जॉर्डन माप

गणित में, जॉर्डन माप आकार (लंबाई, क्षेत्रफल, आयतन) की धारणा का एक विस्तार होता है, उदाहरण के लिए, एक त्रिभुज, डिस्क या समानांतर चतुर्भुज की तुलना में अधिक जटिल आकार होता है।

यह पता चलता है कि एक सेट के लिए जॉर्डन को मापना एक निश्चित प्रतिबंधात्मक अर्थ में अच्छी तरह से व्यवहार किया जाना होता है। इस कारण से, लेबेस्ग उपाय के साथ काम करना अब अधिक सामान्य है, जो सेट के एक बड़े वर्ग के लिए जॉर्डन माप का विस्तार होता है। ऐतिहासिक रूप से बोलते हुए, जॉर्डन माप उन्नीसवीं शताब्दी के अंत में आया था। ऐतिहासिक कारणों से, इस सेट योजना के लिए 'जॉर्डन माप' शब्द अब अच्छी तरह से स्थापित होता है, इस तथ्य के अतिरिक्त यह अपनी आधुनिक परिभाषा में एक सही माप (गणित) नही होती है, क्योंकि जॉर्डन-मापने योग्य सेट एक σ नहीं बनाते है। उदाहरण के लिए, सिंगलटन सेट $\{x\}_{x\in \mathbb {R} }$में $\mathbb {R}$ प्रत्येक के पास जॉर्डन का माप 0 होता है, जबकि $\mathbb {Q} \cap [0,1]$, उनका एक गणनीय संघ, जॉर्डन-मापने योग्य नही होता है। इस कारण कुछ लेखक जॉर्डन सामग्री शब्द का प्रयोग करना अधिक पसंद करते है।

पीआनो-जॉर्डन उपाय का नाम इसके प्रवर्तकों, फ्रांसीसी गणितज्ञ केमिली जॉर्डन और इतालवी गणितज्ञ ग्यूसेप पीनो के नाम पर रखा गया था।

सरल सेटों का जॉर्डन माप

एक साधारण सेट, परिभाषा के अनुसार, (संभवतः अतिव्यापी) आयतों का एक संघ है।

ऊपर से सरल सेट गैर-अतिव्यापी आयतों के संघ के रूप में विघटित हो गया।

यूक्लिडियन स्थान पर विचार करते है $\mathbb {R} ^{n}.$ जॉर्डन माप को पहले बंधे सेट आधे खुले अंतराल (गणित) के उत्पादों पर परिभाषित किया गया है

$$C=[a_{1},b_{1})\times [a_{2},b_{2})\times \cdots \times [a_{n},b_{n})$$

जो बायीं ओर बंद होते है और सभी समापन बिंदुओं के साथ दायीं ओर खुले होते है $a_{i}$ और $b_{i}$ परिमित वास्तविक संख्याएँ (आधा-खुला अंतराल एक तकनीकी विकल्प होता है, जैसा कि हम नीचे देखते है, यदि पसंद हो तो बंद या खुले अंतराल का उपयोग कर सकते है)। ऐसे समुच्चय को a कहा जाता है $n$-आयामी आयत, या बस एक आयत

इस तरह के एक आयत को अंतराल की लंबाई के उत्पाद के रूप में परिभाषित किया गया है:

$$m(C)=(b_{1}-a_{1})(b_{2}-a_{2})\cdots (b_{n}-a_{n}).$$

अगला, कोई सरल सेट पर विचार करता है, कई बार बहुआयताकार, जो आयतों के परिमित संघ (सेट सिद्धांत) है,

$$S=C_{1}\cup C_{2}\cup \cdots \cup C_{k}$$

किसी के लिए $k\geq 1.$

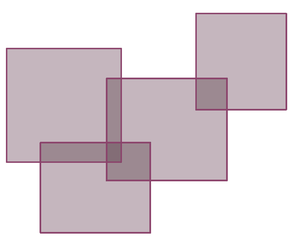
कोई जॉर्डन माप को परिभाषित नहीं कर सकता है $S$ व्यक्तिगत आयतों के उपायों के योग के रूप में, क्योंकि ऐसा प्रतिनिधित्व $S$ अद्वितीय से बहुत दूर होते है, और आयतों के बीच महत्वपूर्ण अधिव्यापन हो सकते है।

सौभाग्य से, ऐसा कोई भी सरल सेट $S$ आयतों के एक और परिमित निकटतम के संघ के रूप में फिर से लिखा जा सकता है, जो इस समय पारस्परिक रूप से अलग होते है, और फिर एक जॉर्डन माप को $m(S)$ असम्बद्ध आयतों के मापों के योग के रूप में परिभाषित करता है।

कोई दिखा सकता है कि जॉर्डन की यह परिभाषा मापती है $S$ के प्रतिनिधित्व से स्वतंत्र है $S$ पुनर्लेखन चरण में यह होता है कि आयतों के आधे-खुले अंतराल से बने होने की धारणा का उपयोग किया जाता है।

अधिक जटिल सेटों का विस्तार

एक सेट (नीले वक्र के अंदर क्षेत्र द्वारा चित्र में दर्शाया गया है) जॉर्डन औसत दर्जे का है यदि और केवल यदि इसे सरल सेटों द्वारा अंदर और बाहर दोनों से अच्छी तरह से अनुमानित किया जा सकता है (उनकी सीमाएं क्रमशः गहरे हरे और गहरे गुलाबी रंग में दिखाई जाती है) .

ध्यान दें कि एक समुच्चय जो संवृत्त अंतरालों का गुणनफल होता है,

$$[a_{1},b_{1}]\times [a_{2},b_{2}]\times \cdots \times [a_{n},b_{n}]$$

एक साधारण समुच्चय नही होता है। इस प्रकार, अब तक जॉर्डन औसत दर्जे का सेट अभी भी बहुत सीमित है। तब एक बंधे हुए सेट को परिभाषित करना होता है जॉर्डन मापने योग्य यदि यह सरल सेटों द्वारा अच्छी तरह से अनुमानित होता है, ठीक उसी तरह जैसे एक फ़ंक्शन रीमैन इंटीग्रल होता है यदि यह स्थिर कार्यों द्वारा अच्छी तरह से अनुमानित होते है।

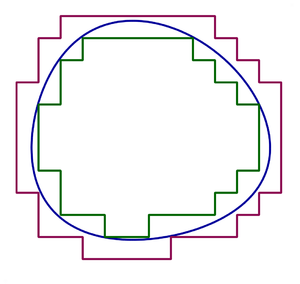
औपचारिक रूप से, एक बंधे हुए सेट के लिए है $B,$ इसे परिभाषित करते है

$$m_{*}(B)=\sup _{S\subseteq B}m(S)$$

और इसके जैसा

$$m^{*}(B)=\inf _{S\supseteq B}m(S)$$

जहांसबसे कम और अंतिम को सरल सेट पर ले जाया जाता है $S.$ सेट $B$ कहा जाता है यदि आंतरिक माप $B$ बाहरी माप के बराबर होता है। दो उपायों के सामान्य मूल्य को कहा जाता है जॉर्डन माप वह सेट फ़ंक्शन है जो जॉर्डन मापने योग्य सेट को उनके जॉर्डन माप में भेजता है।

यह पता चला है कि सभी आयतें (खुली या बंद), संकेतन आदि, जॉर्डन औसत दर्जे की है। इसके अतिरिक्त, यदि कोई दो निरंतर कार्यों पर विचार करता है, तो उन कार्यों के आलेखों के बीच बिंदुओं का सेट जॉर्डन मापने योग्य होता है जब तक कि सेट बाध्य होता है और दो कार्यों का सामान्य डोमेन जॉर्डन मापने योग्य होता है। जॉर्डन मापने योग्य सेटों का कोई भी परिमित संघ और प्रतिच्छेदन जॉर्डन मापने योग्य होता है। एक कॉम्पैक्ट सेट आवश्यक रूप से जॉर्डन औसत दर्जे का नही होता है। उदाहरण के लिए, स्मिथ-वोल्तेरा-कैंटर सेट नही होता है। इसका आंतरिक जॉर्डन माप गायब हो जाता है, क्योंकि इसका पूरक (सेट सिद्धांत) सघन सेट होता है, चूँकि इसका बाहरी जॉर्डन माप गायब नहीं होता है, क्योंकि यह अपने लेबेसेग माप से कम (वास्तव में, बराबर) नही हो सकता है। इसके अतिरिक्त, एक घिरा हुआ खुला सेट जॉर्डन औसत दर्जे का हो यह जरूरी नही होता है। उदाहरण के लिए, वसा कैंटर सेट (अंतराल के भीतर) का पूरक नही होता है। एक घिरा हुआ सेट जॉर्डन मापने योग्य होता है यदि और केवल इसका संकेतक फ़ंक्शन रीमैन इंटीग्रल होता है। रीमैन-इंटीग्रेबल, और इंटीग्रल का मान इसका जॉर्डन उपाय होता है।[1]

समान रूप से, एक बंधे हुए सेट के लिए $B$ आंतरिक जॉर्डन का माप $B$ के आंतरिक (टोपोलॉजी) का लेबेस्ग माप होता है $B$ और बाहरी जॉर्डन माप बंद होने (टोपोलॉजी) का लेबेस्गु माप होता है। इससे यह पता चलता है कि एक घिरा हुआ सेट जॉर्डन मापने योग्य होता है यदि और केवल इसकी सीमा (टोपोलॉजी) में लेबेस्गु माप शून्य होता है। (या समकक्ष रूप से, यदि सीमा में जॉर्डन का माप शून्य होता है, तो सीमा की सघनता के कारण समानता बनी रहती है।)

लेबेस्ग उपाय

यह अंतिम सेटों के प्रकार को बहुत सीमित करती है जो जॉर्डन औसत दर्जे के होते है। उदाहरण के लिए, अंतराल [0,1] में निहित परिमेय संख्याओं का समुच्चय जॉर्डन मापने योग्य नही होता है, क्योंकि इसकी सीमा [0,1] होती है जो जॉर्डन माप शून्य की नही होती है। चूँकि सहज रूप से, परिमेय संख्याओं का समुच्चय एक छोटा समुच्चय होता है, क्योंकि यह गणनीय होता है, और इसका आकार शून्य होता है। यह वास्तव में सच होता है, जब कोई जॉर्डन माप को लेबेस्गु माप से बदल देता है। एक सेट का लेबेस्ग माप इसके जॉर्डन माप के समान होता है। चूंकि, लेबेस्ग माप सेट को एक बहुत व्यापक वर्ग के लिए परिभाषित किया गया है, जैसे कि पहले उल्लिखित अंतराल में परिमेय संख्याओं का सेट, और उन सेटों के लिए भी असीमित या भग्न सेट हो सकते है। इसके अतिरिक्त, लेबेसेग उपाय, जॉर्डन माप के विपरीत, एक वास्तविक माप (गणित) होता है, अर्थात, लेबेसेग मापने योग्य सेटों का कोई भी गणनीय संघ लेबेसेग मापने योग्य होता है, जबकि जॉर्डन मापने योग्य सेटों के गणनीय संघों को जॉर्डन मापने योग्य नही होता है।

संदर्भ

• Emmanuele DiBenedetto (2002). Real analysis. Basel, Switzerland: Birkhäuser. ISBN 0-8176-4231-5.
• Richard Courant; Fritz John (1999). Introduction to Calculus and Analysis Volume II/1: Chapters 1–4 (Classics in Mathematics). Berlin: Springer. ISBN 3-540-66569-2.

बाहरी संबंध

• Derwent, John. "Jordan Measure". MathWorld.
• Terekhin, A.P. (2001) [1994], "Jordan measure", Encyclopedia of Mathematics, EMS Press