पृथक्करण स्वयंसिद्ध
| Separation axioms in topological spaces | |
|---|---|
| Kolmogorov classification | |
| T0 | (Kolmogorov) |
| T1 | (Fréchet) |
| T2 | (Hausdorff) |
| T2½ | (Urysohn) |
| completely T2 | (completely Hausdorff) |
| T3 | (regular Hausdorff) |
| T3½ | (Tychonoff) |
| T4 | (normal Hausdorff) |
| T5 | (completely normal Hausdorff) |
| T6 | (perfectly normal Hausdorff) |
टोपोलॉजी और गणित के संबंधित क्षेत्रों में, कई प्रतिबंध हैं जो अक्सर उन प्रकार के टोपोलॉजिकल स्पेस पर लगाए जाते हैं जिन पर कोई विचार करना चाहता है। इनमें से कुछ प्रतिबंध पृथक्करण अभिगृहीतों द्वारा दिए गए हैं। एंड्री टाइकोनॉफ के बाद, इन्हें कभी-कभी टाइकोनॉफ़ पृथक्करण सिद्धांत कहा जाता है।
जुदाई स्वयंसिद्ध ज़र्मेलो-फ्रेंकेल सेट सिद्धांत की तरह मौलिक स्वयंसिद्ध नहीं हैं, बल्कि गुणों को परिभाषित करते हैं जिन्हें कुछ प्रकार के स्थलीय स्थानों को अलग करने के लिए निर्दिष्ट किया जा सकता है। जुदाई स्वयंसिद्धों को जर्मन भाषा ट्रेन्नुंगसैक्सिओम (पृथक्करण स्वयंसिद्ध) के बाद अक्षर टी से निरूपित किया जाता है, और बढ़ती संख्यात्मक सदस्यताएं मजबूत और मजबूत गुणों को दर्शाती हैं।
पृथक्करण स्वयंसिद्धों के इतिहास की सटीक परिभाषाएँ। विशेष रूप से पुराने साहित्य में, अलग-अलग लेखकों की प्रत्येक स्थिति की अलग-अलग परिभाषाएँ हो सकती हैं।
प्रारंभिक परिभाषाएँ
इससे पहले कि हम स्वयं पृथक्करण अभिगृहीतों को परिभाषित करें, हम सांस्थितिकीय स्थानों में पृथक समुच्चयों (और बिंदुओं) की अवधारणा को ठोस अर्थ देते हैं। (पृथक सेट अलग-अलग रिक्त स्थान के समान नहीं हैं, जिसे अगले खंड में परिभाषित किया गया है।)
अलग-[[अलग सेट]] और डिस्टिक्ट (गणित) बिंदुओं को अलग करने के लिए अलग-अलग स्वयंसिद्ध सांस्थितिक साधनों के उपयोग के बारे में हैं। किसी टोपोलॉजिकल स्पेस के तत्वों के लिए यह पर्याप्त नहीं है कि वे अलग हों (अर्थात, समानता (गणित)); हम चाहते हैं कि वे स्थैतिक रूप से अलग-अलग हों। इसी तरह, किसी टोपोलॉजिकल स्पेस के सबसेट का असंयुक्त होना ही काफी नहीं है; हम चाहते हैं कि उन्हें अलग किया जाए (किसी भी तरह से)। जुदाई स्वयंसिद्ध सभी कहते हैं, एक या दूसरे तरीके से, कि बिंदु या सेट जो अलग-अलग हैं या कुछ कमजोर अर्थों में अलग-अलग हैं, उन्हें भी कुछ मजबूत अर्थों में अलग-अलग या अलग किया जाना चाहिए।
एक्स को टपॉलजी का मूल्य रहने दें। तब X में दो बिंदु x और y 'टोपोलॉजिकल रूप से अलग-अलग' होते हैं यदि उनके पास बिल्कुल समान पड़ोस (गणित) नहीं है (या समान रूप से समान खुले पड़ोस); अर्थात्, उनमें से कम से कम एक का ऐसा पड़ोस है जो दूसरे का पड़ोस नहीं है (या समतुल्य रूप से एक खुला सेट है जो एक बिंदु का है लेकिन दूसरा बिंदु का नहीं है)। यानी कम से कम एक बिंदु दूसरे के क्लोजर (टोपोलॉजी) से संबंधित नहीं है।
दो बिंदु x और y 'पृथक' हैं यदि उनमें से प्रत्येक का एक पड़ोस है जो दूसरे का पड़ोस नहीं है; यानी न तो दूसरे के क्लोजर (टोपोलॉजी) से संबंधित है। अधिक आम तौर पर, एक्स के दो सबसेट ए और बी 'अलग' होते हैं यदि प्रत्येक दूसरे के बंद होने से अलग होता है। (संवरणों को खुद को अलग करने की ज़रूरत नहीं है।) सिंगलटन सेट का उपयोग करके सेटों को अलग करने के लिए शेष सभी शर्तों को बिंदुओं (या एक बिंदु और एक सेट) पर भी लागू किया जा सकता है। अंक x और y को आस-पड़ोस द्वारा, बंद पड़ोस द्वारा, एक निरंतर कार्य द्वारा, एक फ़ंक्शन द्वारा सटीक रूप से अलग माना जाएगा, अगर और केवल अगर उनके सिंगलटन सेट {x} और {y} को संबंधित मानदंड के अनुसार अलग किया जाता है।
सबसेट ए और बी 'पड़ोस से अलग' हैं यदि उनके पड़ोस अलग हैं। यदि वे बंद पड़ोस से अलग हैं तो वे 'बंद पड़ोस से अलग' हैं। वे 'एक निरंतर कार्य द्वारा अलग' होते हैं यदि अंतरिक्ष X से वास्तविक रेखा 'R' तक एक निरंतर कार्य f मौजूद होता है, जैसे कि A preimage f का सबसेट है−1({0}) और B प्रीइमेज f का एक उपसमुच्चय है-1({1})। अंत में, वे एक निरंतर कार्य द्वारा ठीक से अलग हो जाते हैं यदि X से R तक एक निरंतर कार्य f मौजूद होता है, जैसे कि A प्रीइमेज f के बराबर होता है−1({0}) और B बराबर f है-1({1})।
बढ़ती ताकत के क्रम में ये स्थितियां दी गई हैं: किसी भी दो स्थलीय रूप से अलग-अलग बिंदुओं को अलग-अलग होना चाहिए, और किसी भी दो अलग-अलग बिंदुओं को स्थलीय रूप से अलग-अलग होना चाहिए। किन्हीं भी दो अलग-अलग सेटों को अलग होना चाहिए, आस-पड़ोस से अलग किए गए किन्हीं भी दो सेटों को अलग-अलग किया जाना चाहिए, और इसी तरह।
मुख्य परिभाषाएँ
ये सभी परिभाषाएँ उपरोक्त #प्रारंभिक परिभाषाओं का अनिवार्य रूप से उपयोग करती हैं।
इनमें से कई नामों का पृथक्करण स्वयंसिद्धों का इतिहास है; उदाहरण के लिए, सामान्य और टी के अर्थ4कभी-कभी आपस में बदल जाते हैं, इसी तरह नियमित और टी3, आदि। कई अवधारणाओं के भी कई नाम हैं; हालाँकि, पहले सूचीबद्ध एक के अस्पष्ट होने की संभावना हमेशा कम से कम होती है।
इनमें से अधिकांश अभिगृहीतों की समान अर्थ वाली वैकल्पिक परिभाषाएँ हैं; यहाँ दी गई परिभाषाएँ एक सुसंगत पैटर्न में आती हैं जो पिछले खंड में परिभाषित अलगाव की विभिन्न धारणाओं से संबंधित हैं। अन्य संभावित परिभाषाएँ अलग-अलग लेखों में पाई जा सकती हैं।
निम्नलिखित सभी परिभाषाओं में, X फिर से एक सामयिक स्थान है।
- X 'T0 स्पेस है|T0, या कोल्मोगोरोव, यदि X में कोई दो अलग-अलग बिंदु स्थलीय भिन्नता हैं। (यह अलग-अलग स्वयंसिद्धों के बीच एक सामान्य विषय होगा जिसमें एक स्वयंसिद्ध का एक संस्करण होगा जिसके लिए टी की आवश्यकता होती है0 और एक संस्करण जो नहीं करता है।)
- X 'R0 स्पेस है | R0, या सममित, अगर X में कोई भी दो स्थलीय रूप से अलग-अलग बिंदुओं को अलग किया जाता है।
- X T1 स्पेस है|T1, या सुलभ या फ़्रेचेट, यदि X में कोई दो अलग-अलग बिंदु अलग किए गए हैं। समान रूप से, प्रत्येक एकल-बिन्दु समुच्चय एक संवृत समुच्चय होता है। इस प्रकार, 'एक्स' टी है1 अगर और केवल अगर यह दोनों टी है0 और आर0. (हालांकि कोई ऐसी बातें कह सकता है जैसे टी1 अंतरिक्ष, फ्रेचेट टोपोलॉजी, और मान लीजिए कि स्थलीय अंतरिक्ष एक्स फ्रेचेट है; इस संदर्भ में फ्रेचेट स्पेस कहने से बचना चाहिए, क्योंकि कार्यात्मक विश्लेषण में फ्रेचेट स्पेस की एक और पूरी तरह से अलग धारणा है।)
- X 'R1 स्पेस है|R1, या प्रीरेगुलर, अगर X में कोई दो टोपोलॉजिकल रूप से अलग-अलग बिंदुओं को पड़ोस से अलग किया जाता है। हर आर1 अंतरिक्ष भी आर है0.
- X 'हॉसडॉर्फ स्पेस' है, या टी2या अलग, यदि X में किन्हीं दो अलग-अलग बिंदुओं को पड़ोस द्वारा अलग किया जाता है। इस प्रकार, एक्स हौसडॉर्फ है अगर और केवल अगर यह दोनों टी है0 और आर1. प्रत्येक हॉसडॉर्फ स्थान भी T है1.
- X 'यूरीसोहन' है और पूरी तरह से हॉसडॉर्फ स्पेस|टी2½, या उरीसोहन, अगर X में दो अलग-अलग बिंदु बंद पड़ोस से अलग होते हैं। हर टी2½ स्पेस हॉसडॉर्फ भी है।
- X 'पूरी तरह से हौसडॉर्फ स्पेस' है, या पूरी तरह से टी2, यदि X में किन्हीं दो अलग-अलग बिंदुओं को एक निरंतर कार्य द्वारा अलग किया जाता है। हर पूरी तरह से हौसडॉर्फ स्पेस भी टी है2½.
- X 'नियमित स्थान' है, यदि कोई बिंदु x दिया गया है और X में बंद सेट F ऐसा है कि x, F से संबंधित नहीं है, तो वे पड़ोस से अलग हो जाते हैं। (वास्तव में, एक नियमित स्थान में, ऐसे किसी भी x और F को भी बंद पड़ोस द्वारा अलग किया जाएगा।) प्रत्येक नियमित स्थान भी R है1.
- X 'नियमित हौसडॉर्फ स्पेस' है, या टी3, अगर यह दोनों टी0 और नियमित।[1] प्रत्येक नियमित हौसडॉर्फ स्थान भी T है2½.
- X 'पूरी तरह से नियमित स्थान' है, यदि कोई बिंदु x दिया गया है और X में बंद सेट F ऐसा है कि x, F से संबंधित नहीं है, तो वे एक निरंतर कार्य द्वारा अलग हो जाते हैं।[2] प्रत्येक पूर्णतः नियमित स्थान भी नियमित होता है।
- X 'टायचोनॉफ स्पेस ' है, या टी3½, पूरी तरह से टी3, या पूरी तरह से नियमित हौसडॉर्फ, अगर यह दोनों टी है0 और पूरी तरह से नियमित।[3] प्रत्येक टाइकोनॉफ़ स्थान नियमित हौसडॉर्फ और पूरी तरह हॉसडॉर्फ दोनों है।
- X 'सामान्य स्थान' है यदि X के दो अलग-अलग बंद उपसमुच्चय पड़ोस से अलग हो जाते हैं। (वास्तव में, एक स्थान सामान्य है अगर और केवल अगर दो अलग-अलग बंद सेटों को निरंतर कार्य से अलग किया जा सकता है; यह उरीसोहन का लेम्मा है।)
- X 'सामान्य नियमित स्थान' है यदि यह दोनों R है0 और सामान्य। हर सामान्य नियमित स्थान भी पूरी तरह से नियमित है।
- एक्स 'सामान्य हौसडॉर्फ स्पेस' है, या टी4, अगर यह दोनों टी1 और सामान्य। प्रत्येक सामान्य हौसडॉर्फ स्थान टाइकोनॉफ़ और सामान्य नियमित दोनों ही है।
- X 'पूरी तरह से सामान्य स्थान' है यदि किन्हीं भी दो अलग-अलग सेटों को पास-पड़ोस द्वारा अलग किया जाता है। हर पूरी तरह से सामान्य स्थान भी सामान्य होता है।
- X 'पूरी तरह से सामान्य हौसडॉर्फ स्पेस' है, या टी5या पूरी तरह से टी4, अगर यह पूरी तरह से सामान्य है और टी1. हर पूरी तरह से सामान्य हॉउसडॉर्फ स्पेस भी सामान्य हॉसडॉर्फ होता है।
- X 'पूरी तरह से सामान्य स्थान' है यदि कोई भी दो अलग-अलग बंद सेट निरंतर कार्य से ठीक से अलग हो जाते हैं। हर पूरी तरह से सामान्य स्थान भी पूरी तरह से सामान्य और पूरी तरह से नियमित दोनों होता है।
- X 'पूरी तरह से सामान्य हौसडॉर्फ स्पेस' है, या टी6या पूरी तरह से टी4, अगर यह पूरी तरह से सामान्य और टी दोनों है0. हर पूरी तरह से सामान्य हॉउसडॉर्फ स्पेस भी पूरी तरह से सामान्य हॉसडॉर्फ है।
निम्न तालिका पृथक्करण अभिगृहीतों के साथ-साथ उनके बीच निहितार्थों को संक्षेप में प्रस्तुत करती है: कोशिकाएँ जो मर्ज की जाती हैं समतुल्य गुणों का प्रतिनिधित्व करती हैं, प्रत्येक अभिगृहीत का तात्पर्य इसके बाईं ओर की कोशिकाओं से है, और यदि हम टी मानते हैं1 अभिगृहीत, तो प्रत्येक अभिगृहीत का तात्पर्य इसके ऊपर की कोशिकाओं में भी होता है (उदाहरण के लिए, सभी सामान्य टी1 रिक्त स्थान भी पूरी तरह से नियमित हैं)।
| Separated | Separated by neighborhoods | Separated by closed neighborhoods | Separated by function | Precisely separated by function | |
|---|---|---|---|---|---|
| Distinguishable points | Symmetric[4] | Preregular | |||
| Distinct points | Fréchet | Hausdorff | Urysohn | Completely Hausdorff | Perfectly Hausdorff |
| Closed set and point outside | Symmetric[5] | Regular | Completely regular | Perfectly normal | |
| Disjoint closed sets | always | Normal | |||
| Separated sets | always | Completely normal | discrete space | ||
स्वयंसिद्धों के बीच संबंध
टी0 स्वयंसिद्ध इस मायने में खास है कि इसे न केवल एक संपत्ति में जोड़ा जा सकता है (ताकि पूरी तरह से नियमित प्लस टी0 Tychonoff है) लेकिन एक संपत्ति से भी घटाया जा सकता है (ताकि हौसडॉर्फ माइनस टी0 आर है1), काफी सटीक अर्थों में; अधिक जानकारी के लिए कोलमोगोरोव भागफल देखें। पृथक्करण स्वयंसिद्धों पर लागू होने पर, यह तालिका में संबंधों को नीचे बाईं ओर ले जाता है। इस तालिका में T की आवश्यकता को जोड़कर दाईं ओर से बाईं ओर जाता है0, और कोलमोगोरोव भागफल ऑपरेशन का उपयोग करके, उस आवश्यकता को हटाकर बाईं ओर से दाईं ओर जाता है। (इस तालिका के बाईं ओर दिए गए कोष्ठकों में नाम आम तौर पर अस्पष्ट या कम से कम कम प्रसिद्ध हैं, लेकिन उनका उपयोग नीचे दिए गए चित्र में किया गया है।)
| T0 version | Non-T0 version |
|---|---|
| T0 | (No requirement) |
| T1 | R0 |
| Hausdorff (T2) | R1 |
| T2½ | (No special name) |
| Completely Hausdorff | (No special name) |
| Regular Hausdorff (T3) | Regular |
| Tychonoff (T3½) | Completely regular |
| Normal T0 | Normal |
| Normal Hausdorff (T4) | Normal regular |
| Completely normal T0 | Completely normal |
| Completely normal Hausdorff (T5) | Completely normal regular |
| Perfectly normal Hausdorff (T6) | Perfectly normal |
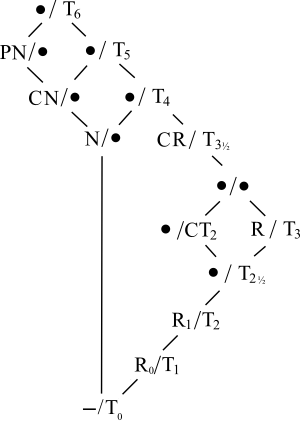
टी के समावेश या बहिष्करण के अलावा0, पृथक्करण अभिगृहीतों के बीच संबंधों को आरेख में दाईं ओर इंगित किया गया है। इस आरेख में, गैर-टी0 स्थिति का संस्करण स्लैश के बाईं ओर है, और T0 संस्करण दाईं ओर है। संक्षिप्त नाम के लिए अक्षरों का प्रयोग इस प्रकार किया जाता है:
पी = पूरी तरह से, सी = पूरी तरह से, एन = सामान्य, और आर (सबस्क्रिप्ट के बिना) = नियमित। एक गोली इंगित करती है कि उस स्थान पर किसी स्थान के लिए कोई विशेष नाम नहीं है। नीचे डैश कोई शर्त नहीं दर्शाता है।
जब तक दोनों शाखाएं मिलती हैं तब तक ऊपर की ओर आरेख का पालन करके इस आरेख का उपयोग करके दो गुणों को जोड़ा जा सकता है। उदाहरण के लिए, यदि कोई स्थान पूरी तरह से सामान्य (CN) और पूरी तरह से हौसडॉर्फ (CT2), दोनों शाखाओं के बाद, एक स्थान पाता है •/टी5. चूंकि पूरी तरह से हौसडॉर्फ रिक्त स्थान टी हैं0 (भले ही पूरी तरह से सामान्य स्थान न हो), कोई टी लेता है0 स्लैश के किनारे, इसलिए पूरी तरह से सामान्य हॉसडॉर्फ स्थान टी के समान है5 अंतरिक्ष (कम अस्पष्ट रूप से पूरी तरह से सामान्य हौसडॉर्फ अंतरिक्ष के रूप में जाना जाता है, जैसा कि उपरोक्त तालिका में देखा जा सकता है)।
जैसा कि आरेख, सामान्य और आर से देखा जा सकता है0 एक साथ अन्य गुणों के एक मेजबान का अर्थ है, क्योंकि दो गुणों के संयोजन से दाईं ओर की शाखा पर कई नोड्स होते हैं। चूँकि नियमितता इनमें से सबसे प्रसिद्ध है, ऐसे स्थान जो सामान्य और R दोनों हैं0 आमतौर पर सामान्य नियमित स्थान कहलाते हैं। कुछ इसी तरह से, रिक्त स्थान जो सामान्य और T दोनों हैं1 अस्पष्ट टी नोटेशन से बचने की इच्छा रखने वाले लोगों द्वारा अक्सर सामान्य हौसडॉर्फ रिक्त स्थान कहा जाता है। इन सम्मेलनों को अन्य नियमित स्थानों और हॉसडॉर्फ स्थानों के लिए सामान्यीकृत किया जा सकता है।
[एनबी: यह आरेख यह नहीं दर्शाता है कि पूरी तरह से सामान्य स्थान हमेशा नियमित होते हैं; संपादक अब इस पर काम कर रहे हैं।]
अन्य पृथक्करण स्वयंसिद्ध
टोपोलॉजिकल स्पेस पर कुछ अन्य शर्तें हैं जिन्हें कभी-कभी पृथक्करण स्वयंसिद्धों के साथ वर्गीकृत किया जाता है, लेकिन ये सामान्य पृथक्करण स्वयंसिद्धों के साथ पूरी तरह से फिट नहीं होते हैं। उनकी परिभाषाओं के अलावा, यहां उनकी चर्चा नहीं की गई है; उनके व्यक्तिगत लेख देखें।
- X 'सोबर स्पेस' है, यदि प्रत्येक बंद सेट C के लिए, जो दो छोटे बंद सेटों का (संभवतः अविच्छिन्न) मिलन नहीं है, एक अद्वितीय बिंदु p है, जैसे कि {p} का समापन C के बराबर है। अधिक संक्षेप में, प्रत्येक इरेड्यूसिबल बंद सेट का एक अनूठा सामान्य बिंदु है। हौसडॉर्फ का कोई भी स्थान शांत होना चाहिए, और कोई भी शांत स्थान टी होना चाहिए0.
- X 'कमजोर हॉसडॉर्फ स्पेस' है, अगर कॉम्पैक्ट हौसडॉर्फ स्पेस से एक्स के प्रत्येक सतत मानचित्र के लिए, एफ की छवि एक्स में बंद है। किसी कमजोर हौसडॉर्फ स्थान को हौसडॉर्फ कमजोर होना चाहिए, और कोई कमजोर हौसडॉर्फ स्पेस टी होना चाहिए1.
- X '[[अर्ध-नियमित स्थान]]' है यदि नियमित खुले सेट X के खुले सेट के लिए एक आधार (टोपोलॉजी) बनाते हैं। कोई भी नियमित स्थान भी अर्ध-नियमित होना चाहिए।
- X 'क्वैसी-रेगुलर स्पेस|क्वैसी-रेगुलर' है अगर किसी भी गैर-खाली ओपन सेट G के लिए, एक नॉन-रिक्त ओपन सेट H है जैसे कि H का क्लोजर G में समाहित है।
- X 'पूरी तरह से सामान्य स्थान' है यदि प्रत्येक खुले आवरण में एक खुला तारा शोधन है। एक्स 'पूरी तरह से टी4 स्पेस है|पूरी तरह से टी4, या पूरी तरह से सामान्य हौसडॉर्फ, अगर यह दोनों टी है1 और पूरी तरह से सामान्य। हर पूरी तरह से सामान्य स्थान सामान्य है और हर पूरी तरह से टी4 अंतरिक्ष टी है4. इसके अलावा, कोई यह दिखा सकता है कि हर पूरी तरह से टी4 अंतरिक्ष परा-सुसंहत है। वास्तव में, पूरी तरह से सामान्य स्थान वास्तव में सामान्य पृथक्करण स्वयंसिद्धों की तुलना में पैराकॉम्पैक्टनेस के साथ अधिक होते हैं।
- सिद्धांत है कि सभी कॉम्पैक्ट उपसमुच्चय बंद हैं, सख्ती से टी के बीच है1 और टी2 (हॉसडॉर्फ) ताकत में। इस अभिगृहीत को संतुष्ट करने वाला स्थान आवश्यक रूप से T है1 क्योंकि प्रत्येक एकल-बिंदु सेट आवश्यक रूप से कॉम्पैक्ट है और इस प्रकार बंद है, लेकिन जरूरी नहीं कि रिवर्स सच हो; असीम रूप से कई बिंदुओं पर सहसंबद्ध टोपोलॉजी के लिए, जो कि टी है1, हर सबसेट कॉम्पैक्ट है लेकिन हर सबसेट बंद नहीं है। इसके अलावा, हर टी2 (हॉसडॉर्फ) स्थान उस स्वयंसिद्ध को संतुष्ट करता है कि सभी कॉम्पैक्ट उपसमुच्चय बंद हैं, लेकिन जरूरी नहीं कि विपरीत सच हो; बेशुमार बिंदुओं पर गणना योग्य टोपोलॉजी के लिए, कॉम्पैक्ट सेट सभी परिमित हैं और इसलिए सभी बंद हैं लेकिन स्थान टी नहीं है2 (हॉसडॉर्फ)।
यह भी देखें
टिप्पणियाँ
- ↑ Schechter 1997, p. 441.
- ↑ Schechter 1997, 16.16, p. 442.
- ↑ Schechter 1997, 16.17, p. 443.
- ↑ Schechter 1997, 16.6(D), p. 438.
- ↑ Schechter 1997, 16.6(C), p. 438.
संदर्भ
- Schechter, Eric (1997). Handbook of Analysis and its Foundations. San Diego: Academic Press. ISBN 0126227608. (has Ri axioms, among others)
- Willard, Stephen (1970). General topology. Reading, Mass.: Addison-Wesley Pub. Co. ISBN 0-486-43479-6. (has all of the non-Ri axioms mentioned in the Main Definitions, with these definitions)
- Merrifield, Richard E.; Simmons, Howard E. (1989). Topological Methods in Chemistry. New York: Wiley. ISBN 0-471-83817-9. (gives a readable introduction to the separation axioms with an emphasis on finite spaces)