निर्देशित अचक्रीय ग्राफ

From Vigyanwiki
Revision as of 09:29, 7 July 2023 by alpha>Artiverma
एक निर्देशित विश्वकोश ग्राफ का उदाहरण

गणित में, विशेष रूप से ग्राफ सिद्धांत और कंप्यूटर विज्ञान में, निर्देशित अचक्रीय ग्राफ (डीएजी) निर्देशित ग्राफ है जिसमें कोई निर्देशित चक्र नहीं है। अर्थात्, इसमें शीर्ष और किनारे (जिन्हें 'चाप' भी कहा जाता है) सम्मिलित हैं, प्रत्येक किनारे को एक शीर्ष से दूसरे तक निर्देशित किया जाता है, जैसे कि उन निर्देशों का पालन करने से कभी भी संवृत लूप नहीं बनेगा। निर्देशित ग्राफ डीएजी है यदि और केवल यह टोपोलॉजिकल ऑर्डरिंग हो सकता है, जो कि रेखीय क्रम के रूप में शीर्षों को व्यवस्थित करता है जो सभी किनारों की दिशाओं के अनुरूप है। डीएजी के कई जीव विज्ञान (विकास, पारिवारिक वृक्ष, महामारी विज्ञान) से लेकर सूचना विज्ञान (उद्धरण नेटवर्क) और संगणना (निर्धारण) तक वैज्ञानिक और कम्प्यूटेशनल अनुप्रयोग हैं,।

निर्देशित अचक्रीय ग्राफ को कभी-कभी अचक्रीय निर्देशित ग्राफ[1] या अचक्रीय डिग्राफ कहा जाता है।[2]

परिभाषाएँ

ग्राफ़ शीर्षों और शीर्षों के जोड़े को जोड़ने वाले किनारों से बनता है, जहाँ शीर्ष किसी भी प्रकार की वस्तु हो सकती है जो किनारों द्वारा जोड़े में जुड़ी होती है। निर्देशित ग्राफ की स्थिति में, प्रत्येक किनारे का एक शीर्ष से दूसरे शीर्ष तक अभिविन्यास होता है। निर्देशित ग्राफ़ में पथ किनारों का अनुक्रम है जिसमें यह गुण होता है कि अनुक्रम में प्रत्येक किनारे का अंतिम शीर्ष अनुक्रम में अगले किनारे के प्रारंभिक शीर्ष के समान होता है; पथ चक्र बनाता है यदि इसके प्रथम किनारे का आरंभिक शीर्ष इसके अंतिम किनारे के अंतिम शीर्ष के समान होता है। निर्देशित अचक्रीय ग्राफ निर्देशित ग्राफ है जिसमें कोई चक्र नहीं है।[1][2][3]

निर्देशित ग्राफ़ के शीर्ष v को दूसरे शीर्ष u से पहुंच योग्य माना जाता है जब कोई पथ उपस्थित होता है जो u से प्रारंभ होता है और v पर समाप्त होता है। विशेष स्थिति के रूप में, प्रत्येक शीर्ष को स्वयं से (शून्य किनारों वाले पथ द्वारा) पहुंच योग्य माना जाता है। यदि कोई शीर्ष गैर-तुच्छ पथ (एक या अधिक किनारों वाला पथ) के माध्यम से स्वयं तक पहुंच सकता है, तो वह पथ चक्र है, इसलिए निर्देशित अचक्रीय ग्राफ को परिभाषित करने का दूसरा प्रकार यह है कि वे ऐसे ग्राफ़ हैं जिनमें कोई भी शीर्ष किसी गैर तुच्छ पथ के माध्यम से स्वयं तक नहीं पहुंच सकता है।[4]

गणितीय गुण

रीचैबिलिटी संबंध, सकर्मक समापन, और सकर्मक अल्पता

A DAG
Its transitive reduction

डीएजी की रीचैबिलिटी संबंध को डीएजी के शीर्ष पर आंशिक क्रम ≤ के रूप में औपचारिक रूप दिया जा सकता है। इस आंशिक क्रम में, दो शीर्षों u और v को u ≤ v के रूप में क्रमित किया जाता है, ठीक उसी समय जब डीएजी में u से v तक निर्देशित पथ उपस्थित होता है; अर्थात्, जब u v तक पहुँच सकते हैं (या v u से पहुंच योग्य है)।[5] चूँकि, भिन्न-भिन्न डीएजी समान रीचैबिलिटी संबंध और समान आंशिक क्रम को उत्पन्न कर सकते हैं।[6] उदाहरण के लिए, दो किनारों u → v और v → w के साथ डीएजी का तीन किनारों u → v, v → w, और u → w के साथ डीएजी के समान ही रीचैबिलिटी संबंध है। ये दोनों डीएजी समान आंशिक क्रम उत्पन्न करते हैं, जिसमें शीर्षों को u ≤ v ≤ w के रूप में क्रमित किया जाता है।

डीएजी का सकर्मक समापन सबसे अधिक किनारों वाला ग्राफ है जिसमें डीएजी के समान ही रीचैबिलिटी संबंध होता है। डीएजी के रीचैबिलिटी संबंध ≤ में शीर्षों की प्रत्येक जोड़ी (u, v) के लिए इसका किनारा u → v है, और इसलिए इसे ग्राफ-सैद्धांतिक शब्दों में रीचैबिलिटी संबंध ≤ के सीधे अनुवाद के रूप में माना जा सकता है। आंशिक आदेशों को डीएजी में अनुवाद करने की विधि सामान्यतः कार्य करती है: प्रत्येक परिमित आंशिक रूप से आदेशित समूह (S, ≤) के लिए, ग्राफ जिसमें S के प्रत्येक तत्व के लिए शीर्ष है और ≤ में तत्वों की प्रत्येक जोड़ी के लिए किनारा स्वचालित रूप से सकर्मक होता है संवृत डीएजी, और इसका रीचैबिलिटी संबंध (S, ≤) है। इस प्रकार, प्रत्येक परिमित आंशिक रूप से आदेशित समूह को डीएजी के रूप में दर्शाया जा सकता है।

तीन-तत्व समूह के सबसमूह के मध्य समूह समावेशन (⊆) के आंशिक क्रम का प्रतिनिधित्व करने वाला हस आरेख

डीएजी की सकर्मक अल्पता सबसे अल्प किनारों वाला ग्राफ है जिसमें डीएजी के समान ही रीचैबिलिटी संबंध है। डीएजी के रीचैबिलिटी संबंध ≤ के कवरिंग संबंध में शीर्षों की प्रत्येक जोड़ी (u, v) के लिए इसका किनारा u → v है। यह डीएजी का उपसमूह है, जो u → v किनारों को विस्थापित करके बनाया गया है, जिसके लिए डीएजी में u से v तक लंबा निर्देशित पथ भी होता है।

सकर्मक समापन के जैसे, सकर्मक अल्पता को डीएजी के लिए विशिष्ट रूप से परिभाषित किया गया है। इसके विपरीत, निर्देशित ग्राफ़ के लिए जो चक्रीय नहीं है, समान रीचैबिलिटी संबंध के साथ एक से अधिक न्यूनतम सबग्राफ हो सकते हैं।[7] सकर्मक कटौती उनके द्वारा प्रतिनिधित्व किए जाने वाले आंशिक आदेशों की कल्पना करने में उपयोगी होती है, क्योंकि उनके पास समान आदेशों का प्रतिनिधित्व करने वाले अन्य ग्राफ़ों की तुलना में अल्प किनारे होते हैं और इसलिए सरल ग्राफ़ आरेखण होते हैं। आंशिक क्रम का हास आरेख सकर्मक अल्पता का चित्र है जिसमें प्रत्येक किनारे के उन्मुखीकरण को किनारे के प्रारंभिक शीर्ष को उसके अंतिम शीर्ष की तुलना में अल्प स्थिति में रखकर दिखाया गया है।[8]

टोपोलॉजिकल ऑर्डरिंग

A topological ordering of a directed acyclic graph: every edge goes from earlier in the ordering (upper left) to later in the ordering (lower right). A directed graph is acyclic if and only if it has a topological ordering.
Adding the red edges to the blue directed acyclic graph produces another DAG, the transitive closure of the blue graph. For each red or blue edge u → v, v is reachable from u: there exists a blue path starting at u and ending at v.

एक निर्देशित ग्राफ़ का टोपोलॉजिकल ऑर्डर अनुक्रम में इसके शीर्षों का क्रम है, जैसे कि प्रत्येक किनारे के लिए किनारे का प्रारंभ शीर्ष किनारे के अंत के शीर्ष से अनुक्रम में पहले होता है। ग्राफ़ जिसमें टोपोलॉजिकल ऑर्डरिंग है, में कोई चक्र नहीं हो सकता है, क्योंकि चक्र के प्रारंभिकशीर्ष में किनारे को गलत तरीके से उन्मुख करना होगा। इसलिए, सांस्थितिक क्रम वाला प्रत्येक ग्राफ अचक्रीय होता है। इसके विपरीत, प्रत्येक निर्देशित अचक्रीय ग्राफ में कम से कम सांस्थितिक क्रम होता है। टोपोलॉजिकल ऑर्डरिंग का अस्तित्व इसलिए निर्देशित अचक्रीय ग्राफ की समकक्ष परिभाषा के रूप में उपयोग किया जा सकता है: वे वास्तव में ग्राफ़ हैं जिनके पास टोपोलॉजिकल ऑर्डरिंग हैं।[2]सामान्य तौर पर, यह क्रम अद्वितीय नहीं है; डीएजी के पास अद्वितीय टोपोलॉजिकल ऑर्डरिंग है यदि और केवल यदि उसके पास निर्देशित पथ है जिसमें सभी शिखर सम्मिलित हैं, इस स्थिति में ऑर्डर उसी क्रम के समान है जिसमें पथ में कोने दिखाई देते हैं।[9] डीएजी के टोपोलॉजिकल ऑर्डरिंग का परिवार डीएजी के लिए रीचैबिलिटी रिलेशन के रैखिक विस्तार के परिवार के समान है,[10] इसलिए ही आंशिक क्रम का प्रतिनिधित्व करने वाले किन्हीं भी दो ग्राफ़ों में सांस्थितिक क्रमों का ही समूह होता है।

मिश्रित गणना

निर्देशित अचक्रीय ग्राफ की गिनती की ग्राफ गणना समस्या का अध्ययन रॉबिन्सन (1973) द्वारा किया गया था।[11] n = 0, 1, 2, 3, … के लिए n लेबल वाले शीर्षों पर डीएजी की संख्या (उस क्रम पर प्रतिबंध के बिना जिसमें ये संख्या डीएजी के टोपोलॉजिकल क्रम में दिखाई देती हैं) है।

1, 1, 3, 25, 543, 29281, 3781503, … (sequence A003024 in the OEIS)

इन संख्याओं की गणना पुनरावृत्ति संबंध द्वारा की जा सकती है।

[11]
एरिक डब्ल्यू वीस्टीन ने अनुमान लगाया,[12] और McKay et al. (2004) ने सिद्ध किया कि समान संख्याएँ (0,1) आव्यूहों की गणना करती हैं, जिसके लिए सभी आइगेनमान ​​​​सकारात्मक वास्तविक संख्याएँ हैं। प्रमाण विशेषण प्रमाण है: आव्यूहA यदि और केवल यदि डीएजीका आसन्न आव्यूहहै A + I (0,1) आव्यूहहै जिसमें सभी आइगेनमान ​​​​सकारात्मक हैं, जहां I पहचान आव्यूहको दर्शाता है। क्योंकि डीएजीमें लूप (ग्राफ़ सिद्धांत) नहीं हो सकता है | स्व-लूप, इसके आसन्न आव्यूहमें शून्य विकर्ण होना चाहिए, इसलिए जोड़ना I संपत्ति को संरक्षित करता है कि सभी आव्यूहगुणांक 0 या 1 हैं।[13]

रेखांकन के संबंधित परिवार

A multitree, a DAG in which the subgraph reachable from any vertex induces an undirected tree (e.g. in red)
A polytree, a DAG formed by orienting the edges of an undirected tree

एक हॉटलाइन (जिसे दृढ़ता से अस्पष्ट ग्राफ या मैंग्रोव भी कहा जाता है) डीएजी है जिसमें किसी भी दो कोने के मध्य अधिकतम निर्देशित पथ होता है। समतुल्य रूप से, यह डीएजी है जिसमें किसी शीर्ष से पहुंचने योग्य सबग्राफ ट्री (ग्राफ सिद्धांत) को प्रेरित करता है।[14] एक polytree (जिसे निर्देशित पेड़ भी कहा जाता है) अप्रत्यक्ष पेड़ के किनारों को उन्मुख करके बनाई गई बहु वृक्ष है।[15] एक आर्बोरेसेंस (ग्राफ थ्योरी) ओरिएंटेशन (ग्राफ थ्योरी) द्वारा बनाई गई पॉलीट्री है जो विशेष वर्टेक्स से दूर अप्रत्यक्ष पेड़ के किनारों को आर्बोरेसेंस की जड़ कहा जाता है।

कम्प्यूटेशनल समस्याएं

सामयिक छँटाई और मान्यता

Main article: टोपोलॉजिकल सॉर्टिंग

टोपोलॉजिकल सॉर्टिंग किसी दिए गए डीएजी के टोपोलॉजिकल ऑर्डरिंग को खोजने की एल्गोरिथम समस्या है। इसे रैखिक समय में हल किया जा सकता है।[16] टोपोलॉजिकल सॉर्टिंग के लिए कहन का एल्गोरिथ्म सीधे वर्टेक्स ऑर्डर बनाता है। यह उन शीर्षों की सूची रखता है जिनमें अन्य शीर्षों से कोई आने वाला किनारा नहीं है जो पहले से ही आंशिक रूप से निर्मित टोपोलॉजिकल ऑर्डरिंग में सम्मिलित नहीं किए गए हैं; प्रारंभ में इस सूची में वे शीर्ष होते हैं जिनमें कोई आने वाला किनारा नहीं होता है। फिर, यह आंशिक रूप से निर्मित टोपोलॉजिकल ऑर्डरिंग के अंत में इस सूची से बार-बार शीर्ष जोड़ता है, और जांचता है कि इसके पड़ोसियों को सूची में जोड़ा जाना चाहिए या नहीं। एल्गोरिथ्म समाप्त हो जाता है जब सभी कोने इस तरह से संसाधित किए जाते हैं।[17]वैकल्पिक रूप से, गहराई-प्रथम खोज ग्राफ़ ट्रैवर्सल के मेल आदेश नंबरिंग को उलट कर टोपोलॉजिकल ऑर्डरिंग का निर्माण किया जा सकता है।[16]

यह जांचना भी संभव है कि क्या दिया गया निर्देशित ग्राफ रैखिक समय में डीएजी है, या तो टोपोलॉजिकल ऑर्डरिंग खोजने का प्रयास करके और फिर प्रत्येक किनारे के लिए परीक्षण करना कि परिणामी ऑर्डरिंग वैध है या नहीं[18] या वैकल्पिक रूप से, कुछ टोपोलॉजिकल सॉर्टिंग एल्गोरिदम के लिए, यह सत्यापित करके कि एल्गोरिथ्म त्रुटि स्थिति को पूरा किए बिना सभी कोने को सफलतापूर्वक ऑर्डर करता है।[17]

चक्रीय रेखांकन से निर्माण

किसी भी अप्रत्यक्ष ग्राफ को उसके शीर्षों के लिए कुल क्रम का चयन करके और बाद के समापन बिंदु के क्रम में पहले के समापन बिंदु से प्रत्येक किनारे को निर्देशित करके डीएजीमें बनाया जा सकता है। किनारों के परिणामी अभिविन्यास (ग्राफ़ सिद्धांत) को अचक्रीय ओरिएंटेशन कहा जाता है। अलग-अलग कुल आदेश ही चक्रीय अभिविन्यास के लिए नेतृत्व कर सकते हैं, इसलिए ए n-वरटेक्स ग्राफ से कम हो सकता है n! चक्रीय अभिविन्यास। अचक्रीय ओरिएंटेशन की संख्या के बराबर है |χ(−1)|, कहाँ χ दिए गए ग्राफ का रंगीन बहुपद है।[19]

पीला निर्देशित विश्वकोश ग्राफ नीले निर्देशित ग्राफ का संघनन (ग्राफ सिद्धांत) है। यह एज संकुचन द्वारा नीले ग्राफ के प्रत्येक दृढ़ता से जुड़े घटक को एकल पीले शीर्ष में बनाया जाता है।

फीडबैक वर्टेक्स समूह या फीडबैक आर्क समूह , कोने या किनारों का समूह (क्रमशः) जो सभी चक्रों को छूता है, को हटाकर किसी भी निर्देशित ग्राफ को डीएजी में बनाया जा सकता है। चूँकि, इस तरह का सबसे छोटा समूह एनपी-मुश्किल है।[20] मनमाने ढंग से निर्देशित ग्राफ को भी डीएजी में परिवर्तित किया जा सकता है, जिसे इसका संघनन (ग्राफ सिद्धांत) कहा जाता है, एज संकुचन द्वारा इसके प्रत्येक दृढ़ता से जुड़े घटकों को एकल सुपरवर्टेक्स में बदल दिया जाता है।[21] जब ग्राफ पहले से ही अचक्रीय होता है, तो इसका सबसे छोटा फीडबैक वर्टेक्स समूह और फीडबैक आर्क समूह खाली समूह होता है, और इसका संक्षेपण ही ग्राफ होता है।

सकर्मक संवृतऔर सकर्मक कमी

किसी दिए गए डीएजीका सकर्मक समापन, के साथ n शिखर और m किनारों, समय में बनाया जा सकता है O(mn) प्रत्येक शीर्ष से पुन: योग्यता का परीक्षण करने के लिए या तो चौड़ाई-पहली खोज या गहराई-पहली खोज का उपयोग करके।[22] वैकल्पिक रूप से, इसे समय पर हल किया जा सकता है O(nω) कहाँ ω < 2.373 आव्यूहगुणन#आव्यूहगुणन घातांक की कम्प्यूटेशनल जटिलता है; यह सैद्धांतिक सुधार है O(mn) घने रेखांकन के लिए बाध्य।[23] इन सभी सकर्मक क्लोजर एल्गोरिदम में, जोड़े से दो या अधिक लंबाई के कम से कम पथ द्वारा पहुंच योग्य जोड़े के जोड़े को अलग करना संभव है जो केवल लंबाई-एक पथ से जुड़ा हो सकता है। सकर्मक कमी में किनारे होते हैं जो लंबाई-एक पथ बनाते हैं जो कि उनके समापन बिंदुओं को जोड़ने वाले एकमात्र पथ हैं। इसलिए, सकर्मक कमी को सकर्मक संवृतहोने के समान स्पर्शोन्मुख समय सीमा में बनाया जा सकता है।[24]

क्लोजर समस्या

Main article: क्लोजर समस्या

क्लोजर समस्या शीर्ष-भारित निर्देशित अचक्रीय ग्राफ को इनपुट के रूप में लेती है और क्लोजर के न्यूनतम (या अधिकतम) वजन की तलाश करती है - शीर्ष सी का समूह , जैसे कि कोई किनारा सी नहीं त्यागता है। समस्या को धारणा के बिना निर्देशित ग्राफ के लिए प्रस्तुत किया जा सकता है। चक्रीयता का, किन्तु अधिक व्यापकता के बिना, क्योंकि इस स्थिति में यह ग्राफ के संक्षेपण पर उसी समस्या के समान है। अधिकतम प्रवाह समस्या में अल्पता का उपयोग करके इसका बहुपद समय में समाधान किया जा सकता है।[25]

पथ एल्गोरिदम

टोपोलॉजिकल ऑर्डरिंग के सिद्धांत के आधार पर, सामान्य ग्राफ़ के अतिरिक्त डीएजी पर उपयोग किए जाने पर कुछ एल्गोरिदम सरल हो जाते हैं। उदाहरण के लिए, शीर्षों को टोपोलॉजिकल क्रम में संसाधित करके और प्रत्येक शीर्ष के लिए पथ की लंबाई की गणना करके किसी भी माध्यम से प्राप्त न्यूनतम या अधिकतम लंबाई के आधार पर रैखिक समय में डीएजी में दिए गए प्रारंभिक शीर्ष से सबसे छोटे पथ और सबसे लंबे पथ को इसके किसी आने वाले किनारे के माध्यम से ज्ञात करना संभव है।[26] इसके विपरीत, इच्छानुसार ग्राफ़ के लिए सबसे छोटे पथ के लिए धीमे एल्गोरिदम की आवश्यकता हो सकती है जैसे कि डिज्क्स्ट्रा का एल्गोरिथ्म या बेलमैन-फोर्ड एल्गोरिथम,[27] और इच्छानुसार ग्राफ़ में सबसे लंबे पथ को ज्ञात करना एनपी-कठिन हैं।[28]

अनुप्रयोग

शेड्यूलिंग

आंशिक ऑर्डरिंग के डायरेक्टेड अचक्रीय ग्राफ प्रस्तुतियों में ऑर्डरिंग बाधाओं के साथ कार्यों की प्रणालियों के लिए अनुसूची में कई अनुप्रयोग हैं।[29] इस प्रकार की समस्याओं का महत्वपूर्ण वर्ग उन वस्तुओं के संग्रह से संबंधित है जिन्हें अद्यतन करने की आवश्यकता है, जैसे कि किसी सेल के बाद स्प्रेडशीट की कोशिकाओं को बदल दिया गया है, या इसके स्रोत कोड के बाद कंप्यूटर सॉफ़्टवेयर के टुकड़े की वस्तु फ़ाइल को बदल दिया गया है। बदला हुआ। इस संदर्भ में, निर्भरता ग्राफ ग्राफ है जिसमें प्रत्येक वस्तु को अद्यतन करने के लिए शीर्ष होता है, और दो वस्तुओं को जोड़ने वाला किनारा जब भी उनमें से को दूसरे से पहले अद्यतन करने की आवश्यकता होती है। इस ग्राफ में चक्र को परिपत्र निर्भरता कहा जाता है, और सामान्यतः इसकी अनुमति नहीं होती है, क्योंकि चक्र में सम्मिलित कार्यों को लगातार शेड्यूल करने का कोई तरीका नहीं होगा। सर्कुलर निर्भरता के बिना निर्भरता ग्राफ डीएजी बनाते हैं।[30] उदाहरण के लिए, जब स्प्रेडशीट का सेल बदलता है, तो अन्य सेल के मानों की पुनर्गणना करना आवश्यक होता है जो बदले गए सेल पर प्रत्यक्ष या अप्रत्यक्ष रूप से निर्भर करते हैं। इस समस्या के लिए, निर्धारित किए जाने वाले कार्य स्प्रेडशीट के अलग-अलग कक्षों के मूल्यों की पुनर्गणना हैं। निर्भरताएँ तब उत्पन्न होती हैं जब कक्ष में कोई व्यंजक किसी अन्य कक्ष के मान का उपयोग करता है। ऐसी स्थिति में, उपयोग किए गए मान का उपयोग करने वाले व्यंजक से पहले पुनर्गणना की जानी चाहिए। टोपोलॉजिकल रूप से डिपेंडेंसी ग्राफ को ऑर्डर करना, और सेल अपडेट को शेड्यूल करने के लिए इस टोपोलॉजिकल ऑर्डर का उपयोग करना, पूरी स्प्रेडशीट को प्रति सेल केवल मूल्यांकन के साथ अपडेट करने की अनुमति देता है।[31] प्रोग्राम संकलन के लिए mac्स में टास्क ऑर्डरिंग की समान समस्याएं उत्पन्न होती हैं[31]और निम्न-स्तरीय कंप्यूटर प्रोग्राम अनुकूलन के लिए निर्देश शेड्यूलिंग।[32]

पांच मील के पत्थर (10-50 लेबल) और छह कार्यों (ए-एफ लेबल) के साथ परियोजना के लिए पीईआरटी चार्ट। दो महत्वपूर्ण रास्ते हैं, एडीएफ और बीसी।

कार्यक्रम मूल्यांकन और समीक्षा तकनीक (पीईआरटी) द्वारा शेड्यूलिंग बाधाओं के कुछ अलग डीएजी-आधारित फॉर्मूलेशन का उपयोग किया जाता है, जो बड़ी मानव परियोजनाओं के प्रबंधन के लिए विधि है जो डीएजी के पहले अनुप्रयोगों में से था। इस पद्धति में, डीएजी के शिखर प्रदर्शन किए जाने वाले विशिष्ट कार्यों के अतिरिक्त किसी परियोजना के माइलस्टोन (परियोजना प्रबंधन) का प्रतिनिधित्व करते हैं। इसके अतिरिक्त, कार्य या गतिविधि को डीएजीके किनारे द्वारा दर्शाया जाता है, जो दो मील के पत्थर को जोड़ता है जो कार्य की शुरुआत और पूर्णता को चिह्नित करता है। इस तरह के प्रत्येक किनारे को अनुमान के साथ लेबल किया जाता है कि कार्य करने के लिए श्रमिकों की टीम को कितना समय लगेगा। इस डीएजी में सबसे लंबी पथ समस्या परियोजना की महत्वपूर्ण पथ विधि का प्रतिनिधित्व करती है, जो कि परियोजना के लिए कुल समय को नियंत्रित करती है। अलग-अलग मील के पत्थर उनके शीर्ष पर समाप्त होने वाले सबसे लंबे रास्तों की लंबाई के अनुसार निर्धारित किए जा सकते हैं।[33]

डाटा प्रोसेसिंग नेटवर्क

प्रसंस्करण तत्वों के नेटवर्क का प्रतिनिधित्व करने के लिए निर्देशित विश्वकोश ग्राफ का उपयोग किया जा सकता है। इस प्रतिनिधित्व में, डेटा अपने आने वाले किनारों के माध्यम से प्रसंस्करण तत्व में प्रवेश करता है और इसके बाहर जाने वाले किनारों के माध्यम से तत्व को छोड़ देता है।

उदाहरण के लिए, इलेक्ट्रॉनिक सर्किट डिजाइन में, स्थिर संयोजन तर्क ब्लॉकों को लॉजिक गेट्स की चक्रीय प्रणाली के रूप में दर्शाया जा सकता है जो इनपुट के फ़ंक्शन की गणना करता है, जहां फ़ंक्शन के इनपुट और आउटपुट को अलग-अलग अंश्स के रूप में दर्शाया जाता है। सामान्य तौर पर, इन ब्लॉकों के आउटपुट को इनपुट के रूप में तब तक उपयोग नहीं किया जा सकता जब तक कि इसे रजिस्टर या राज्य तत्व द्वारा कैप्चर नहीं किया जाता है जो इसके चक्रीय गुणों को बनाए रखता है।[34] इलेक्ट्रॉनिक सर्किट स्कीमैटिक्स या तो कागज पर या डेटाबेस में निर्देशित चक्रीय ग्राफ का रूप है जो निम्न स्तर के घटक के लिए निर्देशित संदर्भ बनाने के लिए उदाहरणों या घटकों का उपयोग करता है। जरूरी नहीं कि इलेक्ट्रॉनिक सर्किट खुद ही चक्रीय या निर्देशित हों।

डेटाफ्लो प्रोग्रामिंग लैंग्वेज आकड़ों का प्रवाह पर ऑपरेशंस के सिस्टम और कुछ ऑपरेशंस के आउटपुट और अन्य के इनपुट के मध्य कनेक्शन का वर्णन करती हैं। ये भाषाएं दोहराए जाने वाले डेटा प्रोसेसिंग कार्यों का वर्णन करने के लिए सुविधाजनक हो सकती हैं, जिसमें कई डेटा आइटमों पर ही चक्रीय रूप से जुड़े संचालन का संग्रह लागू होता है। उन्हें समानांतर एल्गोरिदम के रूप में निष्पादित किया जा सकता है जिसमें प्रत्येक ऑपरेशन समानांतर प्रक्रिया द्वारा किया जाता है जैसे ही इनपुट का और समूह उपलब्ध हो जाता है।[35] कंपाइलर्स में, सीधी रेखा कोड (अर्थात, बिना लूप या सशर्त शाखाओं के बयानों के अनुक्रम) को डीएजी द्वारा कोड के भीतर किए गए प्रत्येक अंकगणितीय संचालन के इनपुट और आउटपुट का वर्णन किया जा सकता है। यह प्रतिनिधित्व संकलक को सामान्य उप-अभिव्यक्ति उन्मूलन को कुशलतापूर्वक करने की अनुमति देता है।[36] कोड संगठन के उच्च स्तर पर, विश्वकोश निर्भरता सिद्धांत बताता है कि बड़े सॉफ्टवेयर सिस्टम के मॉड्यूल या घटकों के मध्य निर्भरता निर्देशित विश्वकोश ग्राफ बनाना चाहिए।[37] फीडफॉरवर्ड न्यूरल नेटवर्क और उदाहरण हैं।

कारण संरचना

Main article: बायेसियन नेटवर्क

ग्राफ़ जिसमें कोने निश्चित समय पर होने वाली घटनाओं का प्रतिनिधित्व करते हैं, और जहां किनारों को हमेशा प्रारंभिक समय के शीर्ष से किनारे के देर से समय के शीर्ष तक इंगित किया जाता है, वे आवश्यक रूप से निर्देशित और अचक्रीय होते हैं। चक्र की कमी का अनुसरण करता है क्योंकि किसी शीर्ष से जुड़ा समय हमेशा बढ़ता है क्योंकि आप ग्राफ़ में किसी भी पथ (ग्राफ़ सिद्धांत) का पालन करते हैं, इसलिए आप किसी पथ पर किसी शीर्ष पर कभी नहीं लौट सकते। यह हमारे प्राकृतिक अंतर्ज्ञान को दर्शाता है कि कार्य-कारण का अर्थ है कि घटनाएं केवल भविष्य को प्रभावित कर सकती हैं, वे कभी भी अतीत को प्रभावित नहीं करती हैं, और इस प्रकार हमारे पास कोई कारण नहीं है। इस प्रकार के निर्देशित विश्वकोश ग्राफ का उदाहरण वे हैं जो कारण समूह में पाए जाते हैं, चूँकि इस स्थिति में जिन ग्राफों पर विचार किया जाता है वे हैं #Transitive क्लोजर और ट्रांजिटिव रिडक्शन। नीचे दिए गए संस्करण इतिहास के उदाहरण में, सॉफ़्टवेयर का प्रत्येक संस्करण अद्वितीय समय के साथ जुड़ा हुआ है, सामान्यतःसंस्करण को सहेजे जाने, प्रतिबद्ध या जारी किए जाने का समय। नीचे दिए गए उद्धरण ग्राफ़ उदाहरणों में, दस्तावेज़ समय में प्रकाशित होते हैं और केवल पुराने दस्तावेज़ों को संदर्भित कर सकते हैं।

कभी-कभी घटनाएँ किसी विशिष्ट भौतिक समय से जुड़ी नहीं होती हैं। बशर्ते कि घटनाओं के जोड़े में विशुद्ध रूप से कारणात्मक संबंध हो, अर्थात किनारे घटनाओं के मध्य कार्य-कारण का प्रतिनिधित्व करते हैं, हमारे पास निर्देशित चक्रीय ग्राफ होगा।[38] उदाहरण के लिए, बायेसियन नेटवर्क संभाव्य घटनाओं की प्रणाली को निर्देशित चक्रीय ग्राफ में कोने के रूप में दर्शाता है, जिसमें किसी घटना की संभावना की गणना डीएजीमें उसके पूर्ववर्तियों की संभावना से की जा सकती है।[39] इस संदर्भ में, डीएजीका नैतिक ग्राफ ही शीर्ष के सभी माता-पिता (कभी-कभी शादी करना) के मध्य (अप्रत्यक्ष) किनारा जोड़कर बनाया गया अप्रत्यक्ष ग्राफ है, और फिर सभी निर्देशित किनारों को अप्रत्यक्ष किनारों से बदल देता है।[40] समान कारण संरचना वाला अन्य प्रकार का ग्राफ प्रभाव आरेख है, जिसके शीर्ष या तो किए जाने वाले निर्णयों या अज्ञात जानकारी का प्रतिनिधित्व करते हैं, और जिसके किनारे शीर्ष से दूसरे शीर्ष पर कारण प्रभावों का प्रतिनिधित्व करते हैं।[41] महामारी विज्ञान में, उदाहरण के लिए, इन आरेखों का उपयोग प्रायः हस्तक्षेप के लिए विभिन्न विकल्पों के अपेक्षित मूल्य का अनुमान लगाने के लिए किया जाता है।[42][43] इसका उलटा भी सच है। यह किसी भी अनुप्रयोग में निर्देशित विश्वकोश ग्राफ द्वारा दर्शाया गया है, कारण संरचना है, या तो उदाहरण में स्पष्ट क्रम या समय या आदेश जो ग्राफ संरचना से प्राप्त किया जा सकता है। यह इस प्रकार है क्योंकि सभी निर्देशित अचक्रीय ग्राफ़ में #सांस्थितिक क्रम होता है, अर्थात वर्टिकल को क्रम में रखने का कम से कम तरीका होता है जैसे कि सभी किनारे उस क्रम के साथ ही दिशा में इंगित करते हैं।

वंशावली और संस्करण इतिहास

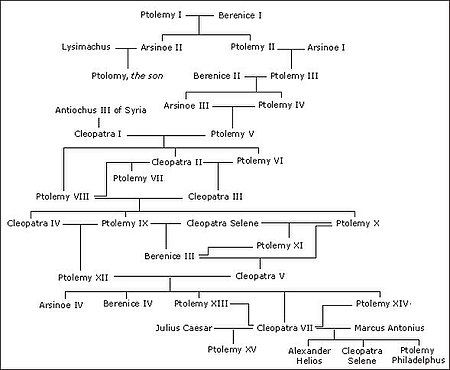
टोलेमिक राजवंश का वंश वृक्ष, रक्त संबंध के मध्य कई विवाहों के कारण वंशावली का पतन हुआ।

परिवार के पेड़ों को प्रत्येक परिवार के सदस्य के लिए शीर्ष और प्रत्येक माता-पिता-बच्चे के रिश्ते के किनारे के साथ निर्देशित अचक्रीय ग्राफ के रूप में देखा जा सकता है।[44] नाम के बावजूद, रिश्तेदारों के मध्य विवाह की संभावना के कारण ये ग्राफ आवश्यक रूप से पेड़ नहीं हैं (इसलिए बच्चे का माता और पिता दोनों पक्षों में सामान्य पूर्वज होता है) जिससे वंशावली का पतन होता है।[45] मातृसत्तात्मक वंश (माँ-बेटी के रिश्ते) और पितृसत्तात्मक वंश (पिता-पुत्र के रिश्ते) के रेखांकन इस ग्राफ के भीतर पेड़ हैं। क्योंकि कोई भी उनका अपना पूर्वज नहीं बन सकता, पारिवारिक वृक्ष चक्रीय होते हैं।[46]

वितरित पुनरीक्षण नियंत्रण प्रणाली के संस्करण इतिहास, जैसे कि गिट, में सामान्यतः निर्देशित अचक्रीय ग्राफ की संरचना होती है, जिसमें प्रत्येक संशोधन के लिए शीर्ष होता है और संशोधनों के जोड़े को जोड़ने वाला किनारा होता है जो सीधे दूसरे से प्राप्त होते हैं। मर्ज के कारण ये सामान्य रूप से पेड़ नहीं हैं।[47] कम्प्यूटेशनल ज्यामिति में कई यादृच्छिककरण एल्गोरिदम में, एल्गोरिदम संरचना में परिवर्तनों के अनुक्रम के दौरान ज्यामितीय संरचना के संस्करण इतिहास का प्रतिनिधित्व करने वाले इतिहास डीएजी को बनाए रखता है। उदाहरण के लिए रेंडमाइज्ड एल्गोरिद्म #ज्यामिति कलन विधि में रेंडमाइज्ड इंक्रीमेंटल कंस्ट्रक्शन Delaunay त्रिभुज के लिए, प्रत्येक बिंदु को जोड़ने पर त्रिकोण को तीन छोटे त्रिकोणों से बदलकर त्रिकोण बदल जाता है, और फ्लिप ऑपरेशंस द्वारा त्रिकोण के जोड़े को त्रिकोण के अलग जोड़े से बदल दिया जाता है। इस एल्गोरिथम के लिए इतिहास डीएजीमें एल्गोरिथम के भाग के रूप में निर्मित प्रत्येक त्रिभुज के लिए शीर्ष है, और प्रत्येक त्रिभुज के किनारों को दो या तीन अन्य त्रिभुजों के लिए जो इसे प्रतिस्थापित करते हैं। यह संरचना बिंदु स्थान प्रश्नों का कुशलतापूर्वक उत्तर देने की अनुमति देती है: क्वेरी बिंदु का स्थान खोजने के लिए q Delaunay त्रिभुज में, इतिहास डीएजीमें पथ का अनुसरण करें, प्रत्येक चरण में उस प्रतिस्थापन त्रिभुज की ओर बढ़ रहा है जिसमें सम्मिलित है q. इस पथ में पहुँचा हुआ अंतिम त्रिभुज Delaunay त्रिभुज होना चाहिए जिसमें समाविष्ट हो q.[48]

उद्धरण रेखांकन

एक उद्धरण ग्राफ़ में शिखर एकल प्रकाशन तिथि वाले दस्तावेज़ होते हैं। किनारे दस्तावेज़ की ग्रंथ सूची से दूसरे आवश्यक रूप से पहले के दस्तावेज़ों के उद्धरणों का प्रतिनिधित्व करते हैं। क्लासिक उदाहरण अकादमिक पत्रों के मध्य उद्धरणों से आता है जैसा कि 1965 के लेख नेटवर्क्स ऑफ साइंटिफिक पेपर्स में बताया गया है[49] डेरेक जे. डी सोला प्राइस द्वारा, जिन्होंने प्रशस्ति पत्र नेटवर्क का पहला मॉडल, प्राइस का मॉडल तैयार किया।[50] इस स्थिति में पेपर का प्रशस्ति पत्र प्रभाव उद्धरण नेटवर्क के संबंधित शीर्ष का केवल इन-डिग्री है। उद्धरण विश्लेषण में यह महत्वपूर्ण उपाय है। निर्णय (कानून) और उदाहरण प्रदान करता है क्योंकि न्यायाधीश पिछले मामलों में किए गए अन्य पूर्व निर्णयों को याद करके स्थिति में अपने निष्कर्ष का समर्थन करते हैं। अंतिम उदाहरण पेटेंट द्वारा प्रदान किया जाता है जो पहले की पूर्व कला को संदर्भित करता है, पहले के पेटेंट जो वर्तमान पेटेंट दावे के लिए प्रासंगिक हैं। निर्देशित विश्वकोश रेखांकन के विशेष गुणों को ध्यान में रखते हुए, नेटवर्क विज्ञान का उपयोग करते हुए कई अध्ययनों में विचार किए गए सामान्य रेखांकन का विश्लेषण करते समय तकनीकों के साथ उद्धरण नेटवर्क का विश्लेषण उपलब्ध नहीं हो सकता है। उदाहरण के लिए #ट्रांजिटिव क्लोजर और ट्रांजिटिव रिडक्शन विभिन्न अनुप्रयोगों में पाए जाने वाले उद्धरण वितरण में नई अंतर्दृष्टि प्रदान करता है, जो विभिन्न संदर्भों में उद्धरण नेटवर्क बनाने वाले तंत्र में स्पष्ट अंतर को उजागर करता है।[51] अन्य तकनीक मुख्य पथ विश्लेषण है, जो उद्धरण लिंक का पता लगाती है और किसी दिए गए उद्धरण ग्राफ़ में सबसे महत्वपूर्ण उद्धरण श्रृंखला का सुझाव देती है।

मूल्य का मॉडल उद्धरण ग्राफ का यथार्थवादी मॉडल होने के लिए बहुत सरल है, किन्तु इसके कुछ गुणों के लिए विश्लेषणात्मक समाधान की अनुमति देने के लिए यह काफी सरल है। इनमें से कई मूल्य के मॉडल, बाराबासी-अल्बर्ट मॉडल के अप्रत्यक्ष संस्करण से प्राप्त परिणामों का उपयोग करके पाया जा सकता है। चूँकि, चूंकि मूल्य का मॉडल निर्देशित अचक्रीय ग्राफ देता है, यह उपयोगी मॉडल है जब निर्देशित अचक्रीय ग्राफ के लिए अद्वितीय गुणों की विश्लेषणात्मक गणना की तलाश में है। उदाहरण के लिए, सबसे लंबे पथ की लंबाई, नेटवर्क में जोड़े गए n-वें नोड से नेटवर्क में पहले नोड तक, स्केल के रूप में[52] .

डेटा संपीड़न

निर्देशित विश्वकोश रेखांकन का उपयोग अनुक्रमों के संग्रह के डेटा संपीड़न के रूप में भी किया जा सकता है। इस प्रकार के आवेदन में, डीएजी मिलता है जिसमें पथ दिए गए अनुक्रमों का निर्माण करते हैं। जब कई अनुक्रम ही अनुवर्ती साझा करते हैं, तो इन साझा अनुक्रमों को डीएजी के साझा भाग द्वारा प्रदर्शित किया जा सकता है, जिससे प्रतिनिधित्व को कम स्थान का उपयोग करने की अनुमति मिलती है, जिससे सभी अनुक्रमों को अलग से सूचीबद्ध किया जा सके। उदाहरण के लिए, नियतात्मक विश्वकोश परिमित अवस्था ऑटोमेटन कंप्यूटर विज्ञान में डेटा संरचना है जो एकल स्रोत के साथ और अक्षरों या प्रतीकों द्वारा लेबल किए गए किनारों के साथ निर्देशित चक्रीय ग्राफ द्वारा बनाई गई है; इस ग्राफ में स्रोत से सिंक तक के रास्ते स्ट्रिंग (कंप्यूटर साइंस) के समूह का प्रतिनिधित्व करते हैं, जैसे कि अंग्रेजी शब्द।[53] अनुक्रम के प्रत्येक उपसर्ग के लिए कोशिश करें वर्टेक्स बनाकर और इन शीर्षों में से किसी के माता-पिता को कम तत्व के साथ अनुक्रम का प्रतिनिधित्व करके अनुक्रमों के किसी भी समूह को पेड़ में पथ के रूप में दर्शाया जा सकता है; स्ट्रिंग्स के समूह के लिए इस तरह से बने पेड़ को ट्री कहा जाता है। निर्देशित अचक्रीय शब्द ग्राफ पथों को मोड़ने और फिर से जुड़ने की अनुमति देकर ट्राई पर जगह बचाता है, जिससे कि ही संभावित प्रत्यय वाले शब्दों का समूह पेड़ के शीर्ष द्वारा प्रदर्शित किया जा सके।[54] पथों के परिवार का प्रतिनिधित्व करने के लिए डीएजीका उपयोग करने का ही विचार द्विआधारी निर्णय आरेख में होता है,[55][56] बाइनरी कार्यों का प्रतिनिधित्व करने के लिए डीएजी-आधारित डेटा संरचना। द्विआधारी निर्णय आरेख में, प्रत्येक गैर-सिंक वर्टेक्स को बाइनरी चर के नाम से लेबल किया जाता है, और प्रत्येक सिंक और प्रत्येक किनारे को 0 या 1 द्वारा लेबल किया जाता है। चर के लिए किसी भी सत्य असाइनमेंट के लिए फ़ंक्शन मान है सिंक पथ का अनुसरण करके पाया जाता है, जो एकल स्रोत वर्टेक्स से प्रारंभहोता है, जो कि प्रत्येक गैर-सिंक वर्टेक्स पर उस वर्टेक्स के चर के मान के साथ लेबल किए गए आउटगोइंग एज का अनुसरण करता है। जिस तरह निर्देशित चक्रीय शब्द रेखांकन को संकुचित रूप में देखा जा सकता है tries, द्विआधारी निर्णय आरेखों को निर्णय वृक्षों के संकुचित रूपों के रूप में देखा जा सकता है जो पथों को फिर से जुड़ने की अनुमति देकर स्थान बचाते हैं जब वे सभी शेष निर्णयों के परिणामों पर सहमत होते हैं।[57]

संदर्भ

  1. ↑ 1.0 1.1 Thulasiraman, K.; Swamy, M. N. S. (1992), "5.7 Acyclic Directed Graphs", Graphs: Theory and Algorithms, John Wiley and Son, p. 118, ISBN 978-0-471-51356-8.
  2. ↑ 2.0 2.1 2.2 Bang-Jensen, Jørgen (2008), "2.1 Acyclic Digraphs", Digraphs: Theory, Algorithms and Applications, Springer Monographs in Mathematics (2nd ed.), Springer-Verlag, pp. 32–34, ISBN 978-1-84800-997-4.
  3. ↑ Christofides, Nicos (1975), Graph theory: an algorithmic approach, Academic Press, pp. 170–174.
  4. ↑ Mitrani, I. (1982), Simulation Techniques for Discrete Event Systems, Cambridge Computer Science Texts, vol. 14, Cambridge University Press, p. 27, ISBN 9780521282826.
  5. ↑ Kozen, Dexter (1992), The Design and Analysis of Algorithms, Monographs in Computer Science, Springer, p. 9, ISBN 978-0-387-97687-7.
  6. ↑ Banerjee, Utpal (1993), "Exercise 2(c)", Loop Transformations for Restructuring Compilers: The Foundations, Springer, p. 19, Bibcode:1993ltfr.book.....B, ISBN 978-0-7923-9318-4.
  7. ↑ Bang-Jensen, Jørgen; Gutin, Gregory Z. (2008), "2.3 Transitive Digraphs, Transitive Closures and Reductions", Digraphs: Theory, Algorithms and Applications, Springer Monographs in Mathematics, Springer, pp. 36–39, ISBN 978-1-84800-998-1.
  8. ↑ Jungnickel, Dieter (2012), Graphs, Networks and Algorithms, Algorithms and Computation in Mathematics, vol. 5, Springer, pp. 92–93, ISBN 978-3-642-32278-5.
  9. ↑ Sedgewick, Robert; Wayne, Kevin (2011), "4,2,25 Unique topological ordering", Algorithms (4th ed.), Addison-Wesley, pp. 598–599, ISBN 978-0-13-276256-4.
  10. ↑ Bender, Edward A.; Williamson, S. Gill (2005), "Example 26 (Linear extensions – topological sorts)", A Short Course in Discrete Mathematics, Dover Books on Computer Science, Courier Dover Publications, p. 142, ISBN 978-0-486-43946-4.
  11. ↑ 11.0 11.1 Robinson, R. W. (1973), "Counting labeled acyclic digraphs", in Harary, F. (ed.), New Directions in the Theory of Graphs, Academic Press, pp. 239–273. See also Harary, Frank; Palmer, Edgar M. (1973), Graphical Enumeration, Academic Press, p. 19, ISBN 978-0-12-324245-7.
  12. ↑ Weisstein, Eric W., "Weisstein's Conjecture", MathWorld
  13. ↑ McKay, B. D.; Royle, G. F.; Wanless, I. M.; Oggier, F. E.; Sloane, N. J. A.; Wilf, H. (2004), "Acyclic digraphs and eigenvalues of (0,1)-matrices", Journal of Integer Sequences, 7: 33, arXiv:math/0310423, Bibcode:2004JIntS...7...33M, Article 04.3.3.
  14. ↑ Furnas, George W.; Zacks, Jeff (1994), "Multitrees: enriching and reusing hierarchical structure", Proc. SIGCHI conference on Human Factors in Computing Systems (CHI '94), pp. 330–336, doi:10.1145/191666.191778, ISBN 978-0897916509, S2CID 18710118.
  15. ↑ Rebane, George; Pearl, Judea (1987), "The recovery of causal poly-trees from statistical data", in Proc. 3rd Annual Conference on Uncertainty in Artificial Intelligence (UAI 1987), Seattle, WA, USA, July 1987 (PDF), pp. 222–228.
  16. ↑ 16.0 16.1 Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford (2001) [1990], Introduction to Algorithms (2nd ed.), MIT Press and McGraw-Hill, ISBN 0-262-03293-7 Section 22.4, Topological sort, pp. 549–552.
  17. ↑ 17.0 17.1 Jungnickel (2012), pp. 50–51.
  18. ↑ For depth-first search based topological sorting algorithm, this validity check can be interleaved with the topological sorting algorithm itself; see e.g. Skiena, Steven S. (2009), The Algorithm Design Manual, Springer, pp. 179–181, ISBN 978-1-84800-070-4.
  19. ↑ Stanley, Richard P. (1973), "Acyclic orientations of graphs" (PDF), Discrete Mathematics, 5 (2): 171–178, doi:10.1016/0012-365X(73)90108-8.
  20. ↑ Garey, Michael R.; Johnson, David S. (1979), Computers and Intractability: A Guide to the Theory of NP-Completeness, W. H. Freeman, ISBN 0-7167-1045-5, Problems GT7 and GT8, pp. 191–192.
  21. ↑ Harary, Frank; Norman, Robert Z.; Cartwright, Dorwin (1965), Structural Models: An Introduction to the Theory of Directed Graphs, John Wiley & Sons, p. 63.
  22. ↑ Skiena (2009), p. 495.
  23. ↑ Skiena (2009), p. 496.
  24. ↑ Bang-Jensen & Gutin (2008), p. 38.
  25. ↑ Picard, Jean-Claude (1976), "Maximal closure of a graph and applications to combinatorial problems", Management Science, 22 (11): 1268–1272, doi:10.1287/mnsc.22.11.1268, MR 0403596.
  26. ↑ Cormen et al. 2001, Section 24.2, Single-source shortest paths in directed acyclic graphs, pp. 592–595.
  27. ↑ Cormen et al. 2001, Sections 24.1, The Bellman–Ford algorithm, pp. 588–592, and 24.3, Dijkstra's algorithm, pp. 595–601.
  28. ↑ Cormen et al. 2001, p. 966.
  29. ↑ Skiena (2009), p. 469.
  30. ↑ Al-Mutawa, H. A.; Dietrich, J.; Marsland, S.; McCartin, C. (2014), "On the shape of circular dependencies in Java programs", 23rd Australian Software Engineering Conference, IEEE, pp. 48–57, doi:10.1109/ASWEC.2014.15, ISBN 978-1-4799-3149-1, S2CID 17570052.
  31. ↑ 31.0 31.1 Gross, Jonathan L.; Yellen, Jay; Zhang, Ping (2013), Handbook of Graph Theory (2nd ed.), CRC Press, p. 1181, ISBN 978-1-4398-8018-0.
  32. ↑ Srikant, Y. N.; Shankar, Priti (2007), The Compiler Design Handbook: Optimizations and Machine Code Generation (2nd ed.), CRC Press, pp. 19–39, ISBN 978-1-4200-4383-9.
  33. ↑ Wang, John X. (2002), What Every Engineer Should Know About Decision Making Under Uncertainty, CRC Press, p. 160, ISBN 978-0-8247-4373-4.
  34. ↑ Sapatnekar, Sachin (2004), Timing, Springer, p. 133, ISBN 978-1-4020-7671-8.
  35. ↑ Dennis, Jack B. (1974), "First version of a data flow procedure language", Programming Symposium, Lecture Notes in Computer Science, vol. 19, pp. 362–376, doi:10.1007/3-540-06859-7_145, ISBN 978-3-540-06859-4.
  36. ↑ Touati, Sid; de Dinechin, Benoit (2014), Advanced Backend Optimization, John Wiley & Sons, p. 123, ISBN 978-1-118-64894-0.
  37. ↑ Garland, Jeff; Anthony, Richard (2003), Large-Scale Software Architecture: A Practical Guide using UML, John Wiley & Sons, p. 215, ISBN 9780470856383.
  38. ↑ Gopnik, Alison; Schulz, Laura (2007), Causal Learning, Oxford University Press, p. 4, ISBN 978-0-19-803928-0.
  39. ↑ Shmulevich, Ilya; Dougherty, Edward R. (2010), Probabilistic Boolean Networks: The Modeling and Control of Gene Regulatory Networks, Society for Industrial and Applied Mathematics, p. 58, ISBN 978-0-89871-692-4.
  40. ↑ Cowell, Robert G.; Dawid, A. Philip; Lauritzen, Steffen L.; Spiegelhalter, David J. (1999), "3.2.1 Moralization", Probabilistic Networks and Expert Systems, Springer, pp. 31–33, ISBN 978-0-387-98767-5.
  41. ↑ Dorf, Richard C. (1998), The Technology Management Handbook, CRC Press, p. 9-7, ISBN 978-0-8493-8577-3.
  42. ↑ Boslaugh, Sarah (2008), Encyclopedia of Epidemiology, Volume 1, SAGE, p. 255, ISBN 978-1-4129-2816-8.
  43. ↑ Pearl, Judea (1995), "Causal diagrams for empirical research", Biometrika, 82 (4): 669–709, doi:10.1093/biomet/82.4.669.
  44. ↑ Kirkpatrick, Bonnie B. (April 2011), "Haplotypes versus genotypes on pedigrees", Algorithms for Molecular Biology, 6 (10): 10, doi:10.1186/1748-7188-6-10, PMC 3102622, PMID 21504603.
  45. ↑ McGuffin, M. J.; Balakrishnan, R. (2005), "Interactive visualization of genealogical graphs" (PDF), IEEE Symposium on Information Visualization (INFOVIS 2005), pp. 16–23, doi:10.1109/INFVIS.2005.1532124, ISBN 978-0-7803-9464-3, S2CID 15449409.
  46. ↑ Bender, Michael A.; Pemmasani, Giridhar; Skiena, Steven; Sumazin, Pavel (2001), "Finding least common ancestors in directed acyclic graphs", Proceedings of the Twelfth Annual ACM-SIAM Symposium on Discrete Algorithms (SODA '01), Philadelphia, PA, USA: Society for Industrial and Applied Mathematics, pp. 845–854, ISBN 978-0-89871-490-6.
  47. ↑ Bartlang, Udo (2010), Architecture and Methods for Flexible Content Management in Peer-to-Peer Systems, Springer, p. 59, Bibcode:2010aamf.book.....B, ISBN 978-3-8348-9645-2.
  48. ↑ Pach, János; Sharir, Micha, Combinatorial Geometry and Its Algorithmic Applications: The Alcalá Lectures, Mathematical surveys and monographs, vol. 152, American Mathematical Society, pp. 93–94, ISBN 978-0-8218-7533-9.
  49. ↑ Price, Derek J. de Solla (July 30, 1965), "Networks of Scientific Papers" (PDF), Science, 149 (3683): 510–515, Bibcode:1965Sci...149..510D, doi:10.1126/science.149.3683.510, PMID 14325149.
  50. ↑ Price, Derek J. de Solla (1976), "A general theory of bibliometric and other cumulative advantage processes", Journal of the American Society for Information Science, 27 (5): 292–306, doi:10.1002/asi.4630270505.
  51. ↑ Clough, James R.; Gollings, Jamie; Loach, Tamar V.; Evans, Tim S. (2015), "Transitive reduction of citation networks", Journal of Complex Networks, 3 (2): 189–203, arXiv:1310.8224, doi:10.1093/comnet/cnu039, S2CID 10228152.
  52. ↑ Evans, T.S.; Calmon, L.; Vasiliauskaite, V. (2020), "The Longest Path in the Price Model", Scientific Reports, 10 (1): 10503, arXiv:1903.03667, Bibcode:2020NatSR..1010503E, doi:10.1038/s41598-020-67421-8, PMC 7324613, PMID 32601403
  53. ↑ Crochemore, Maxime; Vérin, Renaud (1997), "Direct construction of compact directed acyclic word graphs", Combinatorial Pattern Matching, Lecture Notes in Computer Science, vol. 1264, Springer, pp. 116–129, CiteSeerX 10.1.1.53.6273, doi:10.1007/3-540-63220-4_55, ISBN 978-3-540-63220-7, S2CID 17045308.
  54. ↑ Lothaire, M. (2005), Applied Combinatorics on Words, Encyclopedia of Mathematics and its Applications, vol. 105, Cambridge University Press, p. 18, ISBN 9780521848022.
  55. ↑ Lee, C. Y. (1959), "Representation of switching circuits by binary-decision programs", Bell System Technical Journal, 38 (4): 985–999, doi:10.1002/j.1538-7305.1959.tb01585.x.
  56. ↑ Akers, Sheldon B. (1978), "Binary decision diagrams", IEEE Transactions on Computers, C-27 (6): 509–516, doi:10.1109/TC.1978.1675141, S2CID 21028055.
  57. ↑ Friedman, S. J.; Supowit, K. J. (1987), "Finding the optimal variable ordering for binary decision diagrams", Proc. 24th ACM/IEEE Design Automation Conference (DAC '87), New York, NY, USA: ACM, pp. 348–356, doi:10.1145/37888.37941, ISBN 978-0-8186-0781-3, S2CID 14796451.

बाहरी संबंध

Wikimedia Commons has media related to directed acyclic graphs.
Retrieved from ‘https://www.vigyanwiki.in/index.php?title=निर्देशित_अचक्रीय_ग्राफ&oldid=233948’