बिंदु स्थान

बिंदु स्थान समस्या कम्प्यूटेशनल ज्यामिति का एक मौलिक विषय है। यह उन क्षेत्रों में अनुप्रयोग ढूंढता है जो ज्यामितीय डेटा प्रसंस्करण से संबंधित हैं: कंप्यूटर ग्राफिक्स, भौगोलिक सूचना प्रणाली(जीआईएस), गति योजना, और कंप्यूटर एडेड डिजाइन (सीएडी)।

अपने सबसे सामान्य रूप में, समस्या को अलग-अलग क्षेत्रों में स्थान का विभाजन दिया जाता है, जिससे उस क्षेत्र का निर्धारण किया जा सके जहां एक प्रश्न बिंदु स्थित है। एक उदाहरण अनुप्रयोग के रूप में, हर बार जब कोई वेब ब्राउज़र में किसी लिंक का अनुसरण करने के लिए माउस पर क्लिक करता है, तो हल की जाने वाली समस्या यह निर्धारित करना है कि कंप्यूटर स्क्रीन के किस क्षेत्र में माउस पॉइंटर घूम रहा है। बहुभुज समस्या में एक साधारण विशेष मामला एक बिंदु है। इस मामले में, किसी को यह निर्धारित करने की आवश्यकता है कि बिंदु एक बहुभुज की सीमा के अंदर, बाहर या सीमा पर है या नहीं।

कई अनुप्रयोगों में, किसी को स्थान के एक ही विभाजन के संबंध में कई अलग-अलग बिंदुओं का स्थान निर्धारित करने की आवश्यकता होती है। इस समस्या को कुशलता से हल करने के लिए, एक डेटा संरचना का निर्माण करना उपयोगी होता है, जो एक क्वेरी बिंदु दिया जाता है, यह जल्दी से निर्धारित करता है कि किस क्षेत्र में क्वेरी बिंदु (जैसे वोरोनोई आरेख) सम्मिलित है।

प्लानर केस

डिब्बा का सीमा के अंदर एक प्लेनर सबडिवीजन

प्लानर केस में, हमें कई बहुभुजों से बना एक तलीय उपखंड S दिया जाता है, जिसे फलक कहा जाता है, और यह निर्धारित करने की आवश्यकता है कि किस फलक में एक प्रश्न बिंदु है। पॉइंट-इन-पॉलीगॉन एल्गोरिथम का उपयोग करके प्रत्येक चेहरे की क्रूर बल खोज संभव है, लेकिन आमतौर पर उच्च जटिलता के उपखंडों के लिए संभव नहीं है। कई अलग-अलग दृष्टिकोण O(n) स्टोरेज स्पेस और ओ (लॉग एन) क्वेरी टाइम के साथ इष्टतम डेटा संरचनाओं की ओर ले जाते हैं, जहां एन एस में वर्टिकल की कुल संख्या है। शुद्धता के लिए, हम मानते हैं कि प्लानर सबडिवीजन एक वर्गाकार बाउंडिंग बॉक्स के अंदर निहित है।

स्लैब अपघटन

स्लैब में विभाजित एक प्लानर उपखंड।

1976 में डोबकिन और लिप्टन द्वारा O(log n) समय प्राप्त करने के लिए सबसे सरल और सबसे पुरानी डेटा संरचना की खोज की गई थी। यह एस में प्रत्येक शीर्ष से गुजरने वाली लंबवत रेखाओं का उपयोग करके S को उप-विभाजित करने पर आधारित है। दो लगातार लंबवत रेखाओं के बीच के क्षेत्र को स्लैब कहा जाता है। ध्यान दें कि प्रत्येक स्लैब को गैर-प्रतिच्छेदी रेखा खंडों से विभाजित किया गया है जो स्लैब को बाएं से दाएं पूरी तरह से पार करते हैं। एक स्लैब के अंदर लगातार दो खंडों के बीच का क्षेत्र एस के एक अद्वितीय चेहरे से मेल खाता है। इसलिए, हम अपनी बिंदु स्थान समस्या को दो सरल समस्याओं में घटाते हैं:

1. ऊर्ध्वाधर स्लैब में समतल के उपविभाजन को देखते हुए, निर्धारित करें कि किस स्लैब में एक बिंदु है।
2. गैर-अंतर्विभाजक खंडों द्वारा क्षेत्रों में उप-विभाजित एक स्लैब को देखते हुए जो पूरी तरह से बाएं से दाएं स्लैब को पार करता है, निर्धारित करें कि किस क्षेत्र में एक बिंदु है।

पहली समस्या O(log n) समय में लंबवत रेखाओं के एक्स समन्वय पर द्विआधारी खोज द्वारा हल की जा सकती है। दूसरी समस्या को बाइनरी खोज द्वारा O(log n) समय में भी हल किया जा सकता है। यह देखने के लिए कि कैसे, ध्यान दें कि, चूंकि खंड एक दूसरे को नहीं काटते हैं और स्लैब को पूरी तरह से पार करते हैं, इसलिए खंडों को प्रत्येक स्लैब के अंदर लंबवत रूप से क्रमबद्ध किया जा सकता है।

जबकि यह एल्गोरिदम लघुगणकीय समय में बिंदु स्थान की अनुमति देता है और इसे लागू करना आसान है, स्लैब बनाने के लिए आवश्यक स्थान और स्लैब के भीतर निहित क्षेत्र O(n²) जितना ऊंचा हो सकता है, क्योंकि प्रत्येक स्लैब सेगमेंट के एक महत्वपूर्ण अंश को पार करता है।

कई लेखकों ने देखा है कि दो आसन्न स्लैबों को पार करने वाले वर्ग अधिकतर समान हैं। इसलिए, डेटा संरचना के आकार को महत्वपूर्ण रूप से कम किया जा सकता है। अधिक विशेष रूप से, सरनाक और टार्ज़न एक ऊर्ध्वाधर रेखा l को विमान के ऊपर बाएं से दाएं घुमाते हैं, जबकि एक निरंतर लाल-काले पेड़ में l को काटते हुए खंडों को बनाए रखते हैं। यह उन्हें O(log n) प्रश्नचिहन समय को बनाए रखते हुए स्टोरेज स्पेस को O(n) तक कम करने की अनुमति देता है।

मोनोटोन उपखंड

हाइलाइट किए गए कुछ मोनोटोन चेन के साथ एक मोनोटोन प्लानर सबडिवीजन।

ऊर्ध्वाधर मोनोटोन शृंखला एक ऐसा पथ है जिसमें y-निर्देशांक कभी भी पथ के साथ नहीं बढ़ता है। एक साधारण बहुभुज (ऊर्ध्वाधर) मोनोटोन होता है यदि यह दो मोनोटोन श्रृंखलाओं द्वारा बनाया जाता है, जिसमें पहले और अंतिम कोने समान होते हैं। सभी फलक को मोनोटोन बनाने के लिए, एक मोनोटोन सबडिवीजन कहा जाता है, प्राप्त करने के लिए, कुछ किनारों को एक प्लानर उपखंड में जोड़ना संभव है। यह प्रक्रिया उपखंड में किसी भी कोने को नहीं जोड़ती है (इसलिए, आकार O(n) रहता है), और O(log n) समय में प्लेन स्वीप द्वारा किया जा सकता है (यह रैखिक समय में भी किया जा सकता है, बहुभुज त्रिकोणासन का उपयोग करके) ). इसलिए, सामान्यता का कोई नुकसान नहीं है, यदि हम अपनी डेटा संरचना को मोनोटोन उप-विभाजनों के मामले में प्रतिबंधित करते हैं, जैसा कि हम इस खंड में करते हैं।

स्लैब अपघटन की कमजोरी यह है कि लंबवत रेखाएं अपघटन में अतिरिक्त खंड बनाती हैं, जिससे ओ (एन) भंडारण स्थान प्राप्त करना मुश्किल हो जाता है। एडेल्सब्रनर, गुइबास और स्टोल्फी ने एक इष्टतम डेटा संरचना की खोज की जो केवल एक मोनोटोन उपखंड में किनारों का उपयोग करती है। उपखंड को विभाजित करने के लिए ऊर्ध्वाधर रेखाओं का उपयोग करने के बजाय, ऊर्ध्वाधर मोनोटोन श्रृंखलाओं का उपयोग करने का विचार है।

इस सामान्य विचार को एक वास्तविक कुशल डेटा संरचना में परिवर्तित करना कोई आसान काम नहीं है। सबसे पहले, हमें एक मोनोटोन श्रृंखला की गणना करने में सक्षम होने की आवश्यकता है जो उपखंड को समान आकार के दो हिस्सों में विभाजित करती है। दूसरा, चूंकि कुछ किनारों को कई मोनोटोन श्रृंखलाओं में समाहित किया जा सकता है, इसलिए हमें यह सुनिश्चित करने के लिए सावधान रहना होगा कि भंडारण स्थान O(n) है। तीसरा, यह परीक्षण करना कि क्या कोई बिंदु एक मोनोटोन उपखंड के बाईं ओर या दाईं ओर है, अगर सरलता से प्रदर्शन किया जाता है तो O(n) समय लगता है।

पहले दो अभिप्रायों को कैसे हल किया जाए, इस पर विवरण इस आलेख के दायरे से बाहर है। हम संक्षेप में बताते हैं कि तीसरी समस्या का समाधान कैसे किया जाए। बाइनरी खोज का उपयोग करके, हम परीक्षण कर सकते हैं कि O(log n) समय में एक बिंदु एक मोनोटोन श्रृंखला के बाईं या दाईं ओर है या नहीं। जैसा कि हमें बिंदु स्थान को वास्तव में निर्धारित करने के लिए O(log n) श्रृंखलाओं के माध्यम से एक और नेस्टेड बाइनरी खोज करने की आवश्यकता है, क्वेरी समय O(log n) है। O(log n) प्रश्नचिहन समय प्राप्त करने के लिए, हमें अलग-अलग मोनोटोन श्रृंखलाओं के किनारों के बीच पॉइंटर्स रखते हुए आंशिक कैस्केडिंग का उपयोग करने की आवश्यकता है।

त्रिकोणन परिष्करण

त्रिभुज शोधन के क्रमिक चरण।

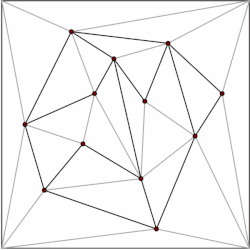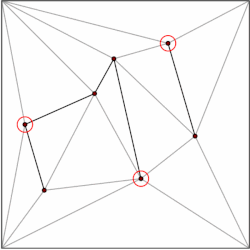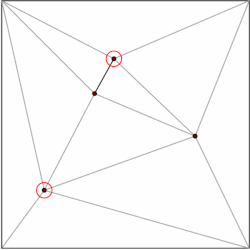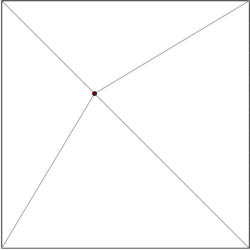
m शीर्ष वाले बहुभुज को m-2 त्रिभुजों में विभाजित किया जा सकता है। जिसे त्रिभुज से प्रारंभ करके प्रेरण द्वारा दिखाया जा सकता है। एक बहुभुज को कुशलतापूर्वक त्रिकोणित करने के लिए कई एल्गोरिदम हैं, सबसे तेज़ O(n) सबसे खराब स्थिति समय है। इसलिए, हम अपने उपखंड के प्रत्येक बहुभुज को त्रिभुजों में विघटित कर सकते हैं, और अपनी डेटा संरचना को केवल त्रिभुजों द्वारा गठित उपविभागों के मामले में प्रतिबंधित कर सकते हैं। किर्कपैट्रिक त्रिभुजित उपखंडों में बिंदु स्थान के लिए O(n) संग्रहण स्थान औरडेटा संरचना को विपरीत क्रम में बनाया गया है, अर्थात नीचे-ऊपर। हम त्रिकोणीय उपखंड से प्रारंभ करते हैं और हटाए जाने वाले शीर्षों का एक स्वतंत्र समुच्चय चुनते हैं। शीर्षों को हटाने के बाद, हम उपखंड को त्रिकोणित करते हैं। क्योंकि उपखंड त्रिभुजों से बनता है, एक लालची एल्गोरिथ्म एक स्वतंत्र सेट पा सकता है जिसमें कोने का एक निरंतर अंश होता है। इसलिए, निष्कासन चरणों की संख्या O(log n) है।प्रश्नचिहन समय के साथ डेटा संरचना देता है।

सामान्य विचार त्रिकोणों का एक पदानुक्रम बनाना है। एक क्वेरी करने के लिए, हम शीर्ष-स्तरीय त्रिभुज को खोजकर प्रारंभ करते हैं जिसमें क्वेरी बिंदु होता है। चूंकि शीर्ष-स्तरीय त्रिकोणों की संख्या एक स्थिरांक से बंधी है, इसलिए यह ऑपरेशन O(1) समय में किया जा सकता है। प्रत्येक त्रिभुज में त्रिभुजों के संकेत होते हैं जो पदानुक्रम के अगले स्तर में प्रतिच्छेद करते हैं, और संकेतकों की संख्या भी एक स्थिरांक द्वारा सीमित होती है। हम क्वेरी के साथ आगे बढ़ते हैं कि किस त्रिभुज में क्वेरी बिंदु स्तर स्तर है।

डेटा संरचना को विपरीत क्रम में बनाया गया है, अर्थात नीचे-ऊपर। हम त्रिकोणीय उपखंड से प्रारंभ करते हैं और हटाए जाने वाले शीर्षों का एक स्वतंत्र समुच्चय चुनते हैं। शीर्षों को हटाने के बाद, हम उपखंड को त्रिकोणित करते हैं। क्योंकि उपखंड त्रिभुजों से बनता है, एक स्पृही कलन विधि एक स्वतंत्र समुच्चय पा सकता है जिसमें कोने का एक निरंतर अंश होता है। इसलिए, निष्कासन चरणों की संख्या O(log n) है।

समलम्बाकार अपघटन

एक ट्रैपेज़ॉयडल अपघटन।

इस समस्या के लिए एक यादृच्छिक दृष्टिकोण, और शायद सबसे व्यावहारिक एक, ट्रैपोज़ाइडल अपघटन, या ट्रेपोज़ाइडल मैप पर आधारित है। मूल उपखंड में प्रत्येक शीर्ष से ऊपर और नीचे दोनों ओर जाने वाली ऊर्ध्वाधर गोलियों की शूटिंग करके एक समलम्बाकार अपघटन प्राप्त किया जाता है। जब वे एक किनारे से टकराते हैं तो गोलियां रुक जाती हैं और उपखंड में एक नया किनारा बना लेती हैं। इस तरह, हम स्लैब अपघटन का एक उपसमुच्चय प्राप्त करते हैं, केवल O(n) किनारों और शीर्षों के साथ, क्योंकि मूल उपखंड में प्रत्येक शीर्ष के लिए हम केवल दो नए कोने जोड़ते हैं और किनारों की संख्या को चार से बढ़ाते हैं।

यह देखना आसान नहीं है कि बिंदु स्थान के लिए ट्रैपोज़ाइडल अपघटन का उपयोग कैसे किया जाए, क्योंकि स्लैब अपघटन में उपयोग की जाने वाली एक बाइनरी खोज अब नहीं की जा सकती है। इसके बजाय, हमें त्रिकोणीय परिशोधन दृष्टिकोण के रूप में उसी तरह से एक प्रश्न का उत्तर देने की आवश्यकता है, लेकिन डेटा संरचना ऊपर-नीचे निर्मित होती है। प्रारंभ में, हम एक ट्रैपेज़ॉइडल अपघटन बनाते हैं जिसमें केवल बाउंडिंग बॉक्स और कोई आंतरिक शीर्ष नहीं होता है। फिर, हम समलम्बाकार अपघटन को परिष्कृत करते हुए, यादृच्छिक क्रम में, एक-एक करके उपखंड से खंडों को जोड़ते हैं। पीछे की ओर विश्लेषण का उपयोग करके, हम दिखा सकते हैं कि प्रत्येक सम्मिलन के लिए बनाए गए ट्रैपेज़ोइड्स की अपेक्षित संख्या एक स्थिरांक से बंधी हुई है।

हम एक निर्देशित अचक्रीय ग्राफ का निर्माण करते हैं, जहां शिखर परिशोधन में किसी बिंदु पर समाहित ट्रेपेज़ॉइड होते हैं, और निर्देशित किनारे उपखंड द्वारा प्राप्त ट्रेपेज़ोइड्स में शामिल होते हैं। इस डिग्राफ में खोज की अपेक्षित गहराई, बाउंडिंग बॉक्स के अनुरूप शीर्ष से शुरू होकर, O(log n) है।.

उच्च आयाम

2 से बड़े आयामों के लिए रैखिक स्थान और लॉगरिदमिक क्वेरी समय के साथ कोई ज्ञात सामान्य बिंदु स्थान डेटा संरचना नहीं है। इसलिए, हमें या तो क्वेरी समय, या संग्रहण स्थान का त्याग करने की आवश्यकता है, या खुद को कुछ कम सामान्य प्रकार के उपखंडों तक सीमित रखने की आवश्यकता है।

त्रि-आयामी स्थान में, O(n log n) स्थान का उपयोग करके O(log² n) में बिंदु स्थान प्रश्नों का उत्तर देना संभव है। सामान्य विचार कई प्लानर पॉइंट स्थान डेटा संरचनाओं को बनाए रखना है, जो उपखंड के चौराहे के अनुरूप एन समांतर विमानों के साथ होता है जिसमें प्रत्येक उपखंड वर्टेक्स होता है। इस विचार का एक सरल उपयोग भंडारण स्थान को O(n²) तक बढ़ा देगा। स्लैब अपघटन की तरह ही, भंडारण स्थान को O(n log n तक कम करने के लिए लगातार डेटा संरचनाओं के बीच समानता का शोषण किया जा सकता है, लेकिन क्वेरी समय O(log² n) तक बढ़ जाता है।

डी-डायमेंशनल स्पेस में, पॉइंट लोकेशन को रिकर्सिवली चेहरों को (d-1) -डायमेंशनल स्पेस में प्रोजेक्ट करके हल किया जा सकता है। जबकि क्वेरी का समय O(log n) है, स्टोरेज स्पेस $O(n^{2^{d}})$ जितना अधिक हो सकता है। डी-डायमेंशनल डेटा स्ट्रक्चर्स की उच्च जटिलता ने विशेष प्रकार के उपखंडों के अध्ययन का नेतृत्व किया।

एक महत्वपूर्ण उदाहरण हाइपरप्लेन की व्यवस्था का मामला है। n हाइपरप्लेन की व्यवस्था O(n^d) सेल को परिभाषित करती है, लेकिन बिंदु स्थान को O(log n) समय में O(n^d) स्थान के साथ चेज़ेल के पदानुक्रमित कटिंग का उपयोग करके किया जा सकता है।

एक अन्य विशेष प्रकार के उपखंड को सीधी रेखा (या ऑर्थोगोनल) उपखंड कहा जाता है। एक आयताकार उपखंड में, सभी किनारे d ऑर्थोगोनल अक्ष में से किसी एक के समानांतर होते हैं। इस मामले में, O(n) स्थान के साथ O(log^d-1 n) समय में बिंदु स्थान का उत्तर दिया जा सकता है।

संदर्भ

• de Berg, Mark; van Kreveld, Marc; Overmars, Mark; Schwarzkopf, Otfried (2000). "Chapter 6: Point location". Computational Geometry (2nd revised ed.). Springer-Verlag. pp. 121–146. ISBN 3-540-65620-0.
• Dobkin, David; Lipton, Richard J. (1976). "Multidimensional searching problems". SIAM Journal on Computing. 5 (2): 181–186. doi:10.1137/0205015.
• Snoeyink, Jack (2004). "Chapter 34: "Point Location". In Goodman, Jacob E.; O'Rourke, Joseph (eds.). Handbook of Discrete and Computational Geometry (2nd ed.). Chapman & Hall/CRC. ISBN 1-58488-301-4.
• Sarnak, Neil; Tarjan, Robert E. (1986). "Planar point location using persistent search trees". Communications of the ACM. 29 (7): 669–679. doi:10.1145/6138.6151.
• Edelsbrunner, Herbert; Guibas, Leonidas J.; Stolfi, Jorge (1986). "Optimal point location in a monotone subdivision". SIAM Journal on Computing. 15 (2): 317–340. doi:10.1137/0215023.
• Kirkpatrick, David G. (1983). "Optimal search in planar subdivisions". SIAM Journal on Computing. 12 (1): 28–35. CiteSeerX 10.1.1.461.1866. doi:10.1137/0212002.

बाहरी संबंध

• Point-Location Source Repository at Stony Brook University
• Point-Location Queries in CGAL, the Computational Geometry Algorithms Library