रुकने का समय

For the musical phenomenon, see stop-time.

रुकने के समय का उदाहरण: एक प्रकार कि गति का हिटिंग समय। प्रक्रिया 0 से शुरू होती है और 1 पर पहुंचते ही रुक जाती है।

संभाव्यता सिद्धांत में, विशेष रूप से स्टोकेस्टिक प्रक्रियाओं के अध्ययन में, एक रुकने का समय (मार्कोव समय, मार्कोव क्षण, वैकल्पिक रुकने का समय या वैकल्पिक समय)) एक विशिष्ट प्रकार का "यादृच्छिक समय" है: एक यादृच्छिक चर जिसका मूल्य उस समय के रूप में व्याख्या किया जाता है जिस पर एक दी गई स्टोकेस्टिक प्रक्रिया रुचि का एक निश्चित व्यवहार प्रदर्शित करती है। रुकने के समय को अक्सर एक रुकने के नियम द्वारा परिभाषित किया जाता है, जो वर्तमान स्थिति और पिछली घटनाओं के आधार पर किसी प्रक्रिया को जारी रखने या रोकने का निर्णय लेने के लिए एक तंत्र है, और जो लगभग हमेशा किसी सीमित समय पर रुकने का निर्णय लेगा।

निर्णय सिद्धांत में रुकने का समय होता है, और वैकल्पिक रोक प्रमेय इस संदर्भ में एक महत्वपूर्ण परिणाम है। जैसा कि चुंग ने अपनी पुस्तक (1982) में कहा है, "समय की सातत्यता को वश में करने" के लिए रुकने के समय को गणितीय प्रमाणों में भी अक्सर लागू किया जाता है।

परिभाषा

असतत समय

होने देना $\tau$ एक यादृच्छिक चर हो, जिसे फ़िल्टर किए गए संभाव्यता स्थान पर परिभाषित किया गया है $(\Omega ,{\mathcal {F}},({\mathcal {F}}_{n})_{n\in \mathbb {N} },P)$ मूल्यों के साथ $\mathbb {N} \cup \{+\infty \}$. तब $\tau$ रुकने का समय कहा जाता है (फ़िल्टरेशन (संभावना सिद्धांत) के संबंध में) $\mathbb {F} =(({\mathcal {F}}_{n})_{n\in \mathbb {N} }$), यदि निम्नलिखित शर्त लागू होती है:

$\{\tau =n\}\in {\mathcal {F}}_{n}$ सभी के लिए $n$

सहज रूप से, इस स्थिति का अर्थ है कि समय पर रुकना है या नहीं इसका निर्णय $n$ केवल समय पर मौजूद जानकारी पर आधारित होना चाहिए $n$, भविष्य की किसी सूचना पर नहीं।

सामान्य मामला

होने देना $\tau$ एक यादृच्छिक चर हो, जिसे फ़िल्टर किए गए संभाव्यता स्थान पर परिभाषित किया गया है $(\Omega ,{\mathcal {F}},({\mathcal {F}}_{t})_{t\in T},P)$ मूल्यों के साथ $T$. अधिकतर परिस्थितियों में, $T=[0,+\infty )$. तब $\tau$ रुकने का समय कहा जाता है (फ़िल्टरेशन (संभावना सिद्धांत) के संबंध में) $\mathbb {F} =({\mathcal {F}}_{t})_{t\in T}$), यदि निम्नलिखित शर्त लागू होती है:

$\{\tau \leq t\}\in {\mathcal {F}}_{t}$ सभी के लिए $t\in T$

अनुकूलित प्रक्रिया के रूप में

होने देना $\tau$ एक यादृच्छिक चर हो, जिसे फ़िल्टर किए गए संभाव्यता स्थान पर परिभाषित किया गया है $(\Omega ,{\mathcal {F}},({\mathcal {F}}_{t})_{t\in T},P)$ मूल्यों के साथ $T$. तब $\tau$ स्टोकेस्टिक प्रक्रिया का रुकने का समय कहा जाता है $X=(X_{t})_{t\in T}$, द्वारा परिभाषित

$X_{t}:={\begin{cases}1&{\text{ if }}t<\tau \\0&{\text{ if }}t\geq \tau \end{cases}}$

निस्पंदन के लिए अनुकूलित प्रक्रिया है $\mathbb {F} =({\mathcal {F}}_{t})_{t\in T}$

टिप्पणियाँ

कुछ लेखक ऐसे मामलों को स्पष्ट रूप से बाहर कर देते हैं $\tau$ हो सकता है $+\infty$, जबकि अन्य लेखक अनुमति देते हैं $\tau$ के समापन में कोई भी मूल्य लेने के लिए $T$.

उदाहरण

यादृच्छिक समय के कुछ उदाहरणों को स्पष्ट करने के लिए जो नियमों को रोक रहे हैं और कुछ जो नहीं हैं, एक जुआरी को एक सामान्य घरेलू बढ़त के साथ रूलेट खेलने पर विचार करें, जो $100 से शुरू होता है और प्रत्येक खेल में लाल रंग पर $1 का दांव लगाता है:

• ठीक पाँच गेम खेलना रुकने के समय τ = 5 से मेल खाता है, और यह रुकने का नियम है।
• जब तक उनके पास पैसे ख़त्म न हो जाएं या 500 गेम न खेल लें, तब तक खेलना बंद करने का नियम है।
• जब तक वे अधिकतम राशि आगे न पहुंच जाएं तब तक खेलना कोई रुकने का नियम नहीं है और न ही रुकने का समय प्रदान करता है, क्योंकि इसके लिए भविष्य के साथ-साथ वर्तमान और अतीत के बारे में जानकारी की आवश्यकता होती है।
• जब तक वे अपना पैसा दोगुना नहीं कर लेते (यदि आवश्यक हो तो उधार लेना) खेलना कोई बंद करने वाला नियम नहीं है, क्योंकि इस बात की सकारात्मक संभावना है कि वे कभी भी अपना पैसा दोगुना नहीं करेंगे।
• जब तक उनका पैसा दोगुना न हो जाए या पैसा खत्म न हो जाए, तब तक खेलना बंद करने का नियम है, भले ही उनके द्वारा खेले जाने वाले गेम की संख्या की संभावित रूप से कोई सीमा नहीं है, क्योंकि उनके एक सीमित समय में बंद होने की संभावना 1 है।

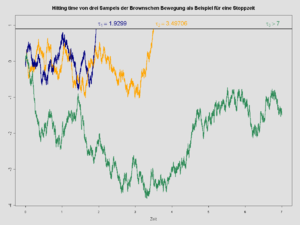
रुकने के समय की अधिक सामान्य परिभाषा को स्पष्ट करने के लिए, ब्राउनियन गति पर विचार करें, जो एक स्टोकेस्टिक प्रक्रिया है $(B_{t})_{t\geq 0}$, जहां प्रत्येक $B_{t}$ संभाव्यता स्थान पर परिभाषित एक यादृच्छिक चर है $(\Omega ,{\mathcal {F}},\mathbb {P} )$. हम इस संभाव्यता स्थान पर एक निस्पंदन को लेट करके परिभाषित करते हैं ${\mathcal {F}}_{t}$ प्रपत्र के सभी सेटों द्वारा उत्पन्न σ-बीजगणित हो $(B_{s})^{-1}(A)$ कहाँ $0\leq s\leq t$ और $A\subseteq \mathbb {R}$ एक बोरेल सेट है. सहज रूप से, एक घटना E में है ${\mathcal {F}}_{t}$ यदि और केवल यदि हम केवल समय 0 से समय t तक ब्राउनियन गति को देखकर यह निर्धारित कर सकते हैं कि E सही है या गलत।

• प्रत्येक स्थिरांक $\tau :=t_{0}$ (तुच्छ रूप से) रुकने का समय है; यह समय पर रुकने के नियम से मेल खाता है $t_{0}$.
• होने देना $a\in \mathbb {R} .$ तब $\tau :=\inf\{t\geq 0\mid B_{t}=a\}$ ब्राउनियन गति के लिए रुकने का समय है, जो रोकने के नियम के अनुरूप है: जैसे ही ब्राउनियन गति मान ए पर पहुंचती है, रुक जाती है।
• एक और रुकने का समय दिया गया है $\tau :=\inf\{t\geq 1\mid B_{s}>0{\text{ for all }}s\in [t-1,t]\}$. यह रोक नियम से मेल खाता है जैसे ही ब्राउनियन गति 1 समय इकाई लंबाई के सन्निहित खिंचाव पर सकारात्मक होती है।
• सामान्य तौर पर, यदि τ₁ और टी₂ बार-बार रुक रहे हैं $\left(\Omega ,{\mathcal {F}},\left\{{\mathcal {F}}_{t}\right\}_{t\geq 0},\mathbb {P} \right)$ फिर उनका न्यूनतम $\tau _{1}\wedge \tau _{2}$, उनकी अधिकतम $\tau _{1}\vee \tau _{2}$, और उनका योग τ₁+ टी₂ समय भी रोक रहे हैं. (यह मतभेदों और उत्पादों के लिए सच नहीं है, क्योंकि इन्हें कब रोकना है यह निर्धारित करने के लिए भविष्य में देखने की आवश्यकता हो सकती है।)

ऊपर दिए गए दूसरे उदाहरण की तरह हिटिंग टाइम, स्टॉपिंग टाइम के महत्वपूर्ण उदाहरण हो सकते हैं। हालाँकि यह दिखाना अपेक्षाकृत सरल है कि अनिवार्य रूप से सभी रुकने के समय हिटिंग समय हैं, यह दिखाना अधिक कठिन हो सकता है कि एक निश्चित हिटिंग समय रुकने का समय है। बाद के प्रकार के परिणामों को हिटिंग टाइम#डेबट प्रमेय|डेबट प्रमेय के रूप में जाना जाता है।

स्थानीयकरण

स्टॉपिंग टाइम का उपयोग अक्सर स्टोकेस्टिक प्रक्रियाओं के कुछ गुणों को उन स्थितियों में सामान्यीकृत करने के लिए किया जाता है जिनमें आवश्यक संपत्ति केवल स्थानीय अर्थ में संतुष्ट होती है। सबसे पहले, यदि X एक प्रक्रिया है और τ रुकने का समय है, तो X^τ का उपयोग प्रक्रिया X को समय τ पर रोकने के लिए किया जाता है।

$X_{t}^{\tau }=X_{\min(t,\tau )}$

फिर, कहा जाता है कि यदि रुकने के समय का कोई क्रम मौजूद है, तो X स्थानीय रूप से कुछ संपत्ति P को संतुष्ट करता है_n, जो अनंत तक बढ़ता है और जिसके लिए प्रक्रियाएं होती हैं

$\mathbf {1} _{\{\tau _{n}>0\}}X^{\tau _{n}}$ संपत्ति पी को संतुष्ट करें। समय सूचकांक सेट I = [0, ∞) के साथ सामान्य उदाहरण इस प्रकार हैं:

<ब्लॉककोट>'स्थानीय मार्टिंगेल प्रक्रिया'। एक प्रक्रिया X एक स्थानीय मार्टिंगेल है यदि यह कैडलैग है और इसमें रुकने के समय का एक क्रम मौजूद है τ_n अनंत तक बढ़ रहा है, जैसे कि

$\mathbf {1} _{\{\tau _{n}>0\}}X^{\tau _{n}}$ प्रत्येक n के लिए एक मार्टिंगेल (संभावना सिद्धांत) है।

<ब्लॉककोट>'स्थानीय रूप से एकीकृत प्रक्रिया'। एक गैर-नकारात्मक और बढ़ती हुई प्रक्रिया X स्थानीय रूप से एकीकृत है यदि रुकने के समय का क्रम मौजूद है τ_n अनंत तक बढ़ रहा है, जैसे कि

$\operatorname {E} \left[\mathbf {1} _{\{\tau _{n}>0\}}X^{\tau _{n}}\right]<\infty$ प्रत्येक n के लिए.

रुकने के समय के प्रकार

समय सूचकांक सेट I = [0,∞) के साथ रुकने के समय को अक्सर कई प्रकारों में से एक में विभाजित किया जाता है, जो इस बात पर निर्भर करता है कि क्या भविष्यवाणी करना संभव है कि वे कब घटित होने वाले हैं।

रुकने का समय τ 'अनुमानित' है यदि यह रुकने के समय के बढ़ते क्रम की सीमा के बराबर है τ_n संतोषजनक τ_n < τ जब भी τ > 0. अनुक्रम τ_n कहा जाता है कि τ की घोषणा की जाती है, और पूर्वानुमानित रुकने के समय को कभी-कभी घोषणा योग्य के रूप में जाना जाता है। पूर्वानुमानित रुकने के समय के उदाहरण निरंतर और अनुकूलित प्रक्रिया प्रक्रियाओं के हिटिंग समय हैं। यदि τ पहली बार है जब एक सतत और वास्तविक मूल्य वाली प्रक्रिया X कुछ मान a के बराबर है, तो इसे अनुक्रम τ द्वारा घोषित किया जाता है_n, कहां τ_n यह पहली बार है जब X, a के 1/n की दूरी के भीतर है।

'सुलभ' रुकने के समय वे हैं जिन्हें पूर्वानुमानित समय के अनुक्रम द्वारा कवर किया जा सकता है। अर्थात्, रुकने का समय τ सुलभ है यदि, P(τ = τ_n कुछ n के लिए) = 1, जहां τ_n पूर्वानुमानित समय हैं.

रुकने का समय τ 'पूरी तरह से दुर्गम' है यदि इसे रुकने के समय के बढ़ते क्रम द्वारा कभी भी घोषित नहीं किया जा सकता है। समान रूप से, प्रत्येक पूर्वानुमानित समय σ के लिए P(τ = σ < ∞) = 0। पूरी तरह से दुर्गम रुकने के समय के उदाहरणों में पॉइसन प्रक्रियाओं का जंप समय शामिल है।

प्रत्येक रुकने के समय को विशिष्ट रूप से सुलभ और पूरी तरह से दुर्गम समय में विघटित किया जा सकता है। अर्थात्, एक अद्वितीय सुलभ रुकने का समय σ और पूरी तरह से दुर्गम समय υ मौजूद है जैसे कि τ = σ जब भी σ < ∞, τ = υ जब भी υ < ∞, और τ = ∞ जब भी σ = υ = ∞। ध्यान दें कि इस अपघटन परिणाम के विवरण में, रुकने का समय लगभग निश्चित रूप से सीमित नहीं होना चाहिए, और ∞ के बराबर हो सकता है।

नैदानिक ​​​​परीक्षणों में रोक के नियम

चिकित्सा में नैदानिक ​​​​परीक्षण अक्सर यह निर्धारित करने के लिए अंतरिम विश्लेषण करते हैं कि क्या परीक्षण पहले ही अपने अंतिम बिंदुओं को पूरा कर चुका है। हालाँकि, अंतरिम विश्लेषण गलत-सकारात्मक परिणामों का जोखिम पैदा करता है, और इसलिए अंतरिम विश्लेषण की संख्या और समय निर्धारित करने के लिए सीमाओं को रोकने का उपयोग किया जाता है (जिसे अल्फा-खर्च के रूप में भी जाना जाता है, झूठी सकारात्मकता की दर को दर्शाने के लिए)। प्रत्येक आर अंतरिम परीक्षण में, यदि संभावना सीमा पी से कम है, तो परीक्षण रोक दिया जाता है, जो उपयोग की गई विधि पर निर्भर करता है। अनुक्रमिक विश्लेषण देखें.

यह भी देखें

• इष्टतम रोक
• ऑड्स एल्गोरिथम
• सचिव समस्या
• हिटिंग टाइम
• रुकी हुई प्रक्रिया
• अव्यवस्था की समस्या
• हिटिंग टाइम#डेबट प्रमेय|डेबट प्रमेय
• अनुक्रमिक विश्लेषण

अग्रिम पठन

• Thomas S. Ferguson, “Who solved the secretary problem?”, Stat. Sci. vol. 4, 282–296, (1989).
• An introduction to stopping times.
• F. Thomas Bruss, “Sum the odds to one and stop”, Annals of Probability, Vol. 4, 1384–1391,(2000)
• Chung, Kai Lai (1982). Lectures from Markov processes to Brownian motion. Grundlehren der Mathematischen Wissenschaften No. 249. New York, NY: Springer-Verlag. ISBN 978-0-387-90618-8.
• H. Vincent Poor and Olympia Hadjiliadis (2008). Quickest Detection (First ed.). Cambridge, England: Cambridge University Press. ISBN 978-0-521-62104-5.
• Protter, Philip E. (2005). Stochastic integration and differential equations. Stochastic Modelling and Applied Probability No. 21 (2nd edition (version 2.1, corrected 3rd printing) ed.). Berlin: Springer-Verlag. ISBN 978-3-540-00313-7.
• Shiryaev, Albert N. (2007). Optimal Stopping Rules. Springer. ISBN 978-3-540-74010-0.