त्वाचिक प्रभाव

अनुप्रस्थ काट में दिखाए गए बेलनाकार सुचालक में धारा प्रवाह का वितरण। प्रत्यावर्ती धारा के लिए, धारा घनत्व सतह से अंदर की ओर तीव्रता से घटता है। त्वचा की गहराई, δ, को उस गहराई के रूप में परिभाषित किया जाता है जहां धारा घनत्व सतह पर मान का सिर्फ 1/e (लगभग 37%) है, यह धारा की आवृत्ति और सुचालक के विद्युत और चुंबकीय गुणों पर निर्भर करता है।

अनुगम कुकर त्वचा के प्रभाव के कारण कॉइल के ताप को कम करने के लिए फंसे हुए कॉइल (लिट्ज तार ) का उपयोग करते हैं। प्रवेश कुकर में उपयोग की जाने वाली एसी आवृत्ति मानक मेन आवृत्ति से बहुत अधिक होती है - सामान्यतः पर लगभग 25-50 किलोहर्ट्ज़।

त्वचा प्रभाव प्रत्यावर्ती धारा (AC) की सुचालक (सामग्री) के भीतर वितरित होने की प्रवृत्ति है, जैसे कि धारा घनत्व सुचालक की सतह के पास सबसे बड़ा है और सुचालक में अधिक गहराई के साथ तीव्रता से घटता है। विद्युत धारा मुख्य रूप से सुचालक की त्वचा पर बाहरी सतह और त्वचा की गहराई के बीच प्रवाह होती है। त्वचा की गहराई प्रत्यावर्ती धारा की आवृत्ति पर निर्भर करती है, जैसे-जैसे आवृत्ति बढ़ती है, धारा का प्रवाह सतह की ओर बढ़ता है, जिसके परिणामस्वरूप त्वचा की गहराई कम होती है। त्वचा का प्रभाव सुचालक के प्रभावी अनुप्रस्थ काट को कम करता है और इस प्रकार इसके प्रभावी विद्युत प्रतिरोध को बढ़ाता है। प्रत्यावर्ती धारा के परिणामस्वरूप बदलते चुंबकीय क्षेत्र से प्रेरित भंवर धारा का विरोध करने के कारण त्वचा का प्रभाव होता है। तांबे में 60 हेटर्स पर, त्वचा की गहराई लगभग 8.5 मिमी होती है। उच्च आवृत्तियों पर त्वचा की गहराई बहुत कम हो जाती है।

विशेष रूप से बुने हुए लिट्ज़ तार का उपयोग करके त्वचा के प्रभाव के कारण बढ़े हुए एसी प्रतिरोध को कम किया जा सकता है। क्योंकि बड़े सुचालक के आंतरिक भाग में इतना कम धारा होता है, भार और मूल्य बचाने के लिए पाइप जैसे नलीदार सुचालक का उपयोग किया जा सकता है। रेडियो -आवृत्ति और माइक्रो तंरग परिपथ, संचरण रेखा (या वेवगाइड), और एंटेना के विश्लेषण और रचना में त्वचा के प्रभाव का व्यावहारिक परिणाम होता है। यह एसी विद्युत शक्ति संचरण प्रणाली में मुख्य आवृत्तियों (50–60 Hz) पर भी महत्वपूर्ण है। यह लंबी दूरी के विद्युत संचरण के लिए उच्च-वोल्टेज प्रत्यक्ष धारा को प्राथमिकता देने के कारणों में से है।

गोलाकार सुचालक के स्थितियों में प्रभाव को पहली बार 1883 में होरेस लैम्ब द्वारा पेपर में वर्णित किया गया था,^[1] और 1885 में ओलिवर हीविसाइड द्वारा किसी भी आकार के सुचालकों के लिए सामान्यीकृत किया गया था।

कारण

त्वचा प्रभाव का कारण। सुचालक के माध्यम से प्रवाहित धारा I चुंबकीय क्षेत्र H को प्रेरित करती है। यदि धारा बढ़ता है, जैसा कि इस आंकड़े में है, तो H में परिणामी वृद्धि परिसंचारी भंवर धारा को प्रेरित करती है I _W जो केंद्र में धारा प्रवाह को आंशिक रूप से रद्द करते हैं और इसे त्वचा के पास ठोस करते हैं।

सुचालक, सामान्यतः तारों के रूप में, उस सुचालक के माध्यम से प्रवाहित वैकल्पिक धारा का उपयोग करके विद्युत ऊर्जा या संकेतों को प्रसारित करने के लिए उपयोग किया जा सकता है। विद्युत ऊर्जा के स्रोत के कारण धारा, सामान्यतः इलेक्ट्रॉन को बनाने वाले आवेश वाहक विद्युत क्षेत्र द्वारा संचालित होते हैं। धारा सुचालक में और उसके आसपास चुंबकीय क्षेत्र उत्पन्न करता है। जब किसी चालक में धारा की तीव्रता बदलती है तो चुंबकीय क्षेत्र भी बदलता है। चुंबकीय क्षेत्र में परिवर्तन, बदले में, विद्युत क्षेत्र बनाता है जो धारा तीव्रता में परिवर्तन का विरोध करता है। इस विरोधी विद्युत क्षेत्र को "काउंटर-इलेक्ट्रोमोटिव बल " (बैक ईएमएफ) कहा जाता है। पिछला EMF सुचालक के केंद्र में सबसे ठोस होता है, और चालक इलेक्ट्रॉनों को सुचालक के बाहर की ओर उत्तेजित करना है, जैसा कि दाईं ओर आरेख में दिखाया गया है।^[2]^[3]

चालन बल के अतिरिक्त, सुचालक की सतह पर धारा घनत्व सबसे बड़ा पाया जाता है, सुचालक में कम परिमाण के साथ। धारा घनत्व में गिरावट को त्वचा प्रभाव के रूप में जाना जाता है और त्वचा की गहराई उस गहराई का माप है जिस पर धारा घनत्व E (गणितीय स्थिरांक) पर गिरता है। सतह के पास इसके मूल्य का 1/e। 98% से अधिक धारा सतह से त्वचा की गहराई से 4 गुना सतह के भीतर प्रवाहित होगी। यह व्यवहार दिष्टधारा से भिन्न है जो सामान्यतः तार के अनुप्रस्थ काट पर समान रूप से वितरित किया जाएगा।

विद्युत चुम्बकीय प्रेरण के नियम के अनुसार वैकल्पिक चुंबकीय क्षेत्र के कारण सुचालक में प्रत्यावर्ती धारा भी प्रेरित हो सकती है। सुचालक पर विद्युत चुम्बकीय तरंग इसलिए सामान्यतः इस प्रकार के धारा का उत्पादन करती है, यह धातुओं से विद्युत चुम्बकीय तरंगों के प्रतिबिंब की व्याख्या करता है। यद्यपि शब्द त्वचा प्रभाव अधिकांशतः विद्युत धाराओं के संचरण से जुड़े अनुप्रयोगों से जुड़ा होता है, त्वचा की गहराई भी विद्युतऔर चुंबकीय क्षेत्रों के घातीय क्षय के साथ-साथ प्रेरित धाराओं की घनत्व का वर्णन करती है, जब विमान लहर टकराती है सामान्य घटना पर उस पर।

सूत्र

धारा घनत्व $J$ सतह पर इसके मूल्य से सुचालक घातीय क्षय में $J$ _S गहराई के अनुसार $d$ सतह से, इस प्रकार:^[4]^[5]

\delta ={\sqrt {{\frac {\,2\rho \,}{\omega \mu }}\;}}\;{\sqrt {\,{\sqrt {1+\left({\rho \omega \varepsilon }\right)^{2}\;}}+\rho \omega \varepsilon \;}}~

जहाँ पे,

\rho

= चालक की प्रतिरोधकता

\omega

= धारा की कोणीय आवृत्ति =

2\pi f~,

जहाँ पे

f

आवृत्ति है।

\mu

= सुचालक की पारगम्यता (विद्युत चुंबकत्व) ,

\mu _{r}\,\mu _{0}

\mu _{r}

= सुचालक की सापेक्ष चुंबकीय पारगम्यता

\mu _{0}

= मुक्त स्थान की पारगम्यता

\varepsilon

= सुचालक की पारगम्यता,

\varepsilon _{r}\,\varepsilon _{0}

\varepsilon _{r}

= सुचालक की सापेक्ष पारगम्यता

\varepsilon _{0}

= मुक्त स्थान की पारगम्यता

बहुत कम आवृत्तियों पर $1/(\rho \epsilon )$ बड़े कण के अंदर की मात्रा के निकट है और सूत्र सामान्यतः इस प्रकार दिया जाता है:

\delta ={\sqrt {{\frac {\,2\rho \,}{\omega \mu }}\,}}~.

यह सूत्र ठोस परमाणु या आणविक अनुनादों (जहां $\epsilon$ बड़ा काल्पनिक भाग होगा) और आवृत्तियों पर जो सामग्री की प्लाज्मा आवृत्ति (सामग्री में मुक्त इलेक्ट्रॉनों के घनत्व पर निर्भर) और चालन इलेक्ट्रॉनों को संयोजित करने वाले टकरावों के बीच औसत समय के पारस्परिक दोनों से बहुत नीचे हैं। धातुओं जैसे अच्छे सुचालकों में उन सभी स्थितियों को कम से कम माइक्रो तंरग आवृत्तियों तक सुनिश्चित किया जाता है, जो इस सूत्र की वैधता को सही ठहराते हैं।^{[note 1]} जैसे उदाहरण के लिए, तांबे के स्थितियों में, यह बहुत कम आवृत्तियों के लिए सही होगा 10¹⁸हर्ट्ज।

चूँकि, बहुत खराब सुचालकों में, पर्याप्त उच्च आवृत्तियों पर,बड़े कण के अनुसार कारक बढ़ जाता है। की तुलना में बहुत अधिक आवृत्तियों पर $1/(\rho \epsilon )$ यह दिखाया जा सकता है कि त्वचा की गहराई, घटने के अतिरिक्त, वास्तविक मूल्य तक पहुँचती है:

\delta \approx {2\rho }{\sqrt {{\frac {\,\varepsilon \,}{\mu }}\,}}~.

सामान्य सूत्र से यह विचलन मात्र कम चालकता की सामग्री के लिए और आवृत्तियों पर लागू होता है जहां वैक्यूम तरंग दैर्ध्य त्वचा की गहराई से बहुत बड़ा नहीं होता है। जैसे उदाहरण के लिए, बल्क सिलिकॉन (पूर्ववत) खराब सुचालक है और इसकी त्वचा की गहराई 100 kHz पर लगभग 40 मीटर है ( $λ$ = 3 किमी)। चूँकि, मेगाहर्ट्ज़ रेंज में आवृत्ति अच्छी प्रकार से बढ़ जाती है, इसकी त्वचा की गहराई कभी भी 11 मीटर के वास्तविक मान से कम नहीं होती है। निष्कर्ष यह है कि खराब ठोस चालकों में, जैसे पूर्ववत सिलिकॉन में, अधिकांश व्यावहारिक स्थितियों में त्वचा के प्रभाव को ध्यान में रखने की आवश्यकता नहीं होती है: किसी भी धारा को सामग्री के अनुप्रस्थ काट में समान रूप से वितरित किया जाता है, यदि इसकी आवृत्ति कुछ भी हो।

गोल सुचालक में धारा घनत्व

जब तार की त्रिज्या के संबंध में त्वचा की गहराई कम नहीं होती है, तो बेसेल कार्यों के संदर्भ में धारा घनत्व का वर्णन किया जा सकता है। अक्ष से दूरी के कार्य के रूप में अन्य क्षेत्रों के प्रभाव से दूर गोल तार के अंदर धारा घनत्व द्वारा दिया गया है:^[6] अनुगम का यह छोटा घटक के मूल्य तक पहुंचता है ${\frac {\mu }{8\pi }}$ (50 nH/m गैर-चुंबकीय तार के लिए) कम आवृत्तियों पर, यदि तार की त्रिज्या कुछ भी हो। बढ़ती आवृत्ति के साथ इसकी कमी, जैसा कि तार की त्रिज्या के लिए त्वचा की गहराई का अनुपात लगभग 1 से नीचे आता है, साथ के ग्राफ में प्लॉट किया जाता है, और टेलीफोन केबल की विशेषताओं में बढ़ती आवृत्ति के साथ टेलीफोन केबल अनुगम में कमी के लिए अधीन है।

एक गोल तार के अनुगम का आंतरिक घटक विरूद्ध त्वचा की गहराई से त्रिज्या का अनुपात। स्वयं प्रवेश का वह घटक μ / 8π से कम हो जाता है क्योंकि त्वचा की गहराई छोटी हो जाती है (जैसे-जैसे आवृत्ति बढ़ती है)।

एक गोल तार के डीसी प्रतिरोध के अनुपात एसी प्रतिरोध विरूद्ध त्वचा की गहराई के तार के त्रिज्या के अनुपात की तुलना में। चूंकि त्वचा की गहराई त्रिज्या के सापेक्ष छोटी हो जाती है, एसी से डीसी प्रतिरोध का अनुपात त्वचा की गहराई के त्रिज्या के अनुपात के आधे हिस्से तक पहुंच जाता है।

प्रतिरोध

एकल तार की प्रतिबाधा पर त्वचा के प्रभाव का सबसे महत्वपूर्ण प्रभाव, चूँकि, तार के प्रतिरोध में वृद्धि और परिणामस्वरूप तांबे की हानि है। बड़े सुचालक की सतह के पास सीमित धारा के कारण प्रभावी प्रतिरोध को हल किया जा सकता है जैसे कि धारा मोटाई की सतह के माध्यम से समान रूप से प्रवाहित होती है $δ$ उस सामग्री की डीसी प्रतिरोधकता के आधार पर प्रभावी अनुप्रस्थ काट क्षेत्र लगभग बराबर है $δ$ सुचालक की परिधि का गुना। इस प्रकार लंबा बेलनाकार सुचालक जैसे तार, जिसका व्यास होता है $D$ की तुलना में बड़ा $δ$ , दीवार की मोटाई के साथ लगभग खोखले नली का प्रतिरोध होता है $δ$ प्रत्यक्ष धारा ले जाना। लंबाई के तार का एसी प्रतिरोध $ℓ$ और प्रतिरोधकता $\rho$ है:

R\approx {{\ell \rho } \over {\pi (D-\delta )\delta }}\approx {{\ell \rho } \over {\pi D\delta }}

उपरोक्त अंतिम सन्निकटन मानता है $D\gg \delta$ .

व्यास के लिए सुविधाजनक सूत्र (फ्रेडरिक टरमन|एफ.ई. टरमन को अधीन ठहराया गया)। $D$ _W वृत्ताकार अनुप्रस्थ काट के तार का जिसका प्रतिरोध आवृत्ति पर 10% बढ़ जाएगा $f$ है:^[7]

D_{\mathrm {W} }={\frac {200~\mathrm {mm} }{\sqrt {f/\mathrm {Hz} }}}

एसी प्रतिरोध में वृद्धि के लिए यह सूत्र मात्र पृथक तार के लिए ठीक है। आस-पास के तारों के लिए, जैसे विद्युत केबल या कॉइल में, एसी प्रतिरोध निकटता प्रभाव (विद्युत चुंबकत्व) से भी प्रभावित होता है, जिससे एसी प्रतिरोध में अतिरिक्त वृद्धि हो सकती है।

त्वचा की गहराई पर भौतिक प्रभाव

एक अच्छे सुचालक में, त्वचा की गहराई प्रतिरोधकता के वर्गमूल के समानुपाती होती है। इसका अर्थ यह है कि उच्चतम संवाहकों की त्वचा की गहराई कम होती है। कम त्वचा की गहराई के साथ भी उच्चतम सुचालक का समग्र प्रतिरोध कम रहता है। चूँकि, उच्च प्रतिरोधकता वाले सुचालक की तुलना में उच्चतम सुचालक अपने एसी और डीसी प्रतिरोध के बीच उच्च अनुपात दिखाएगा। जैसे उदाहरण के लिए, 60 हर्ट्ज पर, अमेरिकी वायर गेज़ (1000 वर्ग मिलीमीटर) तांबे के सुचालक में डीसी की तुलना में 23% अधिक प्रतिरोध होता है। एल्युमीनियम में समान आकार के सुचालक का 60 हर्ट्ज एसी के साथ डीसी की तुलना में मात्र 10% अधिक प्रतिरोध होता है।^[8] सुचालक की पारगम्यता (विद्युत चुंबकत्व) के व्युत्क्रम वर्गमूल के रूप में त्वचा की गहराई भी भिन्न होती है। लोहे के स्थितियों में इसकी चालकता तांबे की तुलना में लगभग 1/7 है। चूँकि लौह-चुंबकीय होने के कारण इसकी पारगम्यता लगभग 10,000 गुना अधिक है। यह लोहे के लिए त्वचा की गहराई को तांबे के लगभग 1/38, 60 Hz पर लगभग 220 माइक्रोमीटर तक कम कर देता है। लोहे के तार इस प्रकार एसी पावर लाइनों के लिए व्यर्थ हैं (एल्यूमीनियम जैसे गैर चुंबकीय सुचालक के लिए कोर के रूप में कार्य करके यांत्रिक शक्ति को जोड़ने के अतिरिक्त)। त्वचा के प्रभाव से विद्युतट्रांसफार्मर में फाड़ना की प्रभावी मोटाई भी कम हो जाती है, जिससे उनका हानि बढ़ जाता है।

लोहे की छड़ें प्रत्यक्ष-धारा (डीसी) वेल्डिंग के लिए अच्छी प्रकार से काम करती हैं किन्तु 60 हर्ट्ज से बहुत अधिक आवृत्तियों पर उनका उपयोग करना असंभव है। कुछ किलोहर्ट्ज़ पर, वेल्डिंग रॉड लाल गर्म चमकेगी क्योंकि चाप वेल्डिंग के लिए अपेक्षाकृत कम शक्ति शेष होने के साथ ही त्वचा के प्रभाव से उत्पन्न बहुत अधिक एसी प्रतिरोध के माध्यम से धारा प्रवाहित होता है। उच्च-आवृत्ति वेल्डिंग के लिए मात्र गैर-चुंबकीय छड़ का उपयोग किया जा सकता है।

1 मेगाहर्ट्ज़ पर गीली मिट्टी में त्वचा के प्रभाव की गहराई लगभग 5.0 मीटर होती है, समुद्री जल में यह लगभग 0.25 मीटर है।^[9]

शमन

एक प्रकार की केबल जिसे लिट्ज़ वायर कहा जाता है ( जर्मन भाषा लिट्जेंड्रहट, ब्रेडेड वायर से) कुछ किलोहर्ट्ज़ से लगभग मेगाहर्ट्ज़ की आवृत्तियों के लिए त्वचा के प्रभाव को कम करने के लिए उपयोग किया जाता है। इसमें सावधानी से डिज़ाइन किए गए पैटर्न में साथ बुने हुए कई इंसुलेटेड तार होते हैं, जिससे कि समग्र चुंबकीय क्षेत्र सभी तारों पर समान रूप से कार्य करे और कुल धारा को उनके बीच समान रूप से वितरित करने का कारण बने। त्वचा के प्रभाव से प्रत्येक पतली किस्में पर थोड़ा प्रभाव पड़ता है, बंडल को एसी प्रतिरोध में समान वृद्धि का सामना नहीं करना पड़ता है, जो कि समान क्रॉस-आंशिक क्षेत्र के ठोस सुचालक त्वचा के प्रभाव के कारण होता है।^[10] त्वचा के प्रभाव और निकटता प्रभाव (विद्युत चुंबकत्व) दोनों को कम करके उनकी दक्षता बढ़ाने के लिए लिट्ज तार का उपयोग अधिकांशतः उच्च-आवृत्ति वाले ट्रांसफार्मर की समापन में किया जाता है। बड़े विद्युतट्रांसफार्मर लिट्ज़ तार के समान निर्माण के फंसे हुए सुचालकों के साथ घाव कर रहे हैं, किन्तु मुख्य आवृत्तियों पर बड़ी त्वचा की गहराई के अनुरूप बड़े अनुप्रस्थ काट को नियोजित करते हैं।Cite error: Closing </ref> missing for <ref> tag

जैसे उदाहरण

फेराइट]

Al – धात्विक [एल्युमिनियम]

Cu – धात्विक [तांबा]

स्टील 410 - चुंबकीय [स्टेनलेस स्टील]

Fe-Si –[अनाज-उन्मुख विद्युत स्टील]

Fe-Ni – उच्च-पारगम्यता [पर्मलॉय](80%Ni-20%Fe)

हम निम्नानुसार त्वचा की गहराई के लिए व्यावहारिक सूत्र प्राप्त कर सकते हैं:

\delta ={\frac {1}{\alpha }}={\sqrt {{2\rho } \over {(2\pi f)(\mu _{0}\mu _{r})}}}=

={\frac {1}{\sqrt {\pi f\mu \sigma }}}\approx 503\,{\sqrt {\frac {\rho }{\mu _{r}f}}}\approx 503\,{\frac {1}{\sqrt {\mu _{r}f\sigma }}},

जहाँ पे

\delta =

मीटर में त्वचा की गहराई

\alpha =

में क्षीणन

{\frac {Np}{m}}

\mu _{0}=

मुक्त स्थान की पारगम्यता

\mu _{r}=

माध्यम की पारगम्यता (विद्युत चुंबकत्व) (तांबे के लिए,

\mu _{r}

= 1.00)

\mu =

माध्यम की पारगम्यता

\rho =

Ω·m में माध्यम की प्रतिरोधकता, इसकी चालकता के व्युत्क्रम के बराबर भी:

\rho ={\frac {1}{\sigma }}

(तांबे के लिए, ρ = 1.68×10⁻⁸ Ω·m)

\sigma =

माध्यम की चालकता (तांबे के लिए,

\sigma \approx

58.5×10⁶ S/m)

f=

हर्ट्ज में धारा की आवृत्ति

सोना प्रतिरोधकता के साथ अच्छा सुचालक है 2.44×10⁻⁸ Ω·m और अनिवार्य रूप से गैर चुंबकीय है: $\mu _{r}=$ 1, इसलिए इसकी त्वचा की गहराई 50 हर्ट्ज की आवृत्ति पर दी गई है

\delta =503\,{\sqrt {\frac {2.44\cdot 10^{-8}}{1\cdot 50}}}=11.1\,\mathrm {mm}

इसके विपरीत, सीसा, प्रतिरोधकता के साथ अपेक्षाकृत खराब सुचालक (धातुओं के बीच) है 2.2×10⁻⁷ Ω·m, सोने से लगभग 9 गुना। 50 हर्ट्ज पर इसकी त्वचा की गहराई भी लगभग 33 मिमी या ${\sqrt {9}}=3$ सोने से गुना पाई जाती है

अत्यधिक चुंबकीय सामग्री में उनकी बड़ी पारगम्यता के कारण त्वचा की गहराई कम होती है $\mu _{r}$ जैसा कि लोहे के स्थितियों में ऊपर बताया गया था, इसकी खराब चालकता के अतिरिक्त। प्रवेश कुकर के उपयोगकर्ताओं द्वारा व्यावहारिक परिणाम देखा जाता है, जहां कुछ प्रकार के स्टेनलेस स्टील कुकवेयर अनुपयोगी होते हैं क्योंकि वे लोह चुम्बकिक नहीं होते हैं।

बहुत उच्च आवृत्तियों पर अच्छे संवाहकों के लिए त्वचा की गहराई छोटी हो जाती है। जैसे उदाहरण के लिए, 10 GHz (माइक्रो तंरग क्षेत्र) की आवृत्ति पर कुछ सामान्य धातुओं की त्वचा की गहराई माइक्रोमीटर से कम होती है:

माइक्रो तंरग आवृत्तियों पर त्वचा की गहराई
सुचालक	त्वचा की गहराई (μm)
अल्युमीनियम	0.820
ताँबा	0.652
सोना	0.753
चाँदी	0.634

इस प्रकार माइक्रो तंरग आवृत्तियों पर, अधिकांश धारा सतह के निकट अत्यंत पतले क्षेत्र में प्रवाहित होती है। इसलिए माइक्रो तंरग आवृत्तियों पर वेवगाइड्स का ओमिक हानि मात्र सामग्री की सतह परत पर निर्भर करता है। कांच के टुकड़े पर 3μm मोटी वाष्पित चांदी की सतह इस प्रकार ऐसी आवृत्तियों पर उत्कृष्ट चालक होती है।

तांबे में, त्वचा की गहराई को आवृत्ति के वर्गमूल के अनुसार गिरते हुए देखा जा सकता है:

तांबे में त्वचा की गहराई
आवृत्ति	त्वचा की गहराई (μm)
50 Hz	9220
60 Hz	8420
10 kHz	652
100 kHz	206
1 MHz	65.2
10 MHz	20.6
100 MHz	6.52
1 GHz	2.06

इंजीनियरिंग इलेक्ट्रोमैग्नेटिक्स में, हेट बताते है कि पावर स्टेशन में 60 Hz पर प्रत्यावर्ती धारा के लिए इंच (8 मिमी) के तिहाई से बड़े त्रिज्या के साथ बस बार तांबे की बर्बादी है, और व्यवहार में भारी एसी धारा के लिए संभवतः ही कभी आधे इंच से अधिक होते हैं (12 मिमी) यांत्रिक कारणों को छोड़कर।

एक सुचालक के आंतरिक अनुगम की त्वचा प्रभाव में कमी

एक समाक्षीय केबल के आंतरिक और बाहरी सुचालकों को दिखाते हुए नीचे दिए गए आरेख का संदर्भ लें। चूंकि त्वचा प्रभाव मुख्य रूप से सुचालक की सतह पर प्रवाहित होने वाली उच्च आवृत्तियों पर धारा का कारण बनता है, यह देखा जा सकता है कि यह तार के अंदर चुंबकीय क्षेत्र को कम कर देगा, अर्थात उस गहराई के नीचे जिस पर धारा प्रवाहित होती है। यह दिखाया जा सकता है कि तार के स्वयं- अनुगम पर इसका साधारण प्रभाव पड़ेगा, इस घटना के गणितीय उपचार के लिए।

इस संदर्भ में माना जाने वाला प्रवेश नंगे सुचालक को संदर्भित करता है, न कि सर्किट तत्व के रूप में उपयोग किए जाने वाले कॉइल का प्रवेश। कॉइल के घुमावों के बीच पारस्परिक अनुगम द्वारा कॉइल का अनुगम प्रभावी होता है जो घुमावों की संख्या के वर्ग के अनुसार इसकी अनुगम बढ़ाता है। चूँकि, जब मात्र तार संयोजित होता है, तो तार के बाहर चुंबकीय क्षेत्र से जुड़े बाहरी अनुगम के अतिरिक्त (तार में कुल धारा के कारण) जैसा कि नीचे की आकृति के सफेद क्षेत्र में देखा जाता है, वहाँ भी बहुत कुछ है तार के अंदर चुंबकीय क्षेत्र के हिस्से के कारण आंतरिक अनुगम का छोटा घटक, आकृति बी में हरा क्षेत्र। प्रेरकत्व का वह छोटा घटक कम हो जाता है जब धारा सुचालक की त्वचा की ओर केंद्रित होता है, अर्थात, जब त्वचा की गहराई तार की त्रिज्या से बहुत बड़ी नहीं है, जैसा कि उच्च आवृत्तियों पर होगा।

एक तार के लिए, यह कमी घटती महत्व हो जाती है क्योंकि तार अपने व्यास की तुलना में लंबा हो जाता है, और सामान्यतः पर उपेक्षित होता है। चूँकि संचरण लाइन के स्थितियों में दूसरे सुचालक की उपस्थिति तार की लंबाई की परवाह किए बिना बाहरी चुंबकीय क्षेत्र (और कुल स्व- अनुगम) की सीमा को कम कर देती है, जिससे कि त्वचा के प्रभाव के कारण अनुगम में कमी अभी भी हो सकती है महत्वपूर्ण। जैसे उदाहरण के लिए, टेलीफोन मुड़ जोड़ी के स्थितियों में, सुचालकों का अनुगम उच्च आवृत्तियों पर अधिक कम हो जाता है जहां त्वचा का प्रभाव महत्वपूर्ण हो जाता है। दूसरी ओर, जब कॉइल की ज्यामिति (घुमावों के बीच पारस्परिक अनुगम के कारण) के कारण प्रवेश के बाहरी घटक को बढ़ाया जाता है, तो आंतरिक प्रवेश घटक का महत्व और भी बौना हो जाता है और इसे नजरअंदाज कर दिया जाता है।

एक समाक्षीय केबल में प्रति लंबाई अनुगम

आयाम ए, बी, और सी को आंतरिक सुचालक त्रिज्या, त्रिज्या के अंदर ढाल (बाहरी सुचालक) और क्रमशः ढाल बाहरी त्रिज्या होने दें, जैसा कि नीचे आकृति ए के अनुप्रस्थ काट में देखा गया है।

अनुगम पर प्रभाव दिखाते हुए कॉक्स में त्वचा के प्रभाव के चार चरण। चित्र समाक्षीय केबल का अनुप्रस्थ काट दिखाते हैं। रंग कोड: काला = समग्र इन्सुलेट म्यान, तन = सुचालक, सफेद = ढांकता हुआ, हरा = आरेख में धारा, नीला = आरेख से बाहर आने वाला, तीर के साथ धराशायी काली रेखाएं = चुंबकीय प्रवाह (बी)। धराशायी काली रेखाओं की चौड़ाई का उद्देश्य उस त्रिज्या पर परिधि पर ीकृत चुंबकीय क्षेत्र की सापेक्ष शक्ति को दर्शाना है। चार चरण, ए, बी, सी और डी हैं: क्रमशः गैर-ऊर्जावान, कम आवृत्ति, मध्य आवृत्ति और उच्च आवृत्ति। ऐसे तीन क्षेत्र हैं जिनमें प्रेरित चुंबकीय क्षेत्र हो सकते हैं: केंद्र सुचालक, ढांकता हुआ और बाहरी सुचालक। चरण बी में, धारा सुचालकों को समान रूप से कवर करता है और तीनों क्षेत्रों में महत्वपूर्ण चुंबकीय क्षेत्र होता है। जैसे-जैसे आवृत्ति बढ़ती है और त्वचा का प्रभाव पकड़ में आता है (सी और डी) ढांकता हुआ क्षेत्र में चुंबकीय क्षेत्र अपरिवर्तित होता है क्योंकि यह केंद्र सुचालक में प्रवाहित कुल धारा के समानुपाती होता है। सी में, चूँकि, आंतरिक सुचालक के गहरे भाग और ढाल (बाहरी सुचालक) के बाहरी भाग में कम चुंबकीय क्षेत्र होता है। इस प्रकार चुंबकीय क्षेत्र में कम ऊर्जा संग्रहित होती है, जो समान कुल धारा को दी जाती है, जो घटे हुए अनुगम के अनुरूप होती है। उच्च आवृत्ति पर भी , डी, त्वचा की गहराई छोटी है सभी धारा सुचालक की सतह तक ही सीमित हैं। सुचालकों के बीच के क्षेत्रों में मात्र चुंबकीय क्षेत्र है मात्र बाहरी अनुगम रहता है।

किसी दिए गए धारा के लिए, चुंबकीय क्षेत्र में संग्रहीत कुल ऊर्जा वैसी ही होनी चाहिए, जैसी गणना की गई विद्युत ऊर्जा कोक्स के अनुगम के माध्यम से बहने वाली धारा के लिए अधीन होती है, वह ऊर्जा केबल के मापे गए अनुगम के समानुपाती होती है।

एक समाक्षीय केबल के अंदर चुंबकीय क्षेत्र को तीन क्षेत्रों में विभाजित किया जा सकता है, इसलिए प्रत्येक केबल की लंबाई द्वारा देखे जाने वाले विद्युत अनुगम में योगदान देगा। अनुगम $L_{\text{cen}}\,$ त्रिज्या वाले क्षेत्र में चुंबकीय क्षेत्र से जुड़ा है $r<a\,$ केंद्र सुचालक के अंदर का क्षेत्र।

अनुगम $L_{\text{ext}}\,$ क्षेत्र में चुंबकीय क्षेत्र से जुड़ा हुआ है $a<r<b\,$ , दो सुचालकों के बीच का क्षेत्र (एक ढांकता हुआ, संभवतः वायु युक्त)।

अनुगम $L_{\text{shd}}\,$ क्षेत्र में चुंबकीय क्षेत्र से जुड़ा हुआ है $b<r<c\,$ शील्ड सुचालक के अंदर का क्षेत्र।

शुद्ध विद्युत अनुगम तीनों योगदानों के कारण होता है:

L_{\text{total}}=L_{\text{cen}}+L_{\text{shd}}+L_{\text{ext}}\,

$L_{\text{ext}}\,$ त्वचा के प्रभाव से नहीं बदला जाता है और समाक्षीय केबल की लंबाई डी प्रति अनुगम एल के लिए अधिकांशतः उद्धृत सूत्र द्वारा दिया जाता है:

L/D={\frac {\mu _{0}}{2\pi }}\ln \left({\frac {b}{a}}\right)\,

कम आवृत्तियों पर, तीनों अनुगम पूरी प्रकार से उपस्तिथ होते हैं जिससे कि $L_{\text{DC}}=L_{\text{cen}}+L_{\text{shd}}+L_{\text{ext}}\,$ .

उच्च आवृत्तियों पर, मात्र ढांकता हुआ क्षेत्र में चुंबकीय प्रवाह होता है, जिससे कि $L_{\infty }=L_{\text{ext}}\,$ .विचार

समाक्षीय संचरण लाइनों की अधिकांश विचार मानती हैं कि उनका उपयोग रेडियो आवृत्ति के लिए किया जाएगा, इसलिए समीकरणों को मात्र बाद के स्थितियों में ही आपूर्ति की जाती है।

जैसे ही त्वचा का प्रभाव बढ़ता है, धाराएं आंतरिक सुचालक के बाहर (आर = ए) और ढाल के अंदर (आर = बी) के पास केंद्रित होती हैं। चूंकि आंतरिक सुचालक में अनिवार्य रूप से कोई गहराई नहीं है, आंतरिक सुचालक की सतह के नीचे कोई चुंबकीय क्षेत्र नहीं है। चूंकि आंतरिक सुचालक में धारा बाहरी सुचालक के अंदर बहने वाली विपरीत धारा से संतुलित होता है, इसलिए बाहरी सुचालक में कोई भी चुंबकीय क्षेत्र शेष नहीं होता है जहां $b<r<c\,$ . मात्र $L_{\text{ext}}$ इन उच्च आवृत्तियों पर विद्युत अनुगम में योगदान देता है।

चूँकि ज्यामिति अलग है, टेलीफोन लाइनों में उपयोग की जाने वाली मुड़ जोड़ी समान रूप से प्रभावित होती है उच्च आवृत्तियों पर अनुगम 20% से अधिक कम हो जाता है जैसा कि निम्न तालिका में देखा जा सकता है।

आवृत्ति के समारोह के रूप में टेलीफोन केबल के लक्षण

24 गेज पीआईसी टेलीफोन केबल के लिए प्रतिनिधि पैरामीटर डेटा 21 °C (70 °F).

आवृत्ति (Hz)	R (Ω/km)	L (mH/km)	G (μS/km)	C (nF/km)
1	172.24	0.6129	0.000	51.57
1k	172.28	0.6125	0.072	51.57
10k	172.70	0.6099	0.531	51.57
100k	191.63	0.5807	3.327	51.57
1M	463.59	0.5062	29.111	51.57
2M	643.14	0.4862	53.205	51.57
5M	999.41	0.4675	118.074	51.57

रीव में अन्य गेज, तापमान और प्रकार के लिए अधिक व्यापक टेबल और टेबल उपलब्ध हैं।^[11] ^[12] उसी डेटा को पैरामिट्रीकृत रूप में देता है जिसके बारे में वह कहता है कि 50 मेगाहर्ट्ज तक प्रयोग करने योग्य है।

^[12]टेलीफोन मुड़ जोड़ी के लिए इस रूप का समीकरण देता है:

L(f)={\frac {l_{0}+l_{\infty }\left({\frac {f}{f_{m}}}\right)^{b}}{1+\left({\frac {f}{f_{m}}}\right)^{b}}}\,

विषम त्वचा प्रभाव

उच्च आवृत्तियों और कम तापमान के लिए त्वचा की गहराई के लिए सामान्य सूत्र टूट जाते हैं। इस प्रभाव को पहली बार 1940 में हेंज लंदन द्वारा देखा गया था, जिन्होंने सही ढंग से प्रस्ताव दिया था कि यह संभवतः त्वचा की गहराई की सीमा तक पहुँचने वाले इलेक्ट्रॉनों की औसत मुक्त पथ लंबाई के कारण है।^[13] धातुओं और अतिचालकता के इस विशिष्ट स्थितियों के लिए मैटिस-बारडीन सिद्धांत विकसित किया गया था।

यह भी देखें

निकटता प्रभाव (विद्युत चुंबकत्व)
प्रवेश की गहराई
भंवर धारा
लिट्ज तार
ट्रांसफार्मर
प्रवेश कुकर ,ऊष्मा जनरेशन
प्रेरण ऊष्मन
चुंबकीय रेनॉल्ड्स संख्या
व्हीलर इंक्रीमेंटल प्रवेश नियम , त्वचा प्रभाव प्रतिरोध का अनुमान लगाने की विधि।

↑ Note that the above equation for the current density inside the conductor as a function of depth applies to cases where the usual approximation for the skin depth holds. In the extreme cases where it doesn't, the exponential decrease with respect to the skin depth still applies to the magnitude of the induced currents, however the imaginary part of the exponent in that equation, and thus the phase velocity inside the material, are altered with respect to that equation.

संदर्भ

↑ Lamb, Horace (1883-01-01). "XIII. On electrical motions in a spherical conductor". Philosophical Transactions of the Royal Society of London. 174: 519–549. doi:10.1098/rstl.1883.0013. S2CID 111283238.
↑ "These emf's are greater at the center than at the circumference, so the potential difference tends to establish currents that oppose the current at the center and assist it at the circumference" Fink, Donald G.; Beaty, H. Wayne (2000). Standard Handbook for Electrical Engineers (14th ed.). McGraw-Hill. pp. 2–50. ISBN 978-0-07-022005-8.
↑ "To understand skin effect, you must first understand how eddy currents operate..." Johnson, Howard; Graham, Martin (2003). High-Speed Signal propagation Advanced Black Magic (3rd ed.). Prentice Hall. pp. 58–78. ISBN 978-0-13-084408-8.
↑ Hayt, William H. (1989), Engineering Electromagnetics (5th ed.), McGraw-Hill, ISBN 978-0070274068</रेफरी>^: 362
$J=J_{\mathrm {S} }\,e^{-{(1+j)d/\delta }}$
कहाँ पे $\delta$ त्वचा की गहराई कहा जाता है। इस प्रकार त्वचा की गहराई को कंडक्टर की सतह के नीचे की गहराई के रूप में परिभाषित किया जाता है जिस पर वर्तमान घनत्व 1/e (गणितीय स्थिरांक) (लगभग 0.37) तक गिर गया है। $J$ _S. प्रतिपादक का काल्पनिक भाग इंगित करता है कि वर्तमान घनत्व का चरण प्रवेश की प्रत्येक त्वचा की गहराई के लिए चरण विलंब 1 रेडियन है। कंडक्टर में एक पूर्ण तरंग दैर्ध्य की आवश्यकता होती है 2 $π$ त्वचा की गहराई, जिस बिंदु पर वर्तमान घनत्व ई के लिए क्षीण हो जाता है^{−2 $π$} (1.87×10⁻³, या -54.6 dB) इसके सतही मान का। कंडक्टर में तरंग दैर्ध्य निर्वात में तरंग दैर्ध्य की तुलना में बहुत कम है, या समतुल्य, कंडक्टर में तरंग # चरण वेग और समूह वेग निर्वात में प्रकाश की गति से बहुत धीमा है। उदाहरण के लिए, 1 मेगाहर्ट्ज रेडियो तरंग का निर्वात में तरंगदैर्घ्य होता है $λ$ _o लगभग 300 मीटर, जबकि तांबे में, तरंग दैर्ध्य केवल लगभग 500 मीटर/सेकेंड के चरण वेग के साथ लगभग 0.5 मिमी तक कम हो जाता है। स्नेल के नियम और कंडक्टर में इस बहुत छोटे चरण के वेग के परिणामस्वरूप, कंडक्टर में प्रवेश करने वाली कोई भी लहर, चराई की घटना पर भी, कंडक्टर की सतह के लंबवत दिशा में अनिवार्य रूप से अपवर्तित होती है। ढांकता हुआ या चुंबकीय नुकसान नहीं होने पर त्वचा की गहराई के लिए सामान्य सूत्र है:<ref name="VanderVorst41">Vander Vorst, Rosen & Kotsuka (2006)
↑ The formula as shown is algebraically equivalent to the formula found on page 130 Jordan (1968, p. 130)
↑ Weeks, Walter L. (1981), Transmission and Distribution of Electrical Energy, Harper & Row, ISBN 978-0060469825</रेफरी>^: 38

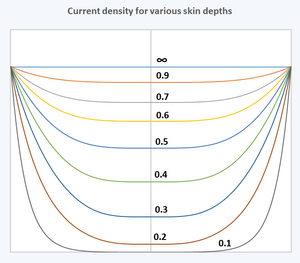विभिन्न त्वचा की गहराई के लिए गोल तार में वर्तमान घनत्व। प्रत्येक वक्र पर दिखाई गई संख्या त्वचा की गहराई से तार की त्रिज्या का अनुपात है। अनंत चिह्न के साथ दिखाया गया वक्र शून्य आवृत्ति (डीसी) का मामला है। सभी वक्रों को सामान्यीकृत किया जाता है ताकि सतह पर वर्तमान घनत्व समान हो। क्षैतिज अक्ष तार के भीतर की स्थिति है जिसमें बाएँ और दाएँ छोर तार की सतह होते हैं। ऊर्ध्वाधर अक्ष सापेक्ष वर्तमान घनत्व है।
: $\mathbf {J} _{r}={\frac {k\mathbf {I} }{2\pi R}}{\frac {J_{0}(kr)}{J_{1}(kR)}}=\mathbf {J} _{R}{\frac {J_{0}(kr)}{J_{0}(kR)}}$
कहाँ पे

$\quad \omega$ = धारा की कोणीय आवृत्ति = 2π × आवृत्ति

$\quad r=$ तार की धुरी से दूरी

$\quad R=$ तार की त्रिज्या

$\quad \mathbf {J} _{r}=$ तार की धुरी से दूरी, आर पर वर्तमान घनत्व फेजर

$\quad \mathbf {J} _{R}=$ तार की सतह पर वर्तमान घनत्व चरण

$\quad \mathbf {I} =$ कुल वर्तमान चरण

$\quad J_{0}=$ प्रथम प्रकार का बेसेल फलन, कोटि 0

$\quad J_{1}=$ प्रथम प्रकार का बेसेल फलन, क्रम 1

$\quad k={\sqrt {\frac {-j\omega \mu }{\rho }}}={\frac {1-j}{\delta }}$ कंडक्टर में तरंग संख्या

$\quad \delta ={\sqrt {\frac {2\rho }{\omega \mu }}}$ त्वचा की गहराई भी कहा जाता है।

$\quad \rho$ = चालक की प्रतिरोधकता

$\quad \mu _{r}$ = कंडक्टर की सापेक्ष चुंबकीय पारगम्यता

$\quad \mu _{0}$ = मुक्त स्थान की पारगम्यता = 4π x 10⁻⁷ एच/एम

$\quad \mu$ = $\mu _{r}$ $\mu _{0}$

तब से $k$ जटिल है, बेसेल कार्य भी जटिल हैं। वर्तमान घनत्व का आयाम और चरण गहराई के साथ बदलता रहता है।

गोल तार का प्रतिबाधा

गोल तार के एक खंड की प्रति यूनिट लंबाई आंतरिक विद्युत प्रतिबाधा द्वारा दी गई है:^: 40

$\mathbf {Z} _{int}={\frac {k\rho }{2\pi R}}{\frac {J_{0}(kR)}{J_{1}(kR)}}$ .

यह प्रतिबाधा एक जटिल संख्या मात्रा है जो तार के आंतरिक स्व-अधिष्ठापन , प्रति इकाई लंबाई के कारण विद्युत प्रतिक्रिया (काल्पनिक) के साथ श्रृंखला में एक प्रतिरोध (वास्तविक) के अनुरूप है।

अधिष्ठापन

एक तार के अधिष्ठापन के एक हिस्से को तार के भीतर ही चुंबकीय क्षेत्र के लिए जिम्मेदार ठहराया जा सकता है जिसे आंतरिक अधिष्ठापन कहा जाता है; यह उपरोक्त सूत्र द्वारा दिए गए आगमनात्मक प्रतिघात (प्रतिबाधा का काल्पनिक भाग) के लिए खाता है। ज्यादातर मामलों में यह एक तार के अधिष्ठापन का एक छोटा सा हिस्सा होता है जिसमें तार में करंट द्वारा उत्पादित तार के बाहर चुंबकीय क्षेत्र से विद्युत चुम्बकीय प्रेरण का प्रभाव शामिल होता है। उस बाहरी अधिष्ठापन के विपरीत, आंतरिक अधिष्ठापन त्वचा के प्रभाव से कम हो जाता है, यानी आवृत्तियों पर जहां कंडक्टर के आकार की तुलना में त्वचा की गहराई अब बड़ी नहीं होती है।<ref name="Hayt303">Hayt (1981, pp. 303)
↑ Terman 1943, p. ??
↑ Fink, Donald G.; Beatty, H. Wayne, eds. (1978), Standard Handbook for Electrical Engineers (11th ed.), McGraw Hill, p. Table 18–21
↑ Popovic & Popovic 1999, p. 385
↑ Xi Nan & Sullivan 2005
↑ Reeve (1995, p. 558)
↑ ^12.0 ^12.1 Chen (2004, p. 26)
↑ R. G. Chambers, The Anomalous Skin Effect, Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences, Vol. 215, No. 1123 (Dec. 22, 1952), pp. 481-497 (17 pages) https://www.jstor.org/stable/99095

Chen, Walter Y. (2004), Home Networking Basics, Prentice Hall, ISBN 978-0-13-016511-4
Hayt, William (1981), Engineering Electromagnetics (4th ed.), McGraw-Hill, ISBN 978-0-07-027395-5
Hayt, William Hart (2006), Engineering Electromagnetics (7th ed.), New York: McGraw Hill, ISBN 978-0-07-310463-8
Nahin, Paul J. Oliver Heaviside: Sage in Solitude. New York: IEEE Press, 1988. ISBN 0-87942-238-6.
Ramo, S., J. R. Whinnery, and T. Van Duzer. Fields and Waves in Communication Electronics. New York: John Wiley & Sons, Inc., 1965.
Ramo, Whinnery, Van Duzer (1994). Fields and Waves in Communications Electronics. John Wiley and Sons.{{cite book}}: CS1 maint: multiple names: authors list (link)
Reeve, Whitman D. (1995), Subscriber Loop Signaling and Transmission Handbook, IEEE Press, ISBN 978-0-7803-0440-6
Skilling, Hugh H. (1951), Electric Transmission Lines, McGraw-Hill
Terman, F. E. (1943), Radio Engineers' Handbook, New York: McGraw-Hill
Xi Nan; Sullivan, C. R. (2005), "An equivalent complex permeability model for litz-wire windings", Industry Applications Conference, 3: 2229–2235, doi:10.1109/IAS.2005.1518758, ISBN 978-0-7803-9208-3, ISSN 0197-2618, S2CID 114947614
Jordan, Edward Conrad (1968), Electromagnetic Waves and Radiating Systems, Prentice Hall, ISBN 978-0-13-249995-8
Vander Vorst, Andre; Rosen, Arye; Kotsuka, Youji (2006), RF/Microwave Interaction with Biological Tissues, John Wiley and Sons, Inc., ISBN 978-0-471-73277-8
Popovic, Zoya; Popovic, Branko (1999), Chapter 20,The Skin Effect, Introductory Electromagnetics, Prentice-Hall, ISBN 978-0-201-32678-9

बाहरी कड़ियाँ

सुचालक Bulk Resistivity & त्वचा की गहराईs

[6] Note that the above equation for the current density inside the conductor as a function of depth applies to cases where the usual approximation for the skin depth holds. In the extreme cases where it doesn't, the exponential decrease with respect to the skin depth still applies to the magnitude of the induced currents, however the imaginary part of the exponent in that equation, and thus the phase velocity inside the material, are altered with respect to that equation.

[1] Lamb, Horace (1883-01-01). "XIII. On electrical motions in a spherical conductor". Philosophical Transactions of the Royal Society of London. 174: 519–549. doi:10.1098/rstl.1883.0013. S2CID 111283238.

[Standard_Handbook_for_Electrical_Engineers_(14th_ed))_p._2-50-2] "These emf's are greater at the center than at the circumference, so the potential difference tends to establish currents that oppose the current at the center and assist it at the circumference" Fink, Donald G.; Beaty, H. Wayne (2000). Standard Handbook for Electrical Engineers (14th ed.). McGraw-Hill. pp. 2–50. ISBN 978-0-07-022005-8.

[Black_Magic-3] "To understand skin effect, you must first understand how eddy currents operate..." Johnson, Howard; Graham, Martin (2003). High-Speed Signal propagation Advanced Black Magic (3rd ed.). Prentice Hall. pp. 58–78. ISBN 978-0-13-084408-8.

[Hayt_5-4] Hayt, William H. (1989), Engineering Electromagnetics (5th ed.), McGraw-Hill, ISBN 978-0070274068</रेफरी>^: 362
$J=J_{\mathrm {S} }\,e^{-{(1+j)d/\delta }}$
कहाँ पे $\delta$ त्वचा की गहराई कहा जाता है। इस प्रकार त्वचा की गहराई को कंडक्टर की सतह के नीचे की गहराई के रूप में परिभाषित किया जाता है जिस पर वर्तमान घनत्व 1/e (गणितीय स्थिरांक) (लगभग 0.37) तक गिर गया है। $J$ _S. प्रतिपादक का काल्पनिक भाग इंगित करता है कि वर्तमान घनत्व का चरण प्रवेश की प्रत्येक त्वचा की गहराई के लिए चरण विलंब 1 रेडियन है। कंडक्टर में एक पूर्ण तरंग दैर्ध्य की आवश्यकता होती है 2 $π$ त्वचा की गहराई, जिस बिंदु पर वर्तमान घनत्व ई के लिए क्षीण हो जाता है^{−2 $π$} (1.87×10⁻³, या -54.6 dB) इसके सतही मान का। कंडक्टर में तरंग दैर्ध्य निर्वात में तरंग दैर्ध्य की तुलना में बहुत कम है, या समतुल्य, कंडक्टर में तरंग # चरण वेग और समूह वेग निर्वात में प्रकाश की गति से बहुत धीमा है। उदाहरण के लिए, 1 मेगाहर्ट्ज रेडियो तरंग का निर्वात में तरंगदैर्घ्य होता है $λ$ _o लगभग 300 मीटर, जबकि तांबे में, तरंग दैर्ध्य केवल लगभग 500 मीटर/सेकेंड के चरण वेग के साथ लगभग 0.5 मिमी तक कम हो जाता है। स्नेल के नियम और कंडक्टर में इस बहुत छोटे चरण के वेग के परिणामस्वरूप, कंडक्टर में प्रवेश करने वाली कोई भी लहर, चराई की घटना पर भी, कंडक्टर की सतह के लंबवत दिशा में अनिवार्य रूप से अपवर्तित होती है। ढांकता हुआ या चुंबकीय नुकसान नहीं होने पर त्वचा की गहराई के लिए सामान्य सूत्र है:<ref name="VanderVorst41">Vander Vorst, Rosen & Kotsuka (2006)

[Jordan-5] The formula as shown is algebraically equivalent to the formula found on page 130 Jordan (1968, p. 130)

[Walter_Weeks-7] Weeks, Walter L. (1981), Transmission and Distribution of Electrical Energy, Harper & Row, ISBN 978-0060469825</रेफरी>^: 38

विभिन्न त्वचा की गहराई के लिए गोल तार में वर्तमान घनत्व। प्रत्येक वक्र पर दिखाई गई संख्या त्वचा की गहराई से तार की त्रिज्या का अनुपात है। अनंत चिह्न के साथ दिखाया गया वक्र शून्य आवृत्ति (डीसी) का मामला है। सभी वक्रों को सामान्यीकृत किया जाता है ताकि सतह पर वर्तमान घनत्व समान हो। क्षैतिज अक्ष तार के भीतर की स्थिति है जिसमें बाएँ और दाएँ छोर तार की सतह होते हैं। ऊर्ध्वाधर अक्ष सापेक्ष वर्तमान घनत्व है।
: $\mathbf {J} _{r}={\frac {k\mathbf {I} }{2\pi R}}{\frac {J_{0}(kr)}{J_{1}(kR)}}=\mathbf {J} _{R}{\frac {J_{0}(kr)}{J_{0}(kR)}}$
कहाँ पे

$\quad \omega$ = धारा की कोणीय आवृत्ति = 2π × आवृत्ति

$\quad r=$ तार की धुरी से दूरी

$\quad R=$ तार की त्रिज्या

$\quad \mathbf {J} _{r}=$ तार की धुरी से दूरी, आर पर वर्तमान घनत्व फेजर

$\quad \mathbf {J} _{R}=$ तार की सतह पर वर्तमान घनत्व चरण

$\quad \mathbf {I} =$ कुल वर्तमान चरण

$\quad J_{0}=$ प्रथम प्रकार का बेसेल फलन, कोटि 0

$\quad J_{1}=$ प्रथम प्रकार का बेसेल फलन, क्रम 1

$\quad k={\sqrt {\frac {-j\omega \mu }{\rho }}}={\frac {1-j}{\delta }}$ कंडक्टर में तरंग संख्या

$\quad \delta ={\sqrt {\frac {2\rho }{\omega \mu }}}$ त्वचा की गहराई भी कहा जाता है।

$\quad \rho$ = चालक की प्रतिरोधकता

$\quad \mu _{r}$ = कंडक्टर की सापेक्ष चुंबकीय पारगम्यता

$\quad \mu _{0}$ = मुक्त स्थान की पारगम्यता = 4π x 10⁻⁷ एच/एम

$\quad \mu$ = $\mu _{r}$ $\mu _{0}$

तब से $k$ जटिल है, बेसेल कार्य भी जटिल हैं। वर्तमान घनत्व का आयाम और चरण गहराई के साथ बदलता रहता है।

गोल तार का प्रतिबाधा

गोल तार के एक खंड की प्रति यूनिट लंबाई आंतरिक विद्युत प्रतिबाधा द्वारा दी गई है:^: 40

$\mathbf {Z} _{int}={\frac {k\rho }{2\pi R}}{\frac {J_{0}(kR)}{J_{1}(kR)}}$ .

यह प्रतिबाधा एक जटिल संख्या मात्रा है जो तार के आंतरिक स्व-अधिष्ठापन , प्रति इकाई लंबाई के कारण विद्युत प्रतिक्रिया (काल्पनिक) के साथ श्रृंखला में एक प्रतिरोध (वास्तविक) के अनुरूप है।

अधिष्ठापन

एक तार के अधिष्ठापन के एक हिस्से को तार के भीतर ही चुंबकीय क्षेत्र के लिए जिम्मेदार ठहराया जा सकता है जिसे आंतरिक अधिष्ठापन कहा जाता है; यह उपरोक्त सूत्र द्वारा दिए गए आगमनात्मक प्रतिघात (प्रतिबाधा का काल्पनिक भाग) के लिए खाता है। ज्यादातर मामलों में यह एक तार के अधिष्ठापन का एक छोटा सा हिस्सा होता है जिसमें तार में करंट द्वारा उत्पादित तार के बाहर चुंबकीय क्षेत्र से विद्युत चुम्बकीय प्रेरण का प्रभाव शामिल होता है। उस बाहरी अधिष्ठापन के विपरीत, आंतरिक अधिष्ठापन त्वचा के प्रभाव से कम हो जाता है, यानी आवृत्तियों पर जहां कंडक्टर के आकार की तुलना में त्वचा की गहराई अब बड़ी नहीं होती है।<ref name="Hayt303">Hayt (1981, pp. 303)

[8] Terman 1943, p. ??

[9] Fink, Donald G.; Beatty, H. Wayne, eds. (1978), Standard Handbook for Electrical Engineers (11th ed.), McGraw Hill, p. Table 18–21

[10] Popovic & Popovic 1999, p. 385

[11] Xi Nan & Sullivan 2005

[Reeve558-12] Reeve (1995, p. 558)

[Chen26-13] 12.0 ^12.1 Chen (2004, p. 26)

[14] R. G. Chambers, The Anomalous Skin Effect, Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences, Vol. 215, No. 1123 (Dec. 22, 1952), pp. 481-497 (17 pages) https://www.jstor.org/stable/99095

[1]

[2]

[3]

[4]

[5]

[note 1]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

Anonymous

Search

त्वाचिक प्रभाव

Namespaces

More

Page actions

Contents

कारण

सूत्र

प्रतिरोध

त्वचा की गहराई पर भौतिक प्रभाव

शमन

जैसे उदाहरण

एक सुचालक के आंतरिक अनुगम की त्वचा प्रभाव में कमी

एक समाक्षीय केबल में प्रति लंबाई अनुगम

आवृत्ति के समारोह के रूप में टेलीफोन केबल के लक्षण

विषम त्वचा प्रभाव

यह भी देखें

टिप्पणियाँ

संदर्भ

गोल तार का प्रतिबाधा

अधिष्ठापन

बाहरी कड़ियाँ

Navigation

Navigation

Wiki tools

Wiki tools

Anonymous

Search

त्वाचिक प्रभाव

कारण

सूत्र

प्रतिरोध

त्वचा की गहराई पर भौतिक प्रभाव

शमन

जैसे उदाहरण

एक सुचालक के आंतरिक अनुगम की त्वचा प्रभाव में कमी

एक समाक्षीय केबल में प्रति लंबाई अनुगम

आवृत्ति के समारोह के रूप में टेलीफोन केबल के लक्षण

विषम त्वचा प्रभाव

यह भी देखें

टिप्पणियाँ

संदर्भ

गोल तार का प्रतिबाधा

अधिष्ठापन

बाहरी कड़ियाँ

Navigation

Wiki tools

Page tools

Other projects

Categories