समदिग्नत कक्षा (होमोक्लिनिक ऑर्बिट)

समदिग्नत कक्षा

उन्मुख समदिग्नत कक्षा

मुड़ी हुई समदिग्नत कक्षा

गतिशील प्रणालियों के अध्ययन में, समदिग्नत कक्षा चरण स्थान के माध्यम से पथ है जो काठी संतुलन बिंदु को स्वयं से जोड़ती है। अधिक सटीक रूप से, समदिग्नत कक्षा संतुलन के स्थिर अनेक गुना और अस्थिर अनेक गुना के प्रतिच्छेदन में स्थित होती है। यह हेटरोक्लिनिक कक्षा है - किन्हीं दो संतुलन बिंदुओं के बीच का पथ - जिसमें समापन बिंदु और समान होते हैं।

साधारण अंतर समीकरण द्वारा वर्णित सतत कार्य गतिशील प्रणाली पर विचार करें

${\dot {x}}=f(x)$

मान लीजिए कि वहाँ संतुलन है $x=x_{0}$, फिर समाधान $\Phi (t)$ यदि समदिग्नत कक्षा है

$\Phi (t)\rightarrow x_{0}\quad \mathrm {as} \quad t\rightarrow \pm \infty$

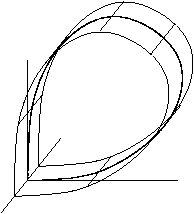
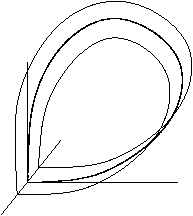
यदि चरण स्थान में तीन या अधिक आयाम हैं, तो सैडल बिंदु के अस्थिर मैनिफोल्ड की टोपोलॉजी पर विचार करना महत्वपूर्ण है। आंकड़े दो मामले दिखाते हैं. पहला, जब स्थिर मैनिफोल्ड टोपोलॉजिकल रूप से सिलेंडर होता है, और दूसरा, जब अस्थिर मैनिफोल्ड टोपोलॉजिकल रूप से मोबियस स्ट्रिप होता है; इस मामले में समदिग्नत कक्षा को मुड़ कहा जाता है।

असतत गतिशील प्रणाली

समदिग्नत कक्षाओं और समदिग्नत बिंदुओं को पुनरावृत्त कार्यों के लिए उसी तरह से परिभाषित किया जाता है, जैसे सिस्टम के कुछ निश्चित बिंदु (गणित) या आवधिक बिंदु के स्थिर मैनिफोल्ड और अस्थिर सेट का प्रतिच्छेदन।

असतत गतिशील प्रणालियों पर विचार करते समय हमारे पास समदिग्नत कक्षा की भी धारणा है। ऐसे में यदि $f:M\rightarrow M$ अनेक गुना की भिन्नता है $M$, हम ऐसा कहते हैं $x$ समदिग्नत बिंदु है यदि इसका अतीत और भविष्य समान है - अधिक विशेष रूप से, यदि कोई निश्चित (या आवधिक) बिंदु मौजूद है $p$ ऐसा है कि

$\lim _{n\rightarrow \pm \infty }f^{n}(x)=p.$

गुण

समदिग्नत बिंदु का अस्तित्व उनकी अनंत संख्या के अस्तित्व को दर्शाता है। यह इसकी परिभाषा से आता है: स्थिर और अस्थिर सेट का प्रतिच्छेदन। दोनों सेट परिभाषा के अनुसार सकारात्मक अपरिवर्तनीय सेट हैं, जिसका अर्थ है कि समदिग्नत बिंदु का आगे का पुनरावृत्ति स्थिर और अस्थिर सेट दोनों पर है। एन बार पुनरावृत्ति करके, नक्शा स्थिर सेट द्वारा संतुलन बिंदु तक पहुंचता है, लेकिन प्रत्येक पुनरावृत्ति में यह अस्थिर मैनिफोल्ड पर भी होता है, जो इस संपत्ति को दर्शाता है।

यह गुण बताता है कि समदिग्नत बिंदु के अस्तित्व से जटिल गतिशीलता उत्पन्न होती है। वास्तव में, स्मेल (1967) पता चला कि ये बिंदु गतिशीलता जैसे घोड़े की नाल के नक्शे की ओर ले जाते हैं, जो अराजकता से जुड़ा है।

प्रतीकात्मक गतिशीलता

मार्कोव विभाजन का उपयोग करके, प्रतीकात्मक गतिशीलता की तकनीकों का उपयोग करके हाइपरबोलिक प्रणाली के दीर्घकालिक व्यवहार का अध्ययन किया जा सकता है। इस मामले में, समदिग्नत कक्षा का विशेष रूप से सरल और स्पष्ट प्रतिनिधित्व होता है। लगता है कि $S=\{1,2,\ldots ,M\}$ एम प्रतीकों का सीमित सेट है। बिंदु x की गतिशीलता को प्रतीकों की द्वि-अनंत स्ट्रिंग द्वारा दर्शाया जाता है

$\sigma =\{(\ldots ,s_{-1},s_{0},s_{1},\ldots ):s_{k}\in S\;\forall k\in \mathbb {Z} \}$

सिस्टम का आवधिक बिंदु केवल अक्षरों का आवर्ती अनुक्रम है। हेटरोक्लिनिक कक्षा तब दो अलग-अलग आवधिक कक्षाओं का जुड़ना है। इसे ऐसे लिखा जा सकता है

$p^{\omega }s_{1}s_{2}\cdots s_{n}q^{\omega }$

कहाँ $p=t_{1}t_{2}\cdots t_{k}$ लंबाई k के प्रतीकों का क्रम है, (बेशक, $t_{i}\in S$), और $q=r_{1}r_{2}\cdots r_{m}$ लंबाई m के प्रतीकों का और क्रम है (इसी प्रकार, $r_{i}\in S$). संकेतन $p^{\omega }$ बस अनंत बार p की पुनरावृत्ति को दर्शाता है। इस प्रकार, हेटरोक्लिनिक कक्षा को आवधिक कक्षा से दूसरे में संक्रमण के रूप में समझा जा सकता है। इसके विपरीत, समदिग्नत कक्षा को इस प्रकार लिखा जा सकता है

$p^{\omega }s_{1}s_{2}\cdots s_{n}p^{\omega }$

मध्यवर्ती अनुक्रम के साथ $s_{1}s_{2}\cdots s_{n}$ गैर-रिक्त होना, और, निश्चित रूप से, पी नहीं होना, अन्यथा, कक्षा बस होगी $p^{\omega }$.

यह भी देखें

• हेटरोक्लिनिक कक्षा
• समदिग्नत द्विभाजन

संदर्भ

• John Guckenheimer and Philip Holmes, Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields (Applied Mathematical Sciences Vol. 42), Springer

बाहरी संबंध

• Homoclinic orbits in Henon map with Java applets and comments