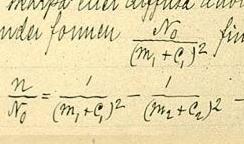रिडबर्ग सूत्र
| के बारे में लेखों की एक श्रृंखला का हिस्सा |
| क्वांटम यांत्रिकी |
|---|
परमाणु भौतिकी में, रिडबर्ग सूत्र कई रासायनिक तत्वों में वर्णक्रमीय रेखा के तरंग दैर्ध्य की गणना करता है। सूत्र को मुख्य रूप से हाइड्रोजन के सभी आणविक अतिसूक्ष्म परमाणु संक्रमण के लिए बामर श्रृंखला के सामान्यीकरण के रूप में प्रस्तुत किया गया था। यह पहली बार अनुभवजन्य रूप से 1888 में स्वीडिश भौतिक विज्ञानी जोहान्स रिडबर्ग द्वारा कहा गया था,[1] फिर सैद्धांतिक रूप से 1913 में नील्स बोह्र द्वारा, जिन्होंने परिमाण यांत्रिकी के एक आदिम रूप का उपयोग किया। सूत्र सीधे हाइड्रोजन वर्णक्रमीय श्रृंखला के तरंग दैर्ध्य की गणना करने के लिए उपयोग किए जाने वाले समीकरणों को सामान्य करता है।
इतिहास
1880 में, रिडबर्ग ने क्षार धातुओं की वर्णक्रमीय रेखाओं में तरंग दैर्ध्य के बीच संबंध का वर्णन करने वाले सूत्र पर काम किया। उन्होंने देखा कि रेखाएं श्रृंखला में आती हैं और उन्होंने पाया कि वह माप की अपनी इकाई के रूप में तरंग संख्या (इकाई लंबाई पर अधिकार करने वाली तरंगों की संख्या, 1/λ के बराबर, तरंग दैर्ध्य के व्युत्क्रम) का उपयोग करके अपनी गणना को सरल बना सकते हैं। उन्होंने लगातार पूर्णांकों के विरुद्ध प्रत्येक श्रृंखला में क्रमिक रेखाओं की तरंगों (n) को आलेख किया जो उस विशेष श्रृंखला में रेखाओं के क्रम का प्रतिनिधित्व करते थे। यह देखते हुए कि परिणामी वक्र समान आकार के थे, जब उपयुक्त स्थिरांक डाले गए थे तब उन्होंने एक एकल कार्य की मांग की जो उन सभी को उत्पन्न कर सके।
पहले उन्होंने: सूत्र जाँचा, जहाँ n रेखा की तरंग संख्या है, n0 श्रृंखला की सीमा है, m श्रृंखला में रेखा की क्रमिक संख्या है, m' अलग श्रृंखला के लिए एक स्थिर भिन्न है और C0 एक सार्वभौमिक स्थिरांक है। यह बहुत अच्छी तरह से काम नहीं किया।
रिडबर्ग का प्रयास कर रहे थे, जब उन्हें हाइड्रोजन विस्तृत श्रेणी के लिए बामर का सूत्र के बारे में पता चला। इस समीकरण में, m एक पूर्णांक है और h एक स्थिरांक है (जिसे बाद के प्लैंक स्थिरांक के साथ भ्रमित नहीं होना चाहिए)।
रिडबर्ग ने इसलिए तरंग संख्या के संदर्भ में बाल्मर के सूत्र को फिर से लिखा, जैसा कि .
इसने सुझाव दिया कि हाइड्रोजन के लिए बामर सूत्र एक विशेष स्तिथि और हो सकती है, जहाँ , बामर के स्थिरांक का व्युत्क्रम है (यह स्थिरांक h बामर समीकरण लेख में B लिखा गया है, फिर से प्लैंक स्थिरांक के साथ भ्रम से बचने के लिए)।
शब्द 4/h के बराबर, सभी तत्वों के लिए एक सार्वभौमिक स्थिरांक सामान्य पाया गया। इस स्थिरांक को अब रिडबर्ग स्थिरांक के रूप में जाना जाता है, और m' को परिमाण त्रुटि के रूप में जाना जाता है।
जैसा कि नील्स बोह्र द्वारा बल दिया गया है,[2] तरंग संख्या के संदर्भ में परिणाम व्यक्त करना, तरंग दैर्ध्य नहीं, रिडबर्ग की खोज की कुंजी थी। 1908 के रिडबर्ग-रिट्ज संयोजन सिद्धांत द्वारा तरंगों की मौलिक भूमिका पर भी महत्त्व दिया गया था। इसका मूल कारण परिमाण यांत्रिकी में निहित है। प्रकाश की तरंग संख्या आवृत्ति के समानुपाती होती है, और इसलिए प्रकाश की परिमाण ऊर्जा E के समानुपाती भी है। इस प्रकार, (इस सूत्र में H प्लैंक स्थिरांक का प्रतिनिधित्व करता है)। आधुनिक समझ यह है कि रेडबर्ग के निष्कर्ष परमाणुओं में अतिसूक्ष्म परमाणु कक्षीय के बीच निश्चित (मात्राबद्ध) ऊर्जा अंतर के संदर्भ में वर्णक्रमीय रेखाओं के व्यवहार की अंतर्निहित सादगी का प्रतिबिंब थे। वर्णक्रमीय श्रृंखला के रूप के लिए रिडबर्ग की 1888 शास्त्रीय अभिव्यक्ति एक भौतिक व्याख्या के साथ नहीं थी। वर्णक्रमीय श्रृंखला के अंतर्निहित तंत्र के लिए वाल्थर रिट्ज की पूर्व-परिमाण 1908 की व्याख्या यह थी कि आणव अतिसूक्ष्म परमाणु चुंबक की तरह व्यवहार करते हैं और चुंबक विद्युत चुम्बकीय विकिरण उत्पन्न करने के लिए परमाणु नाभिक (कम से कम अस्थायी रूप से) के संबंध में कंपन कर सकते हैं।[3] लेकिन इस सिद्धांत को 1913 में नील्स बोह्र के बोहर प्रतिरूप ने अधिलंघित कर दिया।
बोह्र की परमाणु की अवधारणा में, पूर्णांक रिडबर्ग (और बाल्मर) n संख्याएँ परमाणु से विभिन्न अभिन्न दूरी पर अतिसूक्ष्म परमाणु कक्षक का प्रतिनिधित्व करती हैं। एक आवृत्ति (या वर्णक्रमीय ऊर्जा) n1 से n2 के संक्रमण में उत्सर्जित होती है या जब एक अतिसूक्ष्म परमाणु कक्षीय 1 से कक्षीय 2 में कूदता है तब अवशोषित फोटॉन ऊर्जा का प्रतिनिधित्व करता है ।
बाद के प्रतिरूपों ने पाया कि n1 के मान और n2 दो कक्षकों की प्रमुख परिमाण संख्याओं के अनुरूप हैं।
हाइड्रोजन के लिए
- निर्वात में उत्सर्जित विद्युत चुम्बकीय विकिरण की तरंग दैर्ध्य है,
- हाइड्रोजन के लिए रिडबर्ग स्थिरांक है, लगभग 1.09677583×107 m−1,
- एक ऊर्जा स्तर की प्रमुख परिमाण संख्या है, और
- परमाणु अतिसूक्ष्म परमाणु संक्रमण के लिए ऊर्जा स्तर की प्रमुख परिमाण संख्या है।
नोट: यहाँ,
व्यवस्थित करके 1 और दे 2 से अनंत तक चलती हैं, 91 nm तक अभिसरण करने वाली लाइमैन श्रृंखला के रूप में जानी जाने वाली वर्णक्रमीय रेखाएं उसी तरह से प्राप्त की जाती हैं:
| n1 | n2 | नाम | अभिसरित उद्यत |
|---|---|---|---|
| 1 | 2 – ∞ | लाइमैन श्रेणी | 91.13 nm (UV) |
| 2 | 3 – ∞ | बामर श्रेणी | 364.51 nm (Visible) |
| 3 | 4 – ∞ | पाशन श्रेणी | 820.14 nm (IR) |
| 4 | 5 – ∞ | ब्रेकेट श्रेणी | 1458.03 nm (Far IR) |
| 5 | 6 – ∞ | फुंड श्रेणी | 2278.17 nm (Far IR) |
| 6 | 7 – ∞ | हम्फ्री श्रेणी | 3280.56 nm (Far IR) |
किसी भी हाइड्रोजन जैसे तत्व के लिए
उपरोक्त सूत्र को किसी भी हाइड्रोजन जैसे परमाणु | हाइड्रोजन जैसे रासायनिक तत्वों के साथ उपयोग के लिए बढ़ाया जा सकता है
- उत्सर्जित प्रकाश की तरंग दैर्ध्य (निर्वात में) है,
- इस तत्व के लिए रिडबर्ग स्थिरांक है,
- परमाणु संख्या है, अर्थात इस तत्व के परमाणु नाभिक में प्रोटॉन की संख्या,
- निम्न ऊर्जा स्तर की प्रमुख परिमाण संख्या है, और
- परमाणु अतिसूक्ष्म परमाणु संक्रमण के लिए उच्च ऊर्जा स्तर की प्रमुख परिमाण संख्या है।
यह सूत्र केवल हाइड्रोजन-जैसे परमाणु पर ही लागू किया जा सकता है| रासायनिक तत्वों के हाइड्रोजनिक परमाणु भी कहा जाता है, यानी परमाणु एक प्रभावी परमाणु चार्ज (जो आसानी से अनुमान लगाया जाता है) से केवल एक अतिसूक्ष्म परमाणु प्रभावित होता है। उदाहरणों में वह सम्मिलित He+, Li2+, Be3+ आदि, जहां परमाणु में कोई अन्य अतिसूक्ष्म परमाणु उपस्थित नहीं है।
लेकिन रिडबर्ग सूत्र दूर के अतिसूक्ष्म परमाणुों के लिए सही तरंग दैर्ध्य भी प्रदान करता है, जहां प्रभावी परमाणु प्रभार का अनुमान हाइड्रोजन के समान ही लगाया जा सकता है, क्योंकि सभी परमाणु शुल्कों में से एक को अन्य अतिसूक्ष्म परमाणुों द्वारा स्क्रीन किया गया है, और परमाणु के मूल में है +1 का एक प्रभावी सकारात्मक चार्ज।
अंत में, कुछ संशोधनों के साथ (Z का Z - 1 द्वारा प्रतिस्थापन, और ns के लिए पूर्णांक 1 और 2 का उपयोग एक संख्यात्मक मान देने के लिए 3⁄4 उनके व्युत्क्रम वर्गों के अंतर के लिए), रिडबर्ग सूत्र K- कश्मीर अल्फा लाइनों के विशेष मामले में सही मान प्रदान करता है, क्योंकि प्रश्न में संक्रमण 1s कक्षीय से 2p कक्षीय तक अतिसूक्ष्म परमाणु का K- अल्फा संक्रमण है। यह हाइड्रोजन के लिए लाइमन-अल्फा रेखा संक्रमण के अनुरूप है, और समान आवृत्ति कारक है। क्योंकि 2p अतिसूक्ष्म परमाणु नाभिक से परमाणु में किसी भी अन्य अतिसूक्ष्म परमाणु द्वारा प्रदर्शित नहीं होता है, परमाणु आवेश केवल शेष 1s अतिसूक्ष्म परमाणु द्वारा कम होता है, जिससे प्रणाली प्रभावी रूप से एक हाइड्रोजनी परमाणु बन जाती है, लेकिन कम परमाणु आवेश Z - 1 के साथ इस प्रकार इसकी आवृत्ति लाइमन-अल्फ़ा हाइड्रोजन आवृत्ति है, जो (Z - 1) के कारक से बढ़ जाती है। F = C / λ = (लाइमन-अल्फा आवृति) ⋅ (Z - 1) का यह सूत्र2 को ऐतिहासिक रूप से मोसले के नियम के रूप में जाना जाता है (तरंग दैर्घ्य को आवृति में बदलने के लिए एक कारक c जोड़ा गया है), और इसका उपयोग के के रजिस्टर की भविष्यवाणी करने के लिए किया जा सकता है Kα (K-अल्फा) एल्यूमीनियम से सोने तक रासायनिक तत्वों की एक्स-रे वर्णक्रमीय अंतर्निहित लाइनें। इस कानून के ऐतिहासिक महत्व के लिए हेनरी मोस्ले की जीवनी देखें, जो लगभग उसी समय अनुभवजन्य रूप से प्राप्त हुए थे जब इसे परमाणु के बोह्र प्रतिरूप द्वारा समनाया गया था। (Z - 1) का यह सूत्र 2 को ऐतिहासिक रूप से मोसले के नियम के रूप में जाना जाता है (वेवलेंथ को आवृति में बदलने के लिए एक कारक c जोड़ा गया है), और इसका उपयोग के के रजिस्टर की भविष्यवाणी करने के लिए किया जा सकता है Kα (के-अल्फा) एल्यूमीनियम से सोने तक रासायनिक तत्वों की एक्स-रे वर्णक्रमीय अंतर्निहित रेखाएं । इस कानून के ऐतिहासिक महत्व के लिए हेनरी मोस्ले की जीवनी देखें, जो लगभग उसी समय अनुभवजन्य रूप से प्राप्त हुए थे जब इसे परमाणु के बोह्र प्रतिरूप द्वारा समनाया गया था।
बहु-अतिसूक्ष्म परमाणु परमाणुओं में अन्य वर्णक्रमीय संक्रमणों के लिए, रिडबर्ग सूत्र आम तौर पर गलत परिणाम प्रदान करता है, क्योंकि बाहरी-अतिसूक्ष्म परमाणु संक्रमणों के लिए आंतरिक अतिसूक्ष्म परमाणुों की स्क्रीनिंग का परिमाण परिवर्तनशील होता है और उपरोक्त सरल तरीके से क्षतिपूर्ति करना संभव नहीं होता है। इन परमाणुओं के रिडबर्ग सूत्र में सुधार को परिमाण दोष के रूप में जाना जाता है।
यह भी देखें
- बामर श्रृंखला
- हाइड्रोजन रेखा
- रिडबर्ग-रिट्ज संयोजन सिद्धांत
संदर्भ
- ↑ See:
- Rydberg, J.R. (1889). "Researches sur la constitution des spectres d'émission des éléments chimiques" [Investigations of the composition of the emission spectra of chemical elements]. Kongliga Svenska Vetenskaps-Akademiens Handlingar [Proceedings of the Royal Swedish Academy of Science]. 2nd series (in French). 23 (11): 1–177.
{{cite journal}}: CS1 maint: unrecognized language (link) - English summary: Rydberg, J.R. (1890). "On the structure of the line-spectra of the chemical elements". Philosophical Magazine. 5th series. 29: 331–337.
- Rydberg, J.R. (1889). "Researches sur la constitution des spectres d'émission des éléments chimiques" [Investigations of the composition of the emission spectra of chemical elements]. Kongliga Svenska Vetenskaps-Akademiens Handlingar [Proceedings of the Royal Swedish Academy of Science]. 2nd series (in French). 23 (11): 1–177.
- ↑ Bohr, N. (1985). "Rydberg's discovery of the spectral laws". In Kalckar, J. (ed.). Collected works. Vol. 10. Amsterdam: North-Holland Publ. Cy. pp. 373–379.
- ↑ Ritz, W. (1908). "Magnetische Atomfelder und Serienspektren" [The magnetic fields of atoms and spectral series]. Annalen der Physik (in Deutsch). 330 (4): 660–696. Bibcode:1908AnP...330..660R. doi:10.1002/andp.19083300403.
- Sutton, Mike (July 2004). "Getting the numbers right: The lonely struggle of the 19th century physicist/chemist Johannes Rydberg". Chemistry World. 1 (7): 38–41. ISSN 1473-7604.
- Martinson, I.; Curtis, L.J. (2005). "Janne Rydberg – his life and work". Nuclear Instruments and Methods in Physics Research Section B. 235 (1–4): 17–22. Bibcode:2005NIMPB.235...17M. CiteSeerX 10.1.1.602.6210. doi:10.1016/j.nimb.2005.03.137.