ऑप्टिकल चरण समष्टि

चरण समष्टि में एक सुसंगत राज्य के वितरण का ऑप्टिकल चरण आरेख।

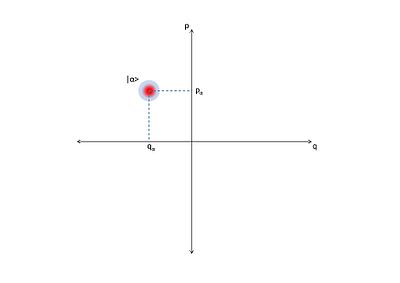
क्वांटम प्रकाशिकी में, एक ऑप्टिकल चरण समष्टि एक चरण समष्टि है जिसमें एक ऑप्टिकल प्रणाली के सभी क्वांटम अवस्थाओ का वर्णन किया गया है। ऑप्टिकल चरण समष्टि में प्रत्येक बिंदु ऑप्टिकल प्रणाली की एक अद्वितीय स्थिति से मेल खाता है। ऐसी किसी भी प्रणाली के लिए, संभवतः समय के कार्यों के रूप में, एक दूसरे के विरुद्ध चतुर्भुज का एक प्लॉट, चरण आरेख कहलाता है। यदि चतुर्भुज समय के कार्य हैं तो ऑप्टिकल चरण आरेख समय के साथ क्वांटम ऑप्टिकल प्रणाली के विकास को दिखा सकता है।

एक ऑप्टिकल चरण आरेख प्रणाली के गुणों और व्यवहारों में अंतर्दृष्टि दे सकता है जो अन्यथा स्पष्ट नहीं हो सकता है। यह उस प्रणाली के गुणों की ओर संकेत कर सकता है जो किसी ऑप्टिकल प्रणाली का अध्ययन करने वाले व्यक्ति के लिए रुचिकर हो सकता है जिसे अन्यथा निकालना बहुत कठिन होगा। जो कि ऑप्टिकल चरण आरेख का एक अन्य उपयोग यह है कि यह एक ऑप्टिकल प्रणाली की स्थिति के विकास को दर्शाता है। इसका उपयोग किसी भी समय ऑप्टिकल प्रणाली की स्थिति निर्धारित करने के लिए किया जा सकता है।

पृष्ठभूमि जानकारी

प्रकाश के क्वांटम सिद्धांत पर विचार करते समय, एक मॉडल के रूप में विद्युत चुम्बकीय दोलन का उपयोग करना बहुत समान्य है। एक विद्युत चुम्बकीय दोलन विद्युत क्षेत्र के दोलन का वर्णन करता है। चूँकि चुंबकीय क्षेत्र विद्युत क्षेत्र के परिवर्तन की दर के समानुपाती होता है, इसलिए यह भी दोलन करता है। ऐसे दोलन प्रकाश का वर्णन करते हैं। ऐसे दोलन से बने प्रणाली को ऑप्टिकल चरण समष्टि द्वारा वर्णित किया जा सकता है।

मान लीजिए कि u(x,t) एक वेक्टर फ़ंक्शन है जो एक सरल हार्मोनिक दोलन के एकल मोड का वर्णन करता है। सरलता के लिए, यह माना जाता है कि यह विद्युत चुम्बकीय दोलन निर्वात में है। इसका एक उदाहरण समतल तरंग द्वारा दिया गया है

$\mathbf {u} (\mathbf {x} ,t)=\mathbf {u_{0}} e^{i(\mathbf {k} \cdot \mathbf {x} -\omega t)}$

जहां u₀ ध्रुवीकरण वेक्टर है, जिसमे k तरंग वेक्टर है, $\omega$ आवृत्ति है, और A.B वेक्टर A और B के बीच डॉट उत्पाद को दर्शाता है। यह एक समतल तरंग के लिए समीकरण है और इस तरह का एक सरल उदाहरण है विद्युत चुम्बकीय दोलन . जिन दोलन की जांच की जा रही है वे या तो अंतरिक्ष में मुक्त तरंगें हो सकते हैं या कुछ गुहा में निहित कुछ सामान्य मोड हो सकते हैं।

इलेक्ट्रोमैग्नेटिक दोलन के एक मोड को प्रणाली के शेष भागो से अलग किया जाता है और उसकी जांच की जाती है। ऐसे दोलन , जब परिमाणित किया जाता है, तो क्वांटम हार्मोनिक दोलन के गणित द्वारा वर्णित किया जाता है। क्वांटम दोलन का वर्णन सृजन और विनाश ऑपरेटरों ${\hat {a}}^{\dagger }$ और ${\hat {a}}$. का उपयोग करके किया गया है। भौतिक मात्राएँ, जैसे विद्युत क्षेत्र की ताकत, फिर क्वांटम ऑपरेटर बन जाती हैं।

इसका वर्णन करने के लिए उपयोग किए जाने वाले क्वांटम मैकेनिकल ऑपरेटर से किसी भौतिक मात्रा को अलग करने के लिए, ऑपरेटर प्रतीकों के ऊपर एक "टोपी" का उपयोग किया जाता है। इस प्रकार, उदाहरण के लिए, जहां $E_{i}$ विद्युत क्षेत्र (के एक घटक) का प्रतिनिधित्व कर सकता है, प्रतीक ${\widehat {E}}_{i}$ क्वांटम-मैकेनिकल ऑपरेटर को दर्शाता है जो $E_{i}$ का वर्णन करता है। इस परिपाटी का उपयोग इस पूरे लेख में किया गया है, किन्तु अधिक उन्नत पाठों में इसका सामान्य उपयोग नहीं किया जाता है, जो टोपी से बचते हैं, क्योंकि यह केवल पाठ को अव्यवस्थित करता है।

क्वांटम दोलन मोड में, भौतिक मात्राओं का प्रतिनिधित्व करने वाले अधिकांश ऑपरेटरों को समान्य रूप से निर्माण और विनाश ऑपरेटरों के संदर्भ में व्यक्त किया जाता है। इस उदाहरण में, विद्युत क्षेत्र की शक्ति इस प्रकार दी गई है:

${\widehat {E}}_{i}=u_{i}^{*}(\mathbf {x} ,t){\widehat {a}}^{\dagger }+u_{i}(\mathbf {x} ,t){\widehat {a}}$

(जहाँ xi, x, स्थिति का एक एकल घटक है)। एक विद्युत चुम्बकीय दोलन के लिए हैमिल्टनियन इस दोलन के लिए विद्युत चुम्बकीय क्षेत्र की मात्रा निर्धारित करके पाया जाता है और सूत्र इस प्रकार दिया जाता है:

${\widehat {H}}=\hbar \omega ({\widehat {a}}^{\dagger }{\widehat {a}}+1/2)$

जहाँ $\omega$ (स्थान-अस्थायी) मोड की आवृत्ति है। सर्वनाश संचालिका बोसोनिक सर्वनाश संचालिका है और इसलिए यह दिए गए विहित रूपान्तरण संबंध का पालन करता है:

$[{\widehat {a}},{\widehat {a}}^{\dagger }]=1$

विनाश संचालिका की मूल अवस्थाओं को सुसंगत अवस्थाएँ कहा जाता है:

${\widehat {a}}|\alpha \rangle =\alpha |\alpha \rangle$

यह ध्यान रखना महत्वपूर्ण है कि विनाश संचालिका हर्मिटियन नहीं है; इसलिए इसके आइजेनवैल्यू $\alpha$ सम्मिश्र हो सकता है. इसके महत्वपूर्ण परिणाम हैं.

अंत में, ऑपरेटर ${\widehat {N}}={\widehat {a}}^{\dagger }{\widehat {a}},$ द्वारा फोटॉन संख्या दी जाती है, जो दिए गए (स्थानिक-लौकिक) मोड यू में फोटॉनों की संख्या देता है।

चतुर्भुज

संचालक (गणित) द्वारा दिया गया है

${\widehat {q}}={\tfrac {1}{2}}({\widehat {a}}^{\dagger }+{\widehat {a}})$

और

${\widehat {p}}={\tfrac {i}{2}}({\widehat {a}}^{\dagger }-{\widehat {a}})$

चतुर्भुज कहलाते हैं और वे सम्मिश्र आयाम के वास्तविक और काल्पनिक भागों का प्रतिनिधित्व करते हैं जो ${\widehat {a}}$ द्वारा दर्शाए जाते हैं। दो चतुर्भुजों के बीच कम्यूटेशन संबंध की गणना सरलता से की जा सकती है:

${\begin{aligned}\left[{\widehat {q}},{\widehat {p}}\right]&={\tfrac {i}{4}}[{\widehat {a}}^{\dagger }+{\widehat {a}},{\widehat {a}}^{\dagger }-{\widehat {a}}]\\&={\tfrac {i}{4}}([{\widehat {a}}^{\dagger },{\widehat {a}}^{\dagger }]-[{\widehat {a}}^{\dagger },{\widehat {a}}]+[{\widehat {a}},{\widehat {a}}^{\dagger }]-[{\widehat {a}},{\widehat {a}}])\\&={\tfrac {i}{4}}(-(-1)+1)\\&={\tfrac {i}{2}}\end{aligned}}$

यह स्थिति और गति ऑपरेटर के कम्यूटेशन संबंध के समान दिखता है। इस प्रकार, चतुर्भुजों को दोलन की स्थिति और गति के रूप में सोचना और व्यवहार करना उपयोगी हो सकता है, चूँकि वास्तव में वे स्थानिक-लौकिक मोड के विद्युत क्षेत्र आयाम के इन-फेज और आउट-ऑफ-फेज घटक हैं, या यू, और वास्तव में विद्युत चुम्बकीय दोलक की स्थिति या गति से कोई लेना-देना नहीं है (क्योंकि यह परिभाषित करना कठिन है कि विद्युत चुम्बकीय दोलक के लिए स्थिति और गति का क्या अर्थ है)।

चतुर्भुज के गुण

चतुर्भुज ऑपरेटरों के eigenstates ${\widehat {q}}$ और ${\widehat {p}}$ चतुर्भुज अवस्थाएँ कहलाती हैं। वे रिश्तों को संतुष्ट करते हैं:

• ${\widehat {q}}|q\rangle =q|q\rangle$ और ${\widehat {p}}|p\rangle =p|p\rangle$
• $\langle q|q'\rangle =\delta (q-q')$ और $\langle p|p'\rangle =\delta (p-p')$
• $\int _{-\infty }^{\infty }|q\rangle \langle q|\,dq=1$ और $\int _{-\infty }^{\infty }|p\rangle \langle p|\,dp=1$

फॉर्म एस के ऑर्थोनॉर्मल आधार सेट।

महत्वपूर्ण परिणाम

निम्नलिखित एक महत्वपूर्ण संबंध है जिसे उपरोक्त से प्राप्त किया जा सकता है जो हमारी व्याख्या को उचित ठहराता है कि चतुर्भुज एक सम्मिश्र के वास्तविक और काल्पनिक भाग हैं $\alpha$ (अर्थात विद्युत चुम्बकीय दोलन के इन-फेज और आउट-ऑफ-फेज घटक)

$\langle \alpha |{\widehat {q}}|\alpha \rangle ={\frac {1}{2}}(\langle \alpha |{\widehat {a}}^{\dagger }|\alpha \rangle +\langle \alpha |{\widehat {a}}|\alpha \rangle )={\frac {1}{2}}(\alpha ^{*}\langle \alpha |\alpha \rangle +\alpha \langle \alpha |\alpha \rangle )$

निम्नलिखित एक संबंध है जिसका उपयोग उपरोक्त का मूल्यांकन करने में सहायता के लिए किया जा सकता है और इसे निम्न द्वारा दिया गया है:

$\langle \alpha '|\alpha \rangle =e^{(-1/2)(|\alpha '|^{2}+|\alpha |^{2})+\alpha '^{*}\alpha }$

इससे हमें यह मिलता है:

$\langle \alpha |{\widehat {q}}|\alpha \rangle ={\frac {1}{2}}(\alpha ^{*}+\alpha )=q_{\alpha }$

$\langle \alpha |{\widehat {p}}|\alpha \rangle ={\frac {i}{2}}(\alpha ^{*}-\alpha )=p_{\alpha }$ उपरोक्त के समान विधि द्वारा।

$\alpha ={\frac {1}{2}}(\langle \alpha |{\widehat {q}}|\alpha \rangle +i\langle \alpha |{\widehat {p}}|\alpha \rangle )={\frac {1}{2}}(q_{\alpha }+ip_{\alpha })$

इस प्रकार, $\alpha$ यह केवल चतुर्भुजों की एक रचना है।

सुसंगत अवस्थाओ की एक और बहुत महत्वपूर्ण संपत्ति इस औपचारिकता में बहुत स्पष्ट हो जाती है। एक सुसंगत अवस्था ऑप्टिकल चरण समष्टि में एक बिंदु नहीं है, बल्कि उस पर एक वितरण है। इसके जरिये देखा जा सकता है

$q_{\alpha }=\langle \alpha |{\widehat {q}}|\alpha \rangle$

और

$p_{\alpha }=\langle \alpha |{\widehat {p}}|\alpha \rangle$.

ये केवल अपेक्षा के मूल्य हैं ${\widehat {q}}$ और ${\widehat {p}}$ राज्य के लिए $|\alpha \rangle$.

यह दिखाया जा सकता है कि चतुर्भुज हाइजेनबर्ग के अनिश्चितता सिद्धांत का पालन करते हैं:

$\Delta q\Delta p\geq 1/2$(जहाँ $\Delta q$ और $\Delta p$ क्रमशः q और p के वितरण के प्रसरण हैं)

यह असमानता आवश्यक रूप से संतृप्त नहीं होती है और ऐसे अवस्थाओ का एक सामान्य उदाहरण निचोड़ा हुआ सुसंगत राज्य है। सुसंगत अवस्थाएँ आस-पास स्थानीयकृत चरण समष्टि पर गाऊसी संभाव्यता वितरण हैं $\alpha$.

चरण समष्टि पर ऑपरेटर

चरण समष्टि के चारों ओर सुसंगत अवस्थाओं को स्थानांतरित करने के लिए ऑपरेटरों को परिभाषित करना संभव है। ये नई सुसंगत अवस्थाएँ उत्पन्न कर सकते हैं और हमें चरण समष्टि के चारों ओर घूमने की अनुमति दे सकते हैं।

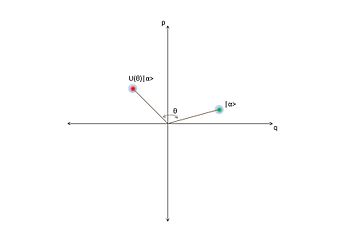
चरण-स्थानांतरण ऑपरेटर

फेज़ शिफ्टिंग ऑपरेटर एक सुसंगत स्थिति पर कार्य करते हुए इसे एक कोण से घुमाता है $\theta$ चरण समष्टि में.

चरण-शिफ्टिंग ऑपरेटर सुसंगत स्थिति को एक कोण से घुमाता है $\theta$ ऑप्टिकल चरण समष्टि में. यह ऑपरेटर द्वारा दिया गया है:

${\widehat {U}}(\theta )=e^{-i\theta {\widehat {N}}}$

महत्वपूर्ण रिश्ता

${\widehat {U}}(\theta )^{\dagger }{\widehat {a}}{\widehat {U}}(\theta )={\widehat {a}}e^{-i\theta }$

इस प्रकार व्युत्पन्न है:

$d/d\theta ({\widehat {U}}^{\dagger }{\widehat {a}}{\widehat {U}})=i{\widehat {N}}{\widehat {U}}^{\dagger }{\widehat {a}}{\widehat {U}}-i{\widehat {U}}^{\dagger }{\widehat {a}}{\widehat {U}}{\widehat {N}}={\widehat {U}}^{\dagger }i[{\widehat {N}},{\widehat {a}}]{\widehat {U}}$

$={\widehat {U}}^{\dagger }i({\widehat {a}}^{\dagger }{\widehat {a}}{\widehat {a}}-{\widehat {a}}{\widehat {a}}^{\dagger }{\widehat {a}}){\widehat {U}}={\widehat {U}}^{\dagger }i[{\widehat {a}}^{\dagger },{\widehat {a}}]{\widehat {a}}{\widehat {U}}=-i{\widehat {U}}^{\dagger }{\widehat {a}}{\widehat {U}}$

और इस अंतर समीकरण को हल करने से वांछित परिणाम प्राप्त होता है।

इस प्रकार उपरोक्त के प्रयोग से यह स्पष्ट हो जाता है कि

${\widehat {U}}(\theta )|\alpha \rangle =|\alpha e^{-i\theta }\rangle$,

या चरण समष्टि में सुसंगत स्थिति पर कोण थीटा द्वारा घूर्णन। निम्नलिखित इसे और अधिक स्पष्ट रूप से दर्शाता है:

${\widehat {a}}({\widehat {U}}|\alpha \rangle )={\widehat {U}}{\widehat {a}}e^{-i\theta }|\alpha \rangle$

(जो इस तथ्य का उपयोग करके प्राप्त किया जाता है कि चरण-शिफ्टिंग ऑपरेटर एकात्मक ऑपरेटर है

${\widehat {a}}({\widehat {U}}|\alpha \rangle )={\widehat {U}}\alpha e^{-i\theta }|\alpha \rangle =\alpha e^{-i\theta }({\widehat {U}}|\alpha \rangle )$

इस प्रकार,

$(\alpha e^{-i\theta },{\widehat {U}}|\alpha \rangle )$

का आइजेनवैल्यू, आइजेनवेक्टर और आइजेनस्पेस है

${\widehat {a}}{\widehat {U}}|\alpha \rangle$.

इससे ये पता चल सकता है

$(\alpha e^{-i\theta }=2^{-1/2}[q_{\alpha }\cos(\theta )+p_{\alpha }\sin(\theta )]+i2^{-1/2}[-q_{\alpha }\sin(\theta )+p_{\alpha }\cos(\theta )],{\widehat {U}}|\alpha \rangle =|\alpha e^{-i\theta }\rangle )$

जो ईजेनपेयर को व्यक्त करने का एक और तरीका है जो सुसंगत अवस्थाओ पर चरण-शिफ्टिंग ऑपरेटर के प्रभावों को अधिक स्पष्ट रूप से दर्शाता है।

विस्थापन ऑपरेटर

विस्थापन ऑपरेटर एक सुसंगत स्थिति पर कार्य करते हुए इसे कुछ मान से विस्थापित करता है $\alpha$ चरण समष्टि में.

विस्थापन संचालिका एक एकात्मक संचालिका है जो एक सुसंगत अवस्था लेती है और उसे दूसरी सुसंगत अवस्था में बदल देती है। विस्थापन ऑपरेटर द्वारा दिया गया है

${\widehat {D}}(\alpha )=e^{\alpha {\widehat {a}}^{\dagger }-\alpha ^{*}{\widehat {a}}}$

और इसका नाम एक महत्वपूर्ण संबंध से आया है

${\widehat {a}}(\alpha )\equiv {\widehat {D}}^{\dagger }(\alpha ){\widehat {a}}{\widehat {D}}(\alpha )={\widehat {a}}+\alpha$.

वास्तव में, आइए अस्थायी रूप से परिचय दें ${\widehat {a}}(s)={\widehat {a}}(s\alpha )$ असली के साथ $s$ और विचार करें कि कैसे ${\widehat {a}}(s)$ कब भिन्न होता है $s$ 0 से 1 में परिवर्तन। विभेद करना ${\widehat {a}}(s)$ इसके संबंध में $s$, हम देखतें है

${\frac {\partial }{\partial s}}{\widehat {a}}(s)=D^{\dagger }(s\alpha )[\alpha ^{*}{\widehat {a}}-\alpha {\widehat {a}}^{\dagger },{\widehat {a}}]D(s\alpha )=\alpha ,$ ताकि ${\widehat {a}}(s)={\widehat {a}}(0)+s\alpha .$ चूँकि सुसंगत अवस्थाएँ संहार संचालक और किसी संख्या से गुणन संचालक दोनों की मूल अवस्थाएँ हैं, इसलिए यह देखना आसान है कि, वास्तव में, विस्थापन संचालक सुसंगत अवस्थाओं को स्थानांतरित करता है, या, अधिक सटीक रूप से,

${\widehat {D}}(\alpha )|\beta \rangle =|\alpha +\beta \rangle .$ दरअसल, ऊपर प्राप्त संबंध को इस प्रकार फिर से लिखा जा सकता है ${\widehat {a}}{\widehat {D}}(\alpha )={\widehat {D}}(\alpha )({\widehat {a}}+\alpha )$, तब

${\widehat {a}}{\widehat {D}}(\alpha )|\beta \rangle ={\widehat {D}}(\alpha )({\widehat {a}}+\alpha )|\beta \rangle =(\alpha +\beta ){\widehat {D}}(\alpha )|\beta \rangle .$ इस प्रकार, ${\widehat {D}}(\alpha )|\beta \rangle$ आइगेनवैल्यू के साथ विनाश संचालिका का एक आइजेनस्टेट है $\alpha +\beta$, इस तरह ${\widehat {D}}(\alpha )|\beta \rangle =|\alpha +\beta \rangle$.

विशेष रूप से,

${\widehat {D}}(-\alpha )|\alpha \rangle =|0\rangle$

जिससे होता है

$|\alpha \rangle ={\widehat {D}}(\alpha )|0\rangle$.

यह महत्वपूर्ण है क्योंकि यह दर्शाता है कि सभी सुसंगत अवस्थाओं को जमीनी अवस्था के विस्थापन के रूप में प्राप्त किया जा सकता है, जो प्रकाशिकी में निर्वात अवस्था भी है।

यह भी देखें

• अशास्त्रीय प्रकाश
• रोटेशन ऑपरेटर (क्वांटम यांत्रिकी)
• क्वांटम हार्मोनिक ऑसिलेटर
• अर्धसंभाव्यता वितरण
• हुसिमी क्यू प्रतिनिधित्व
• निचोड़ा हुआ सुसंगत अवस्था
• विग्नर क्वासिप्रोबेबिलिटी वितरण