परिमित अंतर

परिमित अंतर रूप की गणितीय अभिव्यक्ति है f (x + b) − f (x + a)। यदि एक परिमित अंतर b − a से विभाजित किया जाता है, अंतर भागफल मिलता है। परिमित भिन्नताओं द्वारा अवकलज का अनुमान अंतर समीकरण के संख्यात्मक विश्लेषण समाधान के लिएपरिमित अंतर विधि यों में एक केंद्रीय भूमिका निभाता है विशेष रूप से सीमा मूल्य समस्या के लिए निभाता है।

अंतरसंकारक, आमतौर पर $\Delta$ के रूप में जाना जाता है, वह संकारक (गणित) है जो किसी फलन f को $\Delta [f]$ द्वारा परिभाषित करता है।

$\Delta [f](x)=f(x+1)-f(x).$

अंतर समीकरण एक फलनिक समीकरण है जिसमें परिमित अंतर संकारक उसी तरह शामिल होता है जैसे एक अंतर समीकरण में अवकलज शामिल होते हैं। अंतर समीकरणों और अंतर समीकरणों के बीच कई समानताएं हैं, विशेष रूप से हल करने के तरीकों में। कुछ पुनरावृत्ति संबंधों को परिमित अंतरों के साथ पुनरावृत्ति संकेतन को बदलकर अंतर समीकरणों के रूप में लिखा जा सकता है।

संख्यात्मक विश्लेषण में, अवकलज का अनुमान लगाने के लिए परिमित अंतर का व्यापक रूप से उपयोग किया जाता है, और "परिमित अंतर" शब्द का उपयोग अक्सर "अवकलज के परिमित अंतर सन्निकटन" के संक्षिप्त रूप में किया जाता है। परिमित अंतर सन्निकटन ऊपर नियोजित शब्दावली में परिमित अंतर भागफल हैं।

1715 में ब्रुक टेलर द्वारा परिमित अंतर पेश किए गए थे और जॉर्ज बूले(1860), एल.एम. मिल्ने-थॉमसन (1933), और केरोली जॉर्डन (1939) द्वारा कार्यों में सार स्व-स्थायी गणितीय वस्तुओं के रूप में भी अध्ययन किया गया है। परिमित अंतर अपनी उत्पत्ति को जोस्ट बर्गी के एल्गोरिदम (c. 1592) में से एक में खोजते हैं और आइजैक न्यूटन सहित अन्य लोगों द्वारा काम करते हैं। परिमित अंतरों की औपचारिक गणना को अत्युणु की गणना के विकल्प के रूप में देखा जा सकता है।

मूल प्रकार

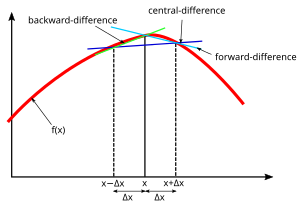
आमतौर पर तीन बुनियादी प्रकारों पर विचार किया जाता है: अग्र, पश्च और केंद्रीय परिमित अंतर।

अग्रांतर सूत्र, $\Delta _{h}[f],$ एक फलन f के रूप में परिभाषित फलन है

$\Delta _{h}[f](x)=f(x+h)-f(x).$

अनुप्रयोग के आधार पर, रिक्ति h परिवर्तनशील या स्थिर हो सकता है। जब छोड़ा गया, h 1 लिया जाता है, वह है,

$\Delta [f](x)=\Delta _{1}[f](x)=f(x+1)-f(x).$

पश्च अंतर फलन मानों x और x − h का उपयोग करता है , x + h औरx के मानों के बजाय::

$\nabla _{h}[f](x)=f(x)-f(x-h)=\Delta _{h}[f](x-h).$

अंत में, केंद्रीय अंतर द्वारा दिया जाता है

$\delta _{h}[f](x)=f(x+{\tfrac {h}{2}})-f(x-{\tfrac {h}{2}})=\Delta _{h/2}[f](x)+\nabla _{h/2}[f](x).$

अवकलज के साथ संबंध

परिमित अंतर अक्सर व्युत्पन्न के सन्निकटन के रूप में प्रयोग किया जाता है, आमतौर पर संख्यात्मक अवकलन में।

फलन का व्युत्पन्न f एक बिंदु पर x फलन की सीमा द्वारा परिभाषित किया गया है।

$f'(x)=\lim _{h\to 0}{\frac {f(x+h)-f(x)}{h}}.$

यदि h शून्य के करीब पहुंचने के बजाय निश्चित (गैर-शून्य) मान है, तो उपरोक्त समीकरण के दाहिने हाथ की ओर लिखा जाएगा

${\frac {f(x+h)-f(x)}{h}}={\frac {\Delta _{h}[f](x)}{h}}.$

इसलिए, जब h छोटा है अग्र के अंतर से विभाजित h अवकलज का अनुमान लगाता है। इस सन्निकटन में त्रुटि टेलर के प्रमेय से प्राप्त की जा सकती है। ये मानते हुए f दो बार अवकलनीय है, हमारे पास है

${\frac {\Delta _{h}[f](x)}{h}}-f'(x)=O(h)\to 0\quad {\text{as }}h\to 0.$

पिछड़े अंतर के लिए समान सूत्र है:

${\frac {\nabla _{h}[f](x)}{h}}-f'(x)=O(h)\to 0\quad {\text{as }}h\to 0.$

हालांकि, केंद्रीय (जिसे केंद्रित भी कहा जाता है) अंतर अधिक सटीक सन्निकटन पैदा करता है। यदि f तीन गुना अवकलनीय है,

${\frac {\delta _{h}[f](x)}{h}}-f'(x)=O\left(h^{2}\right).$

मुख्य समस्या हालांकि, केंद्रीय अंतर विधि के साथ, यह है कि दोलन फलन शून्य व्युत्पन्न प्राप्त कर सकते हैं। यदि f (nh) = 1 के लिए n विषम, और f (nh) = 2 के लिए n फिर भी f ′(nh) = 0 यदि इसकी गणना केंद्रीय अंतर योजना से की जाती है। यह विशेष रूप से परेशानी भरा है अगर का डोमेन f असतत है। सममित व्युत्पन्न भी देखें

लेखक जिनके लिए परिमित अंतर का अर्थ है परिमित अंतर सन्निकटन अग्र/पश्च/केंद्रीय अंतर को इस खंड में दिए गए भागफल के रूप में परिभाषित करते हैं (पिछले खंड में दी गई परिभाषाओं को नियोजित करने के बजाय)।

उच्च-क्रम अंतर

एक समान तरीके से, उच्च ऑर्डर अवकलज और अंतर ऑपरेटरों के लिए परिमित अंतर सन्निकटन प्राप्त कर सकते हैं। उदाहरण के लिए, उपरोक्त केंद्रीय अंतर सूत्र का उपयोग करके f ′(x + h/2) और f ′(x − h/2) और के व्युत्पन्न के लिए एक केंद्रीय अंतर सूत्र लागू करना f ′ पर x, हम के दूसरे व्युत्पन्न का केंद्रीय अंतर सन्निकटन प्राप्त करते हैं f:

दूसरे क्रम का केंद्रीय

$f''(x)\approx {\frac {\delta _{h}^{2}[f](x)}{h^{2}}}={\frac {{\frac {f(x+h)-f(x)}{h}}-{\frac {f(x)-f(x-h)}{h}}}{h}}={\frac {f(x+h)-2f(x)+f(x-h)}{h^{2}}}.$

इसी तरह हम अन्य भिन्न सूत्रों को पुनरावर्ती तरीके से लागू कर सकते हैं।

दूसरा आदेश अग्र

$f''(x)\approx {\frac {\Delta _{h}^{2}[f](x)}{h^{2}}}={\frac {{\frac {f(x+2h)-f(x+h)}{h}}-{\frac {f(x+h)-f(x)}{h}}}{h}}={\frac {f(x+2h)-2f(x+h)+f(x)}{h^{2}}}.$

दूसरा क्रम पिछड़ा

$f''(x)\approx {\frac {\nabla _{h}^{2}[f](x)}{h^{2}}}={\frac {{\frac {f(x)-f(x-h)}{h}}-{\frac {f(x-h)-f(x-2h)}{h}}}{h}}={\frac {f(x)-2f(x-h)+f(x-2h)}{h^{2}}}.$

अधिक आम तौर पर,nवें क्रम अग्र, पश्च, और केंद्रीय अंतर क्रमशः द्वारा दिए गए हैं,

अग्र

$\Delta _{h}^{n}[f](x)=\sum _{i=0}^{n}(-1)^{n-i}{\binom {n}{i}}f{\bigl (}x+ih{\bigr )},$

या के लिए h = 1,

$\Delta ^{n}[f](x)=\sum _{i=0}^{n}{\binom {n}{i}}(-1)^{n-i}f(x+i)$

पिछड़ा

$\nabla _{h}^{n}[f](x)=\sum _{i=0}^{n}(-1)^{i}{\binom {n}{i}}f(x-ih),$

केंद्रीय

$\delta _{h}^{n}[f](x)=\sum _{i=0}^{n}(-1)^{i}{\binom {n}{i}}f\left(x+\left({\frac {n}{2}}-i\right)h\right).$

योग चिह्न के रूप में दिखाए जाने के बाद ये समीकरण द्विपद गुणांक का उपयोग करते हैं (ⁿ
_i). पास्कल के त्रिभुज की प्रत्येक पंक्ति के प्रत्येक मान के लिए गुणांक प्रदान करती है i.

ध्यान दें कि विषम के लिए केंद्रीय अंतर होगा n, पास होना h गैर-पूर्णांक से गुणा। यह अक्सर एक समस्या होती है क्योंकि यह विवेक के अंतराल को बदलने के बराबर होती है। का औसत लेकर समस्या का समाधान किया जा सकता है δⁿ[ f ](x − h/2) और δⁿ[ f ](x + h/2).

एक अनुक्रम पर लागू किए गए अग्र के अंतर को कभी-कभी अनुक्रम का द्विपद परिवर्तन कहा जाता है, और इसमें कई दिलचस्प संयोजी गुण होते हैं। नॉर्लंड-राइस इंटीग्रल का उपयोग करके अग्र के अंतर का मूल्यांकन किया जा सकता है। इस प्रकार की श्रृंखलाओं के लिए अभिन्न प्रतिनिधित्व दिलचस्प है, क्योंकि अभिन्न का मूल्यांकन अक्सर स्पर्शोन्मुख विस्तार या लादने की सीमा तकनीकों का उपयोग करके किया जा सकता है, इसके विपरीत, अग्र की अंतर श्रृंखला संख्यात्मक रूप से मूल्यांकन करने के लिए बेहद कठिन हो सकती है, क्योंकि द्विपद गुणांक बड़े के लिए तेजी से बढ़ते हैं n.

संबंधित अवकलज के साथ इन उच्च-क्रम के अंतरों का संबंध सीधा है,

${\frac {d^{n}f}{dx^{n}}}(x)={\frac {\Delta _{h}^{n}[f](x)}{h^{n}}}+O(h)={\frac {\nabla _{h}^{n}[f](x)}{h^{n}}}+O(h)={\frac {\delta _{h}^{n}[f](x)}{h^{n}}}+O\left(h^{2}\right).$

बेहतर सन्निकटन बनाने के लिए उच्च-क्रम के अंतर का भी उपयोग किया जा सकता है। जैसा कि ऊपर उल्लेख किया गया है, प्रथम-क्रम अंतर आदेश की अवधि तक प्रथम-क्रम व्युत्पन्न का अनुमान लगाता है h. हालाँकि, संयोजन

${\frac {\Delta _{h}[f](x)-{\frac {1}{2}}\Delta _{h}^{2}[f](x)}{h}}=-{\frac {f(x+2h)-4f(x+h)+3f(x)}{2h}}$

अनुमानित f ′(x) आदेश की अवधि तक h². यह टेलर श्रृंखला में उपरोक्त अभिव्यक्ति का विस्तार करके या परिमित अंतरों के कलन का उपयोग करके सिद्ध किया जा सकता है, जिसे नीचे समझाया गया है।

यदि आवश्यक हो, तो अग्र, पश्च और केंद्रीय अंतरों को मिलाकर परिमित अंतर को किसी भी बिंदु पर केंद्रित किया जा सकता है।

बहुपद

डिग्री के दिए गए बहुपद के लिए n ≥ 1फलन में व्यक्त किया P(x), वास्तविक संख्या के साथ a ≠ 0 और b और निचले क्रम की शर्तें (यदि कोई हो) के रूप में चिह्नित l.o.t.:

$P(x)=ax^{n}+bx^{n-1}+l.o.t.$ बाद में n जोड़ो में मतभेद, निम्नलिखित परिणाम प्राप्त किया जा सकता है, जहां h ≠ 0 अंकगणितीय अंतर को चिह्नित करने वाली एक वास्तविक संख्या है:

$\Delta _{h}^{n}[P](x)=ah^{n}n!$ केवल उच्चतम-क्रम पद का गुणांक रहता है। चूंकि यह परिणाम के संबंध में स्थिर है x, किसी भी जोड़ीवार अंतर का मान होगा 0.

आगमनात्मक प्रमाण

बेस केस

होने देना Q(x) डिग्री का बहुपद हो 1:

$\Delta _{h}[Q](x)=Q(x+h)-Q(x)=[a(x+h)+b]-[ax+b]=ah=ah^{1}1!$ यह इसे आधार मामले के लिए साबित करता है।

स्टेप केस

होने देना R(x) डिग्री का बहुपद हो m-1 कहां m ≥ 2 और उच्चतम-क्रम पद का गुणांक हो a ≠ 0. निम्नलिखित को घात के सभी बहुपदों के लिए सत्य मानते हुए m-1:

$\Delta _{h}^{m-1}[R](x)=ah^{m-1}(m-1)!$ होने देना S(x) डिग्री का बहुपद हो m. एक जोड़ो में अंतर के साथ:

$\Delta _{h}[S](x)=[a(x+h)^{m}+b(x+h)^{m-1}+l.o.t.]-[ax^{m}+bx^{m-1}+l.o.t.]=ahmx^{m-1}+l.o.t.=T(x)$ जैसा ahm ≠ 0, इसका परिणाम एक बहुपद में होता है T(x) डिग्री का m-1, साथ ahm उच्चतम-क्रम अवधि के गुणांक के रूप में। उपरोक्त धारणा को देखते हुए और m-1 जोड़ीदार अंतर (जिसके परिणामस्वरूप कुल m जोड़ीदार अंतर के लिए S(x)), यह पाया जा सकता है कि:

$\Delta _{h}^{m-1}[T](x)=ahm\cdot h^{m-1}(m-1)!=ah^{m}m!$ यह प्रमाण को पूरा करता है।

अनुप्रयोग

इस पहचान का उपयोग सबसे कम-डिग्री वाले बहुपद को खोजने के लिए किया जा सकता है जो कई बिंदुओं को रोकता है (x, y) जहाँ x-अक्ष पर एक बिंदु से दूसरे बिंदु का अंतर एक स्थिरांक है h ≠ 0. उदाहरण के लिए, निम्नलिखित बिंदु दिए गए हैं:

x	y
1	4
4	109
7	772
10	2641
13	6364

हम अंतर तालिका का उपयोग कर सकते हैं, जहां सभी कक्ष पहले के दाईं ओर होते हैं y, सेल के लिए तुरंत बाईं ओर कॉलम में सेल्स के लिए निम्न संबंध मौजूद है (a+1, b+1), शीर्ष-बाएँ सेल समन्वय पर होने के साथ (0, 0):

$(a+1,b+1)=(a,b)-(a,b+1)$ पहला पद ज्ञात करने के लिए, निम्न तालिका का उपयोग किया जा सकता है:

x	y	Δy	Δ2y	Δ3y
1	4
4	109	105
7	772	663	558
10	2641	1869	1206	648
13	6364	3723	1854	648

यह एक स्थिरांक पर आता है 648. अंकगणितीय अंतर है h=3, जैसा कि ऊपर स्थापित किया गया है। स्थिरांक तक पहुँचने के लिए जोड़ीदार अंतरों की संख्या को देखते हुए, यह अनुमान लगाया जा सकता है कि यह डिग्री का बहुपद है 3. इस प्रकार, उपरोक्त पहचान का उपयोग करना:

$648=a\cdot 3^{3}\cdot 3!=a\cdot 27\cdot 6=a\cdot 162$ के लिए हल करना a, इसका मान पाया जा सकता है 4. इस प्रकार, बहुपद का पहला पद है 4x³.

फिर, पहले पद को घटाकर, जो बहुपद की घात को कम करता है, और परिमित अंतर को फिर से ज्ञात करता है:

x	y	Δy	Δ2y
1	4 - 4(1)3 = 4 - 4 = 0
4	109 - 4(4)3 = 109 - 256 = -147	-147
7	772 - 4(7)3 = 772 - 1372 = -600	-453	-306
10	2641 - 4(10)3 = 2641 - 4000 = -1359	-759	-306
13	6364 - 4(13)3 = 6364 - 8788 = -2424	-1065	-306

यहाँ, स्थिरांक केवल 2 जोड़ीदार अंतरों के बाद प्राप्त किया जाता है, इस प्रकार निम्न परिणाम:

$-306=a\cdot 3^{2}\cdot 2!=a\cdot 18$ के लिए हल करना a, जो है -17, बहुपद का दूसरा पद है -17x².

दूसरे पद को घटाकर, अगले पद पर जाना:

x	y	Δy
1	0 - (-17(1)2) = 0 + 17 = 17
4	-147 - (-17(4)2) = -147 + 272 = 125	108
7	-600 - (-17(7)2) = -600 + 833 = 233	108
10	-1359 - (-17(10)2) = -1359 + 1700 = 341	108
13	-2424 - (-17(13)2) = -2424 + 2873 = 449	108

इस प्रकार स्थिर केवल 1 जोड़ीदार अंतर के बाद प्राप्त किया जाता है:

$108=a\cdot 3^{1}\cdot 1!=a\cdot 3$ यह पाया जा सकता है a = 36 और इस प्रकार बहुपद का तीसरा पद है 36x. तीसरे पद को घटाना:

x	y
1	17 - 36(1) = 17 - 36 = -19
4	125 - 36(4) = 125 - 144 = -19
7	233 - 36(7) = 233 - 252 = -19
10	341 - 36(10) = 341 - 360 = -19
13	449 - 36(13) = 449 - 468 = -19

बिना किसी युग्मवार अंतर के, यह पाया जाता है कि बहुपद का चौथा और अंतिम पद अचर है -19. इस प्रकार, पहली तालिका में सभी बिंदुओं को इंटरसेप्ट करने वाला निम्नतम-डिग्री बहुपद पाया जाता है:

$4x^{3}-17x^{2}+36x-19$

मनमाने ढंग से गुठली का आकार

Main article: Finite difference coefficient

Further information: Five-point stencil

रेखीय बीजगणित का उपयोग करके परिमित अंतर सन्निकटन का निर्माण किया जा सकता है जो किसी भी आदेश व्युत्पन्न के लिए बाईं ओर बिंदुओं की मनमानी संख्या और मूल्यांकन बिंदु के दाईं ओर (संभवतः भिन्न) अंकों की संख्या का उपयोग करता है। इसमें एक रेखीय प्रणाली को हल करना शामिल है जैसे कि मूल्यांकन बिंदु के चारों ओर उन बिंदुओं के योग का टेलर विस्तार वांछित व्युत्पन्न के टेलर विस्तार का सबसे अच्छा अनुमान लगाता है। इस तरह के सूत्रों को हेक्सागोनल या हीरे के आकार के ग्रिड पर रेखांकन के रूप में दर्शाया जा सकता है। यह एक ग्रिड पर एक फलन को अलग करने के लिए उपयोगी है, जहां एक व्यक्ति ग्रिड के किनारे तक पहुंचता है, उसे एक तरफ कम और कम बिंदुओं का नमूना लेना चाहिए।

विवरण इन नोट्स में दिए गए हैं।

परिमित अंतर गुणांक कैलक्यूलेटर गैर-मानक (और यहां तक ​​कि गैर-पूर्णांक) स्टेंसिल के लिए परिमित अंतर सन्निकटन का निर्माण करता है जिसे मनमाना स्टैंसिल और वांछित व्युत्पन्न क्रम दिया जाता है .

गुण

• सभी सकारात्मक के लिए k और n
  $$\Delta _{kh}^{n}(f,x)=\sum \limits _{i_{1}=0}^{k-1}\sum \limits _{i_{2}=0}^{k-1}\cdots \sum \limits _{i_{n}=0}^{k-1}\Delta _{h}^{n}\left(f,x+i_{1}h+i_{2}h+\cdots +i_{n}h\right).$$
• लीबनिज नियम (सामान्यीकृत उत्पाद नियम) :
  $$\Delta _{h}^{n}(fg,x)=\sum \limits _{k=0}^{n}{\binom {n}{k}}\Delta _{h}^{k}(f,x)\Delta _{h}^{n-k}(g,x+kh).$$

अंतर समीकरणों में

Main article: Finite difference method

परिमित अंतरों का एक महत्वपूर्ण अनुप्रयोग संख्यात्मक विश्लेषण में है, विशेष रूप से संख्यात्मक आंशिक अंतर समीकरण ों में, जो साधारण अंतर समीकरण और आंशिक अंतर समीकरणों के संख्यात्मक समाधान का लक्ष्य रखता है। विचार यह है आंशिक विभेदक समीकरण में दिखाई देने वाले अवकलज को परिमित अंतर से बदल दिया जाए जो उन्हें अनुमानित करता है। परिणामी विधियों को परिमित अंतर विधियाँ कहा जाता है।

कम्प्यूटेशनल विज्ञान और इंजीनियरिंग विषयों में परिमित अंतर विधि के सामान्य अनुप्रयोग हैं, जैसे थर्मल इंजीनियरिंग , द्रव यांत्रिकी, आदि।

न्यूटन की श्रृंखला

न्यूटन बहुपद में न्यूटन फ़ॉरवर्ड डिफ़रेंस समीकरण की शर्तें शामिल हैं, जिसका नाम इसहाक न्यूटन के नाम पर रखा गया है, संक्षेप में, यह न्यूटन इंटरपोलेशन फॉर्मूला है, जो पहली बार 1687 में उनके 'फिलोसोफी नेचुरेलिस प्रिंसिपिया मैथेमेटिका' में प्रकाशित हुआ था। अर्थात् निरंतर टेलर विस्तार का असतत अनुरूप,

$f(x)=\sum _{k=0}^{\infty }{\frac {\Delta ^{k}[f](a)}{k!}}\,(x-a)_{k}=\sum _{k=0}^{\infty }{\binom {x-a}{k}}\,\Delta ^{k}[f](a),$

जो किसी भी बहुपद फलन के लिए है f और कई (लेकिन सभी नहीं) विश्लेषणात्मक फलन ों के लिए। (यह कब पकड़ में नहीं आता है f चरघातांकी प्रकार है $\pi$. यह आसानी से देखा जा सकता है, क्योंकि साइन फलन के पूर्णांक गुणकों पर गायब हो जाता है $\pi$, संबंधित न्यूटन श्रृंखला समान रूप से शून्य है, क्योंकि इस मामले में सभी परिमित अंतर शून्य हैं। फिर भी स्पष्ट रूप से, ज्या फलन शून्य नहीं है।) यहाँ, व्यंजक

${\binom {x}{k}}={\frac {(x)_{k}}{k!}}$

द्विपद गुणांक है, और

$(x)_{k}=x(x-1)(x-2)\cdots (x-k+1)$

खाली उत्पाद होने पर फैक्टोरियल या लोअर फैक्टोरियल गिर रहा है (x)₀ 1 के रूप में परिभाषित किया गया है। इस विशेष मामले में, के मानों में परिवर्तन के लिए इकाई चरणों की धारणा है x, h = 1 नीचे दिए गए सामान्यीकरण का।

टेलर के प्रमेय के इस परिणाम के औपचारिक पत्राचार पर ध्यान दें। ऐतिहासिक रूप से, यह, साथ ही चू-वंडरमोंड पहचान,

$(x+y)_{n}=\sum _{k=0}^{n}{\binom {n}{k}}(x)_{n-k}\,(y)_{k},$

(इससे अनुसरण करते हुए, और द्विपद प्रमेय के अनुरूप), उन टिप्पणियों में शामिल हैं जो अम्ब्रल कैलकुलस की प्रणाली के लिए परिपक्व हैं।

न्यूटन श्रृंखला विस्तार टेलर श्रृंखला विस्तार से बेहतर हो सकता है जब क्वांटम स्पिन (होल्स्टीन-प्रिमाकॉफ परिवर्तन देखें), नॉर्मल_ऑर्डर#बोसोनिक_ऑपरेटर_फंक्शन या असतत गिनती के आंकड़ों जैसी असतत मात्राओं पर लागू किया जाता है। वास्तविक अभ्यास में कोई न्यूटन के सूत्र का उपयोग कैसे कर सकता है, यह समझाने के लिए, फाइबोनैचि अनुक्रम को दोगुना करने के पहले कुछ शब्दों पर विचार करें। f = 2, 2, 4, ... कोई एक बहुपद खोज सकता है जो पहले एक अंतर तालिका की गणना करके, और उसके बाद के अंतरों को प्रतिस्थापित करके इन मानों को पुन: उत्पन्न करता है x₀ (रेखांकित) सूत्र में निम्नानुसार है,

${\begin{matrix}{\begin{array}{|c||c|c|c|}\hline x&f=\Delta ^{0}&\Delta ^{1}&\Delta ^{2}\\\hline 1&{\underline {2}}&&\\&&{\underline {0}}&\\2&2&&{\underline {2}}\\&&2&\\3&4&&\\\hline \end{array}}&\quad {\begin{aligned}f(x)&=\Delta ^{0}\cdot 1+\Delta ^{1}\cdot {\dfrac {(x-x_{0})_{1}}{1!}}+\Delta ^{2}\cdot {\dfrac {(x-x_{0})_{2}}{2!}}\quad (x_{0}=1)\\\\&=2\cdot 1+0\cdot {\dfrac {x-1}{1}}+2\cdot {\dfrac {(x-1)(x-2)}{2}}\\\\&=2+(x-1)(x-2)\\\end{aligned}}\end{matrix}}$

के मानों में गैर-समान चरणों के मामले में x, न्यूटन विभाजित अंतरों की गणना करता है,

$\Delta _{j,0}=y_{j},\qquad \Delta _{j,k}={\frac {\Delta _{j+1,k-1}-\Delta _{j,k-1}}{x_{j+k}-x_{j}}}\quad \ni \quad \left\{k>0,\;j\leq \max \left(j\right)-k\right\},\qquad \Delta 0_{k}=\Delta _{0,k}$

उत्पादों की श्रृंखला,

${P_{0}}=1,\quad \quad P_{k+1}=P_{k}\cdot \left(\xi -x_{k}\right),$

और परिणामी बहुपद अदिश गुणनफल है,

$f(\xi )=\Delta 0\cdot P\left(\xi \right)$ .

पी-एडिक संख्या के साथ विश्लेषण में |p-आदिक संख्या, Mahler के प्रमेय में कहा गया है कि धारणा है कि f एक बहुपद फलन है कि धारणा के लिए सभी तरह से कमजोर किया जा सकता है f केवल निरंतर है।

कार्लसन की प्रमेय न्यूटन श्रृंखला के अद्वितीय होने के लिए आवश्यक और पर्याप्त शर्तें प्रदान करती है, यदि यह मौजूद है। हालाँकि, न्यूटन श्रृंखला सामान्य रूप से मौजूद नहीं है।

न्यूटन श्रृंखला, स्टर्लिंग श्रृंखला और सेलबर्ग वर्ग के साथ, सामान्य अंतर श्रृंखला का एक विशेष मामला है, जिनमें से सभी को उपयुक्त रूप से अग्र बढ़ने वाले अंतरों के संदर्भ में परिभाषित किया गया है।

एक संकुचित और थोड़ा अधिक सामान्य रूप और समदूरस्थ नोड्स में सूत्र पढ़ता है

$f(x)=\sum _{k=0}{\binom {\frac {x-a}{h}}{k}}\sum _{j=0}^{k}(-1)^{k-j}{\binom {k}{j}}f(a+jh).$

परिमित अंतरों की गणना

अग्र के अंतर को एक संकारक (गणित) के रूप में माना जा सकता है, जिसे अंतरसंकारक कहा जाता है, जो फलन को मैप करता है f को Δ_h[ f ]. इस संकारक की राशि है

$\Delta _{h}=T_{h}-I,$

कहां T_h द्वारा परिभाषित चरण एच के साथ शिफ्ट संकारक है T_h[ f ](x) = f (x + h), और I पहचान संकारक है।

उच्च आदेशों के परिमित अंतर को पुनरावर्ती तरीके से परिभाषित किया जा सकता है Δⁿ
_h ≡ Δ_h(Δ^{n − 1}
_h). एक अन्य समकक्ष परिभाषा है Δⁿ
_h = [T_h − I]ⁿ.

अंतरसंकारक Δ_h एक रैखिक संकारक है, इसलिए यह संतुष्ट करता है Δ_h[αf + βg](x) = α Δ_h[ f ](x) + β Δ_h[g](x).

यह ऊपर बताए गए एक विशेष लीबनिज़ नियम (सामान्यीकृत उत्पाद नियम) को भी संतुष्ट करता है, Δ_h(f (x)g(x)) = (Δ_hf (x)) g(x+h) + f (x) (Δ_hg(x)). इसी तरह के बयान पिछड़े और केंद्रीय मतभेदों के लिए हैं।

औपचारिक रूप से टेलर श्रृंखला के संबंध में अनुप्रयोग करना h, सूत्र देता है

$\Delta _{h}=hD+{\frac {1}{2!}}h^{2}D^{2}+{\frac {1}{3!}}h^{3}D^{3}+\cdots =\mathrm {e} ^{hD}-I,$

कहां D निरंतर व्युत्पन्न संकारक, मैपिंग को दर्शाता है f इसके व्युत्पन्न के लिए f ′. विस्तार तब मान्य होता है जब दोनों पक्ष पर्याप्त रूप से छोटे के लिए विश्लेषणात्मक कार्यों पर फलन करते हैं h. इस प्रकार, T_h = e^hD, और औपचारिक रूप से घातीय पैदावार को उलटा करना

$hD=\log(1+\Delta _{h})=\Delta _{h}-{\tfrac {1}{2}}\Delta _{h}^{2}+{\tfrac {1}{3}}\Delta _{h}^{3}-\cdots .$

यह सूत्र इस अर्थ में है कि बहुपद पर लागू होने पर दोनों संकारक समान परिणाम देते हैं।

विश्लेषणात्मक कार्यों के लिए भी, दाईं ओर की श्रृंखला को अभिसरण की गारंटी नहीं है, यह एक स्पर्शोन्मुख श्रृंखला हो सकती है। हालांकि, इसका उपयोग व्युत्पन्न के लिए अधिक सटीक सन्निकटन प्राप्त करने के लिए किया जा सकता है। उदाहरण के लिए, श्रृंखला के पहले दो पदों को बनाए रखने से दूसरे क्रम का सन्निकटन प्राप्त होता है f ′(x) #उच्च-क्रम अंतर|अनुभाग उच्च-क्रम अंतर के अंत में उल्लेख किया गया है।

पिछड़े और केंद्रीय अंतर ऑपरेटरों के लिए समान सूत्र हैं

$hD=-\log(1-\nabla _{h})\quad {\text{and}}\quad hD=2\operatorname {arsinh} \left({\tfrac {1}{2}}\delta _{h}\right).$

परिमित अंतरों की गणना कॉम्बिनेटरिक्स के अम्ब्रल कैलकुलस से संबंधित है। यह उल्लेखनीय रूप से व्यवस्थित पत्राचार अम्ब्रल मात्रा के commutators की पहचान के कारण उनके निरंतर अनुरूप है (h → 0 सीमाएं),

$\left[{\frac {\Delta _{h}}{h}},x\,T_{h}^{-1}\right]=[D,x]=I.$

बड़ी संख्या में मानक कलन के औपचारिक अंतर संबंध शामिल हैं कार्यों f (x) इस प्रकार अम्ब्रल परिमित-अंतर एनालॉग्स को शामिल करने के लिए व्यवस्थित रूप से मैप करें f (xT⁻¹
_h).

उदाहरण के लिए, एक मोनोमियल का उम्ब्रल एनालॉग xⁿ उपरोक्त गिरने वाले फैक्टोरियल (पोचममेर के-प्रतीक) का सामान्यीकरण है,

$~(x)_{n}\equiv \left(xT_{h}^{-1}\right)^{n}=x(x-h)(x-2h)\cdots {\bigl (}x-(n-1)h{\bigr )},$ ताकि

${\frac {\Delta _{h}}{h}}(x)_{n}=n(x)_{n-1},$

इसलिए उपरोक्त न्यूटन इंटरपोलेशन फॉर्मूला (मनमाने फलन के विस्तार में गुणांक मिलान करके f (x) ऐसे प्रतीकों में), और इसी तरह।

उदाहरण के लिए, उम्ब्रल साइन है

$\sin \left(x\,T_{h}^{-1}\right)=x-{\frac {(x)_{3}}{3!}}+{\frac {(x)_{5}}{5!}}-{\frac {(x)_{7}}{7!}}+\cdots$

सातत्य सीमा के रूप में, का आइजनफंक्शन Δ_h/h भी एक घातीय होता है,

${\frac {\Delta _{h}}{h}}(1+\lambda h)^{\frac {x}{h}}={\frac {\Delta _{h}}{h}}e^{\ln(1+\lambda h){\frac {x}{h}}}=\lambda e^{\ln(1+\lambda h){\frac {x}{h}}},$

और इसलिए निरंतर कार्यों के फूरियर योगों को आसानी से अम्ब्रल फूरियर योगों के लिए मैप किया जाता है, यानी, इन umbral आधार घातांकों को गुणा करने वाले समान फूरियर गुणांकों को शामिल करना। यह उम्ब्रल एक्सपोनेंशियल इस प्रकार पोचममेर प्रतीकों के एक्सपोनेंशियल जनरेटिंग फलन की मात्रा है।

इस प्रकार, उदाहरण के लिए, डिराक डेल्टा फलन मैप्स को इसके उम्ब्रल संवाददाता, सिंक फलन ,

$\delta (x)\mapsto {\frac {\sin \left[{\frac {\pi }{2}}\left(1+{\frac {x}{h}}\right)\right]}{\pi (x+h)}},$

इत्यादि। अंतर समीकरणों को अक्सर उन तकनीकों के साथ हल किया जा सकता है जो अंतर समीकरणों को हल करने के लिए बहुत समान हैं।

फ़ॉरवर्ड डिफ़रेंस संकारक का व्युत्क्रम संकारक, इसलिए फिर उम्ब्रल इंटीग्रल, अनिश्चित योग या प्रतिपक्ष संकारक है।

परिमित अंतर ऑपरेटरों की गणना के लिए नियम

भेदभाव नियमों के अनुरूप, हमारे पास है:

• निरंतर नियम : यदि c एक स्थिरांक (गणित) है, तब

$\Delta c=0$

• विभेदन की रैखिकता: यदि a और b स्थिर हैं (गणित),

$\Delta (af+bg)=a\,\Delta f+b\,\Delta g$

उपरोक्त सभी नियम किसी भी अंतरसंकारक पर समान रूप से अच्छी तरह से लागू होते हैं, जिनमें शामिल हैं ∇ के रूप में Δ.

• प्रॉडक्ट नियम :

${\begin{aligned}\Delta (fg)&=f\,\Delta g+g\,\Delta f+\Delta f\,\Delta g\\\nabla (fg)&=f\,\nabla g+g\,\nabla f-\nabla f\,\nabla g\end{aligned}}$

• भागफल नियम :

$\nabla \left({\frac {f}{g}}\right)={\frac {1}{g}}\det {\begin{bmatrix}\nabla f&\nabla g\\f&g\end{bmatrix}}\left(\det {\begin{bmatrix}g&\nabla g\\1&1\end{bmatrix}}\right)^{-1}$

या

$\nabla \left({\frac {f}{g}}\right)={\frac {g\,\nabla f-f\,\nabla g}{g\cdot (g-\nabla g)}}$

• कलन का मौलिक प्रमेय :

${\begin{aligned}\sum _{n=a}^{b}\Delta f(n)&=f(b+1)-f(a)\\\sum _{n=a}^{b}\nabla f(n)&=f(b)-f(a-1)\end{aligned}}$

संदर्भ देखें।

सामान्यीकरण

• एक सामान्यीकृत परिमित अंतर को आमतौर पर इस रूप में परिभाषित किया जाता है
  $$\Delta _{h}^{\mu }[f](x)=\sum _{k=0}^{N}\mu _{k}f(x+kh),$$
  कहां μ = (μ₀, …, μ_N) इसका गुणांक वेक्टर है। एक अनंत अंतर एक और सामान्यीकरण है, जहां ऊपर परिमित योग को एक श्रृंखला (गणित) द्वारा प्रतिस्थापित किया जाता है। सामान्यीकरण का दूसरा तरीका गुणांक बना रहा है μ_k बिन्दु पर निर्भर है x: μ_k = μ_k(x), इस प्रकार भारित परिमित अंतर पर विचार करना। कोई कदम भी उठा सकता है h बिन्दु पर निर्भर है x: h = h(x). इस तरह के सामान्यीकरण निरंतरता के विभिन्न मापांकों के निर्माण के लिए उपयोगी होते हैं।
• सामान्यीकृत अंतर को बहुपद के छल्ले के रूप में देखा जा सकता है R[T_h]. यह अंतर बीजगणित की ओर जाता है।
• डिफरेंस संकारक आंशिक रूप से ऑर्डर किए गए सेट पर मोबियस इनवर्जन का सामान्यीकरण करता है।
• घुमाव संकारक के रूप में: घटना बीजगणित की औपचारिकता के माध्यम से, अंतरसंकारक और अन्य मोबियस व्युत्क्रम को पोसेट पर एक फलन के साथ कनवल्शन द्वारा दर्शाया जा सकता है, जिसे मोबियस फलन कहा जाता है μ, अंतरसंकारक के लिए μ क्रम है (1, −1, 0, 0, 0, …).

बहुभिन्नरूपी परिमित अंतर

परिमित अंतरों को एक से अधिक चरों में माना जा सकता है। वे कई चरों में आंशिक अवकलज के अनुरूप हैं।

कुछ आंशिक व्युत्पन्न सन्निकटन हैं:

${\begin{aligned}f_{x}(x,y)&\approx {\frac {f(x+h,y)-f(x-h,y)}{2h}}\\f_{y}(x,y)&\approx {\frac {f(x,y+k)-f(x,y-k)}{2k}}\\f_{xx}(x,y)&\approx {\frac {f(x+h,y)-2f(x,y)+f(x-h,y)}{h^{2}}}\\f_{yy}(x,y)&\approx {\frac {f(x,y+k)-2f(x,y)+f(x,y-k)}{k^{2}}}\\f_{xy}(x,y)&\approx {\frac {f(x+h,y+k)-f(x+h,y-k)-f(x-h,y+k)+f(x-h,y-k)}{4hk}}.\end{aligned}}$

वैकल्पिक रूप से, उन अनुप्रयोगों के लिए जिनमें की गणना f सबसे महंगा कदम है, और पहले और दूसरे अवकलज दोनों की गणना की जानी चाहिए, अंतिम मामले के लिए एक अधिक कुशल सूत्र है

$f_{xy}(x,y)\approx {\frac {f(x+h,y+k)-f(x+h,y)-f(x,y+k)+2f(x,y)-f(x-h,y)-f(x,y-k)+f(x-h,y-k)}{2hk}},$

चूंकि गणना करने के लिए केवल वही मान हैं जिनकी पहले से ही पिछले चार समीकरणों के लिए आवश्यकता नहीं है f (x + h, y + k) और f (x − h, y − k).

यह भी देखें

• Discrete calculus
• Divided differences
• Finite-difference time-domain method (FDTD)
• Finite volume method
• FTCS scheme
• Gilbreath's conjecture
• Sheffer sequence
• Summation by parts
• Time scale calculus
• Upwind differencing scheme for convection

संदर्भ

• Richardson, C. H. (1954): An Introduction to the Calculus of Finite Differences (Van Nostrand (1954) online copy
• Mickens, R. E. (1991): Difference Equations: Theory and Applications (Chapman and Hall/CRC) ISBN 978-0442001360

इस पेज में लापता आंतरिक लिंक की सूची

• गणना
• बहुत छोता
• फलन (गणित)
• संख्यात्मक विभेदन
• एक फलन की सीमा
• तरल यांत्रिकी
• घातीय प्रकार
• फिबोनाची अनुक्रम
• विभाजित मतभेद
• अदिश उत्पाद
• रैखिक संकारक
• पोछाम्मेर क-सिंबल
• निरंतरता की सीमा
• पोछाम्मेर सिंबल
• मैं अनिश्चित काल के लिए हूं
• विभेदन नियम
• निरंतर (गणित)
• भेदभाव की रैखिकता
• निरंतरता का मापांक
• आंशिक रूप से आदेशित सेट

बाहरी कड़ियाँ

• "Finite-difference calculus", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
• Table of useful finite difference formula generated using Mathematica
• D. Gleich (2005), Finite Calculus: A Tutorial for Solving Nasty Sums
• Discrete Second Derivative from Unevenly Spaced Points

श्रेणी: संख्यात्मक अंतर समीकरण श्रेणी:गणितीय विश्लेषण श्रेणी: क्रमगुणित और द्विपद विषय श्रेणी: कैलकुलस में लीनियर ऑपरेटर्स श्रेणी: संख्यात्मक विश्लेषण श्रेणी: गैर-न्यूटोनियन कलन