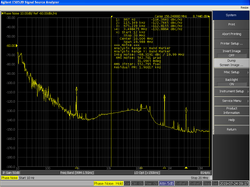
चरण रव

संकेत स्रोत विश्लेषक (एसएसए) द्वारा मापा गया चरण शोर। एसएसए चरण शोर का सकारात्मक हिस्सा दिखाता है। इस तस्वीर में मुख्य वाहक का चरण शोर, 3 अन्य संकेत और शोर पहाड़ी है।

मजबूत संकेत के चरण शोर में एक कमजोर संकेत गायब हो जाता है

संकेत प्रसंस्करण में, चरण शोर एक तरंग के चरण में यादृच्छिक उतार-चढ़ाव का आवृत्ति-कार्यक्षेत्र प्रतिनिधित्व होता है, जो पूर्ण आवधिकता (जिटर) से समय-कार्यक्षेत्र विचलन के अनुरूप होता है। सामान्यतया, आकाशवाणी आवृति इंजीनियर एक थरथरानवाला के चरण शोर की बात करते हैं, जबकि डिजिटल प्रणाली इंजीनियर एक घड़ी के जिटर के साथ काम करते हैं।

परिभाषाएँ

ऐतिहासिक रूप से चरण शोर के लिए दो परस्पर विरोधी अभी तक व्यापक रूप से उपयोग की जाने वाली परिभाषाएँ हैं। कुछ लेखक चरण शोर को केवल संकेत के चरण के वर्णक्रमीय घनत्व के रूप में परिभाषित करते हैं, जबकि दूसरी परिभाषा चरण स्पेक्ट्रम को संदर्भित करती है (जो वर्णक्रमीय घनत्व संबंधित अवधारणाएं) संकेत के वर्णक्रमीय अनुमान से उत्पन्न होती हैं। दोनों परिभाषाएँ वाहक से अच्छी तरह से हटाई गई ऑफ़सेट आवृति पर समान परिणाम देती हैं। हालांकि, क्लोज-इन ऑफ़सेट में, दो परिभाषाएँ भिन्न होती हैं।

IEEE चरण शोर को परिभाषित करता है ℒ(f) = S_φ(f)/2 जहां चरण अस्थिरता S_φ(f) संकेत के चरण विचलन का एक तरफा वर्णक्रमीय घनत्व है। यद्यपि S_φ(f) एक तरफा कार्य है, यह चरण में उतार-चढ़ाव के डबल-साइडबैंड वर्णक्रमीय घनत्व का प्रतिनिधित्व करता है। प्रतीक ℒ को (कैपिटल या अकेस) स्क्रिप्ट L कहा जाता हैं।

पृष्ठभूमि

एक आदर्शइलेक्ट्रॉनिक थरथरानवाला एक शुद्ध साइन तरंग उत्पन्न करेगा। आवृति कार्यक्षेत्र में, यह दोलक की आवृति परडिराक डेल्टा समारोह (पॉज़िटिव और नेगेटिव कॉन्जुगेट्स) की एक जोड़ी के रूप में दर्शाया जाएगा; यानी, सभी संकेत की शक्ति एक ही आवृत्ति पर होती है। सभी वास्तविक दोलकों में चरण संशोधित इलेक्ट्रॉनिक शोर घटक होते हैं। चरण शोर घटक एक संकेत की शक्ति को आसन्न आवृत्तियों तक फैलाते हैं, जिसके परिणामस्वरूप शोर साइडबैंड होते हैं। थरथरानवाला चरण शोर में अक्सर कम आवृत्तिझिलमिलाहट शोर शामिल होता है और इसमें सफेद शोर शामिल हो सकता है।

निम्नलिखित शोर-मुक्त संकेत पर विचार करें:

v(t) = Acos(2πf₀t).

चरण शोर इस संकेत में φ द्वारा दर्शाई गई स्टोकास्टिक प्रक्रिया को संकेत में निम्नानुसार जोड़ा जाता है:

v(t) = Acos(2πf₀t + φ(t)).

चरण शोर इसी प्रकार का साइक्लोस्टेशनरी शोर है और यह जिटर से निकटता से संबंधित है, विशेष रूप से महत्वपूर्ण प्रकार का चरण शोर है जो ऑसीलेटर चरण शोर द्वारा उत्पादित होता है।

चरण शोर (ℒ(f)) समान्यतः dBc /Hz की इकाइयों में व्यक्त किया जाता है, और यह वाहक से एक निश्चित ऑफ़सेट पर केंद्रित 1 Hz बैंडविड्थ में निहित वाहक के सापेक्ष शोर शक्ति का प्रतिनिधित्व करता है। उदाहरण के लिए, एक निश्चित संकेत में 10 kHz के ऑफ़सेट पर -80 dBc/Hz का फेज़ शोर हो सकता है और 100 kHz के ऑफ़सेट पर -95 dBc/Hz हो सकता है। चरण शोर को एकल-साइडबैंड या डबल-साइडबैंड मूल्यों के रूप में मापा और व्यक्त किया जा सकता है, लेकिन जैसा कि पहले उल्लेख किया गया है, IEEE ने परिभाषा को डबल-साइडबैंड PSD के आधे के रूप में अपनाया है।

जिटर रूपांतरण

चरण शोर को कभी-कभी ऑफ़सेट आवृति की एक निश्चित सीमा पर ℒ(f) को एकीकृत करके प्राप्त शक्ति के रूप में भी मापा और व्यक्त किया जाता है। उदाहरण के लिए, चरण शोर -40 dBc हो सकता है जो 1 kHz से 100 kHz की सीमा में एकीकृत कर सकता है। इस एकीकृत चरण शोर (डिग्री में व्यक्त) को निम्न सूत्र का उपयोग करके जिटर (सेकंड में व्यक्त) में परिवर्तित किया जा सकता है:

${\text{jitter (seconds}})={\frac {{\text{phase error (}}{}^{\circ }{\text{)}}}{360^{\circ }\times {\text{frequency (hertz)}}}}$

उस क्षेत्र में 1/f शोर की अनुपस्थिति में जहां चरण शोर -20dBc/दशक ढलान (लीसन का समीकरण) प्रदर्शित करता है, वर्गमूल औसत का वर्ग चक्र जिटर चरण शोर से संबंधित हो सकता है:

$\sigma _{c}^{2}={\frac {f^{2}{\mathcal {L}}\left(f\right)}{f_{\text{osc}}^{3}}}$

वैसे ही:

${\mathcal {L}}\left(f\right)={\frac {f_{\text{osc}}^{3}\sigma _{c}^{2}}{f^{2}}}$

नाप

चरण शोर को स्पेक्ट्रम विश्लेषक का उपयोग करके मापा जा सकता है यदि स्पेक्ट्रम विश्लेषक के स्थानीय ऑसीलेटर के संबंध में परीक्षण (डीयूटी) के तहत डिवाइस का चरण शोर बड़ा है। ध्यान रखा जाना चाहिए कि देखे गए मान मापा संकेत के कारण हैं और स्पेक्ट्रम विश्लेषक के फिल्टर के आकार कारक नहीं हैं। स्पेक्ट्रम विश्लेषक आधारित माप कई दशकों की आवृत्ति पर चरण-शोर शक्ति दिखा सकता है; जैसे 1 Hz से 10 MHz। विभिन्न ऑफसेटआवृत्ति क्षेत्रों में ऑफसेट आवृत्ति वाला ढलान शोर के स्रोत के रूप में सुराग प्रदान कर सकता है; उदाहरण के लिए, कम आवृत्ति झिलमिलाहट का शोर 30 dB प्रति दशक (= 9 dB प्रति सप्तक) घट रहा है।

चरण शोर मापन प्रणाली स्पेक्ट्रम विश्लेषक के विकल्प हैं। ये प्रणालियां आंतरिक और बाहरी संदर्भों का उपयोग कर सकती हैं और अवशिष्ट (योगात्मक) और पूर्ण शोर दोनों के मापन की अनुमति देती हैं। इसके अतिरिक्त, ये सिस्टम कम-शोर, निकट-से-वाहक, माप कर सकते हैं।

स्पेक्ट्रल शुद्धता

एक आदर्श इलेक्ट्रॉनिक दोलक का साइनवेव आउटपुट आवृत्ति स्पेक्ट्रम में सिंगल लाइन है। एक व्यावहारिक दोलक में ऐसी पूर्ण वर्णक्रमीय शुद्धता प्राप्त करने योग्य नहीं है। एक सुपरहेटरोडाइन रिसीवर के लिए स्थानीय दोलक में चरण शोर के कारण स्पेक्ट्रम लाइन का प्रसार कम से कम होना चाहिए क्योंकि यह IF (मध्यवर्ती आवृत्ति) एम्पलीफायर में फिल्टर द्वारा प्राप्तकर्ता आवृत्ति रेंज को प्रतिबंधित करने के उद्देश्य को पराजित करता है।

यह भी देखें

• एलन विचरण
• झिलमिलाहट शोर
• लेसन का समीकरण
• अधिकतम समय अंतराल त्रुटि
• शोर वर्णक्रमीय घनत्व
• वर्णक्रमीय घनत्व
• वर्णक्रमीय चरण
• ऑप्टो-इलेक्ट्रॉनिक दोलक

आगे की पढाई

• Rubiola, Enrico (2008), Phase Noise and Frequency Stability in Oscillators, Cambridge University Press, ISBN 978-0-521-88677-2
• Wolaver, Dan H. (1991), Phase-Locked Loop Circuit Design, Prentice Hall, ISBN 978-0-13-662743-2
• Lax, M. (August 1967), "Classical noise. V. Noise in self-sustained oscillators", Physical Review, 160 (2): 290–307, Bibcode:1967PhRv..160..290L, doi:10.1103/PhysRev.160.290
• Hajimiri, A.; Lee, T. H. (February 1998), "A general theory of phase noise in electrical oscillators" (PDF), IEEE Journal of Solid-State Circuits, 33 (2): 179–194, Bibcode:1998IJSSC..33..179H, doi:10.1109/4.658619, archived from the original (PDF) on 2015-03-05, retrieved 2021-09-16 {{citation}}: |archive-date= / |archive-url= timestamp mismatch (help)
• Pulikkoonattu, R. (June 12, 2007), Oscillator Phase Noise and Sampling Clock Jitter (PDF), Tech Note, Bangalore, India: ST Microelectronics, archived (PDF) from the original on 2022-10-09, retrieved March 29, 2012
• Chorti, A.; Brookes, M. (September 2006), "A spectral model for RF oscillators with power-law phase noise" (PDF), IEEE Transactions on Circuits and Systems I: Regular Papers, 53 (9): 1989–1999, doi:10.1109/TCSI.2006.881182, hdl:10044/1/676, S2CID 8855005, archived (PDF) from the original on 2022-10-09
• Rohde, Ulrich L.; Poddar, Ajay K.; Böck, Georg (May 2005), The Design of Modern Microwave Oscillators for Wireless Applications, New York, NY: John Wiley & Sons, ISBN 978-0-471-72342-4
• Ulrich L. Rohde, A New and Efficient Method of Designing Low Noise Microwave Oscillators, https://depositonce.tu-berlin.de/bitstream/11303/1306/1/Dokument_16.pdf
• Ajay Poddar, Ulrich Rohde, Anisha Apte, “ How Low Can They Go, Oscillator Phase noise model, Theoretical, Experimental Validation, and Phase Noise Measurements”, IEEE Microwave Magazine, Vol. 14, No. 6, pp. 50–72, September/October 2013.
• Ulrich Rohde, Ajay Poddar, Anisha Apte, “Getting Its Measure”, IEEE Microwave Magazine, Vol. 14, No. 6, pp. 73–86, September/October 2013
• U. L. Rohde, A. K. Poddar, Anisha Apte, “Phase noise measurement and its limitations”, Microwave Journal, pp. 22–46, May 2013
• A. K. Poddar, U.L. Rohde, “Technique to Minimize Phase Noise of Crystal Oscillators”, Microwave Journal, pp. 132–150, May 2013.
• A. K. Poddar, U. L. Rohde, and E. Rubiola, “Phase noise measurement: Challenges and uncertainty”, 2014 IEEE IMaRC, Bangalore, Dec 2014.