प्रोटॉन क्षय

जॉर्जी-ग्लाशो मॉडल में कणों के लिए कमजोर आइसोस्पिन, कमजोर हाइपरचार्ज और रंग शुल्क का पैटर्न। यहाँ, एक प्रोटॉन, जिसमें दो अप क्वार्क और एक डाउन होता है, एक पिओन में क्षय होता है, जिसमें एक अप और एंटी-अप होता है, और एक पॉज़िट्रॉन, विद्युत आवेश वाले एक्स बोसोन के माध्यम से -⁴/₃.

कण भौतिकी में, प्रोटॉन क्षय कण क्षय का एक परिकल्पना रूप है जिसमें प्रोटॉन हल्के उप-परमाणु कणों, जैसे कि एक तटस्थ पियॉन और पॉज़िट्रॉन में क्षय होता है। प्रोटॉन क्षय परिकल्पना पहली बार 1967 में आंद्रेई सखारोव के द्वारा तैयार की गई थी। महत्वपूर्ण प्रायोगिक प्रयासों के अतिरिक्त, प्रोटॉन क्षय को कभी नहीं देखा गया था। यदि यह पॉजिट्रॉन के माध्यम से क्षय करता है, तो प्रोटॉन का आधा जीवन कम से कम 1.67×10³⁴ वर्ष का होना चाहिए था।

मानक मॉडल के अनुसार, प्रोटॉन, एक प्रकार का बैरियन, स्थिर है क्योंकि बेरोन संख्या (क्वार्क संख्या) संरक्षित (सामान्य परिस्थितियों में; अपवाद के लिए चिरल विसंगति देखें) है, इसलिए प्रोटॉन अन्य कणों में अपने दम पर क्षय नहीं करते है, क्योंकि वे सबसे हल्के (और इसलिए सबसे कम ऊर्जावान) बैरियन होते है। पॉज़िट्रॉन उत्सर्जन और इलेक्ट्रॉन कैप्चर - रेडियोधर्मी क्षय के रूप जो एक प्रोटॉन को न्यूट्रॉन बनते हुए देखते हैं - वो प्रोटॉन क्षय नहीं होते है, क्योंकि प्रोटॉन परमाणु के भीतर अन्य कणों के साथ संपर्क करते है।

कुछ परे-मानक मॉडल ग्रैंड यूनिफाइड थ्योरी (जीयूटीस) स्पष्ट रूप से बेरोन संख्या समरूपता को तोड़ते हैं, प्रोटॉन को हिग्स कण, चुंबकीय मोनोपोल, या 10³¹ से 10³⁶ वर्षों के आधे जीवन के साथ नए एक्स बोसोन के माध्यम से क्षय करने की अनुमति देते हैं। तुलना के लिए, ब्रह्मांड लगभग 1.38 × 10¹⁰ वर्ष पुराना है। आज तक, जीयूटीस (जैसे प्रोटॉन क्षय या चुंबकीय मोनोपोल के अस्तित्व) द्वारा भविष्यवाणी की गई नई घटनाओं को देखने के सभी प्रयास विफल रहे हैं।

क्वांटम टनलिंग प्रोटॉन क्षय के कई माध्मों में से एक हो सकता है।

क्वांटम गुरुत्वाकर्षण (आभासी ब्लैक होल और हॉकिंग विकिरण के माध्यम से) ऊपर जीयूटी स्केल क्षय सीमा के साथ-साथ सुपरसिमेट्री में अतिरिक्त आयामों से परे परिमाण या जीवनकाल में प्रोटॉन क्षय का एक स्थान प्रदान कर सकता है।

प्रोटॉन क्षय के अतिरिक्त बैरोन उल्लंघन के सैद्धांतिक तरीके हैं जिनमें 1 के अतिरिक्त बैरोन या लेप्टान संख्या के परिवर्तन के साथ वार्तालाप सम्मलित होती है (जैसा कि प्रोटॉन क्षय में आवश्यक है)। इनमें 2, 3, या अन्य नंबरों का B और L उल्लंघन, या B − L उल्लंघन सम्मलित था। ऐसे उदाहरणों में उच्च ऊर्जा और तापमान पर न्यूट्रॉन दोलन और इलेक्ट्रोवीक स्पैलेरॉन विसंगति सम्मलित हैं, जो प्रोटॉन के एंटीलेप्टोन या इसके विपरीत (लेप्टोजेनेसिस (भौतिकी) और गैर-जीयूटी बैरोजेनेसिस में एक प्रमुख कारक) के टकराव के बीच परिणाम दे सकते हैं।

बैरियोजेनेसिस

Main article: बैरियोजेनेसिस

आधुनिक भौतिकी की उत्कृष्ट समस्याओं में से एक ब्रह्मांड में एंटीस्थिति पर पदार्थ की प्रबलता है। ब्रह्मांड, एक पूरे के रूप में गैर-शून्य सकारात्मक बेरोन संख्या घनत्व प्रतीत होता है - अर्थात, पदार्थ उपलब्ध रहता है। चूंकि ब्रह्माण्ड विज्ञान में यह माना जाता है कि हम जो कण देखते हैं वे उसी भौतिकी का उपयोग करके बनाए गए थे जिसे हम आज मापते हैं, सामान्य रूप से यह अपेक्षा की जाती है कि समग्र बेरोन संख्या शून्य होनी चाहिए, क्योंकि पदार्थ और प्रतिपदार्थ समान मात्रा में बनाए गए होंगे। इसने समरूपता को तोड़ने के लिए कई प्रस्तावित तंत्रों को उत्पन्न किया है जो कुछ शर्तों के अनुसार सामान्य पदार्थ (एंटीमैटर के विपरीत) के निर्माण का पक्ष लेते हैं। यह असंतुलन असाधारण रूप से छोटा होता है, प्रत्येक 10000000000 (10¹⁰) कणों में 1 के क्रम में बड़े धमाके के बाद एक सेकेंड का एक छोटा अंश होता है, लेकिन अधिकांश पदार्थ और प्रतिकारक नष्ट हो जाने के बाद, वर्तमान ब्रह्मांड में सभी बाह्य पदार्थ और बहुत अधिक संख्या में बोसॉन के साथ शेष रह जाते है।

अधिकांश भव्य एकीकृत सिद्धांत बेरोन संख्या समरूपता को स्पष्ट रूप से तोड़ते हैं, जो इस विसंगति के लिए जिम्मेदार होते है, सामान्यतः बहुत बड़े एक्स बोसोन (एक्स) या बड़े पैमाने पर हिग्स बोसोन (
H⁰
) द्वारा मध्यस्थता वाली प्रतिक्रियाओं का आह्वान करते हैं। जिस दर पर ये घटनाएँ घटित होती हैं, वह बड़े पैमाने पर मध्यवर्ती एक्स या H⁰ कणों के द्रव्यमान द्वारा नियंत्रित किया जाता है, यह मानकर कि ये प्रतिक्रियाएँ आज देखी जाने वाली अधिकांश बैरियन संख्या के लिए ज़िम्मेदार हैं, जिसके ऊपर दर होता है उसमे एक अधिकतम द्रव्यमान की गणना की जा सकती है आज के समय में पदार्थ की उपस्थिति की व्याख्या करना बहुत ही धीमी प्रक्रिया होती है। ये अनुमान भविष्यवाणी करते हैं कि बड़ी मात्रा में सामग्री कभी-कभी एक सहज प्रोटॉन क्षय प्रदर्शित करेगी।

प्रायोगिक साक्ष्य

प्रोटॉन क्षय 1970 के दशक में प्रस्तावित विभिन्न भव्य एकीकृत सिद्धांतों (जीयूटीस) की प्रमुख भविष्यवाणियों में से एक है, यह अन्य प्रमुख चुंबकीय मोनोपोल का अस्तित्व है। 1980 के दशक की शुरुआत से ही दोनों अवधारणाएं प्रमुख प्रायोगिक भौतिकी प्रयासों का केंद्र रही हैं। आज तक, इन घटनाओं को देखने के सभी प्रयास विफल रहे हैं; चूंकि, ये प्रयोग प्रोटॉन के आधे जीवन पर निचली सीमा स्थापित करने में सक्षम हैं। वर्तमान में, सबसे त्रुटिहीन परिणाम जापान में सुपर-कमियोकांडे वाटर चेरेंकोव विकिरण डिटेक्टर से आते हैं: 2015 के एक विश्लेषण ने पॉज़िट्रॉन क्षय के माध्यम से 1.67 × 10³⁴ वर्षों के प्रोटॉन के आधे जीवन पर एक निचली सीमा रखी गयी थी और इसी प्रकार, 2012 का एक विश्लेषण एंटीम्यूऑन क्षय के माध्यम से 1.08×10³⁴ वर्षों के प्रोटॉन के आधे जीवन के लिए एक निचली सीमा दी गयी थी। 10³⁴-10³⁶ वर्षों की एक सुपरसिमेट्री (एसयूएसवाई) भविष्यवाणी के करीब होती है। एक उन्नत संस्करण, हाइपर-कामीकांडे, संभवतः सुपर-कामीकांडे की तुलना में इसमें 5-10 गुना उत्तम संवेदनशीलता होती है।

सैद्धांतिक प्रेरणा

प्रोटॉन क्षय के लिए अवलोकन प्रमाण की कमी के अतिरिक्त, कुछ भव्य एकीकरण सिद्धांत, जैसे एसयू (5) जॉर्जी-ग्लाशो मॉडल और एसओ (10), उनके सुपरसिमेट्रिक रूपों के साथ, इसकी आवश्यकता होती है। इस प्रकार के सिद्धांतों के अनुसार, प्रोटॉन का आधा जीवन लगभग 10³¹~10³⁶ वर्ष का होता है और एक पॉज़िट्रॉन और एक तटस्थ पिओन में क्षय हो जाता है जो स्वयं तुरंत दो गामा विकिरण फोटोन में क्षय हो जाता है:

p+	→	e+	+	π0
				└→	2 γ

चूंकि पॉज़िट्रॉन एक एंटीलेप्टन है, इसलिए यह क्षय B − L संख्या को संरक्षित करता है, जो कि अधिकांश जीयूटीस में संरक्षित है।

अतिरिक्त क्षय मोड उपलब्ध हैं (जैसे:
p⁺
→
μ⁺
+
π⁰
), दोनों सीधे और जब जीयूटी-अनुमानित चुंबकीय मोनोपोल के साथ वार्तालाप के माध्यम से उत्प्रेरित होते हैं। चूंकि इस प्रक्रिया को प्रयोगात्मक रूप से नहीं देखा जाता है, यह मेगाटन पैमाने पर भविष्य में नियुक्त बहुत बड़े पैमाने के डिटेक्टरों के लिए प्रायोगिक परीक्षण क्षमता के दायरे में है। इस प्रकार के डिटेक्टरों में हाइपर-कमियोकांडे सम्मलित होता हैं।

प्रारंभिक भव्य एकीकरण सिद्धांत (जीयूटीस) जैसे कि जॉर्जी-ग्लाशो मॉडल, जो प्रोटॉन क्षय का सुझाव देने वाले पहले सुसंगत सिद्धांत थे, जिसने माना कि प्रोटॉन का आधा जीवन कम से कम 10³¹ वर्ष का होता है। जैसा कि 1990 के दशक में और प्रयोग और गणनाएँ की गईं जिससे यह स्पष्ट हो गया कि प्रोटॉन का आधा जीवन 10³² वर्ष से कम नहीं हो सकता है। उस अवधि की कई पुस्तकें इस आंकड़े को बायोरोनिक पदार्थ के संभावित क्षय समय के लिए संदर्भित करती हैं। अधिक हाल के निष्कर्षों ने सरल जीयूटीस (न्यूनतम एसयू(5) / जॉर्जी-ग्लाशो सहित) और अधिकांश गैर-एसयूएसवाई मॉडल को खारिज करते हुए न्यूनतम प्रोटॉन आधा जीवन को कम से कम 10³⁴~10³⁵ वर्ष तक धकेल दिया जाता है। प्रोटॉन जीवनकाल पर अधिकतम ऊपरी सीमा (यदि अस्थिर है), की गणना 6 × 10³⁹ वर्षों में की जाती है, जो एसयूएसवाई मॉडल अधिकतम (न्यूनतम) गैर-एसयूएसवाई जीयूटीस के लिए 1.4 × 1036 वर्ष तक लागू होती है।

चूंकि इस परिघटना को "प्रोटॉन क्षय" कहा जाता है, लेकिन इस प्रभाव को परमाणु नाभिक के अंदर स्थित न्यूट्रॉन में भी देखा जा सकता है। मुक्त न्यूट्रॉन - जो एक परमाणु नाभिक के अंदर नहीं हैं - पहले से ही बीटा क्षय नामक प्रक्रिया में प्रोटॉन (और एक इलेक्ट्रॉन और एक एंटीन्यूट्रिनो) में क्षय के लिए जाने जाते हैं। कमजोर अंतःक्रिया के कारण मुक्त न्यूट्रॉन का अर्ध-जीवन 10 मिनट (610.2±0.8 सेकेंड) का होता है। एक नाभिक के अंदर बंधे न्यूट्रॉन का आधा जीवन बहुत लंबा होता है - सामान्यतः प्रोटॉन जितना बड़ा होता है।

प्रक्षेपित प्रोटॉन जीवनकाल

सिद्धांत वर्ग	प्रोटॉन जीवनकाल (वर्ष)	प्रयोगात्मक रूप से खारिज कर दिया?
मिनिमल एसयू(5) (जॉर्जी-ग्लाशो)	1030–1031	Yes
मिनिमल एसयूएसवाई एसयू(5)	1028–1032	Yes
एसयूजीआरऐ एसयू(5)	1032–1034	Yes
एसयूएसवाई एसओ(10)	1032–1035	Partially
एसयूएसवाई एसयू(5) (एमएसएसएम)	~1034	Partially
एसयूएसवाई एसयू(5) - 5 आयाम	1034–1035	Partially
एसयूएसवाई एसओ(10) एमएसएसएम जी(224)	2·1034	No
मिनिमल (बेसिक) एसओ(10) - नॉन-एसयूएसवाई	< ~1035 (अधिकतम सीमा)	No
फ़्लिप एसयू(5) (एमएसएसएम)	1035–1036	No

वैनिला एसयू(5) में प्रोटॉन के जीवनकाल का सहज अनुमान लगाया जा सकता है $\tau _{p}\sim {\frac {M_{X}^{4}}{m_{p}^{5}}}$ जो सामान्यतः वर्तमान प्रयोगात्मक निचली सीमा में लगभग µ ~ 2×1016 GeV/c2 के पुनर्एकीकरण पैमाने के साथ सुपरसिमेट्रिक जीयूटीस 10³⁴ वर्ष का जीवनकाल उत्पन्न करते हैं।

क्षय संचालक

आयाम-6 प्रोटॉन क्षय संचालक

मौलिक स्केलिंग आयाम -6 प्रोटॉन क्षय संकारक हैं ${\frac {qqql}{\Lambda ^{2}}}$, ${\frac {d^{c}u^{c}u^{c}e^{c}}{\Lambda ^{2}}}$, ${\frac {{\overline {e^{c}}}{\overline {u^{c}}}qq}{\Lambda ^{2}}}$ और ${\frac {{\overline {d^{c}}}{\overline {u^{c}}}ql}{\Lambda ^{2}}}$ जहाँ $\Lambda$ मानक मॉडल के लिए कटऑफ (भौतिकी) होता है। ये सभी ऑपरेटर बैरोन संख्या (बी) और लेप्टन संख्या (एल) संरक्षण का उल्लंघन करते हैं, लेकिन ये दोनों बी-एल नहीं होते हैं।

जीयूटी मॉडल में, Λ _{जीयूटी} द्रव्यमान के साथ X या Y बोसोन के आदान-प्रदान से अंतिम दो ऑपरेटरों को दबा दिया जाता है ${\frac {1}{\Lambda _{GUT}^{2}}}$ द्रव्यमान के साथ एक ट्रिपल हिग्स का आदान-प्रदान $M$ सभी ऑपरेटरों को दबा सकता है

${\frac {1}{M^{2}}}$ डबलट-ट्रिपल विभाजन समस्या देखें।

• प्रोटॉन क्षय, ये ग्राफिक्स एक्स बोसोन और हिग्स बोसोन को संदर्भित करते हैं।
• Index.php?title=File:Proton decay2.svg

  आयाम-6 प्रोटॉन क्षय द्वारा मध्यस्थता

• Index.php?title=File:Proton decay3.svg

  आयाम-6 प्रोटॉन क्षय द्वारा मध्यस्थता

• Index.php?title=File:Proton decay4.svg

  आयाम-6 प्रोटॉन क्षय द्वारा मध्यस्थता

आयाम-5 प्रोटॉन क्षय ऑपरेटर्स

सुपरसिमेट्रिक एक्सटेंशन (जैसे कि न्यूनतम सुपरसिमेट्रिक मानक मॉडल) में, हमारे पास आयाम -5 ऑपरेटर भी हो सकते हैं जिनमें द्रव्यमान M के ट्रिपलटिनो के आदान-प्रदान के कारण दो फ़र्मियन और दो स्फ़र्मियन सम्मलित होते हैं। इसके बाद स्फ़र्मियन एक गोगिनो या हिग्सिनो या गुरुत्वाकर्षण का आदान-प्रदान करते है और दो फर्मीनों को छोड़ देते हैं। सम्पूर्ण फेनमैन आरेख में एक लूप (और अन्य जटिलताएं जो प्रबल अन्योन्य भौतिकी के कारण) होता है। इस क्षय दर को दबा दिया जाता है ${\frac {1}{MM_{\text{SUSY}}}}$ जहां M _{एसयूएसवाई} सुपरपार्टनर्स का मास स्केल होता है।

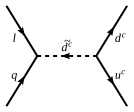
आयाम-4 प्रोटॉन क्षय संचालक

द्रव्य समानता के अभाव में, मानक मॉडल के सुपरसिमेट्रिक एक्सटेंशन से डाउन क्वार्क द्रव्यमान के व्युत्क्रम वर्ग द्वारा दबाए गए अंतिम ऑपरेटर को उत्पन्न किया जा सकता है। यह आयाम-4 ऑपरेटरों के कारण होता है
q

ℓ

d͂
^C और
u
^C
d
^C
d͂
^C.

प्रोटॉन क्षय दर ${\frac {1}{M_{\text{SUSY}}^{2}}}$ द्वारा दबाई जाती है, जो बहुत तेज होती है और यह तबतक दबाई जाती है जब तक कि कपलिंग बहुत छोटी ना हों जाये।

यह भी देखें

• ब्रह्मांड की आयु
• बी - एल
• वर्चुअल ब्लैक होल
• कमजोर हाइपरचार्ज
• एक्स और वाई बोसोन

अग्रिम पठन

• C. Amsler; Particle Data Group (2008). "Review of Particle Physics – N Baryons" (PDF). Physics Letters B. 667 (1): 1–6. Bibcode:2008PhLB..667....1A. doi:10.1016/j.physletb.2008.07.018. hdl:1854/LU-685594. S2CID 227119789.
• K. Hagiwara; Particle Data Group (2002). "Review of Particle Physics – N Baryons" (PDF). Physical Review D. 66 (1): 010001. Bibcode:2002PhRvD..66a0001H. doi:10.1103/PhysRevD.66.010001.
• F. Adams; G. Laughlin (2000-06-19). The Five Ages of the Universe : Inside the Physics of Eternity. ISBN 978-0-684-86576-8.
• L.M. Krauss (2001). Atom : An Odyssey from the Big Bang to Life on Earth. ISBN 978-0-316-49946-0.
• D.-D. Wu; T.-Z. Li (1985). "Proton decay, annihilation or fusion?". Zeitschrift für Physik C. 27 (2): 321–323. Bibcode:1985ZPhyC..27..321W. doi:10.1007/BF01556623. S2CID 121868029.
• P. Nath; P. Fileviez Perez (2007). "Proton stability in grand unified theories, in strings and in branes". Physics Reports. 441 (5–6): 191–317. arXiv:hep-ph/0601023. Bibcode:2007PhR...441..191N. doi:10.1016/j.physrep.2007.02.010. S2CID 119542637.

बाहरी संबंध

• Proton decay at एसयूper-Kamiokande
• Pictorial history of the IMB experiment
• Luciano Maiani (8 February 2006). The problem of proton decay (PDF). Third NO-VE International Workshop on Neutrino Oscillations in Venice. Venice.