क्वांटम स्पिन तरल

From Vigyanwiki

संघनित पदार्थ भौतिकी में क्वांटम स्पिन तरल पदार्थ की अवस्था है जो कुछ चुंबकीय सामग्रियों में स्पिन (भौतिकी) के परस्पर क्रिया द्वारा बनाई जा सकती है। क्वांटम स्पिन तरल पदार्थ (क्यूएसएल) को सामान्यतः उनके लंबी दूरी की क्वांटम उलझाव भिन्नात्मक उत्तेजना, और साधारण चुंबकीय क्रम और विकार की अनुपस्थिति की विशेषता होती है।[1]

क्वांटम स्पिन तरल अवस्था को पहली बार 1973 में भौतिक विज्ञानी फिल एंडरसन द्वारा त्रिकोणीय जाली पर स्पिन की प्रणाली के लिए जमीनी स्थिति के रूप में प्रस्तावित किया गया था जो अपने निकटतम सहवासी के साथ प्रतिलौह चुंबकत्व पर परस्पर क्रिया करता है, अर्थात निकटतम स्पिन विपरीत दिशाओं में संरेखित करना चाहते हैं।[2] क्वांटम स्पिन तरल पदार्थ ने और अधिक रुचि उत्पन्न की जब 1987 में एंडरसन ने सिद्धांत प्रस्तावित किया जो अव्यवस्थित स्पिन-तरल अवस्था के संदर्भ में उच्च तापमान सुपरकंडक्टिविटी का वर्णन करता है।[3][4]

मूल गुण

2:27
कुंठित चुंबकत्व से निकलने वाले स्पिन तरल का उदाहरण

सबसे सरल प्रकार का चुंबकीय चरण एक परमैग्नेट है जहां प्रत्येक अलग-अलग स्पिन आदर्श गैस में परमाणुओं की तरह शेष भागो से स्वतंत्र रूप से व्यवहार करता है। यह अत्यधिक अव्यवस्थित चरण उच्च तापमान पर चुम्बकों की सामान्य अवस्था है, जहाँ तापीय उतार-चढ़ाव हावी होते हैं। ठंडा होने पर स्पिन अधिकांशतः लौह (या एंटीफेरोमैग्नेट) चरण में प्रवेश करेंगे इस चरण में घुमावों के बीच की परस्पर क्रिया उन्हें बड़े मापदंड के प्रतिरूप में संरेखित करने का कारण बनती है, जैसे चुंबकीय डोमेन, पट्टियां, या चेकरबोर्ड इन लंबी दूरी के प्रतिरूप को चुंबकीय क्रम के रूप में संदर्भित किया जाता है, और कई ठोस पदार्थों द्वारा गठित नियमित क्रिस्टल संरचना के अनुरूप होते हैं।[5]

क्वांटम स्पिन तरल पदार्थ इस विशिष्ट व्यवहार के लिए नाटकीय विकल्प प्रदान करते हैं। लौह-चुंबकीय स्पिन स्थिति की तुलना में इस अवस्था का सहज वर्णन आदेश और विकार (भौतिकी) स्पिन के तरल के रूप में है,[6] जिस तरह से क्रिस्टलीय बर्फ की तुलना में तरल पानी अव्यवस्थित अवस्था में होता है। चूंकि अन्य अव्यवस्थित अवस्थाओं के विपरीत, क्वांटम स्पिन तरल अवस्था अपने विकार को बहुत कम तापमान तक बनाए रखती है।[7] क्वांटम स्पिन तरल पदार्थों के अधिक आधुनिक लक्षण वर्णन में उनके सामयिक क्रम लंबी दूरी की क्वांटम उलझाव गुण और कोई भी उत्तेजना सम्मिलित हैं,[8][1][9]

उदाहरण

कई भौतिक मॉडलों में अव्यवस्थित जमीनी अवस्था होती है जिसे क्वांटम स्पिन तरल के रूप में वर्णित किया जा सकता है।

कुंठित चुंबकीय क्षण

निराश ईज़िंग त्रिकोण पर घूमता है।

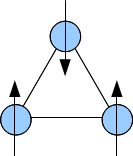
स्थानीय स्पिन निराश हो जाते हैं यदि प्रतिस्पर्धात्मक आदान-प्रदान उपस्थित हैं जो सभी ही समय में संतुष्ट नहीं हो सकते हैं, जिससे प्रणाली की जमीनी स्थिति का बड़ा पतन हो सकता है। इसिंग स्पिन का त्रिकोण (जिसका अर्थ है कि स्पिन का एकमात्र संभावित अभिविन्यास या तो ऊपर या नीचे है), जो एंटीफेरोमैग्नेटिक रूप से परस्पर क्रिया करता है,जो कि निराशा के लिए सरल उदाहरण है। जमीनी अवस्था में दो स्पिन समानांतर हो सकते हैं किन्तु तीसरा नहीं हो सकता है यह जमीनी अवस्था में स्पिन के संभावित झुकाव (इस स्थितियों में छह) की वृद्धि की ओर जाता है, उतार-चढ़ाव को बढ़ाता है और इस प्रकार चुंबकीय क्रम को दबा देता है।

वर्तमान के शोध कार्य ने मस्तिष्क नेटवर्क के विश्लेषण में इस अवधारणा का उपयोग किया और लचीले तंत्रिका अंतःक्रियाओं के अनुरूप मस्तिष्क में आश्चर्यजनक रूप से कुंठित अंतःक्रियाओं का संकेत दिया। यह अवलोकन निराशा की घटना के सामान्यीकरण पर प्रकाश डालता है और जैविक प्रणालियों में इसकी जांच का प्रस्ताव करता है।[10]

रेजोनेटिंग वैलेंस बांड (आरवीबी)

Main article: अनुनाद वैलेंस बांड सिद्धांत
वैलेंस बांड ठोस। बांड विशिष्ट प्रतिरूप बनाते हैं और इसमें उलझे हुए स्पिन के जोड़े होते हैं।

चुंबकीय क्षण के बिना जमीनी स्थिति बनाने के लिए वैलेंस बॉन्ड स्टेट्स का उपयोग किया जा सकता है, जहां एंटीफेरोमैग्नेटिक इंटरैक्शन के कारण दो इलेक्ट्रॉन स्पिन स्पिन 0 सिंगलेट बनाते हैं। यदि प्रणाली में प्रत्येक स्पिन इस तरह से बंधा हुआ है, तो पूरे प्रणाली की स्थिति में भी स्पिन 0 है और यह गैर-चुंबकीय है। बॉन्ड बनाने वाले दो स्पिन अधिकतम रूप से उलझे हुए स्थितिया है, जबकि अन्य स्पिनों से नहीं उलझे हुए हैं। यदि सभी स्पिन कुछ स्थानीयकृत स्थिर बांडों में वितरित किए जाते हैं, तो इसे वैलेंस बॉन्ड ठोस (वीबीएस) कहा जाता है।

दो चीजें हैं जो अभी भी स्पिन तरल से वीबीएस को अलग करती हैं: सबसे पहले, बांड को निश्चित विधि से व्यवस्थित करके जाली समरूपता सामान्यतः टूट जाती है जो स्पिन तरल के स्थितियों में नहीं होती है। दूसरा इस जमीनी अवस्था में लंबी दूरी के उलझाव का अभाव है। इसे प्राप्त करने के लिए वैलेंस बॉन्ड के क्वांटम यांत्रिक उतार-चढ़ाव की अनुमति दी जानी चाहिए, जिससे वैलेंस बॉन्ड में स्पिन के कई अलग-अलग विभाजनों के सुपरपोज़िशन से युक्त जमीनी स्थिति हो। यदि विभाजन समान रूप से वितरित किए जाते हैं (समान क्वांटम आयाम के साथ), तो किसी विशिष्ट विभाजन (वैलेंस बॉन्ड लिक्विड) के लिए कोई वरीयता नहीं है। इस तरह के जमीनी स्थिति तरंग फलन को पीडब्लू एंडरसन द्वारा 1973 में स्पिन तरल पदार्थ की जमीनी स्थिति के रूप में प्रस्तावित किया गया था।[2] और इसे रेज़ोनेटिंग वैलेंस बॉन्ड (आरवीबी ) स्थिति कहा जाता है। ये स्थिति महान सैद्धांतिक रुचि के हैं क्योंकि उन्हें उच्च तापमान अतिचालक भौतिकी में महत्वपूर्ण भूमिका निभाने का प्रस्ताव है।[4]

  • आरवीबी राज्य में स्पिन की एक संभावित शॉर्ट-रेंज जोड़ी।

    आरवीबी राज्य में स्पिन की एक संभावित शॉर्ट-रेंज जोड़ी।

  • स्पिन की लंबी दूरी की जोड़ी।

    स्पिन की लंबी दूरी की जोड़ी।

उत्तेजना

स्पिनॉन स्पिन तरल पदार्थ में घूम रहा है।

वैलेंस बॉन्ड को केवल निकटतम सहवासी द्वारा नहीं बनाया जाना चाहिए और उनके वितरण अलग-अलग सामग्रियों में भिन्न हो सकते हैं। लंबी दूरी के वैलेंस बॉन्ड के बड़े योगदान वाले ग्राउंड स्टेट्स में कम-ऊर्जा रीढ़ की हड्डी उत्तेजना होती है, क्योंकि उन वैलेंस बॉन्ड को तोड़ना आसान होता है। तोड़ने पर वे दो मुक्त चक्रण बनाते हैं। अन्य उत्तेजन वैलेंस बांडों को पुनर्व्यवस्थित करते हैं, जिससे लघु सीमा बॉन्ड्स के लिए भी कम-ऊर्जा उत्तेजनाएं होती हैं। स्पिन तरल पदार्थों के बारे में कुछ खास बात यह है कि वे विदेशी उत्तेजनाओं का समर्थन करते हैं जिसका अर्थ भिन्नात्मक क्वांटम संख्याओं के साथ उत्तेजना है। प्रमुख उदाहरण स्पिनन का उत्तेजना है जो प्रभारी तटस्थ हैं और स्पिन ले जाते हैं स्पिन तरल पदार्थों में स्पिनॉन बनाया जाता है यदि स्पिन को वैलेंस बांड में जोड़ा नहीं जाता है। यह कम ऊर्जा निवेश पर पास के वैलेंस बॉन्ड को पुनर्व्यवस्थित करके स्थानांतरित कर सकता है।

(स्थिर) आरवीबी राज्यों की प्राप्ति

आरवीबी तस्वीर का उपयोग करते हुए स्क्वायर जाली पर आरवीबी स्थिति की पहली चर्चा[11] केवल निकटतम निकटतम बंधनों पर विचार करें जो विभिन्न उप-जालियों को जोड़ते हैं। निर्मित आरवीबी स्थिति सभी निकटतम-निकटतम बांड विन्यासों का समान आयाम सुपरपोजिशन है। ऐसा माना जाता है कि इस तरह के आरवीबी स्थिति में आकस्मिक अंतराल रहित होता है गेज क्षेत्र जो स्पिनोन आदि को सीमित कर सकता है। इसलिए चौकोर जाली पर समान-आयाम निकटतम-निकटतम आरवीबी स्थिति अस्थिर है और क्वांटम स्पिन चरण से मेल नहीं खाता है। यह दो स्थिर चरणों के बीच महत्वपूर्ण चरण संक्रमण बिंदु का वर्णन कर सकता है। आरवीबी स्थिति का संस्करण जो स्थिर है और इसमें डिकॉन्फ़िंड स्पिनन्स सम्मिलित हैं, चिराल स्पिन स्थिति है।[12][13] इसके पश्चात् में स्थिर आरवीबी स्थिति का और संस्करण डिकॉन्फ़िंड स्पिनॉन्स के साथ प्रस्तावित है, जेड2 स्पिन तरल, प्रस्तावित है,[14][15] जो सबसे सरल टोपोलॉजिकल ऑर्डर - जेड2 सामयिक क्रम को साकार करता है। चिरल स्पिन अवस्था और जेड2 स्पिन तरल अवस्था दोनों में लंबे आरवीबी बॉन्ड होते हैं जो ही उप-जाली को जोड़ते हैं। चिरल स्पिन अवस्था में, विभिन्न बॉन्ड कॉन्फ़िगरेशन में जटिल आयाम हो सकते हैं, जबकि जेड2 स्पिन तरल अवस्था में विभिन्न बॉन्ड कॉन्फ़िगरेशन में केवल वास्तविक आयाम होते हैं। त्रिकोण जाली पर आरवीबी स्थिति भी जेड2 स्पिन तरल का अनुभव करता है,[16] जहां विभिन्न बंधन विन्यासों में केवल वास्तविक आयाम होते हैं। टोरिक कोड मॉडल अभी तक जेड2 स्पिन तरल (और जेड2 टोपोलॉजिकल ऑर्डर) का और अनुभव है जो स्पष्ट रूप से स्पिन रोटेशन समरूपता को तोड़ता है और बिल्कुल घुलनशील है।[17]

प्रायोगिक हस्ताक्षर और जांच

चूँकि कोई एकल प्रायोगिक विशेषता नहीं है जो किसी पदार्थ को स्पिन तरल के रूप में पहचानती है विभिन्न गुणों के बारे में जानकारी प्राप्त करने के लिए कई प्रयोग किए जाने हैं जो स्पिन तरल की विशेषता रखते हैं।[18]

चुंबकीय संवेदनशीलता

उच्च तापमान, उत्कृष्ट पैरामैग्नेट चरण में क्यूरी-वीस नियम द्वारा चुंबकीय संवेदनशीलता दी जाती है

इस समीकरण के लिए प्रायोगिक डेटा को फ़िट करना एक फेनोमेनोलॉजिकल क्यूरी-वीस तापमान, निर्धारित करता है। एक दूसरा तापमान है, जहां पदार्थ में चुंबकीय क्रम विकसित होना प्रारंभ हो जाता है, जैसा में एक गैर-विश्लेषणात्मक विशेषता द्वारा प्रमाणित है। इनके अनुपात को फ्रस्ट्रेशन मापदंड कहा जाता है
एक उत्कृष्ट एंटीफेरोमैग्नेट में, दो तापमानों को मेल खाना चाहिए और देना चाहिए। एक आदर्श क्वांटम स्पिन तरल किसी भी तापमान पर चुंबकीय क्रम विकसित नहीं करेगा और इसलिए एक अपसारी निराश मापदंड होगा।[19] एक बड़ा मान इसलिए संभावित स्पिन तरल चरण का एक अच्छा संकेत है। विभिन्न जाली संरचनाओं और उनके क्यूरी-वीस तापमान वाली कुछ निराश पदार्थ नीचे दी गई तालिका में सूचीबद्ध हैं। ये सभी प्रस्तावित स्पिन तरल उम्मीदवार हैं।

पदार्थ जाली
κ-(BEDT-TTF)2Cu2(CN)3 अनिसोट्रोपिक त्रिकोणीय -375
ZnCu3(OH)6Cl2 (हर्बर्टस्मिथाइट) कागोमे -241
BaCu3V2O8(OH)2 (वेसिग्निएइट) कागोमे
Na4Ir3O8 हाइपरकागोम -650
PbCuTe2O6 हाइपरकागोम -22 [20]
Cu-(1,3-बेंजीनडीकार्बोक्सिलेट) कागोमे -33 [21]
Rb2Cu3SnF12 कागोमे [22]
1T-TaS2 त्रिकोणीय

अन्य

चुंबकीय आदेश की अनुपस्थिति के लिए सबसे प्रत्यक्ष प्रमाणों में से एनएमआर या μSR प्रयोग देता है। यदि कोई स्थानीय चुंबकीय क्षेत्र उपस्थित है, तो परमाणु या म्यूऑन स्पिन प्रभावित होगा जिसे मापा जा सकता है। 1H-एनएमआर माप [23] κ-(BEDT-TTF)2Cu2(CN)3 ने 32 mK के नीचे चुंबकीय क्रम का कोई संकेत नहीं दिखाया है, जो हाइजेनबर्ग मॉडल (क्वांटम) J≈250 K से छोटे परिमाण के चार आदेश हैं[24] इस परिसर में निकटतम घुमावों के बीच आगे की जांच में सम्मिलित हैं:

  • विशिष्ट ऊष्मा मापन से राज्यों के निम्न-ऊर्जा घनत्व के बारे में जानकारी मिलती है, जिसकी तुलना सैद्धांतिक मॉडल से की जा सकती है।
  • ऊष्मीय परिवहन माप यह निर्धारित कर सकते हैं कि उत्तेजनाएं स्थानीयकृत हैं या पुनरावृत्त हैं।
  • न्यूट्रॉन प्रकीर्णन से उत्तेजनाओं और सहसंबंधों (जैसे स्पिनॉन) की प्रकृति के बारे में जानकारी मिलती है।
  • परावर्तन माप स्पिनन को उजागर कर सकते हैं, जो विद्युत-नियम ऑप्टिकल चालकता को जन्म देते हुए विद्युत चुम्बकीय क्षेत्र में उभरते गेज क्षेत्रों के माध्यम से जोड़े जाते हैं।[25]
हर्बर्टस्मिथाइट, वह खनिज जिसकी जमीनी अवस्था में QSL व्यवहार दिखाया गया था

उम्मीदवार पदार्थ

आरवीबी प्रकार

सीज़ियम क्लोरोकुप्रेट Cs2CuCl4 के न्यूट्रॉन प्रकीर्णन माप त्रिकोणीय जाली पर स्पिन-1/2 एंटीफेरोमैग्नेट, फैलाना प्रकीर्णन को प्रदर्शित करता है। इसे 2D आरवीबी अवस्था से उत्पन्न होने वाले स्पिनों के लिए उत्तरदाई ठहराया गया था।[26] बाद में सैद्धांतिक काम ने इस तस्वीर को चुनौती दी, यह तर्क देते हुए कि सभी प्रयोगात्मक परिणाम व्यक्तिगत श्रृंखलाओं तक सीमित 1D स्पिनॉन के परिणाम थे।[27]

इसके पश्चात् में यह जैविक Mott इन्सुलेटर ((κ-(BEDT-TTF)2Cu2(CN)3)) 2003 में कानोडा के समूह द्वारा[23] यह स्पिनन फर्मी सतह (तथाकथित यूनिफॉर्म आरवीबी स्टेट) के साथ गैपलेस स्पिन लिक्विड के अनुरूप हो सकता है।[2] इस ऑर्गेनिक क्वांटम स्पिन लिक्विड कंपाउंड के विचित्र फेज डायग्राम को पहले म्यूऑन स्पिन स्पेक्ट्रोस्कोपी का उपयोग करके पूरी तरह से मैप किया गया था।[28]


हर्बर्टस्मिथाइट

हर्बर्टस्मिथाइट सबसे व्यापक रूप से अध्ययन की जाने वाली क्यूएसएल उम्मीदवार पदार्थ में से है।[19] यह रासायनिक संरचना ZnCu3(OH)6Cl2 वाला खनिज है और मुख्यत: रवा क्रिस्टल संरचना विशेष रूप से इस संरचना के अंदर तांबे के आयन कगोम जाली की द्वि-आयामी परतों को संग्रह करते हैं। इसके अतिरिक्त, ऑक्सीजन बॉन्ड पर सुपेरेक्स्चंगे के बीच शक्तिशाली एंटीफेरोमैग्नेटिक इंटरैक्शन बनाता है तांबा परत के अंदर घूमता है, जबकि परतों के बीच युग्मन नगण्य होता है।[19] इसलिए, यह कगोम जाली पर एंटीफेरोमैग्नेटिक स्पिन -1/2 हाइजेनबर्ग मॉडल का अच्छा अनुभव है, जो क्वांटम स्पिन तरल का प्रोटोटाइपिकल सैद्धांतिक उदाहरण है।[29][30]

सिंथेटिक, पॉलीक्रिस्टलाइन हर्बर्टस्मिथाइट पाउडर पहली बार 2005 में सूची किया गया था, और प्रारंभिक चुंबकीय संवेदनशीलता अध्ययन ने 2K के नीचे चुंबकीय क्रम का कोई संकेत नहीं दिखाया।[31] बाद के अध्ययन में, चुंबकीय क्रम की अनुपस्थिति को 50 mK तक सत्यापित किया गया था, अप्रत्यास्थ न्यूट्रॉन प्रकीर्णन मापों ने कम ऊर्जा स्पिन उत्तेजनाओं के व्यापक स्पेक्ट्रम का खुलासा किया, और कम तापमान वाले विशिष्ट ताप मापों में पावर लॉ स्केलिंग थी। इसने गैपलेस स्पिनन उत्तेजना।[32] सहित अतिरिक्त प्रयोगों की विस्तृत श्रृंखला 17O एनएमआर,[33] और गतिशील चुंबकीय संरचना कारक के न्यूट्रॉन स्पेक्ट्रोस्कोपी,[34] गैपलेस स्पिन तरल पदार्थ के रूप में हर्बर्टस्मिथाइट की पहचान को सुदृढ़ किया, चूंकि स्पष्ट लक्षण वर्णन 2010 तक अस्पष्ट रहा है ।[35]

2011 में हर्बर्टस्मिथाइट के बड़े (मिलीमीटर आकार) एकल क्रिस्टल उगाए गए और उनकी विशेषता बताई गई।[36] ये संभावित स्पिन तरल गुणों के अधिक स्पष्ट माप को सक्षम करते हैं। विशेष रूप से संवेग-समाधान अप्रत्यास्थ न्यूट्रॉन प्रकीर्णन प्रयोगों ने उत्तेजनाओं की व्यापक निरंतरता दिखाई। इसे गैपलेस, फ्रैक्शनलाइज्ड स्पिनॉन्स के साक्ष्य के रूप में व्याख्यायित किया गया था।[37] अनुवर्ती प्रयोग (उपयोग 17O एनएमआर और उच्च-रिज़ॉल्यूशन, कम-ऊर्जा न्यूट्रॉन प्रकीर्णन) ने इस तस्वीर को परिष्कृत किया और निर्धारित किया कि वास्तव में 0.07-0.09 meV का छोटा स्पिनॉन उत्तेजना अंतराल था।[38][39]

कुछ माप क्वांटम महत्वपूर्ण बिंदु बिहेवियर के सूचक थे।[40][41] इस पदार्थ की चुंबकीय प्रतिक्रिया थोक एसी इलेक्ट्रिक संवेदनशीलता और कम ऊर्जा गतिशील संवेदनशीलता दोनों में स्केलिंग संबंध प्रदर्शित करती है चुंबकीय क्षेत्र के आधार पर कम तापमान ताप क्षमता के साथ[42][43] यह स्केलिंग कुछ क्वांटम एंटीफेरोमैग्नेट्स, भारी फर्मियन पदार्थ भारी-फर्मियन धातु और द्वि-आयामी में देखा जाता है 3वह क्वांटम क्रिटिकल पॉइंट से निकटता के हस्ताक्षर के रूप में देखा जाता है।।[44]

2020 में हर्बर्टस्मिथाइट (~10 एनएम) के मोनोडिस्पर्स सिंगल-क्रिस्टल नैनोकणों को गैस-प्रसार इलेक्ट्रोक्रिस्टलीकरण का उपयोग करते हुए कमरे के तापमान पर संश्लेषित किया गया था जिससे पता चलता है कि उनकी स्पिन तरल प्रकृति इतने छोटे आयामों पर बनी रहती है।[45]

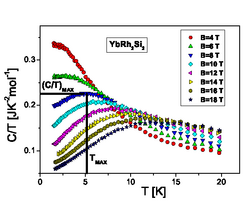
YbRh के इलेक्ट्रॉनिक विशिष्ट ताप C/टी की टी-निर्भरता2और2विभिन्न चुंबकीय क्षेत्रों में [46]जैसा कि पौराणिक कथाओं में दिखाया गया है। (सी/टी) के मानmax और टीmax बी = 8 टेस्ला में दिखाया गया है। अधिकतम (सी/टी)max बढ़ते हुए चुंबकीय क्षेत्र बी के साथ घटता है, जबकि Tmax बी = 18 Tesla पर 14 K तक पहुँचने के लिए उच्च टी पर शिफ्ट होता है। यह देखते हुए कि C/टी~χ~M*, कोई यह निष्कर्ष निकालता है कि ZnCu में SCQSL है3(ओह)6क्लोरीन2 अंजीर में दिखाया गया है। 2 YbRh में भारी फरमिओन्स के समान व्यवहार प्रदर्शित करता है2और2.
चित्र 2: ZnCu के लिए विभिन्न चुंबकीय क्षेत्रों में चुंबकीय संवेदनशीलता χ की टी-निर्भरता3(ओह)6क्लोरीन2.[42]χ का मानmax और टीmax बी = 7 टेस्ला में दिखाया गया है। टी-निर्भरता टी(-2/3) बी=0 पर ठोस वक्र द्वारा दर्शाया गया है। अधिकतम χmax(टी) चुंबकीय क्षेत्र बी बढ़ने पर घटता है, जबकि Tmax(बी) बी = 14 टेस्ला पर 15 के तक पहुंचने वाले उच्च टी में स्थानांतरित हो जाता है। उस χ~C/TM~M* को देखते हुए, कोई यह निष्कर्ष निकालता है कि YbRh की विशिष्ट ऊष्मा2और2 अंजीर में दिखाया गया है। 1 समान व्यवहार प्रदर्शित करता है जो χ करता है। यह, Zn Cu में SQL3(ओह)6क्लोरीन2 YbRh में भारी फरमिओन्स के रूप में व्यवहार करता है2और2.[47]

इसमें U(1)-डिराक स्पिन लिक्विड हो सकता है।[48]

किताएव स्पिन तरल पदार्थ

क्वांटम स्पिन तरल का और प्रमाण अगस्त 2015 में 2-आयामी पदार्थ में देखा गया था। ओक रिज राष्ट्रीय प्रयोगशाला के शोधकर्ता कैम्ब्रिज विश्वविद्यालय के भौतिकविदों और ड्रेसडेन, जर्मनी में मैक्स प्लैंक इंस्टीट्यूट फॉर द फिजिक्स ऑफ कॉम्प्लेक्स सिस्टम्स के साथ सहयोग कर रहे हैं। , ग्राफीन जैसी संरचना वाली दो आयामी पदार्थ में मेजराना फर्मियन के रूप में जाने जाने वाले इन भिन्नात्मक कणों के पहले हस्ताक्षरों को मापा। उनके प्रायोगिक परिणाम क्वांटम स्पिन तरल के लिए मुख्य सैद्धांतिक मॉडल में से के साथ सफलतापूर्वक मेल खाते हैं, जिसे किताएव मधुकोश मॉडल के रूप में जाना जाता है।[49][50]

शक्तिशाली सहसंबद्ध क्वांटम स्पिन तरल

दृढ़ता से सहसंबद्ध क्वांटम स्पिन तरल (एससीक्यूएसएल) संभावित क्वांटम स्पिन तरल (क्यूएसएल) का विशिष्ट अनुभव है।[7][40] नए प्रकार के दृढ़ता से सहसंबद्ध विद्युत इन्सुलेटर (बिजली) (एससीआई) का प्रतिनिधित्व करता है जिसमें अपवाद के साथ भारी फ़र्मियन धातुओं के गुण होते हैं: यह विद्युत आवेश के प्रवाह का प्रतिरोध करता है।[47][51] कम तापमान T पर इस प्रकार के इन्सुलेटर की विशिष्ट ऊष्मा Tn के समानुपाती होती है, n = 3 के अतिरिक्त n कम या समान के साथ, जैसा कि पारंपरिक इन्सुलेटर के स्थितियों में होना चाहिए जिसकी ताप क्षमता T3 के समानुपाती होती है जब चुंबकीय क्षेत्र बी को एससीआई पर प्रयुक्त किया जाता है तो पारंपरिक इंसुलेटर के विपरीत विशिष्ट गर्मी बी पर दृढ़ता से निर्भर करती है। एससीआई के कुछ उम्मीदवार हैं; उनमें से सबसे आशाजनक हर्बर्टस्मिथाइट खनिज है जिसकी रासायनिक संरचना ZnCu3(OH)6Cl2 है।,[51]

कगोम प्रकार

Ca10Cr7O28 कुंठित कगोम धातु है, जो 1 K से भी नीचे लंबी दूरी के क्रम को विकसित नहीं करती है, और इसमें अंतरहीन उत्तेजनाओं का फैला हुआ स्पेक्ट्रम है।

टोरिक कोड प्रकार

दिसंबर 2021 में टोरिक कोड प्रकार के एक क्वांटम स्पिन तरल का पहला प्रत्यक्ष माप बताया गया था[52][53] कि इसे दो टीमों द्वारा प्राप्त किया गया था:[54] एक क्वांटम प्रोसेसर पर जमीनी स्थिति और किसी भी उत्तेजना की खोज और दूसरा रूबी जाली पर परमाणुओं के सैद्धांतिक खाका को प्रयुक्त करना।[55] क्वांटम सिम्युलेटर पर ऑप्टिकल चिमटी के साथ आयोजित किया गया।[56]

विशिष्ट गुण: संस्थानिक फर्मियन संघनन क्वांटम चरण संक्रमण

भारी फ़र्मियन (एचएफ) धातुओं और दो आयामी हीलियम -3 पर एकत्रित प्रयोगात्मक तथ्यों से पता चलता है कि क्यूसिपार्टिकल प्रभावी द्रव्यमान (ठोस अवस्था भौतिकी) M* बहुत बड़ा है, या यहां तक ​​कि विचलन भी करता है। टोपोलॉजिकल फर्मियन कंडेनसेशन क्वांटम फेज ट्रांजिशन (एफसीक्यूपीटी) क्विसी कण को संरक्षित करता है, और फर्मी स्तर पर फ्लैट ऊर्जा बैंड बनाता है। एफसीक्यूपीटी का उद्भव सीधे प्रभावी द्रव्यमान (सॉलिड-स्थिति फिजिक्स) M* की असीमित वृद्धि से संबंधित है।[44] एफसीक्यूपीटी के पास, M* तापमान टी, संख्या घनत्व एक्स, चुंबकीय क्षेत्र 'बी' और अन्य बाहरी मापदंडों जैसे दबाव P, आदि पर निर्भर होना प्रारंभ कर देता है। लैंडौ प्रतिमान के विपरीत यह धारणा है कि प्रभावी द्रव्यमान लगभग स्थिर है, एफसीक्यूपीटी सिद्धांत में नए कुसिक्र्यस्ताल्स का प्रभावी द्रव्यमान दृढ़ता से टी, एक्स, 'बी' आदि पर निर्भर करता है। इसलिए, कई प्रयोगात्मक तथ्यों से सहमत/व्याख्या करने के लिए, एफसीक्यूपीटी पर आधारित विस्तारित क्वासिपार्टिकल्स प्रतिमान प्रस्तुत किया जाना है। यहाँ मुख्य बिंदु यह है कि अच्छी तरह से परिभाषित क्वासिपार्टिकल्स दृढ़ता से सहसंबद्ध फर्मी प्रणाली के थर्मोडायनामिक , विश्राम (भौतिकी), बहुआयामी स्केलिंग और परिवहन गुणों का निर्धारण करते हैं और एम * टी, एक्स, 'बी', पी, आदि का कार्य बन जाता है। बहुत अलग दृढ़ता से सहसंबद्ध फर्मी प्रणाली के लिए एकत्रित डेटा सार्वभौमिक स्केलिंग व्यवहार प्रदर्शित करता है; दूसरे शब्दों में, दृढ़ता से सहसंबद्ध फ़र्मियन के साथ अलग पदार्थ अप्रत्याशित रूप से समान हो जाती है, इस प्रकार एचएफ धातु, क्वासिक क्रिस्टल, क्वांटम स्पिन तरल, दो आयामी हीलियम -3, और उच्च तापमान सुपरकंडक्टिविटी प्रदर्शित करने वाले रासायनिक यौगिक से युक्त पदार्थ की नई स्थिति बनती है।[40][44]

अनुप्रयोग

क्वांटम स्पिन तरल अवस्थाओं का समर्थन करने वाली पदार्थ में डेटा स्टोरेज और मेमोरी में अनुप्रयोग हो सकते हैं।[57] विशेष रूप से, स्पिन-लिक्विड स्टेट्स के माध्यम से टोपोलॉजिकल क्वांटम कम्प्यूटेशन को अनुभूत करना संभव है।[58] क्वांटम स्पिन तरल पदार्थ के विकास से उच्च तापमान अतिचालकता को समझने में भी सहायता मिल सकती है।[59]

संदर्भ

  1. ↑ Jump up to: 1.0 1.1 Savary, L.; Balents, L. (2017). "Quantum spin liquids: a review". Reports on Progress in Physics. 80 (1): 016502. arXiv:1601.03742. Bibcode:2017RPPh...80a6502S. doi:10.1088/0034-4885/80/1/016502. PMID 27823986. S2CID 22285828.
  2. ↑ Jump up to: 2.0 2.1 2.2 P. W. Anderson (1973). "Resonating valence bonds: A new kind of insulator?". Materials Research Bulletin. 8 (2): 153–160. doi:10.1016/0025-5408(73)90167-0.
  3. ↑ Trafton, Anne (March 28, 2011). "A new spin on superconductivity?". MIT News. Retrieved 24 December 2012.
  4. ↑ Jump up to: 4.0 4.1 P. W. Anderson (1987). "The resonating valence bond state in La2CuO4 and superconductivity". Science. 235 (4793): 1196–1198. Bibcode:1987Sci...235.1196A. doi:10.1126/science.235.4793.1196. PMID 17818979. S2CID 28146486.
  5. ↑ Chaikin, Paul M; Lubensky, Tom C (1995). Principles of Condensed-Matter Physics. Cambridge university press. ISBN 9780521432245.
  6. ↑ Wilkins, Alasdair (August 15, 2011). "A Strange New Quantum State of Matter: Spin Liquids". io9. Retrieved 23 December 2012.
  7. ↑ Jump up to: 7.0 7.1 Leon Balents (2010). "Spin liquids in frustrated magnets". Nature. 464 (7286): 199–208. Bibcode:2010Natur.464..199B. doi:10.1038/nature08917. PMID 20220838. S2CID 4408289.
  8. ↑ Wolchover, Natalie (2018-01-03). "Physicists Aim to Classify All Possible Phases of Matter". Quanta Magazine. Retrieved 2019-05-05.
  9. ↑ Wilczek, Frank (2017-02-28). "Inside the Knotty World of 'Anyon' Particles". Quanta Magazine. Retrieved 2019-05-05.
  10. ↑ Saberi M, Khosrowabadi R, Khatibi A, Misic B, Jafari G (October 2022). "कार्यात्मक मस्तिष्क नेटवर्क में हताशा गठन का पैटर्न". Network Neuroscience. 6 (4): 1334-1356. doi:10.1162/netn_a_00268.
  11. ↑ Kivelson, Steven A.; Rokhsar, Daniel S.; Sethna, James P. (1987). "Topology of the resonating valence-bond state: Solitons and high-Tc superconductivity". Physical Review B. 35 (16): 8865–8868. Bibcode:1987PhRvB..35.8865K. doi:10.1103/physrevb.35.8865. PMID 9941277.
  12. ↑ Kalmeyer, V.; Laughlin, R. B. (1987). "Equivalence of the resonating-valence-bond and fractional quantum Hall states". Physical Review Letters. 59 (18): 2095–2098. Bibcode:1987PhRvL..59.2095K. doi:10.1103/physrevlett.59.2095. PMID 10035416.
  13. ↑ Wen, Xiao-Gang; Wilczek, F.; Zee, A. (1989). "Chiral Spin States and Superconductivity". Physical Review B. 39 (16): 11413–11423. Bibcode:1989PhRvB..3911413W. CiteSeerX 10.1.1.676.519. doi:10.1103/physrevb.39.11413. PMID 9947970.
  14. ↑ Read, N.; Sachdev, Subir (1991). "Large-N expansion for frustrated quantum antiferromagnets". Physical Review Letters. 66 (13): 1773–1776. Bibcode:1991PhRvL..66.1773R. doi:10.1103/physrevlett.66.1773. PMID 10043303.
  15. ↑ Wen, Xiao-Gang (1991). "Mean Field Theory of Spin Liquid States with Finite Energy Gaps". Physical Review B. 44 (6): 2664–2672. Bibcode:1991PhRvB..44.2664W. doi:10.1103/physrevb.44.2664. PMID 9999836.
  16. ↑ Moessner, R.; Sondhi, S. L. (2002). "Resonating Valence Bond Liquid Physics on the Triangular Lattice". Progress of Theoretical Physics Supplement. 145: 37–42. arXiv:cond-mat/0205029. Bibcode:2002PThPS.145...37M. doi:10.1143/PTPS.145.37. S2CID 119370249.
  17. ↑ Kitaev, A.Yu.; Balents, Leon (2003). "Fault-tolerant quantum computation by anyons". Annals of Physics. 303 (1): 2–30. arXiv:quant-ph/9707021. Bibcode:2003AnPhy.303....2K. doi:10.1016/S0003-4916(02)00018-0. S2CID 119087885.
  18. ↑ Knolle, Johannes; Moessner, Roderich (2019). "A field guide to spin liquids". Annual Review of Condensed Matter Physics. 10: 451–472. arXiv:1804.02037. Bibcode:2019ARCMP..10..451K. doi:10.1146/annurev-conmatphys-031218-013401. S2CID 85529148.
  19. ↑ Jump up to: 19.0 19.1 19.2 Norman, M.R. (2016). "Herbertsmithite and the Search for the Quantum Spin Liquid". Reviews of Modern Physics. 88 (4): 041002. arXiv:1710.02991. doi:10.1103/RevModPhys.88.041002. S2CID 118727125.
  20. ↑ Phys. Rev. Lett. 116, 107203 (2016)
  21. ↑ Nytko, Emily A.; Helton, Joel S.; Müller, Peter; Nocera, Daniel G. (2008). "A Structurally Perfect S = 1/2 Metal−Organic Hybrid Kagome Antiferromagnet". Journal of the American Chemical Society. 130 (10): 2922–2923. doi:10.1021/ja709991u. PMID 18275194.
  22. ↑ Matan, K.; Ono, T.; Fukumoto, Y.; Sato, T. J.; et al. (2010). "Pinwheel valence-bond solid and triplet excitations in the two-dimensional deformed kagome lattice". Nature Physics. 6 (11): 865–869. arXiv:1007.3625. Bibcode:2010NatPh...6..865M. doi:10.1038/nphys1761. S2CID 118664640.
  23. ↑ Jump up to: 23.0 23.1 Y. Shimizu; K. Miyagawa; K. Kanoda; M. Maesato; et al. (2003). "Spin Liquid State in an Organic Mott Insulator with a Triangular Lattice". Physical Review Letters. 91 (10): 107001. arXiv:cond-mat/0307483. Bibcode:2003PhRvL..91j7001S. doi:10.1103/PhysRevLett.91.107001. PMID 14525498. S2CID 4652670.
  24. ↑ In literature, the value of J is commonly given in units of temperature () instead of energy.
  25. ↑ T. Ng & P. A. Lee (2007). "Power-Law Conductivity inside the Mott Gap: Application to κ-(BEDT-TTF)2Cu2(CN)3". Physical Review Letters. 99 (15): 156402. arXiv:0706.0050. Bibcode:2007PhRvL..99o6402N. doi:10.1103/PhysRevLett.99.156402. PMID 17995193. S2CID 45188091.
  26. ↑ Coldea, R.; Tennant, D.A.; Tsvelik, A.M.; Tylczynski, Z. (12 Feb 2001). "Experimental realization of a 2D fractional quantum spin liquid". Physical Review Letters. 86 (7): 1335–1338. arXiv:cond-mat/0007172. Bibcode:2001PhRvL..86.1335C. doi:10.1103/PhysRevLett.86.1335. PMID 11178077. S2CID 39524266. Note that the preprint was uploaded in 2000.
  27. ↑ Kohno, Masanori; Starkh, Oleg A; Balents, Leon (2007). "Spinons and triplons in spatially anisotropic frustrated antiferromagnets". Nature Physics. 3 (11): 790. arXiv:0706.2012. Bibcode:2007NatPh...3..790K. doi:10.1038/nphys749. S2CID 28004603.
  28. ↑ Pratt, F. L.; Baker, P. J.; Blundell, S. J.; Lancaster, T.; et al. (2011). "Magnetic and non-magnetic phases of a quantum spin liquid". Nature. 471 (7340): 612–616. Bibcode:2011Natur.471..612P. doi:10.1038/nature09910. PMID 21455176. S2CID 4430673.
  29. ↑ Elser, Veit (1989). "Nuclear antiferromagnetism in a registered 3He solid". Physical Review Letters. 62 (20): 2405–2408. Bibcode:1989PhRvL..62.2405E. doi:10.1103/PhysRevLett.62.2405. PMID 10039977.
  30. ↑ Yan, Simeng; Huse, David A; White, Steven R (2011). "Spin-liquid ground state of the S=1/2 kagome Heisenberg antiferromagnet". Science. 332 (6034): 1173–1176. arXiv:1011.6114. Bibcode:2011Sci...332.1173Y. doi:10.1126/science.1201080. PMID 21527676. S2CID 34864628.
  31. ↑ Shores, Matthew P; Nytko, Emily A; Bartlett, Bart M; Nocera, Daniel G (2005). "A Structurally Perfect S=1/2 Kagome Antigerromagnet". Journal of the American Chemical Society. 127 (39): 13462–13463. doi:10.1021/ja053891p. PMID 16190686.
  32. ↑ Helton, J. S.; et al. (2007). "Spin Dynamics of the Spin-1/2 Kagome Lattice Antiferromagnet ZnCu3(OH)6Cl2". Physical Review Letters. 98 (10): 107204. arXiv:cond-mat/0610539. Bibcode:2007PhRvL..98j7204H. doi:10.1103/PhysRevLett.98.107204. PMID 17358563. S2CID 23174611.
  33. ↑ Olariu, A; et al. (2008). "17O NMR Study of the Intrinsic Magnetic Susceptibility and Spin Dynamics of the Quantum Kagome Antiferromagnet ZnCu3(OH)6Cl2". Physical Review Letters. 100 (9): 087202. arXiv:0711.2459. Bibcode:2008PhRvL.100h7202O. doi:10.1103/PhysRevLett.100.087202. PMID 18352658. S2CID 2682652.
  34. ↑ de Vries, M. A.; Stewart, J. R.; Deen, P. P.; Piatek, J. O.; Nilsen, G. J.; Ronnow, H. M.; Harrison, A. (2009). "Scale-free antiferromagnetic fluctuations in the S=1/2 kagome antiferromagnet herbertsmithite". Physical Review Letters. 103 (23): 237201. arXiv:0902.3194. Bibcode:2009PhRvL.103w7201D. doi:10.1103/PhysRevLett.103.237201. ISSN 0031-9007. PMID 20366167. S2CID 2540295.
  35. ↑ Mendels, Philippe; Bert, Fabrice (2010). "Quantum kagome antiferromagnet: ZnCu3(OH)6Cl2". Journal of the Physical Society of Japan. 79 (1): 011001. arXiv:1001.0801. Bibcode:2010JPSJ...79a1001M. doi:10.1143/JPSJ.79.011001. S2CID 118545779.
  36. ↑ Han, TH; Helton, JS; Chu, S; Prodi, Andrea; Singh, DK; Mazzoli, Claudio; Müller, P; Nocera, DG; Lee, Young S (2011). "Synthesis and characterization of single crystals of the spin-1/2 kagome-lattice antiferromagnets Znx Cu4-x(OH)6Cl2" (PDF). Physical Review B. 83 (10): 100402. doi:10.1103/PhysRevB.83.100402.
  37. ↑ Han, Tian-Heng; Helton, Joel S; Chu, Shaoyan; Nocera, Daniel G; Rodriguez-Rivera, Jose A; Broholm, Collin; Lee, Young S (2012). "Fractionalized excitations in the spin-liquid state of a kagome-lattice antiferromagnet". Nature. 492 (7429): 406–410. arXiv:1307.5047. Bibcode:2012Natur.492..406H. doi:10.1038/nature11659. PMID 23257883. S2CID 4344923.
  38. ↑ Fu, Mingxuan; Imai, Takashi; Lee, Young S (2015). "Evidence for a gapped spin-liquid ground state in a kagome Heisenberg antiferromagnet". Science. 350 (6261): 655–658. arXiv:1511.02174. Bibcode:2015Sci...350..655F. doi:10.1126/science.aab2120. PMID 26542565. S2CID 22287797.
  39. ↑ Han, Tian-Heng; Norman, MR; Wen, J-J; Rodriguez-Rivera, Jose A; Helton, Joel S; Broholm, Collin; Lee, Young S (2016). "Correlated impurities and intrinsic spin-liquid physics in the kagome material herbertsmithite". Physical Review B. 94 (6): 060409. arXiv:1512.06807. Bibcode:2016PhRvB..94f0409H. doi:10.1103/PhysRevB.94.060409. S2CID 115149342.
  40. ↑ Jump up to: 40.0 40.1 40.2 Amusia, M.; Popov, K.; Shaginyan, V.; Stephanovich, V. (2014). Theory of Heavy-Fermion Compounds - Theory of Strongly Correlated Fermi-Systems. Springer Series in Solid-State Sciences. Vol. 182. Springer. doi:10.1007/978-3-319-10825-4. ISBN 978-3-319-10825-4.
  41. ↑ Wen, Jinsheng; Yu, Shun-Li; Li, Shiyan; Yu, Weiqiang; Li, Jian-Xin (12 September 2019). "क्वांटम स्पिन तरल पदार्थों की प्रायोगिक पहचान". NPJ Quantum Materials (in English). 4 (1): 12. arXiv:1904.04435. Bibcode:2019npjQM...4...12W. doi:10.1038/s41535-019-0151-6. ISSN 2397-4648. S2CID 104292206.
  42. ↑ Jump up to: 42.0 42.1 Helton, J. S.; et al. (1472). "Dynamic Scaling in the Susceptibility of the Spin-1/2 Kagome Lattice Antiferromagnet Herbertsmithite". Physical Review Letters. 104 (14): 147201. arXiv:1002.1091. Bibcode:2010PhRvL.104n7201H. doi:10.1103/PhysRevLett.104.147201. PMID 20481955. S2CID 10718733.
  43. ↑ de Vries, M. A.; et al. (2008). "The magnetic ground state of an experimental S=1/2 kagomé antiferromagnet". Physical Review Letters. 100 (15): 157205. arXiv:0705.0654. Bibcode:2008PhRvL.100o7205D. doi:10.1103/PhysRevLett.100.157205. PMID 18518149. S2CID 118805305.
  44. ↑ Jump up to: 44.0 44.1 44.2 Shaginyan, V. R.; Amusia, M. Ya.; Msezane, A. Z.; Popov, K. G. (2010). "Scaling Behavior of Heavy Fermion Metals". Physics Reports. 492 (2–3): 31. arXiv:1006.2658. Bibcode:2010PhR...492...31S. CiteSeerX 10.1.1.749.3376. doi:10.1016/j.physrep.2010.03.001. S2CID 119235769.
  45. ↑ Pozo, Guillermo; de la Presa, Patricia; Prato, Rafael; Morales, Irene; Marin, Pilar; Fransaer, Jan; Dominguez-Benetton, Xochitl (2020). "Spin transition nanoparticles made electrochemically". Nanoscale. 12 (9): 5412–5421. doi:10.1039/C9NR09884D. PMID 32080699.
  46. ↑ Gegenwart, P.; et al. (2006). "High-field phase diagram of the heavy-fermion metal YbRh2Si2". New Journal of Physics. 8 (9): 171. Bibcode:2006NJPh....8..171G. doi:10.1088/1367-2630/8/9/171.
  47. ↑ Jump up to: 47.0 47.1 Shaginyan, V. R.; Msezane, A.; Popov, K. (2011). "Thermodynamic Properties of Kagome Lattice in ZnCu3(OH)6Cl2 Herbertsmithite". Physical Review B. 84 (6): 060401. arXiv:1103.2353. Bibcode:2011PhRvB..84f0401S. doi:10.1103/PhysRevB.84.060401. S2CID 118651738.
  48. ↑ Ying Ran, Michael Hermele, Patrick A. Lee, Xiao-Gang Wen, (2006), "Projected wavefunction study of Spin-1/2 Heisenberg model on the Kagome lattice", https://arxiv.org/abs/cond-mat/0611414
  49. ↑ "New state of matter detected in a two-dimensional material". Retrieved 5 April 2016.
  50. ↑ Banerjee, A.; Bridges, C. A.; Yan, J.-Q.; Aczel, A. A.; Li, L.; Stone, M. B.; Granroth, G. E.; Lumsden, M. D.; Yiu, Y.; Knolle, J.; Bhattacharjee, S.; Kovrizhin, D. L.; Moessner, R.; Tennant, D. A.; Mandrus, D. G.; Nagler, S. E. (2016). "Proximate Kitaev quantum spin liquid behaviour in a honeycomb magnet". Nature Materials. 15 (7): 733–740. arXiv:1504.08037. Bibcode:2016NatMa..15..733B. doi:10.1038/nmat4604. PMID 27043779. S2CID 3406627.
  51. ↑ Jump up to: 51.0 51.1 Shaginyan, V. R.; et al. (2012). "Identification of Strongly Correlated Spin Liquid in Herbertsmithite". EPL. 97 (5): 56001. arXiv:1111.0179. Bibcode:2012EL.....9756001S. doi:10.1209/0295-5075/97/56001. S2CID 119288349.
  52. ↑ Wood, Charlie (2021-12-02). "क्वांटम प्रोसेसर पर स्थैतिक रूप से आदेशित राज्यों को साकार करना". Science (in English). 374 (6572): 1237–1241. arXiv:2104.01180. Bibcode:2021Sci...374.1237S. doi:10.1126/science.abi8378. PMID 34855491. S2CID 233025160. Retrieved 2021-12-04.{{cite journal}}: CS1 maint: url-status (link)
  53. ↑ Wood, Charlie (2021-12-02). "क्वांटम सिमुलेटर पदार्थ का एक पूरी तरह से नया चरण बनाते हैं". Quanta Magazine (in English). Retrieved 2022-03-11.
  54. ↑ Satzinger, K. J.; Liu, Y.-J; Smith, A.; Knapp, C.; Newman, M.; Jones, C.; Chen, Z.; Quintana, C.; Mi, X.; Dunsworth, A.; Gidney, C. (2021-12-03). "क्वांटम प्रोसेसर पर स्थैतिक रूप से आदेशित राज्यों को साकार करना". Science. 374 (6572): 1237–1241. arXiv:2104.01180. Bibcode:2021Sci...374.1237S. doi:10.1126/science.abi8378. PMID 34855491. S2CID 233025160.
  55. ↑ Verresen, Ruben; Lukin, Mikhail D.; Vishwanath, Ashvin (2021-07-08). "रिडबर्ग नाकाबंदी से टोरिक कोड टोपोलॉजिकल ऑर्डर की भविष्यवाणी". Physical Review X. 11 (3): 031005. arXiv:2011.12310. Bibcode:2021PhRvX..11c1005V. doi:10.1103/PhysRevX.11.031005. S2CID 227162637.
  56. ↑ Semeghini, G.; Levine, H.; Keesling, A.; Ebadi, S.; Wang, T. T.; Bluvstein, D.; Verresen, R.; Pichler, H.; Kalinowski, M.; Samajdar, R.; Omran, A. (2021-12-03). "एक प्रोग्राम योग्य क्वांटम सिम्युलेटर पर टोपोलॉजिकल स्पिन तरल पदार्थ की जांच करना". Science. 374 (6572): 1242–1247. arXiv:2104.04119. Bibcode:2021Sci...374.1242S. doi:10.1126/science.abi8794. PMID 34855494. S2CID 233204440.
  57. ↑ Aguilar, Mario (December 20, 2012). "This Weird Crystal Demonstrates a New Magnetic Behavior That Works Like Magic". Gizmodo. Retrieved 24 December 2012.
  58. ↑ Fendley, Paul. "Topological Quantum Computation from non-abelian anyons" (PDF). University of Virginia. Archived from the original (PDF) on 2013-07-28. Retrieved 24 December 2012.
  59. ↑ Chandler, David (December 20, 2012). "New kind of magnetism discovered: Experiments demonstrate 'quantum spin liquid'". Phys.org. Retrieved 24 December 2012.
Retrieved from ‘https://www.vigyanwiki.in/index.php?title=क्वांटम_स्पिन_तरल&oldid=214585’