घूर्णन तल

ज्यामिति में, घूर्णन का तल एक अमूर्त वस्तु है जिसका उपयोग स्थल में घूर्णन (गणित) का वर्णन या कल्पना करने के लिए किया जाता है। तीन आयामों में यह एक निश्चित अक्ष के चारों ओर घूमने का एक विकल्प है, लेकिन घूर्णन की धुरी के विपरीत इसका उपयोग अन्य आयामों में किया जा सकता है, जैसे कि दो चार या अधिक आयाम।

गणितीय रूप से इस तरह के तल को कई तरह से वर्णित किया जा सकता है। उन्हें समतल (ज्यामिति) और घूर्णन कोण के संदर्भ में वर्णित किया जा सकता है। उन्हें ज्यामितीय बीजगणित से बायवेक्टर के साथ जोड़ा जा सकता है। वे घूर्णन (गणित) के आइजनवैल्यू ​​​​और आइजन्वेक्टर से संबंधित हैं और विशेष आयामों में वे अन्य बीजगणितीय और ज्यामितीय गुणों से संबंधित हैं, जिन्हें बाद में अन्य आयामों के लिए सामान्यीकृत किया जा सकता है।

घूर्णन के तलों का दो और तीन आयामों में अधिक उपयोग नहीं किया जाता है, क्योंकि दो आयामों में केवल एक ही तल होता है, इसलिए घूर्णन के तल की पहचान तुच्छ और कदाचित ही कभी की जाती है, जबकि तीन आयामों में घूर्णन की धुरी एक ही उद्देश्य को पूरा करती है और और अधिक स्थापित दृष्टिकोण है। उनके लिए मुख्य उपयोग उच्च आयामों में अधिक जटिल घुमावों का वर्णन करने में है, जहाँ उनका उपयोग घुमावों को सरल भागों में तोड़ने के लिए किया जा सकता है। यह बीजगणित में साधारण द्विभाजकों से जुड़े घूर्णन के तलों के साथ ज्यामितीय बीजगणित का उपयोग करके किया जा सकता है।

परिभाषाएँ

तल

इस लेख के लिए, सभी समतल (ज्यामिति) मूल (गणित) से होकर जाने वाले तल हैं, अर्थात उनमें शून्य सदिश होता है। n-आयामी स्थान समष्टि का द्वि-आयामी रैखिक उप-स्थान है। यह पूरी तरह से किसी भी दो गैर-शून्य और गैर-समानांतर सदिशों द्वारा निर्दिष्ट किया जाता है जो तल में स्थित होते हैं, जो कि किसी भी दो सदिश a और b, द्वारा होता है। ऐसा है कि

$\mathbf {a} \wedge \mathbf {b} \neq 0,$

जहाँ ∧ बहिर्भाग बीजगणित या ज्यामितीय बीजगणित से बहिर्भाग उत्पाद है (तीन आयामों में संकरीकरण उत्पाद का उपयोग किया जा सकता है)। अधिक सटीक, मात्रा a ∧ b द्वारा निर्दिष्ट तल से जुड़ा बाइवेक्टर a और b है, और परिमाण है |a| |b| sin φ, जहाँ φ सदिशों के बीच का कोण है; इसलिए आवश्यकता है कि सदिश गैर-शून्य और गैर-समानांतर हों।

अगर बायवेक्टर a ∧ b B लिखा है, तब वह स्थिति जिससे संबद्ध तल पर कोई बिंदु B स्थित है,

$\mathbf {x} \wedge \mathbf {B} =0.$

यह सभी आयामों में सत्य है, और इसे समतल पर परिभाषा के रूप में लिया जा सकता है। विशेष रूप से, बाहरी उत्पाद के गुणों से दोनों a और b से संतुष्ट है, और इसलिए निम्न स्वरुप के किसी भी सदिश द्वारा:

$\mathbf {c} =\lambda \mathbf {a} +\mu \mathbf {b} ,$

वास्तविक संख्याओं λ और μ के साथ है। जैसा λ और μ सभी वास्तविक संख्याओं पर सीमा, c पूरे तल पर पर्वतमाला है, इसलिए इसे तल की एक और परिभाषा के रूप में लिया जा सकता है।

घूर्णन तल

किसी विशेष घूर्णन (गणित) के लिए घूर्णन का समतल एक तल है जो घूर्णन द्वारा स्वयं के लिए रैखिक मानचित्र है। तल स्थिर नहीं है, लेकिन तल के सभी सदिश घूर्णन द्वारा उसी तल में अन्य सदिश के लिए प्रतिचित्र किए जाते हैं। तल का अपने आप में परिवर्तन सदैव उत्पत्ति की ओर एक घूर्णन होता है, एक कोण के माध्यम से जो तल के घूर्णन का कोण होता है।

अस्मिता घूर्णन को छोड़कर हर घूर्णन में घूर्णन का कम से कम एक तल होता है, और निम्न तक

$\left\lfloor {\frac {n}{2}}\right\rfloor$

घूर्णन के तल, जहां n आयाम है। इस तालिका में आठ आयामों तक के तलों की अधिकतम संख्या दर्शाई गई है:

आयाम	2	3	4	5	6	7	8
तल की संख्या	1	1	2	2	3	3	4

जब किसी घूर्णन में घूर्णन के कई तल होते हैं तो वे केवल उदगम उभयनिष्ठ होते हुए सदैव एक दूसरे के लम्बवत होते हैं। यह कहने की तुलना में एक मजबूत स्थिति है कि तल समकोण पर हैं; इसके स्थान पर इसका मतलब है कि तलों में कोई गैर-शून्य सदिश सामान्यतः नहीं है, और यह कि एक तल में प्रत्येक सदिश दूसरे तल में प्रत्येक सदिश के लिए आयतीय है। यह केवल चार या अधिक आयामों में ही हो सकता है। दो आयामों में केवल एक तल होता है, जबकि तीन समतलों में सभी तल में कम से कम एक शून्येतर सदिश उभयनिष्ठ होता है।

तीन से अधिक आयामों में घूर्णन के तल सदैव अद्वितीय नहीं होते हैं। उदाहरण के लिए चार आयामों में पहचान आव्यूह का प्रतिकूल,

${\begin{pmatrix}-1&0&0&0\\0&-1&0&0\\0&0&-1&0\\0&0&0&-1\end{pmatrix}},$

चार आयामों में घूर्णन का वर्णन करता है जिसमें उत्पत्ति के माध्यम से प्रत्येक तल कोण π के माध्यम से घूर्णन का तल होता है, इसलिए आयतीय तल की कोई भी जोड़ी घूर्णन उत्पन्न करती है। लेकिन एक सामान्य घुमाव के लिए कम से कम सैद्धांतिक रूप से आयतीय तल के एक अद्वितीय सम्मुच्चय की पहचान करना संभव है, जिनमें से प्रत्येक बिंदु को एक कोण के माध्यम से घुमाया जाता है, इसलिए तल और कोणों का सम्मुचय पूरी तरह से घूर्णन की विशेषता है।

दो आयाम

द्वि-आयामी स्थल में घूर्णन का केवल एक तल है, स्थल का ही तल। कार्तीय समन्वय प्रणाली में यह कार्तीय तल है, जटिल संख्या में यह जटिल तल है। इसलिए कोई भी घुमाव पूरे तल का होता है, यानी समतल का, केवल व्युत्पत्ति (गणित) को स्थिर रखते हुए। यह घूर्णन के हस्ताक्षरित कोण द्वारा पूरी तरह से निर्दिष्ट है, उदाहरण के लिए -π से π.सीमा में। इसलिए यदि कोण θ है तो जटिल तल में घूर्णन यूलर के सूत्र द्वारा दिया जाता है:

$e^{i\theta }=\cos {\theta }+i\sin {\theta },\,$

जबकि कार्तीय तल में घूर्णन द्वारा 2 × 2 घूर्णन आव्यूह दिया जाता है  :

${\begin{pmatrix}\cos \theta &-\sin \theta \\\sin \theta &\cos \theta \end{pmatrix}}.$

तीन आयाम

एक त्रि-आयामी घूर्णन, घूर्णन की धुरी के साथ z-अक्ष और घूर्णन का तल xy-तल

त्रि-आयामी स्थल में घूर्णन के असीमित संख्या में तल होते हैं, जिनमें से केवल एक ही किसी दिए गए घूर्णन में सम्मिलित होता है। अर्थात्, एक सामान्य घुमाव के लिए ठीक एक तल होता है जो इसके साथ जुड़ा होता है या जिसमें घुमाव होता है। एकमात्र अपवाद साधारण घुमाव है, जो तत्समक आव्यूह के अनुरूप है, जिसमें कोई घुमाव नहीं होता है।

तीन आयामों में किसी भी घुमाव में सदैव एक निश्चित धुरी और घूर्णन की धुरी होती है। इस अक्ष को देकर घूर्णन का वर्णन किया जा सकता है, जिस कोण से घूर्णन इसके चारों ओर घूमता है; यह एक घूर्णन का अक्ष कोण निरूपण है। घूर्णन का तल इस अक्ष के लिए समतल आयतीय है, इसलिए अक्ष तल की सामान्य सतह है। घूर्णन तब इस तल को उसी कोण से घुमाता है जैसे यह मूलबिंदु के चारों ओर घूमता है, अर्थात तल में सब कुछ मूलबिंदु में उसी कोण से घूमता है।

एक उदाहरण आरेख में दिखाया गया है, जहां z-अक्ष घूर्णन के मूलबिंदु में होता है । xy-तल घूर्णन का तल है, तो उस तल में सब कुछ घूर्णन द्वारा तल में रखा जाता है। यह एक आव्यूह द्वारा निम्नलिखित की तरह वर्णित किया जा सकता है, जिसमें एक कोण θ के माध्यम से घूर्णन होता है:

${\begin{pmatrix}\cos \theta &-\sin \theta &0\\\sin \theta &\cos \theta &0\\0&0&1\end{pmatrix}}.$

पृथ्वी अपनी धुरी और घूर्णन के तल को दिखा रही है, दोनों अक्षीय झुकाव तल के सापेक्ष और पृथ्वी की कक्षा के लंबवत हैं

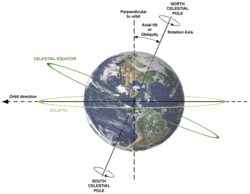
एक अन्य उदाहरण पृथ्वी का घूर्णन है। घूर्णन की धुरी उत्तरी ध्रुव और दक्षिणी ध्रुव को मिलाने वाली रेखा है और घूर्णन का तल भूमध्य रेखा के माध्यम से उत्तरी गोलार्ध और दक्षिणी गोलार्ध के बीच का तल है। अन्य उदाहरणों में घूर्णिका या गतिपालक चक्र जैसे यांत्रिक उपकरण सम्मिलित हैं जो घूर्णी ऊर्जा को द्रव्यमान में सामान्यतः घूर्णन के तल के साथ संग्रहीत करते हैं।

किसी भी तीन आयामी घुमाव में घूर्णन के तल को विशिष्ट रूप से परिभाषित किया जाता है। घूर्णन के कोण के साथ मिलकर यह घूर्णन का पूरी तरह से वर्णन करता है। या एक निरंतर घूमने वाली वस्तु में घूर्णी गुण जैसे घूर्णन की दर को घूर्णन के तल के संदर्भ में वर्णित किया जा सकता है। यह लंबवत है, और इसलिए इसे घूर्णन की धुरी द्वारा परिभाषित किया गया है, इसलिए घूर्णन के तल के संदर्भ में घूर्णन का कोई भी विवरण घूर्णन के अक्ष के संदर्भ में वर्णित, और इसके विपरीत किया जा सकता है। लेकिन घूर्णन की धुरी के विपरीत तल अन्य, विशेष रूप से उच्च, आयामों में सामान्यीकृत होता है।

चार आयाम

Main article: 4-आयामी यूक्लिडिय स्थल में घूर्णन

चार आयामी स्थल में एक सामान्य घुमाव का केवल एक निश्चित बिंदु होता है, मूल बिंदु। इसलिए घूर्णन की धुरी का उपयोग चार आयामों में नहीं किया जा सकता है। लेकिन घूर्णन के तलों का उपयोग किया जा सकता है, और चार आयामों में प्रत्येक गैर-तुच्छ घूर्णन में घूर्णन के एक या दो तल होते हैं।

सरल घुमाव

घूर्णन के केवल एक तल के साथ घूर्णन सरल घूर्णन है। साधारण घुमाव में एक निश्चित तल होता है, और इस तल के बारे में कहा जा सकता है कि घूर्णन होता है, इसलिए जब वे घूमते हैं तो बिंदु इस तल से अपनी दूरी नहीं बदलते हैं। घूर्णन का तल इस तल के लिए आयतीय है, और कहा जा सकता है कि घूर्णन इस तल में होता है।

उदाहरण के लिए निम्न आव्यूह xy-तल ठीक करता है: बिंदु उस तल में और केवल उस तल में अपरिवर्तित हैं। घूर्णन का तल zw-तल है इस तल में बिंदुओं को एक कोण θ से घुमाया जाता है। एक सामान्य बिंदु केवल zw-तल में घूमता है, यानी यह केवल z और w निर्देशांक बदलकर xy-तल के चारों ओर घूमता है।

${\begin{pmatrix}1&0&0&0\\0&1&0&0\\0&0&\cos \theta &-\sin \theta \\0&0&\sin \theta &\cos \theta \end{pmatrix}}$

दो और तीन आयामों में सभी घूर्णन सरल होते हैं, जिसमें उनके घूर्णन का केवल एक तल होता है। केवल चार या अधिक आयामों में ऐसे घुमाव होते हैं जो साधारण घुमाव नहीं होते हैं। विशेष रूप से चार आयामों में दोहरे और समनमनी घुमाव भी होते हैं।

युग्म घूर्णन

युग्म घूर्णन में घूर्णन के दो तल हैं, कोई निश्चित तल नहीं है, और एकमात्र मूलबिंदु निश्चित है। घूर्णन को घूर्णन के दोनों तलों में होने के लिए कहा जा सकता है, क्योंकि उनमें बिंदुओं को तलों के भीतर घुमाया जाता है। ये तल आयतीय हैं, अर्थात इनमें कोई सदिश उभयनिष्ठ नहीं है इसलिए एक तल का प्रत्येक सदिश दूसरे तल के प्रत्येक सदिश के समकोण पर है। दो घूर्णन तल चार-आयामी स्थल में फैले हुए हैं, इसलिए स्थल में प्रत्येक बिंदु को दो बिंदुओं और प्रत्येक तल पर एक बिंदु द्वारा निर्दिष्ट किया जा सकता है।

एक युग्म घूर्णन में घूर्णन के दो कोण होते हैं और घूर्णन के प्रत्येक तल के लिए एक कोण होता है। घूर्णन दो तलों और दो गैर-शून्य कोणों α और β (यदि कोण शून्य है तो घूर्णन सरल है) को देकर निर्दिष्ट किया गया है। पहले तल में α बिंदु घूमते हैं , जबकि दूसरे तल में β बिंदु घूमते हैं, अन्य सभी बिंदु बीच के कोण α और β से घूमते हैं, इसलिए एक मायने में वे एक साथ घूर्णन की मात्रा निर्धारित करते हैं। एक सामान्य दोहरे घूर्णन के लिए घूर्णन और कोण के तल अद्वितीय होते हैं, और एक सामान्य घूर्णन दिए जाने पर उनकी गणना की जा सकती है। उदाहरण के लिए का एक घूर्णन α में xy-तल और β में zw-तल आव्यूह द्वारा दिया जाता है।

${\begin{pmatrix}\cos \alpha &-\sin \alpha &0&0\\\sin \alpha &\cos \alpha &0&0\\0&0&\cos \beta &-\sin \beta \\0&0&\sin \beta &\cos \beta \end{pmatrix}}.$

समनमनी घूर्णन

समनमनी घुमाव के साथ एक टेस्सेरैक्ट का प्रक्षेपण।

दोहरे घुमाव का एक विशेष मामला तब होता है जब कोण बराबर अर्थात α = β ≠ 0 होते हैं, इसे समनमनी घुमाव कहा जाता है, और यह कई तरीकों से सामान्य दोहरे घुमाव से अलग है। उदाहरण के लिए एक समनमनी घूर्णन में, सभी गैर-शून्य बिंदु एक ही कोण α से घूमते हैं। सबसे महत्वपूर्ण बात यह है कि घूर्णन के तलों की विशिष्ट पहचान नहीं की जाती है। इसके स्थान पर आयतीय तलों के अनंत संख्या में जोड़े हैं जिन्हें घूर्णन के तलों के रूप में माना जा सकता है। उदाहरण के लिए किसी भी बिंदु को लिया जा सकता है, और जिस समतल में यह घूमता है, साथ में इसके आयतीय तल के साथ घूर्णन के दो तलों के रूप में उपयोग किया जा सकता है।

उच्च आयाम

जैसा कि पहले ही उल्लेख किया गया है कि घूर्णन के तलों की अधिकतम संख्या n आयाम है

$\left\lfloor {\frac {n}{2}}\right\rfloor ,$

इसलिए जटिलता जल्दी से चार से अधिक आयामों के साथ बढ़ जाती है और उपरोक्त के रूप में घूर्णन को वर्गीकृत करना व्यावहारिक होने के लिए बहुत जटिल हो जाता है, लेकिन कुछ अवलोकन किए जा सकते हैं।

सरल घुमावों को सभी आयामों में घूर्णन के केवल एक तल के साथ घूर्णन के रूप में पहचाना जा सकता है।

एक सामान्य घूर्णन सरल नहीं होता है, और जैसा कि ऊपर दिया गया है, घूर्णन के तलों की अधिकतम संख्या होती है। सामान्य स्थिति में इन तलों में घूर्णन के कोण भिन्न होते हैं और तल विशिष्ट रूप से परिभाषित होते हैं। यदि कोई भी कोण समान है तो तल अद्वितीय नहीं हैं, जैसा कि चार आयामों में एक समनमनी घुमाव के साथ होता है।

समान आयामों में (n = 2, 4, 6...) n/2 तक घूर्णन के तल स्थल में फैले हुए हैं, इसलिए एक सामान्य घुमाव मूल बिंदु को छोड़कर सभी बिंदुओं को घुमाता है जो एकमात्र निश्चित बिंदु है। विषम आयामों में (n = 3, 5, 7, ...) जहाँ n − 1/2 समतल और घूर्णन के समान आयाम के समान एक निचला कोण है। ये स्थल को नहीं फैलाते हैं, लेकिन एक रेखा छोड़ते हैं जो घूमती नहीं है - जैसे कि तीन आयामों में एक निश्चित अक्ष के चारों ओर घूमना, इस रेखा के बारे में घुमावों को छोड़कर, इसके कई तलों में आयतीय नहीं होता है।

गणितीय गुण

ऊपर दिए गए उदाहरणों को घूर्णन के स्पष्ट और सरल उदाहरण के रूप सामान्यतः तीन और चार आयामों में समन्वय अक्षों के समानांतर तलों के साथ में चुना गया था। लेकिन सामान्यतः यह स्थिति नहीं है: तल सामान्यतः अक्ष के समानांतर नहीं होते हैं, और आव्यूहों को आसानी से लिखा नहीं जा सकता है। सभी आयामों में घुमाव पूरी तरह से घूर्णन के तलों और उनके संबंधित कोणों द्वारा वर्णित हैं, इसलिए उन्हें निर्धारित करने में सक्षम होना उपयोगी है, या कम से कम गणितीय रूप से उनका वर्णन करने के तरीके खोजना उपयोगी है।

प्रतिबिंब

हर साधारण घुमाव को दो प्रतिबिंब (गणित) द्वारा उत्पन्न किया जा सकता है।प्रतिबिंबित करने के लिए एक (एन -1) -आयामी उप-स्थान देकर प्रतिबिंबों को एन आयामों में निर्दिष्ट किया जा सकता है, इसलिए एक द्वि-आयामी प्रतिबिंब एक रेखा में है, एक त्रि-आयामी प्रतिबिंब एक विमान में है, और आगे इसी तरह। लेकिन उच्च आयामों में इसे लागू करना कठिन हो जाता है, इसलिए इसके स्थान पर सदिश का उपयोग करना बेहतर होता है।

n आयामों में एक प्रतिबिंब (n − 1)-विमीय उपसमष्टि के लम्बवत् सदिश द्वारा निर्दिष्ट किया जाता है। सरल घुमाव उत्पन्न करने के लिए केवल मूल को ठीक करने वाले प्रतिबिंबों की आवश्यकता होती है, इसलिए सदिश की स्थिति नहीं होती है, केवल दिशा होती है। इससे कोई फर्क नहीं पड़ता कि यह किस तरह से सामना कर रहा है: परिणाम को बदले बिना इसे इसके नकारात्मक से बदला जा सकता है। इसी तरह इकाई सदिश का उपयोग गणनाओं को सरल बनाने के लिए किया जा सकता है।

अतः एक (n − 1) -विमीय स्थान में परावर्तन इसके लंबवत इकाई सदिश द्वारा दिया जाता है, m, इस प्रकार:

$\mathbf {x} '=-\mathbf {mxm} \,$

जहां उत्पाद ज्यामितीय बीजगणित से ज्यामितीय उत्पाद है।

यदि x′ एक अन्य, विशिष्ट, (n − 1)-आयामी स्थल में परिलक्षित होता है, जो एक इकाई सदिश n लंबवत द्वारा वर्णित है, तो परिणाम है

$\mathbf {x} ''=-\mathbf {nx} '\mathbf {n} =-\mathbf {n} (-\mathbf {mxm} )\mathbf {n} =\mathbf {nmxmn}$

यह n आयामों में एक साधारण घुमाव है, जो उप-स्थानों के बीच दो बार कोण के माध्यम से होता है, जो कि सदिश m और n के बीच का कोण भी है। इसे ज्यामितीय बीजगणित का उपयोग करके जांचा जा सकता है कि यह एक घूर्णन है, और यह अपेक्षा के अनुरूप सभी सदिशों को घुमाता है।

मात्रा mn एक घूर्णक (गणित) है, और nm इसका व्युत्क्रम है

$(\mathbf {mn} )(\mathbf {nm} )=\mathbf {mnnm} =\mathbf {mm} =1$

तो घूर्णन लिखा जा सकता है

$\mathbf {x} ''=R\mathbf {x} R^{-1}$

जहाँ R = mn घूर्णक है।

घूर्णन का तल युक्त तल m और n है , जो अलग होना चाहिए अन्यथा प्रतिबिंब समान होते हैं और कोई घुमाव नहीं होता है। जैसा कि किसी भी सदिश को उसके ऋणात्मक द्वारा प्रतिस्थापित किया जा सकता है, उनके बीच का कोण सदैव न्यून या अधिक से अधिक π/2 हो सकता है। घूर्णन सदिशों के बीच के दोगुने कोण से होता है, π तक या अर्ध-मोड़ तक। घूर्णन की भावना m से n की ओर घूमना है: ज्यामितीय उत्पाद क्रम विनिमेय नहीं है इसलिए उत्पाद nm व्युत्क्रम घूर्णन है, जिसका अर्थ n से m है।

इसके विपरीत, सभी सरल घुमावों को इस तरह से दो प्रतिबिंबों के साथ उत्पन्न किया जा सकता है, घूर्णन के तल में दो इकाई सदिशों द्वारा घूर्णन के वांछित कोण के आधे से अलग किया जाता है। घूर्णन के प्रत्येक तल में दो सदिश द्वारा दिए गए प्रतिबिंबों के जोड़े का चयन करके, यदि आयाम n सम है, तो n - 2 यदि n विषम है, तो n प्रतिबिंबों का उपयोग करके अधिक सामान्य घुमाव उत्पन्न करने के लिए इनकी रचना की जा सकती है।।

बायवेक्टर्स

द्विभाजक ज्यामितीय बीजगणित, क्लिफर्ड बीजगणित और बाहरी बीजगणित से मात्राएं हैं, जो सदिश के विचार को दो आयामों में सामान्यीकृत करती हैं। चूंकि सदिश रेखाओं के लिए हैं, इसलिए बाइवेक्टर तलों के लिए हैं। तो हर तल (किसी भी आयाम में) एक बायवेक्टर से जुड़ा हो सकता है, और हर बायवेक्टर एक तल से जुड़ा होता है। यह उन्हें घूर्णन के तलों का वर्णन करने के लिए उपयुक्त बनाता है।

घूर्णन में हर तल में एक साधारण बायवेक्टर जुड़ा होता है। यह समतल के समानांतर है और इसका परिमाण समतल में घूर्णन कोण के बराबर है। इन बायवेक्टरों को पूरे घूर्णन के लिए एकल, सामान्यतः गैर-सरल, बायवेक्टर बनाने के लिए अभिव्यक्त किया जाता है। यह घातांक प्रकार्य के माध्यम से एक घूर्णक (गणित) उत्पन्न कर सकता है, जिसका उपयोग किसी वस्तु को घुमाने के लिए किया जा सकता है।

बाइवेक्टर घातीय मानचित्र के माध्यम से घूर्णाकों से संबंधित हैं (जो डी मोइवर के सूत्र का उपयोग करके घूर्णक और घुमाव उत्पन्न करता है)। विशेष रूप से किसी भी बायवेक्टर को दिया गया B इससे जुड़ा घूर्णक है

$R_{\mathbf {B} }=e^{\frac {\mathbf {B} }{2}}.$

यह एक साधारण घुमाव है यदि बायवेक्टर सरल है, अन्यथा अधिक सामान्य घुमाव है। रुंडित होने पर,

${R_{\mathbf {B} }}^{2}=e^{\frac {\mathbf {B} }{2}}e^{\frac {\mathbf {B} }{2}}=e^{\mathbf {B} },$

यह एक घूर्णक देता है जो दो बार कोण से घूमता है। यदि B सरल है तो यह वही घुमाव है जो उत्पाद के रूप में दो प्रतिबिंबों द्वारा उत्पन्न होता है, क्योंकि गुणनफल mn सदिशों के बीच दुगने कोण से घूर्णन देता है। इनकी बराबरी की जा सकती है,

$\mathbf {mn} =e^{\mathbf {B} },$

जिससे यह पता चलता है कि m और n युक्त क्रमावर्तन के तल से जुड़ा बाइवेक्टर जो m को n में घुमाता है

$\mathbf {B} =\log(\mathbf {mn} ).$

यह एक साधारण बायवेक्टर है, जो वर्णित सरल घुमाव से जुड़ा है। चार या अधिक आयामों में अधिक सामान्य घुमाव साधारण द्विभाजकों के योग से जुड़े होते हैं, घूर्णन के प्रत्येक तल के लिए एक, ऊपर के रूप में गणना की जाती है।

उदाहरणों में ऊपर दिए गए चार आयामों में दो घुमाव सम्मिलित हैं। zw-तल में एक कोण θ द्वारा साधारण घुमाव में बाइवेक्टर e34θ एक साधारण बायवेक्टर है। युग्म घूर्णन द्वारा α और β में xy-तल और zw-तल में बाइवेक्टर e₁₂α + e₃₄β होता है , दो साधारण द्विभाजकों का योग e₁₂α और e₃₄β जो घूर्णन के दो तलों के समानांतर होते हैं और इनके परिमाण घूर्णन कोणों के बराबर होते हैं।

एक घूर्णक को देखते हुए इसके साथ जुड़े बायवेक्टर को घूर्णक के लघुगणक को ले कर पुनर्प्राप्त किया जा सकता है, जिसे बाद में घूर्णन के तलों को निर्धारित करने के लिए सरल बायवेक्टरों में विभाजित किया जा सकता है, हालांकि व्यवहार में सभी के लिए लेकिन सबसे सरल स्थितियों में यह अव्यावहारिक हो सकता है। लेकिन सरल बायवेक्टर दिए जाने पर ज्यामितीय बीजगणित उपरोक्त की तरह बीजगणित का उपयोग करके घूर्णन के तलों का अध्ययन करने के लिए एक उपयोगी उपकरण है।

आइगेनवैल्यू और आइगेनप्लेन

आइगेनवैल्यू ​​का उपयोग कर एक विशेष घुमाव के लिए घूर्णन के तल n आयामों में एक सामान्य घूर्णन आव्यूह को देखते हुए इसकी विशेषता समीकरण में या तो एक (विषम आयामों में) या शून्य (यहां तक ​​कि आयामों में) वास्तविक वर्गमूल हैं। अन्य जड़ें बिल्कुल जटिल संयुग्म जोड़े में हैं

$\left\lfloor {\frac {n}{2}}\right\rfloor ,$

ये घूर्णन के तलों के अनुरूप हैं, आव्यूह के आइगेनप्लेन, जिनकी गणना बीजगणितीय तकनीकों का उपयोग करके की जा सकती है। इसके अलावा जटिल वर्गमूल के तर्क (जटिल विश्लेषण) घूर्णन के तलों से जुड़े बायवेक्टरों के परिमाण हैं। विशेषता समीकरण का रूप तलों से संबंधित है, जिससे इसके बीजगणितीय गुणों को दोहराए जाने वाले जड़ों से संबंधित करना संभव हो जाता है, जहां दोहराए जाने वाले बायवेक्टर परिमाण में विशेष ज्यामितीय व्याख्याएं होती हैं।

यह भी देखें

• SO(3) का लेखाचित्र
• घूर्णन करता है
• चतुष्कोण
• घूर्णन समूह SO(3)
• 4-आयामी यूक्लिडीय स्थल में घूर्णन

संदर्भ

• Hestenes, David (1999). New Foundations for Classical Mechanics (2nd ed.). Kluwer. ISBN 0-7923-5302-1.
• Lounesto, Pertti (2001). Clifford algebras and spinors. Cambridge: Cambridge University Press. ISBN 978-0-521-00551-7.
• Dorst, Leo; Doran, Chris; Lasenby, Joan (2002). Applications of geometric algebra in computer science and engineering. Birkhäuser. ISBN 0-8176-4267-6.