ज्यामितीय हैशिंग
कंप्यूटर विज्ञान में, ज्यामितीय हैशिंग दो आयामी वस्तुओं की कुशलता से जानकारी प्राप्त करने की विधि है जो सतत बिंदुओं द्वारा प्रस्तुत की जाती है, जो परिशोधित परिवर्तन से हुई है, चूँकि एक्सटेंशन अन्य ऑब्जेक्ट प्रस्तुतियों एवं परिवर्तनों के लिए उपस्थित हैं। ऑफलाइन चरण में, प्रत्येक जोड़ी बिंदुओं को ज्यामितीय आधार (रैखिक बीजगणित) के रूप में मानकर वस्तुओं को एन्कोड किया जाता है। शेष बिंदुओं को दो मापदंडों का उपयोग करके इस आधार के संबंध में अपरिवर्तनीय (गणित) प्रचलन में प्रदर्शित किया जा सकता है। प्रत्येक बिंदु के लिए, इसके आकस्मिकता (सिग्नल प्रोसेसिंग) रूपांतरित निर्देशांक को हैश सारणी में कुंजी के रूप में संग्रहीत किया जाता है, एवं आधार बिंदुओं के मान के रूप में होते हैं। आधार बिंदुओं की नई जोड़ी का चयन किया जाता है एवं प्रक्रिया को दोहराया जाता है। ऑनलाइन (मान्यता) चरण में, डेटा बिंदुओं के चयनित जोड़े को प्रत्याशी के आधार के रूप में माना जाता है। प्रत्येक प्रत्याशी के आधार पर, शेष डेटा बिंदुओं को आधार के अनुसार एन्कोड किया गया है एवं वस्तु से संभावित पत्राचार पूर्व निर्मित सारणी में पाए जाते हैं। प्रत्याशी के आधार को स्वीकार किया जाता है यदि पर्याप्त रूप से बड़ी संख्या में डेटा बिंदु सुसंगत वस्तु आधार को अनुक्रमित करते हैं।
ज्यामिति हैशिंग मूल रूप से 2डी एवं 3डी में वस्तु मान्यता के लिए कंप्यूटर दृष्टि में दर्शायी गई थी,[1] तत्पश्चात प्रोटीन के संरचनात्मक संरेखण जैसी विभिन्न समस्याओं पर प्रारम्भ किया गया।[2][3]
कंप्यूटर दृष्टि में ज्यामितीय हैशिंग
ज्यामितीय हैशिंग वस्तु पहचान के लिए उपयोग की जाने वाली विधि है। मान लीजिए कि हम यह जानकारी प्राप्त करना चाहते हैं कि इनपुट छवि में मॉडल छवि देखी जा सकती है या नहीं। यह ज्यामितीय हैशिंग के साथ पूर्ण किया जा सकता है। विधि का उपयोग, आधार में एकाधिक वस्तुओं को पहचानने के लिए किया जा सकता है, इस स्तिथि में हैश सारणी को न केवल मुद्रा जानकारी अर्थात आधार में ऑब्जेक्ट मॉडल की अनुक्रमणिका भी संग्रहित करनी चाहिए।
उदाहरण
सरलता के लिए, यह उदाहरण अत्यधिक बिंदु विशेषताओं का उपयोग नहीं करेगा एवं यह मान लेगा कि उनके विवरणकर्ता केवल उनके निर्देशांक द्वारा दिए गए हैं (व्यवहार में स्थानीय वर्णनकर्ता जैसे कि स्केल का उपयोग अनुक्रमण के लिए किया जा सकता है)।
प्रशिक्षण चरण
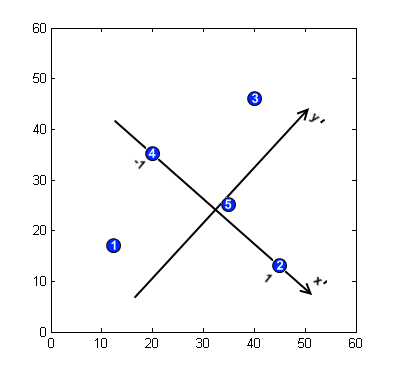
मॉडल के विशेष बिन्दुओ की जानकारी प्राप्त करते है। मान लें कि मॉडल छवि में निर्देशांक के साथ 5 विशेष बिंदु पाए जाते हैं , चित्र को देखें।
- सुविधा बिंदुओं के स्थानों का वर्णन करने के लिए आधार का परिचय देते है। 2डी स्थान एवं अफिन (Affine) परिवर्तन के लिए आधार को बिंदुओं की जोड़ी द्वारा परिभाषित किया गया है। उत्पत्ति के बिंदु को दो बिंदुओं (हमारे उदाहरण में P2, P4) को जोड़ने वाले खंड के मध्य में रखा गया है अक्ष उनमें से एक की ओर निर्देशित है, द ओर्थोगोनल है एवं मूल से होकर जाता है। स्तर का चयन इस प्रकार किया जाता है कि का निरपेक्ष मान दोनों आधार बिंदुओं के लिए 1 है।
- उस आधार के संबंध में विशेष स्थानों का वर्णन करें, अर्थात अनुमानों को नए समन्वय अक्षों पर गणना करें। हम आकार 0.25 लेते हैं। इस प्रकार हम निर्देशांकप्राप्त करते हैंI
- सुविधाओं द्वारा अनुक्रमित हैश सारणी में आधार को एकत्र करें (इस स्तिथि में केवल रूपांतरित निर्देशांक)। यदि युग्मित करने के लिए वस्तुओ को आधार जोड़ी के साथ संग्रहित करनी चाहिए।
- भिन्न आधार जोड़ी (चरण 2) के लिए प्रक्रिया को पुर्नरावृत्ति करे। व्यवधान को आरक्षित करने के लिए इसकी आवश्यकता होती है। आदर्श रूप से, सभी असंरेखता युग्मों की गणना की जानी चाहिए। हम दो पुनरावृत्तियों के पश्चात् हैश सारणी प्रदान करते हैं, जोड़ी (P1, P3) को दूसरे के लिए चयनित किया जाता है।
हैश सारणी:
| वेक्टर (, ) | आधार |
|---|---|
| (P2,P4) | |
| (P2,P4) | |
| (P2,P4) | |
| (P2,P4) | |
| (P2,P4) | |
| (P1,P3) | |
| (P1,P3) | |
| (P1,P3) | |
| (P1,P3) | |
| (P1,P3) |
अधिकांश हैश सारणीओं में भिन्न-भिन्न मानों के लिए मैप की गई समान कुंजियाँ नहीं हो सकती हैं। तो वास्तविक जीवन में हैश सारणी में आधार कुंजी (1.0, 0.0) एवं (-1.0, 0.0) को एन्कोड नहीं किया जाएगा।
मान्यता चरण
- इनपुट छवि में रुचिकर विशेषता बिंदु का शोध करे।
- इच्छानुसार आधार का चयन करे। यदि उपयुक्त इच्छानुसार आधार नहीं है, तो यह संभावना है कि इनपुट छवि में लक्षित वस्तु नहीं है।
- नए आधार में विशेषता बिंदुओं के निर्देशांक का वर्णन करें। प्राप्त निर्देशांक को परिमाणित करें जैसा कि पूर्व में किया गया था।
- हैश सारणी के साथ इनपुट छवि में सभी रूपांतरित बिंदु सुविधाओं की तुलना करें। यदि बिंदु विशेषताएं समान हैं, तो संबंधित आधार (एवं वस्तु का प्रकार, यदि कोई हो) के लिए गिनती बढ़ाएं।
- प्रत्येक आधार के लिए जैसे कि गिनती निश्चित सीमा से अधिक है, परिकल्पना को सत्यापित करें कि यह चरण 2 में चयन किये गए छवि आधार से युग्मित होती है। छवि समन्वय प्रणाली को मॉडल (माना वस्तु के लिए) में स्थानांतरित करें एवं उनका युग्मित करने का प्रयास करें। सफल होने पर वस्तु युग्मित जाती है। अन्यथा, चरण 2 पर वापस जाएँ।
प्रतिबिंबित पैटर्न शोध करना
ऐसा प्रतीत होता है कि यह विधि केवल स्केलिंग, अनुवाद एवं घुमाव को आरक्षित करने में सक्षम है। चूँकि, इनपुट छवि में दर्पण परिवर्तन में वस्तु हो सकती है। इसलिए, ज्यामितीय हैशिंग को भी वस्तु का शोध करने में सक्षम होना चाहिए। प्रतिबिंबित वस्तुओं की जानकारी प्राप्त करने के दो उपाए हैं।
- वेक्टर ग्राफ के लिए, बाईं ओर सकारात्मक एवं दाईं ओर नकारात्मक बनाएं। x स्थिति को -1 से गुणा करने पर वही परिणाम मिलेगा।
- आधार के लिए 3 बिंदुओं का प्रयोग करें। यह दर्पण छवियों (या वस्तुओं) की जानकारी प्राप्त करने की अनुमति देता है। वस्तुतः, आधार के लिए 3 बिंदुओं का उपयोग करना ज्यामितीय हैशिंग के लिए प्रक्रिया है।
उच्च-आयामों में ज्यामितीय हैशिंग
ऊपर दिए गए उदाहरण के समान, हैशिंग उच्च-आयामी डेटा में प्रारम्भ होती है। त्रि-आयामी डेटा बिंदुओं के लिए एवं आधार के लिए तीन बिंदुओं की भी आवश्यकता होती है। प्रथम के दो बिंदु x-अक्ष को परिभाषित करते हैं, एवं तीसरा बिंदु y-अक्ष (प्रथम बिंदु के साथ) को परिभाषित करता है। z-अक्ष दाएँ हाथ के नियम का उपयोग करके बनाए गए अक्ष के लंबवत है। ध्यान दें कि अंकों का क्रम परिणामी आधार को प्रभावित करता हैI
यह भी देखें
संदर्भ
- ↑ A.S. Mian, M. Bennamoun, and R. Owens, Three-dimensional model-based object recognition and segmentation in cluttered scenes., IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 28, Oct. 2006, pp. 1584-601.
- ↑ Moll, Mark; Bryant, Drew H.; Kavraki, Lydia E. (2010-11-11). "अधोसंरचना मिलान के लिए लेबलहैश एल्गोरिथम". BMC Bioinformatics. 11: 555. doi:10.1186/1471-2105-11-555. ISSN 1471-2105. PMC 2996407. PMID 21070651.
- ↑ Nussinov, R.; Wolfson, H. J. (1991-12-01). "कंप्यूटर दृष्टि तकनीकों द्वारा जैविक मैक्रोमोलेक्यूल्स में त्रि-आयामी संरचनात्मक रूपांकनों का कुशल पता लगाना". Proceedings of the National Academy of Sciences of the United States of America. 88 (23): 10495–10499. doi:10.1073/pnas.88.23.10495. ISSN 0027-8424. PMC 52955. PMID 1961713.
- Wolfson, H.J. & Rigoutsos, I (1997). Geometric Hashing: An Overview. IEEE Computational Science and Engineering, 4(4), 10-21.