दो-वस्तु समस्या

This article is about मौलिक यांत्रिकी में दो-वस्तु की समस्या. For सापेक्षतावादी संस्करण, see सामान्य सापेक्षता में दो-वस्तु की समस्या. For कामकाजी जोड़ों की कैरियर प्रबंधन समस्या, see दो वस्तु की समस्या (करियर).

Left: Two bodies with similar mass orbiting a common barycenter external to both bodies, with elliptic orbits—typical of binary stars . Right: Two bodies with a "slight" difference in mass orbiting a common barycenter. The sizes, and this type of orbit are similar to the Pluto–Charon system (in which the barycenter is external to both bodies), and to the Earth–Moon system—where the barycenter is internal to the larger body.

मौलिक यांत्रिकी में, दो-वस्तु की समस्या दो वस्तुओं के गति की भविष्यवाणी करना होता है जिसमे बिंदु कणों को अमूर्त रूप में देखा जा सकता है। समस्या यह मानती है कि दो वस्तुएं केवल एक दूसरे के साथ ही प्रभावित होती है, प्रत्येक वस्तु को प्रभावित करने वाला एकमात्र बल दूसरी वस्तु से उत्पन्न होता है, और अन्य सभी वस्तुओं को अनदेखा कर दिया जाता है।

मौलिक दो-वस्तु समस्या का सबसे प्रमुख स्थिति गुरुत्वाकर्षण की स्थिति होती है (केपलर समस्या भी देखे), उपग्रहों, ग्रहों और सितारों जैसे वस्तुओं की कक्षाओं की भविष्यवाणी करने के लिए खगोल विज्ञान में उत्पन्न होता है। ऐसी प्रणाली का एक दो-बिंदु-कण मॉडल लगभग हमेशा उपयोगी अंतर्दृष्टि और भविष्यवाणियां प्रदान करने के लिए पर्याप्त रूप से अपने व्यवहार का वर्णन करता है।

एक सरल निकाय मॉडल, केंद्रीय-बल समस्या, एक वस्तु को दूसरे पर कार्य करने वाले बल के स्थिर स्रोत के रूप मे मानता है। इसके बाद एक शेष वस्तु की गति की भविष्यवाणी करना चाहता है। इस तरह का सन्निकटन तब उपयोगी परिणाम दे सकता है जब एक वस्तु दूसरे की तुलना में बहुत अधिक विशाल होती है (जैसा कि एक प्रकाश ग्रह एक भारी तारे की परिक्रमा करता है, जहाँ तारे को अनिवार्य रूप से स्थिर माना जाता है)।

चूंकि, एक-निकाय सन्निकटन सामान्यतः अनावश्यक होता है। गुरुत्वाकर्षण सहित कई बलो के लिए, दो-वस्तु की समस्या के सामान्य संस्करण को एक-वस्तु की समस्याओं की एक जोड़ी में कम किया जा सकता है, जिससे इसे पूरी तरह हल किया जा सकता है, और प्रभावी ढंग से उपयोग करने के लिए पर्याप्त सरल समाधान प्रदान किया जा सकता है।

इसके विपरीत, विशेष स्थितियों को छोड़कर, तीन-निकाय समस्या (और, अधिक सामान्यतः, n ≥ 3 के लिए n-निकाय समस्या) को पहले अभिन्न के संदर्भ में हल नही किया जा सकता है।

प्रमुख स्थितियों के लिए परिणाम

गुरुत्वाकर्षण और अन्य व्युत्क्रम-वर्ग उदाहरण

दो वस्तुों की समस्या खगोल विज्ञान में रोचक है क्योंकि खगोलीय वस्तुओं के जोड़े अधिकांशतः मनमानी दिशाओं में तेजी से आगे बढ़ती है (इसलिए उनकी गति रोचक हो जाती है), व्यापक रूप से एक दूसरे से अलग हो जाती है (इसलिए वे टकराती नही है) और अन्य वस्तुओं से भी अधिक व्यापक रूप से अलग हो जाती है ( इसलिए बाहरी प्रभाव इतने छोटे होते है कि उन्हें सुरक्षित रूप से अनदेखा किया जा सकता है)।

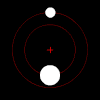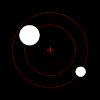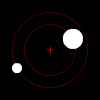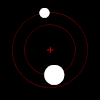
गुरुत्वाकर्षण बल के अनुसार, ऐसी वस्तुओं की एक जोड़ी के प्रत्येक सदस्य एक अण्डाकार नमूने में द्रव्यमान के अपने पारस्परिक केंद्र की परिक्रमा करता है, जब तक कि वे एक दूसरे से पूरी तरह से बचने के लिए पर्याप्त तेजी से आगे नही बढ़ते है, जिस स्थिति में उनके पथ अन्य योजना शंकु वर्गों के साथ अलग हो जाते है। यदि एक वस्तु दूसरे की तुलना में बहुत अधिक भारी होता है, तो वह द्रव्यमान के साझा केंद्र के संदर्भ में दूसरे की तुलना में बहुत उसकी गति कम होती है। द्रव्यमान का आपसी केंद्र बड़ी वस्तु के अंदर भी हो सकता है।

समस्या के समाधान की व्युत्पत्ति के लिए, मौलिक केंद्रीय-बल समस्या या केप्लर समस्या देखे।

सिद्धांत रूप में, एक ही समाधान मैक्रोस्कोपिक समस्याओं पर लागू होता है जिसमें वस्तु न केवल गुरुत्वाकर्षण के माध्यम से प्रभावित होते है, जबकि किसी भी अन्य आकर्षक बल क्षेत्र के माध्यम से व्युत्क्रम-वर्ग नियम का पालन करते है, जिसमें इलेक्ट्रोस्टैटिक आकर्षण स्पष्ट भौतिक उदाहरण है। व्यवहार में, ऐसी समस्याएं संभवतः ही कभी उत्पन्न होती है। संभवतः प्रायोगिक उपकरण या अन्य विशेष उपकरणों को छोड़कर, हम संभवतः ही कभी इलेक्ट्रोस्टैटिक रूप से परस्पर क्रिया करने वाली वस्तुओं का सामना करते है जो अधिक तेजी से आगे बढ़ती है, और इस तरह की दिशा में टकराने से बचने के लिए, अपने परिवेश से पर्याप्त रूप से अलग होते है।

बलाघूर्ण के प्रभाव में दो-निकाय प्रणाली की गतिकीय प्रणाली एक स्टर्म-लिउविल समीकरण बन जाती है।

परमाणुओं और उप-परमाणु कणों के लिए अनुपयुक्तता

यद्यपि दो-वस्तु मॉडल वस्तुओं को बिंदु कणों के रूप में मानता है, मौलिक यांत्रिकी केवल मैक्रोस्कोपिक स्केल की प्रणालियों पर लागू होता है। उप-परमाणु कणों के अधिकांश व्यवहार की भविष्यवाणी इस लेख में निहित मौलिक मान्यताओं के अनुसार या यहाँ गणित का उपयोग करके नही किया सकता है।

नील्स बोह्र (यह शब्द "ऑर्बिटल" का स्रोत है) के प्रारंभिक अनुमान के बाद, एक परमाणु में इलेक्ट्रॉनों को कभी-कभी इसके नाभिक की "कक्षा" के रूप में वर्णित किया जाता है। चूंकि, इलेक्ट्रॉन वास्तव में किसी भी सार्थक अर्थ में नाभिक की परिक्रमा नही करता है, और इलेक्ट्रॉन के वास्तविक व्यवहार की किसी भी उपयोगी समझ के लिए क्वांटम यांत्रिकी आवश्यक है। एक परमाणु नाभिक की परिक्रमा करने वाले एक इलेक्ट्रॉन के लिए मौलिक दो वस्तु समस्या को हल करना कठिन होता है और कई उपयोगी अंतर्दृष्टि उत्पन्न नही होते है।

दो स्वतंत्र, एक-निकाय समस्याओं में कमी

पूर्ण दो-निकाय समस्या को दो एक-निकाय समस्याओं के रूप में पुन: सूत्रित करके हल किया जा सकता है। चूंकि एक-वस्तु की समस्याओं को त्रुटिहीन रूप से हल किया जा सकता है, इसलिए संबंधित दो-वस्तु की समस्या को भी हल किया जा सकता है।

दो-वस्तु की समस्या के लिए जैकोबी समन्वय करता है; जैकोबी निर्देशांक है ${\boldsymbol {R}}={\frac {m_{1}}{M}}{\boldsymbol {x}}_{1}+{\frac {m_{2}}{M}}{\boldsymbol {x}}_{2}$ और ${\boldsymbol {r}}={\boldsymbol {x}}_{1}-{\boldsymbol {x}}_{2}$ साथ $M=m_{1}+m_{2}\$.

x₁ और x₂ को दो वस्तुओं की सदिश स्थिति होने दें, और m₁ और m₂ उनके द्रव्यमान हों। लक्ष्य सभी समय टी के लिए प्रक्षेपवक्र x₁(t) और x₂(t) निर्धारित करना है, प्रारंभिक स्थिति x₁(t = 0) और x₂(t = 0) और प्रारंभिक वेग v₁(t = 0) और v₂(t = 0) दिए गए है।

जब दो द्रव्यमानों पर लागू किया जाता है, तो न्यूटन का दूसरा नियम कहता है कि

$$\mathbf {F} _{12}(\mathbf {x} _{1},\mathbf {x} _{2})=m_{1}{\ddot {\mathbf {x} }}_{1}$$

(Equation 1)

$$\mathbf {F} _{21}(\mathbf {x} _{1},\mathbf {x} _{2})=m_{2}{\ddot {\mathbf {x} }}_{2}$$

(Equation 2)

जहां F₁₂ द्रव्यमान 1 पर द्रव्यमान 2 के साथ इसकी अन्योन्य क्रिया के कारण बल है, और F₂₁ द्रव्यमान 2 पर द्रव्यमान 1 के साथ इसको प्रभावित करने का बल है। x स्थिति वैक्टर के शीर्ष पर स्थित दो बिंदु समय के संबंध में उनके दूसरे व्युत्पन्न या उनके त्वरण वैक्टर को दर्शाता है।

इन दो समीकरणों को जोड़ना और घटाना उन्हें दो एक-निकाय समस्याओं में अलग करता है, जिन्हें स्वतंत्र रूप से हल किया जा सकता है। समीकरणों (1) और (2) को जोड़ने से द्रव्यमान केंद्र गति का वर्णन करने वाला समीकरण प्राप्त होता है। इसके विपरीत, समीकरण (2) को समीकरण (1) से घटाने पर एक ऐसा समीकरण बनता है जो बताता है कि द्रव्यमान के बीच सदिश r = x₁ − x₂ समय के साथ कैसे बदलता है। इन स्वतंत्र एक-निकाय समस्याओं के समाधान को प्रक्षेपवक्र x₁(t) और x₂(t) के समाधान प्राप्त करने के लिए जोड़ा जा सकता है।

द्रव्यमान गति का केंद्र (पहली एक-वस्तु समस्या)

मान लेते है $\mathbf {R}$ निकाय के द्रव्यमान केंद्र की स्थिति है। बल समीकरणों (1) और (2) को जोड़ने पर प्राप्त होता है

$$m_{1}{\ddot {\mathbf {x} }}_{1}+m_{2}{\ddot {\mathbf {x} }}_{2}=(m_{1}+m_{2}){\ddot {\mathbf {R} }}=\mathbf {F} _{12}+\mathbf {F} _{21}=0$$

जहाँ हमने न्यूटन के तीसरे नियम F₁₂ = −F₂₁ का प्रयोग किया है और जहाँ

$${\ddot {\mathbf {R} }}\equiv {\frac {m_{1}{\ddot {\mathbf {x} }}_{1}+m_{2}{\ddot {\mathbf {x} }}_{2}}{m_{1}+m_{2}}}.$$

परिणामी समीकरण:

$${\ddot {\mathbf {R} }}=0$$

वेग दर्शाता है $\mathbf {v} ={\frac {dR}{dt}}$ द्रव्यमान का केंद्र स्थिर है, जिससे कुल संवेग m₁ v₁ + m₂ v₂ भी स्थिर है। इसलिए, प्रारंभिक स्थितियों और वेगों से हर समय द्रव्यमान के केंद्र की स्थिति R(t) निर्धारित की जा सकती है।

विस्थापन वेक्टर गति (द्वितीय एक-निकाय समस्या)

दोनों बल समीकरणों को संबंधित द्रव्यमानों से विभाजित करने पर, पहले से दूसरे समीकरण को घटाने पर, और पुनर्व्यवस्थित करने पर समीकरण प्राप्त होता है

$${\ddot {\mathbf {r} }}={\ddot {\mathbf {x} }}_{1}-{\ddot {\mathbf {x} }}_{2}=\left({\frac {\mathbf {F} _{12}}{m_{1}}}-{\frac {\mathbf {F} _{21}}{m_{2}}}\right)=\left({\frac {1}{m_{1}}}+{\frac {1}{m_{2}}}\right)\mathbf {F} _{12}$$

जहाँ हमने फिर से न्यूटन के तीसरे नियम का प्रयोग किया है F₁₂ = −F₂₁ और जहाँ r द्रव्यमान 2 से द्रव्यमान 1 तक विस्थापन (वेक्टर) है, जैसा कि ऊपर परिभाषित किया गया है।

दो वस्तुओं के बीच बल, जो दो वस्तुओं में उत्पन्न होता है, केवल उनके अलगाव का एक कार्य होता है r और उनके पूर्ण पदों की नही है x₁ और x₂, अन्यथा, अनुवाद संबंधी समरूपता नही होती है, और भौतिकी के नियमों को एक स्थान से दूसरे स्थान पर बदलना होता है। घटाया गया समीकरण इसलिए लिखा जा सकता है:

$$\mu {\ddot {\mathbf {r} }}=\mathbf {F} _{12}(\mathbf {x} _{1},\mathbf {x} _{2})=\mathbf {F} (\mathbf {r} )$$

जहाँ $\mu$ घटा हुआ द्रव्यमान है

$$\mu ={\frac {1}{{\frac {1}{m_{1}}}+{\frac {1}{m_{2}}}}}={\frac {m_{1}m_{2}}{m_{1}+m_{2}}}.$$

इसके लिए समीकरण को हल करता है r(t) दो-वस्तु की समस्या की कुंजी होती है। समाधान निकायों के बीच विशिष्ट बल पर निर्भर करता है, जिसे परिभाषित किया गया है $\mathbf {F} (\mathbf {r} )$ स्थितियों के लिए जहां $\mathbf {F} (\mathbf {r} )$ व्युत्क्रम-वर्ग नियम का पालन करता है, केप्लर समस्या देखे।

एक बार R(t) और r(t) निर्धारित किया जाता है, मूल प्रक्षेपवक्र प्राप्त किया जा सकता है

$$\mathbf {x} _{1}(t)=\mathbf {R} (t)+{\frac {m_{2}}{m_{1}+m_{2}}}\mathbf {r} (t)$$

$$\mathbf {x} _{2}(t)=\mathbf {R} (t)-{\frac {m_{1}}{m_{1}+m_{2}}}\mathbf {r} (t)$$

जैसा कि इन दो समीकरणों के दाहिने हाथ की ओर R और r की परिभाषाओं को प्रतिस्थापित करके सत्यापित किया जा सकता है।

दो वस्तु गति तलीय है

एक दूसरे के संबंध में दो वस्तुों की गति हमेशा समतल होती है।

प्रमाण: रैखिक गति को परिभाषित करता है p और कोणीय गति है L प्रणाली के, द्रव्यमान के केंद्र के संबंध में, समीकरणों है

$$\mathbf {L} =\mathbf {r} \times \mathbf {p} =\mathbf {r} \times \mu {\frac {d\mathbf {r} }{dt}},$$

जहाँ μ घटा हुआ द्रव्यमान है और r सापेक्ष स्थिति है r₂ − r₁ (इनके साथ द्रव्यमान के केंद्र को उत्पत्ति के रूप में लिखा गया है, और इस प्रकार दोनों समानांतर है r) कोणीय गति के परिवर्तन की दर L के बराबर है N

$$\mathbf {N} ={\frac {d\mathbf {L} }{dt}}={\dot {\mathbf {r} }}\times \mu {\dot {\mathbf {r} }}+\mathbf {r} \times \mu {\ddot {\mathbf {r} }}\ ,$$

और वेक्टर उत्पाद का उपयोग करता है v × w = 0 किसी भी वैक्टर के लिए v और w उसी दिशा में संकेत करता है

$$\mathbf {N} \ =\ {\frac {d\mathbf {L} }{dt}}=\mathbf {r} \times \mathbf {F} \ ,$$

साथ F = μ d²r/dt².

धारणा का परिचय देते हुए (अधिकांश भौतिक बलों के लिए सच है, क्योंकि वे न्यूटन के गति के नियमों का पालन करते है | न्यूटन की गति का तीसरा नियम) कि दो कणों के बीच का बल उनकी स्थिति के बीच की रेखा के साथ कार्य करता है, यह इस प्रकार है r × F = 0 और कोणीय गति का संरक्षण | कोणीय गति वेक्टर L स्थिर (संरक्षित) है। इसलिए, विस्थापन वेक्टर r और इसका वेग v हमेशा स्थिर सदिश के लंबवत तल में होते है L.

दो-वस्तु प्रणाली की ऊर्जा

यदि बल F(r) संरक्षी बल है तो तंत्र में स्थिति ऊर्जा होती है U(r), इसलिए कुल यांत्रिक ऊर्जा को इस रूप में लिखा जा सकता है

$$E_{\text{tot}}={\frac {1}{2}}m_{1}{\dot {\mathbf {x} }}_{1}^{2}+{\frac {1}{2}}m_{2}{\dot {\mathbf {x} }}_{2}^{2}+U(\mathbf {r} )={\frac {1}{2}}(m_{1}+m_{2}){\dot {\mathbf {R} }}^{2}+{1 \over 2}\mu {\dot {\mathbf {r} }}^{2}+U(\mathbf {r} )$$

द्रव्यमान के केंद्र में गतिज ऊर्जा संदर्भ सबसे कम होता है और कुल ऊर्जा बन जाती है

$$E={\frac {1}{2}}\mu {\dot {\mathbf {r} }}^{2}+U(\mathbf {r} )$$

निर्देशांक x₁ और x₂ के रूप में व्यक्त किया जा सकता है

$$\mathbf {x} _{1}={\frac {\mu }{m_{1}}}\mathbf {r}$$

$$\mathbf {x} _{2}=-{\frac {\mu }{m_{2}}}\mathbf {r}$$

और इसी प्रकार ऊर्जा E से संबंधित है E₁ और E₂ जिसमें अलग-अलग प्रत्येक वस्तु की गतिज ऊर्जा होती है:

$${\begin{aligned}E_{1}&={\frac {\mu }{m_{1}}}E={\frac {1}{2}}m_{1}{\dot {\mathbf {x} }}_{1}^{2}+{\frac {\mu }{m_{1}}}U(\mathbf {r} )\\[4pt]E_{2}&={\frac {\mu }{m_{2}}}E={\frac {1}{2}}m_{2}{\dot {\mathbf {x} }}_{2}^{2}+{\frac {\mu }{m_{2}}}U(\mathbf {r} )\\[4pt]E_{\text{tot}}&=E_{1}+E_{2}\end{aligned}}$$

केंद्रीय बल

Main article: मौलिक केंद्रीय बल समस्या

कई भौतिक समस्याओं के लिए, बल F(r) एक केंद्रीय बल है, अर्थात यह है

$$\mathbf {F} (\mathbf {r} )=F(r){\hat {\mathbf {r} }}$$

जहाँ r = |r| और r̂ = r/r संगत इकाई सदिश है। अब हमारे पास है:

$$\mu {\ddot {\mathbf {r} }}={F}(r){\hat {\mathbf {r} }}\ ,$$

जहां आकर्षक बल के स्थितियों में F(r) नकारात्मक है।

यह भी देखे

• ऊर्जा बहाव
• केंद्र का समीकरण
• यूलर की तीन-वस्तु की समस्या
• केप्लर कक्षा
• केप्लर प्रॉब्लम
• एन-वस्तु प्रॉब्लम|एन-वस्तु प्रॉब्लम
• वायरल प्रमेय

ग्रन्थसूची

• Landau LD; Lifshitz EM (1976). Mechanics (3rd. ed.). New York: Pergamon Press. ISBN 0-08-029141-4.
• Goldstein H (1980). Classical Mechanics (2nd. ed.). New York: Addison-Wesley. ISBN 0-201-02918-9.

बाहरी संबंध

• Two-body problem at Eric Weisstein's World of Physics