पार्से ट्री
एक पदनिरूपक रेखा चिट्र या पदनिरूपक रेखा चिट्र [1] या वाक्यविग्रह रेखा चिट्र या साकार वाक्य - विन्यास रेखा चिट्र एक आदेशित, सुदृढ़ रेखा चिट्र (डेटा संरचना) है जो कुछ संदर्भ-मुक्त व्याकरण के अनुसार एक स्ट्रिंग(कंप्यूटर विज्ञान) की वाक्य संरचना का प्रतिनिधित्व करता है। पदनिरूपक रेखा चिट्र ' शब्द का प्रयोग मुख्य रूप से संगणनात्मक भाषाविज्ञान में किया जाता है; सैद्धांतिक वाक्य-विन्यास में, वाक्यविन्यास रेखा चिट्र शब्द अधिक सामान्य है।
साकार वाक्य रचना रेखा चिट्र इनपुट भाषा के वाक्य रचना को दर्शाते हैं, जिससे वे कंप्यूटर प्रोग्रामिंग में उपयोग किए जाने वाले संक्षेप वाक्य रचना रेखा चिट्र से अलग हो जाते हैं। व्याकरण पढ़ाने के लिए उपयोग किए जाने वाले रीड-केलॉग वाक्य आरेखों के विपरीत, पदनिरूपक रेखा चिट्र विभिन्न प्रकार के संविधान(भाषाविज्ञान) के लिए अलग-अलग प्रतीक आकार का उपयोग नहीं करते हैं।
पदनिरूपक रेखा चिट्र सामान्यतः पुनर्रचित क्षेत्र व्याकरण (वाक्यांश संरचना व्याकरण) या निर्भरता व्याकरण के निर्भरता संबंध के पुनर्रचित क्षेत्र संबंध के आधार पर बनाए जाते हैं। प्राकृतिक भाषाओं में वाक्य (भाषाविज्ञान) के लिए पदनिरूपक रेखा चिट्र उत्पन्न हो सकते हैं (प्राकृतिक भाषा प्रसंस्करण देखें), साथ ही कंप्यूटर भाषाओं के प्रक्रिया के दौरान, जैसे प्रोग्रामिंग भाषाएं।
एक संबंधित अवधारणा वाक्यांश मार्कर या पी-मार्कर की है, जैसा कि परिवर्तनकारी जनरेटिव व्याकरण में प्रयोग किया जाता है। एक वाक्यांश मार्कर एक भाषाई अभिव्यक्ति है जो इसकी वाक्यांश संरचना के रूप में चिह्नित है। यह एक रेखा चिट्र के रूप में, या एक कोष्ठक अभिव्यक्ति के रूप में प्रस्तुत किया जा सकता है। वाक्यांश मार्कर वाक्यांश संरचना नियमों को लागू करके उत्पन्न होते हैं, और स्वयं आगे परिवर्तनकारी नियमों के अधीन होते हैं।[2] वाक्य-विन्यास की दृष्टि से अस्पष्ट वाक्य के लिए संभावित पदनिरूपक रेखा चिट्र के सम्मुच्चय को पदनिरूपक फ़ॉरेस्ट कहा जाता है।[3]
नामपद्धति
एक पदनिरूपक रेखा चिट्र नोड्स और शाखाओं से बना होता है।[4] तस्वीर में पदनिरूपक रेखा चिट्र पूरी संरचना है, जो S से शुरू होकर प्रत्येक पर्ण आसंधि (जॉन, बॉल, द, हिट) में समाप्त होती है। एक पदनिरूपक रेखा चिट्र में, प्रत्येक आसंधि या तो एक रूट आसंधि, एक शाखा आसंधि या एक लीफ आसंधि होता है। उपरोक्त उदाहरण में, S रूट आसंधि है, NP और VP ब्रांच आसंधि हैं, जबकि जॉन, बॉल, द और हिट सभी लीफ आसंधि हैं।
नोड्स को जनक आसंधि और वंश आसंधि के रूप में भी संदर्भित किया जा सकता है। एक जनक आसंधि वह होता है जिसके अंतर्गत एक शाखा द्वारा कम से कम एक अन्य आसंधि जुड़ा होता है। उदाहरण में, S, NP और VP दोनों का जनक है। वंश आसंधि वह होता है जिसके ठीक ऊपर कम से कम एक आसंधि होता है जिससे वह रेखा चिट्र की एक शाखा से जुड़ा होता है। फिर से हमारे उदाहरण से, हिट V का वंश आसंधि है।
एक 'अंतकेतर फलन एक फलन (आसंधि ) है जो या तो उस रेखा चिट्र में जड़ या शाखा है जबकि एक 'टर्मिनल फलन ' एक पदनिरूपक रेखा चिट्र में एक फलन (आसंधि ) है जो एक पत्ता है।
पुनर्रचित क्षेत्र आधारित पदनिरूपक रेखा चिट्र
पुनर्रचित क्षेत्र आधारित व्याकरण के पदनिरूपक रेखा चिट्र(वाक्यांश संरचना व्याकरण) टर्मिनल और गैर-टर्मिनल नोड्स के बीच अंतर करते हैं। आंतरिक नोड्स को व्याकरण की गैर-टर्मिनल श्रेणियों द्वारा लेबल किया जाता है, जबकि लसीका नोड्स को टर्मिनल प्रतीक श्रेणियों द्वारा लेबल किया जाता है। नीचे दी गई छवि एक पुनर्रचित क्षेत्र-आधारित पदनिरूपक रेखा चिट्र का प्रतिनिधित्व करती है; यह अंग्रेजी भाषा के वाक्य जॉन हिट द बॉल की वाक्य रचना को दर्शाता है:
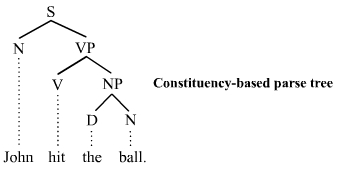 पदनिरूपक रेखा चिट्र संपूर्ण संरचना है, जो S से शुरू होती है और प्रत्येक लीफ आसंधि (जॉन, हिट, द, बॉल) में समाप्त होती है। रेखा चिट्र में निम्नलिखित संक्षेपों का उपयोग किया जाता है:
पदनिरूपक रेखा चिट्र संपूर्ण संरचना है, जो S से शुरू होती है और प्रत्येक लीफ आसंधि (जॉन, हिट, द, बॉल) में समाप्त होती है। रेखा चिट्र में निम्नलिखित संक्षेपों का उपयोग किया जाता है:
- S वाक्य (भाषाविज्ञान) के लिए, इस उदाहरण में शीर्ष-स्तरीय संरचना
- संज्ञा वाक्यांश के लिए एनपी। पहला (सबसे बायां) एनपी, एक संज्ञा जॉन, वाक्य के विषय (व्याकरण) के रूप में कार्य करता है। दूसरा वाक्य का उद्देश्य (व्याकरण) है।
- वीपी [[क्रिया वाक्यांश]] के लिए, जो विधेय (व्याकरण) के रूप में कार्य करता है
- V क्रिया के लिए। इस मामले में, यह एक सकर्मक क्रिया हिट है।
- निर्धारक (वर्ग) के लिए डी, इस उदाहरण में लेख (व्याकरण) है
- एन संज्ञा के लिए
रेखा चिट्र में प्रत्येक आसंधि या तो एक रूट आसंधि, एक शाखा आसंधि या एक पत्ती आसंधि है।[5] रूट आसंधि एक ऐसा आसंधि होता है जिसके शीर्ष पर कोई शाखा नहीं होती है। एक वाक्य के भीतर, केवल एक रूट आसंधि होता है। एक शाखा आसंधि एक जनक आसंधि है जो दो या दो से अधिक वंश आसंधि से जुड़ता है। एक पत्ता आसंधि, हालांकि, एक टर्मिनल आसंधि है जो रेखा चिट्र में अन्य नोड्स पर हावी नहीं होता है। S रूट आसंधि है, NP और VP ब्रांच आसंधि हैं, और जॉन (N), हिट (V), (D), और बॉल (N) सभी लीफ आसंधि हैं। पत्तियाँ वाक्य का शाब्दिक विश्लेषण हैं। एकजनक आसंधि वह होता है जिसके अंतर्गत एक शाखा द्वारा कम से कम एक अन्य आसंधि जुड़ा होता है। उदाहरण में, S, N और VP दोनों का जनक है। एक वंश आसंधि वह होता है जिसके ठीक ऊपर कम से कम एक आसंधि होता है जिससे वह एक रेखा चिट्र की शाखा से जुड़ा होता है। उदाहरण से, हिट V का वंश आसंधि है। कभी-कभी इस रिश्ते के लिए मां और बेटी शब्द का भी उपयोग किया जाता है।
निर्भरता-आधारित पदनिरूपक रेखा चिट्र
निर्भरता आधारित ग्रामर के डिपेंडेंसी-आधारित पदनिरूपक फलन रेखा चिट्र [6] सभी नोड्स को टर्मिनल के रूप में देखें, जिसका अर्थ है कि वे टर्मिनल और गैर-टर्मिनल श्रेणियों के बीच अंतर को स्वीकार नहीं करते हैं। वे पुनर्रचित क्षेत्र-आधारित पदनिरूपक रेखा चिट्र की तुलना में औसतन सरल होते हैं क्योंकि उनमें कम आसंधि होते हैं। उपरोक्त उदाहरण वाक्य के लिए निर्भरता-आधारित पदनिरूपक रेखा चिट्र इस प्रकार है:
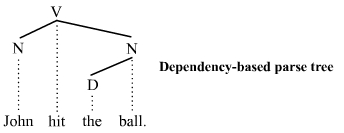 इस पदनिरूपक रेखा चिट्र में उपरोक्त पुनर्रचित क्षेत्र-आधारित प्रतिरूप में दिखाई देने वाली वाक्यांश श्रेणियों (एस, वीपी, और एनपी) का अभाव है। पुनर्रचित क्षेत्र आधारित रेखा चिट्र की तरह, घटक (भाषाविज्ञान) संरचना को स्वीकार किया जाता है। रेखा चिट्र का कोई भी पूर्ण उप-रेखा चिट्र एक घटक है। इस प्रकार यह निर्भरता-आधारित पदनिरूपक रेखा चिट्र सब्जेक्ट संज्ञा जॉन और ऑब्जेक्ट संज्ञा वाक्यांश बॉल को घटक के रूप में स्वीकार करता है, जैसे कि पुनर्रचित क्षेत्र-आधारित पदनिरूपक रेखा चिट्र करता है।
इस पदनिरूपक रेखा चिट्र में उपरोक्त पुनर्रचित क्षेत्र-आधारित प्रतिरूप में दिखाई देने वाली वाक्यांश श्रेणियों (एस, वीपी, और एनपी) का अभाव है। पुनर्रचित क्षेत्र आधारित रेखा चिट्र की तरह, घटक (भाषाविज्ञान) संरचना को स्वीकार किया जाता है। रेखा चिट्र का कोई भी पूर्ण उप-रेखा चिट्र एक घटक है। इस प्रकार यह निर्भरता-आधारित पदनिरूपक रेखा चिट्र सब्जेक्ट संज्ञा जॉन और ऑब्जेक्ट संज्ञा वाक्यांश बॉल को घटक के रूप में स्वीकार करता है, जैसे कि पुनर्रचित क्षेत्र-आधारित पदनिरूपक रेखा चिट्र करता है।
पुनर्रचित क्षेत्र बनाम निर्भरता का अंतर दूरगामी है। क्या पुनर्रचित क्षेत्र-आधारित पदनिरूपक रेखा चिट्र से जुड़ी अतिरिक्त वाक्य रचना संरचना आवश्यक है या लाभकारी है, यह वाद विवाद का विषय है।
वाक्यांश मार्कर
वाक्यांश मार्कर, या पी-मार्कर, प्रारंभिक परिवर्तनकारी जनरेटिव व्याकरण में प्रस्तुत किए गए थे, जैसा कि नोम चौमस्की और अन्य द्वारा विकसित किया गया था। एक वाक्य की गहरी संरचना का प्रतिनिधित्व करने वाला एक वाक्यांश मार्कर वाक्यांश संरचना नियमों को लागू करके उत्पन्न होता है। फिर, यह अनुप्रयोग आगे के परिवर्तनों से गुजर सकता है।
वाक्यांश चिह्नकों को रेखा चिट्र (डेटा संरचना) के रूप में प्रस्तुत किया जा सकता है (जैसा कि निर्वाचन क्षेत्र- आधारित पदनिरूपक रेखा चिट्र | पुनर्रचित क्षेत्र-आधारित पदनिरूपक रेखा चिट्र पर उपरोक्त अनुभाग में है), लेकिन प्रायः इसके अतिरिक्त ब्रैकेटेड एक्सप्रेशन के रूप में दिए जाते हैं, जो कम जगह लेते हैं स्मृति में स्थान। उदाहरण के लिए, ऊपर दिए गए पुनर्रचित क्षेत्र-आधारित रेखा चिट्र से संबंधित एक कोष्ठक अभिव्यक्ति कुछ इस तरह हो सकती है:
रेखा चिट्र की तरह, इस तरह के भावों का सटीक निर्माण और दिखाए गए विवरण की मात्रा लागू किए जा रहे सिद्धांत और उन बिंदुओं पर निर्भर कर सकती है जिन्हें क्वेरी लेखक स्पष्ट करना चाहता है।
यह भी देखें
- सार सिंटैक्स ट्री
- संघटक (भाषाविज्ञान)
- निर्भरता व्याकरण
- अभिकलनात्मक भाषाविज्ञान
- पदच्छेद (वाक्यविन्यास विश्लेषण)
- वाक्यांश संरचना व्याकरण
- वाक्य आरेख
- टर्मिनल और गैर-टर्मिनल प्रतीक
टिप्पणियाँ
- ↑ See Chiswell and Hodges 2007: 34.
- ↑ Noam Chomsky (26 December 2014). Aspects of the Theory of Syntax. MIT Press. ISBN 978-0-262-52740-8.
- ↑ Billot, Sylvie, and Bernard Lang. "The structure of shared forests in ambiguous parsing."
- ↑ "The parsetree Package for Drawing Trees in LaTeX". www1.essex.ac.uk.
- ↑ See Carnie (2013:118ff.) for an introduction to the basic concepts of syntax trees (e.g. root node, terminal node, non-terminal node, etc.).
- ↑ See for example Ágel et al. 2003/2006.
संदर्भ
- Ágel, V., Ludwig Eichinger, Hans-Werner Eroms, Peter Hellwig, Hans Heringer, and Hennig Lobin (eds.) 2003/6. Dependency and valency: An international handbook of contemporary research. Berlin: Walter de Gruyter.
- Carnie, A. 2013. Syntax: A generative introduction, 3rd edition. Malden, MA: Wiley-Blackwell.
- Chiswell, Ian and Wilfrid Hodges 2007. Mathematical logic. Oxford: Oxford University Press.
- Aho, A. V., Sethi, R., and Ullman, J. D. 1986. Compilers: Principles, techniques, & tools. Reading, MA: Addison-Wesley.
बाहरी संबंध
- Syntax Tree Editor
- Linguistic Tree Constructor
- phpSyntaxTree – Online parse tree drawing site
- phpSyntaxTree (Unicode) – Online parse tree drawing site (improved version that supports Unicode)
- rSyntaxTree Enhanced version of phpSyntaxTree in Ruby with Unicode and Vectorized graphics
- Qtree – LaTeX package for drawing parse trees
- TreeForm Syntax Tree Drawing Software
- Visual Introduction to Parse Trees Introduction and Transformation
- OpenCourseOnline Dependency Parse Introduction (Christopher Manning)
- Penn Treebank II Constituent Tags

