बाह्य बिलियर्ड्स
बाह्य बिलियर्ड्स एक गतिशील प्रणाली है जो की समतल में उत्तल समुच्चय आकार पर आधारित है। और मौलिक रूप से, इस प्रणाली को यूक्लिडियन समतल के लिए परिभाषित किया गया है[1] किन्तु कोई प्रणाली को अतिशयोक्तिपूर्ण ज्यामिति में भी मान सकता है[2] या अन्य समष्टिों पर जो समतल को उपयुक्त रूप से सामान्यीकृत करते हैं। इस प्रकार से बाह्य बिलियर्ड्स सामान्य गतिशील बिलियर्ड्स से इस अर्थ में भिन्न होता है कि यह आकार के अंदर के अतिरिक्त बाहर की ओर गति करता है।
परिभाषाएँ
बाह्य बिलियर्ड्स मानचित्र
इस प्रकार से मान लीजिए कि P समतल में एक उत्तल समुच्चय आकृति है।
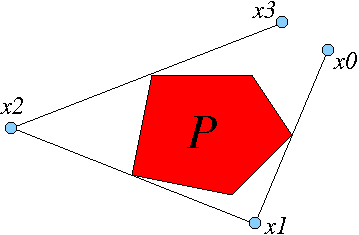
P के बाहर एक बिंदु x0 दिया गया है, सामान्यतः एक अद्वितीय है बिंदु x1 (P के बाहर भी) जिससे x0 को x1 से जोड़ने वाला रेखाखंड इसके मध्य बिंदु पर P की स्पर्शरेखा हो और
x0 से x1 तक चलने वाले व्यक्ति को दाईं ओर P दिखाई देगा। (चित्र देखें।) मानचित्र F: x0 -> X1 को बाह्य बिलियर्ड्स मानचित्र कहा जाता है।
व्युत्क्रम फलन (या पीछे की ओर) बाह्य बिलियर्ड्स मानचित्र को मानचित्र x1 -> x0 के रूप में भी परिभाषित किया गया है।
ऊपर दी गई परिभाषा में दाएँ शब्द को बाएँ शब्द से प्रतिस्थापित करने से ही विपरीत मानचित्र प्राप्त हो जाता है।
यह आंकड़ा यूक्लिडियन समतल में स्थिति को दर्शाता है, किन्तु इसमें परिभाषा को दर्शाता है अतिशयोक्तिपूर्ण ज्यामिति मूलतः समान है।
कक्षाएँ
इस प्रकार से एक बाह्य बिलियर्ड्स कक्षा (गतिशीलता) सभी पुनरावृत्त फलन का समुच्चय है
बिंदु का, अर्थात् ... x0 <--> x1 <--> x2 <--> x3 ... अर्थात, x0 से प्रारंभ करें और बाह्य बिलियर्ड्स मानचित्र और पीछे की ओर बाह्य बिलियर्ड्स मानचित्र दोनों को पुनरावृत्त रूप से प्रस्तुत करें।
जब P एक पूर्णतः उत्तल आकृति हो, जैसे दीर्घवृत्त, P के बाहरी भाग में प्रत्येक बिंदु की एक उचित प्रकार से परिभाषित कक्षा है। जब P एक बहुभुज है, तो प्रासंगिक स्पर्शरेखा रेखा के मध्यबिंदु को चुनने की संभावित अस्पष्टता के कारण, कुछ बिंदुओं में उचित प्रकार से परिभाषित कक्षाएँ नहीं हो सकती हैं। फिर भी, में बहुभुज स्तिथि में, लगभग हर बिंदु की एक उचित प्रकार से परिभाषित कक्षा होती है।
- किसी कक्षा को आवधिक कहा जाता है यदि वह अंततः दोहराती है।
- एक कक्षा को एपेरियोडिक (या गैर-आवधिक) कहा जाता है यदि यह आवधिक नहीं है।
- एक कक्षा को परिबद्ध (या स्थिर) कहा जाता है यदि समतल में किसी परिबद्ध क्षेत्र में पूरी कक्षा समाहित हो।
- किसी कक्षा को असंबद्ध (या अस्थिर) कहा जाता है यदि वह परिबद्ध न हो।
उच्च-आयामी समष्टि
इस प्रकार से उच्च-आयामी समष्टि में बाह्य बिलियर्ड्स प्रणाली को परिभाषित करना इस लेख की सीमा से बाहर है। किन्तु सामान्य गतिशील बिलियर्ड्स के स्तिथि के विपरीत, परिभाषा सीधी नहीं है। अतः मानचित्र के लिए प्राकृतिक सेटिंग एक सम्मिश्र सदिश समष्टि है। इस स्तिथि में, प्रत्येक बिंदु पर उत्तल समुच्चय बॉडी पर स्पर्श रेखा का प्राकृतिक विकल्प होता है। इन स्पर्शरेखाओं को सामान्य से प्रारंभ करके और 90 डिग्री घुमाने के लिए सम्मिश्र संरचना का उपयोग करके प्राप्त किया जाता है। इन विशिष्ट स्पर्शरेखा रेखाओं का उपयोग किया जा सकता है
बाह्य बिलियर्ड्स मानचित्र को लगभग ऊपर बताए अनुसार परिभाषित करने के लिए किया जाता है।[1]
इतिहास
अधिकांश लोग बाह्य बिलियर्ड्स की प्रारंभ का श्रेय 1950 के दशक के अंत में बर्नहार्ड न्यूमैन को देते हैं,[3] चूंकि ऐसा लगता है कि कुछ लोग एम. डे के कारण 1945 में हुए पुराने निर्माण का संकेत देते हैं। इस प्रकार से जर्गेन मोजर ने 1970 के दशक में आकाशीय यांत्रिकी के लिए टॉय मॉडल के रूप में इस प्रणाली को लोकप्रिय बनाया है।[4][5] इस प्रणाली का मौलिक अध्ययन यूक्लिडियन समतल में और वर्तमान ही में किया गया है
इस प्रकार से अतिशयोक्तिपूर्ण ज्यामिति. कोई उच्च-आयामी समष्टिों पर भी विचार कर सकता है, चूंकि अभी तक कोई गंभीर अध्ययन नहीं किया गया है।
बर्नहार्ड न्यूमैन ने अनौपचारिक रूप से यह प्रश्न उठाया कि कोई कर सकता है या नहीं बाह्य बिलियर्ड्स प्रणाली में असीमित कक्षाएँ हैं, और मोजर ने इसे 1973 में लिखित रूप में दिया था।[4]
कभी-कभी इस मूल प्रश्न को मोजर-न्यूमैन प्रश्न कहा जाता है। यह प्रश्न, जो मूल रूप से यूक्लिडियन समतल में आकृतियों के लिए उठाया गया था और वर्तमान में हल किया गया है, इस क्षेत्र में एक मार्गदर्शक समस्या रही है।
मोजर-न्यूमैन प्रश्न
यूक्लिडियन तल में बंधी हुई कक्षाएँ
इस प्रकार से 70 के दशक में, जुर्गन मोजर ने कोलमोगोरोव-अर्नोल्ड-मोजर प्रमेय के.ए.एम. पर आधारित एक प्रमाण तैयार किया। सिद्धांत, वह बाहरी ए के सापेक्ष बिलियर्ड्स धनात्मक वक्रता (गणित) के 6-गुना-विभेदित कार्य आकार में सभी कक्षाएँ सीमित हैं। किन्तु 1982 में राफेल डौडी ने इस नतीजे का पूरा प्रमाण दिया।[6] चूंकि बहुभुज स्तिथि में एक बड़ी प्रगति कई वर्षों की अवधि में हुई जब लेखकों की तीन टीमें, विवाल्डी-शैडेंको,[7] व्हीलराइट,[8] और गुटकिन-मुझे नहीं पता,[9] प्रत्येक विभिन्न विधियों का उपयोग करते हुए, दिखाया गया कि एक अर्धवार्षिक बहुभुज के सापेक्ष बाह्य बिलियर्ड्स की सभी कक्षाएँ परिबद्ध हैं। और द्विवार्षिक की धारणा तकनीकी है (संदर्भ देखें) किन्तु इसमें नियमित बहुभुज और उत्तल तर्कसंगत बहुभुज का वर्ग सम्मिलित है, अर्थात् वे उत्तल बहुभुज जिनके शीर्षों पर परिमेय संख्या निर्देशांक होते हैं। अतः परिमेय बहुभुजों के स्तिथि में, सभी कक्षाएँ हैं किन्तु आवधिक. 1995 में, सर्गेई ताबाचनिकोव ने दिखाया कि नियमित पेंटागन के लिए बाह्य बिलियर्ड्स में कुछ एपेरियोडिक कक्षाएँ होती हैं, इस प्रकार तर्कसंगत और नियमित स्तिथियों में गतिशीलता के मध्य अंतर स्पष्ट हो जाता है।[1] इस प्रकार से 1996 में, फिलिप बॉयलैंड ने दिखाया कि कुछ आकृतियों के सापेक्ष बाह्य बिलियर्ड्स में कक्षाएँ हो सकती हैं जो जमा होती हैं।[10] अर्थात 2005 में, डैनियल जेनिन ने दिखाया कि जब आकृति एक समलम्बाकार होती है तो सभी कक्षाएँ सीमित हो जाती हैं, इस प्रकार यह दर्शाता है कि प्रणाली की सभी कक्षाओं को सीमित करने के लिए अर्ध-तर्कसंगतता आवश्यक नियम नहीं है।[11](सभी समलंब चतुर्भुज नहीं हैं।)
यूक्लिडियन तल में असीमित कक्षाएँ
इस प्रकार से 2007 में, रिचर्ड श्वार्ट्ज (गणितज्ञ) ने दिखाया कि परिभाषित होने पर बाह्य बिलियर्ड्स की कुछ असीमित कक्षाएँ होती हैं रोजर पेनरोज़ पतंग के सापेक्ष, इस प्रकार मूल मोजर-न्यूमैन प्रश्न का उत्तर धनात्मक है।[12] किन्तु पेनरोज़ पतंग पतंग-और-डार्ट्स पेनरोज़ टाइलिंग्स से उत्तल बहुभुज चतुर्भुज है। इसके बाद, श्वार्ट्ज ने दिखाया कि सापेक्ष परिभाषित होने पर बाह्य बिलियर्ड्स की असीमित कक्षाएँ होती हैं
किसी भी तर्कहीन पतंग के लिए.[13] एक अपरिमेय पतंग निम्नलिखित गुण वाला एक चतुर्भुज है:चतुर्भुज का एक विकर्ण क्षेत्र को समान क्षेत्रफल वाले दो त्रिभुजों में विभाजित करता है और दूसरा विकर्ण क्षेत्र को दो त्रिभुजो में विभाजित करता है जिनके क्षेत्रफल एक दूसरे के तर्कसंगत गुणज नहीं हैं। इस प्रकार से 2008 में, दिमित्री डोलगोप्याट और बासम फयाद ने दिखाया कि सेमीडिस्क के सापेक्ष परिभाषित बाह्य बिलियर्ड्स हैं असीमित कक्षाएँ.[14] सेमीडिस्क वह क्षेत्र है जो डिस्क (गणित) को आधा काटने पर प्राप्त होता है।
डोलगोपायत-फ़याद का प्रमाण सशक्त है, और डिस्क को लगभग आधा काटकर प्राप्त क्षेत्रों के लिए भी कार्य करता है, जब लगभग शब्द की उपयुक्त व्याख्या की जाती है।
अतिपरवलयिक तल में असीमित कक्षाएँ
2003 में, फ़िलिज़ डोरू और सर्गेई ताबाचनिकोव ने दिखाया कि हाइपरबोलिक ज्यामिति में उत्तल बहुभुजों के एक निश्चित वर्ग के लिए सभी कक्षाएँ असीमित हैं।[15] लेखक ऐसे बहुभुजों को बड़ा कहते हैं। (परिभाषा के लिए संदर्भ देखें।) फ़िलिज़ डोरू और सैमुअल ओटन ने 2011 में उन नियमों को निर्दिष्ट करके इस काम को बढ़ाया जिसके अधीन हाइपरबोलिक समतल में एक नियमित बहुभुज तालिका में सभी कक्षाएँ असीमित होती हैं, अर्थात उच्च होती हैं।[16]
आवधिक कक्षाओं का अस्तित्व
इस प्रकार से साधारण गतिशील बिलियर्ड्स में, आवधिक का अस्तित्व कक्षाएँ एक प्रमुख अनसुलझी समस्या है। किन्तु उदाहरण के लिए, यह अज्ञात है कि प्रत्येक त्रिकोणीय आकार की मेज में एक आवधिक बिलियर्ड पथ होता है। जिसमे अधिक प्रगति हुई है जो की बाह्य बिलियर्ड्स के लिए बनाया गया है, चूंकि स्थिति अभी भी उचित प्रकार से समझ में नहीं आई है।
जैसा कि ऊपर उल्लेख किया गया है, सभी कक्षाएँ आवधिक होती हैं जब प्रणाली को यूक्लिडियन समतल में उत्तल तर्कसंगत बहुभुज के सापेक्ष परिभाषित किया जाता है। इसके अतिरिक्त यह क्रिस कल्टर (सर्गेई ताबाचनिकोव द्वारा लिखित) का आधुनिक प्रमेय है कि किसी भी उत्तल बहुभुज के सापेक्ष बाह्य बिलियर्ड्स में आवधिक कक्षाएँ होती हैं - वास्तव में किसी भी दिए गए सीमित क्षेत्र के बाहर एक आवधिक कक्षा होती है।[17]
विवृत प्रश्न
इस प्रकार से आउटर बिलियर्ड्स एक ऐसा विषय है जो अभी भी अपने प्रारंभी चरण में है। किन्तु अधिकांश समस्याएँ अभी भी अनसुलझी हैं। और यहां क्षेत्र की कुछ विवृत समस्याएं हैं।
- दिखाएँ कि लगभग हर उत्तल बहुभुज के सापेक्ष बाह्य बिलियर्ड्स की कक्षाएँ असीमित हैं।
- दिखाएँ कि एक नियमित बहुभुज के सापेक्ष बाह्य बिलियर्ड्स की लगभग हर कक्षा आवर्त होती है। समबाहु त्रिभुज और वर्ग के स्तिथि तुच्छ हैं, और ताबाचनिकोव ने नियमित पंचकोण के लिए इसका उत्तर दिया। ये एकमात्र ज्ञात स्तिथि हैं।
- अधिक व्यापक रूप से, विशिष्ट उत्तल बहुभुज के सापेक्ष आवधिक कक्षाओं के समुच्चय की संरचना को चिह्नित करें।
- अतिशयोक्तिपूर्ण तल में सरल आकृतियों, जैसे छोटे समबाहु त्रिभुज, के सापेक्ष आवधिक कक्षाओं की संरचना को समझें।
यह भी देखें
संदर्भ
- ↑ 1.0 1.1 1.2 Tabachnikov, Serge (1995). Billiards. Panoramas et Synthèses. Société Mathématique de France. ISBN 978-2-85629-030-9.
- ↑ Tabachnikov, Sergei (2002). "Dual Billiards in the Hyperbolic Plane". Nonlinearity. 15 (4): 1051–1072. Bibcode:2002Nonli..15.1051T. CiteSeerX 10.1.1.408.9436. doi:10.1088/0951-7715/15/4/305. S2CID 250758250.
- ↑ Neumann, Bernhard H. (25 Jan 1959). "Sharing Ham and Eggs". Iota: The Manchester University Mathematics Students' Journal.
- ↑ 4.0 4.1 Moser, Jürgen (1973). Stable and random motions in dynamical systems. Annals of Mathematics Studies. Vol. 77. Princeton University Press.
- ↑ Moser, Jürgen (1978). "Is the Solar System Stable?". Mathematical Intelligencer. 1 (2): 65–71. doi:10.1007/BF03023062.
- ↑ R. Douady (1982). "these de 3-eme cycle". University of Paris 7.
{{cite journal}}: Cite journal requires|journal=(help) - ↑ Vivaldi, Franco; Shaidenko, Anna V. (1987). "Global Stability of a class of discontinuous billiards". Communications in Mathematical Physics. 110 (4): 625–640. Bibcode:1987CMaPh.110..625V. doi:10.1007/BF01205552. S2CID 111386812.
- ↑ Kołodziej, Rafał (1989). "The antibilliard outside a polygon". Bull. Polish Acad. Sci. Math. 34: 163–168.
- ↑ Gutkin, Eugene; Simanyi, Nandor (1991). "Dual polygonal billiard and necklace dynamics". Communications in Mathematical Physics. 143 (3): 431–450. Bibcode:1992CMaPh.143..431G. doi:10.1007/BF02099259. S2CID 121776396.
- ↑ Boyland, Philip (1996). "Dual billiards, twist maps, and impact oscillators". Nonlinearity. 9 (6): 1411–1438. arXiv:math/9408216. Bibcode:1996Nonli...9.1411B. doi:10.1088/0951-7715/9/6/002. S2CID 18709638.
- ↑ Genin, Daniel I. (2005). Regular and chaotic dynamics of outer billiards (Ph.D. Thesis). Pennsylvania State University.
- ↑ Schwartz, Richard E. (2007). "unbounded orbits for outer billiards I". Journal of Modern Dynamics. 1 (3): 371–424. arXiv:math/0702073. Bibcode:2007math......2073S. doi:10.3934/jmd.2007.1.371. S2CID 119146537.
- ↑ Schwartz, Richard E. (2009). "outer billiards on kites". Annals of Mathematics Studies. 171. Princeton University Press.
{{cite journal}}: Cite journal requires|journal=(help) - ↑ Dolgopyat, Dmitry; Fayad, Bassam (2009). "unbounded orbits for semicircular outer billiards". Annales Henri Poincaré. 10 (2): 357–375. Bibcode:2009AnHP...10..357D. doi:10.1007/s00023-009-0409-9.
- ↑ Doǧru, Filiz; Tabachnikov, Sergei (2003). "On Polygonal Dual Billiards in the Hyperbolic Plane". Regular and Chaotic Dynamics. 8 (1): 67–82. Bibcode:2003RCD.....8...67D. doi:10.1070/RD2003v008n01ABEH000226.
- ↑ Doǧru, Filiz; Otten, Samuel (2011). "Sizing Up Outer Billiard Tables". American Journal of Undergraduate Research. 10: 1–8. doi:10.33697/ajur.2011.008.
- ↑ Tabachnikov, Serge (2007). "A proof of Culter's theorem on existence of periodic orbits in polygonal outer billiards". Geometriae Dedicata. 129: 83–87. arXiv:0706.1003. Bibcode:2007arXiv0706.1003T. doi:10.1007/s10711-007-9196-y.