यंग-लाप्लास समीकरण
भौतिकी में, यंग-लैपलेस समीकरण (/ləˈplɑːs/) एक बीजगणितीय समीकरण है जो सतही तनाव या दीवार तनाव की घटना के कारण पानी और हवा जैसे दो द्रव स्थैतिकी के बीच अंतराफलक में निरंतर केशिका दबाव अंतर का वर्णन करता है, हालांकि बाद का उपयोग केवल तभी लागू होता है जब यह माना जाता है कि दीवार बहुत पतली है. यंग-लाप्लास समीकरण दबाव अंतर को सतह या दीवार के आकार से संबंधित करता है और यह स्थिर केशिका सतहों के अध्ययन में मूलभूत रूप से महत्वपूर्ण है। यह इंटरफ़ेस पर स्थिर तरल पदार्थ की बैठक के लिए सामान्य तनाव संतुलन का बयान है, जहां इंटरफ़ेस को सतह (गणित) (शून्य मोटाई) के रूप में माना जाता है:
समीकरण का नाम थॉमस यंग (वैज्ञानिक) के नाम पर रखा गया है, जिन्होंने 1805 में सतही तनाव के गुणात्मक सिद्धांत को विकसित किया था, और पियरे-साइमन लाप्लास ने अगले वर्ष गणितीय विवरण पूरा किया था। इसे कभी-कभी यंग-लैपलेस-गॉस समीकरण भी कहा जाता है, क्योंकि कार्ल फ्रेडरिक गॉस ने 1830 में यंग और लाप्लास के काम को एकीकृत किया, जोहान बर्नौली के आभासी कार्य सिद्धांतों का उपयोग करके अंतर समीकरण और सीमा शर्तों दोनों को प्राप्त किया।[2]
साबुन फिल्म
यदि दबाव अंतर शून्य है, जैसा कि गुरुत्वाकर्षण के बिना साबुन की फिल्म में होता है, तो इंटरफ़ेस एक न्यूनतम सतह का आकार ले लेगा।
पायसन
समीकरण एक पायस बनाने के लिए आवश्यक ऊर्जा की भी व्याख्या करता है। एक पायस की छोटी, अत्यधिक घुमावदार बूंदों को बनाने के लिए, उनके छोटे त्रिज्या से उत्पन्न बड़े दबाव को दूर करने के लिए अतिरिक्त ऊर्जा की आवश्यकता होती है।
लाप्लास दबाव, जो छोटी बूंदों के लिए अधिक होता है, इमल्शन में सबसे छोटी बूंदों में से अणुओं के प्रसार का कारण बनता है और ऑस्वाल्ड राइपनिंग के माध्यम से इमल्शन को मोटा करता है।[citation needed]
एक ट्यूब में केशिका दबाव
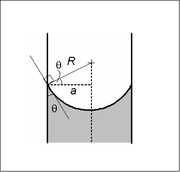
वृत्ताकार क्रॉस-सेक्शन (त्रिज्या a) की एक पर्याप्त रूप से संकीर्ण (यानी, कम बॉन्ड संख्या) ट्यूब में, दो तरल पदार्थों के बीच का इंटरफ़ेस एक मेनिस्कस (तरल) बनाता है जो त्रिज्या आर के साथ एक गोले की सतह का एक हिस्सा है। दबाव कूद इस सतह के पार त्रिज्या और सतह के तनाव γ से संबंधित है
क्षेत्र का त्रिज्या केवल संपर्क कोण, θ का एक कार्य होगा, जो बदले में तरल पदार्थ के सटीक गुणों और कंटेनर सामग्री पर निर्भर करता है जिसके साथ तरल पदार्थ संपर्क/इंटरफेसिंग कर रहे हैं:
हाइड्रोस्टैटिक संतुलन बनाए रखने के लिए, प्रेरित केशिका दबाव को ऊंचाई में परिवर्तन, 'एच' द्वारा संतुलित किया जाता है, जो सकारात्मक या नकारात्मक हो सकता है, यह इस बात पर निर्भर करता है कि गीला कोण 90 डिग्री से कम या अधिक है या नहीं। घनत्व ρ के तरल पदार्थ के लिए:
- γ = 0.0728 जे/एम2 20 डिग्री सेल्सीयस पर
- θ = 20° (0.35 कांति )
- ρ = 1000 किग्रा/मीटर3</उप>
- g = 9.8 मी/से2</उप>
और इसलिए पानी के स्तंभ की ऊंचाई इस प्रकार दी गई है:
सामान्य रूप में केशिका क्रिया
सामान्य मामले में, एक मुक्त सतह के लिए और जहां एक लागू ओवर-दबाव होता है, Δp, संतुलन में इंटरफ़ेस पर, लागू दबावहीड्रास्टाटिक दबाव दबाव और सतह तनाव के प्रभावों के बीच संतुलन होता है। 'यंग-लाप्लास' समीकरण बन जाता है:
तब अविमीय समीकरण बन जाता है:
अक्षीय समीकरण
द्रवस्थैतिक 'यंग-लैपलेस समीकरण' देने के लिए प्रमुख वक्रता के लिए सामान्य अभिव्यक्तियों को प्रतिस्थापित करके एक अक्षीय सतह का (गैर-आयामी) आकार, r(z) पाया जा सकता है:[5]
चिकित्सा में आवेदन
चिकित्सा में इसे अक्सर लाप्लास के नियम के रूप में संदर्भित किया जाता है, जिसका उपयोग कार्डियोवास्कुलर फिजियोलॉजी के संदर्भ में किया जाता है,[6] और श्वसन क्रिया विज्ञान भी, हालांकि बाद वाला प्रयोग अक्सर गलत होता है।[7]
इतिहास
फ्रांसिस हॉक्सबी ने 1709 में कुछ शुरुआती अवलोकन और प्रयोग किए[8] और इन्हें 1718 में जेम्स ज्यूरिन द्वारा दोहराया गया जिन्होंने देखा कि केशिका स्तंभ में द्रव की ऊंचाई केवल सतह पर क्रॉस-सेक्शनल क्षेत्र का कार्य था, स्तंभ के किसी अन्य आयाम का नहीं।[4][9] थॉमस यंग (वैज्ञानिक) ने अपने 1804 के पेपर एन एसे ऑन द कोहेशन ऑफ फ्लुइड्स में समीकरण की नींव रखी[10] जहां उन्होंने वर्णनात्मक शब्दों में तरल पदार्थों के बीच संपर्क को नियंत्रित करने वाले सिद्धांतों (द्रव व्यवहार के कई अन्य पहलुओं के साथ) को निर्धारित किया। पियरे साइमन लाप्लास ने इसके बाद मैकानिक सेलेस्टे में काम किया[11] ऊपर दिए गए औपचारिक गणितीय विवरण के साथ, जो यंग द्वारा पहले वर्णित संबंध को प्रतीकात्मक शब्दों में पुन: प्रस्तुत करता है।
लाप्लास ने हॉक्सबी द्वारा अपनी पुस्तक फिजिको-मैकेनिकल एक्सपेरिमेंट्स (1709) में प्रतिपादित इस विचार को स्वीकार किया कि यह घटना एक आकर्षण बल के कारण थी जो समझदार दूरी पर असंवेदनशील थी।[12][13] वह हिस्सा जो एक तरल पर एक ठोस की क्रिया और दो तरल पदार्थों की पारस्परिक क्रिया से संबंधित है, पूरी तरह से काम नहीं किया गया था, लेकिन अंततः कार्ल फ्रेडरिक गॉस द्वारा पूरा किया गया था।[14] फ्रांज अर्न्स्ट न्यूमैन (1798-1895) ने बाद में कुछ विवरण भरे।[15][9][16]
संदर्भ
- ↑ Surface Tension Module Archived 2007-10-27 at the Wayback Machine, by John W. M. Bush, at MIT OCW.
- ↑ Robert Finn (1999). "Capillary Surface Interfaces" (PDF). AMS.
- ↑ "यूरी का शासन". McGraw-Hill Dictionary of Scientific and Technical Terms. McGraw-Hill on Answers.com. 2003. Retrieved 2007-09-05.
- ↑ 4.0 4.1 See:
- James Jurin (1718) "An account of some experiments shown before the Royal Society; with an enquiry into the cause of some of the ascent and suspension of water in capillary tubes," Philosophical Transactions of the Royal Society of London, 30 : 739–747.
- James Jurin (1719) "An account of some new experiments, relating to the action of glass tubes upon water and quicksilver," Philosophical Transactions of the Royal Society of London, 30 : 1083–1096.
- ↑ Lamb, H. Statics, Including Hydrostatics and the Elements of the Theory of Elasticity, 3rd ed. Cambridge, England: Cambridge University Press, 1928.
- ↑ Basford, Jeffrey R. (2002). "लाप्लास का कानून और समकालीन चिकित्सा और पुनर्वास के लिए इसकी प्रासंगिकता". Archives of Physical Medicine and Rehabilitation. 83 (8): 1165–1170. doi:10.1053/apmr.2002.33985. PMID 12161841.
- ↑ Prange, Henry D. (2003). "Laplace's Law and the Alveolus: A Misconception of Anatomy and a Misapplication of Physics". Advances in Physiology Education. 27 (1): 34–40. doi:10.1152/advan.00024.2002. PMID 12594072. S2CID 7791096.
- ↑ See:
- Francis Hauksbee, Physico-mechanical Experiments on Various Subjects … (London, England: (Self-published by author; printed by R. Brugis), 1709), pages 139–169.
- Francis Hauksbee (1711) "An account of an experiment touching the direction of a drop of oil of oranges, between two glass planes, towards any side of them that is nearest press'd together," Philosophical Transactions of the Royal Society of London, 27 : 374–375.
- Francis Hauksbee (1712) "An account of an experiment touching the ascent of water between two glass planes, in an hyperbolick figure," Philosophical Transactions of the Royal Society of London, 27 : 539–540.
- ↑ 9.0 9.1 Maxwell, James Clerk; Strutt, John William (1911). . Encyclopædia Britannica (in English). Vol. 5 (11th ed.). pp. 256–275.
- ↑ Thomas Young (1805) "An essay on the cohesion of fluids," Philosophical Transactions of the Royal Society of London, 95 : 65–87.
- ↑ Pierre Simon marquis de Laplace, Traité de Mécanique Céleste, volume 4, (Paris, France: Courcier, 1805), Supplément au dixième livre du Traité de Mécanique Céleste, pages 1–79.
- ↑ Pierre Simon marquis de Laplace, Traité de Mécanique Céleste, volume 4, (Paris, France: Courcier, 1805), Supplément au dixième livre du Traité de Mécanique Céleste. On page 2 of the Supplément, Laplace states that capillary action is due to "… les lois dans lesquelles l'attraction n'est sensible qu'à des distances insensibles; …" (… the laws in which attraction is sensible [significant] only at insensible [infinitesimal] distances …).
- ↑ In 1751, Johann Andreas Segner came to the same conclusion that Hauksbee had reached in 1709: J. A. von Segner (1751) "De figuris superficierum fluidarum" (On the shapes of liquid surfaces), Commentarii Societatis Regiae Scientiarum Gottingensis (Memoirs of the Royal Scientific Society at Göttingen), 1 : 301–372. On page 303, Segner proposes that liquids are held together by an attractive force (vim attractricem) that acts over such short distances "that no one could yet have perceived it with their senses" (… ut nullo adhuc sensu percipi poterit.).
- ↑ Carl Friedrich Gauss, Principia generalia Theoriae Figurae Fluidorum in statu Aequilibrii [General principles of the theory of fluid shapes in a state of equilibrium] (Göttingen, (Germany): Dieterichs, 1830). Available on-line at: Hathi Trust.
- ↑ Franz Neumann with A. Wangerin, ed., Vorlesungen über die Theorie der Capillarität [Lectures on the theory of capillarity] (Leipzig, Germany: B. G. Teubner, 1894).
- ↑ Rouse Ball, W. W. [1908] (2003) "Pierre Simon Laplace (1749–1827)", in A Short Account of the History of Mathematics, 4th ed., Dover, ISBN 0-486-20630-0
अग्रिम पठन
- Maxwell, James Clerk; Strutt, John William (1911). . In Chisholm, Hugh (ed.). Encyclopædia Britannica (in English). Vol. 5 (11th ed.). Cambridge University Press. pp. 256–275.
- Batchelor, G. K. (1967) An Introduction To Fluid Dynamics, Cambridge University Press
- Jurin, J. (1716). "An account of some experiments shown before the Royal Society; with an enquiry into the cause of the ascent and suspension of water in capillary tubes". Philosophical Transactions of the Royal Society. 30 (351–363): 739–747. doi:10.1098/rstl.1717.0026. S2CID 186211806.
- Tadros T. F. (1995) Surfactants in Agrochemicals, Surfactant Science series, vol.54, Dekker