रेखा - चित्र

चित्र 1. . मिशेलसन प्रयोग से डेटा का बॉक्स प्लॉट।

वर्णनात्मक आँकड़ों में, बॉक्स प्लॉट या बॉक्सप्लॉट ग्राफिक रूप से स्थानीयता, प्रसार और संख्यात्मक डेटा के तिरछे समूहों को उनके चतुर्थक के माध्यम से प्रदर्शित करने की विधि है। बॉक्स प्लॉट पर बॉक्स के अतिरिक्त, बॉक्स से फैली हुई रेखायें (जिन्हें मूंछ कहा जाता है) हो सकती हैं। जो ऊपरी और निचले चतुर्थक के बाहर परिवर्तनशीलता का संकेत देती हैं। इस प्रकार प्लॉट को 'बॉक्स-एंड-व्हिस्कर प्लॉट' भी कहा जाता है और 'बॉक्स-एंड-व्हिस्कर आरेख' भी कहा जाता है। आउटलेयर जो अन्य डेटासेट से अधिक भिन्न होती हैं। उन्हें बॉक्स-प्लॉट पर मूंछ से बढ़कर भिन्न-भिन्न बिंदुओं के रूप में प्लॉट किया जा सकता है।

सामान्यतः बॉक्स प्लॉट गैर पैरामीट्रिक हैं। वे अंतर्निहित संभाव्यता वितरण की कोई धारणा बनाए बिना सांख्यिकीय जन-संख्या की रचनाओं में भिन्नता प्रदर्शित करते हैं। (चूंकि टकी का बॉक्सप्लॉट मूंछों के लिए समरूपता और उनकी लंबाई के लिए सामान्यता मानता है)। बॉक्स-प्लॉट के प्रत्येक उपखंड में स्पेसिंग डेटा के सांख्यिकीय फैलाव (प्रसार) और डेटा के तिरछापन की डिग्री दर्शाती है। जिसे सामान्यतः पांच-संख्या सारांश का उपयोग करके वर्णित किया जाता है। इसके अतिरिक्त, बॉक्स-प्लॉट व्यक्ति को विभिन्न एल-अनुमानकों, विशेष रूप से अन्तःचतुर्थक श्रेणी, मिडहिंज, श्रेणी (सांख्यिकी), मध्य-श्रेणी और काट-छांट करने का अनुमान लगाने की अनुमति देता है। अतः बॉक्स प्लॉट या तो क्षैतिज या लंबवत रूप से खींचे जा सकते हैं।

इतिहास

श्रेणी-बार पद्धति को प्रथम बार मैरी एलेनोर स्पीयर ने सन् 1952 में अपनी पुस्तक "चार्टिंग स्टैटिस्टिक्स" में प्रस्तुत किया था। इसके पश्चात् सन् 1969 में उनकी पुस्तक "प्रैक्टिकल चार्टिंग टेक्निक्स" में प्रस्तुत किया गया था। चूँकि बॉक्स-एंड-व्हिस्कर प्लॉट प्रथम बार सन् 1970 में जॉन टुकी द्वारा प्रस्तुत किया गया थ। जिन्होंने इसके पश्चात् सन् 1977 में अपनी पुस्तक "एक्सप्लोरेटरी डेटा एनालिसिस" में इस विषय को प्रकाशित किया था।

तत्व

चित्रा 2. न्यूनतम से अधिकतम तक मूंछ के साथ बॉक्स-प्लॉट

चित्रा 3.1.5 आईक्यूआर मान के भीतर मूंछ के साथ समान बॉक्स-प्लॉट।

बॉक्सप्लॉट पाँच अंकों के सारांश के आधार पर डेटासेट प्रदर्शित करने की मानकीकृत विधि है। न्यूनतम, अधिकतम, रचना माध्यिका, और पहला और तीसरा चतुर्थक।

• रचना न्यूनतम (Q₀ या 0 वाँ प्रतिशतक): किसी भी आउटलेयर को छोड़कर डेटा सेट में सबसे कम डेटा बिंदु।
• रचना अधिकतम (Q₄ या 100 वाँ प्रतिशतक): किसी भी आउटलेयर को छोड़कर डेटा सेट में उच्चतम डेटा बिंदु।
• माध्यिका (Q₂ या 50 वाँ प्रतिशतक): डेटा सेट में मध्य मान।
• पहला चतुर्थक (Q₁ या 25वां प्रतिशतक): जिसे निम्न चतुर्थक qn(0.25) के रूप में भी जाना जाता है। यह डेटासेट के निचले आधे भाग की माध्यिका है।
• तीसरा चतुर्थक (Q₃ या 75 वाँ प्रतिशतक): जिसे ऊपरी चतुर्थक q_n(0.75), के रूप में भी जाना जाता है। यह डेटासेट के ऊपरी आधे भाग की माध्यिका है।

बॉक्स-प्लॉट के निर्माण के लिए उपयोग किए जाने वाले न्यूनतम और अधिकतम मानों के अतिरिक्त, अन्य महत्वपूर्ण तत्व जिसे बॉक्स-प्लॉट प्राप्त करने के लिए भी नियोजित किया जा सकता है। जो अन्तःचतुर्थक श्रेणी (आईक्यूआर) है, जैसा कि नीचे दर्शाया गया है।

• इंटरक्वेरटाइल श्रेणी (आईक्यूआर): ऊपरी और निचले चतुर्थक के मध्य की दूरी,

${\text{IQR}}=Q_{3}-Q_{1}=q_{n}(0.75)-q_{n}(0.25)$

बॉक्स-प्लॉट में सामान्यतः दो भाग होते हैं। बॉक्स और मूंछ का सेट जैसा कि चित्र 2 में दिखाया गया है। चूँकि बॉक्स Q₁ से Q₃ के मध्य में खींची गई क्षैतिज रेखा के साथ खींचा जाता है। जो मध्यिका को दर्शाता है। अतः मूंछ को विभिन्न प्रकारों से परिभाषित किया जा सकता है।

सबसे सीधी-आगे की विधि में, निचले मूंछ की सीमा डेटा सेट का न्यूनतम मूल्य है और ऊपरी मूंछ की सीमा डेटा सेट का अधिकतम मूल्य है।

मूंछ की सीमाओं के लिए अन्य लोकप्रिय विकल्प 1.5 आईक्यूआर मान पर आधारित है। ऊपरी चतुर्थक के ऊपर से (Q₃), आईक्यूआर से 1.5 गुना की दूरी मापी जाती है और इस दूरी के अंदर आने वाले डेटासेट से सबसे बड़े देखे गए डेटा बिंदु तक मूंछ खींची जाती है। इसी प्रकार, आईक्यूआर की 1.5 गुना की दूरी को निम्न चतुर्थक (Q₁) के नीचे मापा जाता है और इस दूरी के अंदर आने वाले डेटासेट से सबसे कम देखे गए डेटा बिंदु के लिए मूंछ खींची जाती है। चूँकि मूंछ देखे गए डेटा बिंदु पर समाप्त होनी चाहिए अतः मूंछ की लंबाई असमान दिख सकती है। यदि 1.5 आईक्यूआर दोनों पक्षों के लिए समान होता है। तब व्हिस्कर्स की सीमा के बाहर देखे गए अन्य सभी डेटा बिंदुओं को 'आउटलेयर' के रूप में प्लॉट किया जाता है। अतः आउटलेयर को बॉक्स-प्लॉट पर डॉट, छोटा वृत्त, स्टार, आदि के रूप में प्लॉट किया जा सकता है।

चूँकि, मूंछें कई अन्य चीजों के लिए खड़ी हो सकती हैं। जैसे:

• डेटा सेट का न्यूनतम और अधिकतम मान (जैसा चित्र 2 में दिखाया गया है)।
• डेटा सेट के माध्य से ऊपर और नीचे मानक विचलन।
• डेटा सेट का 9वाँ प्रतिशतक और 91वाँ प्रतिशतक।
• डेटा सेट का दूसरा प्रतिशतक और 98वां प्रतिशतक।

सामान्यतः विरले ही बॉक्स प्लॉट बिना मूंछ के प्लॉट किए जा सकते हैं। यह संवेदनशील जानकारी के लिए उचित हो सकता है। जिससे कि मूंछ (और बाहरी) से बचने के लिए वास्तविक मूल्यों का व्याख्यान किया जा सकता है।

कुछ बॉक्स प्लॉट में डेटा के माध्यम का प्रतिनिधित्व करने के लिए अतिरिक्त वर्ण सम्मिलित होते है।

असामान्य प्रतिशतक 2%, 9%, 91%, 98% का उपयोग कभी-कभी मूंछ क्रॉस-हैच के लिए किया जाता है और सात-संख्या सारांश को दर्शाने के लिए मूंछ समाप्त होती है। यदि डेटा सामान्य वितरण हैं। तब बॉक्स प्लॉट पर सात चिह्नों के स्थान समान रूप से स्थानित होते है। अतः कुछ बॉक्स भूखंडों पर, प्रत्येक मूंछ के अंत से पहले क्रॉस-हैच लगाया जाता है।

इस परिवर्तनशीलता के कारण, बॉक्स-प्लॉट के शीर्षक में व्हिस्कर्स और आउटलेयर के लिए उपयोग किए जा रहे सम्मेलन का वर्णन करना उचित है।

रूपांतर

चित्र 4.चार बॉक्स प्लॉट, नॉच और चर चौड़ाई के साथ और बिना।

चूंकि गणितज्ञ जॉन डब्ल्यू ने तुकी ने प्रथम बार सन् 1969 में इस प्रकार के विज़ुअल डेटा डिस्प्ले को लोकप्रिय बनाया था। क्लासिकल बॉक्स प्लॉट पर कई विविधताएँ विकसित की गई हैं और दो सबसे अधिक पाई जाने वाली विविधताएँ चर चौड़ाई वाले बॉक्स प्लॉट और नॉटेड बॉक्स प्लॉट हैं जो चित्र 4 में दिखाए गए हैं।

परिवर्तनीय चौड़ाई वाले बॉक्स प्लॉट प्रत्येक समूह के आकार का वर्णन करते हैं। जिनके डेटा को समूह के आकार के अनुपात में बॉक्स की चौड़ाई बनाकर प्लॉट किया जा रहा है। समूह के आकार के वर्गमूल के अनुपात में बॉक्स की चौड़ाई को आनुपातिक बनाने की लोकप्रिय परंपरा है।

अधिकाशतः नोकदार बॉक्स प्लॉट माध्यिका के चारों ओर पायदान या बॉक्स की संकीर्णता को प्रयुक्त करते हैं। माध्यिका के अंतर के महत्व की मोटी गाइड की प्रस्तुतीकर करने में पायदान उपयोगी होते हैं। यदि दो बक्सों के पायदान ओवरलैप नहीं होते हैं। तब यह माध्यिका के मध्य सांख्यिकीय रूप से महत्वपूर्ण अंतर का प्रमाण प्रदान करता है। सामान्यतः खांचे की चौड़ाई रचनाओं की अन्तःचतुर्थक श्रेणी (आईक्यूआर) के समानुपाती होती है और रचनाओं के आकार के वर्गमूल के व्युत्क्रमानुपाती होती है। चूंकि, सबसे उपयुक्त गुणक के बारे में अनिश्चितता है (क्योंकि यह रचनाओं के प्रसरणों की समानता के आधार पर भिन्न हो सकता है)।

इन खांचों की सीमाओं को प्राप्त करने के लिए परिपाटी की दूरी का उपयोग करना है। जो $\pm {\frac {1.58{\text{ IQR}}}{\sqrt {n}}}$ मध्य के आसपास होता है।

समायोजित बॉक्स भूखंडों का उद्देश्य तिरछापन का वर्णन करना है और वह तिरछापन के मध्यम आँकड़ों पर समर्थन करते हैं। एमसी के औसत मूल्य के लिए, बॉक्स-प्लॉट पर ऊपरी और निचले मूंछ की लंबाई क्रमशः इस प्रकार परिभाषित की जाती है।

${\begin{matrix}1.5{\text{IQR}}\cdot e^{3{\text{MC}}},&1.5{\text{ IQR}}\cdot e^{-4{\text{MC}}}{\text{ if }}{\text{MC}}\geq 0,\\1.5{\text{IQR}}\cdot e^{4{\text{MC}}},&1.5{\text{ IQR}}\cdot e^{-3{\text{MC}}}{\text{ if }}{\text{MC}}\leq 0.\end{matrix}}$

सममित डेटा वितरण के लिए मेडकूपल शून्य होता है और यह समायोजित बॉक्स-प्लॉट को टकी के बॉक्स-प्लॉट में समांतर मूंछ की लंबाई के साथ कम कर देता है $1.5{\text{ IQR}}$ दोनों मूंछों के लिए होता है।

अन्य प्रकार के बॉक्स प्लॉट, जैसे वायलिन प्लॉट्स और बीन प्लॉट एकल-मोडल और मल्टीमॉडल वितरण के मध्य अंतर दिखा सकते हैं। जिसे मूल मौलिक बॉक्स-प्लॉट से नहीं देखा जा सकता है।

उदाहरण

बाहरी कारकों के बिना उदाहरण

चित्रा 5. बिना किसी आउटलेयर के बाईं ओर उदाहरण का उत्पन्न बॉक्सप्लॉट चित्र।

सामान्यतः घंटे के तापमान की श्रृंखला को पूरे दिन में डिग्री फ़ारेनहाइट में मापा गया है। जिसका रिकॉर्ड किए गए मान के निम्नानुसार सूचीबद्ध हैं (°F): 57, 57, 57, 58, 63, 66, 66, 67, 67, 68, 69, 70, 70, 70, 70, 72, 73, 75, 75, 76, 76, 78, 79, 81।

डेटा सेट का बॉक्स प्लॉट पहले इस डेटा सेट के पांच प्रासंगिक मानों की गणना करके उत्पन्न किया जा सकता है: न्यूनतम, अधिकतम, माध्यिका (Q₂), पहला चतुर्थक (Q₁), और तीसरा चतुर्थक (Q₃)।

न्यूनतम डेटा सेट की सबसे छोटी संख्या है। इस स्थिति में, न्यूनतम अंकित दिन का तापमान 57 डिग्री फारेनहाइट है।

अधिकतम डेटा सेट की सबसे बड़ी संख्या है। इस स्थिति में, अधिकतम रिकॉर्ड किया गया दिन का तापमान 81 °F है।

माध्यिका आदेशित डेटा सेट की मध्य संख्या है। इसका तात्पर्य यह है कि 50% तत्व माध्यिका से कम हैं और 50% तत्व माध्यिका से अधिक हैं। इस आदेशित डेटा सेट का माध्यिका 70 °F है।

प्रथम चतुर्थक मान (Q₁या 25 वाँ प्रतिशतक) वह संख्या है जो आदेशित डेटा सेट के चौथाई को चिह्नित करता है। दूसरे शब्दों में, ठीक 25% ऐसे तत्व हैं। जो प्रथम चतुर्थक से कम हैं और ठीक 75% ऐसे तत्व हैं जो इससे अधिक हैं। न्यूनतम और माध्यिका के मध्य की मध्य संख्या ज्ञात करके प्रथम चतुर्थक मान सरलता से निर्धारित किया जा सकता है। अतः प्रति घंटा तापमान के लिए, 57 °F और 70 °F के मध्य पाई जाने वाली मध्य संख्या 66 °F है।

तीसरा चतुर्थक मान (Q₃या 75 वाँ प्रतिशतक) वह संख्या है जो आदेशित डेटा सेट के तीन चौथाई को चिह्नित करती है। दूसरे शब्दों में, ठीक 75% तत्व ऐसे हैं। जो तीसरे चतुर्थक से कम हैं और 25% ऐसे तत्व हैं। जो इससे अधिक हैं। माध्यिका और अधिकतम के मध्य की संख्या ज्ञात करके तीसरा चतुर्थक मान सरलता से प्राप्त किया जा सकता है। प्रति घंटा तापमान के लिए, 70 °F और 81 °F के मध्य की संख्या 75 °F है।

अन्तःचतुर्थक श्रेणी या आईक्यूआर की गणना प्रथम चतुर्थक मान (Q₁) को घटाकर की जा सकती है। तीसरे चतुर्थक मान (Q₃) से घटाकर की जा सकती है।

${\text{IQR}}=Q_{3}-Q_{1}=75^{\circ }F-66^{\circ }F=9^{\circ }F.$

इस प्रकार, $1.5{\text{IQR}}=1.5\cdot 9^{\circ }F=13.5^{\circ }F.$

1.5 आईक्यूआर तीसरे चतुर्थक से ऊपर है।

$Q_{3}+1.5{\text{ IQR}}=75^{\circ }F+13.5^{\circ }F=88.5^{\circ }F.$

प्रथम चतुर्थक के नीचे 1.5 आईक्यूआर है।

$Q_{1}-1.5{\text{ IQR}}=66^{\circ }F-13.5^{\circ }F=52.5^{\circ }F.$

बॉक्स-प्लॉट की ऊपरी मूंछ सीमा सबसे बड़ा डेटा मान है। जो तीसरे चतुर्थक के ऊपर 1.5 आईक्यूआर के अंदर है। यहाँ तीसरे चतुर्थक के ऊपर 1.5 आईक्यूआर 88.5 °F और अधिकतम 81 °F है। इस प्रकार ऊपरी मूंछ अधिकतम के मान पर खींची जाती है, जो कि 81 °F है।

इसी प्रकार, बॉक्स प्लॉट की निचली मूंछ सीमा सबसे छोटा डेटा मान है जो पहले चतुर्थांश के नीचे 1.5 आईक्यूआर के अंदर है। यहां, पहले चतुर्थक के नीचे 1.5 आईक्यूआर 52.5 °F और न्यूनतम 57 °F है। इस प्रकार निचला मूंछ न्यूनतम के मान पर खींचा जाता है, जो कि 57 °F है।

आउटलेर्स के साथ उदाहरण

चित्रा 6. आउटलेयर के साथ बाईं ओर उदाहरण का उत्पन्न बॉक्सप्लॉट।

ऊपर आउटलेयर के बिना उदाहरण है। आउटलेर्स के साथ बॉक्स-प्लॉट बनाने के लिए यहां अनुवर्ती उदाहरण दिया गया है।

रिकॉर्ड किए गए तापमान के लिए निर्धारित सेट है (°F): 52, 57, 57, 58, 63, 66, 66, 67, 67, 68, 69, 70, 70, 70, 70, 72, 73, 75, 75 , 76, 76, 78, 79, 89।

इस उदाहरण में केवल पहली और आखिरी संख्या परिवर्तित की गई है। अतः माध्यिका, तृतीय चतुर्थक और प्रथम चतुर्थक समान रहते हैं।

इस स्थिति में, इस डेटा सेट में अधिकतम मान 89 °F है और तीसरे चतुर्थक के ऊपर 1.5 आईक्यूआर 88.5 °F है। अधिकतम 1.5 आईक्यूआर और तीसरे चतुर्थक से अधिक है, इसलिए अधिकतम बाहरी है। जिससे कि ऊपरी मूंछ तीसरे चतुर्थक के ऊपर 1.5 आईक्यूआर से छोटे सबसे बड़े मूल्य पर खींची जाती है, जो कि 79 ° F है।

इसी प्रकार, इस डेटा सेट में न्यूनतम मान 52 °F है और पहली चतुर्थक के नीचे 1.5 आईक्यूआर 52.5 °F है। न्यूनतम 1.5 आईक्यूआर माइनस प्रथम चतुर्थक से छोटा है। इसलिए न्यूनतम भी आउटलायर है। जिससे कि निचली मूंछ पहले चतुर्थक के नीचे 1.5 आईक्यूआर से अधिक के सबसे छोटे मूल्य पर खींची जाती है, जो कि 57 ° F है।

बड़े डेटासेट के स्थिति में,

बड़ी संख्या में डेटा बिंदुओं वाले डेटा सेट से बॉक्स-प्लॉट प्राप्त करने का अतिरिक्त उदाहरण है।

अनुभवजन्य मात्राओं की गणना करने के लिए सामान्य समीकरण

$q_{n}(p)=x_{(k)}+\alpha (x_{(k+1)}-x_{(k)})$

${\text{with }}k=[p(n+1)]{\text{ and }}\alpha =p(n+1)-k$

यहाँ $x_{(k)}$ डेटा बिंदुओं के सामान्य क्रम के लिए खड़ा है (अर्थात यदि $i<k$, तब $x_{(i)}<x_{(k)}$ )

उपरोक्त उदाहरण का उपयोग करते हुए जिसमें 24 डेटा बिंदु (n = 24) हैं। अतः कोई भी गणितीय या दृष्टिगत रूप से माध्यिका, प्रथम और तृतीय चतुर्थक की गणना कर सकता है।

'मध्य' : $q_{n}(0.5)=x_{(12)}+(0.5\cdot 25-12)\cdot (x_{(13)}-x_{(12)})=70+(0.5\cdot 25-12)\cdot (70-70)=70^{\circ }F$

पहला चतुर्थक : $q_{n}(0.25)=x_{(6)}+(0.25\cdot 25-6)\cdot (x_{(7)}-x_{(6)})=66+(0.25\cdot 25-6)\cdot (66-66)=66^{\circ }F$

तीसरा चतुर्थक : $q_{n}(0.75)=x_{(18)}+(0.75\cdot 25-18)\cdot (x_{(19)}-x_{(18)})=75+(0.75\cdot 25-18)\cdot (75-75)=75^{\circ }F$

विज़ुअलाइज़ेशन

चित्रा 7. सामान्य एन (0,1σ²) का बॉक्स-प्लॉट और प्रायिकता घनत्व फ़ंक्शन (पीडीएफ) जनसंख्या।

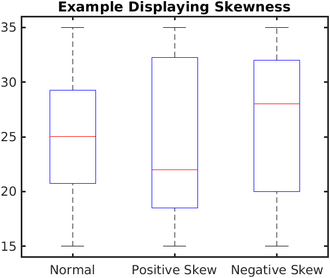
चूंकि बॉक्स प्लॉट हिस्टोग्राम या कर्नेल घनत्व अनुमान से अधिक प्राचीन लग सकते हैं। अतः उनके कई लाभ होते हैं। सबसे पहले, बॉक्स प्लॉट सांख्यिकीविदों को या अधिक डेटा सेटों पर त्वरित ग्राफिकल परीक्षा करने में सक्षम बनाता है। बॉक्स-प्लॉट भी कम जगह लेते हैं और इसलिए समानांतर में कई समूहों या डेटा के सेट के मध्य वितरण की तुलना करने के लिए विशेष रूप से उपयोगी होते हैं। (उदाहरण के लिए चित्र 1 देखें) अंत में, हिस्टोग्राम और कर्नेल घनत्व अनुमान की समग्र संरचना क्रमशः हिस्टोग्राम बॉक्स की संख्या और चौड़ाई तकनीकों और बैंडविड्थ की पसंद से दृढ़ता से प्रभावित हो सकती है।

चूंकि बॉक्स प्लॉट को देखने की तुलना में सांख्यिकीय वितरण को देखना अधिक सामान्य है। यह सामान्य एन (0, σ²) के लिए प्रायिकता घनत्व फ़ंक्शन (सैद्धांतिक हिस्टोग्राम) के विरुद्ध बॉक्स प्लॉट की तुलना करने के लिए उपयोगी हो सकता है। वितरण और सीधे उनकी विशेषताओं का निरीक्षण किया जाता है। (जैसा चित्र 7 में दिखाया गया है)।

चित्र 8. डेटा सेट के तिरछापन को प्रदर्शित करने वाले बॉक्स-प्लॉट

यह भी देखें

• बैगप्लॉट
• कैंडलस्टिक चार्ट
• डेटा और सूचना विज़ुअलाइज़ेशन
• अन्वेषणात्मक डेटा विश्लेषण
• फैन चार्ट (आँकड़े)
• पांच अंकों का सारांश
• कार्यात्मक बॉक्सप्लॉट
• सात अंकों का सारांश

अग्रिम पठन

• Tukey, John W. (1977). Exploratory Data Analysis. Addison-Wesley. ISBN 9780201076165.
• Benjamini, Y. (1988). "Opening the Box of a Boxplot". The American Statistician. 42 (4): 257–262. doi:10.2307/2685133. JSTOR 2685133.
• Rousseeuw, P. J.; Ruts, I.; Tukey, J. W. (1999). "The Bagplot: A Bivariate Boxplot". The American Statistician. 53 (4): 382–387. doi:10.2307/2686061. JSTOR 2686061.

बाहरी संबंध

• Beeswarm Boxplot - superimposing a frequency-jittered stripchart on top of a box plot