विटर्बी डिकोडर

एक विटरबी डिकोडर बिटस्ट्रीम को डिकोड करने के लिए विटरबी एल्गोरिदम का उपयोग करता है कन्वोल्यूशनल कोड या ट्रेलिस मॉड्यूलेशन का उपयोग करके एन्कोड किया गया।

एक विटरबी डिकोडर एक बिटस्ट्रीम को डिकोड करने के लिए विटरबी एल्गोरिदम का उपयोग करता है जिसे एक कनवल्शनल कोड या ट्रेलिस कोड का उपयोग करके एन्कोड किया गया है।

कनवल्शनल रूप से एन्कोडेड स्ट्रीम को डिकोड करने के लिए अन्य एल्गोरिदम हैं (उदाहरण के लिए, अनुक्रमिक डिकोडिंग या फैनो एल्गोरिदम)। विटर्बी एल्गोरिदम सबसे अधिक संसाधन-खपत वाला है, किंतु यह अधिकतम संभावना डिकोडिंग करता है। इसका उपयोग अधिकांशत: बाधा लंबाई k≤3 के साथ दृढ़ कोड को डिकोड करने के लिए किया जाता है, किंतु k=15 तक के मान व्यवहार में उपयोग किए जाते हैं।

विटरबी डिकोडिंग एंड्रयू जे. विटरबी द्वारा विकसित किया गया था और पेपर में प्रकाशित किया गया था Viterbi, A. (April 1967). "कनवल्शनल कोड के लिए त्रुटि सीमाएं और एक एसिम्प्टोटिक रूप से इष्टतम डिकोडिंग एल्गोरिदम". सूचना सिद्धांत पर आईईईई लेनदेन. 13 (2): 260–269. doi:10.1109/tit.1967.1054010.

विटरबी डिकोडर के हार्डवेयर (मॉडेम में) और सॉफ्टवेयर दोनों कार्यान्वयन हैं।

विटरबी डिकोडिंग का उपयोग पुनरावृत्त विटर्बी डिकोडिंग एल्गोरिदम में किया जाता है।

हार्डवेयर कार्यान्वयन

हार्डवेयर विटरबी डिकोडर को प्रयुक्त करने का एक सामान्य विधि

मूलभूत (छिद्रित नहीं) कोड के लिए एक हार्डवेयर विटरबी डिकोडर में समान्यत: निम्नलिखित प्रमुख ब्लॉक होते हैं:

• शाखा मीट्रिक इकाई (बीएमयू)
• पथ मीट्रिक इकाई (पीएमयू)
• ट्रेसबैक यूनिट (टीबीयू)

शाखा मीट्रिक इकाई (बीएमयू)

शाखा मीट्रिक इकाई का एक नमूना कार्यान्वयन

एक शाखा मीट्रिक इकाई का कार्य शाखा मीट्रिक की गणना करना है, जो कोड वर्णमाला में प्रत्येक संभावित प्रतीक और प्राप्त प्रतीक के बीच मानक दूरी है।

कठोर निर्णय और नरम निर्णय विटर्बी डिकोडर हैं। एक कठिन निर्णय विटर्बी डिकोडर अपने इनपुट पर एक सरल बिटस्ट्रीम प्राप्त करता है, और हैमिंग दूरी को मीट्रिक के रूप में उपयोग किया जाता है। एक नरम निर्णय विटर्बी डिकोडर एक बिटस्ट्रीम प्राप्त करता है जिसमें प्रत्येक प्राप्त प्रतीक की विश्वसनीयता के बारे में जानकारी होती है। उदाहरण के लिए, 3-बिट एन्कोडिंग में, इस विश्वसनीयता जानकारी को निम्नानुसार एन्कोड किया जा सकता है:

मान	अर्थ
000	प्रबल	0
001	अपेक्षाकृत प्रबल	0
010	अपेक्षाकृत दुर्बल	0
011	दुर्बल	0
100	दुर्बल	1
101	अपेक्षाकृत दुर्बल	1
110	अपेक्षाकृत प्रबल	1
111	प्रबल	1

परन्तु , यह विश्वसनीयता डेटा को एन्कोड करने का एकमात्र विधि नहीं है।

वर्गाकार यूक्लिडियन दूरी का उपयोग नरम निर्णय डिकोडर्स के लिए एक मीट्रिक के रूप में किया जाता है।

पथ मीट्रिक इकाई (पीएमयू)

एक विशिष्ट K=4 डिकोडर के लिए पथ मीट्रिक इकाई का एक नमूना कार्यान्वयन

एक पथ मीट्रिक इकाई $2^{K-1}$ पथों के लिए मीट्रिक प्राप्त करने के लिए शाखा मीट्रिक का सारांश प्रस्तुत करती है, जहां K कोड की बाधा लंबाई है, जिनमें से एक को अंततः इष्टतम के रूप में चुना जा सकता है। हर घड़ी यह $2^{K-1}$ निर्णय लेता है, जानबूझकर गैर-इष्टतम पथों को फेंक देता है। इन निर्णयों के परिणाम ट्रेसबैक इकाई की मेमोरी में लिखे जाते हैं।

पीएमयू के मुख्य तत्व एसीएस (ऐड-कंपेयर-सेलेक्ट) इकाइयां हैं। जिस तरह से वे आपस में जुड़े हुए हैं उसे एक विशिष्ट कोड के ट्रेलिस आरेख द्वारा परिभाषित किया गया है।

चूंकि शाखा आव्यूह सदैव $\geq 0$ होते हैं, इसलिए मीट्रिक काउंटरों को अतिप्रवाह से रोकने के लिए एक अतिरिक्त परिपथ (छवि पर नहीं दिखाया गया) होना चाहिए। एक वैकल्पिक विधि जो पथ मीट्रिक वृद्धि की निगरानी करने की आवश्यकता को समाप्त करती है, वह है पथ मीट्रिक को "रोल ओवर" करने की अनुमति देना; इस पद्धति का उपयोग करने के लिए यह सुनिश्चित करना आवश्यक है कि पथ मीट्रिक संचायक में "सर्वोत्तम" और "सबसे व्यर्थ " मानों को एक दूसरे के 2(n-1) के अंदर आने से रोकने के लिए पर्याप्त बिट्स हों। तुलना परिपथ मूलतः अपरिवर्तित है।

एसीएस इकाई का एक नमूना कार्यान्वयन

सर्वोत्तम पथ मीट्रिक की वृद्धि दर की निगरानी करके आने वाली बिट स्ट्रीम पर ध्वनि स्तर की निगरानी करना संभव है। ऐसा करने का एक सरल विधि यह है कि किसी एक स्थान या स्थिति की निगरानी की जाए और इसे संचायक की सीमा के अंदर चार अलग-अलग स्तरों से निकलते हुए देखा जाए। जैसे ही यह इनमें से प्रत्येक सीमा से ऊपर की ओर गुजरता है, एक काउंटर बढ़ जाता है जो आने वाले सिग्नल पर उपस्थित ध्वनि को दर्शाता है।

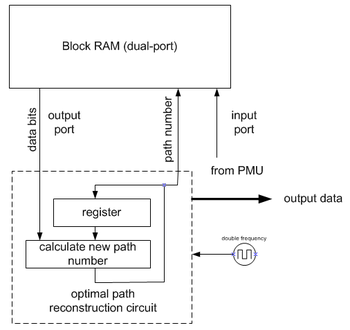
ट्रेसबैक यूनिट (टीबीयू)

ट्रेसबैक इकाई का एक नमूना कार्यान्वयन

बैक-ट्रेस इकाई पीएमयू द्वारा लिए गए निर्णयों से (लगभग) अधिकतम-संभावना पथ को पुनर्स्थापित करती है। चूँकि यह इसे विपरीत दिशा में करता है, एक विटरबी डिकोडर में सही क्रम का पुनर्निर्माण करने के लिए एक एफआईएलओ (फर्स्ट-इन-लास्ट-आउट) बफर सम्मिलित होता है।

ध्यान दें कि छवि पर दिखाए गए कार्यान्वयन के लिए दोहरी आवृत्ति की आवश्यकता होती है। कुछ विधियाँ हैं जो इस आवश्यकता को समाप्त कर देती हैं।

कार्यान्वयन मुद्दे

नरम निर्णय डिकोडिंग के लिए परिमाणीकरण

सॉफ्ट डिसीजन डिकोडिंग के लाभों का पूरी तरह से लाभ उठाने के लिए, किसी को इनपुट सिग्नल को ठीक से परिमाणित करने की आवश्यकता है। इष्टतम परिमाणीकरण क्षेत्र की चौड़ाई निम्नलिखित सूत्र द्वारा परिभाषित की गई है:

$\,\!T={\sqrt {\frac {N_{0}}{2^{k}}}},$

जहाँ $N_{0}$ एक ध्वनि शक्ति वर्णक्रमीय घनत्व है, और k नरम निर्णय के लिए बिट्स की एक संख्या है।

यूक्लिडियन मीट्रिक गणना

वर्ग मानदंड (गणित) ($\ell _{2}$) कोड वर्णमाला में प्राप्त और वास्तविक प्रतीकों के बीच की दूरी को एक रैखिक योग/अंतर रूप में और सरल बनाया जा सकता है, जो इसे कम कम्प्यूटेशनल रूप से गहन बनाता है।

1/2 कनवल्शनल कोड पर विचार करें, जो प्रत्येक इनपुट बिट (1 या 0) के लिए 2 बिट्स (00, 01, 10 या 11) उत्पन्न करता है। इन रिटर्न-टू-जीरो संकेतों को साथ में दिखाए गए नॉन-रिटर्न-टू-जीरो फॉर्म में अनुवादित किया गया है।

कोड वर्णमाला	वेक्टर मानचित्रण
00	+1, +1
01	+1, −1
10	−1, +1
11	−1, −1

प्रत्येक प्राप्त प्रतीक को वेक्टर रूप में v_r = {r₀, r₁} के रूप में दर्शाया जा सकता है, जहां r₀ और r₁ नरम निर्णय मान हैं, जिनके परिमाण प्राप्त वेक्टर, v_r की संयुक्त विश्वसनीयता को दर्शाते हैं।

इसी तरह, कोड वर्णमाला में प्रत्येक प्रतीक को वेक्टर v_i = {±1, ±1}. द्वारा दर्शाया जा सकता है

यूक्लिडियन दूरी मीट्रिक की वास्तविक गणना है:

$\,\!D=({\overrightarrow {v_{r}}}-{\overrightarrow {v_{i}}})^{2}={\overrightarrow {v_{r}}}^{2}-2{\overrightarrow {v_{r}}}{\overrightarrow {v_{i}}}+{\overrightarrow {v_{i}}}^{2}$

प्रत्येक वर्ग पद एक मानक दूरी है, जो प्रतीक की ऊर्जा को दर्शाता है। उदाहरण के लिए, प्रतीक 'v_i= {±1, ±1}' की ऊर्जा की गणना इस प्रकार की जा सकती है

$\,\!{\overrightarrow {v_{i}}}^{2}=(\pm 1)^{2}+(\pm 1)^{2}=2$

इस प्रकार, कोड वर्णमाला में सभी प्रतीकों का ऊर्जा शब्द स्थिर है ((सामान्यीकृत) मान 2 पर)।

ऐड-तुलना-चयन (एसीएस) ऑपरेशन प्राप्त प्रतीक के बीच मीट्रिक दूरी की तुलना करता है ||v_r|| और कोड वर्णमाला में कोई भी 2 प्रतीक जिनके पथ संबंधित सलाखें में एक नोड पर विलीन हो जाते हैं, ||v_i⁽⁰⁾|| and ||v_i⁽¹⁾||. यह तुलना करने के समान है

$\,\!D_{0}={\overrightarrow {v_{r}}}^{2}-2{\overrightarrow {v_{r}}}{\overrightarrow {v_{i}^{0}}}+{\overrightarrow {v_{i}^{0}}}^{2}$

और

$\,\!D_{1}={\overrightarrow {v_{r}}}^{2}-2{\overrightarrow {v_{r}}}{\overrightarrow {v_{i}^{1}}}+{\overrightarrow {v_{i}^{1}}}^{2}$

किंतु , ऊपर से हम जानते हैं कि v_i की ऊर्जा स्थिर (2 के (सामान्यीकृत) मान के समान ) है, और v_r की ऊर्जा दोनों स्थितियों में समान है। यह 2 (मध्य) डॉट उत्पाद नियमों के बीच मिनिमा फलन की तुलना को कम करता है,

$\,\!\min(-2{\overrightarrow {v_{r}}}{\overrightarrow {v_{i}^{0}}},-2{\overrightarrow {v_{r}}}{\overrightarrow {v_{i}^{1}}})=\max({\overrightarrow {v_{r}}}{\overrightarrow {v_{i}^{0}}},{\overrightarrow {v_{r}}}{\overrightarrow {v_{i}^{1}}})$

चूँकि ऋणात्मक संख्याओं पर न्यूनतम संक्रिया को धनात्मक राशियों पर समतुल्य अधिकतम संक्रिया के रूप में समझा जा सकता है।

प्रत्येक डॉट उत्पाद शब्द को इस प्रकार विस्तारित किया जा सकता है

$\,\!\max(\pm r_{0}\pm r_{1},\pm r_{0}\pm r_{1})$

जहां, प्रत्येक पद के चिह्न प्रतीकों, v_i⁽⁰⁾ and v_i⁽¹⁾ पर निर्भर करते हैं, जिनकी तुलना की जा रही है। इस प्रकार, शाखा मीट्रिक की गणना करने के लिए वर्गित यूक्लिडियन मीट्रिक दूरी की गणना एक सरल जोड़/घटाव ऑपरेशन के साथ की जा सकती है।

ट्रेसबैक

ट्रेसबैक के लिए सामान्य दृष्टिकोण बाधा लंबाई (5 (के - 1)) से पांच गुना तक पथ आव्यूह जमा करना है, सबसे बड़ी संचित निवेश के साथ नोड खोजना , और इस नोड से ट्रेसबैक प्रारंभ करना है।

कन्वेन्शनल कोड की मेमोरी (बाधा लंबाई K-1) की पांच गुना की ट्रंकेशन गहराई का समान्यत: उपयोग किया जाने वाला वलय का नियम केवल दर 1/2 कोड के लिए स्पष्ट है। एक इच्छित दर के लिए, स्पष्ट नियम 2.5(K - 1)/(1−r) है जहां r कोड दर है।

चूँकि , उस नोड की गणना करना जिसने सबसे बड़ी निवेश (या तो सबसे बड़ी या सबसे छोटी अभिन्न पथ मीट्रिक) जमा की है, इसमें कई (समान्यत: 2^K-1) की मैक्सिमा या मिनिमा का पता लगाना सम्मिलित है) नंबर, जिन्हें एंबेडेड हार्डवेयर सिस्टम पर प्रयुक्त करने में समय लग सकता है।

अधिकांश संचार प्रणालियाँ विटरबी डिकोडिंग का उपयोग करती हैं, जिसमें निश्चित आकार के डेटा पैकेट सम्मिलित होते हैं, जिसमें डेटा पैकेट की प्रारंभ में या/और अंत में एक निश्चित अंश /बाइट पैटर्न होता है। संदर्भ के रूप में ज्ञात बिट/बाइट पैटर्न का उपयोग करके, प्रारंभ नोड को एक निश्चित मान पर सेट किया जा सकता है, जिससे ट्रेसबैक के समय एक आदर्श अधिकतम संभावना पथ प्राप्त होता है।

सीमाएँ

विटरबी डिकोडर के भौतिक कार्यान्वयन से इनपुट सिग्नल, शाखा और पथ आव्यूह के परिमाणीकरण (सिग्नल प्रोसेसिंग), और सीमित ट्रेसबैक लंबाई के कारण स्पष्ट अधिकतम-संभावना स्ट्रीम नहीं मिलेगी। व्यावहारिक कार्यान्वयन आदर्श के 1 डीबी के अंदर होता है।

विटर्बी डिकोडर के आउटपुट में, जब एक एडिटिव गॉसियन चैनल द्वारा क्षतिग्रस्त संदेश को डिकोड किया जाता है, तो त्रुटियों को एरर बर्स्ट में समूहीकृत किया जाता है।

हैमिंग कोड या अकेले एकल-त्रुटि-सुधार करने वाले कोड ऐसे विस्फोटों को ठीक नहीं कर सकते हैं, इसलिए या तो कन्वेन्शनल कोड और विटरबी डिकोडर को त्रुटियों को स्वीकार्य दर तक लाने के लिए पर्याप्त शक्तिशाली डिज़ाइन किया जाना चाहिए, या बर्स्ट त्रुटि-सुधार करने वाले कोड का उपयोग किया जाना चाहिए।

छिद्रित कोड

पंचर कोड कोड का एक हार्डवेयर विटरबी डिकोडर समान्यत: इस तरह से कार्यान्वित किया जाता है:

• एक डिपंक्चरर, जो इनपुट स्ट्रीम को उस स्ट्रीम में परिवर्तन कर देता है जो मूल (गैर पंचर) स्ट्रीम की तरह दिखती है, जहां बिट्स मिटाए गए स्थानों पर ERASE निशान होते हैं।
• एक मूलभूत विटरबी डिकोडर जो इन ERASE चिह्नों को समझता है (अर्थात, शाखा मीट्रिक गणना के लिए उनका उपयोग नहीं कर रहा है)।

सॉफ्टवेयर कार्यान्वयन

Main article: विटर्बी एल्गोरिदम

सबसे अधिक समय लेने वाले ऑपरेशनों में से एक एसीएस बटरफ्लाई है, जिसे समान्यत: डिकोडिंग समय को तेज करने के लिए असेंबली लैंग्वेज और उपयुक्त निर्देश सेट एक्सटेंशन (जैसे व्यर्थ 2) का उपयोग करके कार्यान्वित किया जाता है।

अनुप्रयोग

विटरबी डिकोडिंग एल्गोरिदम का व्यापक रूप से निम्नलिखित क्षेत्रों में उपयोग किया जाता है:

• रेडियो संचार: डिजिटल टीवी (एटीएससी, क्यूएएम (टेलीविजन), डीवीबी-टी, आदि), रेडियो रिले लिंक, उपग्रह संचार, शौकिया रेडियो के लिए सरलता से1 डिजिटल मोड है।
• डिकोडिंग ट्रेलिस-कोडित मॉड्यूलेशन (टीसीएम), 3 किलोहर्ट्ज़-बैंडविड्थ एनालॉग टेलीफोन लाइनों से उच्च वर्णक्रमीय दक्षता को निचोड़ने के लिए टेलीफोन-लाइन मॉडेम में उपयोग की जाने वाली तकनीक है।
• कंप्यूटर स्टोरेज डिवाइस जैसे हार्ड डिस्क ड्राइव है।
• स्वचालित वाक् पहचान

बाहरी संबंध

• Forney, G. David, Jr (29 Apr 2005). "The Viterbi Algorithm: A Personal History". arXiv:cs/0504020.{{cite arXiv}}: CS1 maint: multiple names: authors list (link)
• Details on Viterbi decoding, as well as a bibliography.
• Viterbi algorithm explanation with the focus on hardware implementation issues.
• r=1/6 k=15 coding for the Cassini mission to Saturn.
• Online Generator of optimized software Viterbi decoders (GPL).
• GPL Viterbi decoder software for four standard codes.
• Description of a k=24 Viterbi decoder, believed to be the largest ever in practical use.
• Generic Viterbi decoder hardware (GPL).