शून्य-ज्ञान प्रमाण

"जेडकेपी" redirects here. For रूस में हवाई अड्डा, see ज़िर्यंका हवाई अड्डा. For अन्य उपयोग, see शून्य ज्ञान.

क्रिप्टोग्राफी में, शून्य-ज्ञान प्रमाण या शून्य-ज्ञान प्रोटोकॉल ऐसी विधि है जिसके द्वारा एक पक्ष (प्रस्तावकर्ता) दूसरे पक्ष (सत्यापनकर्ता) को यह सिद्ध कर सकता है कि दिया गया कथन सत्य है, जबकि प्रस्तावक इसके अतिरिक्त कोई अतिरिक्त जानकारी देने से बचता है। तथ्य यह है कि कथन वास्तव में सत्य है। शून्य-ज्ञान प्रमाणों का सार यह है कि यह सिद्ध करना तुच्छ है कि किसी व्यक्ति के पास कुछ सूचनाओं का ज्ञान है, केवल उसे प्रकट करके; चुनौती स्वयं जानकारी या किसी अतिरिक्त जानकारी का विवरण दिये बिना इस प्रकार के कब्जे को सिद्ध करना है।

यदि किसी कथन को सिद्ध करने के लिए यह आवश्यक है कि प्रस्तावक के पास कुछ गुप्त जानकारी हो, तो सत्यापनकर्ता गुप्त जानकारी के बिना किसी अन्य को कथन को सिद्ध करने में सक्षम नहीं होगा। सिद्ध किए जा रहे कथन में यह अभिकथन सम्मिलित होना चाहिए कि कहावत को ऐसा ज्ञान है, किन्तु बिना स्वयं अभिकथन में ज्ञान को सम्मिलित किए या प्रसारित किए। अन्यथा, कथन शून्य-ज्ञान में सिद्ध नहीं होगा क्योंकि यह सत्यापनकर्ता को प्रोटोकॉल के अंत तक कथन के बारे में अतिरिक्त जानकारी प्रदान करता है। ज्ञान का शून्य-ज्ञान प्रमाण विशेष स्थिति है जब कथन में केवल इस तथ्य का समावेश होता है कि कहावत में गुप्त जानकारी होती है।

इंटरएक्टिव शून्य-ज्ञान प्रमाणों को व्यक्ति (या कंप्यूटर प्रणाली) के बीच उनके ज्ञान को सिद्ध करने और प्रमाण को मान्य करने वाले व्यक्ति के बीच बातचीत की आवश्यकता होती है। गैर-संवादात्मक शून्य-ज्ञान प्रमाण किसी भी संवादात्मक योजना से फिएट-शमीर अनुमानी पर विश्वाश करके बनाया जा सकता है, जो आज इस प्रकार के प्रमाणों का सबसे सामान्य तात्कालिकता है। चूंकि, प्रमाण की वैधता कम्प्यूटेशनल मान्यताओं (सामान्यतः आदर्श क्रिप्टोग्राफ़िक हैश फ़ंक्शन की धारणा) पर निर्भर करती है।

ज्ञान के शून्य-ज्ञान प्रमाण को प्रायुक्त करने वाला प्रोटोकॉल अधिकांश प्रतिलिपि के रूप में प्रस्तुत किया जाता है जहां समर्थक सत्यापनकर्ता से इंटरैक्टिव इनपुट का जवाब देता है। यह इंटरएक्टिव इनपुट सामान्यतः या से अधिक चुनौतियों के रूप में होता है, जैसे कि प्रस्तावक की प्रतिक्रियाएँ सत्यापनकर्ता को विश्वास दिलाती हैं कि यदि और केवल यदि कथन सत्य है, अर्थात, यदि प्रस्तावक के पास दावा किया गया ज्ञान है। यदि ऐसा नहीं होता, तो सत्यापनकर्ता प्रोटोकॉल के निष्पादन को रिकॉर्ड कर सकता था और किसी और को यह विश्वास दिलाने के लिए इसे फिर से चला सकता था कि उनके पास गुप्त जानकारी है। नई पार्टी की स्वीकृति या तो उचित है क्योंकि रिप्लेयर के पास जानकारी (जिसका अर्थ है कि प्रोटोकॉल लीक हुई जानकारी है, और इस प्रकार, शून्य-ज्ञान में सिद्ध नहीं है) है, या स्वीकृति नकली है, अर्थात, किसी ऐसे व्यक्ति से स्वीकार किया गया था जो नहीं करता है वास्तव में जानकारी रखते हैं।

सार उदाहरण

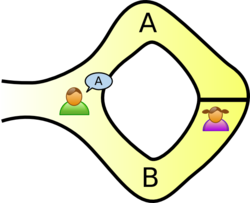
अली बाबा गुफा

Peggy randomly takes either path A or B, while Victor waits outside

Victor chooses an exit path

Peggy reliably appears at the exit Victor names

शून्य-ज्ञान प्रमाण के मौलिक विचारों को प्रस्तुत करने वाली प्रसिद्ध कहानी है, जो पहली बार 1990 में जीन-जैक्स क्विस्क्वाटर और अन्य लोगों द्वारा अपने पेपर हाउ टू एक्सप्लेन जीरो-नॉलेज प्रोटोकॉल टू योर चिल्ड्रन में प्रकाशित हुई थी। दो पक्षों को शून्य-ज्ञान प्रमाण में पैगी (बयान का समर्थक) और विक्टर (बयान का सत्यापनकर्ता) के रूप में लेबल करना सामान्य बात है।

इस कहानी में पैगी ने गुफा में जादुई दरवाजा खोलने के लिए उपयोग किए गए गुप्त शब्द का विवरण किया है। गुफा अंगूठी के आकार की है, जिसके तरफ प्रवेश द्वार है और विपरीत दिशा में जादू का दरवाजा अवरुद्ध है। विक्टर जानना चाहता है कि क्या पैगी गुप्त शब्द जानती है; किन्तु पैगी, बहुत ही निजी व्यक्ति होने से संबंधित, अपने ज्ञान (गुप्त शब्द) को विक्टर को प्रकट नहीं करना चाहती या अपने ज्ञान के तथ्य को सामान्य रूप से संसार के सामने प्रकट नहीं करना चाहती।

वे A और B के प्रवेश द्वार से बाएं और दाएं रास्तों को लेबल करते हैं। सबसे पहले, विक्टर गुफा के बाहर इंतजार करता है क्योंकि पैगी अंदर जाती है। पेगी या तो रास्ता ए या बी लेती है; विक्टर को यह देखने की अनुमति नहीं है कि वह कौन सा रास्ता अपनाती है। फिर, विक्टर गुफा में प्रवेश करता है और उस रास्ते का नाम चिल्लाता है जिसे वह चाहता है कि वह वापसी के लिए A या B का उपयोग करे, यादृच्छिक रूप से चुना गया। परन्तु वह वास्तव में जादू शब्द जानती हो, यह आसान है: यदि आवश्यक हो, तो वह दरवाजा खोलती है, और वांछित पथ के साथ वापस आती है।

चूँकि, मान लीजिए कि वह शब्द नहीं जानती थी। तब, वह नामित पथ से तभी वापस लौट पाएगी जब विक्टर उसी पथ का नाम बताए जिससे उसने प्रवेश किया था। चूंकि विक्टर यादृच्छिक रूप से A या B को चुनेगी, इसलिए उसके पास सही अनुमान लगाने का 50% मौका होगा। यदि वे इस योजना को कई बार दोहराते हैं, तो कहें कि लगातार 20 बार, विक्टर के सभी अनुरोधों का सफलतापूर्वक अनुमान लगाने की उनकी संभावना बहुत कम (2²⁰ में 1, या लगभग एक मिलियन में 1) हो जाएगी।

इस प्रकार, यदि पैगी बार-बार बाहर निकलने वाले विक्टर के नामों पर प्रकट होती है, तो वह निष्कर्ष निकाल सकता है कि यह बेहद संभव है कि पेगी वास्तव में गुप्त शब्द को जानती है।

तीसरे पक्ष के पर्यवेक्षकों के संबंध में तरफ ध्यान दें: तथापि विक्टर ने छिपा हुआ कैमरा पहना हो जो पूरे लेनदेन को रिकॉर्ड करता है, केवल चीज जो कैमरा रिकॉर्ड करेगा, स्थिति में विक्टर ए चिल्ला रहा है! और पेगी ए या दूसरे स्थिति में विक्टर चिल्लाते हुए B! और पैगी बी पर दिखाई दे रही है। इस प्रकार की रिकॉर्डिंग किसी भी दो लोगों के नकली (केवल यह आवश्यक है कि पैगी और विक्टर ए और बी के अनुक्रम पर पहले से सहमत हों कि विक्टर चिल्लाएगा) होने के लिए तुच्छ होगी। इस प्रकार की रिकॉर्डिंग निश्चित रूप से मूल प्रतिभागियों को छोड़कर किसी के लिए भी आश्वस्त नहीं होगी। वास्तव में, यहां तक ​​कि व्यक्ति जो मूल प्रयोग में पर्यवेक्षक के रूप में उपस्थित था, वह असंबद्ध होगा, क्योंकि विक्टर और पैगी ने पूरे प्रयोग को प्रारंभ से अंत तक ऑर्केस्ट्रेट किया होगा।

आगे ध्यान दें कि यदि विक्टर कैमरे पर सिक्के को फ़्लिप करके अपने A और B को चुनता है, तो यह प्रोटोकॉल अपनी शून्य-ज्ञान संपत्ति खो देता है; ऑन-कैमरा सिक्का फ्लिप संभवतः बाद में रिकॉर्डिंग देखने वाले किसी भी व्यक्ति के लिए आश्वस्त होगा। इस प्रकार, चूंकि यह विक्टर के लिए गुप्त शब्द प्रकट नहीं करता है, यह विक्टर के लिए सामान्य रूप से संसार को समझाने के लिए संभव बनाता है कि पैगी के पास वह ज्ञान है - पेगी की घोषित इच्छाओं के विपरीत। चूंकि, डिजिटल क्रिप्टोग्राफी सामान्यतः छद्म-यादृच्छिक संख्या जनरेटर पर विश्वाश करके सिक्कों को फ़्लिप करती है, जो सिक्के के समान है, जिसमें सिर और पूंछ का निश्चित पैटर्न होता है, जिसे केवल सिक्के के मालिक के लिए जाना जाता है। यदि विक्टर का सिक्का इस प्रकार से व्यवहार करता है, तो फिर से विक्टर और पैगी के लिए यह संभव होगा कि उन्होंने प्रयोग को विफल कर दिया हो, इसलिए छद्म-यादृच्छिक संख्या जनरेटर का उपयोग करने से पेगी के ज्ञान को उसी प्रकार से संसार में प्रकट नहीं किया जाएगा, जिस प्रकार से फ़्लिप किए गए सिक्के का उपयोग किया जाएगा।

ध्यान दें कि पैगी विक्टर को यह सिद्ध कर सकती है कि वह एक ही परीक्षण में उसे बताए बिना जादुई शब्द जानती है। यदि विक्टर और पेगी दोनों साथ गुफा के प्रारंभ पर जाते हैं, तो विक्टर A के माध्यम से पेगी को अंदर जाते हुए और B के माध्यम से बाहर आते हुए देख सकता है। यह निश्चित रूप से सिद्ध होगा कि विक्टर को जादू शब्द का विवरण किए बिना पैगी जादू शब्द जानता है। चूँकि, ऐसा प्रमाण किसी तीसरे पक्ष द्वारा देखा जा सकता है, या विक्टर द्वारा रिकॉर्ड किया जा सकता है और ऐसा प्रमाण किसी के लिए भी यथार्थपूर्ण होगा। दूसरे शब्दों में, पेगी विक्टर के साथ मिलीभगत का दावा करके इस प्रकार के प्रमाण का खंडन नहीं कर सकती थी, और इसलिए वह अब इस बात पर नियंत्रण नहीं रखती कि कौन उसके ज्ञान के बारे में जानता है।

दो गेंदें और वर्णान्ध दोस्त

कल्पना करें कि आपका दोस्त विक्टर लाल-हरे रंग का अंधापन है। वर्णान्ध (जबकि आप नहीं हैं) और आपके पास दो गेंदें हैं: लाल और हरी, किन्तु अन्यथा समान। विक्टर को गेंदें बिल्कुल जैसी लगती हैं। विक्टर को संदेह है कि गेंदें वास्तव में भिन्न-भिन्न हैं। आप विक्टर को यह सिद्ध करना चाहते हैं कि गेंदें वास्तव में भिन्न-भिन्न रंग की हैं, किन्तु कुछ और नहीं। विशेष रूप से, आप यह प्रकट नहीं करना चाहते हैं कि कौन सी गेंद लाल है और कौन सी हरी है।

यहाँ प्रमाण प्रणाली है। आप दो गेंदों को विक्टर को देते हैं और वह उन्हें अपनी पीठ के पीछे रखता है। इसके बाद, वह गेंदों में से लेता है और उसे अपनी पीठ के पीछे से बाहर लाता है और प्रदर्शित करता है। फिर वह इसे फिर से अपनी पीठ के पीछे रखता है और फिर दो गेंदों में से केवल को प्रकट करने का विकल्प चुनता है, दोनों में से को समान संभावना के साथ यादृच्छिक रूप से चुनता है। वह आपसे पूछेगा, क्या मैंने गेंद को स्विच किया? यह पूरी प्रक्रिया तब जितनी बार आवश्यक हो दोहराई जाती है।

गेंदों के रंगों को देखकर, आप निश्चित रूप से निश्चित रूप से कह सकते हैं कि उसने उन्हें बदल दिया या नहीं। दूसरी ओर, यदि गेंदें ही रंग की थीं और इसलिए भिन्न-भिन्न नहीं थीं, तो कोई विधि नहीं है कि आप 50% से अधिक प्रायिकता के साथ सही विधि से अनुमान लगा सकें।

चूँकि संभावना है कि आप प्रत्येक स्विच/गैर-स्विच की पहचान करने में यादृच्छिक रूप से सफल होंगे, 50% है, 'सभी' स्विच/गैर-स्विच पर यादृच्छिक रूप से सफल होने की संभावना शून्य (ध्वनि) तक पहुंचती है। यदि आप और आपका मित्र इस प्रमाण को कई बार (जैसे 20 बार) दोहराते हैं, तो आपके मित्र को आश्वस्त (पूर्णता) हो जाना चाहिए कि गेंदें वास्तव में भिन्न-भिन्न रंग की हैं।

उपरोक्त प्रमाण शून्य-ज्ञान है क्योंकि आपका मित्र कभी नहीं सीखता कि कौन सी गेंद हरी है और कौन सी लाल; वास्तव में, उन्हें इस बारे में कोई ज्ञान नहीं है कि गेंदों को कैसे अलग किया जाए।

परिभाषा

किसी कथन के शून्य-ज्ञान प्रमाण को तीन गुणों को पूरा करना चाहिए:

1. पूर्णता: यदि कथन सत्य है, तो ईमानदार सत्यापनकर्ता (अर्थात, प्रोटोकॉल का ठीक से पालन करने वाला) ईमानदार समर्थक द्वारा इस तथ्य के प्रति आश्वस्त होगा।
2. सुदृढ़ता: यदि कथन झूठा है, तो कोई भी धोखाधड़ी करने वाला ईमानदार सत्यापनकर्ता को विश्वास नहीं दिला सकता है कि यह सत्य है, अतिरिक्त कुछ छोटी संभावना के।
3. शून्य-ज्ञान: यदि कथन सत्य है, तो कोई भी सत्यापनकर्ता इस तथ्य के अलावा और कुछ नहीं सीखता है कि कथन सत्य है। दूसरे शब्दों में, केवल कथन को जानना (रहस्य नहीं) एक परिदृश्य की कल्पना करने के लिए पर्याप्त है जो यह दर्शाता है कि नीतिवचन रहस्य जानता है। यह दिखाते हुए इसे औपचारिक रूप दिया गया है कि प्रत्येक सत्यापनकर्ता के पास कुछ सिम्युलेटर है, जो केवल सिद्ध किए जाने वाले कथन (और प्रोवर तक पहुंच नहीं) को देखते हुए, एक प्रतिलेख उत्पन्न कर सकता है जो एक ईमानदार कहावत और प्रश्न में सत्यापनकर्ता के बीच एक बातचीत "जैसा दिखता है"।

इनमें से पहले दो अधिक सामान्य इंटरैक्टिव प्रमाण प्रणाली के गुण हैं। तीसरा वह है जो प्रमाण को शून्य-ज्ञान बनाता है।

शून्य-ज्ञान प्रमाण शब्द के गणितीय अर्थ में प्रमाण नहीं हैं क्योंकि कुछ छोटी संभावना है, ध्वनि त्रुटि, कि धोखा देने वाला झूठे बयान के सत्यापनकर्ता को समझाने में सक्षम होगा। दूसरे शब्दों में, शून्य-ज्ञान प्रमाण नियतात्मक प्रमाण के अतिरिक्त संभाव्य प्रमाण हैं। चूँकि, साउंडनेस त्रुटि को नगण्य रूप से छोटे मानों (उदाहरण के लिए सौ या हज़ार बाइनरी निर्णयों पर सही विधि से अनुमान लगाने में क्रमशः 1/2^100 या 1/2^1000 होता है। जैसे-जैसे बिट्स की संख्या बढ़ती है, साउंडनेस त्रुटि शून्य की ओर घटता है) तक कम करने की विधियाँ हैं।

शून्य-ज्ञान की औपचारिक परिभाषा में कुछ कम्प्यूटेशनल मॉडल का उपयोग करना पड़ता है, सबसे सामान्य एक ट्यूरिंग मशीन है। बता दें कि $P$, $V$, और $S$ ट्यूरिंग मशीन हैं। एक भाषा $L$ के लिये$(P,V)$ के साथ एक इंटरैक्टिव प्रमाण प्रणाली शून्य-ज्ञान है यदि किसी संभाव्य बहुपद समय (पीपीटी) सत्यापनकर्ता ${\hat {V}}$ के लिए पीपीटी सिम्युलेटर $S$ उपस्थित है जैसे कि

$\forall x\in L,z\in \{0,1\}^{*},\operatorname {View} _{\hat {V}}\left[P(x)\leftrightarrow {\hat {V}}(x,z)\right]=S(x,z)$

जहाँ $\operatorname {View} _{\hat {V}}\left[P(x)\leftrightarrow {\hat {V}}(x,z)\right]$ $P(x)$ और ${\hat {V}}(x,z)$ के बीच की बातचीत का रिकॉर्ड है। कहावत $P$ असीमित संगणना शक्ति के रूप में तैयार किया गया है (व्यवहार में, $P$ सामान्यतः संभाव्य ट्यूरिंग मशीन है)। सहज रूप से, परिभाषा बताती है कि इंटरैक्टिव प्रमाण प्रणाली $(P,V)$ किसी सत्यापनकर्ता ${\hat {V}}$ के लिए शून्य-ज्ञान है कुशल सिम्युलेटर $S$ (${\hat {V}}$ पर निर्भर करते हुए) उपस्थित है जो $P$ और ${\hat {V}}$ किसी दिए गए इनपुट पर बीच की बातचीत को पुन: उत्पन्न कर सकता है। परिभाषा में सहायक स्ट्रिंग $z$ "पूर्व ज्ञान" (${\hat {V}}$ के यादृच्छिक सिक्कों सहित) की भूमिका निभाता है। परिभाषा का तात्पर्य है कि ${\hat {V}}$ $P$ के साथ अपनी बातचीत से जानकारी निकालने के लिए किसी पूर्व ज्ञान स्ट्रिंग $z$ का उपयोग नहीं कर सकता है, क्योंकि यदि $S$ को भी यह पूर्व ज्ञान दिया जाता है तो यह ${\hat {V}}$ और $P$ के बीच पहले की प्रकार बातचीत को पुन: उत्पन्न कर सकता है।

दी गई परिभाषा पूर्ण शून्य-ज्ञान की है। कम्प्यूटेशनल शून्य-ज्ञान सत्यापनकर्ता के विचारों की आवश्यकता के द्वारा प्राप्त किया जाता है ${\hat {V}}$ और सिम्युलेटर केवल कम्प्यूटेशनल अप्रभेद्यता है, सहायक स्ट्रिंग दी गई है।

व्यावहारिक उदाहरण

किसी दिए गए मान का असतत लॉग

हम इन विचारों को अधिक यथार्थवादी क्रिप्टोग्राफी एप्लिकेशन पर प्रायुक्त कर सकते हैं। पैगी विक्टर को यह सिद्ध करना चाहती है कि वह दिए गए समूह सिद्धांत में दिए गए मान के असतत लघुगणक को जानती है।

उदाहरण के लिए, एक मान $y$, एक बड़ा अभाज्य संख्या $p$ और एक जनरेटर $g$ दिया गया है, वह यह सिद्ध करना चाहती है कि वह एक मान $x$ जानती है जैसे कि $g^{x}{\bmod {p}}=y$, बिना $x$ प्रकट किए। वास्तव में, $x$ के ज्ञान को पहचान के प्रमाण के रूप में उपयोग किया जा सकता है, जिसमें पैगी को ऐसा ज्ञान हो सकता है क्योंकि उसने एक यादृच्छिक मान $x$ चुना है जिसे उसने किसी को प्रकट नहीं किया, $y=g^{x}{\bmod {p}}$ की गणना की और सभी संभावितों को $y$ का मान वितरित किया सत्यापनकर्ता, जैसे कि बाद के समय में, $x$ का ज्ञान सिद्ध करना पैगी के रूप में पहचान सिद्ध करने के बराबर है।

प्रोटोकॉल निम्नानुसार आगे बढ़ता है: प्रत्येक चरण में, पैगी यादृच्छिक संख्या $r$ उत्पन्न करती है, $C=g^{r}{\bmod {p}}$ की गणना करती है और विक्टर को इसका विवरण करता है। $C$ प्राप्त करने के बाद, विक्टर यादृच्छिक विधि से निम्नलिखित दो अनुरोधों में से जारी करता है: वह या तो अनुरोध करता है कि पैगी $r$ के मान का विवरण करे, या $(x+r){\bmod {(p-1)}}$ के मान को प्रकाशित करे। किसी भी उत्तर के साथ, पैगी केवल यादृच्छिक मान का विवरण कर रही है, इसलिए प्रोटोकॉल के चरण के सही निष्पादन से कोई जानकारी प्रकट नहीं होती है।

विक्टर या तो उत्तर सत्यापित कर सकता है; यदि उसने $r$ का अनुरोध किया, वह फिर $g^{r}{\bmod {p}}$ की गणना कर सकता है और सत्यापित करें कि यह $C$ से मेल खाता है। यदि उसने $(x+r){\bmod {(p-1)}}$ अनुरोध किया, वह $C$ की पुष्टि कर सकता है इसके अनुरूप है, कंप्यूटिंग द्वारा $g^{(x+r){\bmod {(p-1)}}}{\bmod {p}}$ और यह सत्यापित करना कि यह $(C\cdot y){\bmod {p}}$ से मेल खाता है। यदि पैगी वास्तव में $x$ मान जानती है, वह विक्टर की संभावित चुनौतियों में से किसी का जवाब दे सकती है।

यदि पेगी जानती थी या अनुमान लगा सकती थी कि विक्टर किस चुनौती को जारी करने जा रहा है, तो वह आसानी से विक्टर को धोखा दे सकती है और उसे विश्वास दिला सकती है कि वह जानती है $x$ जब वह नहीं करती: यदि वह जानती है कि विक्टर अनुरोध करने जा रहा है $r$, तो वह सामान्य रूप से आगे बढ़ती है: वह चुनती है $r$, गणना करता है $C=g^{r}{\bmod {p}}$ और प्रकट करता है $C$ विक्टर को; वह विक्टर की चुनौती का जवाब दे सकेगी। दूसरी ओर, यदि वह जानती है कि विक्टर अनुरोध करेगा $(x+r){\bmod {(p-1)}}$, फिर वह यादृच्छिक मान चुनती है $r'$, गणना करता है $C'=g^{r'}\cdot \left(g^{x}\right)^{-1}{\bmod {p}}$, और प्रकट करता है $C'$ विक्टर के मान के रूप में $C$ कि वह उम्मीद कर रहा है। जब विक्टर उसे प्रकट करने की चुनौती देता है $(x+r){\bmod {(p-1)}}$, वह प्रकट करती है $r'$, जिसके लिए विक्टर निरंतरता की पुष्टि करेगा, क्योंकि वह बदले में गणना करेगा $g^{r'}{\bmod {p}}$, जो मेल खाता है $C'\cdot y$, चूंकि पैगी को मॉड्यूलर गुणक व्युत्क्रम से गुणा किया जाता है $y$.

चूंकि, यदि उपरोक्त परिदृश्यों में से किसी में विक्टर अपनी अपेक्षा के अतिरिक्त चुनौती जारी करता है और जिसके लिए उसने परिणाम तैयार किया है, तो वह असतत लॉग को हल करने की अक्षमता की धारणा के तहत चुनौती का जवाब देने में असमर्थ होगा। इस समूह। यदि उसने उठाया $r$ और विवरण किया $C=g^{r}{\bmod {p}}$, तो वह वैध उत्पादन करने में असमर्थ होगी $(x+r){\bmod {(p-1)}}$ यह विक्टर के सत्यापन को पास करेगा, यह देखते हुए कि वह नहीं जानती $x$. और यदि उसने कोई मान चुना $r'$ के रूप में प्रस्तुत करता है $(x+r){\bmod {(p-1)}}$, तो उसे अपने द्वारा बताए गए मान के असतत लॉग के साथ जवाब देना होगा – किन्तु पैगी इस असतत लॉग को नहीं जानती है, क्योंकि उसके द्वारा बताए गए मान सी को अंकगणित के माध्यम से ज्ञात मूल्यों के साथ प्राप्त किया गया था, न कि ज्ञात प्रतिपादक के साथ शक्ति की गणना करके।

इस प्रकार, धोखा देने वाले खिलाड़ी के पास चरण में सफलतापूर्वक धोखा देने की 0.5 संभावना होती है। बड़ी संख्या में राउंड को परिणाम देकर, धोखा देने वाले के सफल होने की संभावना को स्वैच्छिक विधि से कम किया जा सकता है।

संक्षिप्त सारांश

पैगी एक्स का मान जानती है (उदाहरण के लिए उसका पासवर्ड)।

1. पैगी और विक्टर फ़ील्ड $\mathbb {Z} _{p}$ के गुणात्मक समूह के प्राइम $p$ और जनरेटर $g$ पर सहमत हैं।
2. पैगी मान $y=g^{x}{\bmod {p}}$ की गणना करता है और विक्टर को मान स्थानांतरित करता है।
3. निम्नलिखित दो चरणों को (बड़ी) संख्या में दोहराया जाता है।
   1. पैगी बार-बार यादृच्छिक मान $r\in U[0,p-2]$ चुनती है और $C=g^{r}{\bmod {p}}$ की गणना करता है। ववह मान $C$ को विक्टर को हस्तांतरित करती है।
   2. विक्टर ने पैगी को या तो मान $(x+r){\bmod {(p-1)}}$ या मान $r$ की गणना करने और स्थानांतरित करने के लिए कहा। पहले स्थिति में विक्टर $(C\cdot y){\bmod {p}}\equiv g^{(x+r){\bmod {(p-1)}}}{\bmod {p}}$ की पुष्टि करता है। दूसरे स्थिति में वह $C\equiv g^{r}{\bmod {p}}$ की पुष्टि करता है।

मान $(x+r){\bmod {(}}p-1)$ के एन्क्रिप्टेड मान $x{\bmod {(}}p-1)$ के रूप में देखा जा सकता है। यदि $r$ वास्तव में यादृच्छिक है, समान रूप से शून्य और $(p-2)$ के बीच वितरित किया जाता है, $x$ (वन-टाइम पैड देखें) के बारे में कोई जानकारी लीक नहीं होती है।

बड़े ग्राफ के लिए हैमिल्टनियन चक्र

निम्नलिखित योजना मैनुअल ब्लम के कारण है।

इस परिदृश्य में, पेगी बड़े ग्राफ़ (असतत गणित) के लिए हैमिल्टनियन पथ जानता है G. विक्टर जानता है G किन्तु चक्र नहीं (जैसे, पैगी ने G को उत्पन्न किया है और उसे यह पता चला।) बड़े ग्राफ को दिए गए हैमिल्टनियन चक्र को ढूँढना कम्प्यूटेशनल रूप से अक्षम माना जाता है, क्योंकि इसके संबंधित निर्णय संस्करण को एनपी-पूर्ण माना जाता है। पैगी यह सिद्ध कर देगी कि वह चक्र को केवल प्रकट किए बिना जानती है (संभवतः विक्टर इसे खरीदने में रुचि रखता है किन्तु पहले सत्यापन चाहता है, या संभवतः पैगी ही एकमात्र है जो इस जानकारी को जानती है और विक्टर को अपनी पहचान सिद्ध कर रही है)।

यह दिखाने के लिए कि पैगी हैमिल्टनियन चक्र को जानती है, वह और विक्टर गेम के कई राउंड खेलते हैं।

• प्रत्येक चरण के प्रारंभ में, पैगी H बनाती है, एक ग्राफ जो G (अर्थात H बिल्कुल G की प्रकार है अतिरिक्त इसके कि सभी शीर्षों के भिन्न-भिन्न नाम हैं) ग्राफ समरूपता है। चूँकि ज्ञात समरूपता के साथ आइसोमोर्फिक ग्राफ़ के बीच हैमिल्टनियन चक्र का अनुवाद करना तुच्छ है, यदि पेगी G के लिए हैमिल्टनियन चक्र जानता है उसे भी के लिए पता होना चाहिए.
• पैगी H के लिए प्रतिबद्ध है। वह एक क्रिप्टोग्राफिक प्रतिबद्धता योजना का उपयोग करके ऐसा कर सकती है। वैकल्पिक रूप से, वह H के शीर्षों को क्रमांकित कर सकती है। अगला, H के प्रत्येक किनारे के लिए, कागज के एक छोटे से टुकड़े पर, वह उन दो शीर्षों को लिखती है जिनसे किनारा जुड़ता है। फिर वह कागज के इन सभी टुकड़ों को एक मेज पर उलट कर रख देती है। इस प्रतिबद्धता का उद्देश्य यह है कि पैगी H को बदलने में सक्षम नहीं है, वहीं विक्टर को H के बारे में कोई जानकारी नहीं है।
• विक्टर तब पैगी से पूछने के लिए यादृच्छिक रूप से दो प्रश्नों में से एक चुनता है। वह या तो उससे H और G के बीच समरूपता दिखाने के लिए कह सकता है (ग्राफ़ समरूपता समस्या देखें), या वह उसे H में हैमिल्टनियन चक्र दिखाने के लिए कह सकता है।
• यदि पेगी को यह दिखाने के लिए कहा जाता है कि दो ग्राफ़ आइसोमॉर्फिक हैं, तो वह पहले सभी एच को प्रकाशित करती है (उदाहरण के लिए टेबल पर रखे सभी कागज़ों के टुकड़ों को पलट कर) और फिर वर्टेक्स अनुवाद प्रदान करती है जो G को H से मैप करती है। विक्टर सत्यापित कर सकता है कि वे वास्तव में आइसोमॉर्फिक हैं।
• अगर पैगी को यह सिद्ध करने के लिए कहा जाता है कि वह H में हैमिल्टनियन चक्र को जानती है, तो वह अपने हैमिल्टनियन चक्र को G पर H पर अनुवाद करती है और केवल हैमिल्टनियन चक्र पर किनारों को प्रकाशित करती है। विक्टर के लिए यह जाँचने के लिए पर्याप्त है कि H में वास्तव में एक हैमिल्टनियन चक्र है।

यह महत्वपूर्ण है कि ग्राफ़ के प्रति वचनबद्धता ऐसी हो कि दूसरे स्थिति में विक्टर सत्यापित कर सके कि चक्र वास्तव में H से किनारों से बना है। उदाहरण के लिए इसे प्रत्येक किनारे (या इसकी कमी) को अलग से कमिट करके किया जा सकता है।

संपूर्णता

यदि पैगी G में हैमिल्टनियन चक्र को जानती है तो वह H से G उत्पन्न करने वाले ग्राफ आइसोमोर्फिज्म या H में हैमिल्टनियन चक्र के लिए विक्टर की मांग को आसानी से पूरा (जो उसने पहले चरण में प्रतिबद्ध किया था) कर सकती है (जिसे वह G में चक्र के लिए आइसोमोर्फिज्म प्रायुक्त करके बना सकती है)।

शून्य-ज्ञान

पैगी के उत्तर G में मूल हैमिल्टनियन चक्र को प्रकट नहीं करते हैं। प्रत्येक दौर में, विक्टर केवल H के आइसोमोर्फिज्म को G या H में हैमिल्टनियन चक्र को सीखेंगे। उन्हें G में चक्र की खोज के लिए एकल H के लिए दोनों उत्तरों की आवश्यकता होगी, इसलिए जानकारी बनी हुई है अज्ञात जब तक पैगी हर दौर में एक अलग H उत्पन्न कर सकती है। यदि पैगी G में हैमिल्टनियन चक्र के बारे में नहीं जानती है, लेकिन किसी प्रकार पहले से जानती है कि विक्टर प्रत्येक दौर को देखने के लिए क्या कहेगा तो वह धोखा दे सकती है। उदाहरण के लिए, यदि पैगी समय से पहले जानती थी कि विक्टर H में हैमिल्टनियन चक्र को देखने के लिए कहेगा तो वह एक असंबंधित ग्राफ के लिए हैमिल्टनियन चक्र उत्पन्न कर सकती थी। इसी प्रकार, अगर पैगी को पहले से पता था कि विक्टर समरूपता को देखने के लिए कहेगा तो वह बस एक समरूपी ग्राफ H (जिसमें वह एक हैमिल्टनियन चक्र भी नहीं जानती) उत्पन्न कर सकती है। विक्टर स्वयं (पैगी के बिना) प्रोटोकॉल का अनुकरण कर सकता है क्योंकि वह जानता है कि वह क्या देखने के लिए कहेगा। इसलिए, प्रत्येक चरण में सामने आई जानकारी से विक्टर को G में हैमिल्टनियन चक्र के बारे में कोई जानकारी नहीं मिली।

सुदृढ़ता

यदि पेगी जानकारी नहीं जानती है, तो वह अनुमान लगा सकती है कि विक्टर कौन सा प्रश्न पूछेगा और एक असंबंधित ग्राफ के लिए या तो G के लिए आइसोमोर्फिक ग्राफ या हैमिल्टनियन चक्र उत्पन्न करेगा, लेकिन चूंकि वह G के लिए हैमिल्टनियन चक्र नहीं जानता है, वह दोनों नहीं कर सकता है। इस अनुमान के साथ, विक्टर को मूर्ख बनाने का उसका मौका 2⁻ⁿ है, जहां n राउंड की संख्या है। सभी यथार्थवादी उद्देश्यों के लिए, इस प्रकार से उचित संख्या में राउंड के साथ शून्य-ज्ञान प्रमाण को पराजित करना असंभव रूप से कठिन है।

शून्य-ज्ञान के पर्याय

शून्य-ज्ञान के विभिन्न रूपों को निम्नलिखित तरीकों से वास्तविक प्रमाण प्रोटोकॉल के निष्पादन की प्रकार दिखने वाले सिम्युलेटर के आउटपुट से क्या अर्थ है, इसकी सहज अवधारणा को औपचारिक रूप से परिभाषित किया जा सकता है:

• हम पूर्ण शून्य-ज्ञान की बात करते हैं यदि सिम्युलेटर और प्रूफ प्रोटोकॉल द्वारा उत्पादित वितरण बिल्कुल समान वितरित किए जाते हैं। यह उदाहरण के लिए ऊपर के पहले उदाहरण में स्थिति है।
• सांख्यिकीय शून्य-ज्ञान इसका अर्थ यह है कि वितरण बिल्कुल समान नहीं हैं, किन्तु वे सांख्यिकीय रूप से करीब हैं, जिसका अर्थ है कि उनका सांख्यिकीय अंतर नगण्य कार्य है।
• हम कम्प्यूटेशनल शून्य-ज्ञान की बात करते हैं यदि कोई कुशल एल्गोरिदम दो वितरणों को अलग नहीं कर सकता है।

शून्य ज्ञान प्रकार

• ज्ञान का प्रमाण: ऊपर दिखाए गए उदाहरण की प्रकार एक्सपोनेंट में भी ज्ञान छिपा होता है।
• पेयरिंग आधारित क्रिप्टोग्राफी: दिए गए f(x) और f(y), x और y को जाने बिना,f(x×y) की गणना करना संभव है।
• साक्षी अप्रभेद्य प्रमाण: सत्यापनकर्ता यह नहीं जान सकते हैं कि प्रमाण प्रस्तुत करने के लिए किस साक्षी का उपयोग किया गया है।
• बहुदलीय संगणना: जबकि प्रत्येक पक्ष अपने संबंधित रहस्य रख सकता है, वे साथ परिणाम उत्पन्न करते हैं।
• अंगूठी हस्ताक्षर: बाहरी लोगों को पता नहीं है कि हस्ताक्षर करने के लिए किस कुंजी का उपयोग किया जाता है।

अनुप्रयोग

प्रमाणीकरण प्रणाली

शून्य-ज्ञान प्रमाण में शोध प्रमाणीकरण प्रणाली से प्रेरित है, जहां पक्ष किसी गुप्त सूचना (जैसे पासवर्ड) के माध्यम से दूसरे पक्ष को अपनी पहचान सिद्ध करना चाहता है, किन्तु नहीं चाहता कि दूसरा पक्ष इस रहस्य के बारे में कुछ भी सीखे। इसे ज्ञान का शून्य-ज्ञान प्रमाण कहा जाता है। चूँकि, पासवर्ड सामान्यतः ज्ञान के शून्य-ज्ञान प्रमाण के लिए कई योजनाओं में उपयोग करने के लिए बहुत छोटा या अपर्याप्त रूप से यादृच्छिक होता है। शून्य-ज्ञान पासवर्ड प्रमाण विशेष प्रकार का ज्ञान का शून्य-ज्ञान प्रमाण है जो पासवर्ड के सीमित आकार को संबोधित करता है।

अप्रैल 2015 में, ज्ञान का प्रमाण सिग्मा प्रोटोकॉल (कई प्रमाणों में से एक) प्रस्तुत किया गया था। अगस्त 2021 में, क्लाउडफ्लेयर, अमेरिकी वेब इंफ्रास्ट्रक्चर और सुरक्षा कंपनी ने वेंडर हार्डवेयर का उपयोग करके निजी वेब सत्यापन के लिए एक-आउट-ऑफ-द-मैनी प्रूफ मैकेनिज्म का उपयोग करने का निर्णय लिया।

नैतिक व्यवहार

क्रिप्टोग्राफ़िक प्रोटोकॉल के भीतर शून्य-ज्ञान प्रमाण का उपयोग गोपनीयता बनाए रखते हुए ईमानदार व्यवहार को प्रायुक्त करना है। सामान्यतः, विचार शून्य-ज्ञान प्रमाण का उपयोग करके उपयोगकर्ता को यह सिद्ध करने के लिए मजबूर करना है कि उसका व्यवहार प्रोटोकॉल के अनुसार सही है। सुदृढ़ता के कारण, हम जानते हैं कि वैध प्रमाण प्रदान करने में सक्षम होने के लिए उपयोगकर्ता को वास्तव में ईमानदारी से कार्य करना चाहिए। शून्य ज्ञान के कारण, हम जानते हैं कि प्रमाण प्रदान करने की प्रक्रिया में उपयोगकर्ता अपने रहस्यों की गोपनीयता से समझौता नहीं करता है।

परमाणु निरस्त्रीकरण

2016 में, प्रिंसटन प्लाज़्मा भौतिकी प्रयोगशाला और प्रिंसटन विश्वविद्यालय ने ऐसी तकनीक का प्रदर्शन किया जो भविष्य में परमाणु निरस्त्रीकरण वार्ता के लिए उपयुक्त हो सकती है। यह निरीक्षकों को यह पुष्टि करने की अनुमति देगा कि कोई वस्तु वास्तव में परमाणु हथियार है या नहीं, बिना रिकॉर्डिंग, साझा या आंतरिक कार्यकलापों का विवरण किए जो गुप्त हो सकता है।

ब्लॉकचैन

ज़ेरोकॉइन प्रोटोकॉल और ज़ीरोकैश प्रोटोकॉल में शून्य-ज्ञान प्रमाण प्रायुक्त किए गए थे, जो ज़कॉइन(बाद में 2020 में फिरो (क्रिप्टोक्यूरेंसी) के रूप में पुनः ब्रांडेड) और 2016 में ज़कैश क्रिप्टोकरेंसी के जन्म में समाप्त हुआ। ज़ेरोकॉइन में अंतर्निहित मिक्सिंग मॉडल है जो गुमनामी सुनिश्चित करने के लिए किसी भी सहकर्मी या केंद्रीकृत मिक्सिंग प्रदाताओं पर विश्वाश नहीं करता है। उपयोगकर्ता आधार मुद्रा में लेन-देन कर सकते हैं और मुद्रा को ज़ीरोकॉइन में और बाहर चक्रित कर सकते हैं। ज़ेरोकैश प्रोटोकॉल समान मॉडल का उपयोग करता है (संस्करण जिसे गैर-संवादात्मक शून्य-ज्ञान प्रमाण के रूप में जाना जाता है) अतिरिक्त इसके कि यह लेन-देन की राशि को अस्पष्ट कर सकता है, जबकि ज़ीरोकॉइन नहीं कर सकता। ज़ेरोकैश नेटवर्क पर लेन-देन डेटा के महत्वपूर्ण प्रतिबंधों को देखते हुए, ज़ेरोकैश में ज़ेरोकॉइन की तुलना में गोपनीयता समय के हमलों का खतरा कम है। चूँकि, गोपनीयता की यह अतिरिक्त परत ज़ीरोकैश आपूर्ति के संभावित अनपेक्षित हाइपरफ्लिनेशन का कारण बन सकती है क्योंकि धोखाधड़ी वाले सिक्कों को ट्रैक नहीं किया जा सकता है।

2018 में, बुलेटप्रूफ प्रस्तुत किए गए थे। बुलेटप्रूफ गैर-संवादात्मक शून्य-ज्ञान प्रमाण से सुधार है जहां विश्वसनीय सेटअप की आवश्यकता नहीं होती है। इसे बाद में मिम्बलविंबल प्रोटोकॉल (जो ग्रिन और बीम क्रिप्टोकरेंसी पर आधारित हैं) और मोनेरो (क्रिप्टोक्यूरेंसी) में प्रायुक्त किया गया था। 2019 में, फ़िरो ने सिग्मा प्रोटोकॉल को प्रायुक्त किया, जो बिना विश्वसनीय सेटअप के ज़ेरोकॉइन प्रोटोकॉल में सुधार है। उसी वर्ष, फ़िरो ने लेलंटस प्रोटोकॉल प्रस्तुत किया, सिग्मा प्रोटोकॉल पर सुधार, जहां पूर्व लेन-देन की उत्पत्ति और राशि को छुपाता है।

इतिहास

ज़ीरो-नॉलेज प्रूफ की कल्पना सबसे पहले 1985 में शफी गोल्डवेसर, सिल्वियो मिकाली और चार्ल्स रैकॉफ ने अपने पेपर द नॉलेज कॉम्प्लेक्सिटी ऑफ इंटरएक्टिव प्रूफ-सिस्टम्स में की थी। इस पत्र ने इंटरएक्टिव प्रमाण प्रणाली के आईपी पदानुक्रम (इंटरैक्टिव प्रमाण प्रणाली देखें) की प्रारंभ की और नॉलेज कॉम्प्लेक्सिटी की अवधारणा की कल्पना की, जो प्रोवर से सत्यापनकर्ता को हस्तांतरित प्रूफ के बारे में ज्ञान की मात्रा का माप है। उन्होंने ठोस समस्या के लिए पहला शून्य-ज्ञान प्रमाण भी दिया, जो द्विघात अवशेष मॉड m को तय करने का था। लेज़्लो बाबई और श्लोमो मोरन के पेपर के साथ, इस लैंडमार्क पेपर ने इंटरएक्टिव प्रमाण प्रणाली का आविष्कार किया, जिसके लिए सभी पांच लेखकों ने 1993 में पहला गोडेल पुरस्कार जीता था।

उनके अपने शब्दों में, गोल्डवेसर, मिकाली और रैकॉफ कहते हैं:

विशेष रूप से रुचि का स्थिति है जहां यह अतिरिक्त ज्ञान अनिवार्य रूप से 0 है और हम दिखाते हैं कि [यह] अंतःक्रियात्मक रूप से सिद्ध करना संभव है कि संख्या द्विघात गैर अवशेष मॉड एम है जो 0 अतिरिक्त ज्ञान जारी करती है। यह आश्चर्यजनक है क्योंकि m का गुणनखंड नहीं दिए जाने पर द्विघात अवशिष्टता मोड़ m ज्ञात करने के लिए कोई कुशल एल्गोरिदम ज्ञात नहीं है। इसके अतिरिक्त, इस समस्या के लिए सभी ज्ञात एनपी प्रमाण एम के प्रमुख गुणन को प्रदर्शित करते हैं। यह निरुपित करता है कि सिद्ध करने की प्रक्रिया में बातचीत जोड़ने से ज्ञान की मात्रा कम हो सकती है जिसे प्रमेय सिद्ध करने के लिए संप्रेषित किया जाना चाहिए।

द्विघात गैर-अवशेष समस्या में 'एनपी (जटिलता)' और 'सह-एनपी' एल्गोरिदम दोनों हैं, और इसलिए 'एनपी' और 'सह-एनपी' के चौराहे पर स्थित है। यह कई अन्य समस्याओं के बारे में भी सच था, जिसके लिए बाद में शून्य-ज्ञान प्रमाण की खोज की गई, जैसे कि ओडेड गोल्ड्रेइच द्वारा अप्रकाशित प्रमाण प्रणाली जो यह सत्यापित करती है कि दो-प्रमुख मापांक ब्लम पूर्णांक नहीं है।

ओडेड गोल्ड्रेइच, सिल्वियो मिकाली और एवी विगडरसन ने यह कदम आगे बढ़ाया, यह दिखाते हुए कि, अटूट एन्क्रिप्शन के अस्तित्व को मानते हुए, तीन रंगों के साथ एनपी-पूर्ण ग्राफ रंग समस्या के लिए शून्य-ज्ञान प्रमाण प्रणाली बना सकते हैं। चूंकि एनपी में हर समस्या को इस समस्या में कुशलता से कम किया जा सकता है, इसका अर्थ यह है कि, इस धारणा के तहत, एनपी में सभी समस्याओं का शून्य-ज्ञान प्रमाण है। धारणा का कारण यह है कि, जैसा कि ऊपर के उदाहरण में है, उनके प्रोटोकॉल को एन्क्रिप्शन की आवश्यकता होती है। अटूट एन्क्रिप्शन के अस्तित्व के लिए सामान्यतः उद्धृत पर्याप्त स्थिति तरफ़ा कार्यों का अस्तित्व है, किन्तु यह बोधगम्य है कि कुछ भौतिक साधन भी इसे प्राप्त कर सकते हैं।

इसके शीर्ष पर, उन्होंने यह भी दिखाया कि ग्राफ गैर-समरूपता समस्या, ग्राफ समरूपता समस्या की पूरक (जटिलता), शून्य-ज्ञान प्रमाण है। यह समस्या सह-एनपी में है, किन्तु वर्तमान में एनपी या किसी भी व्यावहारिक वर्ग में नहीं है। अधिक सामान्यतः, रसेल इम्पैग्लियाज़ो और मोती युंग के साथ-साथ बेन-ऑर एट अल। यह दिखाने के लिए आगे बढ़ेंगे कि, तरफा समारोह या अटूट एन्क्रिप्शन को भी मानते हुए, कि IP = PSPACE में सभी समस्याओं के लिए शून्य-ज्ञान प्रमाण हैं, या दूसरे शब्दों में, कुछ भी जो इंटरैक्टिव प्रूफ द्वारा सिद्ध किया जा सकता है प्रणाली को शून्य ज्ञान के साथ सिद्ध किया जा सकता है।

अनावश्यक धारणाएँ बनाना पसंद नहीं करते, कई सिद्धांतकारों ने तरफ़ा कार्यों की आवश्यकता को समाप्त करने का विधि खोजा। ऐसा करने का विधि मल्टी-प्रोवर इंटरएक्टिव प्रमाण प्रणाली (इंटरैक्टिव प्रमाण प्रणाली देखें) के साथ किया गया था, जिसमें केवल के अतिरिक्त कई स्वतंत्र प्रोवर होते हैं, जिससे सत्यापनकर्ता को गुमराह होने से बचने के लिए आइसोलेशन में प्रोवर्स की जांच करने की अनुमति मिलती है। यह दिखाया जा सकता है कि, बिना किसी सहज धारणा के, 'एनपी' में सभी भाषाओं में ऐसी प्रणाली में शून्य-ज्ञान प्रमाण हैं।

यह पता चला है कि इंटरनेट जैसी सेटिंग में, जहां कई प्रोटोकॉल समवर्ती रूप से निष्पादित किए जा सकते हैं, शून्य-ज्ञान प्रमाण बनाना अधिक चुनौतीपूर्ण है। सिंथिया डवर्क, मोनी नोर और अमित सहाई के काम से समवर्ती शून्य-ज्ञान प्रमाण की जांच करने वाली शोध की रेखा प्रारंभ हुई थी। इन पंक्तियों के साथ विशेष विकास साक्षी-अविभेद्य प्रमाण प्रोटोकॉल का विकास रहा है। साक्षी-अविभेद्यता की संपत्ति शून्य-ज्ञान से संबंधित है, फिर भी साक्षी-अविभेद्य प्रोटोकॉल समवर्ती निष्पादन की समान समस्याओं से ग्रस्त नहीं हैं।

शून्य-ज्ञान प्रमाण का अन्य प्रकार गैर-संवादात्मक शून्य-ज्ञान प्रमाण है। ब्लम, फेल्डमैन और मिकाली ने दिखाया कि प्रोवर और सत्यापनकर्ता के बीच साझा किया गया सामान्य यादृच्छिक स्ट्रिंग बिना किसी सहभागिता की आवश्यकता के कम्प्यूटेशनल शून्य-ज्ञान प्राप्त करने के लिए पर्याप्त है।

जीरो-नॉलेज प्रूफ प्रोटोकॉल

सबसे लोकप्रिय संवादात्मक या गैर-संवादात्मक शून्य-ज्ञान प्रमाण (जैसे, जेडके-स्नार्क) प्रोटोकॉल को सामान्यतः निम्नलिखित चार श्रेणियों में वर्गीकृत किया जा सकता है: ज्ञान के संक्षिप्त गैर-संवादात्मक तर्क (स्नार्क), ज्ञान के स्केलेबल पारदर्शी तर्क (STARK), सत्यापन योग्य बहुपद प्रतिनिधिमंडल (वीपीडी), और संक्षिप्त गैर-संवादात्मक तर्क (एसएनएआरजी)। पारदर्शिता, सार्वभौमिकता, प्रशंसनीय पोस्ट-क्वांटम सुरक्षा और प्रोग्रामिंग प्रतिमान के आधार पर तुलना के साथ शून्य-ज्ञान प्रमाण प्रोटोकॉल और पुस्तकालयों की सूची नीचे दी गई है। पारदर्शी प्रोटोकॉल वह है जिसे किसी विश्वसनीय सेटअप की आवश्यकता नहीं होती है और यह सार्वजनिक यादृच्छिकता का उपयोग करता है। सार्वभौमिक प्रोटोकॉल वह है जिसे प्रत्येक सर्किट के लिए अलग विश्वसनीय सेटअप की आवश्यकता नहीं होती है। अंत में, प्रशंसनीय रूप से पोस्ट-क्वांटम प्रोटोकॉल वह है जो क्वांटम एल्गोरिदम से जुड़े ज्ञात हमलों के लिए अतिसंवेदनशील नहीं है।

शून्य-ज्ञान प्रमाण (जेडकेपी) प्रणाली

जेडकेपी प्रणाली	प्रकाशन वर्ष	प्रोटोकॉल	पारदर्शी	सार्वभौमिक	संभावित रूप से पोस्ट-क्वांटम सुरक्षित	प्रोग्रामिंग प्रतिमान
पिनोच्चियो	2013	जेडके-स्नार्क	No	No	No	प्रक्रियात्मक
गेपेटो	2015	जेडके-स्नार्क	No	No	No	प्रक्रियात्मक
टिनीरैम	2013	जेडके-स्नार्क	No	No	No	प्रक्रियात्मक
बुफ़ेट	2015	जेडके-स्नार्क	No	No	No	प्रक्रियात्मक
ज़ोक्रेट्स	2018	जेडके-स्नार्क	No	No	No	प्रक्रियात्मक
एक्सजेस्नार्क	2018	जेडके-स्नार्क	No	No	No	प्रक्रियात्मक
विरैम	2018	जेडके-स्नार्ग	No	Yes	No	असेंबली
वीएन टिनीरैम	2014	जेडके-स्नार्क	No	Yes	No	प्रक्रियात्मक
मिराज	2020	जेडके-स्नार्क	No	Yes	No	अंकगणितीय परिपथ
सोनिक	2019	जेडके-स्नार्क	No	Yes	No	अंकगणितीय परिपथ
मर्लिन	2020	जेडके-स्नार्क	No	Yes	No	अंकगणितीय परिपथ
प्लैंक	2019	जेडके-स्नार्क	No	Yes	No	अंकगणितीय परिपथ
सुपरसोनिक	2020	जेडके-स्नार्क	Yes	Yes	No	अंकगणितीय परिपथ
बुलेटप्रूफ	2018	Bulletproofs	Yes	Yes	No	अंकगणितीय परिपथ
हाईरेक्स	2018	जेडके-स्नार्क	Yes	Yes	No	अंकगणितीय परिपथ
हालो	2019	जेडके-स्नार्क	Yes	Yes	No	अंकगणितीय परिपथ
विर्गो	2020	जेडके-स्नार्क	Yes	Yes	Yes	अंकगणितीय परिपथ
लिगेरो	2017	जेडके-स्नार्क	Yes	Yes	Yes	अंकगणितीय परिपथ
ऑरोरा	2019	जेडके-स्नार्क	Yes	Yes	Yes	अंकगणितीय परिपथ
जेडके-स्टार्क	2019	जेडके-स्टार्क	Yes	Yes	Yes	असेंबली
ज़िल्च	2021	जेडके-स्टार्क	Yes	Yes	Yes	वस्तु के उन्मुख

यह भी देखें

• तीर सूचना विरोधाभास
• क्रिप्टोग्राफिक प्रोटोकॉल
• फीज-फिएट-शमीर पहचान योजना
• ज्ञान का प्रमाण
• क्रिप्टोग्राफी में विषय
• साक्षी-अभेद्य प्रमाण
• जीरो-नॉलेज पासवर्ड प्रूफ
• गैर-संवादात्मक शून्य-ज्ञान प्रमाण