सूचक यंत्र

सैद्धांतिक कंप्यूटर विज्ञान में, पॉइंटर मशीन रैंडम-्सेस मशीन के समान अटॉमिस्टिक सार मशीन मॉडल है। पॉइंटर एल्गोरिदम पॉइंटर मशीन मॉडल तक सीमित एल्गोरिदम भी हो सकता है।प्रकार के आधार पर, पॉइंटर मशीन को लिंकिंग ऑटोमेटन, केयू-मशीन, एसएमएम, अटॉमिस्टिक एलआईएसपी मशीन, ट्री-पॉइंटर मशीन, आदि कहा जा सकता है (सीएफ बेन-अम्राम 1995)। साहित्य में कम से कम तीन प्रमुख प्रकार - कोलमोगोरोव-उसपेन्स्की मॉडल (केयूएम, केयू-मशीन), नुथ लिंकिंग ऑटोमेटन, एवं शॉनहेज स्टोरेज मॉडिफिकेशन मशीन मॉडल (एसएमएम) उपस्थित हैं। एसएमएम सबसे सामान्य प्रतीत होता है।

अपने रीड-ओनली टेप (या समतुल्य) से पॉइंटर मशीन इनपुट प्राप्त करती है - कम से कम दो प्रतीकों से बने प्रतीक-अनुक्रम है। { 0, 1 } - एवं यह आउटपुट "केवल-लेखन" टेप (या समतुल्य) पर आउटपुट प्रतीक-अनुक्रम लिखता है। प्रतीक-अनुक्रम (इनपुट शब्द) को आउटपुट प्रतीक-अनुक्रम में परिवर्तित करने के लिए मशीन प्रोग्राम - परिमित-स्टेट मशीन (मेमोरी एवं निर्देशों की सूची) से सुसज्जित है। अपनी स्टेट मशीन के माध्यम से प्रोग्राम इनपुट प्रतीकों को पढ़ता है, इसकी स्टोरेज संरचना पर कार्य करता है - किनारों से जुड़े नोड्स (रजिस्टर) का संग्रह (प्रतीकों जैसे कि {0, 1} के साथ लेबल किए गए पॉइंटर्स), एवं आउटपुट टेप पर प्रतीकों को लिखता है।

पॉइंटर मशीनें सामान्य उपायों से अंकगणित नहीं कर सकतीं है। गणना केवल इनपुट प्रतीकों को पढ़ने, संशोधित करने एवं इसकी स्टोरेज संरचना पर विभिन्न परीक्षण करने - नोड्स एवं पॉइंटर्स के पैटर्न, एवं परीक्षणों के आधार पर प्रतीकों को आउटपुट करने से अग्रसर होती है। सूचना स्टोरेज संरचना में है।

पॉइंटर मशीनों के प्रकार

गुरेविच एवं बेन-अम्राम दोनों ने एब्स्ट्रैक्ट मशीनों के कई समान अटॉमिस्टिक मॉडलों की सूची बनाई है; बेन-अम्राम का मानना ​​है कि 6 अटॉमिस्टिक मॉडल को उच्च-स्तरीय मॉडल से भिन्न किया जाना चाहिए। यह लेख विशेष रूप से निम्नलिखित 3 अटॉमिस्टिक मॉडलों पर विचार करेगा:

• शॉनहेज की स्टोरेज संशोधन मशीनें (एसएमएम),
• कोलमोगोरोव-उसपेन्स्की मशीनें (केयूएम या केयू-मशीनें),
• नुथ का लिंकिंग ऑटोमेटन

किन्तु बेन-अम्राम जोड़ता है:

• अटॉमिस्टिक प्योर-एलआईएसपी मशीन (एपीएलएम)
• अटॉमिस्टिक पूर्ण-एलआईएसपी मशीन (एएफएलएम),
• सामान्य अटॉमिस्टिक सूचक मशीनें,
• जोन की भाषा (दो प्रकार)

पॉइंटर-मशीन मॉडल के साथ समस्याएं

समष्टिता सिद्धांत में मॉडल का उपयोग: वैन एम्डे बोस (1990) विचार व्यक्त करते हैं कि एब्सट्रैक्ट मॉडल का यह रूप है:

सैद्धांतिक मॉडल, किन्तु ... समष्टिता सिद्धांत के लिए मौलिक मॉडल के रूप में इसका आकर्षण संदिग्ध है। इसका समय माप ऐसे संदर्भ में समान समय पर आधारित है जहां यह माप वास्तविक समय समष्टिता को कम आंकने के लिए जाना जाता है। मशीन के लिए स्थान माप के लिए भी यही अवलोकन प्रस्तावित होता है (वैन एम्डे बोस (1990) पृष्ठ 35)।

गुरेविच 1988 भी विचार व्यक्त करते हैं:

व्यावहारिक रूप से कहें तो, शॉनहेज मॉडल कला की वर्तमान स्थिति में समय की समष्टिता का उत्तम माप प्रदान करता है, (गुरेविच (1988) पृष्ठ 6 एंग्लुइन डी एवं वैलेंट एल.जी. के संदर्भ में, हैमिल्टनियन परिपथ एवं मिलान के लिए फास्ट प्रोबेबिलिस्टिक एल्गोरिदम, जर्नल ऑफ कंप्यूटर एंड सिस्टम साइंसेज 18 (1979) ) 155-193) है।

तथ्य यह है कि, §3 एवं §4 (पीपी. 494-497) में, शॉनहेज (1980) अपने दो रैंडम-्सेस मशीन मॉडल RAM0 एवं RAM1 की वास्तविक समय तुल्यता को प्रदर्शित करता है, जो समष्टिता अध्ययन के लिए एसएमएम की आवश्यकता पर प्रश्न उठाता है।

मॉडल के लिए संभावित उपयोग: चूंकि, शॉनहेज (1980) अपने §6, रैखिक समय में पूर्णांक-गुणन में प्रदर्शित करता है। एवं गुरेविच को आश्चर्य है कि समानांतर केयू मशीन कुछ सीमा तक मानव मस्तिष्क से मिलती है या नहीं मिलती है (गुरेविच (1988) पृष्ठ 5)।

शॉनहेज की स्टोरेज संशोधन मशीन (एसएमएम) मॉडल

शॉनहेज का एसएमएम मॉडल सबसे सामान्य एवं सबसे स्वीकार्य प्रतीत होता है। यह रजिस्टर मशीन मॉडल एवं अन्य सामान्य कम्प्यूटेशनल मॉडल से अधिक भिन्न है, उदाहरण टेप-आधारित ट्यूरिंग मशीन या काउंटर मशीन के लेबल होल्स एवं अप्रभेद्य पेब्ब्लेस है।कंप्यूटर में इनपुट प्रतीकों की निश्चित वर्णमाला होती है, एवं परिवर्तनशील निर्देशित ग्राफ (स्टेट डायग्राम) होता है जिसके एरो वर्णमाला प्रतीकों द्वारा लेबल किए जाते हैं। ग्राफ़ के प्रत्येक नोड में प्रत्येक प्रतीक के साथ लेबल किया गया आउटगोइंग एरो होता है, चूँकि इनमें से कुछ मूल नोड में वापस लूप हो सकते हैं। ग्राफ़ के निश्चित नोड को प्रारंभ या सक्रिय नोड के रूप में पहचाना जाता है।

वर्णमाला के प्रतीकों के प्रत्येक शब्द को मशीन के माध्यम से पथ में अनुवादित किया जा सकता है; उदाहरण के लिए, 10011 प्रारंभ नोड से पथ 1, तत्पश्चात परिणामी नोड से पथ 0, तत्पश्चात पथ 0, तत्पश्चात पथ 1, तत्पश्चात पथ 1 लेने में अनुवादित होगा। पथ, परिवर्तित में, परिणामी नोड से पहचाना जा सकता है, किन्तु गणना के समय ग्राफ़ परिवर्तित होते ही यह पहचान परिवर्तित हो जाएगी।

मशीन निर्देश प्राप्त कर सकती है जो ग्राफ़ का लेआउट परिवर्तित कर देती है। मूल निर्देश नवीन w निर्देश हैं, जो नवीन नोड बनाता है जो स्ट्रिंग w का अनुसरण करने का परिणाम है, एवं w से v निर्देश सेट करता है जो (पुनः) किनारे को भिन्न नोड पर निर्देशित करता है। यहां w एवं v शब्दों को परिवर्तित करते हैं। v पूर्व शब्द है—अर्थात् प्रतीकों की पूर्व-निर्मित स्ट्रिंग - जिससे पुनर्निर्देशित किनारा पीछे की ओर पूर्व नोड की ओर प्रदर्शित करेगा जो कि उस स्ट्रिंग का परिणाम है।

2-प्रतीक {0,1} मशीन में नवीन नोड के निर्माण के चरण: जब उपन्यास शब्द (यहां: 11) के साथ सामना किया जाता है, तो मशीन उत्तरदायी होती है (i) नवीन नोड 3 बनाना एवं उस पर उपयुक्त 1-किनारे को प्रदर्शित करना, तत्पश्चात (ii) दो नवीन पॉइंटर्स बनाना ( 0-किनारे एवं 1-किनारे) जो दोनों पूर्व नोड पर वापस प्रदर्शित करते हैं (यहां: नोड 2)।

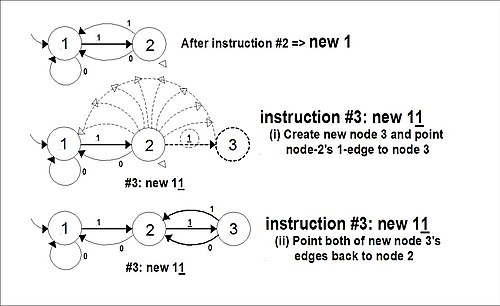
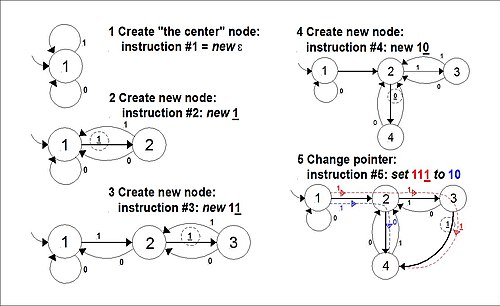
(1) नवीन w: नवीन नोड बनाता है। w नवीन शब्द का प्रतिनिधित्व करता है जो नवीन नोड बनाता है। मशीन w शब्द को पढ़ती है, w के प्रतीकों द्वारा प्रदर्शित किए पथ का अनुसरण करते हुए जब तक मशीन शब्द के अंतिम, अतिरिक्त प्रतीक तक नहीं पहुंच जाती है। अतिरिक्त प्रतीक अंतिम स्थिति को नवीन नोड बनाने के लिए बाध्य करता है, एवं उसके संबंधित एरो (उस प्रतीक के साथ लेबल किया गया) को उसकी पूर्व स्थिति से नवीन नोड पर प्रदर्शित करने के लिए फ़्लिप करता है। परिवर्तित होे में नवीन नोड अपने सभी किनारों को पूर्व अंतिम स्थिति में वापस प्रदर्शित करता है, जहां वे किसी अन्य सेट द्वारा पुनर्निर्देशित होने तक आराम करते हैं। नवीन नोड स्लीपिंग मोड में हैं, असाइनमेंट की प्रतीक्षा कर रहे हैं। आरंभिक या केंद्र नोड के विषय में हम इसी प्रकार इसके दोनों किनारों को स्वयं की ओर प्रदर्शित करके प्रारंभ करते हैं।

• उदाहरण: मान लीजिए w 10110[1] है, जहां अंतिम वर्ण इसकी विशेष स्थिति को प्रदर्शित करने के लिए कोष्ठक में है। हम 10110 तक पहुंचने वाले नोड के 1 किनारे को लेते हैं (पांच-किनारे के अंत में, इसलिए छह-नोड, पथ), एवं इसे नवीन 7वें नोड पर प्रदर्शित करते हैं। इस नवीन नोड के दो किनारे तत्पश्चात पथ के छठे नोड की ओर, पीछे की ओर प्रदर्शित करते हैं।

(2) w को v पर सेट करें: w शब्द द्वारा प्रदर्शित किए पथ से किनारे (एरो) को पूर्व नोड पर रीडायरेक्ट (स्थानांतरित) करता है जो v शब्द का प्रतिनिधित्व करता है। पुनः यह पथ का अंतिम एरो है जिसे पुनर्निर्देशित किया गया है।

• उदाहरण: उपरोक्त निर्देश के पश्चात 1011011 को 1011 पर सेट करें, 101101 पर नवीन नोड के 1 एरो को परिवर्तित करके 1011 पर पहुंचने वाले पथ में पांचवें नोड को प्रदर्शित करता है। इस प्रकार पथ 1011011 का परिणाम अब 1011 जैसा ही होता है।

(3) यदि v = w तो निर्देश z: सशर्त निर्देश जो w एवं v शब्दों द्वारा प्रदर्शित किए दो पथों की अपेक्षा करता है यह देखने के लिए कि क्या वे समान नोड पर समाप्त होते हैं; यदि ऐसा है तो अनुदेश z पर जाएं अन्यथा निरंतर रखें। यह निर्देश रजिस्टर मशीन या वांग बी-मशीन में अपने समकक्ष के समान उद्देश्य को पूर्ण करता है, जो ट्यूरिंग मशीन की नई स्थिति में जाने की क्षमता के अनुरूप है।

2-प्रतीक {0,1} मशीन में नवीन नोड्स के निर्माण के चरण है। जैसे ही शब्द - प्रतीक 0 एवं 1 की स्ट्रिंग - मशीन में आते हैं, मशीन ग्राफ़ बनाती है। जैसा कि यहां प्रदर्शित किया गया है, 5वें चरण के पश्चात दो शब्द - 111 एवं 10 - दोनों नोड 4 की ओर प्रदर्शित करते हैं। इस समय, यदि मशीन को यदि 10=111 तो xxx करना है, तो परीक्षण सफल होता है एवं मशीन वास्तव में xxx पर पहुंच जाता है।

नुथ का लिंकिंग ऑटोमेटन मॉडल

स्कोनहेज के अनुसार, नुथ ने कहा कि एसएमएम मॉडल विशेष प्रकार के लिंकिंग ऑटोमेटा से समान होता है जिसे कंप्यूटर प्रोग्रामिंग की कला के खंड में संक्षेप में बताया गया है (सीएफ. [4, पीपी. 462-463])।

कोलमोगोरोव-उसपेन्स्की मशीन (केयू-मशीन) मॉडल

केयूएम केवल उलटे पॉइंटर्स की अनुमति देने में एसएमएम से भिन्न है: नोड x से नोड y तक प्रत्येक पॉइंटर के लिए, y से x तक व्युत्क्रम पॉइंटर उपस्थित होना चाहिए। चूँकि आउटगोइंग पॉइंटर्स को वर्णमाला के भिन्न-भिन्न प्रतीकों द्वारा लेबल किया जाना चाहिए, केयूएम एवं एसएमएम दोनों ग्राफ़ में O(1) आउटडिग्री है। चूंकि, केयूएम पॉइंटर्स की व्युत्क्रमता इन-डिग्री को O(1) तक सीमित करती है। यह भौतिक (विशुद्ध रूप से सूचनात्मक के विपरीत) यथार्थवाद के लिए कुछ समस्याओं जैसे उपरोक्त वैन एम्डे बोस उद्धरण को संबोधित करता है।

अतिरिक्त अंतर यह है कि केयूएम का उद्देश्य ट्यूरिंग मशीन के सामान्यीकरण के रूप में था, एवं इसलिए यह वर्तमान में सक्रिय नोड को ग्राफ़ के चारों ओर ले जाने की अनुमति देता है। तदनुसार, नोड्स को शब्दों के अतिरिक्त भिन्न-भिन्न वर्णों द्वारा निर्दिष्ट किया जा सकता है, एवं की जाने वाली कार्रवाई को निर्देशों की निश्चित सूची के अतिरिक्त स्टेट तालिका द्वारा निर्धारित किया जा सकता है।

यह भी देखें

रजिस्टर मशीन-जेनेरिक रजिस्टर-आधारित एब्सट्रैक्ट मशीन कम्प्यूटेशनल मॉडल

• काउंटर मशीन-सबसे प्रिमिटिव मशीन, बेस मॉडल के निर्देश-सेट का उपयोग रजिस्टर मशीनों की पूर्ण श्रेणी में किया जाता है।
• रैंडम-्सेस मशीन-रैम: अतिरिक्त अप्रत्यक्ष एड्रेसिंग क्षमता वाली काउंटर मशीन है।
• रैंडम-्सेस संग्रहित-प्रोग्राम मशीन -आरएएसपी: यूनिवर्सल ट्यूरिंग मशीन अर्थात वॉन न्यूमैन आर्किटेक्चर के विषय में रजिस्टरों में पाए जाने वाले निर्देशों के प्रोग्राम के साथ काउंटर-आधारित या रैम-आधारित मशीन है।

ट्यूरिंग मशीन-जेनेरिक टेप-आधारित एब्सट्रैक्ट मशीन कम्प्यूटेशनल मॉडल

• पोस्ट-ट्यूरिंग मशीन-न्यूनतम -टेप, दो-दिशा, 1 प्रतीक {रिक्त, चिह्न} ट्यूरिंग जैसी मशीन किन्तु मूल 3-निर्देश काउंटर मशीनों के समान डिफ़ॉल्ट अनुक्रमिक निर्देश निष्पादन के साथ है।

संदर्भ

Most references and a bibliography are to be found at the article Register machine. The following are particular to this article:

• Amir Ben-Amram (1995), What is a "Pointer machine"?, SIGACTN: SIGACT News (ACM Special Interest Group on Automata and Computability Theory)", volume 26, 1995. also: DIकेयू, Department of Computer Science, University of Copenhagen, amirben@diku.dk. Wherein Ben-Amram describes the types and subtypes: (type 1a) Abstract Machines: Atomistic models including Kolmogorov-Uspenskii Machines (केयूएम), Schönhage's Storage Modification Machines (एसएमएम), Knuth's "Linking Automaton", APLM and AFLM (Atomistic Pure-LISP Machine) and (Atomistic Full-LISP machine), General atomistic Pointer Machines, Jone's I Language; (type 1b) Abstract Machines: High-level models, (type 2) Pointer algorithms.
• Andrey Kolmogorov and V. Uspenskii, On the definition of an algorithm, Uspekhi Mat. Nauk 13 (1958), 3-28. English translation in American Mathematical Society Translations, Series II, Volume 29 (1963), pp. 217–245.
• Yuri Gurevich (2000), Sequential Abstract State Machines Capture Sequential Algorithms, ACM Transactions on Computational Logic, vol. 1, no. 1, (July 2000), pages 77–111. In a single sentence Gurevich compares the Schönhage [1980] "storage modification machines" to Knuth's "pointer machines." For more, similar models such as "random access machines" Gurevich references:
  • John E. Savage (1998), Models of Computation: Exploring the Power of Computing. Addison Wesley Longman.
• Yuri Gurevich (1988), On Kolmogorov Machines and Related Issues, the column on "Logic in Computer Science", Bulletin of European Association for Theoretical Computer Science, Number 35, June 1988, 71-82. Introduced the unified description of Schönhage and Kolmogorov-Uspenskii machines used here.
• Arnold Schönhage (1980), Storage Modification Machines, Society for Industrial and Applied Mathematics, SIAM J. Comput. Vol. 9, No. 3, August 1980. Wherein Schönhage shows the equivalence of his एसएमएम with the "successor RAM" (Random Access Machine), etc. He refers to an earlier paper where he introduces the एसएमएम:
  • Arnold Schönhage (1970), Universelle Turing Speicherung, Automatentheorie und Formale Sprachen, Dörr, Hotz, eds. Bibliogr. Institut, Mannheim, 1970, pp. 69–383.
• Peter van Emde Boas, Machine Models and Simulations pp. 3–66, appearing in:

Jan van Leeuwen, ed. "Handbook of Theoretical Computer Science. Volume A: Algorithms and Complexity, The MIT PRESS/Elsevier, 1990. ISBN 0-444-88071-2 (volume A). QA 76.H279 1990.

van Emde Boas' treatment of एसएमएमs appears on pp. 32-35. This treatment clarifies Schönhage 1980 -- it closely follows but expands slightly the Schönhage treatment. Both references may be needed for effective understanding.