1/एन विस्तार
क्वांटम क्षेत्र सिद्धांत और सांख्यिकीय यांत्रिकी में, 1/एन विस्तार (जिसे बड़े एन विस्तार के रूप में भी जाना जाता है) विशेष ऑर्थोगोनल जैसे आंतरिक समरूपता समूह सिद्धांत के साथ क्वांटम क्षेत्र सिद्धांतों का एक विशेष गड़बड़ी सिद्धांत विश्लेषण है। समूह|एसओ(एन) या विशेष एकात्मक समूह|एसयू(एन)। इसमें शक्तियों में सिद्धांत के गुणों का विस्तार प्राप्त करना शामिल है , जिसे एक छोटे पैरामीटर के रूप में माना जाता है।
इस तकनीक का उपयोग क्वांटम क्रोमोडायनामिक्स में किया जाता है (भले ही वहां केवल 3 है) गेज समूह एसयू(3) के साथ। कण भौतिकी में एक अन्य अनुप्रयोग AdS/CFT द्वंद्वों का अध्ययन है।
इसका उपयोग संघनित पदार्थ भौतिकी में भी बड़े पैमाने पर किया जाता है जहां इसका उपयोग माध्य-क्षेत्र सिद्धांत के लिए कठोर आधार प्रदान करने के लिए किया जा सकता है।
उदाहरण
एक सरल उदाहरण से शुरू करते हुए - ऑर्थोगोनल समूह |ओ(एन) क्वार्टिक इंटरेक्शन|φ4- अदिश क्षेत्र φ O(N) के वास्तविक संख्या वेक्टर प्रतिनिधित्व में मान लेता है। आइंस्टीन सारांश सम्मेलन के साथ एन फ्लेवर (कण भौतिकी) के लिए सूचकांक संकेतन का उपयोग करना और क्योंकि ओ (एन) ऑर्थोगोनल है, सहसंयोजक और विरोधाभासी सूचकांकों के बीच कोई अंतर नहीं किया जाएगा। लैग्रेंजियन घनत्व द्वारा दिया गया है
कहाँ 1 से N तक चलता है। ध्यान दें कि N को युग्मन स्थिरांक λ में अवशोषित कर लिया गया है। यह यहाँ महत्वपूर्ण है.
एक सहायक क्षेत्र एफ का परिचय;
फेनमैन आरेखों में, ग्राफ असंयुक्त चक्र (ग्राफ सिद्धांत) में टूट जाता है, प्रत्येक एक ही स्वाद के φ किनारों से बना होता है और चक्र एफ किनारों से जुड़े होते हैं (जिनमें कोई प्रचारक रेखा नहीं होती है क्योंकि सहायक क्षेत्र प्रचारित नहीं होते हैं)।
प्रत्येक 4-बिंदु शीर्ष λ/N का योगदान देता है और इसलिए, 1/N का योगदान देता है। प्रत्येक स्वाद चक्र एन का योगदान देता है क्योंकि योग करने के लिए एन ऐसे स्वाद हैं। ध्यान दें कि सभी संवेग प्रवाह चक्र स्वाद चक्र नहीं हैं।
कम से कम परेशान करने वाली बात यह है कि 2k-बिंदु जुड़े सहसंबंध फ़ंक्शन में प्रमुख योगदान क्रम का है (1/N)k-1और अन्य पद 1/N की उच्च शक्तियाँ हैं। 1/एन विस्तार का निष्पादन बड़ी एन सीमा में अधिक से अधिक सटीक हो जाता है। निर्वात ऊर्जा घनत्व N के समानुपाती होता है, लेकिन सामान्य सापेक्षता मान्यताओं का अनुपालन न होने के कारण इसे अनदेखा किया जा सकता है।[clarification needed]
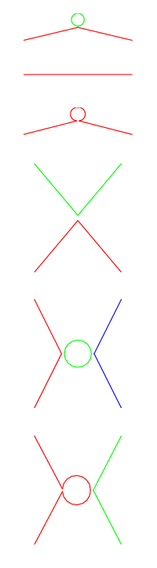
इस संरचना के कारण, फेनमैन आरेखों को दर्शाने के लिए एक अलग ग्राफिकल नोटेशन का उपयोग किया जा सकता है। प्रत्येक स्वाद चक्र को एक शीर्ष द्वारा दर्शाया जा सकता है। दो बाहरी शीर्षों को जोड़ने वाले स्वाद पथों को एक ही शीर्ष द्वारा दर्शाया जाता है। एक ही स्वाद पथ के साथ दो बाहरी शीर्ष स्वाभाविक रूप से युग्मित होते हैं और इन्हें एक एकल शीर्ष और एक किनारे (एफ किनारे नहीं) द्वारा प्रतिस्थापित किया जा सकता है जो इसे स्वाद पथ से जोड़ता है। एफ किनारे दो स्वाद चक्रों/पथों को एक-दूसरे से जोड़ने वाले किनारे हैं (या स्वयं एक स्वाद चक्र/पथ)। स्वाद चक्र/पथ के साथ होने वाली अंतःक्रियाओं का एक निश्चित चक्रीय क्रम होता है और यह एक विशेष प्रकार के ग्राफ का प्रतिनिधित्व करता है, जहां शीर्ष पर पड़ने वाले किनारों का क्रम मायने रखता है, लेकिन केवल चक्रीय क्रमपरिवर्तन तक, और चूंकि यह वास्तविक अदिशों का एक सिद्धांत है, एक ऑर्डर रिवर्सल भी (लेकिन अगर हमारे पास SU(2) के बजाय SU(N) है, तो ऑर्डर रिवर्सल मान्य नहीं है)। प्रत्येक एफ किनारे को एक संवेग (संवेग स्थानांतरण) सौंपा गया है और प्रत्येक स्वाद चक्र के साथ एक आंतरिक संवेग अभिन्न अंग जुड़ा हुआ है।
क्यूसीडी
QCD एक SU(3) गेज सिद्धांत है जिसमें ग्लूऑन और क्वार्क शामिल हैं। वेइल फर्मियन | बाएं हाथ के क्वार्क एक त्रिक प्रतिनिधित्व से संबंधित हैं, दाएँ हाथ के क्वार्क एक एंटीट्रिपलेट प्रतिनिधित्व (उन्हें चार्ज-संयुग्मित करने के बाद) और ग्लून्स एक वास्तविक संख्या के निकटवर्ती प्रतिनिधित्व से संबंधित हैं। एक क्वार्क किनारे को एक रंग और अभिविन्यास सौंपा गया है और एक ग्लूऑन किनारे को एक रंग जोड़ी सौंपी गई है।
बड़ी एन सीमा में, हम केवल प्रमुख शब्द पर विचार करते हैं। विज्ञापन/सीएफटी देखें।
संदर्भ
- G. 't Hooft (1974). "A planar diagram theory for strong interactions". Nuclear Physics B. 72 (3): 461. Bibcode:1974NuPhB..72..461T. doi:10.1016/0550-3213(74)90154-0. Archived from the original on 2006-10-11.