तापमान

Temperature
Temperature
	Thermal vibration of a segment of protein alpha helix. Its amplitude increases with temperature
सामान्य प्रतीक	T
Si इकाई	K
अन्य इकाइयां	°C, °F, °R, °Rø, °Ré, °N, °D, °L, °W
गहन?	Yes
अन्य मात्राओं से ; व्युत्पत्तियां	,
आयाम	Script error: The module returned a nil value. It is supposed to return an export table.

तापमान एक भौतिक राशि है जो पदार्थ या विकिरण की गर्मी को व्यक्त करता है।

तीन प्रकार के तापमान पैमाने हैं - वे, जैसे कि एसआई (SI) पैमाना, जो कि एक पिण्ड में परमाणु, अणु, या इलेक्ट्रॉन जैसे मुक्त रूप से चलने वाले सूक्ष्म कण, औसत अनुवादकीय गतिज ऊर्जा के संदर्भ में परिभाषित किए जाते हैं वे जो पूरी तरह से मैक्रोस्कोपिक गुणों और ऊष्मागतिकी सिद्धांतों पर निर्भर करते हैं, जैसे कि केल्विन की मूल परिभाषा, और वे जो सैद्धांतिक सिद्धांतों द्वारा परिभाषित नहीं हैं, लेकिन विशेष पदार्थों के सुविधाजनक अनुभवजन्य गुणों द्वारा परिभाषित किए गए हैं।

तापमान को तापमापी (थर्मामीटर) से मापा जाता है। यह विभिन्न तापमान पैमानों में अंशांकित है जो ऐतिहासिक रूप से परिभाषा के लिए विभिन्न संदर्भ बिंदुओं और तापमितीय पदार्थों पर निर्भर है। सबसे आम पैमाने हैं सेल्सियस पैमाना (पूर्व में "सेंटीग्रेड" कहा जाता था, इकाई डिग्री सेल्सियस (°C) के साथ), फ़ारेनहाइट पैमाना (इकाई डिग्री फ़ारेनहाइट (°F) के साथ), और केल्विन पैमाना (इकाई K के साथ), बाद वाले का मुख्य रूप से उपयोग किया जा रहा है। वैज्ञानिक उद्देश्य और प्राथमिक तापमान पैमाना है जिसे अंतर्राष्ट्रीय इकाइयों की प्रणाली (SI) द्वारा परिभाषित किया गया है।

सबसे ठंडे निकाय की कल्पना तब की जा सकती है जब उसका तापमान परम शून्य हो। प्रायोगिक तौर पर, इसे केवल बहुत करीब से देखा जा सकता है लेकिन वास्तव में नहीं पहुंचा जा सकता है, जैसा कि ऊष्मागतिकी के तीसरे नियम में मान्यता प्राप्त है। उस तापमान पर किसी निकाय से ऊष्मा के रूप में ऊर्जा निकालना असंभव होगा। किसी निकाय का शारीरिक रूप से परिभाषित ऊष्मागतिकी तापमान तभी हो सकता है जब वह ऊष्मागतिकी संतुलन की स्थिति में हो। ऊष्मागतिकी संतुलन की स्थिति में प्रत्येक वास्तविक भौतिक निकाय में एसआई (SI) और ऊष्मागतिकी दोनों का सकारात्मक पूर्ण तापमान होता है।

ऊर्जा के सावधानीपूर्वक विनियमित छोटे प्रवाह के साथ, एक निकाय को ऐसी स्थिति में रखा जा सकता है जो व्यावहारिक रूप से स्थिर है, हालांकि ऊष्मागतिकी का संतुलन नहीं है जिसमें निकाय के सूक्ष्म घटकों को गणितीय रूप से परिभाषित ऋणात्मक पूर्ण ऊष्मागतिकी तापमान के रूप में माना जा सकता है, लेकिन ऐसा निकाय उस निकाय की तुलना में अधिक गर्म होता है जिसकी कल्पना परम शून्य तापमान पर की जाती है। ऐसे घटकों के लिए एसआई (SI) तापमान परिभाषित नहीं है क्योंकि वे स्वतंत्र रूप से गतिमान नहीं होते हैं।

भौतिक विज्ञान, रसायन विज्ञान, पृथ्वी विज्ञान, खगोल विज्ञान, चिकित्सा, जीव विज्ञान, पारिस्थितिकी, भौतिक विज्ञान, धातु विज्ञान, यांत्रिक इंजीनियरिंग और भूगोल के साथ-साथ दैनिक जीवन के अधिकांश पहलुओं सहित प्राकृतिक विज्ञान के सभी क्षेत्रों में तापमान महत्वपूर्ण है।

प्रभाव

मानव शरीर के तापमान में औसत दैनिक भिन्नता

कई भौतिक प्रक्रियाएं तापमान से संबंधित हैं, उनमें से कुछ नीचे दी गई हैं।

चरण (ठोस, तरल, गैसीय या प्लाज्मा), घनत्व, घुलनशीलता, वाष्प दबाव, विद्युत चालकता, कठोरता, घिसाव प्रतिरोध, तापीय चालकता, संक्षारण प्रतिरोध, शक्ति सहित पदार्थ के भौतिक गुण।
रासायनिक अभिक्रियाएँ होने की दर और सीमा तक।^[1]
किसी वस्तु की सतह से उत्सर्जित तापीय विकिरण की राशि और गुण।
वायु का तापमान सभी जीवित जीवों को प्रभावित करता है।
ध्वनि की गति, जो गैस में परम तापमान के वर्गमूल के समानुपाती होती है।^[2]

पैमाने

सेल्सियस और फ़ारेनहाइट में तापमान दिखाने वाले दो थर्मामीटर

तापमान के पैमाने दो तरह से भिन्न होते हैं- शून्य डिग्री के रूप में चुना गया बिंदु और तापमान की वृद्धिशील इकाई का परिमाण।

आमतौर पर उपयोग किए जाने वाले पैमाने

सेल्सियस पैमाने (डिग्री सेल्सियस) का उपयोग दुनिया के अधिकांश हिस्सों में सामान्य तापमान माप के लिए किया जाता है। यह एक अनुभवजन्य पैमाना है जो ऐतिहासिक रूप से विकसित हुआ, जिसके कारण इसके शून्य बिंदु 0 °C को पानी के हिमांक के रूप में, और 100 °C को पानी के क्वथनांक के रूप में, दोनों समुद्र तल पर वायुमंडलीय दबाव पर के रूप में परिभाषित किया गया हैं। 100-डिग्री के अंतराल के कारण, इसे सेंटीग्रेड पैमाना कहा जाता था।^[3] इकाइयों की अंतर्राष्ट्रीय प्रणाली में केल्विन के मानकीकरण के बाद से, इसे बाद में केल्विन पैमाने पर समतुल्य प्रतिष्ठापन बिंदुओं के रूप में फिर से परिभाषित किया गया है, और इसलिए कि एक डिग्री सेल्सियस की तापमान वृद्धि एक केल्विन की वृद्धि के समान है, हालांकि संख्यात्मक रूप से वे ठीक 273.15 के योगात्मक समायोजन से भिन्न होते हैं।

फारेनहाइट पैमाना संयुक्त राज्य अमेरिका में सामान्य रूप से उपयोग में है। पानी 32 °F पर जम जाता है और समुद्र के स्तर के वायुमंडलीय दबाव में 212 °F पर उबलता है।

निरपेक्ष शून्य

तापमान के परम शून्य पर, ऊष्मा के रूप में किसी भी ऊर्जा को पदार्थ से नहीं हटाया जा सकता है, यह तथ्य ऊष्मागतिकी के तीसरे नियम में व्यक्त किया गया है। इस तापमान पर, पदार्थ में कोई मैक्रोस्कोपिक ऊष्मीय ऊर्जा नहीं होती है, लेकिन फिर भी क्वांटम-मैकेनिकल शून्य-बिंदु ऊर्जा होती है, जैसा कि अनिश्चितता सिद्धांत द्वारा भविष्यवाणी की गई है, हालांकि यह पूर्ण तापमान की परिभाषा में प्रवेश नहीं करता है। प्रयोगात्मक रूप से, निरपेक्ष शून्य को केवल बहुत निकट से ही देखा जा सकता है यह कभी नहीं पहुँचा सकता (प्रयोग द्वारा प्राप्त न्यूनतम तापमान 100 pK है)।^{[citation needed]} सैद्धांतिक रूप से, किसी निकाय में परम शून्य के तापमान पर, उसके कणों की सभी चिरसम्मत गति समाप्त हो जाती है और वे इस चिरसम्मत अर्थ में पूर्ण विराम पर होते हैं। निरपेक्ष शून्य, जिसे 0 K के रूप में परिभाषित किया गया है, −273.15 °C, या −459.67 °F के बिल्कुल बराबर है।

निरपेक्ष पैमाने

मैक्सवेल-बोल्ट्ज़मान वितरण के लिए बोल्ट्ज़मान स्थिरांक का उल्लेख करते हुए, और बोल्ट्ज़मान सांख्यिकीय यांत्रिक परिभाषा एन्ट्रॉपी के लिए,स्वतंत्र रूप से गतिमान सूक्ष्म कणों के लिए गिब्स की परिभाषा से अलग,^[4] अंतर-कण संभावित ऊर्जा की अवहेलना करते हुए, अंतर्राष्ट्रीय समझौते द्वारा, एक तापमान पैमाने को परिभाषित किया जाता है और इसे निरपेक्ष कहा जाता है क्योंकि यह विशेष तापमितीय पदार्थों और थर्मामीटर तंत्र की विशेषताओं से स्वतंत्र होता है। निरपेक्ष शून्य के अलावा, इसका कोई संदर्भ तापमान नहीं होता है। इसे केल्विन पैमाने के रूप में जाना जाता है, जिसका व्यापक रूप से विज्ञान और प्रौद्योगिकी में उपयोग किया जाता है। केल्विन (इकाई का नाम लोअर-केस 'k' के साथ लिखा गया है) अंतर्राष्ट्रीय इकाइयों की प्रणाली (SI) में तापमान की इकाई है। ऊष्मागतिकी संतुलन की स्थिति में किसी निकाय का तापमान परम शून्य के सापेक्ष हमेशा सकारात्मक होता है।

अंतरराष्ट्रीय स्तर पर सहमत केल्विन पैमाने के अलावा, लॉर्ड केल्विन द्वारा आविष्कार किया गया एक ऊष्मागतिकी तापमान पैमाना भी है, जिसका तापमान के पूर्ण शून्य पर संख्यात्मक शून्य भी है, लेकिन सीधे मैक्रोस्कोपिक एंट्रोपी सहित विशुद्ध रूप से मैक्रोस्कोपिक ऊष्मागतिकी अवधारणाओं से संबंधित है, हालांकि विहित समूह के लिए, एंट्रोपी की गिब्स सांख्यिकीय यांत्रिक परिभाषा के लिए सूक्ष्म रूप से संदर्भित है, जो कि अंतर-कण संभावित ऊर्जा को ध्यान में रखती है, साथ ही साथ स्वतंत्र कण गति को भी ध्यान में लेती है ताकि यह पूर्ण शून्य के करीब तापमान के माप के लिए जिम्मेदार हो सके।^[4] इस पैमाने का पानी के त्रिगुण बिंदु पर एक संदर्भ तापमान होता है, जिसका संख्यात्मक मान उपर्युक्त अंतरराष्ट्रीय स्तर पर सहमत केल्विन पैमाने का उपयोग करके माप द्वारा परिभाषित किया जाता है।

केल्विन पैमाना

कई वैज्ञानिक माप केल्विन तापमान पैमाने (इकाई प्रतीक- K) का उपयोग करते हैं, जिसका नाम उस भौतिक विज्ञानी के सम्मान में रखा गया है जिसने इसे पहले परिभाषित किया था। यह एक निरपेक्ष पैमाना है। इसका संख्यात्मक शून्य बिंदु, 0 K, तापमान के परम शून्य पर होता है। मई, 2019 से, केल्विन को कण गतिज सिद्धांत और सांख्यिकीय यांत्रिकी के माध्यम से परिभाषित किया गया है। अंतरराष्ट्रीय इकाइयों की प्रणाली (SI) में, केल्विन के परिमाण को बोल्ट्जमान स्थिरांक के रूप में परिभाषित किया गया है, जिसका मान अंतरराष्ट्रीय सम्मेलन द्वारा निर्धारित के रूप में परिभाषित किया गया है।^[5]^[6]

सांख्यिकीय यांत्रिक बनाम ऊष्मागतिकी तापमान पैमाने

मई 2019 से, केल्विन के परिमाण को सूक्ष्म घटनाओं के संबंध में परिभाषित किया गया है, जो सांख्यिकीय यांत्रिकी के संदर्भ में विशेषता है। पहले, लेकिन 1954 के बाद से, अंतरराष्ट्रीय इकाइयों की प्रणाली ने केल्विन के लिए एक ऊष्मागतिकी तापमान के रूप में एक पैमाने और इकाई को परिभाषित किया, दूसरे संदर्भ बिंदु के रूप में पानी के ट्रिपल बिंदु के विश्वसनीय प्रतिलिपि प्रस्तुत करने योग्य तापमान का उपयोग करके, पहला संदर्भ बिंदु निरपेक्ष शून्य पर 0 K है।^{[citation needed]}

ऐतिहासिक रूप से, पानी के त्रिगुण बिंदु का तापमान ठीक 273.16 K के रूप में परिभाषित किया गया था। आज यह एक आनुभविक रूप से मापी गई राशि है। समुद्र के स्तर के वायुमंडलीय दबाव पर पानी का हिमांक 273.15 K (0 °C) के बहुत करीब होता है।

पैमाने का वर्गीकरण

तापमान पैमाने के विभिन्न प्रकार हैं। अनुभवजन्य और सैद्धांतिक रूप से उन्हें वर्गीकृत करना सुविधाजनक हो सकता है। अनुभवजन्य तापमान पैमाने ऐतिहासिक रूप से पुराने हैं, जबकि सैद्धांतिक रूप से आधारित पैमाने उन्नीसवीं सदी के मध्य में उत्पन्न हुए थे।^[7]^[8]

अनुभवजन्य पैमाने

अनुभवजन्य रूप से आधारित तापमान पैमाने सीधे पदार्थ के सरल मैक्रोस्कोपिक भौतिक गुणों के माप पर निर्भर करते हैं। उदाहरण के लिए, एक कांच की दीवार वाली केशिका ट्यूब में सीमित पारा के एक स्तंभ की लंबाई काफी हद तक तापमान पर निर्भर होती है और यह बहुत उपयोगी पारा-इन-ग्लास थर्मामीटर का आधार है। इस तरह के पैमाने केवल तापमान की सुविधाजनक सीमाओं के भीतर ही मान्य होते हैं। उदाहरण के लिए, पारा के क्वथनांक से ऊपर, पारा-इन-ग्लास थर्मामीटर अव्यावहारिक है। अधिकांश पदार्थ तापमान में वृद्धि के साथ विस्तारित होती है, लेकिन कुछ पदार्थ, जैसे पानी, तापमान के साथ अनुबंध कुछ विशिष्ट सीमा पर बढ़ता है, और फिर वे तापमितीय पदार्थ के रूप में शायद ही उपयोगी होते हैं। एक पदार्थ अपने चरण-परिवर्तन तापमान में से एक के पास थर्मामीटर के रूप में उपयोग नहीं किए जाते है, उदाहरण के लिए, इसका क्वथनांक।

इन सीमाओं के बावजूद, सामान्यतः उपयोग किए जाने वाले व्यावहारिक थर्मामीटर अनुभवजन्य रूप से आधारित होते हैं। विशेष रूप से, इसका उपयोगउष्मामिति के लिए किया गया था, जिसने ऊष्मागतिकी की खोज में बहुत योगदान दिया। फिर भी, सैद्धांतिक भौतिकी के आधार के रूप में निर्णय लेने पर अनुभवजन्य थर्मोमेट्री में गंभीर कमियां हैं। अनुभवजन्य रूप से आधारित थर्मामीटर, उनके आधार से परे, तापमितीय पदार्थ के सामान्य भौतिक गुणों के सरल प्रत्यक्ष माप के रूप में, सैद्धांतिक भौतिक तर्क के उपयोग से पुन: जांच किए जा सकते हैं, और यह उनकी पर्याप्तता की सीमा का विस्तार कर सकते हैं।

सैद्धांतिक पैमाने

सैद्धांतिक रूप से आधारित तापमान पैमाने सीधे सैद्धांतिक तर्कों पर आधारित होते हैं, विशेष रूप से गतिज सिद्धांत और ऊष्मागतिकी के। वे व्यावहारिक रूप से व्यवहार्य भौतिक उपकरणों और पदार्थों में लगभग आदर्श रूप से महसूस किए जाते हैं। सैद्धांतिक रूप से आधारित तापमान पैमानों का उपयोग व्यावहारिक अनुभवजन्य रूप से आधारित थर्मामीटरों के लिए अंशांकन मानकों को प्रदान करने के लिए किया जाता है।

माइक्रोस्कोपिक सांख्यिकीय यांत्रिक पैमाने

भौतिकी में, अंतरराष्ट्रीय स्तर पर स्वीकृत पारंपरिक तापमान पैमाने को केल्विन पैमाना कहा जाता है। यह बोल्ट्ज़मान स्थिरांक के अंतरराष्ट्रीय स्तर पर सहमत और निर्धारित मान के माध्यम से प्राप्त किया जाता है,^[5]^[6] सूक्ष्म कणों, जैसे परमाणुओं, अणुओं और इलेक्ट्रॉनों की गति का जिक्र करते हुए, निकाय में घटक जिसका तापमान मापा जाना है। केल्विन द्वारा आविष्कार किए गए ऊष्मागतिकी तापमान पैमाने के विपरीत, वर्तमान में पारंपरिक केल्विन तापमान को एक मानक निकाय के संदर्भ अवस्था के तापमान के साथ तुलना करके और न ही मैक्रोस्कोपिक ऊष्मागतिकी के संदर्भ में परिभाषित किया जाता है।

तापमान के पूर्ण शून्य के अलावा, आंतरिक ऊष्मागतिकी संतुलन की स्थिति में एक निकाय के केल्विन तापमान को उसके भौतिक गुणों के उपयुक्त रूप से चुने गए मापों द्वारा परिभाषित किया जाता है, जैसे कि बोल्ट्ज़मान स्थिरांक के संदर्भ में सटीक रूप से ज्ञात सैद्धांतिक स्पष्टीकरण है।^{[citation needed]} वह स्थिरांक निकाय की बनावट में सूक्ष्म कणों की चुनिंदा प्रकार की गति को संदर्भित करता है। इस प्रकार की गति में, कण आपस में परस्पर क्रिया के बिना, व्यक्तिगत रूप से चलते हैं। इस तरह की गतियां सामान्यतः अंतर-कण टकराव से बाधित होती हैं, लेकिन तापमान माप के लिए, गतियों को चुना जाता है, ताकि टकराव के बीच, उनके प्रक्षेपवक्र के गैर-संवादात्मक खंड सटीक माप के लिए सुलभ हो सकें। इस उद्देश्य के लिए, अंतर-कण संभावित ऊर्जा की अवहेलना की जाती है।

एक आदर्श गैस में, और अन्य सैद्धांतिक रूप से समझ में आने वाले निकायों में, केल्विन तापमान को गैर-अंतःक्रियात्मक रूप से चलने वाले सूक्ष्म कणों की औसत गतिज ऊर्जा के आनुपातिक होने के रूप में परिभाषित किया जाता है, जिसे उपयुक्त तकनीकों द्वारा मापा जा सकता है। आनुपातिकता स्थिरांक बोल्ट्जमान नियतांक का एक साधारण गुणज है। यदि अणु, परमाणु, या इलेक्ट्रॉन,^[9]^[10] पदार्थ से उत्सर्जित होते हैं और उनके वेगों को मापा जाता है, तो उनके वेगों का स्पेक्ट्रम प्रायः मैक्सवेल-बोल्ट्जमैन वितरण नामक एक सैद्धांतिक नियम का पालन करता है, जो तापमान का एक अच्छी तरह से स्थापित माप देता है जिसके लिए नियम रखता है।^[11] इस तरह के अभी तक सफल प्रयोग नहीं हुए हैं जो सीधे थर्मोमेट्री के लिए फर्मी-डिराक वितरण का उपयोग करते हैं, लेकिन शायद यह भविष्य में हासिल किया जाएगा।

एक गैस में ध्वनि की गति सैद्धांतिक रूप से गैस के आणविक चरित्र से, उसके तापमान और दबाव से, और बोल्ट्जमान स्थिरांक के मान से गणना की जा सकती है। ज्ञात आणविक चरित्र और दबाव की गैस के लिए, यह तापमान और बोल्ट्जमान स्थिरांक के बीच संबंध प्रदान करता है। उन राशिओं को ऊष्मागतिकी चर की तुलना में अधिक सटीक रूप से जाना या मापा जा सकता है जो पानी के नमूने की स्थिति को उसके त्रिगुण बिंदु पर परिभाषित करते हैं। नतीजतन, बोल्ट्ज़मान स्थिरांक के मान को प्राथमिक रूप से परिभाषित मान के एक परिभाषित संदर्भ के रूप में लेते हुए, ध्वनि की गति का एक माप, गैस के तापमान का अधिक सटीक माप प्रदान कर सकता है।^[12]

एक आदर्श त्रि-आयामी श्याम पिंड से विद्युत चुम्बकीय विकिरण के स्पेक्ट्रम का मापन एक सटीक तापमान माप प्रदान कर सकता है क्योंकि श्याम पिंड विकिरण की अधिकतम वर्णक्रमीय चमक की आवृत्ति सीधे श्याम पिंड के तापमान के समानुपाती होती है इसे विएन के विस्थापन नियम के रूप में जाना जाता है और प्लैंक के नियम और बोस-आइंस्टीन नियम में इसकी सैद्धांतिक व्याख्या है।

एक विद्युत प्रतिरोधी द्वारा उत्पादित शोर-शक्ति के स्पेक्ट्रम का मापन सटीक तापमान माप भी प्रदान कर सकता है। प्रतिरोधी के दो टर्मिनल होते हैं और यह वास्तव में एक आयामी निकाय होता है। इस मामले के लिए बोस-आइंस्टीन नियम इंगित करता है कि शोर-शक्ति प्रतिरोधी के तापमान और उसके प्रतिरोध के मान और शोर बैंडविड्थ के सीधे आनुपातिक है। किसी दिए गए आवृत्ति बैंड में, प्रत्येक आवृत्ति से शोर-शक्ति का समान योगदान होता है और इसे जॉनसन शोर कहा जाता है। यदि प्रतिरोध का मान ज्ञात हो तो तापमान ज्ञात किया जा सकता है।^[13]^[14]

मैक्रोस्कोपिक ऊष्मागतिकी पैमाना

ऐतिहासिक रूप से, मई 2019 तक, केल्विन पैमाने की परिभाषा यह थी कि केल्विन द्वारा आविष्कार किया गया था, जो पूरी तरह से मैक्रोस्कोपिक ऊष्मागतिकी के संदर्भ में एक आदर्श कार्नोट इंजन में प्रक्रियाओं में ऊर्जा की राशि के अनुपात पर आधारित था।^{[citation needed]} वह कार्नोट इंजन दो तापमानों के बीच काम करता था जिसका तापमान मापा जाना था और एक संदर्भ, जो पानी के त्रिगुण बिंदु के तापमान पर होता है। तब संदर्भ तापमान, जो कि त्रिगुण बिंदु का था, को ठीक 273.16 K के रूप में परिभाषित किया गया था। मई 2019 से, उस मान को परिभाषा द्वारा तय नहीं किया गया था, लेकिन सूक्ष्म घटना के माध्यम से मापा जाना है, जिसमें बोल्ट्ज़मैन स्थिरांक सम्मिलित है, जैसा कि ऊपर वर्णित है। सूक्ष्म सांख्यिकीय यांत्रिक परिभाषा में संदर्भ तापमान नहीं होता है।

आदर्श गैस

एक पदार्थ जिस पर मैक्रोस्कोपिक रूप से परिभाषित तापमान पैमाना आधारित हो सकता है वह आदर्श गैस है। एक आदर्श गैस के निश्चित आयतन और द्रव्यमान द्वारा लगाया गया दबाव उसके तापमान के सीधे आनुपातिक होता है। कुछ प्राकृतिक गैसें उपयुक्त तापमान परास में इतने आदर्श गुण प्रदर्शित करती हैं कि उनका उपयोग थर्मोमेट्री के लिए किया जा सकता है ऊष्मागतिकी के विकास के दौरान यह महत्वपूर्ण था और आज भी व्यावहारिक महत्व का है।^[15]^[16] आदर्श गैस थर्मामीटर, हालांकि, ऊष्मागतिकी के लिए सैद्धांतिक रूप से सही नहीं है। इसका कारण यह है कि किसी आदर्श गैस की उसके परम शून्य तापमान पर एन्ट्रापी एक धनात्मक अर्ध-निश्चित राशि नहीं होती है, जो गैस को ऊष्मागतिकी के तीसरे नियम का उल्लंघन करती है। वास्तविक पदार्थ के विपरीत, आदर्श गैस कितनी भी ठंडी क्यों न हो, द्रवीभूत या ठोस नहीं होती है। वैकल्पिक रूप से सोच, आदर्श गैस नियम, असीम रूप से उच्च तापमान और शून्य दबाव की सीमा को संदर्भित करता है ये स्थितियां घटक अणुओं के गैर-संवादात्मक गति की गारंटी देती हैं।^[17]^[18]^[19]

गतिज सिद्धांत दृष्टिकोण

केल्विन के परिमाण को अब गतिज सिद्धांत के रूप में परिभाषित किया गया है, जो बोल्ट्जमान स्थिरांक के मान से प्राप्त होता है।

गतिज सिद्धांत पदार्थ के कुछ निकायों, विशेष रूप से गैसों के लिए तापमान की एक सूक्ष्म गणना प्रदान करता है, जो मैक्रोस्कोपिक प्रणाली पर आधारित होता है, जो कई सूक्ष्म कणों से बना होता है, जैसे कि विभिन्न प्रजातियों के अणु और आयन, एक प्रजाति के कण सभी समान होते हैं। यह सूक्ष्म कणों के चिरसम्मत यांत्रिकी के माध्यम से मैक्रोस्कोपिक घटना की व्याख्या करता है। गतिज सिद्धांत के समविभाजन प्रमेय का दावा है कि स्वतंत्र रूप से गतिमान कण की प्रत्येक चिरसम्मत स्वतंत्रता की कोटि में kBT/2 की औसत गतिज ऊर्जा होती है, जहां kB बोल्ट्जमान स्थिरांक को दर्शाता है।^{[citation needed]} कण की अनुवाद गति में तीन स्वतंत्रता की कोटि होती है, ताकि, बहुत कम तापमानों को छोड़कर, जहां क्वांटम प्रभाव प्रबल होते हैं, तापमान T वाली प्रणाली में स्वतंत्र रूप से चलने वाले कण की औसत अनुवादकीय गतिज ऊर्जा 3kBT/2 होगी।

अणु, जैसे कि ऑक्सीजन (O2) में एकल गोलाकार परमाणुओं की तुलना में अधिक स्वतंत्रता की कोटि होती है वे घूर्णी और कंपन गति के साथ-साथ अनुवाद से भी गुजरते हैं। परितप्त के परिणामस्वरूप अणुओं की औसत स्थानान्तरण गतिज ऊर्जा में वृद्धि के कारण ताप में वृद्धि होती है। ताप भी समविभाजन के माध्यम से, कंपन और घूर्णी मोड से जुड़ी ऊर्जा में वृद्धि का कारण होगा। इस प्रकार एक द्विपरमाणुक गैस को अपने तापमान को एक निश्चित राशि में बढ़ाने के लिए अधिक ऊर्जा इनपुट की आवश्यकता होगी, अर्थात इसमें एक एकपरमाणुक गैस की तुलना में अधिक ऊष्मा क्षमता होगी।

जैसा कि ऊपर उल्लेख किया गया है, गैस में ध्वनि की गति की गणना गैस के आणविक चरित्र से, उसके तापमान और दबाव से और बोल्ट्जमैन स्थिरांक के मान से की जा सकती है। बोल्ट्ज़मान स्थिरांक के मान को प्राथमिक रूप से परिभाषित मान के एक परिभाषित संदर्भ के रूप में लेते हुए, ध्वनि की गति का एक माप गैस के तापमान का अधिक सटीक माप प्रदान कर सकता है।^[12]

घटक सूक्ष्म कणों की औसत गतिज ऊर्जा को मापना संभव है यदि उन्हें युक्त दीवार में एक छोटे से छेद के माध्यम से प्रणाली के ढेर से बाहर निकलने की अनुमति दी जाती है। वेगों के स्पेक्ट्रम को मापना होता है, और औसत की गणना उसी से की जाती है। यह जरूरी नहीं है कि जो कण बच जाते हैं और मापे जाते हैं, उनका वेग वितरण उतना ही होता है जितना कि प्रणाली के ढेर में रहने वाले कणों का, लेकिन कभी-कभी एक अच्छा नमूना संभव होता है।

ऊष्मागतिकी दृष्टिकोण

ऊष्मागतिकी के अध्ययन में तापमान प्रमुख राशिओं में से एक है। पूर्व में, केल्विन के परिमाण को ऊष्मागतिकी शब्दों में परिभाषित किया गया था, लेकिन आजकल, जैसा कि ऊपर उल्लेख किया गया है, इसे गतिज सिद्धांत के संदर्भ में परिभाषित किया गया है।

ऊष्मागतिकी तापमान को दो कारणों से निरपेक्ष कहा जाता है। एक यह है कि इसका औपचारिक स्वरूप विशेष पदार्थ के गुणों से स्वतंत्र होता है। दूसरा कारण यह है कि इसका शून्य, एक अर्थ में, निरपेक्ष है, जिसमें यह पदार्थ के घटक कणों की सूक्ष्म चिरसम्मत गति की अनुपस्थिति को इंगित करता है, ताकि ऊष्मागतिकी के तीसरे नियम के अनुसार, शून्य तापमान के लिए उनके पास शून्य की एक सीमित विशिष्ट गर्मी हो। फिर भी, एक ऊष्मागतिकी तापमान का वास्तव में एक निश्चित संख्यात्मक मान होता है जिसे परंपरा द्वारा मनमाने ढंग से चुना गया है और यह विशेष पदार्थों के गुणों पर निर्भर है यह सापेक्ष "डिग्री" पैमानों जैसे सेल्सियस और फ़ारेनहाइट की तुलना में केवल कम मनमाना है। एक निश्चित बिंदु (शून्य) के साथ एक निरपेक्ष पैमाना होने के नाते, सापेक्ष पैमानों में दो के बजाय मनमाने ढंग से चुनाव करने के लिए केवल एक स्वतंत्रता की कोटि बची है, मई 2019 से केल्विन पैमाने के लिए, अंतर्राष्ट्रीय सम्मेलन द्वारा, आणविक गति के बारे में सूक्ष्म गतिज सिद्धांतों पर भरोसा करते हुए, विभिन्न थर्मोमेट्रिक उपकरणों के संचालन के तरीकों के ज्ञान का उपयोग करने का विकल्प बनाया गया है। संख्यात्मक पैमाने को बोल्ट्ज़मान स्थिरांक के मान की एक पारंपरिक परिभाषा द्वारा तय किया जाता है, जो अणुओं जैसे कणों की औसत सूक्ष्म गतिज ऊर्जा के लिए मैक्रोस्कोपिक तापमान से संबंधित है। इसका संख्यात्मक मान मनमाना है, और एक वैकल्पिक, कम व्यापक रूप से उपयोग किया जाने वाला निरपेक्ष तापमान पैमाना मौजूद है जिसे रैंकिन पैमाना कहा जाता है, जिसे फ़ारेनहाइट पैमाने के साथ संरेखित किया जाता है क्योंकि केल्विन सेल्सियस के साथ होता है।

तापमान की ऊष्मागतिकी परिभाषा केल्विन के कारण होती है। इसे एक आदर्श उपकरण के रूप में तैयार किया गया है जिसे कार्नोट इंजन कहा जाता है, जिसकी कल्पना लगातार प्रक्रियाओं के एक कल्पित निरंतर चक्र में चलने के लिए की जाती है जो इसके कार्यशील निकाय की अवस्थाओं के चक्र को पार करती है। इंजन एक गर्म संग्रह से ऊष्मा Q1 की राशि लेता है और कम राशि में अपशिष्ट ऊष्मा Q2 <0 को ठंडे संग्रह में भेजता है। कार्यशील निकाय द्वारा अवशोषित शुद्ध ऊष्मा ऊर्जा, थर्मोडायनामिक कार्य के रूप में, एक कार्य संग्रह में पारित की जाती है, और इसे इंजन का आउटपुट माना जाता है। चक्र को इतनी धीमी गति से चलने की कल्पना की जाती है कि चक्र के प्रत्येक बिंदु पर कार्यशील निकाय ऊष्मागतिकी संतुलन की स्थिति में हो। इस प्रकार चक्र की क्रमिक प्रक्रियाओं को बिना एन्ट्रापी उत्पादन के विपरीत रूप से चलाने की कल्पना की जाती है। फिर काम करने वाले निकाय को गर्म करने पर गर्म संग्रह से ली गई एन्ट्रापी की राशि , काम करने वाले निकाय के ठंडा होने पर ठंडे संग्रह में जाने वाली एन्ट्रापी के बराबर होती है। फिर संग्रहो के निरपेक्ष या ऊष्मागतिकी तापमान, T1 और T2 को इस तरह परिभाषित किया जाता है कि^[20]

${\displaystyle {\frac {T_{1}}{T_{2}}}=-{\frac {Q_{1}}{Q_{2}}}.}$

ऊष्मागतिकी का शून्य नियम इस परिभाषा को स्र्झान के एक मनमाने निकाय के निरपेक्ष या ऊष्मागतिकी तापमान को मापने के लिए उपयोग करने की अनुमति देता है, जिससे अन्य गर्म संग्रह में स्र्झान के निकाय के समान तापमान होता है।

केल्विन का मूल कार्य निरपेक्ष तापमान को 1848 में प्रकाशित किया गया था। यह ऊष्मागतिकी के पहले कानून के निर्माण से पहले कार्नोट के काम पर आधारित था। कार्नोट को ऊष्मा की कोई अच्छी समझ नहीं थी और न ही एन्ट्रापी की कोई विशिष्ट अवधारणा थी। उन्होंने 'कैलोरी' के बारे में लिखा और कहा कि गर्म संग्रह से गुजरने वाली सारी कैलोरी ठंडे संग्रह में चली गई। केल्विन ने अपने 1848 के पेपर में लिखा था कि उनका पैमाना इस मायने में निरपेक्ष था कि इसे "किसी विशेष प्रकार के पदार्थ के गुणों से स्वतंत्र रूप से" परिभाषित किया गया था। उनका निश्चित प्रकाशन, जो अभी बताई गई परिभाषा को निर्धारित करता है, 1853 में, 1851 में पढ़ा गया एक पेपर में छपा था।^[21]^[22]^[23]^[24]

संख्यात्मक विवरण पूर्व में ताप जलाशयों में से एक को पानी के त्रिगुण बिंदु पर एक सेल बनाकर तय किया गया था, जिसे 273.16 K के पूर्ण तापमान के लिए परिभाषित किया गया था।^[25] आजकल, संख्यात्मक मान माप से प्राप्त करने के बजाय सूक्ष्म सांख्यिकीय यांत्रिक अंतर्राष्ट्रीय परिभाषा के माध्यम से प्राप्त किया जाता है, जैसा कि ऊपर बताया गया है।

गहन परिवर्तनशीलता

ऊष्मागतिकी शब्दों में, तापमान एक गहन चर है क्योंकि यह किसी दिए गए निकाय के लिए दूसरे के संबंध में एक व्यापक चर के अंतर गुणांक के बराबर है। इस प्रकार इसमें दो व्यापक चरों के अनुपात के आयाम हैं। ऊष्मागतिकी में, दो निकायों को प्रायः एक सामान्य दीवार के संपर्क से जुड़ा माना जाता है, जिसमें कुछ विशिष्ट पारगम्यता गुण होते हैं। इस तरह की विशिष्ट पारगम्यता को एक विशिष्ट गहन चर के रूप में संदर्भित किया जा सकता है। उदाहरण- एक डायथर्मिक दीवार है जो केवल गर्मी के लिए पारगम्य है इस मामले के लिए गहन चर तापमान है। जब दो निकायों को विशेष रूप से पारगम्य दीवार के माध्यम से बहुत लंबे समय तक जोड़ा गया है, और एक स्थायी स्थिर स्थिति में बस गए हैं, प्रासंगिक गहन चर दोनों निकायों में बराबर हैं एक डायथर्मल दीवार के लिए, इस कथन को कभी-कभी ऊष्मागतिकी का शून्य नियम कहा जाता है।^[26]^[27]^[28]

विशेष रूप से, जब निकाय को इसकी आंतरिक ऊर्जा U, एक व्यापक चर, इसकी एन्ट्रॉपी S के एक समारोह के रूप में, एक व्यापक चर, और अन्य अवस्था चर V, N, U = U (S, V, N) के साथ वर्णित किया जाता है, तो तापमान एन्ट्रापी के संबंध में आंतरिक ऊर्जा के आंशिक व्युत्पन्न के बराबर होता है^[27]^[28]

${\displaystyle T=\left({\frac {\partial U}{\partial S}}\right)_{V,N}.}{\displaystyle T=\left({\frac {\partial U}{\partial S}}\right)_{V,N}.}$

इसी तरह, जब निकाय को इसकी आंतरिक ऊर्जा U के एक फलन के रूप में अपनी एन्ट्रॉपी S बताते हुए वर्णित किया जाता है, और अन्य अवस्था चर V, N, S = S (U, V, N) के साथ, तब तापमान का व्युत्क्रम आंतरिक ऊर्जा के संबंध में एन्ट्रापी के आंशिक व्युत्पन्न के बराबर होता है।^[27]^[29]

${\displaystyle {\frac {1}{T}}=\left({\frac {\partial S}{\partial U}}\right)_{V,N}.}$

निरपेक्ष तापमान की उपरोक्त परिभाषा, समीकरण (1), केल्विन के कारण है। यह पदार्थ के हस्तांतरण के लिए बंद प्रणालियों को संदर्भित करता है और सीधे प्रयोगात्मक प्रक्रियाओं पर विशेष जोर देता है। गिब्स द्वारा ऊष्मागतिकी की एक प्रस्तुति अधिक सार स्तर पर प्रारम्भ होती है और पदार्थ के हस्तांतरण के लिए खुली प्रणालियों से संबंधित होती है ऊष्मागतिकी के इस विकास में, उपरोक्त समीकरण (2) और (3) वास्तव में तापमान की वैकल्पिक परिभाषाएँ हैं।^[30]

स्थानीय ऊष्मागतिकी संतुलन

वास्तविक-विश्व निकाय प्रायः ऊष्मागतिकी संतुलन में नहीं होते हैं और सजातीय नहीं होते हैं। चिरसम्मत अपरिवर्तनीय ऊष्मागतिकी के तरीकों के अध्ययन के लिए, एक निकाय सामान्यतः स्थानिक और अस्थायी रूप से छोटे आकार के 'कोशिकाओं' में अवधारणात्मक रूप से विभाजित होता है। यदि इस तरह के 'सेल' में पदार्थ के लिए चिरसम्मत ऊष्मागतिकी संतुलन की स्थिति को अच्छे सन्निकटन के लिए पूरा किया जाता है, तो यह सजातीय है और इसके लिए एक तापमान मौजूद है। यदि निकाय की प्रत्येक 'कोशिका' के लिए ऐसा है, तो कहा जाता है कि स्थानीय उष्मागतिकी संतुलन पूरे निकाय में प्रबल होता है।^[31]^[32]^[33]^[34]^[35]

यह अच्छी समझ में आता है, उदाहरण के लिए, व्यापक चर U, या व्यापक चर S के बारे में कहने के लिए, कि प्रति इकाई राशि में घनत्व या प्रणाली के प्रति इकाई द्रव्यमान की राशि है, लेकिन प्रति इकाई आयतन तापमान के घनत्व या प्रणाली के प्रति इकाई द्रव्यमान तापमान की राशि के बारे में बात करने का कोई मतलब नहीं है। दूसरी ओर, एक बिंदु पर आंतरिक ऊर्जा की बात करने का कोई मतलब नहीं है, जबकि जब स्थानीय ऊष्मागतिकी संतुलन बना रहता है, तो एक बिंदु पर तापमान की बात करना अच्छा होता है। नतीजतन, तापमान एक बिंदु से दूसरे बिंदु पर भिन्न हो सकता है जो वैश्विक ऊष्मागतिकी संतुलन में नहीं है, लेकिन जिसमें स्थानीय ऊष्मागतिकी संतुलन है।

इस प्रकार, जब एक निकाय में स्थानीय ऊष्मागतिकी संतुलन होता है, तो तापमान को उस निकाय में स्थानिक रूप से भिन्न स्थानीय गुणों के रूप में माना जा सकता है, और ऐसा इसलिए है क्योंकि तापमान एक गहन चर है।

मूल सिद्धांत

तापमान पदार्थ की अवस्था की गुणवत्ता की एक माप है।^[36] गुणवत्ता को किसी विशेष तापमान पैमाने की तुलना में अधिक सार तत्व के रूप में माना जा सकता है जो इसे मापता है, और कुछ लेखकों द्वारा इसे गर्माहट (हॉटनेस) कहा जाता है।^[37]^[38]^[39] गर्माहट की गुणवत्ता केवल एक विशेष स्थान में पदार्थ की स्थिति को संदर्भित करती है, और सामान्य तौर पर, ऊष्मागतिकी संतुलन की एक स्थिर स्थिति में रखे गए निकायों के अलावा, गर्माहट एक स्थान से दूसरे स्थान पर भिन्न होती है। यह जरूरी नहीं है कि किसी विशेष स्थान पर कोई पदार्थ ऐसी स्थिति में हो जो स्थिर और लगभग सजातीय हो ताकि उसे एक अच्छी तरह से परिभाषित गर्माहट या तापमान मिल सके। गर्माहट को अमूर्त रूप से एक आयामी कई गुना के रूप में दर्शाया जा सकता है। हर मान्य तापमान पैमाने का अपना एक-से-एक नक्शा कई गुना गर्माहट में होता है।^[40]^[41]

जब तापीय संपर्क में दो प्रणालियाँ एक ही तापमान पर होती हैं तो उनके बीच कोई ऊष्मा स्थानान्तरण नहीं होता है। जब एक तापमान अंतर मौजूद होता है तो ऊष्मा स्वचालित रूप से गर्म प्रणाली से ठंडी प्रणाली में तब तक प्रवाहित होती है जब तक कि वे तापीय संतुलन में नहीं हो जाते। ऐसा ऊष्मा स्थानांतरण चालन या तापीय विकिरण द्वारा होता है।^[42]^[43]^[44]^[45]^[46]^[47]^[48]^[49]

प्रायोगिक भौतिकविदों, उदाहरण के लिए गैलीलियो और न्यूटन,^[50] ने पाया कि अनिश्चित काल तक कई अनुभवजन्य तापमान पैमाने हैं। फिर भी, ऊष्मागतिकी का शून्य नियम कहता है कि वे सभी एक ही गुणवत्ता को मापते हैं। इसका मतलब यह है कि एक निकाय के लिए आंतरिक ऊष्मागतिकी संतुलन की अपनी स्थिति में, प्रत्येक सही ढंग से कैलिब्रेटेड थर्मामीटर, चाहे वह किसी भी प्रकार का हो, जो शरीर के तापमान को मापता है, एक ही तापमान को रिकॉर्ड करता है। एक निकाय के लिए जो आंतरिक ऊष्मागतिकी संतुलन की अपनी स्थिति में नहीं है, अलग-अलग थर्मामीटर अलग-अलग तापमान रिकॉर्ड कर सकते हैं, जो क्रमशः थर्मामीटर के संचालन के तंत्र पर निर्भर करता है।

ऊष्मागतिकी संतुलन में निकाय

प्रायोगिक भौतिकी के लिए, गर्माहट का अर्थ है कि, किन्हीं दो निकायों की तुलना उनके अलग-अलग ऊष्मागतिकी संतुलन में करते समय, संख्यात्मक पैमाने के रीडिंग के साथ उपयुक्त रूप से दिए गए दो अनुभवजन्य थर्मामीटर इस बात से सहमत होंगे कि दो दिए गए निकायों में से कौन सा सबसे गर्म है, या उनके पास समान तापमान है।^[51] इसके लिए यह आवश्यक नहीं है कि दो थर्मामीटर अपने संख्यात्मक पैमाने के रीडिंग के बीच एक रैखिक संबंध रखें, लेकिन इसके लिए यह आवश्यक है कि उनके संख्यात्मक रीडिंग के बीच का संबंध सख्ती से मोनोटोनिक हो।^[52]^[53] तापीय विकिरण के विएन के विस्थापन नियम से, कैलोरीमेट्री, ऊष्मागतिकी और विशेष पदार्थों के गुणों से स्वतंत्र रूप से अधिक गर्माहट का एक निश्चित अर्थ हो सकता है थर्मल विकिरण के स्नान का तापमान आनुपातिक है, एक सार्वभौमिक स्थिरांक द्वारा इसकी आवृत्ति स्पेक्ट्रम की अधिकतम आवृत्ति होती है यह आवृत्ति हमेशा सकारात्मक होती है, लेकिन इसके मान शून्य हो सकते हैं। ऊष्मागतिकी संतुलन में एक गुहा के लिए प्रारम्भ में तापीय विकिरण को परिभाषित किया गया है। ये भौतिक तथ्य एक गणितीय कथन को सही ठहराते हैं कि गर्माहट एक क्रमबद्ध एक-आयामी कई गुना मौजूद है। यह अपने स्वयं के ऊष्मागतिकी संतुलन में निकायों के लिए तापमान और थर्मामीटर का एक मौलिक चरित्र है।^[7]^[40]^[41]^[54]^[55]

पहले क्रम के चरण परिवर्तन से गुजरने वाली प्रणाली को छोड़कर, जैसे कि बर्फ का पिघलना, एक बंद प्रणाली के रूप में ऊष्मा प्राप्त होती है, इसके आयतन में बदलाव के बिना और बाहरी बल क्षेत्रों में बदलाव के बिना इसका तापमान बढ़ जाता है। इस तरह के चरण परिवर्तन से गुजरने वाली प्रणाली के लिए इतनी धीमी गति से कि ऊष्मागतिकी संतुलन से प्रस्थान की उपेक्षा की जा सकती है, इसका तापमान स्थिर रहता है क्योंकि प्रणाली को गुप्त ऊष्मा की आपूर्ति की जाती है। इसके विपरीत, एक बंद प्रणाली से ऊष्मा की हानि, चरण परिवर्तन के बिना, राशि में परिवर्तन के बिना, और उस पर समूह करने वाले बाहरी बल क्षेत्रों में बदलाव के बिना, इसका तापमान कम हो जाता है।^[56]

निकाय स्थिर अवस्था में हैं लेकिन ऊष्मागतिकी संतुलन में नहीं हैं

जबकि अपने स्वयं के ऊष्मागतिकी संतुलन अवस्थाओं में निकायों के लिए, तापमान की धारणा के लिए आवश्यक है कि सभी अनुभवजन्य थर्मामीटर इस बात से सहमत हों कि दो में से कौन सा निकाय अधिक गर्म है या वे एक ही तापमान पर हैं, यह आवश्यकता उन निकायों के लिए सुरक्षित नहीं है जो स्थिर हैं। हालांकि ऊष्मागतिकी संतुलन में नहीं। यह तब अच्छी तरह से हो सकता है कि विभिन्न अनुभवजन्य थर्मामीटर इस बात से असहमत हैं कि कौन सा गर्म है, और यदि ऐसा है, तो कम से कम एक निकाय में एक अच्छी तरह से परिभाषित पूर्ण ऊष्मागतिकी तापमान नहीं होता है। फिर भी, किसी ने निकाय दिया है और कोई भी उपयुक्त अनुभवजन्य थर्मामीटर अभी भी प्रक्रियाओं की एक उपयुक्त श्रेणी के लिए अनुभवजन्य, गैर-पूर्ण, गर्माहट और तापमान की धारणाओं का समर्थन कर सकता है। यह गैर-संतुलन ऊष्मागतिकी में अध्ययन का विषय है।^{[citation needed]}

निकाय स्थिर अवस्था में नहीं

जब कोई निकाय स्थिर अवस्था में नहीं होता है, तो तापमान की धारणा एक स्थिर अवस्था में निकाय के लिए ऊष्मागतिकी संतुलन में नहीं होने से भी कम सुरक्षित हो जाती है। यह गैर-संतुलन ऊष्मागतिकी में भी अध्ययन का विषय है।

ऊष्मागतिकी संतुलन स्वयंसिद्धता

ऊष्मागतिकी संतुलन के स्वयंसिद्ध उपचार के लिए, 1930 के दशक से, ऊष्मागतिकी के शून्य नियम को संदर्भित करने की प्रथा बन गई है। इस तरह के नियम को पारंपरिक रूप से कहा गया न्यूनतम संस्करण केवल यह बताता है कि सभी निकाय, जो ऊष्मीय रूप से जुड़े होने पर ऊष्मीय संतुलन में होंगे, को परिभाषा के अनुसार समान तापमान कहा जाना चाहिए, लेकिन अपने आप में तापमान को पैमाने पर वास्तविक संख्या के रूप में व्यक्त की गई राशि के रूप में स्थापित नहीं करता है। इस तरह के नियम का एक अधिक भौतिक रूप से सूचनात्मक संस्करण अनुभवजन्य तापमान को कई गुना गर्माहट पर एक चार्ट के रूप में देखता है।^[40]^[55]^[57] जबकि शून्य नियम तापमान के कई अलग-अलग अनुभवजन्य पैमानों की परिभाषा की अनुमति देता है, ऊष्मागतिकी का दूसरा नियम एकल अधिमानित, निरपेक्ष तापमान की परिभाषा का चयन करता है, जो एक मनमाने पैमाने के कारक तक अद्वितीय है, जहां से ऊष्मागतिकी तापमान कहा जाता है।^[7]^[40]^[58]^[59]^[60]^[61] यदि आंतरिक ऊर्जा को ऊष्मागतिकी संतुलन में एक सजातीय प्रणाली के आयतन और एन्ट्रापी के कार्य के रूप में माना जाता है, तो ऊष्मागतिकी निरपेक्ष तापमान स्थिर राशि में एन्ट्रापी के संबंध में आंतरिक ऊर्जा के आंशिक व्युत्पन्न के रूप में प्रकट होता है। इसका प्राकृतिक, आंतरिक मूल या अशक्त बिंदु पूर्ण शून्य है जिस पर किसी भी प्रणाली की एन्ट्रापी न्यूनतम होती है। यद्यपि यह मॉडल द्वारा वर्णित न्यूनतम निरपेक्ष तापमान है, ऊष्मागतिकी का तीसरा नियम यह मानता है कि किसी भी भौतिक प्रणाली द्वारा पूर्ण शून्य प्राप्त नहीं किया जा सकता है।

ऊष्मा क्षमता

जब किसी निकाय में या उससे ऊर्जा का स्थानांतरण केवल ऊष्मा के रूप में होता है, तो निकाय की स्थिति बदल जाती है। परिवेश और उन्हें निकाय से अलग करने वाली दीवारों के आधार पर, निकाय में विभिन्न परिवर्तन संभव हैं। इनमें रासायनिक प्रतिक्रियाएं, दबाव में वृद्धि, तापमान में वृद्धि और चरण परिवर्तन सम्मिलित होते हैं। निर्दिष्ट परिस्थितियों में प्रत्येक प्रकार के परिवर्तन के लिए, ऊष्मा क्षमता परिवर्तन के परिमाण में स्थानांतरित ऊष्मा की राशि का अनुपात है।^[62] उदाहरण के लिए, यदि परिवर्तन स्थिर आयतन पर तापमान में वृद्धि है, जिसमें कोई चरण परिवर्तन नहीं होता है और कोई रासायनिक परिवर्तन नहीं होता है, तो निकाय का तापमान बढ़ जाता है और उसका दबाव बढ़ जाता है। स्थानांतरित ऊष्मा की राशि , $Δ Q$ , देखे गए तापमान परिवर्तन से विभाजित, $Δ T$ , स्थिर राशि में निकाय की ऊष्मा क्षमता है।

C_{V}={\frac {\Delta Q}{\Delta T}}.

यदि ऊष्मा क्षमता को पदार्थ की एक अच्छी तरह से परिभाषित राशि के लिए मापा जाता है, तो विशिष्ट ऊष्मा उस ऊष्मा का माप है जो ऐसी इकाई राशि के तापमान को एक इकाई तापमान तक बढ़ाने के लिए आवश्यक है। उदाहरण के लिए, पानी का तापमान एक केल्विन (एक डिग्री सेल्सियस के बराबर) बढ़ाने के लिए 4186 जूल प्रति किलोग्राम (J/kg) की आवश्यकता होती है।

माप

एक विशिष्ट सेल्सियस थर्मामीटर सर्दियों के दिन के तापमान को −17 °C . मापता है

आधुनिक वैज्ञानिक थर्मामीटर और तापमान पैमानों का उपयोग करते हुए तापमान माप कम से कम 18 वीं शताब्दी की शुरुआत तक चला जाता है, जब डैनियल गेब्रियल फ़ारेनहाइट ने एक थर्मामीटर (पारा में स्विच करना) और एक पैमाने को ओले क्रिस्टेंसेन रोमर द्वारा विकसित किया था। संयुक्त राज्य अमेरिका में गैर-वैज्ञानिक अनुप्रयोगों के लिए फ़ारेनहाइट का पैमाना अभी भी उपयोग में है।

तापमान को थर्मामीटर से मापा जाता है जिसे विभिन्न प्रकार के तापमान पैमानों पर अंशांकित अंशांकन किया जा सकता है। अधिकांश दुनिया में (बेलीज, म्यांमार, लाइबेरिया और संयुक्त राज्य अमेरिका को छोड़कर), सेल्सियस पैमाने का उपयोग अधिकांश तापमान मापने के उद्देश्यों के लिए किया जाता है। अधिकांश वैज्ञानिक केल्विन पैमाने का उपयोग करके सेल्सियस पैमाने और ऊष्मागतिकी तापमान का उपयोग करके तापमान को मापते हैं, जो कि सेल्सियस पैमाने ऑफ़सेट है ताकि इसका शून्य बिंदु 0 K = −273.15 °C, या पूर्ण शून्य हो। अमेरिका में कई इंजीनियरिंग क्षेत्र, विशेष रूप से उच्च तकनीक और अमेरिकी संघीय विनिर्देश (नागरिक और सैन्य), केल्विन और सेल्सियस पैमाने का भी उपयोग करते हैं। अमेरिका में अन्य इंजीनियरिंग क्षेत्र भी दहन जैसे ऊष्मागतिकी-संबंधित विषयों में काम करते समय रैंकिन पैमाने (एक स्थानांतरित फ़ारेनहाइट पैमाने) पर भरोसा करते हैं।

इकाइयाँ

अंतर्राष्ट्रीय इकाई प्रणाली (एसआई) में तापमान की मूल इकाई केल्विन है। इसका प्रतीक K है।

रोज़मर्रा के अनुप्रयोगों के लिए, सेल्सियस पैमाने का उपयोग करना प्रायः सुविधाजनक होता है, जिसमें 0 डिग्री सेल्सियस पानी के हिमांक से बहुत निकटता से मेल खाता है और 100 डिग्री सेल्सियस समुद्र तल पर इसका क्वथनांक होता है। चूंकि तरल बूंदें आमतौर पर उप-शून्य तापमान पर बादलों में मौजूद होती हैं, इसलिए 0 डिग्री सेल्सियस को बर्फ के गलनांक के रूप में बेहतर परिभाषित किया जाता है। इस पैमाने में, 1 डिग्री सेल्सियस का तापमान अंतर 1 केल्विन वृद्धि के समान होता है, लेकिन पैमाने की भरपाई उस तापमान से होती है जिस पर बर्फ पिघलती है (273.15 K)।

अंतरराष्ट्रीय समझौते के अनुसार,^[63]मई 2019 तक, केल्विन और सेल्सियस के पैमाने को दो फिक्सिंग बिंदुओं द्वारा परिभाषित किया गया था- पूर्ण शून्य और वियना मानक माध्य समुद्री जल का त्रिगुण बिंदु, जो विशेष रूप से हाइड्रोजन और ऑक्सीजन आइसोटोप के एक निर्दिष्ट मिश्रण के साथ तैयार किया गया पानी है। निरपेक्ष शून्य को सटीक रूप से 0 K और −273.15 °C के रूप में परिभाषित किया गया था। यह वह तापमान है जिस पर पदार्थ वाले कणों की सभी चिरसम्मत अनुवाद गति समाप्त हो जाती है और वे चिरम्मत मॉडल में पूर्ण विराम पर होते हैं। क्वांटम-यांत्रिक रूप से, हालांकि, शून्य-बिंदु गति बनी रहती है और इसमें एक संबद्ध ऊर्जा, शून्य-बिंदु ऊर्जा होती है। पदार्थ अपनी जमीनी अवस्था में है,^[64] और इसमें कोई तापीय ऊर्जा नहीं होती है। तापमान 273.16 के और 0.01 डिग्री सेल्सियस को पानी के त्रिगुण बिंदु के रूप में परिभाषित किया गया था। इस परिभाषा ने निम्नलिखित उद्देश्यों की पूर्ति की इसने केल्विन के परिमाण को निरपेक्ष शून्य और पानी के त्रिगुण बिंदु के बीच के अंतर के 273.16 भागों में ठीक 1 भाग के रूप में निर्धारित किया इसने स्थापित किया कि एक केल्विन का परिमाण ठीक वैसा ही है जैसा कि सेल्सियस पैमाने पर एक डिग्री का होता है; और इसने इन पैमानों के शून्य बिंदुओं के बीच का अंतर 273.15 K (0 K = −273.15 °C और 273.16 K = 0.01 °C) के रूप में स्थापित किया। 2019 के बाद से, बोल्ट्ज़मैन स्थिरांक पर आधारित एक नई परिभाषा आई है,^[65] लेकिन पैमानों में शायद ही कोई बदलाव किया गया है।

संयुक्त राज्य अमेरिका में, फारेनहाइट पैमाने का सबसे व्यापक रूप से उपयोग किया जाता है। इस पैमाने पर पानी का हिमांक 32 °F और क्वथनांक 212 °F के अनुरूप होता है। रैंकिन पैमाना, जो अभी भी अमेरिका में केमिकल इंजीनियरिंग के क्षेत्रों में उपयोग किया जाता है, फ़ारेनहाइट वृद्धि पर आधारित एक निरपेक्ष पैमाना है।

ऐतिहासिक पैमाने

तापमान मापने के लिए निम्नलिखित तापमान पैमानों का उपयोग किया जाता है या ऐतिहासिक रूप से उपयोग किया जाता है।

केल्विन पैमाना

सेल्सियस पैमाना

फारेनहाइट पैमाना

रैंकिन पैमाना

डेलीले पैमाना

न्यूटन पैमाना

रेउमुर पैमाना

रोमर पैमाना

प्लाज्मा भौतिकी

प्लाज्मा भौतिकी का क्षेत्र विद्युत चुम्बकीय प्रकृति की घटनाओं से संबंधित है जिसमें बहुत अधिक तापमान सम्मिलित होता है। यह इलेक्ट्रॉनवोल्ट या किलोइलेक्ट्रॉनवोल्ट (ईवी/केबी या केवी/केबी) से संबंधित एक इकाई में तापमान को ऊर्जा के रूप में व्यक्त करने के लिए प्रथागत है। संबंधित ऊर्जा, जो तापमान से आयामी रूप से भिन्न होती है, की गणना बोल्ट्ज़मान स्थिरांक और तापमान के गुणनफल के रूप में की जाती है, $E=k_{\text{B}}T$ । फिर, 1 eV/kB 11605 K होता है। QCD पदार्थ के अध्ययन में एक नियमित रूप से कुछ सौ MeV/kB के तापमान का सामना करता है, जो लगभग 1012 K के बराबर होता है।

सैद्धांतिक नींव

ऐतिहासिक रूप से, तापमान की व्याख्या के लिए कई वैज्ञानिक दृष्टिकोण हैं मैक्रोस्कोपिक अनुभवजन्य चर पर आधारित चिरसम्मत ऊष्मागतिकी विवरण जिसे प्रयोगशाला में मापा जा सकता है। गैसों का गतिज सिद्धांत जो गैस कणों की गति की ऊर्जा के प्रायिकता वितरण के लिए मैक्रोस्कोपिक विवरण से संबंधित है और सांख्यिकीय भौतिकी और क्वांटम यांत्रिकी पर आधारित एक सूक्ष्म व्याख्या। इसके अलावा, कठोर और विशुद्ध गणितीय उपचारों ने चिरम्मत ऊष्मागतिकी और तापमान के लिए एक स्वयंसिद्ध दृष्टिकोण प्रदान किया है।^[66] सांख्यिकीय भौतिकी पदार्थ के परमाणु व्यवहार का वर्णन करके एक गहरी समझ प्रदान करती है और चिरसम्मत और क्वांटम दोनों अवस्थाओं सहित सूक्ष्म अवस्थाओं के सांख्यिकीय औसत से मैक्रोस्कोपिक गुण प्राप्त करती है। मौलिक भौतिक विवरण में, तापमान को सीधे ऊर्जा की इकाइयों में मापा जा सकता है। हालांकि, विज्ञान, प्रौद्योगिकी और वाणिज्य के लिए माप की व्यावहारिक प्रणालियों में, जैसे कि इकाइयों की आधुनिक मीट्रिक प्रणाली, मैक्रोस्कोपिक और सूक्ष्म विवरण बोल्ट्ज़मान स्थिरांक द्वारा परस्पर जुड़े हुए हैं, एक आनुपातिक कारक जो सूक्ष्म माध्य गतिज ऊर्जा के तापमान को मापता है।

सांख्यिकीय यांत्रिकी में सूक्ष्म विवरण एक ऐसे मॉडल पर आधारित होता है जो एक प्रणाली को पदार्थ के मूलभूत कणों में या चिरम्मत या क्वांटम-मैकेनिकल दोलनों के एक सेट में विश्लेषण करता है और प्रणाली को सूक्ष्म अवस्थाओं के एक सांख्यिकीय समूह के रूप में मानता है। चिरम्मत भौतिक कणों के संग्रह के रूप में, तापमान गति की औसत ऊर्जा का एक उपाय है, जिसे कणों की अनुवादिक गतिज ऊर्जा कहा जाता है, चाहे वह ठोस, तरल पदार्थ, गैसों या प्लाज़्मा में हो। गतिज ऊर्जा, चिरम्मत यांत्रिकी की एक अवधारणा, एक कण का आधा द्रव्यमान उसकी गति के वर्ग से गुणा है। ऊष्मा गति की इस यांत्रिक व्याख्या में, भौतिक कणों की गतिज ऊर्जा उनके अनुवाद या कंपन गति के कणों के वेग में या उनके घूर्णन मोड की जड़त्व में रह सकती है। एकपरमाणुक परिपूर्ण गैसों में और, लगभग, अधिकांश गैसों में और साधारण धातुओं में, तापमान माध्य कण अनुवादकीय गतिज ऊर्जा, 3/2 kBT का एक माप है। यह ऊर्जा के प्रायिकता वितरण फलन को भी निर्धारित करता है। संघनित पदार्थ में, और विशेष रूप से ठोस पदार्थों में, यह विशुद्ध रूप से यांत्रिक विवरण प्रायः कम उपयोगी होता है और थरथरानवाला मॉडल क्वांटम यांत्रिक घटनाओं के लिए बेहतर विवरण प्रदान करता है। तापमान समूह के सूक्ष्म अवस्थाओं के सांख्यिकीय व्यवसाय को निर्धारित करता है। तापमान की सूक्ष्म परिभाषा केवल ऊष्मागतिकी सीमा में सार्थक है, जिसका अर्थ है कि अवस्थाओं या कणों के बड़े समूह के लिए, सांख्यिकीय मॉडल की आवश्यकताओं को पूरा करना।

गतिज ऊर्जा को तापीय ऊर्जा का एक घटक भी माना जाता है। तापीय ऊर्जा को स्वतंत्र घटकों में विभाजित किया जा सकता है, जो कि कणों की स्वतंत्रता की डिग्री या थर्मोडायनामिक सिस्टम में ऑसिलेटर्स के तरीकों के कारण होता है। सामान्य तौर पर, ऊर्जा के समविभाजन के लिए उपलब्ध स्वतंत्रता की इन डिग्री की संख्या तापमान पर निर्भर करती है, अर्थात विचाराधीन अंतःक्रियाओं का ऊर्जा क्षेत्र। ठोस पदार्थों के लिए, तापीय ऊर्जा मुख्य रूप से इसके परमाणुओं या अणुओं के कंपन से उनकी संतुलन स्थिति के बारे में जुड़ी होती है। एक आदर्श एकपरमाणुक गैस में, गतिज ऊर्जा विशेष रूप से कणों की विशुद्ध रूप से स्थानान्तरण गति में पाई जाती है। अन्य प्रणालियों में, कंपन और घूर्णी गति भी स्वतंत्रता की डिग्री में योगदान करती हैं।

गैसों का गतिज सिद्धांत

गतिज सिद्धांत से गैस के कठोर क्षेत्र मॉडल में तापमान की सैद्धांतिक समझ प्राप्त की जा सकती है।

मैक्सवेल और बोल्ट्जमैन ने एक गतिज सिद्धांत विकसित किया जो गैसों में तापमान की एक मौलिक समझ पैदा करता है।^[67] यह सिद्धांत आदर्श गैस नियम और एकपरमाणुक (या 'महान') गैसों की प्रेक्षित ऊष्मा क्षमता की भी व्याख्या करता है।^[68]^[69]^[70]

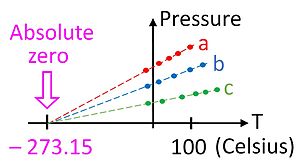
तीन अलग-अलग गैस नमूनों के लिए दबाव बनाम तापमान के प्लॉट को निरपेक्ष शून्य पर बहिर्विष्ट किया गया।

आदर्श गैस कानून दबाव (P), आयतन (V), और तापमान (T) के बीच देखे गए अनुभवजन्य संबंधों पर आधारित है, और गैसों के गतिज सिद्धांत विकसित होने से बहुत पहले पहचाना गया था (बॉयल और चार्ल्स के नियम देखें)। आदर्श गैस नियम में कहा गया है।^[71]

pV=nRT,

जहां n गैस के मोलों की संख्या है और R = 8.314462618... J⋅mol⁻¹⋅K⁻¹^[72] गैस स्थिरांक है।

यह संबंध हमें हमारा पहला संकेत देता है कि तापमान पैमाने पर एक पूर्ण शून्य होता है, क्योंकि यह केवल तभी होता है जब तापमान को केल्विन जैसे पूर्ण पैमाने पर मापा जाता है। आदर्श गैस नियम गैस थर्मामीटर का उपयोग करके इस निरपेक्ष पैमाने पर तापमान को मापने की अनुमति देता है। केल्विन में तापमान को गैस स्थिरांक से विभाजित एक घन मीटर के कंटेनर में गैस के एक मोल के पास्कल में दबाव के रूप में परिभाषित किया जा सकता है।

हालांकि यह एक विशेष रूप से सुविधाजनक उपकरण नहीं है, गैस थर्मामीटर एक आवश्यक सैद्धांतिक आधार प्रदान करता है जिसके द्वारा सभी थर्मामीटरों को अंशांकित किया जा सकता है। एक व्यावहारिक मामले के रूप में, पूर्ण शून्य तापमान को मापने के लिए गैस थर्मामीटर का उपयोग करना संभव नहीं है क्योंकि तापमान के शून्य तक पहुंचने से बहुत पहले गैसें द्रव में संघनित हो जाती हैं। हालांकि, आदर्श गैस नियम का उपयोग करके निरपेक्ष शून्य पर बहिर्विष्ट करना संभव है, जैसा कि चित्र में दिखाया गया है।

गतिज सिद्धांत मानता है कि दबाव दीवारों से टकराने वाले अलग-अलग परमाणुओं से जुड़े बल के कारण होता है, और यह सारी ऊर्जा अनुवाद की गतिज ऊर्जा है। एक परिष्कृत समरूपता तर्क का उपयोग करते हुए,^[73] बोल्ट्ज़मैन ने एक आदर्श गैस में कणों के वेग के लिए मैक्सवेल-बोल्ट्ज़मैन संभाव्यता वितरण फलन को घटाया। उस संभाव्यता वितरण फलन से, एक एकपरमाणुक आदर्श गैस की औसत गतिज ऊर्जा (प्रति कण) है।^[69]^[74]

E_{\text{k}}={\frac {1}{2}}mv_{\text{rms}}^{2}={\frac {3}{2}}k_{\text{B}}T,

जहां बोल्ट्जमान स्थिरांक kB आदर्श गैस स्थिरांक है जिसे एवोगैड्रो संख्या से विभाजित किया जाता है, और ${\textstyle v_{\text{rms}}={\sqrt {\langle v^{2}\rangle }}={\sqrt {\langle \mathbf {v\cdot v} \rangle }}}$ मूल-माध्य-वर्ग गति है।^[75] तापमान और माध्य आणविक गतिज ऊर्जा के बीच यह प्रत्यक्ष आनुपातिकता समविभाजन प्रमेय का एक विशेष मामला है, और केवल एक आदर्श गैस की चिरसम्मत सीमा में ही है। यह अधिकांश पदार्थों के लिए सटीक रूप से धारण नहीं करता है।

ऊष्मागतिकी का शून्य नियम

जब दो अलग-अलग निकाय पदार्थ के लिए अभेद्य कठोर भौतिक पथ द्वारा एक साथ जुड़े होते हैं, तो ऊष्मा के रूप में गर्म से ठंडे में ऊर्जा का सहज हस्तांतरण होता है। अंततः, वे आपसी तापीय संतुलन की स्थिति में पहुंच जाते हैं, जिसमें ऊष्मा हस्तांतरण बंद हो गया है, और निकायों के संबंधित राज्य चर अपरिवर्तनीय हो गए हैं।^[76]^[77]^[78]

ऊष्मागतिकी का शून्य नियम का एक कथन यह है कि यदि दो प्रणालियाँ एक तीसरे प्रणाली के साथ तापीय संतुलन में हैं, तो वे एक दूसरे के साथ तापीय संतुलन में भी हैं।^[79]^[80]^[81]

यह कथन तापमान को परिभाषित करने में मदद करता है लेकिन यह अपने आप परिभाषा को पूरा नहीं करता है। एक ऊष्मागतिकी प्रणाली की गर्माहट के लिए एक अनुभवजन्य तापमान एक संख्यात्मक पैमाना है। इस तरह की गर्माहट को एक-आयामी कई गुना पर विद्यमान के रूप में परिभाषित किया जा सकता है, जो गर्म और ठंडे के बीच फैली हुई है। कभी-कभी शून्य नियम में एक अद्वितीय सार्वभौमिक गर्माहट कई गुना, और उस पर संख्यात्मक पैमाने के अस्तित्व को सम्मिलित करने के लिए कहा जाता है, ताकि अनुभवजन्य तापमान की पूरी परिभाषा प्रदान की जा सके।^[57] अनुभवजन्य थर्मोमेट्री के लिए उपयुक्त होने के लिए, एक पदार्थ में गर्माहट और कुछ आसानी से मापी गई अवस्था चर, जैसे दबाव या आयतन के बीच एक एकदिष्ट संबंध होना चाहिए, जब अन्य सभी प्रासंगिक निर्देशांक तय हो जाते हैं। एक असाधारण रूप से उपयुक्त प्रणाली आदर्श गैस है, जो एक ऐसा तापमान पैमाना प्रदान कर सकती है जो निरपेक्ष केल्विन पैमाने से मेल खाता हो। केल्विन पैमाने को ऊष्मागतिकी के दूसरे नियम के आधार पर परिभाषित किया गया है।

ऊष्मागतिकी का दूसरा नियम

ऊष्मागतिकी के शून्य नियम पर विचार करने या परिभाषित करने के विकल्प के रूप में, ऊष्मागतिकी के दूसरे नियम के संदर्भ में तापमान को परिभाषित करना ऊष्मागतिकी में ऐतिहासिक विकास था जो एन्ट्रापी से संबंधित है।^{[citation needed]} दूसरा नियम कहता है कि किसी भी प्रक्रिया के परिणामस्वरूप या तो कोई परिवर्तन नहीं होगा या ब्रह्मांड की एन्ट्रापी में शुद्ध वृद्धि होगी। इसे संभाव्यता के संदर्भ में समझा जा सकता है।

उदाहरण के लिए, सिक्का उछालने की एक श्रृंखला में, एक पूरी तरह से आदेशित प्रणाली वह होगी जिसमें या तो हर उछाल ऊपर आता है या हर उछाल टेल आता है। इसका मतलब है कि परिणाम हमेशा 100% समान परिणाम होता है। इसके विपरीत, कई मिश्रित (अव्यवस्थित) परिणाम संभव हैं, और प्रत्येक उछाल के साथ उनकी संख्या बढ़ जाती है। आखिरकार, ~ 50% हेड्स और ~ 50% टेल्स का संयोजन हावी हो जाता है, और 50/50 से काफी भिन्न परिणाम प्राप्त करना तेजी से असंभव हो जाता है। इस प्रकार प्रणाली स्वाभाविक रूप से अधिकतम विकार या एन्ट्रापी की स्थिति में प्रगति करती है।

चूंकि तापमान दो प्रणालियों के बीच गर्मी के हस्तांतरण को नियंत्रित करता है और ब्रह्मांड अधिकतम एन्ट्रॉपी की ओर बढ़ता है, यह अपेक्षा की जाती है कि तापमान और एन्ट्रॉपी के बीच कुछ संबंध है। एक ऊष्मा इंजन तापीय ऊर्जा को यांत्रिक ऊर्जा में परिवर्तित करने के लिए एक उपकरण है, जिसके परिणामस्वरूप कार्य का प्रदर्शन होता है। कार्नोट ऊष्मा इंजन का विश्लेषण आवश्यक संबंध प्रदान करता है। ऊर्जा संरक्षण और ऊर्जा के अनुसार एक अवस्था फलन होने के कारण जो एक पूर्ण चक्र में नहीं बदलता है, एक पूर्ण चक्र पर ऊष्मा इंजन से काम शुद्ध ऊष्मा के बराबर होता है, यानी उच्च तापमान पर प्रणाली में डाली गई ऊष्मा का योग, q_H > 0, और कम तापमान पर छोड़ी गई अपशिष्ट ऊष्मा, q_C < 0 है।^[82]

दक्षता गर्मी इनपुट द्वारा विभाजित कार्य है।

${\displaystyle {\text{efficiency}}={\frac {w_{\text{cy}}}{q_{\text{H}}}}={\frac {q_{\text{H}}+q_{\text{C}}}{q_{\text{H}}}}=1-{\frac {|q_{\text{C}}|}{q_{\text{H}}}},}$

जहां w_cy प्रति चक्र किया जाने वाला कार्य है। दक्षता केवल |q_C|/q_H पर निर्भर करती है। क्योंकि q_C और q_H क्रमशः टीसी और टीएच तापमान पर गर्मी हस्तांतरण के अनुरूप हैं, q_C|/q_H इन तापमानों का कुछ फलन होना चाहिए।

${\displaystyle {\frac {|q_{\text{C}}|}{q_{\text{H}}}}=f\left(T_{\text{H}},T_{\text{C}}\right).}$

कार्नोट के प्रमेय में कहा गया है कि एक ही ऊष्मा भंडार के बीच काम करने वाले सभी प्रतिवर्ती इंजन समान रूप से कुशल होते हैं।^{[citation needed]} इस प्रकार, T1 और T3 के बीच काम करने वाले एक ताप इंजन की दक्षता उतनी ही होनी चाहिए जितनी एक में दो चक्र होते हैं, एक T1 और T2 के बीच, और दूसरा T2 और T3 के बीच होता है। ऐसा तभी हो सकता है जब

q_{13}={\frac {q_{1}q_{2}}{q_{2}q_{3}}},

जो ये दर्शाता है।

q_{13}=f\left(T_{1},T_{3}\right)=f\left(T_{1},T_{2}\right)f\left(T_{2},T_{3}\right).

चूंकि पहला फ़ंक्शन T₂ से स्वतंत्र है, यह तापमान दाईं ओर रद्द होना चाहिए, जिसका अर्थ है कि f(T₁, T₃) जो g(T₁)/g(T₃) के रूप में है (यानी f(T₁, T₃) = f(T₁, T₂)f(T₂, T₃) = g(T₁)/g(T₂) · g(T₂)/g(T₃) = g(T₁)/g(T₃)), जहां g एकल तापमान का एक फलन है। एक तापमान पैमाना अब इस गुण के साथ चुना जा सकता है कि

${\displaystyle {\frac {|q_{\text{C}}|}{q_{\text{H}}}}={\frac {T_{\text{C}}}{T_{\text{H}}}}.}$

(6) को वापस (4) में प्रतिस्थापित करने पर तापमान के संदर्भ में दक्षता के लिए एक संबंध मिलता है-

${\displaystyle {\text{efficiency}}=1-{\frac {|q_{\text{C}}|}{q_{\text{H}}}}=1-{\frac {T_{\text{C}}}{T_{\text{H}}}}.}$

T_C = 0 के लिए दक्षता 100% है और यह दक्षता 0 के नीचे 100% से अधिक हो जाती है। चूंकि 100% से अधिक दक्षता थर्मोडायनामिक्स के पहले कानून का उल्लंघन करती है, इसका मतलब है कि 0 के न्यूनतम संभव तापमान है। वास्तव में, मैक्रोस्कोपिक प्रणाली में अब तक का सबसे कम तापमान 20 nK था, जो 1995 में NIST में हासिल किया गया था। दाहिने हाथ की तरफ (5) को मध्य भाग से घटाना और पुनर्व्यवस्थित करना देता है^[20]^[82]

{\frac {q_{\text{H}}}{T_{\text{H}}}}+{\frac {q_{\text{C}}}{T_{\text{C}}}}=0,

जहां ऋणात्मक चिन्ह प्रणाली से निकलने वाली गर्मी को इंगित करता है। यह संबंध एक अवस्था फलन, S के अस्तित्व का सुझाव देता है, जिसका परिवर्तन विशेष रूप से एक पूर्ण चक्र के लिए गायब हो जाता है यदि इसे परिभाषित किया जाता है

${\displaystyle dS={\frac {dq_{\text{rev}}}{T}},}$

जहां सबस्क्रिप्ट एक प्रतिवर्ती प्रक्रिया को दर्शाता है। यह फलन प्रणाली की एन्ट्रॉपी से मेल खाती है, जिसे पहले वर्णित किया गया था। पुनर्व्यवस्थित (8) एंट्रोपी और ऊष्मा के काल्पनिक अनंतिम अर्ध-प्रतिवर्ती तत्वों के संदर्भ में तापमान के लिए एक सूत्र देता है

${\displaystyle T={\frac {dq_{\text{rev}}}{dS}}.}$

एक स्थिर-आयतन प्रणाली के लिए जहां एन्ट्रापी S(E) इसकी ऊर्जा E का एक फलन है, dE = dqrev और (9) देता है

${\displaystyle T^{-1}={\frac {d}{dE}}S(E),}$

यानी तापमान का व्युत्क्रम स्थिर आयतन पर ऊर्जा के संबंध में एन्ट्रापी की वृद्धि की दर है।

सांख्यिकीय यांत्रिकी से परिभाषा

सांख्यिकीय यांत्रिकी एक प्रणाली की स्वतंत्रता की मौलिक डिग्री के आधार पर तापमान को परिभाषित करती है। समीकरण (10) तापमान का परिभाषित संबंध है, जहां एन्ट्रॉपी S को दिए गए सूक्ष्म अवस्था में प्रणाली की स्थूल अवस्थाओं की संख्या के लॉगरिदम द्वारा परिभाषित (स्थिर तक) किया जाता है (जैसा कि माइक्रोकैनोनिकल समूह में निर्दिष्ट है)।

S=k_{\mathrm {B} }\ln(W)

जहाँ $k_{\mathrm {B} }$ बोल्ट्जमैन स्थिरांक है और W प्रणाली की ऊर्जा E (पतन) के साथ सूक्ष्म अवस्थाओं की संख्या है।

जब अलग-अलग तापमान वाली दो प्रणालियों को विशुद्ध रूप से तापीय संपर्क में डाल दिया जाता है, तो ऊष्मा उच्च तापमान प्रणाली से निम्न तापमान प्रणाली में प्रवाहित होगी ऊष्मागतिकी रूप से इसे ऊष्मागतिकी के दूसरे नियम द्वारा समझा जाता है ऊर्जा के हस्तांतरण के बाद एन्ट्रापी में कुल परिवर्तन $\Delta E$ प्रणाली 1 से प्रणाली 2 में है।

\Delta S=-(dS/dE)_{1}\cdot \Delta E+(dS/dE)_{2}\cdot \Delta E=\left({\frac {1}{T_{2}}}-{\frac {1}{T_{1}}}\right)\Delta E

और इस प्रकार सकारात्मक है यदि $T_{1}>T_{2}$

सांख्यिकीय यांत्रिकी के दृष्टिकोण से, संयुक्त प्रणाली 1 + प्रणाली 2 में सूक्ष्म अवस्थाओं की कुल संख्या $N_{1}\cdot N_{2}$ है, जिसका लघुगणक (बोल्ट्ज़मान स्थिरांक से गुणा) उनकी एन्ट्रॉपी का योग है इस प्रकार उच्च से निम्न तापमान तक ऊष्मा का प्रवाह, जो कुल एन्ट्रॉपी में वृद्धि लाता है, किसी भी अन्य परिदृश्य की तुलना में अधिक संभावना है (सामन्यता इसकी अधिक संभावना है), क्योंकि परिणामी स्थूल अवस्था में अधिक सूक्ष्म अवस्था होती हैं।

एकल-कण सांख्यिकी से सामान्यीकृत तापमान

तापमान की परिभाषा को कुछ कणों की प्रणालियों तक भी विस्तारित करना संभव है, जैसे कि क्वांटम डॉट में। सामान्यीकृत तापमान एक एकल/दोगुना-अधिभोग प्रणाली के साथ फर्मियन की एक छोटी प्रणाली (N यहां तक कि 10 से कम) के बीच ऊष्मा और कण विनिमय के मामले में सांख्यिकीय यांत्रिकी में दिए गए विन्यास-स्थान समूह के बजाय समय के टुकड़ों पर विचार करके प्राप्त किया जाता है।^[83] अभ्यतिप्रायता और रूढ़िवादिता की परिकल्पना के तहत प्राप्त परिमित क्वांटम भव्य विहित समूह,^[84] व्यवसाय के औसत समय के अनुपात से सामान्यीकृत तापमान को व्यक्त करने की अनुमति देता है $\tau _{1}$ तथा $\tau _{2}$ सिंगल/डबल-अधिभोग प्रणाली की।^[85]

T={\frac {E-E_{\text{F}}\left(1+{\frac {3}{2N}}\right)}{k_{\text{B}}\ln \left(2{\frac {\tau _{2}}{\tau _{1}}}\right)}},

जहां E_F फर्मी ऊर्जा है। जब N अनंत तक जाता है तो यह सामान्यीकृत तापमान सामान्य तापमान की ओर जाता है।

ऋणात्मक तापमान

अनुभवजन्य तापमान पैमानों पर जिन्हें निरपेक्ष शून्य के लिए संदर्भित नहीं किया जाता है, एक ऋणात्मक तापमान उपयोग किए गए पैमाने के शून्य-बिंदु से एक नीचे होता है। उदाहरण के लिए, सूखी बर्फ का उच्च बनाने की क्रिया तापमान −78.5 °C होता है जो -109.3 °F के बराबर होता है।^[86] निरपेक्ष केल्विन पैमाने पर यह तापमान 194.6 K है। किसी भी परिमित व्यावहारिक प्रक्रिया द्वारा किसी भी वस्तु को 0 K (आदर्श रूप से सबसे ठंडे संभव निकाय का तापमान) तक नहीं लाया जा सकता है; यह ऊष्मागतिकी के तीसरे नियम का परिणाम है।^[87]^[88]^[89]

किसी निकाय का अंतर्राष्ट्रीय गतिज सिद्धांत तापमान ऋणात्मक मान नहीं ले सकता है। हालाँकि, ऊष्मागतिकी तापमान पैमाना इतना विवश नहीं है।

पदार्थ के निकाय के लिए, कभी-कभी अवधारणात्मक रूप से परिभाषित किया जा सकता है, स्वतंत्रता की सूक्ष्म डिग्री के संदर्भ में, अर्थात् कण चक्रण, एक उपप्रणाली, पूरे निकाय के तापमान के अलावा अन्य तापमान के साथ। जब निकाय आंतरिक ऊष्मागतिकी संतुलन की अपनी स्थिति में होता है, तो पूरे निकाय और उपप्रणाली का तापमान समान होना चाहिए। दो तापमान अलग-अलग हो सकते हैं, जब बाहरी रूप से लगाए गए बल क्षेत्रों के माध्यम से, ऊर्जा को निकाय के बाकी हिस्सों से अलग, उपप्रणाली में और उससे स्थानांतरित किया जा सकता है तब पूरा निकाय आंतरिक ऊष्मागतिकी संतुलन की अपनी स्थिति में नहीं होता है। ऊर्जा की एक ऊपरी सीमा होती है जिसे एक चक्रण उपप्रणाली प्राप्त कर सकती है।

उपप्रणाली को आभासी ऊष्मागतिकी संतुलन की अस्थायी स्थिति में देखते हुए, ऊष्मागतिकी पैमाने पर एक ऋणात्मक तापमान प्राप्त करना संभव है। ऊष्मागतिकी तापमान अपनी आंतरिक ऊर्जा के संबंध में उपप्रणाली की एन्ट्रापी के व्युत्पन्न का व्युत्क्रम है। जैसे-जैसे उपप्रणाली की आंतरिक ऊर्जा बढ़ती है, कुछ सीमा के लिए एन्ट्रापी बढ़ जाती है, लेकिन अंततः अधिकतम मान प्राप्त कर लेती है और फिर घटने लगती है क्योंकि उच्चतम ऊर्जा अवस्था भरना प्रारम्भ कर देते हैं। अधिकतम एन्ट्रापी के बिंदु पर, तापमान फलन एक विलक्षणता के व्यवहार को दर्शाता है, क्योंकि ऊर्जा के कार्य के रूप में एन्ट्रापी का ढलान शून्य हो जाता है और फिर ऋणात्मक हो जाता है। जैसे ही उपप्रणाली की एन्ट्रापी अपने अधिकतम तक पहुँचती है, इसका ऊष्मागतिकी तापमान सकारात्मक अनंत तक जाता है, ढलान ऋणात्मक होने पर ऋणात्मक अनंत में बदल जाता है। इस तरह के ऋणात्मक तापमान किसी भी सकारात्मक तापमान की तुलना में अधिक गर्म होते हैं। समय के साथ, जब उपप्रणाली निकाय के बाकी हिस्सों के संपर्क में आता है, जिसमें एक सकारात्मक तापमान होता है, ऊर्जा को ऋणात्मक तापमान उपप्रणाली से सकारात्मक तापमान प्रणाली में गर्मी के रूप में स्थानांतरित किया जाता है।^[90] ऐसे उप-प्रणालियों के लिए गतिज सिद्धांत तापमान परिभाषित नहीं है।

उदाहरण

विभिन्न पैमानों में तापमान की तुलना
	तापमान		श्याम पिंड विकिरण की शिखर उत्सर्जन तरंग दैर्ध्य^[91]
	केल्विन	सेल्सियस	श्याम पिंड विकिरण की शिखर उत्सर्जन तरंग दैर्ध्य^[91]
निरपेक्ष शून्य (बिल्कुल परिभाषा के अनुसार)	0 K	−273.15 °C	Infinity
ब्लैक होल का ब्लैकबॉडी तापमान हमारी आकाशगंगा का केंद्र, Sagittarius A*^[92]	15 fK	−273.149999999999985 °C	2.5×10⁸ km (1.7 AU)
न्यूनतम तापमान हासिल किया^[93]	100 pK	−273.149999999900 °C	29000 km
सबसे ठंडा बोस-आइंस्टीन कंडेनसेट^[94]	450 pK	−273.14999999955 °C	6400 km
एक मिलीकेल्विन (ठीक परिभाषा के अनुसार)	0.001 K	−273.149 °C	2.89777 m (रेडियो, FM बैंंड)^[95]
ब्रह्मांडीय माइक्रोवेव पृष्ठभूमि (2013 माप)	2.7260 K	−270.424 °C	0.00106301 m (मिलीमीटर-तरंग दैर्ध्य माइक्रोवेव)
जल त्रिगुण बिंदु (ठीक परिभाषा के अनुसार)	273.16 K	0.01 °C	10608.3 nm (लंबी तरंग दैर्ध्य IR)
पानी का क्वथनांक [ए]	373.1339 K	99.9839 °C	7766.03 nm (मध्य तरंगदैर्घ्य IR)
लोहे का गलनांक	1811 K	1538 °C	1600 nm (सुदूर अवरक्त)
तापदीप्त दीपक [बी]	2500 K	≈2200 °C	1160 nm (निकट अवरक्त)
सूर्य की दृश्यमान सतह[D]^[96]	5778 K	5505 °C	501.5 nm (हरा-नीला प्रकाश)
बिजली चैनल [ई]	28 kK	28000 °C	100 nm (दूर का पराबैंगनी प्रकाश )
सूर्य का कोर [ई]	16 MK	16 million °C	0.18 nm (एक्स-रे)
थर्मोन्यूक्लियर हथियार (उच्चतम तापमान) [ई]^[97]	350 MK	350 million °C	8.3×10⁻³ nm (गामा किरणें)
सैंडिया नेशनल लैब्स' Z मशीन [ई]^[98]	2 GK	2 billion °C	1.4×10⁻³ nm (गामा किरणें)
अपने अंतिम दिन एक उच्च-द्रव्यमान तारे का कोर^[99]	3 GK	3 billion °C	1×10⁻³ nm (गामा किरणें)
बाइनरी का विलय न्यूट्रॉन तारा प्रणाली [ई]^[100]	350 GK	350 billion °C	8×10⁻⁶ nm (गामा किरणें)
आपेक्षिक भारी आयन कोलाइडर [ई]^[101]	1 TK	1 trillion °C	3×10⁻⁶ nm (गामा किरणें)
CERN's का प्रोटॉन बनाम नाभिकीय टक्कर[ई]^[102]	10 TK	10 trillion °C	3×10⁻⁷ nm (गामा किरणें)
ब्रह्मांड 5.391×10⁻⁴⁴ s बिग बैंग के बाद	1.417×10³² K (प्लैंक तापमान)	1.417×10³² °C	1.616×10⁻²⁷ nm (प्लैंक लंबाई)^[103]

^A For Vienna Standard Mean Ocean Water at one standard atmosphere (101.325 kPa) when calibrated strictly per the two-point definition of thermodynamic temperature.
^B The 2500 K value is approximate. The 273.15 K difference between K and °C is rounded to 300 K to avoid false precision in the Celsius value.
^C For a true black-body (which tungsten filaments are not). Tungsten filament emissivity is greater at shorter wavelengths, which makes them appear whiter.
^D Effective photosphere temperature. The 273.15 K difference between K and °C is rounded to 273 K to avoid false precision in the Celsius value.
^E The 273.15 K difference between K and °C is within the precision of these values.
^F For a true black-body (which the plasma was not). The Z machine's dominant emission originated from 40 MK electrons (soft x-ray emissions) within the plasma.

यह भी देखें

वायुमंडलीय तापमान
शरीर का तापमान - किसी जीव की अपने शरीर के तापमान को कुछ सीमाओं (थर्मोरेग्यूलेशन) के भीतर रखने की क्षमता
रंग तापमान - श्याम पिंड के विकिरण से संबंधित प्रकाश स्रोतों के गुण
शुष्क-बल्ब तापमान - विकिरण और नमी से परिरक्षित थर्मामीटर द्वारा मापा गया हवा का तापमान
ऊष्मीय चालन - कणों के टकराव और इलेक्ट्रॉन की गति के कारण शरीर के भीतर आंतरिक ऊर्जा का स्थानांतरण
संवहनी ऊष्मा हस्तांतरण
वाद्य तापमान रिकॉर्ड - स्वस्थानी माप में जो पृथ्वी की जलवायु प्रणाली का तापमान प्रदान करते हैं
आईएसओ 1 - आईएसओ मानक तापमान, 20 डिग्री सेल्सियस
1990 का अंतर्राष्ट्रीय तापमान पैमाना (ITS-90) - व्यावहारिक तापमान पैमाना
लेजर श्लेरेन डिफ्लेक्टोमेट्री
औसत तापमान के अनुसार शहरों की सूची
मैक्सवेल का दानव - 1867 का विचार प्रयोग
परिमाण के क्रम (तापमान) - तापमान की सीमा परम शून्य से बहुत अधिक
बाहरी हवा का तापमान
प्लैंक तापमान
रैंकिन पैमाना - फ़ारेनहाइट डिग्री का उपयोग करके पूर्ण तापमान पैमाना
सापेक्षिक ऊष्मा चालन - विशेष सापेक्षता के साथ संगत मॉडल
उपग्रह तापमान माप
तापमान का पैमाना - तापमान को मात्रात्मक रूप से मापने की विधि
समुद्र की सतह का तापमान - समुद्र की सतह के समीप पानी का तापमान
निश्चलता तापमान
ऊष्मीय विकिरण - कणों की ऊष्मीय गति से उत्पन्न विद्युत चुम्बकीय विकिरण
थर्मोसेप्शन - तापमान उत्तेजना ऊष्मा प्रवाह से अनुमानित और आणविक संकेत में परिवर्तित हो जाती है
थर्मोडायनामिक (पूर्ण) तापमान - पूर्ण तापमान का माप
थर्मोग्राफी - संरचनाओं या क्षेत्रों में ऊष्मा वितरण का अध्ययन करने के लिए थर्मोग्राम का उपयोग
थर्मामीटर - तापमान मापने के लिए उपकरण
आभासी तापमान
वेट-बल्ब ग्लोब तापमान - मनुष्यों पर तापमान और अन्य कारकों के प्रभाव का अनुमान लगाने के लिए उपयोग किए जाने वाले स्पष्ट तापमान का प्रकार
वेट-बल्ब तापमान - जल सिक्त कपड़े में ढके थर्मामीटर द्वारा पढ़ा जाने वाला तापमान

नोट्स और संदर्भ

↑ Agency, International Atomic Energy (1974). Thermal discharges at nuclear power stations: their management and environmental impacts: a report prepared by a group of experts as the result of a panel meeting held in Vienna, 23–27 October 1972. International Atomic Energy Agency.
↑ Watkinson, John (2001). The Art of Digital Audio. Taylor & Francis. ISBN 978-0-240-51587-8.
↑ Middleton, W.E.K. (1966), pp. 89–105.
↑ ^4.0 ^4.1 Jaynes, E.T. (1965), pp. 391–398.
↑ ^5.0 ^5.1 Cryogenic Society (2019).
↑ ^6.0 ^6.1 Draft Resolution A "On the revision of the International System of Units (SI)" to be submitted to the CGPM at its 26th meeting (2018) (PDF), archived from the original (PDF) on 2018-04-29, retrieved 2019-10-20
↑ ^7.0 ^7.1 ^7.2 Truesdell, C.A. (1980), Sections 11 B, 11H, pp. 306–310, 320–332.
↑ Quinn, T. J. (1983).
↑ Germer, L.H. (1925). 'The distribution of initial velocities among thermionic electrons', Phys. Rev., 25: 795–807. here
↑ Turvey, K. (1990). 'Test of validity of Maxwellian statistics for electrons thermionically emitted from an oxide cathode', European Journal of Physics, 11(1): 51–59. here
↑ Zeppenfeld, M., Englert, B.G.U., Glöckner, R., Prehn, A., Mielenz, M., Sommer, C., van Buuren, L.D., Motsch, M., Rempe, G. (2012).
↑ ^12.0 ^12.1 de Podesta, M., Underwood, R., Sutton, G., Morantz, P, Harris, P, Mark, D.F., Stuart, F.M., Vargha, G., Machin, M. (2013). A low-uncertainty measurement of the Boltzmann constant, Metrologia, 50 (4): S213–S216, BIPM & IOP Publishing Ltd
↑ Quinn, T.J. (1983), pp. 98–107.
↑ Schooley, J.F. (1986), pp. 138–143.
↑ Quinn, T.J. (1983), pp. 61–83.
↑ Schooley, J.F. (1986), pp. 115–138.
↑ Adkins, C.J. (1968/1983), pp. 119–120.
↑ Buchdahl, H.A. (1966), pp. 137–138.
↑ Tschoegl, N.W. (2000), p. 88.
↑ ^20.0 ^20.1 Fermi, E. (1956). Thermodynamics. Dover Publications (still in print). p. 48. eq.(64).
↑ Thomson, W. (Lord Kelvin) (1848).
↑ Thomson, W. (Lord Kelvin) (1851).
↑ Partington, J.R. (1949), pp. 175–177.
↑ Roberts, J.K., Miller, A.R. (1928/1960), pp. 321–322.
↑ Quinn, T.J. (1983). Temperature, Academic Press, London, ISBN 0-12-569680-9, pp. 160–162.
↑ Tisza, L. (1966). Generalized Thermodynamics, M.I.T. Press, Cambridge MA, pp. 47, 57.
↑ ^27.0 ^27.1 ^27.2 Münster, A. (1970), Classical Thermodynamics, translated by E.S. Halberstadt, Wiley–Interscience, London, ISBN 0-471-62430-6, pp. 49, 69.
↑ ^28.0 ^28.1 Bailyn, M. (1994). A Survey of Thermodynamics, American Institute of Physics Press, New York, ISBN 0-88318-797-3, pp. 14–15, 214.
↑ Kondepudi, D., Prigogine, I. (1998). Modern Thermodynamics. From Heat Engines to Dissipative Structures, John Wiley, Chichester, ISBN 0-471-97394-7, pp. 115–116.
↑ Tisza, L. (1966). Generalized Thermodynamics, M.I.T. Press, Cambridge MA, p. 58.
↑ Milne, E.A. (1929). The effect of collisions on monochromatic radiative equilibrium, Monthly Notices of the Royal Astronomical Society, 88: 493–502.
↑ Gyarmati, I. (1970). Non-equilibrium Thermodynamics. Field Theory and Variational Principles, translated by E. Gyarmati and W.F. Heinz, Springer, Berlin, pp. 63–66.
↑ Glansdorff, P., Prigogine, I., (1971). Thermodynamic Theory of Structure, Stability and Fluctuations, Wiley, London, ISBN 0-471-30280-5, pp. 14–16.
↑ Bailyn, M. (1994). A Survey of Thermodynamics, American Institute of Physics Press, New York, ISBN 0-88318-797-3, pp. 133–135.
↑ Callen, H.B. (1960/1985), Thermodynamics and an Introduction to Thermostatistics, (first edition 1960), second edition 1985, John Wiley & Sons, New York, ISBN 0-471-86256-8, pp. 309–310.
↑ Bryan, G.H. (1907). Thermodynamics. An Introductory Treatise dealing mainly with First Principles and their Direct Applications, B.G. Teubner, Leipzig, p. 3. "Thermodynamics by George Hartley Bryan". Archived from the original on 2011-11-18. Retrieved 2011-10-02.
↑ Pippard, A.B. (1957/1966), p. 18.
↑ Adkins,C.J. (1968/1983), p. 20.
↑ Bryan, G.H. (1907). Thermodynamics. An Introductory Treatise dealing mainly with First Principles and their Direct Applications, B.G. Teubner, Leipzig, p. 5: "... when a body is spoken of as growing hotter or colder an increase of temperature is always implied, for the hotness and coldness of a body are qualitative terms which can only refer to temperature." "Thermodynamics by George Hartley Bryan". Archived from the original on 2011-11-18. Retrieved 2011-10-02.
↑ ^40.0 ^40.1 ^40.2 ^40.3 Mach, E. (1900). Die Principien der Wärmelehre. Historisch-kritisch entwickelt, Johann Ambrosius Barth, Leipzig, section 22, pp. 56–57.
↑ ^41.0 ^41.1 Serrin, J. (1986). Chapter 1, 'An Outline of Thermodynamical Structure', pp. 3–32, especially p. 6, in New Perspectives in Thermodynamics, edited by J. Serrin, Springer, Berlin, ISBN 3-540-15931-2.
↑ Maxwell, J.C. (1872). Theory of Heat, third edition, Longmans, Green, London, p. 32.
↑ Tait, P.G. (1884). Heat, Macmillan, London, Chapter VII, pp. 39–40.
↑ Planck, M. (1897/1903). Treatise on Thermodynamics, translated by A. Ogg, Longmans, Green, London, pp. 1–2.
↑ Planck, M. (1914), The Theory of Heat Radiation Archived 2011-11-18 at the Wayback Machine, second edition, translated into English by M. Masius, Blakiston's Son & Co., Philadelphia, reprinted by Kessinger.
↑ J.S. Dugdale (1996). Entropy and its Physical Interpretation. Taylor & Francis. p. 13. ISBN 978-0-7484-0569-5.
↑ F. Reif (1965). Fundamentals of Statistical and Thermal Physics. McGraw-Hill. p. 102. ISBN 9780070518001.
↑ M.J. Moran; H.N. Shapiro (2006). "1.6.1". Fundamentals of Engineering Thermodynamics (5 ed.). John Wiley & Sons, Ltd. p. 14. ISBN 978-0-470-03037-0.{{cite book}}: CS1 maint: multiple names: authors list (link)
↑ T.W. Leland, Jr. "Basic Principles of Classical and Statistical Thermodynamics" (PDF). p. 14. Archived (PDF) from the original on 2011-09-28. Consequently we identify temperature as a driving force which causes something called heat to be transferred.
↑ Tait, P.G. (1884). Heat, Macmillan, London, Chapter VII, pp. 42, 103–117.
↑ Beattie, J.A., Oppenheim, I. (1979). Principles of Thermodynamics, Elsevier Scientific Publishing Company, Amsterdam, ISBN 978-0-444-41806-7, p. 29.
↑ Landsberg, P.T. (1961). Thermodynamics with Quantum Statistical Illustrations, Interscience Publishers, New York, p. 17.
↑ Thomsen, J.S. (1962). "A restatement of the zeroth law of thermodynamics". Am. J. Phys. 30 (4): 294–296. Bibcode:1962AmJPh..30..294T. doi:10.1119/1.1941991.
↑ Maxwell, J.C. (1872). Theory of Heat, third edition, Longman's, Green & Co, London, p. 45.
↑ ^55.0 ^55.1 Pitteri, M. (1984). On the axiomatic foundations of temperature, Appendix G6 on pp. 522–544 of Rational Thermodynamics, C. Truesdell, second edition, Springer, New York, ISBN 0-387-90874-9.
↑ Truesdell, C., Bharatha, S. (1977). The Concepts and Logic of Classical Thermodynamics as a Theory of Heat Engines, Rigorously Constructed upon the Foundation Laid by S. Carnot and F. Reech, Springer, New York, ISBN 0-387-07971-8, p. 20.
↑ ^57.0 ^57.1 Serrin, J. (1978). The concepts of thermodynamics, in Contemporary Developments in Continuum Mechanics and Partial Differential Equations. Proceedings of the International Symposium on Continuum Mechanics and Partial Differential Equations, Rio de Janeiro, August 1977, edited by G.M. de La Penha, L.A.J. Medeiros, North-Holland, Amsterdam, ISBN 0-444-85166-6, pp. 411–451.
↑ Maxwell, J.C. (1872). Theory of Heat, third edition, Longmans, Green, London, pp. 155–158.
↑ Tait, P.G. (1884). Heat, Macmillan, London, Chapter VII, Section 95, pp. 68–69.
↑ Buchdahl, H.A. (1966), p. 73.
↑ Kondepudi, D. (2008). Introduction to Modern Thermodynamics, Wiley, Chichester, ISBN 978-0-470-01598-8, Section 32., pp. 106–108.
↑ Green, Don; Perry, Robert H. (2008). Perry's Chemical Engineers' Handbook, Eighth Edition (8th ed.). McGraw-Hill Education. p. 660. ISBN 978-0071422949.
↑ The kelvin in the SI Brochure Archived 2007-09-26 at the Wayback Machine
↑ "Absolute Zero". Calphad.com. Archived from the original on 2011-07-08. Retrieved 2010-09-16.
↑ Definition agreed by the 26th General Conference on Weights and Measures (CGPM) Archived 2020-10-09 at the Wayback Machine in November 2018, implemented 20 May 2019
↑ C. Caratheodory (1909). "Untersuchungen über die Grundlagen der Thermodynamik". Mathematische Annalen. 67 (3): 355–386. doi:10.1007/BF01450409. S2CID 118230148.
↑ Swendsen, Robert (March 2006). "Statistical mechanics of colloids and Boltzmann's definition of entropy" (PDF). American Journal of Physics. 74 (3): 187–190. Bibcode:2006AmJPh..74..187S. doi:10.1119/1.2174962. S2CID 59471273. Archived from the original (PDF) on 2020-02-28.
↑ Balescu, R. (1975). Equilibrium and Nonequilibrium Statistical Mechanics, Wiley, New York, ISBN 0-471-04600-0, pp. 148–154.
↑ ^69.0 ^69.1 Kittel, Charles; Kroemer, Herbert (1980). Thermal Physics (2nd ed.). W.H. Freeman Company. pp. 391–397. ISBN 978-0-7167-1088-2.
↑ Kondepudi, D.K. (1987). "Microscopic aspects implied by the second law". Foundations of Physics. 17 (7): 713–722. Bibcode:1987FoPh...17..713K. doi:10.1007/BF01889544. S2CID 120576357.
↑ Feynman, R.P., Leighton, R.B., Sands, M. (1963). The Feynman Lectures on Physics, Addison–Wesley, Reading MA, volume 1, pp. 39-6 to 39-12.
↑ "2018 CODATA Value: molar gas constant". The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
↑ "Kinetic Theory". galileo.phys.virginia.edu. Archived from the original on 16 July 2017. Retrieved 27 January 2018.
↑ Tolman, R.C. (1938). The Principles of Statistical Mechanics, Oxford University Press, London, pp. 93, 655.
↑ Peter Atkins, Julio de Paula (2006). Physical Chemistry (8 ed.). Oxford University Press. p. 9.
↑ Maxwell, J.C. (1872). Theory of Heat, third edition, Longman's, Green & Co, London, p. 32.
↑ Bailyn, M. (1994). A Survey of Thermodynamics, American Institute of Physics Press, New York, ISBN 0-88318-797-3, p. 23, "..., if a temperature gradient exists, ..., then a flow of heat, ..., must occur to achieve a uniform temperature."
↑ Guggenheim, E.A. (1967). Thermodynamics. An Advanced Treatment for Chemists and Physicists, North-Holland Publishing Company., Amsterdam, (1st edition 1949) fifth edition 1965, p. 8, "... will gradually adjust themselves until eventually they do reach mutual equilibrium after which there will of course be no further change."
↑ Bailyn, M. (1994). A Survey of Thermodynamics, American Institute of Physics Press, New York, ISBN 0-88318-797-3, p. 22.
↑ Guggenheim, E.A. (1967). Thermodynamics. An Advanced Treatment for Chemists and Physicists, North-Holland Publishing Company., Amsterdam, (1st edition 1949) fifth edition 1965, p. 8: "If two systems are both in thermal equilibrium with a third system then they are in thermal equilibrium with each other."
↑ Buchdahl, H.A. (1966). The Concepts of Classical Thermodynamics, Cambridge University Press, Cambridge, p. 29: "... if each of two systems is in equilibrium with a third system then they are in equilibrium with each other."
↑ ^82.0 ^82.1 Planck, M. (1945). Treatise on Thermodynamics. Dover Publications. p. §90 & §137. eqs.(39), (40), & (65).
↑ Prati, E. (2010). "The finite quantum grand canonical ensemble and temperature from single-electron statistics for a mesoscopic device". J. Stat. Mech. 1 (1): P01003. arXiv:1001.2342. Bibcode:2010JSMTE..01..003P. doi:10.1088/1742-5468/2010/01/P01003. S2CID 118339343. arxiv.org Archived 2017-11-22 at the Wayback Machine
↑ "Archived copy" (PDF). Archived (PDF) from the original on 2014-04-13. Retrieved 2014-04-11.{{cite web}}: CS1 maint: archived copy as title (link)
↑ Prati, E.; et al. (2010). "Measuring the temperature of a mesoscopic electron system by means of single electron statistics". Applied Physics Letters. 96 (11): 113109. arXiv:1002.0037. Bibcode:2010ApPhL..96k3109P. doi:10.1063/1.3365204. S2CID 119209143. Archived from the original on 2016-05-14. Retrieved 2022-03-02. arxiv.org Archived 2017-11-22 at the Wayback Machine
↑ Water Science School. "Frozen carbon dioxide (dry ice) sublimates directly into a vapor". USGS.
↑ Guggenheim, E.A. (1967) [1949], Thermodynamics. An Advanced Treatment for Chemists and Physicists (fifth ed.), Amsterdam: North-Holland Publishing Company., p. 157: "It is impossible by any procedure, no matter how idealized, to reduce the temperature of any system to zero temperature in a finite number of finite operations."
↑ Pippard, A.B. (1957/1966). Elements of Classical Thermodynamics for Advanced Students of Physics, original publication 1957, reprint 1966, Cambridge University Press, Cambridge, page 51: "By no finite series of processes is the absolute zero attainable."
↑ Tisza, L. (1966). Generalized Thermodynamics, MIT Press, Cambridge MA, page 96: "It is impossible to reach absolute zero as a result of a finite sequence of operations."
↑ Kittel, Charles; Kroemer, Herbert (1980). Thermal Physics (2nd ed.). W.H. Freeman Company. p. Appendix E. ISBN 978-0-7167-1088-2.
↑ The cited emission wavelengths are for black bodies in equilibrium. CODATA 2006 recommended value of 2.8977685(51)×10⁻³ m K used for Wien displacement law constant b.
↑ This the Hawking Radiation for a Schwarzschild black hole of mass M = 4.145×10⁶ M_☉. It is too faint to be observed.
↑ "World record in low temperatures". Archived from the original on 2009-06-18. Retrieved 2009-05-05.
↑ A temperature of 450 ±80 pK in a Bose–Einstein condensate (BEC) of sodium atoms was achieved in 2003 by researchers at MIT. Citation: Cooling Bose–Einstein Condensates Below 500 Picokelvin, A.E. Leanhardt et al., Science 301, 12 Sept. 2003, p. 1515. It's noteworthy that this record's peak emittance black-body wavelength of 6,400 kilometers is roughly the radius of Earth.
↑ The peak emittance wavelength of 2.89777 m is a frequency of 103.456 MHz
↑ Measurement was made in 2002 and has an uncertainty of ±3 kelvins. A 1989 measurement Archived 2010-02-11 at the Wayback Machine produced a value of 5,777.0±2.5 K. Citation: Overview of the Sun (Chapter 1 lecture notes on Solar Physics by Division of Theoretical Physics, Dept. of Physical Sciences, University of Helsinki).
↑ The 350 MK value is the maximum peak fusion fuel temperature in a thermonuclear weapon of the Teller–Ulam configuration (commonly known as a hydrogen bomb). Peak temperatures in Gadget-style fission bomb cores (commonly known as an atomic bomb) are in the range of 50 to 100 MK. Citation: Nuclear Weapons Frequently Asked Questions, 3.2.5 Matter At High Temperatures. Link to relevant Web page. Archived 2007-05-03 at the Wayback Machine All referenced data was compiled from publicly available sources.
↑ Peak temperature for a bulk quantity of matter was achieved by a pulsed-power machine used in fusion physics experiments. The term bulk quantity draws a distinction from collisions in particle accelerators wherein high temperature applies only to the debris from two subatomic particles or nuclei at any given instant. The >2 GK temperature was achieved over a period of about ten nanoseconds during shot Z1137. In fact, the iron and manganese ions in the plasma averaged 3.58±0.41 GK (309±35 keV) for 3 ns (ns 112 through 115). Ion Viscous Heating in a Magnetohydrodynamically Unstable Z Pinch at Over 2×10⁹ Kelvin, M.G. Haines et al., Physical Review Letters 96 (2006) 075003. Link to Sandia's news release. Archived 2010-05-30 at the Wayback Machine
↑ Core temperature of a high–mass (>8–11 solar masses) star after it leaves the main sequence on the Hertzsprung–Russell diagram and begins the alpha process (which lasts one day) of fusing silicon–28 into heavier elements in the following steps: sulfur–32 → argon–36 → calcium–40 → titanium–44 → chromium–48 → iron–52 → nickel–56. Within minutes of finishing the sequence, the star explodes as a Type II supernova. Citation: Stellar Evolution: The Life and Death of Our Luminous Neighbors (by Arthur Holland and Mark Williams of the University of Michigan). Link to Web site Archived 2009-01-16 at the Wayback Machine. More informative links can be found here "Chapter 21 Stellar Explosions". Archived from the original on 2013-04-11. Retrieved 2016-02-08., and here "Trans". Archived from the original on 2011-08-14. Retrieved 2016-02-08., and a concise treatise on stars by NASA is here "NASA - Star". Archived from the original on 2010-10-24. Retrieved 2010-10-12.. "Stellar". Archived from the original on January 16, 2009. Retrieved 2010-10-12.{{cite web}}: CS1 maint: bot: original URL status unknown (link)
↑ Based on a computer model that predicted a peak internal temperature of 30 MeV (350 GK) during the merger of a binary neutron star system (which produces a gamma–ray burst). The neutron stars in the model were 1.2 and 1.6 solar masses respectively, were roughly 20 km in diameter, and were orbiting around their barycenter (common center of mass) at about 390 Hz during the last several milliseconds before they completely merged. The 350 GK portion was a small volume located at the pair's developing common core and varied from roughly 1 to 7 km across over a time span of around 5 ms. Imagine two city-sized objects of unimaginable density orbiting each other at the same frequency as the G4 musical note (the 28th white key on a piano). It's also noteworthy that at 350 GK, the average neutron has a vibrational speed of 30% the speed of light and a relativistic mass (m) 5% greater than its rest mass (m₀). Torus Formation in Neutron Star Mergers and Well-Localized Short Gamma-Ray Bursts Archived 2017-11-22 at the Wayback Machine, R. Oechslin et al. of Max Planck Institute for Astrophysics. Archived 2005-04-03 at the Wayback Machine, arXiv:astro-ph/0507099 v2, 22 Feb. 2006. An html summary Archived 2010-11-09 at the Wayback Machine.
↑ Results of research by Stefan Bathe using the PHENIX Archived 2008-11-20 at the Wayback Machine detector on the Relativistic Heavy Ion Collider Archived 2016-03-03 at the Wayback Machine at Brookhaven National Laboratory Archived 2012-06-24 at the Wayback Machine in Upton, New York. Bathe has studied gold-gold, deuteron-gold, and proton-proton collisions to test the theory of quantum chromodynamics, the theory of the strong force that holds atomic nuclei together. Link to news release. Archived 2009-02-11 at the Wayback Machine
↑ How do physicists study particles? Archived 2007-10-11 at the Wayback Machine by CERN Archived 2012-07-07 at the Wayback Machine.
↑ The Planck frequency equals 1.85487(14)×10⁴³ Hz (which is the reciprocal of one Planck time). Photons at the Planck frequency have a wavelength of one Planck length. The Planck temperature of 1.41679(11)×10³² K equates to a calculated b /T = λ_max wavelength of 2.04531(16)×10⁻²⁶ nm. However, the actual peak emittance wavelength quantizes to the Planck length of 1.61624(12)×10⁻²⁶ nm.

उद्धृत संदर्भों की ग्रंथ सूची

एडकिंस, सी। जे। (1968/1983)।संतुलन थर्मोडायनामिक्स, (प्रथम संस्करण 1968), तीसरा संस्करण 1983, कैम्ब्रिज यूनिवर्सिटी प्रेस, कैम्ब्रिज यूके, ISBN 0-521-25445-0।
बुचदहल, एच.ए.(1966)।शास्त्रीय थर्मोडायनामिक्स, कैम्ब्रिज यूनिवर्सिटी प्रेस, कैम्ब्रिज की अवधारणाएं।
जेनेस, ई.टी.(1965)।गिब्स बनाम बोल्ट्जमैन एंट्रोपीज़, अमेरिकन जर्नल ऑफ फिजिक्स, '33' (5), 391-398।
मिडलटन, डब्ल्यू.ई.के.(1966)।थर्मामीटर का एक इतिहास और मेट्रोलॉजी में इसका उपयोग, जॉन्स हॉपकिंस प्रेस, बाल्टीमोर।
Miller, J (2013). "Cooling molecules the optoelectric way". Physics Today. 66 (1): 12–14. Bibcode:2013PhT....66a..12M. doi:10.1063/pt.3.1840. Archived from the original on 2016-05-15. Retrieved 2013-07-25.
जे। आर। पार्टिंगटन | पार्टिंगटन, जे.आर. (1949)।भौतिक रसायन विज्ञान, खंड 1, मौलिक सिद्धांतों पर एक उन्नत ग्रंथ।गैसों, लॉन्गमैन, ग्रीन एंड कंपनी, लंदन, पीपी। & nbsp; 175–177 के गुण।
ब्रायन पिपार्ड | पिपार्ड, ए.बी.(1957/1966)।भौतिकी के उन्नत छात्रों के लिए शास्त्रीय थर्मोडायनामिक्स के तत्व, मूल प्रकाशन 1957, पुनर्मुद्रण 1966, कैम्ब्रिज यूनिवर्सिटी प्रेस, कैम्ब्रिज यूके।
क्विन, टी.जे.(1983)।तापमान, अकादमिक प्रेस, लंदन, ISBN 0-12-569680-9।
स्कूल, जे.एफ. (1986)।थर्मोमेट्री, सीआरसी प्रेस, बोका रैटन, ISBN 0-8493-5833-7।
रॉबर्ट्स, जे.के., मिलर, ए.आर.(1928/1960)।हीट एंड थर्मोडायनामिक्स, (फर्स्ट एडिशन 1928), फिफ्थ एडिशन, ब्लैकी एंड सोन लिमिटेड, ग्लासगो।
विलियम थॉमसन, 1 बैरन केल्विन | थॉमसन, डब्ल्यू। (लॉर्ड केल्विन) (1848)।एक पूर्ण तापमितीय पैमाने पर, कार्नोट के सिद्धांत के रूप में गर्मी के मकसद शक्ति के सिद्धांत पर स्थापित, और Regnault की टिप्पणियों से गणना की गई, Proc।कैम्ब।फिल।सोसाइटी।(1843/1863) '1', नंबर 5: 66–71।
Thomson, W. (Lord Kelvin) (March 1851). "On the Dynamical Theory of Heat, with numerical results deduced from Mr Joule's equivalent of a Thermal Unit, and M. Regnault's Observations on Steam". Transactions of the Royal Society of Edinburgh. XX (part II): 261–268, 289–298.
Truesdell, C.A.(1980)।थर्मोडायनामिक्स का दुखद इतिहास, 1822-1854, स्प्रिंगर, न्यूयॉर्क, ISBN 0-387-90403-4।
Tschoegl, N.W.(2000)।संतुलन और स्थिर-राज्य थर्मोडायनामिक्स, एल्सेवियर, एम्स्टर्डम के मूल सिद्धांतों, ISBN 0-444-50426-5।
Zeppenfeld, M.; Englert, B.G.U.; Glöckner, R.; Prehn, A.; Mielenz, M.; Sommer, C.; van Buuren, L.D.; Motsch, M.; Rempe, G. (2012). "Sysiphus cooling of electrically trapped polyatomic molecules". Nature. 491 (7425): 570–573. arXiv:1208.0046. Bibcode:2012Natur.491..570Z. doi:10.1038/nature11595. PMID 23151480. S2CID 4367940.

अग्रिम पठन

Chang, Hasok (2004). Inventing Temperature: Measurement and Scientific Progress. Oxford: Oxford University Press. ISBN 978-0-19-517127-3.
Zemansky, Mark Waldo (1964). Temperatures Very Low and Very High. Princeton, NJ: Van Nostrand.

बाहरी संबंध

Current map of global surface temperatures

] ]

[1] Agency, International Atomic Energy (1974). Thermal discharges at nuclear power stations: their management and environmental impacts: a report prepared by a group of experts as the result of a panel meeting held in Vienna, 23–27 October 1972. International Atomic Energy Agency.

[2] Watkinson, John (2001). The Art of Digital Audio. Taylor & Francis. ISBN 978-0-240-51587-8.

[3] Middleton, W.E.K. (1966), pp. 89–105.

[BoltzmannvsGibbs-4] 4.0 ^4.1 Jaynes, E.T. (1965), pp. 391–398.

[Boltzmann_constant-5] 5.0 ^5.1 Cryogenic Society (2019).

[draft-resolution-A-6] 6.0 ^6.1 Draft Resolution A "On the revision of the International System of Units (SI)" to be submitted to the CGPM at its 26th meeting (2018) (PDF), archived from the original (PDF) on 2018-04-29, retrieved 2019-10-20

[Truesdell_1980-7] 7.0 ^7.1 ^7.2 Truesdell, C.A. (1980), Sections 11 B, 11H, pp. 306–310, 320–332.

[8] Quinn, T. J. (1983).

[9] Germer, L.H. (1925). 'The distribution of initial velocities among thermionic electrons', Phys. Rev., 25: 795–807. here

[10] Turvey, K. (1990). 'Test of validity of Maxwellian statistics for electrons thermionically emitted from an oxide cathode', European Journal of Physics, 11(1): 51–59. here

[11] Zeppenfeld, M., Englert, B.G.U., Glöckner, R., Prehn, A., Mielenz, M., Sommer, C., van Buuren, L.D., Motsch, M., Rempe, G. (2012).

[de_Podesta-12] 12.0 ^12.1 de Podesta, M., Underwood, R., Sutton, G., Morantz, P, Harris, P, Mark, D.F., Stuart, F.M., Vargha, G., Machin, M. (2013). A low-uncertainty measurement of the Boltzmann constant, Metrologia, 50 (4): S213–S216, BIPM & IOP Publishing Ltd

[13] Quinn, T.J. (1983), pp. 98–107.

[14] Schooley, J.F. (1986), pp. 138–143.

[15] Quinn, T.J. (1983), pp. 61–83.

[16] Schooley, J.F. (1986), pp. 115–138.

[17] Adkins, C.J. (1968/1983), pp. 119–120.

[18] Buchdahl, H.A. (1966), pp. 137–138.

[19] Tschoegl, N.W. (2000), p. 88.

[FermiBook-20] 20.0 ^20.1 Fermi, E. (1956). Thermodynamics. Dover Publications (still in print). p. 48. eq.(64).

[21] Thomson, W. (Lord Kelvin) (1848).

[22] Thomson, W. (Lord Kelvin) (1851).

[23] Partington, J.R. (1949), pp. 175–177.

[24] Roberts, J.K., Miller, A.R. (1928/1960), pp. 321–322.

[25] Quinn, T.J. (1983). Temperature, Academic Press, London, ISBN 0-12-569680-9, pp. 160–162.

[26] Tisza, L. (1966). Generalized Thermodynamics, M.I.T. Press, Cambridge MA, pp. 47, 57.

[Munster_49_69-27] 27.0 ^27.1 ^27.2 Münster, A. (1970), Classical Thermodynamics, translated by E.S. Halberstadt, Wiley–Interscience, London, ISBN 0-471-62430-6, pp. 49, 69.

[Bailyn_14_214-28] 28.0 ^28.1 Bailyn, M. (1994). A Survey of Thermodynamics, American Institute of Physics Press, New York, ISBN 0-88318-797-3, pp. 14–15, 214.

[29] Kondepudi, D., Prigogine, I. (1998). Modern Thermodynamics. From Heat Engines to Dissipative Structures, John Wiley, Chichester, ISBN 0-471-97394-7, pp. 115–116.

[30] Tisza, L. (1966). Generalized Thermodynamics, M.I.T. Press, Cambridge MA, p. 58.

[31] Milne, E.A. (1929). The effect of collisions on monochromatic radiative equilibrium, Monthly Notices of the Royal Astronomical Society, 88: 493–502.

[32] Gyarmati, I. (1970). Non-equilibrium Thermodynamics. Field Theory and Variational Principles, translated by E. Gyarmati and W.F. Heinz, Springer, Berlin, pp. 63–66.

[33] Glansdorff, P., Prigogine, I., (1971). Thermodynamic Theory of Structure, Stability and Fluctuations, Wiley, London, ISBN 0-471-30280-5, pp. 14–16.

[34] Bailyn, M. (1994). A Survey of Thermodynamics, American Institute of Physics Press, New York, ISBN 0-88318-797-3, pp. 133–135.

[35] Callen, H.B. (1960/1985), Thermodynamics and an Introduction to Thermostatistics, (first edition 1960), second edition 1985, John Wiley & Sons, New York, ISBN 0-471-86256-8, pp. 309–310.

[36] Bryan, G.H. (1907). Thermodynamics. An Introductory Treatise dealing mainly with First Principles and their Direct Applications, B.G. Teubner, Leipzig, p. 3. "Thermodynamics by George Hartley Bryan". Archived from the original on 2011-11-18. Retrieved 2011-10-02.

[37] Pippard, A.B. (1957/1966), p. 18.

[38] Adkins,C.J. (1968/1983), p. 20.

[39] Bryan, G.H. (1907). Thermodynamics. An Introductory Treatise dealing mainly with First Principles and their Direct Applications, B.G. Teubner, Leipzig, p. 5: "... when a body is spoken of as growing hotter or colder an increase of temperature is always implied, for the hotness and coldness of a body are qualitative terms which can only refer to temperature." "Thermodynamics by George Hartley Bryan". Archived from the original on 2011-11-18. Retrieved 2011-10-02.

[Mach_1900-40] 40.0 ^40.1 ^40.2 ^40.3 Mach, E. (1900). Die Principien der Wärmelehre. Historisch-kritisch entwickelt, Johann Ambrosius Barth, Leipzig, section 22, pp. 56–57.

[Serrin_1986-41] 41.0 ^41.1 Serrin, J. (1986). Chapter 1, 'An Outline of Thermodynamical Structure', pp. 3–32, especially p. 6, in New Perspectives in Thermodynamics, edited by J. Serrin, Springer, Berlin, ISBN 3-540-15931-2.

[Maxwell_1872-42] Maxwell, J.C. (1872). Theory of Heat, third edition, Longmans, Green, London, p. 32.

[Tait_1884_39-40-43] Tait, P.G. (1884). Heat, Macmillan, London, Chapter VII, pp. 39–40.

[Planck_1897-44] Planck, M. (1897/1903). Treatise on Thermodynamics, translated by A. Ogg, Longmans, Green, London, pp. 1–2.

[45] Planck, M. (1914), The Theory of Heat Radiation Archived 2011-11-18 at the Wayback Machine, second edition, translated into English by M. Masius, Blakiston's Son & Co., Philadelphia, reprinted by Kessinger.

[dugdale-46] J.S. Dugdale (1996). Entropy and its Physical Interpretation. Taylor & Francis. p. 13. ISBN 978-0-7484-0569-5.

[reif-47] F. Reif (1965). Fundamentals of Statistical and Thermal Physics. McGraw-Hill. p. 102. ISBN 9780070518001.

[Moran-48] M.J. Moran; H.N. Shapiro (2006). "1.6.1". Fundamentals of Engineering Thermodynamics (5 ed.). John Wiley & Sons, Ltd. p. 14. ISBN 978-0-470-03037-0.{{cite book}}: CS1 maint: multiple names: authors list (link)

[49] T.W. Leland, Jr. "Basic Principles of Classical and Statistical Thermodynamics" (PDF). p. 14. Archived (PDF) from the original on 2011-09-28. Consequently we identify temperature as a driving force which causes something called heat to be transferred.

[50] Tait, P.G. (1884). Heat, Macmillan, London, Chapter VII, pp. 42, 103–117.

[51] Beattie, J.A., Oppenheim, I. (1979). Principles of Thermodynamics, Elsevier Scientific Publishing Company, Amsterdam, ISBN 978-0-444-41806-7, p. 29.

[52] Landsberg, P.T. (1961). Thermodynamics with Quantum Statistical Illustrations, Interscience Publishers, New York, p. 17.

[53] Thomsen, J.S. (1962). "A restatement of the zeroth law of thermodynamics". Am. J. Phys. 30 (4): 294–296. Bibcode:1962AmJPh..30..294T. doi:10.1119/1.1941991.

[54] Maxwell, J.C. (1872). Theory of Heat, third edition, Longman's, Green & Co, London, p. 45.

[Pitteri_1984-55] 55.0 ^55.1 Pitteri, M. (1984). On the axiomatic foundations of temperature, Appendix G6 on pp. 522–544 of Rational Thermodynamics, C. Truesdell, second edition, Springer, New York, ISBN 0-387-90874-9.

[56] Truesdell, C., Bharatha, S. (1977). The Concepts and Logic of Classical Thermodynamics as a Theory of Heat Engines, Rigorously Constructed upon the Foundation Laid by S. Carnot and F. Reech, Springer, New York, ISBN 0-387-07971-8, p. 20.

[Serrin_1978-57] 57.0 ^57.1 Serrin, J. (1978). The concepts of thermodynamics, in Contemporary Developments in Continuum Mechanics and Partial Differential Equations. Proceedings of the International Symposium on Continuum Mechanics and Partial Differential Equations, Rio de Janeiro, August 1977, edited by G.M. de La Penha, L.A.J. Medeiros, North-Holland, Amsterdam, ISBN 0-444-85166-6, pp. 411–451.

[Maxwell_1872_155-158-58] Maxwell, J.C. (1872). Theory of Heat, third edition, Longmans, Green, London, pp. 155–158.

[Tait_1884_68-69-59] Tait, P.G. (1884). Heat, Macmillan, London, Chapter VII, Section 95, pp. 68–69.

[60] Buchdahl, H.A. (1966), p. 73.

[61] Kondepudi, D. (2008). Introduction to Modern Thermodynamics, Wiley, Chichester, ISBN 978-0-470-01598-8, Section 32., pp. 106–108.

[62] Green, Don; Perry, Robert H. (2008). Perry's Chemical Engineers' Handbook, Eighth Edition (8th ed.). McGraw-Hill Education. p. 660. ISBN 978-0071422949.

[63] The kelvin in the SI Brochure Archived 2007-09-26 at the Wayback Machine

[64] "Absolute Zero". Calphad.com. Archived from the original on 2011-07-08. Retrieved 2010-09-16.

[65] Definition agreed by the 26th General Conference on Weights and Measures (CGPM) Archived 2020-10-09 at the Wayback Machine in November 2018, implemented 20 May 2019

[caratheodory-66] C. Caratheodory (1909). "Untersuchungen über die Grundlagen der Thermodynamik". Mathematische Annalen. 67 (3): 355–386. doi:10.1007/BF01450409. S2CID 118230148.

[67] Swendsen, Robert (March 2006). "Statistical mechanics of colloids and Boltzmann's definition of entropy" (PDF). American Journal of Physics. 74 (3): 187–190. Bibcode:2006AmJPh..74..187S. doi:10.1119/1.2174962. S2CID 59471273. Archived from the original (PDF) on 2020-02-28.

[68] Balescu, R. (1975). Equilibrium and Nonequilibrium Statistical Mechanics, Wiley, New York, ISBN 0-471-04600-0, pp. 148–154.

[K&K_391_397-69] 69.0 ^69.1 Kittel, Charles; Kroemer, Herbert (1980). Thermal Physics (2nd ed.). W.H. Freeman Company. pp. 391–397. ISBN 978-0-7167-1088-2.

[70] Kondepudi, D.K. (1987). "Microscopic aspects implied by the second law". Foundations of Physics. 17 (7): 713–722. Bibcode:1987FoPh...17..713K. doi:10.1007/BF01889544. S2CID 120576357.

[71] Feynman, R.P., Leighton, R.B., Sands, M. (1963). The Feynman Lectures on Physics, Addison–Wesley, Reading MA, volume 1, pp. 39-6 to 39-12.

[physconst-R-72] "2018 CODATA Value: molar gas constant". The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.

[73] "Kinetic Theory". galileo.phys.virginia.edu. Archived from the original on 16 July 2017. Retrieved 27 January 2018.

[74] Tolman, R.C. (1938). The Principles of Statistical Mechanics, Oxford University Press, London, pp. 93, 655.

[atkins-75] Peter Atkins, Julio de Paula (2006). Physical Chemistry (8 ed.). Oxford University Press. p. 9.

[76] Maxwell, J.C. (1872). Theory of Heat, third edition, Longman's, Green & Co, London, p. 32.

[77] Bailyn, M. (1994). A Survey of Thermodynamics, American Institute of Physics Press, New York, ISBN 0-88318-797-3, p. 23, "..., if a temperature gradient exists, ..., then a flow of heat, ..., must occur to achieve a uniform temperature."

[78] Guggenheim, E.A. (1967). Thermodynamics. An Advanced Treatment for Chemists and Physicists, North-Holland Publishing Company., Amsterdam, (1st edition 1949) fifth edition 1965, p. 8, "... will gradually adjust themselves until eventually they do reach mutual equilibrium after which there will of course be no further change."

[79] Bailyn, M. (1994). A Survey of Thermodynamics, American Institute of Physics Press, New York, ISBN 0-88318-797-3, p. 22.

[80] Guggenheim, E.A. (1967). Thermodynamics. An Advanced Treatment for Chemists and Physicists, North-Holland Publishing Company., Amsterdam, (1st edition 1949) fifth edition 1965, p. 8: "If two systems are both in thermal equilibrium with a third system then they are in thermal equilibrium with each other."

[81] Buchdahl, H.A. (1966). The Concepts of Classical Thermodynamics, Cambridge University Press, Cambridge, p. 29: "... if each of two systems is in equilibrium with a third system then they are in equilibrium with each other."

[PlanckBook-82] 82.0 ^82.1 Planck, M. (1945). Treatise on Thermodynamics. Dover Publications. p. §90 & §137. eqs.(39), (40), & (65).

[finense-83] Prati, E. (2010). "The finite quantum grand canonical ensemble and temperature from single-electron statistics for a mesoscopic device". J. Stat. Mech. 1 (1): P01003. arXiv:1001.2342. Bibcode:2010JSMTE..01..003P. doi:10.1088/1742-5468/2010/01/P01003. S2CID 118339343. arxiv.org Archived 2017-11-22 at the Wayback Machine

[84] "Archived copy" (PDF). Archived (PDF) from the original on 2014-04-13. Retrieved 2014-04-11.{{cite web}}: CS1 maint: archived copy as title (link)

[singlepart-85] Prati, E.; et al. (2010). "Measuring the temperature of a mesoscopic electron system by means of single electron statistics". Applied Physics Letters. 96 (11): 113109. arXiv:1002.0037. Bibcode:2010ApPhL..96k3109P. doi:10.1063/1.3365204. S2CID 119209143. Archived from the original on 2016-05-14. Retrieved 2022-03-02. arxiv.org Archived 2017-11-22 at the Wayback Machine

[86] Water Science School. "Frozen carbon dioxide (dry ice) sublimates directly into a vapor". USGS.

[87] Guggenheim, E.A. (1967) [1949], Thermodynamics. An Advanced Treatment for Chemists and Physicists (fifth ed.), Amsterdam: North-Holland Publishing Company., p. 157: "It is impossible by any procedure, no matter how idealized, to reduce the temperature of any system to zero temperature in a finite number of finite operations."

[88] Pippard, A.B. (1957/1966). Elements of Classical Thermodynamics for Advanced Students of Physics, original publication 1957, reprint 1966, Cambridge University Press, Cambridge, page 51: "By no finite series of processes is the absolute zero attainable."

[89] Tisza, L. (1966). Generalized Thermodynamics, MIT Press, Cambridge MA, page 96: "It is impossible to reach absolute zero as a result of a finite sequence of operations."

[90] Kittel, Charles; Kroemer, Herbert (1980). Thermal Physics (2nd ed.). W.H. Freeman Company. p. Appendix E. ISBN 978-0-7167-1088-2.

[91] The cited emission wavelengths are for black bodies in equilibrium. CODATA 2006 recommended value of 2.8977685(51)×10⁻³ m K used for Wien displacement law constant b.

[92] This the Hawking Radiation for a Schwarzschild black hole of mass M = 4.145×10⁶ M_☉. It is too faint to be observed.

[ltl-93] "World record in low temperatures". Archived from the original on 2009-06-18. Retrieved 2009-05-05.

[recordcold-94] A temperature of 450 ±80 pK in a Bose–Einstein condensate (BEC) of sodium atoms was achieved in 2003 by researchers at MIT. Citation: Cooling Bose–Einstein Condensates Below 500 Picokelvin, A.E. Leanhardt et al., Science 301, 12 Sept. 2003, p. 1515. It's noteworthy that this record's peak emittance black-body wavelength of 6,400 kilometers is roughly the radius of Earth.

[95] The peak emittance wavelength of 2.89777 m is a frequency of 103.456 MHz

[96] Measurement was made in 2002 and has an uncertainty of ±3 kelvins. A 1989 measurement Archived 2010-02-11 at the Wayback Machine produced a value of 5,777.0±2.5 K. Citation: Overview of the Sun (Chapter 1 lecture notes on Solar Physics by Division of Theoretical Physics, Dept. of Physical Sciences, University of Helsinki).

[97] The 350 MK value is the maximum peak fusion fuel temperature in a thermonuclear weapon of the Teller–Ulam configuration (commonly known as a hydrogen bomb). Peak temperatures in Gadget-style fission bomb cores (commonly known as an atomic bomb) are in the range of 50 to 100 MK. Citation: Nuclear Weapons Frequently Asked Questions, 3.2.5 Matter At High Temperatures. Link to relevant Web page. Archived 2007-05-03 at the Wayback Machine All referenced data was compiled from publicly available sources.

[98] Peak temperature for a bulk quantity of matter was achieved by a pulsed-power machine used in fusion physics experiments. The term bulk quantity draws a distinction from collisions in particle accelerators wherein high temperature applies only to the debris from two subatomic particles or nuclei at any given instant. The >2 GK temperature was achieved over a period of about ten nanoseconds during shot Z1137. In fact, the iron and manganese ions in the plasma averaged 3.58±0.41 GK (309±35 keV) for 3 ns (ns 112 through 115). Ion Viscous Heating in a Magnetohydrodynamically Unstable Z Pinch at Over 2×10⁹ Kelvin, M.G. Haines et al., Physical Review Letters 96 (2006) 075003. Link to Sandia's news release. Archived 2010-05-30 at the Wayback Machine

[99] Core temperature of a high–mass (>8–11 solar masses) star after it leaves the main sequence on the Hertzsprung–Russell diagram and begins the alpha process (which lasts one day) of fusing silicon–28 into heavier elements in the following steps: sulfur–32 → argon–36 → calcium–40 → titanium–44 → chromium–48 → iron–52 → nickel–56. Within minutes of finishing the sequence, the star explodes as a Type II supernova. Citation: Stellar Evolution: The Life and Death of Our Luminous Neighbors (by Arthur Holland and Mark Williams of the University of Michigan). Link to Web site Archived 2009-01-16 at the Wayback Machine. More informative links can be found here "Chapter 21 Stellar Explosions". Archived from the original on 2013-04-11. Retrieved 2016-02-08., and here "Trans". Archived from the original on 2011-08-14. Retrieved 2016-02-08., and a concise treatise on stars by NASA is here "NASA - Star". Archived from the original on 2010-10-24. Retrieved 2010-10-12.. "Stellar". Archived from the original on January 16, 2009. Retrieved 2010-10-12.{{cite web}}: CS1 maint: bot: original URL status unknown (link)

[100] Based on a computer model that predicted a peak internal temperature of 30 MeV (350 GK) during the merger of a binary neutron star system (which produces a gamma–ray burst). The neutron stars in the model were 1.2 and 1.6 solar masses respectively, were roughly 20 km in diameter, and were orbiting around their barycenter (common center of mass) at about 390 Hz during the last several milliseconds before they completely merged. The 350 GK portion was a small volume located at the pair's developing common core and varied from roughly 1 to 7 km across over a time span of around 5 ms. Imagine two city-sized objects of unimaginable density orbiting each other at the same frequency as the G4 musical note (the 28th white key on a piano). It's also noteworthy that at 350 GK, the average neutron has a vibrational speed of 30% the speed of light and a relativistic mass (m) 5% greater than its rest mass (m₀). Torus Formation in Neutron Star Mergers and Well-Localized Short Gamma-Ray Bursts Archived 2017-11-22 at the Wayback Machine, R. Oechslin et al. of Max Planck Institute for Astrophysics. Archived 2005-04-03 at the Wayback Machine, arXiv:astro-ph/0507099 v2, 22 Feb. 2006. An html summary Archived 2010-11-09 at the Wayback Machine.

[101] Results of research by Stefan Bathe using the PHENIX Archived 2008-11-20 at the Wayback Machine detector on the Relativistic Heavy Ion Collider Archived 2016-03-03 at the Wayback Machine at Brookhaven National Laboratory Archived 2012-06-24 at the Wayback Machine in Upton, New York. Bathe has studied gold-gold, deuteron-gold, and proton-proton collisions to test the theory of quantum chromodynamics, the theory of the strong force that holds atomic nuclei together. Link to news release. Archived 2009-02-11 at the Wayback Machine

[102] How do physicists study particles? Archived 2007-10-11 at the Wayback Machine by CERN Archived 2012-07-07 at the Wayback Machine.

[103] The Planck frequency equals 1.85487(14)×10⁴³ Hz (which is the reciprocal of one Planck time). Photons at the Planck frequency have a wavelength of one Planck length. The Planck temperature of 1.41679(11)×10³² K equates to a calculated b /T = λ_max wavelength of 2.04531(16)×10⁻²⁶ nm. However, the actual peak emittance wavelength quantizes to the Planck length of 1.61624(12)×10⁻²⁶ nm.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

[28]

[29]

[30]

[31]

[32]

[33]

[34]

[35]

[36]

[37]

[38]

[39]

[40]

[41]

[42]

[43]

[44]

[45]

[46]

[47]

[48]

[49]

[50]

[51]

[52]

[53]

[54]

[55]

[56]

[57]

[58]

[59]

[60]

[61]

[62]

[63]

[64]

[65]

[66]

[67]

[68]

[69]

[70]

[71]

[72]

[73]

[74]

[75]

[76]

[77]

[78]

[79]

[80]

[81]

[82]

[83]

[84]

[85]

[86]

[87]

[88]

[89]

[90]

[91]

[92]

[93]

[94]

[95]

[96]

[97]

[98]

[99]

[100]

v t e Meteorological data and variables
General	Adiabatic processes Advection Buoyancy Lapse rate Lightning Surface solar radiation Surface weather analysis Visibility Vorticity Wind Wind shear
Condensation	Cloud Cloud condensation nuclei (CCN) Fog Convective condensation level (CCL) Lifted condensation level (LCL) Precipitation Water vapor
Convection	Convective available potential energy (CAPE) Convective inhibition (CIN) Convective instability Convective momentum transport Conditional symmetric instability Convective temperature (T_c) Equilibrium level (EL) Free convective layer (FCL) Helicity K Index Level of free convection (LFC) Lifted index (LI) Maximum parcel level (MPL) Bulk Richardson number (BRN)
Temperature	Dew point (T_d) Dew point depression Dry-bulb temperature Equivalent temperature (T_e) Forest fire weather index Haines Index Heat index Humidex Humidity Relative humidity (RH) Mixing ratio Potential temperature (θ) Equivalent potential temperature (θ_e) Sea surface temperature (SST) Temperature anomaly Thermodynamic temperature Vapor pressure Virtual temperature Wet-bulb temperature Wet-bulb globe temperature Wet-bulb potential temperature Wind chill
Pressure	Atmospheric pressure Baroclinity Barotropicity Pressure gradient Pressure-gradient force (PGF)
Velocity	Maximum potential intensity

v t e Scales of temperature
Celsius Delisle Fahrenheit Gas mark Kelvin Leiden Newton Rankine Réaumur Rømer Wedgwood
Conversion formulas and comparison

Anonymous

Search