फिक के प्रसार के नियम

For मापने की तकनीक कार्डियक आउटपुट, see फिक सिद्धांत.

सूक्ष्म और स्थूल दृष्टिकोण से आणविक प्रसार। प्रारंभ में, एक बाधा (बैंगनी रेखा) के बाईं ओर विलेय अणु होते हैं और दाईं ओर कोई नहीं होता है। बाधा हटा दी जाती है, और विलेय पूरे कंटेनर को भरने के लिए विसरित हो जाता है। शीर्ष: एक एकल अणु बेतरतीब ढंग से घूमता है। मध्य: अधिक अणुओं के साथ, एक स्पष्ट प्रवृत्ति होती है जहां विलेय कंटेनर को अधिक से अधिक समान रूप से भरता है। नीचे: विलेय अणुओं की एक विशाल संख्या के साथ, यादृच्छिकता ज्ञानी नहीं हो पाती है: विलेय उच्च-सघनता वाले क्षेत्रों से कम-सांद्रता वाले क्षेत्रों में सुचारू रूप से और व्यवस्थित रूप से चलता प्रतीत होता है। इस सहज प्रवाह का वर्णन फिक के नियमों द्वारा किया गया है।

फिक के प्रसार के नियम प्रसार का वर्णन करते हैं और बड़े पैमाने पर प्रायोगिक परिणामों के आधार पर पहली बार 1855 में एडॉल्फ फिक द्वारा प्रस्तुत किए गए थे। उनका उपयोग प्रसार गुणांक, D को लिए हल करने के लिए किया जा सकता है। फिक का पहला नियम उनके दूसरे नियम को प्राप्त करने के लिए उपयोग किया जा सकता है जो बदले में प्रसार समीकरण के समान है।

फिक के नियमों का पालन करने वाली प्रसार प्रक्रियाओं को सामान्य या फिकियन प्रसार कहा जाता है; अन्यथा, इसे विषम प्रसार या गैर-स्थानीय विसरण भी कहा जाता है।

इतिहास

1855 में, फिजियोलॉजिस्ट एडॉल्फ फिक ने पहली बार अपने अब तक के जाने-माने नियमों के माध्यम से बड़े पैमाने पर परिवहन को नियंत्रित करने वाले नियमों की सूचना दी थी। फिक का काम थॉमस ग्राहम के पहले के प्रयोगों से प्रेरित था, जो मूलभूत नियमों का प्रस्ताव करने में कमी आई थी जिसके लिए फिक प्रसिद्ध हो गया था। फिक का नियम अन्य प्रसिद्ध वैज्ञानिकों द्वारा उसी युग में खोजे गए संबंधों के अनुरूप है: डार्सी का नियम (हाइड्रोलिक प्रवाह), ओम का नियम (चार्ज ट्रांसपोर्ट), और फूरियर का नियम (हीट ट्रांसपोर्ट)।

फिक के प्रयोग (ग्राहम के मॉडल पर आधारित) ने पानी की नलियों के माध्यम से दो जलाशयों के बीच फैले नमक की सांद्रता और प्रवाह को मापा। यह उल्लेखनीय है कि फिक का काम मुख्य रूप से तरल पदार्थों में प्रसार से संबंधित था, क्योंकि उस समय ठोस पदार्थों में प्रसार को सामान्यतः संभव नहीं माना जाता था। आज, फिक के नियम ठोस, तरल पदार्थ और गैसों में प्रसार की हमारी समझ का मूल रूप बनाते हैं (बाद के दो मामलों में थोक द्रव गति के अभाव में)। जब प्रसार प्रक्रिया फिक के नियमों का पालन नहीं करती है (जो झरझरा मीडिया के माध्यम से प्रसार के मामलों में होता है और अन्य लोगों के बीच सूजन के प्रवेशकों का प्रसार होता है), इसे गैर-फिकियन कहा जाता है।

फिक का पहला नियम

फिक का पहला नियम विसरित प्रवाह को सांद्रण की प्रवणता से संबंधित करता है। यह मानता है कि प्रवाह उच्च सांद्रता वाले क्षेत्रों से कम सांद्रता वाले क्षेत्रों में जाता है, परिमाण के साथ जो कि सांद्रता प्रवणता (स्थानिक व्युत्पन्न) के समानुपाती होता है।

या सरलीकृत शब्दों में यह अवधारणा है कि विलेय उच्च सांद्रता वाले क्षेत्र से कम सांद्रता वाले क्षेत्र में सांद्रता प्रवणता में चला जाएगा। (स्थानिक) आयाम में, नियम को विभिन्न रूपों में लिखा जा सकता है, जहां सबसे सामान्य रूप (देखें) मोलर के आधार पर है:

$J=-D{\frac {d\varphi }{dx}}$

जहाँ

• J प्रसार प्रवाह है, जिसमें से आयामी विश्लेषण प्रति इकाई समय प्रति इकाई क्षेत्र में पदार्थ की मात्रा है। J इकाई समय अंतराल के समय इकाई क्षेत्र से प्रवाहित होने वाले पदार्थ की मात्रा का माप।
• D विसरण गुणांक या द्रव्यमान विसारकता है। इसका आयाम क्षेत्र प्रति इकाई समय है।
• φ (आदर्श मिश्रण के लिए) सान्द्रता है, जिसका आयाम प्रति इकाई आयतन में पदार्थ की मात्रा है।
• x स्थिति है, जिसका आयाम लंबाई है।

D विसरित कणों के वर्ग वेग के समानुपाती होता है, जो स्टोक्स-आइंस्टीन संबंध के अनुसार तापमान, तरल पदार्थ की श्यानता और कणों के आकार पर निर्भर करता है। तनु जलीय घोल में, अधिकांश आयनों के प्रसार गुणांक समान होते हैं और उनके मान कमरे के तापमान पर (0.6–2)×10⁻⁹ m²/s की सीमा में होते हैं। जैविक अणुओं के लिए, विसरण गुणांक सामान्यतः 10⁻¹⁰ से 10⁻¹¹ m²/s के बीच होता है।

दो या दो से अधिक आयामों में हमें ∇, डेल या ग्रेडियेंट संक्रियक का उपयोग करना चाहिए, जो पहले यौगिक का सामान्यीकरण करता है, प्राप्त करता है

$\mathbf {J} =-D\nabla \varphi$

जहाँ J प्रसार प्रवाह सदिश को दर्शाता है।

आयामी प्रसार के लिए प्रेरक शक्ति मात्रा है −∂φ/∂x, जो आदर्श मिश्रण के लिए सघनता प्रवणता है।

पहले नियम के रूपांतर

पहले नियम के लिए एक अन्य रूप इसे प्राथमिक चर (y_i उदाहरण के लिए किग्रा / किग्रा में दिया गया) के साथ बड़े पैमाने पर अंश के रूप में लिखना है, फिर समीकरण में परिवर्तन होता है:

$\mathbf {J_{i}} =-{\frac {\rho D}{M_{i}}}\nabla y_{i}$

जहाँ नियम

• अनुक्रमणिका i दर्शाता है iवें वर्ण,
• J_i का प्रसार प्रवाह सदिश है iवीं वर्ण (उदाहरण के लिए mol/m²-s),
• M_i का मोलर द्रव्यमान है iवें वर्ण, और
• ρ मिश्रण का घनत्व है (उदाहरण के लिए किग्रा/मी³).

ध्यान दें कि $\rho$ ग्रेडिएंट संक्रियक के बाहर है। यह है क्योंकि:

$y_{i}={\frac {\rho _{si}}{\rho }}$

जहाँ ρ_si का iवीं वर्ण आंशिक घनत्व है।

इसके अलावा, आदर्श समाधान या मिश्रण के अलावा अन्य रासायनिक प्रणालियों में, प्रत्येक वर्ण के प्रसार के लिए प्रेरक बल इस वर्ण की रासायनिक क्षमता का आवरण है। फिर फिक का पहला नियम (आयामी स्थिति) लिखा जा सकता है

$J_{i}=-{\frac {Dc_{i}}{RT}}{\frac {\partial \mu _{i}}{\partial x}}$

जहाँ

• अनुक्रमणिका i दर्शाता है iवीं वर्ण।
• c एकाग्रता है (मोल/एम³).
• R सार्वभौमिक गैस स्थिरांक (जे/के/मोल) है।
• T पूर्ण तापमान (के) है।
• μ रासायनिक क्षमता (जे/मोल) है।

फिक के नियम की प्रेरक शक्ति को एक उग्रता अंतर के रूप में व्यक्त किया जा सकता है:

$J_{i}=-{\frac {D}{RT}}{\frac {\partial f_{i}}{\partial x}}$

उग्रता $f_{i}$ Pa इकाइयां हैं। $f_{i}$ वाष्प में घटक i का आंशिक दबाव $f_{i}^{G}$ या तरल $f_{i}^{L}$ अवस्था है। वाष्प तरल संतुलन पर वाष्पीकरण प्रवाह शून्य होता है क्योंकि $f_{i}^{G}=f_{i}^{L}$.

गैसों के लिए फिक के प्रथम नियम की व्युत्पत्ति

बाइनरी गैस मिश्रणों के लिए फिक के नियम के चार संस्करण नीचे दिए गए हैं। ये मान लेते हैं: उष्मीय प्रसार नगण्य है; दोनों वर्णों पर प्रति यूनिट द्रव्यमान का शरीर बल समान है; और या तो दबाव स्थिर रहता है या दोनों वर्णों का मोलर द्रव्यमान समान होता है। इन शर्तों के तहत, संदर्भ विस्तार से दिखाता है कि गैसों के गतिज सिद्धांत से प्रसार समीकरण कैसे फिक के नियम के इस संस्करण में कम हो जाता है:

$$\mathbf {V_{i}} =-D\nabla \ln y_{i},$$

जहां V_i वर्णों i का प्रसार वेग है। वर्णों के प्रवाह के संदर्भ में, यह है

$$\mathbf {J_{i}} =-{\frac {\rho D}{M_{i}}}\nabla y_{i}.$$

अगर, इसके अतिरिक्त, $\nabla \rho =0$, यह फिक के नियम के सबसे सामान्य रूप को कम करता है,

$$\mathbf {J_{i}} =-D\nabla \varphi .$$

यदि (इसके बदले में या इसके अतिरिक्त $\nabla \rho =0$) दोनों वर्णों का मोलर द्रव्यमान समान है, फिक का नियम बन जाता है

$$\mathbf {J_{i}} =-{\frac {\rho D}{M_{i}}}\nabla x_{i},$$

जहां $x_{i}$ वर्णों का मोल अंश i है।

फिक का दूसरा नियम

फिक का दूसरा नियम भविष्यवाणी करता है कि समय के संबंध में प्रसार किस प्रकार एकाग्रता को बदलता है। यह एक आंशिक अवकल समीकरण है जो एक आयाम में पढ़ता है:

${\frac {\partial \varphi }{\partial t}}=D\,{\frac {\partial ^{2}\varphi }{\partial x^{2}}}$

जहाँ

• φ के आयामों में एकाग्रता है $[{\mathsf {N}}{\mathsf {L}}^{-3}]$, उदाहरण मोल / मी³; φ = φ(x,t) एक ऐसा कार्य है जो स्थिति x और समय t पर निर्भर करता है
• t समय है, उदाहरण s
• D के आयामों में प्रसार गुणांक है $[{\mathsf {L}}^{2}{\mathsf {T}}^{-1}]$, उदाहरण m²/s
• x स्थिति है, उदाहरण m

दो या दो से अधिक आयामों में हमें लाप्लासियन का उपयोग करना चाहिए Δ = ∇², C

${\frac {\partial \varphi }{\partial t}}=D\Delta \varphi$

दो या अधिक आयामों में हमें लाप्लासियन Δ = ∇2 का उपयोग करना चाहिए, जो दूसरे व्युत्पन्न को सामान्य करता है, समीकरण प्राप्त करता है

फिक के दूसरे नियम का वही गणितीय रूप है जो ऊष्मा समीकरण का होता है और इसका मूल समाधान ऊष्मा गिरी के समान होता है, तापीय चालकता को छोड़कर - प्रसार गुणांक के साथ $k$-$D$:

$$\varphi (x,t)={\frac {1}{\sqrt {4\pi Dt}}}\exp \left(-{\frac {x^{2}}{4Dt}}\right).$$

तरल पदार्थ में फिक का प्रवाह

जब दो घुलनशील तरल पदार्थ संपर्क में लाए जाते हैं, और प्रसार होता है, तो मैक्रोस्कोपिक (या औसत) एकाग्रता फिक के नियम के अनुसार विकसित होती है। मेसोस्कोपिक पैमाने पर, अर्थात्, फिक के नियम और आणविक पैमाने द्वारा वर्णित मैक्रोस्कोपिक पैमाने के बीच, जहां आणविक यादृच्छिक चलता है, उतार-चढ़ाव की उपेक्षा नहीं की जा सकती है। ऐसी स्थितियों को लैंडौ-लिफ्शिट्ज़ के उतार-चढ़ाव वाले हाइड्रोडायनामिक्स के साथ सफलतापूर्वक तैयार किया जा सकता है। इस सैद्धांतिक ढांचे में, प्रसार उन उतार-चढ़ावों के कारण होता है, जिनके आयाम आणविक पैमाने से लेकर मैक्रोस्कोपिक पैमाने तक होते हैं।

विशेष रूप से, उतार-चढ़ाव वाले हाइड्रोडायनामिक समीकरणों में एक दिए गए प्रसार गुणांक के साथ-साथ हाइड्रोडायनामिक्स समीकरणों और उतार-चढ़ाव का वर्णन करने वाले स्टोकेस्टिक शब्दों के साथ फिक का प्रवाह शब्द सम्मिलित है। व्यथित दृष्टिकोण के साथ उतार-चढ़ाव की गणना करते समय, शून्य-क्रम सन्निकटन फिक का नियम है। पहला आदेश उतार-चढ़ाव देता है, और यह पता चलता है कि उतार-चढ़ाव प्रसार में योगदान देता है। यह किसी भी तरह से तनातनी का प्रतिनिधित्व करता है क्योंकि निम्न क्रम सन्निकटन द्वारा वर्णित घटना एक उच्च सन्निकटन का परिणाम है: यह समस्या उतार-चढ़ाव वाले हाइड्रोडायनामिक्स समीकरणों को सामान्य करके ही हल की जाती है।

विलयन दर और तनु विलेय की संघट्टन आवृत्ति

समाधान में आणविक प्रसार की योजना। ऑरेंज डॉट विलेय अणु हैं, सॉल्वेंट के अणु नहीं खींचे जाते हैं, काला तीर एक उदाहरण यादृच्छिक चलने वाला प्रक्षेपवक्र है, और लाल वक्र फिक के प्रसार के नियम से विसारक गॉसियन व्यापक संभाव्यता कार्य है।^{:अंजीर। 9</उप>}

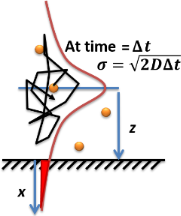
(गैस या तरल) समाधान में सतह या इंटरफ़ेस के लिए तनु विलेय की अवशोषण या अवशोषण दर की गणना फिक के प्रसार के नियमों का उपयोग करके की जा सकती है। सतह पर अधिशोषित अणुओं की संचित संख्या को लैंगमुइर-शेफर समीकरण द्वारा समय के साथ प्रसार प्रवाह समीकरण को एकीकृत करके कम समय सीमा पर व्यक्त किया जाता है:

$\Gamma =2AC{\sqrt {\frac {Dt}{\pi }}}$

• $\Gamma$ समय के समय अवशोषित इकाई $t$ अणुओं में अणुओं की संख्या है
• A इकाई $m^{2}$ में सतह क्षेत्र है
• C इकाई अणुओं में थोक समाधान में $m^{3}$अवशोषक अणुओं की संख्या सांद्रता है
• D इकाई में अवशोषक का प्रसार गुणांक $m^{2}/s$ है.
• t इकाई में बीता हुआ समय $s$ है

समीकरण का नाम अमेरिकी रसायनज्ञ इरविंग लैंगमुइर और विन्सेंट शेफर के नाम पर रखा गया है।

लैंगमुइर-शेफ़र समीकरण को सतह से अस्वीकृत अणुओं के "बैक-डिफ्यूजन" के लिए खाते में वार्ड-तोरदाई समीकरण तक विस्तारित किया जा सकता है:

$\Gamma =2AC{\sqrt {\frac {Dt}{\pi }}}-A{\sqrt {\frac {D}{\pi }}}\int _{0}^{\sqrt {t}}{\frac {C_{b}(\tau )}{\sqrt {t-\tau }}}\,d\tau$ जहाँ $C$ थोक एकाग्रता है, $C_{b}$ उप-सतह एकाग्रता है (जो अवशोषण के प्रतिक्रिया मॉडल के आधार पर समय का कार्य है), और $\tau$ डमी चर है।

मोंटे कार्लो सिमुलेशन दिखाते हैं कि ये दो समीकरण उन प्रणालियों की सोखने की दर की भविष्यवाणी करने के लिए काम करते हैं जो सतह के पास अनुमानित एकाग्रता ग्रेडियेंट बनाते हैं लेकिन अप्रत्याशित एकाग्रता ग्रेडियेंट के बिना या उनके साथ सिस्टम के लिए परेशानी होती है, जैसे कि विशिष्ट बायोसेंसिंग सिस्टम या जब प्रवाह और संवहन महत्वपूर्ण होते हैं।

विसारक अवशोषण पर सिद्धांतों का एक संक्षिप्त इतिहास।

विसरित अधिशोषण का संक्षिप्त इतिहास सही चित्र में दिखाया गया है। एकल-अणु स्तर पर विसरित अवशोषण को समझने की एक उल्लेखनीय चुनौती विसरण की भग्न प्रकृति है। अधिकांश कंप्यूटर सिमुलेशन प्रसार के लिए एक समय कदम चुनते हैं जो इस तथ्य की उपेक्षा करता है कि प्रत्येक चरण के भीतर स्व-समान महीन प्रसार घटनाएं (फ्रैक्टल्स) होती हैं। फ्रैक्टल डिफ्यूज़न को अनुकरण करने से पता चलता है कि एक निश्चित टाइम-स्टेप अवशोषण सिमुलेशन के परिणाम के लिए दो सुधारों का कारक पेश किया जाना चाहिए, जिससे यह उपरोक्त दो समीकरणों के अनुरूप हो।

उपरोक्त समीकरणों का अधिक समस्याग्रस्त परिणाम यह है कि वे आदर्श स्थितियों के तहत अधिशोषण की निचली सीमा की भविष्यवाणी करते हैं लेकिन वास्तविक अधिशोषण दरों की भविष्यवाणी करना बहुत कठिन है। समीकरण लंबी-समय-सीमा की स्थिति में प्राप्त होते हैं जब सतह के पास एक स्थिर सांद्रता प्रवणता बन जाती है। लेकिन वास्तविक अवशोषण प्रायः इस अनंत समय सीमा की तुलना में बहुत तेजी से किया जाता है, यानी, एकाग्रता आवरण, उप-सतह पर एकाग्रता का क्षय, सतह के संतृप्त होने से पहले केवल आंशिक रूप से बनता है, इस प्रकार मापी गई अवशोषण दर लगभग हमेशा तेज होती है समीकरणों ने कम या शून्य ऊर्जा अवरोधक सोखने की भविष्यवाणी की है (जब तक कि कोई महत्वपूर्ण अवशोषण ऊर्जा अवरोध न हो जो अवशोषण को काफी धीमा कर देता है), उदाहरण के लिए, जल-हवा या पानी में मोनोलेयर्स के स्व-विधानसभा में हजारों से लाखों गुना तेजी से -सब्सट्रेट इंटरफेस। इस प्रकार, सतह के पास एकाग्रता प्रवणता के विकास की गणना करना और व्यावहारिक अनुप्रयोगों के लिए कल्पित अनंत विकास को रोकने के लिए उचित समय का पता लगाना आवश्यक है। हालांकि यह भविष्यवाणी करना मुश्किल है कि कब रुकना है लेकिन कम से कम समय की गणना करना काफी आसान है, महत्वपूर्ण समय जब सब्सट्रेट सतह से पहला निकटतम पड़ोसी एकाग्रता आवरण के निर्माण को महसूस करता है। यह एक आदर्श स्थिति के तहत अवशोषण दर की ऊपरी सीमा पैदा करता है जब अवशोषक गतिशीलता को प्रभावित करने वाले प्रसार के अलावा कोई अन्य कारक नहीं होता है:

$<r>={\frac {4}{\pi }}Ac_{b}^{4/3}D$

• $<r>$ R इकाई s में, अवशोषण ऊर्जा अवरोध मुक्त स्थिति के तहत सोखने की दर है।
• $A$ इकाई m² में अनंत और सपाट सब्सट्रेट पर ब्याज की सतह का क्षेत्रफल है।
• $C_{b}$ इकाई m³ में थोक समाधान में अवशोषक अणु की एकाग्रता है।
• $D$ इकाई m² में समाधान में अवशोषक का प्रसार स्थिरांक है।
• इन इकाइयों का विमीय विश्लेषण संतुष्ट है।

इस समीकरण का उपयोग किसी भी प्रणाली की प्रारंभिक अधिशोषण दर का अनुमान लगाने के लिए किया जा सकता है; इसका उपयोग एक विशिष्ट बायोसेंसिंग सिस्टम की स्थिर-अवस्था सोखने की दर का अनुमान लगाने के लिए किया जा सकता है, जब बाध्यकारी साइट सब्सट्रेट सतह का बहुत अल्प अंश है और निकट-सतह एकाग्रता आवरण कभी नहीं बनती है; इसका उपयोग सतह पर अणुओं के सोखने की दर का अनुमान लगाने के लिए भी किया जा सकता है, जब उप-सतह में बहुत उथल-पुथल से एकाग्रता आवरण को प्रेरित करने के लिए एक महत्वपूर्ण प्रवाह होता है।

अल्ट्राशॉर्ट समय सीमा में, प्रसार समय a²/D के क्रम में, जहां a कण त्रिज्या है,लैंग्विन समीकरण द्वारा प्रसार का वर्णन किया गया है। एक लंबे समय में, लैंगविन समीकरण स्टोक्स-आइंस्टीन समीकरण में विलीन हो जाता है। बाद वाला पतला घोल की स्थिति के लिए उपयुक्त है, जहां लंबी दूरी के प्रसार पर विचार किया जाता है। लंबे समय की सीमा में लैंगविन समीकरण पर आधारित उतार-चढ़ाव-अपव्यय प्रमेय के अनुसार और जब कण आसपास के तरल पदार्थ की तुलना में काफी सघन होता है, तो समय-निर्भर प्रसार स्थिरांक है:

$D(t)=\mu \,k_{\rm {B}}T\left(1-e^{-t/(m\mu )}\right)$

जहां (सभी एसआई इकाइयों में)

• k_B बोल्ट्जमैन स्थिरांक है।
• t पूर्ण तापमान है।
• μ द्रव या गैस में कण की गतिशीलता है, जिसकी गणना आइंस्टीन संबंध (गतिज सिद्धांत) का उपयोग करके की जा सकती है।
• m कण का द्रव्यमान है।
• t समय है।

पानी में कार्बनिक अणुओं या बायोमोलिक्यूल (जैसे प्रोटीन) जैसे एकल अणु के लिए, पिकोसेकंड क्षेत्र में mμ के अल्प उत्पाद के कारण घातीय अवधि नगण्य है।

जब रुचि का क्षेत्र अणु के आकार का हो (विशेष रूप से, डीएनए जैसा लंबा बेलनाकार अणु), अवशोषण दर समीकरण पतला समाधान में दो अणुओं की टक्कर आवृत्ति का प्रतिनिधित्व करता है, जिसमें एक अणु विशिष्ट पक्ष और दूसरा कोई स्थैतिक निर्भरता नहीं है, अर्थात, अणु (यादृच्छिक अभिविन्यास) दूसरे के एक तरफ से टकराता है। विसरण स्थिरांक को दो विसरित अणुओं के बीच सापेक्ष विसरण स्थिरांक में अद्यतन किए जाने की आवश्यकता है। यह अनुमान विशेष रूप से एक अल्प अणु और प्रोटीन जैसे बड़े अणु के बीच की बातचीत का अध्ययन करने में उपयोगी है। प्रभावी विसरण स्थिरांक पर अल्प वाले का प्रभुत्व होता है जिसका विसरण स्थिरांक इसके बदले में उपयोग किया जा सकता है।

सतह पर आणविक स्व-संयोजन के कैनेटीक्स की भविष्यवाणी करने के लिए उपरोक्त हिटिंग दर समीकरण भी उपयोगी है। अणु थोक समाधान में यादृच्छिक रूप से उन्मुख होते हैं। यह मानते हुए कि 1/6 अणुओं का सतह बंधन स्थलों के लिए सही अभिविन्यास है, अर्थात x, y, और z तीन आयामों में 1/2 z- दिशा, इस प्रकार ब्याज की एकाग्रता थोक एकाग्रता का सिर्फ 1/6 है इस मान को समीकरण में रखने के लिए लैंगमुइर अवशोषण मॉडल का उपयोग करके सैद्धांतिक अवशोषण गतिज वक्र की गणना करने में सक्षम होना चाहिए। एक अधिक कठोर चित्र में, 1/6 को बाइंडिंग ज्योमेट्री के स्टेरिक कारक द्वारा प्रतिस्थापित किया जा सकता है।

प्रोटीन जमावट/एकत्रीकरण सहित कई प्रतिक्रियाओं से संबंधित द्विआण्विक टक्कर आवृत्ति को शुरू में 1916 के एक मौलिक प्रकाशन में मैरियन स्मोलुचोव्स्की द्वारा प्रस्तावित स्मोलुचोव्स्की जमावट समीकरण द्वारा वर्णित किया गया है, [17] जो ब्राउनियन गति और फिक के प्रसार के नियमों से लिया गया है। A+B-> उत्पाद के लिए एक पतला समाधान में आदर्श प्रतिक्रिया स्थिति के तहत, स्मोलुचोव्स्की ने सुझाव दिया कि अनंत समय सीमा पर आणविक प्रवाह की गणना फिक के प्रसार के नियमों से की जा सकती है, जो लक्ष्य अणु से एक निश्चित/स्थिर सांद्रता प्रवणता उत्पन्न करता है, उदा। बी लक्ष्य अणु है जो अपेक्षाकृत स्थिर रहता है, और ए गतिमान अणु है जो ए और बी के बीच जमावट प्रतिक्रिया के कारण लक्ष्य अणु बी के पास एकाग्रता आवरण बनाता है। स्मोलुचोव्स्की ने इकाई #/s/ के साथ समाधान में ए और बी के बीच टक्कर आवृत्ति की गणना की 3

टक्कर सिद्धांत और विसरित टक्कर सिद्धांत की तुलना करना।

प्रोटीन जमावट/एकत्रीकरण सहित कई प्रतिक्रियाओं से संबंधित द्वि-आणविक टक्कर आवृत्ति को प्रारंभिक रूप से मैरियन स्मोलुचोव्स्की द्वारा 1916 के मौलिक प्रकाशन में प्रस्तावित स्मोलुचोव्स्की जमावट समीकरण द्वारा वर्णित किया गया है। ब्राउनियन गति और फिक के प्रसार के नियमों से व्युत्पन्न। A+B-> उत्पाद के लिए पतला समाधान में आदर्श प्रतिक्रिया स्थिति के तहत, स्मोलुचोव्स्की ने सुझाव दिया कि अनंत समय सीमा पर आणविक प्रवाह की गणना फिक के प्रसार के नियमों से की जा सकती है, जो लक्ष्य अणु से एक निश्चित/स्थिर सांद्रता प्रवणता प्रदान करता है, उदा। B लक्ष्य अणु है जो अपेक्षाकृत स्थिर है, और A गतिमान अणु है जो A और B के बीच जमावट प्रतिक्रिया के कारण लक्ष्य अणु B के पास सांद्रता प्रवणता बनाता है। स्मोलुचोव्स्की ने इकाई /s/$m^{3}$ के साथ समाधान में A और B के बीच टक्कर आवृत्ति की गणना की

$Z_{AB}=4{\pi }RD_{r}C_{A}C_{B}$

जहाँ,

• $R$ टक्कर की त्रिज्या है।
• $D_{r}$ A और B के बीच सापेक्ष प्रसार स्थिरांक इकाई $m^{2}/s$ है,
• $C_{A}$ और $C_{B}$ क्रमशः A और B की संख्या सांद्रता इकाई /$m^{3}$हैं,

इस द्विध्रुवीय प्रतिक्रिया का प्रतिक्रिया क्रम 2 है जो अणु की गतिमान गति को विसरित प्रवाह के साथ बदलकर टक्कर सिद्धांत के परिणाम के अनुरूप है। टक्कर सिद्धांत में, A और B के बीच यात्रा का समय दूरी के समानुपाती होता है जो प्रवाह के स्थिर होने पर प्रसार मामले के लिए एक समान संबंध है।

हालाँकि, व्यावहारिक स्थिति के तहत, लक्ष्य अणु के पास सांद्रता प्रवणता समय के साथ आणविक प्रवाह के साथ-साथ विकसित हो रही है, और औसतन प्रवाह स्मोलुचोव्स्की द्वारा प्रस्तावित अनंत समय सीमा प्रवाह से बहुत बड़ा है। इस प्रकार, यह स्मोलुचोव्स्की आवृत्ति वास्तविक टक्कर आवृत्ति की निचली सीमा का प्रतिनिधित्व करती है।

2022 में, चेन समाधान में A और B के बीच टक्कर आवृत्ति की ऊपरी सीमा की गणना करता है, यह मानते हुए कि चलती अणु की थोक एकाग्रता लक्ष्य अणु के पहले निकटतम पड़ोसी के बाद तय की जाती है। इस प्रकार वास्तविक प्रवाह की गणना करने के लिए स्टॉप-टाइम दिए जाने पर एकाग्रता आवरण विकास पहली निकटतम पड़ोसी परत पर रुक जाता है। उन्होंने इसे महत्वपूर्ण समय का नाम दिया और इकाई #/s/$m^{3}$ में विसारक टक्कर आवृत्ति प्राप्त की।

$Z_{AB}={\frac {8}{\pi }}{\sigma }D_{r}C_{A}C_{B}{\sqrt[{3}]{C_{A}+C_{B}}}$

जहाँ,

• ${\sigma }$ टक्कर, इकाई $m^{2}$के क्रॉस-सेक्शन का क्षेत्र है
• $D_{r}$ A और B, इकाई $m^{2}/s$ के बीच सापेक्ष प्रसार स्थिरांक है .
• $C_{A}$ और $C_{B}$ क्रमशः A और B की संख्या सांद्रता इकाई # /$m^{3}$हैं

यह समीकरण A और B के बीच विसारक टक्कर आवृत्ति की ऊपरी सीमा मानता है जब पहली पड़ोसी परत एकाग्रता आवरण के विकास को महसूस करना शुरू कर देती है, जिसका प्रतिक्रिया क्रम 2 के बदले में $2{\frac {1}{3}}$ है । स्मोलुचोव्स्की समीकरण और जेचेन समीकरण दोनों एसआई इकाइयों के साथ आयामी जाँच को संतुष्ट करते हैं। लेकिन पूर्व त्रिज्या पर निर्भर है और बाद वाला टक्कर क्षेत्र के क्षेत्र पर है। द्विध्रुवीय इकाई प्रतिक्रिया के लिए वास्तविक प्रतिक्रिया क्रम 2 और के बीच हो सकता है $2{\frac {1}{3}}$, जो समझ में आता है क्योंकि विसरित टक्कर का समय दो अणुओं के बीच की दूरी पर निर्भर करता है।

जैविक परिप्रेक्ष्य

पहला नियम निम्नलिखित सूत्र को जन्म देता है:

${\text{flux}}={-P\left(c_{2}-c_{1}\right)}$

जिसमें

• P पारगम्यता है, एक दिए गए तापमान पर किसी दिए गए गैस के लिए प्रयोगात्मक रूप से निर्धारित झिल्ली विद्युत चालकता है।
• c₂ − c₁ प्रवाह की दिशा के लिए कृत्रिम झिल्ली में गैस की सांद्रता में अंतर है (से c₁ को c₂).

फिक का प्रथम नियम विकिरण अंतरण समीकरणों में भी महत्वपूर्ण है। हालाँकि, इस संदर्भ में, यह तब गलत हो जाता है जब प्रसार स्थिरांक कम होता है और विकिरण उस सामग्री के प्रतिरोध के बदले में प्रकाश की गति से सीमित हो जाता है जिससे विकिरण प्रवाहित हो रहा है। इस स्थिति में, फ्लक्स सीमक का उपयोग किया जा सकता है।

ग्राहम के नियम के साथ मिलकर इस नियम का उपयोग करके द्रव झिल्ली में गैस की विनिमय दर निर्धारित की जा सकती है।

पतला समाधान की स्थिति के तहत जब प्रसार नियंत्रण लेता है, उपरोक्त खंड में उल्लिखित झिल्ली पारगम्यता को सैद्धांतिक रूप से अंतिम खंड में उल्लिखित समीकरण का उपयोग करके विलेय के लिए गणना की जा सकती है (विशेष देखभाल के साथ उपयोग करें क्योंकि समीकरण घने विलेय के लिए प्राप्त होता है, जबकि जैविक अणु पानी से सघन नहीं हैं):

$P=2A_{p}\eta _{tm}{\sqrt {D/(\pi t)}}$

जहाँ

• $A_{P}$ झिल्ली पर छिद्रों का कुल क्षेत्रफल है (इकाई m²).
• $\eta _{tm}$ ट्रांसमेम्ब्रेन दक्षता (यूनिटलेस), जिसकी गणना क्रोमैटोग्राफी के स्टोकेस्टिक सिद्धांत से की जा सकती है।
• D विलेय इकाई m²s⁻¹ का प्रसार स्थिरांक है।
• t टाइम यूनिट s है।
• c₂, c₁ एकाग्रता इकाई मोल m⁻³ का उपयोग करना चाहिए, इसलिए फ्लक्स इकाई मोल s⁻¹ बन जाती है।

प्रवाह समय के वर्गमूल पर क्षय होता है क्योंकि आदर्श परिस्थितियों में समय के साथ झिल्ली के पास एक सांद्रता प्रवणता बनती है। जब प्रवाह और संवहन होता है, तो प्रवाह समीकरण की भविष्यवाणी से काफी अलग हो सकता है और एक निश्चित मूल्य के साथ एक प्रभावी समय टी दिखा सकता है, जो समय के साथ क्षय के बदले में फ्लक्स को स्थिर बनाता है। जब कोई आवरण नहीं बनती है तो आदर्श प्रवाह स्थितियों के तहत एक महत्वपूर्ण समय का अनुमान लगाया गया है। यह रणनीति जीव विज्ञान में अपनाई जाती है जैसे रक्त परिसंचरण।

अर्धचालक निर्माण अनुप्रयोग

अर्धचालक उपकरणों की श्रृंखला के लिए एक सामूहिक शब्द है। इसमें मुख्य रूप से तीन श्रेणियां सम्मिलित हैं: दो-टर्मिनल उपकरण, तीन-टर्मिनल उपकरण और चार-टर्मिनल उपकरण। अर्धचालक के संयोजन को एकीकृत परिपथ कहा जाता है।

फिक के नियम और अर्धचालकों के बीच संबंध: अर्धचालक का सिद्धांत रसायनों या डोपेंट को परत से परत में स्थानांतरित कर रहा है। फिक के नियम का उपयोग गणित के माध्यम से प्रति मीटर और सेकंड में डोपेंट या रसायनों की सांद्रता कितनी है, यह जानकर प्रसार को नियंत्रित करने और भविष्यवाणी करने के लिए किया जा सकता है।

इसलिए, अर्धचालकों के विभिन्न प्रकार और स्तरों का निर्माण किया जा सकता है।

इंटीग्रेटेड सर्किट फैब्रिकेशन टेक्नोलॉजी, मॉडल प्रोसेस जैसे सीवीडी, थर्मल ऑक्सीडेशन, वेट ऑक्सीडेशन, डोपिंग आदि फिक के नियम से प्राप्त प्रसार समीकरणों का उपयोग करते हैं।

अर्धचालक बनाने की सीवीडी विधि

वेफर प्रकार का अर्धचालक है जिसका सिलिकॉन सब्सट्रेट सीवीडी-निर्मित बहुलक श्रृंखला और फिल्मों की परत के साथ लेपित होता है। इस फिल्म में एन-टाइप और पी-टाइप डोपेंट सम्मिलित हैं और डोपेंट चालन की जिम्मेदारी लेती है। सीवीडी का सिद्धांत पतली फिल्म बनाने के लिए गैस चरण और गैस-ठोस रासायनिक प्रतिक्रिया पर निर्भर करता है।

सीवीडी का चिपचिपा प्रवाह शासन दबाव प्रवणता द्वारा संचालित होता है। सीवीडी में एडाटम्स के सतह प्रसार से अलग प्रसार घटक भी सम्मिलित है। सीवीडी में, अभिकारकों और उत्पादों को सब्सट्रेट के बगल में उपस्थित स्थिर गैस की एक सीमा परत के माध्यम से भी फैलाना चाहिए। सीवीडी फिल्म के विकास के लिए आवश्यक चरणों की कुल संख्या सीमा परत के माध्यम से अभिकारकों का गैस चरण प्रसार, एडटॉम्स का अवशोषण और सतह प्रसार, सब्सट्रेट पर प्रतिक्रियाएं और सीमा परत के माध्यम से उत्पादों का गैस चरण प्रसार है।

गैस प्रवाह के लिए वेग रूपरेखा है:

$$\delta (x)=\left({\frac {5x}{\mathrm {Re} ^{1/2}}}\right)\mathrm {Re} ={\frac {v\rho L}{\eta }}$$

जहाँ

• $\delta$ मोटाई है
• $\mathrm {Re}$ रेनॉल्ड्स संख्या है
• x सब्सट्रेट की लंबाई है।
• v = 0 किसी भी सतह पर
• $\eta$ श्यानता है
• $\rho$ घनत्व है।

एकीकृत x से 0 को L, यह औसत मोटाई देता है:

$$\delta ={\frac {10L}{3\mathrm {Re} ^{1/2}}}$$

प्रतिक्रिया को संतुलित रखने के लिए, अभिकारकों को स्थिर सीमा परत के माध्यम से सब्सट्रेट तक पहुंचने के लिए फैलाना चाहिए। इसलिए पतली सीमा परत वांछनीय है। समीकरणों के अनुसार, vo में वृद्धि से अधिक व्यर्थ अभिकारकों का परिणाम होगा। यदि प्रवाह अशांत हो जाता है तो अभिकारक सब्सट्रेट तक समान रूप से नहीं पहुंचेंगे। एक अन्य विकल्प कम श्यानता या घनत्व वाली नई वाहक गैस पर स्विच करना है। फिक का पहला नियम सीमा परत के माध्यम से प्रसार का वर्णन करता है। गैस में दबाव (P) और तापमान (T) के कार्य के रूप में, प्रसार निर्धारित किया जाता है।

$$D=D_{0}\left({\frac {P_{0}}{P}}\right)\left({\frac {T}{T_{0}}}\right)^{3/2}$$

जहाँ

• $P_{0}$ मानक दबाव है।
• $T_{0}$ मानक तापमान है।
• $D_{0}$ मानक प्रसार है।

समीकरण बताता है कि तापमान बढ़ाने या दबाव कम करने से विसारकता बढ़ सकती है।

फिक का पहला नियम अभिकारकों के प्रवाह को सब्सट्रेट और उत्पाद को सब्सट्रेट से दूर करने की भविष्यवाणी करता है:

$$J=-D_{i}\left({\frac {dc_{i}}{dx}}\right)$$

जहाँ

• $x$ मोटाई है $\delta$
• $dc_{i}$ पहले अभिकारक की एकाग्रता है।

आदर्श गैस नियम में $PV=nRT$, गैस की सांद्रता आंशिक दबाव द्वारा व्यक्त की जाती है।

$$J=-D_{i}\left({\frac {P_{i}-P_{0}}{\delta RT}}\right)$$

जहाँ

• $R$ गैस नियतांक है।
• ${\frac {P_{i}-P_{0}}{\delta }}$ आंशिक दबाव प्रवणता है।

परिणामस्वरूप, फिक का पहला नियम हमें बताता है कि हम विसारकता को नियंत्रित करने और अर्धचालकों की पतली फिल्मों के विकास को नियंत्रित करने के लिए आंशिक दबाव प्रवणता का उपयोग कर सकते हैं।

कई यथार्थवादी स्थितियों में, साधारण फिक का नियम अर्धचालक समस्या के लिए पर्याप्त सूत्रीकरण नहीं है। यह केवल कुछ शर्तों पर लागू होता है, उदाहरण के लिए, अर्धचालक सीमा की स्थिति: निरंतर स्रोत एकाग्रता प्रसार, सीमित स्रोत एकाग्रता, या चलती सीमा प्रसार (जहां जंक्शन की गहराई सब्सट्रेट में चलती रहती है)।

फिकियन प्रसार की अमान्यता

यह नोट करना महत्वपूर्ण है कि भले ही प्रारंभिक दिनों में सेमीकंडक्टर निर्माण (सीवीडी रिएक्टरों सहित) में प्रसार प्रक्रियाओं को मॉडल करने के लिए फिकियन प्रसार का उपयोग किया गया हो, यह प्रायः उन्नत अर्धचालक नोड्स (<90 एनएम) में प्रसार को मान्य करने में विफल रहता है। यह ज्यादातर फिकियन प्रसार की अक्षमता से आणविक स्तर और अल्प पर मॉडल प्रसार प्रक्रियाओं की अक्षमता से उत्पन्न होता है। उन्नत अर्धचालक निर्माण में, परमाणु पैमानों पर गति को समझना महत्वपूर्ण है, जो निरंतर प्रसार द्वारा विफल हो गया है। आज, अधिकांश सेमीकंडक्टर निर्माता प्रसार प्रक्रियाओं का अध्ययन और मॉडल करने के लिए यादृच्छिक चाल का उपयोग करते हैं। यह हमें अलग-अलग परमाणुओं, अणुओं, प्लाज्मा आदि की गति को समझने के लिए विसरण के प्रभावों का अलग-अलग तरीके से अध्ययन करने की अनुमति देता है।

इस तरह की प्रक्रिया में, सीवीडी रिएक्टर, सीमा परत, सामग्री संरचनाओं आदि के माध्यम से एक यादृच्छिक चलने के बाद, फैलाने वाली वर्णों (परमाणु, अणु, प्लाज्मा इत्यादि) के आंदोलनों को असतत इकाई के रूप में माना जाता है। कभी-कभी, आंदोलन पक्षपातपूर्ण हो सकते हैं -प्रसंस्करण की स्थिति के आधार पर यादृच्छिक चलना। सांख्यिकीय विश्लेषण वर्णों के यादृच्छिक चलने से उत्पन्न भिन्नता/स्टोचैस्टिसिटी को समझने के लिए किया जाता है, जो बदले में समग्र प्रक्रिया और विद्युत विविधताओं को प्रभावित करता है।

खाद्य उत्पादन और भोजन पकाने

फिक के पहले नियम का सूत्रीकरण भोजन और खाना पकाने के संदर्भ में विभिन्न प्रकार की जटिल घटनाओं की व्याख्या कर सकता है: एथिलीन जैसे अणुओं का प्रसार पौधे की वृद्धि और पकने को बढ़ावा देता है, नमक और चीनी के अणु मांस लाने और मैरीनेट करने को बढ़ावा देते हैं, और पानी के अणु निर्जलीकरण को बढ़ावा देते हैं। फिक के पहले नियम का उपयोग एक स्पेगेटी नूडल में बदलते नमी प्रोफाइल की भविष्यवाणी करने के लिए भी किया जा सकता है क्योंकि यह खाना पकाने के समय हाइड्रेट करता है। ये घटनाएँ सांद्रण प्रवणता द्वारा संचालित विलेय के कणों के स्वतःस्फूर्त संचलन के बारे में हैं। अलग-अलग स्थितियों में अलग-अलग विसरणशीलता होती है जो एक स्थिर होती है।

सघनता प्रवणता को नियंत्रित करके, भोजन पकाने का समय, आकार और नमक को नियंत्रित किया जा सकता है।

यह भी देखें

• अभिवहन
• चर्चिल-बर्नस्टीन समीकरण
• प्रसार
• मिथ्या प्रसार
• गैस विनिमय
• द्रव्यमान प्रवाह
• मैक्सवेल-स्टीफन प्रसार
• नर्नस्ट-प्लैंक समीकरण
• असमस

अग्रिम पठन

• Berg HC (1977). Random Walks in Biology. Princeton.
• Bird RB, Stewart WE, Lightfoot EN (1976). Transport Phenomena. John Wiley & Sons.
• Bokshtein BS, Mendelev MI, Srolovitz DJ, eds. (2005). Thermodynamics and Kinetics in Materials Science: A Short Course. Oxford: Oxford University Press. pp. 167–171.
• Crank J (1980). The Mathematics of Diffusion. Oxford University Press.
• Fick A (1855). "On liquid diffusion". Annalen der Physik und Chemie. 94: 59. – reprinted in Fick, Adolph (1995). "On liquid diffusion". Journal of Membrane Science. 100: 33–38. doi:10.1016/0376-7388(94)00230-v.
• Smith WF (2004). Foundations of Materials Science and Engineering (3rd ed.). McGraw-Hill.

बाहरी संबंध

• Fick's equations, Boltzmann's transformation, etc. (with figures and animations)
• Fick's Second Law on OpenStax