स्वतंत्र कोटि: Difference between revisions

External images
External images
	https://chem.libretexts.org/@api/deki/files/9669/h2ovibrations.gif?revision=1
	https://chem.libretexts.org/@api/deki/files/9668/co2vibrations.gif?revision=1

Latest revision as of 11:38, 20 April 2023

भौतिकी और रसायन विज्ञान में, भौतिक प्रणाली की स्थिति के औपचारिक विवरण में स्वतंत्र कोटि एक स्वतंत्र भौतिक मापदण्ड है। प्रणाली की सभी अवस्था के सम्मुच्चय को प्रणाली के प्रावस्था समष्टि के रूप में जाना जाता है, और प्रणाली की स्वतंत्र कोटि प्रावस्था समष्टि के आयाम हैं।

त्रि-आयामी अंतरिक्ष में एक कण के स्थान के लिए तीन समन्वय प्रणाली की आवश्यकता होती है। इसी तरह, जिस दिशा और गति पर एक कण चलता है, प्रत्येक अंतरिक्ष के तीन आयामों के संदर्भ में उसे वेग के तीन घटकों के रूप में वर्णित किया जा सकता है। यदि प्रणाली का समय विकास नियतात्मक प्रणाली है (जहां एक पल में अवस्था विशिष्ट रूप से अपने अतीत और भविष्य की स्थिति और वेग को समय के कार्य के रूप में निर्धारित करता है) तो ऐसी प्रणाली में स्वतंत्र की छह कोटि होती है।^{[citation needed]} यदि कण की गति आयामों की कम संख्या तक सीमित है - उदाहरण के लिए, कण को एक तार के साथ या एक निश्चित सतह पर चलना चाहिए - तो प्रणाली में स्वतंत्र की छह कोटि से कम है। दूसरी ओर, एक विस्तारित वस्तु वाली एक प्रणाली जो घूम सकती है या कंपन कर सकती है, स्वतंत्र की छह कोटि से अधिक हो सकती है।

शास्त्रीय यांत्रिकी में, किसी भी समय एक बिंदु कण की स्थिति को लैग्रैंगियन यांत्रिकी औपचारिकता में स्थिति और वेग निर्देशांक के साथ वर्णित किया जाता है, या हैमिल्टनियन (परिमाण यांत्रिकी) औपचारिकता में स्थिति और गति निर्देशांक के साथ वर्णित किया जाता है।

सांख्यिकीय यांत्रिकी में, स्वतंत्र की एक कोटि प्रणाली के सूक्ष्म अवस्था (सांख्यिकीय यांत्रिकी) का वर्णन करने वाला एक एकल अदिश (भौतिकी) संख्या है।^[1] प्रणाली के सभी सूक्ष्म अवस्था का विनिर्देश प्रणाली के प्रावस्था समष्टि में एक बिंदु है।

रसायन विज्ञान में 3D आदर्श श्रृंखला प्रतिरूप में, प्रत्येक एकलक के अभिविन्यास का वर्णन करने के लिए दो कोण आवश्यक हैं।

स्वतंत्र की द्विघात कोटि निर्दिष्ट करना अक्सर उपयोगी होता है। ये स्वतंत्र कोटि हैं जो प्रणाली की ऊर्जा के द्विघात कार्य में योगदान करती हैं।

जो गिन रहा है उसके आधार पर, कई अलग-अलग तरीके हैं जिनसे स्वतंत्र कोटि को परिभाषित किया जा सकता है, प्रत्येक एक अलग मूल्य के साथ।^[2]

गैसों के लिए स्वतंत्र की ऊष्मागतिक कोटि

समविभाजन प्रमेय द्वारा, गैस की प्रति मोल आंतरिक ऊर्जा $c v T$ बराबर होती है, जहाँ $T$ निरपेक्ष तापमान है और स्थिर आयतन पर विशिष्ट ऊष्मा c_v = (f)(R/2 है। R = 8.314 J/(K mol) सार्वभौमिक गैस स्थिरांक है, और f स्वतंत्र की ऊष्मागतिक (द्विघात) कोटि की संख्या है, ऊर्जा उत्पन्न करने के तरीकों की संख्या की गणना करना है।

किसी भी परमाणु या अणु में x, y, और z अक्षों के संबंध में द्रव्यमान के केंद्र के स्थानांतरीय गति (गतिज ऊर्जा) से जुड़ी स्वतंत्र की तीन कोटि होती है। एकपरमाण्विक प्रजातियों के लिए स्वतंत्र की ये एकमात्र कोटि हैं, जैसे उत्कृष्ट गैस परमाणु।

दो या दो से अधिक परमाणुओं वाली संरचना के लिए, पूरी संरचना में घूर्णी गतिज ऊर्जा भी होती है, जहाँ पूरी संरचना एक अक्ष के चारों ओर घूमती है।

एक रेखीय आणविक ज्यामिति, जहाँ सभी परमाणु एक अक्ष के साथ होते हैं, जैसे कोई द्विपरमाणुक अणु और कुछ अन्य अणु जैसे कार्बन डाईऑक्साइड (CO₂), स्वतंत्र की दो घूर्णी कोटि होती है, क्योंकि यह आणविक अक्ष के लम्बवत दो अक्षों में से किसी एक के बारे में घूम सकती है। एक अरैखिक अणु, जहां परमाणु एक धुरी के साथ नहीं रहते हैं, जैसे पानी (H₂O), स्वतंत्र की तीन घूर्णी कोटि है, क्योंकि यह किसी भी तीन लंबवत अक्षों के चारों ओर घूम सकती है। विशेष स्तिथियों में, जैसे अधिशोषित बड़े अणु में, स्वतंत्र की घूर्णी कोटि केवल एक तक सीमित हो सकती है।^[3]

दो या दो से अधिक परमाणुओं वाली संरचना में कंपन ऊर्जा भी होती है, जहां व्यक्तिगत परमाणु एक दूसरे के संबंध में गति करते हैं। एक द्विपरमाणुक अणु में एक आणविक कंपन प्रणाली होता है: दो परमाणु स्प्रिंग के रूप में कार्य करने वाले रासायनिक बंधन के साथ आगे और आगे बढ़ते हैं। $N$ परमाणुओं के साथ एक अणु में आणविक कंपन के अधिक जटिल तरीके होते हैं एक रैखिक अणु के लिए $3 N - 5$ कंपन प्रणाली और एक अरेखीय अणु के लिए $3 N - 6$ प्रणाली।^[4] विशिष्ट उदाहरण के रूप में, रैखिक CO₂ अणु में दोलन के 4 तरीके होते हैं,^[5] और अरैखिक जल अणु में दोलन के 3 तरीके होते हैं^[6] प्रत्येक कंपन प्रणाली में दो ऊर्जा शब्द होते हैं: गतिमान परमाणुओं की गतिज ऊर्जा और वसंत जैसे रासायनिक बंधों की संभावित ऊर्जा। इसलिए, कंपन ऊर्जा शर्तों की संख्या एक रैखिक अणु के लिए $2(3 N - 5)$ है और एक अरेखीय अणु के लिए $2(3 N - 6)$ प्रणाली है।

घूर्णी और कंपन प्रणाली दोनों को परिमाणित किया जाता है, जिसके लिए न्यूनतम तापमान को सक्रिय करने की आवश्यकता होती है।^[7] कई गैसों के लिए स्वतंत्र की घूर्णी कोटि को सक्रिय करने के लिए घूर्णी तापमान 100 K से कम है। N₂ और O₂ के लिए, यह 3 K से कम है।^[1] पर्याप्त कंपन के लिए आवश्यक कंपन तापमान 10³ और 10⁴ के बीच है, 3521 K N₂ के लिए और 2156 K O₂ के लिए हैं।^[1] N₂ और O₂ में कंपन को सक्रिय करने के लिए विशिष्ट वायुमंडलीय तापमान पर्याप्त नहीं हैं, जिसमें अधिकांश वातावरण सम्मिलित है। (अगला आंकड़ा देखें।) हालांकि, बहुत कम प्रचुर मात्रा में ग्रीनहाउस गैस पृथ्वी की सतह से अवरक्त को अवशोषित करके क्षोभमंडल को गर्म रखती हैं, जो उनके कंपन प्रणाली को उत्तेजित करता है।^[8] इस ऊर्जा का अधिकांश भाग ग्रीनहाउस प्रभाव के माध्यम से अवरक्त में सतह पर वापस आ जाता है।

क्योंकि कमरे का तापमान (≈298 K) विशिष्ट घूर्णी तापमान से अधिक है, लेकिन विशिष्ट कंपन तापमान से कम है, केवल स्वतंत्र के अनुवाद और घूर्णी कोटि, समान मात्रा में, ताप क्षमता अनुपात में योगदान करते हैं। इसलिए $γ$ ≈ $.mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output .sfrac.tion,.mw-parser-output .sfrac .tion{display:inline-block;vertical-align:-0.5em;font-size:85%;text-align:center}.mw-parser-output .sfrac .num,.mw-parser-output .sfrac .den{display:block;line-height:1em;margin:0 0.1em}.mw-parser-output .sfrac .den{border-top:1px solid}.mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px}5/3$ एकपरमाण्विक गैसों के लिए और $γ$ ≈ $7 / 5$ कमरे के तापमान पर द्विपरमाण्विक गैसों के लिए है।^[1]

स्थिर आयतन पर शुष्क वायु की विशिष्ट ऊष्मा का ग्राफ, c_v, तापमान के एक फलन के रूप में संख्यात्मक मूल्यों को तालिका से हवा - लगातार दबाव और भिन्न तापमान पर विशिष्ट गर्मी में लिया जाता है ।^[9] उन मूल्यों में J / (के किलो) की इकाइयां हैं, इसलिए आलेख किए गए संदर्भ रेखाएं (5/2)

R

_d और (7/2)

R

_d हैं, जहाँ

R

_d =

R d

M

शुष्क हवा के लिए गैस नियतांक है,

R

= 8.314 J/(K mol) सार्वभौमिक गैस नियतांक है, और M_d = 28.965369 g/mol शुष्क वायु का मोलीय द्रव्यमान है।^[10]T = 140, 160, 200, 220, 320, 340, 360, 380 के, C_v पर = 718.4, 717.2, 716.3, 716.3, 719.2, 720.6, 722.3, 724.3 J/(K किलो)। इस प्रकार, 140 के <T <360 K, C के लिए_v (5/2) R_d से भिन्न है, 1% से भी कम।

चूंकि पृथ्वी के वायुमंडल में द्विपरमाणुक गैसों (नाइट्रोजन और ऑक्सीजन का योगदान लगभग 99% है) का प्रभुत्व है, इसकी दाढ़ आंतरिक ऊर्जा करीब $c v T$ = (5/2) $R$ $T$ है, द्विपरमाणुक गैसों द्वारा प्रदर्शित स्वतंत्र की 5 कोटि द्वारा निर्धारित है।^{[citation needed]}^[11]^{[circular reference]}

ग्राफ़ को दाईं ओर देखें। 140 K < $T$ <380 K, c_v (5/2) से भिन्न $R$ _d 1% से भी कम है। केवल क्षोभमंडल और समताप मंडल में तापमान से काफी ऊपर के तापमान पर ही कुछ अणुओं में पर्याप्त ऊर्जा होती है जिससे वे N₂ और O₂ के कंपन प्रणाली को सक्रिय कर सकें। स्थिर आयतन पर विशिष्ट ऊष्मा, c_v, धीरे-धीरे (7/2) की ओर बढ़ता है $R$ जैसे-जैसे तापमान T = 400 K से ऊपर बढ़ता है, जहाँ c_v (5/2) $R$ _d = 717.5 जे / (के किलो) से 1.3% ऊपर है।

एन परमाणुओं के लिए स्वतंत्र की घटक कोटि (3 $N$ कुल समन्वय गति)
	एकपरमाण्विक	रैखिक अणु	अरैखिक अणु
अनुवाद ( $x$ , $y$ , and $z$ )	3	3	3
क्रमावर्तन ( $x$ , $y$ , and $z$ )	0	2	3
कंपन (संरचनात्मक विभिन्नता)	0	$(3 N - 5)$	$(3 N - 6)$

एक स्थिति निर्दिष्ट करने के लिए निर्देशांक की न्यूनतम संख्या की गणना

किसी स्थिति को निर्दिष्ट करने के लिए आवश्यक न्यूनतम संख्या में निर्देशांक का उपयोग करके कोई भी स्वतंत्र कोटि की गणना कर सकता है। यह अग्रानुसार होगा:

एक कण के लिए हमें इसकी स्थिति निर्दिष्ट करने के लिए 2-D तल में 2 निर्देशांक और 3-D अंतरिक्ष में 3 निर्देशांक की आवश्यकता होती है। इस प्रकार 3-D अंतरिक्ष में इसकी स्वतंत्र कोटि 3 है।
एक 3-D अंतरिक्ष में 2 कणों (उदाहरण के लिए एक द्विपरमाणुक अणु) से युक्त शरीर के लिए उनके बीच निरंतर दूरी के साथ (मान लें कि D) हम इसकी स्वतंत्र कोटि (नीचे) 5 दिखा सकते हैं।

मान लीजिए कि इस शरीर में एक कण का समन्वय $(x 1, y 1, z 1)$ है और दूसरे ने समन्वय $(x 2, y 2, z 2)$ अज्ञात $z 2$ के साथ किया है। दो निर्देशांकों के बीच की दूरी के सूत्र का अनुप्रयोग

d={\sqrt {(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}+(z_{2}-z_{1})^{2}}}

एक अज्ञात के साथ एक समीकरण में परिणाम, जिसमें हम $z 2$ के लिए हल कर सकते हैं। $x 1$ , $x 2$ , $y 1$ , $y 2$ , $z 1$ , या $z 2$ में से एक अज्ञात हो सकता है।

शास्त्रीय समविभाजन प्रमेय के विपरीत, कमरे के तापमान पर, अणुओं की कंपन गति सामान्यतः ताप क्षमता में उपेक्षणीय योगदान देती है। ऐसा इसलिए है क्योंकि स्वतंत्र की ये कोटि जमी हुई हैं क्योंकि ऊर्जा के बीच की दूरी परिवेश के तापमान ( $k B T$ ) के अनुरूप ऊर्जा से अधिक है।^[1]

स्वतंत्र की स्वतंत्र कोटि

स्वतंत्र कोटि का सम्मुच्चय {{math|X₁, ..., X_N} एक प्रणाली का} स्वतंत्र है यदि सम्मुच्चय से जुड़ी ऊर्जा को निम्नलिखित रूप में लिखा जा सकता है:

E=\sum _{i=1}^{N}E_{i}(X_{i}),

जहाँ $E i$ एकमात्र चर का एक कार्य $X i$ है।

उदाहरण: अगर $X 1$ और $X 2$ स्वतंत्र की दो कोटि हैं, और $E$ संबंधित ऊर्जा है:

अगर $E=X_{1}^{4}+X_{2}^{4}$ है, तो स्वतंत्र की दो कोटि स्वतंत्र हैं।
अगर $E=X_{1}^{4}+X_{1}X_{2}+X_{2}^{4}$ है, तब स्वतंत्र की दो कोटि स्वतंत्र नहीं हैं। $X 1$ और $X 2$ के उत्पाद को सम्मिलित करने वाला शब्द एक युग्मन शब्द है जो स्वतंत्र की दो कोटि के बीच की बातचीत का वर्णन करता है।

1 से $N$ तक $i$ के लिए, $i$ का मूल्य स्वतंत्र कोटि $X i$ बोल्ट्जमैन वितरण के अनुसार वितरित किया जाता है। इसकी संभाव्यता घनत्व फलन निम्न है:

p_{i}(X_{i})={\frac {e^{-{\frac {E_{i}}{k_{B}T}}}}{\int dX_{i}\,e^{-{\frac {E_{i}}{k_{B}T}}}}}

,

इस खंड में, और पूरे लेख में कोष्ठक $\langle \rangle$ उनके द्वारा संलग्न मात्रा के माध्य को निरूपित करें।

प्रणाली की आंतरिक ऊर्जा स्वतंत्र की प्रत्येक कोटि से जुड़ी औसत ऊर्जाओं का योग है:

\langle E\rangle =\sum _{i=1}^{N}\langle E_{i}\rangle .

स्वतंत्र की द्विघात कोटि

स्वतंत्र की एक कोटि $X i$ द्विघात है यदि स्वतंत्र की इस कोटि से जुड़ी ऊर्जा शर्तों को इस रूप में लिखा जा सकता है

E=\alpha _{i}\,\,X_{i}^{2}+\beta _{i}\,\,X_{i}Y

,

जहाँ $Y$ स्वतंत्र की अन्य द्विघात कोटि का एक रेखीय संयोजन है।

उदाहरण: अगर $X 1$ और $X 2$ स्वतंत्र की दो कोटि हैं, और $E$ संबंधित ऊर्जा है:

अगर $E=X_{1}^{4}+X_{1}^{3}X_{2}+X_{2}^{4}$ है, तो स्वतंत्र की दो कोटि स्वतंत्र और गैर-द्विघात नहीं हैं।
अगर $E=X_{1}^{4}+X_{2}^{4}$ है, तो स्वतंत्र की दो कोटि स्वतंत्र और गैर-द्विघात हैं।
अगर $E=X_{1}^{2}+X_{1}X_{2}+2X_{2}^{2}$ है, तब स्वतंत्र की दो कोटि स्वतंत्र नहीं हैं बल्कि द्विघात हैं।
अगर $E=X_{1}^{2}+2X_{2}^{2}$ है, तो स्वतंत्र की दो कोटि स्वतंत्र और द्विघात हैं।

उदाहरण के लिए, न्यूटोनियन यांत्रिकी में, स्वतंत्र की द्विघात कोटि की एक प्रणाली की गतिशीलता (यांत्रिकी) को निरंतर गुणांक वाले सजातीय रैखिक अंतर समीकरण के एक सम्मुच्चय द्वारा नियंत्रित किया जाता है।

स्वतंत्र की द्विघात और स्वतंत्र कोटि

$X 1, ... , X N$ स्वतंत्र की द्विघात और स्वतंत्र कोटि हैं यदि उनके द्वारा प्रतिनिधित्व की जाने वाली प्रणाली के एक सूक्ष्म अवस्था से जुड़ी ऊर्जा को इस प्रकार लिखा जा सकता है:

E=\sum _{i=1}^{N}\alpha _{i}X_{i}^{2}

समविभाजन प्रमेय

सांख्यिकीय यांत्रिकी की शास्त्रीय सीमा में, ऊष्मागतिक संतुलन पर, एक प्रणाली की आंतरिक ऊर्जा $N$ स्वतंत्र की द्विघात और स्वतंत्र कोटि है:

U=\langle E\rangle =N\,{\frac {k_{B}T}{2}}

यहाँ, स्वतंत्र कोटि से जुड़ी औसत ऊर्जा निम्न है:

\langle E_{i}\rangle =\int dX_{i}\,\,\alpha _{i}X_{i}^{2}\,\,p_{i}(X_{i})={\frac {\int dX_{i}\,\,\alpha _{i}X_{i}^{2}\,\,e^{-{\frac {\alpha _{i}X_{i}^{2}}{k_{B}T}}}}{\int dX_{i}\,\,e^{-{\frac {\alpha _{i}X_{i}^{2}}{k_{B}T}}}}}

\langle E_{i}\rangle ={\frac {k_{B}T}{2}}{\frac {\int dx\,\,x^{2}\,\,e^{-{\frac {x^{2}}{2}}}}{\int dx\,\,e^{-{\frac {x^{2}}{2}}}}}={\frac {k_{B}T}{2}}

चूंकि स्वतंत्र कोटि स्वतंत्र हैं, प्रणाली की आंतरिक ऊर्जा स्वतंत्र की प्रत्येक कोटि से जुड़ी औसत ऊर्जा के योग के बराबर होती है, जो परिणाम प्रदर्शित करती है।

सामान्यीकरण

अपने प्रावस्था समष्टि में बिंदु (ज्यामिति) के रूप में एक प्रणाली की स्थिति का वर्णन, हालांकि गणितीय रूप से सुविधाजनक है, परन्तु मौलिक रूप से गलत माना जाता है। परिमाण यांत्रिकी में, स्वतंत्र की गति की कोटि तरंग फलन की अवधारणा से अलग हो जाती है, और संचालक (भौतिकी) में बिंदु वर्णक्रम होता है जो स्वतंत्र की अन्य कोटि के अनुरूप होती है। उदाहरण के लिए, एक इलेक्ट्रॉन या फोटॉन के लिए कोणीय संवेग संचालिका, कक्षीय, और कुल कोणीय संवेग संचालिका (जो घूर्णी स्वतंत्र से मेल खाती है) में केवल दो आइगेनवैल्यू होते हैं। यह असततता तब स्पष्ट हो जाती है जब क्रिया (भौतिकी) में प्लैंक स्थिरांक के परिमाण का एक क्रम होता है, और स्वतंत्र की अलग-अलग कोटि को अलग किया जा सकता है।

संदर्भ

↑ ^1.0 ^1.1 ^1.2 ^1.3 ^1.4 Reif, F. (2009). सांख्यिकीय और तापीय भौतिकी के मूल सिद्धांत. Long Grove, IL: Waveland Press, Inc. p. 51. ISBN 978-1-57766-612-7.
↑ "Physical chemistry - Does a diatomic gas have one or two vibrational degrees of freedom?".
↑ Waldmann, Thomas; Klein, Jens; Hoster, Harry E.; Behm, R. Jürgen (2013). "Stabilization of Large Adsorbates by Rotational Entropy: A Time-Resolved Variable-Temperature STM Study". ChemPhysChem. 14 (1): 162–9. doi:10.1002/cphc.201200531. PMID 23047526.
↑ Molecular vibration^{[user-generated source]}
↑ For drawings, see http://www.colby.edu/chemistry/PChem/notes/NormalModesText.pdf
↑ For drawings, see https://sites.cns.utexas.edu/jones_ch431/normal-modes-vibration
↑ Section 12-7 (pp. 376-379) of Sears and Salinger, 1975: Thermodynamics, Kinetic Theory, and Statistical Thermodynamics. Third edition. Addison-Wesley Publishing Co.
↑ "अणु कंपन करते हैं". UCAR Center for Science Education. Archived from the original on 2014-10-10. Retrieved 2021-01-19.
↑ "Air - Specific Heat vs. Temperature at Constant Pressure".
↑ Gatley, D. P., S. Herrmann, H.-J. Kretzshmar, 2008: A twenty-first century molar mass for dry air. HVAC&R Research, vol. 14, pp. 655-662.
↑ Equipartition theorem#Diatomic gases

[:0-1] 1.0 ^1.1 ^1.2 ^1.3 ^1.4 Reif, F. (2009). सांख्यिकीय और तापीय भौतिकी के मूल सिद्धांत. Long Grove, IL: Waveland Press, Inc. p. 51. ISBN 978-1-57766-612-7.

[2] "Physical chemistry - Does a diatomic gas have one or two vibrational degrees of freedom?".

[3] Waldmann, Thomas; Klein, Jens; Hoster, Harry E.; Behm, R. Jürgen (2013). "Stabilization of Large Adsorbates by Rotational Entropy: A Time-Resolved Variable-Temperature STM Study". ChemPhysChem. 14 (1): 162–9. doi:10.1002/cphc.201200531. PMID 23047526.

[4] Molecular vibration^{[user-generated source]}

[5] For drawings, see http://www.colby.edu/chemistry/PChem/notes/NormalModesText.pdf

[6] For drawings, see https://sites.cns.utexas.edu/jones_ch431/normal-modes-vibration

[7] Section 12-7 (pp. 376-379) of Sears and Salinger, 1975: Thermodynamics, Kinetic Theory, and Statistical Thermodynamics. Third edition. Addison-Wesley Publishing Co.

[8] "अणु कंपन करते हैं". UCAR Center for Science Education. Archived from the original on 2014-10-10. Retrieved 2021-01-19.

[9] "Air - Specific Heat vs. Temperature at Constant Pressure".

[10] Gatley, D. P., S. Herrmann, H.-J. Kretzshmar, 2008: A twenty-first century molar mass for dry air. HVAC&R Research, vol. 14, pp. 655-662.

[11] Equipartition theorem#Diatomic gases

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

@@ Line 1: / Line 1: @@
-{{Short description|Independent parameter describing the state of a physical system}}
+{{Short description|Independent parameter describing the state of a physical system}}भौतिकी और [[रसायन विज्ञान]] में, [[भौतिक प्रणाली]] की स्थिति के औपचारिक विवरण में स्वतंत्र कोटि एक स्वतंत्र भौतिक [[पैरामीटर|मापदण्ड]] है। प्रणाली की सभी अवस्था के सम्मुच्चय को प्रणाली के [[चरण स्थान|प्रावस्था समष्टि]] के रूप में जाना जाता है, और प्रणाली की स्वतंत्र कोटि प्रावस्था समष्टि के [[आयाम]] हैं।
-{{About||other fields|Degrees of freedom}}
-{{More citations needed|date=November 2009}}
-भौतिकी और [[रसायन विज्ञान]] में, [[भौतिक प्रणाली]] की स्थिति के औपचारिक विवरण में स्वतंत्रता की डिग्री एक स्वतंत्र भौतिक [[पैरामीटर]] है। सिस्टम के सभी राज्यों के सेट को सिस्टम के [[चरण स्थान]] के रूप में जाना जाता है, और सिस्टम की स्वतंत्रता की डिग्री चरण स्थान के [[आयाम]] हैं।
+त्रि-आयामी अंतरिक्ष में एक [[कण]] के स्थान के लिए तीन समन्वय प्रणाली की आवश्यकता होती है। इसी तरह, जिस दिशा और गति पर एक कण चलता है, प्रत्येक अंतरिक्ष के तीन आयामों के संदर्भ में उसे वेग के तीन घटकों के रूप में वर्णित किया जा सकता है। यदि प्रणाली का [[समय विकास]] [[नियतात्मक प्रणाली]] है (जहां एक पल में अवस्था विशिष्ट रूप से अपने अतीत और भविष्य की स्थिति और वेग को समय के कार्य के रूप में निर्धारित करता है) तो ऐसी प्रणाली में स्वतंत्र की छह कोटि होती है।{{citation needed|date=November 2015}} यदि कण की [[गति]] आयामों की कम संख्या तक सीमित है - उदाहरण के लिए, कण को एक तार के साथ या एक निश्चित सतह पर चलना चाहिए - तो प्रणाली में स्वतंत्र की छह कोटि से कम है। दूसरी ओर, एक विस्तारित वस्तु वाली एक प्रणाली जो घूम सकती है या कंपन कर सकती है, स्वतंत्र की छह कोटि से अधिक हो सकती है।
-त्रि-आयामी अंतरिक्ष में एक [[कण]] के स्थान के लिए तीन समन्वय प्रणाली की आवश्यकता होती है। इसी तरह, जिस दिशा और गति पर एक कण चलता है, उसे वेग के तीन घटकों के रूप में वर्णित किया जा सकता है, प्रत्येक अंतरिक्ष के तीन आयामों के संदर्भ में। यदि प्रणाली का [[समय विकास]] [[नियतात्मक प्रणाली]] है (जहां एक पल में राज्य विशिष्ट रूप से अपने अतीत और भविष्य की स्थिति और वेग को समय के कार्य के रूप में निर्धारित करता है) तो ऐसी प्रणाली में स्वतंत्रता की छह डिग्री होती है।{{citation needed|date=November 2015}} यदि कण की [[गति]] आयामों की कम संख्या तक सीमित है - उदाहरण के लिए, कण को एक तार के साथ या एक निश्चित सतह पर चलना चाहिए - तो सिस्टम में स्वतंत्रता की छह डिग्री से कम है। दूसरी ओर, एक विस्तारित वस्तु वाली एक प्रणाली जो घूम सकती है या कंपन कर सकती है, स्वतंत्रता की छह डिग्री से अधिक हो सकती है।
+[[शास्त्रीय यांत्रिकी]] में, किसी भी समय एक [[बिंदु कण]] की स्थिति को लैग्रैंगियन यांत्रिकी औपचारिकता में स्थिति और वेग निर्देशांक के साथ वर्णित किया जाता है, या [[हैमिल्टनियन (क्वांटम यांत्रिकी)|हैमिल्टनियन (परिमाण यांत्रिकी)]] औपचारिकता में स्थिति और गति निर्देशांक के साथ वर्णित किया जाता है।
-[[शास्त्रीय यांत्रिकी]] में, किसी भी समय एक [[बिंदु कण]] की स्थिति को लैग्रैंगियन यांत्रिकी औपचारिकता में स्थिति और वेग निर्देशांक के साथ वर्णित किया जाता है, या [[हैमिल्टनियन (क्वांटम यांत्रिकी)]] औपचारिकता में स्थिति और गति निर्देशांक के साथ।
+[[सांख्यिकीय यांत्रिकी]] में, स्वतंत्र की एक कोटि प्रणाली के [[माइक्रोस्टेट (सांख्यिकीय यांत्रिकी)|सूक्ष्म अवस्था (सांख्यिकीय यांत्रिकी)]] का वर्णन करने वाला एक एकल [[अदिश (भौतिकी)]] संख्या है।<ref name=":0">{{cite book |last=Reif |first=F. |title=सांख्यिकीय और तापीय भौतिकी के मूल सिद्धांत|year=2009 |publisher=Waveland Press, Inc. |location=Long Grove, IL |isbn=978-1-57766-612-7 |page=51}}</ref> प्रणाली के सभी सूक्ष्म अवस्था का विनिर्देश प्रणाली के प्रावस्था समष्टि में एक बिंदु है।
-[[सांख्यिकीय यांत्रिकी]] में, स्वतंत्रता की एक डिग्री एक प्रणाली के [[माइक्रोस्टेट (सांख्यिकीय यांत्रिकी)]] का वर्णन करने वाला एक एकल [[अदिश (भौतिकी)]] संख्या है।<ref name=":0">{{cite book |last=Reif |first=F. |title=सांख्यिकीय और तापीय भौतिकी के मूल सिद्धांत|year=2009 |publisher=Waveland Press, Inc. |location=Long Grove, IL |isbn=978-1-57766-612-7 |page=51}}</ref> सिस्टम के सभी माइक्रोस्टेट्स का विनिर्देश सिस्टम के चरण स्थान में एक बिंदु है।
+रसायन विज्ञान में 3D आदर्श श्रृंखला प्रतिरूप में, प्रत्येक एकलक के अभिविन्यास का वर्णन करने के लिए दो [[कोण]] आवश्यक हैं।
-रसायन विज्ञान में 3डी आदर्श श्रृंखला मॉडल में, प्रत्येक मोनोमर के अभिविन्यास का वर्णन करने के लिए दो [[कोण]] आवश्यक हैं।
+स्वतंत्र की द्विघात कोटि निर्दिष्ट करना अक्सर उपयोगी होता है। ये स्वतंत्र कोटि हैं जो प्रणाली की ऊर्जा के द्विघात कार्य में योगदान करती हैं।
-स्वतंत्रता की द्विघात कोटि निर्दिष्ट करना अक्सर उपयोगी होता है। ये स्वतंत्रता की डिग्री हैं जो सिस्टम की ऊर्जा के द्विघात कार्य में योगदान करती हैं।
+जो गिन रहा है उसके आधार पर, कई अलग-अलग तरीके हैं जिनसे स्वतंत्र कोटि को परिभाषित किया जा सकता है, प्रत्येक एक अलग मूल्य के साथ।<ref>{{Cite web|url=https://chemistry.stackexchange.com/questions/83840/does-a-diatomic-gas-have-one-or-two-vibrational-degrees-of-freedom|title = Physical chemistry - Does a diatomic gas have one or two vibrational degrees of freedom?}}</ref>
-कोई क्या गिन रहा है इसके आधार पर, कई अलग-अलग तरीके हैं जिनसे स्वतंत्रता की डिग्री को परिभाषित किया जा सकता है,
-प्रत्येक एक अलग मूल्य के साथ।<ref>{{Cite web|url=https://chemistry.stackexchange.com/questions/83840/does-a-diatomic-gas-have-one-or-two-vibrational-degrees-of-freedom|title = Physical chemistry - Does a diatomic gas have one or two vibrational degrees of freedom?}}</ref>
+== गैसों के लिए स्वतंत्र की ऊष्मागतिक कोटि ==
-== गैसों के लिए स्वतंत्रता की थर्मोडायनामिक डिग्री ==
 {{External image|Link=|image1=https://chem.libretexts.org/@api/deki/files/9669/h2ovibrations.gif?revision=1|image2=https://chem.libretexts.org/@api/deki/files/9668/co2vibrations.gif?revision=1}}
-[[समविभाजन प्रमेय]] द्वारा, गैस की प्रति मोल आंतरिक ऊर्जा बराबर होती है {{math|''c''<sub>v</sub> ''T''}}, कहाँ {{mvar|T}} [[निरपेक्ष तापमान]] है और स्थिर आयतन पर विशिष्ट ऊष्मा c है<sub>v</sub> = (च)(आर/2).
+[[समविभाजन प्रमेय]] द्वारा, गैस की प्रति मोल आंतरिक ऊर्जा {{math|''c''<sub>v</sub> ''T''}} बराबर होती है, जहाँ {{mvar|T}} [[निरपेक्ष तापमान]] है और स्थिर आयतन पर विशिष्ट ऊष्मा c<sub>v</sub> = (f)(R/2 है। R = 8.314 J/(K mol) सार्वभौमिक गैस स्थिरांक है, और f स्वतंत्र की ऊष्मागतिक (द्विघात) कोटि की संख्या है, ऊर्जा उत्पन्न करने के तरीकों की संख्या की गणना करना है।
-R = 8.314 J/(K mol) सार्वभौमिक गैस स्थिरांक है, और f स्वतंत्रता की थर्मोडायनामिक (द्विघात) डिग्री की संख्या है,
-उन तरीकों की संख्या की गिनती करना जिनमें ऊर्जा उत्पन्न हो सकती है।
-किसी भी परमाणु या अणु में x, y, और z अक्षों के संबंध में द्रव्यमान के केंद्र के स्थानांतरीय गति (गतिज ऊर्जा) से जुड़ी स्वतंत्रता की तीन डिग्री होती है। मोनोआटोमिक प्रजातियों के लिए स्वतंत्रता की ये एकमात्र डिग्री हैं, जैसे महान गैस परमाणु।
+किसी भी परमाणु या अणु में x, y, और z अक्षों के संबंध में द्रव्यमान के केंद्र के स्थानांतरीय गति (गतिज ऊर्जा) से जुड़ी स्वतंत्र की तीन कोटि होती है। एकपरमाण्विक प्रजातियों के लिए स्वतंत्र की ये एकमात्र कोटि हैं, जैसे उत्कृष्ट गैस परमाणु।
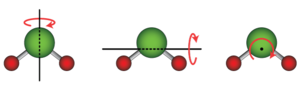
 [[File:Rotations in water molecule.png|thumb|]]दो या दो से अधिक परमाणुओं वाली संरचना के लिए, पूरी संरचना में घूर्णी गतिज ऊर्जा भी होती है, जहाँ पूरी संरचना एक अक्ष के चारों ओर घूमती है।
-एक रेखीय आणविक ज्यामिति, जहाँ सभी परमाणु एक अक्ष के साथ होते हैं,
+एक रेखीय आणविक ज्यामिति, जहाँ सभी परमाणु एक अक्ष के साथ होते हैं, जैसे कोई द्विपरमाणुक अणु और कुछ अन्य अणु जैसे [[कार्बन डाईऑक्साइड]] (CO<sub>2</sub>), स्वतंत्र की दो घूर्णी कोटि होती है, क्योंकि यह आणविक अक्ष के लम्बवत दो अक्षों में से किसी एक के बारे में घूम सकती है। एक अरैखिक अणु, जहां परमाणु एक धुरी के साथ नहीं रहते हैं, जैसे [[पानी के गुण|पानी]] (H<sub>2</sub>O), स्वतंत्र की तीन घूर्णी कोटि है, क्योंकि यह किसी भी तीन लंबवत अक्षों के चारों ओर घूम सकती है। विशेष स्तिथियों में, जैसे अधिशोषित बड़े अणु में, स्वतंत्र की घूर्णी कोटि केवल एक तक सीमित हो सकती है।<ref>{{cite journal|doi=10.1002/cphc.201200531|pmid=23047526|title=Stabilization of Large Adsorbates by Rotational Entropy: A Time-Resolved Variable-Temperature STM Study|journal=ChemPhysChem|volume=14 |issue=1|pages=162–9|year=2013 | last1=Waldmann|first1=Thomas |last2=Klein|first2=Jens|last3=Hoster|first3=Harry E.|last4=Behm|first4=R. Jürgen}}</ref>
-जैसे कोई द्विपरमाणुक अणु और कुछ अन्य अणु जैसे [[कार्बन डाईऑक्साइड]] (CO<sub>2</sub>),
-स्वतंत्रता की दो घूर्णी कोटि होती है, क्योंकि यह आणविक अक्ष के लम्बवत दो अक्षों में से किसी एक के बारे में घूम सकती है।
-एक अरैखिक अणु, जहां परमाणु एक धुरी के साथ नहीं रहते हैं, जैसे [[पानी के गुण]] (H<sub>2</sub>O), स्वतंत्रता की तीन घूर्णी डिग्री है, क्योंकि यह किसी भी तीन लंबवत अक्षों के चारों ओर घूम सकती है।
-विशेष मामलों में, जैसे अधिशोषित बड़े अणु, स्वतंत्रता की घूर्णी डिग्री केवल एक तक सीमित हो सकती है।<ref>{{cite journal|doi=10.1002/cphc.201200531|pmid=23047526|title=Stabilization of Large Adsorbates by Rotational Entropy: A Time-Resolved Variable-Temperature STM Study|journal=ChemPhysChem|volume=14 |issue=1|pages=162–9|year=2013 | last1=Waldmann|first1=Thomas |last2=Klein|first2=Jens|last3=Hoster|first3=Harry E.|last4=Behm|first4=R. Jürgen}}</ref>
-दो या दो से अधिक परमाणुओं वाली संरचना में कंपन ऊर्जा भी होती है, जहां व्यक्तिगत परमाणु एक दूसरे के संबंध में गति करते हैं। एक डायटोमिक अणु में एक [[आणविक कंपन]] मोड होता है: दो परमाणु वसंत के रूप में कार्य करने वाले रासायनिक बंधन के साथ आगे और आगे बढ़ते हैं। के साथ एक अणु {{mvar|N}} परमाणुओं में आणविक कंपन के अधिक जटिल तरीके होते हैं {{math|3''N'' − 5}} एक रैखिक अणु के लिए कंपन मोड और {{math|3''N'' − 6}} एक अरेखीय अणु के लिए मोड।<ref>[[Molecular vibration]]{{User-generated source|date=January 2021}}</ref>
-विशिष्ट उदाहरण के रूप में, रैखिक CO<sub>2</sub> अणु में दोलन के 4 तरीके होते हैं,<ref>For drawings, see http://www.colby.edu/chemistry/PChem/notes/NormalModesText.pdf</ref> और अरैखिक जल अणु में दोलन के 3 तरीके होते हैं<ref>For drawings, see https://sites.cns.utexas.edu/jones_ch431/normal-modes-vibration</ref>
-प्रत्येक कंपन मोड में दो ऊर्जा शब्द होते हैं: गतिमान परमाणुओं की [[गतिज ऊर्जा]] और वसंत जैसे रासायनिक बंधों की [[संभावित ऊर्जा]]।
-इसलिए, कंपन ऊर्जा शर्तों की संख्या {{math|2(3''N'' − 5)}} एक रैखिक अणु के लिए और {{math|2(3''N'' − 6)}} एक अरेखीय अणु के लिए मोड।
-घूर्णी और कंपन मोड दोनों को परिमाणित किया जाता है, जिसके लिए न्यूनतम तापमान को सक्रिय करने की आवश्यकता होती है।<ref>Section 12-7 (pp. 376-379) of Sears and Salinger, 1975: Thermodynamics, Kinetic Theory, and Statistical Thermodynamics. Third edition. Addison-Wesley Publishing Co.</ref> कई गैसों के लिए स्वतंत्रता की घूर्णी डिग्री को सक्रिय करने के लिए [[घूर्णी तापमान]] 100 K से कम है। एन के लिए<sub>2</sub> और ओ<sub>2</sub>, यह 3 K से कम है।<ref name=":0" />पर्याप्त कंपन के लिए आवश्यक [[कंपन तापमान]] 10 के बीच है<sup>3</sup> के और 10<sup>4</sup> के, 3521 के एन के लिए<sub>2</sub> और 2156 के ओ के लिए<sub>2</sub>.<ref name=":0" />एन में कंपन को सक्रिय करने के लिए विशिष्ट वायुमंडलीय तापमान पर्याप्त नहीं हैं<sub>2</sub> और ओ<sub>2</sub>, जिसमें अधिकांश वातावरण शामिल है। (अगला आंकड़ा देखें।) हालांकि, बहुत कम प्रचुर मात्रा में [[ग्रीनहाउस गैस]]ें पृथ्वी की सतह से [[ अवरक्त ]] को अवशोषित करके क्षोभमंडल को गर्म रखती हैं, जो उनके कंपन मोड को उत्तेजित करता है।<ref>{{Cite web|last=|first=|date=|title=अणु कंपन करते हैं|url=https://scied.ucar.edu/molecular-vibration-modes|url-status=live|archive-url=https://web.archive.org/web/20141010161149/http://scied.ucar.edu:80/molecular-vibration-modes |archive-date=2014-10-10 |access-date=2021-01-19|website=UCAR Center for Science Education}}</ref>
+दो या दो से अधिक परमाणुओं वाली संरचना में कंपन ऊर्जा भी होती है, जहां व्यक्तिगत परमाणु एक दूसरे के संबंध में गति करते हैं। एक द्विपरमाणुक अणु में एक [[आणविक कंपन]] प्रणाली होता है: दो परमाणु स्प्रिंग के रूप में कार्य करने वाले रासायनिक बंधन के साथ आगे और आगे बढ़ते हैं। {{mvar|N}} परमाणुओं के साथ एक अणु में आणविक कंपन के अधिक जटिल तरीके होते हैं  एक रैखिक अणु के लिए {{math|3''N'' − 5}} कंपन प्रणाली और एक अरेखीय अणु के लिए {{math|3''N'' − 6}} प्रणाली।<ref>[[Molecular vibration]]{{User-generated source|date=January 2021}}</ref> विशिष्ट उदाहरण के रूप में, रैखिक CO<sub>2</sub> अणु में दोलन के 4 तरीके होते हैं,<ref>For drawings, see http://www.colby.edu/chemistry/PChem/notes/NormalModesText.pdf</ref> और अरैखिक जल अणु में दोलन के 3 तरीके होते हैं<ref>For drawings, see https://sites.cns.utexas.edu/jones_ch431/normal-modes-vibration</ref> प्रत्येक कंपन प्रणाली में दो ऊर्जा शब्द होते हैं: गतिमान परमाणुओं की [[गतिज ऊर्जा]] और वसंत जैसे रासायनिक बंधों की [[संभावित ऊर्जा]]। इसलिए, कंपन ऊर्जा शर्तों की संख्या एक रैखिक अणु के लिए {{math|2(3''N'' − 5)}} है और  एक अरेखीय अणु के लिए {{math|2(3''N'' − 6)}} प्रणाली है।
-इस ऊर्जा का अधिकांश भाग [[ग्रीनहाउस प्रभाव]] के माध्यम से इन्फ्रारेड में सतह पर वापस आ जाता है।
-क्योंकि कमरे का तापमान (≈298 K) विशिष्ट घूर्णी तापमान से अधिक है, लेकिन विशिष्ट कंपन तापमान से कम है, केवल स्वतंत्रता के अनुवाद और घूर्णी डिग्री, समान मात्रा में, [[ताप क्षमता अनुपात]] में योगदान करते हैं। इसलिए {{mvar|γ}}≈{{math|{{sfrac|5|3}}}} [[एकपरमाण्विक]] गैसों के लिए और {{mvar|γ}}≈{{math|{{sfrac|7|5}}}} कमरे के तापमान पर [[दो परमाणुओंवाला]] गैसों के लिए।<ref name=":0" />
+घूर्णी और कंपन प्रणाली दोनों को परिमाणित किया जाता है, जिसके लिए न्यूनतम तापमान को सक्रिय करने की आवश्यकता होती है।<ref>Section 12-7 (pp. 376-379) of Sears and Salinger, 1975: Thermodynamics, Kinetic Theory, and Statistical Thermodynamics. Third edition. Addison-Wesley Publishing Co.</ref> कई गैसों के लिए स्वतंत्र की घूर्णी कोटि को सक्रिय करने के लिए [[घूर्णी तापमान]] 100 K से कम है। N<sub>2</sub> और O<sub>2</sub> के लिए, यह 3 K से कम है।<ref name=":0" /> पर्याप्त कंपन के लिए आवश्यक [[कंपन तापमान]] 10<sup>3</sup> और 10<sup>4</sup> के बीच है, 3521 K N<sub>2</sub> के लिए और 2156 K O<sub>2</sub> के लिए हैं।<ref name=":0" /> N<sub>2</sub> और O<sub>2</sub> में कंपन को सक्रिय करने के लिए विशिष्ट वायुमंडलीय तापमान पर्याप्त नहीं हैं, जिसमें अधिकांश वातावरण सम्मिलित है। (अगला आंकड़ा देखें।) हालांकि, बहुत कम प्रचुर मात्रा में [[ग्रीनहाउस गैस]] पृथ्वी की सतह से [[ अवरक्त |अवरक्त]] को अवशोषित करके क्षोभमंडल को गर्म रखती हैं, जो उनके कंपन प्रणाली को उत्तेजित करता है।<ref>{{Cite web|last=|first=|date=|title=अणु कंपन करते हैं|url=https://scied.ucar.edu/molecular-vibration-modes|url-status=live|archive-url=https://web.archive.org/web/20141010161149/http://scied.ucar.edu:80/molecular-vibration-modes |archive-date=2014-10-10 |access-date=2021-01-19|website=UCAR Center for Science Education}}</ref> इस ऊर्जा का अधिकांश भाग [[ग्रीनहाउस प्रभाव]] के माध्यम से अवरक्त में सतह पर वापस आ जाता है।
-[[File:Specific heat at constant volume for dry air vs T.png|thumb|स्थिर आयतन पर शुष्क वायु की विशिष्ट ऊष्मा का ग्राफ, c<sub>v</sub>, तापमान के एक समारोह के रूप में संख्यात्मक मूल्यों को तालिका से हवा में लिया जाता है - लगातार दबाव और भिन्न तापमान पर विशिष्ट गर्मी।<ref>{{Cite web|url=https://www.engineeringtoolbox.com/air-specific-heat-capacity-d_705.html|title=Air - Specific Heat vs. Temperature at Constant Pressure}}</ref> उन मूल्यों में जे / (के किलो) की इकाइयां हैं, इसलिए प्लॉट किए गए संदर्भ रेखाएं (5/2) {{mvar|R}}<sub>d</sub> और (7/2) {{mvar|R}}<sub>d</sub>, कहाँ {{mvar|R}}<sub>d</sub> = {{sfrac|{{mvar|R<sub>d</sub>}}|{{mvar|M}}}} शुष्क हवा के लिए गैस नियतांक है, {{mvar|R}} = 8.314 J/(K mol) सार्वभौमिक गैस नियतांक है, और M<sub>d</sub> = 28.965369 g/mol शुष्क वायु का मोलर द्रव्यमान है।<ref>Gatley, D. P., S. Herrmann, H.-J. Kretzshmar, 2008: A twenty-first century molar mass for dry air. HVAC&R Research, vol. 14, pp. 655-662.</ref>
-टी = 140, 160, 200, 220, 320, 340, 360, 380 के, सी पर<sub>v</sub> = 718.4, 717.2, 716.3, 716.3, 719.2, 720.6, 722.3, 724.3 J/(K किलो)। इस प्रकार, 140 के <टी <360 के, सी के लिए<sub>v</sub> (5/2) आर से भिन्न है<sub>d</sub> 1% से भी कम।]]चूंकि पृथ्वी के वायुमंडल में डायटोमिक गैसों ([[नाइट्रोजन]] और [[ऑक्सीजन]] का योगदान लगभग 99% है) का प्रभुत्व है, इसकी दाढ़ आंतरिक ऊर्जा करीब है {{math|c<sub>v</sub> T}} = (5/2){{mvar|R}}{{mvar|T}}, डायटोमिक गैसों द्वारा प्रदर्शित स्वतंत्रता की 5 डिग्री द्वारा निर्धारित।{{cn|date=October 2022}}<ref>[[Equipartition theorem#Diatomic gases]]</ref>{{circular ref|date=January 2021}}
+क्योंकि कमरे का तापमान (≈298 K) विशिष्ट घूर्णी तापमान से अधिक है, लेकिन विशिष्ट कंपन तापमान से कम है, केवल स्वतंत्र के अनुवाद और घूर्णी कोटि, समान मात्रा में, [[ताप क्षमता अनुपात]] में योगदान करते हैं। इसलिए {{mvar|γ}}≈{{math|{{sfrac|5|3}}}} [[एकपरमाण्विक]] गैसों के लिए और {{mvar|γ}}≈{{math|{{sfrac|7|5}}}} कमरे के तापमान पर [[दो परमाणुओंवाला|द्विपरमाण्विक]] गैसों के लिए है।<ref name=":0" />
-ग्राफ़ को दाईं ओर देखें। 140 के < {{mvar|T}} <380 के, सी<sub>v</sub> (5/2) से भिन्न {{mvar|R}}<sub>d</sub> 1% से भी कम।
+[[File:Specific heat at constant volume for dry air vs T.png|thumb|स्थिर आयतन पर शुष्क वायु की विशिष्ट ऊष्मा का ग्राफ, c<sub>v</sub>, तापमान के एक फलन के रूप में संख्यात्मक मूल्यों को तालिका से हवा - लगातार दबाव और भिन्न तापमान पर विशिष्ट गर्मी में लिया जाता है ।<ref>{{Cite web|url=https://www.engineeringtoolbox.com/air-specific-heat-capacity-d_705.html|title=Air - Specific Heat vs. Temperature at Constant Pressure}}</ref> उन मूल्यों में J / (के किलो) की इकाइयां हैं, इसलिए आलेख किए गए संदर्भ रेखाएं (5/2) {{mvar|R}}<sub>d</sub> और (7/2) {{mvar|R}}<sub>d</sub> हैं, जहाँ {{mvar|R}}<sub>d</sub> = {{sfrac|{{mvar|R<sub>d</sub>}}|{{mvar|M}}}} शुष्क हवा के लिए गैस नियतांक है, {{mvar|R}} = 8.314 J/(K mol) सार्वभौमिक गैस नियतांक है, और M<sub>d</sub> = 28.965369 g/mol शुष्क वायु का मोलीय द्रव्यमान है।<ref>Gatley, D. P., S. Herrmann, H.-J. Kretzshmar, 2008: A twenty-first century molar mass for dry air. HVAC&R Research, vol. 14, pp. 655-662.</ref>T = 140, 160, 200, 220, 320, 340, 360, 380 के, C<sub>v</sub> पर = 718.4, 717.2, 716.3, 716.3, 719.2, 720.6, 722.3, 724.3 J/(K किलो)। इस प्रकार, 140 के <T <360 K, C के लिए<sub>v</sub> (5/2) R<sub>d</sub> से भिन्न है, 1% से भी कम।
-केवल क्षोभमंडल और [[समताप मंडल]] में तापमान से काफी ऊपर के तापमान पर ही कुछ अणुओं में पर्याप्त ऊर्जा होती है जिससे वे N के कंपन मोड को सक्रिय कर सकें।<sub>2</sub> और ओ<sub>2</sub>. स्थिर आयतन पर विशिष्ट ऊष्मा, c<sub>v</sub>, धीरे-धीरे (7/2) की ओर बढ़ता है {{mvar|R}} जैसे-जैसे तापमान T = 400 K से ऊपर बढ़ता है, जहाँ c<sub>v</sub> 1.3% ऊपर है (5/2) {{mvar|R}}<sub>d</sub> = 717.5 जे / (के किलो)।
+]]चूंकि पृथ्वी के वायुमंडल में द्विपरमाणुक गैसों ([[नाइट्रोजन]] और [[ऑक्सीजन]] का योगदान लगभग 99% है) का प्रभुत्व है, इसकी दाढ़ आंतरिक ऊर्जा करीब {{math|c<sub>v</sub> T}} = (5/2){{mvar|R}}{{mvar|T}} है, द्विपरमाणुक गैसों द्वारा प्रदर्शित स्वतंत्र की 5 कोटि द्वारा निर्धारित है।{{cn|date=October 2022}}<ref>[[Equipartition theorem#Diatomic gases]]</ref>{{circular ref|date=January 2021}}
+ग्राफ़ को दाईं ओर देखें। 140 K < {{mvar|T}} <380 K, c<sub>v</sub> (5/2) से भिन्न {{mvar|R}}<sub>d</sub> 1% से भी कम है। केवल क्षोभमंडल और [[समताप मंडल]] में तापमान से काफी ऊपर के तापमान पर ही कुछ अणुओं में पर्याप्त ऊर्जा होती है जिससे वे N<sub>2</sub> और O<sub>2</sub> के कंपन प्रणाली को सक्रिय कर सकें। स्थिर आयतन पर विशिष्ट ऊष्मा, c<sub>v</sub>, धीरे-धीरे (7/2) की ओर बढ़ता है {{mvar|R}} जैसे-जैसे तापमान T = 400 K से ऊपर बढ़ता है, जहाँ c<sub>v</sub>  (5/2) {{mvar|R}}<sub>d</sub> = 717.5 जे / (के किलो) से 1.3% ऊपर है।
 {| class="wikitable"
-|+Component degrees of freedom for {{Mvar|N}} atoms (3{{Mvar|N}} total coordinate motions)
+|+एन परमाणुओं के लिए स्वतंत्र की घटक कोटि (3{{Mvar|N}} कुल समन्वय गति)
 |-
 !
-! [[Monatomic]]
+! [[Monatomic|एकपरमाण्विक]]
-! [[Linear molecule]]s
+! [[Linear molecule|रैखिक अणु]]
-! [[molecular geometry|Non-linear molecules]]
+! [[molecular geometry|अरैखिक अणु]]
 |-
-| Translation ({{mvar|x}}, {{mvar|y}}, and {{mvar|z}})
+| अनुवाद ({{mvar|x}}, {{mvar|y}}, and {{mvar|z}})
 | align="center" | 3
 | align="center" | 3
 | align="center" | 3
 |-
-| Rotation ({{mvar|x}}, {{mvar|y}}, and {{mvar|z}})
+| क्रमावर्तन ({{mvar|x}}, {{mvar|y}}, and {{mvar|z}})
 | align="center" | 0
 | align="center" | 2
 | align="center" | 3
 |-
-| Vibration (structural variations)
+| कंपन (संरचनात्मक विभिन्नता)
 | align="center" | 0
 | align="center" | {{math|(3''N'' − 5)}}
@@ Line 73: / Line 59: @@
 === एक स्थिति निर्दिष्ट करने के लिए निर्देशांक की न्यूनतम संख्या की गणना ===
-किसी स्थिति को निर्दिष्ट करने के लिए आवश्यक न्यूनतम संख्या में निर्देशांक का उपयोग करके कोई भी स्वतंत्रता की डिग्री की गणना कर सकता है। यह अग्रानुसार होगा:
+किसी स्थिति को निर्दिष्ट करने के लिए आवश्यक न्यूनतम संख्या में निर्देशांक का उपयोग करके कोई भी स्वतंत्र कोटि की गणना कर सकता है। यह अग्रानुसार होगा:
-# एक कण के लिए हमें इसकी स्थिति निर्दिष्ट करने के लिए 2-डी विमान में 2 निर्देशांक और 3-डी अंतरिक्ष में 3 निर्देशांक की आवश्यकता होती है। इस प्रकार 3-डी अंतरिक्ष में इसकी स्वतंत्रता की डिग्री 3 है।
+# एक कण के लिए हमें इसकी स्थिति निर्दिष्ट करने के लिए 2-D तल में 2 निर्देशांक और 3-D अंतरिक्ष में 3 निर्देशांक की आवश्यकता होती है। इस प्रकार 3-D अंतरिक्ष में इसकी स्वतंत्र कोटि 3 है।
-# एक 3-डी अंतरिक्ष में 2 कणों (उदाहरण के लिए एक डायटोमिक अणु) से युक्त शरीर के लिए उनके बीच निरंतर दूरी के साथ (मान लें कि डी) हम इसकी स्वतंत्रता की डिग्री (नीचे) 5 दिखा सकते हैं।
+# एक 3-D अंतरिक्ष में 2 कणों (उदाहरण के लिए एक द्विपरमाणुक अणु) से युक्त शरीर के लिए उनके बीच निरंतर दूरी के साथ (मान लें कि D) हम इसकी स्वतंत्र कोटि (नीचे) 5 दिखा सकते हैं।
-मान लीजिए कि इस शरीर में एक कण का समन्वय है {{math|(''x''<sub>1</sub>, ''y''<sub>1</sub>, ''z''<sub>1</sub>)}} और दूसरे ने समन्वय किया है {{math|(''x''<sub>2</sub>, ''y''<sub>2</sub>, ''z''<sub>2</sub>)}} साथ {{math| ''z''<sub>2</sub>}} अज्ञात। दो निर्देशांकों के बीच की दूरी के सूत्र का अनुप्रयोग
+मान लीजिए कि इस शरीर में एक कण का समन्वय {{math|(''x''<sub>1</sub>, ''y''<sub>1</sub>, ''z''<sub>1</sub>)}} है और दूसरे ने समन्वय {{math|(''x''<sub>2</sub>, ''y''<sub>2</sub>, ''z''<sub>2</sub>)}} अज्ञात {{math| ''z''<sub>2</sub>}} के साथ किया है। दो निर्देशांकों के बीच की दूरी के सूत्र का अनुप्रयोग
 :<math>d=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2+(z_2-z_1)^2}</math>
-एक अज्ञात के साथ एक समीकरण में परिणाम, जिसमें हम के लिए हल कर सकते हैं {{math|''z''<sub>2</sub>}}.
+एक अज्ञात के साथ एक समीकरण में परिणाम, जिसमें हम {{math|''z''<sub>2</sub>}} के लिए हल कर सकते हैं।  {{math|''x''<sub>1</sub>}}, {{math|''x''<sub>2</sub>}}, {{math|''y''<sub>1</sub>}}, {{math|''y''<sub>2</sub>}}, {{math|''z''<sub>1</sub>}}, या {{math|''z''<sub>2</sub>}} में से एक अज्ञात हो सकता है।
-में से एक {{math|''x''<sub>1</sub>}}, {{math|''x''<sub>2</sub>}}, {{math|''y''<sub>1</sub>}}, {{math|''y''<sub>2</sub>}}, {{math|''z''<sub>1</sub>}}, या {{math|''z''<sub>2</sub>}} अज्ञात हो सकता है।
-क्लासिकल समविभाजन प्रमेय के विपरीत, कमरे के [[तापमान]] पर, अणुओं की कंपन गति आमतौर पर ताप क्षमता में नगण्य योगदान देती है। ऐसा इसलिए है क्योंकि स्वतंत्रता की ये डिग्री जमी हुई हैं क्योंकि ऊर्जा के बीच की दूरी परिवेश के तापमान के अनुरूप ऊर्जा से अधिक है ({{math|''k''<sub>B</sub>''T''}}).<ref name=":0" />
+शास्त्रीय समविभाजन प्रमेय के विपरीत, कमरे के [[तापमान]] पर, अणुओं की कंपन गति सामान्यतः ताप क्षमता में उपेक्षणीय योगदान देती है। ऐसा इसलिए है क्योंकि स्वतंत्र की ये कोटि जमी हुई हैं क्योंकि ऊर्जा के बीच की दूरी परिवेश के तापमान ({{math|''k''<sub>B</sub>''T''}}) के अनुरूप ऊर्जा से अधिक है।<ref name=":0" />
-== स्वतंत्रता की स्वतंत्र डिग्री ==
+== स्वतंत्र की स्वतंत्र कोटि ==
-स्वतंत्रता की डिग्री का सेट {{math|''X''<sub>1</sub>, ... , ''X''<sub>''N''</sub>}एक प्रणाली का } स्वतंत्र है यदि सेट से जुड़ी ऊर्जा को निम्नलिखित रूप में लिखा जा सकता है:
+<nowiki>स्वतंत्र कोटि का सम्मुच्चय {{math|</nowiki>''X''<sub>1</sub>, ..., ''X''<sub>''N''</sub>} एक प्रणाली का} स्वतंत्र है यदि सम्मुच्चय से जुड़ी ऊर्जा को निम्नलिखित रूप में लिखा जा सकता है:
 :<math>E = \sum_{i=1}^N E_i(X_i),</math>
-कहाँ {{mvar|E<sub>i</sub>}} एकमात्र चर का एक कार्य है {{mvar|X<sub>i</sub>}}.
+जहाँ {{mvar|E<sub>i</sub>}} एकमात्र चर का एक कार्य {{mvar|X<sub>i</sub>}} है।
-उदाहरण: अगर {{math|''X''<sub>1</sub>}} और {{math|''X''<sub>2</sub>}} स्वतंत्रता की दो डिग्री हैं, और {{mvar|E}} संबंधित ऊर्जा है:
+उदाहरण: अगर {{math|''X''<sub>1</sub>}} और {{math|''X''<sub>2</sub>}} स्वतंत्र की दो कोटि हैं, और {{mvar|E}} संबंधित ऊर्जा है:
-* अगर <math>E = X_1^4 + X_2^4</math>, तो स्वतंत्रता की दो डिग्री स्वतंत्र हैं।
+* अगर <math>E = X_1^4 + X_2^4</math> है, तो स्वतंत्र की दो कोटि स्वतंत्र हैं।
-* अगर <math>E = X_1^4 + X_1 X_2 + X_2^4</math>, तब स्वतंत्रता की दो कोटि स्वतंत्र नहीं हैं। के उत्पाद को शामिल करने वाला शब्द {{math|''X''<sub>1</sub>}} और {{math|''X''<sub>2</sub>}} एक युग्मन शब्द है जो स्वतंत्रता की दो डिग्री के बीच की बातचीत का वर्णन करता है।
+* अगर <math>E = X_1^4 + X_1 X_2 + X_2^4</math> है, तब स्वतंत्र की दो कोटि स्वतंत्र नहीं हैं। {{math|''X''<sub>1</sub>}} और {{math|''X''<sub>2</sub>}} के उत्पाद को सम्मिलित करने वाला शब्द एक युग्मन शब्द है जो स्वतंत्र की दो कोटि के बीच की बातचीत का वर्णन करता है।
-के लिए {{mvar|i}} 1 से {{mvar|N}}, का मूल्य {{mvar|i}} स्वतंत्रता की डिग्री {{mvar|X<sub>i</sub>}} [[बोल्ट्जमैन वितरण]] के अनुसार वितरित किया जाता है। इसकी संभाव्यता घनत्व फ़ंक्शन निम्न है:
+से {{mvar|N}} तक {{mvar|i}} के लिए, {{mvar|i}} का मूल्य स्वतंत्र कोटि {{mvar|X<sub>i</sub>}} [[बोल्ट्जमैन वितरण]] के अनुसार वितरित किया जाता है। इसकी संभाव्यता घनत्व फलन निम्न है:
 : <math>p_i(X_i) = \frac{e^{-\frac{E_i}{k_B T}}}{\int dX_i \, e^{-\frac{E_i}{k_B T}}}</math>,
 इस खंड में, और पूरे लेख में कोष्ठक <math>\langle \rangle</math> उनके द्वारा संलग्न मात्रा के माध्य को निरूपित करें।
-सिस्टम की [[आंतरिक ऊर्जा]] स्वतंत्रता की प्रत्येक डिग्री से जुड़ी औसत ऊर्जाओं का योग है:
+प्रणाली की [[आंतरिक ऊर्जा]] स्वतंत्र की प्रत्येक कोटि से जुड़ी औसत ऊर्जाओं का योग है:
 :<math>\langle E \rangle = \sum_{i=1}^N \langle E_i \rangle.</math>
-== स्वतंत्रता की द्विघात डिग्री ==
+== स्वतंत्र की द्विघात कोटि ==
-स्वतंत्रता की एक डिग्री {{mvar|X<sub>i</sub>}} द्विघात है यदि स्वतंत्रता की इस डिग्री से जुड़ी ऊर्जा शर्तों को इस रूप में लिखा जा सकता है
+स्वतंत्र की एक कोटि {{mvar|X<sub>i</sub>}} द्विघात है यदि स्वतंत्र की इस कोटि से जुड़ी ऊर्जा शर्तों को इस रूप में लिखा जा सकता है
 :<math>E = \alpha_i\,\,X_i^2 + \beta_i \,\, X_i Y </math>,
-कहाँ {{mvar|Y}} स्वतंत्रता की अन्य द्विघात कोटि का एक रेखीय संयोजन है।
+जहाँ {{mvar|Y}} स्वतंत्र की अन्य द्विघात कोटि का एक रेखीय संयोजन है।
-उदाहरण: अगर {{math|''X''<sub>1</sub>}} और {{math|''X''<sub>2</sub>}} स्वतंत्रता की दो डिग्री हैं, और {{mvar|E}} संबंधित ऊर्जा है:
+उदाहरण: अगर {{math|''X''<sub>1</sub>}} और {{math|''X''<sub>2</sub>}} स्वतंत्र की दो कोटि हैं, और {{mvar|E}} संबंधित ऊर्जा है:
-* अगर <math>E = X_1^4 + X_1^3 X_2 + X_2^4</math>, तो स्वतंत्रता की दो डिग्री स्वतंत्र और गैर-द्विघात नहीं हैं।
+* अगर <math>E = X_1^4 + X_1^3 X_2 + X_2^4</math> है, तो स्वतंत्र की दो कोटि स्वतंत्र और गैर-द्विघात नहीं हैं।
-* अगर <math>E = X_1^4 + X_2^4</math>, तो स्वतंत्रता की दो डिग्री स्वतंत्र और गैर-द्विघात हैं।
+* अगर <math>E = X_1^4 + X_2^4</math> है, तो स्वतंत्र की दो कोटि स्वतंत्र और गैर-द्विघात हैं।
-* अगर <math>E = X_1^2 + X_1 X_2 + 2X_2^2</math>, तब स्वतंत्रता की दो कोटि स्वतंत्र नहीं हैं बल्कि द्विघात हैं।
+* अगर <math>E = X_1^2 + X_1 X_2 + 2X_2^2</math> है, तब स्वतंत्र की दो कोटि स्वतंत्र नहीं हैं बल्कि द्विघात हैं।
-* अगर <math>E = X_1^2 + 2X_2^2</math>, तो स्वतंत्रता की दो डिग्री स्वतंत्र और द्विघात हैं।
+* अगर <math>E = X_1^2 + 2X_2^2</math> है, तो स्वतंत्र की दो कोटि स्वतंत्र और द्विघात हैं।
-उदाहरण के लिए, [[न्यूटोनियन यांत्रिकी]] में, स्वतंत्रता की द्विघात डिग्री की एक प्रणाली की गतिशीलता (यांत्रिकी) को निरंतर गुणांक वाले सजातीय [[रैखिक अंतर समीकरण]]ों के एक सेट द्वारा नियंत्रित किया जाता है।
+उदाहरण के लिए, [[न्यूटोनियन यांत्रिकी]] में, स्वतंत्र की द्विघात कोटि की एक प्रणाली की गतिशीलता (यांत्रिकी) को निरंतर गुणांक वाले सजातीय [[रैखिक अंतर समीकरण]] के एक सम्मुच्चय द्वारा नियंत्रित किया जाता है।
-=== स्वतंत्रता की द्विघात और स्वतंत्र डिग्री ===
+=== स्वतंत्र की द्विघात और स्वतंत्र कोटि ===
-{{math|''X''<sub>1</sub>, ... , ''X''<sub>''N''</sub>}} स्वतंत्रता की द्विघात और स्वतंत्र डिग्री हैं यदि उनके द्वारा प्रतिनिधित्व की जाने वाली प्रणाली के एक माइक्रोस्टेट से जुड़ी ऊर्जा को इस प्रकार लिखा जा सकता है:
+{{math|''X''<sub>1</sub>, ... , ''X''<sub>''N''</sub>}} स्वतंत्र की द्विघात और स्वतंत्र कोटि हैं यदि उनके द्वारा प्रतिनिधित्व की जाने वाली प्रणाली के एक सूक्ष्म अवस्था से जुड़ी ऊर्जा को इस प्रकार लिखा जा सकता है:
 :<math>E = \sum_{i=1}^N \alpha_i X_i^2</math>
 === समविभाजन प्रमेय ===
-{{main|Equipartition theorem}}
+{{main|समविभाजन प्रमेय}}
-सांख्यिकीय यांत्रिकी की शास्त्रीय सीमा में, [[थर्मोडायनामिक संतुलन]] पर, एक प्रणाली की आंतरिक ऊर्जा {{mvar|N}} स्वतंत्रता की द्विघात और स्वतंत्र डिग्री है:
+सांख्यिकीय यांत्रिकी की शास्त्रीय सीमा में, [[थर्मोडायनामिक संतुलन|ऊष्मागतिक संतुलन]] पर, एक प्रणाली की आंतरिक ऊर्जा {{mvar|N}} स्वतंत्र की द्विघात और स्वतंत्र कोटि है:
 : <math>U = \langle E \rangle = N\,\frac{k_B T}{2}</math>
-यहाँ, स्वतंत्रता की डिग्री से जुड़ी औसत ऊर्जा है:
+यहाँ, स्वतंत्र कोटि से जुड़ी औसत ऊर्जा निम्न है:
 :<math>\langle E_i \rangle = \int dX_i\,\,\alpha_i X_i^2\,\, p_i(X_i) = \frac{\int dX_i\,\,\alpha_i X_i^2\,\, e^{-\frac{\alpha_i X_i^2}{k_B T}}}{\int dX_i\,\, e^{-\frac{\alpha_i X_i^2}{k_B T}}} </math>
 :<math>\langle E_i \rangle = \frac{k_B T}{2}\frac{\int dx\,\,x^2\,\, e^{-\frac{x^2}{2}}}{\int dx\,\, e^{-\frac{x^2}{2}}} = \frac{k_B T}{2} </math>
-चूंकि स्वतंत्रता की डिग्री स्वतंत्र हैं, सिस्टम की आंतरिक ऊर्जा स्वतंत्रता की प्रत्येक डिग्री से जुड़ी औसत ऊर्जा के योग के बराबर होती है, जो परिणाम प्रदर्शित करती है।
+चूंकि स्वतंत्र कोटि स्वतंत्र हैं, प्रणाली की आंतरिक ऊर्जा स्वतंत्र की प्रत्येक कोटि से जुड़ी औसत ऊर्जा के योग के बराबर होती है, जो परिणाम प्रदर्शित करती है।
 == सामान्यीकरण ==
-अपने चरण स्थान में एक [[बिंदु (ज्यामिति)]] के रूप में एक प्रणाली की स्थिति का वर्णन, हालांकि गणितीय रूप से सुविधाजनक है, मौलिक रूप से गलत माना जाता है। [[क्वांटम यांत्रिकी]] में, स्वतंत्रता की गति की डिग्री तरंग फ़ंक्शन की अवधारणा से अलग हो जाती है, और [[ऑपरेटर (भौतिकी)]] जो स्वतंत्रता की अन्य डिग्री के अनुरूप होती है, में [[बिंदु स्पेक्ट्रम]] होता है। उदाहरण के लिए, एक [[इलेक्ट्रॉन]] या फोटॉन के लिए कोणीय संवेग संचालिका #स्पिन, कक्षीय, और कुल कोणीय संवेग संचालिका (जो घूर्णी स्वतंत्रता से मेल खाती है) में केवल दो eigenvalues होते हैं। यह असततता तब स्पष्ट हो जाती है जब [[क्रिया (भौतिकी)]] में [[प्लैंक स्थिरांक]] के परिमाण का एक क्रम होता है, और स्वतंत्रता की अलग-अलग डिग्री को अलग किया जा सकता है।
+अपने प्रावस्था समष्टि में [[बिंदु (ज्यामिति)]] के रूप में एक प्रणाली की स्थिति का वर्णन, हालांकि गणितीय रूप से सुविधाजनक है, परन्तु मौलिक रूप से गलत माना जाता है। [[क्वांटम यांत्रिकी|परिमाण यांत्रिकी]] में, स्वतंत्र की गति की कोटि तरंग फलन की अवधारणा से अलग हो जाती है, और [[ऑपरेटर (भौतिकी)|संचालक (भौतिकी)]] में [[बिंदु स्पेक्ट्रम|बिंदु वर्णक्रम]] होता है जो स्वतंत्र की अन्य कोटि के अनुरूप होती है। उदाहरण के लिए, एक [[इलेक्ट्रॉन]] या फोटॉन के लिए कोणीय संवेग संचालिका, कक्षीय, और कुल कोणीय संवेग संचालिका (जो घूर्णी स्वतंत्र से मेल खाती है) में केवल दो आइगेनवैल्यू होते हैं। यह असततता तब स्पष्ट हो जाती है जब [[क्रिया (भौतिकी)]] में [[प्लैंक स्थिरांक]] के परिमाण का एक क्रम होता है, और स्वतंत्र की अलग-अलग कोटि को अलग किया जा सकता है।
 ==संदर्भ==
@@ Line 137: / Line 122: @@
 {{Authority control}}
-[[Category: भौतिक मात्रा]] [[Category: आयाम]]
-[[Category: Machine Translated Page]]
+[[Category:Accuracy disputes from January 2021]]
+[[Category:All articles lacking reliable references]]
+[[Category:All articles with unsourced statements]]
+[[Category:Articles lacking reliable references from January 2021]]
+[[Category:Articles with hatnote templates targeting a nonexistent page]]
+[[Category:Articles with invalid date parameter in template]]
+[[Category:Articles with unsourced statements from November 2015]]
+[[Category:Articles with unsourced statements from October 2022]]
 [[Category:Created On 09/03/2023]]
+[[Category:Lua-based templates]]
+[[Category:Machine Translated Page]]
+[[Category:Pages with script errors]]
+[[Category:Short description with empty Wikidata description]]
+[[Category:Templates Vigyan Ready]]
+[[Category:Templates that add a tracking category]]
+[[Category:Templates that generate short descriptions]]
+[[Category:Templates using TemplateData]]
+[[Category:आयाम]]
+[[Category:भौतिक मात्रा]]

Anonymous

Search

स्वतंत्र कोटि: Difference between revisions

Namespaces

More

Page actions

Latest revision as of 11:38, 20 April 2023

Contents

गैसों के लिए स्वतंत्र की ऊष्मागतिक कोटि

एक स्थिति निर्दिष्ट करने के लिए निर्देशांक की न्यूनतम संख्या की गणना

स्वतंत्र की स्वतंत्र कोटि

स्वतंत्र की द्विघात कोटि

स्वतंत्र की द्विघात और स्वतंत्र कोटि

समविभाजन प्रमेय

सामान्यीकरण

संदर्भ

Navigation

Navigation

Wiki tools

Wiki tools

Anonymous

Search

स्वतंत्र कोटि: Difference between revisions

Latest revision as of 11:38, 20 April 2023

गैसों के लिए स्वतंत्र की ऊष्मागतिक कोटि

एक स्थिति निर्दिष्ट करने के लिए निर्देशांक की न्यूनतम संख्या की गणना

स्वतंत्र की स्वतंत्र कोटि

स्वतंत्र की द्विघात कोटि

स्वतंत्र की द्विघात और स्वतंत्र कोटि

समविभाजन प्रमेय

सामान्यीकरण

संदर्भ

Navigation

Wiki tools

Page tools

Other projects

Categories