इलेक्ट्रॉन घनत्व

This article is about the quantum mechanical probability density of an electron. For the number density of electrons in a plasma, also called "electron density", see Plasma (physics).

इलेक्ट्रॉन घनत्व या इलेक्ट्रॉनिक घनत्व किसी दिए गए बिंदु के आस-पास अंतरिक्ष के एक अतिसूक्ष्म तत्व पर एक इलेक्ट्रॉन के मौजूद होने की संभावना का माप है। यह तीन स्थानिक चर के आधार पर एक अदिश राशि है और इसे आमतौर पर या तो के रूप में दर्शाया जाता है $\rho ({\textbf {r}})$ या $n({\textbf {r}})$. घनत्व निर्धारित किया जाता है, परिभाषा के माध्यम से, सामान्यीकृत द्वारा $N$-इलेक्ट्रॉन तरंग क्रिया जो खुद पर निर्भर करता है $4N$ चर (${\textstyle 3N}$ स्थानिक और $N$ स्पिन (भौतिकी) निर्देशांक)। इसके विपरीत, घनत्व एक चरण कारक तक तरंग फ़ंक्शन मॉड्यूल को निर्धारित करता है, जो घनत्व कार्यात्मक सिद्धांत की औपचारिक नींव प्रदान करता है।

क्वांटम यांत्रिकी के अनुसार, परमाणु पैमाने पर अनिश्चितता सिद्धांत के कारण एक इलेक्ट्रॉन के सटीक स्थान की भविष्यवाणी नहीं की जा सकती है, केवल इसके दिए गए स्थान पर होने की संभावना है; इसलिए परमाणुओं और अणुओं में इलेक्ट्रॉन ऐसे कार्य करते हैं मानो वे अंतरिक्ष में बिखर गए हों। एक-इलेक्ट्रॉन प्रणालियों के लिए, किसी भी बिंदु पर इलेक्ट्रॉन घनत्व वेवफंक्शन के वर्ग परिमाण के समानुपाती होता है।

परिभाषा

एक सामान्यीकृत के अनुरूप इलेक्ट्रॉनिक घनत्व $N$-इलेक्ट्रॉन वेवफंक्शन $\Psi$ (साथ ${\textbf {r}}$ और $s$ क्रमशः स्थानिक और स्पिन चर को दर्शाते हुए) के रूप में परिभाषित किया गया है

$\rho (\mathbf {r} )=\langle \Psi |{\hat {\rho }}(\mathbf {r} )|\Psi \rangle ,$

जहां देखने योग्य घनत्व के अनुरूप ऑपरेटर है

${\hat {\rho }}(\mathbf {r} )=\sum _{i=1}^{N}\ \delta (\mathbf {r} -\mathbf {r} _{i}).$

कम्प्यूटिंग $\rho (\mathbf {r} )$ जैसा कि ऊपर परिभाषित किया गया है, हम निम्नानुसार अभिव्यक्ति को सरल बना सकते हैं।

${\begin{aligned}\rho (\mathbf {r} )&=\sum _{{s}_{1}}\cdots \sum _{{s}_{N}}\int \ \mathrm {d} \mathbf {r} _{1}\ \cdots \int \ \mathrm {d} \mathbf {r} _{N}\ \left(\sum _{i=1}^{N}\delta (\mathbf {r} -\mathbf {r} _{i})\right)|\Psi (\mathbf {r} _{1},s_{1},\mathbf {r} _{2},s_{2},...,\mathbf {r} _{N},s_{N})|^{2}\\&=N\sum _{{s}_{1}}\cdots \sum _{{s}_{N}}\int \ \mathrm {d} \mathbf {r} _{2}\ \cdots \int \ \mathrm {d} \mathbf {r} _{N}\ |\Psi (\mathbf {r} ,s_{1},\mathbf {r} _{2},s_{2},...,\mathbf {r} _{N},s_{N})|^{2}\end{aligned}}$ शब्दों में: स्थिति में अभी भी एक इलेक्ट्रॉन धारण करना ${\textbf {r}}$ हम अन्य इलेक्ट्रॉनों की सभी संभावित व्यवस्थाओं का योग करते हैं। कारक एन उत्पन्न होता है क्योंकि सभी इलेक्ट्रॉन अप्रभेद्य होते हैं, और इसलिए सभी अभिन्न एक ही मूल्य का मूल्यांकन करते हैं।

हार्ट्री-फॉक और घनत्व कार्यात्मक सिद्धांत सिद्धांतों में, तरंग फ़ंक्शन को आम तौर पर एकल स्लेटर निर्धारक के रूप में दर्शाया जाता है $N$ कक्षीय, $\varphi _{k}$, संबंधित व्यवसायों के साथ $n_{k}$. इन स्थितियों में, घनत्व सरल हो जाता है

$\rho (\mathbf {r} )=\sum _{k=1}^{N}n_{k}|\varphi _{k}(\mathbf {r} )|^{2}.$

सामान्य गुण

इसकी परिभाषा से, इलेक्ट्रॉन घनत्व इलेक्ट्रॉनों की कुल संख्या को एकीकृत करने वाला एक गैर-नकारात्मक कार्य है। इसके अलावा, गतिज ऊर्जा टी वाले सिस्टम के लिए, घनत्व असमानताओं को संतुष्ट करता है

${\frac {1}{2}}\int \mathrm {d} \mathbf {r} \ {\big (}\nabla {\sqrt {\rho (\mathbf {r} )}}{\big )}^{2}\leq T.$

${\frac {3}{2}}\left({\frac {\pi }{2}}\right)^{4/3}\left(\int \mathrm {d} \mathbf {r} \ \rho ^{3}(\mathbf {r} )\right)^{1/3}\leq T.$

परिमित गतिज ऊर्जाओं के लिए, पहली (मजबूत) असमानता सोबोलिव अंतरिक्ष में घनत्व के वर्गमूल को रखती है $H^{1}(\mathbb {R} ^{3})$. सामान्यीकरण और गैर-नकारात्मकता के साथ यह शारीरिक रूप से स्वीकार्य घनत्व वाले स्थान को परिभाषित करता है

${\mathcal {J}}_{N}=\left\{\rho \left|\rho (\mathbf {r} )\geq 0,\ \rho ^{1/2}(\mathbf {r} )\in H^{1}(\mathbf {R} ^{3}),\ \int \mathrm {d} \mathbf {r} \ \rho (\mathbf {r} )=N\right.\right\}.$

दूसरी असमानता घनत्व को Lp स्पेस|L में रखती है³ स्थान। सामान्यीकरण संपत्ति के साथ एल के चौराहे के भीतर स्वीकार्य घनत्व रखता है¹ और एल³ – का सुपरसेट ${\mathcal {J}}_{N}$.

टोपोलॉजी

एक परमाणु की जमीनी स्थिति इलेक्ट्रॉनिक घनत्व को परमाणु नाभिक से दूरी के एक मोनोटोनिक फ़ंक्शन क्षयकारी फ़ंक्शन के रूप में माना जाता है।

परमाणु पुच्छल स्थिति

असीमित इलेक्ट्रॉन-नाभिक कूलम्ब क्षमता के परिणामस्वरूप इलेक्ट्रॉनिक घनत्व एक अणु में प्रत्येक नाभिक पर क्यूप्स प्रदर्शित करता है। गोलाकार औसत घनत्व के संदर्भ में तैयार किए गए काटो पुच्छल स्थिति द्वारा इस व्यवहार की मात्रा निर्धारित की जाती है, ${\bar {\rho }}$, किसी दिए गए नाभिक के बारे में

$\left.{\frac {\partial }{\partial r_{\alpha }}}{\bar {\rho }}(r_{\alpha })\right|_{r_{\alpha }=0}=-2Z_{\alpha }{\bar {\rho }}(0).$

अर्थात्, गोलाकार रूप से औसत घनत्व का रेडियल व्युत्पन्न, किसी भी नाभिक पर मूल्यांकन किया जाता है, उस नाभिक पर घनत्व के दोगुने के बराबर होता है जो परमाणु संख्या के ऋणात्मक से गुणा होता है ($Z$).

स्पर्शोन्मुख व्यवहार

परमाणु पुच्छल स्थिति निकट-परमाणु प्रदान करती है (छोटा $r$) घनत्व व्यवहार के रूप में

$\rho (r)\sim e^{-2Z_{\alpha }r}\,.$

लंबी दूरी (बड़ा $r$) घनत्व का व्यवहार रूप लेते हुए भी जाना जाता है

$\rho (r)\sim e^{-2{\sqrt {2\mathrm {I} }}r}\,.$

जहाँ I निकाय की आयनन ऊर्जा है।

प्रतिक्रिया घनत्व

घनत्व की एक और अधिक सामान्य परिभाषा रैखिक-प्रतिक्रिया घनत्व है। यह घनत्व है कि जब अनुबंधित होता है किसी भी स्पिन-मुक्त के साथ, एक-इलेक्ट्रॉन ऑपरेटर ऊर्जा के व्युत्पन्न के रूप में परिभाषित संबंधित संपत्ति का उत्पादन करता है। उदाहरण के लिए, एक द्विध्रुवीय क्षण बाहरी चुंबकीय क्षेत्र के संबंध में ऊर्जा का व्युत्पन्न होता है और वेवफंक्शन पर ऑपरेटर का अपेक्षित मूल्य नहीं है। कुछ सिद्धांतों के लिए वे वही हैं जब वेवफंक्शन अभिसरित है। व्यवसाय संख्या शून्य से दो तक सीमित नहीं है, और इसलिए कभी-कभी अंतरिक्ष के कुछ क्षेत्रों में प्रतिक्रिया घनत्व भी नकारात्मक हो सकता है।

सिंहावलोकन

अणुओं में, बड़े इलेक्ट्रॉन घनत्व के क्षेत्र आमतौर पर परमाणु और उसके बंधनों के आसपास पाए जाते हैं। डी-लोकलाइज्ड या संयुग्मित प्रणालियों में, जैसे कि फिनोल, बेंजीन और हीमोग्लोबिन और क्लोरोफिल जैसे यौगिकों में, इलेक्ट्रॉन घनत्व पूरे क्षेत्र में महत्वपूर्ण होता है, यानी बेंजीन में वे प्लानर रिंग के ऊपर और नीचे पाए जाते हैं। इसे कभी-कभी आरेखीय रूप से वैकल्पिक सिंगल और डबल बॉन्ड की श्रृंखला के रूप में दिखाया जाता है। फिनोल और बेंजीन के मामले में, एक षट्भुज के अंदर एक चक्र यौगिक की विस्थानीकृत प्रकृति को दर्शाता है। यह नीचे दिखाया गया है:

कई रिंग सिस्टम वाले यौगिकों में जो आपस में जुड़े हुए हैं, यह अब सटीक नहीं है, इसलिए बारी-बारी से सिंगल और डबल बॉन्ड का उपयोग किया जाता है। क्लोरोफिल और फिनोल जैसे यौगिकों में, कुछ आरेख उन क्षेत्रों के निरूपण का प्रतिनिधित्व करने के लिए एक बिंदीदार या धराशायी रेखा दिखाते हैं जहां एकल बांड के बगल में इलेक्ट्रॉन घनत्व अधिक होता है। संयुग्मित प्रणालियां कभी-कभी उन क्षेत्रों का प्रतिनिधित्व कर सकती हैं जहां विभिन्न तरंग दैर्ध्य पर विद्युत चुम्बकीय विकिरण अवशोषित होता है जिसके परिणामस्वरूप यौगिक रंगीन दिखाई देते हैं। पॉलीमर में, इन क्षेत्रों को क्रोमोफोरस के रूप में जाना जाता है।

क्वांटम रसायन विज्ञान में, इलेक्ट्रॉन घनत्व, ρ(r), निर्देशांक r का एक कार्य है, इसलिए परिभाषित किया गया है कि ρ(r)dr एक छोटी मात्रा में इलेक्ट्रॉनों की संख्या है। खुला खोल | क्लोज्ड-शेल अणुओं के लिए, $\rho (\mathbf {r} )$ आधार कार्यों के उत्पादों के योग के रूप में लिखा जा सकता है, φ:

$\rho (\mathbf {r} )=\sum _{\mu }\sum _{\nu }P_{\mu \nu }\phi _{\mu }(\mathbf {r} )\phi _{\nu }(\mathbf {r} )$

एनिलिन के लिए गणना की गई इलेक्ट्रॉन घनत्व, उच्च घनत्व मान परमाणु की स्थिति को इंगित करते हैं, मध्यवर्ती घनत्व मान रासायनिक बंधन पर जोर देते हैं, कम मान अणु के आकार और आकार के बारे में जानकारी प्रदान करते हैं।

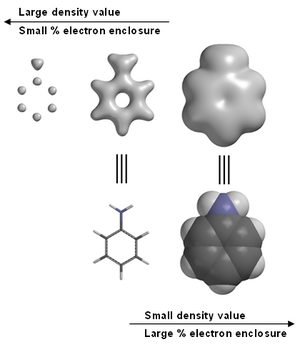
जहां पी घनत्व मैट्रिक्स है। इलेक्ट्रॉन घनत्व अक्सर चुने गए घनत्व के मान द्वारा निर्धारित सतह के आकार और आकार के साथ एक आइसोसफेस (एक आइसोडेनसिटी सतह) के संदर्भ में प्रस्तुत किया जाता है, या संलग्न कुल इलेक्ट्रॉनों के प्रतिशत के संदर्भ में।

क्वांटम रसायन विज्ञान और ठोस अवस्था भौतिकी सॉफ्टवेयर की सूची अक्सर इलेक्ट्रॉन घनत्व की चित्रमय छवियां प्रदान करती है। उदाहरण के लिए, एनिलिन में (दाईं ओर छवि देखें)। इलेक्ट्रॉन घनत्व सहित ग्राफिकल मॉडल, रसायन विज्ञान शिक्षा में आमतौर पर नियोजित उपकरण हैं। ध्यान दें कि एनिलिन की सबसे बाईं ओर की छवि में, उच्च इलेक्ट्रॉन घनत्व कार्बन और नाइट्रोजन से जुड़े हैं, लेकिन उनके नाभिक में केवल एक प्रोटॉन वाले हाइड्रोजन दिखाई नहीं दे रहे हैं। यही कारण है कि एक्स-रे विवर्तन में हाइड्रोजन की स्थिति का पता लगाने में मुश्किल होती है।

अधिकांश आणविक मॉडलिंग सॉफ़्टवेयर पैकेज उपयोगकर्ता को इलेक्ट्रॉन घनत्व के लिए एक मान चुनने की अनुमति देते हैं, जिसे अक्सर आइसोवैल्यू कहा जाता है। कुछ सॉफ्टवेयर संलग्न कुल इलेक्ट्रॉनों के प्रतिशत के संदर्भ में इलेक्ट्रॉन घनत्व के विनिर्देशन की भी अनुमति देता है। आइसोवैल्यू के आधार पर (प्रति घन बोह्र त्रिज्या में विशिष्ट इकाइयां इलेक्ट्रॉन हैं), या संलग्न कुल इलेक्ट्रॉनों का प्रतिशत, इलेक्ट्रॉन घनत्व सतह का उपयोग परमाणुओं का पता लगाने के लिए किया जा सकता है, रासायनिक बंधों से जुड़े इलेक्ट्रॉन घनत्व पर जोर दिया जा सकता है, या समग्र आणविक आकार और आकार को इंगित करने के लिए . ग्राफिक रूप से, इलेक्ट्रॉन घनत्व सतह एक कैनवास के रूप में भी कार्य करती है जिस पर अन्य इलेक्ट्रॉनिक गुण प्रदर्शित किए जा सकते हैं। इलेक्ट्रोस्टैटिक क्षमता मैप (इलेक्ट्रॉन घनत्व पर मैप किए गए इलेक्ट्रोस्टैटिक पोटेंशियल का गुण) एक अणु में चार्ज वितरण के लिए एक संकेतक प्रदान करता है। स्थानीय आयनीकरण संभावित नक्शा (इलेक्ट्रॉन घनत्व पर मैप किए गए आयनीकरण ऊर्जा की संपत्ति) इलेक्ट्रोफिलिसिटी का एक संकेतक प्रदान करता है। और LUMO मानचित्र (लूमो इलेक्ट्रॉन घनत्व पर मैप किया गया) न्यूक्लियोफिलिसिटी के लिए एक संकेतक प्रदान कर सकता है।

प्रयोग

कई प्रायोगिक तकनीकें इलेक्ट्रॉन घनत्व को माप सकती हैं। उदाहरण के लिए, एक्स-रे विवर्तन स्कैनिंग के माध्यम से क्वांटम क्रिस्टलोग्राफी, जहां एक उपयुक्त तरंग दैर्ध्य की एक्स-रे को एक नमूने की ओर लक्षित किया जाता है और समय के साथ मापन किया जाता है, इलेक्ट्रॉनों के स्थानों का एक संभाव्य प्रतिनिधित्व देता है। इन स्थितियों से, आणविक संरचनाओं, साथ ही सटीक चार्ज घनत्व वितरण, अक्सर क्रिस्टलीकृत सिस्टम के लिए निर्धारित किए जा सकते हैं। क्वांटम इलेक्ट्रोडायनामिक्स और क्वांटम क्षेत्र सिद्धांत की कुछ शाखाएँ भी इलेक्ट्रॉन सुपरपोजिशन सिद्धांत और अन्य संबंधित घटनाओं का अध्ययन और विश्लेषण करती हैं, जैसे गैर-सहसंयोजक इंटरैक्शन इंडेक्स जो इलेक्ट्रॉन घनत्व का उपयोग करके गैर-सहसंयोजक इंटरैक्शन के अध्ययन की अनुमति देता है। मुल्लिकेन जनसंख्या विश्लेषण अणुओं में इलेक्ट्रॉन घनत्व पर आधारित है और परमाणु आवेशों का अनुमान देने के लिए परमाणुओं के बीच घनत्व को विभाजित करने का एक तरीका है।

ट्रांसमिशन इलेक्ट्रॉन माइक्रोस्कोपी (टीईएम) और गहरे अप्रत्यास्थ बिखरने के साथ-साथ अन्य उच्च ऊर्जा कण प्रयोगों में, उच्च ऊर्जा इलेक्ट्रॉन, इलेक्ट्रॉन घनत्व के प्रत्यक्ष प्रतिनिधित्व देने के लिए इलेक्ट्रॉन बादल के साथ संपर्क करते हैं। टीईएम, स्कैनिंग टनलिंग माइक्रोस्कोप (एसटीएम) और परमाणु-बल माइक्रोस्कोपी (एएफएम) का उपयोग विशिष्ट व्यक्तिगत परमाणुओं के इलेक्ट्रॉन घनत्व की जांच के लिए किया जा सकता है।

स्पिन घनत्व

स्पिन घनत्व इलेक्ट्रॉन घनत्व है जो मुक्त कणों पर लागू होता है। इसे एक स्पिन ऋण के इलेक्ट्रॉनों के कुल इलेक्ट्रॉन घनत्व के रूप में परिभाषित किया जाता है, जो दूसरे स्पिन के इलेक्ट्रॉनों के कुल इलेक्ट्रॉन घनत्व का होता है। प्रयोगात्मक रूप से इसे मापने के तरीकों में से एक इलेक्ट्रॉन स्पिन अनुनाद है, न्यूट्रॉन विवर्तन 3डी-स्पेस में स्पिन घनत्व के प्रत्यक्ष मानचित्रण की अनुमति देता है।

यह भी देखें

• अंतर घनत्व नक्शा
• इलेक्ट्रॉन बादल
• ऋणावेशित सूक्ष्म अणु का विन्यास
• संकल्प (इलेक्ट्रॉन घनत्व)
• चार्ज का घनत्व
• सघनता व्यावहारिक सिद्धांत
• संभावना वर्तमान