बार्न्स जी-फ़ंक्शन: Difference between revisions
(Created page with "File:Plot of the Barnes G aka double gamma function G(z) in the complex plane from -2-2i to 2+2i with colors created with Mathematica 13.1 function ComplexPlot3D.svg|alt=Plo...") |
No edit summary |
||
| (8 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
गणित में, '''बार्न्स G-फलन''' ''G''(''z'') [[फ़ंक्शन (गणित)|फलन (गणित)]] है जोकी [[जटिल संख्या]]ओं के लिए [[सुपरफैक्टोरियल]] का विस्तार है। यह [[गामा फ़ंक्शन|गामा फलन]] , [[K-फ़ंक्शन|K-]]फलन और ग्लैशर-किंकलिन स्थिरांक से संबंधित है, और इसका नाम [[गणितज्ञ]] [[अर्नेस्ट विलियम बार्न्स]] के नाम पर रखा गया था।<ref>E. W. Barnes, "The theory of the G-function", ''Quarterly Journ. Pure and Appl. Math.'' '''31''' (1900), 264–314.</ref> इसे दोहरे गामा फलन के संदर्भ में लिखा जा सकता है। | |||
औपचारिक रूप से, बार्न्स | इस प्रकार से औपचारिक रूप से, बार्न्स G-फलन को निम्नलिखित [[वीयरस्ट्रैस उत्पाद]] रूप में परिभाषित किया गया है: | ||
:<math> G(1+z)=(2\pi)^{z/2} \exp\left(- \frac{z+z^2(1+\gamma)}{2} \right) \, \prod_{k=1}^\infty \left\{ \left(1+\frac{z}{k}\right)^k \exp\left(\frac{z^2}{2k}-z\right) \right\}</math> | :<math> G(1+z)=(2\pi)^{z/2} \exp\left(- \frac{z+z^2(1+\gamma)}{2} \right) \, \prod_{k=1}^\infty \left\{ \left(1+\frac{z}{k}\right)^k \exp\left(\frac{z^2}{2k}-z\right) \right\}</math> | ||
जहां <math>\, \gamma </math> यूलर-माशेरोनी स्थिरांक है, exp(''x'') = ''e<sup>x</sup>'' घातीय फलन है, और Π गुणन (कैपिटल पाई नोटेशन) को दर्शाता जाता है। | |||
संपूर्ण फलन के रूप में, ''G'' क्रम दो का और अनंत प्रकार का है। इसका अनुमान दिए गए स्पर्शोन्मुख विस्तार से लगाया जा सकता है नीचे दिया गया.[[File:2022-08-09 12 43 26-Barnes-G from -6 to 4.png|बार्न्स जी वास्तविक अक्ष के भाग के साथ कार्य करता है]] | |||
==[[कार्यात्मक समीकरण]] और पूर्णांक तर्क== | ==[[कार्यात्मक समीकरण]] और पूर्णांक तर्क== | ||
बार्न्स | बार्न्स ''G'' -फलन कार्यात्मक समीकरण को संतुष्ट करता है | ||
:<math> G(z+1)=\Gamma(z)\, G(z) </math> | :<math> G(z+1)=\Gamma(z)\, G(z) </math> | ||
सामान्यीकरण | सामान्यीकरण ''G(1) = 1'' के साथ। बार्न्स ''G'' -फलन के कार्यात्मक समीकरण और यूलर गामा फलन के कार्यात्मक समीकरण के बीच समानता पर ध्यान दें: | ||
:<math> \Gamma(z+1)=z \, \Gamma(z) .</math> | :<math> \Gamma(z+1)=z \, \Gamma(z) .</math> | ||
कार्यात्मक समीकरण का तात्पर्य है कि G [[पूर्णांक]] तर्कों पर निम्नलिखित मान लेता है: | कार्यात्मक समीकरण का तात्पर्य है कि ''G'' [[पूर्णांक]] तर्कों पर निम्नलिखित मान लेता है: | ||
:<math>G(n)=\begin{cases} 0&\text{if }n=0,-1,-2,\dots\\ \prod_{i=0}^{n-2} i!&\text{if }n=1,2,\dots\end{cases}</math> | :<math>G(n)=\begin{cases} 0&\text{if }n=0,-1,-2,\dots\\ \prod_{i=0}^{n-2} i!&\text{if }n=1,2,\dots\end{cases}</math> | ||
(विशेष रूप से, | (विशेष रूप से, <math>\,G(0)=0, G(1)=1</math>) | ||
और इस | |||
और इस प्रकार से | |||
:<math>G(n)=\frac{(\Gamma(n))^{n-1}}{K(n)}</math> | :<math>G(n)=\frac{(\Gamma(n))^{n-1}}{K(n)}</math> | ||
जहाँ <math>\,\Gamma(x)</math> गामा फलन को दर्शाता है और K, K-फलन को दर्शाता है। कार्यात्मक समीकरण विशिष्ट रूप से G फलन को परिभाषित करता है यदि उत्तलता की स्थिति, | |||
:<math>\, \frac{d^3}{dx^3}G(x)\geq 0</math> जोड़ दिया गया है।<ref>M. F. Vignéras, ''L'équation fonctionelle de la fonction zêta de Selberg du groupe mudulaire SL<math>(2,\mathbb{Z})</math>'', Astérisque '''61''', 235–249 (1979).</ref> इसके अतिरिक्त, बार्न्स | :<math>\, \frac{d^3}{dx^3}G(x)\geq 0</math> जोड़ दिया गया है।<ref>M. F. Vignéras, ''L'équation fonctionelle de la fonction zêta de Selberg du groupe mudulaire SL<math>(2,\mathbb{Z})</math>'', Astérisque '''61''', 235–249 (1979).</ref> इसके अतिरिक्त, बार्न्स ''G'' फलन दोहराव सूत्र को संतुष्ट करता है,<ref>{{cite journal | url=https://koreascience.kr/article/JAKO199611919482150.page | title=A duplication formula for the double gamma function $Gamma_2$ | journal=Bulletin of the Korean Mathematical Society | year=1996 | volume=33 | issue=2 | pages=289–294 | last1=Park | first1=Junesang }}</ref> | ||
:<math>G(x)G\left(x+\frac{1}{2}\right)^{2}G(x+1)=e^{\frac{1}{4}}A^{-3}2^{-2x^{2}+3x-\frac{11}{12}}\pi^{x-\frac{1}{2}}G\left(2x\right)</math> | :<math>G(x)G\left(x+\frac{1}{2}\right)^{2}G(x+1)=e^{\frac{1}{4}}A^{-3}2^{-2x^{2}+3x-\frac{11}{12}}\pi^{x-\frac{1}{2}}G\left(2x\right)</math> | ||
== लक्षण वर्णन == | |||
गामा फलन के लिए बोहर-मोलेरुप प्रमेय|बोहर-मोलेरुप प्रमेय के समान, स्थिरांक <math>c>0</math>,के लिए हमारे समीप <math>f(x)=cG(x)</math><ref>{{Cite book |last=Marichal |first=Jean Luc |title=A Generalization of Bohr-Mollerup’s Theorem for Higher Order Convex Functions |publisher=Springer |url=https://orbi.uliege.be/bitstream/2268/294009/1/Marichal-Zena%C3%AFdi2022_Book_AGeneralizationOfBohr-Mollerup.pdf |pages=218}}</ref> | |||
<math>f(x+1)=\Gamma(x)f(x)</math> के लिए है | |||
और के लिए <math>x>0</math> | |||
<math>f(x+ | <math>f(x+n)\sim \Gamma(x)^nn^{{x\choose 2}}f(n) </math> | ||
जैसा <math>n\to\infty</math>. | |||
जैसा <math>n\to\infty</math>. | |||
==1/2 पर | ==मान 1/2 पर == | ||
:<math>G\left(\tfrac{1}{2}\right) = 2^{\frac{1}{24}} e^{\frac32 \zeta'(-1)}\pi^{-\frac14}.</math> | :<math>G\left(\tfrac{1}{2}\right) = 2^{\frac{1}{24}} e^{\frac32 \zeta'(-1)}\pi^{-\frac14}.</math> | ||
==परावर्तन सूत्र 1.0== | ==परावर्तन सूत्र 1.0 == | ||
इस प्रकार से G-फलन के लिए [[अंतर समीकरण]], गामा फलन के कार्यात्मक समीकरण के साथ, बार्न्स G-फलन के लिए निम्नलिखित [[प्रतिबिंब सूत्र]] प्राप्त करने के लिए उपयोग किया जा सकता है (मूल रूप से [[हरमन किंकेलिन]] द्वारा सिद्ध) किया गया है: | |||
:<math> \log G(1-z) = \log G(1+z)-z\log 2\pi+ \int_0^z \pi x \cot \pi x \, dx.</math> | :<math> \log G(1-z) = \log G(1+z)-z\log 2\pi+ \int_0^z \pi x \cot \pi x \, dx.</math> | ||
दाहिनी ओर लॉगटैन्जेंट इंटीग्रल का मूल्यांकन [[क्लॉज़ेन फ़ंक्शन]] (क्रम 2 के) के संदर्भ में किया जा सकता है, जैसा कि नीचे दिखाया गया है: | दाहिनी ओर लॉगटैन्जेंट इंटीग्रल का मूल्यांकन [[क्लॉज़ेन फ़ंक्शन|क्लॉज़ेन]] फलन (क्रम 2 के) के संदर्भ में किया जा सकता है, जैसा कि नीचे दिखाया गया है: | ||
:<math>2\pi \log\left( \frac{G(1-z)}{G(1+z)} \right)= 2\pi z\log\left(\frac{\sin\pi z}{\pi} \right) + \operatorname{Cl}_2(2\pi z)</math> | :<math>2\pi \log\left( \frac{G(1-z)}{G(1+z)} \right)= 2\pi z\log\left(\frac{\sin\pi z}{\pi} \right) + \operatorname{Cl}_2(2\pi z)</math> | ||
इस परिणाम का प्रमाण कोटैंजेंट इंटीग्रल के निम्नलिखित मूल्यांकन पर निर्भर करता है: | इस परिणाम का प्रमाण कोटैंजेंट इंटीग्रल के निम्नलिखित मूल्यांकन पर निर्भर करता है: लॉगकोटैंजेंट इंटीग्रल के लिए नोटेशन <math>\operatorname{Lc}(z)</math> का परिचय देना, और इस तथ्य का उपयोग करना कि <math>\,(d/dx) \log(\sin\pi x)=\pi\cot\pi x</math> भागों द्वारा एक एकीकरण देता है | ||
:<math>\begin{align} | :<math>\begin{align} | ||
| Line 57: | Line 61: | ||
&= z\log(2\sin \pi z)-\int_0^z\log(2\sin \pi x)\,dx . | &= z\log(2\sin \pi z)-\int_0^z\log(2\sin \pi x)\,dx . | ||
\end{align}</math> | \end{align}</math> | ||
अभिन्न प्रतिस्थापन करना <math>\, y=2\pi x \Rightarrow dx=dy/(2\pi)</math> देता है | अभिन्न प्रतिस्थापन करना <math>\, y=2\pi x \Rightarrow dx=dy/(2\pi)</math> देता है | ||
:<math>z\log(2\sin \pi z)-\frac{1}{2\pi}\int_0^{2\pi z}\log\left(2\sin \frac{y}{2} \right)\,dy.</math> | :<math>z\log(2\sin \pi z)-\frac{1}{2\pi}\int_0^{2\pi z}\log\left(2\sin \frac{y}{2} \right)\,dy.</math> | ||
क्लॉज़ेन | क्लॉज़ेन फलन - दूसरे क्रम का - अभिन्न प्रतिनिधित्व है | ||
:<math>\operatorname{Cl}_2(\theta) = -\int_0^{\theta}\log\Bigg|2\sin \frac{x}{2} \Bigg|\,dx.</math> | :<math>\operatorname{Cl}_2(\theta) = -\int_0^{\theta}\log\Bigg|2\sin \frac{x}{2} \Bigg|\,dx.</math> | ||
चूंकि , अंतराल के अंदर <math>\, 0 < \theta < 2\pi </math>, [[ एकीकृत |एकीकृत]] के अंदर पूर्ण मूल्य चिह्न को छोड़ा जा सकता है, क्योंकि सीमा के अंदर इंटीग्रल में 'अर्ध-साइन' फलन जटिलता से सकारात्मक माने जाते है, और यह जटिलता से गैर-शून्य होते है। लॉगटैन्जेंट इंटीग्रल के लिए उपरोक्त परिणाम के साथ इस परिभाषा की तुलना करने पर, निम्नलिखित संबंध स्पष्ट रूप से सामने आते है: | |||
:<math>\operatorname{Lc}(z)=z\log(2\sin \pi z)+\frac{1}{2\pi} \operatorname{Cl}_2(2\pi z).</math> | :<math>\operatorname{Lc}(z)=z\log(2\sin \pi z)+\frac{1}{2\pi} \operatorname{Cl}_2(2\pi z).</math> | ||
इस प्रकार, शब्दों की थोड़ी सी पुनर्व्यवस्था के | इस प्रकार, शब्दों की थोड़ी सी पुनर्व्यवस्था के पश्चात , प्रमाण पूर्ण हो जाता है: | ||
:<math>2\pi \log\left( \frac{G(1-z)}{G(1+z)} \right)= 2\pi z\log\left(\frac{\sin\pi z}{\pi} \right)+\operatorname{Cl}_2(2\pi z)\, . \, \Box </math> | :<math>2\pi \log\left( \frac{G(1-z)}{G(1+z)} \right)= 2\pi z\log\left(\frac{\sin\pi z}{\pi} \right)+\operatorname{Cl}_2(2\pi z)\, . \, \Box </math> | ||
संबंध | संबंध <math>\, G(1+z)=\Gamma(z)\, G(z) </math>का उपयोग करना और प्रतिबिंब सूत्र को <math>\, 2\pi </math> कारक से विभाजित करना समतुल्य रूप दिया जाता है: | ||
:<math> \log\left( \frac{G(1-z)}{G(z)} \right)= z\log\left(\frac{\sin\pi z}{\pi} | :<math> \log\left( \frac{G(1-z)}{G(z)} \right)= z\log\left(\frac{\sin\pi z}{\pi} | ||
\right)+\log\Gamma(z)+\frac{1}{2\pi}\operatorname{Cl}_2(2\pi z) </math> | \right)+\log\Gamma(z)+\frac{1}{2\pi}\operatorname{Cl}_2(2\pi z) </math> | ||
संदर्भ: प्रतिबिंब सूत्र के समतुल्य रूप के लिए नीचे एडमचिक देखें, | संदर्भ: प्रतिबिंब सूत्र के समतुल्य रूप के लिए नीचे एडमचिक देखें, किन्तु इसे अलग प्रमाण के साथ उपयोग किया जाता है । | ||
==परावर्तन सूत्र 2.0== | ==परावर्तन सूत्र 2.0 == | ||
पिछले प्रतिबिंब सूत्र में ''z'' को '''(1/2) − ''z<nowiki>''</nowiki>''''' से परिवर्तित करने पर, कुछ सरलीकरण के पश्चात , नीचे दिखाया गया समतुल्य सूत्र मिलता है ([[बर्नौली बहुपद]] को सम्मिलित करते हुए): किया जाता है। | |||
:<math>\log\left( \frac{ G\left(\frac{1}{2}+z\right) }{ G\left(\frac{1}{2}-z\right) } \right) = \log \Gamma \left(\frac{1}{2}-z \right) + B_1(z) \log 2\pi+\frac{1}{2}\log 2+\pi \int_0^z B_1(x) \tan \pi x \,dx</math> | |||
==टेलर श्रृंखला विस्तार == | |||
टेलर के प्रमेय द्वारा, और बार्न्स फलन के लघुगणकीय व्युत्पन्न पर विचार करते हुए, निम्नलिखित श्रृंखला विस्तार प्राप्त किया जा सकता है: | |||
== | :<math>\log G(1+z) = \frac{z}{2}\log 2\pi -\left( \frac{z+(1+\gamma)z^2}{2} \right) + \sum_{k=2}^{\infty}(-1)^k\frac{\zeta(k)}{k+1}z^{k+1}.</math> | ||
यह <math>\, 0 < z < 1 </math>, के लिए मान्य है . यहाँ <math>\, \zeta(x) </math> [[रीमैन ज़ेटा फ़ंक्शन|रीमैन ज़ेटा]] फलन है: | |||
:<math> \zeta(s)=\sum_{n=1}^{\infty}\frac{1}{n^s}. </math> | |||
टेलर विस्तार के दोनों पक्षों का प्रतिपादन करने पर यह प्राप्त होता है: | |||
:<math> \zeta(s)=\sum_{n=1}^{\infty}\frac{1}{n^s}. </math> | |||
टेलर विस्तार के दोनों पक्षों का प्रतिपादन करने पर यह | |||
:<math>\begin{align} G(1+z) &= \exp \left[ \frac{z}{2}\log 2\pi -\left( \frac{z+(1+\gamma)z^2}{2} \right) + \sum_{k=2}^{\infty}(-1)^k\frac{\zeta(k)}{k+1}z^{k+1} \right] \\ | :<math>\begin{align} G(1+z) &= \exp \left[ \frac{z}{2}\log 2\pi -\left( \frac{z+(1+\gamma)z^2}{2} \right) + \sum_{k=2}^{\infty}(-1)^k\frac{\zeta(k)}{k+1}z^{k+1} \right] \\ | ||
&=(2\pi)^{z/2}\exp\left[ -\frac{z+(1+\gamma)z^2}{2} \right] \exp \left[\sum_{k=2}^{\infty}(-1)^k\frac{\zeta(k)}{k+1}z^{k+1} \right].\end{align}</math> | &=(2\pi)^{z/2}\exp\left[ -\frac{z+(1+\gamma)z^2}{2} \right] \exp \left[\sum_{k=2}^{\infty}(-1)^k\frac{\zeta(k)}{k+1}z^{k+1} \right].\end{align}</math> | ||
इसकी तुलना बार्न्स | इसकी तुलना बार्न्स फलन के वीयरस्ट्रैस उत्पाद रूप से करने पर निम्नलिखित संबंध देखने को मिलते है: | ||
:<math>\exp \left[\sum_{k=2}^\infty (-1)^k\frac{\zeta(k)}{k+1}z^{k+1} \right] = \prod_{k=1}^{\infty} \left\{ \left(1+\frac{z}{k}\right)^k \exp \left(\frac{z^2}{2k}-z\right) \right\}</math> | :<math>\exp \left[\sum_{k=2}^\infty (-1)^k\frac{\zeta(k)}{k+1}z^{k+1} \right] = \prod_{k=1}^{\infty} \left\{ \left(1+\frac{z}{k}\right)^k \exp \left(\frac{z^2}{2k}-z\right) \right\}</math> | ||
==गुणन सूत्र == | |||
गामा फलन की तरह, G-फलन में भी गुणन सूत्र होता है:<ref>I. Vardi, ''Determinants of Laplacians and multiple gamma functions'', SIAM J. Math. Anal. '''19''', 493–507 (1988).</ref> | |||
गामा | |||
:<math> | :<math> | ||
G(nz)= K(n) n^{n^{2}z^{2}/2-nz} (2\pi)^{-\frac{n^2-n}{2}z}\prod_{i=0}^{n-1}\prod_{j=0}^{n-1}G\left(z+\frac{i+j}{n}\right) | G(nz)= K(n) n^{n^{2}z^{2}/2-nz} (2\pi)^{-\frac{n^2-n}{2}z}\prod_{i=0}^{n-1}\prod_{j=0}^{n-1}G\left(z+\frac{i+j}{n}\right) | ||
</math> | </math> | ||
जहाँ <math>K(n)</math> द्वारा दिया गया स्थिरांक है: | |||
:<math> K(n)= e^{-(n^2-1)\zeta^\prime(-1)} \cdot | :<math> K(n)= e^{-(n^2-1)\zeta^\prime(-1)} \cdot | ||
n^{\frac{5}{12}}\cdot(2\pi)^{(n-1)/2}\,=\, | n^{\frac{5}{12}}\cdot(2\pi)^{(n-1)/2}\,=\, | ||
(Ae^{-\frac{1}{12}})^{n^2-1}\cdot n^{\frac{5}{12}}\cdot (2\pi)^{(n-1)/2}.</math> | (Ae^{-\frac{1}{12}})^{n^2-1}\cdot n^{\frac{5}{12}}\cdot (2\pi)^{(n-1)/2}.</math> | ||
यहाँ <math>\zeta^\prime</math> [[रीमैन ज़ेटा फ़ंक्शन]] का व्युत्पन्न है और <math>A</math> ग्लैशर-किंकलिन स्थिरांक है। | यहाँ <math>\zeta^\prime</math> [[रीमैन ज़ेटा फ़ंक्शन|रीमैन ज़ेटा]] फलन का व्युत्पन्न है और <math>A</math> ग्लैशर-किंकलिन स्थिरांक माना जाता है। | ||
==पूर्ण मान== | ==पूर्ण मान == | ||
यह सच है <math>G(\overline z)=\overline{G(z)}</math>, इस प्रकार <math>|G(z)|^2=G(z)G(\overline z)</math>. इस संबंध से और ऊपर प्रस्तुत वीयरस्ट्रैस उत्पाद प्रपत्र से कोई यह दिखा सकता है | यह सच है <math>G(\overline z)=\overline{G(z)}</math>, इस प्रकार <math>|G(z)|^2=G(z)G(\overline z)</math>. इस संबंध से और ऊपर प्रस्तुत वीयरस्ट्रैस उत्पाद प्रपत्र से कोई यह दिखा सकता है | ||
:<math> | :<math> | ||
|G(x+iy)|=|G(x)|\exp\left(y^2\frac{1+\gamma}{2}\right)\sqrt{1+\frac{y^2}{x^2}}\sqrt{\prod_{k=1}^\infty\left(1+\frac{y^2}{(x+k)^2}\right)^{k+1}\exp\left(-\frac{y^2}{k}\right)}. | |G(x+iy)|=|G(x)|\exp\left(y^2\frac{1+\gamma}{2}\right)\sqrt{1+\frac{y^2}{x^2}}\sqrt{\prod_{k=1}^\infty\left(1+\frac{y^2}{(x+k)^2}\right)^{k+1}\exp\left(-\frac{y^2}{k}\right)}. | ||
</math> | </math> | ||
यह संबंध | यह संबंध इच्छा अनुसार <math>x\in\mathbb{R}\setminus\{0,-1,-2,\dots\}</math> , और <math>y\in\mathbb{R}</math> के लिए मान्य है यदि <math>x=0</math>, तो इसके अतिरिक्त नीचे दिया गया सूत्र मान्य है | ||
:<math> | :<math> | ||
|G(iy)|=y\exp\left(y^2\frac{1+\gamma}{2}\right)\sqrt{\prod_{k=1}^\infty\left(1+\frac{y^2}{k^2}\right)^{k+1}\exp\left(-\frac{y^2}{k}\right)} | |G(iy)|=y\exp\left(y^2\frac{1+\gamma}{2}\right)\sqrt{\prod_{k=1}^\infty\left(1+\frac{y^2}{k^2}\right)^{k+1}\exp\left(-\frac{y^2}{k}\right)} | ||
</math> | </math> | ||
इच्छा अनुसार वास्तविक y के लिए। | |||
==स्पर्शोन्मुख विस्तार== | ==स्पर्शोन्मुख विस्तार == | ||
G(z + 1) के लघुगणक में निम्नलिखित स्पर्शोन्मुख विस्तार है, जैसा कि बार्न्स द्वारा स्थापित किया गया है: | ''G(z + 1)'' के लघुगणक में निम्नलिखित स्पर्शोन्मुख विस्तार है, जैसा कि बार्न्स द्वारा स्थापित किया गया है: | ||
:<math>\begin{align} | :<math>\begin{align} | ||
| Line 133: | Line 134: | ||
& {} + \left(\frac{1}{12}-\log A \right) | & {} + \left(\frac{1}{12}-\log A \right) | ||
+\sum_{k=1}^N \frac{B_{2k + 2}}{4k\left(k + 1\right)z^{2k}}~+~O\left(\frac{1}{z^{2N + 2}}\right). | +\sum_{k=1}^N \frac{B_{2k + 2}}{4k\left(k + 1\right)z^{2k}}~+~O\left(\frac{1}{z^{2N + 2}}\right). | ||
\end{align}</math> | \end{align}</math> | ||
यहां ही <math>B_k</math> [[बर्नौली संख्या]]एँ हैं और <math>A</math> ग्लैशर-किंकलिन स्थिरांक है। (ध्यान दें कि बार्न्स के समय यह कुछ | यहां ही <math>B_k</math> [[बर्नौली संख्या]]एँ हैं और <math>A</math> ग्लैशर-किंकलिन स्थिरांक है। (ध्यान दें कि बार्न्स के समय यह कुछ सीमा तक भ्रमित करने वाला था <ref>[[E. T. Whittaker]] and [[G. N. Watson]], "[[A Course of Modern Analysis]]", CUP.</ref> [[बर्नौली संख्या]] <math>B_{2k}</math> के रूप में लिखा गया होगा <math>(-1)^{k+1} B_k </math>, किन्तु यह परिपाटी अब प्रचलित नहीं है।) यह विस्तार इसके लिए मान्य <math>z </math> है किसी भी ऐसे सेक्टर में जिसमें नकारात्मक वास्तविक अक्ष <math>|z|</math> उच्चय न हो। | ||
==लॉगगामा इंटीग्रल से संबंध== | ==लॉगगामा इंटीग्रल से संबंध == | ||
पैरामीट्रिक लॉगगामा का मूल्यांकन बार्न्स | पैरामीट्रिक लॉगगामा का मूल्यांकन बार्न्स G-फलन के संदर्भ में किया जा सकता है (संदर्भ: यह परिणाम नीचे एडमचिक में पाया गया है, किन्तु बिना प्रमाण में दर्शाया गया है): | ||
:<math> \int_0^z \log \Gamma(x)\,dx=\frac{z(1-z)}{2}+\frac{z}{2}\log 2\pi +z\log\Gamma(z) -\log G(1+z) </math> | :<math> \int_0^z \log \Gamma(x)\,dx=\frac{z(1-z)}{2}+\frac{z}{2}\log 2\pi +z\log\Gamma(z) -\log G(1+z) </math> | ||
प्रमाण कुछ | प्रमाण कुछ सीमा तक अप्रत्यक्ष होते है, और इसमें पहले गामा फलन और बार्न्स G-फलन के लघुगणकीय अंतर पर विचार करना सम्मिलित होता है: | ||
:<math>z\log \Gamma(z)-\log G(1+z)</math> | :<math>z\log \Gamma(z)-\log G(1+z)</math> | ||
जहाँ | |||
:<math>\frac{1}{\Gamma(z)}= z e^{\gamma z} \prod_{k=1}^\infty \left\{ \left(1+\frac{z}{k}\right)e^{-z/k} \right\}</math> | :<math>\frac{1}{\Gamma(z)}= z e^{\gamma z} \prod_{k=1}^\infty \left\{ \left(1+\frac{z}{k}\right)e^{-z/k} \right\}</math> | ||
और <math>\,\gamma</math> यूलर-माशेरोनी स्थिरांक है। | और <math>\,\gamma</math> यूलर-माशेरोनी स्थिरांक है। | ||
बार्न्स | बार्न्स फलन और गामा फलन के वीयरस्ट्रैस उत्पाद रूपों का लघुगणक लेने पर यह मिलता है: | ||
:<math> | :<math> | ||
| Line 157: | Line 158: | ||
& {} -\left[ \frac{z}{2}\log 2\pi -\frac{z}{2}-\frac{z^2}{2} -\frac{z^2 \gamma}{2} + \sum_{k=1}^\infty \Bigg\{k\log\left(1+\frac{z}{k}\right) +\frac{z^2}{2k} -z \Bigg\} \right] | & {} -\left[ \frac{z}{2}\log 2\pi -\frac{z}{2}-\frac{z^2}{2} -\frac{z^2 \gamma}{2} + \sum_{k=1}^\infty \Bigg\{k\log\left(1+\frac{z}{k}\right) +\frac{z^2}{2k} -z \Bigg\} \right] | ||
\end{align} | \end{align} | ||
</math> | </math> | ||
शब्दों का थोड़ा सरलीकरण और पुनः क्रम लगाने से श्रृंखला का विस्तार होता है: | शब्दों का थोड़ा सरलीकरण और पुनः क्रम लगाने से श्रृंखला का विस्तार होता है: | ||
:<math> | :<math> | ||
| Line 165: | Line 166: | ||
= {} & {-z}\log z-\frac{z}{2}\log 2\pi +\frac{z}{2} +\frac{z^2}{2}- \frac{z^2 \gamma}{2}- z\log\Gamma(z) +\log G(1+z) | = {} & {-z}\log z-\frac{z}{2}\log 2\pi +\frac{z}{2} +\frac{z^2}{2}- \frac{z^2 \gamma}{2}- z\log\Gamma(z) +\log G(1+z) | ||
\end{align} | \end{align} | ||
</math> | </math> | ||
अंत में, गामा | अंत में, गामा फलन के वीयरस्ट्रैस उत्पाद रूप का लघुगणक लें, और अंतराल <math>\, [0,\,z]</math> पर एकीकृत करें प्राप्त करने के लिए: | ||
:<math> | :<math> | ||
| Line 173: | Line 174: | ||
= {} & {-(z\log z-z)}-\frac{z^2 \gamma}{2}- \sum_{k=1}^\infty \Bigg\{ (k+z)\log \left(1+\frac{z}{k}\right)-\frac{z^2}{2k}-z \Bigg\} | = {} & {-(z\log z-z)}-\frac{z^2 \gamma}{2}- \sum_{k=1}^\infty \Bigg\{ (k+z)\log \left(1+\frac{z}{k}\right)-\frac{z^2}{2k}-z \Bigg\} | ||
\end{align} | \end{align} | ||
</math> | </math> | ||
दोनों मूल्यांकनों को | दोनों मूल्यांकनों को समान करने से प्रमाण पूर्ण हो जाता है: | ||
:<math> \int_0^z \log \Gamma(x)\,dx=\frac{z(1-z)}{2}+\frac{z}{2}\log 2\pi +z\log\Gamma(z) -\log G(1+z)</math> | |||
और जब से <math>\, G(1+z)=\Gamma(z)\, G(z) </math> जब , | |||
==संदर्भ== | :<math> \int_0^z \log \Gamma(x)\,dx=\frac{z(1-z)}{2}+\frac{z}{2}\log 2\pi -(1-z)\log\Gamma(z) -\log G(z)\, .</math> | ||
==संदर्भ == | |||
<references/> | <references/> | ||
*{{dlmf|first=R.A. |last=Askey|first2=R.|last2=Roy|id=5.17}} | *{{dlmf|first=R.A. |last=Askey|first2=R.|last2=Roy|id=5.17}} | ||
{{DEFAULTSORT:Barnes G-Function}} | {{DEFAULTSORT:Barnes G-Function}} | ||
*{{cite arXiv|last=Adamchik|first=Viktor S.|title=Contributions to the Theory of the Barnes function|year=2003|eprint=math/0308086}} | *{{cite arXiv|last=Adamchik|first=Viktor S.|title=Contributions to the Theory of the Barnes function|year=2003|eprint=math/0308086}} | ||
[[Category:Created On 05/07/2023|Barnes G-Function]] | |||
[[Category:Machine Translated Page|Barnes G-Function]] | |||
[[Category: Machine Translated Page]] | [[Category:Templates Vigyan Ready|Barnes G-Function]] | ||
[[Category: | [[Category:विशेष कार्य|Barnes G-Function]] | ||
[[Category:संख्या सिद्धांत|Barnes G-Function]] | |||
Latest revision as of 17:40, 13 July 2023
गणित में, बार्न्स G-फलन G(z) फलन (गणित) है जोकी जटिल संख्याओं के लिए सुपरफैक्टोरियल का विस्तार है। यह गामा फलन , K-फलन और ग्लैशर-किंकलिन स्थिरांक से संबंधित है, और इसका नाम गणितज्ञ अर्नेस्ट विलियम बार्न्स के नाम पर रखा गया था।[1] इसे दोहरे गामा फलन के संदर्भ में लिखा जा सकता है।
इस प्रकार से औपचारिक रूप से, बार्न्स G-फलन को निम्नलिखित वीयरस्ट्रैस उत्पाद रूप में परिभाषित किया गया है:
जहां यूलर-माशेरोनी स्थिरांक है, exp(x) = ex घातीय फलन है, और Π गुणन (कैपिटल पाई नोटेशन) को दर्शाता जाता है।
संपूर्ण फलन के रूप में, G क्रम दो का और अनंत प्रकार का है। इसका अनुमान दिए गए स्पर्शोन्मुख विस्तार से लगाया जा सकता है नीचे दिया गया.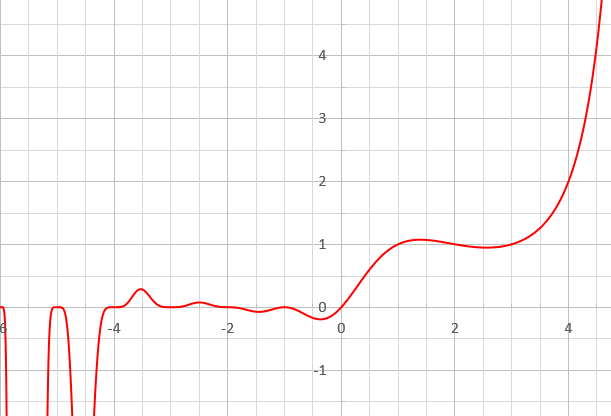
कार्यात्मक समीकरण और पूर्णांक तर्क
बार्न्स G -फलन कार्यात्मक समीकरण को संतुष्ट करता है
सामान्यीकरण G(1) = 1 के साथ। बार्न्स G -फलन के कार्यात्मक समीकरण और यूलर गामा फलन के कार्यात्मक समीकरण के बीच समानता पर ध्यान दें:
कार्यात्मक समीकरण का तात्पर्य है कि G पूर्णांक तर्कों पर निम्नलिखित मान लेता है:
(विशेष रूप से, )
और इस प्रकार से
जहाँ गामा फलन को दर्शाता है और K, K-फलन को दर्शाता है। कार्यात्मक समीकरण विशिष्ट रूप से G फलन को परिभाषित करता है यदि उत्तलता की स्थिति,
लक्षण वर्णन
गामा फलन के लिए बोहर-मोलेरुप प्रमेय|बोहर-मोलेरुप प्रमेय के समान, स्थिरांक ,के लिए हमारे समीप [4]
के लिए है
और के लिए
जैसा .
मान 1/2 पर
परावर्तन सूत्र 1.0
इस प्रकार से G-फलन के लिए अंतर समीकरण, गामा फलन के कार्यात्मक समीकरण के साथ, बार्न्स G-फलन के लिए निम्नलिखित प्रतिबिंब सूत्र प्राप्त करने के लिए उपयोग किया जा सकता है (मूल रूप से हरमन किंकेलिन द्वारा सिद्ध) किया गया है:
दाहिनी ओर लॉगटैन्जेंट इंटीग्रल का मूल्यांकन क्लॉज़ेन फलन (क्रम 2 के) के संदर्भ में किया जा सकता है, जैसा कि नीचे दिखाया गया है:
इस परिणाम का प्रमाण कोटैंजेंट इंटीग्रल के निम्नलिखित मूल्यांकन पर निर्भर करता है: लॉगकोटैंजेंट इंटीग्रल के लिए नोटेशन का परिचय देना, और इस तथ्य का उपयोग करना कि भागों द्वारा एक एकीकरण देता है
अभिन्न प्रतिस्थापन करना देता है
क्लॉज़ेन फलन - दूसरे क्रम का - अभिन्न प्रतिनिधित्व है
चूंकि , अंतराल के अंदर , एकीकृत के अंदर पूर्ण मूल्य चिह्न को छोड़ा जा सकता है, क्योंकि सीमा के अंदर इंटीग्रल में 'अर्ध-साइन' फलन जटिलता से सकारात्मक माने जाते है, और यह जटिलता से गैर-शून्य होते है। लॉगटैन्जेंट इंटीग्रल के लिए उपरोक्त परिणाम के साथ इस परिभाषा की तुलना करने पर, निम्नलिखित संबंध स्पष्ट रूप से सामने आते है:
इस प्रकार, शब्दों की थोड़ी सी पुनर्व्यवस्था के पश्चात , प्रमाण पूर्ण हो जाता है:
संबंध का उपयोग करना और प्रतिबिंब सूत्र को कारक से विभाजित करना समतुल्य रूप दिया जाता है:
संदर्भ: प्रतिबिंब सूत्र के समतुल्य रूप के लिए नीचे एडमचिक देखें, किन्तु इसे अलग प्रमाण के साथ उपयोग किया जाता है ।
परावर्तन सूत्र 2.0
पिछले प्रतिबिंब सूत्र में z को (1/2) − z'' से परिवर्तित करने पर, कुछ सरलीकरण के पश्चात , नीचे दिखाया गया समतुल्य सूत्र मिलता है (बर्नौली बहुपद को सम्मिलित करते हुए): किया जाता है।
टेलर श्रृंखला विस्तार
टेलर के प्रमेय द्वारा, और बार्न्स फलन के लघुगणकीय व्युत्पन्न पर विचार करते हुए, निम्नलिखित श्रृंखला विस्तार प्राप्त किया जा सकता है:
यह , के लिए मान्य है . यहाँ रीमैन ज़ेटा फलन है:
टेलर विस्तार के दोनों पक्षों का प्रतिपादन करने पर यह प्राप्त होता है:
इसकी तुलना बार्न्स फलन के वीयरस्ट्रैस उत्पाद रूप से करने पर निम्नलिखित संबंध देखने को मिलते है:
गुणन सूत्र
गामा फलन की तरह, G-फलन में भी गुणन सूत्र होता है:[5]
जहाँ द्वारा दिया गया स्थिरांक है:
यहाँ रीमैन ज़ेटा फलन का व्युत्पन्न है और ग्लैशर-किंकलिन स्थिरांक माना जाता है।
पूर्ण मान
यह सच है , इस प्रकार . इस संबंध से और ऊपर प्रस्तुत वीयरस्ट्रैस उत्पाद प्रपत्र से कोई यह दिखा सकता है
यह संबंध इच्छा अनुसार , और के लिए मान्य है यदि , तो इसके अतिरिक्त नीचे दिया गया सूत्र मान्य है
इच्छा अनुसार वास्तविक y के लिए।
स्पर्शोन्मुख विस्तार
G(z + 1) के लघुगणक में निम्नलिखित स्पर्शोन्मुख विस्तार है, जैसा कि बार्न्स द्वारा स्थापित किया गया है:
यहां ही बर्नौली संख्याएँ हैं और ग्लैशर-किंकलिन स्थिरांक है। (ध्यान दें कि बार्न्स के समय यह कुछ सीमा तक भ्रमित करने वाला था [6] बर्नौली संख्या के रूप में लिखा गया होगा , किन्तु यह परिपाटी अब प्रचलित नहीं है।) यह विस्तार इसके लिए मान्य है किसी भी ऐसे सेक्टर में जिसमें नकारात्मक वास्तविक अक्ष उच्चय न हो।
लॉगगामा इंटीग्रल से संबंध
पैरामीट्रिक लॉगगामा का मूल्यांकन बार्न्स G-फलन के संदर्भ में किया जा सकता है (संदर्भ: यह परिणाम नीचे एडमचिक में पाया गया है, किन्तु बिना प्रमाण में दर्शाया गया है):
प्रमाण कुछ सीमा तक अप्रत्यक्ष होते है, और इसमें पहले गामा फलन और बार्न्स G-फलन के लघुगणकीय अंतर पर विचार करना सम्मिलित होता है:
जहाँ
और यूलर-माशेरोनी स्थिरांक है।
बार्न्स फलन और गामा फलन के वीयरस्ट्रैस उत्पाद रूपों का लघुगणक लेने पर यह मिलता है:
शब्दों का थोड़ा सरलीकरण और पुनः क्रम लगाने से श्रृंखला का विस्तार होता है:
अंत में, गामा फलन के वीयरस्ट्रैस उत्पाद रूप का लघुगणक लें, और अंतराल पर एकीकृत करें प्राप्त करने के लिए:
दोनों मूल्यांकनों को समान करने से प्रमाण पूर्ण हो जाता है:
और जब से जब ,
संदर्भ
- ↑ E. W. Barnes, "The theory of the G-function", Quarterly Journ. Pure and Appl. Math. 31 (1900), 264–314.
- ↑ M. F. Vignéras, L'équation fonctionelle de la fonction zêta de Selberg du groupe mudulaire SL, Astérisque 61, 235–249 (1979).
- ↑ Park, Junesang (1996). "A duplication formula for the double gamma function $Gamma_2$". Bulletin of the Korean Mathematical Society. 33 (2): 289–294.
- ↑ Marichal, Jean Luc. A Generalization of Bohr-Mollerup’s Theorem for Higher Order Convex Functions (PDF). Springer. p. 218.
- ↑ I. Vardi, Determinants of Laplacians and multiple gamma functions, SIAM J. Math. Anal. 19, 493–507 (1988).
- ↑ E. T. Whittaker and G. N. Watson, "A Course of Modern Analysis", CUP.
- Askey, R.A.; Roy, R. (2010), "बार्न्स जी-फ़ंक्शन", in Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W. (eds.), NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0-521-19225-5, MR 2723248
- Adamchik, Viktor S. (2003). "Contributions to the Theory of the Barnes function". arXiv:math/0308086.