वर्णक्रमीय घनत्व अनुमान: Difference between revisions
No edit summary |
No edit summary |
||
| (19 intermediate revisions by 3 users not shown) | |||
| Line 3: | Line 3: | ||
{{broader| | {{broader| | ||
वर्णक्रमीय घनत्व}} | वर्णक्रमीय घनत्व}} | ||
[[सांख्यिकीय सिग्नल प्रोसेसिंग]] में, [[वर्णक्रमीय घनत्व]] अनुमान (एसडीई) या केवल वर्णक्रमीय अनुमान का लक्ष्य सिग्नल के समय प्रतिरूप के अनुक्रम से सिग्नल के वर्णक्रमीय घनत्व (जिसे [[पावर स्पेक्ट्रम|शक्ति वर्णक्रम]] के रूप में भी जाना जाता है) का अनुमान लगाना है।<ref>[[Peter Stoica|P Stoica]] and R Moses, Spectral Analysis of Signals, Prentice Hall, 2005.</ref> सहज रूप से कहें तो, वर्णक्रमीय घनत्व सिग्नल की [[आवृत्ति]] सामग्री को दर्शाता है। वर्णक्रमीय घनत्व का अनुमान लगाने का उद्देश्य इन आवधिकों के अनुरूप आवृत्तियों पर चोटियों को देखकर, डेटा में किसी भी आवधिक | [[सांख्यिकीय सिग्नल प्रोसेसिंग]] में, '''[[वर्णक्रमीय घनत्व]] अनुमान''' (एसडीई) या केवल वर्णक्रमीय अनुमान का लक्ष्य सिग्नल के समय प्रतिरूप के अनुक्रम से सिग्नल के वर्णक्रमीय घनत्व (जिसे [[पावर स्पेक्ट्रम|शक्ति वर्णक्रम]] के रूप में भी जाना जाता है) का अनुमान लगाना है।<ref>[[Peter Stoica|P Stoica]] and R Moses, Spectral Analysis of Signals, Prentice Hall, 2005.</ref> सहज रूप से कहें तो, वर्णक्रमीय घनत्व सिग्नल की [[आवृत्ति]] सामग्री को दर्शाता है। वर्णक्रमीय घनत्व का अनुमान लगाने का उद्देश्य इन आवधिकों के अनुरूप आवृत्तियों पर चोटियों को देखकर, डेटा में किसी भी आवधिक फलन की जानकारी ज्ञात करना है। | ||
कुछ एसडीई प्रविधियां मानती हैं कि सिग्नल सीमित (सामान्यतः अल्प) संख्या में उत्पन्न आवृत्तियों और शोर से बना होता है और उत्पन्न आवृत्तियों के स्थान और तीव्रता की जानकारी ज्ञात करने का प्रयत्न करता है। अन्य लोग घटकों की संख्या पर कोई धारणा नहीं बनाते हैं और संपूर्ण उत्पादन वर्णक्रम का अनुमान लगाना चाहते हैं। | कुछ एसडीई प्रविधियां मानती हैं कि सिग्नल सीमित (सामान्यतः अल्प) संख्या में उत्पन्न आवृत्तियों और शोर से बना होता है और उत्पन्न आवृत्तियों के स्थान और तीव्रता की जानकारी ज्ञात करने का प्रयत्न करता है। अन्य लोग घटकों की संख्या पर कोई धारणा नहीं बनाते हैं और संपूर्ण उत्पादन वर्णक्रम का अनुमान लगाना चाहते हैं। | ||
== | == अवलोकन == | ||
[[Image:Voice waveform and spectrum.png|thumb|ध्वनि | [[Image:Voice waveform and spectrum.png|thumb|ध्वनि तरंग रूप और उसके आवृत्ति वर्णक्रम का उदाहरण]] | ||
[[Image:triangle-td and fd.png|thumb|आवधिक तरंगरूप ([[त्रिकोण तरंग]]) और उसका आवृत्ति वर्णक्रम, 220 हर्ट्ज पर मौलिक आवृत्ति और उसके | [[Image:triangle-td and fd.png|thumb|आवधिक तरंगरूप ([[त्रिकोण तरंग]]) और उसका आवृत्ति वर्णक्रम, 220 हर्ट्ज पर मौलिक आवृत्ति और उसके पश्चात 220 हर्ट्ज के गुणक (हार्मोनिक्स) दर्शाता है।]] | ||
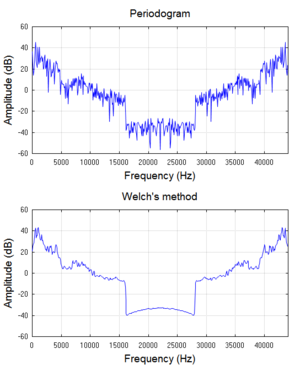
[[File:Comparison of periodogram and Welch methods of spectral density estimation.png|thumb|तुलना के लिए, संगीत के | [[File:Comparison of periodogram and Welch methods of spectral density estimation.png|thumb|तुलना के लिए, संगीत के भाग की शक्ति वर्णक्रमीय घनत्व का अनुमान दो भिन्न-भिन्न प्रविधियों से लगाया जाता है।]]वर्णक्रम विश्लेषण, जिसे [[आवृत्ति डोमेन]] विश्लेषण या वर्णक्रमीय घनत्व अनुमान भी कहा जाता है, जटिल सिग्नल को सरल भागों में विघटित करने की प्रौद्योगिकी प्रक्रिया है। जैसा कि ऊपर वर्णित है, कई भौतिक प्रक्रियाओं को कई व्यक्तिगत आवृत्ति घटकों के योग के रूप में सबसे उचित रूप से वर्णित किया गया है। कोई भी प्रक्रिया जो विभिन्न मात्राओं (जैसे आयाम, शक्तियाँ, तीव्रता) के प्रति आवृत्ति (या चरण (तरंगें)) की मात्रा निर्धारित करती है, उसे वर्णक्रम विश्लेषण कहा जा सकता है। | ||
वर्णक्रम विश्लेषण पूर्ण सिग्नल पर किया जा सकता है। वैकल्पिक रूप से, सिग्नल को अल्प भागो (कभी-कभी फ़्रेम कहा जाता है) में विभक्त किया जा सकता है, और वर्णक्रम विश्लेषण को इन व्यक्तिगत भागो पर प्रारम्भ किया जा सकता है। आवधिक कार्य (जैसे <math>\sin (t)</math>) इस उप-विभाजन के लिए विशेष रूप से उपयुक्त होते हैं। गैर-आवधिक कार्यों के विश्लेषण के लिए सामान्य गणितीय प्रविधियां [[फूरियर विश्लेषण]] की श्रेणी के अंतर्गत आती हैं। | वर्णक्रम विश्लेषण पूर्ण सिग्नल पर किया जा सकता है। वैकल्पिक रूप से, सिग्नल को अल्प भागो (कभी-कभी फ़्रेम कहा जाता है) में विभक्त किया जा सकता है, और वर्णक्रम विश्लेषण को इन व्यक्तिगत भागो पर प्रारम्भ किया जा सकता है। आवधिक कार्य (जैसे <math>\sin (t)</math>) इस उप-विभाजन के लिए विशेष रूप से उपयुक्त होते हैं। गैर-आवधिक कार्यों के विश्लेषण के लिए सामान्य गणितीय प्रविधियां [[फूरियर विश्लेषण]] की श्रेणी के अंतर्गत आती हैं। | ||
किसी | किसी फलन का [[फूरियर रूपांतरण]] आवृत्ति वर्णक्रम उत्पन्न करता है जिसमें मूल सिग्नल के विषय में सम्पूर्ण जानकारी होती है, किन्तु भिन्न रूप में इसका अर्थ यह है कि मूल फलन को व्युत्क्रम फूरियर रूपांतरण द्वारा पूर्ण रूप से पुनर्निर्मित (संश्लेषित) किया जा सकता है। उचित पुनर्निर्माण के लिए, वर्णक्रम विश्लेषक को प्रत्येक आवृत्ति घटक के [[आयाम]] और [[चरण]] (तरंगों) दोनों को संरक्षित करना होगा, जानकारी के इन दो भागो को 2-आयामी सदिश के रूप में, [[जटिल संख्या]] के रूप में, या ध्रुवीय निर्देशांक में परिमाण (आयाम) और चरण के रूप में (अर्थात, चरण के रूप में) दर्शाया जा सकता है।[[नमूनाकरण (सिग्नल प्रोसेसिंग)|सिग्नल प्रोसेसिंग]] में सामान्य प्रविधि वर्ग आयाम, या [[शक्ति (भौतिकी)]] पर विचार करना है, इस विषय में परिणामी प्लॉट को पावर वर्णक्रम के रूप में जाना जाता है। | ||
उत्क्रमणीयता के कारण, फूरियर रूपांतरण को समय के अतिरिक्त आवृत्ति के संदर्भ में | उत्क्रमणीयता के कारण, फूरियर रूपांतरण को समय के अतिरिक्त आवृत्ति के संदर्भ में फलन का प्रतिनिधित्व कहा जाता है, इस प्रकार यह आवृत्ति डोमेन प्रतिनिधित्व होती है। समय डोमेन में निष्पादित किए जा सकने वाले रैखिक परिचालनों में ऐसे समकक्ष होते हैं जिन्हें प्रायः आवृत्ति डोमेन में अधिक सरलता से निष्पादित किया जा सकता है। आवृत्ति विश्लेषण रैखिक और गैर-रेखीय दोनों, विभिन्न समय-डोमेन संचालन के प्रभावों के विचार और व्याख्या को भी सरल बनाता है। उदाहरण के लिए, केवल गैर-रैखिकता या समय-संस्करण प्रणाली संचालन ही आवृत्ति वर्णक्रम में नई आवृत्तियाँ बना सकते हैं। | ||
व्यवहार में, लगभग सभी सॉफ्टवेयर और इलेक्ट्रॉनिक उपकरण जो आवृत्ति वर्ण-पट उत्पन्न करते हैं, [[उलटा फूरियर रूपांतरण]] (डीएफटी) का उपयोग करते हैं, जो सिग्नल के प्रतिरूपो (सिग्नल प्रोसेसिंग) पर कार्य करता है, और जो पूर्ण अभिन्न समाधान के लिए गणितीय अनुमान प्रदान करता है। डीएफटी लगभग सदैव कुशल एल्गोरिदम द्वारा कार्यान्वित किया जाता है जिसे [[[[असतत फूरियर रूपांतरण]]]] (एफएफटी) कहा जाता है। डीएफटी के वर्ग-परिमाण घटकों की सरणी प्रकार का पावर वर्णक्रम है जिसे [[ periodogram | पीरियोडोग्राम]] कहा जाता है, जिसका व्यापक रूप से [[आवेग प्रतिक्रिया]] और [[विंडो फ़ंक्शन]] जैसे शोर-मुक्त कार्यों की आवृत्ति विशेषताओं के परीक्षण के लिए उपयोग किया जाता है। किन्तु कम सिग्नल-टू-शोर अनुपात पर शोर जैसे संकेतों या यहां तक कि साइनसोइड्स पर प्रारम्भ होने पर पीरियोडोग्राम प्रसंस्करण-लाभ प्रदान नहीं करता है। दूसरे शब्दों में, किसी दी गई आवृत्ति पर इसके वर्णक्रमीय अनुमान का विचरण कम नहीं होता है क्योंकि गणना में उपयोग किए गए प्रतिरूपो की संख्या बढ़ जाती है। इसे समय के साथ औसत करके (वेल्च की विधि <ref>{{Citation|last=Welch|first=P. D.|title=The use of Fast Fourier Transform for the estimation of power spectra: A method based on time averaging over short, modified periodograms|journal=IEEE Transactions on Audio and Electroacoustics|volume=AU-15|issue=2|year=1967|pages=70–73|doi=10.1109/TAU.1967.1161901|bibcode=1967ITAE...15...70W}}</ref>या अधिक आवृत्ति ([[ चौरसाई ]]) किया जा सकता है। वर्णक्रमीय घनत्व आकलन (एसडीई) के लिए वेल्च की विधि का व्यापक रूप से उपयोग किया जाता है। चूंकि, पीरियोडोग्राम-आधारित प्रविधियां अल्प पूर्वाग्रह प्रस्तुत करती हैं, जो कुछ अनुप्रयोगों में अस्वीकार्य हैं। इसलिए अन्य विकल्प आगामी भाग में प्रस्तुत किए गए हैं। | व्यवहार में, लगभग सभी सॉफ्टवेयर और इलेक्ट्रॉनिक उपकरण जो आवृत्ति वर्ण-पट उत्पन्न करते हैं, [[उलटा फूरियर रूपांतरण]] (डीएफटी) का उपयोग करते हैं, जो सिग्नल के प्रतिरूपो (सिग्नल प्रोसेसिंग) पर कार्य करता है, और जो पूर्ण अभिन्न समाधान के लिए गणितीय अनुमान प्रदान करता है। डीएफटी लगभग सदैव कुशल एल्गोरिदम द्वारा कार्यान्वित किया जाता है जिसे [[[[असतत फूरियर रूपांतरण]]]] (एफएफटी) कहा जाता है। डीएफटी के वर्ग-परिमाण घटकों की सरणी प्रकार का पावर वर्णक्रम है जिसे [[ periodogram | पीरियोडोग्राम]] कहा जाता है, जिसका व्यापक रूप से [[आवेग प्रतिक्रिया]] और [[विंडो फ़ंक्शन|विंडो फलन]] जैसे शोर-मुक्त कार्यों की आवृत्ति विशेषताओं के परीक्षण के लिए उपयोग किया जाता है। किन्तु कम सिग्नल-टू-शोर अनुपात पर शोर जैसे संकेतों या यहां तक कि साइनसोइड्स पर प्रारम्भ होने पर पीरियोडोग्राम प्रसंस्करण-लाभ प्रदान नहीं करता है। दूसरे शब्दों में, किसी दी गई आवृत्ति पर इसके वर्णक्रमीय अनुमान का विचरण कम नहीं होता है क्योंकि गणना में उपयोग किए गए प्रतिरूपो की संख्या बढ़ जाती है। इसे समय के साथ औसत करके (वेल्च की विधि <ref>{{Citation|last=Welch|first=P. D.|title=The use of Fast Fourier Transform for the estimation of power spectra: A method based on time averaging over short, modified periodograms|journal=IEEE Transactions on Audio and Electroacoustics|volume=AU-15|issue=2|year=1967|pages=70–73|doi=10.1109/TAU.1967.1161901|bibcode=1967ITAE...15...70W}}</ref>या अधिक आवृत्ति ([[ चौरसाई |चौरसाई]]) किया जा सकता है। वर्णक्रमीय घनत्व आकलन (एसडीई) के लिए वेल्च की विधि का व्यापक रूप से उपयोग किया जाता है। चूंकि, पीरियोडोग्राम-आधारित प्रविधियां अल्प पूर्वाग्रह प्रस्तुत करती हैं, जो कुछ अनुप्रयोगों में अस्वीकार्य हैं। इसलिए अन्य विकल्प आगामी भाग में प्रस्तुत किए गए हैं। | ||
== प्रविधि == | == प्रविधि == | ||
| Line 49: | Line 49: | ||
=== पैरामीट्रिक अनुमान === | === पैरामीट्रिक अनुमान === | ||
पैरामीट्रिक वर्णक्रमीय अनुमान में, कोई यह मानता है कि सिग्नल स्थिर प्रक्रिया द्वारा प्रस्तुत किया गया है जिसमें वर्णक्रमीय घनत्व | पैरामीट्रिक वर्णक्रमीय अनुमान में, कोई यह मानता है कि सिग्नल स्थिर प्रक्रिया द्वारा प्रस्तुत किया गया है जिसमें वर्णक्रमीय घनत्व फलन (एसडीएफ) <math>S(f; a_1, \ldots, a_p)</math> है, यह आवृत्ति का कार्य है <math>f</math> और <math>p</math> पैरामीटर <math>a_1, \ldots, a_p</math>.<ref name=Percival1993>{{cite book |last1=Percival|first1=Donald B.|last2=Walden|first2=Andrew T.|title=भौतिक अनुप्रयोगों के लिए वर्णक्रमीय विश्लेषण|date=1992|publisher=Cambridge University Press|isbn=9780521435413}}</ref> तत्पश्चात अनुमान की समस्या इन मापदंडों का अनुमान लगाने में से बन जाती है। | ||
पैरामीट्रिक एसडीएफ अनुमान का सबसे सामान्य रूप मॉडल के रूप में ऑटोरेग्रेसिव मॉडल <math>\text{AR}(p)</math> का उपयोग करता है। <math>p</math> ऑर्डर की {{r|Percival1993|page1=392}} संकेत अनुक्रम <math>\{Y_t\}</math> शून्य माध्य का पालन करना <math>\text{AR}(p)</math> प्रक्रिया समीकरण को संतुष्ट करती है। | पैरामीट्रिक एसडीएफ अनुमान का सबसे सामान्य रूप मॉडल के रूप में ऑटोरेग्रेसिव मॉडल <math>\text{AR}(p)</math> का उपयोग करता है। <math>p</math> ऑर्डर की {{r|Percival1993|page1=392}} संकेत अनुक्रम <math>\{Y_t\}</math> शून्य माध्य का पालन करना <math>\text{AR}(p)</math> प्रक्रिया समीकरण को संतुष्ट करती है। | ||
:<math>Y_t = \phi_1Y_{t-1} + \phi_2Y_{t-2} + \cdots + \phi_pY_{t-p} + \epsilon_t,</math> | :<math>Y_t = \phi_1Y_{t-1} + \phi_2Y_{t-2} + \cdots + \phi_pY_{t-p} + \epsilon_t,</math> | ||
जहां <math>\phi_1,\ldots,\phi_p</math> निश्चित गुणांक हैं और <math>\epsilon_t</math> शून्य माध्य और नवीनता विचरण वाली श्वेत प्रक्रिया है, इस प्रक्रिया के लिए <math>\sigma^2_p</math> एसडीएफ है | जहां <math>\phi_1,\ldots,\phi_p</math> निश्चित गुणांक हैं और <math>\epsilon_t</math> शून्य माध्य और नवीनता विचरण वाली श्वेत प्रक्रिया है, इस प्रक्रिया के लिए <math>\sigma^2_p</math> एसडीएफ है, | ||
:<math> | :<math> | ||
| Line 62: | Line 62: | ||
साथ <math>\Delta t</math> प्रतिरूपकरण समय अंतराल और <math>f_N</math> [[नाइक्विस्ट आवृत्ति]] | साथ <math>\Delta t</math> प्रतिरूपकरण समय अंतराल और <math>f_N</math> [[नाइक्विस्ट आवृत्ति]] | ||
<math>\phi_1, \ldots, \phi_p,\sigma^2_p</math> की <math>\text{AR}(p)</math> प्रक्रिया और इस प्रकार वर्णक्रमीय घनत्व | मापदंडों का अनुमान लगाने के लिए कई दृष्टिकोण हैं <math>\phi_1, \ldots, \phi_p,\sigma^2_p</math> की <math>\text{AR}(p)</math> प्रक्रिया और इस प्रकार वर्णक्रमीय घनत्व है। | ||
* | * <math>\text{AR}(p)</math> प्रक्रिया यूल-वॉकर अनुमानक यूल-वॉकर समीकरणों को पुनरावर्ती रूप से हल करके पाए जाते हैं। | ||
* बर्ग अनुमानक यूल-वॉकर समीकरणों को सामान्य न्यूनतम वर्ग समस्या के रूप में मानकर पाए जाते हैं। बर्ग अनुमानकों को सामान्यतः पर यूल-वॉकर अनुमानकों से | * बर्ग अनुमानक यूल-वॉकर समीकरणों को सामान्य न्यूनतम वर्ग समस्या के रूप में मानकर पाए जाते हैं। बर्ग अनुमानकों को सामान्यतः पर यूल-वॉकर अनुमानकों से उत्तम माना जाता है।{{r|Percival1993|page1=452}} बर्ग ने इन्हें अधिकतम एन्ट्रॉपी वर्णक्रमीय अनुमान के साथ जोड़ा था।<ref name=Burg>Burg, J.P. (1967) "Maximum Entropy Spectral Analysis", ''Proceedings of the 37th Meeting of the Society of Exploration Geophysicists'', Oklahoma City, Oklahoma.</ref> | ||
* आगे-पीछे | * आगे-पीछे <math>\text{AR}(p)</math> न्यूनतम-वर्ग अनुमानक का व्यवहार करते हैं, प्रतिगमन समस्या के रूप में प्रक्रिया करें और आगे-पीछे विधि का उपयोग करके उस समस्या का समाधान करें। वे बर्ग अनुमानकर्ताओं के साथ प्रतिस्पर्धी होते हैं। | ||
* अधिकतम संभावना अनुमानक अधिकतम संभावना दृष्टिकोण का उपयोग करके मापदंडों का अनुमान लगाते हैं। इसमें अरेखीय अनुकूलन | * अधिकतम संभावना अनुमानक अधिकतम संभावना दृष्टिकोण का उपयोग करके मापदंडों का अनुमान लगाते हैं। इसमें अरेखीय अनुकूलन सम्मिलित है और यह प्रथम तीन की तुलना में अधिक जटिल है। | ||
वैकल्पिक पैरामीट्रिक | वैकल्पिक पैरामीट्रिक प्रविधियों में [[ चलती औसत मॉडल ]] (एमए) और पूर्ण ऑटोरेग्रेसिव मूविंग एवरेज मॉडल (एआरएमए) में उपयुक्त होना सम्मिलित है। | ||
==आवृत्ति अनुमान == | ==आवृत्ति अनुमान == | ||
आवृत्ति अनुमान अनुमान सिद्धांत की प्रक्रिया है जो घटकों की संख्या के | आवृत्ति अनुमान अनुमान सिद्धांत की प्रक्रिया है जो घटकों की संख्या के विषय में दी गई धारणाओं के [[शोर]] की उपस्थिति में [[ अंकीय संकेत प्रक्रिया ]] की आवृत्ति, आयाम और चरण-शिफ्ट होती है।<ref>Hayes, Monson H., ''Statistical Digital Signal Processing and Modeling'', John Wiley & Sons, Inc., 1996. {{ISBN|0-471-59431-8}}.</ref> यह उपरोक्त सामान्य प्रविधियों के विपरीत होती है, जो घटकों के विषय में पूर्व धारणा नहीं बनाते हैं। | ||
=== एकल स्वर === | === एकल स्वर === | ||
{{See also| | {{See also| | ||
यदि कोई केवल सबसे ऊंची आवृत्ति का अनुमान लगाना चाहता है, तो वह [[पिच का पता लगाने का एल्गोरिदम]] का उपयोग कर सकता है। यदि प्रमुख आवृत्ति समय के साथ | साइनसॉइडल मॉडल}} | ||
यदि कोई प्राप्त सिग्नल के सभी (संभवतः जटिल) आवृत्ति घटकों (संचरित सिग्नल और शोर सहित) को जानना चाहता है, तो वह मल्टी-टोन दृष्टिकोण का उपयोग करता है। | यदि कोई केवल सबसे ऊंची आवृत्ति का अनुमान लगाना चाहता है, तो वह [[पिच का पता लगाने का एल्गोरिदम|पिच का पता ज्ञात करने के लिए एल्गोरिदम]] का उपयोग कर सकता है। यदि प्रमुख आवृत्ति समय के साथ परिवर्तित होती है, तो समस्या [[तात्कालिक आवृत्ति]] के अनुमान की हो जाती है जैसा कि समय-आवृत्ति प्रतिनिधित्व में परिभाषित किया गया है। तात्कालिक आवृत्ति अनुमान के प्रविधियों में [[विग्नर-विले वितरण]] और उच्च क्रम अस्पष्टता कार्यों पर आधारित प्रविधियां सम्मिलित होती हैं।<ref name=Lerga>{{cite web|last=Lerga|first=Jonatan|title=सिग्नल तात्कालिक आवृत्ति अनुमान विधियों का अवलोकन|url=http://www.fer.unizg.hr/_download/repository/Jonatan_Lerga_-_kvalifikacijski_rad.pdf|publisher=University of Rijeka|access-date=22 March 2014}}</ref>यदि कोई प्राप्त सिग्नल के सभी (संभवतः जटिल) आवृत्ति घटकों (संचरित सिग्नल और शोर सहित) को जानना चाहता है, तो वह मल्टी-टोन दृष्टिकोण का उपयोग करता है। | ||
=== एकाधिक स्वर === | === एकाधिक स्वर === | ||
सिग्नल के लिए विशिष्ट मॉडल <math>x(n)</math> | सिग्नल के लिए विशिष्ट मॉडल का योग <math>x(n)</math> होता है, सफ़ेद शोर की उपस्थिति में <math>p</math> जटिल घातांक,<math>w(n)</math> | ||
:<math>x(n) = \sum_{i=1}^p A_i e^{j n \omega_i} + w(n)</math>. | :<math>x(n) = \sum_{i=1}^p A_i e^{j n \omega_i} + w(n)</math>. | ||
की शक्ति वर्णक्रमीय घनत्व <math>x(n)</math> से बना है <math>p</math> शोर के कारण वर्णक्रमीय घनत्व | की शक्ति वर्णक्रमीय घनत्व <math>x(n)</math> से बना है, <math>p</math> आवेग शोर के कारण वर्णक्रमीय घनत्व फलन के अतिरिक्त कार्य करता है। | ||
आवृत्ति अनुमान के लिए सबसे | आवृत्ति अनुमान के लिए सबसे सरल प्रविधियों में इन घटकों को निकालने के लिए शोर [[रैखिक उपस्थान]] की पहचान करना सम्मिलित होता है। ये विधियाँ सिग्नल उप-स्थान और शोर उप-स्थान में ऑटोसहसंबंध मैट्रिक्स के [[Eigendecomposition|सिग्नल उप-स्थान और शोर उप-स्थान में ईजिन अपघटन]] पर आधारित हैं। इन उप-स्थानों की पहचान होने के पश्चात, शोर उप-स्थान से घटक आवृत्तियों का शोध करने के लिए आवृत्ति अनुमान फलन का उपयोग किया जाता है। शोर उप-स्थान आधारित आवृत्ति अनुमान की सबसे लोकप्रिय विधियाँ हैं पिसारेंको की विधि, मल्टीपल सिग्नल वर्गीकरण (संगीत) विधि, ईजेन सदिश विधि और न्यूनतम मानक विधि होती है। | ||
; | ; पिसारेंको की विधि: <math>\hat{P}_\text{PHD}\left(e^{j \omega}\right) = \frac{1}{\left|\mathbf{e}^H \mathbf{v}_\text{min}\right|^2}</math> | ||
; एकाधिक सिग्नल वर्गीकरण: <math>\hat{P}_\text{MU}\left(e^{j \omega}\right) = \frac{1}{\sum_{i=p+1}^M \left|\mathbf{e}^H \mathbf{v}_i\right|^2}</math>, | ; एकाधिक सिग्नल वर्गीकरण: <math>\hat{P}_\text{MU}\left(e^{j \omega}\right) = \frac{1}{\sum_{i=p+1}^M \left|\mathbf{e}^H \mathbf{v}_i\right|^2}</math>, | ||
; | ; आइजेन सदिश विधि: <math>\hat{P}_\text{EV}\left(e^{j \omega}\right) = \frac{1}{\sum_{i=p+1}^M \frac{1}{\lambda_i} \left|\mathbf{e}^H \mathbf{v}_i\right|^2}</math> | ||
; न्यूनतम मानक विधि: <math>\hat{P}_\text{MN}\left(e^{j \omega}\right) = \frac{1}{\left|\mathbf{e}^H \mathbf{a}\right|^2} ; \ \mathbf{a} = \lambda \mathbf{P}_n \mathbf{u}_1</math> | ; न्यूनतम मानक विधि: <math>\hat{P}_\text{MN}\left(e^{j \omega}\right) = \frac{1}{\left|\mathbf{e}^H \mathbf{a}\right|^2} ; \ \mathbf{a} = \lambda \mathbf{P}_n \mathbf{u}_1</math> | ||
| Line 102: | Line 102: | ||
&= \sum_k \left(\overbrace{a_k}^{A_k \sin(\phi_k)} \cos(2\pi\nu_k n) + \overbrace{b_k}^{A_k \cos(\phi_k)} \sin(2\pi\nu_k n)\right) | &= \sum_k \left(\overbrace{a_k}^{A_k \sin(\phi_k)} \cos(2\pi\nu_k n) + \overbrace{b_k}^{A_k \cos(\phi_k)} \sin(2\pi\nu_k n)\right) | ||
\end{align}</math> | \end{align}</math> | ||
<math>x_n</math> का विचरण जैसा कि ऊपर दिया गया है, शून्य-माध्य फलन के लिए है | |||
:<math>\frac{1}{N} \sum_{n=0}^{N-1} x_n^2.</math> | :<math>\frac{1}{N} \sum_{n=0}^{N-1} x_n^2.</math> | ||
यदि ये डेटा विद्युत सिग्नल से लिए गए | यदि ये डेटा विद्युत सिग्नल से लिए गए प्रतिरूप थे, तो यह इसकी औसत शक्ति होगी (शक्ति प्रति यूनिट समय ऊर्जा है, इसलिए यदि ऊर्जा आयाम वर्ग के अनुरूप है तो यह विचरण के अनुरूप है)। | ||
अब, सरलता के लिए, मान लीजिए कि संकेत समय में अनंत रूप से | अब, सरलता के लिए, मान लीजिए कि संकेत समय में अनंत रूप से विस्तृत होता है, इसलिए हम सीमा को पार कर जाते हैं <math>N\to \infty.</math> यदि औसत शक्ति सीमित है, जो वास्तविकता में लगभग सदैव विषय होता है, तो निम्न सीमा उपस्थित होती है और डेटा की भिन्नता होती है। | ||
:<math>\lim_{N \to \infty} \frac{1}{N} \sum_{n=0}^{N-1} x_n^2.</math> | :<math>\lim_{N \to \infty} \frac{1}{N} \sum_{n=0}^{N-1} x_n^2.</math> | ||
तत्पश्चात, सरलता के लिए, हम निरंतर समय पर जाएंगे, और मान लेंगे कि संकेत दोनों दिशाओं में समय में अनंत रूप से विस्तृत होता है। तब ये दो सूत्र बन जाते हैं, | |||
:<math>x(t) = \sum_k A_k \sin(2\pi\nu_k t + \phi_k)</math> | :<math>x(t) = \sum_k A_k \sin(2\pi\nu_k t + \phi_k)</math> | ||
| Line 116: | Line 116: | ||
:<math>\lim_{T\to\infty} \frac{1}{2T} \int_{-T}^T x(t)^2 dt.</math> | :<math>\lim_{T\to\infty} \frac{1}{2T} \int_{-T}^T x(t)^2 dt.</math> | ||
मूल माध्य का वर्ग <math>\sin</math> है <math>1/\sqrt{2}</math>, तो का विचरण <math>A_k \sin(2\pi\nu_k t + \phi_k)</math> है <math>\tfrac{1}{2} A_k^2.</math> इसलिए, | मूल माध्य का वर्ग <math>\sin</math> है <math>1/\sqrt{2}</math>, तो का विचरण <math>A_k \sin(2\pi\nu_k t + \phi_k)</math> है <math>\tfrac{1}{2} A_k^2.</math> इसलिए, <math>x(t)</math> की औसत शक्ति में योगदान आवृत्ति के साथ <math>\nu_k</math> घटक से आ रहा है, ये सभी योगदान <math>\tfrac{1}{2}A_k^2.</math> औसत शक्ति में जुड़ जाते हैं, तत्पश्चात आवृत्ति के फलन <math>x(t).</math> के रूप में <math>\tfrac{1}{2}A_k^2,</math> शक्ति है और इसका सांख्यिकीय [[संचयी वितरण कार्य]] <math>S(\nu)</math> होगा। | ||
:<math>S(\nu) = \sum _ {k : \nu_k < \nu} \frac{1}{2} A_k^2.</math> | :<math>S(\nu) = \sum _ {k : \nu_k < \nu} \frac{1}{2} A_k^2.</math> | ||
<math>S</math> चरणीय | <math>S</math> चरणीय फलन है, जो नीरस रूप से घटता नहीं है। इसकी छलांग अवधि (रिंग) घटकों की आवृत्तियों पर होती है, <math>x</math> और प्रत्येक छलांग का मूल्य उस घटक की शक्ति या भिन्नता है। | ||
विचरण स्वयं के साथ डेटा का सहप्रसरण है। यदि हम अब उसी डेटा पर विचार करें किन्तु | विचरण स्वयं के साथ डेटा का सहप्रसरण है। यदि हम अब उसी डेटा पर विचार करें, किन्तु <math>\tau</math> थोड़े अंतराल के साथ, हम इसका सहप्रसरण ले सकते हैं, <math>x(t)</math> साथ <math>x(t + \tau)</math>, और इसे स्वतः सहसंबंध फलन के रूप में <math>c</math> सिग्नल (या डेटा) का <math>x</math> परिभाषित करें: | ||
:<math>c(\tau) = \lim_{T\to\infty} \frac{1}{2T} \int_{-T}^T x(t) x(t + \tau) dt.</math> | :<math>c(\tau) = \lim_{T\to\infty} \frac{1}{2T} \int_{-T}^T x(t) x(t + \tau) dt.</math> | ||
यदि यह | यदि यह <math>\tau.</math> अस्तित्व में है तो यह सम कार्य है, यदि औसत शक्ति परिबद्ध है, तो <math>c</math> सर्वत्र विद्यमान है, परिमित है और सीमाबद्ध <math>c(0),</math> है, जो डेटा की औसत शक्ति या विचरण है। | ||
ऐसा दिखाया जा सकता है <math>c</math> समान अवधियों के साथ आवधिक घटकों में | ऐसा दिखाया जा सकता है, <math>c</math> समान अवधियों के साथ आवधिक घटकों में <math>x</math> विघटित किया जा सकता है। | ||
:<math>c(\tau) = \sum_k \frac{1}{2} A_k^2 \cos(2\pi\nu_k\tau).</math> | :<math>c(\tau) = \sum_k \frac{1}{2} A_k^2 \cos(2\pi\nu_k\tau).</math> | ||
यह वास्तव में का वर्णक्रमीय अपघटन है <math>c</math> विभिन्न आवृत्तियों पर, | यह वास्तव में का वर्णक्रमीय अपघटन है <math>c</math> विभिन्न आवृत्तियों पर, <math>x</math> और शक्ति के वितरण से संबंधित है, आवृत्तियों पर आवृत्ति घटक का आयाम <math>c</math> सिग्नल की औसत शक्ति में इसका योगदान है। | ||
इस उदाहरण का पावर वर्णक्रम निरंतर नहीं है, और इसलिए इसका कोई व्युत्पन्न नहीं है, और इसलिए इस सिग्नल में पावर | इस उदाहरण का पावर वर्णक्रम निरंतर नहीं है, और इसलिए इसका कोई व्युत्पन्न नहीं है, और इसलिए इस सिग्नल में पावर वर्णक्रम घनत्व फलन नहीं है। सामान्यतः, पावर वर्णक्रम सामान्यतः पर दो भागों का योग होगा, लाइन वर्णक्रम जैसे कि इस उदाहरण में, जो निरंतर नहीं है और इसमें घनत्व फलन नहीं है, और अवशेष, जो निरंतर है और इसमें घनत्व फलन होता है। . | ||
== यह भी देखें == | == यह भी देखें == | ||
| Line 139: | Line 138: | ||
* पीरियोडोग्राम | * पीरियोडोग्राम | ||
* [[सिगस्पेक]] | * [[सिगस्पेक]] | ||
* [[ spectrogram ]] | * [[ spectrogram | स्पेक्ट्रोग्राम]] | ||
* समय-आवृत्ति विश्लेषण | * समय-आवृत्ति विश्लेषण | ||
* समय-आवृत्ति प्रतिनिधित्व | * समय-आवृत्ति प्रतिनिधित्व | ||
* | * अर्घ्य संभावना | ||
* [[वर्णक्रमीय विद्युत वितरण]] | * [[वर्णक्रमीय विद्युत वितरण]] | ||
| Line 178: | Line 177: | ||
{{Statistics|analysis}} | {{Statistics|analysis}} | ||
[[Category:Articles with hatnote templates targeting a nonexistent page]] | |||
[[Category:CS1]] | |||
[[Category: | [[Category:Collapse templates]] | ||
[[Category:Created On 04/07/2023]] | [[Category:Created On 04/07/2023]] | ||
[[Category:Lua-based templates]] | |||
[[Category:Machine Translated Page]] | |||
[[Category:Navigational boxes| ]] | |||
[[Category:Navigational boxes without horizontal lists]] | |||
[[Category:Pages with empty portal template]] | |||
[[Category:Pages with script errors]] | |||
[[Category:Portal-inline template with redlinked portals]] | |||
[[Category:Sidebars with styles needing conversion]] | |||
[[Category:Template documentation pages|Documentation/doc]] | |||
[[Category:Templates Vigyan Ready]] | |||
[[Category:Templates generating microformats]] | |||
[[Category:Templates that add a tracking category]] | |||
[[Category:Templates that are not mobile friendly]] | |||
[[Category:Templates that generate short descriptions]] | |||
[[Category:Templates using TemplateData]] | |||
[[Category:Wikipedia metatemplates]] | |||
[[Category:फ़्रिक्वेंसी-डोमेन विश्लेषण]] | |||
[[Category:संकेत अनुमान]] | |||
[[Category:सांख्यिकीय सिग्नल प्रोसेसिंग]] | |||
Latest revision as of 17:16, 16 July 2023
सांख्यिकीय सिग्नल प्रोसेसिंग में, वर्णक्रमीय घनत्व अनुमान (एसडीई) या केवल वर्णक्रमीय अनुमान का लक्ष्य सिग्नल के समय प्रतिरूप के अनुक्रम से सिग्नल के वर्णक्रमीय घनत्व (जिसे शक्ति वर्णक्रम के रूप में भी जाना जाता है) का अनुमान लगाना है।[1] सहज रूप से कहें तो, वर्णक्रमीय घनत्व सिग्नल की आवृत्ति सामग्री को दर्शाता है। वर्णक्रमीय घनत्व का अनुमान लगाने का उद्देश्य इन आवधिकों के अनुरूप आवृत्तियों पर चोटियों को देखकर, डेटा में किसी भी आवधिक फलन की जानकारी ज्ञात करना है।
कुछ एसडीई प्रविधियां मानती हैं कि सिग्नल सीमित (सामान्यतः अल्प) संख्या में उत्पन्न आवृत्तियों और शोर से बना होता है और उत्पन्न आवृत्तियों के स्थान और तीव्रता की जानकारी ज्ञात करने का प्रयत्न करता है। अन्य लोग घटकों की संख्या पर कोई धारणा नहीं बनाते हैं और संपूर्ण उत्पादन वर्णक्रम का अनुमान लगाना चाहते हैं।
अवलोकन

वर्णक्रम विश्लेषण, जिसे आवृत्ति डोमेन विश्लेषण या वर्णक्रमीय घनत्व अनुमान भी कहा जाता है, जटिल सिग्नल को सरल भागों में विघटित करने की प्रौद्योगिकी प्रक्रिया है। जैसा कि ऊपर वर्णित है, कई भौतिक प्रक्रियाओं को कई व्यक्तिगत आवृत्ति घटकों के योग के रूप में सबसे उचित रूप से वर्णित किया गया है। कोई भी प्रक्रिया जो विभिन्न मात्राओं (जैसे आयाम, शक्तियाँ, तीव्रता) के प्रति आवृत्ति (या चरण (तरंगें)) की मात्रा निर्धारित करती है, उसे वर्णक्रम विश्लेषण कहा जा सकता है।
वर्णक्रम विश्लेषण पूर्ण सिग्नल पर किया जा सकता है। वैकल्पिक रूप से, सिग्नल को अल्प भागो (कभी-कभी फ़्रेम कहा जाता है) में विभक्त किया जा सकता है, और वर्णक्रम विश्लेषण को इन व्यक्तिगत भागो पर प्रारम्भ किया जा सकता है। आवधिक कार्य (जैसे ) इस उप-विभाजन के लिए विशेष रूप से उपयुक्त होते हैं। गैर-आवधिक कार्यों के विश्लेषण के लिए सामान्य गणितीय प्रविधियां फूरियर विश्लेषण की श्रेणी के अंतर्गत आती हैं।
किसी फलन का फूरियर रूपांतरण आवृत्ति वर्णक्रम उत्पन्न करता है जिसमें मूल सिग्नल के विषय में सम्पूर्ण जानकारी होती है, किन्तु भिन्न रूप में इसका अर्थ यह है कि मूल फलन को व्युत्क्रम फूरियर रूपांतरण द्वारा पूर्ण रूप से पुनर्निर्मित (संश्लेषित) किया जा सकता है। उचित पुनर्निर्माण के लिए, वर्णक्रम विश्लेषक को प्रत्येक आवृत्ति घटक के आयाम और चरण (तरंगों) दोनों को संरक्षित करना होगा, जानकारी के इन दो भागो को 2-आयामी सदिश के रूप में, जटिल संख्या के रूप में, या ध्रुवीय निर्देशांक में परिमाण (आयाम) और चरण के रूप में (अर्थात, चरण के रूप में) दर्शाया जा सकता है।सिग्नल प्रोसेसिंग में सामान्य प्रविधि वर्ग आयाम, या शक्ति (भौतिकी) पर विचार करना है, इस विषय में परिणामी प्लॉट को पावर वर्णक्रम के रूप में जाना जाता है।
उत्क्रमणीयता के कारण, फूरियर रूपांतरण को समय के अतिरिक्त आवृत्ति के संदर्भ में फलन का प्रतिनिधित्व कहा जाता है, इस प्रकार यह आवृत्ति डोमेन प्रतिनिधित्व होती है। समय डोमेन में निष्पादित किए जा सकने वाले रैखिक परिचालनों में ऐसे समकक्ष होते हैं जिन्हें प्रायः आवृत्ति डोमेन में अधिक सरलता से निष्पादित किया जा सकता है। आवृत्ति विश्लेषण रैखिक और गैर-रेखीय दोनों, विभिन्न समय-डोमेन संचालन के प्रभावों के विचार और व्याख्या को भी सरल बनाता है। उदाहरण के लिए, केवल गैर-रैखिकता या समय-संस्करण प्रणाली संचालन ही आवृत्ति वर्णक्रम में नई आवृत्तियाँ बना सकते हैं।
व्यवहार में, लगभग सभी सॉफ्टवेयर और इलेक्ट्रॉनिक उपकरण जो आवृत्ति वर्ण-पट उत्पन्न करते हैं, उलटा फूरियर रूपांतरण (डीएफटी) का उपयोग करते हैं, जो सिग्नल के प्रतिरूपो (सिग्नल प्रोसेसिंग) पर कार्य करता है, और जो पूर्ण अभिन्न समाधान के लिए गणितीय अनुमान प्रदान करता है। डीएफटी लगभग सदैव कुशल एल्गोरिदम द्वारा कार्यान्वित किया जाता है जिसे [[असतत फूरियर रूपांतरण]] (एफएफटी) कहा जाता है। डीएफटी के वर्ग-परिमाण घटकों की सरणी प्रकार का पावर वर्णक्रम है जिसे पीरियोडोग्राम कहा जाता है, जिसका व्यापक रूप से आवेग प्रतिक्रिया और विंडो फलन जैसे शोर-मुक्त कार्यों की आवृत्ति विशेषताओं के परीक्षण के लिए उपयोग किया जाता है। किन्तु कम सिग्नल-टू-शोर अनुपात पर शोर जैसे संकेतों या यहां तक कि साइनसोइड्स पर प्रारम्भ होने पर पीरियोडोग्राम प्रसंस्करण-लाभ प्रदान नहीं करता है। दूसरे शब्दों में, किसी दी गई आवृत्ति पर इसके वर्णक्रमीय अनुमान का विचरण कम नहीं होता है क्योंकि गणना में उपयोग किए गए प्रतिरूपो की संख्या बढ़ जाती है। इसे समय के साथ औसत करके (वेल्च की विधि [2]या अधिक आवृत्ति (चौरसाई) किया जा सकता है। वर्णक्रमीय घनत्व आकलन (एसडीई) के लिए वेल्च की विधि का व्यापक रूप से उपयोग किया जाता है। चूंकि, पीरियोडोग्राम-आधारित प्रविधियां अल्प पूर्वाग्रह प्रस्तुत करती हैं, जो कुछ अनुप्रयोगों में अस्वीकार्य हैं। इसलिए अन्य विकल्प आगामी भाग में प्रस्तुत किए गए हैं।
प्रविधि
मूलभूत आवर्त सारणी की कमियों को अर्घ्य करने के लिए वर्णक्रमीय आकलन की कई अन्य प्रविधियां विकसित की गई हैं। इन प्रविधियों को सामान्यतः पर गैर-पैरामीट्रिक सांख्यिकी, पैरामीट्रिक अनुमान, और शीघ्र ही में अर्ध-पैरामीट्रिक मॉडल (जिसे विरल भी कहा जाता है) विधियों में विभाजित किया जा सकता है।[3] गैर-पैरामीट्रिक दृष्टिकोण स्पष्ट रूप से सहप्रसरण या प्रक्रिया के वर्णक्रम का अनुमान लगाते हैं, बिना यह माने कि प्रक्रिया में कोई विशेष संरचना है। मूलभूत अनुप्रयोगों (उदाहरण के लिए वेल्च की विधि) के लिए उपयोग में आने वाले कुछ सबसे सरल अनुमानक गैर-पैरामीट्रिक अनुमानक हैं जो पीरियोडोग्राम से निकटता से संबंधित होता हैं। इसके विपरीत, पैरामीट्रिक दृष्टिकोण यह मानना हैं कि अंतर्निहित स्थिर प्रक्रिया में निश्चित संरचना होती है जिसे कम संख्या में मापदंडों का उपयोग करके वर्णित किया जा सकता है (उदाहरण के लिए, ऑटो-प्रतिगामी या चलती औसत मॉडल का उपयोग करके)। इन दृष्टिकोणों में, कार्य उस मॉडल के मापदंडों का अनुमान लगाना है जो स्टोकेस्टिक प्रक्रिया का वर्णन करता है। अर्ध-पैरामीट्रिक विधियों का उपयोग करते समय, अंतर्निहित प्रक्रिया को गैर-पैरामीट्रिक प्रतिमा का उपयोग करके मॉडलिंग किया जाता है, अतिरिक्त धारणा के साथ कि मॉडल के गैर-शून्य घटकों की संख्या अल्प होती है (अर्थात, मॉडल विरल है)। गुम डेटा पुनर्प्राप्ति के लिए भी इसी प्रकार की प्रविधियों का उपयोग लापता डेटा रिकवरी उपयोग किया जा [4]के साथ-साथ सिग्नल पुनर्निर्माण के लिए भी किया जा सकता है।
गैर-पैरामीट्रिक वर्णक्रमीय घनत्व आकलन तकनीकों की आंशिक सूची निम्नलिखित है:
- पीरियोडोग्राम, असतत फूरियर रूपांतरण का मापांक वर्ग होता है।
- लोम्ब-स्कार्गल पीरियोडोग्राम, जिसके लिए डेटा को समान रूप से स्थान देने की आवश्यकता नहीं है।
- बार्टलेट की विधि वर्णक्रमीय घनत्व अनुमान के विचरण को कम करने के लिए सिग्नल के कई भागो से लिए गए पीरियडोग्राम का औसत है।
- वेल्च की विधि बार्टलेट की विधि का विंडो संस्करण है, जो ओवरलैपिंग सेगमेंट का उपयोग करती है।
- मल्टीटेपर पीरियडोग्राम-आधारित विधि है, जो वर्णक्रमीय घनत्व अनुमान के विचरण को कम करने के लिए वर्णक्रमीय घनत्व का स्वतंत्र अनुमान बनाने के लिए कई टेपर या विंडो का उपयोग करती है।
- न्यूनतम-वर्ग वर्णक्रमीय विश्लेषण, ज्ञात आवृत्तियों के अनुरूप न्यूनतम वर्गों पर आधारित होता है।
- गैर-समान असतत फूरियर ट्रांसफॉर्म का उपयोग तब किया जाता है, जब सिग्नल प्रतिरूप असमान रूप से समय श्रृंखला में होते हैं।
- एकवचन वर्णक्रम विश्लेषण गैरपैरामीट्रिक विधि है, जो वर्णक्रमीय घनत्व का अनुमान लगाने के लिए सहप्रसरण मैट्रिक्स के एकवचन मूल्य अपघटन का उपयोग करता है।
- अल्पकालीन फूरियर रूपांतरण
- सूचना क्षेत्र सिद्धांत पर आधारित गैर-पैरामीट्रिक विधि है जो शोर, अपूर्ण डेटा और वाद्य प्रतिक्रिया कार्यों से कल्पित कर सकती है।
नीचे पैरामीट्रिक प्रविधियों की आंशिक सूची दी गई है:
- ऑटोरेग्रेसिव मॉडल (एआर) अनुमान, जो मानता है कि एनवां प्रतिरूप पूर्व पी प्रतिरूपो के साथ सहसंबद्ध है।
- मूविंग-एवरेज मॉडल (एमए) अनुमान, जो मानता है कि एनवां प्रतिरूप पूर्व पी प्रतिरूपो में शोर नियमो के साथ सहसंबद्ध है।
- ऑटोरेग्रेसिव मूविंग एवरेज (एआरएमए) अनुमान, जो एआर और एमए मॉडल का सामान्यीकरण करता है।
- संगीत (एल्गोरिदम) (संगीत) लोकप्रिय सुपर-समाधान विधि है।
- अधिकतम एन्ट्रापी वर्णक्रमीय आकलन पूर्ण-ध्रुव विधि है जो एसडीई के लिए उपयोगी है जब एकल वर्णक्रमीय विशेषताएं, जैसे तीव्र चोटियां, अपेक्षित होती हैं।
और अंत में अर्ध-पैरामीट्रिक प्रविधियों के कुछ उदाहरण:
- विरल पुनरावृत्तीय सहप्रसरण-आधारित अनुमान (स्पाइस) अनुमान,[3]और अधिक सामान्यीकृत -स्पाइस।[5] *पुनरावृत्तीय अनुकूली दृष्टिकोण (आईएए) अनुमान।[6] *लैस्सो (सांख्यिकी), कम से कम वर्ग वर्णक्रमीय विश्लेषण के समान किन्तु विरल दंड प्रारम्भ करने के साथ होता है।[7]
पैरामीट्रिक अनुमान
पैरामीट्रिक वर्णक्रमीय अनुमान में, कोई यह मानता है कि सिग्नल स्थिर प्रक्रिया द्वारा प्रस्तुत किया गया है जिसमें वर्णक्रमीय घनत्व फलन (एसडीएफ) है, यह आवृत्ति का कार्य है और पैरामीटर .[8] तत्पश्चात अनुमान की समस्या इन मापदंडों का अनुमान लगाने में से बन जाती है।
पैरामीट्रिक एसडीएफ अनुमान का सबसे सामान्य रूप मॉडल के रूप में ऑटोरेग्रेसिव मॉडल का उपयोग करता है। ऑर्डर की [8]: 392 संकेत अनुक्रम शून्य माध्य का पालन करना प्रक्रिया समीकरण को संतुष्ट करती है।
जहां निश्चित गुणांक हैं और शून्य माध्य और नवीनता विचरण वाली श्वेत प्रक्रिया है, इस प्रक्रिया के लिए एसडीएफ है,
साथ प्रतिरूपकरण समय अंतराल और नाइक्विस्ट आवृत्ति
मापदंडों का अनुमान लगाने के लिए कई दृष्टिकोण हैं की प्रक्रिया और इस प्रकार वर्णक्रमीय घनत्व है।
- प्रक्रिया यूल-वॉकर अनुमानक यूल-वॉकर समीकरणों को पुनरावर्ती रूप से हल करके पाए जाते हैं।
- बर्ग अनुमानक यूल-वॉकर समीकरणों को सामान्य न्यूनतम वर्ग समस्या के रूप में मानकर पाए जाते हैं। बर्ग अनुमानकों को सामान्यतः पर यूल-वॉकर अनुमानकों से उत्तम माना जाता है।[8]: 452 बर्ग ने इन्हें अधिकतम एन्ट्रॉपी वर्णक्रमीय अनुमान के साथ जोड़ा था।[9]
- आगे-पीछे न्यूनतम-वर्ग अनुमानक का व्यवहार करते हैं, प्रतिगमन समस्या के रूप में प्रक्रिया करें और आगे-पीछे विधि का उपयोग करके उस समस्या का समाधान करें। वे बर्ग अनुमानकर्ताओं के साथ प्रतिस्पर्धी होते हैं।
- अधिकतम संभावना अनुमानक अधिकतम संभावना दृष्टिकोण का उपयोग करके मापदंडों का अनुमान लगाते हैं। इसमें अरेखीय अनुकूलन सम्मिलित है और यह प्रथम तीन की तुलना में अधिक जटिल है।
वैकल्पिक पैरामीट्रिक प्रविधियों में चलती औसत मॉडल (एमए) और पूर्ण ऑटोरेग्रेसिव मूविंग एवरेज मॉडल (एआरएमए) में उपयुक्त होना सम्मिलित है।
आवृत्ति अनुमान
आवृत्ति अनुमान अनुमान सिद्धांत की प्रक्रिया है जो घटकों की संख्या के विषय में दी गई धारणाओं के शोर की उपस्थिति में अंकीय संकेत प्रक्रिया की आवृत्ति, आयाम और चरण-शिफ्ट होती है।[10] यह उपरोक्त सामान्य प्रविधियों के विपरीत होती है, जो घटकों के विषय में पूर्व धारणा नहीं बनाते हैं।
एकल स्वर
यदि कोई केवल सबसे ऊंची आवृत्ति का अनुमान लगाना चाहता है, तो वह पिच का पता ज्ञात करने के लिए एल्गोरिदम का उपयोग कर सकता है। यदि प्रमुख आवृत्ति समय के साथ परिवर्तित होती है, तो समस्या तात्कालिक आवृत्ति के अनुमान की हो जाती है जैसा कि समय-आवृत्ति प्रतिनिधित्व में परिभाषित किया गया है। तात्कालिक आवृत्ति अनुमान के प्रविधियों में विग्नर-विले वितरण और उच्च क्रम अस्पष्टता कार्यों पर आधारित प्रविधियां सम्मिलित होती हैं।[11]यदि कोई प्राप्त सिग्नल के सभी (संभवतः जटिल) आवृत्ति घटकों (संचरित सिग्नल और शोर सहित) को जानना चाहता है, तो वह मल्टी-टोन दृष्टिकोण का उपयोग करता है।
एकाधिक स्वर
सिग्नल के लिए विशिष्ट मॉडल का योग होता है, सफ़ेद शोर की उपस्थिति में जटिल घातांक,
- .
की शक्ति वर्णक्रमीय घनत्व से बना है, आवेग शोर के कारण वर्णक्रमीय घनत्व फलन के अतिरिक्त कार्य करता है।
आवृत्ति अनुमान के लिए सबसे सरल प्रविधियों में इन घटकों को निकालने के लिए शोर रैखिक उपस्थान की पहचान करना सम्मिलित होता है। ये विधियाँ सिग्नल उप-स्थान और शोर उप-स्थान में ऑटोसहसंबंध मैट्रिक्स के सिग्नल उप-स्थान और शोर उप-स्थान में ईजिन अपघटन पर आधारित हैं। इन उप-स्थानों की पहचान होने के पश्चात, शोर उप-स्थान से घटक आवृत्तियों का शोध करने के लिए आवृत्ति अनुमान फलन का उपयोग किया जाता है। शोर उप-स्थान आधारित आवृत्ति अनुमान की सबसे लोकप्रिय विधियाँ हैं पिसारेंको की विधि, मल्टीपल सिग्नल वर्गीकरण (संगीत) विधि, ईजेन सदिश विधि और न्यूनतम मानक विधि होती है।
- पिसारेंको की विधि
- एकाधिक सिग्नल वर्गीकरण
- ,
- आइजेन सदिश विधि
- न्यूनतम मानक विधि
उदाहरण गणना
कल्पना करना , से को शून्य माध्य वाली समय श्रृंखला (भिन्न समय) है। मान लीजिए कि यह आवधिक घटकों की सीमित संख्या का योग है (सभी आवृत्तियाँ सकारात्मक हैं):
का विचरण जैसा कि ऊपर दिया गया है, शून्य-माध्य फलन के लिए है
यदि ये डेटा विद्युत सिग्नल से लिए गए प्रतिरूप थे, तो यह इसकी औसत शक्ति होगी (शक्ति प्रति यूनिट समय ऊर्जा है, इसलिए यदि ऊर्जा आयाम वर्ग के अनुरूप है तो यह विचरण के अनुरूप है)।
अब, सरलता के लिए, मान लीजिए कि संकेत समय में अनंत रूप से विस्तृत होता है, इसलिए हम सीमा को पार कर जाते हैं यदि औसत शक्ति सीमित है, जो वास्तविकता में लगभग सदैव विषय होता है, तो निम्न सीमा उपस्थित होती है और डेटा की भिन्नता होती है।
तत्पश्चात, सरलता के लिए, हम निरंतर समय पर जाएंगे, और मान लेंगे कि संकेत दोनों दिशाओं में समय में अनंत रूप से विस्तृत होता है। तब ये दो सूत्र बन जाते हैं,
और
मूल माध्य का वर्ग है , तो का विचरण है इसलिए, की औसत शक्ति में योगदान आवृत्ति के साथ घटक से आ रहा है, ये सभी योगदान औसत शक्ति में जुड़ जाते हैं, तत्पश्चात आवृत्ति के फलन के रूप में शक्ति है और इसका सांख्यिकीय संचयी वितरण कार्य होगा।
चरणीय फलन है, जो नीरस रूप से घटता नहीं है। इसकी छलांग अवधि (रिंग) घटकों की आवृत्तियों पर होती है, और प्रत्येक छलांग का मूल्य उस घटक की शक्ति या भिन्नता है।
विचरण स्वयं के साथ डेटा का सहप्रसरण है। यदि हम अब उसी डेटा पर विचार करें, किन्तु थोड़े अंतराल के साथ, हम इसका सहप्रसरण ले सकते हैं, साथ , और इसे स्वतः सहसंबंध फलन के रूप में सिग्नल (या डेटा) का परिभाषित करें:
यदि यह अस्तित्व में है तो यह सम कार्य है, यदि औसत शक्ति परिबद्ध है, तो सर्वत्र विद्यमान है, परिमित है और सीमाबद्ध है, जो डेटा की औसत शक्ति या विचरण है।
ऐसा दिखाया जा सकता है, समान अवधियों के साथ आवधिक घटकों में विघटित किया जा सकता है।
यह वास्तव में का वर्णक्रमीय अपघटन है विभिन्न आवृत्तियों पर, और शक्ति के वितरण से संबंधित है, आवृत्तियों पर आवृत्ति घटक का आयाम सिग्नल की औसत शक्ति में इसका योगदान है।
इस उदाहरण का पावर वर्णक्रम निरंतर नहीं है, और इसलिए इसका कोई व्युत्पन्न नहीं है, और इसलिए इस सिग्नल में पावर वर्णक्रम घनत्व फलन नहीं है। सामान्यतः, पावर वर्णक्रम सामान्यतः पर दो भागों का योग होगा, लाइन वर्णक्रम जैसे कि इस उदाहरण में, जो निरंतर नहीं है और इसमें घनत्व फलन नहीं है, और अवशेष, जो निरंतर है और इसमें घनत्व फलन होता है। .
यह भी देखें
- बहुआयामी वर्णक्रमीय अनुमान
- पीरियोडोग्राम
- सिगस्पेक
- स्पेक्ट्रोग्राम
- समय-आवृत्ति विश्लेषण
- समय-आवृत्ति प्रतिनिधित्व
- अर्घ्य संभावना
- वर्णक्रमीय विद्युत वितरण
संदर्भ
- ↑ P Stoica and R Moses, Spectral Analysis of Signals, Prentice Hall, 2005.
- ↑ Welch, P. D. (1967), "The use of Fast Fourier Transform for the estimation of power spectra: A method based on time averaging over short, modified periodograms", IEEE Transactions on Audio and Electroacoustics, AU-15 (2): 70–73, Bibcode:1967ITAE...15...70W, doi:10.1109/TAU.1967.1161901
- ↑ 3.0 3.1 Stoica, Petre; Babu, Prabhu; Li, Jian (January 2011). "अलग-अलग मॉडलों में विरल पैरामीटर अनुमान की नई विधि और अनियमित रूप से नमूना किए गए डेटा के वर्णक्रमीय विश्लेषण के लिए इसका उपयोग". IEEE Transactions on Signal Processing. 59 (1): 35–47. Bibcode:2011ITSP...59...35S. doi:10.1109/TSP.2010.2086452. ISSN 1053-587X. S2CID 15936187.
- ↑ Stoica, Petre; Li, Jian; Ling, Jun; Cheng, Yubo (April 2009). "एक गैरपैरामीट्रिक पुनरावृत्त अनुकूली दृष्टिकोण के माध्यम से गुम डेटा पुनर्प्राप्ति". 2009 IEEE International Conference on Acoustics, Speech and Signal Processing. IEEE: 3369–3372. doi:10.1109/icassp.2009.4960347. ISBN 978-1-4244-2353-8.
- ↑ Sward, Johan; Adalbjornsson, Stefan Ingi; Jakobsson, Andreas (March 2017). "विरल पुनरावृत्तीय सहप्रसरण-आधारित अनुमानक का एक सामान्यीकरण". 2017 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP). IEEE: 3954–3958. doi:10.1109/icassp.2017.7952898. ISBN 978-1-5090-4117-6. S2CID 5640068.
- ↑ Yardibi, Tarik; Li, Jian; Stoica, Petre; Xue, Ming; Baggeroer, Arthur B. (January 2010). "Source Localization and Sensing: A Nonparametric Iterative Adaptive Approach Based on Weighted Least Squares". IEEE Transactions on Aerospace and Electronic Systems. 46 (1): 425–443. Bibcode:2010ITAES..46..425Y. doi:10.1109/TAES.2010.5417172. hdl:1721.1/59588. ISSN 0018-9251. S2CID 18834345.
- ↑ Panahi, Ashkan; Viberg, Mats (February 2011). "LASSO-आधारित DOA आकलन पद्धति के रिज़ॉल्यूशन पर". 2011 International ITG Workshop on Smart Antennas. IEEE: 1–5. doi:10.1109/wsa.2011.5741938. ISBN 978-1-61284-075-8. S2CID 7013162.
- ↑ 8.0 8.1 8.2 Percival, Donald B.; Walden, Andrew T. (1992). भौतिक अनुप्रयोगों के लिए वर्णक्रमीय विश्लेषण. Cambridge University Press. ISBN 9780521435413.
- ↑ Burg, J.P. (1967) "Maximum Entropy Spectral Analysis", Proceedings of the 37th Meeting of the Society of Exploration Geophysicists, Oklahoma City, Oklahoma.
- ↑ Hayes, Monson H., Statistical Digital Signal Processing and Modeling, John Wiley & Sons, Inc., 1996. ISBN 0-471-59431-8.
- ↑ Lerga, Jonatan. "सिग्नल तात्कालिक आवृत्ति अनुमान विधियों का अवलोकन" (PDF). University of Rijeka. Retrieved 22 March 2014.
अग्रिम पठन
- Porat, B. (1994). Digital Processing of Random Signals: Theory & Methods. Prentice Hall. ISBN 978-0-13-063751-2.
- Priestley, M.B. (1991). Spectral Analysis and Time Series. Academic Press. ISBN 978-0-12-564922-3.
- Stoica, P.; Moses, R. (2005). Spectral Analysis of Signals. Prentice Hall. ISBN 978-0-13-113956-5.
- Thomson, D. J. (1982). "Spectrum estimation and harmonic analysis". Proceedings of the IEEE. 70 (9): 1055–1096. Bibcode:1982IEEEP..70.1055T. CiteSeerX 10.1.1.471.1278. doi:10.1109/PROC.1982.12433. S2CID 290772.