समरूपता (ज्यामिति): Difference between revisions
No edit summary |
No edit summary |
||
| (10 intermediate revisions by 3 users not shown) | |||
| Line 3: | Line 3: | ||
किसी ज्यामितीय वस्तु के लिए संभव समरूपता के प्रकार उपलब्ध ज्यामितीय परिवर्तनों के समूह पर निर्भर करते हैं, और परिवर्तन के पश्चात् किस वस्तु के गुण अपरिवर्तित रहने चाहिए। क्योंकि दो परिवर्तनों की संरचना भी परिवर्तन है और प्रत्येक परिवर्तन में, परिभाषा के अनुसार, विपरीत परिवर्तन होता है जो इसे पूर्ववत करता है, परिवर्तनों का समूह जिसके अंतर्गत वस्तु सममित होती है, गणितीय [[समूह (गणित)]], वस्तु का [[समरूपता समूह]] बनाती है।<ref>{{cite book | last=Miller | first=Willard Jr. | year=1972 | title=समरूपता समूह और उनके अनुप्रयोग| publisher=Academic Press | location=New York | oclc=589081 | url=http://www.ima.umn.edu/~miller/symmetrygroups.html | access-date=2009-09-28 | url-status=dead | archive-url=https://web.archive.org/web/20100217091244/http://www.ima.umn.edu/~miller/symmetrygroups.html | archive-date=2010-02-17 }}</ref> | किसी ज्यामितीय वस्तु के लिए संभव समरूपता के प्रकार उपलब्ध ज्यामितीय परिवर्तनों के समूह पर निर्भर करते हैं, और परिवर्तन के पश्चात् किस वस्तु के गुण अपरिवर्तित रहने चाहिए। क्योंकि दो परिवर्तनों की संरचना भी परिवर्तन है और प्रत्येक परिवर्तन में, परिभाषा के अनुसार, विपरीत परिवर्तन होता है जो इसे पूर्ववत करता है, परिवर्तनों का समूह जिसके अंतर्गत वस्तु सममित होती है, गणितीय [[समूह (गणित)]], वस्तु का [[समरूपता समूह]] बनाती है।<ref>{{cite book | last=Miller | first=Willard Jr. | year=1972 | title=समरूपता समूह और उनके अनुप्रयोग| publisher=Academic Press | location=New York | oclc=589081 | url=http://www.ima.umn.edu/~miller/symmetrygroups.html | access-date=2009-09-28 | url-status=dead | archive-url=https://web.archive.org/web/20100217091244/http://www.ima.umn.edu/~miller/symmetrygroups.html | archive-date=2010-02-17 }}</ref> | ||
== | == सामान्यतः यूक्लिडियन समरूपता == | ||
वस्तुओं पर | वस्तुओं पर प्रस्तावित होने वाले परिवर्तनों के सबसे सामान्य समूह को [[आइसोमेट्री]] के [[यूक्लिडियन स्थान]] कहा जाता है, जो अंतरिक्ष में दूरी-संरक्षण परिवर्तन होते हैं जिन्हें सामान्यतः दो-आयामी या त्रि-आयामी (समतल ज्यामिति या ठोस ज्यामिति [[यूक्लिडियन समूह]] स्थान में) के रूप में जाना जाता है। इन आइसोमेट्री में प्रतिबिंब (गणित), घूर्णन, अनुवाद (ज्यामिति) और इन बुनियादी संचालन के संयोजन सम्मिलित होते हैं।<ref name="Higher dimensional group theory'">{{cite web | url=http://www.bangor.ac.uk/r.brown/hdaweb2.htm| title=उच्च आयामी समूह सिद्धांत| access-date=2013-04-16 | url-status=dead | archive-url=https://archive.today/20120723235509/http://www.bangor.ac.uk/r.brown/hdaweb2.htm | archive-date=2012-07-23 }}</ref> सममितीय परिवर्तन के अंतर्गत, ज्यामितीय वस्तु को सममित कहा जाता है यदि, परिवर्तन के पश्चात्, वस्तु परिवर्तन से पूर्व की वस्तु से अप्रभेद्य हो।<ref>{{Cite web|url=https://www.ck12.org/book/CK-12-Interactive-Geometry-for-CCSS/section/2.6/|title=2.6 Reflection Symmetry|website=CK-12 Foundation|access-date=2019-12-06}}</ref> ज्यामितीय वस्तु सामान्यतः केवल सभी आइसोमेट्री के [[उपसमूह]] या उपसमूह के अंतर्गत सममित होती है। आइसोमेट्री उपसमूहों के प्रकारों का वर्णन नीचे किया गया है, इसके पश्चात् अन्य प्रकार के परिवर्तन समूहों और ज्यामिति में संभव ऑब्जेक्ट इनवेरिएंस के प्रकारों का वर्णन किया गया है। | ||
कार्टन-ड्युडोने प्रमेय के अनुसार, | कार्टन-ड्युडोने प्रमेय के अनुसार, n-आयामी अंतरिक्ष में [[ऑर्थोगोनल परिवर्तन]] को अधिकतम n प्रतिबिंबों की संरचना द्वारा प्रदर्शित जा सकता है। | ||
{| class=wikitable | {| class=wikitable | ||
|+ | |+ आयाम के अनुसार मूलरूप आइसोमेट्री | ||
|- align=center | |- align=center | ||
| | | | ||
| Line 16: | Line 16: | ||
|colspan=2|'''4D''' | |colspan=2|'''4D''' | ||
|- align=center | |- align=center | ||
! | !प्रतिबिंब | ||
|BGCOLOR="#ffe0e0"|''' | |BGCOLOR="#ffe0e0"|'''बिंदु'''||BGCOLOR="#ffe0e0"|'''एफ़िन''' | ||
|''' | |'''बिंदु'''||'''एफ़िन''' | ||
|BGCOLOR="#ffe0e0"|''' | |BGCOLOR="#ffe0e0"|'''बिंदु'''||BGCOLOR="#ffe0e0"|'''एफ़िन''' | ||
|''' | |'''बिंदु'''||'''एफ़िन''' | ||
|- align=center | |- align=center | ||
!1 | !1 | ||
|BGCOLOR="#ffe0e0" colspan=2| | |BGCOLOR="#ffe0e0" colspan=2|प्रतिबिंब | ||
|colspan=2| | |colspan=2|प्रतिबिंब | ||
|BGCOLOR="#ffe0e0" colspan=2| | |BGCOLOR="#ffe0e0" colspan=2|प्रतिबिंब | ||
|colspan=2| | |colspan=2|प्रतिबिंब | ||
|- align=center | |- align=center | ||
!2 | !2 | ||
|BGCOLOR="#ffe0e0"| ||BGCOLOR="#ffe0e0"| | |BGCOLOR="#ffe0e0"| ||BGCOLOR="#ffe0e0"| अनुवाद | ||
| | | घूर्णन ||अनुवाद | ||
|BGCOLOR="#ffe0e0"| | |BGCOLOR="#ffe0e0"| घूर्णन || bgcolor="#ffe0e0" |अनुवाद | ||
| | | घूर्णन ||अनुवाद | ||
|- align=center | |- align=center | ||
!3 | !3 | ||
| colspan=2| | | colspan=2| | ||
| | | | ||
| | | ट्रांसफ़्लेक्शन | ||
| BGCOLOR="#ffe0e0"| [[Rotoreflection]] | | BGCOLOR="#ffe0e0"| [[Rotoreflection|रोटोरफ्लेक्शन]] | ||
| BGCOLOR="#ffe0e0"| | | BGCOLOR="#ffe0e0"| ट्रांसफ़्लेक्शन | ||
| | | रोटोरफ्लेक्शन | ||
| | | ट्रांसफ़्लेक्शन | ||
|- align=center | |- align=center | ||
!4 | !4 | ||
| colspan=4| | | colspan=4| | ||
|BGCOLOR="#ffe0e0"| ||BGCOLOR="#ffe0e0"| | |BGCOLOR="#ffe0e0"| ||BGCOLOR="#ffe0e0"| घूर्णी अनुवाद | ||
| [[Double rotation]] || | | [[Double rotation|दोहरा घूर्णन]] || घूर्णी अनुवाद | ||
|- align=center | |- align=center | ||
!5 | !5 | ||
| colspan=6| | | colspan=6| | ||
| || | | || घूर्णी ट्रांसफ़्लेक्शन | ||
|} | |} | ||
== परावर्तक समरूपता == | == परावर्तक समरूपता == | ||
{{Main| | {{Main|परावर्तक समरूपता}} | ||
परावर्तन के संबंध में परावर्तक समरूपता, रैखिक समरूपता, दर्पण समरूपता, दर्पण-छवि समरूपता या द्विपक्षीय | परावर्तन के संबंध में परावर्तक समरूपता, रैखिक समरूपता, दर्पण समरूपता, दर्पण-छवि समरूपता या द्विपक्षीय समरूपता है।<ref>{{cite book |title=समरूपता|last=Weyl |first=Hermann |author-link=Hermann Weyl |year=1982 |orig-year=1952 |publisher=Princeton University Press |location=Princeton | isbn=0-691-02374-3 |ref=Weyl 1982}}</ref> आयाम में, समरूपता का बिंदु होता है जिसके सम्बन्ध में प्रतिबिंब होता है; दो आयामों में, समरूपता का अक्ष (a.k.a., समरूपता की रेखा) है, और तीन आयामों में समरूपता का तल है।<ref name=":1" /><ref>{{cite book |last1=Cowin |first1=Stephen C. |last2=Doty |first2=Stephen B. |year=2007 |title=ऊतक यांत्रिकी|url=https://archive.org/details/tissuemechanics00cowi_776 |url-access=limited |publisher=Springer |page=[https://archive.org/details/tissuemechanics00cowi_776/page/n162 152]|isbn=9780387368252 }}</ref> वस्तु या आकृति जिसके लिए प्रत्येक बिंदु का दूसरे पर मानचित्रण होता है, जो सामान्य तल के विपरीत पक्षों से समान दूरी पर होता है, दर्पण सममिति कहलाता है (अधिक जानकारी के लिए, [[दर्पण छवि]] देखें)। | ||
द्वि-आयामी आकृति की समरूपता की धुरी | द्वि-आयामी आकृति की समरूपता की धुरी रेखा है, जैसे कि यदि लंबवत का निर्माण किया जाता है, तो समरूपता की धुरी से समान दूरी पर लंबवत पर स्थित कोई भी दो बिंदु समान होते हैं। इसके सम्बन्ध में विचार करने का दूसरा उपाय यह है कि यदि आकृति को अक्ष के ऊपर अर्ध मोड़ दिया जाए, तो दोनों भाग एक-दूसरे की दर्पण छवियों के समान होंगे। उदाहरण के लिए [[वर्ग (ज्यामिति)]] में समरूपता के चार अक्ष होते हैं, क्योंकि इसे मोड़ने और किनारों को एक-दूसरे से मिलाने के चार भिन्न-भिन्न उपाय होते हैं। अन्य उदाहरण वृत्त का होगा, जिसके केंद्र से समान कारण से सममिति के अनंत कई अक्ष गुजरते हैं।<ref>{{cite book | author=Caldecott, Stratford | year=2009 | title=Beauty for Truth's Sake: On the Re-enchantment of Education | publisher=Brazos Press |page=70}}</ref> यदि अक्षर T ऊर्ध्वाधर अक्ष पर प्रतिबिंबित होता है, तो यह वैसा ही दिखाई देता है। इसे कभी-कभी ऊर्ध्वाधर समरूपता भी कहा जाता है। इस प्रकार कोई इस घटना का स्पष्ट रूप से यह कहकर वर्णन कर सकता है कि T में ऊर्ध्वाधर समरूपता अक्ष है, या कि T में बाएँ-दाएँ समरूपता है। | ||
यदि अक्षर T ऊर्ध्वाधर अक्ष पर प्रतिबिंबित होता है, तो यह वैसा ही दिखाई देता है। इसे कभी-कभी ऊर्ध्वाधर समरूपता भी कहा जाता है। इस प्रकार कोई इस घटना का स्पष्ट रूप से यह कहकर वर्णन कर सकता है कि T में ऊर्ध्वाधर समरूपता अक्ष है, या कि T में बाएँ-दाएँ समरूपता है। | |||
परावर्तन समरूपता वाले त्रिभुज [[समद्विबाहु]] होते हैं, इस समरूपता वाले [[चतुर्भुज]] काइट (ज्यामिति) और समद्विबाहु समलंब चतुर्भुज होते हैं।<ref>{{cite book | title=प्राथमिक विद्यालय के शिक्षकों के लिए गणित| author=Bassarear, Tom |edition=5 | publisher=Cengage Learning | year=2011 |page =499}}</ref> | परावर्तन समरूपता वाले त्रिभुज [[समद्विबाहु]] होते हैं, इस समरूपता वाले [[चतुर्भुज]] काइट (ज्यामिति) और समद्विबाहु समलंब चतुर्भुज होते हैं।<ref>{{cite book | title=प्राथमिक विद्यालय के शिक्षकों के लिए गणित| author=Bassarear, Tom |edition=5 | publisher=Cengage Learning | year=2011 |page =499}}</ref> प्रतिबिंब की प्रत्येक रेखा या तल के लिए, समरूपता समूह C<sub>s</sub> के साथ [[समरूपी|समरूP]] है (अधिक जानकारी के लिए तीन आयामों में [[बिंदु समूह]] देखें), तीन प्रकार के क्रम दो (अंतर्विरोध (गणित) एस) में से एक है, इसलिए बीजगणितीय रूप से C<sub>2</sub> के लिए आइसोमोर्फिक [[मौलिक डोमेन]] अर्ध-तल या अर्ध-स्थान है।<ref>{{cite book | author-link=Norman Johnson (mathematician) | author=Johnson, N. W. Johnson | title=ज्यामिति और परिवर्तन| year=2018 | chapter=11: Finite symmetry groups | publisher=Cambridge University Press}}</ref> | ||
प्रतिबिंब की प्रत्येक रेखा या तल के लिए, समरूपता समूह C के साथ [[समरूपी]] है | |||
== बिंदु प्रतिबिंब और अन्य समावेशी आइसोमेट्री == | == बिंदु प्रतिबिंब और अन्य समावेशी आइसोमेट्री == | ||
[[File:Point Reflection.png|thumb|upright=0.6|2 आयामों में, एक बिंदु प्रतिबिंब 180 डिग्री का घूर्णन है।]] | [[File:Point Reflection.png|thumb|upright=0.6|2 आयामों में, एक बिंदु प्रतिबिंब 180 डिग्री का घूर्णन है।]] | ||
{{Main| | {{Main|बिंदु प्रतिबिंब}} | ||
परावर्तन समरूपता को अन्य आइसोमेट्री के लिए सामान्यीकृत किया जा सकता है {{mvar|m}}-आयामी स्थान जो | परावर्तन समरूपता को अन्य आइसोमेट्री के लिए सामान्यीकृत किया जा सकता है, {{mvar|m}}-आयामी स्थान जो अंतर्विरोध (गणित) हैं, जैसे | ||
:{{math|(''x''<sub>1</sub>, ..., ''x''<sub>''m''</sub>) ↦ (−''x''<sub>1</sub>, ..., −''x''<sub>''k''</sub>, ''x''<sub>''k''+1</sub>, ..., ''x''<sub>''m''</sub>)}} | :{{math|(''x''<sub>1</sub>, ..., ''x''<sub>''m''</sub>) ↦ (−''x''<sub>1</sub>, ..., −''x''<sub>''k''</sub>, ''x''<sub>''k''+1</sub>, ..., ''x''<sub>''m''</sub>)}} | ||
कार्टेशियन निर्देशांक की | कार्टेशियन निर्देशांक की निश्चित प्रणाली में यह {{math|(''m''−''k'')}}-आयामी एफ़िन उपस्थान के साथ स्थान को प्रदर्शित करता है ।<ref>{{cite book | author=Hertrich-Jeromin, Udo | year=2003 | title=Introduction to Möbius Differential Geometry | publisher=Cambridge University Press}}</ref> यदि {{mvar|k}} = {{mvar|m}}, तो ऐसे परिवर्तन को [[बिंदु प्रतिबिंब]], या बिंदु के माध्यम से व्युत्क्रमण के रूप में जाना जाता है। समतल पर (ज्यामिति) ({{mvar|m}} = 2), बिंदु प्रतिबिंब अर्ध-[[मोड़ (ज्यामिति)]] (180°) घूर्णन के समान है; नीचे देखें। एंटीपोडल समरूपता मूल बिंदु के माध्यम से बिंदु प्रतिबिंब समरूपता का वैकल्पिक नाम है।<ref>{{cite book |last=Dieck |first=Tammo |title=बीजगणितीय टोपोलॉजी|url=https://archive.org/details/algebraictopolog00diec |url-access=limited |year=2008 |publisher=European Mathematical Society |isbn=9783037190487 |pages=[https://archive.org/details/algebraictopolog00diec/page/n273 261]}}</ref> ऐसा प्रतिबिंब [[अभिविन्यास (वेक्टर स्थान)|अभिविन्यास (सदिश स्थान)]] को संरक्षित करता है यदि और केवल यदि {{mvar|k}} [[सम संख्या]] है.<ref>William H. Barker, Roger Howe ''Continuous Symmetry: From Euclid to Klein (Google eBook)'' American Mathematical Soc</ref> इसका तात्पर्य यह है कि त्रि-आयामी अंतरिक्ष के लिए {{mvar|m}}=3 (साथ ही अन्य विषम के लिए भी {{mvar|m}}), बिंदु प्रतिबिंब दर्पण-छवि समरूपता की जैसे, अंतरिक्ष के अभिविन्यास को परिवर्तित करता है। यह बताता है कि क्यों भौतिकी में, शब्द P-[[समरूपता (भौतिकी)]] (P का अर्थ [[समता (भौतिकी)]] है) का उपयोग बिंदु प्रतिबिंब और दर्पण समरूपता दोनों के लिए किया जाता है। चूंकि तीन आयामों में बिंदु प्रतिबिंब [[बाएं हाथ की समन्वय प्रणाली]] को दाएं हाथ की समन्वय प्रणाली में परिवर्तित कर देता है, बिंदु प्रतिबिंब के अंतर्गत समरूपता को बाएं-दाएं समरूपता भी कहा जाता है।<ref name=Gibson1980>{{cite book |author1=W.M. Gibson |author2=B.R. Pollard |name-list-style=amp |title=प्राथमिक कण भौतिकी में समरूपता सिद्धांत|year=1980 |publisher=Cambridge University Press |isbn=0-521-29964-0 |pages=120–122}}</ref> | ||
ऐसा प्रतिबिंब [[अभिविन्यास (वेक्टर स्थान)]] को संरक्षित करता है यदि और केवल यदि {{mvar|k}} | |||
== घूर्णी समरूपता == | == घूर्णी समरूपता == | ||
{{Main| | {{Main|घूर्णी समरूपता}} | ||
[[File:The armoured triskelion on the flag of the Isle of Man.svg|thumb|upright=0.6|[[ट्रिस्केलियन]] में तीन गुना घूर्णी समरूपता है।]]घूर्णी समरूपता कुछ या सभी घुमावों के संबंध | [[File:The armoured triskelion on the flag of the Isle of Man.svg|thumb|upright=0.6|[[ट्रिस्केलियन]] में तीन गुना घूर्णी समरूपता है।]]घूर्णी समरूपता कुछ या सभी घुमावों के संबंध {{mvar|m}}-आयामी यूक्लिडियन स्थान में समरूपता होती है । घूर्णन एसई (n) हैं, जो आइसोमेट्री हैं जो [[अभिविन्यास (गणित)]] को संरक्षित करते हैं।<ref>Vladimir G. Ivancevic, Tijana T. Ivancevic (2005) ''Natural Biodynamics'' World Scientific</ref> इसलिए, घूर्णी समरूपता का समूह विशेष यूक्लिडियन समूह एसई(3) का उपसमूह है I | ||
सभी बिंदुओं के सम्बन्ध में सभी घुमावों के संबंध में समरूपता का तात्पर्य सभी अनुवादों के संबंध में अनुवादात्मक समरूपता से है (क्योंकि अनुवाद | सभी बिंदुओं के सम्बन्ध में सभी घुमावों के संबंध में समरूपता का तात्पर्य सभी अनुवादों के संबंध में अनुवादात्मक समरूपता से है (क्योंकि अनुवाद भिन्न-भिन्न बिंदुओं के सम्बन्ध में घुमावों की रचनाएं हैं),<ref>{{cite book | author=Singer, David A. | year=1998 | title=Geometry: Plane and Fancy | url=https://archive.org/details/geometryplanefan0000sing | url-access=registration | publisher=Springer Science & Business Media}}</ref> और समरूपता समूह संपूर्ण E<sup>+</sup>({{mvar|m}}) है I यह वस्तुओं पर प्रस्तावित नहीं होता क्योंकि यह स्थान को सजातीय बनाता है, किन्तु यह भौतिक नियमों पर प्रस्तावित हो सकता है। | ||
किसी बिंदु के चारों ओर घूर्णन के संबंध में समरूपता के लिए, कोई उस बिंदु को मूल बिंदु के रूप में ले सकता है। ये घुमाव [[विशेष ऑर्थोगोनल समूह]] SO( | किसी बिंदु के चारों ओर घूर्णन के संबंध में समरूपता के लिए, कोई उस बिंदु को मूल बिंदु के रूप में ले सकता है। ये घुमाव [[विशेष ऑर्थोगोनल समूह]] SO({{mvar|m}}) बनाते हैं, जिसे समूह द्वारा प्रदर्शित किया जा सकता है, {{math|''m'' × ''m''}} निर्धारक 1 के साथ [[ऑर्थोगोनल मैट्रिक्स]] {{mvar|m}}=3, यह [[घूर्णन समूह SO(3)]] है।<ref>{{cite book | author=Joshi, A. W. | title=भौतिकविदों के लिए समूह सिद्धांत के तत्व| year=2007 | publisher=New Age International | pages=111ff}}</ref> भिन्न उपाय से कहें तो, किसी वस्तु का घूर्णन समूह E<sup>+</sup>({{mvar|m}}) के अंदर समरूपता समूह है, कठोर गतियों का समूह;<ref>{{cite book | author=Hartshorne, Robin | year=2000 | title=Geometry: Euclid and Beyond | publisher=Springer Science & Business Media}}</ref> अर्थात्, पूर्ण समरूपता समूह और कठोर गतियों के समूह का प्रतिच्छेदन चिरल वस्तुओं के लिए, यह पूर्ण समरूपता समूह के समान है। | ||
भौतिकी के नियम SO(3)-अपरिवर्तनीय हैं यदि वे अंतरिक्ष में विभिन्न दिशाओं में अंतर नहीं करते हैं। नोएथर के प्रमेय के कारण, | भौतिकी के नियम SO(3)-अपरिवर्तनीय हैं यदि वे अंतरिक्ष में विभिन्न दिशाओं में अंतर नहीं करते हैं। नोएथर के प्रमेय के कारण, भौतिक प्रणाली की घूर्णी समरूपता कोणीय गति [[संरक्षण कानून (भौतिकी)]] के सामान है।<ref name=Noether>{{Cite book | last = Kosmann-Schwarzbach | first = Yvette | author-link = Yvette Kosmann-Schwarzbach | title = The Noether theorems: Invariance and conservation laws in the twentieth century | publisher = [[Springer Science+Business Media|Springer-Verlag]] | series = Sources and Studies in the History of Mathematics and Physical Sciences | year = 2010 | isbn = 978-0-387-87867-6}}</ref> अधिक जानकारी के लिए, [[घूर्णी अपरिवर्तनीयता]] देखें। | ||
==अनुवादात्मक समरूपता== | ==अनुवादात्मक समरूपता== | ||
[[File:Frieze hop.png|thumb|ट्रांसलेशनल समरूपता के साथ | [[File:Frieze hop.png|thumb|ट्रांसलेशनल समरूपता के साथ [[फ्रिज़ पैटर्न]]]] | ||
{{Main| | {{Main|अनुवादात्मक समरूपता}} | ||
अनुवाद संबंधी समरूपता किसी वस्तु को अनुवाद के | |||
अनुवाद संबंधी समरूपता किसी वस्तु को अनुवाद के भिन्न या निरंतर समूह (ज्यामिति) <math>\scriptstyle T_a(p) \;=\; p \,+\, a</math> के अंतर्गत अपरिवर्तनीय छोड़ देती है I<ref>Stenger, Victor J. (2000) and Mahou Shiro (2007). ''Timeless Reality''. Prometheus Books. Especially chapter 12. Nontechnical.</ref> दाईं ओर का चित्रण तीर के साथ अनुवाद द्वारा उत्पन्न चार सर्वांगसम पदचिह्न प्रदर्शित करता है। यदि पदचिह्नों की रेखा दोनों दिशाओं में अनंत तक विस्तारित होती, तो उनमें भिन्न अनुवादात्मक समरूपता होती; कोई भी अनुवाद जो एक पदचिह्न को दूसरे पदचिह्न पर मैप करता है, पूरी पंक्ति को अपरिवर्तित छोड़ देगा। | |||
==ग्लाइड प्रतिबिंब समरूपता== | ==ग्लाइड प्रतिबिंब समरूपता== | ||
[[File:Frieze step.png|thumb|ग्लाइड प्रतिबिंब समरूपता के साथ | [[File:Frieze step.png|thumb|ग्लाइड प्रतिबिंब समरूपता के साथ फ्रिज़ पैटर्न]] | ||
{{Main| | {{Main|ग्लाइड प्रतिबिंब }} | ||
2डी में, ग्लाइड परावर्तन समरूपता (3डी में [[ सरकना विमान ]] समरूपता और सामान्य रूप से ट्रांसफ़्लेक्शन भी कहा जाता है) का अर्थ है कि | 2डी में, ग्लाइड परावर्तन समरूपता (3डी में [[ सरकना विमान |ग्लाइड समतल]] समरूपता और सामान्य रूप से ट्रांसफ़्लेक्शन भी कहा जाता है) का अर्थ है कि रेखा या समतल में प्रतिबिंब, रेखा के साथ या समतल में अनुवाद के साथ मिलकर, एक ही वस्तु में परिणत होता है ( जैसे कि पैरों के चिन्ह के सम्बन्ध में) है।<ref name=":0" /><ref>{{citation |title=Transformation Geometry: An Introduction to Symmetry |series=[[Undergraduate Texts in Mathematics]] |first=George E. |last=Martin |publisher=Springer |year=1982 |isbn=9780387906362 |page=64|url=https://books.google.com/books?id=KW4EwONsQJgC&pg=PA64}}.</ref> दो ग्लाइड प्रतिबिंबों की संरचना के परिणामस्वरूप दोगुने अनुवाद सदिश के साथ अनुवाद समरूपता होती है। ग्लाइड प्रतिबिंब और संबंधित अनुवादों वाला समरूपता समूह फ़्रीज़ समूह p11g है, और अनंत चक्रीय समूह Z के साथ समरू P है। | ||
===रोटोरफ्लेक्शन समरूपता=== | ===रोटोरफ्लेक्शन समरूपता=== | ||
[[File:Rotoreflection example antiprism.png|thumb|upright=0.8|चिह्नित किनारों वाला | [[File:Rotoreflection example antiprism.png|thumb|upright=0.8|चिह्नित किनारों वाला पंचकोणीय एंटीप्रिज्म 10 के क्रम के साथ रोटोरफ्लेक्शनल समरूपता प्रदर्शित करता है।]] | ||
{{Main| | {{Main|अनुचित घुमाव}} | ||
3डी में, | |||
3डी में, रोटरी परावर्तन, रोटोरफ्लेक्शन या अनुचित घुमाव अक्ष के सम्बन्ध में घूर्णन होता है, जो उस अक्ष के लंबवत समतल में प्रतिबिंब के साथ संयुक्त होता है।<ref>Robert O. Gould, Steffen Borchardt-Ott (2011)''Crystallography: An Introduction'' Springer Science & Business Media</ref> रोटोरफ्लेक्शन से जुड़े समरूपता समूहों में सम्मिलित हैं: | |||
* यदि घूर्णन कोण में 360° के साथ कोई उभयनिष्ठ भाजक नहीं है, तो समरूपता समूह असतत नहीं है। | * यदि घूर्णन कोण में 360° के साथ कोई उभयनिष्ठ भाजक नहीं है, तो समरूपता समूह असतत नहीं है। | ||
* यदि रोटरफ्लेक्शन में 2n-गुना घूर्णन कोण (180°/n का कोण) है, तो समरूपता समूह S | * यदि रोटरफ्लेक्शन में 2n-गुना घूर्णन कोण (180°/n का कोण) है, तो समरूपता समूह S<sub>2''n''</sub> है क्रम 2n का ([[सममित समूह|सममित समूहों]] के साथ भ्रमित न हों, जिसके लिए समान संकेतन का उपयोग किया जाता है; अमूर्त समूह C<sub>2n</sub> है) I एक विशेष विषय n = 1 है, बिंदु में व्युत्क्रमण, क्योंकि यह अक्ष और तल पर निर्भर नहीं करता है। इसकी विशेषता केवल व्युत्क्रम बिंदु है। | ||
* ग्रुप | * ग्रुप C<sub>nh</sub> (360°/n का कोण); विषम n के लिए, यह एकल समरूपता द्वारा उत्पन्न होता है, और अमूर्त समूह C<sub>2''n''</sub> है, सम n के लिए यह मूल समरूपता नहीं किन्तु संयोजन है। | ||
अधिक जानकारी के लिए, [[तीन आयामों में बिंदु समूह]] देखें। | अधिक जानकारी के लिए, [[तीन आयामों में बिंदु समूह]] देखें। | ||
== | ==कुंडलित समरूपता== | ||
{{See also| | {{See also|स्क्रू अक्ष}} | ||
3डी ज्यामिति और उच्चतर में, | 3डी ज्यामिति और उच्चतर में, स्क्रू अक्ष (या रोटरी अनुवाद) घूर्णन अक्ष के साथ घूर्णन और अनुवाद का संयोजन है।<ref>Bottema, O, and B. Roth, ''Theoretical Kinematics,'' Dover Publications (September 1990)</ref> [[ कुंडलित वक्रता |कुंडलित वक्रता]] समरूपता प्रतिदिन की वस्तुओं जैसे [[ वसंत (उपकरण) |वसंत (उपकरण)]] , [[स्लिंकी]], [[ड्रिल बिट्स]] और [[बरमा (ड्रिल)|ऑगर्स (ड्रिल)]] में देखी जाने वाली समरूपता है। कुंडलित समरूपता की अवधारणा को त्रि-आयामी अंतरिक्ष में अनुरेखण के रूप में देखा जा सकता है जो किसी वस्तु को निरंतर [[कोणीय गति]] से घुमाने के साथ-साथ घूर्णन की धुरी के साथ निरंतर रैखिक गति से अनुवाद करने के परिणामस्वरूप होता है। किसी भी समय, ये दोनों गतियाँ मिलकर कुंडलित कोण प्रदान करती हैं जो ट्रेस किए गए कुंडलित के गुणों को परिभाषित करने में सहायता करता है।<ref>George R. McGhee (2006) ''The Geometry of Evolution: Adaptive Landscapes and Theoretical Morphospaces'' Cambridge University Press p.64</ref> जब ट्रेसिंग वस्तु तीव्रता से घूमता है और धीरे-धीरे अनुवाद करता है, तो कॉइलिंग कोण 0° के निकट होगा। इसके विपरीत, यदि वस्तु धीरे-धीरे घूमती है और तीव्रता से अनुवाद करती है, तो कुंडलित कोण 90° तक पहुंच जाएगा। | ||
[[ कुंडलित वक्रता ]] समरूपता | [[File:Helix.svg|150px|thumb|left|सतत कुंडलित]]धुरी के साथ कुंडलित कोण और अनुवाद समरूपता के परस्पर क्रिया के अर्ध पर, कुंडलित समरूपता के तीन मुख्य वर्गों को प्रतिष्ठित किया जा सकता है: | ||
[[File:Helix.svg|150px|thumb|left| | [[File:Triangular helix.png|thumb|नियमित तिरछा-एपिरोगोन में भिन्न (यहां 3-गुना) स्क्रू-अक्ष समरूपता होती है, जो परिप्रेक्ष्य (ग्राफिकल) में खींची जाती है।]] | ||
[[File:Triangular helix.png|thumb| | [[File:Coxeter helix 3 colors.png|thumb|बोएर्डिज्क-कॉक्समूहर कुंडलित, संवर्धित नियमित टेट्राहेड्रा द्वारा निर्मित, स्क्रू अक्ष समरूपता का उदाहरण है जो अन्य-आवधिक है।]]* अनंत कुंडलित समरूपता: यदि कुंडलित जैसी वस्तु की लंबाई के साथ कोई विशिष्ट विशेषताएं नहीं हैं, तो वस्तु में वृत्त की जैसे अनंत समरूपता होगी, किन्तु वस्तु की लंबी धुरी के साथ अनुवाद की अतिरिक्त आवश्यकता के साथ इसे इसके मूल स्वरूप में पुनः लाने के लिए<ref>Anna Ursyn(2012) ''Biologically-inspired Computing for the Arts: Scientific Data Through Graphics'' IGI Global Snippet p.209 {{clarify|date=November 2014}}</ref> कुंडलित-जैसी वस्तु होती है जिसमें प्रत्येक बिंदु पर कुंडलित होने का नियमित कोण होता है, किन्तु इसमें अनिश्चित काल तक उच्च जटिलता का [[क्रॉस सेक्शन (ज्यामिति)|अनुप्रस्थ काट (ज्यामिति)]] भी हो सकता है, नियमानुसार वही अनुप्रस्थ काट उपस्थित हो (सामान्यतः एक के पश्चात्) वस्तु की लंबाई के अनुदिश प्रत्येक बिंदु पर घूर्णन)। सरल उदाहरणों में समान रूप से कुंडलित स्प्रिंग्स, स्लिंकी, ड्रिल बिट्स और ऑगर्स सम्मिलित होते हैं। अधिक त्रुटिहीन रूप से कहा जाए तो, किसी वस्तु में अनंत कुंडलित समरूपताएं होती हैं यदि वस्तु के केंद्रीय अक्ष के चारों ओर किसी भी छोटे घूर्णन के लिए, उस अक्ष पर निकट में बिंदु (अनुवाद दूरी) उपस्थित होता है, जिस पर वस्तु वैसी ही दिखाई देगी जैसी वह पूर्व दिखाई देती थी। यह अनंत कुंडलित समरूपता है जो घुमाए जा रहे ऑगर्स या स्क्रू बिट की लंबाई के साथ गति के विचित्र भ्रम को जन्म देती है। यह ऐसे उपकरणों को उनकी लंबाई के साथ सामग्री को स्थानांतरित करने की यांत्रिक रूप से उपयोगी क्षमता भी प्रदान करता है, नियमानुसार कि वे गुरुत्वाकर्षण या घर्षण जैसे बल के साथ संयुक्त हों जो सामग्री को ड्रिल या ऑगर्स के साथ घूमने का विरोध करने की अनुमति प्रदान करता है। | ||
[[File:Coxeter helix 3 colors.png|thumb|बोएर्डिज्क-कॉक्समूहर | *''n''-गुना कुंडलित समरूपता: यदि कुंडलित वस्तु के प्रत्येक अनुप्रस्थ काट के समान होने की आवश्यकता में कमी दी जाती है, तो अतिरिक्त कम कुंडलित समरूपता संभव हो जाएगी। उदाहरण के लिए, कुंडलित वस्तु का अनुप्रस्थ काट परिवर्तित हो सकता है, किन्तु फिर भी कुंडलित वस्तु की धुरी के साथ नियमित रूप से स्वयं को दोहरा सकता है। परिणामस्वरूप, इस प्रकार की वस्तुएं कुछ निश्चित कोण θ द्वारा घूर्णन और कुछ निश्चित दूरी द्वारा अनुवाद के पश्चात् समरूपता प्रदर्शित करेंगी, किन्तु सामान्यतः किसी भी घूर्णन कोण के लिए अपरिवर्तनीय नहीं होंगी। यदि घूर्णन का कोण जिस पर समरूपता होती है, समान रूप से पूर्ण वृत्त (360°) में विभाजित होता है, तो परिणाम नियमित बहुभुज के कुंडलित समकक्ष होता है। इस सम्बन्ध को n-विविध कुंडलित समरूपता कहा जाता है, जहां ''n'' = 360° (जैसे कि [[ दोहरी कुंडली |दोहरी कुंडली]] का विषय)। ऐसे विषयों को सम्मिलित करके इस अवधारणा को और अधिक सामान्यीकृत किया जा सकता है, <math>\scriptstyle m\theta</math> घुमाव (ज्यामिति) 360° का गुणज है - यानी, चक्र अंततः दोहराता है, किन्तु कुंडलित वस्तु के एक से अधिक पूर्ण घूर्णन के पश्चात् ही। | ||
*'' | * अन्य-दोहराई जाने वाली कुंडलित समरूपता: यह वह विषय है जिसमें समरूपता का निरीक्षण करने के लिए आवश्यक घूर्णन कोण θ [[अपरिमेय कोण]] है। घूर्णन का कोण कभी भी त्रुटिहीन रूप से नहीं दोहराता, चाहे कुंडलित को कितनी भी बार घुमाया जाए। ऐसी समरूपताएं अन्य-दोहराए जाने वाले बिंदु समूह दो आयामों में उपयोग करके बनाई जाती हैं। [[डीएनए]], प्रति मोड़ लगभग 10.5 अर्ध जोड़े के साथ, इस प्रकार की अन्य-दोहराई जाने वाली कुंडलित समरूपता का उदाहरण है।<ref>{{cite book |last=Sinden |first=Richard R. |title=डीएनए संरचना और कार्य|year=1994 |publisher=Gulf Professional Publishing |isbn=9780126457506 |page=101}}</ref> | ||
* | |||
== दोहरा घूर्णन समरूपता == | == दोहरा घूर्णन समरूपता == | ||
[[File:Torus vectors oblique.jpg|thumb| | [[File:Torus vectors oblique.jpg|thumb|4D क्लिफ़ोर्ड [[ टोरस्र्स |टोरस्र्स,]] स्टीरियोग्राफ़िक रूप से 3D में प्रक्षेपित, टोरस जैसा दिखता है। दोहरे घुमाव को कुंडलित पथ के रूप में देखा जा सकता है।]] | ||
{{See also| | {{See also|4-आयामी यूक्लिडियन अंतरिक्ष में घूर्णन दोहरा घूर्णन}} | ||
4डी में, दो ऑर्थोगोनल घुमावों के संयोजन के रूप में | 4डी में, दो ऑर्थोगोनल घुमावों के संयोजन के रूप में डबल रोटेशन समरूपता उत्पन्न की जा सकती है।<ref>Charles Howard Hinton | ||
(1906) ''The Fourth Dimension (Google eBook)'' S. Sonnenschein & Company p.223</ref> यह 3डी स्क्रू अक्ष के समान है जो | (1906) ''The Fourth Dimension (Google eBook)'' S. Sonnenschein & Company p.223</ref> यह 3डी स्क्रू अक्ष के समान है जो घूर्णन और ऑर्थोगोनल अनुवाद का सम्मिश्रण होती है। | ||
== | ==अन्य-आइसोमेट्रिक समरूपता== | ||
ज्यामितीय समरूपता की | ज्यामितीय समरूपता की व्यापक परिभाषा आइसोमेट्री के यूक्लिडियन समूह की तुलना में बड़े समूह से संचालन की अनुमति प्रदान करती है। बड़े ज्यामितीय समरूपता समूहों के उदाहरण इस प्रकार हैं: | ||
*[[समानता परिवर्तन (ज्यामिति)]] का समूह;<ref>[[H.S.M. Coxeter]] (1961,9) ''Introduction to Geometry'', §5 Similarity in the Euclidean Plane, pp. 67–76, §7 Isometry and Similarity in Euclidean Space, pp 96–104, [[John Wiley & Sons]].</ref> | *[[समानता परिवर्तन (ज्यामिति)]] का समूह;<ref>[[H.S.M. Coxeter]] (1961,9) ''Introduction to Geometry'', §5 Similarity in the Euclidean Plane, pp. 67–76, §7 Isometry and Similarity in Euclidean Space, pp 96–104, [[John Wiley & Sons]].</ref> [[मैट्रिक्स (गणित)]] द्वारा प्रदर्शित किये गए [[एफ़िन परिवर्तन]] {{mvar|A}} यह ऑर्थोगोनल मैट्रिक्स का अदिश गुना है। इस प्रकार [[सजातीय परिवर्तन]] जोड़ा जाता है, स्व-समानता को समरूपता माना जाता है। | ||
* | *मैट्रिक्स द्वारा प्रदर्शित किये गए एफ़िन परिवर्तनों का समूह {{mvar|A}} निर्धारक 1 या −1 के साथ परिवर्तन जो क्षेत्र को संरक्षित करते हैं।<ref>William Thurston. ''Three-dimensional geometry and topology. Vol. 1''. Edited by Silvio Levy. Princeton Mathematical Series, 35. Princeton University Press, Princeton, NJ, 1997. x+311 pp. {{isbn|0-691-08304-5}}</ref> | ||
*: यह, उदाहरण के लिए, तिरछी परावर्तन समरूपता जोड़ता है। | *: यह, उदाहरण के लिए, तिरछी परावर्तन समरूपता जोड़ता है। | ||
*सभी विशेषण एफ़िन परिवर्तनों का | *सभी विशेषण एफ़िन परिवर्तनों का समूह है। | ||
*मोबियस परिवर्तनों का समूह जो क्रॉस-अनुपात को संरक्षित करता है। | *मोबियस परिवर्तनों का समूह जो क्रॉस-अनुपात को संरक्षित करता है। | ||
*: यह जोड़ता है, उदाहरण के लिए, [[व्युत्क्रम ज्यामिति]] प्रतिबिंब जैसे कि समतल पर वृत्त | *: यह जोड़ता है, उदाहरण के लिए, [[व्युत्क्रम ज्यामिति]] प्रतिबिंब जैसे कि समतल पर वृत्त प्रतिबिंब है। | ||
[[फ़ेलिक्स क्लेन]] के [[एर्लांगेन कार्यक्रम]] में, समरूपता का प्रत्येक संभावित समूह | [[फ़ेलिक्स क्लेन]] के [[एर्लांगेन कार्यक्रम]] में, समरूपता का प्रत्येक संभावित समूह ज्यामिति को परिभाषित करता है जिसमें समरूपता समूह के सदस्य से संबंधित वस्तुओं को समकक्ष माना जाता है।<ref>[[Felix Klein|Klein, Felix]], 1872. "Vergleichende Betrachtungen über neuere geometrische Forschungen" ('A comparative review of recent researches in geometry'), Mathematische Annalen, 43 (1893) pp. 63–100 (Also: Gesammelte Abh. Vol. 1, Springer, 1921, pp. 460–497). | ||
:An English translation by Mellen Haskell appeared in ''Bull. N. Y. Math. Soc'' 2 (1892–1893): 215–249. | :An English translation by Mellen Haskell appeared in ''Bull. N. Y. Math. Soc'' 2 (1892–1893): 215–249. | ||
</ref> उदाहरण के लिए, यूक्लिडियन समूह [[यूक्लिडियन ज्यामिति]] को परिभाषित करता है, जबकि मोबियस परिवर्तनों का समूह [[प्रक्षेप्य ज्यामिति]] को परिभाषित करता है। | </ref> उदाहरण के लिए, यूक्लिडियन समूह [[यूक्लिडियन ज्यामिति]] को परिभाषित करता है, जबकि मोबियस परिवर्तनों का समूह [[प्रक्षेप्य ज्यामिति]] को परिभाषित करता है। | ||
==स्केल समरूपता और | ==स्केल समरूपता और फ्रैक्टल== | ||
[[File:Julia set (ice).png|thumb|[[जूलिया सेट|जूलिया समूह]] में स्केल समरूपता होती है]]स्केल समरूपता का अर्थ है कि यदि किसी वस्तु का आकार बढ़ाया या घटाया जाता है, तो नई वस्तु में मूल वस्तु के समान गुण होते हैं।<ref>Tian Yu Cao ''Conceptual Foundations of Quantum Field Theory'' Cambridge University Press p.154-155</ref> यह आत्म-समानता कई प्राकृतिक संरचनाओं जैसे कि क्यूम्यलस | [[File:Julia set (ice).png|thumb|[[जूलिया सेट|जूलिया समूह]] में स्केल समरूपता होती है]]स्केल समरूपता का अर्थ है कि यदि किसी वस्तु का आकार बढ़ाया या घटाया जाता है, तो नई वस्तु में मूल वस्तु के समान गुण होते हैं।<ref>Tian Yu Cao ''Conceptual Foundations of Quantum Field Theory'' Cambridge University Press p.154-155</ref> यह आत्म-समानता कई प्राकृतिक संरचनाओं जैसे कि क्यूम्यलस क्लाउड्स, विद्युत्, फ़र्न और समुद्र तट में व्यापक पैमाने पर देखी जाती है। यह सामान्यतः गुरुत्वाकर्षण से बंधी संरचनाओं में नहीं पाया जाता है, उदाहरण के लिए [[हाथी]] और चूहे के पैरों का आकार (तथाकथित [[एलोमेट्रिक स्केलिंग]]) आदि। इसी प्रकार, यदि कोमल मोम को ऊंचे पेड़ के आकार तक बड़ा कर दिया जाए, तो यह तुरंत अपने वजन के नीचे ढह जाएगी। | ||
स्केल समरूपता का अधिक सूक्ष्म रूप [[ भग्न ]] | स्केल समरूपता का अधिक सूक्ष्म रूप [[ भग्न |फ्रैक्टल]] द्वारा प्रदर्शित किया जाता है। जैसा कि बेनोइट मैंडेलब्रॉट ने कल्पना की थी, फ्रैक्टल गणितीय अवधारणा है जिसमें जटिल रूप की संरचना किसी भी आवर्धन स्तर पर समान दिखती है,<ref name="Gouyet">{{cite book | last = Gouyet | first = Jean-François | title = भौतिकी और भग्न संरचनाएँ| publisher = Masson Springer | location = Paris/New York | year = 1996 | isbn = 978-0-387-94153-0 }}</ref> [[मैंडेलब्रॉट सेट|मैंडेलब्रॉट समूह]] में अच्छी प्रकार से देखा गया। तट प्राकृतिक रूप से पाए जाने वाले फ्रैक्टल का उदाहरण है, क्योंकि यह उपग्रह के दृश्य से लेकर रेत के भिन्न-भिन्न कणों के विपरीत पानी के बहाव की सूक्ष्म जांच तक विपरीत स्तर पर समान दिखने वाली जटिलता को बनाये रखता है। पेड़ों की शाखाएँ, जो छोटी टहनियों को [[चित्रावली]] में पूर्ण पेड़ों के लिए खड़े होने में सक्षम बनाती हैं, उदाहरण है। | ||
चूँकि फ्रैक्टल [[प्रकृति में पैटर्न]] की उपस्थिति उत्पन्न कर सकते हैं, उनमें | चूँकि फ्रैक्टल [[प्रकृति में पैटर्न|प्रकृति में स्वरुप]] की उपस्थिति उत्पन्न कर सकते हैं, उनमें सुंदरता और परिचितता होती है जो सामान्यतः गणितीय रूप से उत्पन्न कार्यों के साथ नहीं देखी जाती है। फ्रैक्टल्स को [[कंप्यूटर जनित कल्पना]] प्रभावों में भी स्थान मिली है, जहां फ्रैक्टल समरूपता के साथ जटिल वक्र बनाने की उनकी क्षमता के परिणामस्वरूप अधिक यथार्थवादी [[आभासी दुनिया|आभासी संसार]] बनते है। | ||
==अमूर्त समरूपता== | ==अमूर्त समरूपता== | ||
===क्लेन का दृष्टिकोण=== | ===क्लेन का दृष्टिकोण=== | ||
प्रत्येक ज्यामिति के साथ, फेलिक्स क्लेन ने | प्रत्येक ज्यामिति के साथ, फेलिक्स क्लेन ने अंतर्निहित समरूपता समूह को जोड़ा है। इस प्रकार ज्यामिति के पदानुक्रम को गणितीय रूप से इन समूहों (गणित) के पदानुक्रम और उनके अपरिवर्तनीय (गणित) के पदानुक्रम के रूप में प्रदर्शित किया जाता है। उदाहरण के लिए, लंबाई, कोण और क्षेत्रों को समरूपता की यूक्लिडियन ज्यामिति के संबंध में संरक्षित किया जाता है, जबकि केवल [[घटना संरचना]] और क्रॉस-अनुपात को सबसे सामान्य प्रक्षेप्य ज्यामिति के अंतर्गत संरक्षित किया जाता है। [[समानांतर (ज्यामिति)]] अनुवाद की अवधारणा, जो एफ़िन ज्यामिति में संरक्षित है, प्रक्षेप्य ज्यामिति में सार्थक नहीं है। ज्यामिति से समरूपता के अंतर्निहित समूह (गणित) को भिन्न करके, समूह स्तर पर उनके मध्य संबंधों को पुनः स्थापित किया जा सकता है। चूंकि एफ़िन ज्यामिति का समूह प्रक्षेप्य ज्यामिति के समूह का उपसमूह है, इसलिए प्रक्षेप्य ज्यामिति में अपरिवर्तनीय कोई भी धारणा एफ़िन ज्यामिति में प्राथमिक अर्थपूर्ण है; किन्तु इसके विपरीत नहीं. यदि आप आवश्यक समरूपताएँ जोड़ते हैं, तो आपके निकट अधिक शक्तिशाली सिद्धांत होगा किन्तु कम अवधारणाएँ और प्रमेय होंगे (जो अधिक गहरे और अधिक सामान्य होंगे)। | ||
===थर्स्टन का दृष्टिकोण=== | ===थर्स्टन का दृष्टिकोण=== | ||
[[विलियम थर्स्टन]] ने ज्यामिति में समरूपता का | [[विलियम थर्स्टन]] ने ज्यामिति में समरूपता का समान संस्करण प्रस्तुत किया है। मॉडल ज्योमेट्री कॉम्पैक्ट स्टेबलाइजर्स के साथ ''X'' पर [[झूठ समूह|लाई समूह]] ''G'' की सकर्मक क्रिया के साथ सरल रूप से जुड़ा हुआ [[ चिकनी कई गुना |स्मूथ विविध]] X है। लाई समूह को ज्यामिति की समरूपताओं के समूह के रूप में सोचा जा सकता है। | ||
मॉडल ज्यामिति को अधिकतम कहा जाता है यदि G कॉम्पैक्ट स्टेबलाइजर्स के साथ X पर सुचारू रूप से और परिवर्तनीय रूप से कार्य करने वाले समूहों के मध्य अधिकतम है, यदि यह समरूपता का अधिकतम समूह है। कभी-कभी इस स्थिति को मॉडल ज्यामिति की परिभाषा में सम्मिलित किया जाता है। | |||
विविध M पर ज्यामितीय संरचना कुछ मॉडल ज्यामिति ''X'' के लिए ''M'' से ''X''/Γतक भिन्नता है, जहां Γ G का भिन्न उपसमूह है, ''X'' पर स्वतंत्र रूप से कार्य करना। यदि कोई दिया गया विविध ज्यामितीय संरचना को स्वीकार करता है, तो यह उसे स्वीकार करता है जिसका मॉडल अधिकतम है। | |||
ज्यामितिकरण अनुमान 3-आयामी मॉडल ज्यामिति ''X'' ज्यामितिकरण अनुमान के लिए प्रासंगिक है यदि यह अधिकतम है और यदि ''X'' पर अर्धरित ज्यामितीय संरचना के साथ कम से कम कॉम्पैक्ट विविध है। थर्स्टन ने इन नियमो को पूर्ण करने वाले 8 मॉडल ज्यामिति को वर्गीकृत किया; वे नीचे सूचीबद्ध हैं और कभी-कभी उन्हें थर्स्टन ज्यामिति भी कहा जाता है। (संक्षिप्त भागफल के अतिरिक्त भी अनगिनत मॉडल ज्यामिति हैं।) | |||
== यह भी देखें == | == यह भी देखें == | ||
* | * फ्रैक्टल | ||
* [[सममित संबंध]] | * [[सममित संबंध]] | ||
| Line 169: | Line 165: | ||
==बाहरी संबंध== | ==बाहरी संबंध== | ||
*[https://web.archive.org/web/20141111041507/http://www.teachersnetwork.org/teachnet/westchester/symmetry.htm Calotta: A World of Symmetry] | *[https://web.archive.org/web/20141111041507/http://www.teachersnetwork.org/teachnet/westchester/symmetry.htm Calotta: A World of Symmetry] | ||
*[http://www.uwgb.edu/dutchs/SYMMETRY/2DPTGRP.HTM Dutch: Symmetry Around a | *[http://www.uwgb.edu/dutchs/SYMMETRY/2DPTGRP.HTM Dutch: Symmetry Around a बिंदु in the Plane] | ||
[[Category: | [[Category:Articles with hatnote templates targeting a nonexistent page]] | ||
[[Category:Created On 13/07/2023]] | [[Category:Created On 13/07/2023]] | ||
[[Category:Lua-based templates]] | |||
[[Category:Machine Translated Page]] | |||
[[Category:Pages with script errors]] | |||
[[Category:Short description with empty Wikidata description]] | |||
[[Category:Templates Vigyan Ready]] | |||
[[Category:Templates that add a tracking category]] | |||
[[Category:Templates that generate short descriptions]] | |||
[[Category:Templates using TemplateData]] | |||
[[Category:Wikipedia articles needing clarification from November 2014]] | |||
[[Category:समरूपता]] | |||
Latest revision as of 15:55, 2 August 2023
ज्यामिति में, किसी वस्तु में समरूपता होती है यदि कोई संचालन (गणित) या परिवर्तन (फलन) (जैसे अनुवाद (ज्यामिति), मापक (ज्यामिति), घूर्णन (गणित) या प्रतिबिंब (गणित)) होता है जो आकृति या वस्तु को मैप करता है स्वयं (अर्थात, वस्तु में परिवर्तन के अंतर्गत अपरिवर्तनीय (गणित) है)।[1] इस प्रकार, समरूपता को परिवर्तन के प्रति प्रतिरक्षा के रूप में सोचा जा सकता है।[2] उदाहरण के लिए, अपने केंद्र के चारों ओर घूमने वाले वृत्त का आकार और मूल वृत्त के आकार के समान होगा, क्योंकि परिवर्तन से पूर्व और पश्चात् के सभी बिंदु अप्रभेद्य होंगे। इस प्रकार वृत्त को घूर्णन के अंतर्गत सममित या घूर्णी समरूपता वाला कहा जाता है। यदि आइसोमेट्री रेखा के सम्बन्ध में समतल आकृति का प्रतिबिंब है, तो कहा जाता है कि आकृति में परावर्तन समरूपता या रेखा समरूपता है;[3] किसी आकृति या वस्तु में समरूपता की एक से अधिक रेखाएँ होना भी संभव है।[4]
किसी ज्यामितीय वस्तु के लिए संभव समरूपता के प्रकार उपलब्ध ज्यामितीय परिवर्तनों के समूह पर निर्भर करते हैं, और परिवर्तन के पश्चात् किस वस्तु के गुण अपरिवर्तित रहने चाहिए। क्योंकि दो परिवर्तनों की संरचना भी परिवर्तन है और प्रत्येक परिवर्तन में, परिभाषा के अनुसार, विपरीत परिवर्तन होता है जो इसे पूर्ववत करता है, परिवर्तनों का समूह जिसके अंतर्गत वस्तु सममित होती है, गणितीय समूह (गणित), वस्तु का समरूपता समूह बनाती है।[5]
सामान्यतः यूक्लिडियन समरूपता
वस्तुओं पर प्रस्तावित होने वाले परिवर्तनों के सबसे सामान्य समूह को आइसोमेट्री के यूक्लिडियन स्थान कहा जाता है, जो अंतरिक्ष में दूरी-संरक्षण परिवर्तन होते हैं जिन्हें सामान्यतः दो-आयामी या त्रि-आयामी (समतल ज्यामिति या ठोस ज्यामिति यूक्लिडियन समूह स्थान में) के रूप में जाना जाता है। इन आइसोमेट्री में प्रतिबिंब (गणित), घूर्णन, अनुवाद (ज्यामिति) और इन बुनियादी संचालन के संयोजन सम्मिलित होते हैं।[6] सममितीय परिवर्तन के अंतर्गत, ज्यामितीय वस्तु को सममित कहा जाता है यदि, परिवर्तन के पश्चात्, वस्तु परिवर्तन से पूर्व की वस्तु से अप्रभेद्य हो।[7] ज्यामितीय वस्तु सामान्यतः केवल सभी आइसोमेट्री के उपसमूह या उपसमूह के अंतर्गत सममित होती है। आइसोमेट्री उपसमूहों के प्रकारों का वर्णन नीचे किया गया है, इसके पश्चात् अन्य प्रकार के परिवर्तन समूहों और ज्यामिति में संभव ऑब्जेक्ट इनवेरिएंस के प्रकारों का वर्णन किया गया है।
कार्टन-ड्युडोने प्रमेय के अनुसार, n-आयामी अंतरिक्ष में ऑर्थोगोनल परिवर्तन को अधिकतम n प्रतिबिंबों की संरचना द्वारा प्रदर्शित जा सकता है।
| 1D | 2D | 3D | 4D | |||||
| प्रतिबिंब | बिंदु | एफ़िन | बिंदु | एफ़िन | बिंदु | एफ़िन | बिंदु | एफ़िन |
|---|---|---|---|---|---|---|---|---|
| 1 | प्रतिबिंब | प्रतिबिंब | प्रतिबिंब | प्रतिबिंब | ||||
| 2 | अनुवाद | घूर्णन | अनुवाद | घूर्णन | अनुवाद | घूर्णन | अनुवाद | |
| 3 | ट्रांसफ़्लेक्शन | रोटोरफ्लेक्शन | ट्रांसफ़्लेक्शन | रोटोरफ्लेक्शन | ट्रांसफ़्लेक्शन | |||
| 4 | घूर्णी अनुवाद | दोहरा घूर्णन | घूर्णी अनुवाद | |||||
| 5 | घूर्णी ट्रांसफ़्लेक्शन | |||||||
परावर्तक समरूपता
परावर्तन के संबंध में परावर्तक समरूपता, रैखिक समरूपता, दर्पण समरूपता, दर्पण-छवि समरूपता या द्विपक्षीय समरूपता है।[8] आयाम में, समरूपता का बिंदु होता है जिसके सम्बन्ध में प्रतिबिंब होता है; दो आयामों में, समरूपता का अक्ष (a.k.a., समरूपता की रेखा) है, और तीन आयामों में समरूपता का तल है।[3][9] वस्तु या आकृति जिसके लिए प्रत्येक बिंदु का दूसरे पर मानचित्रण होता है, जो सामान्य तल के विपरीत पक्षों से समान दूरी पर होता है, दर्पण सममिति कहलाता है (अधिक जानकारी के लिए, दर्पण छवि देखें)।
द्वि-आयामी आकृति की समरूपता की धुरी रेखा है, जैसे कि यदि लंबवत का निर्माण किया जाता है, तो समरूपता की धुरी से समान दूरी पर लंबवत पर स्थित कोई भी दो बिंदु समान होते हैं। इसके सम्बन्ध में विचार करने का दूसरा उपाय यह है कि यदि आकृति को अक्ष के ऊपर अर्ध मोड़ दिया जाए, तो दोनों भाग एक-दूसरे की दर्पण छवियों के समान होंगे। उदाहरण के लिए वर्ग (ज्यामिति) में समरूपता के चार अक्ष होते हैं, क्योंकि इसे मोड़ने और किनारों को एक-दूसरे से मिलाने के चार भिन्न-भिन्न उपाय होते हैं। अन्य उदाहरण वृत्त का होगा, जिसके केंद्र से समान कारण से सममिति के अनंत कई अक्ष गुजरते हैं।[10] यदि अक्षर T ऊर्ध्वाधर अक्ष पर प्रतिबिंबित होता है, तो यह वैसा ही दिखाई देता है। इसे कभी-कभी ऊर्ध्वाधर समरूपता भी कहा जाता है। इस प्रकार कोई इस घटना का स्पष्ट रूप से यह कहकर वर्णन कर सकता है कि T में ऊर्ध्वाधर समरूपता अक्ष है, या कि T में बाएँ-दाएँ समरूपता है।
परावर्तन समरूपता वाले त्रिभुज समद्विबाहु होते हैं, इस समरूपता वाले चतुर्भुज काइट (ज्यामिति) और समद्विबाहु समलंब चतुर्भुज होते हैं।[11] प्रतिबिंब की प्रत्येक रेखा या तल के लिए, समरूपता समूह Cs के साथ समरूP है (अधिक जानकारी के लिए तीन आयामों में बिंदु समूह देखें), तीन प्रकार के क्रम दो (अंतर्विरोध (गणित) एस) में से एक है, इसलिए बीजगणितीय रूप से C2 के लिए आइसोमोर्फिक मौलिक डोमेन अर्ध-तल या अर्ध-स्थान है।[12]
बिंदु प्रतिबिंब और अन्य समावेशी आइसोमेट्री
परावर्तन समरूपता को अन्य आइसोमेट्री के लिए सामान्यीकृत किया जा सकता है, m-आयामी स्थान जो अंतर्विरोध (गणित) हैं, जैसे
- (x1, ..., xm) ↦ (−x1, ..., −xk, xk+1, ..., xm)
कार्टेशियन निर्देशांक की निश्चित प्रणाली में यह (m−k)-आयामी एफ़िन उपस्थान के साथ स्थान को प्रदर्शित करता है ।[13] यदि k = m, तो ऐसे परिवर्तन को बिंदु प्रतिबिंब, या बिंदु के माध्यम से व्युत्क्रमण के रूप में जाना जाता है। समतल पर (ज्यामिति) (m = 2), बिंदु प्रतिबिंब अर्ध-मोड़ (ज्यामिति) (180°) घूर्णन के समान है; नीचे देखें। एंटीपोडल समरूपता मूल बिंदु के माध्यम से बिंदु प्रतिबिंब समरूपता का वैकल्पिक नाम है।[14] ऐसा प्रतिबिंब अभिविन्यास (सदिश स्थान) को संरक्षित करता है यदि और केवल यदि k सम संख्या है.[15] इसका तात्पर्य यह है कि त्रि-आयामी अंतरिक्ष के लिए m=3 (साथ ही अन्य विषम के लिए भी m), बिंदु प्रतिबिंब दर्पण-छवि समरूपता की जैसे, अंतरिक्ष के अभिविन्यास को परिवर्तित करता है। यह बताता है कि क्यों भौतिकी में, शब्द P-समरूपता (भौतिकी) (P का अर्थ समता (भौतिकी) है) का उपयोग बिंदु प्रतिबिंब और दर्पण समरूपता दोनों के लिए किया जाता है। चूंकि तीन आयामों में बिंदु प्रतिबिंब बाएं हाथ की समन्वय प्रणाली को दाएं हाथ की समन्वय प्रणाली में परिवर्तित कर देता है, बिंदु प्रतिबिंब के अंतर्गत समरूपता को बाएं-दाएं समरूपता भी कहा जाता है।[16]
घूर्णी समरूपता

घूर्णी समरूपता कुछ या सभी घुमावों के संबंध m-आयामी यूक्लिडियन स्थान में समरूपता होती है । घूर्णन एसई (n) हैं, जो आइसोमेट्री हैं जो अभिविन्यास (गणित) को संरक्षित करते हैं।[17] इसलिए, घूर्णी समरूपता का समूह विशेष यूक्लिडियन समूह एसई(3) का उपसमूह है I
सभी बिंदुओं के सम्बन्ध में सभी घुमावों के संबंध में समरूपता का तात्पर्य सभी अनुवादों के संबंध में अनुवादात्मक समरूपता से है (क्योंकि अनुवाद भिन्न-भिन्न बिंदुओं के सम्बन्ध में घुमावों की रचनाएं हैं),[18] और समरूपता समूह संपूर्ण E+(m) है I यह वस्तुओं पर प्रस्तावित नहीं होता क्योंकि यह स्थान को सजातीय बनाता है, किन्तु यह भौतिक नियमों पर प्रस्तावित हो सकता है।
किसी बिंदु के चारों ओर घूर्णन के संबंध में समरूपता के लिए, कोई उस बिंदु को मूल बिंदु के रूप में ले सकता है। ये घुमाव विशेष ऑर्थोगोनल समूह SO(m) बनाते हैं, जिसे समूह द्वारा प्रदर्शित किया जा सकता है, m × m निर्धारक 1 के साथ ऑर्थोगोनल मैट्रिक्स m=3, यह घूर्णन समूह SO(3) है।[19] भिन्न उपाय से कहें तो, किसी वस्तु का घूर्णन समूह E+(m) के अंदर समरूपता समूह है, कठोर गतियों का समूह;[20] अर्थात्, पूर्ण समरूपता समूह और कठोर गतियों के समूह का प्रतिच्छेदन चिरल वस्तुओं के लिए, यह पूर्ण समरूपता समूह के समान है।
भौतिकी के नियम SO(3)-अपरिवर्तनीय हैं यदि वे अंतरिक्ष में विभिन्न दिशाओं में अंतर नहीं करते हैं। नोएथर के प्रमेय के कारण, भौतिक प्रणाली की घूर्णी समरूपता कोणीय गति संरक्षण कानून (भौतिकी) के सामान है।[21] अधिक जानकारी के लिए, घूर्णी अपरिवर्तनीयता देखें।
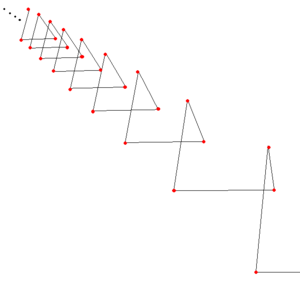
अनुवादात्मक समरूपता
अनुवाद संबंधी समरूपता किसी वस्तु को अनुवाद के भिन्न या निरंतर समूह (ज्यामिति) के अंतर्गत अपरिवर्तनीय छोड़ देती है I[22] दाईं ओर का चित्रण तीर के साथ अनुवाद द्वारा उत्पन्न चार सर्वांगसम पदचिह्न प्रदर्शित करता है। यदि पदचिह्नों की रेखा दोनों दिशाओं में अनंत तक विस्तारित होती, तो उनमें भिन्न अनुवादात्मक समरूपता होती; कोई भी अनुवाद जो एक पदचिह्न को दूसरे पदचिह्न पर मैप करता है, पूरी पंक्ति को अपरिवर्तित छोड़ देगा।
ग्लाइड प्रतिबिंब समरूपता
2डी में, ग्लाइड परावर्तन समरूपता (3डी में ग्लाइड समतल समरूपता और सामान्य रूप से ट्रांसफ़्लेक्शन भी कहा जाता है) का अर्थ है कि रेखा या समतल में प्रतिबिंब, रेखा के साथ या समतल में अनुवाद के साथ मिलकर, एक ही वस्तु में परिणत होता है ( जैसे कि पैरों के चिन्ह के सम्बन्ध में) है।[2][23] दो ग्लाइड प्रतिबिंबों की संरचना के परिणामस्वरूप दोगुने अनुवाद सदिश के साथ अनुवाद समरूपता होती है। ग्लाइड प्रतिबिंब और संबंधित अनुवादों वाला समरूपता समूह फ़्रीज़ समूह p11g है, और अनंत चक्रीय समूह Z के साथ समरू P है।
रोटोरफ्लेक्शन समरूपता
3डी में, रोटरी परावर्तन, रोटोरफ्लेक्शन या अनुचित घुमाव अक्ष के सम्बन्ध में घूर्णन होता है, जो उस अक्ष के लंबवत समतल में प्रतिबिंब के साथ संयुक्त होता है।[24] रोटोरफ्लेक्शन से जुड़े समरूपता समूहों में सम्मिलित हैं:
- यदि घूर्णन कोण में 360° के साथ कोई उभयनिष्ठ भाजक नहीं है, तो समरूपता समूह असतत नहीं है।
- यदि रोटरफ्लेक्शन में 2n-गुना घूर्णन कोण (180°/n का कोण) है, तो समरूपता समूह S2n है क्रम 2n का (सममित समूहों के साथ भ्रमित न हों, जिसके लिए समान संकेतन का उपयोग किया जाता है; अमूर्त समूह C2n है) I एक विशेष विषय n = 1 है, बिंदु में व्युत्क्रमण, क्योंकि यह अक्ष और तल पर निर्भर नहीं करता है। इसकी विशेषता केवल व्युत्क्रम बिंदु है।
- ग्रुप Cnh (360°/n का कोण); विषम n के लिए, यह एकल समरूपता द्वारा उत्पन्न होता है, और अमूर्त समूह C2n है, सम n के लिए यह मूल समरूपता नहीं किन्तु संयोजन है।
अधिक जानकारी के लिए, तीन आयामों में बिंदु समूह देखें।
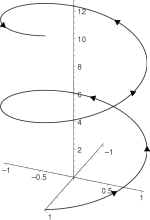
कुंडलित समरूपता
3डी ज्यामिति और उच्चतर में, स्क्रू अक्ष (या रोटरी अनुवाद) घूर्णन अक्ष के साथ घूर्णन और अनुवाद का संयोजन है।[25] कुंडलित वक्रता समरूपता प्रतिदिन की वस्तुओं जैसे वसंत (उपकरण) , स्लिंकी, ड्रिल बिट्स और ऑगर्स (ड्रिल) में देखी जाने वाली समरूपता है। कुंडलित समरूपता की अवधारणा को त्रि-आयामी अंतरिक्ष में अनुरेखण के रूप में देखा जा सकता है जो किसी वस्तु को निरंतर कोणीय गति से घुमाने के साथ-साथ घूर्णन की धुरी के साथ निरंतर रैखिक गति से अनुवाद करने के परिणामस्वरूप होता है। किसी भी समय, ये दोनों गतियाँ मिलकर कुंडलित कोण प्रदान करती हैं जो ट्रेस किए गए कुंडलित के गुणों को परिभाषित करने में सहायता करता है।[26] जब ट्रेसिंग वस्तु तीव्रता से घूमता है और धीरे-धीरे अनुवाद करता है, तो कॉइलिंग कोण 0° के निकट होगा। इसके विपरीत, यदि वस्तु धीरे-धीरे घूमती है और तीव्रता से अनुवाद करती है, तो कुंडलित कोण 90° तक पहुंच जाएगा।
धुरी के साथ कुंडलित कोण और अनुवाद समरूपता के परस्पर क्रिया के अर्ध पर, कुंडलित समरूपता के तीन मुख्य वर्गों को प्रतिष्ठित किया जा सकता है:
* अनंत कुंडलित समरूपता: यदि कुंडलित जैसी वस्तु की लंबाई के साथ कोई विशिष्ट विशेषताएं नहीं हैं, तो वस्तु में वृत्त की जैसे अनंत समरूपता होगी, किन्तु वस्तु की लंबी धुरी के साथ अनुवाद की अतिरिक्त आवश्यकता के साथ इसे इसके मूल स्वरूप में पुनः लाने के लिए[27] कुंडलित-जैसी वस्तु होती है जिसमें प्रत्येक बिंदु पर कुंडलित होने का नियमित कोण होता है, किन्तु इसमें अनिश्चित काल तक उच्च जटिलता का अनुप्रस्थ काट (ज्यामिति) भी हो सकता है, नियमानुसार वही अनुप्रस्थ काट उपस्थित हो (सामान्यतः एक के पश्चात्) वस्तु की लंबाई के अनुदिश प्रत्येक बिंदु पर घूर्णन)। सरल उदाहरणों में समान रूप से कुंडलित स्प्रिंग्स, स्लिंकी, ड्रिल बिट्स और ऑगर्स सम्मिलित होते हैं। अधिक त्रुटिहीन रूप से कहा जाए तो, किसी वस्तु में अनंत कुंडलित समरूपताएं होती हैं यदि वस्तु के केंद्रीय अक्ष के चारों ओर किसी भी छोटे घूर्णन के लिए, उस अक्ष पर निकट में बिंदु (अनुवाद दूरी) उपस्थित होता है, जिस पर वस्तु वैसी ही दिखाई देगी जैसी वह पूर्व दिखाई देती थी। यह अनंत कुंडलित समरूपता है जो घुमाए जा रहे ऑगर्स या स्क्रू बिट की लंबाई के साथ गति के विचित्र भ्रम को जन्म देती है। यह ऐसे उपकरणों को उनकी लंबाई के साथ सामग्री को स्थानांतरित करने की यांत्रिक रूप से उपयोगी क्षमता भी प्रदान करता है, नियमानुसार कि वे गुरुत्वाकर्षण या घर्षण जैसे बल के साथ संयुक्त हों जो सामग्री को ड्रिल या ऑगर्स के साथ घूमने का विरोध करने की अनुमति प्रदान करता है।
- n-गुना कुंडलित समरूपता: यदि कुंडलित वस्तु के प्रत्येक अनुप्रस्थ काट के समान होने की आवश्यकता में कमी दी जाती है, तो अतिरिक्त कम कुंडलित समरूपता संभव हो जाएगी। उदाहरण के लिए, कुंडलित वस्तु का अनुप्रस्थ काट परिवर्तित हो सकता है, किन्तु फिर भी कुंडलित वस्तु की धुरी के साथ नियमित रूप से स्वयं को दोहरा सकता है। परिणामस्वरूप, इस प्रकार की वस्तुएं कुछ निश्चित कोण θ द्वारा घूर्णन और कुछ निश्चित दूरी द्वारा अनुवाद के पश्चात् समरूपता प्रदर्शित करेंगी, किन्तु सामान्यतः किसी भी घूर्णन कोण के लिए अपरिवर्तनीय नहीं होंगी। यदि घूर्णन का कोण जिस पर समरूपता होती है, समान रूप से पूर्ण वृत्त (360°) में विभाजित होता है, तो परिणाम नियमित बहुभुज के कुंडलित समकक्ष होता है। इस सम्बन्ध को n-विविध कुंडलित समरूपता कहा जाता है, जहां n = 360° (जैसे कि दोहरी कुंडली का विषय)। ऐसे विषयों को सम्मिलित करके इस अवधारणा को और अधिक सामान्यीकृत किया जा सकता है, घुमाव (ज्यामिति) 360° का गुणज है - यानी, चक्र अंततः दोहराता है, किन्तु कुंडलित वस्तु के एक से अधिक पूर्ण घूर्णन के पश्चात् ही।
- अन्य-दोहराई जाने वाली कुंडलित समरूपता: यह वह विषय है जिसमें समरूपता का निरीक्षण करने के लिए आवश्यक घूर्णन कोण θ अपरिमेय कोण है। घूर्णन का कोण कभी भी त्रुटिहीन रूप से नहीं दोहराता, चाहे कुंडलित को कितनी भी बार घुमाया जाए। ऐसी समरूपताएं अन्य-दोहराए जाने वाले बिंदु समूह दो आयामों में उपयोग करके बनाई जाती हैं। डीएनए, प्रति मोड़ लगभग 10.5 अर्ध जोड़े के साथ, इस प्रकार की अन्य-दोहराई जाने वाली कुंडलित समरूपता का उदाहरण है।[28]
दोहरा घूर्णन समरूपता

4डी में, दो ऑर्थोगोनल घुमावों के संयोजन के रूप में डबल रोटेशन समरूपता उत्पन्न की जा सकती है।[29] यह 3डी स्क्रू अक्ष के समान है जो घूर्णन और ऑर्थोगोनल अनुवाद का सम्मिश्रण होती है।
अन्य-आइसोमेट्रिक समरूपता
ज्यामितीय समरूपता की व्यापक परिभाषा आइसोमेट्री के यूक्लिडियन समूह की तुलना में बड़े समूह से संचालन की अनुमति प्रदान करती है। बड़े ज्यामितीय समरूपता समूहों के उदाहरण इस प्रकार हैं:
- समानता परिवर्तन (ज्यामिति) का समूह;[30] मैट्रिक्स (गणित) द्वारा प्रदर्शित किये गए एफ़िन परिवर्तन A यह ऑर्थोगोनल मैट्रिक्स का अदिश गुना है। इस प्रकार सजातीय परिवर्तन जोड़ा जाता है, स्व-समानता को समरूपता माना जाता है।
- मैट्रिक्स द्वारा प्रदर्शित किये गए एफ़िन परिवर्तनों का समूह A निर्धारक 1 या −1 के साथ परिवर्तन जो क्षेत्र को संरक्षित करते हैं।[31]
- यह, उदाहरण के लिए, तिरछी परावर्तन समरूपता जोड़ता है।
- सभी विशेषण एफ़िन परिवर्तनों का समूह है।
- मोबियस परिवर्तनों का समूह जो क्रॉस-अनुपात को संरक्षित करता है।
- यह जोड़ता है, उदाहरण के लिए, व्युत्क्रम ज्यामिति प्रतिबिंब जैसे कि समतल पर वृत्त प्रतिबिंब है।
फ़ेलिक्स क्लेन के एर्लांगेन कार्यक्रम में, समरूपता का प्रत्येक संभावित समूह ज्यामिति को परिभाषित करता है जिसमें समरूपता समूह के सदस्य से संबंधित वस्तुओं को समकक्ष माना जाता है।[32] उदाहरण के लिए, यूक्लिडियन समूह यूक्लिडियन ज्यामिति को परिभाषित करता है, जबकि मोबियस परिवर्तनों का समूह प्रक्षेप्य ज्यामिति को परिभाषित करता है।
स्केल समरूपता और फ्रैक्टल

स्केल समरूपता का अर्थ है कि यदि किसी वस्तु का आकार बढ़ाया या घटाया जाता है, तो नई वस्तु में मूल वस्तु के समान गुण होते हैं।[33] यह आत्म-समानता कई प्राकृतिक संरचनाओं जैसे कि क्यूम्यलस क्लाउड्स, विद्युत्, फ़र्न और समुद्र तट में व्यापक पैमाने पर देखी जाती है। यह सामान्यतः गुरुत्वाकर्षण से बंधी संरचनाओं में नहीं पाया जाता है, उदाहरण के लिए हाथी और चूहे के पैरों का आकार (तथाकथित एलोमेट्रिक स्केलिंग) आदि। इसी प्रकार, यदि कोमल मोम को ऊंचे पेड़ के आकार तक बड़ा कर दिया जाए, तो यह तुरंत अपने वजन के नीचे ढह जाएगी।
स्केल समरूपता का अधिक सूक्ष्म रूप फ्रैक्टल द्वारा प्रदर्शित किया जाता है। जैसा कि बेनोइट मैंडेलब्रॉट ने कल्पना की थी, फ्रैक्टल गणितीय अवधारणा है जिसमें जटिल रूप की संरचना किसी भी आवर्धन स्तर पर समान दिखती है,[34] मैंडेलब्रॉट समूह में अच्छी प्रकार से देखा गया। तट प्राकृतिक रूप से पाए जाने वाले फ्रैक्टल का उदाहरण है, क्योंकि यह उपग्रह के दृश्य से लेकर रेत के भिन्न-भिन्न कणों के विपरीत पानी के बहाव की सूक्ष्म जांच तक विपरीत स्तर पर समान दिखने वाली जटिलता को बनाये रखता है। पेड़ों की शाखाएँ, जो छोटी टहनियों को चित्रावली में पूर्ण पेड़ों के लिए खड़े होने में सक्षम बनाती हैं, उदाहरण है।
चूँकि फ्रैक्टल प्रकृति में स्वरुप की उपस्थिति उत्पन्न कर सकते हैं, उनमें सुंदरता और परिचितता होती है जो सामान्यतः गणितीय रूप से उत्पन्न कार्यों के साथ नहीं देखी जाती है। फ्रैक्टल्स को कंप्यूटर जनित कल्पना प्रभावों में भी स्थान मिली है, जहां फ्रैक्टल समरूपता के साथ जटिल वक्र बनाने की उनकी क्षमता के परिणामस्वरूप अधिक यथार्थवादी आभासी संसार बनते है।
अमूर्त समरूपता
क्लेन का दृष्टिकोण
प्रत्येक ज्यामिति के साथ, फेलिक्स क्लेन ने अंतर्निहित समरूपता समूह को जोड़ा है। इस प्रकार ज्यामिति के पदानुक्रम को गणितीय रूप से इन समूहों (गणित) के पदानुक्रम और उनके अपरिवर्तनीय (गणित) के पदानुक्रम के रूप में प्रदर्शित किया जाता है। उदाहरण के लिए, लंबाई, कोण और क्षेत्रों को समरूपता की यूक्लिडियन ज्यामिति के संबंध में संरक्षित किया जाता है, जबकि केवल घटना संरचना और क्रॉस-अनुपात को सबसे सामान्य प्रक्षेप्य ज्यामिति के अंतर्गत संरक्षित किया जाता है। समानांतर (ज्यामिति) अनुवाद की अवधारणा, जो एफ़िन ज्यामिति में संरक्षित है, प्रक्षेप्य ज्यामिति में सार्थक नहीं है। ज्यामिति से समरूपता के अंतर्निहित समूह (गणित) को भिन्न करके, समूह स्तर पर उनके मध्य संबंधों को पुनः स्थापित किया जा सकता है। चूंकि एफ़िन ज्यामिति का समूह प्रक्षेप्य ज्यामिति के समूह का उपसमूह है, इसलिए प्रक्षेप्य ज्यामिति में अपरिवर्तनीय कोई भी धारणा एफ़िन ज्यामिति में प्राथमिक अर्थपूर्ण है; किन्तु इसके विपरीत नहीं. यदि आप आवश्यक समरूपताएँ जोड़ते हैं, तो आपके निकट अधिक शक्तिशाली सिद्धांत होगा किन्तु कम अवधारणाएँ और प्रमेय होंगे (जो अधिक गहरे और अधिक सामान्य होंगे)।
थर्स्टन का दृष्टिकोण
विलियम थर्स्टन ने ज्यामिति में समरूपता का समान संस्करण प्रस्तुत किया है। मॉडल ज्योमेट्री कॉम्पैक्ट स्टेबलाइजर्स के साथ X पर लाई समूह G की सकर्मक क्रिया के साथ सरल रूप से जुड़ा हुआ स्मूथ विविध X है। लाई समूह को ज्यामिति की समरूपताओं के समूह के रूप में सोचा जा सकता है।
मॉडल ज्यामिति को अधिकतम कहा जाता है यदि G कॉम्पैक्ट स्टेबलाइजर्स के साथ X पर सुचारू रूप से और परिवर्तनीय रूप से कार्य करने वाले समूहों के मध्य अधिकतम है, यदि यह समरूपता का अधिकतम समूह है। कभी-कभी इस स्थिति को मॉडल ज्यामिति की परिभाषा में सम्मिलित किया जाता है।
विविध M पर ज्यामितीय संरचना कुछ मॉडल ज्यामिति X के लिए M से X/Γतक भिन्नता है, जहां Γ G का भिन्न उपसमूह है, X पर स्वतंत्र रूप से कार्य करना। यदि कोई दिया गया विविध ज्यामितीय संरचना को स्वीकार करता है, तो यह उसे स्वीकार करता है जिसका मॉडल अधिकतम है।
ज्यामितिकरण अनुमान 3-आयामी मॉडल ज्यामिति X ज्यामितिकरण अनुमान के लिए प्रासंगिक है यदि यह अधिकतम है और यदि X पर अर्धरित ज्यामितीय संरचना के साथ कम से कम कॉम्पैक्ट विविध है। थर्स्टन ने इन नियमो को पूर्ण करने वाले 8 मॉडल ज्यामिति को वर्गीकृत किया; वे नीचे सूचीबद्ध हैं और कभी-कभी उन्हें थर्स्टन ज्यामिति भी कहा जाता है। (संक्षिप्त भागफल के अतिरिक्त भी अनगिनत मॉडल ज्यामिति हैं।)
यह भी देखें
- फ्रैक्टल
- सममित संबंध
संदर्भ
- ↑ Martin, G. (1996). Transformation Geometry: An Introduction to Symmetry. Springer. p. 28.
- ↑ 2.0 2.1 "Symmetry | Thinking about Geometry | Underground Mathematics". undergroundmathematics.org. Retrieved 2019-12-06.
- ↑ 3.0 3.1 "समरूपता - मैथबिट्सनोटबुक(जियो - सीसीएसएस गणित)". mathbitsnotebook.com. Retrieved 2019-12-06.
- ↑ Freitag, Mark (2013). Mathematics for Elementary School Teachers: A Process Approach. Cengage Learning. p. 721.
- ↑ Miller, Willard Jr. (1972). समरूपता समूह और उनके अनुप्रयोग. New York: Academic Press. OCLC 589081. Archived from the original on 2010-02-17. Retrieved 2009-09-28.
- ↑ "उच्च आयामी समूह सिद्धांत". Archived from the original on 2012-07-23. Retrieved 2013-04-16.
- ↑ "2.6 Reflection Symmetry". CK-12 Foundation. Retrieved 2019-12-06.
- ↑ Weyl, Hermann (1982) [1952]. समरूपता. Princeton: Princeton University Press. ISBN 0-691-02374-3.
- ↑ Cowin, Stephen C.; Doty, Stephen B. (2007). ऊतक यांत्रिकी. Springer. p. 152. ISBN 9780387368252.
- ↑ Caldecott, Stratford (2009). Beauty for Truth's Sake: On the Re-enchantment of Education. Brazos Press. p. 70.
- ↑ Bassarear, Tom (2011). प्राथमिक विद्यालय के शिक्षकों के लिए गणित (5 ed.). Cengage Learning. p. 499.
- ↑ Johnson, N. W. Johnson (2018). "11: Finite symmetry groups". ज्यामिति और परिवर्तन. Cambridge University Press.
- ↑ Hertrich-Jeromin, Udo (2003). Introduction to Möbius Differential Geometry. Cambridge University Press.
- ↑ Dieck, Tammo (2008). बीजगणितीय टोपोलॉजी. European Mathematical Society. pp. 261. ISBN 9783037190487.
- ↑ William H. Barker, Roger Howe Continuous Symmetry: From Euclid to Klein (Google eBook) American Mathematical Soc
- ↑ W.M. Gibson & B.R. Pollard (1980). प्राथमिक कण भौतिकी में समरूपता सिद्धांत. Cambridge University Press. pp. 120–122. ISBN 0-521-29964-0.
- ↑ Vladimir G. Ivancevic, Tijana T. Ivancevic (2005) Natural Biodynamics World Scientific
- ↑ Singer, David A. (1998). Geometry: Plane and Fancy. Springer Science & Business Media.
- ↑ Joshi, A. W. (2007). भौतिकविदों के लिए समूह सिद्धांत के तत्व. New Age International. pp. 111ff.
- ↑ Hartshorne, Robin (2000). Geometry: Euclid and Beyond. Springer Science & Business Media.
- ↑ Kosmann-Schwarzbach, Yvette (2010). The Noether theorems: Invariance and conservation laws in the twentieth century. Sources and Studies in the History of Mathematics and Physical Sciences. Springer-Verlag. ISBN 978-0-387-87867-6.
- ↑ Stenger, Victor J. (2000) and Mahou Shiro (2007). Timeless Reality. Prometheus Books. Especially chapter 12. Nontechnical.
- ↑ Martin, George E. (1982), Transformation Geometry: An Introduction to Symmetry, Undergraduate Texts in Mathematics, Springer, p. 64, ISBN 9780387906362.
- ↑ Robert O. Gould, Steffen Borchardt-Ott (2011)Crystallography: An Introduction Springer Science & Business Media
- ↑ Bottema, O, and B. Roth, Theoretical Kinematics, Dover Publications (September 1990)
- ↑ George R. McGhee (2006) The Geometry of Evolution: Adaptive Landscapes and Theoretical Morphospaces Cambridge University Press p.64
- ↑ Anna Ursyn(2012) Biologically-inspired Computing for the Arts: Scientific Data Through Graphics IGI Global Snippet p.209[clarification needed]
- ↑ Sinden, Richard R. (1994). डीएनए संरचना और कार्य. Gulf Professional Publishing. p. 101. ISBN 9780126457506.
- ↑ Charles Howard Hinton (1906) The Fourth Dimension (Google eBook) S. Sonnenschein & Company p.223
- ↑ H.S.M. Coxeter (1961,9) Introduction to Geometry, §5 Similarity in the Euclidean Plane, pp. 67–76, §7 Isometry and Similarity in Euclidean Space, pp 96–104, John Wiley & Sons.
- ↑ William Thurston. Three-dimensional geometry and topology. Vol. 1. Edited by Silvio Levy. Princeton Mathematical Series, 35. Princeton University Press, Princeton, NJ, 1997. x+311 pp. ISBN 0-691-08304-5
- ↑ Klein, Felix, 1872. "Vergleichende Betrachtungen über neuere geometrische Forschungen" ('A comparative review of recent researches in geometry'), Mathematische Annalen, 43 (1893) pp. 63–100 (Also: Gesammelte Abh. Vol. 1, Springer, 1921, pp. 460–497).
- An English translation by Mellen Haskell appeared in Bull. N. Y. Math. Soc 2 (1892–1893): 215–249.
- ↑ Tian Yu Cao Conceptual Foundations of Quantum Field Theory Cambridge University Press p.154-155
- ↑ Gouyet, Jean-François (1996). भौतिकी और भग्न संरचनाएँ. Paris/New York: Masson Springer. ISBN 978-0-387-94153-0.