चरण-स्थान सूत्रीकरण

क्वांटम यांत्रिकी का चरण-स्थान सूत्रीकरण चरण स्थान में स्थितिऔर गति चर को समान स्तर पर रखता है। इसके विपरीत, श्रोडिंगर चित्र स्थिति या संवेग निरूपण का उपयोग करता है (स्थिति और संवेग स्थान भी देखें)। चरण-अंतरिक्ष सूत्रीकरण की दो प्रमुख विशेषताएं यह हैं कि जितना क्वांटम स्थिति को अर्धसंभाव्यता वितरण (तरंग फ़ंक्शन, क्वांटम स्थिति या घनत्व मैट्रिक्स के बजाय) द्वारा वर्णित किया जाता है और ऑपरेटर गुणन को स्टार उत्पाद द्वारा प्रतिस्थापित किया जाता है।

यह सिद्धांत पूरी तरह से हिलब्रांड जे. ग्रोएनवॉल्ड द्वारा 1946 में अपनी पीएचडी थीसिस में विकसित किया गया था, और स्वतंत्र रूप से जोस एनरिक मोयल द्वारा, प्रत्येक इमारत हरमन वेइल के पहले के विचारों पर आधारित है और यूजीन विग्नर. चरण-अंतरिक्ष सूत्रीकरण का मुख्य लाभ यह है कि यह ऑपरेटर औपचारिकता से बचकर क्वांटम यांत्रिकी को यथासंभव हैमिल्टनियन यांत्रिकी के समान बनाता है, जिससे हिल्बर्ट अंतरिक्ष के 'बोझ' की मात्रा को 'मुक्त' किया जाता है। यह सूत्रीकरण प्रकृति में सांख्यिकीय है और क्वांटम यांत्रिकी और शास्त्रीय सांख्यिकीय यांत्रिकी के बीच तार्किक संबंध प्रदान करता है, जिससे दोनों के बीच प्राकृतिक तुलना संभव हो जाती है (शास्त्रीय सीमा देखें)। चरण स्थान में क्वांटम यांत्रिकी को अक्सर कुछ क्वांटम प्रकाशिकी अनुप्रयोगों (ऑप्टिकल चरण स्थान देखें), या असम्बद्धता और विशेष तकनीकी समस्याओं की एक श्रृंखला के अध्ययन में पसंद किया जाता है, हालांकि अन्यथा व्यावहारिक स्थितियों में औपचारिकता कम आम तौर पर नियोजित होती है। चरण स्थान में क्वांटम यांत्रिकी के विकास में अंतर्निहित वैचारिक विचार कोंटसेविच के विरूपण-परिमाणीकरण (कोंत्सेविच परिमाणीकरण सूत्र देखें) और गैर-अनुवांशिक ज्यामिति जैसे गणितीय शाखाओं में विभाजित हो गए हैं।

चरण-अंतरिक्ष वितरण

Main articles: Wigner quasiprobability distribution, Quasiprobability distribution, and Wigner–Weyl transform

चरण-अंतरिक्ष वितरण f(x, p)क्वांटम अवस्था का एक अर्धसंभाव्यता वितरण है। चरण-अंतरिक्ष सूत्रीकरण में, चरण-अंतरिक्ष वितरण को तरंग कार्यों या घनत्व मैट्रिक्स के किसी भी संदर्भ के बिना, क्वांटम प्रणाली के मौलिक, आदिम विवरण के रूप में माना जा सकता है। वितरण को दर्शाने के कई अलग-अलग तरीके हैं, सभी एक दूसरे से संबंधित हैं। सबसे उल्लेखनीय विग्नर क्वासिप्रोबेबिलिटी वितरण है, W(x, p), सबसे पहले खोजा गया। अन्य अभ्यावेदन (साहित्य में प्रचलन के लगभग घटते क्रम में) में ग्लौबर-सुदर्शन पी-प्रतिनिधित्व|ग्लौबर-सुदर्शन पी, शामिल हैं। हुसिमी क्यू प्रतिनिधित्व, किर्कवुड-रिहाज़ेक, मेहता, रिवियर और बोर्न-जॉर्डन प्रतिनिधित्व। ये विकल्प तब सबसे उपयोगी होते हैं जब हैमिल्टनियन एक विशेष रूप लेता है, जैसे कि ग्लौबर-सुदर्शन पी-प्रतिनिधित्व के लिए सामान्य क्रम। चूंकि विग्नर प्रतिनिधित्व सबसे आम है, इसलिए यह लेख आम तौर पर इस पर कायम रहेगा, जब तक कि अन्यथा निर्दिष्ट न किया गया हो।

चरण-स्थान वितरण में 2n-आयामी चरण स्थान में संभाव्यता घनत्व के समान गुण होते हैं। उदाहरण के लिए, आम तौर पर जटिल-मूल्यवान तरंग फ़ंक्शन के विपरीत, यह वास्तविक-मूल्यवान है। हम किसी स्थिति अंतराल के भीतर झूठ बोलने की संभावना को समझ सकते हैं, उदाहरण के लिए, सभी संवेगों और स्थिति अंतराल पर विग्नर फ़ंक्शन को एकीकृत करके:

$\operatorname {P} [a\leq X\leq b]=\int _{a}^{b}\int _{-\infty }^{\infty }W(x,p)\,dp\,dx.$

अगर Â(x, p) एक ऑपरेटर है जो एक अवलोकनीय का प्रतिनिधित्व करता है, इसे चरण स्थान पर मैप किया जा सकता है A(x, p) विग्नर-वेइल परिवर्तन के माध्यम से। इसके विपरीत, इस ऑपरेटर को विग्नर-वेइल ट्रांसफॉर्म द्वारा पुनर्प्राप्त किया जा सकता है।

चरण-अंतरिक्ष वितरण के संबंध में अवलोकन योग्य का अपेक्षित मूल्य है

$\langle {\hat {A}}\rangle =\int A(x,p)W(x,p)\,dp\,dx.$

हालाँकि, सावधानी की बात: दिखने में समानता के बावजूद, W(x, p) एक वास्तविक संयुक्त संभाव्यता वितरण नहीं है, क्योंकि इसके अंतर्गत आने वाले क्षेत्र परस्पर अनन्य राज्यों का प्रतिनिधित्व नहीं करते हैं, जैसा कि संभाव्यता सिद्धांतों#तीसरे सिद्धांत में आवश्यक है। इसके अलावा, यह, सामान्य तौर पर, संभाव्यता सिद्धांतों # प्रथम सिद्धांत के उल्लंघन में, (वैकल्पिक रूप से निचोड़ा हुआ सुसंगत राज्य) सुसंगत राज्यों के अनूठे अपवाद के साथ, शुद्ध राज्यों के लिए भी नकारात्मक संभाव्यता ले सकता है।

ऐसे नकारात्मक मूल्य वाले क्षेत्र छोटे साबित हो सकते हैं: वे कुछ से बड़े क्षेत्रों तक विस्तारित नहीं हो सकते हैं ħ, और इसलिए शास्त्रीय सीमा में गायब हो जाते हैं। वे अनिश्चितता सिद्धांत द्वारा परिरक्षित हैं, जो इससे छोटे चरण-स्थान क्षेत्रों के भीतर सटीक स्थानीयकरण की अनुमति नहीं देता है ħ, और इस प्रकार ऐसी नकारात्मक संभावनाओं को कम विरोधाभासी बना देता है। यदि समीकरण के बाईं ओर को एक ऑपरेटर के संबंध में हिल्बर्ट स्पेस में एक अपेक्षा मूल्य के रूप में व्याख्या किया जाना है, तो क्वांटम ऑप्टिक्स के संदर्भ में इस समीकरण को ऑप्टिकल तुल्यता प्रमेय के रूप में जाना जाता है। (विग्नर फ़ंक्शन के गुणों और व्याख्या के विवरण के लिए, इसका विग्नर क्वासिप्रोबेबिलिटी वितरण देखें।)

क्वांटम यांत्रिकी के लिए एक वैकल्पिक चरण-अंतरिक्ष दृष्टिकोण चरण स्थान पर एक तरंग फ़ंक्शन (केवल एक अर्धसंभाव्यता घनत्व नहीं) को परिभाषित करना चाहता है, आमतौर पर सेगल-बार्गमैन स्पेस#द सेगल-बार्गमैन ट्रांसफॉर्म|सेगल-बार्गमैन ट्रांसफॉर्म के माध्यम से। अनिश्चितता सिद्धांत के अनुकूल होने के लिए, चरण-अंतरिक्ष तरंग फ़ंक्शन एक मनमाना कार्य नहीं हो सकता है, अन्यथा इसे चरण स्थान के एक मनमाने ढंग से छोटे क्षेत्र में स्थानीयकृत किया जा सकता है। बल्कि, सेगल-बार्गमैन परिवर्तन एक होलोमोर्फिक फ़ंक्शन है $x+ip$. चरण-अंतरिक्ष तरंग फ़ंक्शन से जुड़ी एक अर्धसंभाव्यता घनत्व है; यह स्थिति तरंग फ़ंक्शन का हुसिमी क्यू प्रतिनिधित्व है।

स्टार उत्पाद

Main article: Moyal product

चरण-अंतरिक्ष सूत्रीकरण में मौलिक गैर-अनुवांशिक बाइनरी ऑपरेटर जो मानक ऑपरेटर गुणन को प्रतिस्थापित करता है वह मोयल उत्पाद है, जिसे प्रतीक द्वारा दर्शाया गया है ★.चरण-अंतरिक्ष वितरण के प्रत्येक प्रतिनिधित्व में एक अलग विशेषता सितारा उत्पाद होता है। संक्षिप्तता के लिए, हम इस चर्चा को विग्नर-वेइल प्रतिनिधित्व से संबंधित स्टार उत्पाद तक सीमित रखते हैं।

सांकेतिक सुविधा के लिए, हम ऑपरेटर साहचर्य की धारणा का परिचय देते हैं। फ़ंक्शन f और g की एक जोड़ी के लिए, बाएँ और दाएँ डेरिवेटिव को इस प्रकार परिभाषित किया गया है

${\begin{aligned}f{\overset {_{\gets }}{\partial }}_{x}g&={\frac {\partial f}{\partial x}}\cdot g,\\f{\vec {\partial }}_{x}g&=f\cdot {\frac {\partial g}{\partial x}}.\end{aligned}}$

स्टार उत्पाद का छद्म-अंतर ऑपरेटर है

$f\star g=f\,\exp {\left({\frac {i\hbar }{2}}\left({\overset {_{\gets }}{\partial }}_{x}{\vec {\partial }}_{p}-{\overset {_{\gets }}{\partial }}_{p}{\vec {\partial }}_{x}\right)\right)}g,$

जहां घातीय फलन के तर्क की व्याख्या घात श्रृंखला के रूप में की जा सकती है। अतिरिक्त अंतर संबंध इसे एफ और जी के तर्कों में बदलाव के संदर्भ में लिखने की अनुमति देते हैं:

${\begin{aligned}(f\star g)(x,p)&=f\left(x+{\tfrac {i\hbar }{2}}{\vec {\partial }}_{p},p-{\tfrac {i\hbar }{2}}{\vec {\partial }}_{x}\right)\cdot g(x,p)\\&=f(x,p)\cdot g\left(x-{\tfrac {i\hbar }{2}}{\overset {_{\gets }}{\partial }}_{p},p+{\tfrac {i\hbar }{2}}{\overset {_{\gets }}{\partial }}_{x}\right)\\&=f\left(x+{\tfrac {i\hbar }{2}}{\vec {\partial }}_{p},p\right)\cdot g\left(x-{\tfrac {i\hbar }{2}}{\overset {_{\gets }}{\partial }}_{p},p\right)\\&=f\left(x,p-{\tfrac {i\hbar }{2}}{\vec {\partial }}_{x}\right)\cdot g\left(x,p+{\tfrac {i\hbar }{2}}{\overset {_{\gets }}{\partial }}_{x}\right).\end{aligned}}$

को परिभाषित करना भी संभव है ★-एक दृढ़ अभिन्न रूप में उत्पाद, अनिवार्य रूप से फूरियर रूपांतरण के माध्यम से:

$(f\star g)(x,p)={\frac {1}{\pi ^{2}\hbar ^{2}}}\,\int f(x+x',p+p')\,g(x+x'',p+p'')\,\exp {\left({\tfrac {2i}{\hbar }}(x'p''-x''p')\right)}\,dx'dp'dx''dp''.$

(इस प्रकार, उदा.,गाऊसी हाइपरबोलिक फ़ंक्शन की रचना करते हैं#वृत्ताकार फ़ंक्शंस के साथ तुलना:

$\exp {\big (}{-a}(x^{2}+p^{2}){\big )}\star \exp {\big (}{-b}(x^{2}+p^{2}){\big )}={\frac {1}{1+\hbar ^{2}ab}}\exp \left(-{\frac {a+b}{1+\hbar ^{2}ab}}(x^{2}+p^{2})\right),$

या

$\delta (x)\star \delta (p)={\frac {2}{h}}\exp \left(2i{\frac {xp}{\hbar }}\right),$

वगैरह।)

ऊर्जा ईजेनस्टेट वितरण को स्टारजेनस्टेट्स के रूप में जाना जाता है, ★-जेनस्टेट्स, स्टारजेनफ़ंक्शंस, या ★-जेन फ़ंक्शन, और संबंधित ऊर्जाओं को स्टारजेन मान या के रूप में जाना जाता है ★-जेनवैल्यू. इन्हें समय-स्वतंत्र श्रोडिंगर समीकरण के अनुरूप हल किया जाता है ★-जेनवैल्यू समीकरण,

$H\star W=E\cdot W,$

कहाँ H हैमिल्टनियन है, एक सादा चरण-अंतरिक्ष फ़ंक्शन, जो अक्सर शास्त्रीय हैमिल्टनियन के समान होता है।

समय विकास

चरण अंतरिक्ष वितरण का समय विकास लिउविले के प्रमेय (हैमिल्टनियन) के क्वांटम संशोधन द्वारा दिया गया है। यह सूत्र क्वांटम लिउविले समीकरण के घनत्व मैट्रिक्स संस्करण में विग्नर परिवर्तन को लागू करने से उत्पन्न होता है, वॉन न्यूमैन समीकरण.

इसके संबद्ध सितारा उत्पाद के साथ चरण अंतरिक्ष वितरण के किसी भी प्रतिनिधित्व में, यह है

${\frac {\partial f}{\partial t}}=-{\frac {1}{i\hbar }}\left(f\star H-H\star f\right),$

या, विशेष रूप से विग्नर फ़ंक्शन के लिए,

${\frac {\partial W}{\partial t}}=-\{\{W,H\}\}=-{\frac {2}{\hbar }}W\sin \left({\frac {\hbar }{2}}({\overset {_{\gets }}{\partial }}_{x}{\vec {\partial }}_{p}-{\overset {_{\gets }}{\partial }}_{p}{\vec {\partial }}_{x})\right)H=-\{W,H\}+O(\hbar ^{2}),$

जहां <नोविकी> · </nowiki> मोयल ब्रैकेट है, क्वांटम कम्यूटेटर का विग्नर ट्रांसफॉर्म है, जबकि { , } क्लासिकल पॉइसन ब्रैकेट है।

इससे पत्राचार सिद्धांत का एक संक्षिप्त चित्रण प्राप्त होता है: यह समीकरण स्पष्ट रूप से सीमा ħ → 0 में शास्त्रीय लिउविले समीकरण को कम कर देता है। प्रवाह के क्वांटम विस्तार में, हालांकि, चरण स्थान में बिंदुओं का घनत्व संरक्षित नहीं है; प्रायिकता द्रव विसरित और संकुचित प्रतीत होता है। इसलिए क्वांटम प्रक्षेपवक्र की अवधारणा यहां एक नाजुक मुद्दा है। क्वांटम चरण प्रवाह की गैर-स्थानीयता की सराहना करने के लिए, नीचे मोर्स क्षमता के लिए फिल्म देखें।

एन.बी. स्थानीयकरण पर अनिश्चितता सिद्धांत द्वारा लगाए गए प्रतिबंधों को देखते हुए, नील्स बोह्र ने सूक्ष्म पैमाने पर ऐसे प्रक्षेप पथों के भौतिक अस्तित्व को सख्ती से नकार दिया। औपचारिक चरण-अंतरिक्ष प्रक्षेप पथ के माध्यम से, विग्नर फ़ंक्शन की समय विकास समस्या को पथ-अभिन्न विधि का उपयोग करके कठोरता से हल किया जा सकता है और क्वांटम विशेषताओं की विधि, हालाँकि दोनों ही मामलों में गंभीर व्यावहारिक बाधाएँ हैं।

उदाहरण

सरल हार्मोनिक थरथरानवाला

Main article: quantum harmonic oscillator

विग्नर क्वासिप्रोबेबिलिटी वितरण F_n(u) सरल हार्मोनिक थरथरानवाला के लिए a) n = 0, b) n = 1, c) n = 5

विग्नर-वेइल प्रतिनिधित्व में एक स्थानिक आयाम में सरल हार्मोनिक ऑसिलेटर के लिए हैमिल्टनियन है

$H={\frac {1}{2}}m\omega ^{2}x^{2}+{\frac {p^{2}}{2m}}.$

★ll>-स्थैतिक विग्नर फ़ंक्शन के लिए जेनवैल्यू समीकरण फिर पढ़ता है

${\begin{aligned}H\star W&=\left({\frac {1}{2}}m\omega ^{2}x^{2}+{\frac {p^{2}}{2m}}\right)\star W\\&=\left({\frac {1}{2}}m\omega ^{2}\left(x+{\frac {i\hbar }{2}}{\vec {\partial }}_{p}\right)^{2}+{\frac {1}{2m}}\left(p-{\frac {i\hbar }{2}}{\vec {\partial }}_{x}\right)^{2}\right)W\\&=\left({\frac {1}{2}}m\omega ^{2}\left(x^{2}-{\frac {\hbar ^{2}}{4}}{\vec {\partial }}_{p}^{2}\right)+{\frac {1}{2m}}\left(p^{2}-{\frac {\hbar ^{2}}{4}}{\vec {\partial }}_{x}^{2}\right)\right)W\\&\quad {}+{\frac {i\hbar }{2}}\left(m\omega ^{2}x{\vec {\partial }}_{p}-{\frac {p}{m}}{\vec {\partial }}_{x}\right)W\\&=E\cdot W.\end{aligned}}$

Time evolution of combined ground and 1st excited state Wigner function for the simple harmonic oscillator. Note the rigid motion in phase space corresponding to the conventional oscillations in coordinate space.

Wigner function for the harmonic oscillator ground state, displaced from the origin of phase space, i.e., a coherent state. Note the rigid rotation, identical to classical motion: this is a special feature of the SHO, illustrating the correspondence principle. From the general pedagogy web-site.

सबसे पहले, इसके काल्पनिक भाग पर विचार करें ★-जेनवैल्यू समीकरण,

${\frac {\hbar }{2}}\left(m\omega ^{2}x{\vec {\partial }}_{p}-{\frac {p}{m}}{\vec {\partial }}_{x}\right)\cdot W=0$

इसका तात्पर्य यह है कि कोई भी लिख सकता है ★-एकल तर्क के कार्यों के रूप में बताता है:

$W(x,p)=F\left({\frac {1}{2}}m\omega ^{2}x^{2}+{\frac {p^{2}}{2m}}\right)\equiv F(u).$

चरों के इस परिवर्तन से इसका वास्तविक भाग लिखना संभव है ★-एक संशोधित लैगुएरे समीकरण के रूप में जेनवैल्यू समीकरण (हर्माइट बहुपद नहीं#हर्माइट कार्यों के विग्नर वितरण|हर्माइट का समीकरण!), जिसके समाधान में लैगुएरे बहुपद शामिल हैं: $F_{n}(u)={\frac {(-1)^{n}}{\pi \hbar }}L_{n}\left(4{\frac {u}{\hbar \omega }}\right)e^{-2u/\hbar \omega },$ ग्रोनवॉल्ड द्वारा प्रस्तुत,संबद्ध के साथ ★-मूल्य

$E_{n}=\hbar \omega \left(n+{\frac {1}{2}}\right).$

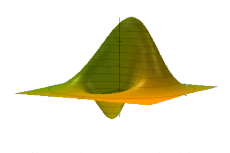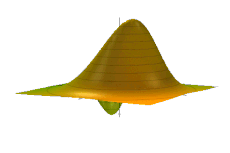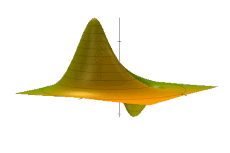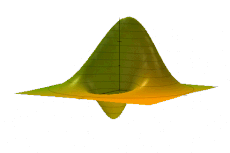
हार्मोनिक ऑसिलेटर के लिए, एक मनमाना विग्नर वितरण का समय विकास सरल है। एक शुरुआती W(x, p; t = 0) = F(u) दिए गए ऑसिलेटर हैमिल्टनियन द्वारा संचालित उपरोक्त विकास समीकरण द्वारा विकसित होता है, बस चरण स्थान में कठोरता से घूमते हुए,: $W(x,p;t)=W(m\omega x\cos \omega t-p\sin \omega t,p\cos \omega t+\omega mx\sin \omega t;0).$ आमतौर पर, ऊर्जा का एक उभार (या सुसंगत अवस्था)। E ≫ ħω एक स्थूल मात्रा का प्रतिनिधित्व कर सकता है और चरण स्थान में समान रूप से घूमते हुए एक शास्त्रीय वस्तु की तरह दिखाई दे सकता है, एक सादा यांत्रिक थरथरानवाला (एनिमेटेड आंकड़े देखें)। ऐसी वस्तुओं के सभी चरणों (t = 0 पर प्रारंभिक स्थिति) को एकीकृत करने से, एक सतत पलिसडे, उपरोक्त स्थिर के समान एक समय-स्वतंत्र कॉन्फ़िगरेशन उत्पन्न करता है ★-पुनर्स्थापित F(u), बड़े-एक्शन सिस्टम के लिए शास्त्रीय सीमा का एक सहज दृश्य।

मुक्त कण कोणीय संवेग

मान लीजिए कि एक कण प्रारंभ में क्वांटम यांत्रिकी में न्यूनतम अनिश्चित वेव पैकेट # गॉसियन वेवपैकेट में है, स्थिति और गति के अपेक्षित मूल्य दोनों चरण स्थान में मूल पर केंद्रित हैं। ऐसे राज्य के लिए विग्नर फ़ंक्शन स्वतंत्र रूप से प्रचारित होता है

$W(\mathbf {x} ,\mathbf {p} ;t)={\frac {1}{(\pi \hbar )^{3}}}\exp {\left(-\alpha ^{2}r^{2}-{\frac {p^{2}}{\alpha ^{2}\hbar ^{2}}}\left(1+\left({\frac {t}{\tau }}\right)^{2}\right)+{\frac {2t}{\hbar \tau }}\mathbf {x} \cdot \mathbf {p} \right)}~,$

जहां α गॉसियन की प्रारंभिक चौड़ाई का वर्णन करने वाला एक पैरामीटर है, और τ = m/α²ħ.

प्रारंभ में, स्थिति और संवेग असंबद्ध हैं। इस प्रकार, 3 आयामों में, हम उम्मीद करते हैं कि स्थिति और संवेग सदिश एक-दूसरे के समानांतर होने की संभावना से दोगुना होंगे।

हालाँकि, जैसे-जैसे राज्य विकसित होता है, स्थिति और गति तेजी से सहसंबद्ध हो जाती है, क्योंकि स्थिति में मूल से दूर वितरण के कुछ हिस्सों तक पहुँचने के लिए एक बड़ी गति की आवश्यकता होती है: स्पर्शोन्मुख रूप से,

$W\longrightarrow {\frac {1}{(\pi \hbar )^{3}}}\exp \left[-\alpha ^{2}\left(\mathbf {x} -{\frac {\mathbf {p} t}{m}}\right)^{2}\right]\,.$

(यह सापेक्ष निचोड़ित सुसंगत अवस्था | निचोड़ना समन्वय स्थान में मुक्त तरंग पैकेट के प्रसार को दर्शाता है।)

वास्तव में, यह दिखाना संभव है कि मानक के अनुरूप कण की गतिज ऊर्जा केवल स्पर्शोन्मुख रेडियल हो जाती है अभिविन्यास स्वतंत्रता को निर्दिष्ट करते हुए ग्राउंड-स्टेट गैर-शून्य कोणीय गति की क्वांटम-मैकेनिकल धारणा:

$K_{\text{rad}}={\frac {\alpha ^{2}\hbar ^{2}}{2m}}\left({\frac {3}{2}}-{\frac {1}{1+(t/\tau )^{2}}}\right)$

$K_{\text{ang}}={\frac {\alpha ^{2}\hbar ^{2}}{2m}}{\frac {1}{1+(t/\tau )^{2}}}~.$

मोर्स क्षमता

मोर्स क्षमता का उपयोग डायटोमिक अणु की कंपन संरचना का अनुमान लगाने के लिए किया जाता है।

मोर्स क्षमता U(x) = 20(1 - e) का विग्नर क्वासिप्रोबेबिलिटी वितरण समय-विकास^−0.16x)²परमाणु इकाइयों में (ए.यू.)। ठोस रेखाएँ हैमिल्टनियन यांत्रिकी H(x, p) = p के स्तर सेट का प्रतिनिधित्व करती हैं²/2 + U(x).

क्वांटम टनलिंग

क्वांटम टनलिंग एक विशिष्ट क्वांटम प्रभाव है जहां एक क्वांटम कण, ऊपर उड़ने के लिए पर्याप्त ऊर्जा नहीं होने के बावजूद, एक बाधा से गुजरता है। यह प्रभाव शास्त्रीय यांत्रिकी में मौजूद नहीं है।

संभावित अवरोध U(x) = 8e के माध्यम से क्वांटम टनलिंग के लिए विग्नर क्वासिप्रोबेबिलिटी वितरण^−0.25x2परमाणु इकाइयों में (ए.यू.)। ठोस रेखाएँ हैमिल्टनियन यांत्रिकी H(x, p) = p के स्तर सेट का प्रतिनिधित्व करती हैं²/2 + U(x).

चतुर्थक विभव

संभावित U(x) = 0.1x के लिए विग्नर क्वासिप्रोबेबिलिटी वितरण समय विकास⁴परमाणु इकाइयों में (ए.यू.)। ठोस रेखाएँ हैमिल्टनियन यांत्रिकी H(x, p) = p के स्तर सेट का प्रतिनिधित्व करती हैं²/2 + U(x).

श्रोडिंगर बिल्ली स्थिति

#सरल हार्मोनिक ऑसिलेटर हैमिल्टनियन के माध्यम से विकसित होने वाले दो हस्तक्षेप करने वाले सुसंगत राज्यों का विग्नर फ़ंक्शन। संबंधित गति और समन्वय अनुमानों को दाईं ओर और चरण स्थान प्लॉट के नीचे प्लॉट किया गया है।