जियोमीट्रिक श्रंखला

ज्यामितीय श्रृंखला 1/4 + 1/16 + 1/64 + 1/256 + ... को बैंगनी वर्गों के क्षेत्रों के रूप में दर्शाया गया है। प्रत्येक बैंगनी वर्ग का क्षेत्रफल अगले बड़े वर्ग (1/2×)।1/2 = 1/4, 1/4×1/4 = 1/16, आदि) का 1/4 है। बैंगनी वर्गों के क्षेत्रफल का योग बड़े वर्ग के क्षेत्रफल का एक तिहाई है।

एक अन्य ज्यामितीय श्रृंखला (गुणांक a = 4/9 और सामान्य अनुपात r = 1/9) को बैंगनी वर्गों के क्षेत्रों के रूप में दर्शाया गया है। कुल बैंगनी क्षेत्र S = a / (1 - r) = (4/9) / (1 - (1/9)) = 1/2 है, जिसकी पुष्टि यह देखकर की जा सकती है कि इकाई वर्ग को अनंत में विभाजित किया गया है L-आकार के क्षेत्रों की संख्या, जिनमें से प्रत्येक में चार बैंगनी वर्ग और चार पीले वर्ग हैं, जो आधा बैंगनी है।

गणित में, एक ज्यामितीय श्रृंखला अनंत संख्याओं का योग है जिसमें क्रमिक पदों के मध्य एक स्थिर अनुपात होता है। उदाहरण के लिए, श्रृंखला

${\frac {1}{2}}\,+\,{\frac {1}{4}}\,+\,{\frac {1}{8}}\,+\,{\frac {1}{16}}\,+\,\cdots$

ज्यामितीय है, क्योंकि प्रत्येक क्रमिक पद पिछले पद को $1/2$ से गुणा करके प्राप्त किया जा सकता है। सामान्य तौर पर, एक ज्यामितीय श्रृंखला को इस प्रकार $a+ar+ar^{2}+ar^{3}+...$ लिखा जाता है, जहाँ $a$ प्रत्येक पद का गुणांक है और $r$ आसन्न पदों के मध्य सामान्य अनुपात है। गणना के प्रारंभिक विकास में ज्यामितीय श्रृंखला की महत्वपूर्ण भूमिका थी, इसका उपयोग सम्पूर्ण गणित में किया जाता है और यह टेलर श्रृंखला, सम्मिश्र फूरियर श्रृंखला और आव्यूह घातांक जैसे प्रायः उपयोग किए जाने वाले गणितीय उपकरणों के परिचय के रूप में कार्य कर सकता है।

नाम ज्यामितीय श्रृंखला इंगित करती है कि प्रत्येक पद अपने दो निकटवर्ती पदों का ज्यामितीय माध्य है, उसी तरह जैसे नाम अंकगणितीय श्रृंखला इंगित करता है कि प्रत्येक पद अपने दो निकटवर्ती पदों का अंकगणितीय माध्य है। ज्यामितीय श्रृंखला (गणित) पदों के अनुक्रम (बिना किसी जोड़ के) को ज्यामितीय अनुक्रम या ज्यामितीय प्रगति कहा जाता है।

निरूपण

गुणांक a

ज्यामितीय श्रृंखला 1 + r + r² + r³ ...के पहले नौ पद |r| < 1 की सीमा के भीतर फलन (लाल, हरा, नीला, लाल, हरा, नीला, क्रम में रंगे हुए) के रूप में खींचे गए हैं। संवृत रूप वाली ज्यामितीय श्रृंखला 1 / (1 - r) काली धराशायी रेखा है।

ज्यामितीय श्रृंखला a + ar + ar² + ar³+...विस्तारित रूप में लिखा गया है। ज्यामितीय श्रृंखला में प्रत्येक गुणांक समान है। इसके विपरीत, विस्तारित रूप में a₀ + a₁r + a₂r² + a₃r³ + ... के रूप में लिखी गई घात श्रृंखला में गुणांक ai है जो पद दर पद भिन्न हो सकता है। दूसरे शब्दों में, ज्यामितीय श्रृंखला घात श्रृंखला की एक विशेष स्थिति है। विस्तारित रूप में किसी ज्यामितीय श्रृंखला का पहला पद उस ज्यामितीय श्रृंखला का गुणांक a है।

ज्यामितीय श्रृंखला के विस्तारित रूप के अतिरिक्त, ज्यामितीय श्रृंखला का एक जनक रूपभी लिखा गया है।

$\sum _{k=0}^{\infty }ar^{k}$

और ज्यामितीय श्रृंखला का एक संवृत रूप इस प्रकार लिखा गया है;

${\frac {a}{1-r}}{\text{ for }}|r|<1.$

विस्तारित रूप से संवृत रूप की व्युत्पत्ति इस आलेख के § योग अनुभाग में दिखाई गई है। हालाँकि, उस व्युत्पत्ति के बिना भी, परिणाम की पुष्टि लंबे विभाजन के साथ की जा सकती है: a को (1 - r) से विभाजित करने पर परिणाम a + ar + ar² + ar³ + ... प्राप्त होता है, जो कि ज्यामितीय श्रृंखला का विस्तारित रूप है।

अंकन में प्रायः श्रृंखला को योग s के बराबर व्यवस्थित करना और ज्यामितीय श्रृंखला के साथ कार्य करना एक सुविधा होती है।

s = a + ar + ar² + ar³ + ar⁴ + ... अपने सामान्यीकृत रूप में,

s / a = 1 + r + r² + r³ + r⁴ + ... या इसके सामान्यीकृत सदिश रूप में,

s / a = [1 1 1 1 1 ...][1 r r² r³ r⁴ ...]^T या इसके सामान्यीकृत आंशिक श्रृंखला रूप में,

s_n / a = 1 + r + r² + r³ + r⁴ + ... + rⁿ, जहां n आंशिक योग s_n में सम्मिलित अंतिम पद की घात (या कोटि) है।

गुणांकों में से किसी एक को भी गुणांक a के अतिरिक्त किसी अन्य चीज़ में बदलने से परिणामी फलनों का योग |r| < 1 सीमा के भीतर a / (1 − r) के अतिरिक्त किसी अन्य फलन में बदल जाएगा। एक तरफ, गुणांकों में एक विशेष रूप से उपयोगी परिवर्तन टेलर श्रृंखला द्वारा परिभाषित किया गया है, जो वर्णन करता है कि गुणांकों को कैसे बदला जाए ताकि फलनों का योग किसी भी उपयोगकर्ता द्वारा चयनित, एक सीमा के भीतर पर्याप्त रूप से सुचारू फलन में परिवर्तित हो जाए।

सामान्य अनुपात r

r=1/2 और a=1/2 के साथ ज्यामितीय श्रृंखला का अभिसरण।

r=1/2 और a=1 के साथ ज्यामितीय श्रृंखला का अभिसरण।

ज्यामितीय श्रृंखला 1 + r + r² + r³ + ... के पहले 11 पदों को जोड़े जाने पर श्रेणी -1 < r < -0.5 के भीतर फलनों के संचयी योग का निकट चित्रण अप दृश्य है। ज्यामितीय श्रृंखला 1 / (1 - r) लाल धराशायी रेखा है।

सम्मिश्र ज्यामितीय श्रृंखला (गुणांक a = 1 और सामान्य अनुपात r =0.5 e^iω₀t) एक वृत्त में परिवर्तित होती है। एनीमेशन में, ज्यामितीय श्रृंखला के प्रत्येक पद को दो बार सदिश के रूप में खींचा जाता है: एक बार मूल पर और फिर शीर्ष पुच्छ सदिश योग के भीतर जो वृत्त में परिवर्तित होता है। वृत्त वास्तविक अक्ष को 2 (= 1/(1-1/2) जब θ = 0) पर और 2/3 (= 1/(1-(-1/2)) पर जब θ = 180 डिग्री) पर प्रतिच्छेद करता है।

ज्यामितीय श्रृंखला a + ar + ar² + ar³+... केवल दो मापदंडों द्वारा परिभाषित एक अनंत श्रृंखला है: गुणांक a और सामान्य अनुपात r है। सामान्य अनुपात r श्रृंखला में किसी भी पद का पिछले पद से अनुपात है या समकक्ष, सामान्य अनुपात r पद गुणक है जिसका उपयोग श्रृंखला में अगले पद की गणना के लिए किया जाता है। निम्न तालिका कई ज्यामितीय श्रृंखलाएँ दर्शाती है:

a	r	उदाहरण शृंखला
4	10	4 + 40 + 400 + 4000 + 40,000 + ···
3	1	3 + 3 + 3 + 3 + 3 + ···
1	2/3	1 + 2/3 + 4/9 + 8/27 + 16/81 + ···
1/2	1/2	1/2 + 1/4 + 1/8 + 1/16 + 1/32 + ···
9	1/3	9 + 3 + 1 + 1/3 + 1/9 + ···
7	1/10	7 + 0.7 + 0.07 + 0.007 + 0.0007 + ···
1	−1/2	1 − 1/2 + 1/4 − 1/8 + 1/16 − 1/32 + ···
3	−1	3 − 3 + 3 − 3 + 3 − ···

ज्यामितीय श्रृंखला का अभिसरण सामान्य अनुपात r के मान पर निर्भर करता है:

• यदि |r| <1, श्रृंखला के पद सीमा में शून्य तक पहुंचते हैं (परिमाण में छोटे और छोटे होते जाते हैं), और श्रृंखला योग a / (1 - r) में परिवर्तित हो जाती है।
• यदि |r| = 1, श्रृंखला अभिसरित नहीं होती है। जब r = 1 होता है, तो श्रृंखला के सभी पद समान होते हैं और श्रृंखला अनंत होती है। जब r = −1, पद बारी-बारी से दो मान लेते हैं (उदाहरण के लिए, 2, −2, 2, −2, 2,... )। पदों का योग दो मानों के मध्य दोलन करता है (उदाहरण के लिए, 2, 0, 2, 0, 2,... )। यह एक अलग प्रकार का विचलन है। उदाहरण के लिए ग्रैंडी की श्रृंखला: 1 − 1 + 1 − 1 + ···· देखें।
• यदि |r| > 1, श्रृंखला के पद परिमाण में बड़े और बड़े होते जाते हैं। पदों का योग भी बड़ा होता जाता है और श्रृंखला योग में परिवर्तित नहीं होती है (श्रृंखला अपसारित हो जाती है)।

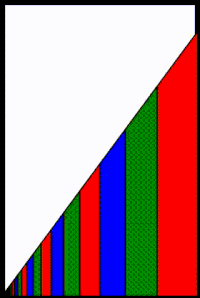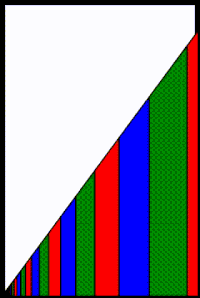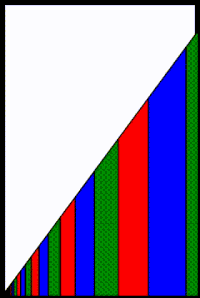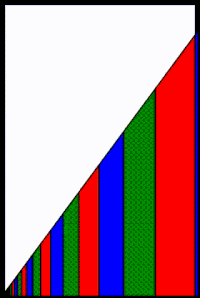
अभिसरण की दर सामान्य अनुपात r के मान पर भी निर्भर करती है। विशेष रूप से, जैसे-जैसे r, 1 या −1 के निकट पहुंचता है, अभिसरण की दर धीमी हो जाती है। उदाहरण के लिए, a = 1 के साथ ज्यामितीय श्रृंखला 1 + r + r² + r³ + ... है और 1 / (1 - r) में परिवर्तित हो जाती है जब |r| < 1 है। हालाँकि, जैसे-जैसे r, 1 के निकट पहुंचता है, अभिसरण के लिए आवश्यक पदों की संख्या अनंत तक पहुंचती है क्योंकि a / (1 - r) अनंत तक पहुंचता है और श्रृंखला का प्रत्येक पद एक से कम या उसके बराबर होता है। इसके विपरीत, जैसे-जैसे r, −1 के निकट पहुंचता है, ज्यामितीय श्रृंखला के पहले कई पदों का योग 1/2 में परिवर्तित होने लगता है, लेकिन थोड़ा ऊपर या नीचे हो जाता है, यह इस पर निर्भर करता है कि सबसे हाल ही में जोड़े गए पद में r की घात है या नहीं, जो कि सम या विषम है। r = −1 के निकट फ़्लिपिंग व्यवहार को आसन्न छवि में चित्रित किया गया है जिसमें a = 1 और |r| < 1 के साथ ज्यामितीय श्रृंखला के पहले 11 पद दिखाए गए हैं।

सामान्य अनुपात r और गुणांक a भी ज्यामितीय प्रगति को परिभाषित करते हैं, जो कि ज्यामितीय श्रृंखला के पदों की एक सूची है परन्तु बिना जोड़ के है। इसलिए ज्यामितीय श्रृंखला a + ar + ar² + ar³ +... में ज्यामितीय प्रगति होती है (जिसे ज्यामितीय अनुक्रम भी कहा जाता है) a, ar, ar², ar³, ... ज्यामितीय प्रगति - जितनी सरल है - प्राकृतिक घटनाओं की एक आश्चर्यजनक संख्या का प्रतिरूप बनाती है:

• ब्रह्मांड के विस्तार जैसे कुछ सबसे बड़े अवलोकनों से जहां सामान्य अनुपात r को हबल के स्थिरांक द्वारा परिभाषित किया गया है,
• कुछ सबसे छोटे अवलोकनों जैसे कि रेडियोधर्मी कार्बन-14 परमाणुओं का क्षय जहां सामान्य अनुपात आर को कार्बन-14 के आधे जीवन से परिभाषित किया जाता है।

एक तरफ, सामान्य अनुपात r एक सम्मिश्र संख्या हो सकती है जैसे |r|e^iθ जहाँ |r| सदिश का परिमाण (या लंबाई) है, θ सम्मिश्र समतल में सदिश का कोण (या अभिविन्यास) है और i²= -1 है। एक सामान्य अनुपात |r|e^iθ के साथ, ज्यामितीय श्रृंखला का विस्तारित रूप a + a|r|e^iθ + a|r|²e^i2θ + a|r|³e^i3θ + ... है। कोण θ को समय के साथ रैखिक रूप से बढ़ते हुए मॉडलिंग करना कुछ कोणीय आवृत्ति ω₀ की दर (दूसरे शब्दों में, प्रतिस्थापन θ = ω₀tबनाते हुए), ज्यामितीय श्रृंखला का विस्तारित रूप a + a|r|e^iω₀t + a|r|²e^i2ω₀t + a|r|³e^i3ω₀t + ... हो जाता है। जहां पहला पद लंबाई का एक सदिश है जो बिल्कुल नहीं घूमता है और अन्य सभी पद मौलिक कोणीय आवृत्ति ω₀ के गुणवृत्ति पर घूमने वाले विभिन्न लंबाई के सदिश हैं। व्यवरोध |r|<1 एक वृत्त का पता लगाने में अलग-अलग गति से घूमने वाले विभिन्न लंबाई के सदिशों की इस अनंत संख्या को समन्वयित करने के लिए पर्याप्त है, जैसा कि आसन्न वीडियो में दर्शाया गया है। टेलर श्रृंखला बताती है कि गुणांकों को कैसे बदला जाए ताकि श्रृंखला एक सीमा के भीतर उपयोगकर्ता द्वारा चयनित पर्याप्त सुचारू फलन में परिवर्तित हो जाए, फूरियर श्रृंखला बताती है कि गुणांकों को कैसे बदला जाए (जो सदिशों के प्रारंभिक कोणों को निर्दिष्ट करने के लिए सम्मिश्र संख्याएँ भी हो सकती हैं) इसलिए श्रृंखला उपयोगकर्ता द्वारा चयनित आवधिक फलन में परिवर्तित हो जाती है।

योग

एक ज्यामितीय श्रृंखला के पहले n पदों का योग, r ^n-1 पद तक और इसमें सम्मिलित, संवृत-रूप सूत्र द्वारा दिया गया है:

$${\begin{aligned}s_{n}&=ar^{0}+ar^{1}+\cdots +ar^{n-1}\\&=\sum _{k=0}^{n-1}ar^{k}=\sum _{k=1}^{n}ar^{k-1}\\&={\begin{cases}a\left({\frac {1-r^{n}}{1-r}}\right),{\text{ for }}r\neq 1\\an,{\text{ for }}r=1\end{cases}}\end{aligned}}$$

जहाँ r सामान्य अनुपात है। आंशिक योग, s_n सूत्र को निम्नानुसार कई स्वयं-समान शब्दों को घटाकर प्राप्त किया जा सकता है:

$${\begin{aligned}s_{n}&=ar^{0}+ar^{1}+\cdots +ar^{n-1},\\rs_{n}&=ar^{1}+ar^{2}+\cdots +ar^{n},\\s_{n}-rs_{n}&=ar^{0}-ar^{n},\\s_{n}\left(1-r\right)&=a\left(1-r^{n}\right),\\s_{n}&=a\left({\frac {1-r^{n}}{1-r}}\right),{\text{ for }}r\neq 1.\end{aligned}}$$

जैसे-जैसे n अनंत की ओर बढ़ता है, श्रृंखला के अभिसरण के लिए r का निरपेक्ष मान एक से कम होना चाहिए। तो योग बन जाता है;

$${\begin{aligned}s&=a+ar+ar^{2}+ar^{3}+ar^{4}+\cdots \\&=\sum _{k=0}^{\infty }ar^{k}=\sum _{k=1}^{\infty }ar^{k-1}\\&={\frac {a}{1-r}},{\text{ for }}|r|<1.\end{aligned}}$$

सूत्र सम्मिश्र r के लिए भी अनुप्रयुक्त होता है, इसी प्रतिबंध के साथ कि r मापांक दृढता से एक से कम है।

एक तरफ, यह प्रश्न कि क्या एक अनंत श्रृंखला अभिसरण करती है, मूल रूप से दो मानों के मध्य की दूरी के विषय में एक प्रश्न है: पर्याप्त पदों को देखते हुए, क्या आंशिक योग का मान यादृच्छिक रूप से उस परिमित मान के निकट हो जाता है जो वह आ रहा है? ज्यामितीय श्रृंखला के संवृत रूप की उपरोक्त व्युत्पत्ति में, दो मानों के मध्य की दूरी की व्याख्या संख्या रेखा पर उनके स्थानों के मध्य की दूरी है। यह दो मानों के मध्य की दूरी की सबसे सामान्य व्याख्या है। हालाँकि, p-एडिक मापीय, जो आधुनिक संख्या सिद्धांत में एक महत्वपूर्ण धारणा बन गई है, दूरी की एक परिभाषा प्रदान करती है जैसे कि ज्यामितीय श्रृंखला 1 + 2 + 4 + 8 + ..., a = 1 और r = 2 के साथ वास्तव में होती है। a / (1 - r) = 1 / (1 - 2) = -1 में अभिसरण करें, भले ही r विशिष्ट अभिसरण सीमा |r| <1 से बाहर हो।

अभिसरण का प्रमाण

हम यह सिद्ध कर सकते हैं कि ज्यामितीय श्रृंखला एक ज्यामितीय प्रगति के लिए योग सूत्र का उपयोग करके अभिसरण करती है:

$${\begin{aligned}1+r+r^{2}+r^{3}+\cdots \ &=\lim _{n\to \infty }\left(1+r+r^{2}+\cdots +r^{n}\right)\\&=\lim _{n\to \infty }{\frac {1-r^{n+1}}{1-r}}.\end{aligned}}$$

दूसरी समानता सत्य है क्योंकि यदि $|r|<1,$ तब $r^{n+1}\to 0$ जैसे $n\to \infty$ और

$${\begin{aligned}\left(1+r+r^{2}+\cdots +r^{n}\right)(1-r)&=\left((1-r)+(r-r^{2})+(r^{2}-r^{3})+\dots +(r^{n}-r^{n+1})\right)\\&=1+(-r+r)+(-r^{2}+r^{2})+\dots +(-r^{n}+r^{n})-r^{n+1}\\&=1-r^{n+1}.\end{aligned}}$$

वैकल्पिक रूप से, अभिसरण की एक ज्यामितीय व्याख्या आसन्न चित्र में दिखाई गई है। सफ़ेद त्रिभुज का क्षेत्रफल श्रृंखला शेषफल = s − s_n = arⁿ⁺¹ / (1 − r) है। आंशिक श्रृंखला में प्रत्येक अतिरिक्त पद जोड़े गए पद का प्रतिनिधित्व करने वाले समलम्ब चतुर्भुज के क्षेत्रफल द्वारा उस सफेद त्रिभुज के शेष भाग का क्षेत्रफल कम कर देता है। समलम्बाकार क्षेत्र (अर्थात, पदों के मान) उत्तरोत्तर पतले और छोटे होते जाते हैं और मूल बिंदु के निकट होते जाते हैं। सीमा में, जैसे-जैसे समलंब की संख्या अनंत तक पहुंचती है, सफेद त्रिकोण शेष लुप्त हो जाते है क्योंकि यह समलंब से भर जाता है और इसलिए s_n, s में परिवर्तित हो जाता है, बशर्ते |r|<1 हैं। इसके विपरीत, यदि |r|>1, तो श्रृंखला की पदों का प्रतिनिधित्व करने वाले समलम्बाकार क्षेत्र मूल से उत्तरोत्तर व्यापक और लम्बे और दूर होते जाते हैं, मूल में परिवर्तित नहीं होते हैं और एक श्रृंखला के रूप में परिवर्तित नहीं होते हैं।

अभिसरण की दर

सामान्य अनुपात r = -1/2 और गुणांक a = 1 के साथ वैकल्पिक ज्यामितीय श्रृंखला को परिवर्तित करना। (शीर्ष) धनात्मक और ऋणात्मक क्षेत्रों को वैकल्पिक करना। (मध्य) आसन्न क्षेत्रों के जुड़ने से उत्पन्न अंतराल। (नीचे) अलग-अलग समलंब की ऊंचाई को चौड़ा करने और घटाने से भरे गए अंतराल।

यह जानने के बाद कि एक श्रृंखला अभिसरण करती है, कुछ अनुप्रयोग ऐसे हैं जिनमें यह जानना भी महत्वपूर्ण है कि श्रृंखला कितनी तीव्रता से अभिसरण करती है। ज्यामितीय श्रृंखला के लिए, अभिसरण दर का एक सुविधाजनक माप यह है कि आंशिक श्रृंखला के अंतिम पद के कारण पिछली श्रृंखला का शेष कितना कम हो जाता है। दिया गया है कि अंतिम पद arⁿ है और पिछली श्रृंखला का शेषफल s - s_n-1 = arⁿ / (1 - r) है, ज्यामितीय श्रृंखला की अभिसरण दर का यह माप arⁿ / (arⁿ / (1 - r)) = 1 - r है, यदि 0 ≤ r < 1 हैं।

यदि r < 0, तो ज्यामितीय श्रृंखला में आसन्न पद धनात्मक और ऋणात्मक होने के मध्य वैकल्पिक होते हैं। एक अभिसारी प्रत्यावर्ती ज्यामितीय श्रृंखला की एक ज्यामितीय व्याख्या आसन्न आरेख में दिखाई गई है जिसमें ऋणात्मक पदों के क्षेत्र x अक्ष के नीचे दिखाए गए हैं। प्रत्येक धनात्मक क्षेत्र को उसके ऋणात्मक छोटे क्षेत्र निकटवर्ती के साथ जोड़ने और सारांशित करने से अंतराल द्वारा अलग किए गए अनतिव्यापी समलंब प्राप्त होते हैं। अंतराल को दूर करने के लिए, प्रत्येक समलंब को केवल सबसे दाहिनी ओर 1 - |r| के बजाय मूल त्रिभुज क्षेत्र के सबसे दाहिनी ओर 1 - r² को समाविष्ट करने के लिए चौड़ा करें। हालाँकि, इस व्यापक परिवर्तन के पर्यन्त समान समलम्बाकार क्षेत्रों को बनाए रखने के लिए, क्रम गणक की आवश्यकता है: स्केल*(1 - आर²) = (1 - |r|), या पैमाना = (1 - |r|) / (1 - r²) = (1 + r) / (1 - r²) = (1 + r) / ((1 + r)(1 - r)) = 1 / (1 - r) जहां -1 < r ≤ 0 है। ध्यान दें कि क्योंकि r < 0 यह पैमाना विभाजन अंतराल को भरने के लिए अलग किए गए समलंब के आयाम को कम करता है। इसके विपरीत, स्थिति r > 0 के लिए समान पैमाना 1 / (1 - r) ओवरलैप किए गए क्षेत्रों की हानि को ध्यान में रखते हुए अनतिव्यापी समलंब के आयाम को बढ़ाता है।

अंतरालों को हटाने के साथ, एक अभिसारी प्रत्यावर्ती ज्यामितीय श्रृंखला में पदों के जोड़े एक अभिसारी (गैर-वैकल्पिक) ज्यामितीय श्रृंखला बन जाते हैं, जिसमें पदों के युग्म के लिए सामान्य अनुपात r² और गुणांक a = 1 / (1 - r) होता है। अंतराल पूरक और आंशिक श्रृंखला की घात (अर्थात, उच्चतम चालित पद) को n के बजाय m कहा जाता है ताकि इस बात पर जोर दिया जा सके कि पदों को जोड़ा गया है। r > 0 स्थिति के समान, r < 0 अभिसरण दर = ar^2m / (s - s_m-1) = 1 - r², जो एक गैर-वैकल्पिक ज्यामितीय श्रृंखला के अभिसरण दर के समान है यदि इसके पद समान रूप से जोड़े गए हों। इसलिए, अभिसरण दर n या m पर निर्भर नहीं करती है और सम्भवतः अधिक आश्चर्य की बात है, सामान्य अनुपात के संकेत पर निर्भर नहीं करती है। एक परिप्रेक्ष्य जो अभिसरण की परिवर्तनीय दर को समझाने में सहायता करता है जो r = 0 के विषय में सममित है, वह यह है कि आंशिक श्रृंखला का प्रत्येक युग्म पद r = 1 पर अनंत योग में एक सीमित योगदान देता है और आंशिक श्रृंखला का प्रत्येक युग्म पद r = -1 पर अनंत प्रवणता तक एक सीमित योगदान देता है।

व्युत्पत्ति

परिमित श्रृंखला

इस सूत्र को प्राप्त करने के लिए, पहले एक सामान्य ज्यामितीय श्रृंखला इस प्रकार लिखें:

$$\sum _{k=1}^{n}ar^{k-1}=ar^{0}+ar^{1}+ar^{2}+ar^{3}+\cdots +ar^{n-1}.$$

हम उपरोक्त समीकरण के दोनों पक्षों को 1 - r से गुणा करके इस योग के लिए एक सरल सूत्र प्राप्त कर सकते हैं और हम देखेंगे कि

$${\begin{aligned}(1-r)\sum _{k=1}^{n}ar^{k-1}&=(1-r)\left(ar^{0}+ar^{1}+ar^{2}+ar^{3}+\cdots +ar^{n-1}\right)\\&=ar^{0}+ar^{1}+ar^{2}+ar^{3}+\cdots +ar^{n-1}-ar^{1}-ar^{2}-ar^{3}-\cdots -ar^{n-1}-ar^{n}\\&=a-ar^{n}\end{aligned}}$$

चूँकि अन्य सभी पद निरसित हो जाते हैं। यदि r ≠ 1 है, तो हम एक ज्यामितीय श्रृंखला के लिए सुविधाजनक सूत्र प्राप्त करने के लिए उपरोक्त को पुनर्व्यवस्थित कर सकते हैं जो n पदों के योग की गणना करता है:

$$\sum _{k=1}^{n}ar^{k-1}={\frac {a(1-r^{n})}{1-r}}.$$

संबंधित सूत्र

यदि किसी को योग का प्रारंभ k=1 या 0 से नहीं, बल्कि किसी भिन्न मान से करना हो, तो मान लीजिए $m$, तब

$${\begin{aligned}\sum _{k=m}^{n}ar^{k-1}&={\begin{cases}{\frac {a(r^{m-1}-r^{n})}{1-r}}&{\text{if }}r\neq 1\\a(n-m+1)&{\text{if }}r=1\end{cases}}\\\sum _{k=m}^{n}ar^{k}&={\begin{cases}a(n-m+1)&{\text{if }}r=1\\{\frac {a(r^{m}-r^{n+1})}{1-r}}&{\text{if }}r\neq 1\end{cases}}\end{aligned}}$$

इस सूत्र को $r$ के संबंध में विभेदित करने से हमें रूप के योग के लिए सूत्र प्राप्त करने की अनुमति मिलती है।

$$G_{s}(n,r):=\sum _{k=0}^{n}k^{s}r^{k}.$$

उदाहरण के लिए:

$${\frac {d}{dr}}\sum _{k=0}^{n}r^{k}=\sum _{k=1}^{n}kr^{k-1}={\frac {1-r^{n+1}}{(1-r)^{2}}}-{\frac {(n+1)r^{n}}{1-r}}.$$

एक ज्यामितीय श्रृंखला के लिए जिसमें केवल $r$ की सम घातें हों, $1-r^{2}$ से गुणा करें:

$${\begin{aligned}(1-r^{2})\sum _{k=0}^{n}ar^{2k}&=a-ar^{2n+2}\\\sum _{k=0}^{n}ar^{2k}&={\frac {a(1-r^{2n+2})}{1-r^{2}}}\end{aligned}}$$

समान रूप से, $r^{2}$ को सामान्य अनुपात के रूप में लें और मानक सूत्रीकरण का उपयोग करें।

$r$ की केवल विषम घातो वाली श्रृंखला के लिए:

$${\begin{aligned}(1-r^{2})\sum _{k=0}^{n}ar^{2k+1}&=ar-ar^{2n+3}\\\sum _{k=0}^{n}ar^{2k+1}&={\frac {ar(1-r^{2n+2})}{1-r^{2}}}&={\frac {a(r-r^{2n+3})}{1-r^{2}}}\end{aligned}}$$

सामान्यीकृत योग के लिए एक सटीक सूत्र $G_{s}(n,r)$ जब $s\in \mathbb {N}$ दूसरे प्रकार के स्टर्लिंग संख्याओं द्वारा विस्तारित किया गया है।

$$G_{s}(n,r)=\sum _{j=0}^{s}\left\lbrace {s \atop j}\right\rbrace x^{j}{\frac {d^{j}}{dx^{j}}}\left[{\frac {1-x^{n+1}}{1-x}}\right].$$

अनंत शृंखला

एक अनंत ज्यामितीय श्रृंखला एक अनंत श्रृंखला होती है जिसके क्रमिक पदों का एक सामान्य अनुपात होता है। ऐसी श्रृंखला अभिसरित होती है यदि और केवल यदि सामान्य अनुपात का निरपेक्ष मान एक (|r| <1) से कम हो। इसके मान की गणना परिमित योग सूत्र से की जा सकती है;

$$\sum _{k=0}^{\infty }ar^{k}=\lim _{n\to \infty }{\sum _{k=0}^{n}ar^{k}}=\lim _{n\to \infty }{\frac {a(1-r^{n+1})}{1-r}}={\frac {a}{1-r}}-\lim _{n\to \infty }{\frac {ar^{n+1}}{1-r}}$$

एनीमेशन, ज्यामितीय प्रगति $\sum \limits _{k=0}^{n}q^{k}$ (लाल रेखा), इसके योग तक ${1 \over 1-q}$ (नीली रेखा), $|q|<1$ के लिए आंशिक योगों का अभिसरण दर्शा रहा है।

आरेख ज्यामितीय श्रृंखला 1 + 1/2 + 1/4 + 1/8 + ⋯ दिखा रहा है जो 2 में परिवर्तित होती है।

तब से:

$$r^{n+1}\to 0{\mbox{ as }}n\to \infty {\mbox{ when }}|r|<1.$$

तब:

$$\sum _{k=0}^{\infty }ar^{k}={\frac {a}{1-r}}-0={\frac {a}{1-r}}$$

एक श्रृंखला के लिए जिसमें केवल $r$ की सम घातें हों,

$$\sum _{k=0}^{\infty }ar^{2k}={\frac {a}{1-r^{2}}}$$

और केवल विषम घातो के लिए,

$$\sum _{k=0}^{\infty }ar^{2k+1}={\frac {ar}{1-r^{2}}}$$

ऐसे स्थितियों में जहां योग k = 0 से प्रारंभ नहीं होता है,

$$\sum _{k=m}^{\infty }ar^{k}={\frac {ar^{m}}{1-r}}$$

ऊपर दिए गए सूत्र केवल |r| < 1 के लिए मान्य हैं। बाद वाला सूत्र प्रत्येक बानाच बीजगणित में मान्य है, जब तक कि r का मान एक से कम है, और p-एडिक संख्याओं के क्षेत्र में भी यदि |r|_p< 1, जैसा कि एक सीमित योग के स्थिति में होता है, हम संबंधित योगों के लिए सूत्रों की गणना करने के लिए अंतर कर सकते हैं।

उदाहरण के लिए,

$${\frac {d}{dr}}\sum _{k=0}^{\infty }r^{k}=\sum _{k=1}^{\infty }kr^{k-1}={\frac {1}{(1-r)^{2}}}$$

यह सूत्र केवल |r| < 1 के लिए भी कार्य करता है। |r| < 1 के लिए, इससे यह निष्कर्ष निकलता है कि

$$\sum _{k=0}^{\infty }kr^{k}={\frac {r}{\left(1-r\right)^{2}}}\,;\,\sum _{k=0}^{\infty }k^{2}r^{k}={\frac {r\left(1+r\right)}{\left(1-r\right)^{3}}}\,;\,\sum _{k=0}^{\infty }k^{3}r^{k}={\frac {r\left(1+4r+r^{2}\right)}{\left(1-r\right)^{4}}}$$

साथ ही, अनंत श्रृंखला 1/2 + 1/4 + 1/8 + 1/16 + ⋯ एक श्रृंखला का एक प्रारंभिक उदाहरण है जो पूर्ण रूप से अभिसरण करती है।

यह एक ज्यामितीय श्रृंखला है जिसका पहला पद 1/2 है और जिसका सामान्य अनुपात 1/2 है, इसलिए इसका योग है

$${\frac {1}{2}}+{\frac {1}{4}}+{\frac {1}{8}}+{\frac {1}{16}}+\cdots ={\frac {1/2}{1-(+1/2)}}=1.$$

उपरोक्त श्रृंखला का व्युत्क्रम 1/2 - 1/4 + 1/8 - 1/16 + ⋯ एक वैकल्पिक श्रृंखला का एक सरल उदाहरण है जो पूर्ण रूप से अभिसरण करता है।

यह एक ज्यामितीय श्रृंखला है जिसका पहला पद 1/2 है और जिसका सामान्य अनुपात -1/2 है, इसलिए इसका योग है

$${\frac {1}{2}}-{\frac {1}{4}}+{\frac {1}{8}}-{\frac {1}{16}}+\cdots ={\frac {1/2}{1-(-1/2)}}={\frac {1}{3}}.$$

सम्मिश्र श्रृंखला

ज्यामितीय श्रृंखला के लिए योग सूत्र तब भी मान्य रहता है जब उभयनिष्ठ अनुपात एक सम्मिश्र संख्या हो। इस स्थिति में प्रतिबन्ध यह है कि r का निरपेक्ष मान 1 से कम हो, r का मापांक 1 से कम हो। कुछ गैर-स्पष्ट ज्यामितीय श्रृंखलाओं के योग की गणना करना संभव है। उदाहरण के लिए, कथन पर विचार करें;

$$\sum _{k=0}^{\infty }{\frac {\sin(kx)}{r^{k}}}={\frac {r\sin(x)}{1+r^{2}-2r\cos(x)}}$$

इसका प्रमाण इस बात से मिलता है,

$$\sin(kx)={\frac {e^{ikx}-e^{-ikx}}{2i}},$$

जो यूलर के सूत्र का परिणाम है। इसे मूल श्रृंखला में प्रतिस्थापित करने पर प्राप्त होता है।

$$\sum _{k=0}^{\infty }{\frac {\sin(kx)}{r^{k}}}={\frac {1}{2i}}\left[\sum _{k=0}^{\infty }\left({\frac {e^{ix}}{r}}\right)^{k}-\sum _{k=0}^{\infty }\left({\frac {e^{-ix}}{r}}\right)^{k}\right].$$

यह दो ज्यामितीय श्रृंखलाओं का अंतर है और इसलिए यह अनंत ज्यामितीय श्रृंखला के सूत्र का सीधा अनुप्रयोग है जो प्रमाण को पूर्ण करता है।

इतिहास

एलिया का ज़ेनो (सी.495 - सी.430 ईसा पूर्व)

2,500 वर्ष पहले, ग्रीक गणितज्ञों को एक स्थान से दूसरे स्थान तक चलने में समस्या होती थी: उन्होंने सोचा था कि शून्य से बड़ी संख्याओं की एक अनंत लंबी सूची अनंत तक होती है। इसलिए, यह एक विरोधाभास था जब एलिया के ज़ेनो ने बताया कि एक स्थान से दूसरे स्थान तक चलने के लिए, आपको पहले आधी दूरी तक चलना होगा और फिर आपको शेष दूरी का आधा चलना होगा और फिर आपको आधी दूरी तक चलना होगा। उस शेष दूरी का और आप शेष दूरी को अनंत बार आधा-आधा करते रहें क्योंकि शेष दूरी चाहे कितनी भी छोटी क्यों न हो, फिर भी आपको उसका पहला आधा भाग चलना होगा। इस प्रकार, एलिया के ज़ेनो ने एक छोटी दूरी को आधी शेष दूरियों की एक अनंत लंबी सूची में बदल दिया, जो सभी शून्य से अधिक हैं। और यही समस्या थी: सीधे मापने पर कोई दूरी छोटी कैसे हो सकती है और आधे शेषफलों की अनंत सूची में योग करने पर अनंत भी कैसे हो सकती है? विरोधाभास से पता चला कि इस धारणा में कुछ त्रुटि थी कि शून्य से बड़ी संख्याओं की अनंत रूप से लंबी सूची अनंत तक होती ।

अलेक्जेंड्रिया के यूक्लिड (लगभग 300 ईसा पूर्व)

ज्यामिति के तत्व, पुस्तक IX, कथन 35।"यदि लगातार आनुपातिक संख्याओं में से कुछ भी हो और पहले के बराबर दूसरे और अंतिम से घटाया जाता है, तो दूसरे से पहले की अधिकता के रूप में, इसलिए अतिरिक्त अंतिम भाग उन सभी के लिए होगा जो इससे पहले थे।"

यूक्लिड के ज्यामिति के तत्व पुस्तक IX, कथन 35, प्रमाण है (आसन्न आरेख के शीर्षक में कथन का):

मान लीजिए कि AA', BC, DD', EF न्यूनतम AA' से आरंभ करते हुए निरंतर आनुपातिक संख्याओं का कोई भी समूह हो। और मान लीजिए कि BG और FH, प्रत्येक AA' के बराबर हैं, BC और EF से घटा दिए गए हैं। मैं कहता हूं कि जैसे GC का अर्थ AA' है, वैसे ही EH का अर्थ AA', BC, DD' है।

मान लीजिए कि FK को BC के बराबर और FL को DD' के बराबर कर दिया गया है और चूँकि FK, BC के बराबर है, जिसमें से FH, BG के बराबर है, शेष HK इस प्रकार शेष GC के बराबर है और चूंकि EF का अर्थ DD' है, इसलिए DD' का अर्थ BC है और BC का अर्थ AA' है [कथन. 7.13], और DD' FL के बराबर है और BC से FK और AA' से FH है, इस प्रकार जैसे EF, FL के लिए है, वैसे ही LF से FK और FK से FH है। विभाजन द्वारा, जैसे EL से LF, इसलिए LK से FK, और KH से FH [कथन. 7.11, 7.13] है और इस प्रकार जैसे कि अग्रणी में से एक निम्नलिखित में से एक के लिए है, इसलिए सभी अग्रणी में से एक (का योग) निम्नलिखित में से एक के लिए है [कथन. 7.12]. इस प्रकार, जैसे KH से FH है, वैसे ही EL, LK, KH से LF, FK, HF है और KH, CG के बराबर है और FH से AA', और LF, FK, HF से DD', BC, AA' है। इस प्रकार, जैसे CG से AA' है, वैसे ही EH से DD', BC, AA' है। इस प्रकार, जैसे दूसरे का आधिक्य पहले के लिए है, वैसे ही अंतिम का आधिक्य उससे पहले वाले सभी के लिए है। वही जो दिखाना आवश्यक था।

यूक्लिड के कथनों और प्रमाणों की संक्षिप्तता एक आवश्यकता रही होगी। वैसे, ज्यामिति के तत्व 500 पृष्ठों से अधिक के कथनों और प्रमाणों से भरे हुए हैं। इस लोकप्रिय पाठ्यपुस्तक की प्रतियां बनाना श्रमसाध्य था, क्योंकि मुद्रणालय का आविष्कार 1440 तक नहीं हुआ था और पुस्तक की लोकप्रियता लंबे समय तक रही: जैसा कि एक अंग्रेजी अनुवाद के उद्धृत परिचय में कहा गया है, "ज्यामिति के तत्वों को" दुनिया का सबसे प्रतिष्ठित होने का गौरव प्राप्त है। सबसे पुरानी निरंतर उपयोग की जाने वाली गणितीय पाठ्यपुस्तक है, इसलिए बहुत संक्षिप्त होना बहुत व्यावहारिक होना था। पुस्तक IX में कथन 35 का प्रमाण और भी अधिक संक्षिप्त हो सकता था यदि यूक्लिड किसी तरह श्रृंखला में विभिन्न पदों से विशिष्ट रेखा खंडों की लंबाई को स्पष्ट रूप से बराबर करने से बच सकता था। उदाहरण के लिए, ज्यामितीय श्रृंखला के लिए समसामयिक संकेतन (अर्थात्, a + ar + ar² + ar³ + ... + arⁿ) उन शब्दों के विशिष्ट भागों को लेबल नहीं करता है जो एक दूसरे के बराबर हैं।

साथ ही उद्धृत परिचय में संपादक टिप्पणी करता है,

तत्वों में दिखाई देने वाले अधिकांश प्रमेय यूक्लिड द्वारा स्वयं नहीं खोजे गए थे, बल्कि पाइथागोरस (और उनके शिक्षालय), चियोस के हिप्पोक्रेट्स, एथेंस के थेएटेटस और कनिडोस के यूडोक्सस जैसे पहले ग्रीक गणितज्ञों के कार्य थे। हालाँकि, यूक्लिड को सामान्य तौर पर इन प्रमेयों को तार्किक तरीके से व्यवस्थित करने का श्रेय दिया जाता है, ताकि यह प्रदर्शित किया जा सके (माना जाता है कि, सदैव आधुनिक गणित द्वारा मांग की गई कठोरता के साथ नहीं) कि वे आवश्यक रूप से पांच सरल सिद्धांतों का पालन करते हैं। यूक्लिड को पहले खोजे गए प्रमेयों के कई विशेष रूप से सरल प्रमाण तैयार करने का श्रेय भी दिया जाता है (उदाहरण के लिए, पुस्तक 1 ​​में प्रमेय 48)।

वर्तमान संकेतन का उपयोग करने वाले रूप में कथन और प्रमाण का अनुवाद करने में सहायता के लिए, आरेख में कुछ संशोधन हैं। सर्वप्रथम, एक ज्यामितीय श्रृंखला के पहले चार पदों के मानों का प्रतिनिधित्व करने वाली चार क्षैतिज रेखा की लंबाई को अब आरेख के बाएं सीमा में a, ar, ar², ar³ लेबल किया गया है। दूसरा, नए लेबल A' और D' अब पहली और तीसरी पंक्तियों पर हैं ताकि आरेख के सभी रेखा खंड नाम निरन्तर खंड के प्रारंभिक बिंदु और समाप्ति बिंदु को निर्दिष्ट करें।

यहां कथन की वाक्यांश दर वाक्यांश व्याख्या दी गई है:

कथन	समसामयिक संकेतन में
"यदि निरंतर आनुपातिक संख्याओं में से किसी भी प्रकार की कोई बहु संख्या है।"	एक ज्यामितीय श्रृंखला के पहले n+1 पद लेने पर Sn = a + ar + ar2 + ar3 + ... + arn हैं।
"और पहले के बराबर दूसरे और अंतिम से घटाया जाता है।"	और ar और arn में से a घटाना,
"फिर जैसे पहले के लिए दूसरे की अधिकता होगी, वैसे ही पिछले सभी के लिए अधिकता होगी।"	तब (ar-a) / a = (arn-a) / (a + ar + ar2 + ar3 + ... + arn-1) = (arn-a) / Sn-1, जिसे अधिक में पुनर्व्यवस्थित किया जा सकता है, परिचित रूप Sn-1 = a(rn-1) / (r-1) हैं।

इसी प्रकार, यहां प्रमाण की वाक्य-दर-वाक्य व्याख्या दी गई है:

प्रमाण	समसामयिक संकेतन में
"मान लीजिए AA', BC, DD', EF न्यूनतम AA' से आरंभ करते हुए निरंतर आनुपातिक संख्याओं का कोई भी समूह हो।"	स्थिति r>1 और n=3 के लिए ज्यामितीय श्रृंखला Sn = a + ar + ar2 + ar3 + ... + arn के पहले n+1 पदों पर विचार करें।
"और माना कि BG और FH, प्रत्येक AA' के ​​बराबर हैं, BC और EF से घटा दिए गए हैं।"	ar और ar3 में से a घटाएँ।
"मैं कहता हूं कि जैसे GC का अर्थ AA' है, वैसे ही EH का अर्थ AA', BC, DD' है।"	मैं कहता हूं कि (ar-a) / a = (ar3-a) / (a + ar + ar2) है।
"मान लीजिए कि FK को BC के बराबर और FL को DD के बराबर बना दिया जाए।"
"और चूंकि FK BC के बराबर है, जिसमें से FH, BG के बराबर है, शेष HK इस प्रकार शेष GC के बराबर है।"
"और चूँकि EF, DD' है, इसलिए DD', BC है और BC, AA' [कथन 7.13] है और DD', FL के बराबर है और BC, FK है और AA', FH है, इस प्रकार EF, FL है, तो LF से FK और FK से FH है।"
"विभाजन द्वारा, जैसे EL से LF, इसलिए LK से FK और KH से FH [कथन. 7.11, 7.13] है।"	विभाजन से, (ar3-ar2) / ar2 = (ar2-ar) / ar = (ar-a) / a = r-1 है।
"और इस प्रकार जैसे एक अग्रणी निम्नलिखित में से एक के लिए है, वैसे ही सभी अग्रणियों का (योग) निम्नलिखित में से एक के लिए है [कथन 7.12]।"	उन अंशों का योग और उन हरों का योग समान अनुपात बनाता है: ((ar3-ar2) + (ar2-ar) + (ar-a)) / (ar2 + ar + a) = r-1.
"और इस प्रकार जैसे एक अग्रणी निम्नलिखित में से एक के लिए है, वैसे ही सभी अग्रणियों का (योग) निम्नलिखित में से एक के लिए है [कथन 7.12]।"	और समान अनुपातों के इस योग को (arn-arn-1) / arn-1 तक के सभी अनुपातों को शामिल करने के लिए (ar3-ar2) / ar2 से आगे बढ़ाया जा सकता है।
"इस प्रकार, जैसे KH से FH है, वैसे ही EL, LK, KH से LF, FK, HF है।"
"और KH बराबर CG, और FH से AA' और LF, FK, HF से DD', BC, AA' है।"
"इस प्रकार, जैसे CG से AA' है, वैसे ही EH से DD', BC, AA' है।"
"इस प्रकार, जैसे दूसरे की अधिकता पहले के लिए है, वैसे ही अंतिम की अधिकता उसके पहले के सभी लोगों के लिए है।"	इस प्रकार, (ar-a) / a = (ar3-a) / S2 या अधिक सामान्यतः, (ar-a) / a = (arn-a) / Sn-1, जिसे अधिक सामान्य रूप Sn-1 = a(rn-1) / (r-1) में पुनर्व्यवस्थित किया जा सकता है।
"वही चीज़ जो दिखाना आवश्यक था।"	क्यू.ई.डी.

सिरैक्यूज़ के आर्किमिडीज़ (सी.287 - सी.212 ईसा पूर्व)

आर्किमिडीज़ द्वारा एक परवलयिक खंड को अनंत अनेक त्रिभुजों में विच्छेदित करना।

Main article: परवलय का चतुर्भुज

आर्किमिडीज ने एक परवलय और एक सीधी रेखा से घिरे क्षेत्र की गणना करने के लिए एक ज्यामितीय श्रृंखला के योग का उपयोग किया। उनका तरीका क्षेत्र को अनंत संख्या में त्रिकोणों में विच्छेदित करना था।

आर्किमिडीज़ प्रमेय में कहा गया है कि परवलय के नीचे का कुल क्षेत्रफल नीले त्रिकोण के क्षेत्रफल का 4/3 है।

आर्किमिडीज़ ने निर्धारित किया कि प्रत्येक हरे त्रिकोण का क्षेत्रफल नीले त्रिकोण का 1/8 है, प्रत्येक पीले त्रिकोण का क्षेत्रफल हरे त्रिकोण का 1/8 है, इत्यादि।

यह मानते हुए कि नीले त्रिभुज का क्षेत्रफल 1 है, कुल क्षेत्रफल एक अनंत योग है:

$1\,+\,2\left({\frac {1}{8}}\right)\,+\,4\left({\frac {1}{8}}\right)^{2}\,+\,8\left({\frac {1}{8}}\right)^{3}\,+\,\cdots .$

पहला पद नीले त्रिभुज के क्षेत्रफल को दर्शाता है, दूसरा पद दो हरे त्रिभुजों के क्षेत्रफल को दर्शाता है, तीसरा पद चार पीले त्रिभुजों के क्षेत्रफल को दर्शाता है, इत्यादि। भिन्नों को सरल बनाने से प्राप्त होता है।

$1\,+\,{\frac {1}{4}}\,+\,{\frac {1}{16}}\,+\,{\frac {1}{64}}\,+\,\cdots .$

यह उभयनिष्ठ अनुपात 1/4 वाली एक ज्यामितीय श्रृंखला है और भिन्नात्मक भाग बराबर है।

$\sum _{n=0}^{\infty }4^{-n}=1+4^{-1}+4^{-2}+4^{-3}+\cdots ={4 \over 3}.$

योग है;

${\frac {1}{1-r}}\;=\;{\frac {1}{1-{\frac {1}{4}}}}\;=\;{\frac {4}{3}}.$

यह गणना निश्शेषण विधि का उपयोग करती है, जो एकीकरण का प्रारंभिक संस्करण है। गणना का उपयोग करके, वही क्षेत्र एक निश्चित अभिन्न द्वारा पाया जा सकता है।

निकोल ओरेस्मे (सी.1323 - 1382)

एक दो आयामी ज्यामितीय श्रृंखला आरेख निकोल ओरेस्मे ने यह निर्धारित करने के लिए उपयोग किया कि अनंत श्रृंखला 1/2 + 2/4 + 3/8 + 4/16 + 5/32 + 6/64 + 7/128 + ... , 2 में परिवर्तित हो जाती है।

अनंत श्रृंखला में उनकी अंतर्दृष्टि के अतिरिक्त, गुणित स्वर श्रृंखला के विचलन के उनके सुंदर सरल प्रमाण के अतिरिक्त, निकोल ओरेस्मे ने सिद्ध किया कि श्रृंखला 1/2 + 2/4 + 3/8 + 4/16 + 5/32 + 6/64 + 7/128 + ..., 2 में परिवर्तित होता है। उसके ज्यामितीय प्रमाण के लिए उसका आरेख, आसन्न आरेख के समान, एक दो आयामी ज्यामितीय श्रृंखला दर्शाता है। पहला आयाम क्षैतिज है, निचली पंक्ति में ज्यामितीय श्रृंखला S = 1/2 + 1/4 + 1/8 + 1/16 + ... दिखाई देती है, जो कि गुणांक a = 1/2 और उभयनिष्ठ के साथ ज्यामितीय श्रृंखला है अनुपात r = 1/2 जो s = a / (1-r) = (1/2) / (1-1/2) = 1 में परिवर्तित होता है। दूसरा आयाम ऊर्ध्वाधर है, जहां नीचे की पंक्ति एक नया गुणांक है। S के बराबर और इसके ऊपर की प्रत्येक बाद की पंक्ति को समान सामान्य अनुपात r = 1/2 द्वारा माप क्रमित किया जाता है, जिससे एक और ज्यामितीय श्रृंखला T = 1 + 1/2 + 1/4 + 1/8 + ... बनती है, जो कि ज्यामितीय है गुणांक a_T = S = 1 और सामान्य अनुपात r = 1/2 के साथ श्रृंखला जो T = a_T / (1-r) = S / (1-r) = a / (1-r) / (1-r) = (1/2) / (1-1/2) / (1-1/2) = 2 में परिवर्तित होती है।

यद्यपि तीन आयामों से परे कल्पना करना कठिन है, ओरेस्मे की अंतर्दृष्टि किसी भी आयाम को सामान्यीकृत करती है। ज्यामितीय श्रृंखला के d-1 आयाम के योग को ज्यामितीय श्रृंखला के d आयाम में गुणांक a के रूप में उपयोग करने से d-आयामी ज्यामितीय श्रृंखला का परिणाम सीमा |r|<1 के भीतर S^d / a = 1 / (1-r)^d में परिवर्तित हो जाता है। पास्कल का त्रिकोण और लंबा विभाजन इन बहुआयामी ज्यामितीय श्रृंखला के गुणांकों को प्रकट करता है, जहां संवृत रूप केवल |r|<1 की सीमा के भीतर मान्य है।

${\begin{matrix}1\\1\quad 1\\1\quad 2\quad 1\\1\quad 3\quad 3\quad 1\\1\quad 4\quad 6\quad 4\quad 1\end{matrix}}$

$d$	$S^{d}$ (संवृत्त रूप)	$S^{d}$ (विस्तारित रूप)
$1$	$1/(1-r)$	$1+r+r^{2}+r^{3}+r^{4}+\cdots$
$2$	$1/(1-r)^{2}$	$1+2r+3r^{2}+4r^{3}+5r^{4}+\cdots$
$3$	$1/(1-r)^{3}$	$1+3r+6r^{2}+10r^{3}+15r^{4}+\cdots$
$4$	$1/(1-r)^{4}$	$1+4r+10r^{2}+20r^{3}+35r^{4}+\cdots$

एक तरफ, लंबे विभाजन का उपयोग करने के बजाय, आयाम d−1 के गुणांकों को एकीकृत करके d-आयामी ज्यामितीय श्रृंखला के गुणांकों की गणना करना भी संभव है। घात श्रृंखला योग कार्यक्षेत्र में 1-r द्वारा विभाजन से लेकर घात श्रृंखला गुणांक कार्यक्षेत्र में एकीकरण तक की यह मानचित्रण लाप्लास रूपांतर द्वारा निष्पादित मानचित्रण का एक भिन्न रूप है। एमआईटी के प्रोफेसर आर्थर मैटक इस व्याख्यान वीडियो में दिखाते हैं कि घात श्रृंखला से लाप्लास रूपांतर कैसे प्राप्त किया जाए, जहां घात श्रृंखला असतत गुणांक और योग के मध्य एक मानचित्रण है और लाप्लास रूपांतर सतत भार और एक अभिन्न के मध्य एक मानचित्रण है।

अनुप्रयोग

अर्थशास्त्र

Main article: मुद्रा का समय मूल्य

अर्थशास्त्र में, वार्षिकी वर्तमान मान (नियमित अंतराल में भुगतान की जाने वाली धनराशि) को दर्शाने के लिए ज्यामितीय श्रृंखला का उपयोग किया जाता है।

उदाहरण के लिए, मान लीजिए कि वार्षिकी के मालिक को प्रति वर्ष एक बार (वर्ष के अंत में) $100 का भुगतान किया जाएगा। अब से प्रति वर्ष $100 प्राप्त करना तत्काल $100 से कम मूल्य का है, क्योंकि कोई भी तब तक पैसा निवेश नहीं कर सकता जब तक वह इसे प्राप्त न कर ले। विशेष रूप से, भविष्य में एक वर्ष के लिए $100 का वर्तमान मान $100 / (1 + $I$) है, जहां $I$ वार्षिक ब्याज दर है।

इसी प्रकार, भविष्य में दो वर्षों के लिए $100 के भुगतान का वर्तमान मान $100 / (1 + $I$)² (चुकता क्योंकि अभी पैसा न मिलने से दो साल का ब्याज नष्ट हो जाता है)। इसलिए, शाश्वत रूप से प्रति वर्ष $100 प्राप्त करने का वर्तमान मान है।

$\sum _{n=1}^{\infty }{\frac {\$100}{(1+I)^{n}}},$

जो अनंत श्रृंखला है:

${\frac {\$100}{(1+I)}}\,+\,{\frac {\$100}{(1+I)^{2}}}\,+\,{\frac {\$100}{(1+I)^{3}}}\,+\,{\frac {\$100}{(1+I)^{4}}}\,+\,\cdots .$

यह एक ज्यामितीय श्रृंखला है जिसका सामान्य अनुपात 1/(1+ $I$ ) है। योग पहला पद है जिसे (सामान्य अनुपात से एक घटाकर) विभाजित किया जाता है:

${\frac {\$100/(1+I)}{1-1/(1+I)}}\;=\;{\frac {\$100}{I}}.$

उदाहरण के लिए, यदि वार्षिक ब्याज दर 10% ($I$= 0.10) है, तो संपूर्ण वार्षिकी का वर्तमान मान $100 / 0.10 = $1000 है।

इस प्रकार की गणना का उपयोग ऋण की वार्षिक प्रतिशत दर (जैसे बंधक ऋण) की गणना करने के लिए किया जाता है। इसका उपयोग अपेक्षित लाभांश के वर्तमान मान, या स्थिर विकास दर मानकर किसी वित्तीय परिसंपत्ति के आवधिक मूल्य का अनुमान लगाने के लिए भी किया जा सकता है।

आंशिक ज्यामिति

कोच हिमकण का आंतरिक भाग अनंत कई त्रिभुजों का एक संघ है। आंशिक के अध्ययन में, ज्यामितीय श्रृंखला प्रायः परिधि, क्षेत्र, या आयतन के रूप में स्व-समान आकृति के रूप में उत्पन्न होती है।

यदि |r| < 1, प्रत्येक ज्यामितीय श्रृंखला पद को एक समान त्रिभुज के क्षेत्र के रूप में प्रस्तुत करने से एक आंशिक बनता है जिसमें अधिक आकारवर्धन करने से सदैव अधिक समान त्रिभुज प्रकट होते हैं।

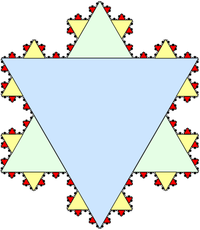
कोच हिमकण के भीतर के क्षेत्र को अनंत कई समबाहु त्रिभुजों के मिलन के रूप में वर्णित किया जा सकता है (चित्र देखें)। हरे त्रिभुज की प्रत्येक भुजा बड़े नीले त्रिभुज की भुजा के आकार का ठीक 1/3 है और इसलिए इसका क्षेत्रफल बिल्कुल 1/9 है। इसी प्रकार, प्रत्येक पीले त्रिभुज का क्षेत्रफल हरे त्रिभुज का 1/9 है, इत्यादि। नीले त्रिकोण को क्षेत्रफल की एक इकाई के रूप में लेते हुए, हिमकण का कुल क्षेत्रफल है।

$1\,+\,3\left({\frac {1}{9}}\right)\,+\,12\left({\frac {1}{9}}\right)^{2}\,+\,48\left({\frac {1}{9}}\right)^{3}\,+\,\cdots .$

इस श्रृंखला का पहला पद नीले त्रिभुज के क्षेत्रफल को दर्शाता है, दूसरा पद तीन हरे त्रिभुजों के कुल क्षेत्रफल को दर्शाता है, तीसरा पद बारह पीले त्रिभुजों के कुल क्षेत्रफल को दर्शाता है, इत्यादि। आरंभिक 1 को छोड़कर, यह श्रृंखला निरंतर अनुपात r = 4/9 के साथ ज्यामितीय है। ज्यामितीय श्रृंखला का पहला पद a = 3(1/9) = 1/3 है, इसलिए योग है;

$1\,+\,{\frac {a}{1-r}}\;=\;1\,+\,{\frac {\frac {1}{3}}{1-{\frac {4}{9}}}}\;=\;{\frac {8}{5}}.$

इस प्रकार कोच हिमकण का क्षेत्रफल आधार त्रिभुज का 8/5 है।

एकीकरण

$f(x)=\arctan(u(x)){\text{ is }}f'(x)=u'(x)/(1+[u(x)]^{2})$ का व्युत्पन्न है क्योंकि,$y{\text{ and }}u{\text{ represent }}f(x){\text{ and }}u(x),$

${\begin{aligned}y&=\arctan(u)&&\quad {\text{ implies }}\\u&=\tan(y)&&\quad {\text{ in the range }}-\pi /2<y<\pi /2{\text{ and }}\\u'&=\sec ^{2}y\cdot y'&&\quad {\text{ by applying the quotient rule to }}\tan(y)=\sin(y)/\cos(y),\\y'&=u'/\sec ^{2}y&&\quad {\text{ by dividing both sides by }}\sec ^{2}y,\\&=u'/(1+\tan ^{2}y)&&\quad {\text{ by using the trigonometric identity derived by dividing }}\sin ^{2}y+\cos ^{2}y=1{\text{ by }}\cos ^{2}y,\\&=u'/(1+u^{2})&&\quad {\text{ by recalling }}u=\tan(y).\end{aligned}}$

इसलिए, $u(x)=x,\arctan(x)$ अभिन्न है।

${\begin{aligned}\arctan(x)&=\int {\frac {dx}{1+x^{2}}}\quad &&{\text{in the range }}-\pi /2<\arctan(x)<\pi /2,\\&=\int {\frac {dx}{1-(-x^{2})}}\quad &&{\text{by writing integrand as closed form of geometric series with }}r=-x^{2},\\&=\int \left(1+\left(-x^{2}\right)+\left(-x^{2}\right)^{2}+\left(-x^{2}\right)^{3}+\cdots \right)dx\quad &&{\text{by writing geometric series in expanded form}},\\&=\int \left(1-x^{2}+x^{4}-x^{6}+\cdots \right)dx\quad &&{\text{by calculating the sign and power of each term in integrand}},\\&=x-{\frac {x^{3}}{3}}+{\frac {x^{5}}{5}}-{\frac {x^{7}}{7}}+\cdots \quad &&{\text{by integrating each term}},\\&=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{2n+1}}x^{2n+1}\quad &&{\text{by writing series in generator form}},\end{aligned}}$

जिसे ग्रेगरी की श्रृंखला कहा जाता है और इसका श्रेय सामान्यतौर पर संगमग्राम के माधव (सी. 1340 - सी. 1425) को दिया जाता है।

उदाहरण

• ग्रैंडी की श्रृंखला: 1 − 1 + 1 − 1 + ⋯
• 1 + 2 + 4 + 8 + ⋯
• 1 − 2 + 4 − 8 + ⋯
• 1/2 + 1/4 + 1/8 + 1/16 + ⋯
• 1/2 − 1/4 + 1/8 − 1/16 + ⋯
• 1/4 + 1/16 + 1/64 + 1/256 + ⋯
• एक ज्यामितीय श्रृंखला एक इकाई श्रृंखला है (श्रृंखला का योग एक में परिवर्तित होता है) यदि और केवल यदि |r| <1 और a + r = 1 (अधिक परिचित रूप S = a / (1 - r) = 1 के बराबर जब |r| <1) है। इसलिए, एक प्रत्यावर्ती श्रृंखला भी एक इकाई श्रृंखला होती है जब -1 < r < 0 और a + r = 1 (उदाहरण के लिए, गुणांक a = 1.7 और सामान्य अनुपात r = -0.7) है।
• एक ज्यामितीय श्रृंखला के पद भी एक सामान्यीकृत फाइबोनैचि अनुक्रम (F_n = F_n-1 + F_n-2 लेकिन F₀ = 0 और F₁ = 1 की आवश्यकता के बिना) के पद हैं, जब एक ज्यामितीय श्रृंखला सामान्य अनुपात r व्यवरोध 1 + r = r² को संतुष्ट करता है, जो द्विघात सूत्र के अनुसार तब होता है जब सामान्य अनुपात r स्वर्णिम अनुपात के बराबर होता है (अर्थात, सामान्य अनुपात r = (1 ± √5)/2)।
• एकमात्र ज्यामितीय श्रृंखला जो एक इकाई श्रृंखला है और इसमें सामान्यीकृत फाइबोनैचि अनुक्रम के पद भी हैं, इसका गुणांक a के रूप में स्वर्णिम अनुपात और इसके सामान्य अनुपात आर के रूप में संयुग्मित स्वर्णिम अनुपात है (अर्थात, a = (1 + √5)/2 और r = (1 - √5)/2) । यह एक इकाई श्रृंखला है क्योंकि a + r = 1 और |r| <1, यह एक सामान्यीकृत फाइबोनैचि अनुक्रम है क्योंकि 1 + r = r² और यह एक वैकल्पिक श्रृंखला है क्योंकि r < 0 है।

ज्यामितीय श्रृंखला

परिप्रेक्ष्य स्विचन को सरल बनाने के लिए ज्यामितीय श्रृंखला पर विभिन्न परिप्रेक्ष्यों का एक संक्षिप्त चित्रण है। वृत्तपाद A1 में क्यों परिप्रेक्ष्य सम्मिलित है जो संक्षेप में वर्णन करता है कि ज्यामितीय श्रृंखला क्यों मायने रखती है। वृत्तपाद A2 में जूलिया कूट के एक कतरन को सूचीबद्ध करने वाला परिप्रेक्ष्य सम्मिलित है जो ज्यामितीय श्रृंखला की गणना करता है। चतुर्भुज A3 में ज्यामितीय श्रृंखला संवृत रूप सूत्र के बीजगणितीय प्रमाण के साथ क्या (बीजगणित) परिप्रेक्ष्य सम्मिलित है। वृत्तपाद A4 में क्या (ज्यामिति) परिप्रेक्ष्य सम्मिलित है जो ज्यामितीय श्रृंखला के संवृत रूप सूत्र के ज्यामितीय प्रमाण के तीन चरणों को दर्शाता है और दायी सीमा ज्यामितीय श्रृंखला के बारे में कुछ ऐतिहासिक अंतर्दृष्टि की समयरेखा दर्शाती है।

ज्यामितीय श्रृंखला में स्वतंत्रता की दो घाते: एक इसके गुणांक के लिए और दूसरा इसके सामान्य अनुपात r के लिए हैं। बहुपदों के मानचित्र में, बड़ा लाल वृत्त सभी ज्यामितीय श्रृंखलाओं के समुच्चय का प्रतिनिधित्व करता है।

अभिसरण ज्यामितीय श्रृंखला

सभी ज्यामितीय श्रृंखलाओं का केवल एक उपसमुच्चय अभिसरित होता है। विशेष रूप से, एक ज्यामितीय श्रृंखला अभिसरण करती है यदि और केवल यदि इसका सामान्य अनुपात |r| < 1 है।बहुपदों के मानचित्र में, लाल त्रिकोण अभिसरण ज्यामितीय श्रृंखला के समुच्चय का प्रतिनिधित्व करता है और सभी ज्यामितीय श्रृंखलाओं के समुच्चय का प्रतिनिधित्व करने वाले बड़े लाल वृत्त के भीतर खींचा जाना इंगित करता है कि अभिसरण ज्यामितीय श्रृंखला ज्यामितीय श्रृंखला का एक उपसमुच्चय है।

पुनरावर्ती दशमलव

Main article: दशमलव पुनरावृत्ति

सभी अभिसरण ज्यामितीय श्रृंखलाओं का केवल एक उपसमुच्चय दशमलव अंशों में परिवर्तित होता है जिनके प्रतिरुप दोहराए जाते हैं जो सदैव के लिए जारी रहते हैं (उदाहरण के लिए, 0.7777... या 0.9999... या 0.123412341234...)। बहुपदों के मानचित्र में, छोटा पीला त्रिकोण ज्यामितीय श्रृंखला के समुच्चय का प्रतिनिधित्व करता है जो अनंत रूप से दोहराए गए दशमलव प्रतिरुप में परिवर्तित होता है। यह इंगित करने के लिए लाल त्रिकोण के भीतर खींचा गया है कि यह अभिसारी ज्यामितीय श्रृंखला का एक उपसमूह है, जो बदले में बड़े लाल वृत्त के भीतर खींचा गया है जो दर्शाता है कि अभिसरण ज्यामितीय श्रृंखला और ज्यामितीय श्रृंखला दोनों जो अनंत रूप से दोहराए गए प्रतिरुप में परिवर्तित होती हैं, ज्यामितीय के उपसमुच्चय शृंखला हैं।

यद्यपि अनंत रूप से पुनरावर्ती दशमलव प्रतिरुप वाले अंशों का अनुमान केवल तब लगाया जा सकता है जब उन्हें चल बिंदु संख्याओं के रूप में कोडित किया जाता है, उन्हें सदैव दो पूर्णांकों के अनुपात के रूप में परिभाषित किया जा सकता है और उन दो पूर्णांकों की गणना ज्यामितीय श्रृंखला का उपयोग करके की जा सकती है। उदाहरण के लिए, पुनरावर्ती दशमलव अंश 0.7777... को ज्यामितीय श्रृंखला के रूप में लिखा जा सकता है।

$0.7777\ldots \;=\;{\frac {7}{10}}\,+\,{\frac {7}{10}}{\frac {1}{10}}\,+\,{\frac {7}{10}}{\frac {1}{10^{2}}}\,+\,{\frac {7}{10}}{\frac {1}{10^{3}}}\,+\,\cdots$

जहाँ गुणांक a = 7/10 और सार्व अनुपात r = 1/10 है। ज्यामितीय श्रृंखला का संवृत रूप दो पूर्णांकों को प्रकट करता है जो पुनरावर्ती प्रतिरुप को निर्दिष्ट करते हैं:

$0.7777\ldots \;=\;{\frac {a}{1-r}}\;=\;{\frac {7/10}{1-1/10}}\;=\;{\frac {7/10}{9/10}}\;=\;{\frac {7}{9}}.$

यह दृष्टिकोण मूल अंक-दस संख्याओं से आगे तक फैला हुआ है। वास्तव में, कोई भी भिन्न जिसका प्रतिरुप मूल अंक-दस संख्याओं में अनंत रूप से दोहराया जाता है, किसी अन्य आधार में लिखी संख्याओं में भी अनंत रूप से दोहराया जाने वाला प्रतिरुप होता है। उदाहरण के लिए, संख्या 0.7777... के लिए चल बिंदु कोडन को देखते हुए। julia> bitstring(Float32(0.77777777777777777777))
"00111111010001110001110001110010"

द्विआधारी अंश 0.110001110001110001... को प्रकट करता है जहां द्विआधारी प्रतिरुप 0b110001 अनिश्चित काल तक दोहराता है और ज्यादातर (घातो को छोड़कर) द्विआधारी संख्याओं में लिखा जा सकता है।

$0.110001110001110001\ldots \;=\;{\frac {110001}{1000000}}\,+\,{\frac {110001}{1000000}}{\frac {1}{1000000}}\,+\,{\frac {110001}{1000000}}{\frac {1}{1000000^{2}}}\,+\,{\frac {110001}{1000000}}{\frac {1}{1000000^{3}}}\,+\,\cdots$

जहां गुणांक a = 0b110001 / 0b1000000 = 49 / 64 और सामान्य अनुपात r = 1 / 0b1000000 = 1 / 64 है। पहले की तरह ज्यामितीय श्रृंखला संवृत रूप का उपयोग करना।

$0.7777\ldots \;=\;0b0.110001110001110001\ldots \;=\;{\frac {a}{1-r}}\;=\;{\frac {49/64}{1-1/64}}\;=\;{\frac {49/64}{63/64}}\;=\;{\frac {49}{63}}\;=\;{\frac {7}{9}}.$

आपने देखा होगा कि चल बिंदु कोडन पिछले कुछ (कम से कम महत्वपूर्ण) द्वयंकों में 0b110001 पुनरावृत्त प्रतिरुप को कैप्चर नहीं करता है। ऐसा इसलिए है क्योंकि चल बिंदु कोडन शेष को छोटा करने के बजाय उसे गोल कर देती है। इसलिए, यदि शेषफल का सबसे महत्वपूर्ण द्वयंक 1 है, तो कूटबद्‍ध अंश का सबसे कम महत्वपूर्ण द्वयंक बढ़ जाता है और यदि अंश का सबसे कम महत्वपूर्ण द्वयंक पहले से ही 1 है, तो यह एक ऋणी का कारण बनेगा, जो कि उस द्वयंक के एक और ऋणी का कारण बन सकता है। अंश पहले से ही 1 है, जो एक और ऋणी आदि का कारण बन सकता है। यह चल बिंदु निष्कोणन और उसके बाद का ऋणी प्रसार बताता है कि क्यों 0.99999... के लिए चल बिंदु कोडन 1 के लिए चल बिंदु कोडन के समान ही है।

julia> bitstring(Float32(0.99999999999999999999))
"00111111100000000000000000000000"

julia> bitstring(Float32(1.0))
"00111111100000000000000000000000"

एक उदाहरण के रूप में, जिसमें पुनरावर्ती प्रतिरुप में चार अंक हैं, 0.123412341234... को ज्यामितीय श्रृंखला के रूप में लिखा जा सकता है;

$0.123412341234\ldots \;=\;{\frac {1234}{10000}}\,+\,{\frac {1234}{10000}}{\frac {1}{10000}}\,+\,{\frac {1234}{10000}}{\frac {1}{10000^{2}}}\,+\,{\frac {1234}{10000}}{\frac {1}{10000^{3}}}\,+\,\cdots$

जहाँ गुणांक a = 1234/10000 और सार्व अनुपात r = 1/10000 है। ज्यामितीय श्रृंखला का संवृत रूप दो पूर्णांकों को प्रकट करता है जो पुनरावर्ती प्रतिरुप को निर्दिष्ट करते हैं:

$0.123412341234\ldots \;=\;{\frac {a}{1-r}}\;=\;{\frac {1234/10000}{1-1/10000}}\;=\;{\frac {1234/10000}{9999/10000}}\;=\;{\frac {1234}{9999}}.$

घात श्रृंखला

Main article: घात श्रृंखला

ज्यामितीय श्रृंखला की तरह, घात श्रृंखला में इसके सामान्य अनुपात r (x-अक्ष के साथ) के लिए स्वतंत्रता की एक घात होती है, लेकिन इसके गुणांकों (y-अक्ष के साथ) के लिए n+1 घात की स्वतंत्रता होती है, जहाँ n आंशिक श्रृंखला में अंतिम पद की घात को दर्शाता है। बहुपदों के मानचित्र में, बड़ा नीला वृत्त सभी घात श्रृंखलाओं के समुच्चय को दर्शाता है।

टेलर श्रृंखला

गणित में, टेलर श्रृंखला या किसी फलन का टेलर विस्तार शब्दों का एक अनंत योग है जो एक ही बिंदु पर फलन के व्युत्पन्न के संदर्भ में व्यक्त किया जाता है। अधिकांश सामान्य फलनों के लिए, फलन और उसकी टेलर श्रृंखला का योग इस बिंदु के निकट बराबर होते हैं। टेलर श्रृंखला का नाम ब्रुक टेलर के नाम पर रखा गया है, जिन्होंने उन्हें 1715 में प्रस्तुत किया था। टेलर श्रृंखला को मैकलॉरिन श्रृंखला भी कहा जाता है जब 0 वह बिंदु होता है जहां व्युत्पन्न पर विचार किया जाता है, कॉलिन मैकलॉरिन के नाम पर, जिन्होंने 18वीं सदी के मध्य में, टेलर श्रृंखला की इस विशेष स्थिति का व्यापक उपयोग किया था।

टेलर श्रृंखला के पहले n + 1 पदों द्वारा गठित आंशिक योग घात n का एक बहुपद है जिसे फलन का nवाँ टेलर बहुपद कहा जाता है। टेलर बहुपद एक फलन के सन्निकटन हैं, जो सामान्यतः n बढ़ने पर अधिक सटीक हो जाते हैं। टेलर का प्रमेय ऐसे सन्निकटनों के उपयोग से उत्पन्न त्रुटि पर मात्रात्मक अनुमान देता है। यदि किसी फलन की टेलर श्रृंखला अभिसरण है, तो इसका योग टेलर बहुपदों के अनंत अनुक्रम की सीमा है। एक फलन उसकी टेलर श्रृंखला के योग से भिन्न हो सकता है, भले ही उसकी टेलर श्रृंखला अभिसरण हो। एक फलन एक बिंदु x पर विश्लेषणात्मक होता है यदि यह x युक्त किसी विवृत अंतराल (या जटिल समतल में विवृत चक्रिका) में इसकी टेलर श्रृंखला के योग के बराबर है। इसका तात्पर्य यह है कि फलन अंतराल (या चक्रिका) के प्रत्येक बिंदु पर विश्लेषणात्मक है।

द्विआधारी कूटबद्‍ध संख्याएँ

Main article: द्विआधारी संख्या

Main article: एकल-परिशुद्धता चल बिंदु प्रारूप

गुणांक a=1/2 और सामान्य अनुपात r=1/2 के साथ एलिया की ज्यामितीय श्रृंखला का ज़ेनो अंकीय संगणक में भिन्नों के द्विआधारी कूटबद्‍ध अनुमानों की नींव है। सीधे तौर पर, अपने सामान्यीकृत सदिश रूप में लिखी गई ज्यामितीय श्रृंखला s/a = [1 1 1 1 1 …][1 r r² r³ r⁴ …]^T है। आधार फलनों के स्तम्भ सदिश को ध्यान में रखते हुए [1 r r² r³ r⁴ …]^T को समान रखा गया है, लेकिन पंक्ति सदिश [1 1 1 1 1…] को सामान्यीकृत किया गया है ताकि प्रत्येक प्रविष्टि या तो 0 या 1 हो सके, किसी भी अंश के अनुमानित कोडन की अनुमति देता है। उदाहरण के लिए, मान v = 0.34375 को v/a = [0 1 0 1 1 0 …][1 r r² r³ r⁴ …]^T के रूप में कोडित किया गया है, जहां गुणांक a = 1/2 और सामान्य अनुपात r = 1/2 है। सामान्यतौर पर, पंक्ति सदिश अधिक सुसंहत द्विआधारी रूप v = 0.010110 में लिखा जाता है जो दशमलव में 0.34375 है।

इसी प्रकार, गुणांक a=1 और सामान्य अनुपात r=2 के साथ ज्यामितीय श्रृंखला अंकीय संगणक में द्विआधारी कूटबद्‍ध पूर्णांकों की नींव है। पुनः, अपने सामान्यीकृत सदिश रूप में लिखी गई ज्यामितीय श्रृंखला s/a = [1 1 1 1 1 …][1 r r² r³ r⁴ …]^T है। आधार फलनों के स्तम्भ सदिश को ध्यान में रखते हुए [1 r r² r³ r⁴ …]^T को समान रखा गया है, लेकिन पंक्ति सदिश [1 1 1 1 1…] को सामान्यीकृत किया जा रहा है ताकि प्रत्येक प्रविष्टि या तो 0 या 1 हो सके, किसी भी पूर्णांक के कोडन की अनुमति देता है। उदाहरण के लिए, मान v = 151 को v/a = [1 1 1 0 1 0 0 1 0 …][1 r r² r³ r⁴ r⁵ r⁶ r⁷ r⁸ …]^T इस प्रकार कोडित किया गया है, जहां गुणांक a = 1 और सामान्य अनुपात r = 2 है। सामान्यतौर पर, पंक्ति सदिश को अधिक सुसंहत द्विआधारी रूप v = ...010010111 = 10010111 में उल्टे क्रम में लिखा जाता है (ताकि सबसे महत्वपूर्ण द्वयंक पहले हो) जो दशमलव में 151 है।

आईईईई 754 मानक के अनुसार 32-द्वयंक चल बिंदु संख्याओं को कोडित करने के लिए द्वयंक क्षेत्र।

जैसा कि आसन्न चित्र में दिखाया गया है, 32-द्वयंक चल बिंदु संख्या का मानक द्विआधारी कोडन एक द्विआधारी कूटबद्‍ध पूर्णांक और एक द्विआधारी कूटबद्‍ध अंश का संयोजन है, जो सबसे महत्वपूर्ण द्वयंक से प्रारंभ होता है:

• चिन्ह द्वयंक, इसके बाद
• 127 के मानित अंतलंब के साथ एक 8-द्वयंक पूर्णांक घातांक क्षेत्र (इसलिए 127 का मान 0 के घातांक मान को दर्शाता है) और 2 के आधार के साथ जिसका अर्थ है कि घातांक मान भिन्न क्षेत्र में थोड़ा बदलाव निर्दिष्ट करता है, जिसके बाद
• एक 23-द्वयंक अंश क्षेत्र जिसमें मान लिया गया है लेकिन कूटबद्‍ध नहीं है, 1 अंश के सबसे महत्वपूर्ण गैर-शून्य द्वयंक के रूप में कार्य करता है, जो कूटबद्‍ध किए जाने पर द्वयंक स्थिति 23 में होगा।

0.010110 की द्विआधारी कोडन वाले 0.34375 के पिछले उदाहरण के आधार पर, 0.34375 की एक चल बिंदु कोडन (आईईईई 754 मानक के अनुसार) है:

• चिन्ह द्वयंक जो 0 है क्योंकि संख्या ऋणात्मक नहीं है,
• एक 8-द्वयंक पूर्णांक घातांक क्षेत्र जिसमें एक विस्थापन निर्दिष्ट करना होगा जो 0.010110 से 1.0110 तक मूल द्विआधारी कोडन प्राप्त करने के लिए 2 द्वयंक बाईं विस्थापन को प्रत्युत्तर करता है, और मूल द्विआधारी कोडन को पुनर्प्राप्त करने के लिए वह प्रत्युत्तर विस्थापन 2 द्वयंक की एक दाईं विस्थापन है जो 125 के घातांक मान द्वारा निर्दिष्ट किया जाता है (क्योंकि 125 − 127 = -2 जो 2 द्वयंक का दायां बदलाव है) जो द्विआधारी में 0111 1101 है,
• एक 23-द्वयंक अंश क्षेत्र: .0110 0000 0000 0000 0000 000.

हालाँकि इस तरह से चल बिंदु संख्याओं को हाथ से कोडित करना संभव है, संगणक को ऐसा करने देना सरल है और त्रुटि की संभावना कम है। निम्नलिखित जूलिया कूट संख्या 0.34375 की हाथ से गणना की गई चल बिंदु कोडन की पुष्टि करता है:

julia> bitstring(Float32(0.34375))
"00111110101100000000000000000000"

लॉरेंट श्रृंखला

गणित में, एक सम्मिश्र फलन की लॉरेंट श्रृंखला f(z) उस फलन का एक घात श्रृंखला के रूप में प्रतिनिधित्व है जिसमें ऋणात्मक घात की शर्तें सम्मिलित हैं। इसका उपयोग उन स्थितियों में सम्मिश्र फलनों को व्यक्त करने के लिए किया जा सकता है जहां टेलर श्रृंखला विस्तार अनुप्रयुक्त नहीं किया जा सकता है। लॉरेंट श्रृंखला का नाम पियरे अल्फोंस लॉरेंट के नाम पर रखा गया था और इसे पहली बार 1843 में प्रकाशित किया गया था। कार्ल वीयरस्ट्रैस ने इसे सबसे पहले 1841 में लिखे एक लेख्य में खोजा था, लेकिन यह उनकी मृत्यु के बाद तक प्रकाशित नहीं हुआ था।

सम्मिश्र फूरियर श्रृंखला

Main article: फोरियर शृंखला

आगे और पीछे के तल सम्मिश्र फूरियर श्रृंखला के पहले +/-n पदों का योग दर्शाते हैं जिसमें घातांक के लिए अक्षर 'e' के अनुरेखण में परिवर्तित होने के लिए गुणांक निर्धारित हैं (जूलिया स्रोत कूट जो इस एनीमेशन के क्षणचित्र और श्रव्य उत्पन्न करता है वह यहां परिशिष्ट B में है)।

किसी भी 2डी संवृत आकृति का पता लगाने के लिए सम्मिश्र फूरियर श्रृंखला की क्षमता के एक उदाहरण के रूप में, आसन्न एनीमेशन में एक सम्मिश्र फूरियर श्रृंखला अक्षर 'e' (घातांक के लिए) का पता लगाती है। एनीमेशन में दिखाए गए गतियों के सम्मिश्र समन्वय को देखते हुए, सम्मिश्र फूरियर श्रृंखला की परिभाषा केवल दो समीकरणों में आश्चर्यजनक रूप से संक्षिप्त की जा सकती है:

${\begin{aligned}s(t)&=\sum _{n=-\infty }^{\infty }c_{n}e^{2\pi int}\\c_{n}&=\int _{0}^{1}s(t)e^{-2\pi int}dt\\\end{aligned}}$

जहां पैरामिट्रीकृत फलन s(t) सम्मिश्र समतल में कुछ 2डी संवृत आकृति का पता लगाता है क्योंकि मापदण्ड t, 0 से 1 की अवधि के पर्यन्त आगे बढ़ता है।

सम्मिश्र फूरियर श्रृंखला को परिभाषित करने वाले इन सघन समीकरणों को समझने में सहायता के लिए, ध्यान दें कि सम्मिश्र फूरियर श्रृंखला का योग सम्मिश्र ज्यामितीय श्रृंखला के समान दिखता है, अतिरिक्त इसके कि सम्मिश्र फूरियर श्रृंखला मूल रूप से दो सम्मिश्र ज्यामितीय श्रृंखलाएं हैं (धनात्मक दिशा में घूमने वाले पदों का एक समुच्चय) और ऋणात्मक दिशा में घूमने वाले पदों का एक और समुच्चय), और सम्मिश्र फूरियर श्रृंखला के गुणांक सम्मिश्र स्थिरांक हैं जो एक पद से दूसरे पद में भिन्न हो सकते हैं। पदों को किसी भी दिशा में घूमने की अनुमति देकर, श्रृंखला किसी भी 2डी संवृत आकृति का पता लगाने में सक्षम हो जाती है। इसके विपरीत, सम्मिश्र ज्यामितीय श्रृंखला में सभी पद एक ही दिशा में घूमते हैं और यह केवल वृत्तों का पता लगा सकता है। सम्मिश्र ज्यामितीय श्रृंखला के गुणांकों को पद दर पद भिन्न-भिन्न करने की अनुमति देने से उन आकृतियों का विस्तार होगा जिनका वह पता लगा सकता है लेकिन सभी संभावित आकार अभी भी उभरे हुए और बादल जैसे होने तक ही सीमित रहेंगे, एक सरल रेखा खंड के आकार का पता लगाने में सक्षम नहीं होंगे , उदाहरण के लिए 1 + i0 और -1 + i0 के मध्य आगे और पीछे जाना है। हालाँकि, यूलर के सूत्र से पता चलता है कि विपरीत दिशाओं में घूमने वाले केवल दो पदों को जोड़ने से 1 + i0 और -1 + i0 के मध्य उस रेखा खंड का पता लगाया जा सकता है:

${\begin{aligned}e^{i\theta }&=\cos \theta +i\sin \theta \\e^{-i\theta }&=\cos \theta -i\sin \theta \\\cos \theta &={\frac {e^{i\theta }+e^{-i\theta }}{2}}.\\\end{aligned}}$

गुणांकों की गणना करने के तरीके को परिभाषित करने वाले सम्मिश्र फूरियर श्रृंखला के दूसरे समीकरण के संबंध में, अघूर्णी पद c₀ के गुणांक की गणना 0 से 1 तक की एक अवधि की सीमा पर सम्मिश्र फूरियर श्रृंखला के पहले समीकरण को एकीकृत करके की जा सकती है। उस सीमा पर, सभी घूर्णी पद केवल c₀ छोड़कर शून्य में एकीकृत हो जाते हैं। इसी प्रकार, सम्मिश्र फूरियर श्रृंखला के पहले समीकरण में किसी भी पद को समीकरण $e^{-2\pi int}$ के दोनों पक्षों को गुणा करके एक अघूर्णी पद बनाया जा सकता है। c_n की गणना करने के लिए एकीकृत करने से पहले, और वह सम्मिश्र फूरियर श्रृंखला दूसरा समीकरण है।

यह भी देखें

• 0.999...
• अनंतस्पर्शी – Limit of the tangent line at a point that tends to infinity
• अपसारी ज्यामितीय श्रृंखला
• सामान्यीकृत हाइपरज्यामेट्रिक फलन
• [[

ज्यामितीय अनुक्रम| ज्यामितीय अनुक्रम]] – Mathematical sequence of numbers

• न्यूमैन श्रृंखला
• अनुपात परीक्षण
• वर्गमूल परीक्षण
• श्रृंखला (गणित) – Infinite sum
• अंकगणित श्रृंखला

संदर्भ

• Abramowitz, M.; Stegun, I. A., eds. (1972). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables (9th printing ed.). New York: Dover. p. 10.
• Andrews, George E. (1998). "The geometric series in calculus". The American Mathematical Monthly. Mathematical Association of America. 105 (1): 36–40. doi:10.2307/2589524. JSTOR 2589524.
• Arfken, G. Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 278–279, 1985.
• Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, p. 8, 1987.
• Courant, R. and Robbins, H. "The Geometric Progression." §1.2.3 in What Is Mathematics?: An Elementary Approach to Ideas and Methods, 2nd ed. Oxford, England: Oxford University Press, pp. 13–14, 1996.
• Hall, Brian C. (2015), Lie groups, Lie algebras, and representations: An elementary introduction, Graduate Texts in Mathematics, vol. 222 (2nd ed.), Springer, ISBN 978-3-319-13466-6
• Horn, Roger A.; Johnson, Charles R. (1990). Matrix Analysis. Cambridge University Press. ISBN 978-0-521-38632-6..
• James Stewart (2002). Calculus, 5th ed., Brooks Cole. ISBN 978-0-534-39339-7
• Larson, Hostetler, and Edwards (2005). Calculus with Analytic Geometry, 8th ed., Houghton Mifflin Company. ISBN 978-0-618-50298-1
• Moise, Edwin E. (1967), Calculus: Complete, Reading: Addison-Wesley
• Pappas, T. "Perimeter, Area & the Infinite Series." The Joy of Mathematics. San Carlos, CA: Wide World Publ./Tetra, pp. 134–135, 1989.
• Protter, Murray H.; Morrey, Charles B. Jr. (1970), College Calculus with Analytic Geometry (2nd ed.), Reading: Addison-Wesley, LCCN 76087042
• Roger B. Nelsen (1997). Proofs without Words: Exercises in Visual Thinking, The Mathematical Association of America. ISBN 978-0-88385-700-7

इतिहास और दर्शन

• सी. एच. एडवर्ड्स जूनियर (1994)। कैलकुलस का ऐतिहासिक विकास, तीसरा संस्करण, स्प्रिंगर। ISBN 978-0-387-94313-8.
• Swain, Gordon and Thomas Dence (April 1998). "आर्किमिडीज़ के परवलय के चतुर्भुज पर दोबारा गौर किया गया". Mathematics Magazine. 71 (2): 123–30. doi:10.2307/2691014. JSTOR 2691014.
• वह माओरी है (1991)। टू इनफिनिटी एंड बियॉन्ड: ए कल्चरल हिस्ट्री ऑफ द इनफिनिटी, प्रिंसटन यूनिवर्सिटी प्रेस। ISBN 978-0-691-02511-7
• मोर लेज़ेरोविट्ज़ (2000)। तत्वमीमांसा की संरचना (दर्शनशास्त्र का अंतर्राष्ट्रीय पुस्तकालय), रूटलेज। ISBN 978-0-415-22526-7

अर्थशास्त्र

• कार्ल पी. साइमन और लॉरेंस ब्लूम (1994)। अर्थशास्त्रियों के लिए गणित, डब्ल्यू डब्ल्यू नॉर्टन एंड कंपनी। ISBN 978-0-393-95733-4
• माइक रोसेर (2003)। अर्थशास्त्रियों के लिए बुनियादी गणित, दूसरा संस्करण, रूटलेज। ISBN 978-0-415-26784-7

जीवविज्ञान

• एडवर्ड बैट्स्चेलेट (1992)। जीवन वैज्ञानिकों के लिए गणित का परिचय, तीसरा संस्करण, स्प्रिंगर। ISBN 978-0-387-09648-3
• रिचर्ड एफ. बर्टन (1998)। संख्याओं द्वारा जीवविज्ञान: मात्रात्मक सोच के लिए एक प्रोत्साहन, कैम्ब्रिज यूनिवर्सिटी प्रेस। ISBN 978-0-521-57698-7

कंप्यूटर विज्ञान

• जॉन रास्ट हबर्ड (2000)। शाउम की सिद्धांत की रूपरेखा और जावा, मैकग्रा-हिल के साथ डेटा संरचनाओं की समस्याएं। ISBN 978-0-07-137870-3

बाहरी संबंध

• "Geometric progression", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
• Weisstein, Eric W. "Geometric Series". MathWorld.
• Geometric Series at PlanetMath.
• Peppard, Kim. "College Algebra Tutorial on Geometric Sequences and Series". West Texas A&M University.
• Casselman, Bill. "A Geometric Interpretation of the Geometric Series". Archived from the original (Applet) on 2007-09-29.
• "Geometric Series" by Michael Schreiber, Wolfram Demonstrations Project, 2007.