परिमित अंतर: Difference between revisions
(Created page with "{{Use American English|date = March 2019}} {{Short description|Discrete analog of a derivative}} {{Use mdy dates|date=September 2011}} एक परिमित अंतर...") |
No edit summary |
||
| (13 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
'''परिमित अंतर''' रूप की गणितीय अभिव्यक्ति है {{math|''f'' (''x'' + ''b'') − ''f'' (''x'' + ''a'')}}। यदि एक परिमित अंतर {{math|''b'' − ''a''}} से विभाजित किया जाता है, [[ अंतर भागफल |अंतर भागफल]] मिलता है। परिमित भिन्नताओं द्वारा [[ यौगिक | अवकलज]] का अनुमान [[ अंतर समीकरण |अवकल समीकरण]] के [[ संख्यात्मक विश्लेषण |संख्यात्मक विश्लेषण]] समाधान के लिए[[ परिमित अंतर विधि ]]यों में एक केंद्रीय भूमिका निभाता है विशेष रूप से [[ सीमा मूल्य समस्या |सीमा मूल्य समस्या]] के लिए निभाता है। | |||
[[ अंतर ऑपरेटर ]], | [[ अंतर ऑपरेटर |अंतरसंकारक]], सामान्यतः <math>\Delta</math> के रूप में जाना जाता है, वह [[ ऑपरेटर (गणित) |संकारक (गणित)]] है जो किसी फलन {{mvar|f}} को <math>\Delta[f]</math> द्वारा परिभाषित करता है। | ||
:<math>\Delta[f](x)= f(x+1)-f(x).</math> | :<math>\Delta[f](x)= f(x+1)-f(x).</math> | ||
[[ अंतर समीकरण |अवकल समीकरण]] एक [[ कार्यात्मक समीकरण |फलनिक समीकरण]] है जिसमें परिमित अंतर संकारक उसी तरह सम्मलित होता है जैसे एक अवकल समीकरण में अवकलज सम्मलित होते हैं। अवकल समीकरण और अवकल समीकरण के बीच कई समानताएं हैं, विशेष रूप से हल करने के तरीकों में। कुछ पुनरावृत्ति संबंधों को परिमित अंतरों के साथ पुनरावृत्ति संकेतन को बदलकर अवकल समीकरण के रूप में लिखा जा सकता है। | |||
संख्यात्मक विश्लेषण में, | संख्यात्मक विश्लेषण में, अवकलज का अनुमान लगाने के लिए परिमित अंतर का व्यापक रूप से उपयोग किया जाता है, और "परिमित अंतर" शब्द का उपयोग अधिकांशतः "अवकलज के परिमित अंतर सन्निकटन" के संक्षिप्त रूप में किया जाता है।<ref name="WilmottHowison1995">{{cite book|author1=Paul Wilmott|author2=Sam Howison|author3=Jeff Dewynne|title=वित्तीय डेरिवेटिव का गणित: एक छात्र परिचय|year=1995|publisher=Cambridge University Press|isbn=978-0-521-49789-3|page=[https://archive.org/details/mathematicsoffin00wilm/page/137 137]|url-access=registration|url=https://archive.org/details/mathematicsoffin00wilm/page/137}}</ref><ref name="Olver2013">{{cite book|author=Peter Olver|author-link=Peter J. Olver|title=आंशिक विभेदक समीकरणों का परिचय|year=2013|publisher=Springer Science & Business Media|isbn=978-3-319-02099-0|page=182}}</ref><ref name="Chaudhry2007">{{cite book|author=M Hanif Chaudhry|title=ओपन-चैनल फ्लो|year=2007|publisher=Springer|isbn=978-0-387-68648-6|pages=369}}</ref> परिमित अंतर सन्निकटन ऊपर नियोजित शब्दावली में परिमित अंतर भागफल हैं। | ||
1715 में [[ ब्रुक टेलर ]] द्वारा परिमित अंतर पेश किए गए थे और [[ जॉर्ज बूले ]] (1860), एल.एम. मिल्ने-थॉमसन (1933) द्वारा | 1715 में [[ ब्रुक टेलर |ब्रुक टेलर]] द्वारा परिमित अंतर पेश किए गए थे और [[ जॉर्ज बूले |जॉर्ज बूले]](1860), एल.एम. मिल्ने-थॉमसन (1933), और {{interlanguage link|केरोली जॉर्डन|डी}} (1939) द्वारा फलन में सार स्व-स्थायी गणितीय वस्तुओं के रूप में भी अध्ययन किया गया है। परिमित अंतर अपनी उत्पत्ति को जोस्ट बर्गी के एल्गोरिदम (c. 1592) में से एक में खोजते हैं और [[ आइजैक न्यूटन |आइजैक न्यूटन]] सहित अन्य लोगों द्वारा काम करते हैं। परिमित अंतरों की औपचारिक गणना को अत्युणु की गणना के विकल्प के रूप में देखा जा सकता है।<ref>Jordán, op. cit., p. 1 and Milne-Thomson, p. xxi. | ||
Milne-Thomson, Louis Melville (2000): ''The Calculus of Finite Differences'' (Chelsea Pub Co, 2000) {{ISBN|978-0821821077}}</ref> | Milne-Thomson, Louis Melville (2000): ''The Calculus of Finite Differences'' (Chelsea Pub Co, 2000) {{ISBN|978-0821821077}}</ref> | ||
== मूल प्रकार == | |||
[[File:Finite difference method.svg|तीन प्रकार के परिमित अंतर। x के बारे में केंद्रीय अंतर x.|307x307px|thumb पर फ़ंक्शन के डेरिवेटिव का सबसे अच्छा सन्निकटन देता है]] | |||
सामान्यतः तीन बुनियादी प्रकारों पर विचार किया जाता है: अग्र, पश्च और केंद्रीय परिमित अंतर।<ref name="WilmottHowison1995" /><ref name="Olver2013" /><ref name="Chaudhry2007" /> | |||
अग्रांतर सूत्र, <math>\Delta_h[f],</math> एक फलन {{mvar|f}} के रूप में परिभाषित फलन है | |||
:<math> \Delta_h[f](x) = f(x + h) - f(x). </math> | :<math> \Delta_h[f](x) = f(x + h) - f(x). </math> | ||
अनुप्रयोग के आधार पर, रिक्ति {{mvar|h}} परिवर्तनशील या स्थिर हो सकता है। जब छोड़ा गया, {{mvar|h}} 1 लिया जाता है, वह है, | |||
:<math> \Delta[f](x) = \Delta_1[f](x) =f(x+1)-f(x) .</math> | :<math> \Delta[f](x) = \Delta_1[f](x) =f(x+1)-f(x) .</math> | ||
पश्च अंतर फलन मानों {{mvar|x}} और {{math|''x'' − ''h''}} का उपयोग करता है , {{math|''x'' + ''h''}} और{{mvar|x}} के मानों के अतिरिक्त:: | |||
:<math> \nabla_h[f](x) = f(x) - f(x-h)=\Delta_h[f](x-h). </math> | :<math> \nabla_h[f](x) = f(x) - f(x-h)=\Delta_h[f](x-h). </math> | ||
अंत में, केंद्रीय अंतर द्वारा दिया जाता है | अंत में, केंद्रीय अंतर द्वारा दिया जाता है | ||
:<math> \delta_h[f](x) = f(x+\tfrac{h}2)-f(x-\tfrac{h}2)=\Delta_{h/2}[f](x)+\nabla_{h/2}[f](x).</math> | :<math> \delta_h[f](x) = f(x+\tfrac{h}2)-f(x-\tfrac{h}2)=\Delta_{h/2}[f](x)+\nabla_{h/2}[f](x).</math> | ||
== अवकलज के साथ संबंध == | |||
परिमित अंतर अधिकांशतः व्युत्पन्न के सन्निकटन के रूप में प्रयोग किया जाता है, सामान्यतः संख्यात्मक अवकलन में। | |||
फलन का व्युत्पन्न {{mvar|f}} एक बिंदु पर {{mvar|x}} फलन की सीमा द्वारा परिभाषित किया गया है। | |||
:<math> f'(x) = \lim_{h\to0} \frac{f(x+h) - f(x)}{h}. </math> | :<math> f'(x) = \lim_{h\to0} \frac{f(x+h) - f(x)}{h}. </math> | ||
यदि {{mvar|h}} शून्य के करीब पहुंचने के | यदि {{mvar|h}} शून्य के करीब पहुंचने के अतिरिक्त निश्चित (गैर-शून्य) मान है, तो उपरोक्त समीकरण के दाहिने हाथ की ओर लिखा जाएगा | ||
:<math> \frac{f(x + h) - f(x)}{h} = \frac{\Delta_h[f](x)}{h}. </math> | :<math> \frac{f(x + h) - f(x)}{h} = \frac{\Delta_h[f](x)}{h}. </math> | ||
इसलिए, | इसलिए, जब {{mvar|h}} छोटा है अग्र के अंतर से विभाजित {{mvar|h}} अवकलज का अनुमान लगाता है। इस सन्निकटन में त्रुटि टेलर के प्रमेय से प्राप्त की जा सकती है। ये मानते हुए {{mvar|f}} दो बार अवकलनीय है, हमारे पास है | ||
:<math> \frac{\Delta_h[f](x)}{h} - f'(x) = O(h)\to 0 \quad \text{as }h \to 0. </math> | :<math> \frac{\Delta_h[f](x)}{h} - f'(x) = O(h)\to 0 \quad \text{as }h \to 0. </math> | ||
पश्च अंतर के लिए समान सूत्र है: | |||
:<math> \frac{\nabla_h[f](x)}{h} - f'(x) = O(h)\to 0 \quad \text{as }h \to 0. </math> | :<math> \frac{\nabla_h[f](x)}{h} - f'(x) = O(h)\to 0 \quad \text{as }h \to 0. </math> | ||
चूंकि, केंद्रीय (जिसे केंद्रित भी कहा जाता है) अंतर अधिक सटीक सन्निकटन पैदा करता है। यदि {{mvar|f}} तीन गुना अवकलनीय है, | |||
:<math> \frac{\delta_h[f](x)}{h} - f'(x) = O\left(h^2\right) . </math> | :<math> \frac{\delta_h[f](x)}{h} - f'(x) = O\left(h^2\right) . </math> | ||
मुख्य समस्या | मुख्य समस्या केंद्रीय अंतर विधि के साथ, चूंकि, यह है कि दोलन कार्य शून्य व्युत्पन्न प्राप्त कर सकते हैं। यदि {{math|''f'' (''nh'') {{=}} 1}}, {{mvar|n}} विषम के लिए, और {{math|''f'' (''nh'') {{=}} 2}}, {{mvar|n}} के लिए भी फिर भी {{math|''f'' ′(''nh'') {{=}} 0}} यदि इसकी गणना[[ केंद्रीय अंतर योजना | केंद्रीय अंतर योजना]] से की जाती है। यदि {{mvar|f}} का प्रांत असतत है तो यह विशेष रूप से कठिन है।[[ सममित व्युत्पन्न | सममित व्युत्पन्न]] भी देखें | ||
लेखक जिनके लिए परिमित अंतर का अर्थ है परिमित अंतर सन्निकटन अग्र/पश्च/केंद्रीय अंतर को इस खंड में दिए गए भागफल के रूप में परिभाषित करता है (पिछले खंड में दी गई परिभाषाओं को नियोजित करने के अतिरिक्त)।<ref name="WilmottHowison1995"/><ref name="Olver2013"/><ref name="Chaudhry2007"/> | |||
== उच्च-क्रम अंतर == | == उच्च-क्रम अंतर == | ||
एक समान तरीके से, उच्चतर क्रम अवकलज और अंतर संकारक के लिए परिमित अंतर सन्निकटन प्राप्त कर सकते हैं। उदाहरण के लिए, उपरोक्त केंद्रीय अंतर सूत्र का उपयोग करके {{math|''f'' ′(''x'' + {{sfrac|''h''|2}})}} और {{math|''f'' ′(''x'' − {{sfrac|''h''|2}})}} और {{mvar|x}} पर {{math|''f'' ′}} के अवकलज के लिए केंद्रीय अंतर सूत्र लागू करते हुए, हम {{mvar|f}} के दूसरे अवकलज का केंद्रीय अंतर सन्निकटन प्राप्त करते हैं: | |||
एक समान तरीके से, | ; दूसरा क्रम केंद्रीय | ||
; | |||
:<math> f''(x) \approx \frac{\delta_h^2[f](x)}{h^2} = \frac{ \frac{f(x+h) - f(x)}{h} - \frac{f(x) - f(x-h)}{h} }{h} = \frac{f(x+h) - 2 f(x) + f(x-h)}{h^{2}} . </math> | :<math> f''(x) \approx \frac{\delta_h^2[f](x)}{h^2} = \frac{ \frac{f(x+h) - f(x)}{h} - \frac{f(x) - f(x-h)}{h} }{h} = \frac{f(x+h) - 2 f(x) + f(x-h)}{h^{2}} . </math> | ||
इसी तरह हम अन्य भिन्न सूत्रों को पुनरावर्ती तरीके से लागू कर सकते हैं। | इसी तरह हम अन्य भिन्न सूत्रों को पुनरावर्ती तरीके से लागू कर सकते हैं। | ||
;दूसरा | ;दूसरा क्रम अग्र | ||
:<math> f''(x) \approx \frac{\Delta_h^2[f](x)}{h^2} = \frac{ \frac{f(x+2h) - f(x+h)}{h} - \frac{f(x+h) - f(x)}{h} }{h} = \frac{f(x+2h) - 2 f(x+h) + f(x)}{h^{2}} . </math> | :<math> f''(x) \approx \frac{\Delta_h^2[f](x)}{h^2} = \frac{ \frac{f(x+2h) - f(x+h)}{h} - \frac{f(x+h) - f(x)}{h} }{h} = \frac{f(x+2h) - 2 f(x+h) + f(x)}{h^{2}} . </math> | ||
;दूसरा क्रम | ;दूसरा क्रम पश्च | ||
:<math> f''(x) \approx \frac{\nabla_h^2[f](x)}{h^2} = \frac{ \frac{f(x) - f(x-h)}{h} - \frac{f(x-h) - f(x-2h)}{h} }{h} = \frac{f(x) - 2 f(x-h) + f(x - 2h)}{h^{2}} . </math> | :<math> f''(x) \approx \frac{\nabla_h^2[f](x)}{h^2} = \frac{ \frac{f(x) - f(x-h)}{h} - \frac{f(x-h) - f(x-2h)}{h} }{h} = \frac{f(x) - 2 f(x-h) + f(x - 2h)}{h^{2}} . </math> | ||
अधिक | अधिक सामान्यतः,{{mvar|n}} वें क्रम अग्र, पश्च, और केंद्रीय अंतर क्रमशः द्वारा दिए गए हैं, | ||
; | ;अग्र | ||
:<math>\Delta^n_h[f](x) = \sum_{i = 0}^{n} (-1)^{n-i} \binom{n}{i} f\bigl(x + i h\bigr),</math> | :<math>\Delta^n_h[f](x) = \sum_{i = 0}^{n} (-1)^{n-i} \binom{n}{i} f\bigl(x + i h\bigr),</math> | ||
या | या {{math|''h'' {{=}} 1}} के लिए, | ||
:<math>\Delta^n [f](x)= \sum_{i=0}^n\binom ni(-1)^{n-i}f(x + i)</math> | :<math>\Delta^n [f](x)= \sum_{i=0}^n\binom ni(-1)^{n-i}f(x + i)</math> | ||
पश्च | |||
:<math>\nabla^n_h[f](x) = \sum_{i = 0}^{n} (-1)^i \binom{n}{i} f(x - ih),</math> | :<math>\nabla^n_h[f](x) = \sum_{i = 0}^{n} (-1)^i \binom{n}{i} f(x - ih),</math> | ||
;केंद्रीय | ;केंद्रीय | ||
:<math>\delta^n_h[f](x) = \sum_{i = 0}^{n} (-1)^i \binom{n}{i} f\left(x + \left(\frac{n}{2} - i\right) h\right).</math> | :<math>\delta^n_h[f](x) = \sum_{i = 0}^{n} (-1)^i \binom{n}{i} f\left(x + \left(\frac{n}{2} - i\right) h\right).</math> | ||
योग चिह्न | इन समीकरणों में योग चिह्न के बाद [[ द्विपद गुणांक |द्विपद गुणांक]] का उपयोग किया जाता है, जैसा कि दिखाया गया है {{math|<big><big>(</big></big>{{su|p=''n''|b=''i''|a=c}}<big><big>)</big></big>}}। पास्कल के त्रिभुज की प्रत्येक पंक्ति i के प्रत्येक मान के लिए गुणांक प्रदान करती है। | ||
ध्यान दें कि | ध्यान दें कि केंद्रीय अंतर, विषम {{mvar|n}} के लिए, {{mvar|h}} को गैर-पूर्णांक से गुणा करेगा। यह अधिकांशतः एक समस्या होती है क्योंकि यह विवेक के अंतराल को बदलने के बराबर होती है। {{math|''δ<sup>n</sup>''[ ''f'' ](''x'' − {{sfrac|''h''|2}})}} और {{math|''δ<sup>n</sup>''[ ''f'' ](''x'' + {{sfrac|''h''|2}})}} का औसत लेकर समस्या का समाधान किया जा सकता है | ||
[[ क्रम |अनुक्रम]] पर लागू किए गए अग्र अंतर को कभी-कभी अनुक्रम का [[ द्विपद परिवर्तन | द्विपद परिवर्तन]] कहा जाता है, और इसमें कई रोचक संयोजी गुण होते हैं। नॉर्लंड-राइस इंटीग्रल का उपयोग करके आगे के अंतर का मूल्यांकन किया जा सकता है। इस प्रकार की श्रृंखलाओं के लिए अभिन्न प्रतिनिधित्व रोचक है, क्योंकि अभिन्न का मूल्यांकन अधिकांशतः [[ स्पर्शोन्मुख विस्तार |स्पर्शोन्मुख विस्तार]] या सैडल-पॉइंट तकनीकों का उपयोग करके किया जा सकता है, इसके विपरीत, आगे की अंतर श्रृंखला संख्यात्मक रूप से मूल्यांकन करने के लिए बेहद कठिन हो सकती है, क्योंकि बड़े {{mvar|n}} के लिए द्विपद गुणांक तेजी से बढ़ते हैं। | |||
संबंधित | संबंधित अवकलज के साथ इन उच्च-क्रम के अंतरों का संबंध सीधा है, | ||
:<math>\frac{d^n f}{d x^n}(x) = \frac{\Delta_h^n[f](x)}{h^n}+O(h) = \frac{\nabla_h^n[f](x)}{h^n}+O(h) = \frac{\delta_h^n[f](x)}{h^n} + O\left(h^2\right).</math> | :<math>\frac{d^n f}{d x^n}(x) = \frac{\Delta_h^n[f](x)}{h^n}+O(h) = \frac{\nabla_h^n[f](x)}{h^n}+O(h) = \frac{\delta_h^n[f](x)}{h^n} + O\left(h^2\right).</math> | ||
बेहतर सन्निकटन बनाने के लिए उच्च-क्रम के अंतर का भी उपयोग किया जा सकता है। जैसा कि ऊपर उल्लेख किया गया है, प्रथम-क्रम अंतर | बेहतर सन्निकटन बनाने के लिए उच्च-क्रम के अंतर का भी उपयोग किया जा सकता है। जैसा कि ऊपर उल्लेख किया गया है, प्रथम-क्रम अंतर क्रम {{mvar|h}} की अवधि तक प्रथम-क्रम व्युत्पन्न का अनुमान लगाता है। हालाँकि, संयोजन | ||
:<math> \frac{\Delta_h[f](x) - \frac12 \Delta_h^2[f](x)}{h} = - \frac{f(x+2h)-4f(x+h)+3f(x)}{2h} </math> | :<math> \frac{\Delta_h[f](x) - \frac12 \Delta_h^2[f](x)}{h} = - \frac{f(x+2h)-4f(x+h)+3f(x)}{2h} </math> | ||
अनुमानित {{math|''f'' ′(''x'')}} | अनुमानित {{math|''f'' ′(''x'')}} क्रम {{math|''h''<sup>2</sup>}} की अवधि तक। यह [[ टेलर श्रृंखला |टेलर श्रृंखला]] में उपरोक्त अभिव्यक्ति का विस्तार करके या परिमित अंतरों के कलन का उपयोग करके सिद्ध किया जा सकता है, जिसे नीचे समझाया गया है। | ||
यदि आवश्यक हो, तो | यदि आवश्यक हो, तो अग्र, पश्च और केंद्रीय अंतरों को मिलाकर परिमित अंतर को किसी भी बिंदु पर केंद्रित किया जा सकता है। | ||
== [[ बहुपद ]] == | == [[ बहुपद ]] == | ||
घात के दिए गए बहुपद के लिए {{math|''n'' ≥ 1}} फलन {{math|''P(x)''}} में व्यक्त किया, वास्तविक संख्या के साथ {{math|''a'' ≠ 0}} और {{math|''b''}} और निचले क्रम की शर्तें (यदि कोई हो) के रूप में चिह्नित {{math|''l.o.t.''}}: | |||
<math>P(x) = ax^n + bx^{n-1} + l.o.t.</math> | <math>P(x) = ax^n + bx^{n-1} + l.o.t.</math> | ||
{{math|''n''}} युग्मानूसार अंतरों के बाद, निम्न परिणाम प्राप्त किया जा सकता है, जहाँ {{math|''h'' ≠ 0}} अंकगणितीय अंतर को चिह्नित करने वाली एक वास्तविक संख्या है:<ref>{{cite web | url=https://divisbyzero.com/2018/02/13/finite-differences-of-polynomials/ | title=बहुपदों के परिमित अंतर| date=February 13, 2018 }}</ref> | |||
<math>\Delta_h^n [P](x) = ah^nn!</math> | <math>\Delta_h^n [P](x) = ah^nn!</math> | ||
केवल उच्चतम-क्रम पद का गुणांक रहता है। चूंकि यह परिणाम | |||
केवल उच्चतम-क्रम पद का गुणांक रहता है। चूंकि यह परिणाम {{math|''x''}} के संबंध में स्थिर है , किसी भी युग्मानूसार अंतर का मान {{math|0}} होगा। | |||
=== आगमनात्मक प्रमाण === | === आगमनात्मक प्रमाण === | ||
==== | ==== आधार मामले ==== | ||
मान लीजिए {{math|''Q(x)''}} घात {{math|1}}का एक बहुपद है: | |||
<math>\Delta_h [Q](x) = Q(x + h) - Q(x) = [a(x + h) + b] - [ax + b] = ah = ah^11!</math> | <math>\Delta_h [Q](x) = Q(x + h) - Q(x) = [a(x + h) + b] - [ax + b] = ah = ah^11!</math>यह इसे आधार मामले के लिए सिद्ध करता है। | ||
यह इसे आधार मामले के लिए | |||
==== स्टेप केस ==== | ==== स्टेप केस ==== | ||
मान लें कि {{math|''R(x)''}} घात {{math|''m''-1}} का बहुपद है जहाँ {{math|''m'' ≥ 2}} और उच्चतम क्रम वाले पद का गुणांक {{math|''a'' ≠ 0}} है। यह मानते हुए कि घात {{math|''m''-1}} के सभी बहुपदों के लिए निम्नलिखित सही है: | |||
<math>\Delta_h^{m-1} [R](x) = ah^{m-1}(m-1)!</math> | <math>\Delta_h^{m-1} [R](x) = ah^{m-1}(m-1)!</math> | ||
<math>\Delta_h [S](x) = [a(x+h)^{m} + b(x+h)^{m-1} + l.o.t.] - [ax^m + bx^{m-1} + l.o.t.] = ahmx^{m-1} + l.o.t. = T(x)</math> | मान लीजिए कि {{math|''S(x)''}} घात {{math|''m''}} का एक बहुपद है। एक युग्मानूसार अंतर के साथ: | ||
<math>\Delta_h [S](x) = [a(x+h)^{m} + b(x+h)^{m-1} + l.o.t.] - [ax^m + bx^{m-1} + l.o.t.] = ahmx^{m-1} + l.o.t. = T(x)</math> {{math|''ahm'' ≠ 0}},के रूप में, इसका परिणाम {{math|''m''-1}} घात के बहुपद {{math|''T(x)''}} में होता है, जिसमें {{math|''ahm''}} उच्चतम-क्रम पद का गुणांक होता है। उपरोक्त धारणा और {{math|''m''-1}} युग्मानूसार अंतरों को देखते हुए (परिणामस्वरूप {{math|''S(x)''}} के लिए कुल {{math|''m''}} युग्मानूसार अंतर), यह पाया जा सकता है कि: | |||
<math>\Delta_h^{m-1} [T](x) = ahm \cdot h^{m-1}(m-1)! = ah^mm!</math> | <math>\Delta_h^{m-1} [T](x) = ahm \cdot h^{m-1}(m-1)! = ah^mm!</math> | ||
यह प्रमाण को पूरा करता है। | यह प्रमाण को पूरा करता है। | ||
=== | === अनुप्रयोग === | ||
इस पहचान का उपयोग सबसे कम- | इस पहचान का उपयोग सबसे कम-घात वाले बहुपद को खोजने के लिए किया जा सकता है जो कई बिंदुओं {{math|(x, y)}} को रोकता है जहाँ x-अक्ष पर एक बिंदु से दूसरे बिंदु का अंतर एक स्थिरांक{{math|h ≠ 0}} है, उदाहरण के लिए, निम्नलिखित बिंदु दिए गए हैं: | ||
{| class="wikitable" | {| class="wikitable" | ||
| Line 132: | Line 123: | ||
| 13 || 6364 | | 13 || 6364 | ||
|} | |} | ||
हम अंतर तालिका का उपयोग कर सकते हैं, जहां | हम अंतर तालिका का उपयोग कर सकते हैं, जहां पहले {{math|y}}, के दाईं ओर सभी सेल, कॉलम में सेल के लिए निम्न संबंध तुरंत बाईं ओर सेल {{math|(a+1, b+1)}} के लिए सम्मलित है, सबसे ऊपर-बाएं सेल निर्देशांक पर है {{math|(0, 0)}}: | ||
<math>(a+1, b+1) = (a, b) - (a, b+1)</math> | <math>(a+1, b+1) = (a, b) - (a, b+1)</math> | ||
पहला पद ज्ञात करने के लिए, निम्न तालिका का उपयोग किया जा सकता है: | पहला पद ज्ञात करने के लिए, निम्न तालिका का उपयोग किया जा सकता है: | ||
| Line 156: | Line 148: | ||
| 6364 || 3723 || 1854 || 648 | | 6364 || 3723 || 1854 || 648 | ||
|} | |} | ||
यह | यह स्थिरांक {{math|648}} पर आता है। अंकगणितीय अंतर {{math|h{{=}}3}} है, जैसा कि ऊपर स्थापित किया गया है। स्थिरांक तक पहुँचने के लिए युग्मानूसार अंतरों की संख्या को देखते हुए, यह अनुमान लगाया जा सकता है कि यह घात {{math|3}} का बहुपद है। इस प्रकार, उपरोक्त पहचान का उपयोग करना: | ||
<math>648 = a \cdot 3^3 \cdot 3! = a \cdot 27 \cdot 6 = a \cdot 162</math> | <math>648 = a \cdot 3^3 \cdot 3! = a \cdot 27 \cdot 6 = a \cdot 162</math> | ||
{{math|a}} को हल करने पर, इसका मान 4 पाया जा सकता है। इस प्रकार, बहुपद का पहला पद है {{math|'''4x<sup>3</sup>'''}}. | |||
फिर, पहले पद को घटाकर, जो बहुपद की घात को कम करता है, और परिमित अंतर को फिर से ज्ञात करता है: | फिर, पहले पद को घटाकर, जो बहुपद की घात को कम करता है, और परिमित अंतर को फिर से ज्ञात करता है: | ||
| Line 182: | Line 175: | ||
| {{math|6364 - 4(13)<sup>3</sup> {{=}} 6364 - 8788 {{=}} -2424}} || -1065 || -306 | | {{math|6364 - 4(13)<sup>3</sup> {{=}} 6364 - 8788 {{=}} -2424}} || -1065 || -306 | ||
|} | |} | ||
यहाँ, स्थिरांक केवल 2 | यहाँ, स्थिरांक केवल 2 युग्मानूसार अंतरों के बाद प्राप्त किया जाता है, इस प्रकार निम्न परिणाम: | ||
<math>-306 = a \cdot 3^2 \cdot 2! = a \cdot 18</math> | <math>-306 = a \cdot 3^2 \cdot 2! = a \cdot 18</math> | ||
{{math|a}} को हल करने पर, जो {{math|-17}} है, बहुपद का दूसरा पद {{math|'''-17x<sup>2</sup>'''}} है . | |||
दूसरे पद को घटाकर, अगले पद पर जाना: | दूसरे पद को घटाकर, अगले पद पर जाना: | ||
| Line 208: | Line 202: | ||
| {{math|-2424 - (-17(13)<sup>2</sup>) {{=}} -2424 + 2873 {{=}} 449 }} || 108 | | {{math|-2424 - (-17(13)<sup>2</sup>) {{=}} -2424 + 2873 {{=}} 449 }} || 108 | ||
|} | |} | ||
इस प्रकार स्थिर केवल 1 | इस प्रकार स्थिर केवल 1 युग्मानूसार अंतर के बाद प्राप्त किया जाता है: | ||
<math>108 = a \cdot 3^1 \cdot 1! = a \cdot 3</math> | <math>108 = a \cdot 3^1 \cdot 1! = a \cdot 3</math> | ||
यह पाया जा सकता है {{math|a {{=}} 36}} और इस प्रकार बहुपद का तीसरा पद | |||
यह पाया जा सकता है {{math|a {{=}} 36}} और इस प्रकार बहुपद का तीसरा पद{{math|'''36x'''}} है, तीसरे पद को घटाना: | |||
{| class="wikitable" | {| class="wikitable" | ||
| Line 232: | Line 227: | ||
| {{math|449 - 36(13) {{=}} 449 - 468 {{=}} -19}} | | {{math|449 - 36(13) {{=}} 449 - 468 {{=}} -19}} | ||
|} | |} | ||
बिना किसी युग्मवार अंतर के, यह पाया जाता है कि बहुपद का चौथा और अंतिम पद अचर | बिना किसी युग्मवार अंतर के, यह पाया जाता है कि बहुपद का चौथा और अंतिम पद अचर {{math|-19}} है, इस प्रकार, पहली तालिका में सभी बिंदुओं को अंतर्रोधक करने वाला निम्नतम-घात बहुपद पाया जाता है: | ||
<math>4x^3 - 17x^2 + 36x - 19</math> | <math>4x^3 - 17x^2 + 36x - 19</math> | ||
== अव्यवस्थित आकार मूल == | |||
{{main|परिमित अंतर गुणांक}} | |||
{{further|पांच सूत्री स्टैंसिल}} | |||
रेखीय बीजगणित का उपयोग करके परिमित अंतर सन्निकटन का निर्माण किया जा सकता है जो किसी भी क्रम व्युत्पन्न के लिए बाईं ओर बिंदुओं की अव्यवस्थित संख्या और मूल्यांकन बिंदु के दाईं ओर (संभवतः भिन्न) अंकों की संख्या का उपयोग करता है। इसमें रेखीय प्रणाली को हल करना सम्मलित है जैसे कि मूल्यांकन बिंदु के चारों ओर उन बिंदुओं के योग का [[ टेलर विस्तार |टेलर विस्तार]] वांछित व्युत्पन्न के टेलर विस्तार का सबसे अच्छा अनुमान लगाता है। इस तरह के सूत्रों को हेक्सागोनल या हीरे के आकार के ग्रिड पर रेखांकन के रूप में दर्शाया जा सकता है।<ref>{{cite journal|last1=Fraser|first1=Duncan C.|title=इंटरपोलेशन फॉर्मूले के ग्राफिक चित्रण पर|journal=Journal of the Institute of Actuaries|date=1 January 1909|volume=43|issue=2|pages=235–241|doi=10.1017/S002026810002494X|url=https://archive.org/stream/journal43instuoft#page/236/mode/2up|access-date=17 April 2017}}</ref> | |||
यह ग्रिड पर फलन को अलग करने के लिए उपयोगी है, जहां एक ग्रिड के किनारे तक पहुंचता है, उसे एक तरफ कम और कम बिंदुओं का नमूना लेना चाहिए। | |||
यह | |||
विवरण इन [http://commons.wikimedia.org/wiki/File:FDnotes.djvu नोट्स] में दिए गए हैं। | विवरण इन [http://commons.wikimedia.org/wiki/File:FDnotes.djvu नोट्स] में दिए गए हैं। | ||
[http://web.media.mit.edu/~crtaylor/calculator.html परिमित अंतर गुणांक कैलक्यूलेटर] गैर-मानक (और यहां तक कि गैर-पूर्णांक) स्टेंसिल के लिए परिमित अंतर सन्निकटन का निर्माण करता है जिसे | [http://web.media.mit.edu/~crtaylor/calculator.html परिमित अंतर गुणांक कैलक्यूलेटर] गैर-मानक (और यहां तक कि गैर-पूर्णांक) स्टेंसिल के लिए परिमित अंतर सन्निकटन का निर्माण करता है जिसे अव्यवस्थित स्टैंसिल और वांछित व्युत्पन्न क्रम दिया जाता है . | ||
=== गुण === | === गुण === | ||
* सभी | * सभी घनात्मक {{mvar|k}} और {{mvar|n}} के लिए<math display="block">\Delta^n_{kh} (f, x) = \sum\limits_{i_1=0}^{k-1} \sum\limits_{i_2=0}^{k-1} \cdots \sum\limits_{i_n=0}^{k-1} \Delta^n_h \left(f, x+i_1h+i_2h+\cdots+i_nh\right).</math> | ||
* [[ लीबनिज नियम (सामान्यीकृत उत्पाद नियम) ]]: <math display="block">\Delta^n_h (fg, x) = \sum\limits_{k=0}^n \binom{n}{k} \Delta^k_h (f, x) \Delta^{n-k}_h(g, x+kh).</math> | * [[ लीबनिज नियम (सामान्यीकृत उत्पाद नियम) ]]: <math display="block">\Delta^n_h (fg, x) = \sum\limits_{k=0}^n \binom{n}{k} \Delta^k_h (f, x) \Delta^{n-k}_h(g, x+kh).</math> | ||
== अवकल समीकरण में == | |||
{{main article|परिमित अंतर विधि}} | |||
परिमित अंतरों का महत्वपूर्ण अनुप्रयोग संख्यात्मक विश्लेषण में है, विशेष रूप से [[ संख्यात्मक आंशिक अंतर समीकरण |संख्यात्मक आंशिक अवकल समीकरण]] में, जो [[ साधारण अंतर समीकरण |साधारण अवकल समीकरण]] और आंशिक अवकल समीकरण के संख्यात्मक समाधान का लक्ष्य रखता है। विचार यह है [[ आंशिक विभेदक समीकरण |आंशिक विभेदक समीकरण]] में दिखाई देने वाले अवकलज को परिमित अंतर से बदल दिया जाए जो उन्हें अनुमानित करता है। परिणामी विधियों को परिमित अंतर विधियाँ कहा जाता है। | |||
कम्प्यूटेशनल विज्ञान और इंजीनियरिंग विषयों में परिमित अंतर विधि के सामान्य अनुप्रयोग हैं, जैसे [[ थर्मल इंजीनियरिंग |ऊष्मा इंजीनियरी]], द्रव यांत्रिकी, आदि। | |||
कम्प्यूटेशनल विज्ञान और इंजीनियरिंग विषयों में परिमित अंतर विधि के सामान्य अनुप्रयोग हैं, जैसे [[ थर्मल इंजीनियरिंग ]], द्रव यांत्रिकी, आदि। | |||
== न्यूटन की श्रृंखला == | == न्यूटन की श्रृंखला == | ||
[[ न्यूटन बहुपद ]] में न्यूटन | [[ न्यूटन बहुपद |न्यूटन बहुपद]] में न्यूटन अग्रांतर समीकरण की शर्तें सम्मलित हैं, जिसका नाम इसहाक न्यूटन के नाम पर रखा गया है, संक्षेप में, यह न्यूटन अंतर्वेशन सूत्र है, जो पहली बार 1687 में उनके 'फिलोसोफी नेचुरेलिस प्रिंसिपिया मैथेमेटिका' में प्रकाशित हुआ था।<ref>Newton, Isaac, (1687). [https://archive.org/details/bub_gb_KaAIAAAAIAAJ/page/n459 <!-- pg=466 quote=sir isaac newton principia mathematica. --> ''Principia'', Book III, Lemma V, Case 1]</ref> अर्थात् निरंतर टेलर विस्तार का असतत अनुरूप, | ||
{{Equation box 1 | {{Equation box 1 | ||
| Line 270: | Line 263: | ||
|border colour = #0073CF | |border colour = #0073CF | ||
|background colour=#F9FFF7}} | |background colour=#F9FFF7}} | ||
जो किसी भी बहुपद | जो किसी भी बहुपद फलन {{mvar|f}} के लिए और कई (लेकिन सभी नहीं) [[ विश्लेषणात्मक कार्य |विश्लेषणात्मक फलन]] के लिए है। (यह धारण नहीं करता है जब {{mvar|f}} चरघातांकी प्रकार <math>\pi</math> है ,इसे आसानी से देखा जा सकता है, क्योंकि <math>\pi</math>, संबंधित न्यूटन श्रृंखला समान रूप से शून्य है, क्योंकि इस मामले में सभी परिमित अंतर शून्य हैं। फिर भी स्पष्ट रूप से, ज्या फलन शून्य नहीं है।) यहाँ, व्यंजक | ||
:<math>\binom{x}{k} = \frac{(x)_k}{k!}</math> | :<math>\binom{x}{k} = \frac{(x)_k}{k!}</math> | ||
द्विपद गुणांक है, और | द्विपद गुणांक है, और | ||
:<math>(x)_k=x(x-1)(x-2)\cdots(x-k+1)</math> | :<math>(x)_k=x(x-1)(x-2)\cdots(x-k+1)</math> | ||
"फॉलिंग फैक्टोरियल" या "लोअर फैक्टोरियल" है, जबकि खाली उत्पाद {{math|(''x'')<sub>0</sub>}} को 1 के रूप में परिभाषित किया गया है। इस विशेष मामले में, {{math|''x'', ''h'' {{=}} 1}} के मान में परिवर्तन के लिए इकाई चरणों की धारणा है। नीचे दिए गए सामान्यीकरण का। | |||
टेलर के प्रमेय के इस परिणाम के औपचारिक पत्राचार पर ध्यान दें। ऐतिहासिक रूप से, यह, साथ ही चू-वंडरमोंड पहचान, | टेलर के प्रमेय के इस परिणाम के औपचारिक पत्राचार पर ध्यान दें। ऐतिहासिक रूप से, यह, साथ ही चू-वंडरमोंड पहचान हैं, | ||
:<math>(x+y)_n=\sum_{k=0}^n \binom{n}{k} (x)_{n-k} \,(y)_k ,</math> | :<math>(x+y)_n=\sum_{k=0}^n \binom{n}{k} (x)_{n-k} \,(y)_k ,</math> | ||
(इससे अनुसरण करते हुए, और [[ द्विपद प्रमेय ]] के अनुरूप), उन टिप्पणियों में | (इससे अनुसरण करते हुए, और [[ द्विपद प्रमेय |द्विपद प्रमेय]] के अनुरूप), उन टिप्पणियों में सम्मलित हैं जो [[ अम्ब्रल कैलकुलस | अम्ब्रल कैलकुलस]] की प्रणाली के लिए परिपक्व हैं। | ||
न्यूटन श्रृंखला विस्तार टेलर श्रृंखला विस्तार से बेहतर हो सकता है जब क्वांटम स्पिन (होल्स्टीन-प्रिमाकॉफ परिवर्तन देखें), | न्यूटन श्रृंखला विस्तार टेलर श्रृंखला विस्तार से बेहतर हो सकता है जब क्वांटम स्पिन (होल्स्टीन-प्रिमाकॉफ परिवर्तन देखें), बोसोनिक ऑपरेटर फलन या असतत गिनती सांख्यिकी जैसी असतत मात्राओं पर लागू किया जाता है।<ref name="Hucht">Jürgen König and Alfred Hucht, [https://scipost.org/10.21468/SciPostPhys.10.1.007 ''SciPost Phys. '' '''10''', 007 (2021)] {{doi| 10.21468/SciPostPhys.10.1.007}}</ref> | ||
वास्तविक अभ्यास में कोई न्यूटन के सूत्र का उपयोग कैसे कर सकता है, यह समझाने के लिए, फाइबोनैचि अनुक्रम को दोगुना करने के पहले कुछ शब्दों पर विचार करें। {{math|''f'' {{=}} 2, 2, 4, ...}} कोई | |||
वास्तविक अभ्यास में कोई न्यूटन के सूत्र का उपयोग कैसे कर सकता है, यह समझाने के लिए, फाइबोनैचि अनुक्रम को दोगुना करने के पहले कुछ शब्दों पर विचार करें। {{math|''f'' {{=}} 2, 2, 4, ...}} कोई बहुपद खोज सकता है जो पहले एक अंतर तालिका की गणना करके, और फिर {{math|''x''<sub>0</sub>}} (रेखांकित) के अनुरूप अंतर को सूत्र में निम्नानुसार प्रतिस्थापित करना,<math> | |||
\begin{matrix} | \begin{matrix} | ||
| Line 308: | Line 301: | ||
\end{matrix} | \end{matrix} | ||
</math> | </math> | ||
{{mvar|x}} के मानों में असमान चरणों के मामले में, न्यूटन विभाजित अंतरों की गणना करता है, | |||
:<math>\Delta _{j,0}=y_j,\qquad \Delta _{j,k}=\frac{\Delta _{j+1,k-1}-\Delta _{j,k-1}}{x_{j+k}-x_j}\quad \ni \quad \left\{ k>0,\; j\le \max \left( j \right)-k \right\},\qquad \Delta 0_k=\Delta _{0,k}</math> | :<math>\Delta _{j,0}=y_j,\qquad \Delta _{j,k}=\frac{\Delta _{j+1,k-1}-\Delta _{j,k-1}}{x_{j+k}-x_j}\quad \ni \quad \left\{ k>0,\; j\le \max \left( j \right)-k \right\},\qquad \Delta 0_k=\Delta _{0,k}</math> | ||
उत्पादों की श्रृंखला, | उत्पादों की श्रृंखला, | ||
| Line 315: | Line 309: | ||
:<math>f(\xi ) = \Delta 0 \cdot P\left( \xi \right)</math> . | :<math>f(\xi ) = \Delta 0 \cdot P\left( \xi \right)</math> . | ||
पी-एडिक | पी-एडिक संख्याओं के विश्लेषण में, महलर के प्रमेय में कहा गया है कि यह धारणा कि {{mvar|f}} बहुपद फलन है इस धारणा के लिए सभी तरह से कमजोर हो सकती है कि {{mvar|f}} केवल निरंतर है। | ||
कार्लसन की प्रमेय न्यूटन श्रृंखला के अद्वितीय होने के लिए आवश्यक और पर्याप्त शर्तें प्रदान करती है, यदि यह | कार्लसन की प्रमेय न्यूटन श्रृंखला के अद्वितीय होने के लिए आवश्यक और पर्याप्त शर्तें प्रदान करती है, यदि यह सम्मलित है। हालाँकि, न्यूटन श्रृंखला सामान्य रूप से सम्मलित नहीं है। | ||
न्यूटन श्रृंखला, [[ स्टर्लिंग श्रृंखला ]] और [[ सेलबर्ग वर्ग ]] के साथ, सामान्य [[ अंतर श्रृंखला ]] का एक विशेष मामला है, जिनमें से सभी को उपयुक्त रूप से | न्यूटन श्रृंखला, [[ स्टर्लिंग श्रृंखला |स्टर्लिंग श्रृंखला]] और [[ सेलबर्ग वर्ग |सेलबर्ग वर्ग]] के साथ, सामान्य [[ अंतर श्रृंखला |अंतर श्रृंखला]] का एक विशेष मामला है, जिनमें से सभी को उपयुक्त रूप से अग्र बढ़ने वाले अंतरों के संदर्भ में परिभाषित किया गया है। | ||
एक संकुचित और थोड़ा अधिक सामान्य रूप और समदूरस्थ नोड्स में सूत्र पढ़ता है | एक संकुचित और थोड़ा अधिक सामान्य रूप और समदूरस्थ नोड्स में सूत्र पढ़ता है | ||
:<math>f(x)=\sum_{k=0}\binom{\frac{x-a}h}{k} \sum_{j=0}^k (-1)^{k-j}\binom{k}{j}f(a+j h).</math> | :<math>f(x)=\sum_{k=0}\binom{\frac{x-a}h}{k} \sum_{j=0}^k (-1)^{k-j}\binom{k}{j}f(a+j h).</math> | ||
== परिमित अंतरों की गणना == | == परिमित अंतरों की गणना == | ||
अग्र के अंतर को संकारक (गणित) के रूप में माना जा सकता है, जिसे अंतरसंकारक कहा जाता है, जो फलन को {{mvar|f}} को {{math|Δ<sub>''h''</sub>[ ''f'' ]}} मैप करता है<ref>[[George Boole|Boole, George]], (1872). ''A Treatise On The Calculus of Finite Differences'', 2nd ed., Macmillan and Company. [https://archive.org/details/cu31924031240934 On line]. Also, [Dover edition 1960]</ref><ref>Jordan, Charles, (1939/1965). "Calculus of Finite Differences", Chelsea Publishing. On-line: [https://books.google.com/books?hl=en&lr=&id=3RfZOsDAyQsC&oi=fnd&pg=PA1&ots=AqSuAgOKs3&sig=fzPpAdvnzp7sG6PorqIe5qFjD2Q#v=onepage]</ref> इस संकारक की राशि है | |||
::<math>\Delta_h = T_h-I, </math> | ::<math>\Delta_h = T_h-I, </math> | ||
जहाँ {{math|''T''<sub>''h''</sub>}} चरण ''h''वाला[[ शिफ्ट ऑपरेटर | शिफ्ट ऑपरेटर]] है जिसे {{math|''T''<sub>''h''</sub>[ ''f'' ](''x'') {{=}} ''f'' (''x'' + ''h'')}} द्वारा परिभाषित किया गया है, और {{mvar|I}} [[ पहचान ऑपरेटर | पहचान]] [[ शिफ्ट ऑपरेटर |ऑपरेटर]] है। | |||
उच्च आदेशों के परिमित अंतर को पुनरावर्ती तरीके से परिभाषित किया जा सकता है {{math|Δ{{su|b=''h''|p=''n''}} ≡ Δ<sub>''h''</sub>(Δ{{su|b=''h''|p=''n'' − 1}})}}, एक अन्य समकक्ष परिभाषा है {{math|Δ{{su|b=''h''|p=''n''}} {{=}} [''T''<sub>''h''</sub> − ''I'']<sup>''n''</sup>}}. | |||
अंतरसंकारक {{math|Δ<sub>''h''</sub>}} रैखिक संकारक है, इसलिए यह संतुष्ट करता है {{math|Δ<sub>''h''</sub>[''αf'' + ''βg''](''x'') {{=}} ''α'' Δ<sub>''h''</sub>[ ''f'' ](''x'') + ''β'' Δ<sub>''h''</sub>[''g''](''x'')}}. | |||
यह ऊपर बताए गए विशेष लीबनिज़ नियम (सामान्यीकृत उत्पाद नियम) को भी संतुष्ट करता है, | |||
{{math|Δ<sub>''h''</sub>(''f'' (''x'')''g''(''x'')) {{=}} (Δ<sub>''h''</sub>''f'' (''x'')) ''g''(''x''+''h'') + ''f'' (''x'') (Δ<sub>''h''</sub>''g''(''x''))}}, इसी तरह के बयान पश्च और केंद्रीय अंतर के लिए हैं। | |||
{{math|Δ<sub>''h''</sub>(''f'' (''x'')''g''(''x'')) {{=}} (Δ<sub>''h''</sub>''f'' (''x'')) ''g''(''x''+''h'') + ''f'' (''x'') (Δ<sub>''h''</sub>''g''(''x''))}} | |||
{{mvar|h}} के संबंध में टेलर श्रृंखला को औपचारिक रूप से लागू करने से सूत्र प्राप्त होता है | |||
:<math> \Delta_h = hD + \frac{1}{2!} h^2D^2 + \frac{1}{3!} h^3D^3 + \cdots = \mathrm{e}^{hD} - I , </math> | :<math> \Delta_h = hD + \frac{1}{2!} h^2D^2 + \frac{1}{3!} h^3D^3 + \cdots = \mathrm{e}^{hD} - I , </math> | ||
जहाँ {{mvar|D}} निरंतर व्युत्पन्न संकारक, मैपिंग को दर्शाता है {{mvar|f}} को इसके डेरिवेटिव {{math|''f'' ′}} मैपिंग करता है। विस्तार तब मान्य होता है जब दोनों पक्ष पर्याप्त रूप से छोटे {{mvar|h}} के लिए विश्लेषणात्मक फलन पर कार्य करते हैं। इस प्रकार, {{math|''T''<sub>''h''</sub> {{=}} ''e''<sup>''hD''</sup>}}, और औपचारिक रूप से घातांकीय प्रतिफल को उलटा करना | |||
:<math> hD = \log(1+\Delta_h) = \Delta_h - \tfrac{1}{2} \Delta_h^2 + \tfrac{1}{3} \Delta_h^3 - \cdots. </math> | :<math> hD = \log(1+\Delta_h) = \Delta_h - \tfrac{1}{2} \Delta_h^2 + \tfrac{1}{3} \Delta_h^3 - \cdots. </math> | ||
यह सूत्र इस अर्थ में है कि बहुपद पर लागू होने पर दोनों संकारक समान परिणाम देते हैं। | यह सूत्र इस अर्थ में है कि बहुपद पर लागू होने पर दोनों संकारक समान परिणाम देते हैं। | ||
विश्लेषणात्मक | विश्लेषणात्मक फलन के लिए भी, दाईं ओर की श्रृंखला को अभिसरण की गारंटी नहीं है, यह[[ स्पर्शोन्मुख श्रृंखला |स्पर्शोन्मुख श्रृंखला]] हो सकती है। चूंकि, इसका उपयोग व्युत्पन्न के लिए अधिक सटीक सन्निकटन प्राप्त करने के लिए किया जा सकता है। उदाहरण के लिए, श्रृंखला के पहले दो शब्दों को बनाए रखने से खंड उच्च-क्रम के अंतर के अंत में उल्लिखित {{math|''f'' ′(''x'')}} के लिए दूसरे क्रम का सन्निकटन प्राप्त होता है। | ||
पश्च और केंद्रीय अंतर संकारक के लिए समान सूत्र हैं | |||
:<math> hD = -\log(1-\nabla_h) \quad\text{and}\quad hD = 2 \operatorname{arsinh}\left(\tfrac12\delta_h\right). </math> | :<math> hD = -\log(1-\nabla_h) \quad\text{and}\quad hD = 2 \operatorname{arsinh}\left(\tfrac12\delta_h\right). </math> | ||
परिमित अंतरों की गणना कॉम्बिनेटरिक्स के अम्ब्रल कैलकुलस से संबंधित है। यह उल्लेखनीय रूप से व्यवस्थित पत्राचार अम्ब्रल मात्रा के [[ commutators ]] की पहचान के कारण उनके निरंतर अनुरूप है ({{math|''h'' → 0}} सीमाएं), | परिमित अंतरों की गणना कॉम्बिनेटरिक्स के अम्ब्रल कैलकुलस से संबंधित है। यह उल्लेखनीय रूप से व्यवस्थित पत्राचार अम्ब्रल मात्रा के [[ commutators |कम्यूटेटरों]] की पहचान के कारण उनके निरंतर अनुरूप है ({{math|''h'' → 0}} सीमाएं), | ||
{{Equation box 1 | {{Equation box 1 | ||
| Line 358: | Line 351: | ||
|border colour = #0073CF | |border colour = #0073CF | ||
|background colour=#F9FFF7}} | |background colour=#F9FFF7}} | ||
फलन {{math|''f'' (''x'')}} वाले मानक कैलकुलस के औपचारिक अंतर संबंधों की बड़ी संख्या इस प्रकार व्यवस्थित रूप से {{math|''f'' (''xT''{{su|b=''h''|p=−1}})}} वाले अम्ब्रल परिमित-अंतर एनालॉग के लिए मैप करती है | |||
उदाहरण के लिए, | उदाहरण के लिए, एकपद {{mvar|x<sup>n</sup>}} का उम्ब्रल एनालॉग उपरोक्त फॉलिंग फैक्टोरियल (पोचममेर के-प्रतीक) का सामान्यीकरण है, | ||
:<math>~(x)_n\equiv \left(xT_h^{-1}\right)^n=x (x-h) (x-2h) \cdots \bigl(x-(n-1)h\bigr),</math> | :<math>~(x)_n\equiv \left(xT_h^{-1}\right)^n=x (x-h) (x-2h) \cdots \bigl(x-(n-1)h\bigr),</math> जिससे कि | ||
:<math>\frac{\Delta_h}{h} (x)_n=n (x)_{n-1} ,</math> | :<math>\frac{\Delta_h}{h} (x)_n=n (x)_{n-1} ,</math> | ||
इसलिए उपरोक्त न्यूटन | इसलिए उपरोक्त न्यूटन अंतर्वेशन सूत्र (इस तरह के प्रतीकों में मनमाने फलन {{math|''f'' (''x'')}} के विस्तार में गुणांक मिलान करके), और इसी तरह। | ||
उदाहरण के लिए, उम्ब्रल | उदाहरण के लिए, उम्ब्रल ज्या है | ||
:<math>\sin \left(x\,T_h^{-1}\right) = x -\frac{(x)_3}{3!} + \frac{(x)_5}{5!} - \frac{(x)_7}{7!} + \cdots</math> | :<math>\sin \left(x\,T_h^{-1}\right) = x -\frac{(x)_3}{3!} + \frac{(x)_5}{5!} - \frac{(x)_7}{7!} + \cdots</math> | ||
सातत्य सीमा के रूप में, का आइजनफंक्शन {{math|{{sfrac|Δ<sub>''h''</sub>|''h''}}}} भी | सातत्य सीमा के रूप में, का आइजनफंक्शन {{math|{{sfrac|Δ<sub>''h''</sub>|''h''}}}} भी घातीय होता है, | ||
:<math>\frac{\Delta_h}{h}(1+\lambda h)^\frac{x}{h} =\frac{\Delta_h}{h} e^{\ln (1+\lambda h) \frac{x}{h}}= \lambda e^{\ln (1+\lambda h) \frac{x}{h}} ,</math> | :<math>\frac{\Delta_h}{h}(1+\lambda h)^\frac{x}{h} =\frac{\Delta_h}{h} e^{\ln (1+\lambda h) \frac{x}{h}}= \lambda e^{\ln (1+\lambda h) \frac{x}{h}} ,</math> | ||
और इसलिए निरंतर | और इसलिए निरंतर फलन के फूरियर योगों को आसानी से अंब्रल फूरियर योगों के लिए मैप किया जाता है, अर्थात, समान फूरियर गुणांकों को सम्मलित करते हुए इन अम्ब्रल आधार घातांकों को गुणा करते हैं।<ref>{{cite journal |last =Zachos|first =C.| author-link =Cosmas Zachos| year =2008| title =डिस्क्रीट स्पेस-टाइम पर अम्ब्रल विरूपण| journal =International Journal of Modern Physics A| volume =23 | issue=13| pages =2005–2014 | doi = 10.1142/S0217751X08040548 | arxiv =0710.2306| bibcode =2008IJMPA..23.2005Z|s2cid =16797959}}</ref> यह उम्ब्रल घातीय इस प्रकार पोचममेर प्रतीकों के घातीय [[ जनरेटिंग फ़ंक्शन |जनरेटिंग फलन]] की मात्रा है। | ||
इस प्रकार, उदाहरण के लिए, [[ डिराक डेल्टा समारोह ]] मैप्स को इसके उम्ब्रल संवाददाता, [[ सिंक समारोह ]], | इस प्रकार, उदाहरण के लिए, [[ डिराक डेल्टा समारोह |डिराक डेल्टा फलन]] मैप्स को इसके उम्ब्रल संवाददाता, [[ सिंक समारोह | कार्डिनल साइन फ़ंक्शन]] , | ||
:<math>\delta (x) \mapsto \frac{\sin \left[ \frac{\pi}{2}\left(1+\frac{x}{h}\right) \right]}{ \pi (x+h) },</math> | :<math>\delta (x) \mapsto \frac{\sin \left[ \frac{\pi}{2}\left(1+\frac{x}{h}\right) \right]}{ \pi (x+h) },</math> | ||
इत्यादि।<ref>{{Cite journal | last1 = Curtright | first1 = T. L. | last2 = Zachos | first2 = C. K. | doi = 10.3389/fphy.2013.00015 | title = अम्ब्राल वेड मेकुम| journal = Frontiers in Physics | volume = 1 | year = 2013 | pages = 15 | arxiv = 1304.0429 | bibcode = 2013FrP.....1...15C | s2cid = 14106142 | doi-access = free }}</ref> | इत्यादि।<ref>{{Cite journal | last1 = Curtright | first1 = T. L. | last2 = Zachos | first2 = C. K. | doi = 10.3389/fphy.2013.00015 | title = अम्ब्राल वेड मेकुम| journal = Frontiers in Physics | volume = 1 | year = 2013 | pages = 15 | arxiv = 1304.0429 | bibcode = 2013FrP.....1...15C | s2cid = 14106142 | doi-access = free }}</ref> अवकल समीकरण को अधिकांशतः उन तकनीकों के साथ हल किया जा सकता है जो अवकल समीकरण को हल करने के लिए बहुत समान हैं। | ||
अग्रांतर संकारक का व्युत्क्रम संकारक, इसलिए फिर उम्ब्रल इंटीग्रल, अनिश्चित योग या प्रतिपक्ष संकारक है। | |||
=== परिमित अंतर | === परिमित अंतर संकारक की गणना के लिए नियम === | ||
अवकलजों की सूची के अनुरूप, हमारे पास है: | |||
*निरंतर नियम : यदि {{mvar|c}} | *निरंतर नियम : यदि {{mvar|c}} स्थिरांक (गणित) है, तब | ||
::<math>\Delta c = 0</math> | ::<math>\Delta c = 0</math> | ||
* | * भेदन की रैखिकता: यदि {{mvar|a}} और {{mvar|b}} स्थिर हैं (गणित), | ||
::<math>\Delta (a f + b g) = a \,\Delta f + b \,\Delta g</math> | ::<math>\Delta (a f + b g) = a \,\Delta f + b \,\Delta g</math> | ||
उपरोक्त सभी नियम किसी भी | उपरोक्त सभी नियम किसी भी अंतरसंकारक पर समान रूप से अच्छी तरह से लागू होते हैं, जिनमें {{math|∇}} के रूप में {{math|Δ}} सम्मलित हैं | ||
* [[ प्रॉडक्ट नियम ]]: | * [[ प्रॉडक्ट नियम | गुणन नियम]] : | ||
::<math> \begin{align} \Delta (f g) &= f \,\Delta g + g \,\Delta f + \Delta f \,\Delta g \\ \nabla (f g) &= f \,\nabla g + g \,\nabla f - \nabla f \,\nabla g \end{align}</math> | ::<math> \begin{align} \Delta (f g) &= f \,\Delta g + g \,\Delta f + \Delta f \,\Delta g \\ \nabla (f g) &= f \,\nabla g + g \,\nabla f - \nabla f \,\nabla g \end{align}</math> | ||
* [[ भागफल नियम ]]: | * [[ भागफल नियम ]]: | ||
| Line 395: | Line 387: | ||
* [[ कलन का मौलिक प्रमेय ]]: | * [[ कलन का मौलिक प्रमेय ]]: | ||
::<math>\begin{align} \sum_{n=a}^{b} \Delta f(n) &= f(b+1)-f(a) \\ \sum_{n=a}^{b} \nabla f(n) &= f(b)-f(a-1) \end{align}</math> | ::<math>\begin{align} \sum_{n=a}^{b} \Delta f(n) &= f(b+1)-f(a) \\ \sum_{n=a}^{b} \nabla f(n) &= f(b)-f(a-1) \end{align}</math> | ||
संदर्भ देखें।<ref>{{cite book|last=Levy|first=H.|author2=Lessman, F.|title=परिमित अंतर समीकरण|year=1992|publisher=Dover|isbn=0-486-67260-3}}</ref><ref>Ames, W. F., (1977). ''Numerical Methods for Partial Differential Equations'', Section 1.6. Academic Press, New York. {{ISBN|0-12-056760-1}}.</ref><ref>[[Francis B. Hildebrand|Hildebrand, F. B.]], (1968). ''Finite-Difference Equations and Simulations'', Section 2.2, Prentice-Hall, Englewood Cliffs, New Jersey.</ref><ref>{{Cite journal | |||
== संदर्भ देखें।<ref>{{cite book|last=Levy|first=H.|author2=Lessman, F.|title=परिमित अंतर समीकरण|year=1992|publisher=Dover|isbn=0-486-67260-3}}</ref><ref>Ames, W. F., (1977). ''Numerical Methods for Partial Differential Equations'', Section 1.6. Academic Press, New York. {{ISBN|0-12-056760-1}}.</ref><ref>[[Francis B. Hildebrand|Hildebrand, F. B.]], (1968). ''Finite-Difference Equations and Simulations'', Section 2.2, Prentice-Hall, Englewood Cliffs, New Jersey.</ref><ref>{{Cite journal | |||
| first1 = Philippe | last1 = Flajolet | | first1 = Philippe | last1 = Flajolet | ||
| author-link2 = Robert Sedgewick (computer scientist) | first2 = Robert | last2 = Sedgewick | | author-link2 = Robert Sedgewick (computer scientist) | first2 = Robert | last2 = Sedgewick | ||
| Line 402: | Line 395: | ||
| volume = 144 | issue = 1–2 | year = 1995 | pages = 101–124 | | volume = 144 | issue = 1–2 | year = 1995 | pages = 101–124 | ||
| doi = 10.1016/0304-3975(94)00281-M | | doi = 10.1016/0304-3975(94)00281-M | ||
}}.</ref> | }}.</ref> == | ||
== सामान्यीकरण == | == सामान्यीकरण == | ||
* | *सामान्यीकृत परिमित अंतर को सामान्यतः इस रूप में परिभाषित किया जाता है <math display="block">\Delta_h^\mu[f](x) = \sum_{k=0}^N \mu_k f(x+kh),</math> जहाँ {{math|1=''μ'' = (''μ''<sub>0</sub>, …, ''μ<sub>N</sub>'')}} इसका गुणांक सदिश है। अनंत अंतर एक और सामान्यीकरण है, जहां ऊपर परिमित योग को अनंत[[ श्रृंखला (गणित) ]]से बदल दिया जाता है। सामान्यीकरण का अन्य तरीका गुणांक बना रहा है {{math|''μ<sub>k</sub>''}} बिन्दु पर निर्भर है {{mvar|x}}: {{math|1=''μ<sub>k</sub>'' = ''μ<sub>k</sub>''(''x'')}}, इस प्रकार भारित परिमित अंतर पर विचार किया जाता है। साथ ही कोई चरण {{mvar|h}} को बिंदु {{mvar|x}}: {{math|1=''h'' = ''h''(''x'')}} पर निर्भर कर सकता है। इस तरह के सामान्यीकरण निरंतरता के विभिन्न मापांकों के निर्माण के लिए उपयोगी होते हैं। | ||
* सामान्यीकृत अंतर को बहुपद के | * सामान्यीकृत अंतर को बहुपद के रिंग {{math|''R''[''T<sub>h</sub>'']}} के रूप में देखा जा सकता है, यह अंतर बीजगणित की ओर जाता है। | ||
* | * अंतरसंकारक आंशिक ऑर्डर समुच्चय पर मोबियस इनवर्जन का सामान्यीकरण करता है। | ||
*[[ घुमाव ]] | *[[ घुमाव | घुमाव]] संकारक के रूप में: [[ घटना बीजगणित | आपतन बीजगणित]] की औपचारिकता के माध्यम से, अंतरसंकारक और अन्य मोबियस व्युत्क्रम को पोसेट पर फलन के साथ संवलन द्वारा दर्शाया जा सकता है, जिसे मोबियस फलन कहा जाता है {{mvar|μ}}, अंतरसंकारक के लिए {{mvar|μ}} क्रम {{nowrap|(1, −1, 0, 0, 0, …)}}है। | ||
== बहुभिन्नरूपी परिमित अंतर == | == बहुभिन्नरूपी परिमित अंतर == | ||
परिमित अंतरों को एक से अधिक चरों में माना जा सकता है। वे कई चरों में आंशिक | परिमित अंतरों को एक से अधिक चरों में माना जा सकता है। वे कई चरों में आंशिक अवकलज के अनुरूप हैं। | ||
कुछ [[ आंशिक व्युत्पन्न ]] सन्निकटन हैं: | कुछ [[ आंशिक व्युत्पन्न |आंशिक व्युत्पन्न]] सन्निकटन हैं: | ||
:<math>\begin{align} | :<math>\begin{align} | ||
| Line 425: | Line 417: | ||
f_{xy}(x,y) &\approx \frac{f(x+h,y+k) - f(x+h,y-k) - f(x-h,y+k) + f(x-h,y-k)}{4hk} . | f_{xy}(x,y) &\approx \frac{f(x+h,y+k) - f(x+h,y-k) - f(x-h,y+k) + f(x-h,y-k)}{4hk} . | ||
\end{align}</math> | \end{align}</math> | ||
वैकल्पिक रूप से, उन अनुप्रयोगों के लिए जिनमें की गणना {{mvar|f}} सबसे महंगा कदम है, और पहले और दूसरे | वैकल्पिक रूप से, उन अनुप्रयोगों के लिए जिनमें की गणना {{mvar|f}} सबसे महंगा कदम है, और पहले और दूसरे अवकलज दोनों की गणना की जानी चाहिए, अंतिम मामले के लिए अधिक कुशल सूत्र है | ||
:<math> f_{xy}(x,y) \approx \frac{f(x+h, y+k) - f(x+h, y) - f(x, y+k) + 2 f(x,y) - f(x-h, y) - f(x, y-k) + f(x-h, y-k)}{2hk},</math> | :<math> f_{xy}(x,y) \approx \frac{f(x+h, y+k) - f(x+h, y) - f(x, y+k) + 2 f(x,y) - f(x-h, y) - f(x, y-k) + f(x-h, y-k)}{2hk},</math> | ||
चूंकि गणना करने के लिए केवल वही मान हैं जिनकी पहले से ही पिछले चार समीकरणों | चूंकि गणना करने के लिए केवल वही मान हैं जिनकी पहले से ही पिछले चार समीकरणों {{math|''f'' (''x'' + ''h'', ''y'' + ''k'')}} और {{math|''f'' (''x'' − ''h'', ''y'' − ''k'')}} के लिए आवश्यकता नहीं है | ||
== यह भी देखें == | == यह भी देखें == | ||
{{columns-list|colwidth=20em| | {{columns-list|colwidth=20em| | ||
* [[ | * [[असतत कलन]] | ||
* [[ | * [[विभाजित अंतर]] | ||
* [[ | * [[परिमित-अंतर समय-डोमेन विधि]] (एफडीटीडी) | ||
* [[ | * [[परिमित मात्रा विधि]] | ||
* [[ | * [[एफटीसीएस योजना]] | ||
* [[ | * [[एफटीसीएस योजना]] | ||
* [[ | * [[शेफर अनुक्रम]] | ||
* [[ | * [[भागों द्वारा योग]] | ||
* [[ | * [[समय पैमाने की गणना]] | ||
* [[ | * [[संवहन के लिए अपविंड विभेदक योजना]] | ||
}} | }} | ||
| Line 450: | Line 442: | ||
* Mickens, R. E. (1991): ''Difference Equations: Theory and Applications'' (Chapman and Hall/CRC) {{ISBN|978-0442001360}} | * Mickens, R. E. (1991): ''Difference Equations: Theory and Applications'' (Chapman and Hall/CRC) {{ISBN|978-0442001360}} | ||
== बाहरी कड़ियाँ == | == बाहरी कड़ियाँ == | ||
* {{springer|title=Finite-difference calculus|id=p/f040230}} | * {{springer|title=Finite-difference calculus|id=p/f040230}} | ||
| Line 481: | Line 449: | ||
{{Calculus topics}} | {{Calculus topics}} | ||
[[Category: | [[Category:Articles with hatnote templates targeting a nonexistent page]] | ||
[[Category:CS1]] | |||
[[Category:CS1 français-language sources (fr)]] | |||
[[Category:CS1 maint]] | |||
[[Category:CS1 Ελληνικά-language sources (el)]] | |||
[[Category:Citation Style 1 templates|W]] | |||
[[Category:Collapse templates]] | |||
[[Category:Created On 27/12/2022]] | [[Category:Created On 27/12/2022]] | ||
[[Category:Lua-based templates]] | |||
[[Category:Machine Translated Page]] | |||
[[Category:Multi-column templates]] | |||
[[Category:Navigational boxes| ]] | |||
[[Category:Navigational boxes without horizontal lists]] | |||
[[Category:Pages using div col with small parameter]] | |||
[[Category:Pages with script errors]] | |||
[[Category:Sidebars with styles needing conversion]] | |||
[[Category:Template documentation pages|Documentation/doc]] | |||
[[Category:Templates Vigyan Ready]] | |||
[[Category:Templates based on the Citation/CS1 Lua module]] | |||
[[Category:Templates generating COinS|Cite web]] | |||
[[Category:Templates generating microformats]] | |||
[[Category:Templates that add a tracking category]] | |||
[[Category:Templates that are not mobile friendly]] | |||
[[Category:Templates used by AutoWikiBrowser|Cite web]] | |||
[[Category:Templates using TemplateData]] | |||
[[Category:Templates using under-protected Lua modules]] | |||
[[Category:Wikipedia fully protected templates|Div col]] | |||
[[Category:Wikipedia metatemplates]] | |||
Latest revision as of 17:16, 25 August 2023
परिमित अंतर रूप की गणितीय अभिव्यक्ति है f (x + b) − f (x + a)। यदि एक परिमित अंतर b − a से विभाजित किया जाता है, अंतर भागफल मिलता है। परिमित भिन्नताओं द्वारा अवकलज का अनुमान अवकल समीकरण के संख्यात्मक विश्लेषण समाधान के लिएपरिमित अंतर विधि यों में एक केंद्रीय भूमिका निभाता है विशेष रूप से सीमा मूल्य समस्या के लिए निभाता है।
अंतरसंकारक, सामान्यतः के रूप में जाना जाता है, वह संकारक (गणित) है जो किसी फलन f को द्वारा परिभाषित करता है।
अवकल समीकरण एक फलनिक समीकरण है जिसमें परिमित अंतर संकारक उसी तरह सम्मलित होता है जैसे एक अवकल समीकरण में अवकलज सम्मलित होते हैं। अवकल समीकरण और अवकल समीकरण के बीच कई समानताएं हैं, विशेष रूप से हल करने के तरीकों में। कुछ पुनरावृत्ति संबंधों को परिमित अंतरों के साथ पुनरावृत्ति संकेतन को बदलकर अवकल समीकरण के रूप में लिखा जा सकता है।
संख्यात्मक विश्लेषण में, अवकलज का अनुमान लगाने के लिए परिमित अंतर का व्यापक रूप से उपयोग किया जाता है, और "परिमित अंतर" शब्द का उपयोग अधिकांशतः "अवकलज के परिमित अंतर सन्निकटन" के संक्षिप्त रूप में किया जाता है।[1][2][3] परिमित अंतर सन्निकटन ऊपर नियोजित शब्दावली में परिमित अंतर भागफल हैं।
1715 में ब्रुक टेलर द्वारा परिमित अंतर पेश किए गए थे और जॉर्ज बूले(1860), एल.एम. मिल्ने-थॉमसन (1933), और केरोली जॉर्डन (1939) द्वारा फलन में सार स्व-स्थायी गणितीय वस्तुओं के रूप में भी अध्ययन किया गया है। परिमित अंतर अपनी उत्पत्ति को जोस्ट बर्गी के एल्गोरिदम (c. 1592) में से एक में खोजते हैं और आइजैक न्यूटन सहित अन्य लोगों द्वारा काम करते हैं। परिमित अंतरों की औपचारिक गणना को अत्युणु की गणना के विकल्प के रूप में देखा जा सकता है।[4]
मूल प्रकार
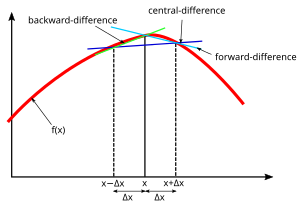
सामान्यतः तीन बुनियादी प्रकारों पर विचार किया जाता है: अग्र, पश्च और केंद्रीय परिमित अंतर।[1][2][3]
अग्रांतर सूत्र, एक फलन f के रूप में परिभाषित फलन है
अनुप्रयोग के आधार पर, रिक्ति h परिवर्तनशील या स्थिर हो सकता है। जब छोड़ा गया, h 1 लिया जाता है, वह है,
पश्च अंतर फलन मानों x और x − h का उपयोग करता है , x + h औरx के मानों के अतिरिक्त::
अंत में, केंद्रीय अंतर द्वारा दिया जाता है
अवकलज के साथ संबंध
परिमित अंतर अधिकांशतः व्युत्पन्न के सन्निकटन के रूप में प्रयोग किया जाता है, सामान्यतः संख्यात्मक अवकलन में।
फलन का व्युत्पन्न f एक बिंदु पर x फलन की सीमा द्वारा परिभाषित किया गया है।
यदि h शून्य के करीब पहुंचने के अतिरिक्त निश्चित (गैर-शून्य) मान है, तो उपरोक्त समीकरण के दाहिने हाथ की ओर लिखा जाएगा
इसलिए, जब h छोटा है अग्र के अंतर से विभाजित h अवकलज का अनुमान लगाता है। इस सन्निकटन में त्रुटि टेलर के प्रमेय से प्राप्त की जा सकती है। ये मानते हुए f दो बार अवकलनीय है, हमारे पास है
पश्च अंतर के लिए समान सूत्र है:
चूंकि, केंद्रीय (जिसे केंद्रित भी कहा जाता है) अंतर अधिक सटीक सन्निकटन पैदा करता है। यदि f तीन गुना अवकलनीय है,
मुख्य समस्या केंद्रीय अंतर विधि के साथ, चूंकि, यह है कि दोलन कार्य शून्य व्युत्पन्न प्राप्त कर सकते हैं। यदि f (nh) = 1, n विषम के लिए, और f (nh) = 2, n के लिए भी फिर भी f ′(nh) = 0 यदि इसकी गणना केंद्रीय अंतर योजना से की जाती है। यदि f का प्रांत असतत है तो यह विशेष रूप से कठिन है। सममित व्युत्पन्न भी देखें
लेखक जिनके लिए परिमित अंतर का अर्थ है परिमित अंतर सन्निकटन अग्र/पश्च/केंद्रीय अंतर को इस खंड में दिए गए भागफल के रूप में परिभाषित करता है (पिछले खंड में दी गई परिभाषाओं को नियोजित करने के अतिरिक्त)।[1][2][3]
उच्च-क्रम अंतर
एक समान तरीके से, उच्चतर क्रम अवकलज और अंतर संकारक के लिए परिमित अंतर सन्निकटन प्राप्त कर सकते हैं। उदाहरण के लिए, उपरोक्त केंद्रीय अंतर सूत्र का उपयोग करके f ′(x + h/2) और f ′(x − h/2) और x पर f ′ के अवकलज के लिए केंद्रीय अंतर सूत्र लागू करते हुए, हम f के दूसरे अवकलज का केंद्रीय अंतर सन्निकटन प्राप्त करते हैं:
- दूसरा क्रम केंद्रीय
इसी तरह हम अन्य भिन्न सूत्रों को पुनरावर्ती तरीके से लागू कर सकते हैं।
- दूसरा क्रम अग्र
- दूसरा क्रम पश्च
अधिक सामान्यतः,n वें क्रम अग्र, पश्च, और केंद्रीय अंतर क्रमशः द्वारा दिए गए हैं,
- अग्र
या h = 1 के लिए,
पश्च
- केंद्रीय
इन समीकरणों में योग चिह्न के बाद द्विपद गुणांक का उपयोग किया जाता है, जैसा कि दिखाया गया है (n
i)। पास्कल के त्रिभुज की प्रत्येक पंक्ति i के प्रत्येक मान के लिए गुणांक प्रदान करती है।
ध्यान दें कि केंद्रीय अंतर, विषम n के लिए, h को गैर-पूर्णांक से गुणा करेगा। यह अधिकांशतः एक समस्या होती है क्योंकि यह विवेक के अंतराल को बदलने के बराबर होती है। δn[ f ](x − h/2) और δn[ f ](x + h/2) का औसत लेकर समस्या का समाधान किया जा सकता है
अनुक्रम पर लागू किए गए अग्र अंतर को कभी-कभी अनुक्रम का द्विपद परिवर्तन कहा जाता है, और इसमें कई रोचक संयोजी गुण होते हैं। नॉर्लंड-राइस इंटीग्रल का उपयोग करके आगे के अंतर का मूल्यांकन किया जा सकता है। इस प्रकार की श्रृंखलाओं के लिए अभिन्न प्रतिनिधित्व रोचक है, क्योंकि अभिन्न का मूल्यांकन अधिकांशतः स्पर्शोन्मुख विस्तार या सैडल-पॉइंट तकनीकों का उपयोग करके किया जा सकता है, इसके विपरीत, आगे की अंतर श्रृंखला संख्यात्मक रूप से मूल्यांकन करने के लिए बेहद कठिन हो सकती है, क्योंकि बड़े n के लिए द्विपद गुणांक तेजी से बढ़ते हैं।
संबंधित अवकलज के साथ इन उच्च-क्रम के अंतरों का संबंध सीधा है,
बेहतर सन्निकटन बनाने के लिए उच्च-क्रम के अंतर का भी उपयोग किया जा सकता है। जैसा कि ऊपर उल्लेख किया गया है, प्रथम-क्रम अंतर क्रम h की अवधि तक प्रथम-क्रम व्युत्पन्न का अनुमान लगाता है। हालाँकि, संयोजन
अनुमानित f ′(x) क्रम h2 की अवधि तक। यह टेलर श्रृंखला में उपरोक्त अभिव्यक्ति का विस्तार करके या परिमित अंतरों के कलन का उपयोग करके सिद्ध किया जा सकता है, जिसे नीचे समझाया गया है।
यदि आवश्यक हो, तो अग्र, पश्च और केंद्रीय अंतरों को मिलाकर परिमित अंतर को किसी भी बिंदु पर केंद्रित किया जा सकता है।
बहुपद
घात के दिए गए बहुपद के लिए n ≥ 1 फलन P(x) में व्यक्त किया, वास्तविक संख्या के साथ a ≠ 0 और b और निचले क्रम की शर्तें (यदि कोई हो) के रूप में चिह्नित l.o.t.:
n युग्मानूसार अंतरों के बाद, निम्न परिणाम प्राप्त किया जा सकता है, जहाँ h ≠ 0 अंकगणितीय अंतर को चिह्नित करने वाली एक वास्तविक संख्या है:[5]
केवल उच्चतम-क्रम पद का गुणांक रहता है। चूंकि यह परिणाम x के संबंध में स्थिर है , किसी भी युग्मानूसार अंतर का मान 0 होगा।
आगमनात्मक प्रमाण
आधार मामले
मान लीजिए Q(x) घात 1का एक बहुपद है:
यह इसे आधार मामले के लिए सिद्ध करता है।
स्टेप केस
मान लें कि R(x) घात m-1 का बहुपद है जहाँ m ≥ 2 और उच्चतम क्रम वाले पद का गुणांक a ≠ 0 है। यह मानते हुए कि घात m-1 के सभी बहुपदों के लिए निम्नलिखित सही है:
मान लीजिए कि S(x) घात m का एक बहुपद है। एक युग्मानूसार अंतर के साथ:
ahm ≠ 0,के रूप में, इसका परिणाम m-1 घात के बहुपद T(x) में होता है, जिसमें ahm उच्चतम-क्रम पद का गुणांक होता है। उपरोक्त धारणा और m-1 युग्मानूसार अंतरों को देखते हुए (परिणामस्वरूप S(x) के लिए कुल m युग्मानूसार अंतर), यह पाया जा सकता है कि:
यह प्रमाण को पूरा करता है।
अनुप्रयोग
इस पहचान का उपयोग सबसे कम-घात वाले बहुपद को खोजने के लिए किया जा सकता है जो कई बिंदुओं (x, y) को रोकता है जहाँ x-अक्ष पर एक बिंदु से दूसरे बिंदु का अंतर एक स्थिरांकh ≠ 0 है, उदाहरण के लिए, निम्नलिखित बिंदु दिए गए हैं:
| x | y |
|---|---|
| 1 | 4 |
| 4 | 109 |
| 7 | 772 |
| 10 | 2641 |
| 13 | 6364 |
हम अंतर तालिका का उपयोग कर सकते हैं, जहां पहले y, के दाईं ओर सभी सेल, कॉलम में सेल के लिए निम्न संबंध तुरंत बाईं ओर सेल (a+1, b+1) के लिए सम्मलित है, सबसे ऊपर-बाएं सेल निर्देशांक पर है (0, 0):
पहला पद ज्ञात करने के लिए, निम्न तालिका का उपयोग किया जा सकता है:
| x | y | Δy | Δ2y | Δ3y |
|---|---|---|---|---|
| 1 | 4 | |||
| 4 | 109 | 105 | ||
| 7 | 772 | 663 | 558 | |
| 10 | 2641 | 1869 | 1206 | 648 |
| 13 | 6364 | 3723 | 1854 | 648 |
यह स्थिरांक 648 पर आता है। अंकगणितीय अंतर h=3 है, जैसा कि ऊपर स्थापित किया गया है। स्थिरांक तक पहुँचने के लिए युग्मानूसार अंतरों की संख्या को देखते हुए, यह अनुमान लगाया जा सकता है कि यह घात 3 का बहुपद है। इस प्रकार, उपरोक्त पहचान का उपयोग करना:
a को हल करने पर, इसका मान 4 पाया जा सकता है। इस प्रकार, बहुपद का पहला पद है 4x3.
फिर, पहले पद को घटाकर, जो बहुपद की घात को कम करता है, और परिमित अंतर को फिर से ज्ञात करता है:
| x | y | Δy | Δ2y |
|---|---|---|---|
| 1 | 4 - 4(1)3 = 4 - 4 = 0 | ||
| 4 | 109 - 4(4)3 = 109 - 256 = -147 | -147 | |
| 7 | 772 - 4(7)3 = 772 - 1372 = -600 | -453 | -306 |
| 10 | 2641 - 4(10)3 = 2641 - 4000 = -1359 | -759 | -306 |
| 13 | 6364 - 4(13)3 = 6364 - 8788 = -2424 | -1065 | -306 |
यहाँ, स्थिरांक केवल 2 युग्मानूसार अंतरों के बाद प्राप्त किया जाता है, इस प्रकार निम्न परिणाम:
a को हल करने पर, जो -17 है, बहुपद का दूसरा पद -17x2 है .
दूसरे पद को घटाकर, अगले पद पर जाना:
| x | y | Δy |
|---|---|---|
| 1 | 0 - (-17(1)2) = 0 + 17 = 17 | |
| 4 | -147 - (-17(4)2) = -147 + 272 = 125 | 108 |
| 7 | -600 - (-17(7)2) = -600 + 833 = 233 | 108 |
| 10 | -1359 - (-17(10)2) = -1359 + 1700 = 341 | 108 |
| 13 | -2424 - (-17(13)2) = -2424 + 2873 = 449 | 108 |
इस प्रकार स्थिर केवल 1 युग्मानूसार अंतर के बाद प्राप्त किया जाता है:
यह पाया जा सकता है a = 36 और इस प्रकार बहुपद का तीसरा पद36x है, तीसरे पद को घटाना:
| x | y |
|---|---|
| 1 | 17 - 36(1) = 17 - 36 = -19 |
| 4 | 125 - 36(4) = 125 - 144 = -19 |
| 7 | 233 - 36(7) = 233 - 252 = -19 |
| 10 | 341 - 36(10) = 341 - 360 = -19 |
| 13 | 449 - 36(13) = 449 - 468 = -19 |
बिना किसी युग्मवार अंतर के, यह पाया जाता है कि बहुपद का चौथा और अंतिम पद अचर -19 है, इस प्रकार, पहली तालिका में सभी बिंदुओं को अंतर्रोधक करने वाला निम्नतम-घात बहुपद पाया जाता है:
अव्यवस्थित आकार मूल
रेखीय बीजगणित का उपयोग करके परिमित अंतर सन्निकटन का निर्माण किया जा सकता है जो किसी भी क्रम व्युत्पन्न के लिए बाईं ओर बिंदुओं की अव्यवस्थित संख्या और मूल्यांकन बिंदु के दाईं ओर (संभवतः भिन्न) अंकों की संख्या का उपयोग करता है। इसमें रेखीय प्रणाली को हल करना सम्मलित है जैसे कि मूल्यांकन बिंदु के चारों ओर उन बिंदुओं के योग का टेलर विस्तार वांछित व्युत्पन्न के टेलर विस्तार का सबसे अच्छा अनुमान लगाता है। इस तरह के सूत्रों को हेक्सागोनल या हीरे के आकार के ग्रिड पर रेखांकन के रूप में दर्शाया जा सकता है।[6]
यह ग्रिड पर फलन को अलग करने के लिए उपयोगी है, जहां एक ग्रिड के किनारे तक पहुंचता है, उसे एक तरफ कम और कम बिंदुओं का नमूना लेना चाहिए।
विवरण इन नोट्स में दिए गए हैं।
परिमित अंतर गुणांक कैलक्यूलेटर गैर-मानक (और यहां तक कि गैर-पूर्णांक) स्टेंसिल के लिए परिमित अंतर सन्निकटन का निर्माण करता है जिसे अव्यवस्थित स्टैंसिल और वांछित व्युत्पन्न क्रम दिया जाता है .
गुण
- सभी घनात्मक k और n के लिए
- लीबनिज नियम (सामान्यीकृत उत्पाद नियम) :
अवकल समीकरण में
परिमित अंतरों का महत्वपूर्ण अनुप्रयोग संख्यात्मक विश्लेषण में है, विशेष रूप से संख्यात्मक आंशिक अवकल समीकरण में, जो साधारण अवकल समीकरण और आंशिक अवकल समीकरण के संख्यात्मक समाधान का लक्ष्य रखता है। विचार यह है आंशिक विभेदक समीकरण में दिखाई देने वाले अवकलज को परिमित अंतर से बदल दिया जाए जो उन्हें अनुमानित करता है। परिणामी विधियों को परिमित अंतर विधियाँ कहा जाता है।
कम्प्यूटेशनल विज्ञान और इंजीनियरिंग विषयों में परिमित अंतर विधि के सामान्य अनुप्रयोग हैं, जैसे ऊष्मा इंजीनियरी, द्रव यांत्रिकी, आदि।
न्यूटन की श्रृंखला
न्यूटन बहुपद में न्यूटन अग्रांतर समीकरण की शर्तें सम्मलित हैं, जिसका नाम इसहाक न्यूटन के नाम पर रखा गया है, संक्षेप में, यह न्यूटन अंतर्वेशन सूत्र है, जो पहली बार 1687 में उनके 'फिलोसोफी नेचुरेलिस प्रिंसिपिया मैथेमेटिका' में प्रकाशित हुआ था।[7] अर्थात् निरंतर टेलर विस्तार का असतत अनुरूप,
जो किसी भी बहुपद फलन f के लिए और कई (लेकिन सभी नहीं) विश्लेषणात्मक फलन के लिए है। (यह धारण नहीं करता है जब f चरघातांकी प्रकार है ,इसे आसानी से देखा जा सकता है, क्योंकि , संबंधित न्यूटन श्रृंखला समान रूप से शून्य है, क्योंकि इस मामले में सभी परिमित अंतर शून्य हैं। फिर भी स्पष्ट रूप से, ज्या फलन शून्य नहीं है।) यहाँ, व्यंजक
द्विपद गुणांक है, और
"फॉलिंग फैक्टोरियल" या "लोअर फैक्टोरियल" है, जबकि खाली उत्पाद (x)0 को 1 के रूप में परिभाषित किया गया है। इस विशेष मामले में, x, h = 1 के मान में परिवर्तन के लिए इकाई चरणों की धारणा है। नीचे दिए गए सामान्यीकरण का।
टेलर के प्रमेय के इस परिणाम के औपचारिक पत्राचार पर ध्यान दें। ऐतिहासिक रूप से, यह, साथ ही चू-वंडरमोंड पहचान हैं,
(इससे अनुसरण करते हुए, और द्विपद प्रमेय के अनुरूप), उन टिप्पणियों में सम्मलित हैं जो अम्ब्रल कैलकुलस की प्रणाली के लिए परिपक्व हैं।
न्यूटन श्रृंखला विस्तार टेलर श्रृंखला विस्तार से बेहतर हो सकता है जब क्वांटम स्पिन (होल्स्टीन-प्रिमाकॉफ परिवर्तन देखें), बोसोनिक ऑपरेटर फलन या असतत गिनती सांख्यिकी जैसी असतत मात्राओं पर लागू किया जाता है।[8]
वास्तविक अभ्यास में कोई न्यूटन के सूत्र का उपयोग कैसे कर सकता है, यह समझाने के लिए, फाइबोनैचि अनुक्रम को दोगुना करने के पहले कुछ शब्दों पर विचार करें। f = 2, 2, 4, ... कोई बहुपद खोज सकता है जो पहले एक अंतर तालिका की गणना करके, और फिर x0 (रेखांकित) के अनुरूप अंतर को सूत्र में निम्नानुसार प्रतिस्थापित करना,
x के मानों में असमान चरणों के मामले में, न्यूटन विभाजित अंतरों की गणना करता है,
उत्पादों की श्रृंखला,
और परिणामी बहुपद अदिश गुणनफल है,[9]
- .
पी-एडिक संख्याओं के विश्लेषण में, महलर के प्रमेय में कहा गया है कि यह धारणा कि f बहुपद फलन है इस धारणा के लिए सभी तरह से कमजोर हो सकती है कि f केवल निरंतर है।
कार्लसन की प्रमेय न्यूटन श्रृंखला के अद्वितीय होने के लिए आवश्यक और पर्याप्त शर्तें प्रदान करती है, यदि यह सम्मलित है। हालाँकि, न्यूटन श्रृंखला सामान्य रूप से सम्मलित नहीं है।
न्यूटन श्रृंखला, स्टर्लिंग श्रृंखला और सेलबर्ग वर्ग के साथ, सामान्य अंतर श्रृंखला का एक विशेष मामला है, जिनमें से सभी को उपयुक्त रूप से अग्र बढ़ने वाले अंतरों के संदर्भ में परिभाषित किया गया है।
एक संकुचित और थोड़ा अधिक सामान्य रूप और समदूरस्थ नोड्स में सूत्र पढ़ता है
परिमित अंतरों की गणना
अग्र के अंतर को संकारक (गणित) के रूप में माना जा सकता है, जिसे अंतरसंकारक कहा जाता है, जो फलन को f को Δh[ f ] मैप करता है[10][11] इस संकारक की राशि है
जहाँ Th चरण hवाला शिफ्ट ऑपरेटर है जिसे Th[ f ](x) = f (x + h) द्वारा परिभाषित किया गया है, और I पहचान ऑपरेटर है।
उच्च आदेशों के परिमित अंतर को पुनरावर्ती तरीके से परिभाषित किया जा सकता है Δn
h ≡ Δh(Δn − 1
h), एक अन्य समकक्ष परिभाषा है Δn
h = [Th − I]n.
अंतरसंकारक Δh रैखिक संकारक है, इसलिए यह संतुष्ट करता है Δh[αf + βg](x) = α Δh[ f ](x) + β Δh[g](x).
यह ऊपर बताए गए विशेष लीबनिज़ नियम (सामान्यीकृत उत्पाद नियम) को भी संतुष्ट करता है,
Δh(f (x)g(x)) = (Δhf (x)) g(x+h) + f (x) (Δhg(x)), इसी तरह के बयान पश्च और केंद्रीय अंतर के लिए हैं।
h के संबंध में टेलर श्रृंखला को औपचारिक रूप से लागू करने से सूत्र प्राप्त होता है
जहाँ D निरंतर व्युत्पन्न संकारक, मैपिंग को दर्शाता है f को इसके डेरिवेटिव f ′ मैपिंग करता है। विस्तार तब मान्य होता है जब दोनों पक्ष पर्याप्त रूप से छोटे h के लिए विश्लेषणात्मक फलन पर कार्य करते हैं। इस प्रकार, Th = ehD, और औपचारिक रूप से घातांकीय प्रतिफल को उलटा करना
यह सूत्र इस अर्थ में है कि बहुपद पर लागू होने पर दोनों संकारक समान परिणाम देते हैं।
विश्लेषणात्मक फलन के लिए भी, दाईं ओर की श्रृंखला को अभिसरण की गारंटी नहीं है, यहस्पर्शोन्मुख श्रृंखला हो सकती है। चूंकि, इसका उपयोग व्युत्पन्न के लिए अधिक सटीक सन्निकटन प्राप्त करने के लिए किया जा सकता है। उदाहरण के लिए, श्रृंखला के पहले दो शब्दों को बनाए रखने से खंड उच्च-क्रम के अंतर के अंत में उल्लिखित f ′(x) के लिए दूसरे क्रम का सन्निकटन प्राप्त होता है।
पश्च और केंद्रीय अंतर संकारक के लिए समान सूत्र हैं
परिमित अंतरों की गणना कॉम्बिनेटरिक्स के अम्ब्रल कैलकुलस से संबंधित है। यह उल्लेखनीय रूप से व्यवस्थित पत्राचार अम्ब्रल मात्रा के कम्यूटेटरों की पहचान के कारण उनके निरंतर अनुरूप है (h → 0 सीमाएं),
फलन f (x) वाले मानक कैलकुलस के औपचारिक अंतर संबंधों की बड़ी संख्या इस प्रकार व्यवस्थित रूप से f (xT−1
h) वाले अम्ब्रल परिमित-अंतर एनालॉग के लिए मैप करती है
उदाहरण के लिए, एकपद xn का उम्ब्रल एनालॉग उपरोक्त फॉलिंग फैक्टोरियल (पोचममेर के-प्रतीक) का सामान्यीकरण है,
- जिससे कि
इसलिए उपरोक्त न्यूटन अंतर्वेशन सूत्र (इस तरह के प्रतीकों में मनमाने फलन f (x) के विस्तार में गुणांक मिलान करके), और इसी तरह।
उदाहरण के लिए, उम्ब्रल ज्या है
सातत्य सीमा के रूप में, का आइजनफंक्शन Δh/h भी घातीय होता है,
और इसलिए निरंतर फलन के फूरियर योगों को आसानी से अंब्रल फूरियर योगों के लिए मैप किया जाता है, अर्थात, समान फूरियर गुणांकों को सम्मलित करते हुए इन अम्ब्रल आधार घातांकों को गुणा करते हैं।[12] यह उम्ब्रल घातीय इस प्रकार पोचममेर प्रतीकों के घातीय जनरेटिंग फलन की मात्रा है।
इस प्रकार, उदाहरण के लिए, डिराक डेल्टा फलन मैप्स को इसके उम्ब्रल संवाददाता, कार्डिनल साइन फ़ंक्शन ,
इत्यादि।[13] अवकल समीकरण को अधिकांशतः उन तकनीकों के साथ हल किया जा सकता है जो अवकल समीकरण को हल करने के लिए बहुत समान हैं।
अग्रांतर संकारक का व्युत्क्रम संकारक, इसलिए फिर उम्ब्रल इंटीग्रल, अनिश्चित योग या प्रतिपक्ष संकारक है।
परिमित अंतर संकारक की गणना के लिए नियम
अवकलजों की सूची के अनुरूप, हमारे पास है:
- निरंतर नियम : यदि c स्थिरांक (गणित) है, तब
- भेदन की रैखिकता: यदि a और b स्थिर हैं (गणित),
उपरोक्त सभी नियम किसी भी अंतरसंकारक पर समान रूप से अच्छी तरह से लागू होते हैं, जिनमें ∇ के रूप में Δ सम्मलित हैं
- या
संदर्भ देखें।[14][15][16][17]
सामान्यीकरण
- सामान्यीकृत परिमित अंतर को सामान्यतः इस रूप में परिभाषित किया जाता है जहाँ μ = (μ0, …, μN) इसका गुणांक सदिश है। अनंत अंतर एक और सामान्यीकरण है, जहां ऊपर परिमित योग को अनंतश्रृंखला (गणित) से बदल दिया जाता है। सामान्यीकरण का अन्य तरीका गुणांक बना रहा है μk बिन्दु पर निर्भर है x: μk = μk(x), इस प्रकार भारित परिमित अंतर पर विचार किया जाता है। साथ ही कोई चरण h को बिंदु x: h = h(x) पर निर्भर कर सकता है। इस तरह के सामान्यीकरण निरंतरता के विभिन्न मापांकों के निर्माण के लिए उपयोगी होते हैं।
- सामान्यीकृत अंतर को बहुपद के रिंग R[Th] के रूप में देखा जा सकता है, यह अंतर बीजगणित की ओर जाता है।
- अंतरसंकारक आंशिक ऑर्डर समुच्चय पर मोबियस इनवर्जन का सामान्यीकरण करता है।
- घुमाव संकारक के रूप में: आपतन बीजगणित की औपचारिकता के माध्यम से, अंतरसंकारक और अन्य मोबियस व्युत्क्रम को पोसेट पर फलन के साथ संवलन द्वारा दर्शाया जा सकता है, जिसे मोबियस फलन कहा जाता है μ, अंतरसंकारक के लिए μ क्रम (1, −1, 0, 0, 0, …)है।
बहुभिन्नरूपी परिमित अंतर
परिमित अंतरों को एक से अधिक चरों में माना जा सकता है। वे कई चरों में आंशिक अवकलज के अनुरूप हैं।
कुछ आंशिक व्युत्पन्न सन्निकटन हैं:
वैकल्पिक रूप से, उन अनुप्रयोगों के लिए जिनमें की गणना f सबसे महंगा कदम है, और पहले और दूसरे अवकलज दोनों की गणना की जानी चाहिए, अंतिम मामले के लिए अधिक कुशल सूत्र है
चूंकि गणना करने के लिए केवल वही मान हैं जिनकी पहले से ही पिछले चार समीकरणों f (x + h, y + k) और f (x − h, y − k) के लिए आवश्यकता नहीं है
यह भी देखें
संदर्भ
- ↑ 1.0 1.1 1.2 Paul Wilmott; Sam Howison; Jeff Dewynne (1995). वित्तीय डेरिवेटिव का गणित: एक छात्र परिचय. Cambridge University Press. p. 137. ISBN 978-0-521-49789-3.
- ↑ 2.0 2.1 2.2 Peter Olver (2013). आंशिक विभेदक समीकरणों का परिचय. Springer Science & Business Media. p. 182. ISBN 978-3-319-02099-0.
- ↑ 3.0 3.1 3.2 M Hanif Chaudhry (2007). ओपन-चैनल फ्लो. Springer. p. 369. ISBN 978-0-387-68648-6.
- ↑ Jordán, op. cit., p. 1 and Milne-Thomson, p. xxi. Milne-Thomson, Louis Melville (2000): The Calculus of Finite Differences (Chelsea Pub Co, 2000) ISBN 978-0821821077
- ↑ "बहुपदों के परिमित अंतर". February 13, 2018.
- ↑ Fraser, Duncan C. (1 January 1909). "इंटरपोलेशन फॉर्मूले के ग्राफिक चित्रण पर". Journal of the Institute of Actuaries. 43 (2): 235–241. doi:10.1017/S002026810002494X. Retrieved 17 April 2017.
- ↑ Newton, Isaac, (1687). Principia, Book III, Lemma V, Case 1
- ↑ Jürgen König and Alfred Hucht, SciPost Phys. 10, 007 (2021) doi:10.21468/SciPostPhys.10.1.007
- ↑ Richtmeyer, D. and Morton, K.W., (1967). Difference Methods for Initial Value Problems, 2nd ed., Wiley, New York.
- ↑ Boole, George, (1872). A Treatise On The Calculus of Finite Differences, 2nd ed., Macmillan and Company. On line. Also, [Dover edition 1960]
- ↑ Jordan, Charles, (1939/1965). "Calculus of Finite Differences", Chelsea Publishing. On-line: [1]
- ↑ Zachos, C. (2008). "डिस्क्रीट स्पेस-टाइम पर अम्ब्रल विरूपण". International Journal of Modern Physics A. 23 (13): 2005–2014. arXiv:0710.2306. Bibcode:2008IJMPA..23.2005Z. doi:10.1142/S0217751X08040548. S2CID 16797959.
- ↑ Curtright, T. L.; Zachos, C. K. (2013). "अम्ब्राल वेड मेकुम". Frontiers in Physics. 1: 15. arXiv:1304.0429. Bibcode:2013FrP.....1...15C. doi:10.3389/fphy.2013.00015. S2CID 14106142.
- ↑ Levy, H.; Lessman, F. (1992). परिमित अंतर समीकरण. Dover. ISBN 0-486-67260-3.
- ↑ Ames, W. F., (1977). Numerical Methods for Partial Differential Equations, Section 1.6. Academic Press, New York. ISBN 0-12-056760-1.
- ↑ Hildebrand, F. B., (1968). Finite-Difference Equations and Simulations, Section 2.2, Prentice-Hall, Englewood Cliffs, New Jersey.
- ↑ Flajolet, Philippe; Sedgewick, Robert (1995). "मेलिन ट्रांसफॉर्म और एसिम्प्टोटिक्स: परिमित अंतर और राइस इंटीग्रल" (PDF). Theoretical Computer Science. 144 (1–2): 101–124. doi:10.1016/0304-3975(94)00281-M..
- Richardson, C. H. (1954): An Introduction to the Calculus of Finite Differences (Van Nostrand (1954) online copy
- Mickens, R. E. (1991): Difference Equations: Theory and Applications (Chapman and Hall/CRC) ISBN 978-0442001360