आंशिक अवकल समीकरण: Difference between revisions
(Created page with "{{short description|Type of differential equation}} {{Differential equations}} File:Heat.gif|thumb|ऊर्ध्वाधर दिशा और रंग द्वार...") |
No edit summary |
||
| (21 intermediate revisions by 7 users not shown) | |||
| Line 1: | Line 1: | ||
{{short description|Type of differential equation}} | {{short description|Type of differential equation}} | ||
{{Differential equations}} | {{Differential equations}} | ||
[[File:Heat.gif|thumb|ऊर्ध्वाधर दिशा और रंग द्वारा दर्शाए गए तापमान के साथ द्वि-आयामी ताप समीकरण के समाधान का एक दृश्य।]]गणित में, | [[File:Heat.gif|thumb|ऊर्ध्वाधर दिशा और रंग द्वारा दर्शाए गए तापमान के साथ द्वि-आयामी [[ ताप समीकरण ]] के समाधान का एक दृश्य।]]गणित में, '''आंशिक अवकल समीकरण''' (पीडीई) एक समीकरण है जो बहुविकल्पीय फलन के विभिन्न आंशिक डेरिवेटिव (व्युत्पन्न) के बीच संबंध स्थापित करता है। | ||
फ़ंक्शन को | फ़ंक्शन को प्रायः एक "अज्ञात" के रूप में माना जाता है जिसे हल किया जाना है, इसी तरह x को बीजगणितीय समीकरण जैसे {{math|1=''x''<sup>2</sup> − 3''x'' + 2 = 0}} में हल करने के लिए एक अज्ञात संख्या के रूप में कैसे सोचा जाता है। हालांकि, आंशिक अंतर समीकरणों के समाधान के लिए स्पष्ट सूत्रों को लिखना असंभव है। तदनुसार, कंप्यूटर का उपयोग करके कुछ आंशिक अंतर समीकरणों के संख्यात्मक रूप से अनुमानित समाधानों के तरीकों पर आधुनिक गणितीय और वैज्ञानिक अनुसंधान की एक बड़ी मात्रा है। आंशिक अवकल समीकरण भी [[ शुद्ध गणित |शुद्ध गणितीय]] अनुसंधान के एक बड़े क्षेत्र पर कब्जा कर लेते हैं, जिसमें सामान्य प्रश्न, मोटे तौर पर बोलते हैं, विभिन्न आंशिक अंतर समीकरणों के समाधान की सामान्य गुणात्मक विशेषताओं की पहचान पर, जैसे कि अस्तित्व, विशिष्टता, नियमितता और स्थिरता। कई खुले प्रश्नों में नेवियर-स्टोक्स समीकरणों के समाधान की मौजूदगी और सुगमता है, जिसे 2000 में मिलेनियम पुरस्कार समस्याओं में से एक के रूप में नामित किया गया था। | ||
भौतिक विज्ञान और | [[ भौतिक विज्ञान |भौतिक विज्ञान]] और [[ अभियांत्रिकी |अभियांत्रिकी]] जैसे गणितीय रूप से उन्मुख वैज्ञानिक क्षेत्रों में आंशिक अंतर समीकरण सर्वव्यापी हैं। उदाहरण के लिए, वे ध्वनि, ऊष्मा, [[ प्रसार |प्रसार]], [[ इलेक्ट्रोस्टाटिक्स |इलेक्ट्रोस्टैटिक्स]], इलेक्ट्रोडायनामिक्स, [[ ऊष्मप्रवैगिकी |ऊष्मप्रवैगिकी]], द्रव गतिकी, [[ लोच (भौतिकी) |लोच]], [[ सामान्य सापेक्षता |सामान्य सापेक्षता]] और [[ क्वांटम यांत्रिकी |क्वांटम यांत्रिकी]] (श्रोडिंगर समीकरण, [[ पाउली समीकरण |पाउली समीकरण]], आदि) की आधुनिक वैज्ञानिक समझ में मूलभूत हैं। वे कई शुद्ध गणितीय विचारों से भी उत्पन्न होते हैं, जैसे [[ अंतर ज्यामिति |अंतर ज्यामिति]] और विविधताओं की कलन; अन्य उल्लेखनीय अनुप्रयोगों में, वे [[ ज्यामितीय टोपोलॉजी |ज्यामितीय टोपोलॉजी]] से पॉइंकेयर अनुमान के प्रमाण में मूलभूत उपकरण हैं। | ||
आंशिक रूप से इस प्रकार के स्रोतों के कारण, विभिन्न प्रकार के आंशिक अंतर समीकरणों का एक विस्तृत स्पेक्ट्रम है, और उत्पन्न होने वाले कई अलग-अलग समीकरणों से निपटने के लिए विधियों का विकास किया गया है। जैसे, यह | आंशिक रूप से इस प्रकार के स्रोतों के कारण, विभिन्न प्रकार के आंशिक अंतर समीकरणों का एक विस्तृत स्पेक्ट्रम है, और उत्पन्न होने वाले कई अलग-अलग समीकरणों से निपटने के लिए विधियों का विकास किया गया है। जैसे, यह सामान्यतः स्वीकार किया जाता है कि आंशिक अवकल समीकरणों का कोई "सामान्य सिद्धांत" नहीं है, जिसमें विशेषज्ञ ज्ञान कुछ हद तक अनिवार्य रूप से अलग-अलग उपक्षेत्रों के बीच विभाजित होता है।<ref>{{cite book |authorlink=Sergiu Klainerman |last=Klainerman |first=Sergiu |year=2010 |chapter=PDE as a Unified Subject |editor-last=Alon |editor-first=N. |editor2-last=Bourgain |editor2-first=J. |editor3-last=Connes |editor3-first=A. |editor4-last=Gromov |editor4-first=M. |editor5-last=Milman |editor5-first=V. |title=गणित में दर्शन|series=Modern Birkhäuser Classics |publisher=Birkhäuser |location=Basel |pages=279–315 |isbn=978-3-0346-0421-5 |doi=10.1007/978-3-0346-0422-2_10 }}</ref> | ||
साधारण अवकल समीकरण आंशिक अवकल समीकरणों का एक उपवर्ग बनाते हैं, जो एकल चर के फलनों के अनुरूप होते हैं। स्टोचैस्टिक आंशिक अंतर समीकरण और | |||
साधारण अवकल समीकरण आंशिक अवकल समीकरणों का एक उपवर्ग बनाते हैं, जो एकल चर के फलनों के अनुरूप होते हैं। स्टोचैस्टिक आंशिक अंतर समीकरण और गैर-स्थानीय समीकरण, 2020 तक, "पीडीई" धारणा के विशेष रूप से व्यापक रूप से अध्ययन किए गए विस्तार हैं। अधिक शास्त्रीय विषय, जिन पर अभी भी बहुत सक्रिय शोध है, में दीर्घवृत्तक और परावर्तक आंशिक अवकल समीकरण, द्रव यांत्रिकी, [[ बोल्ट्जमैन समीकरण |बोल्ट्जमैन समीकरण]] और फैलाने वाले आंशिक अंतर समीकरण शामिल हैं। | |||
== परिचय == | == परिचय == | ||
एक | एक का कहना है कि तीन चर का एक फ़ंक्शन {{math|''u''(''x'', ''y'', ''z'')}} "[[ हार्मोनिक फ़ंक्शन |हार्मोनिक]]" या "लाप्लास समीकरण का समाधान" है यदि यह स्थिति को संतुष्ट करता है।<math display="block">\frac{\partial^2u}{\partial x^2}+\frac{\partial^2u}{\partial y^2}+\frac{\partial^2u}{\partial z^2}=0.</math>चिरसम्मत [[ शास्त्रीय यांत्रिकी |यांत्रिकी]] के लिए उनकी प्रासंगिकता के कारण उन्नीसवीं शताब्दी में इस तरह के कार्यों का व्यापक रूप से अध्ययन किया गया था, उदाहरण के लिए, एक सजातीय ठोस का संतुलन तापमान वितरण एक हार्मोनिक फ़ंक्शन है। यदि स्पष्ट रूप से एक फ़ंक्शन दिया गया है, तो यह सामान्यतः यह जांचने के लिए सीधी गणना का विषय है कि यह हार्मोनिक है या नहीं। उदाहरण के लिए:<math display="block">u(x,y,z) = \frac{1}{\sqrt{x^2 - 2x + y^2 + z^2 + 1}}</math>और<math display="block">u(x,y,z) = 2x^2 - y^2 - z^2</math>जबकि दोनों हार्मोनिक हैं<math display="block">u(x,y,z)=\sin(xy)+z</math>यह आश्चर्यजनक हो सकता है कि हार्मोनिक कार्यों के दिए गए दो उदाहरण एक दूसरे से आश्चर्यजनक रूप से भिन्न रूप हैं। यह इस तथ्य का प्रतिबिंब है कि वे किसी भी तरह से लाप्लास समीकरण के "सामान्य समाधान सूत्र" के विशेष मामले नहीं हैं। यह साधारण अंतर समीकरणों (ओडीई) के मामले के विपरीत है, जो मोटे तौर पर लाप्लास समीकरण के समान है, जिसमें कई परिचयात्मक पाठ्यपुस्तकों का उद्देश्य सामान्य समाधान सूत्रों के लिए एल्गोरिदम खोजना है। लाप्लास समीकरण के लिए, बड़ी संख्या में आंशिक अवकल समीकरणों की तरह, ऐसे समाधान सूत्र मौजूद नहीं होते हैं। | ||
<math display="block">\frac{\partial^2u}{\partial x^2}+\frac{\partial^2u}{\partial y^2}+\frac{\partial^2u}{\partial z^2}=0.</math> | |||
शास्त्रीय यांत्रिकी के लिए उनकी प्रासंगिकता के कारण उन्नीसवीं शताब्दी में इस तरह के कार्यों का व्यापक रूप से अध्ययन किया गया था, उदाहरण के लिए एक सजातीय ठोस का संतुलन तापमान वितरण एक हार्मोनिक | निम्नलिखित पीडीई के मामले में इस विफलता की प्रकृति को और अधिक स्पष्ट रूप से देखा जा सकता है: दो चरों के फ़ंक्शन {{math|''v''(''x'', ''y'')}} के लिए, समीकरण पर विचार करें।<math display="block">\frac{\partial^2v}{\partial x\partial y}=0.</math>इसे प्रत्यक्ष रूप से जांचा जा सकता है कि किसी एकल-चर फलन {{mvar|f}} और {{mvar|g}} के लिए {{math|1=''v''(''x'', ''y'') = ''f''(''x'') + ''g''(''y'')}} रूप का कोई भी फलन {{mvar|v}}, इस शर्त को पूरा करेगा। यह ओडीई समाधान फ़ार्मुलों में उपलब्ध विकल्पों से कहीं अधिक है, जो आम तौर पर कुछ संख्याओं के मुक्त चयन की अनुमति देता है। पीडीई के अध्ययन में, आम तौर पर कार्यों का मुफ्त विकल्प होता है। | ||
<math display="block">u(x,y,z) = \frac{1}{\sqrt{x^2 - 2x + y^2 + z^2 + 1}}</math> | |||
जबकि दोनों हार्मोनिक हैं | |||
<math display="block">u(x,y,z)=\sin(xy)+z</math> | |||
इस पसंद की प्रकृति पीडीई से पीडीई में भिन्न होती है। किसी दिए गए समीकरण | इस पसंद की प्रकृति पीडीई से पीडीई में भिन्न होती है। किसी दिए गए समीकरण को समझने के लिए, अस्तित्व और विशिष्टता प्रमेय सामान्यतः महत्वपूर्ण संगठनात्मक सिद्धांत होते हैं। कई परिचयात्मक पाठ्यपुस्तकों में, मुक्त एवं दूरस्थ शिक्षा के लिए अस्तित्व और विशिष्टता प्रमेयों की भूमिका कुछ हद तक अपारदर्शी हो सकती है; अस्तित्व आधा सामान्यतः अनावश्यक होता है क्योंकि कोई भी प्रस्तावित समाधान सूत्र की सीधे जांच कर सकता है, जबकि विशिष्टता आधा प्रायः पृष्ठभूमि में मौजूद होती है ताकि यह सुनिश्चित किया जा सके कि प्रस्तावित समाधान सूत्र जितना संभव हो उतना सामान्य है। इसके विपरीत, पीडीई के लिए, अस्तित्व और विशिष्टता प्रमेय प्रायः एकमात्र साधन होते हैं जिसके द्वारा कोई भी विभिन्न समाधानों के ढेरों के माध्यम से नेविगेट कर सकता है। इस कारण से, विशुद्ध रूप से संख्यात्मक अनुकरण करते समय वे मौलिक भी होते हैं, क्योंकि किसी को यह समझ होनी चाहिए कि उपयोगकर्ता द्वारा कौन सा डेटा निर्धारित किया जाना है और गणना करने के लिए कंप्यूटर पर क्या छोड़ा जाना है। | ||
इस तरह के अस्तित्व और | इस तरह के अस्तित्व और अद्वितीयता प्रमेयों पर चर्चा करने के लिए, "अज्ञात फ़ंक्शन" के डोमेन के बारे में सटीक होना आवश्यक है। अन्यथा, केवल "दो चरों का एक कार्य" जैसे शब्दों में बोलना, परिणामों को अर्थपूर्ण रूप से तैयार करना असंभव है। अर्थात्, अज्ञात फलन के क्षेत्र को स्वयं पीडीई की संरचना के भाग के रूप में माना जाना चाहिए। | ||
निम्नलिखित ऐसे अस्तित्व और | निम्नलिखित ऐसे अस्तित्व और अद्वितीयता प्रमेय के दो उत्कृष्ट उदाहरण प्रदान करता है। भले ही प्रश्न में दो पीडीई समान हैं, व्यवहार में एक महत्वपूर्ण अंतर है: पहले पीडीई के लिए, एक के पास एक ही फ़ंक्शन का मुफ्त नुस्खा है, जबकि दूसरे पीडीई के लिए, दो कार्यों का मुफ्त निर्धारण है। | ||
* | * बता दें कि {{mvar|B}} समतल में मूल बिंदु के चारों ओर इकाई-त्रिज्या डिस्क को दर्शाता है। यूनिट सर्कल पर किसी भी निरंतर फ़ंक्शन {{mvar|U}} के लिए, {{mvar|B}} पर ठीक एक फ़ंक्शन {{mvar|u}} होता है जैसे कि<math display="block">\frac{\partial^2u}{\partial x^2} + \frac{\partial^2u}{\partial y^2} = 0</math>और यूनिट सर्कल के लिए किसका प्रतिबंध {{mvar|U}} द्वारा दिया गया है। | ||
* | * वास्तविक रेखा {{math|'''R'''}} पर किसी भी फ़ंक्शन {{mvar|f}} और {{mvar|g}} के लिए, {{math|'''R''' × (−1, 1)}} पर बिल्कुल एक फ़ंक्शन {{mvar|u}} होता है जैसे कि<math display="block">\frac{\partial^2u}{\partial x^2} - \frac{\partial^2u}{\partial y^2} = 0</math>और {{math|1=''u''(''x'', 0) = ''f''(''x'')}} और {{math|1={{sfrac|∂''u''|∂''y''}}(''x'', 0) = ''g''(''x'')}} के साथ {{mvar|x}} के सभी मानों के लिए। | ||
इससे भी अधिक घटनाएं संभव हैं। उदाहरण के लिए, निम्नलिखित पीडीई, अंतर ज्यामिति के क्षेत्र में स्वाभाविक रूप से उत्पन्न होता है, एक उदाहरण दिखाता है जहां एक सरल और पूरी तरह से स्पष्ट समाधान सूत्र है, लेकिन केवल तीन संख्याओं के स्वतंत्र विकल्प के साथ और एक भी फ़ंक्शन नहीं है। | |||
* यदि {{mvar|u}} | * यदि {{mvar|u}} {{math|'''R'''<sup>2</sup>}} पर एक फ़ंक्शन है<math display="block">\frac{\partial}{\partial x} \frac{\frac{\partial u}{\partial x}}{\sqrt{1 + \left(\frac{\partial u}{\partial x}\right)^2 + \left(\frac{\partial u}{\partial y}\right)^2}} + | ||
\frac{\partial}{\partial y} \frac{\frac{\partial u}{\partial y}}{\sqrt{1 + \left(\frac{\partial u}{\partial x}\right)^2 + \left(\frac{\partial u}{\partial y}\right)^2}}=0,</math> फिर संख्याएँ हैं {{mvar|a}}, {{mvar|b}}, | \frac{\partial}{\partial y} \frac{\frac{\partial u}{\partial y}}{\sqrt{1 + \left(\frac{\partial u}{\partial x}\right)^2 + \left(\frac{\partial u}{\partial y}\right)^2}}=0,</math> फिर संख्याएँ हैं {{mvar|a}}, {{mvar|b}}, और {{mvar|c}} साथ {{math|1=''u''(''x'', ''y'') = ''ax'' + ''by'' + ''c''}}. | ||
पहले के उदाहरणों के विपरीत, यह पीडीई वर्गमूलों और वर्गों के कारण अरैखिक है। एक | पहले के उदाहरणों के विपरीत, यह '''पीडीई वर्गमूलों''' और वर्गों के कारण अरैखिक है। एक '''अरैखिक पीडीई''' एक ऐसा है कि, यदि यह सजातीय है, तो किन्हीं भी दो समाधानों का योग भी एक समाधान है, और किसी भी समाधान का कोई भी स्थिर गुणक भी एक समाधान है। | ||
== | == वेल-पोसेड्नेस == | ||
अच्छी स्थिति एक पीडीई के बारे में सूचना के एक सामान्य योजनाबद्ध पैकेज को संदर्भित करती है। यह कहने के लिए कि एक पीडीई अच्छी स्थिति में है, एक व्यक्ति में होना चाहिए: | |||
=== ऊर्जा | * एक अस्तित्व और विशिष्टता प्रमेय, यह दावा करते हुए कि कुछ स्वतंत्र रूप से चुने गए कार्यों के नुस्खे से, पीडीई के एक विशिष्ट समाधान को अलग किया जा सकता है | ||
ऊर्जा | * नि: शुल्क विकल्पों को लगातार बदलते रहने से, व्यक्ति लगातार इसी समाधान को बदलता रहता है | ||
<math display="block">\frac{\partial u}{\partial t} + \alpha \frac{\partial u}{\partial x} = 0, \quad x \in [a,b], t > 0,</math> | |||
यह, कई अलग-अलग पीडीई पर लागू होने की आवश्यकता के कारण, कुछ हद तक अस्पष्ट है। विशेष रूप से "निरंतरता" की आवश्यकता अस्पष्ट है क्योंकि आम तौर पर कई असमान साधन होते हैं जिनके द्वारा इसे कड़ाई से परिभाषित किया जा सकता है। हालांकि, पीडीई का अध्ययन करना असामान्य है, बिना यह निर्दिष्ट किए कि यह अच्छी तरह से प्रस्तुत किया गया है। | |||
<math display="block">\int_a^b u \frac{\partial u}{\partial t} \mathrm dx + \alpha \int _a ^b u \frac{\partial u}{\partial x} \mathrm dx = 0.</math> | |||
उसका उपयोग करना | === ऊर्जा पद्धति === | ||
<math display="block">\int _a ^b u \frac{\partial u}{\partial t} \mathrm dx = \frac{1}{2} \frac{\partial}{\partial t} \| u \| ^2 \quad \text{and} \quad \int _a ^b u \frac{\partial u}{\partial x} \mathrm dx = \frac{1}{2} u(b,t)^2 - \frac{1}{2} u(a,t)^2,</math> | ऊर्जा विधि एक गणितीय प्रक्रिया है जिसका उपयोग प्रारंभिक-सीमा-मूल्य-समस्याओं की अच्छी स्थिति को सत्यापित करने के लिए किया जा सकता है।<ref>{{cite book |title=टाइम डिपेंडेंट पीडीई के लिए हाई ऑर्डर डिफरेंस मेथड्स|first=Bertil |last=Gustafsson|series=Springer Series in Computational Mathematics |publisher=Springer |year=2008 |volume=38 |isbn=978-3-540-74992-9 |doi=10.1007/978-3-540-74993-6}}</ref> निम्नलिखित उदाहरण में ऊर्जा पद्धति का उपयोग यह तय करने के लिए किया जाता है कि कहां और कौन सी सीमा शर्तों को लगाया जाना चाहिए ताकि परिणामी आईबीवीपी अच्छी तरह से तैयार हो। द्वारा दिए गए एक आयामी अतिपरवलयिक पीडीई पर विचार करें।<math display="block">\frac{\partial u}{\partial t} + \alpha \frac{\partial u}{\partial x} = 0, \quad x \in [a,b], t > 0,</math>जहां <math>\alpha \neq 0</math> एक स्थिरांक है और <math>u(x,t)</math> प्रारंभिक स्थिति <math>u(x,0) = f(x)</math> के साथ एक अज्ञात फलन है। <math>u</math> से गुणा करने और डोमेन पर एकीकृत करने से मिलता है।<math display="block">\int_a^b u \frac{\partial u}{\partial t} \mathrm dx + \alpha \int _a ^b u \frac{\partial u}{\partial x} \mathrm dx = 0.</math>उसका उपयोग करना<math display="block">\int _a ^b u \frac{\partial u}{\partial t} \mathrm dx = \frac{1}{2} \frac{\partial}{\partial t} \| u \| ^2 \quad \text{and} \quad \int _a ^b u \frac{\partial u}{\partial x} \mathrm dx = \frac{1}{2} u(b,t)^2 - \frac{1}{2} u(a,t)^2,</math>जहां दूसरे संबंध के लिए [[ भागों द्वारा एकीकरण |भागों द्वारा एकीकरण]] का उपयोग किया गया है, हम प्राप्त करते हैं:<math display="block">\frac{\partial}{\partial t} \| u \| ^2 + \alpha u(b,t)^2 - \alpha u(a,t)^2 = 0.</math>यहाँ <math>\| \cdot \|</math> मानक <math>L^2</math> मानक को दर्शाता है। अच्छी स्थिति के लिए हमें आवश्यकता है कि समाधान की ऊर्जा गैर-बढ़ती है, यानी कि <math display="inline">\frac{\partial}{\partial t} \| u \| ^2 \leq 0</math>, जो <math>u</math> को <math>x = a</math> यदि <math>\alpha > 0</math> और <math>x = b</math> पर यदि <math>\alpha < 0</math> निर्दिष्ट करके प्राप्त किया जाता है। यह अंतर्वाह पर केवल थोपने वाली सीमा स्थितियों से संबंधित है। ध्यान दें कि सुव्यवस्थितता डेटा (प्रारंभिक और सीमा) के संदर्भ में वृद्धि की अनुमति देती है और इस प्रकार यह दिखाने के लिए पर्याप्त है कि <math display="inline">\frac{\partial}{\partial t} \| u \| ^2 \leq 0</math> धारण करता है जब सभी डेटा शून्य पर समुच्चय होते हैं। | ||
जहां दूसरे संबंध के लिए भागों द्वारा एकीकरण का उपयोग किया गया है, हम प्राप्त करते हैं | |||
<math display="block">\frac{\partial}{\partial t} \| u \| ^2 + \alpha u(b,t)^2 - \alpha u(a,t)^2 = 0.</math> | |||
=== स्थानीय समाधानों का अस्तित्व === | === स्थानीय समाधानों का अस्तित्व === | ||
कॉची प्रारंभिक मूल्य समस्याओं के लिए कॉची-कोवाल्स्की प्रमेय अनिवार्य रूप से बताता है कि यदि आंशिक अंतर समीकरण में सभी शब्द [[ विश्लेषणात्मक कार्य |विश्लेषणात्मक]] कार्यों से बने होते हैं और एक निश्चित ट्रांसवर्सलिटी की स्थिति संतुष्ट होती है (हाइपरप्लेन या अधिक आम तौर पर हाइपरसफेस जहां प्रारंभिक डेटा सामने आता है) आंशिक अंतर ऑपरेटर के संबंध में गैर-विशेषता), तो कुछ क्षेत्रों पर, आवश्यक रूप से समाधान मौजूद होते हैं जो विश्लेषणात्मक कार्य भी होते हैं। यह विश्लेषणात्मक आंशिक अवकल समीकरणों के अध्ययन का एक मूलभूत परिणाम है। हैरानी की बात है, प्रमेय सुचारू कार्यों की समायोजन में नहीं है; 1957 में [[ हंस लेवी |हैंस लेवी]] द्वारा खोजे गए एक उदाहरण में एक रेखीय आंशिक अंतर समीकरण शामिल है, जिसके गुणांक चिकने हैं (अर्थात, सभी आदेशों के व्युत्पन्न हैं) लेकिन विश्लेषणात्मक नहीं हैं जिसके लिए कोई समाधान मौजूद नहीं है। अतः कौशी-कोवालेव्स्की प्रमेय अनिवार्य रूप से विश्लेषणात्मक कार्यों के दायरे में सीमित है। | |||
== वर्गीकरण == | == वर्गीकरण == | ||
=== अंकन === | === अंकन === | ||
पीडीई लिखते समय, सबस्क्रिप्ट का उपयोग करके | पीडीई लिखते समय, आंशिक डेरिवेटिव को सबस्क्रिप्ट का उपयोग करके निरूपित करना आम है। उदाहरण के लिए:<math display="block">u_x = \frac{\partial u}{\partial x},\quad u_{xx} = \frac{\partial^2 u}{\partial x^2},\quad u_{xy} = \frac{\partial^2 u}{\partial y\, \partial x} = \frac{\partial}{\partial y } \left(\frac{\partial u}{\partial x}\right). </math>सामान्य स्थिति में कि {{mvar|u}} का एक कार्य है {{mvar|n}} चर, फिर {{math|''u''<sub>''i''</sub>}} के सापेक्ष पहले आंशिक व्युत्पन्न को दर्शाता है {{mvar|i}}-वें इनपुट, {{math|''u''<sub>''ij''</sub>}} के सापेक्ष दूसरे आंशिक व्युत्पन्न को दर्शाता है {{mvar|i}}-वें और {{mvar|j}}-वें इनपुट, और इसी तरह। | ||
<math display="block">u_x = \frac{\partial u}{\partial x},\quad u_{xx} = \frac{\partial^2 u}{\partial x^2},\quad u_{xy} = \frac{\partial^2 u}{\partial y\, \partial x} = \frac{\partial}{\partial y } \left(\frac{\partial u}{\partial x}\right). </math> | |||
सामान्य स्थिति में कि {{mvar|u}} का एक कार्य है {{mvar|n}} चर, फिर {{math|''u''<sub>''i''</sub>}} के सापेक्ष पहले आंशिक व्युत्पन्न को दर्शाता है {{mvar|i}}-वें इनपुट, {{math|''u''<sub>''ij''</sub>}} के सापेक्ष दूसरे आंशिक व्युत्पन्न को दर्शाता है {{mvar|i}}-वें और {{mvar|j}}-वें इनपुट, और इसी तरह। | |||
ग्रीक अक्षर {{math|Δ}} लाप्लास ऑपरेटर को दर्शाता है; यदि {{mvar|u}} का एक कार्य है {{mvar|n}} चर, फिर | ग्रीक अक्षर {{math|Δ}} [[ लाप्लास ऑपरेटर |लाप्लास ऑपरेटर]] को दर्शाता है; यदि {{mvar|u}} का एक कार्य है {{mvar|n}} चर, फिर<math display="block">\Delta u = u_{11} + u_{22} + \cdots + u_{nn}.</math>भौतिकी साहित्य में, लाप्लास ऑपरेटर को प्रायः {{math|∇<sup>2</sup>}} द्वारा निरूपित किया जाता है; गणित साहित्य में, {{math|∇<sup>2</sup>''u''}} भी {{mvar|u}} के [[ हेसियन मैट्रिक्स |हेसियन मैट्रिक्स]] को निरूपित कर सकता है। | ||
<math display="block">\Delta u = u_{11} + u_{22} + \cdots + u_{nn}.</math> | |||
भौतिकी साहित्य में, लाप्लास | |||
=== पहले क्रम के समीकरण === | === पहले क्रम के समीकरण === | ||
{{main| | {{main|प्रथम-क्रम आंशिक अंतर समीकरण}} | ||
=== रेखीय और अरेखीय समीकरण === | === रेखीय और अरेखीय समीकरण === | ||
==== रैखिक समीकरण ==== | ==== रैखिक समीकरण ==== | ||
एक | एक पीडीई को रैखिक कहा जाता है यदि यह अज्ञात और उसके डेरिवेटिव में रैखिक है। उदाहरण के लिए, {{mvar|x}} और {{mvar|y}} के फलन {{mvar|u}} के लिए, एक द्वितीय कोटि रैखिक पीडीई का रूप होता है<math display="block"> a_1(x,y)u_{xx} + a_2(x,y)u_{xy} + a_3(x,y)u_{yx} + a_4(x,y)u_{yy} + a_5(x,y)u_x + a_6(x,y)u_y + a_7(x,y)u = f(x,y) | ||
<math display="block"> a_1(x,y)u_{xx} + a_2(x,y)u_{xy} + a_3(x,y)u_{yx} + a_4(x,y)u_{yy} + a_5(x,y)u_x + a_6(x,y)u_y + a_7(x,y)u = f(x,y) | </math>जहाँ {{math|''a<sub>i</sub>''}} और {{mvar|''f''}} केवल स्वतंत्र चरों के फलन हैं। (प्रायः मिश्रित-आंशिक डेरिवेटिव्स {{math|''u<sub>xy</sub>''}} और {{math|''u<sub>yx</sub>''}} को समान किया जाएगा, लेकिन रैखिकता की चर्चा के लिए इसकी आवश्यकता नहीं है।) यदि {{math|''a<sub>i</sub>''}} स्थिरांक हैं ({{mvar|x}} और {{mvar|y}} से स्वतंत्र) तो पीडीई को निरंतर गुणांक के साथ रैखिक कहा जाता है। यदि हर जगह {{mvar|''f''}} शून्य है तो रैखिक पीडीई समांगी है, अन्यथा यह असमघाती है। (यह [[ स्पर्शोन्मुख समरूपता |स्पर्शोन्मुख समरूपता]] से अलग है, जो पीडीई के समाधान पर गुणांक में उच्च आवृत्ति दोलनों के प्रभावों का अध्ययन करता है।) | ||
</math> | |||
==== अरैखिक समीकरण ==== | ==== अरैखिक समीकरण ==== | ||
तीन मुख्य प्रकार के | तीन मुख्य प्रकार के अरैखिक पीडीई अर्धरेखीय पीडीई, रैखिककल्प पीडीई और पूरी तरह से अरैखिक पीडीई हैं। | ||
रेखीय पीडीई के निकटतम सेमीलीनियर पीडीई हैं, जहां केवल उच्चतम क्रम के डेरिवेटिव रैखिक शब्दों के रूप में | रेखीय पीडीई के निकटतम सेमीलीनियर (अर्धरेखीय) पीडीई हैं, जहां केवल उच्चतम क्रम के डेरिवेटिव रैखिक शब्दों के रूप में प्रकट होते हैं, गुणांक के साथ जो स्वतंत्र चर के कार्य हैं। निचले क्रम के डेरिवेटिव और अज्ञात फ़ंक्शन मनमाने ढंग से प्रकट हो सकते हैं। उदाहरण के लिए, दो चरों में एक सामान्य द्वितीय-क्रम सेमीलीनियर पीडीई है।<math display="block"> a_1(x,y)u_{xx} + a_2(x,y)u_{xy} + a_3(x,y)u_{yx} + a_4(x,y)u_{yy} + f(u_x, u_y, u, x, y) = 0 </math>क्वासिलिनियर (रैखिककल्प) पीडीई में उच्चतम क्रम डेरिवेटिव इसी प्रकार केवल रैखिक शर्तों के रूप में दिखाई देते हैं, लेकिन गुणांक के साथ संभवतः अज्ञात और निम्न-क्रम डेरिवेटिव के कार्य होते हैं:<math display="block"> a_1(u_x, u_y, u, x, y)u_{xx} + a_2(u_x, u_y, u, x, y)u_{xy} + a_3(u_x, u_y, u, x, y)u_{yx} + a_4(u_x, u_y, u, x, y)u_{yy} + f(u_x, u_y, u, x, y) = 0 </math>भौतिकी में कई मौलिक पीडीई क्वैसिलिनियर हैं, जैसे सामान्य सापेक्षता के [[ आइंस्टीन समीकरण |आइंस्टीन समीकरण]] और तरल गति का वर्णन करने वाले नेवियर-स्टोक्स समीकरण। | ||
<math display="block"> a_1(x,y)u_{xx} + a_2(x,y)u_{xy} + a_3(x,y)u_{yx} + a_4(x,y)u_{yy} + f(u_x, u_y, u, x, y) = 0 </math> | |||
क्वासिलिनियर पीडीई में उच्चतम | |||
<math display="block"> a_1(u_x, u_y, u, x, y)u_{xx} + a_2(u_x, u_y, u, x, y)u_{xy} + a_3(u_x, u_y, u, x, y)u_{yx} + a_4(u_x, u_y, u, x, y)u_{yy} + f(u_x, u_y, u, x, y) = 0 </math> | |||
भौतिकी में कई मौलिक पीडीई क्वैसिलिनियर हैं, जैसे सामान्य सापेक्षता के आइंस्टीन समीकरण और तरल गति का वर्णन करने वाले नेवियर-स्टोक्स समीकरण। | |||
किसी रैखिकता गुण के बिना पीडीई को पूरी तरह से गैर-रैखिक कहा जाता है और एक या अधिक उच्चतम-क्रम डेरिवेटिव पर गैर-रैखिकता रखता है। एक उदाहरण मोंज-एम्पीयर समीकरण है, जो विभेदक ज्यामिति में उत्पन्न होता है।<ref name="PrincetonCompanion">{{Citation|last = Klainerman|first = Sergiu|year = 2008|title =Partial Differential Equations|editor-last1 = Gowers|editor-first1 = Timothy|editor-last2 = Barrow-Green|editor-first2 = June|editor-last3 = Leader|editor-first3 = Imre|encyclopedia = The Princeton Companion to Mathematics|pages = 455–483|publisher = Princeton University Press}}</ref> | |||
=== दूसरे क्रम के रैखिक समीकरण === | |||
बीसवीं शताब्दी की शुरुआत के बाद से क्रम दो के दीर्घवृत्तीय, परवलयिक और [[ अतिशयोक्तिपूर्ण आंशिक अंतर समीकरण |अतिशयोक्तिपूर्ण आंशिक]] अंतर समीकरणों का व्यापक रूप से अध्ययन किया गया है। हालाँकि, कई अन्य महत्वपूर्ण प्रकार के पीडीई हैं, जिनमें कॉर्टेवेग-डी व्रीज़ समीकरण शामिल है। यूलर-ट्रिकोमी समीकरण जैसे संकर भी हैं, जो डोमेन के विभिन्न क्षेत्रों के लिए दीर्घवृत्त से अतिपरवलयिक में भिन्न होते हैं। इन मूल प्रकारों के उच्च-क्रम पीडीई के लिए महत्वपूर्ण विस्तार भी हैं, लेकिन ऐसा ज्ञान अधिक विशिष्ट है। | |||
दीर्घवृत्तीय/परवलयिक/अतिशयोक्तिपूर्ण वर्गीकरण उपयुक्त प्रारंभिक और सीमा स्थितियों और समाधानों की समतलता के लिए एक मार्गदर्शक प्रदान करता है। {{math|1=''u<sub>xy</sub>'' = ''u<sub>yx</sub>''}} मानते हुए, दो स्वतंत्र चरों में सामान्य रैखिक द्वितीय-क्रम पीडीई का रूप है। | |||
<math display="block">Au_{xx} + 2Bu_{xy} + Cu_{yy} + \cdots \mbox{(lower order terms)} = 0,</math> | <math display="block">Au_{xx} + 2Bu_{xy} + Cu_{yy} + \cdots \mbox{(lower order terms)} = 0,</math> | ||
जहां गुणांक {{mvar|A}}, {{mvar|B}}, {{mvar|C}}... {{mvar|x}} और {{mvar|y}} पर निर्भर हो सकता है। यदि {{math|''A''<sup>2</sup> + ''B''<sup>2</sup> + ''C''<sup>2</sup> > 0}} के एक क्षेत्र पर {{mvar|xy}}-प्लेन, पीडीई उस क्षेत्र में दूसरे क्रम का है। यह प्रपत्र शंकु खंड के समीकरण के अनुरूप है: | |||
<math display="block">Ax^2 + 2Bxy + Cy^2 + \cdots = 0.</math>अधिक सटीक रूप से, {{math|∂<sub>''x''</sub>}} को {{mvar|X}} द्वारा प्रतिस्थापित करना, और इसी तरह अन्य चरों के लिए (औपचारिक रूप से यह एक [[ फूरियर रूपांतरण |फूरियर रूपांतरण]] द्वारा किया जाता है), एक स्थिर-गुणांक पीडीई को समान डिग्री के बहुपद में उच्चतम डिग्री (एक [[ सजातीय बहुपद |सजातीय बहुपद]]) के साथ परिवर्तित करता है। यहाँ एक [[ द्विघात रूप |द्विघात रूप]]) वर्गीकरण के लिए सर्वाधिक महत्वपूर्ण है। | |||
# {{math|''B''<sup>2</sup> − ''AC'' < 0}} ( | जिस तरह विविक्तकर {{math|''B''<sup>2</sup> − 4''AC''}} के आधार पर शंक्वाकार वर्गों और द्विघात रूपों को परवलयिक, अतिशयोक्तिपूर्ण और दीर्घवृत्त में वर्गीकृत किया जाता है, उसी तरह किसी दिए गए बिंदु पर दूसरे क्रम के पीडीई के लिए भी किया जा सकता है। हालाँकि, पीडीई में विविक्तकर {{math|''B''<sup>2</sup> − ''AC''}} द्वारा दिया जाता है क्योंकि {{mvar|xy}} पद की अभ्यास {{mvar|B}} के बजाय {{math|2''B''}} है; औपचारिक रूप से, विविक्तकर (संबंधित द्विघात रूप का) {{math|1=(2''B'')<sup>2</sup> − 4''AC'' = 4(''B''<sup>2</sup> − ''AC'')}} है, जिसमें सरलता के लिए 4 का गुणनखंड हटा दिया गया है। | ||
# {{math|''B''<sup>2</sup> − ''AC'' < 0}} (दीर्घवृत्त आंशिक अंतर समीकरण): अण्डाकार आंशिक अंतर समीकरण के समाधान उतने ही चिकने होते हैं जितने कि गुणांक अनुमति देते हैं, उस क्षेत्र के आंतरिक भाग में जहाँ समीकरण और समाधान परिभाषित होते हैं। उदाहरण के लिए, लाप्लास के समीकरण के समाधान डोमेन के भीतर विश्लेषणात्मक होते हैं जहां उन्हें परिभाषित किया जाता है, लेकिन समाधान सीमा मान मान सकते हैं जो चिकनी नहीं हैं। सबसोनिक गति पर तरल पदार्थ की गति को दीर्घवृत्त पीडीई के साथ अनुमानित किया जा सकता है, और यूलर-ट्रिकोमी समीकरण अंडाकार है जहां {{math|''x'' < 0}}. | |||
# {{math|1=''B''<sup>2</sup> − ''AC'' = 0}} (परवलयिक आंशिक अंतर समीकरण): समीकरण जो हर बिंदु पर परवलयिक आंशिक अंतर समीकरण होते हैं, उन्हें स्वतंत्र चर के परिवर्तन द्वारा ताप समीकरण के अनुरूप रूप में परिवर्तित किया जा सकता है। परिवर्तित समय चर बढ़ने पर समाधान सुचारू हो जाते हैं। यूलर-ट्रिकोमी समीकरण में उस रेखा पर परवलयिक प्रकार है जहां {{math|1=''x'' = 0}}. | # {{math|1=''B''<sup>2</sup> − ''AC'' = 0}} (परवलयिक आंशिक अंतर समीकरण): समीकरण जो हर बिंदु पर परवलयिक आंशिक अंतर समीकरण होते हैं, उन्हें स्वतंत्र चर के परिवर्तन द्वारा ताप समीकरण के अनुरूप रूप में परिवर्तित किया जा सकता है। परिवर्तित समय चर बढ़ने पर समाधान सुचारू हो जाते हैं। यूलर-ट्रिकोमी समीकरण में उस रेखा पर परवलयिक प्रकार है जहां {{math|1=''x'' = 0}}. | ||
# {{math|''B''<sup>2</sup> − ''AC'' > 0}} (अतिपरवलयिक आंशिक अंतर समीकरण): अतिशयोक्तिपूर्ण आंशिक अंतर समीकरण समीकरण प्रारंभिक डेटा में कार्यों या डेरिवेटिव के किसी भी विच्छिन्नता को बनाए रखते हैं। एक उदाहरण तरंग समीकरण है। सुपरसोनिक गति पर द्रव की गति को हाइपरबोलिक पीडीई के साथ अनुमानित किया जा सकता है, और यूलर-ट्रिकोमी समीकरण हाइपरबॉलिक है जहां {{math|''x'' > 0}}. | # {{math|''B''<sup>2</sup> − ''AC'' > 0}} (अतिपरवलयिक आंशिक अंतर समीकरण): अतिशयोक्तिपूर्ण आंशिक अंतर समीकरण समीकरण प्रारंभिक डेटा में कार्यों या डेरिवेटिव के किसी भी विच्छिन्नता को बनाए रखते हैं। एक उदाहरण [[ तरंग समीकरण | तरंग समीकरण]] है। सुपरसोनिक गति पर द्रव की गति को हाइपरबोलिक पीडीई के साथ अनुमानित किया जा सकता है, और यूलर-ट्रिकोमी समीकरण हाइपरबॉलिक है जहां {{math|''x'' > 0}}. | ||
अगर वहाँ {{mvar|n}} स्वतंत्र प्रभावित करने वाली वस्तुएँ {{math|''x''<sub>1</sub>, ''x''<sub>2 </sub>, …, ''x''<sub>''n''</sub>}}दूसरे क्रम के एक सामान्य रैखिक आंशिक अंतर समीकरण का रूप है | अगर वहाँ {{mvar|n}} स्वतंत्र प्रभावित करने वाली वस्तुएँ {{math|''x''<sub>1</sub>, ''x''<sub>2 </sub>, …, ''x''<sub>''n''</sub>}}दूसरे क्रम के एक सामान्य रैखिक आंशिक अंतर समीकरण का रूप है<math display="block">L u =\sum_{i=1}^n\sum_{j=1}^n a_{i,j} \frac{\partial^2 u}{\partial x_i \partial x_j} \quad+ \text{lower-order terms} = 0.</math>वर्गीकरण गुणांक मैट्रिक्स के [[ eigenvalues |आइगेनवैल्यू]] के हस्ताक्षर पर निर्भर करता है {{math|''a''<sub>''i'',''j''</sub>}}. | ||
<math display="block">L u =\sum_{i=1}^n\sum_{j=1}^n a_{i,j} \frac{\partial^2 u}{\partial x_i \partial x_j} \quad+ \text{lower-order terms} = 0.</math> | # दीर्घवृत्त: आइगेनवैल्यू सभी धनात्मक या सभी ऋणात्मक हैं। | ||
वर्गीकरण गुणांक मैट्रिक्स के eigenvalues के हस्ताक्षर पर निर्भर करता है {{math|''a''<sub>''i'',''j''</sub>}}. | # परवलयिक: आइगेनवैल्यू सभी धनात्मक या सभी नकारात्मक हैं, एक को छोड़कर जो शून्य है। | ||
# अतिपरवलयिक: केवल एक ऋणात्मक आइगेनवैल्यू है और बाकी सभी धनात्मक हैं, या केवल एक धनात्मक आइगेनवैल्यू है और बाकी सभी ऋणात्मक हैं। | |||
# दीर्घवृत्त: | # अल्ट्राहाइपरबोलिक: एक से अधिक धनात्मक आइगेनवैल्यू और एक से अधिक ऋणात्मक आइगेनवैल्यू होते हैं, और कोई शून्य आइगेनवैल्यू नहीं होते हैं।<ref>Courant and Hilbert (1962), p.182.</ref> | ||
# परवलयिक: | दीर्घवृत्त, परवलयिक, और अतिपरवलयिक समीकरणों के सिद्धांत का सदियों से अध्ययन किया गया है, जो काफी हद तक [[ लाप्लास समीकरण | लाप्लास समीकरण]] , ऊष्मा समीकरण और तरंग समीकरण के मानक उदाहरणों के आसपास या उसके आधार पर केंद्रित है। | ||
# अतिपरवलयिक: केवल एक | |||
# अल्ट्राहाइपरबोलिक: एक से अधिक | |||
=== प्रथम-क्रम समीकरणों और विशिष्ट सतहों की प्रणाली === | === प्रथम-क्रम समीकरणों और विशिष्ट सतहों की प्रणाली === | ||
आंशिक अंतर समीकरणों के वर्गीकरण को प्रथम-क्रम समीकरणों की प्रणालियों तक विस्तारित किया जा सकता है, जहां अज्ञात {{mvar|u}} अब | आंशिक अंतर समीकरणों के वर्गीकरण को प्रथम-क्रम समीकरणों की प्रणालियों तक विस्तारित किया जा सकता है, जहां अज्ञात {{mvar|u}} अब {{mvar|m}} घटकों के साथ एक वेक्टर है, और गुणांक मैट्रिसेस {{mvar|A<sub>ν</sub>}}, {{math|1=''ν'' = 1, 2, …, ''n''}} के लिए {{mvar|m}} द्वारा {{mvar|m}} मेट्रिसेस हैं। आंशिक अवकल समीकरण का रूप ले लेता है।<math display="block">Lu = \sum_{\nu=1}^{n} A_\nu \frac{\partial u}{\partial x_\nu} + B=0,</math>जहां गुणांक मेट्रिसेस {{mvar|A<sub>ν</sub>}} और वेक्टर {{mvar|B}} पर निर्भर हो सकता है {{mvar|x}} और {{mvar|u}}. यदि एक [[ ऊनविम पृष्ठ |ऊनविम पृष्ठ]] {{mvar|S}} निहित रूप में दिया गया है।<math display="block">\varphi(x_1, x_2, \ldots, x_n)=0,</math> | ||
<math display="block">Lu = \sum_{\nu=1}^{n} A_\nu \frac{\partial u}{\partial x_\nu} + B=0,</math> | |||
जहां गुणांक मेट्रिसेस {{mvar|A<sub>ν</sub>}} और वेक्टर {{mvar|B}} पर निर्भर हो सकता है {{mvar|x}} | |||
<math display="block">\varphi(x_1, x_2, \ldots, x_n)=0,</math | |||
जहां {{mvar|φ}} एक गैर-शून्य है, तब {{mvar|S}} ऑपरेटर के लिए एक विशिष्ट सतह है {{mvar|L}} किसी दिए गए बिंदु पर यदि विशेषता रूप गायब हो जाता है: | |||
<math display="block">Q\left(\frac{\partial\varphi}{\partial x_1}, \ldots, \frac{\partial\varphi}{\partial x_n}\right) = \det\left[\sum_{\nu=1}^n A_\nu \frac{\partial \varphi}{\partial x_\nu}\right] = 0.</math>इस स्थिति की ज्यामितीय व्याख्या इस प्रकार है: यदि {{mvar|u}} के लिए डेटा सतह {{mvar|S}} पर निर्धारित किया गया है, तो यह संभव हो सकता है कि अंतर समीकरण से {{mvar|u}} के सामान्य व्युत्पन्न को निर्धारित किया जा सके। यदि {{mvar|S}} पर डेटा और अवकल समीकरण, {{mvar|S}} पर {{mvar|u}} का सामान्य अवकलज निर्धारित करते हैं, तो {{mvar|S}} गैर-लक्षण है। यदि {{mvar|S}} पर डेटा और अंतर समीकरण {{mvar|S}} पर {{mvar|u}} के सामान्य व्युत्पन्न का निर्धारण नहीं करते हैं, तो सतह विशेषता है, और अंतर समीकरण डेटा को {{mvar|S}} पर प्रतिबंधित करता है: अंतर समीकरण {{mvar|S}} के लिए आंतरिक है। | |||
# एक प्रथम-क्रम प्रणाली {{math|1=''Lu'' = 0}} दीर्घवृत्तीय है यदि कोई सतह {{mvar|L}} के लिए विशेषता नहीं है: {{mvar|S}} पर {{mvar|u}} के मान और अंतर समीकरण हमेशा {{mvar|S}} पर {{mvar|u}} के सामान्य व्युत्पन्न को निर्धारित करते हैं। | |||
#एक प्रथम-क्रम प्रणाली एक बिंदु पर अतिशयोक्तिपूर्ण है यदि उस बिंदु पर सामान्य {{mvar|ξ}} के साथ एक अंतरिक्ष जैसी सतह {{mvar|S}} है। इसका मतलब यह है कि, किसी भी गैर-तुच्छ वेक्टर {{mvar|η}} ऑर्थोगोनल को {{mvar|ξ}}, और एक स्केलर गुणक {{mvar|λ}} दिया गया है, समीकरण ({{math|1=''Q''(''λξ'' + ''η'') = 0}} में {{mvar|m}} वास्तविक जड़ें {{math|''λ''<sub>1</sub>, ''λ''<sub>2</sub>, …, ''λ''<sub>''m''</sub>}} हैं। अगर ये जड़ें हमेशा अलग-अलग हों तो सिस्टम सख्ती से अतिशयोक्तिपूर्ण है। इस स्थिति की ज्यामितीय व्याख्या इस प्रकार है: विशेषता रूप {{math|1=''Q''(''ζ'') = 0}} सजातीय निर्देशांक ζ के साथ एक शंकु (सामान्य शंकु) को परिभाषित करता है। अतिशयोक्तिपूर्ण मामले में, इस शंकु में {{mvar|m}} शीट हैं, और अक्ष {{math|1=''ζ'' = ''λξ''}} इन शीटों के अंदर चलता है: यह उनमें से किसी को नहीं काटता है। लेकिन जब η द्वारा मूल से विस्थापित किया जाता है, तो यह अक्ष प्रत्येक शीट को प्रतिच्छेद करती है। दीर्घवृत्तीय मामले में, सामान्य शंकु में कोई वास्तविक शीट नहीं होती है। | |||
== विश्लेषणात्मक समाधान == | == विश्लेषणात्मक समाधान == | ||
=== चरों का पृथक्करण === | === चरों का पृथक्करण === | ||
{{main| | {{main|वियोज्य आंशिक अंतर समीकरण}} | ||
चरों को अलग करने की महत्वपूर्ण तकनीक द्वारा रेखीय पीडीई को साधारण अंतर समीकरणों की प्रणालियों में घटाया जा सकता है। यह तकनीक अंतर समीकरणों के समाधान की एक विशेषता पर टिकी हुई है: यदि कोई ऐसा समाधान ढूंढ सकता है जो समीकरण को हल करता है और सीमा शर्तों को संतुष्ट करता है, तो यह समाधान है (यह ओडीई पर भी लागू होता है)। हम एक ansatz के रूप में मानते हैं कि | चरों को अलग करने की महत्वपूर्ण तकनीक द्वारा रेखीय पीडीई को साधारण अंतर समीकरणों की प्रणालियों में घटाया जा सकता है। यह तकनीक अंतर समीकरणों के समाधान की एक विशेषता पर टिकी हुई है: यदि कोई ऐसा समाधान ढूंढ सकता है जो समीकरण को हल करता है और सीमा शर्तों को संतुष्ट करता है, तो यह समाधान है (यह ओडीई पर भी लागू होता है)। हम एक [[ ansatz |ansatz]] के रूप में मानते हैं कि पैरामीटर स्थान और समय पर एक समाधान की निर्भरता को उन शर्तों के उत्पाद के रूप में लिखा जा सकता है जो प्रत्येक एक पैरामीटर पर निर्भर करते हैं, और फिर देखते हैं कि समस्या को हल करने के लिए इसे बनाया जा सकता है या नहीं।<ref>{{cite book |last1=Gershenfeld |first1=Neil |title=गणितीय मॉडलिंग की प्रकृति|url=https://archive.org/details/naturemathematic00gers_334 |url-access=limited|date=2000|publisher=Cambridge Univ. Press|location=Cambridge|isbn=0521570956|page=[https://archive.org/details/naturemathematic00gers_334/page/n32 27]|edition=Reprinted (with corr.)}}</ref> | ||
चरों को अलग करने की विधि में, कम चरों में एक | |||
चरों को अलग करने की विधि में, कम चरों में एक पीडीई को एक पीडीई में घटाया जाता है, जो एक सामान्य अंतर समीकरण है यदि एक चर में - इन्हें हल करना आसान होता है। | |||
यह सरल पीडीई के लिए संभव है, जिसे [[ वियोज्य आंशिक अंतर समीकरण |वियोज्य आंशिक अंतर समीकरण]] कहा जाता है, और डोमेन आम तौर पर एक आयत (अंतराल का एक उत्पाद) होता है। वियोज्य पीडीई विकर्ण मैट्रिसेस के अनुरूप हैं - एक समन्वय के रूप में "निश्चित x के मान" के बारे में सोचते हुए, प्रत्येक निर्देशांक को अलग से समझा जा सकता है। | |||
यह | यह [[ विशेषताओं की विधि |विशेषताओं की विधि]] का सामान्यीकरण करता है और इसका उपयोग [[ अभिन्न परिवर्तन |अभिन्न]] परिवर्तनों में भी किया जाता है। | ||
=== विशेषताओं का तरीका === | |||
{{main|विशेषताओं का तरीका}} | |||
विशेष मामलों में, कोई विशेषता वक्र पा सकता है जिस पर समीकरण ओडीई में कम हो जाता है - इन वक्रों को सीधा करने के लिए डोमेन में बदलते निर्देशांक चर के पृथक्करण की अनुमति देते हैं और इसे विशेषताओं की विधि कहा जाता है। | |||
विशेष मामलों में, कोई विशेषता वक्र पा सकता है जिस पर समीकरण | |||
अधिक आम तौर पर, किसी को विशिष्ट सतहें मिल सकती हैं। | अधिक आम तौर पर, किसी को विशिष्ट सतहें मिल सकती हैं। द्वितीय कोटि के आंशिक अवकल समीकरण हल के लिए, चार्पिट विधि देखें। | ||
=== इंटीग्रल ट्रांसफॉर्म === | === इंटीग्रल ट्रांसफॉर्म === | ||
एक अभिन्न परिवर्तन पीडीई को एक सरल रूप में बदल सकता है, विशेष रूप से एक वियोज्य पीडीई। यह एक ऑपरेटर को | एक अभिन्न परिवर्तन पीडीई को एक सरल रूप में बदल सकता है, विशेष रूप से एक वियोज्य पीडीई। यह एक ऑपरेटर को विकर्णित करने के अनुरूप है। | ||
इसका एक महत्वपूर्ण उदाहरण फूरियर विश्लेषण है, जो साइनसोइडल तरंगों के ईजेनबेसिस का उपयोग करके गर्मी समीकरण को | इसका एक महत्वपूर्ण उदाहरण [[ फूरियर विश्लेषण |फूरियर विश्लेषण]] है, जो साइनसोइडल तरंगों के ईजेनबेसिस का उपयोग करके गर्मी समीकरण को विकर्णित करता है। | ||
यदि डोमेन परिमित या आवधिक है, तो फूरियर श्रृंखला जैसे समाधानों का एक अनंत योग उपयुक्त है, लेकिन फूरियर | यदि डोमेन परिमित या आवधिक है, तो फूरियर श्रृंखला जैसे समाधानों का एक अनंत योग उपयुक्त है, लेकिन [[ फूरियर अभिन्न |फूरियर अभिन्न]] जैसे समाधानों का एक अभिन्न अंग सामान्यतः अनंत डोमेन के लिए आवश्यक है। ऊपर दिए गए ताप समीकरण के लिए एक बिंदु स्रोत का समाधान फूरियर इंटीग्रल के उपयोग का एक उदाहरण है। | ||
=== चर का परिवर्तन === | === चर का परिवर्तन === | ||
चरों के उपयुक्त परिवर्तन द्वारा प्रायः पीडीई को ज्ञात समाधान के साथ सरल रूप में कम किया जा सकता है। उदाहरण के लिए, ब्लैक-स्कोल्स समीकरण<math display="block"> \frac{\partial V}{\partial t} + \tfrac{1}{2} \sigma^2 S^2 \frac{\partial^2 V}{\partial S^2} + rS \frac{\partial V}{\partial S} - rV = 0 </math>ऊष्मा समीकरण के लिए कम करने योग्य है।<math display="block"> \frac{\partial u}{\partial \tau} = \frac{\partial^2 u}{\partial x^2}</math>चर के परिवर्तन से<ref>{{cite book |first1=Paul |last1=Wilmott |first2=Sam |last2=Howison |first3=Jeff |last3=Dewynne |title=वित्तीय डेरिवेटिव का गणित|location= |publisher=Cambridge University Press |year=1995 |isbn=0-521-49789-2 |pages=76–81 |url=https://www.google.com/books/edition/The_Mathematics_of_Financial_Derivatives/VYVhnC3fIVEC?hl=en&gbpv=1&pg=PA76 }}</ref><math display="block">\begin{align} | |||
<math display="block"> \frac{\partial V}{\partial t} + \tfrac{1}{2} \sigma^2 S^2 \frac{\partial^2 V}{\partial S^2} + rS \frac{\partial V}{\partial S} - rV = 0 </math> | |||
ऊष्मा समीकरण के लिए कम करने योग्य | |||
<math display="block"> \frac{\partial u}{\partial \tau} = \frac{\partial^2 u}{\partial x^2}</math> | |||
चर के परिवर्तन से<ref>{{cite book |first1=Paul |last1=Wilmott |first2=Sam |last2=Howison |first3=Jeff |last3=Dewynne |title=वित्तीय डेरिवेटिव का गणित|location= |publisher=Cambridge University Press |year=1995 |isbn=0-521-49789-2 |pages=76–81 |url=https://www.google.com/books/edition/The_Mathematics_of_Financial_Derivatives/VYVhnC3fIVEC?hl=en&gbpv=1&pg=PA76 }}</ref> | |||
<math display="block">\begin{align} | |||
V(S,t) &= v(x,\tau),\\[5px] | V(S,t) &= v(x,\tau),\\[5px] | ||
x &= \ln\left(S \right),\\[5px] | x &= \ln\left(S \right),\\[5px] | ||
| Line 172: | Line 131: | ||
\end{align}</math> | \end{align}</math> | ||
=== मौलिक समाधान === | |||
{{main|मौलिक समाधान}} | |||
[[ मौलिक समाधान |मौलिक समाधान]] (एक बिंदु स्रोत के लिए समाधान) को खोजने के द्वारा अमानवीय समीकरणों को प्रायः हल किया जा सकता है (निरंतर गुणांक पीडीई के लिए, हमेशा हल किया जाता है), फिर समाधान प्राप्त करने के लिए सीमा शर्तों के साथ संवलयी होता है। | |||
यह सिग्नल प्रोसेसिंग में एक फिल्टर को उसकी आवेग प्रतिक्रिया द्वारा समझने के अनुरूप है। | यह सिग्नल प्रोसेसिंग में एक फिल्टर को उसकी [[ आवेग प्रतिक्रिया |आवेग प्रतिक्रिया]] द्वारा समझने के अनुरूप है। | ||
=== सुपरपोजिशन सिद्धांत === | === सुपरपोजिशन सिद्धांत === | ||
{{further| | {{further|सुपरपोजिशन सिद्धांत}} | ||
सुपरपोज़िशन सिद्धांत पीडीई के रैखिक सिस्टम सहित किसी भी रैखिक प्रणाली पर लागू होता है। इस अवधारणा का एक सामान्य दृश्य | |||
सुपरपोज़िशन सिद्धांत पीडीई के रैखिक सिस्टम सहित किसी भी रैखिक प्रणाली पर लागू होता है। इस अवधारणा का एक सामान्य दृश्य चरण में दो तरंगों की परस्पर क्रिया है, जिसके परिणामस्वरूप एक बड़ा आयाम होता है, उदाहरण के लिए, {{math|1=sin ''x'' + sin ''x'' = 2 sin ''x''}} पीडीई में समान सिद्धांत देखा जा सकता है जहां समाधान वास्तविक या जटिल और योगात्मक हो सकते हैं। यदि {{math|''u''<sub>1</sub>}} और {{math|''u''<sub>2</sub>}} किसी फंक्शन स्पेस {{mvar|R}} में रैखिक पीडीई के समाधान हैं, तो {{math|1=''u'' = ''c''<sub>1</sub>''u''<sub>1</sub> + ''c''<sub>2</sub>''u''<sub>2</sub>}} किसी भी स्थिरांक {{math|''c''<sub>1</sub>}}और {{math|''c''<sub>2</sub>}} के साथ भी उसी फ़ंक्शन स्पेस में उस पीडीई का एक समाधान है। | |||
=== गैर-रैखिक समीकरणों के लिए तरीके === | === गैर-रैखिक समीकरणों के लिए तरीके === | ||
{{see also| | {{see also|अरेखीय आंशिक अवकल समीकरण}} | ||
अरेखीय पीडीई को हल करने के लिए आम तौर पर लागू होने वाली कोई विधियाँ नहीं हैं। फिर भी, अस्तित्व और अद्वितीयता के परिणाम (जैसे कॉची-कोवालेव्स्की प्रमेय) प्रायः संभव होते हैं, जैसा कि समाधानों के महत्वपूर्ण गुणात्मक और मात्रात्मक गुणों के प्रमाण हैं (इन परिणामों को प्राप्त करना [[ गणितीय विश्लेषण |विश्लेषण]] का एक प्रमुख हिस्सा है)। गैर-रैखिक पीडीई के लिए कम्प्यूटेशनल समाधान, विभाजन-चरण विधि, गैर-रैखिक श्रोडिंगर समीकरण जैसे विशिष्ट समीकरणों के लिए मौजूद है। | |||
फिर भी, कुछ तकनीकों का | फिर भी, कुछ तकनीकों का प्रयोग अनेक प्रकार के समीकरणों के लिए किया जा सकता है। अनिर्धारित समीकरणों को हल करने के लिए {{mvar|h}}-सिद्धांत सबसे शक्तिशाली तरीका है। कई विश्लेषणात्मक [[ अतिनिर्धारित प्रणाली |अतिनिर्धारित]] प्रणालियों के बारे में जानकारी प्राप्त करने के लिए रिक्वायर-जेनेट सिद्धांत एक प्रभावी तरीका है। | ||
विशेषताओं की विधि का उपयोग कुछ विशेष मामलों में | विशेषताओं की विधि का उपयोग कुछ विशेष मामलों में अरैखिक आंशिक अवकल समीकरणों को हल करने के लिए किया जा सकता है।<ref>{{cite book |first=J. David |last=Logan |title=अरैखिक आंशिक विभेदक समीकरणों का परिचय|location=New York |publisher=John Wiley & Sons |year=1994 |isbn=0-471-59916-6 |chapter=First Order Equations and Characteristics |pages=51–79 }}</ref> | ||
कुछ मामलों में, पीडीई को गड़बड़ी विश्लेषण के माध्यम से हल किया जा सकता है जिसमें समाधान को ज्ञात समाधान के साथ समीकरण में सुधार माना जाता है। विकल्प [[ संख्यात्मक विश्लेषण |संख्यात्मक विश्लेषण]] तकनीक हैं जो साधारण [[ परिमित अंतर |परिमित अंतर]] योजनाओं से लेकर अधिक परिपक्व मल्टीग्रिड और परिमित तत्व विधियों तक हैं। [[ कंप्यूटर |कंप्यूटर]], कभी-कभी उच्च-प्रदर्शन वाले [[ सुपर कंप्यूटर |सुपर कंप्यूटर]] का उपयोग करके विज्ञान और इंजीनियरिंग की कई दिलचस्प समस्याओं को इस तरह से हल किया जाता है। | |||
=== लाई ग्रुप विधि === | |||
1870 में सोफस ली के कार्य ने अवकल समीकरणों के सिद्धांत को एक अधिक संतोषजनक आधार पर रखा। उन्होंने दिखाया कि पुराने गणितज्ञों के एकीकरण सिद्धांतों को, जिसे अब लाई समूह कहा जाता है, एक सामान्य स्रोत के रूप में संदर्भित किया जा सकता है; और वह साधारण अवकल समीकरण जो समान अतिसूक्ष्म परिवर्तनों को स्वीकार करते हैं, एकीकरण की तुलनात्मक कठिनाइयाँ प्रस्तुत करते हैं। उन्होंने संपर्क के परिवर्तन के विषय पर भी जोर दिया। | |||
गणित, भौतिकी, इंजीनियरिंग और कई अन्य विषयों में उत्पन्न होने वाले | पीडीई को हल करने के लिए एक सामान्य दृष्टिकोण अंतर समीकरणों की समरूपता संपत्ति का उपयोग करता है, समाधानों के समाधान के निरंतर अत्यल्प रूपांतरण (लाई सिद्धांत)। निरंतर [[ समूह सिद्धांत |समूह सिद्धांत]], ले बीजगणित और अंतर ज्यामिति का उपयोग पूर्णांक समीकरणों को उत्पन्न करने के लिए रैखिक और गैर-रैखिक आंशिक अंतर समीकरणों की संरचना को समझने के लिए किया जाता है, इसके लक्स जोड़े, पुनरावर्तन संचालकों को खोजने के लिए, बैकलंड रूपांतरण (Bäcklund transform) और अंत में पीडीई के लिए सटीक विश्लेषणात्मक समाधान ढूंढते हैं। | ||
गणित, भौतिकी, इंजीनियरिंग और कई अन्य विषयों में उत्पन्न होने वाले विभेदक समीकरणों का अध्ययन करने के लिए सममिति विधियों को मान्यता दी गई है। | |||
=== अर्धविश्लेषणात्मक तरीके === | === अर्धविश्लेषणात्मक तरीके === | ||
एडोमियन अपघटन विधि,<ref>{{cite book |title=भौतिकी की सीमांत समस्याओं का समाधान: अपघटन विधि|first=G. |last=Adomian|author-link=George Adomian|publisher=Kluwer Academic Publishers |year=1994 |isbn=9789401582896 |url=https://books.google.com/books?id=UKPqCAAAQBAJ&q=%22partial+differential%22}}</ref> | [[ एडोमियन अपघटन विधि |एडोमियन अपघटन विधि]],<ref>{{cite book |title=भौतिकी की सीमांत समस्याओं का समाधान: अपघटन विधि|first=G. |last=Adomian|author-link=George Adomian|publisher=Kluwer Academic Publishers |year=1994 |isbn=9789401582896 |url=https://books.google.com/books?id=UKPqCAAAQBAJ&q=%22partial+differential%22}}</ref> लायपुनोव कृत्रिम छोटे पैरामीटर विधि, और उनकी [[ होमोटॉपी गड़बड़ी विधि |होमोटॉपी क्षोभ विधि]] सभी अधिक सामान्य समरूपता विश्लेषण पद्धति के विशेष मामले हैं।<ref>{{Citation | last=Liao | first=S.J. |author-link=Liao Shijun| title=Beyond Perturbation: Introduction to the Homotopy Analysis Method | publisher=Chapman & Hall/ CRC Press | location=Boca Raton | year=2003 | isbn=1-58488-407-X }}</ref> ये श्रृंखला विस्तार के तरीके हैं, और लायपुनोव विधि को छोड़कर, प्रसिद्ध [[ गड़बड़ी सिद्धांत |गड़बड़ी सिद्धांत]] की तुलना में छोटे भौतिक मापदंडों से स्वतंत्र हैं, इस प्रकार इन तरीकों को अधिक लचीलापन और समाधान व्यापकता प्रदान करते हैं। | ||
== संख्यात्मक समाधान == | == संख्यात्मक समाधान == | ||
{{main| | {{main|आंशिक अवकल समीकरणों के संख्यात्मक हल}} | ||
तीन सबसे व्यापक रूप से उपयोग | |||
पीडीई को हल करने के लिए तीन सबसे व्यापक रूप से उपयोग की जाने वाली [[ संख्यात्मक आंशिक अंतर समीकरण |संख्यात्मक]] विधियाँ परिमित तत्व विधि (एफईएम), परिमित आयतन विधि (एफवीएम) और [[ परिमित अंतर विधि |परिमित अंतर विधि]] (एफडीएम) हैं, साथ ही अन्य प्रकार की विधियाँ जिन्हें मेशफ्री विधियाँ कहा जाता है, जो उन समस्याओं को हल करने के लिए बनाई गई थीं जहाँ उपरोक्त तरीके सीमित हैं। इन विधियों में FEM का एक प्रमुख स्थान है और विशेष रूप से इसके असाधारण कुशल उच्च-क्रम संस्करण एचपी-एफईएम। एफईएम और मेशफ्री विधियों के अन्य संकर संस्करणों में सामान्यीकृत परिमित तत्व विधि (जीएफएम), [[ विस्तारित परिमित तत्व विधि |विस्तारित परिमित तत्व विधि]] (एक्सएफईएम), [[ वर्णक्रमीय तत्व विधि |वर्णक्रमीय]] परिमित तत्व विधि (एसएफईएम), मेशफ्री परिमित तत्व विधि, असतत गैलेरकिन परिमित तत्व विधि (डीजीएफईएम), तत्व- शामिल हैं। फ्री गैलेरकिन मेथड (ईएफजीएम), इंटरपोलिंग एलिमेंट-फ्री गैलेर्किन मेथड (आईईएफजीएम), आदि। | |||
=== परिमित तत्व विधि === | === परिमित तत्व विधि === | ||
{{main| | {{main|परिमित तत्व विधि}} | ||
परिमित तत्व विधि (एफईएम) (इसका व्यावहारिक अनुप्रयोग | परिमित तत्व विधि (एफईएम) (इसका व्यावहारिक अनुप्रयोग प्रायः परिमित तत्व विश्लेषण (एफईए) के रूप में जाना जाता है) आंशिक अंतर समीकरणों (पीडीई) के साथ-साथ अभिन्न समीकरणों के अनुमानित समाधान खोजने के लिए एक संख्यात्मक तकनीक है।<ref>{{Citation |first=P. |last=Solin |title=Partial Differential Equations and the Finite Element Method |publisher=J. Wiley & Sons |location=Hoboken, NJ |year=2005 |isbn=0-471-72070-4 }}</ref><ref>{{Citation |first1=P. |last1=Solin |first2=K. |last2=Segeth |name-list-style=amp |first3=I. |last3=Dolezel |title=Higher-Order Finite Element Methods |publisher=Chapman & Hall/CRC Press |location=Boca Raton |year=2003 |isbn=1-58488-438-X }}</ref> समाधान दृष्टिकोण या तो अंतर समीकरण को पूरी तरह से समाप्त करने (स्थिर स्थिति की समस्याओं) पर आधारित है, या पीडीई को सामान्य अंतर समीकरणों की अनुमानित प्रणाली में प्रस्तुत करना है, जो तब मानक तकनीकों जैसे यूलर की विधि, रनगे-कुट्टा, आदि का उपयोग करके संख्यात्मक रूप से एकीकृत होते हैं। | ||
=== परिमित अंतर विधि === | === परिमित अंतर विधि === | ||
{{main| | {{main|परिमित अंतर विधि}} | ||
परिमित-अंतर विधियाँ अवकल समीकरणों के समाधान का अनुमान लगाने के लिए संख्यात्मक विधियाँ | |||
परिमित-अंतर विधियाँ अनुमानित डेरिवेटिव के लिए परिमित-अंतर समीकरणों का उपयोग करते हुए अवकल समीकरणों के समाधान का अनुमान लगाने के लिए संख्यात्मक विधियाँ हैं। | |||
=== परिमित आयतन विधि === | |||
{{main|परिमित आयतन विधि}} | |||
परिमित अंतर विधि या परिमित तत्व विधि के समान, मानों की गणना मेश्ड ज्यामिति पर अलग-अलग स्थानों पर की जाती है। "परिमित मात्रा" एक जाल पर प्रत्येक नोड बिंदु के आसपास की छोटी मात्रा को संदर्भित करता है। परिमित आयतन विधि में, [[ विचलन प्रमेय |विचलन प्रमेय]] का उपयोग करते हुए, एक आंशिक अंतर समीकरण में सतह समाकलन जिसमें एक विचलन शब्द होता है, आयतन समाकलन में परिवर्तित हो जाता है। इन शर्तों का मूल्यांकन प्रत्येक परिमित मात्रा की सतहों पर प्रवाह के रूप में किया जाता है। चूँकि किसी दिए गए आयतन में प्रवेश करने वाला प्रवाह आसन्न आयतन को छोड़ने के समान है, इसलिए ये विधियाँ डिज़ाइन द्वारा द्रव्यमान का संरक्षण करती हैं। | |||
परिमित अंतर विधि या परिमित तत्व विधि के समान, मानों की गणना | |||
== यह भी देखें == | == यह भी देखें == | ||
| Line 223: | Line 188: | ||
* तरंग समीकरण | * तरंग समीकरण | ||
* लाप्लास का समीकरण | * लाप्लास का समीकरण | ||
* हेल्महोल्ट्ज़ समीकरण | * [[ हेल्महोल्ट्ज़ समीकरण ]] | ||
* क्लेन-गॉर्डन समीकरण | * क्लेन-गॉर्डन समीकरण | ||
* पॉसों का समीकरण | * पॉसों का समीकरण | ||
* | * नेवियर-स्टोक्स समीकरण | ||
* बर्गर | * बर्गर समीकरण | ||
सीमा | सीमा की स्थिति के प्रकार | ||
* | * डिरिक्लेट सीमा स्थिति | ||
* न्यूमैन सीमा की स्थिति | * [[ न्यूमैन सीमा की स्थिति ]] | ||
* रॉबिन सीमा की स्थिति | * [[ रॉबिन सीमा की स्थिति ]] | ||
* कॉची समस्या | * [[ कॉची समस्या ]] | ||
विभिन्न विषय | |||
* जेट बंडल | * [[ जेट बंडल ]] | ||
* लाप्लास परिवर्तन अंतर समीकरणों पर लागू होता है | * [[ लाप्लास परिवर्तन अंतर समीकरणों पर लागू होता है |लाप्लास रूपांतरण अवकल समीकरणों पर लागू होता है]] | ||
* डायनेमिक सिस्टम और डिफरेंशियल इक्वेशन विषयों की सूची | * [[ डायनेमिक सिस्टम और डिफरेंशियल इक्वेशन विषयों की सूची |गतिशील प्रणालियों और अवकल समीकरण विषयों की सूची]] | ||
* मैट्रिक्स अंतर समीकरण | * [[ मैट्रिक्स अंतर समीकरण ]] | ||
* संख्यात्मक आंशिक | * संख्यात्मक आंशिक अवकल समीकरण | ||
* आंशिक अंतर बीजगणितीय समीकरण | * [[ आंशिक अंतर बीजगणितीय समीकरण |आंशिक अवकल बीजीय समीकरण]] | ||
* पुनरावृत्ति संबंध | * [[ पुनरावृत्ति संबंध ]] | ||
* स्टोकेस्टिक प्रक्रियाएं और सीमा मूल्य समस्याएं | * [[ स्टोकेस्टिक प्रक्रियाएं और सीमा मूल्य समस्याएं ]] | ||
==टिप्पणियाँ== | ==टिप्पणियाँ== | ||
{{Reflist}} | {{Reflist}} | ||
== संदर्भ == | == संदर्भ == | ||
{{refbegin|2}} | {{refbegin|2}} | ||
| Line 272: | Line 235: | ||
* {{cite book |title=High Order Difference Methods for Time Dependent PDE|first=Bertil |last=Gustafsson|series=Springer Series in Computational Mathematics|author-link=Bertil Gustafsson |publisher=Springer |year=2008 |volume=38 |isbn=978-3-540-74992-9 |doi=10.1007/978-3-540-74993-6}} | * {{cite book |title=High Order Difference Methods for Time Dependent PDE|first=Bertil |last=Gustafsson|series=Springer Series in Computational Mathematics|author-link=Bertil Gustafsson |publisher=Springer |year=2008 |volume=38 |isbn=978-3-540-74992-9 |doi=10.1007/978-3-540-74993-6}} | ||
{{refend}} | {{refend}} | ||
== अग्रिम पठन == | == अग्रिम पठन == | ||
* {{Cite journal|last=Cajori|first=Florian|author-link=Florian Cajori|year=1928|title=The Early History of Partial Differential Equations and of Partial Differentiation and Integration|url=http://www.math.harvard.edu/archive/21a_fall_14/exhibits/cajori/cajori.pdf|journal=The American Mathematical Monthly|volume=35|issue=9|pages=459–467|doi=10.2307/2298771|jstor=2298771|access-date=2016-05-15|archive-url=https://web.archive.org/web/20181123102253/http://www.math.harvard.edu/archive/21a_fall_14/exhibits/cajori/cajori.pdf|archive-date=2018-11-23|url-status=dead}} | * {{Cite journal|last=Cajori|first=Florian|author-link=Florian Cajori|year=1928|title=The Early History of Partial Differential Equations and of Partial Differentiation and Integration|url=http://www.math.harvard.edu/archive/21a_fall_14/exhibits/cajori/cajori.pdf|journal=The American Mathematical Monthly|volume=35|issue=9|pages=459–467|doi=10.2307/2298771|jstor=2298771|access-date=2016-05-15|archive-url=https://web.archive.org/web/20181123102253/http://www.math.harvard.edu/archive/21a_fall_14/exhibits/cajori/cajori.pdf|archive-date=2018-11-23|url-status=dead}} | ||
| Line 288: | Line 249: | ||
| doi=10.1006/aima.1997.1713 | doi-access=free}} | | doi=10.1006/aima.1997.1713 | doi-access=free}} | ||
* | |||
== बाहरी कड़ियाँ == | |||
== बाहरी | |||
{{Sister project links| wikt=no | commons=Category:Solutions of PDE | b=Partial Differential Equations | n=no | q=Partial differential equation | s=no | v=no | voy=no | species=no | d=no}} | {{Sister project links| wikt=no | commons=Category:Solutions of PDE | b=Partial Differential Equations | n=no | q=Partial differential equation | s=no | v=no | voy=no | species=no | d=no}} | ||
* {{springer|title=Differential equation, partial|id=p/d031920}} | * {{springer|title=Differential equation, partial|id=p/d031920}} | ||
| Line 308: | Line 266: | ||
{{Analysis-footer}} | {{Analysis-footer}} | ||
{{Authority control}} | {{Authority control}} | ||
[[ | [[श्रेणी:आंशिक अवकल समीकरण| ]][[श्रेणी:बहुभिन्नरूपी कलन]] | ||
[[ | [[श्रेणी:गणितीय भौतिकी]] | ||
[[ | |||
[[श्रेणी:विभेदक समीकरण|श्रेणी:अवकल समीकरण]] | |||
[[Category: | [[Category:Articles with hatnote templates targeting a nonexistent page]] | ||
[[Category:Created On | [[Category:Collapse templates]] | ||
[[Category:Created On 27/12/2022]] | |||
[[Category:Interwiki link templates| ]] | |||
[[Category:Lua-based templates]] | |||
[[Category:Machine Translated Page]] | |||
[[Category:Mathematics navigational boxes]] | |||
[[Category:Navigational boxes| ]] | |||
[[Category:Navigational boxes without horizontal lists]] | |||
[[Category:Pages with script errors]] | |||
[[Category:Short description with empty Wikidata description]] | |||
[[Category:Sidebars with styles needing conversion]] | |||
[[Category:Template documentation pages|Documentation/doc]] | |||
[[Category:Templates Translated in Hindi]] | |||
[[Category:Templates Vigyan Ready]] | |||
[[Category:Templates generating microformats]] | |||
[[Category:Templates that add a tracking category]] | |||
[[Category:Templates that are not mobile friendly]] | |||
[[Category:Templates that generate short descriptions]] | |||
[[Category:Templates using TemplateData]] | |||
[[Category:Templates using under-protected Lua modules]] | |||
[[Category:Wikipedia fully protected templates|Sister project links]] | |||
[[Category:Wikipedia metatemplates]] | |||
Latest revision as of 13:23, 4 September 2023
| अंतर समीकरण |
|---|
 |
| दायरा |
| वर्गीकरण |
| समाधान |
| लोग |
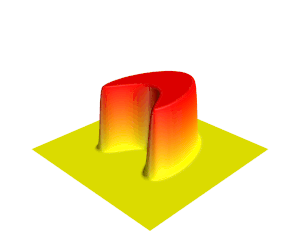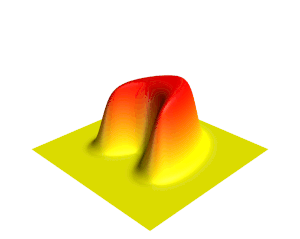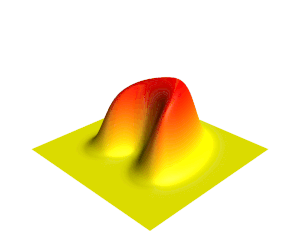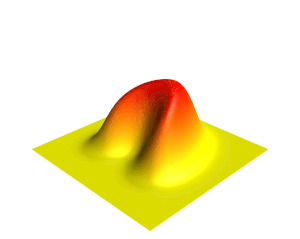
गणित में, आंशिक अवकल समीकरण (पीडीई) एक समीकरण है जो बहुविकल्पीय फलन के विभिन्न आंशिक डेरिवेटिव (व्युत्पन्न) के बीच संबंध स्थापित करता है।
फ़ंक्शन को प्रायः एक "अज्ञात" के रूप में माना जाता है जिसे हल किया जाना है, इसी तरह x को बीजगणितीय समीकरण जैसे x2 − 3x + 2 = 0 में हल करने के लिए एक अज्ञात संख्या के रूप में कैसे सोचा जाता है। हालांकि, आंशिक अंतर समीकरणों के समाधान के लिए स्पष्ट सूत्रों को लिखना असंभव है। तदनुसार, कंप्यूटर का उपयोग करके कुछ आंशिक अंतर समीकरणों के संख्यात्मक रूप से अनुमानित समाधानों के तरीकों पर आधुनिक गणितीय और वैज्ञानिक अनुसंधान की एक बड़ी मात्रा है। आंशिक अवकल समीकरण भी शुद्ध गणितीय अनुसंधान के एक बड़े क्षेत्र पर कब्जा कर लेते हैं, जिसमें सामान्य प्रश्न, मोटे तौर पर बोलते हैं, विभिन्न आंशिक अंतर समीकरणों के समाधान की सामान्य गुणात्मक विशेषताओं की पहचान पर, जैसे कि अस्तित्व, विशिष्टता, नियमितता और स्थिरता। कई खुले प्रश्नों में नेवियर-स्टोक्स समीकरणों के समाधान की मौजूदगी और सुगमता है, जिसे 2000 में मिलेनियम पुरस्कार समस्याओं में से एक के रूप में नामित किया गया था।
भौतिक विज्ञान और अभियांत्रिकी जैसे गणितीय रूप से उन्मुख वैज्ञानिक क्षेत्रों में आंशिक अंतर समीकरण सर्वव्यापी हैं। उदाहरण के लिए, वे ध्वनि, ऊष्मा, प्रसार, इलेक्ट्रोस्टैटिक्स, इलेक्ट्रोडायनामिक्स, ऊष्मप्रवैगिकी, द्रव गतिकी, लोच, सामान्य सापेक्षता और क्वांटम यांत्रिकी (श्रोडिंगर समीकरण, पाउली समीकरण, आदि) की आधुनिक वैज्ञानिक समझ में मूलभूत हैं। वे कई शुद्ध गणितीय विचारों से भी उत्पन्न होते हैं, जैसे अंतर ज्यामिति और विविधताओं की कलन; अन्य उल्लेखनीय अनुप्रयोगों में, वे ज्यामितीय टोपोलॉजी से पॉइंकेयर अनुमान के प्रमाण में मूलभूत उपकरण हैं।
आंशिक रूप से इस प्रकार के स्रोतों के कारण, विभिन्न प्रकार के आंशिक अंतर समीकरणों का एक विस्तृत स्पेक्ट्रम है, और उत्पन्न होने वाले कई अलग-अलग समीकरणों से निपटने के लिए विधियों का विकास किया गया है। जैसे, यह सामान्यतः स्वीकार किया जाता है कि आंशिक अवकल समीकरणों का कोई "सामान्य सिद्धांत" नहीं है, जिसमें विशेषज्ञ ज्ञान कुछ हद तक अनिवार्य रूप से अलग-अलग उपक्षेत्रों के बीच विभाजित होता है।[1]
साधारण अवकल समीकरण आंशिक अवकल समीकरणों का एक उपवर्ग बनाते हैं, जो एकल चर के फलनों के अनुरूप होते हैं। स्टोचैस्टिक आंशिक अंतर समीकरण और गैर-स्थानीय समीकरण, 2020 तक, "पीडीई" धारणा के विशेष रूप से व्यापक रूप से अध्ययन किए गए विस्तार हैं। अधिक शास्त्रीय विषय, जिन पर अभी भी बहुत सक्रिय शोध है, में दीर्घवृत्तक और परावर्तक आंशिक अवकल समीकरण, द्रव यांत्रिकी, बोल्ट्जमैन समीकरण और फैलाने वाले आंशिक अंतर समीकरण शामिल हैं।
परिचय
एक का कहना है कि तीन चर का एक फ़ंक्शन u(x, y, z) "हार्मोनिक" या "लाप्लास समीकरण का समाधान" है यदि यह स्थिति को संतुष्ट करता है।
निम्नलिखित पीडीई के मामले में इस विफलता की प्रकृति को और अधिक स्पष्ट रूप से देखा जा सकता है: दो चरों के फ़ंक्शन v(x, y) के लिए, समीकरण पर विचार करें।
इस पसंद की प्रकृति पीडीई से पीडीई में भिन्न होती है। किसी दिए गए समीकरण को समझने के लिए, अस्तित्व और विशिष्टता प्रमेय सामान्यतः महत्वपूर्ण संगठनात्मक सिद्धांत होते हैं। कई परिचयात्मक पाठ्यपुस्तकों में, मुक्त एवं दूरस्थ शिक्षा के लिए अस्तित्व और विशिष्टता प्रमेयों की भूमिका कुछ हद तक अपारदर्शी हो सकती है; अस्तित्व आधा सामान्यतः अनावश्यक होता है क्योंकि कोई भी प्रस्तावित समाधान सूत्र की सीधे जांच कर सकता है, जबकि विशिष्टता आधा प्रायः पृष्ठभूमि में मौजूद होती है ताकि यह सुनिश्चित किया जा सके कि प्रस्तावित समाधान सूत्र जितना संभव हो उतना सामान्य है। इसके विपरीत, पीडीई के लिए, अस्तित्व और विशिष्टता प्रमेय प्रायः एकमात्र साधन होते हैं जिसके द्वारा कोई भी विभिन्न समाधानों के ढेरों के माध्यम से नेविगेट कर सकता है। इस कारण से, विशुद्ध रूप से संख्यात्मक अनुकरण करते समय वे मौलिक भी होते हैं, क्योंकि किसी को यह समझ होनी चाहिए कि उपयोगकर्ता द्वारा कौन सा डेटा निर्धारित किया जाना है और गणना करने के लिए कंप्यूटर पर क्या छोड़ा जाना है।
इस तरह के अस्तित्व और अद्वितीयता प्रमेयों पर चर्चा करने के लिए, "अज्ञात फ़ंक्शन" के डोमेन के बारे में सटीक होना आवश्यक है। अन्यथा, केवल "दो चरों का एक कार्य" जैसे शब्दों में बोलना, परिणामों को अर्थपूर्ण रूप से तैयार करना असंभव है। अर्थात्, अज्ञात फलन के क्षेत्र को स्वयं पीडीई की संरचना के भाग के रूप में माना जाना चाहिए।
निम्नलिखित ऐसे अस्तित्व और अद्वितीयता प्रमेय के दो उत्कृष्ट उदाहरण प्रदान करता है। भले ही प्रश्न में दो पीडीई समान हैं, व्यवहार में एक महत्वपूर्ण अंतर है: पहले पीडीई के लिए, एक के पास एक ही फ़ंक्शन का मुफ्त नुस्खा है, जबकि दूसरे पीडीई के लिए, दो कार्यों का मुफ्त निर्धारण है।
- बता दें कि B समतल में मूल बिंदु के चारों ओर इकाई-त्रिज्या डिस्क को दर्शाता है। यूनिट सर्कल पर किसी भी निरंतर फ़ंक्शन U के लिए, B पर ठीक एक फ़ंक्शन u होता है जैसे किऔर यूनिट सर्कल के लिए किसका प्रतिबंध U द्वारा दिया गया है।
- वास्तविक रेखा R पर किसी भी फ़ंक्शन f और g के लिए, R × (−1, 1) पर बिल्कुल एक फ़ंक्शन u होता है जैसे किऔर u(x, 0) = f(x) और ∂u/∂y(x, 0) = g(x) के साथ x के सभी मानों के लिए।
इससे भी अधिक घटनाएं संभव हैं। उदाहरण के लिए, निम्नलिखित पीडीई, अंतर ज्यामिति के क्षेत्र में स्वाभाविक रूप से उत्पन्न होता है, एक उदाहरण दिखाता है जहां एक सरल और पूरी तरह से स्पष्ट समाधान सूत्र है, लेकिन केवल तीन संख्याओं के स्वतंत्र विकल्प के साथ और एक भी फ़ंक्शन नहीं है।
- यदि u R2 पर एक फ़ंक्शन हैफिर संख्याएँ हैं a, b, और c साथ u(x, y) = ax + by + c.
पहले के उदाहरणों के विपरीत, यह पीडीई वर्गमूलों और वर्गों के कारण अरैखिक है। एक अरैखिक पीडीई एक ऐसा है कि, यदि यह सजातीय है, तो किन्हीं भी दो समाधानों का योग भी एक समाधान है, और किसी भी समाधान का कोई भी स्थिर गुणक भी एक समाधान है।
वेल-पोसेड्नेस
अच्छी स्थिति एक पीडीई के बारे में सूचना के एक सामान्य योजनाबद्ध पैकेज को संदर्भित करती है। यह कहने के लिए कि एक पीडीई अच्छी स्थिति में है, एक व्यक्ति में होना चाहिए:
- एक अस्तित्व और विशिष्टता प्रमेय, यह दावा करते हुए कि कुछ स्वतंत्र रूप से चुने गए कार्यों के नुस्खे से, पीडीई के एक विशिष्ट समाधान को अलग किया जा सकता है
- नि: शुल्क विकल्पों को लगातार बदलते रहने से, व्यक्ति लगातार इसी समाधान को बदलता रहता है
यह, कई अलग-अलग पीडीई पर लागू होने की आवश्यकता के कारण, कुछ हद तक अस्पष्ट है। विशेष रूप से "निरंतरता" की आवश्यकता अस्पष्ट है क्योंकि आम तौर पर कई असमान साधन होते हैं जिनके द्वारा इसे कड़ाई से परिभाषित किया जा सकता है। हालांकि, पीडीई का अध्ययन करना असामान्य है, बिना यह निर्दिष्ट किए कि यह अच्छी तरह से प्रस्तुत किया गया है।
ऊर्जा पद्धति
ऊर्जा विधि एक गणितीय प्रक्रिया है जिसका उपयोग प्रारंभिक-सीमा-मूल्य-समस्याओं की अच्छी स्थिति को सत्यापित करने के लिए किया जा सकता है।[2] निम्नलिखित उदाहरण में ऊर्जा पद्धति का उपयोग यह तय करने के लिए किया जाता है कि कहां और कौन सी सीमा शर्तों को लगाया जाना चाहिए ताकि परिणामी आईबीवीपी अच्छी तरह से तैयार हो। द्वारा दिए गए एक आयामी अतिपरवलयिक पीडीई पर विचार करें।
स्थानीय समाधानों का अस्तित्व
कॉची प्रारंभिक मूल्य समस्याओं के लिए कॉची-कोवाल्स्की प्रमेय अनिवार्य रूप से बताता है कि यदि आंशिक अंतर समीकरण में सभी शब्द विश्लेषणात्मक कार्यों से बने होते हैं और एक निश्चित ट्रांसवर्सलिटी की स्थिति संतुष्ट होती है (हाइपरप्लेन या अधिक आम तौर पर हाइपरसफेस जहां प्रारंभिक डेटा सामने आता है) आंशिक अंतर ऑपरेटर के संबंध में गैर-विशेषता), तो कुछ क्षेत्रों पर, आवश्यक रूप से समाधान मौजूद होते हैं जो विश्लेषणात्मक कार्य भी होते हैं। यह विश्लेषणात्मक आंशिक अवकल समीकरणों के अध्ययन का एक मूलभूत परिणाम है। हैरानी की बात है, प्रमेय सुचारू कार्यों की समायोजन में नहीं है; 1957 में हैंस लेवी द्वारा खोजे गए एक उदाहरण में एक रेखीय आंशिक अंतर समीकरण शामिल है, जिसके गुणांक चिकने हैं (अर्थात, सभी आदेशों के व्युत्पन्न हैं) लेकिन विश्लेषणात्मक नहीं हैं जिसके लिए कोई समाधान मौजूद नहीं है। अतः कौशी-कोवालेव्स्की प्रमेय अनिवार्य रूप से विश्लेषणात्मक कार्यों के दायरे में सीमित है।
वर्गीकरण
अंकन
पीडीई लिखते समय, आंशिक डेरिवेटिव को सबस्क्रिप्ट का उपयोग करके निरूपित करना आम है। उदाहरण के लिए:
ग्रीक अक्षर Δ लाप्लास ऑपरेटर को दर्शाता है; यदि u का एक कार्य है n चर, फिर
पहले क्रम के समीकरण
रेखीय और अरेखीय समीकरण
रैखिक समीकरण
एक पीडीई को रैखिक कहा जाता है यदि यह अज्ञात और उसके डेरिवेटिव में रैखिक है। उदाहरण के लिए, x और y के फलन u के लिए, एक द्वितीय कोटि रैखिक पीडीई का रूप होता है
अरैखिक समीकरण
तीन मुख्य प्रकार के अरैखिक पीडीई अर्धरेखीय पीडीई, रैखिककल्प पीडीई और पूरी तरह से अरैखिक पीडीई हैं।
रेखीय पीडीई के निकटतम सेमीलीनियर (अर्धरेखीय) पीडीई हैं, जहां केवल उच्चतम क्रम के डेरिवेटिव रैखिक शब्दों के रूप में प्रकट होते हैं, गुणांक के साथ जो स्वतंत्र चर के कार्य हैं। निचले क्रम के डेरिवेटिव और अज्ञात फ़ंक्शन मनमाने ढंग से प्रकट हो सकते हैं। उदाहरण के लिए, दो चरों में एक सामान्य द्वितीय-क्रम सेमीलीनियर पीडीई है।
किसी रैखिकता गुण के बिना पीडीई को पूरी तरह से गैर-रैखिक कहा जाता है और एक या अधिक उच्चतम-क्रम डेरिवेटिव पर गैर-रैखिकता रखता है। एक उदाहरण मोंज-एम्पीयर समीकरण है, जो विभेदक ज्यामिति में उत्पन्न होता है।[3]
दूसरे क्रम के रैखिक समीकरण
बीसवीं शताब्दी की शुरुआत के बाद से क्रम दो के दीर्घवृत्तीय, परवलयिक और अतिशयोक्तिपूर्ण आंशिक अंतर समीकरणों का व्यापक रूप से अध्ययन किया गया है। हालाँकि, कई अन्य महत्वपूर्ण प्रकार के पीडीई हैं, जिनमें कॉर्टेवेग-डी व्रीज़ समीकरण शामिल है। यूलर-ट्रिकोमी समीकरण जैसे संकर भी हैं, जो डोमेन के विभिन्न क्षेत्रों के लिए दीर्घवृत्त से अतिपरवलयिक में भिन्न होते हैं। इन मूल प्रकारों के उच्च-क्रम पीडीई के लिए महत्वपूर्ण विस्तार भी हैं, लेकिन ऐसा ज्ञान अधिक विशिष्ट है।
दीर्घवृत्तीय/परवलयिक/अतिशयोक्तिपूर्ण वर्गीकरण उपयुक्त प्रारंभिक और सीमा स्थितियों और समाधानों की समतलता के लिए एक मार्गदर्शक प्रदान करता है। uxy = uyx मानते हुए, दो स्वतंत्र चरों में सामान्य रैखिक द्वितीय-क्रम पीडीई का रूप है।
जहां गुणांक A, B, C... x और y पर निर्भर हो सकता है। यदि A2 + B2 + C2 > 0 के एक क्षेत्र पर xy-प्लेन, पीडीई उस क्षेत्र में दूसरे क्रम का है। यह प्रपत्र शंकु खंड के समीकरण के अनुरूप है:
- B2 − AC < 0 (दीर्घवृत्त आंशिक अंतर समीकरण): अण्डाकार आंशिक अंतर समीकरण के समाधान उतने ही चिकने होते हैं जितने कि गुणांक अनुमति देते हैं, उस क्षेत्र के आंतरिक भाग में जहाँ समीकरण और समाधान परिभाषित होते हैं। उदाहरण के लिए, लाप्लास के समीकरण के समाधान डोमेन के भीतर विश्लेषणात्मक होते हैं जहां उन्हें परिभाषित किया जाता है, लेकिन समाधान सीमा मान मान सकते हैं जो चिकनी नहीं हैं। सबसोनिक गति पर तरल पदार्थ की गति को दीर्घवृत्त पीडीई के साथ अनुमानित किया जा सकता है, और यूलर-ट्रिकोमी समीकरण अंडाकार है जहां x < 0.
- B2 − AC = 0 (परवलयिक आंशिक अंतर समीकरण): समीकरण जो हर बिंदु पर परवलयिक आंशिक अंतर समीकरण होते हैं, उन्हें स्वतंत्र चर के परिवर्तन द्वारा ताप समीकरण के अनुरूप रूप में परिवर्तित किया जा सकता है। परिवर्तित समय चर बढ़ने पर समाधान सुचारू हो जाते हैं। यूलर-ट्रिकोमी समीकरण में उस रेखा पर परवलयिक प्रकार है जहां x = 0.
- B2 − AC > 0 (अतिपरवलयिक आंशिक अंतर समीकरण): अतिशयोक्तिपूर्ण आंशिक अंतर समीकरण समीकरण प्रारंभिक डेटा में कार्यों या डेरिवेटिव के किसी भी विच्छिन्नता को बनाए रखते हैं। एक उदाहरण तरंग समीकरण है। सुपरसोनिक गति पर द्रव की गति को हाइपरबोलिक पीडीई के साथ अनुमानित किया जा सकता है, और यूलर-ट्रिकोमी समीकरण हाइपरबॉलिक है जहां x > 0.
अगर वहाँ n स्वतंत्र प्रभावित करने वाली वस्तुएँ x1, x2 , …, xnदूसरे क्रम के एक सामान्य रैखिक आंशिक अंतर समीकरण का रूप है
- दीर्घवृत्त: आइगेनवैल्यू सभी धनात्मक या सभी ऋणात्मक हैं।
- परवलयिक: आइगेनवैल्यू सभी धनात्मक या सभी नकारात्मक हैं, एक को छोड़कर जो शून्य है।
- अतिपरवलयिक: केवल एक ऋणात्मक आइगेनवैल्यू है और बाकी सभी धनात्मक हैं, या केवल एक धनात्मक आइगेनवैल्यू है और बाकी सभी ऋणात्मक हैं।
- अल्ट्राहाइपरबोलिक: एक से अधिक धनात्मक आइगेनवैल्यू और एक से अधिक ऋणात्मक आइगेनवैल्यू होते हैं, और कोई शून्य आइगेनवैल्यू नहीं होते हैं।[4]
दीर्घवृत्त, परवलयिक, और अतिपरवलयिक समीकरणों के सिद्धांत का सदियों से अध्ययन किया गया है, जो काफी हद तक लाप्लास समीकरण , ऊष्मा समीकरण और तरंग समीकरण के मानक उदाहरणों के आसपास या उसके आधार पर केंद्रित है।
प्रथम-क्रम समीकरणों और विशिष्ट सतहों की प्रणाली
आंशिक अंतर समीकरणों के वर्गीकरण को प्रथम-क्रम समीकरणों की प्रणालियों तक विस्तारित किया जा सकता है, जहां अज्ञात u अब m घटकों के साथ एक वेक्टर है, और गुणांक मैट्रिसेस Aν, ν = 1, 2, …, n के लिए m द्वारा m मेट्रिसेस हैं। आंशिक अवकल समीकरण का रूप ले लेता है।
जहां φ एक गैर-शून्य है, तब S ऑपरेटर के लिए एक विशिष्ट सतह है L किसी दिए गए बिंदु पर यदि विशेषता रूप गायब हो जाता है:
- एक प्रथम-क्रम प्रणाली Lu = 0 दीर्घवृत्तीय है यदि कोई सतह L के लिए विशेषता नहीं है: S पर u के मान और अंतर समीकरण हमेशा S पर u के सामान्य व्युत्पन्न को निर्धारित करते हैं।
- एक प्रथम-क्रम प्रणाली एक बिंदु पर अतिशयोक्तिपूर्ण है यदि उस बिंदु पर सामान्य ξ के साथ एक अंतरिक्ष जैसी सतह S है। इसका मतलब यह है कि, किसी भी गैर-तुच्छ वेक्टर η ऑर्थोगोनल को ξ, और एक स्केलर गुणक λ दिया गया है, समीकरण (Q(λξ + η) = 0 में m वास्तविक जड़ें λ1, λ2, …, λm हैं। अगर ये जड़ें हमेशा अलग-अलग हों तो सिस्टम सख्ती से अतिशयोक्तिपूर्ण है। इस स्थिति की ज्यामितीय व्याख्या इस प्रकार है: विशेषता रूप Q(ζ) = 0 सजातीय निर्देशांक ζ के साथ एक शंकु (सामान्य शंकु) को परिभाषित करता है। अतिशयोक्तिपूर्ण मामले में, इस शंकु में m शीट हैं, और अक्ष ζ = λξ इन शीटों के अंदर चलता है: यह उनमें से किसी को नहीं काटता है। लेकिन जब η द्वारा मूल से विस्थापित किया जाता है, तो यह अक्ष प्रत्येक शीट को प्रतिच्छेद करती है। दीर्घवृत्तीय मामले में, सामान्य शंकु में कोई वास्तविक शीट नहीं होती है।
विश्लेषणात्मक समाधान
चरों का पृथक्करण
चरों को अलग करने की महत्वपूर्ण तकनीक द्वारा रेखीय पीडीई को साधारण अंतर समीकरणों की प्रणालियों में घटाया जा सकता है। यह तकनीक अंतर समीकरणों के समाधान की एक विशेषता पर टिकी हुई है: यदि कोई ऐसा समाधान ढूंढ सकता है जो समीकरण को हल करता है और सीमा शर्तों को संतुष्ट करता है, तो यह समाधान है (यह ओडीई पर भी लागू होता है)। हम एक ansatz के रूप में मानते हैं कि पैरामीटर स्थान और समय पर एक समाधान की निर्भरता को उन शर्तों के उत्पाद के रूप में लिखा जा सकता है जो प्रत्येक एक पैरामीटर पर निर्भर करते हैं, और फिर देखते हैं कि समस्या को हल करने के लिए इसे बनाया जा सकता है या नहीं।[5]
चरों को अलग करने की विधि में, कम चरों में एक पीडीई को एक पीडीई में घटाया जाता है, जो एक सामान्य अंतर समीकरण है यदि एक चर में - इन्हें हल करना आसान होता है।
यह सरल पीडीई के लिए संभव है, जिसे वियोज्य आंशिक अंतर समीकरण कहा जाता है, और डोमेन आम तौर पर एक आयत (अंतराल का एक उत्पाद) होता है। वियोज्य पीडीई विकर्ण मैट्रिसेस के अनुरूप हैं - एक समन्वय के रूप में "निश्चित x के मान" के बारे में सोचते हुए, प्रत्येक निर्देशांक को अलग से समझा जा सकता है।
यह विशेषताओं की विधि का सामान्यीकरण करता है और इसका उपयोग अभिन्न परिवर्तनों में भी किया जाता है।
विशेषताओं का तरीका
विशेष मामलों में, कोई विशेषता वक्र पा सकता है जिस पर समीकरण ओडीई में कम हो जाता है - इन वक्रों को सीधा करने के लिए डोमेन में बदलते निर्देशांक चर के पृथक्करण की अनुमति देते हैं और इसे विशेषताओं की विधि कहा जाता है।
अधिक आम तौर पर, किसी को विशिष्ट सतहें मिल सकती हैं। द्वितीय कोटि के आंशिक अवकल समीकरण हल के लिए, चार्पिट विधि देखें।
इंटीग्रल ट्रांसफॉर्म
एक अभिन्न परिवर्तन पीडीई को एक सरल रूप में बदल सकता है, विशेष रूप से एक वियोज्य पीडीई। यह एक ऑपरेटर को विकर्णित करने के अनुरूप है।
इसका एक महत्वपूर्ण उदाहरण फूरियर विश्लेषण है, जो साइनसोइडल तरंगों के ईजेनबेसिस का उपयोग करके गर्मी समीकरण को विकर्णित करता है।
यदि डोमेन परिमित या आवधिक है, तो फूरियर श्रृंखला जैसे समाधानों का एक अनंत योग उपयुक्त है, लेकिन फूरियर अभिन्न जैसे समाधानों का एक अभिन्न अंग सामान्यतः अनंत डोमेन के लिए आवश्यक है। ऊपर दिए गए ताप समीकरण के लिए एक बिंदु स्रोत का समाधान फूरियर इंटीग्रल के उपयोग का एक उदाहरण है।
चर का परिवर्तन
चरों के उपयुक्त परिवर्तन द्वारा प्रायः पीडीई को ज्ञात समाधान के साथ सरल रूप में कम किया जा सकता है। उदाहरण के लिए, ब्लैक-स्कोल्स समीकरण
मौलिक समाधान
मौलिक समाधान (एक बिंदु स्रोत के लिए समाधान) को खोजने के द्वारा अमानवीय समीकरणों को प्रायः हल किया जा सकता है (निरंतर गुणांक पीडीई के लिए, हमेशा हल किया जाता है), फिर समाधान प्राप्त करने के लिए सीमा शर्तों के साथ संवलयी होता है।
यह सिग्नल प्रोसेसिंग में एक फिल्टर को उसकी आवेग प्रतिक्रिया द्वारा समझने के अनुरूप है।
सुपरपोजिशन सिद्धांत
सुपरपोज़िशन सिद्धांत पीडीई के रैखिक सिस्टम सहित किसी भी रैखिक प्रणाली पर लागू होता है। इस अवधारणा का एक सामान्य दृश्य चरण में दो तरंगों की परस्पर क्रिया है, जिसके परिणामस्वरूप एक बड़ा आयाम होता है, उदाहरण के लिए, sin x + sin x = 2 sin x पीडीई में समान सिद्धांत देखा जा सकता है जहां समाधान वास्तविक या जटिल और योगात्मक हो सकते हैं। यदि u1 और u2 किसी फंक्शन स्पेस R में रैखिक पीडीई के समाधान हैं, तो u = c1u1 + c2u2 किसी भी स्थिरांक c1और c2 के साथ भी उसी फ़ंक्शन स्पेस में उस पीडीई का एक समाधान है।
गैर-रैखिक समीकरणों के लिए तरीके
अरेखीय पीडीई को हल करने के लिए आम तौर पर लागू होने वाली कोई विधियाँ नहीं हैं। फिर भी, अस्तित्व और अद्वितीयता के परिणाम (जैसे कॉची-कोवालेव्स्की प्रमेय) प्रायः संभव होते हैं, जैसा कि समाधानों के महत्वपूर्ण गुणात्मक और मात्रात्मक गुणों के प्रमाण हैं (इन परिणामों को प्राप्त करना विश्लेषण का एक प्रमुख हिस्सा है)। गैर-रैखिक पीडीई के लिए कम्प्यूटेशनल समाधान, विभाजन-चरण विधि, गैर-रैखिक श्रोडिंगर समीकरण जैसे विशिष्ट समीकरणों के लिए मौजूद है।
फिर भी, कुछ तकनीकों का प्रयोग अनेक प्रकार के समीकरणों के लिए किया जा सकता है। अनिर्धारित समीकरणों को हल करने के लिए h-सिद्धांत सबसे शक्तिशाली तरीका है। कई विश्लेषणात्मक अतिनिर्धारित प्रणालियों के बारे में जानकारी प्राप्त करने के लिए रिक्वायर-जेनेट सिद्धांत एक प्रभावी तरीका है।
विशेषताओं की विधि का उपयोग कुछ विशेष मामलों में अरैखिक आंशिक अवकल समीकरणों को हल करने के लिए किया जा सकता है।[7]
कुछ मामलों में, पीडीई को गड़बड़ी विश्लेषण के माध्यम से हल किया जा सकता है जिसमें समाधान को ज्ञात समाधान के साथ समीकरण में सुधार माना जाता है। विकल्प संख्यात्मक विश्लेषण तकनीक हैं जो साधारण परिमित अंतर योजनाओं से लेकर अधिक परिपक्व मल्टीग्रिड और परिमित तत्व विधियों तक हैं। कंप्यूटर, कभी-कभी उच्च-प्रदर्शन वाले सुपर कंप्यूटर का उपयोग करके विज्ञान और इंजीनियरिंग की कई दिलचस्प समस्याओं को इस तरह से हल किया जाता है।
लाई ग्रुप विधि
1870 में सोफस ली के कार्य ने अवकल समीकरणों के सिद्धांत को एक अधिक संतोषजनक आधार पर रखा। उन्होंने दिखाया कि पुराने गणितज्ञों के एकीकरण सिद्धांतों को, जिसे अब लाई समूह कहा जाता है, एक सामान्य स्रोत के रूप में संदर्भित किया जा सकता है; और वह साधारण अवकल समीकरण जो समान अतिसूक्ष्म परिवर्तनों को स्वीकार करते हैं, एकीकरण की तुलनात्मक कठिनाइयाँ प्रस्तुत करते हैं। उन्होंने संपर्क के परिवर्तन के विषय पर भी जोर दिया।
पीडीई को हल करने के लिए एक सामान्य दृष्टिकोण अंतर समीकरणों की समरूपता संपत्ति का उपयोग करता है, समाधानों के समाधान के निरंतर अत्यल्प रूपांतरण (लाई सिद्धांत)। निरंतर समूह सिद्धांत, ले बीजगणित और अंतर ज्यामिति का उपयोग पूर्णांक समीकरणों को उत्पन्न करने के लिए रैखिक और गैर-रैखिक आंशिक अंतर समीकरणों की संरचना को समझने के लिए किया जाता है, इसके लक्स जोड़े, पुनरावर्तन संचालकों को खोजने के लिए, बैकलंड रूपांतरण (Bäcklund transform) और अंत में पीडीई के लिए सटीक विश्लेषणात्मक समाधान ढूंढते हैं।
गणित, भौतिकी, इंजीनियरिंग और कई अन्य विषयों में उत्पन्न होने वाले विभेदक समीकरणों का अध्ययन करने के लिए सममिति विधियों को मान्यता दी गई है।
अर्धविश्लेषणात्मक तरीके
एडोमियन अपघटन विधि,[8] लायपुनोव कृत्रिम छोटे पैरामीटर विधि, और उनकी होमोटॉपी क्षोभ विधि सभी अधिक सामान्य समरूपता विश्लेषण पद्धति के विशेष मामले हैं।[9] ये श्रृंखला विस्तार के तरीके हैं, और लायपुनोव विधि को छोड़कर, प्रसिद्ध गड़बड़ी सिद्धांत की तुलना में छोटे भौतिक मापदंडों से स्वतंत्र हैं, इस प्रकार इन तरीकों को अधिक लचीलापन और समाधान व्यापकता प्रदान करते हैं।
संख्यात्मक समाधान
पीडीई को हल करने के लिए तीन सबसे व्यापक रूप से उपयोग की जाने वाली संख्यात्मक विधियाँ परिमित तत्व विधि (एफईएम), परिमित आयतन विधि (एफवीएम) और परिमित अंतर विधि (एफडीएम) हैं, साथ ही अन्य प्रकार की विधियाँ जिन्हें मेशफ्री विधियाँ कहा जाता है, जो उन समस्याओं को हल करने के लिए बनाई गई थीं जहाँ उपरोक्त तरीके सीमित हैं। इन विधियों में FEM का एक प्रमुख स्थान है और विशेष रूप से इसके असाधारण कुशल उच्च-क्रम संस्करण एचपी-एफईएम। एफईएम और मेशफ्री विधियों के अन्य संकर संस्करणों में सामान्यीकृत परिमित तत्व विधि (जीएफएम), विस्तारित परिमित तत्व विधि (एक्सएफईएम), वर्णक्रमीय परिमित तत्व विधि (एसएफईएम), मेशफ्री परिमित तत्व विधि, असतत गैलेरकिन परिमित तत्व विधि (डीजीएफईएम), तत्व- शामिल हैं। फ्री गैलेरकिन मेथड (ईएफजीएम), इंटरपोलिंग एलिमेंट-फ्री गैलेर्किन मेथड (आईईएफजीएम), आदि।
परिमित तत्व विधि
परिमित तत्व विधि (एफईएम) (इसका व्यावहारिक अनुप्रयोग प्रायः परिमित तत्व विश्लेषण (एफईए) के रूप में जाना जाता है) आंशिक अंतर समीकरणों (पीडीई) के साथ-साथ अभिन्न समीकरणों के अनुमानित समाधान खोजने के लिए एक संख्यात्मक तकनीक है।[10][11] समाधान दृष्टिकोण या तो अंतर समीकरण को पूरी तरह से समाप्त करने (स्थिर स्थिति की समस्याओं) पर आधारित है, या पीडीई को सामान्य अंतर समीकरणों की अनुमानित प्रणाली में प्रस्तुत करना है, जो तब मानक तकनीकों जैसे यूलर की विधि, रनगे-कुट्टा, आदि का उपयोग करके संख्यात्मक रूप से एकीकृत होते हैं।
परिमित अंतर विधि
परिमित-अंतर विधियाँ अनुमानित डेरिवेटिव के लिए परिमित-अंतर समीकरणों का उपयोग करते हुए अवकल समीकरणों के समाधान का अनुमान लगाने के लिए संख्यात्मक विधियाँ हैं।
परिमित आयतन विधि
परिमित अंतर विधि या परिमित तत्व विधि के समान, मानों की गणना मेश्ड ज्यामिति पर अलग-अलग स्थानों पर की जाती है। "परिमित मात्रा" एक जाल पर प्रत्येक नोड बिंदु के आसपास की छोटी मात्रा को संदर्भित करता है। परिमित आयतन विधि में, विचलन प्रमेय का उपयोग करते हुए, एक आंशिक अंतर समीकरण में सतह समाकलन जिसमें एक विचलन शब्द होता है, आयतन समाकलन में परिवर्तित हो जाता है। इन शर्तों का मूल्यांकन प्रत्येक परिमित मात्रा की सतहों पर प्रवाह के रूप में किया जाता है। चूँकि किसी दिए गए आयतन में प्रवेश करने वाला प्रवाह आसन्न आयतन को छोड़ने के समान है, इसलिए ये विधियाँ डिज़ाइन द्वारा द्रव्यमान का संरक्षण करती हैं।
यह भी देखें
कुछ सामान्य पीडीई
- ऊष्मा समीकरण
- तरंग समीकरण
- लाप्लास का समीकरण
- हेल्महोल्ट्ज़ समीकरण
- क्लेन-गॉर्डन समीकरण
- पॉसों का समीकरण
- नेवियर-स्टोक्स समीकरण
- बर्गर समीकरण
सीमा की स्थिति के प्रकार
- डिरिक्लेट सीमा स्थिति
- न्यूमैन सीमा की स्थिति
- रॉबिन सीमा की स्थिति
- कॉची समस्या
विभिन्न विषय
- जेट बंडल
- लाप्लास रूपांतरण अवकल समीकरणों पर लागू होता है
- गतिशील प्रणालियों और अवकल समीकरण विषयों की सूची
- मैट्रिक्स अंतर समीकरण
- संख्यात्मक आंशिक अवकल समीकरण
- आंशिक अवकल बीजीय समीकरण
- पुनरावृत्ति संबंध
- स्टोकेस्टिक प्रक्रियाएं और सीमा मूल्य समस्याएं
टिप्पणियाँ
- ↑ Klainerman, Sergiu (2010). "PDE as a Unified Subject". In Alon, N.; Bourgain, J.; Connes, A.; Gromov, M.; Milman, V. (eds.). गणित में दर्शन. Modern Birkhäuser Classics. Basel: Birkhäuser. pp. 279–315. doi:10.1007/978-3-0346-0422-2_10. ISBN 978-3-0346-0421-5.
- ↑ Gustafsson, Bertil (2008). टाइम डिपेंडेंट पीडीई के लिए हाई ऑर्डर डिफरेंस मेथड्स. Springer Series in Computational Mathematics. Vol. 38. Springer. doi:10.1007/978-3-540-74993-6. ISBN 978-3-540-74992-9.
- ↑ Klainerman, Sergiu (2008), "Partial Differential Equations", in Gowers, Timothy; Barrow-Green, June; Leader, Imre (eds.), The Princeton Companion to Mathematics, Princeton University Press, pp. 455–483
- ↑ Courant and Hilbert (1962), p.182.
- ↑ Gershenfeld, Neil (2000). गणितीय मॉडलिंग की प्रकृति (Reprinted (with corr.) ed.). Cambridge: Cambridge Univ. Press. p. 27. ISBN 0521570956.
- ↑ Wilmott, Paul; Howison, Sam; Dewynne, Jeff (1995). वित्तीय डेरिवेटिव का गणित. Cambridge University Press. pp. 76–81. ISBN 0-521-49789-2.
- ↑ Logan, J. David (1994). "First Order Equations and Characteristics". अरैखिक आंशिक विभेदक समीकरणों का परिचय. New York: John Wiley & Sons. pp. 51–79. ISBN 0-471-59916-6.
- ↑ Adomian, G. (1994). भौतिकी की सीमांत समस्याओं का समाधान: अपघटन विधि. Kluwer Academic Publishers. ISBN 9789401582896.
- ↑ Liao, S.J. (2003), Beyond Perturbation: Introduction to the Homotopy Analysis Method, Boca Raton: Chapman & Hall/ CRC Press, ISBN 1-58488-407-X
- ↑ Solin, P. (2005), Partial Differential Equations and the Finite Element Method, Hoboken, NJ: J. Wiley & Sons, ISBN 0-471-72070-4
- ↑ Solin, P.; Segeth, K. & Dolezel, I. (2003), Higher-Order Finite Element Methods, Boca Raton: Chapman & Hall/CRC Press, ISBN 1-58488-438-X
संदर्भ
- Courant, R. & Hilbert, D. (1962), Methods of Mathematical Physics, vol. II, New York: Wiley-Interscience, ISBN 9783527617241.
- Evans, L. C. (1998), Partial Differential Equations, Providence: American Mathematical Society, ISBN 0-8218-0772-2.
- Drábek, Pavel; Holubová, Gabriela (2007). Elements of partial differential equations (Online ed.). Berlin: de Gruyter. ISBN 9783110191240.
- Ibragimov, Nail H. (1993), CRC Handbook of Lie Group Analysis of Differential Equations Vol. 1-3, Providence: CRC-Press, ISBN 0-8493-4488-3.
- John, F. (1982), Partial Differential Equations (4th ed.), New York: Springer-Verlag, ISBN 0-387-90609-6.
- Jost, J. (2002), Partial Differential Equations, New York: Springer-Verlag, ISBN 0-387-95428-7.
- Olver, P.J. (1995), Equivalence, Invariants and Symmetry, Cambridge Press.
- Petrovskii, I. G. (1967), Partial Differential Equations, Philadelphia: W. B. Saunders Co..
- Pinchover, Y. & Rubinstein, J. (2005), An Introduction to Partial Differential Equations, New York: Cambridge University Press, ISBN 0-521-84886-5.
- Polyanin, A. D. (2002), Handbook of Linear Partial Differential Equations for Engineers and Scientists, Boca Raton: Chapman & Hall/CRC Press, ISBN 1-58488-299-9.
- Polyanin, A. D. & Zaitsev, V. F. (2004), Handbook of Nonlinear Partial Differential Equations, Boca Raton: Chapman & Hall/CRC Press, ISBN 1-58488-355-3.
- Polyanin, A. D.; Zaitsev, V. F. & Moussiaux, A. (2002), Handbook of First Order Partial Differential Equations, London: Taylor & Francis, ISBN 0-415-27267-X.
- Roubíček, T. (2013), Nonlinear Partial Differential Equations with Applications (PDF), International Series of Numerical Mathematics, vol. 153 (2nd ed.), Basel, Boston, Berlin: Birkhäuser, doi:10.1007/978-3-0348-0513-1, ISBN 978-3-0348-0512-4, MR 3014456
- Stephani, H. (1989), MacCallum, M. (ed.), Differential Equations: Their Solution Using Symmetries, Cambridge University Press.
- Wazwaz, Abdul-Majid (2009). Partial Differential Equations and Solitary Waves Theory. Higher Education Press. ISBN 978-3-642-00251-9.
- Wazwaz, Abdul-Majid (2002). Partial Differential Equations Methods and Applications. A.A. Balkema. ISBN 90-5809-369-7.
- Zwillinger, D. (1997), Handbook of Differential Equations (3rd ed.), Boston: Academic Press, ISBN 0-12-784395-7.
- Gershenfeld, N. (1999), The Nature of Mathematical Modeling (1st ed.), New York: Cambridge University Press, New York, NY, USA, ISBN 0-521-57095-6.
- Krasil'shchik, I.S. & Vinogradov, A.M., Eds. (1999), Symmetries and Conserwation Laws for Differential Equations of Mathematical Physics, American Mathematical Society, Providence, Rhode Island, USA, ISBN 0-8218-0958-X
{{citation}}: CS1 maint: multiple names: authors list (link). - Krasil'shchik, I.S.; Lychagin, V.V. & Vinogradov, A.M. (1986), Geometry of Jet Spaces and Nonlinear Partial Differential Equations, Gordon and Breach Science Publishers, New York, London, Paris, Montreux, Tokyo, ISBN 2-88124-051-8.
- Vinogradov, A.M. (2001), Cohomological Analysis of Partial Differential Equations and Secondary Calculus, American Mathematical Society, Providence, Rhode Island, USA, ISBN 0-8218-2922-X.
- Gustafsson, Bertil (2008). High Order Difference Methods for Time Dependent PDE. Springer Series in Computational Mathematics. Vol. 38. Springer. doi:10.1007/978-3-540-74993-6. ISBN 978-3-540-74992-9.
अग्रिम पठन
- Cajori, Florian (1928). "The Early History of Partial Differential Equations and of Partial Differentiation and Integration" (PDF). The American Mathematical Monthly. 35 (9): 459–467. doi:10.2307/2298771. JSTOR 2298771. Archived from the original (PDF) on 2018-11-23. Retrieved 2016-05-15.
- Nirenberg, Louis (1994). "Partial differential equations in the first half of the century." Development of mathematics 1900–1950 (Luxembourg, 1992), 479–515, Birkhäuser, Basel.
- Brezis, Haïm; Browder, Felix (1998). "Partial Differential Equations in the 20th Century". Advances in Mathematics. 135 (1): 76–144. doi:10.1006/aima.1997.1713.
बाहरी कड़ियाँ
- "Differential equation, partial", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
- Partial Differential Equations: Exact Solutions at EqWorld: The World of Mathematical Equations.
- Partial Differential Equations: Index at EqWorld: The World of Mathematical Equations.
- Partial Differential Equations: Methods at EqWorld: The World of Mathematical Equations.
- Example problems with solutions at exampleproblems.com
- Partial Differential Equations at mathworld.wolfram.com
- Partial Differential Equations with Mathematica
- Partial Differential Equations in Cleve Moler: Numerical Computing with MATLAB
- Partial Differential Equations at nag.com
- Sanderson, Grant (April 21, 2019). "But what is a partial differential equation?". 3Blue1Brown. Archived from the original on 2021-11-02 – via YouTube.