आंशिक अवकल समीकरण: Difference between revisions

Latest revision as of 13:23, 4 September 2023

ऊर्ध्वाधर दिशा और रंग द्वारा दर्शाए गए तापमान के साथ द्वि-आयामी ताप समीकरण के समाधान का एक दृश्य।

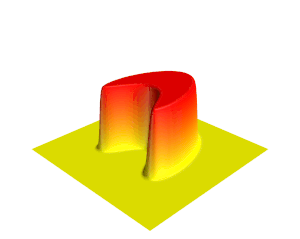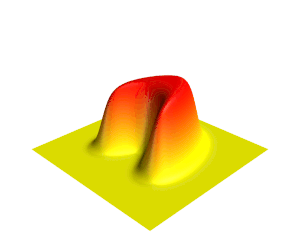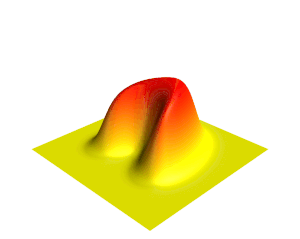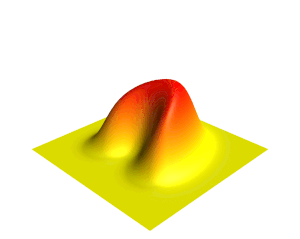
गणित में, आंशिक अवकल समीकरण (पीडीई) एक समीकरण है जो बहुविकल्पीय फलन के विभिन्न आंशिक डेरिवेटिव (व्युत्पन्न) के बीच संबंध स्थापित करता है।

फ़ंक्शन को प्रायः एक "अज्ञात" के रूप में माना जाता है जिसे हल किया जाना है, इसी तरह x को बीजगणितीय समीकरण जैसे $x 2 - 3 x + 2 = 0$ में हल करने के लिए एक अज्ञात संख्या के रूप में कैसे सोचा जाता है। हालांकि, आंशिक अंतर समीकरणों के समाधान के लिए स्पष्ट सूत्रों को लिखना असंभव है। तदनुसार, कंप्यूटर का उपयोग करके कुछ आंशिक अंतर समीकरणों के संख्यात्मक रूप से अनुमानित समाधानों के तरीकों पर आधुनिक गणितीय और वैज्ञानिक अनुसंधान की एक बड़ी मात्रा है। आंशिक अवकल समीकरण भी शुद्ध गणितीय अनुसंधान के एक बड़े क्षेत्र पर कब्जा कर लेते हैं, जिसमें सामान्य प्रश्न, मोटे तौर पर बोलते हैं, विभिन्न आंशिक अंतर समीकरणों के समाधान की सामान्य गुणात्मक विशेषताओं की पहचान पर, जैसे कि अस्तित्व, विशिष्टता, नियमितता और स्थिरता। कई खुले प्रश्नों में नेवियर-स्टोक्स समीकरणों के समाधान की मौजूदगी और सुगमता है, जिसे 2000 में मिलेनियम पुरस्कार समस्याओं में से एक के रूप में नामित किया गया था।

भौतिक विज्ञान और अभियांत्रिकी जैसे गणितीय रूप से उन्मुख वैज्ञानिक क्षेत्रों में आंशिक अंतर समीकरण सर्वव्यापी हैं। उदाहरण के लिए, वे ध्वनि, ऊष्मा, प्रसार, इलेक्ट्रोस्टैटिक्स, इलेक्ट्रोडायनामिक्स, ऊष्मप्रवैगिकी, द्रव गतिकी, लोच, सामान्य सापेक्षता और क्वांटम यांत्रिकी (श्रोडिंगर समीकरण, पाउली समीकरण, आदि) की आधुनिक वैज्ञानिक समझ में मूलभूत हैं। वे कई शुद्ध गणितीय विचारों से भी उत्पन्न होते हैं, जैसे अंतर ज्यामिति और विविधताओं की कलन; अन्य उल्लेखनीय अनुप्रयोगों में, वे ज्यामितीय टोपोलॉजी से पॉइंकेयर अनुमान के प्रमाण में मूलभूत उपकरण हैं।

आंशिक रूप से इस प्रकार के स्रोतों के कारण, विभिन्न प्रकार के आंशिक अंतर समीकरणों का एक विस्तृत स्पेक्ट्रम है, और उत्पन्न होने वाले कई अलग-अलग समीकरणों से निपटने के लिए विधियों का विकास किया गया है। जैसे, यह सामान्यतः स्वीकार किया जाता है कि आंशिक अवकल समीकरणों का कोई "सामान्य सिद्धांत" नहीं है, जिसमें विशेषज्ञ ज्ञान कुछ हद तक अनिवार्य रूप से अलग-अलग उपक्षेत्रों के बीच विभाजित होता है।^[1]

साधारण अवकल समीकरण आंशिक अवकल समीकरणों का एक उपवर्ग बनाते हैं, जो एकल चर के फलनों के अनुरूप होते हैं। स्टोचैस्टिक आंशिक अंतर समीकरण और गैर-स्थानीय समीकरण, 2020 तक, "पीडीई" धारणा के विशेष रूप से व्यापक रूप से अध्ययन किए गए विस्तार हैं। अधिक शास्त्रीय विषय, जिन पर अभी भी बहुत सक्रिय शोध है, में दीर्घवृत्तक और परावर्तक आंशिक अवकल समीकरण, द्रव यांत्रिकी, बोल्ट्जमैन समीकरण और फैलाने वाले आंशिक अंतर समीकरण शामिल हैं।

परिचय

एक का कहना है कि तीन चर का एक फ़ंक्शन $u (x, y, z)$ "हार्मोनिक" या "लाप्लास समीकरण का समाधान" है यदि यह स्थिति को संतुष्ट करता है।

{\frac {\partial ^{2}u}{\partial x^{2}}}+{\frac {\partial ^{2}u}{\partial y^{2}}}+{\frac {\partial ^{2}u}{\partial z^{2}}}=0.

चिरसम्मत यांत्रिकी के लिए उनकी प्रासंगिकता के कारण उन्नीसवीं शताब्दी में इस तरह के कार्यों का व्यापक रूप से अध्ययन किया गया था, उदाहरण के लिए, एक सजातीय ठोस का संतुलन तापमान वितरण एक हार्मोनिक फ़ंक्शन है। यदि स्पष्ट रूप से एक फ़ंक्शन दिया गया है, तो यह सामान्यतः यह जांचने के लिए सीधी गणना का विषय है कि यह हार्मोनिक है या नहीं। उदाहरण के लिए:

u(x,y,z)={\frac {1}{\sqrt {x^{2}-2x+y^{2}+z^{2}+1}}}

और

u(x,y,z)=2x^{2}-y^{2}-z^{2}

जबकि दोनों हार्मोनिक हैं

u(x,y,z)=\sin(xy)+z

यह आश्चर्यजनक हो सकता है कि हार्मोनिक कार्यों के दिए गए दो उदाहरण एक दूसरे से आश्चर्यजनक रूप से भिन्न रूप हैं। यह इस तथ्य का प्रतिबिंब है कि वे किसी भी तरह से लाप्लास समीकरण के "सामान्य समाधान सूत्र" के विशेष मामले नहीं हैं। यह साधारण अंतर समीकरणों (ओडीई) के मामले के विपरीत है, जो मोटे तौर पर लाप्लास समीकरण के समान है, जिसमें कई परिचयात्मक पाठ्यपुस्तकों का उद्देश्य सामान्य समाधान सूत्रों के लिए एल्गोरिदम खोजना है। लाप्लास समीकरण के लिए, बड़ी संख्या में आंशिक अवकल समीकरणों की तरह, ऐसे समाधान सूत्र मौजूद नहीं होते हैं।

निम्नलिखित पीडीई के मामले में इस विफलता की प्रकृति को और अधिक स्पष्ट रूप से देखा जा सकता है: दो चरों के फ़ंक्शन $v (x, y)$ के लिए, समीकरण पर विचार करें।

{\frac {\partial ^{2}v}{\partial x\partial y}}=0.

इसे प्रत्यक्ष रूप से जांचा जा सकता है कि किसी एकल-चर फलन

f

और

g

के लिए

v (x, y) = f (x) + g (y)

रूप का कोई भी फलन

v

, इस शर्त को पूरा करेगा। यह ओडीई समाधान फ़ार्मुलों में उपलब्ध विकल्पों से कहीं अधिक है, जो आम तौर पर कुछ संख्याओं के मुक्त चयन की अनुमति देता है। पीडीई के अध्ययन में, आम तौर पर कार्यों का मुफ्त विकल्प होता है।

इस पसंद की प्रकृति पीडीई से पीडीई में भिन्न होती है। किसी दिए गए समीकरण को समझने के लिए, अस्तित्व और विशिष्टता प्रमेय सामान्यतः महत्वपूर्ण संगठनात्मक सिद्धांत होते हैं। कई परिचयात्मक पाठ्यपुस्तकों में, मुक्त एवं दूरस्थ शिक्षा के लिए अस्तित्व और विशिष्टता प्रमेयों की भूमिका कुछ हद तक अपारदर्शी हो सकती है; अस्तित्व आधा सामान्यतः अनावश्यक होता है क्योंकि कोई भी प्रस्तावित समाधान सूत्र की सीधे जांच कर सकता है, जबकि विशिष्टता आधा प्रायः पृष्ठभूमि में मौजूद होती है ताकि यह सुनिश्चित किया जा सके कि प्रस्तावित समाधान सूत्र जितना संभव हो उतना सामान्य है। इसके विपरीत, पीडीई के लिए, अस्तित्व और विशिष्टता प्रमेय प्रायः एकमात्र साधन होते हैं जिसके द्वारा कोई भी विभिन्न समाधानों के ढेरों के माध्यम से नेविगेट कर सकता है। इस कारण से, विशुद्ध रूप से संख्यात्मक अनुकरण करते समय वे मौलिक भी होते हैं, क्योंकि किसी को यह समझ होनी चाहिए कि उपयोगकर्ता द्वारा कौन सा डेटा निर्धारित किया जाना है और गणना करने के लिए कंप्यूटर पर क्या छोड़ा जाना है।

इस तरह के अस्तित्व और अद्वितीयता प्रमेयों पर चर्चा करने के लिए, "अज्ञात फ़ंक्शन" के डोमेन के बारे में सटीक होना आवश्यक है। अन्यथा, केवल "दो चरों का एक कार्य" जैसे शब्दों में बोलना, परिणामों को अर्थपूर्ण रूप से तैयार करना असंभव है। अर्थात्, अज्ञात फलन के क्षेत्र को स्वयं पीडीई की संरचना के भाग के रूप में माना जाना चाहिए।

निम्नलिखित ऐसे अस्तित्व और अद्वितीयता प्रमेय के दो उत्कृष्ट उदाहरण प्रदान करता है। भले ही प्रश्न में दो पीडीई समान हैं, व्यवहार में एक महत्वपूर्ण अंतर है: पहले पीडीई के लिए, एक के पास एक ही फ़ंक्शन का मुफ्त नुस्खा है, जबकि दूसरे पीडीई के लिए, दो कार्यों का मुफ्त निर्धारण है।

बता दें कि $B$ समतल में मूल बिंदु के चारों ओर इकाई-त्रिज्या डिस्क को दर्शाता है। यूनिट सर्कल पर किसी भी निरंतर फ़ंक्शन $U$ के लिए, $B$ पर ठीक एक फ़ंक्शन $u$ होता है जैसे कि ${\frac {\partial ^{2}u}{\partial x^{2}}}+{\frac {\partial ^{2}u}{\partial y^{2}}}=0$ और यूनिट सर्कल के लिए किसका प्रतिबंध $U$ द्वारा दिया गया है।
वास्तविक रेखा $R$ पर किसी भी फ़ंक्शन $f$ और $g$ के लिए, $R \times (-1, 1)$ पर बिल्कुल एक फ़ंक्शन $u$ होता है जैसे कि ${\frac {\partial ^{2}u}{\partial x^{2}}}-{\frac {\partial ^{2}u}{\partial y^{2}}}=0$ और $u (x, 0) = f (x)$ और $.mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output .sfrac.tion,.mw-parser-output .sfrac .tion{display:inline-block;vertical-align:-0.5em;font-size:85%;text-align:center}.mw-parser-output .sfrac .num,.mw-parser-output .sfrac .den{display:block;line-height:1em;margin:0 0.1em}.mw-parser-output .sfrac .den{border-top:1px solid}.mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px}∂u/∂y(x, 0) = g(x)$ के साथ $x$ के सभी मानों के लिए।

इससे भी अधिक घटनाएं संभव हैं। उदाहरण के लिए, निम्नलिखित पीडीई, अंतर ज्यामिति के क्षेत्र में स्वाभाविक रूप से उत्पन्न होता है, एक उदाहरण दिखाता है जहां एक सरल और पूरी तरह से स्पष्ट समाधान सूत्र है, लेकिन केवल तीन संख्याओं के स्वतंत्र विकल्प के साथ और एक भी फ़ंक्शन नहीं है।

यदि $u$ $R 2$ पर एक फ़ंक्शन है ${\frac {\partial }{\partial x}}{\frac {\frac {\partial u}{\partial x}}{\sqrt {1+\left({\frac {\partial u}{\partial x}}\right)^{2}+\left({\frac {\partial u}{\partial y}}\right)^{2}}}}+{\frac {\partial }{\partial y}}{\frac {\frac {\partial u}{\partial y}}{\sqrt {1+\left({\frac {\partial u}{\partial x}}\right)^{2}+\left({\frac {\partial u}{\partial y}}\right)^{2}}}}=0,$ फिर संख्याएँ हैं $a$ , $b$ , और $c$ साथ $u (x, y) = ax + by + c$ .

पहले के उदाहरणों के विपरीत, यह पीडीई वर्गमूलों और वर्गों के कारण अरैखिक है। एक अरैखिक पीडीई एक ऐसा है कि, यदि यह सजातीय है, तो किन्हीं भी दो समाधानों का योग भी एक समाधान है, और किसी भी समाधान का कोई भी स्थिर गुणक भी एक समाधान है।

वेल-पोसेड्नेस

अच्छी स्थिति एक पीडीई के बारे में सूचना के एक सामान्य योजनाबद्ध पैकेज को संदर्भित करती है। यह कहने के लिए कि एक पीडीई अच्छी स्थिति में है, एक व्यक्ति में होना चाहिए:

एक अस्तित्व और विशिष्टता प्रमेय, यह दावा करते हुए कि कुछ स्वतंत्र रूप से चुने गए कार्यों के नुस्खे से, पीडीई के एक विशिष्ट समाधान को अलग किया जा सकता है
नि: शुल्क विकल्पों को लगातार बदलते रहने से, व्यक्ति लगातार इसी समाधान को बदलता रहता है

यह, कई अलग-अलग पीडीई पर लागू होने की आवश्यकता के कारण, कुछ हद तक अस्पष्ट है। विशेष रूप से "निरंतरता" की आवश्यकता अस्पष्ट है क्योंकि आम तौर पर कई असमान साधन होते हैं जिनके द्वारा इसे कड़ाई से परिभाषित किया जा सकता है। हालांकि, पीडीई का अध्ययन करना असामान्य है, बिना यह निर्दिष्ट किए कि यह अच्छी तरह से प्रस्तुत किया गया है।

ऊर्जा पद्धति

ऊर्जा विधि एक गणितीय प्रक्रिया है जिसका उपयोग प्रारंभिक-सीमा-मूल्य-समस्याओं की अच्छी स्थिति को सत्यापित करने के लिए किया जा सकता है।^[2] निम्नलिखित उदाहरण में ऊर्जा पद्धति का उपयोग यह तय करने के लिए किया जाता है कि कहां और कौन सी सीमा शर्तों को लगाया जाना चाहिए ताकि परिणामी आईबीवीपी अच्छी तरह से तैयार हो। द्वारा दिए गए एक आयामी अतिपरवलयिक पीडीई पर विचार करें।

{\frac {\partial u}{\partial t}}+\alpha {\frac {\partial u}{\partial x}}=0,\quad x\in [a,b],t>0,

जहां

\alpha \neq 0

एक स्थिरांक है और

u(x,t)

प्रारंभिक स्थिति

u(x,0)=f(x)

के साथ एक अज्ञात फलन है।

u

से गुणा करने और डोमेन पर एकीकृत करने से मिलता है।

\int _{a}^{b}u{\frac {\partial u}{\partial t}}\mathrm {d} x+\alpha \int _{a}^{b}u{\frac {\partial u}{\partial x}}\mathrm {d} x=0.

उसका उपयोग करना

\int _{a}^{b}u{\frac {\partial u}{\partial t}}\mathrm {d} x={\frac {1}{2}}{\frac {\partial }{\partial t}}\|u\|^{2}\quad {\text{and}}\quad \int _{a}^{b}u{\frac {\partial u}{\partial x}}\mathrm {d} x={\frac {1}{2}}u(b,t)^{2}-{\frac {1}{2}}u(a,t)^{2},

जहां दूसरे संबंध के लिए भागों द्वारा एकीकरण का उपयोग किया गया है, हम प्राप्त करते हैं:

{\frac {\partial }{\partial t}}\|u\|^{2}+\alpha u(b,t)^{2}-\alpha u(a,t)^{2}=0.

यहाँ

\|\cdot \|

मानक

L^{2}

मानक को दर्शाता है। अच्छी स्थिति के लिए हमें आवश्यकता है कि समाधान की ऊर्जा गैर-बढ़ती है, यानी कि

{\textstyle {\frac {\partial }{\partial t}}\|u\|^{2}\leq 0}

, जो

u

को

x=a

यदि

\alpha >0

और

x=b

पर यदि

\alpha <0

निर्दिष्ट करके प्राप्त किया जाता है। यह अंतर्वाह पर केवल थोपने वाली सीमा स्थितियों से संबंधित है। ध्यान दें कि सुव्यवस्थितता डेटा (प्रारंभिक और सीमा) के संदर्भ में वृद्धि की अनुमति देती है और इस प्रकार यह दिखाने के लिए पर्याप्त है कि

{\textstyle {\frac {\partial }{\partial t}}\|u\|^{2}\leq 0}

धारण करता है जब सभी डेटा शून्य पर समुच्चय होते हैं।

स्थानीय समाधानों का अस्तित्व

कॉची प्रारंभिक मूल्य समस्याओं के लिए कॉची-कोवाल्स्की प्रमेय अनिवार्य रूप से बताता है कि यदि आंशिक अंतर समीकरण में सभी शब्द विश्लेषणात्मक कार्यों से बने होते हैं और एक निश्चित ट्रांसवर्सलिटी की स्थिति संतुष्ट होती है (हाइपरप्लेन या अधिक आम तौर पर हाइपरसफेस जहां प्रारंभिक डेटा सामने आता है) आंशिक अंतर ऑपरेटर के संबंध में गैर-विशेषता), तो कुछ क्षेत्रों पर, आवश्यक रूप से समाधान मौजूद होते हैं जो विश्लेषणात्मक कार्य भी होते हैं। यह विश्लेषणात्मक आंशिक अवकल समीकरणों के अध्ययन का एक मूलभूत परिणाम है। हैरानी की बात है, प्रमेय सुचारू कार्यों की समायोजन में नहीं है; 1957 में हैंस लेवी द्वारा खोजे गए एक उदाहरण में एक रेखीय आंशिक अंतर समीकरण शामिल है, जिसके गुणांक चिकने हैं (अर्थात, सभी आदेशों के व्युत्पन्न हैं) लेकिन विश्लेषणात्मक नहीं हैं जिसके लिए कोई समाधान मौजूद नहीं है। अतः कौशी-कोवालेव्स्की प्रमेय अनिवार्य रूप से विश्लेषणात्मक कार्यों के दायरे में सीमित है।

वर्गीकरण

अंकन

पीडीई लिखते समय, आंशिक डेरिवेटिव को सबस्क्रिप्ट का उपयोग करके निरूपित करना आम है। उदाहरण के लिए:

u_{x}={\frac {\partial u}{\partial x}},\quad u_{xx}={\frac {\partial ^{2}u}{\partial x^{2}}},\quad u_{xy}={\frac {\partial ^{2}u}{\partial y\,\partial x}}={\frac {\partial }{\partial y}}\left({\frac {\partial u}{\partial x}}\right).

सामान्य स्थिति में कि

u

का एक कार्य है

n

चर, फिर

u i

के सापेक्ष पहले आंशिक व्युत्पन्न को दर्शाता है

i

-वें इनपुट,

u ij

के सापेक्ष दूसरे आंशिक व्युत्पन्न को दर्शाता है

i

-वें और

j

-वें इनपुट, और इसी तरह।

ग्रीक अक्षर $Δ$ लाप्लास ऑपरेटर को दर्शाता है; यदि $u$ का एक कार्य है $n$ चर, फिर

\Delta u=u_{11}+u_{22}+\cdots +u_{nn}.

भौतिकी साहित्य में, लाप्लास ऑपरेटर को प्रायः

\nabla 2

द्वारा निरूपित किया जाता है; गणित साहित्य में,

\nabla 2 u

भी

u

के हेसियन मैट्रिक्स को निरूपित कर सकता है।

पहले क्रम के समीकरण

रेखीय और अरेखीय समीकरण

रैखिक समीकरण

एक पीडीई को रैखिक कहा जाता है यदि यह अज्ञात और उसके डेरिवेटिव में रैखिक है। उदाहरण के लिए, $x$ और $y$ के फलन $u$ के लिए, एक द्वितीय कोटि रैखिक पीडीई का रूप होता है

a_{1}(x,y)u_{xx}+a_{2}(x,y)u_{xy}+a_{3}(x,y)u_{yx}+a_{4}(x,y)u_{yy}+a_{5}(x,y)u_{x}+a_{6}(x,y)u_{y}+a_{7}(x,y)u=f(x,y)

जहाँ

a i

और

f

केवल स्वतंत्र चरों के फलन हैं। (प्रायः मिश्रित-आंशिक डेरिवेटिव्स

u xy

और

u yx

को समान किया जाएगा, लेकिन रैखिकता की चर्चा के लिए इसकी आवश्यकता नहीं है।) यदि

a i

स्थिरांक हैं (

x

और

y

से स्वतंत्र) तो पीडीई को निरंतर गुणांक के साथ रैखिक कहा जाता है। यदि हर जगह

f

शून्य है तो रैखिक पीडीई समांगी है, अन्यथा यह असमघाती है। (यह स्पर्शोन्मुख समरूपता से अलग है, जो पीडीई के समाधान पर गुणांक में उच्च आवृत्ति दोलनों के प्रभावों का अध्ययन करता है।)

अरैखिक समीकरण

तीन मुख्य प्रकार के अरैखिक पीडीई अर्धरेखीय पीडीई, रैखिककल्प पीडीई और पूरी तरह से अरैखिक पीडीई हैं।

रेखीय पीडीई के निकटतम सेमीलीनियर (अर्धरेखीय) पीडीई हैं, जहां केवल उच्चतम क्रम के डेरिवेटिव रैखिक शब्दों के रूप में प्रकट होते हैं, गुणांक के साथ जो स्वतंत्र चर के कार्य हैं। निचले क्रम के डेरिवेटिव और अज्ञात फ़ंक्शन मनमाने ढंग से प्रकट हो सकते हैं। उदाहरण के लिए, दो चरों में एक सामान्य द्वितीय-क्रम सेमीलीनियर पीडीई है।

a_{1}(x,y)u_{xx}+a_{2}(x,y)u_{xy}+a_{3}(x,y)u_{yx}+a_{4}(x,y)u_{yy}+f(u_{x},u_{y},u,x,y)=0

क्वासिलिनियर (रैखिककल्प) पीडीई में उच्चतम क्रम डेरिवेटिव इसी प्रकार केवल रैखिक शर्तों के रूप में दिखाई देते हैं, लेकिन गुणांक के साथ संभवतः अज्ञात और निम्न-क्रम डेरिवेटिव के कार्य होते हैं:

a_{1}(u_{x},u_{y},u,x,y)u_{xx}+a_{2}(u_{x},u_{y},u,x,y)u_{xy}+a_{3}(u_{x},u_{y},u,x,y)u_{yx}+a_{4}(u_{x},u_{y},u,x,y)u_{yy}+f(u_{x},u_{y},u,x,y)=0

भौतिकी में कई मौलिक पीडीई क्वैसिलिनियर हैं, जैसे सामान्य सापेक्षता के आइंस्टीन समीकरण और तरल गति का वर्णन करने वाले नेवियर-स्टोक्स समीकरण।

किसी रैखिकता गुण के बिना पीडीई को पूरी तरह से गैर-रैखिक कहा जाता है और एक या अधिक उच्चतम-क्रम डेरिवेटिव पर गैर-रैखिकता रखता है। एक उदाहरण मोंज-एम्पीयर समीकरण है, जो विभेदक ज्यामिति में उत्पन्न होता है।^[3]

दूसरे क्रम के रैखिक समीकरण

बीसवीं शताब्दी की शुरुआत के बाद से क्रम दो के दीर्घवृत्तीय, परवलयिक और अतिशयोक्तिपूर्ण आंशिक अंतर समीकरणों का व्यापक रूप से अध्ययन किया गया है। हालाँकि, कई अन्य महत्वपूर्ण प्रकार के पीडीई हैं, जिनमें कॉर्टेवेग-डी व्रीज़ समीकरण शामिल है। यूलर-ट्रिकोमी समीकरण जैसे संकर भी हैं, जो डोमेन के विभिन्न क्षेत्रों के लिए दीर्घवृत्त से अतिपरवलयिक में भिन्न होते हैं। इन मूल प्रकारों के उच्च-क्रम पीडीई के लिए महत्वपूर्ण विस्तार भी हैं, लेकिन ऐसा ज्ञान अधिक विशिष्ट है।

दीर्घवृत्तीय/परवलयिक/अतिशयोक्तिपूर्ण वर्गीकरण उपयुक्त प्रारंभिक और सीमा स्थितियों और समाधानों की समतलता के लिए एक मार्गदर्शक प्रदान करता है। $u xy = u yx$ मानते हुए, दो स्वतंत्र चरों में सामान्य रैखिक द्वितीय-क्रम पीडीई का रूप है।

Au_{xx}+2Bu_{xy}+Cu_{yy}+\cdots {\mbox{(lower order terms)}}=0,

जहां गुणांक $A$ , $B$ , $C$ ... $x$ और $y$ पर निर्भर हो सकता है। यदि $A 2 + B 2 + C 2 > 0$ के एक क्षेत्र पर $xy$ -प्लेन, पीडीई उस क्षेत्र में दूसरे क्रम का है। यह प्रपत्र शंकु खंड के समीकरण के अनुरूप है:

Ax^{2}+2Bxy+Cy^{2}+\cdots =0.

अधिक सटीक रूप से,

\partial x

को

X

द्वारा प्रतिस्थापित करना, और इसी तरह अन्य चरों के लिए (औपचारिक रूप से यह एक फूरियर रूपांतरण द्वारा किया जाता है), एक स्थिर-गुणांक पीडीई को समान डिग्री के बहुपद में उच्चतम डिग्री (एक सजातीय बहुपद) के साथ परिवर्तित करता है। यहाँ एक द्विघात रूप) वर्गीकरण के लिए सर्वाधिक महत्वपूर्ण है। जिस तरह विविक्तकर

B 2 - 4 AC

के आधार पर शंक्वाकार वर्गों और द्विघात रूपों को परवलयिक, अतिशयोक्तिपूर्ण और दीर्घवृत्त में वर्गीकृत किया जाता है, उसी तरह किसी दिए गए बिंदु पर दूसरे क्रम के पीडीई के लिए भी किया जा सकता है। हालाँकि, पीडीई में विविक्तकर

B 2 - AC

द्वारा दिया जाता है क्योंकि

xy

पद की अभ्यास

B

के बजाय

2 B

है; औपचारिक रूप से, विविक्तकर (संबंधित द्विघात रूप का)

(2 B) 2 - 4 AC = 4(B 2 - AC)

है, जिसमें सरलता के लिए 4 का गुणनखंड हटा दिया गया है।

$B 2 - AC < 0$ (दीर्घवृत्त आंशिक अंतर समीकरण): अण्डाकार आंशिक अंतर समीकरण के समाधान उतने ही चिकने होते हैं जितने कि गुणांक अनुमति देते हैं, उस क्षेत्र के आंतरिक भाग में जहाँ समीकरण और समाधान परिभाषित होते हैं। उदाहरण के लिए, लाप्लास के समीकरण के समाधान डोमेन के भीतर विश्लेषणात्मक होते हैं जहां उन्हें परिभाषित किया जाता है, लेकिन समाधान सीमा मान मान सकते हैं जो चिकनी नहीं हैं। सबसोनिक गति पर तरल पदार्थ की गति को दीर्घवृत्त पीडीई के साथ अनुमानित किया जा सकता है, और यूलर-ट्रिकोमी समीकरण अंडाकार है जहां $x < 0$ .
$B 2 - AC = 0$ (परवलयिक आंशिक अंतर समीकरण): समीकरण जो हर बिंदु पर परवलयिक आंशिक अंतर समीकरण होते हैं, उन्हें स्वतंत्र चर के परिवर्तन द्वारा ताप समीकरण के अनुरूप रूप में परिवर्तित किया जा सकता है। परिवर्तित समय चर बढ़ने पर समाधान सुचारू हो जाते हैं। यूलर-ट्रिकोमी समीकरण में उस रेखा पर परवलयिक प्रकार है जहां $x = 0$ .
$B 2 - AC > 0$ (अतिपरवलयिक आंशिक अंतर समीकरण): अतिशयोक्तिपूर्ण आंशिक अंतर समीकरण समीकरण प्रारंभिक डेटा में कार्यों या डेरिवेटिव के किसी भी विच्छिन्नता को बनाए रखते हैं। एक उदाहरण तरंग समीकरण है। सुपरसोनिक गति पर द्रव की गति को हाइपरबोलिक पीडीई के साथ अनुमानित किया जा सकता है, और यूलर-ट्रिकोमी समीकरण हाइपरबॉलिक है जहां $x > 0$ .

अगर वहाँ $n$ स्वतंत्र प्रभावित करने वाली वस्तुएँ $x 1, x 2, \dots, x n$ दूसरे क्रम के एक सामान्य रैखिक आंशिक अंतर समीकरण का रूप है

Lu=\sum _{i=1}^{n}\sum _{j=1}^{n}a_{i,j}{\frac {\partial ^{2}u}{\partial x_{i}\partial x_{j}}}\quad +{\text{lower-order terms}}=0.

वर्गीकरण गुणांक मैट्रिक्स के आइगेनवैल्यू के हस्ताक्षर पर निर्भर करता है

a i, j

.

दीर्घवृत्त: आइगेनवैल्यू सभी धनात्मक या सभी ऋणात्मक हैं।
परवलयिक: आइगेनवैल्यू सभी धनात्मक या सभी नकारात्मक हैं, एक को छोड़कर जो शून्य है।
अतिपरवलयिक: केवल एक ऋणात्मक आइगेनवैल्यू है और बाकी सभी धनात्मक हैं, या केवल एक धनात्मक आइगेनवैल्यू है और बाकी सभी ऋणात्मक हैं।
अल्ट्राहाइपरबोलिक: एक से अधिक धनात्मक आइगेनवैल्यू और एक से अधिक ऋणात्मक आइगेनवैल्यू होते हैं, और कोई शून्य आइगेनवैल्यू नहीं होते हैं।^[4]

दीर्घवृत्त, परवलयिक, और अतिपरवलयिक समीकरणों के सिद्धांत का सदियों से अध्ययन किया गया है, जो काफी हद तक लाप्लास समीकरण , ऊष्मा समीकरण और तरंग समीकरण के मानक उदाहरणों के आसपास या उसके आधार पर केंद्रित है।

प्रथम-क्रम समीकरणों और विशिष्ट सतहों की प्रणाली

आंशिक अंतर समीकरणों के वर्गीकरण को प्रथम-क्रम समीकरणों की प्रणालियों तक विस्तारित किया जा सकता है, जहां अज्ञात $u$ अब $m$ घटकों के साथ एक वेक्टर है, और गुणांक मैट्रिसेस $A ν$ , $ν = 1, 2, \dots, n$ के लिए $m$ द्वारा $m$ मेट्रिसेस हैं। आंशिक अवकल समीकरण का रूप ले लेता है।

Lu=\sum _{\nu =1}^{n}A_{\nu }{\frac {\partial u}{\partial x_{\nu }}}+B=0,

जहां गुणांक मेट्रिसेस

A ν

और वेक्टर

B

पर निर्भर हो सकता है

x

और

u

. यदि एक ऊनविम पृष्ठ

S

निहित रूप में दिया गया है।

\varphi (x_{1},x_{2},\ldots ,x_{n})=0,

जहां $φ$ एक गैर-शून्य है, तब $S$ ऑपरेटर के लिए एक विशिष्ट सतह है $L$ किसी दिए गए बिंदु पर यदि विशेषता रूप गायब हो जाता है:

Q\left({\frac {\partial \varphi }{\partial x_{1}}},\ldots ,{\frac {\partial \varphi }{\partial x_{n}}}\right)=\det \left[\sum _{\nu =1}^{n}A_{\nu }{\frac {\partial \varphi }{\partial x_{\nu }}}\right]=0.

इस स्थिति की ज्यामितीय व्याख्या इस प्रकार है: यदि

u

के लिए डेटा सतह

S

पर निर्धारित किया गया है, तो यह संभव हो सकता है कि अंतर समीकरण से

u

के सामान्य व्युत्पन्न को निर्धारित किया जा सके। यदि

S

पर डेटा और अवकल समीकरण,

S

पर

u

का सामान्य अवकलज निर्धारित करते हैं, तो

S

गैर-लक्षण है। यदि

S

पर डेटा और अंतर समीकरण

S

पर

u

के सामान्य व्युत्पन्न का निर्धारण नहीं करते हैं, तो सतह विशेषता है, और अंतर समीकरण डेटा को

S

पर प्रतिबंधित करता है: अंतर समीकरण

S

के लिए आंतरिक है।

एक प्रथम-क्रम प्रणाली $Lu = 0$ दीर्घवृत्तीय है यदि कोई सतह $L$ के लिए विशेषता नहीं है: $S$ पर $u$ के मान और अंतर समीकरण हमेशा $S$ पर $u$ के सामान्य व्युत्पन्न को निर्धारित करते हैं।
एक प्रथम-क्रम प्रणाली एक बिंदु पर अतिशयोक्तिपूर्ण है यदि उस बिंदु पर सामान्य $ξ$ के साथ एक अंतरिक्ष जैसी सतह $S$ है। इसका मतलब यह है कि, किसी भी गैर-तुच्छ वेक्टर $η$ ऑर्थोगोनल को $ξ$ , और एक स्केलर गुणक $λ$ दिया गया है, समीकरण ( $Q (λξ + η) = 0$ में $m$ वास्तविक जड़ें $λ 1, λ 2, \dots, λ m$ हैं। अगर ये जड़ें हमेशा अलग-अलग हों तो सिस्टम सख्ती से अतिशयोक्तिपूर्ण है। इस स्थिति की ज्यामितीय व्याख्या इस प्रकार है: विशेषता रूप $Q (ζ) = 0$ सजातीय निर्देशांक ζ के साथ एक शंकु (सामान्य शंकु) को परिभाषित करता है। अतिशयोक्तिपूर्ण मामले में, इस शंकु में $m$ शीट हैं, और अक्ष $ζ = λξ$ इन शीटों के अंदर चलता है: यह उनमें से किसी को नहीं काटता है। लेकिन जब η द्वारा मूल से विस्थापित किया जाता है, तो यह अक्ष प्रत्येक शीट को प्रतिच्छेद करती है। दीर्घवृत्तीय मामले में, सामान्य शंकु में कोई वास्तविक शीट नहीं होती है।

विश्लेषणात्मक समाधान

चरों का पृथक्करण

चरों को अलग करने की महत्वपूर्ण तकनीक द्वारा रेखीय पीडीई को साधारण अंतर समीकरणों की प्रणालियों में घटाया जा सकता है। यह तकनीक अंतर समीकरणों के समाधान की एक विशेषता पर टिकी हुई है: यदि कोई ऐसा समाधान ढूंढ सकता है जो समीकरण को हल करता है और सीमा शर्तों को संतुष्ट करता है, तो यह समाधान है (यह ओडीई पर भी लागू होता है)। हम एक ansatz के रूप में मानते हैं कि पैरामीटर स्थान और समय पर एक समाधान की निर्भरता को उन शर्तों के उत्पाद के रूप में लिखा जा सकता है जो प्रत्येक एक पैरामीटर पर निर्भर करते हैं, और फिर देखते हैं कि समस्या को हल करने के लिए इसे बनाया जा सकता है या नहीं।^[5]

चरों को अलग करने की विधि में, कम चरों में एक पीडीई को एक पीडीई में घटाया जाता है, जो एक सामान्य अंतर समीकरण है यदि एक चर में - इन्हें हल करना आसान होता है।

यह सरल पीडीई के लिए संभव है, जिसे वियोज्य आंशिक अंतर समीकरण कहा जाता है, और डोमेन आम तौर पर एक आयत (अंतराल का एक उत्पाद) होता है। वियोज्य पीडीई विकर्ण मैट्रिसेस के अनुरूप हैं - एक समन्वय के रूप में "निश्चित x के मान" के बारे में सोचते हुए, प्रत्येक निर्देशांक को अलग से समझा जा सकता है।

यह विशेषताओं की विधि का सामान्यीकरण करता है और इसका उपयोग अभिन्न परिवर्तनों में भी किया जाता है।

विशेषताओं का तरीका

विशेष मामलों में, कोई विशेषता वक्र पा सकता है जिस पर समीकरण ओडीई में कम हो जाता है - इन वक्रों को सीधा करने के लिए डोमेन में बदलते निर्देशांक चर के पृथक्करण की अनुमति देते हैं और इसे विशेषताओं की विधि कहा जाता है।

अधिक आम तौर पर, किसी को विशिष्ट सतहें मिल सकती हैं। द्वितीय कोटि के आंशिक अवकल समीकरण हल के लिए, चार्पिट विधि देखें।

इंटीग्रल ट्रांसफॉर्म

एक अभिन्न परिवर्तन पीडीई को एक सरल रूप में बदल सकता है, विशेष रूप से एक वियोज्य पीडीई। यह एक ऑपरेटर को विकर्णित करने के अनुरूप है।

इसका एक महत्वपूर्ण उदाहरण फूरियर विश्लेषण है, जो साइनसोइडल तरंगों के ईजेनबेसिस का उपयोग करके गर्मी समीकरण को विकर्णित करता है।

यदि डोमेन परिमित या आवधिक है, तो फूरियर श्रृंखला जैसे समाधानों का एक अनंत योग उपयुक्त है, लेकिन फूरियर अभिन्न जैसे समाधानों का एक अभिन्न अंग सामान्यतः अनंत डोमेन के लिए आवश्यक है। ऊपर दिए गए ताप समीकरण के लिए एक बिंदु स्रोत का समाधान फूरियर इंटीग्रल के उपयोग का एक उदाहरण है।

चर का परिवर्तन

चरों के उपयुक्त परिवर्तन द्वारा प्रायः पीडीई को ज्ञात समाधान के साथ सरल रूप में कम किया जा सकता है। उदाहरण के लिए, ब्लैक-स्कोल्स समीकरण

{\frac {\partial V}{\partial t}}+{\tfrac {1}{2}}\sigma ^{2}S^{2}{\frac {\partial ^{2}V}{\partial S^{2}}}+rS{\frac {\partial V}{\partial S}}-rV=0

ऊष्मा समीकरण के लिए कम करने योग्य है।

{\frac {\partial u}{\partial \tau }}={\frac {\partial ^{2}u}{\partial x^{2}}}

चर के परिवर्तन से^[6]

{\begin{aligned}V(S,t)&=v(x,\tau ),\\[5px]x&=\ln \left(S\right),\\[5px]\tau &={\tfrac {1}{2}}\sigma ^{2}(T-t),\\[5px]v(x,\tau )&=e^{-\alpha x-\beta \tau }u(x,\tau ).\end{aligned}}

मौलिक समाधान

मौलिक समाधान (एक बिंदु स्रोत के लिए समाधान) को खोजने के द्वारा अमानवीय समीकरणों को प्रायः हल किया जा सकता है (निरंतर गुणांक पीडीई के लिए, हमेशा हल किया जाता है), फिर समाधान प्राप्त करने के लिए सीमा शर्तों के साथ संवलयी होता है।

यह सिग्नल प्रोसेसिंग में एक फिल्टर को उसकी आवेग प्रतिक्रिया द्वारा समझने के अनुरूप है।

सुपरपोजिशन सिद्धांत

सुपरपोज़िशन सिद्धांत पीडीई के रैखिक सिस्टम सहित किसी भी रैखिक प्रणाली पर लागू होता है। इस अवधारणा का एक सामान्य दृश्य चरण में दो तरंगों की परस्पर क्रिया है, जिसके परिणामस्वरूप एक बड़ा आयाम होता है, उदाहरण के लिए, $sin x + sin x = 2 sin x$ पीडीई में समान सिद्धांत देखा जा सकता है जहां समाधान वास्तविक या जटिल और योगात्मक हो सकते हैं। यदि $u 1$ और $u 2$ किसी फंक्शन स्पेस $R$ में रैखिक पीडीई के समाधान हैं, तो $u = c 1 u 1 + c 2 u 2$ किसी भी स्थिरांक $c 1$ और $c 2$ के साथ भी उसी फ़ंक्शन स्पेस में उस पीडीई का एक समाधान है।

गैर-रैखिक समीकरणों के लिए तरीके

अरेखीय पीडीई को हल करने के लिए आम तौर पर लागू होने वाली कोई विधियाँ नहीं हैं। फिर भी, अस्तित्व और अद्वितीयता के परिणाम (जैसे कॉची-कोवालेव्स्की प्रमेय) प्रायः संभव होते हैं, जैसा कि समाधानों के महत्वपूर्ण गुणात्मक और मात्रात्मक गुणों के प्रमाण हैं (इन परिणामों को प्राप्त करना विश्लेषण का एक प्रमुख हिस्सा है)। गैर-रैखिक पीडीई के लिए कम्प्यूटेशनल समाधान, विभाजन-चरण विधि, गैर-रैखिक श्रोडिंगर समीकरण जैसे विशिष्ट समीकरणों के लिए मौजूद है।

फिर भी, कुछ तकनीकों का प्रयोग अनेक प्रकार के समीकरणों के लिए किया जा सकता है। अनिर्धारित समीकरणों को हल करने के लिए $h$ -सिद्धांत सबसे शक्तिशाली तरीका है। कई विश्लेषणात्मक अतिनिर्धारित प्रणालियों के बारे में जानकारी प्राप्त करने के लिए रिक्वायर-जेनेट सिद्धांत एक प्रभावी तरीका है।

विशेषताओं की विधि का उपयोग कुछ विशेष मामलों में अरैखिक आंशिक अवकल समीकरणों को हल करने के लिए किया जा सकता है।^[7]

कुछ मामलों में, पीडीई को गड़बड़ी विश्लेषण के माध्यम से हल किया जा सकता है जिसमें समाधान को ज्ञात समाधान के साथ समीकरण में सुधार माना जाता है। विकल्प संख्यात्मक विश्लेषण तकनीक हैं जो साधारण परिमित अंतर योजनाओं से लेकर अधिक परिपक्व मल्टीग्रिड और परिमित तत्व विधियों तक हैं। कंप्यूटर, कभी-कभी उच्च-प्रदर्शन वाले सुपर कंप्यूटर का उपयोग करके विज्ञान और इंजीनियरिंग की कई दिलचस्प समस्याओं को इस तरह से हल किया जाता है।

लाई ग्रुप विधि

1870 में सोफस ली के कार्य ने अवकल समीकरणों के सिद्धांत को एक अधिक संतोषजनक आधार पर रखा। उन्होंने दिखाया कि पुराने गणितज्ञों के एकीकरण सिद्धांतों को, जिसे अब लाई समूह कहा जाता है, एक सामान्य स्रोत के रूप में संदर्भित किया जा सकता है; और वह साधारण अवकल समीकरण जो समान अतिसूक्ष्म परिवर्तनों को स्वीकार करते हैं, एकीकरण की तुलनात्मक कठिनाइयाँ प्रस्तुत करते हैं। उन्होंने संपर्क के परिवर्तन के विषय पर भी जोर दिया।

पीडीई को हल करने के लिए एक सामान्य दृष्टिकोण अंतर समीकरणों की समरूपता संपत्ति का उपयोग करता है, समाधानों के समाधान के निरंतर अत्यल्प रूपांतरण (लाई सिद्धांत)। निरंतर समूह सिद्धांत, ले बीजगणित और अंतर ज्यामिति का उपयोग पूर्णांक समीकरणों को उत्पन्न करने के लिए रैखिक और गैर-रैखिक आंशिक अंतर समीकरणों की संरचना को समझने के लिए किया जाता है, इसके लक्स जोड़े, पुनरावर्तन संचालकों को खोजने के लिए, बैकलंड रूपांतरण (Bäcklund transform) और अंत में पीडीई के लिए सटीक विश्लेषणात्मक समाधान ढूंढते हैं।

गणित, भौतिकी, इंजीनियरिंग और कई अन्य विषयों में उत्पन्न होने वाले विभेदक समीकरणों का अध्ययन करने के लिए सममिति विधियों को मान्यता दी गई है।

अर्धविश्लेषणात्मक तरीके

एडोमियन अपघटन विधि,^[8] लायपुनोव कृत्रिम छोटे पैरामीटर विधि, और उनकी होमोटॉपी क्षोभ विधि सभी अधिक सामान्य समरूपता विश्लेषण पद्धति के विशेष मामले हैं।^[9] ये श्रृंखला विस्तार के तरीके हैं, और लायपुनोव विधि को छोड़कर, प्रसिद्ध गड़बड़ी सिद्धांत की तुलना में छोटे भौतिक मापदंडों से स्वतंत्र हैं, इस प्रकार इन तरीकों को अधिक लचीलापन और समाधान व्यापकता प्रदान करते हैं।

संख्यात्मक समाधान

पीडीई को हल करने के लिए तीन सबसे व्यापक रूप से उपयोग की जाने वाली संख्यात्मक विधियाँ परिमित तत्व विधि (एफईएम), परिमित आयतन विधि (एफवीएम) और परिमित अंतर विधि (एफडीएम) हैं, साथ ही अन्य प्रकार की विधियाँ जिन्हें मेशफ्री विधियाँ कहा जाता है, जो उन समस्याओं को हल करने के लिए बनाई गई थीं जहाँ उपरोक्त तरीके सीमित हैं। इन विधियों में FEM का एक प्रमुख स्थान है और विशेष रूप से इसके असाधारण कुशल उच्च-क्रम संस्करण एचपी-एफईएम। एफईएम और मेशफ्री विधियों के अन्य संकर संस्करणों में सामान्यीकृत परिमित तत्व विधि (जीएफएम), विस्तारित परिमित तत्व विधि (एक्सएफईएम), वर्णक्रमीय परिमित तत्व विधि (एसएफईएम), मेशफ्री परिमित तत्व विधि, असतत गैलेरकिन परिमित तत्व विधि (डीजीएफईएम), तत्व- शामिल हैं। फ्री गैलेरकिन मेथड (ईएफजीएम), इंटरपोलिंग एलिमेंट-फ्री गैलेर्किन मेथड (आईईएफजीएम), आदि।

परिमित तत्व विधि

परिमित तत्व विधि (एफईएम) (इसका व्यावहारिक अनुप्रयोग प्रायः परिमित तत्व विश्लेषण (एफईए) के रूप में जाना जाता है) आंशिक अंतर समीकरणों (पीडीई) के साथ-साथ अभिन्न समीकरणों के अनुमानित समाधान खोजने के लिए एक संख्यात्मक तकनीक है।^[10]^[11] समाधान दृष्टिकोण या तो अंतर समीकरण को पूरी तरह से समाप्त करने (स्थिर स्थिति की समस्याओं) पर आधारित है, या पीडीई को सामान्य अंतर समीकरणों की अनुमानित प्रणाली में प्रस्तुत करना है, जो तब मानक तकनीकों जैसे यूलर की विधि, रनगे-कुट्टा, आदि का उपयोग करके संख्यात्मक रूप से एकीकृत होते हैं।

परिमित अंतर विधि

परिमित-अंतर विधियाँ अनुमानित डेरिवेटिव के लिए परिमित-अंतर समीकरणों का उपयोग करते हुए अवकल समीकरणों के समाधान का अनुमान लगाने के लिए संख्यात्मक विधियाँ हैं।

परिमित आयतन विधि

परिमित अंतर विधि या परिमित तत्व विधि के समान, मानों की गणना मेश्ड ज्यामिति पर अलग-अलग स्थानों पर की जाती है। "परिमित मात्रा" एक जाल पर प्रत्येक नोड बिंदु के आसपास की छोटी मात्रा को संदर्भित करता है। परिमित आयतन विधि में, विचलन प्रमेय का उपयोग करते हुए, एक आंशिक अंतर समीकरण में सतह समाकलन जिसमें एक विचलन शब्द होता है, आयतन समाकलन में परिवर्तित हो जाता है। इन शर्तों का मूल्यांकन प्रत्येक परिमित मात्रा की सतहों पर प्रवाह के रूप में किया जाता है। चूँकि किसी दिए गए आयतन में प्रवेश करने वाला प्रवाह आसन्न आयतन को छोड़ने के समान है, इसलिए ये विधियाँ डिज़ाइन द्वारा द्रव्यमान का संरक्षण करती हैं।

यह भी देखें

कुछ सामान्य पीडीई

ऊष्मा समीकरण
तरंग समीकरण
लाप्लास का समीकरण
हेल्महोल्ट्ज़ समीकरण
क्लेन-गॉर्डन समीकरण
पॉसों का समीकरण
नेवियर-स्टोक्स समीकरण
बर्गर समीकरण

सीमा की स्थिति के प्रकार

विभिन्न विषय

↑ Klainerman, Sergiu (2010). "PDE as a Unified Subject". In Alon, N.; Bourgain, J.; Connes, A.; Gromov, M.; Milman, V. (eds.). गणित में दर्शन. Modern Birkhäuser Classics. Basel: Birkhäuser. pp. 279–315. doi:10.1007/978-3-0346-0422-2_10. ISBN 978-3-0346-0421-5.
↑ Gustafsson, Bertil (2008). टाइम डिपेंडेंट पीडीई के लिए हाई ऑर्डर डिफरेंस मेथड्स. Springer Series in Computational Mathematics. Vol. 38. Springer. doi:10.1007/978-3-540-74993-6. ISBN 978-3-540-74992-9.
↑ Klainerman, Sergiu (2008), "Partial Differential Equations", in Gowers, Timothy; Barrow-Green, June; Leader, Imre (eds.), The Princeton Companion to Mathematics, Princeton University Press, pp. 455–483
↑ Courant and Hilbert (1962), p.182.
↑ Gershenfeld, Neil (2000). गणितीय मॉडलिंग की प्रकृति (Reprinted (with corr.) ed.). Cambridge: Cambridge Univ. Press. p. 27. ISBN 0521570956.
↑ Wilmott, Paul; Howison, Sam; Dewynne, Jeff (1995). वित्तीय डेरिवेटिव का गणित. Cambridge University Press. pp. 76–81. ISBN 0-521-49789-2.
↑ Logan, J. David (1994). "First Order Equations and Characteristics". अरैखिक आंशिक विभेदक समीकरणों का परिचय. New York: John Wiley & Sons. pp. 51–79. ISBN 0-471-59916-6.
↑ Adomian, G. (1994). भौतिकी की सीमांत समस्याओं का समाधान: अपघटन विधि. Kluwer Academic Publishers. ISBN 9789401582896.
↑ Liao, S.J. (2003), Beyond Perturbation: Introduction to the Homotopy Analysis Method, Boca Raton: Chapman & Hall/ CRC Press, ISBN 1-58488-407-X
↑ Solin, P. (2005), Partial Differential Equations and the Finite Element Method, Hoboken, NJ: J. Wiley & Sons, ISBN 0-471-72070-4
↑ Solin, P.; Segeth, K. & Dolezel, I. (2003), Higher-Order Finite Element Methods, Boca Raton: Chapman & Hall/CRC Press, ISBN 1-58488-438-X

संदर्भ

Courant, R. & Hilbert, D. (1962), Methods of Mathematical Physics, vol. II, New York: Wiley-Interscience, ISBN 9783527617241.
Evans, L. C. (1998), Partial Differential Equations, Providence: American Mathematical Society, ISBN 0-8218-0772-2.
Drábek, Pavel; Holubová, Gabriela (2007). Elements of partial differential equations (Online ed.). Berlin: de Gruyter. ISBN 9783110191240.
Ibragimov, Nail H. (1993), CRC Handbook of Lie Group Analysis of Differential Equations Vol. 1-3, Providence: CRC-Press, ISBN 0-8493-4488-3.
John, F. (1982), Partial Differential Equations (4th ed.), New York: Springer-Verlag, ISBN 0-387-90609-6.
Jost, J. (2002), Partial Differential Equations, New York: Springer-Verlag, ISBN 0-387-95428-7.
Olver, P.J. (1995), Equivalence, Invariants and Symmetry, Cambridge Press.
Petrovskii, I. G. (1967), Partial Differential Equations, Philadelphia: W. B. Saunders Co..
Pinchover, Y. & Rubinstein, J. (2005), An Introduction to Partial Differential Equations, New York: Cambridge University Press, ISBN 0-521-84886-5.
Polyanin, A. D. (2002), Handbook of Linear Partial Differential Equations for Engineers and Scientists, Boca Raton: Chapman & Hall/CRC Press, ISBN 1-58488-299-9.
Polyanin, A. D. & Zaitsev, V. F. (2004), Handbook of Nonlinear Partial Differential Equations, Boca Raton: Chapman & Hall/CRC Press, ISBN 1-58488-355-3.
Polyanin, A. D.; Zaitsev, V. F. & Moussiaux, A. (2002), Handbook of First Order Partial Differential Equations, London: Taylor & Francis, ISBN 0-415-27267-X.
Roubíček, T. (2013), Nonlinear Partial Differential Equations with Applications (PDF), International Series of Numerical Mathematics, vol. 153 (2nd ed.), Basel, Boston, Berlin: Birkhäuser, doi:10.1007/978-3-0348-0513-1, ISBN 978-3-0348-0512-4, MR 3014456
Stephani, H. (1989), MacCallum, M. (ed.), Differential Equations: Their Solution Using Symmetries, Cambridge University Press.
Wazwaz, Abdul-Majid (2009). Partial Differential Equations and Solitary Waves Theory. Higher Education Press. ISBN 978-3-642-00251-9.
Wazwaz, Abdul-Majid (2002). Partial Differential Equations Methods and Applications. A.A. Balkema. ISBN 90-5809-369-7.
Zwillinger, D. (1997), Handbook of Differential Equations (3rd ed.), Boston: Academic Press, ISBN 0-12-784395-7.
Gershenfeld, N. (1999), The Nature of Mathematical Modeling (1st ed.), New York: Cambridge University Press, New York, NY, USA, ISBN 0-521-57095-6.
Krasil'shchik, I.S. & Vinogradov, A.M., Eds. (1999), Symmetries and Conserwation Laws for Differential Equations of Mathematical Physics, American Mathematical Society, Providence, Rhode Island, USA, ISBN 0-8218-0958-X{{citation}}: CS1 maint: multiple names: authors list (link).
Krasil'shchik, I.S.; Lychagin, V.V. & Vinogradov, A.M. (1986), Geometry of Jet Spaces and Nonlinear Partial Differential Equations, Gordon and Breach Science Publishers, New York, London, Paris, Montreux, Tokyo, ISBN 2-88124-051-8.
Vinogradov, A.M. (2001), Cohomological Analysis of Partial Differential Equations and Secondary Calculus, American Mathematical Society, Providence, Rhode Island, USA, ISBN 0-8218-2922-X.
Gustafsson, Bertil (2008). High Order Difference Methods for Time Dependent PDE. Springer Series in Computational Mathematics. Vol. 38. Springer. doi:10.1007/978-3-540-74993-6. ISBN 978-3-540-74992-9.

अग्रिम पठन

Cajori, Florian (1928). "The Early History of Partial Differential Equations and of Partial Differentiation and Integration" (PDF). The American Mathematical Monthly. 35 (9): 459–467. doi:10.2307/2298771. JSTOR 2298771. Archived from the original (PDF) on 2018-11-23. Retrieved 2016-05-15.
Nirenberg, Louis (1994). "Partial differential equations in the first half of the century." Development of mathematics 1900–1950 (Luxembourg, 1992), 479–515, Birkhäuser, Basel.
Brezis, Haïm; Browder, Felix (1998). "Partial Differential Equations in the 20th Century". Advances in Mathematics. 135 (1): 76–144. doi:10.1006/aima.1997.1713.

बाहरी कड़ियाँ

"Differential equation, partial", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
Partial Differential Equations: Exact Solutions at EqWorld: The World of Mathematical Equations.
Partial Differential Equations: Index at EqWorld: The World of Mathematical Equations.
Partial Differential Equations: Methods at EqWorld: The World of Mathematical Equations.
Example problems with solutions at exampleproblems.com
Partial Differential Equations at mathworld.wolfram.com
Partial Differential Equations with Mathematica
Partial Differential Equations in Cleve Moler: Numerical Computing with MATLAB
Partial Differential Equations at nag.com
Sanderson, Grant (April 21, 2019). "But what is a partial differential equation?". 3Blue1Brown. Archived from the original on 2021-11-02 – via YouTube.

श्रेणी:बहुभिन्नरूपी कलन श्रेणी:गणितीय भौतिकी

श्रेणी:अवकल समीकरण

[1] Klainerman, Sergiu (2010). "PDE as a Unified Subject". In Alon, N.; Bourgain, J.; Connes, A.; Gromov, M.; Milman, V. (eds.). गणित में दर्शन. Modern Birkhäuser Classics. Basel: Birkhäuser. pp. 279–315. doi:10.1007/978-3-0346-0422-2_10. ISBN 978-3-0346-0421-5.

[2] Gustafsson, Bertil (2008). टाइम डिपेंडेंट पीडीई के लिए हाई ऑर्डर डिफरेंस मेथड्स. Springer Series in Computational Mathematics. Vol. 38. Springer. doi:10.1007/978-3-540-74993-6. ISBN 978-3-540-74992-9.

[PrincetonCompanion-3] Klainerman, Sergiu (2008), "Partial Differential Equations", in Gowers, Timothy; Barrow-Green, June; Leader, Imre (eds.), The Princeton Companion to Mathematics, Princeton University Press, pp. 455–483

[4] Courant and Hilbert (1962), p.182.

[5] Gershenfeld, Neil (2000). गणितीय मॉडलिंग की प्रकृति (Reprinted (with corr.) ed.). Cambridge: Cambridge Univ. Press. p. 27. ISBN 0521570956.

[6] Wilmott, Paul; Howison, Sam; Dewynne, Jeff (1995). वित्तीय डेरिवेटिव का गणित. Cambridge University Press. pp. 76–81. ISBN 0-521-49789-2.

[7] Logan, J. David (1994). "First Order Equations and Characteristics". अरैखिक आंशिक विभेदक समीकरणों का परिचय. New York: John Wiley & Sons. pp. 51–79. ISBN 0-471-59916-6.

[8] Adomian, G. (1994). भौतिकी की सीमांत समस्याओं का समाधान: अपघटन विधि. Kluwer Academic Publishers. ISBN 9789401582896.

[9] Liao, S.J. (2003), Beyond Perturbation: Introduction to the Homotopy Analysis Method, Boca Raton: Chapman & Hall/ CRC Press, ISBN 1-58488-407-X

[10] Solin, P. (2005), Partial Differential Equations and the Finite Element Method, Hoboken, NJ: J. Wiley & Sons, ISBN 0-471-72070-4

[11] Solin, P.; Segeth, K. & Dolezel, I. (2003), Higher-Order Finite Element Methods, Boca Raton: Chapman & Hall/CRC Press, ISBN 1-58488-438-X

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

v t e गणितीय विश्लेषण में प्रमुख विषय
'पथरी' : एकीकरण भेदभाव अंतर समीकरण साधारण आंशिक स्टोचस्टिक कैलकुलस का मौलिक प्रमेय भिन्नता का पथरी वेक्टर कैलकुलस टेंसर कैलकुलस मैट्रिक्स कैलकुलस अभिन्न की सूची डेरिवेटिव की तालिका
वास्तविक विश्लेषण जटिल विश्लेषण हाइपरकम्प्लेक्स विश्लेषण (चतुर्भुज विश्लेषण) कार्यात्मक विश्लेषण फूरियर विश्लेषण सबसे कम-वर्ग वर्णक्रमीय विश्लेषण हार्मोनिक विश्लेषण पी-एडिक विश्लेषण (पी-एडिक नंबर) माप सिद्धांत प्रतिनिधित्व सिद्धांत कार्य निरंतर कार्य विशेष कार्य सीमा श्रृंखला अनंतता
' गणित पोर्टल' '

@@ Line 1: / Line 1: @@
 {{short description|Type of differential equation}}
 {{Differential equations}}
-[[File:Heat.gif|thumb|ऊर्ध्वाधर दिशा और रंग द्वारा दर्शाए गए तापमान के साथ द्वि-आयामी [[ ताप समीकरण ]] के समाधान का एक दृश्य।]]गणित में, एक आंशिक अवकल समीकरण (पीडीई) एक समीकरण है जो एक बहुविकल्पीय फलन के विभिन्न आंशिक डेरिवेटिव (व्युत्पन्न) के बीच संबंध स्थापित करता है।
+[[File:Heat.gif|thumb|ऊर्ध्वाधर दिशा और रंग द्वारा दर्शाए गए तापमान के साथ द्वि-आयामी [[ ताप समीकरण ]] के समाधान का एक दृश्य।]]गणित में, '''आंशिक अवकल समीकरण''' (पीडीई) एक समीकरण है जो बहुविकल्पीय फलन के विभिन्न आंशिक डेरिवेटिव (व्युत्पन्न) के बीच संबंध स्थापित करता है।
-फ़ंक्शन को अक्सर एक "अज्ञात" के रूप में माना जाता है जिसे हल किया जाना है, इसी तरह x को बीजगणितीय समीकरण जैसे {{math|1=''x''<sup>2</sup> − 3''x'' + 2 = 0}} में हल करने के लिए एक अज्ञात संख्या के रूप में कैसे सोचा जाता है। हालांकि, यह आमतौर पर असंभव है आंशिक अवकल समीकरणों के हल के लिए स्पष्ट सूत्र लिखने के लिए। तदनुसार, कंप्यूटर का उपयोग करके कुछ आंशिक अंतर समीकरणों के संख्यात्मक रूप से अनुमानित समाधानों के तरीकों पर आधुनिक गणितीय और वैज्ञानिक अनुसंधान की एक बड़ी मात्रा है। आंशिक अवकल समीकरण भी [[ शुद्ध गणित |शुद्ध गणितीय]] अनुसंधान के एक बड़े क्षेत्र पर कब्जा कर लेते हैं, जिसमें सामान्य प्रश्न, मोटे तौर पर बोलते हैं, विभिन्न आंशिक अंतर समीकरणों के समाधान की सामान्य गुणात्मक विशेषताओं की पहचान पर, जैसे कि अस्तित्व, विशिष्टता, नियमितता और स्थिरता।{{Citation needed|date=September 2020}} कई खुले प्रश्नों में नेवियर-स्टोक्स समीकरणों के समाधान की मौजूदगी और सुगमता है, जिसे 2000 में मिलेनियम पुरस्कार समस्याओं में से एक के रूप में नामित किया गया था।
+फ़ंक्शन को प्रायः एक "अज्ञात" के रूप में माना जाता है जिसे हल किया जाना है, इसी तरह x को बीजगणितीय समीकरण जैसे {{math|1=''x''<sup>2</sup> − 3''x'' + 2 = 0}} में हल करने के लिए एक अज्ञात संख्या के रूप में कैसे सोचा जाता है। हालांकि, आंशिक अंतर समीकरणों के समाधान के लिए स्पष्ट सूत्रों को लिखना असंभव है। तदनुसार, कंप्यूटर का उपयोग करके कुछ आंशिक अंतर समीकरणों के संख्यात्मक रूप से अनुमानित समाधानों के तरीकों पर आधुनिक गणितीय और वैज्ञानिक अनुसंधान की एक बड़ी मात्रा है। आंशिक अवकल समीकरण भी [[ शुद्ध गणित |शुद्ध गणितीय]] अनुसंधान के एक बड़े क्षेत्र पर कब्जा कर लेते हैं, जिसमें सामान्य प्रश्न, मोटे तौर पर बोलते हैं, विभिन्न आंशिक अंतर समीकरणों के समाधान की सामान्य गुणात्मक विशेषताओं की पहचान पर, जैसे कि अस्तित्व, विशिष्टता, नियमितता और स्थिरता। कई खुले प्रश्नों में नेवियर-स्टोक्स समीकरणों के समाधान की मौजूदगी और सुगमता है, जिसे 2000 में मिलेनियम पुरस्कार समस्याओं में से एक के रूप में नामित किया गया था।
 [[ भौतिक विज्ञान |भौतिक विज्ञान]] और [[ अभियांत्रिकी |अभियांत्रिकी]] जैसे गणितीय रूप से उन्मुख वैज्ञानिक क्षेत्रों में आंशिक अंतर समीकरण सर्वव्यापी हैं। उदाहरण के लिए, वे ध्वनि, ऊष्मा, [[ प्रसार |प्रसार]], [[ इलेक्ट्रोस्टाटिक्स |इलेक्ट्रोस्टैटिक्स]], इलेक्ट्रोडायनामिक्स, [[ ऊष्मप्रवैगिकी |ऊष्मप्रवैगिकी]], द्रव गतिकी, [[ लोच (भौतिकी) |लोच]], [[ सामान्य सापेक्षता |सामान्य सापेक्षता]] और [[ क्वांटम यांत्रिकी |क्वांटम यांत्रिकी]] (श्रोडिंगर समीकरण, [[ पाउली समीकरण |पाउली समीकरण]], आदि) की आधुनिक वैज्ञानिक समझ में मूलभूत हैं। वे कई शुद्ध गणितीय विचारों से भी उत्पन्न होते हैं, जैसे [[ अंतर ज्यामिति |अंतर ज्यामिति]] और विविधताओं की कलन; अन्य उल्लेखनीय अनुप्रयोगों में, वे [[ ज्यामितीय टोपोलॉजी |ज्यामितीय टोपोलॉजी]] से पॉइंकेयर अनुमान के प्रमाण में मूलभूत उपकरण हैं।
-आंशिक रूप से इस प्रकार के स्रोतों के कारण, विभिन्न प्रकार के आंशिक अंतर समीकरणों का एक विस्तृत स्पेक्ट्रम है, और उत्पन्न होने वाले कई अलग-अलग समीकरणों से निपटने के लिए विधियों का विकास किया गया है। जैसे, यह आमतौर पर स्वीकार किया जाता है कि आंशिक अवकल समीकरणों का कोई "सामान्य सिद्धांत" नहीं है, जिसमें विशेषज्ञ ज्ञान कुछ हद तक अनिवार्य रूप से अलग-अलग उपक्षेत्रों के बीच विभाजित होता है।<ref>{{cite book |authorlink=Sergiu Klainerman |last=Klainerman |first=Sergiu |year=2010 |chapter=PDE as a Unified Subject |editor-last=Alon |editor-first=N. |editor2-last=Bourgain |editor2-first=J. |editor3-last=Connes |editor3-first=A. |editor4-last=Gromov |editor4-first=M. |editor5-last=Milman |editor5-first=V. |title=गणित में दर्शन|series=Modern Birkhäuser Classics |publisher=Birkhäuser |location=Basel |pages=279–315 |isbn=978-3-0346-0421-5 |doi=10.1007/978-3-0346-0422-2_10 }}</ref>
+आंशिक रूप से इस प्रकार के स्रोतों के कारण, विभिन्न प्रकार के आंशिक अंतर समीकरणों का एक विस्तृत स्पेक्ट्रम है, और उत्पन्न होने वाले कई अलग-अलग समीकरणों से निपटने के लिए विधियों का विकास किया गया है। जैसे, यह सामान्यतः स्वीकार किया जाता है कि आंशिक अवकल समीकरणों का कोई "सामान्य सिद्धांत" नहीं है, जिसमें विशेषज्ञ ज्ञान कुछ हद तक अनिवार्य रूप से अलग-अलग उपक्षेत्रों के बीच विभाजित होता है।<ref>{{cite book |authorlink=Sergiu Klainerman |last=Klainerman |first=Sergiu |year=2010 |chapter=PDE as a Unified Subject |editor-last=Alon |editor-first=N. |editor2-last=Bourgain |editor2-first=J. |editor3-last=Connes |editor3-first=A. |editor4-last=Gromov |editor4-first=M. |editor5-last=Milman |editor5-first=V. |title=गणित में दर्शन|series=Modern Birkhäuser Classics |publisher=Birkhäuser |location=Basel |pages=279–315 |isbn=978-3-0346-0421-5 |doi=10.1007/978-3-0346-0422-2_10 }}</ref>
 साधारण अवकल समीकरण आंशिक अवकल समीकरणों का एक उपवर्ग बनाते हैं, जो एकल चर के फलनों के अनुरूप होते हैं। स्टोचैस्टिक आंशिक अंतर समीकरण और गैर-स्थानीय समीकरण, 2020 तक, "पीडीई" धारणा के विशेष रूप से व्यापक रूप से अध्ययन किए गए विस्तार हैं। अधिक शास्त्रीय विषय, जिन पर अभी भी बहुत सक्रिय शोध है, में दीर्घवृत्तक और परावर्तक आंशिक अवकल समीकरण, द्रव यांत्रिकी, [[ बोल्ट्जमैन समीकरण |बोल्ट्जमैन समीकरण]] और फैलाने वाले आंशिक अंतर समीकरण शामिल हैं।
 == परिचय ==
-एक का कहना है कि तीन चर का एक फ़ंक्शन {{math|''u''(''x'', ''y'', ''z'')}} "[[ हार्मोनिक फ़ंक्शन |हार्मोनिक]]" या "लाप्लास समीकरण का समाधान" है यदि यह स्थिति को संतुष्ट करता है।<math display="block">\frac{\partial^2u}{\partial x^2}+\frac{\partial^2u}{\partial y^2}+\frac{\partial^2u}{\partial z^2}=0.</math>चिरसम्मत [[ शास्त्रीय यांत्रिकी |यांत्रिकी]] के लिए उनकी प्रासंगिकता के कारण उन्नीसवीं शताब्दी में इस तरह के कार्यों का व्यापक रूप से अध्ययन किया गया था, उदाहरण के लिए, एक सजातीय ठोस का संतुलन तापमान वितरण एक हार्मोनिक फ़ंक्शन है। यदि स्पष्ट रूप से एक फ़ंक्शन दिया गया है, तो यह आमतौर पर यह जांचने के लिए सीधी गणना का विषय है कि यह हार्मोनिक है या नहीं। उदाहरण के लिए:<math display="block">u(x,y,z) = \frac{1}{\sqrt{x^2 - 2x + y^2 + z^2 + 1}}</math>और<math display="block">u(x,y,z) = 2x^2 - y^2 - z^2</math>जबकि दोनों हार्मोनिक हैं<math display="block">u(x,y,z)=\sin(xy)+z</math>यह आश्चर्यजनक हो सकता है कि हार्मोनिक कार्यों के दिए गए दो उदाहरण एक दूसरे से आश्चर्यजनक रूप से भिन्न रूप हैं। यह इस तथ्य का प्रतिबिंब है कि वे किसी भी तरह से लाप्लास समीकरण के "सामान्य समाधान सूत्र" के विशेष मामले नहीं हैं। यह साधारण अंतर समीकरणों (ओडीई) के मामले के विपरीत है, जो मोटे तौर पर लाप्लास समीकरण के समान है, जिसमें कई परिचयात्मक पाठ्यपुस्तकों का उद्देश्य सामान्य समाधान सूत्रों के लिए एल्गोरिदम खोजना है। लाप्लास समीकरण के लिए, बड़ी संख्या में आंशिक अवकल समीकरणों की तरह, ऐसे समाधान सूत्र मौजूद नहीं होते हैं।
+एक का कहना है कि तीन चर का एक फ़ंक्शन {{math|''u''(''x'', ''y'', ''z'')}} "[[ हार्मोनिक फ़ंक्शन |हार्मोनिक]]" या "लाप्लास समीकरण का समाधान" है यदि यह स्थिति को संतुष्ट करता है।<math display="block">\frac{\partial^2u}{\partial x^2}+\frac{\partial^2u}{\partial y^2}+\frac{\partial^2u}{\partial z^2}=0.</math>चिरसम्मत [[ शास्त्रीय यांत्रिकी |यांत्रिकी]] के लिए उनकी प्रासंगिकता के कारण उन्नीसवीं शताब्दी में इस तरह के कार्यों का व्यापक रूप से अध्ययन किया गया था, उदाहरण के लिए, एक सजातीय ठोस का संतुलन तापमान वितरण एक हार्मोनिक फ़ंक्शन है। यदि स्पष्ट रूप से एक फ़ंक्शन दिया गया है, तो यह सामान्यतः यह जांचने के लिए सीधी गणना का विषय है कि यह हार्मोनिक है या नहीं। उदाहरण के लिए:<math display="block">u(x,y,z) = \frac{1}{\sqrt{x^2 - 2x + y^2 + z^2 + 1}}</math>और<math display="block">u(x,y,z) = 2x^2 - y^2 - z^2</math>जबकि दोनों हार्मोनिक हैं<math display="block">u(x,y,z)=\sin(xy)+z</math>यह आश्चर्यजनक हो सकता है कि हार्मोनिक कार्यों के दिए गए दो उदाहरण एक दूसरे से आश्चर्यजनक रूप से भिन्न रूप हैं। यह इस तथ्य का प्रतिबिंब है कि वे किसी भी तरह से लाप्लास समीकरण के "सामान्य समाधान सूत्र" के विशेष मामले नहीं हैं। यह साधारण अंतर समीकरणों (ओडीई) के मामले के विपरीत है, जो मोटे तौर पर लाप्लास समीकरण के समान है, जिसमें कई परिचयात्मक पाठ्यपुस्तकों का उद्देश्य सामान्य समाधान सूत्रों के लिए एल्गोरिदम खोजना है। लाप्लास समीकरण के लिए, बड़ी संख्या में आंशिक अवकल समीकरणों की तरह, ऐसे समाधान सूत्र मौजूद नहीं होते हैं।
+निम्नलिखित पीडीई के मामले में इस विफलता की प्रकृति को और अधिक स्पष्ट रूप से देखा जा सकता है: दो चरों के फ़ंक्शन {{math|''v''(''x'', ''y'')}} के लिए, समीकरण पर विचार करें।<math display="block">\frac{\partial^2v}{\partial x\partial y}=0.</math>इसे प्रत्यक्ष रूप से जांचा जा सकता है कि किसी एकल-चर फलन {{mvar|f}} और {{mvar|g}} के लिए {{math|1=''v''(''x'', ''y'') = ''f''(''x'') + ''g''(''y'')}} रूप का कोई भी फलन {{mvar|v}}, इस शर्त को पूरा करेगा। यह ओडीई समाधान फ़ार्मुलों में उपलब्ध विकल्पों से कहीं अधिक है, जो आम तौर पर कुछ संख्याओं के मुक्त चयन की अनुमति देता है। पीडीई के अध्ययन में, आम तौर पर कार्यों का मुफ्त विकल्प होता है।
-निम्नलिखित पीडीई के मामले में इस विफलता की प्रकृति को और अधिक स्पष्ट रूप से देखा जा सकता है: दो चरों के फ़ंक्शन {{math|''v''(''x'', ''y'')}} के लिए, समीकरण पर विचार करें।<math display="block">\frac{\partial^2v}{\partial x\partial y}=0.</math>इसे प्रत्यक्ष रूप से जांचा जा सकता है कि किसी एकल-चर फलन {{mvar|f}} और {{mvar|g}} के लिए {{math|1=''v''(''x'', ''y'') = ''f''(''x'') + ''g''(''y'')}} रूप का कोई भी फलन {{mvar|v}}, इस शर्त को पूरा करेगा। यह ओडीई समाधान फ़ार्मुलों में उपलब्ध विकल्पों से कहीं अधिक है, जो आम तौर पर कुछ संख्याओं के मुक्त चयन की अनुमति देता है। पीडीई के अध्ययन में, आम तौर पर कार्यों का मुफ्त विकल्प होता है।
-इस पसंद की प्रकृति पीडीई से पीडीई में भिन्न होती है। किसी दिए गए समीकरण को समझने के लिए, अस्तित्व और विशिष्टता प्रमेय आमतौर पर महत्वपूर्ण संगठनात्मक सिद्धांत होते हैं। कई परिचयात्मक पाठ्यपुस्तकों में, मुक्त एवं दूरस्थ शिक्षा के लिए अस्तित्व और विशिष्टता प्रमेयों की भूमिका कुछ हद तक अपारदर्शी हो सकती है; अस्तित्व आधा आमतौर पर अनावश्यक होता है क्योंकि कोई भी प्रस्तावित समाधान सूत्र की सीधे जांच कर सकता है, जबकि विशिष्टता आधा अक्सर पृष्ठभूमि में मौजूद होती है ताकि यह सुनिश्चित किया जा सके कि प्रस्तावित समाधान सूत्र जितना संभव हो उतना सामान्य है। इसके विपरीत, पीडीई के लिए, अस्तित्व और विशिष्टता प्रमेय अक्सर एकमात्र साधन होते हैं जिसके द्वारा कोई भी विभिन्न समाधानों के ढेरों के माध्यम से नेविगेट कर सकता है। इस कारण से, विशुद्ध रूप से संख्यात्मक अनुकरण करते समय वे मौलिक भी होते हैं, क्योंकि किसी को यह समझ होनी चाहिए कि उपयोगकर्ता द्वारा कौन सा डेटा निर्धारित किया जाना है और गणना करने के लिए कंप्यूटर पर क्या छोड़ा जाना है।
+इस पसंद की प्रकृति पीडीई से पीडीई में भिन्न होती है। किसी दिए गए समीकरण को समझने के लिए, अस्तित्व और विशिष्टता प्रमेय सामान्यतः महत्वपूर्ण संगठनात्मक सिद्धांत होते हैं। कई परिचयात्मक पाठ्यपुस्तकों में, मुक्त एवं दूरस्थ शिक्षा के लिए अस्तित्व और विशिष्टता प्रमेयों की भूमिका कुछ हद तक अपारदर्शी हो सकती है; अस्तित्व आधा सामान्यतः अनावश्यक होता है क्योंकि कोई भी प्रस्तावित समाधान सूत्र की सीधे जांच कर सकता है, जबकि विशिष्टता आधा प्रायः पृष्ठभूमि में मौजूद होती है ताकि यह सुनिश्चित किया जा सके कि प्रस्तावित समाधान सूत्र जितना संभव हो उतना सामान्य है। इसके विपरीत, पीडीई के लिए, अस्तित्व और विशिष्टता प्रमेय प्रायः एकमात्र साधन होते हैं जिसके द्वारा कोई भी विभिन्न समाधानों के ढेरों के माध्यम से नेविगेट कर सकता है। इस कारण से, विशुद्ध रूप से संख्यात्मक अनुकरण करते समय वे मौलिक भी होते हैं, क्योंकि किसी को यह समझ होनी चाहिए कि उपयोगकर्ता द्वारा कौन सा डेटा निर्धारित किया जाना है और गणना करने के लिए कंप्यूटर पर क्या छोड़ा जाना है।
 इस तरह के अस्तित्व और अद्वितीयता प्रमेयों पर चर्चा करने के लिए, "अज्ञात फ़ंक्शन" के डोमेन के बारे में सटीक होना आवश्यक है। अन्यथा, केवल "दो चरों का एक कार्य" जैसे शब्दों में बोलना, परिणामों को अर्थपूर्ण रूप से तैयार करना असंभव है। अर्थात्, अज्ञात फलन के क्षेत्र को स्वयं पीडीई की संरचना के भाग के रूप में माना जाना चाहिए।
@@ Line 28: / Line 28: @@
 * यदि {{mvar|u}} {{math|'''R'''<sup>2</sup>}} पर एक फ़ंक्शन है<math display="block">\frac{\partial}{\partial x} \frac{\frac{\partial u}{\partial x}}{\sqrt{1 + \left(\frac{\partial u}{\partial x}\right)^2 + \left(\frac{\partial u}{\partial y}\right)^2}} +
 \frac{\partial}{\partial y} \frac{\frac{\partial u}{\partial y}}{\sqrt{1 + \left(\frac{\partial u}{\partial x}\right)^2 + \left(\frac{\partial u}{\partial y}\right)^2}}=0,</math> फिर संख्याएँ हैं {{mvar|a}}, {{mvar|b}}, और {{mvar|c}} साथ {{math|1=''u''(''x'', ''y'') = ''ax'' + ''by'' + ''c''}}.
-पहले के उदाहरणों के विपरीत, यह पीडीई वर्गमूलों और वर्गों के कारण अरैखिक है। एक रैखिक पीडीई एक ऐसा है कि, यदि यह सजातीय है, तो किन्हीं भी दो समाधानों का योग भी एक समाधान है, और किसी भी समाधान का कोई भी स्थिर गुणक भी एक समाधान है।
+पहले के उदाहरणों के विपरीत, यह '''पीडीई वर्गमूलों''' और वर्गों के कारण अरैखिक है। एक  '''अरैखिक पीडीई''' एक ऐसा है कि, यदि यह सजातीय है, तो किन्हीं भी दो समाधानों का योग भी एक समाधान है, और किसी भी समाधान का कोई भी स्थिर गुणक भी एक समाधान है।
 == वेल-पोसेड्नेस ==
@@ Line 47: / Line 47: @@
 === अंकन ===
-पीडीई लिखते समय, आंशिक डेरिवेटिव को सबस्क्रिप्ट का उपयोग करके निरूपित करना आम है। उदाहरण के लिए:<math display="block">u_x = \frac{\partial u}{\partial x},\quad u_{xx} = \frac{\partial^2 u}{\partial x^2},\quad u_{xy} = \frac{\partial^2 u}{\partial y\, \partial x} = \frac{\partial}{\partial y } \left(\frac{\partial u}{\partial x}\right). </math>
+पीडीई लिखते समय, आंशिक डेरिवेटिव को सबस्क्रिप्ट का उपयोग करके निरूपित करना आम है। उदाहरण के लिए:<math display="block">u_x = \frac{\partial u}{\partial x},\quad u_{xx} = \frac{\partial^2 u}{\partial x^2},\quad u_{xy} = \frac{\partial^2 u}{\partial y\, \partial x} = \frac{\partial}{\partial y } \left(\frac{\partial u}{\partial x}\right). </math>सामान्य स्थिति में कि {{mvar|u}} का एक कार्य है {{mvar|n}} चर, फिर {{math|''u''<sub>''i''</sub>}} के सापेक्ष पहले आंशिक व्युत्पन्न को दर्शाता है {{mvar|i}}-वें इनपुट, {{math|''u''<sub>''ij''</sub>}} के सापेक्ष दूसरे आंशिक व्युत्पन्न को दर्शाता है {{mvar|i}}-वें और {{mvar|j}}-वें इनपुट, और इसी तरह।
-सामान्य स्थिति में कि {{mvar|u}} का एक कार्य है {{mvar|n}} चर, फिर {{math|''u''<sub>''i''</sub>}} के सापेक्ष पहले आंशिक व्युत्पन्न को दर्शाता है {{mvar|i}}-वें इनपुट, {{math|''u''<sub>''ij''</sub>}} के सापेक्ष दूसरे आंशिक व्युत्पन्न को दर्शाता है {{mvar|i}}-वें और {{mvar|j}}-वें इनपुट, और इसी तरह।
-ग्रीक अक्षर {{math|Δ}} [[ लाप्लास ऑपरेटर ]] को दर्शाता है; यदि {{mvar|u}} का एक कार्य है {{mvar|n}} चर, फिर
+ग्रीक अक्षर {{math|Δ}} [[ लाप्लास ऑपरेटर |लाप्लास ऑपरेटर]] को दर्शाता है; यदि {{mvar|u}} का एक कार्य है {{mvar|n}} चर, फिर<math display="block">\Delta u = u_{11} + u_{22} + \cdots + u_{nn}.</math>भौतिकी साहित्य में, लाप्लास ऑपरेटर को प्रायः {{math|∇<sup>2</sup>}} द्वारा निरूपित किया जाता है; गणित साहित्य में, {{math|∇<sup>2</sup>''u''}} भी {{mvar|u}} के [[ हेसियन मैट्रिक्स |हेसियन मैट्रिक्स]] को निरूपित कर सकता है।
-<math display="block">\Delta u = u_{11} + u_{22} + \cdots + u_{nn}.</math>
-भौतिकी साहित्य में, लाप्लास संकारक को प्राय: निरूपित किया जाता है {{math|∇<sup>2</sup>}}; गणित साहित्य में, {{math|∇<sup>2</sup>''u''}} के [[ हेसियन मैट्रिक्स ]] को भी निरूपित कर सकता है {{mvar|u}}.
 === पहले क्रम के समीकरण ===
-{{main|First-order partial differential equation}}
+{{main|प्रथम-क्रम आंशिक अंतर समीकरण}}
 === रेखीय और अरेखीय समीकरण ===
 ==== रैखिक समीकरण ====
-एक PDE को रैखिक कहा जाता है यदि यह अज्ञात और इसके डेरिवेटिव में रैखिक हो। उदाहरण के लिए, एक समारोह के लिए {{mvar|u}} का {{mvar|x}} और {{mvar|y}}, एक द्वितीय कोटि रैखिक PDE रूप का है
+एक पीडीई को रैखिक कहा जाता है यदि यह अज्ञात और उसके डेरिवेटिव में रैखिक है। उदाहरण के लिए, {{mvar|x}} और {{mvar|y}} के फलन {{mvar|u}} के लिए, एक द्वितीय कोटि रैखिक पीडीई का रूप होता है<math display="block"> a_1(x,y)u_{xx} + a_2(x,y)u_{xy} + a_3(x,y)u_{yx} + a_4(x,y)u_{yy} + a_5(x,y)u_x + a_6(x,y)u_y + a_7(x,y)u = f(x,y)
-<math display="block"> a_1(x,y)u_{xx} + a_2(x,y)u_{xy} + a_3(x,y)u_{yx} + a_4(x,y)u_{yy} + a_5(x,y)u_x + a_6(x,y)u_y + a_7(x,y)u = f(x,y)
+</math>जहाँ {{math|''a<sub>i</sub>''}} और {{mvar|''f''}} केवल स्वतंत्र चरों के फलन हैं। (प्रायः मिश्रित-आंशिक डेरिवेटिव्स {{math|''u<sub>xy</sub>''}} और {{math|''u<sub>yx</sub>''}} को समान किया जाएगा, लेकिन रैखिकता की चर्चा के लिए इसकी आवश्यकता नहीं है।) यदि {{math|''a<sub>i</sub>''}} स्थिरांक हैं ({{mvar|x}} और {{mvar|y}} से स्वतंत्र) तो पीडीई को निरंतर गुणांक के साथ रैखिक कहा जाता है। यदि हर जगह {{mvar|''f''}} शून्य है तो रैखिक पीडीई समांगी है, अन्यथा यह असमघाती है। (यह [[ स्पर्शोन्मुख समरूपता |स्पर्शोन्मुख समरूपता]] से अलग है, जो पीडीई के समाधान पर गुणांक में उच्च आवृत्ति दोलनों के प्रभावों का अध्ययन करता है।)
-</math>
-कहां {{math|''a<sub>i</sub>''}} और {{mvar|''f''}} केवल स्वतंत्र चरों के कार्य हैं। (अक्सर मिश्रित-आंशिक डेरिवेटिव {{math|''u<sub>xy</sub>''}} और {{math|''u<sub>yx</sub>''}} समान होगा, लेकिन रैखिकता की चर्चा के लिए इसकी आवश्यकता नहीं है।)
-अगर {{math|''a<sub>i</sub>''}} स्थिरांक हैं (से स्वतंत्र {{mvar|x}} और {{mvar|y}}) तब PDE को अचर गुणांकों वाला रैखिक कहा जाता है। यदि {{mvar|''f''}} हर जगह शून्य है तो रैखिक पीडीई सजातीय है, अन्यथा यह विषम है। (यह [[ स्पर्शोन्मुख समरूपता ]] से अलग है, जो पीडीई के समाधान पर गुणांक में उच्च आवृत्ति दोलनों के प्रभावों का अध्ययन करता है।)
 ==== अरैखिक समीकरण ====
-तीन मुख्य प्रकार के गैर-रैखिक आंशिक अंतर समीकरण सेमीलीनियर पीडीई, क्वैसिलिनियर पीडीई और पूरी तरह से नॉनलाइनियर पीडीई हैं।
+तीन मुख्य प्रकार के अरैखिक पीडीई अर्धरेखीय पीडीई, रैखिककल्प पीडीई और पूरी तरह से अरैखिक पीडीई हैं।
-रेखीय पीडीई के निकटतम सेमिलिनियर पीडीई हैं, जहां केवल उच्चतम क्रम के डेरिवेटिव रैखिक शब्दों के रूप में दिखाई देते हैं, गुणांक के साथ जो स्वतंत्र चर के कार्य हैं। निचले क्रम के डेरिवेटिव और अज्ञात फ़ंक्शन मनमाने ढंग से प्रकट हो सकते हैं। उदाहरण के लिए, दो चरों में एक सामान्य द्वितीय कोटि अर्धरैखिक PDE है
+रेखीय पीडीई के निकटतम सेमीलीनियर (अर्धरेखीय) पीडीई हैं, जहां केवल उच्चतम क्रम के डेरिवेटिव रैखिक शब्दों के रूप में प्रकट होते हैं, गुणांक के साथ जो स्वतंत्र चर के कार्य हैं। निचले क्रम के डेरिवेटिव और अज्ञात फ़ंक्शन मनमाने ढंग से प्रकट हो सकते हैं। उदाहरण के लिए, दो चरों में एक सामान्य द्वितीय-क्रम सेमीलीनियर पीडीई है।<math display="block"> a_1(x,y)u_{xx} + a_2(x,y)u_{xy} + a_3(x,y)u_{yx} + a_4(x,y)u_{yy} + f(u_x, u_y, u, x, y) = 0 </math>क्वासिलिनियर (रैखिककल्प) पीडीई में उच्चतम क्रम डेरिवेटिव इसी प्रकार केवल रैखिक शर्तों के रूप में दिखाई देते हैं, लेकिन गुणांक के साथ संभवतः अज्ञात और निम्न-क्रम डेरिवेटिव के कार्य होते हैं:<math display="block"> a_1(u_x, u_y, u, x, y)u_{xx} + a_2(u_x, u_y, u, x, y)u_{xy} + a_3(u_x, u_y, u, x, y)u_{yx} + a_4(u_x, u_y, u, x, y)u_{yy} + f(u_x, u_y, u, x, y) = 0 </math>भौतिकी में कई मौलिक पीडीई क्वैसिलिनियर हैं, जैसे सामान्य सापेक्षता के [[ आइंस्टीन समीकरण |आइंस्टीन समीकरण]] और तरल गति का वर्णन करने वाले नेवियर-स्टोक्स समीकरण।
-<math display="block"> a_1(x,y)u_{xx} + a_2(x,y)u_{xy} + a_3(x,y)u_{yx} + a_4(x,y)u_{yy} + f(u_x, u_y, u, x, y) = 0 </math>
-क्वासिलिनियर पीडीई में उच्चतम ऑर्डर डेरिवेटिव इसी प्रकार केवल रैखिक शर्तों के रूप में दिखाई देते हैं, लेकिन गुणांक के साथ संभवतः अज्ञात और निम्न-क्रम डेरिवेटिव के कार्य होते हैं:
-<math display="block"> a_1(u_x, u_y, u, x, y)u_{xx} + a_2(u_x, u_y, u, x, y)u_{xy} + a_3(u_x, u_y, u, x, y)u_{yx} + a_4(u_x, u_y, u, x, y)u_{yy} + f(u_x, u_y, u, x, y) = 0 </math>
-भौतिकी में कई मौलिक पीडीई क्वैसिलिनियर हैं, जैसे सामान्य सापेक्षता के [[ आइंस्टीन समीकरण ]] और तरल गति का वर्णन करने वाले नेवियर-स्टोक्स समीकरण।
-किसी रैखिकता गुण के बिना पीडीई को पूरी तरह से गैर-रैखिक कहा जाता है, और एक या अधिक उच्चतम क्रम के डेरिवेटिव पर गैर-रैखिकता रखता है। एक उदाहरण Monge-Ampère समीकरण है, जो अवकल ज्यामिति में उत्पन्न होता है।<ref name="PrincetonCompanion">{{Citation|last = Klainerman|first = Sergiu|year = 2008|title =Partial Differential Equations|editor-last1 = Gowers|editor-first1 = Timothy|editor-last2 = Barrow-Green|editor-first2 = June|editor-last3 = Leader|editor-first3 = Imre|encyclopedia = The Princeton Companion to Mathematics|pages = 455–483|publisher = Princeton University Press}}</ref>
+किसी रैखिकता गुण के बिना पीडीई को पूरी तरह से गैर-रैखिक कहा जाता है और एक या अधिक उच्चतम-क्रम डेरिवेटिव पर गैर-रैखिकता रखता है। एक उदाहरण मोंज-एम्पीयर समीकरण है, जो विभेदक ज्यामिति में उत्पन्न होता है।<ref name="PrincetonCompanion">{{Citation|last = Klainerman|first = Sergiu|year = 2008|title =Partial Differential Equations|editor-last1 = Gowers|editor-first1 = Timothy|editor-last2 = Barrow-Green|editor-first2 = June|editor-last3 = Leader|editor-first3 = Imre|encyclopedia = The Princeton Companion to Mathematics|pages = 455–483|publisher = Princeton University Press}}</ref>
+=== दूसरे क्रम के रैखिक समीकरण ===
+बीसवीं शताब्दी की शुरुआत के बाद से क्रम दो के दीर्घवृत्तीय, परवलयिक और [[ अतिशयोक्तिपूर्ण आंशिक अंतर समीकरण |अतिशयोक्तिपूर्ण आंशिक]] अंतर समीकरणों का व्यापक रूप से अध्ययन किया गया है। हालाँकि, कई अन्य महत्वपूर्ण प्रकार के पीडीई हैं, जिनमें कॉर्टेवेग-डी व्रीज़ समीकरण शामिल है। यूलर-ट्रिकोमी समीकरण जैसे संकर भी हैं, जो डोमेन के विभिन्न क्षेत्रों के लिए दीर्घवृत्त से अतिपरवलयिक में भिन्न होते हैं। इन मूल प्रकारों के उच्च-क्रम पीडीई के लिए महत्वपूर्ण विस्तार भी हैं, लेकिन ऐसा ज्ञान अधिक विशिष्ट है।
+दीर्घवृत्तीय/परवलयिक/अतिशयोक्तिपूर्ण वर्गीकरण उपयुक्त प्रारंभिक और सीमा स्थितियों और समाधानों की समतलता के लिए एक मार्गदर्शक प्रदान करता है। {{math|1=''u<sub>xy</sub>'' = ''u<sub>yx</sub>''}} मानते हुए, दो स्वतंत्र चरों में सामान्य रैखिक द्वितीय-क्रम पीडीई का रूप है।
-=== दूसरे क्रम के रैखिक समीकरण ===
-अण्डाकार आंशिक अंतर समीकरण, परवलयिक आंशिक अंतर समीकरण, और [[ अतिशयोक्तिपूर्ण आंशिक अंतर समीकरण ]] क्रम दो के आंशिक अंतर समीकरणों का बीसवीं शताब्दी की शुरुआत से व्यापक रूप से अध्ययन किया गया है। हालाँकि, कई अन्य महत्वपूर्ण प्रकार के PDE हैं, जिनमें Korteweg-de Vries समीकरण शामिल है। यूलर-ट्रिकोमी समीकरण जैसे संकर भी हैं, जो डोमेन के विभिन्न क्षेत्रों के लिए अण्डाकार से अतिपरवलयिक तक भिन्न होते हैं। उच्च-क्रम पीडीई के लिए इन मूल प्रकारों के महत्वपूर्ण विस्तार भी हैं, लेकिन ऐसा ज्ञान अधिक विशिष्ट है।
-दीर्घवृत्तीय/परवलयिक/अतिशयोक्तिपूर्ण वर्गीकरण उचित प्रारंभिक और [[ सीमा मूल्य समस्या ]] और समाधानों की सहजता के लिए एक गाइड प्रदान करता है। यह मानते हुए {{math|1=''u<sub>xy</sub>'' = ''u<sub>yx</sub>''}}, दो स्वतंत्र चरों में सामान्य रेखीय द्वितीय-क्रम PDE का रूप है
 <math display="block">Au_{xx} + 2Bu_{xy} + Cu_{yy} + \cdots \mbox{(lower order terms)} = 0,</math>
-जहां गुणांक {{mvar|A}}, {{mvar|B}}, {{mvar|C}}... पर निर्भर हो सकता है {{mvar|x}} और {{mvar|y}}. यदि {{math|''A''<sup>2</sup> + ''B''<sup>2</sup> + ''C''<sup>2</sup> > 0}} के एक क्षेत्र पर {{mvar|xy}}-प्लेन, पीडीई उस क्षेत्र में दूसरे क्रम का है। यह प्रपत्र शंकु खंड के समीकरण के अनुरूप है:
-<math display="block">Ax^2 + 2Bxy + Cy^2 + \cdots = 0.</math>
-अधिक सटीक, प्रतिस्थापित करना {{math|∂<sub>''x''</sub>}} द्वारा {{mvar|X}}, और इसी तरह अन्य चर के लिए (औपचारिक रूप से यह एक [[ फूरियर रूपांतरण ]] द्वारा किया जाता है), एक स्थिर-गुणांक PDE को उसी डिग्री के बहुपद में परिवर्तित करता है, जिसमें उच्चतम डिग्री (एक [[ सजातीय बहुपद ]], यहां एक [[ द्विघात रूप ]]) की शर्तें सबसे अधिक होती हैं। वर्गीकरण के लिए महत्वपूर्ण।
-जिस तरह कोई विवेचक के आधार पर शंकु वर्गों और द्विघात रूपों को परवलयिक, अतिशयोक्तिपूर्ण और दीर्घवृत्त में वर्गीकृत करता है {{math|''B''<sup>2</sup> − 4''AC''}}, किसी दिए गए बिंदु पर दूसरे क्रम के पीडीई के लिए भी ऐसा ही किया जा सकता है। हालाँकि, PDE में विविक्तकर द्वारा दिया जाता है {{math|''B''<sup>2</sup> − ''AC''}} सम्मेलन के कारण {{mvar|xy}} टर्म जा रहा है {{math|2''B''}} इसके बजाय {{mvar|B}}; औपचारिक रूप से, विवेचक (संबंधित द्विघात रूप का) है {{math|1=(2''B'')<sup>2</sup> − 4''AC'' = 4(''B''<sup>2</sup> − ''AC'')}}, सरलता के लिए 4 के कारक के साथ हटा दिया गया।
+जहां गुणांक {{mvar|A}}, {{mvar|B}}, {{mvar|C}}... {{mvar|x}} और {{mvar|y}} पर निर्भर हो सकता है। यदि {{math|''A''<sup>2</sup> + ''B''<sup>2</sup> + ''C''<sup>2</sup> > 0}} के एक क्षेत्र पर {{mvar|xy}}-प्लेन, पीडीई उस क्षेत्र में दूसरे क्रम का है। यह प्रपत्र शंकु खंड के समीकरण के अनुरूप है:
+<math display="block">Ax^2 + 2Bxy + Cy^2 + \cdots = 0.</math>अधिक सटीक रूप से, {{math|∂<sub>''x''</sub>}} को {{mvar|X}} द्वारा प्रतिस्थापित करना, और इसी तरह अन्य चरों के लिए (औपचारिक रूप से यह एक [[ फूरियर रूपांतरण |फूरियर रूपांतरण]] द्वारा किया जाता है), एक स्थिर-गुणांक पीडीई को समान डिग्री के बहुपद में उच्चतम डिग्री (एक [[ सजातीय बहुपद |सजातीय बहुपद]]) के साथ परिवर्तित करता है। यहाँ एक [[ द्विघात रूप |द्विघात रूप]]) वर्गीकरण के लिए सर्वाधिक महत्वपूर्ण है।
-# {{math|''B''<sup>2</sup> − ''AC'' < 0}} (अण्डाकार आंशिक अंतर समीकरण): अण्डाकार आंशिक अंतर समीकरण के समाधान उतने ही चिकने होते हैं जितने कि गुणांक अनुमति देते हैं, उस क्षेत्र के आंतरिक भाग में जहाँ समीकरण और समाधान परिभाषित होते हैं। उदाहरण के लिए, लाप्लास के समीकरण के समाधान डोमेन के भीतर विश्लेषणात्मक होते हैं जहां उन्हें परिभाषित किया जाता है, लेकिन समाधान सीमा मान मान सकते हैं जो चिकनी नहीं हैं। सबसोनिक गति पर तरल पदार्थ की गति को अंडाकार पीडीई के साथ अनुमानित किया जा सकता है, और यूलर-ट्रिकोमी समीकरण अंडाकार है जहां {{math|''x'' < 0}}.
+जिस तरह विविक्तकर {{math|''B''<sup>2</sup> − 4''AC''}} के आधार पर शंक्वाकार वर्गों और द्विघात रूपों को परवलयिक, अतिशयोक्तिपूर्ण और दीर्घवृत्त में वर्गीकृत किया जाता है, उसी तरह किसी दिए गए बिंदु पर दूसरे क्रम के पीडीई के लिए भी किया जा सकता है। हालाँकि, पीडीई में विविक्तकर {{math|''B''<sup>2</sup> − ''AC''}} द्वारा दिया जाता है क्योंकि {{mvar|xy}} पद की अभ्यास {{mvar|B}} के बजाय {{math|2''B''}} है; औपचारिक रूप से, विविक्तकर (संबंधित द्विघात रूप का) {{math|1=(2''B'')<sup>2</sup> − 4''AC'' = 4(''B''<sup>2</sup> − ''AC'')}} है, जिसमें सरलता के लिए 4 का गुणनखंड हटा दिया गया है।
+# {{math|''B''<sup>2</sup> − ''AC'' < 0}} (दीर्घवृत्त आंशिक अंतर समीकरण): अण्डाकार आंशिक अंतर समीकरण के समाधान उतने ही चिकने होते हैं जितने कि गुणांक अनुमति देते हैं, उस क्षेत्र के आंतरिक भाग में जहाँ समीकरण और समाधान परिभाषित होते हैं। उदाहरण के लिए, लाप्लास के समीकरण के समाधान डोमेन के भीतर विश्लेषणात्मक होते हैं जहां उन्हें परिभाषित किया जाता है, लेकिन समाधान सीमा मान मान सकते हैं जो चिकनी नहीं हैं। सबसोनिक गति पर तरल पदार्थ की गति को दीर्घवृत्त पीडीई के साथ अनुमानित किया जा सकता है, और यूलर-ट्रिकोमी समीकरण अंडाकार है जहां {{math|''x'' < 0}}.
 # {{math|1=''B''<sup>2</sup> − ''AC'' = 0}} (परवलयिक आंशिक अंतर समीकरण): समीकरण जो हर बिंदु पर परवलयिक आंशिक अंतर समीकरण होते हैं, उन्हें स्वतंत्र चर के परिवर्तन द्वारा ताप समीकरण के अनुरूप रूप में परिवर्तित किया जा सकता है। परिवर्तित समय चर बढ़ने पर समाधान सुचारू हो जाते हैं। यूलर-ट्रिकोमी समीकरण में उस रेखा पर परवलयिक प्रकार है जहां {{math|1=''x'' = 0}}.
-# {{math|''B''<sup>2</sup> − ''AC'' > 0}} (अतिपरवलयिक आंशिक अंतर समीकरण): अतिशयोक्तिपूर्ण आंशिक अंतर समीकरण समीकरण प्रारंभिक डेटा में कार्यों या डेरिवेटिव के किसी भी विच्छिन्नता को बनाए रखते हैं। एक उदाहरण [[ तरंग समीकरण ]] है। सुपरसोनिक गति पर द्रव की गति को हाइपरबोलिक पीडीई के साथ अनुमानित किया जा सकता है, और यूलर-ट्रिकोमी समीकरण हाइपरबॉलिक है जहां {{math|''x'' > 0}}.
+# {{math|''B''<sup>2</sup> − ''AC'' > 0}} (अतिपरवलयिक आंशिक अंतर समीकरण): अतिशयोक्तिपूर्ण आंशिक अंतर समीकरण समीकरण प्रारंभिक डेटा में कार्यों या डेरिवेटिव के किसी भी विच्छिन्नता को बनाए रखते हैं। एक उदाहरण [[ तरंग समीकरण | तरंग समीकरण]]  है। सुपरसोनिक गति पर द्रव की गति को हाइपरबोलिक पीडीई के साथ अनुमानित किया जा सकता है, और यूलर-ट्रिकोमी समीकरण हाइपरबॉलिक है जहां {{math|''x'' > 0}}.
-अगर वहाँ {{mvar|n}} स्वतंत्र प्रभावित करने वाली वस्तुएँ {{math|''x''<sub>1</sub>, ''x''<sub>2 </sub>, …, ''x''<sub>''n''</sub>}}दूसरे क्रम के एक सामान्य रैखिक आंशिक अंतर समीकरण का रूप है
+अगर वहाँ {{mvar|n}} स्वतंत्र प्रभावित करने वाली वस्तुएँ {{math|''x''<sub>1</sub>, ''x''<sub>2 </sub>, …, ''x''<sub>''n''</sub>}}दूसरे क्रम के एक सामान्य रैखिक आंशिक अंतर समीकरण का रूप है<math display="block">L u =\sum_{i=1}^n\sum_{j=1}^n a_{i,j} \frac{\partial^2 u}{\partial x_i \partial x_j} \quad+ \text{lower-order terms} = 0.</math>वर्गीकरण गुणांक मैट्रिक्स के [[ eigenvalues |आइगेनवैल्यू]] के हस्ताक्षर पर निर्भर करता है {{math|''a''<sub>''i'',''j''</sub>}}.
-<math display="block">L u =\sum_{i=1}^n\sum_{j=1}^n a_{i,j} \frac{\partial^2 u}{\partial x_i \partial x_j} \quad+ \text{lower-order terms} = 0.</math>
+# दीर्घवृत्त: आइगेनवैल्यू सभी धनात्मक या सभी ऋणात्मक हैं।
-वर्गीकरण गुणांक मैट्रिक्स के [[ eigenvalues ]] के हस्ताक्षर पर निर्भर करता है {{math|''a''<sub>''i'',''j''</sub>}}.
+# परवलयिक: आइगेनवैल्यू सभी धनात्मक या सभी नकारात्मक हैं, एक को छोड़कर जो शून्य है।
+# अतिपरवलयिक: केवल एक ऋणात्मक आइगेनवैल्यू है और बाकी सभी धनात्मक हैं, या केवल एक धनात्मक आइगेनवैल्यू है और बाकी सभी ऋणात्मक हैं।
-# दीर्घवृत्त: eigenvalues सभी सकारात्मक या सभी नकारात्मक हैं।
+# अल्ट्राहाइपरबोलिक: एक से अधिक धनात्मक आइगेनवैल्यू और एक से अधिक ऋणात्मक आइगेनवैल्यू होते हैं, और कोई शून्य आइगेनवैल्यू नहीं होते हैं।<ref>Courant and Hilbert (1962), p.182.</ref>
-# परवलयिक: eigenvalues सभी सकारात्मक या सभी नकारात्मक हैं, एक को छोड़कर जो शून्य है।
+दीर्घवृत्त, परवलयिक, और अतिपरवलयिक समीकरणों के सिद्धांत का सदियों से अध्ययन किया गया है, जो काफी हद तक [[ लाप्लास समीकरण | लाप्लास समीकरण]] , ऊष्मा समीकरण और तरंग समीकरण के मानक उदाहरणों के आसपास या उसके आधार पर केंद्रित है।
-# अतिपरवलयिक: केवल एक नकारात्मक eigenvalue है और बाकी सभी सकारात्मक हैं, या केवल एक सकारात्मक eigenvalue है और बाकी सभी नकारात्मक हैं।
-# अल्ट्राहाइपरबोलिक: एक से अधिक सकारात्मक आइगेनवैल्यू और एक से अधिक नेगेटिव आइगेनवैल्यू होते हैं, और कोई शून्य आइगेनवैल्यू नहीं होते हैं।<ref>Courant and Hilbert (1962), p.182.</ref>
-अण्डाकार, परवलयिक, और अतिपरवलयिक समीकरणों के सिद्धांत का सदियों से अध्ययन किया गया है, जो काफी हद तक [[ लाप्लास समीकरण ]], ऊष्मा समीकरण और तरंग समीकरण के मानक उदाहरणों के आसपास या उसके आधार पर केंद्रित है।
 === प्रथम-क्रम समीकरणों और विशिष्ट सतहों की प्रणाली ===
-आंशिक अंतर समीकरणों के वर्गीकरण को प्रथम-क्रम समीकरणों की प्रणालियों तक विस्तारित किया जा सकता है, जहां अज्ञात {{mvar|u}} अब एक [[ यूक्लिडियन वेक्टर ]] है {{mvar|m}} घटक, और गुणांक मैट्रिसेस {{mvar|A<sub>ν</sub>}} हैं {{mvar|m}} द्वारा {{mvar|m}} के लिए मेट्रिसेस {{math|1=''ν'' = 1, 2, …, ''n''}}. आंशिक अंतर समीकरण रूप लेता है
+आंशिक अंतर समीकरणों के वर्गीकरण को प्रथम-क्रम समीकरणों की प्रणालियों तक विस्तारित किया जा सकता है, जहां अज्ञात {{mvar|u}} अब {{mvar|m}} घटकों के साथ एक वेक्टर है, और गुणांक मैट्रिसेस {{mvar|A<sub>ν</sub>}}, {{math|1=''ν'' = 1, 2, …, ''n''}} के लिए {{mvar|m}} द्वारा {{mvar|m}} मेट्रिसेस हैं। आंशिक अवकल समीकरण का रूप ले लेता है।<math display="block">Lu = \sum_{\nu=1}^{n} A_\nu \frac{\partial u}{\partial x_\nu} + B=0,</math>जहां गुणांक मेट्रिसेस {{mvar|A<sub>ν</sub>}} और वेक्टर {{mvar|B}} पर निर्भर हो सकता है {{mvar|x}} और {{mvar|u}}. यदि एक [[ ऊनविम पृष्ठ |ऊनविम पृष्ठ]] {{mvar|S}} निहित रूप में दिया गया है।<math display="block">\varphi(x_1, x_2, \ldots, x_n)=0,</math>
-<math display="block">Lu = \sum_{\nu=1}^{n} A_\nu \frac{\partial u}{\partial x_\nu} + B=0,</math>
-जहां गुणांक मेट्रिसेस {{mvar|A<sub>ν</sub>}} और वेक्टर {{mvar|B}} पर निर्भर हो सकता है {{mvar|x}} और {{mvar|u}}. यदि एक [[ ऊनविम पृष्ठ ]] {{mvar|S}} निहित रूप में दिया गया है
-<math display="block">\varphi(x_1, x_2, \ldots, x_n)=0,</math>
-कहां {{mvar|φ}} एक गैर-शून्य ढाल है, तब {{mvar|S}} ऑपरेटर के लिए एक विशिष्ट सतह है {{mvar|L}} किसी दिए गए बिंदु पर यदि विशेषता रूप गायब हो जाता है:
-<math display="block">Q\left(\frac{\partial\varphi}{\partial x_1}, \ldots, \frac{\partial\varphi}{\partial x_n}\right) = \det\left[\sum_{\nu=1}^n A_\nu \frac{\partial \varphi}{\partial x_\nu}\right] = 0.</math>
-इस स्थिति की ज्यामितीय व्याख्या इस प्रकार है: यदि डेटा के लिए {{mvar|u}} सतह पर निर्धारित हैं {{mvar|S}}, तो इसका सामान्य व्युत्पन्न निर्धारित करना संभव हो सकता है {{mvar|u}} पर {{mvar|S}} अंतर समीकरण से। यदि डेटा चालू है {{mvar|S}} और अंतर समीकरण के सामान्य व्युत्पन्न का निर्धारण करते हैं {{mvar|u}} पर {{mvar|S}}, तब {{mvar|S}} गैर-विशेषता है। यदि डेटा चालू है {{mvar|S}} और अंतर समीकरण के सामान्य व्युत्पन्न का निर्धारण नहीं करते हैं {{mvar|u}} पर {{mvar|S}}, तो सतह विशेषता है, और अंतर समीकरण डेटा को प्रतिबंधित करता है {{mvar|S}}: अंतर समीकरण आंतरिक है {{mvar|S}}.
-# एक प्रथम-क्रम प्रणाली {{math|1=''Lu'' = 0}} अण्डाकार है यदि कोई सतह विशेषता नहीं है {{mvar|L}}: के मान {{mvar|u}} पर {{mvar|S}} और अंतर समीकरण हमेशा के सामान्य व्युत्पन्न का निर्धारण करते हैं {{mvar|u}} पर {{mvar|S}}.
-# एक प्रथम-क्रम प्रणाली एक बिंदु पर अतिशयोक्तिपूर्ण है यदि कोई 'स्पेसलाइक' सतह है {{mvar|S}} सामान्य के साथ {{mvar|ξ}} उस बिंदु पर। इसका मतलब यह है कि, कोई गैर-तुच्छ वेक्टर दिया गया है {{mvar|η}} इसके लिए ऑर्थोगोनल {{mvar|ξ}}, और एक अदिश गुणक {{mvar|λ}}, समीकरण {{math|1=''Q''(''λξ'' + ''η'') = 0}} है {{mvar|m}} असली जड़ें {{math|''λ''<sub>1</sub>, ''λ''<sub>2</sub>, …, ''λ''<sub>''m''</sub>}}. अगर ये जड़ें हमेशा अलग-अलग हों तो सिस्टम सख्ती से अतिशयोक्तिपूर्ण है। इस स्थिति की ज्यामितीय व्याख्या इस प्रकार है: चारित्रिक रूप {{math|1=''Q''(''ζ'') = 0}} सजातीय निर्देशांक ζ के साथ एक शंकु (सामान्य शंकु) को परिभाषित करता है। अतिशयोक्तिपूर्ण मामले में, इस शंकु के पास है {{mvar|m}} चादरें, और अक्ष {{math|1=''ζ'' = ''λξ''}} इन शीट्स के अंदर चलता है: यह उनमें से किसी को भी काटता नहीं है। लेकिन जब η द्वारा मूल से विस्थापित किया जाता है, तो यह अक्ष प्रत्येक शीट को प्रतिच्छेद करती है। अण्डाकार मामले में, सामान्य शंकु में कोई वास्तविक चादरें नहीं होती हैं।
-<!--
-''fill in: Dirichlet and Neumann boundaries, hyperbolic/parabolic/elliptic separation of variables, [[Fourier analysis]], [[Green's function]]s ...-->
+जहां {{mvar|φ}} एक गैर-शून्य है, तब {{mvar|S}} ऑपरेटर के लिए एक विशिष्ट सतह है {{mvar|L}} किसी दिए गए बिंदु पर यदि विशेषता रूप गायब हो जाता है:
+<math display="block">Q\left(\frac{\partial\varphi}{\partial x_1}, \ldots, \frac{\partial\varphi}{\partial x_n}\right) = \det\left[\sum_{\nu=1}^n A_\nu \frac{\partial \varphi}{\partial x_\nu}\right] = 0.</math>इस स्थिति की ज्यामितीय व्याख्या इस प्रकार है: यदि {{mvar|u}} के लिए डेटा सतह {{mvar|S}} पर निर्धारित किया गया है, तो यह संभव हो सकता है कि अंतर समीकरण से {{mvar|u}} के सामान्य व्युत्पन्न को निर्धारित किया जा सके। यदि {{mvar|S}} पर डेटा और अवकल समीकरण, {{mvar|S}} पर {{mvar|u}} का सामान्य अवकलज निर्धारित करते हैं, तो {{mvar|S}} गैर-लक्षण है। यदि {{mvar|S}} पर डेटा और अंतर समीकरण {{mvar|S}} पर {{mvar|u}} के सामान्य व्युत्पन्न का निर्धारण नहीं करते हैं, तो सतह विशेषता है, और अंतर समीकरण डेटा को {{mvar|S}} पर प्रतिबंधित करता है: अंतर समीकरण {{mvar|S}} के लिए आंतरिक है।
+# एक प्रथम-क्रम प्रणाली {{math|1=''Lu'' = 0}} दीर्घवृत्तीय है यदि कोई सतह {{mvar|L}} के लिए विशेषता नहीं है: {{mvar|S}} पर {{mvar|u}} के मान और अंतर समीकरण हमेशा {{mvar|S}} पर {{mvar|u}} के सामान्य व्युत्पन्न को निर्धारित करते हैं।
+#एक प्रथम-क्रम प्रणाली एक बिंदु पर अतिशयोक्तिपूर्ण है यदि उस बिंदु पर सामान्य {{mvar|ξ}} के साथ एक अंतरिक्ष जैसी सतह {{mvar|S}} है। इसका मतलब यह है कि, किसी भी गैर-तुच्छ वेक्टर {{mvar|η}} ऑर्थोगोनल को {{mvar|ξ}}, और एक स्केलर गुणक {{mvar|λ}} दिया गया है, समीकरण ({{math|1=''Q''(''λξ'' + ''η'') = 0}} में {{mvar|m}} वास्तविक जड़ें {{math|''λ''<sub>1</sub>, ''λ''<sub>2</sub>, …, ''λ''<sub>''m''</sub>}} हैं। अगर ये जड़ें हमेशा अलग-अलग हों तो सिस्टम सख्ती से अतिशयोक्तिपूर्ण है। इस स्थिति की ज्यामितीय व्याख्या इस प्रकार है: विशेषता रूप {{math|1=''Q''(''ζ'') = 0}} सजातीय निर्देशांक ζ के साथ एक शंकु (सामान्य शंकु) को परिभाषित करता है। अतिशयोक्तिपूर्ण मामले में, इस शंकु में {{mvar|m}} शीट हैं, और अक्ष {{math|1=''ζ'' = ''λξ''}} इन शीटों के अंदर चलता है: यह उनमें से किसी को नहीं काटता है। लेकिन जब η द्वारा मूल से विस्थापित किया जाता है, तो यह अक्ष प्रत्येक शीट को प्रतिच्छेद करती है। दीर्घवृत्तीय मामले में, सामान्य शंकु में कोई वास्तविक शीट नहीं होती है।
 == विश्लेषणात्मक समाधान ==
 === चरों का पृथक्करण ===
-{{main|Separable partial differential equation}}
+{{main|वियोज्य आंशिक अंतर समीकरण}}
-चरों को अलग करने की महत्वपूर्ण तकनीक द्वारा रेखीय पीडीई को साधारण अंतर समीकरणों की प्रणालियों में घटाया जा सकता है। यह तकनीक अंतर समीकरणों के समाधान की एक विशेषता पर टिकी हुई है: यदि कोई ऐसा समाधान ढूंढ सकता है जो समीकरण को हल करता है और सीमा शर्तों को संतुष्ट करता है, तो यह समाधान है (यह ओडीई पर भी लागू होता है)। हम एक [[ ansatz ]] के रूप में मानते हैं कि मापदंडों के स्थान और समय पर एक समाधान की निर्भरता को उन शब्दों के उत्पाद के रूप में लिखा जा सकता है जो प्रत्येक एक पैरामीटर पर निर्भर करते हैं, और फिर देखें कि क्या समस्या को हल करने के लिए इसे बनाया जा सकता है।<ref>{{cite book |last1=Gershenfeld |first1=Neil |title=गणितीय मॉडलिंग की प्रकृति|url=https://archive.org/details/naturemathematic00gers_334 |url-access=limited|date=2000|publisher=Cambridge Univ. Press|location=Cambridge|isbn=0521570956|page=[https://archive.org/details/naturemathematic00gers_334/page/n32 27]|edition=Reprinted (with corr.)}}</ref>
+चरों को अलग करने की महत्वपूर्ण तकनीक द्वारा रेखीय पीडीई को साधारण अंतर समीकरणों की प्रणालियों में घटाया जा सकता है। यह तकनीक अंतर समीकरणों के समाधान की एक विशेषता पर टिकी हुई है: यदि कोई ऐसा समाधान ढूंढ सकता है जो समीकरण को हल करता है और सीमा शर्तों को संतुष्ट करता है, तो यह समाधान है (यह ओडीई पर भी लागू होता है)। हम एक [[ ansatz |ansatz]] के रूप में मानते हैं कि पैरामीटर स्थान और समय पर एक समाधान की निर्भरता को उन शर्तों के उत्पाद के रूप में लिखा जा सकता है जो प्रत्येक एक पैरामीटर पर निर्भर करते हैं, और फिर देखते हैं कि समस्या को हल करने के लिए इसे बनाया जा सकता है या नहीं।<ref>{{cite book |last1=Gershenfeld |first1=Neil |title=गणितीय मॉडलिंग की प्रकृति|url=https://archive.org/details/naturemathematic00gers_334 |url-access=limited|date=2000|publisher=Cambridge Univ. Press|location=Cambridge|isbn=0521570956|page=[https://archive.org/details/naturemathematic00gers_334/page/n32 27]|edition=Reprinted (with corr.)}}</ref>
-चरों को अलग करने की विधि में, कम चरों में एक PDE को एक PDE में घटाया जाता है, जो एक सामान्य अंतर समीकरण है यदि एक चर में - इन्हें हल करना आसान होता है।
+चरों को अलग करने की विधि में, कम चरों में एक पीडीई को एक पीडीई में घटाया जाता है, जो एक सामान्य अंतर समीकरण है यदि एक चर में - इन्हें हल करना आसान होता है।
-यह सरल पीडीई के लिए संभव है, जिसे [[ वियोज्य आंशिक अंतर समीकरण ]] कहा जाता है, और डोमेन आम तौर पर एक आयत (अंतराल का एक उत्पाद) होता है। वियोज्य पीडीई विकर्ण मैट्रिसेस के अनुरूप हैं - निश्चित के लिए मान के बारे में सोच रहे हैं {{mvar|x}}एक निर्देशांक के रूप में, प्रत्येक निर्देशांक को अलग से समझा जा सकता है।
+यह सरल पीडीई के लिए संभव है, जिसे [[ वियोज्य आंशिक अंतर समीकरण |वियोज्य आंशिक अंतर समीकरण]] कहा जाता है, और डोमेन आम तौर पर एक आयत (अंतराल का एक उत्पाद) होता है। वियोज्य पीडीई विकर्ण मैट्रिसेस के अनुरूप हैं - एक समन्वय के रूप में "निश्चित x के मान" के बारे में सोचते हुए, प्रत्येक निर्देशांक को अलग से समझा जा सकता है।
-यह [[ विशेषताओं की विधि ]] का सामान्यीकरण करता है, और इसका उपयोग [[ अभिन्न परिवर्तन ]]ों में भी किया जाता है।
+यह [[ विशेषताओं की विधि |विशेषताओं की विधि]] का सामान्यीकरण करता है और इसका उपयोग [[ अभिन्न परिवर्तन |अभिन्न]] परिवर्तनों में भी किया जाता है।
-=== विशेषताओं की विधि ===
+=== विशेषताओं का तरीका ===
-{{main|Method of characteristics}}
+{{main|विशेषताओं का तरीका}}
-विशेष मामलों में, कोई विशेषता वक्र पा सकता है जिस पर समीकरण एक ODE में कम हो जाता है - इन वक्रों को सीधा करने के लिए डोमेन में बदलते निर्देशांक चर को अलग करने की अनुमति देते हैं, और इसे विशेषताओं की विधि कहा जाता है।
-अधिक आम तौर पर, किसी को विशिष्ट सतहें मिल सकती हैं। दूसरे क्रम के आंशिक अंतर समीकरण समाधान के लिए, चार्पिट विधि देखें।
+विशेष मामलों में, कोई विशेषता वक्र पा सकता है जिस पर समीकरण ओडीई में कम हो जाता है - इन वक्रों को सीधा करने के लिए डोमेन में बदलते निर्देशांक चर के पृथक्करण की अनुमति देते हैं और इसे विशेषताओं की विधि कहा जाता है।
+अधिक आम तौर पर, किसी को विशिष्ट सतहें मिल सकती हैं। द्वितीय कोटि के आंशिक अवकल समीकरण हल के लिए, चार्पिट विधि देखें।
 === इंटीग्रल ट्रांसफॉर्म ===
-एक अभिन्न परिवर्तन पीडीई को एक सरल रूप में बदल सकता है, विशेष रूप से एक वियोज्य पीडीई। यह एक ऑपरेटर को विकर्ण करने से मेल खाता है।
+एक अभिन्न परिवर्तन पीडीई को एक सरल रूप में बदल सकता है, विशेष रूप से एक वियोज्य पीडीई। यह एक ऑपरेटर को विकर्णित करने के अनुरूप है।
-इसका एक महत्वपूर्ण उदाहरण [[ फूरियर विश्लेषण ]] है, जो साइनसोइडल तरंगों के [[ खुद का आधार ]] का उपयोग करके गर्मी समीकरण को विकर्ण करता है।
+इसका एक महत्वपूर्ण उदाहरण [[ फूरियर विश्लेषण |फूरियर विश्लेषण]] है, जो साइनसोइडल तरंगों के ईजेनबेसिस का उपयोग करके गर्मी समीकरण को विकर्णित करता है।
-यदि डोमेन परिमित या आवधिक है, तो फूरियर श्रृंखला जैसे समाधानों का एक अनंत योग उपयुक्त है, लेकिन [[ फूरियर अभिन्न ]] जैसे समाधानों का एक अभिन्न अंग आमतौर पर अनंत डोमेन के लिए आवश्यक होता है। ऊपर दिए गए ऊष्मा समीकरण के लिए बिंदु स्रोत का समाधान फूरियर इंटीग्रल के उपयोग का एक उदाहरण है।
+यदि डोमेन परिमित या आवधिक है, तो फूरियर श्रृंखला जैसे समाधानों का एक अनंत योग उपयुक्त है, लेकिन [[ फूरियर अभिन्न |फूरियर अभिन्न]] जैसे समाधानों का एक अभिन्न अंग सामान्यतः अनंत डोमेन के लिए आवश्यक है। ऊपर दिए गए ताप समीकरण के लिए एक बिंदु स्रोत का समाधान फूरियर इंटीग्रल के उपयोग का एक उदाहरण है।
 === चर का परिवर्तन ===
-अक्सर एक पीडीई को एक उपयुक्त चर परिवर्तन (पीडीई) द्वारा ज्ञात समाधान के साथ एक सरल रूप में कम किया जा सकता है। उदाहरण के लिए, ब्लैक-स्कोल्स समीकरण
+चरों के उपयुक्त परिवर्तन द्वारा प्रायः पीडीई को ज्ञात समाधान के साथ सरल रूप में कम किया जा सकता है। उदाहरण के लिए, ब्लैक-स्कोल्स समीकरण<math display="block"> \frac{\partial V}{\partial t} + \tfrac{1}{2} \sigma^2 S^2 \frac{\partial^2 V}{\partial S^2} + rS \frac{\partial V}{\partial S} - rV = 0 </math>ऊष्मा समीकरण के लिए कम करने योग्य है।<math display="block"> \frac{\partial u}{\partial \tau} = \frac{\partial^2 u}{\partial x^2}</math>चर के परिवर्तन से<ref>{{cite book |first1=Paul |last1=Wilmott |first2=Sam |last2=Howison |first3=Jeff |last3=Dewynne |title=वित्तीय डेरिवेटिव का गणित|location= |publisher=Cambridge University Press |year=1995 |isbn=0-521-49789-2 |pages=76–81 |url=https://www.google.com/books/edition/The_Mathematics_of_Financial_Derivatives/VYVhnC3fIVEC?hl=en&gbpv=1&pg=PA76 }}</ref><math display="block">\begin{align}
-<math display="block"> \frac{\partial V}{\partial t} + \tfrac{1}{2} \sigma^2 S^2 \frac{\partial^2 V}{\partial S^2} + rS \frac{\partial V}{\partial S} - rV = 0 </math>
-ऊष्मा समीकरण के लिए कम करने योग्य है
-<math display="block"> \frac{\partial u}{\partial \tau} = \frac{\partial^2 u}{\partial x^2}</math>
-चर के परिवर्तन से<ref>{{cite book |first1=Paul |last1=Wilmott |first2=Sam |last2=Howison |first3=Jeff |last3=Dewynne |title=वित्तीय डेरिवेटिव का गणित|location= |publisher=Cambridge University Press |year=1995 |isbn=0-521-49789-2 |pages=76–81 |url=https://www.google.com/books/edition/The_Mathematics_of_Financial_Derivatives/VYVhnC3fIVEC?hl=en&gbpv=1&pg=PA76 }}</ref>
-<math display="block">\begin{align}
 V(S,t) &= v(x,\tau),\\[5px]
 x &= \ln\left(S \right),\\[5px]
@@ Line 159: / Line 131: @@
 \end{align}</math>
+=== मौलिक समाधान ===
+{{main|मौलिक समाधान}}
-=== मूल समाधान ===
+[[ मौलिक समाधान |मौलिक समाधान]] (एक बिंदु स्रोत के लिए समाधान) को खोजने के द्वारा अमानवीय समीकरणों को प्रायः हल किया जा सकता है (निरंतर गुणांक पीडीई के लिए, हमेशा हल किया जाता है), फिर समाधान प्राप्त करने के लिए सीमा शर्तों के साथ संवलयी होता है।
-{{main|Fundamental solution}}
-विषम समीकरण{{clarification needed|date=July 2020}} [[ मौलिक समाधान ]] (बिंदु स्रोत के लिए समाधान) ढूंढकर अक्सर हल किया जा सकता है (निरंतर गुणांक पीडीई के लिए, हमेशा हल किया जाता है), फिर समाधान प्राप्त करने के लिए सीमा शर्तों के साथ दृढ़ संकल्प लेना।
-यह [[ संकेत प्रसंस्करण ]] में एक फिल्टर को उसकी [[ आवेग प्रतिक्रिया ]] द्वारा समझने के अनुरूप है।
+यह सिग्नल प्रोसेसिंग में एक फिल्टर को उसकी [[ आवेग प्रतिक्रिया |आवेग प्रतिक्रिया]] द्वारा समझने के अनुरूप है।
 === सुपरपोजिशन सिद्धांत ===
-{{further| Superposition principle }}
+{{further|सुपरपोजिशन सिद्धांत}}
-सुपरपोज़िशन सिद्धांत पीडीई के रैखिक सिस्टम सहित किसी भी रैखिक प्रणाली पर लागू होता है। इस अवधारणा का एक सामान्य दृश्य उदाहरण के लिए, अधिक आयाम में परिणाम के लिए चरण में दो तरंगों की बातचीत को संयुक्त किया जा रहा है {{math|1=sin ''x'' + sin ''x'' = 2 sin ''x''}}. पीडीई में समान सिद्धांत देखा जा सकता है जहां समाधान वास्तविक या जटिल और योगात्मक हो सकते हैं। यदि {{math|''u''<sub>1</sub>}} और {{math|''u''<sub>2</sub>}} कुछ कार्य स्थान में रैखिक पीडीई के समाधान हैं {{mvar|R}}, तब {{math|1=''u'' = ''c''<sub>1</sub>''u''<sub>1</sub> + ''c''<sub>2</sub>''u''<sub>2</sub>}} किसी स्थिरांक के साथ {{math|''c''<sub>1</sub>}} और {{math|''c''<sub>2</sub>}} उसी कार्य स्थान में उस PDE का एक समाधान भी हैं।
+सुपरपोज़िशन सिद्धांत पीडीई के रैखिक सिस्टम सहित किसी भी रैखिक प्रणाली पर लागू होता है। इस अवधारणा का एक सामान्य दृश्य चरण में दो तरंगों की परस्पर क्रिया है, जिसके परिणामस्वरूप एक बड़ा आयाम होता है, उदाहरण के लिए, {{math|1=sin ''x'' + sin ''x'' = 2 sin ''x''}} पीडीई में समान सिद्धांत देखा जा सकता है जहां समाधान वास्तविक या जटिल और योगात्मक हो सकते हैं। यदि {{math|''u''<sub>1</sub>}} और {{math|''u''<sub>2</sub>}} किसी फंक्शन स्पेस {{mvar|R}} में रैखिक पीडीई के समाधान हैं, तो {{math|1=''u'' = ''c''<sub>1</sub>''u''<sub>1</sub> + ''c''<sub>2</sub>''u''<sub>2</sub>}} किसी भी स्थिरांक {{math|''c''<sub>1</sub>}}और {{math|''c''<sub>2</sub>}} के साथ भी उसी फ़ंक्शन स्पेस में उस पीडीई का एक समाधान है।
 === गैर-रैखिक समीकरणों के लिए तरीके ===
-{{see also|nonlinear partial differential equation}}
+{{see also|अरेखीय आंशिक अवकल समीकरण}}
-अरैखिक पीडीई को हल करने के लिए आम तौर पर लागू होने वाली कोई विधि नहीं है। फिर भी, अस्तित्व और अद्वितीयता के परिणाम (जैसे कॉची-कोवलेव्स्की प्रमेय) अक्सर संभव होते हैं, जैसा कि समाधान के महत्वपूर्ण गुणात्मक और मात्रात्मक गुणों के प्रमाण हैं (इन परिणामों को प्राप्त करना [[ गणितीय विश्लेषण ]] का एक प्रमुख हिस्सा है)। गैर-रैखिक पीडीई के लिए कम्प्यूटेशनल समाधान, विभाजन-चरण विधि, गैर-रैखिक श्रोडिंगर समीकरण जैसे विशिष्ट समीकरणों के लिए मौजूद है।
+अरेखीय पीडीई को हल करने के लिए आम तौर पर लागू होने वाली कोई विधियाँ नहीं हैं। फिर भी, अस्तित्व और अद्वितीयता के परिणाम (जैसे कॉची-कोवालेव्स्की प्रमेय) प्रायः संभव होते हैं, जैसा कि समाधानों के महत्वपूर्ण गुणात्मक और मात्रात्मक गुणों के प्रमाण हैं (इन परिणामों को प्राप्त करना [[ गणितीय विश्लेषण |विश्लेषण]] का एक प्रमुख हिस्सा है)। गैर-रैखिक पीडीई के लिए कम्प्यूटेशनल समाधान, विभाजन-चरण विधि, गैर-रैखिक श्रोडिंगर समीकरण जैसे विशिष्ट समीकरणों के लिए मौजूद है।
+फिर भी, कुछ तकनीकों का प्रयोग अनेक प्रकार के समीकरणों के लिए किया जा सकता है। अनिर्धारित समीकरणों को हल करने के लिए {{mvar|h}}-सिद्धांत सबसे शक्तिशाली तरीका है। कई विश्लेषणात्मक [[ अतिनिर्धारित प्रणाली |अतिनिर्धारित]] प्रणालियों के बारे में जानकारी प्राप्त करने के लिए रिक्वायर-जेनेट सिद्धांत एक प्रभावी तरीका है।
-फिर भी, कुछ तकनीकों का उपयोग कई प्रकार के समीकरणों के लिए किया जा सकता है। एच-सिद्धांत |{{mvar|h}}-अंडरसेटिन सिस्टम समीकरणों को हल करने के लिए सिद्धांत सबसे शक्तिशाली तरीका है। कई विश्लेषणात्मक [[ अतिनिर्धारित प्रणाली ]] प्रणालियों के बारे में जानकारी प्राप्त करने के लिए रिक्वायर-जेनेट सिद्धांत एक प्रभावी तरीका है।
+विशेषताओं की विधि का उपयोग कुछ विशेष मामलों में अरैखिक आंशिक अवकल समीकरणों को हल करने के लिए किया जा सकता है।<ref>{{cite book |first=J. David |last=Logan |title=अरैखिक आंशिक विभेदक समीकरणों का परिचय|location=New York |publisher=John Wiley & Sons |year=1994 |isbn=0-471-59916-6 |chapter=First Order Equations and Characteristics |pages=51–79 }}</ref>
-विशेषताओं की विधि का उपयोग कुछ विशेष मामलों में गैर-रैखिक आंशिक अंतर समीकरणों को हल करने के लिए किया जा सकता है।<ref>{{cite book |first=J. David |last=Logan |title=अरैखिक आंशिक विभेदक समीकरणों का परिचय|location=New York |publisher=John Wiley & Sons |year=1994 |isbn=0-471-59916-6 |chapter=First Order Equations and Characteristics |pages=51–79 }}</ref>
+कुछ मामलों में, पीडीई को गड़बड़ी विश्लेषण के माध्यम से हल किया जा सकता है जिसमें समाधान को ज्ञात समाधान के साथ समीकरण में सुधार माना जाता है। विकल्प [[ संख्यात्मक विश्लेषण |संख्यात्मक विश्लेषण]] तकनीक हैं जो साधारण [[ परिमित अंतर |परिमित अंतर]] योजनाओं से लेकर अधिक परिपक्व मल्टीग्रिड और परिमित तत्व विधियों तक हैं। [[ कंप्यूटर |कंप्यूटर]], कभी-कभी उच्च-प्रदर्शन वाले [[ सुपर कंप्यूटर |सुपर कंप्यूटर]] का उपयोग करके विज्ञान और इंजीनियरिंग की कई दिलचस्प समस्याओं को इस तरह से हल किया जाता है।
-कुछ मामलों में, पीडीई को [[ गड़बड़ी विश्लेषण ]] के माध्यम से हल किया जा सकता है जिसमें समाधान को ज्ञात समाधान के साथ समीकरण में सुधार माना जाता है। विकल्प [[ संख्यात्मक विश्लेषण ]] तकनीक हैं जो साधारण [[ परिमित अंतर ]] योजनाओं से लेकर अधिक परिपक्व [[ multigrid ]] और परिमित तत्व विधियों तक हैं। [[ कंप्यूटर ]], कभी-कभी उच्च प्रदर्शन वाले [[ सुपर कंप्यूटर ]] का उपयोग करके विज्ञान और इंजीनियरिंग की कई दिलचस्प समस्याओं को इस तरह हल किया जाता है।
-=== [[ झूठ समूह ]] विधि ===
+=== लाई ग्रुप विधि ===
-से [[ सोफस झूठ ]] के काम ने अंतर समीकरणों के सिद्धांत को अधिक संतोषजनक आधार पर रखा। उन्होंने दिखाया कि पुराने गणितज्ञों के एकीकरण सिद्धांतों को, जिसे अब झूठ समूह कहा जाता है, एक सामान्य स्रोत के रूप में संदर्भित किया जा सकता है; और वह साधारण अवकल समीकरण जो समान [[ अतिसूक्ष्म परिवर्तन ]]ों को स्वीकार करते हैं, एकीकरण की तुलनात्मक कठिनाइयाँ प्रस्तुत करते हैं। उन्होंने [[ संपर्क परिवर्तन ]] के विषय पर भी जोर दिया।
+में सोफस ली के कार्य ने अवकल समीकरणों के सिद्धांत को एक अधिक संतोषजनक आधार पर रखा। उन्होंने दिखाया कि पुराने गणितज्ञों के एकीकरण सिद्धांतों को, जिसे अब लाई समूह कहा जाता है, एक सामान्य स्रोत के रूप में संदर्भित किया जा सकता है; और वह साधारण अवकल समीकरण जो समान अतिसूक्ष्म परिवर्तनों को स्वीकार करते हैं, एकीकरण की तुलनात्मक कठिनाइयाँ प्रस्तुत करते हैं। उन्होंने संपर्क के परिवर्तन के विषय पर भी जोर दिया।
-पीडीई को हल करने के लिए एक सामान्य दृष्टिकोण अंतर समीकरणों की समरूपता संपत्ति का उपयोग करता है, समाधानों के समाधान के निरंतर अत्यल्प रूपांतरण (झूठे सिद्धांत)। सतत [[ समूह सिद्धांत ]], लाई बीजगणित और अंतर ज्यामिति का उपयोग एकीकृत समीकरणों को उत्पन्न करने के लिए रैखिक और गैर-रैखिक आंशिक अंतर समीकरणों की संरचना को समझने के लिए किया जाता है, इसके लक्स जोड़े, रिकर्सन ऑपरेटरों, बैकलंड ट्रांसफॉर्म को खोजने और अंत में पीडीई के लिए सटीक विश्लेषणात्मक समाधान खोजने के लिए।
+पीडीई को हल करने के लिए एक सामान्य दृष्टिकोण अंतर समीकरणों की समरूपता संपत्ति का उपयोग करता है, समाधानों के समाधान के निरंतर अत्यल्प रूपांतरण (लाई सिद्धांत)। निरंतर [[ समूह सिद्धांत |समूह सिद्धांत]], ले बीजगणित और अंतर ज्यामिति का उपयोग पूर्णांक समीकरणों को उत्पन्न करने के लिए रैखिक और गैर-रैखिक आंशिक अंतर समीकरणों की संरचना को समझने के लिए किया जाता है, इसके लक्स जोड़े, पुनरावर्तन संचालकों को खोजने के लिए, बैकलंड रूपांतरण (Bäcklund transform) और अंत में पीडीई के लिए सटीक विश्लेषणात्मक समाधान ढूंढते हैं।
-गणित, भौतिकी, इंजीनियरिंग और कई अन्य विषयों में उत्पन्न होने वाले अंतर समीकरणों का अध्ययन करने के लिए समरूपता विधियों को मान्यता दी गई है।
+गणित, भौतिकी, इंजीनियरिंग और कई अन्य विषयों में उत्पन्न होने वाले विभेदक समीकरणों का अध्ययन करने के लिए सममिति विधियों को मान्यता दी गई है।
 === अर्धविश्लेषणात्मक तरीके ===
-[[ एडोमियन अपघटन विधि ]],<ref>{{cite book |title=भौतिकी की सीमांत समस्याओं का समाधान: अपघटन विधि|first=G. |last=Adomian|author-link=George Adomian|publisher=Kluwer Academic Publishers |year=1994 |isbn=9789401582896 |url=https://books.google.com/books?id=UKPqCAAAQBAJ&q=%22partial+differential%22}}</ref> एलेक्जेंडर लायपुनोव कृत्रिम छोटे पैरामीटर विधि, और उनकी [[ होमोटॉपी गड़बड़ी विधि ]] सभी अधिक सामान्य होमोटोपी विश्लेषण पद्धति के विशेष मामले हैं।<ref>{{Citation | last=Liao | first=S.J. |author-link=Liao Shijun| title=Beyond Perturbation: Introduction to the Homotopy Analysis Method | publisher=Chapman & Hall/ CRC Press | location=Boca Raton | year=2003 | isbn=1-58488-407-X }}</ref> ये श्रृंखला विस्तार विधियां हैं, और लायपुनोव विधि को छोड़कर, प्रसिद्ध [[ गड़बड़ी सिद्धांत ]] की तुलना में छोटे भौतिक मापदंडों से स्वतंत्र हैं, इस प्रकार इन विधियों को अधिक लचीलापन और समाधान व्यापकता प्रदान करते हैं।
+[[ एडोमियन अपघटन विधि |एडोमियन अपघटन विधि]],<ref>{{cite book |title=भौतिकी की सीमांत समस्याओं का समाधान: अपघटन विधि|first=G. |last=Adomian|author-link=George Adomian|publisher=Kluwer Academic Publishers |year=1994 |isbn=9789401582896 |url=https://books.google.com/books?id=UKPqCAAAQBAJ&q=%22partial+differential%22}}</ref> लायपुनोव कृत्रिम छोटे पैरामीटर विधि, और उनकी [[ होमोटॉपी गड़बड़ी विधि |होमोटॉपी क्षोभ विधि]] सभी अधिक सामान्य समरूपता विश्लेषण पद्धति के विशेष मामले हैं।<ref>{{Citation | last=Liao | first=S.J. |author-link=Liao Shijun| title=Beyond Perturbation: Introduction to the Homotopy Analysis Method | publisher=Chapman & Hall/ CRC Press | location=Boca Raton | year=2003 | isbn=1-58488-407-X }}</ref> ये श्रृंखला विस्तार के तरीके हैं, और लायपुनोव विधि को छोड़कर, प्रसिद्ध [[ गड़बड़ी सिद्धांत |गड़बड़ी सिद्धांत]] की तुलना में छोटे भौतिक मापदंडों से स्वतंत्र हैं, इस प्रकार इन तरीकों को अधिक लचीलापन और समाधान व्यापकता प्रदान करते हैं।
 == संख्यात्मक समाधान ==
-{{main|Numerical solutions of partial differential equations}}
+{{main|आंशिक अवकल समीकरणों के संख्यात्मक हल}}
-तीन सबसे व्यापक रूप से उपयोग किए जाने वाले [[ संख्यात्मक आंशिक अंतर समीकरण ]] परिमित तत्व विश्लेषण (FEM), परिमित आयतन विधियाँ (FVM) और [[ परिमित अंतर विधि ]]याँ (FDM) हैं, साथ ही अन्य प्रकार की विधियाँ जिन्हें मेशफ्री विधियाँ कहा जाता है, जो उन समस्याओं को हल करने के लिए बनाई गई थीं जहाँ उपरोक्त तरीके सीमित हैं। इन विधियों में FEM का एक प्रमुख स्थान है और विशेष रूप से इसके असाधारण कुशल उच्च-क्रम संस्करण [[ hp-FEM ]]। FEM और मेशफ्री विधियों के अन्य संकर संस्करणों में सामान्यीकृत परिमित तत्व विधि (GFEM), [[ विस्तारित परिमित तत्व विधि ]] (XFEM), [[ वर्णक्रमीय तत्व विधि ]] (SFEM), मेशफ्री विधियाँ, असंतुलित गैलेर्किन विधि (DGFEM), [[ तत्व-मुक्त गैलेर्किन विधि ]] (EFGM) शामिल हैं। ), [[ इंटरपोलिंग एलिमेंट-फ्री गैलेर्किन विधि ]] (IEFGM), आदि।
+पीडीई को हल करने के लिए तीन सबसे व्यापक रूप से उपयोग की जाने वाली [[ संख्यात्मक आंशिक अंतर समीकरण |संख्यात्मक]] विधियाँ परिमित तत्व विधि (एफईएम), परिमित आयतन विधि (एफवीएम) और [[ परिमित अंतर विधि |परिमित अंतर विधि]] (एफडीएम) हैं, साथ ही अन्य प्रकार की विधियाँ जिन्हें मेशफ्री विधियाँ कहा जाता है, जो उन समस्याओं को हल करने के लिए बनाई गई थीं जहाँ उपरोक्त तरीके सीमित हैं। इन विधियों में FEM का एक प्रमुख स्थान है और विशेष रूप से इसके असाधारण कुशल उच्च-क्रम संस्करण एचपी-एफईएम। एफईएम और मेशफ्री विधियों के अन्य संकर संस्करणों में सामान्यीकृत परिमित तत्व विधि (जीएफएम), [[ विस्तारित परिमित तत्व विधि |विस्तारित परिमित तत्व विधि]] (एक्सएफईएम), [[ वर्णक्रमीय तत्व विधि |वर्णक्रमीय]] परिमित तत्व विधि (एसएफईएम), मेशफ्री परिमित तत्व विधि, असतत गैलेरकिन परिमित तत्व विधि (डीजीएफईएम), तत्व- शामिल हैं। फ्री गैलेरकिन मेथड (ईएफजीएम), इंटरपोलिंग एलिमेंट-फ्री गैलेर्किन मेथड (आईईएफजीएम), आदि।
 === परिमित तत्व विधि ===
-{{main|Finite element method}}
+{{main|परिमित तत्व विधि}}
-परिमित तत्व विधि (एफईएम) (इसका व्यावहारिक अनुप्रयोग अक्सर परिमित तत्व विश्लेषण (एफईए) के रूप में जाना जाता है) आंशिक अंतर समीकरणों (पीडीई) के साथ-साथ अभिन्न समीकरणों के अनुमानित समाधान खोजने के लिए एक संख्यात्मक तकनीक है।<ref>{{Citation |first=P. |last=Solin |title=Partial Differential Equations and the Finite Element Method |publisher=J. Wiley & Sons |location=Hoboken, NJ |year=2005 |isbn=0-471-72070-4 }}</ref><ref>{{Citation |first1=P. |last1=Solin |first2=K. |last2=Segeth |name-list-style=amp |first3=I. |last3=Dolezel |title=Higher-Order Finite Element Methods |publisher=Chapman & Hall/CRC Press |location=Boca Raton |year=2003 |isbn=1-58488-438-X }}</ref> समाधान दृष्टिकोण या तो अंतर समीकरण को पूरी तरह से समाप्त करने (स्थिर स्थिति की समस्याओं) पर आधारित है, या पीडीई को साधारण अंतर समीकरणों की अनुमानित प्रणाली में प्रस्तुत करना है, जो तब यूलर की विधि, रनगे-कुट्टा, आदि जैसी मानक तकनीकों का उपयोग करके संख्यात्मक रूप से एकीकृत होते हैं।
+परिमित तत्व विधि (एफईएम) (इसका व्यावहारिक अनुप्रयोग प्रायः परिमित तत्व विश्लेषण (एफईए) के रूप में जाना जाता है) आंशिक अंतर समीकरणों (पीडीई) के साथ-साथ अभिन्न समीकरणों के अनुमानित समाधान खोजने के लिए एक संख्यात्मक तकनीक है।<ref>{{Citation |first=P. |last=Solin |title=Partial Differential Equations and the Finite Element Method |publisher=J. Wiley & Sons |location=Hoboken, NJ |year=2005 |isbn=0-471-72070-4 }}</ref><ref>{{Citation |first1=P. |last1=Solin |first2=K. |last2=Segeth |name-list-style=amp |first3=I. |last3=Dolezel |title=Higher-Order Finite Element Methods |publisher=Chapman & Hall/CRC Press |location=Boca Raton |year=2003 |isbn=1-58488-438-X }}</ref> समाधान दृष्टिकोण या तो अंतर समीकरण को पूरी तरह से समाप्त करने (स्थिर स्थिति की समस्याओं) पर आधारित है, या पीडीई को सामान्य अंतर समीकरणों की अनुमानित प्रणाली में प्रस्तुत करना है, जो तब मानक तकनीकों जैसे यूलर की विधि, रनगे-कुट्टा, आदि का उपयोग करके संख्यात्मक रूप से एकीकृत होते हैं।
 === परिमित अंतर विधि ===
-{{main|Finite difference method}}
+{{main|परिमित अंतर विधि}}
-परिमित-अंतर विधियाँ अवकल समीकरणों के समाधान का अनुमान लगाने के लिए संख्यात्मक विधियाँ हैं जो परिमित अंतर समीकरणों का उपयोग अनुमानित डेरिवेटिव के लिए करती हैं।
-=== परिमित मात्रा विधि ===
+परिमित-अंतर विधियाँ अनुमानित डेरिवेटिव के लिए परिमित-अंतर समीकरणों का उपयोग करते हुए अवकल समीकरणों के समाधान का अनुमान लगाने के लिए संख्यात्मक विधियाँ हैं।
-{{main|Finite volume method}}
-परिमित अंतर विधि या परिमित तत्व विधि के समान, मानों की गणना जालीदार ज्यामिति पर असतत स्थानों पर की जाती है। परिमित मात्रा जाल पर प्रत्येक नोड बिंदु के आस-पास की छोटी मात्रा को संदर्भित करती है। परिमित आयतन विधि में, [[ विचलन प्रमेय ]] का उपयोग करते हुए, एक आंशिक अंतर समीकरण में सतह अभिन्न, जिसमें एक विचलन शब्द होता है, मात्रा अभिन्न में परिवर्तित हो जाते हैं। इन शर्तों का मूल्यांकन तब प्रत्येक परिमित मात्रा की सतहों पर फ्लक्स के रूप में किया जाता है। क्योंकि किसी दिए गए आयतन में प्रवेश करने वाला प्रवाह आसन्न आयतन को छोड़ने के समान है, ये विधियाँ डिज़ाइन द्वारा द्रव्यमान का संरक्षण करती हैं।
+=== परिमित आयतन विधि ===
+{{main|परिमित आयतन विधि}}
+परिमित अंतर विधि या परिमित तत्व विधि के समान, मानों की गणना मेश्ड ज्यामिति पर अलग-अलग स्थानों पर की जाती है। "परिमित मात्रा" एक जाल पर प्रत्येक नोड बिंदु के आसपास की छोटी मात्रा को संदर्भित करता है। परिमित आयतन विधि में, [[ विचलन प्रमेय |विचलन प्रमेय]] का उपयोग करते हुए, एक आंशिक अंतर समीकरण में सतह समाकलन जिसमें एक विचलन शब्द होता है, आयतन समाकलन में परिवर्तित हो जाता है। इन शर्तों का मूल्यांकन प्रत्येक परिमित मात्रा की सतहों पर प्रवाह के रूप में किया जाता है। चूँकि किसी दिए गए आयतन में प्रवेश करने वाला प्रवाह आसन्न आयतन को छोड़ने के समान है, इसलिए ये विधियाँ डिज़ाइन द्वारा द्रव्यमान का संरक्षण करती हैं।
 == यह भी देखें ==
@@ Line 213: / Line 191: @@
 * क्लेन-गॉर्डन समीकरण
 * पॉसों का समीकरण
-* नेवियर-स्टोक्स समीकरण | नेवियर-स्टोक्स समीकरण
+* नेवियर-स्टोक्स समीकरण
-* बर्गर का समीकरण
+* बर्गर समीकरण
-सीमा शर्तों के प्रकार
+सीमा की स्थिति के प्रकार
-* डिरिचलेट सीमा स्थिति
+* डिरिक्लेट सीमा स्थिति
 * [[ न्यूमैन सीमा की स्थिति ]]
 * [[ रॉबिन सीमा की स्थिति ]]
 * [[ कॉची समस्या ]]
-कई विषय
+विभिन्न विषय
 * [[ जेट बंडल ]]
-* [[ लाप्लास परिवर्तन अंतर समीकरणों पर लागू होता है ]]
+* [[ लाप्लास परिवर्तन अंतर समीकरणों पर लागू होता है |लाप्लास रूपांतरण अवकल समीकरणों पर लागू होता है]]
-* [[ डायनेमिक सिस्टम और डिफरेंशियल इक्वेशन विषयों की सूची ]]
+* [[ डायनेमिक सिस्टम और डिफरेंशियल इक्वेशन विषयों की सूची |गतिशील प्रणालियों और अवकल समीकरण विषयों की सूची]]
 * [[ मैट्रिक्स अंतर समीकरण ]]
-* संख्यात्मक आंशिक अंतर समीकरण
+* संख्यात्मक आंशिक अवकल समीकरण
-* [[ आंशिक अंतर बीजगणितीय समीकरण ]]
+* [[ आंशिक अंतर बीजगणितीय समीकरण |आंशिक अवकल बीजीय समीकरण]]
 * [[ पुनरावृत्ति संबंध ]]
 * [[ स्टोकेस्टिक प्रक्रियाएं और सीमा मूल्य समस्याएं ]]
@@ Line 232: / Line 210: @@
 ==टिप्पणियाँ==
 {{Reflist}}
 == संदर्भ ==
 {{refbegin|2}}
@@ Line 259: / Line 235: @@
 * {{cite book |title=High Order Difference Methods for Time Dependent PDE|first=Bertil |last=Gustafsson|series=Springer Series in Computational Mathematics|author-link=Bertil Gustafsson |publisher=Springer |year=2008 |volume=38 |isbn=978-3-540-74992-9 |doi=10.1007/978-3-540-74993-6}}
 {{refend}}
+== अग्रिम पठन ==
-== आगे की पढाई ==
 * {{Cite journal|last=Cajori|first=Florian|author-link=Florian Cajori|year=1928|title=The Early History of Partial Differential Equations and of Partial Differentiation and Integration|url=http://www.math.harvard.edu/archive/21a_fall_14/exhibits/cajori/cajori.pdf|journal=The American Mathematical Monthly|volume=35|issue=9|pages=459–467|doi=10.2307/2298771|jstor=2298771|access-date=2016-05-15|archive-url=https://web.archive.org/web/20181123102253/http://www.math.harvard.edu/archive/21a_fall_14/exhibits/cajori/cajori.pdf|archive-date=2018-11-23|url-status=dead}}
 * [[Louis Nirenberg|Nirenberg, Louis]] (1994). "Partial differential equations in the first half of the century." Development of mathematics 1900–1950 (Luxembourg, 1992), 479–515, Birkhäuser, Basel.
@@ Line 274: / Line 248: @@
 | pages=76–144
 | doi=10.1006/aima.1997.1713 | doi-access=free}}
 *
@@ Line 294: / Line 266: @@
 {{Analysis-footer}}
 {{Authority control}}
-[[श्रेणी:आंशिक अवकल समीकरण| ]]
+[[श्रेणी:आंशिक अवकल समीकरण| ]][[श्रेणी:बहुभिन्नरूपी कलन]]
-[[श्रेणी:बहुभिन्नरूपी कलन]]
 [[श्रेणी:गणितीय भौतिकी]]
 [[श्रेणी:विभेदक समीकरण|श्रेणी:अवकल समीकरण]]
+[[Category:Articles with hatnote templates targeting a nonexistent page]]
-[[Category: Machine Translated Page]]
+[[Category:Collapse templates]]
 [[Category:Created On 27/12/2022]]
+[[Category:Interwiki link templates| ]]
+[[Category:Lua-based templates]]
+[[Category:Machine Translated Page]]
+[[Category:Mathematics navigational boxes]]
+[[Category:Navigational boxes| ]]
+[[Category:Navigational boxes without horizontal lists]]
+[[Category:Pages with script errors]]
+[[Category:Short description with empty Wikidata description]]
+[[Category:Sidebars with styles needing conversion]]
+[[Category:Template documentation pages|Documentation/doc]]
+[[Category:Templates Translated in Hindi]]
+[[Category:Templates Vigyan Ready]]
+[[Category:Templates generating microformats]]
+[[Category:Templates that add a tracking category]]
+[[Category:Templates that are not mobile friendly]]
+[[Category:Templates that generate short descriptions]]
+[[Category:Templates using TemplateData]]
+[[Category:Templates using under-protected Lua modules]]
+[[Category:Wikipedia fully protected templates|Sister project links]]
+[[Category:Wikipedia metatemplates]]

Anonymous

Search