विशेष सापेक्षता: Difference between revisions
No edit summary |
|||
| (14 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
{{short description|Theory of interwoven space and time by Albert Einstein}} | {{short description|Theory of interwoven space and time by Albert Einstein}} | ||
[[File:Einstein patentoffice.jpg|thumb|260px|1905 के | [[File:Einstein patentoffice.jpg|thumb|260px|1905 के करीब [[ अल्बर्ट आइंस्टीन ]], जिस वर्ष उनके एनस मिराबिलिस पेपर प्रकाशित हुए थे। इनमें गतिमान पिंडों के विद्युतगतिकी पर सम्मिलित हैं<!-- ("On the Electrodynamics of Moving Bodies")-->, विशेष सापेक्षता की स्थापना करने वाला पेपर।]] | ||
{{Special relativity sidebar}} | {{Special relativity sidebar}} | ||
भौतिक विज्ञान में, सापेक्षता का विशेष सिद्धांत, या संक्षेप में विशेष सापेक्षता, अंतरिक्ष और समय के बीच संबंध में एक वैज्ञानिक सिद्धांत है। अल्बर्ट आइंस्टीन के मूल उपचार में | भौतिक विज्ञान में, सापेक्षता का विशेष सिद्धांत, या संक्षेप में विशेष सापेक्षता, अंतरिक्ष और समय के बीच संबंध में एक वैज्ञानिक सिद्धांत है। अल्बर्ट आइंस्टीन के मूल उपचार में दिया गया सिद्धांत दो अभिधारणाओं पर आधारित है:<ref name="electro" group="p"/><ref name = ":0">{{Cite book | last = Griffiths | first = David J. | title = Introduction to Electrodynamics | title-link = Introduction to Electrodynamics | publisher = Pearson | year = 2013 | isbn = 978-0-321-85656-2 | edition = 4th | at = Chapter 12 | chapter = Electrodynamics and Relativity | author-link = David J. Griffiths}}</ref><ref name = ":1">{{Cite book | last = Jackson | first = John D. | title = Classical Electrodynamics | title-link = Classical Electrodynamics (book) | publisher = John Wiley & Sons, Inc. | year = 1999 | isbn = 0-471-30932-X | edition = 3rd | at = Chapter 11 |chapter = Special Theory of Relativity | author-link = John David Jackson (physicist)}}</ref> | ||
# संदर्भ के सभी जड़त्वीय | # संदर्भ के सभी जड़त्वीय सीमा रेखा(अर्थात, बिना किसी [[ त्वरण | त्वरण]] के संदर्भ के सीमा रेखा) में [[ भौतिकी के नियम ]][[ अपरिवर्तनीय (भौतिकी) |अपरिवर्तनीय (भौतिकी)]] (अर्थात समान) हैं। | ||
# निर्वात में प्रकाश की गति सभी प्रेक्षकों के लिए समान होती है, चाहे प्रकाश स्रोत या प्रेक्षक की गति कुछ भी हो। | # निर्वात में प्रकाश की गति सभी प्रेक्षकों के लिए समान होती है, चाहे प्रकाश स्रोत या प्रेक्षक की गति कुछ भी हो। | ||
== मूल और महत्व == | == मूल और महत्व == | ||
{{Main| | {{Main|विशेष सापेक्षता का इतिहास}} | ||
विशेष सापेक्षता मूल रूप से अल्बर्ट आइंस्टीन द्वारा 26 सितंबर 1905 को "विद्युतगतिकी पर गतिमान पिंड" शीर्षक से प्रकाशित एक पेपर में प्रस्तावित की गई थी।<ref name="electro" group="p">[[Albert Einstein]] (1905) "[https://web.archive.org/web/20050220050316/http://www.pro-physik.de/Phy/pdfs/ger_890_921.pdf ''Zur Elektrodynamik bewegter Körper'']", ''Annalen der Physik'' 17: 891; English translation [http://www.fourmilab.ch/etexts/einstein/specrel/www/ On the Electrodynamics of Moving Bodies] by [[George Barker Jeffery]] and Wilfrid Perrett (1923); Another English translation [[s:On the Electrodynamics of Moving Bodies|On the Electrodynamics of Moving Bodies]] by [[Megh Nad Saha]] (1920).</ref> मैक्सवेल के विद्युत चुंबकत्व के समीकरणों के साथ [[ न्यूटनियन यांत्रिकी ]] असंगति और, प्रयोगात्मक रूप से, माइकलसन-मॉर्ले नल परिणाम (और बाद में इसी तरह के प्रयोगों) ने प्रदर्शित किया कि ऐतिहासिक रूप से परिकल्पित [[ चमकदार ईथर ]] | विशेष सापेक्षता मूल रूप से अल्बर्ट आइंस्टीन द्वारा 26 सितंबर 1905 को "विद्युतगतिकी पर गतिमान पिंड" शीर्षक से प्रकाशित एक पेपर में प्रस्तावित की गई थी।<ref name="electro" group="p">[[Albert Einstein]] (1905) "[https://web.archive.org/web/20050220050316/http://www.pro-physik.de/Phy/pdfs/ger_890_921.pdf ''Zur Elektrodynamik bewegter Körper'']", ''Annalen der Physik'' 17: 891; English translation [http://www.fourmilab.ch/etexts/einstein/specrel/www/ On the Electrodynamics of Moving Bodies] by [[George Barker Jeffery]] and Wilfrid Perrett (1923); Another English translation [[s:On the Electrodynamics of Moving Bodies|On the Electrodynamics of Moving Bodies]] by [[Megh Nad Saha]] (1920).</ref> मैक्सवेल के विद्युत चुंबकत्व के समीकरणों के साथ [[ न्यूटनियन यांत्रिकी | न्यूटनियन यांत्रिकी]] असंगति और, प्रयोगात्मक रूप से, माइकलसन-मॉर्ले नल परिणाम(और बाद में इसी तरह के प्रयोगों) ने प्रदर्शित किया कि ऐतिहासिक रूप से परिकल्पित [[ चमकदार ईथर | प्रकाशवाही ईथर]] उपलब्ध नहीं था। इसने आइंस्टीन के विशेष सापेक्षता के विकास को जन्म दिया, जो सभी गतियों को सम्मिलित करने वाली स्थितियों को संभालने के लिए यांत्रिकी को विनिर्मित करता है और विशेष रूप से प्रकाश की गति के निकटतम गति पर(जिसे {{vanchor|आपेक्षित वेग|आपेक्षित वेग}} के नाम से जाना जाता है) आज, विशेष सापेक्षता किसी भी गति से गति का सबसे सटीक मॉडल साबित होती है जब गुरुत्वाकर्षण और क्वांटम प्रभाव नगण्य होते हैं।<ref>{{Cite book|last=Goldstein|first=Herbert|title=Classical Mechanics|title-link=Classical Mechanics (Goldstein book)|publisher=Addison-Wesley Publishing Company|year=1980|isbn=0-201-02918-9|edition=2nd|chapter=Chapter 7: Special Relativity in Classical Mechanics|author-link=Herbert Goldstein}}</ref><ref name=":2">{{Cite book|last=Lanczos|first=Cornelius|title=The Variational Principles of Mechanics|publisher=Dover Publications|year=1970|isbn=978-0-486-65067-8|edition=4th|chapter=Chapter IX: Relativistic Mechanics|author-link=Cornelius Lanczos}}</ref> फिर भी, न्यूटोनियन मॉडल अभी भी कम वेग(प्रकाश की गति के सापेक्ष) पर एक सरल और सटीक सन्निकटन के रूप में मान्य है, उदाहरण के लिए, पृथ्वी पर प्रतिदिन परिक्रमण की गति। | ||
विशेष सापेक्षता के व्यापक परिणाम हैं जिन्हें प्रयोगात्मक रूप से सत्यापित किया गया है। | विशेष सापेक्षता के व्यापक परिणाम हैं जिन्हें प्रयोगात्मक रूप से सत्यापित किया गया है। वे [[ एक साथ सापेक्षता | एक साथ सापेक्षता]], [[ लंबाई संकुचन |लंबाई संकुचन]], समय विस्तार, सापेक्षतावादी वेग जोड़ सूत्र, सापेक्षतावादी [[ डॉपलर प्रभाव |डॉपलर प्रभाव]], [[ विशेष सापेक्षता में द्रव्यमान |विशेष सापेक्षता में द्रव्यमान]], प्रकाश की गति पर ऊपरी सीमा, द्रव्यमान-ऊर्जा तुल्यता, कार्य-कारण और थॉमस पूर्वसर्ग इत्यादि की गति सम्मिलित हैं ।<ref name=":0" /><ref name=":1" />उदाहरण के लिए, इसने एक पूर्ण सार्वभौमिक समय की पारंपरिक धारणा को उस समय की धारणा से बदल दिया है जो निर्देश तंत्र और अंतरिक्ष स्थिति पर निर्भर है। दो घटनाओं के बीच एक अपरिवर्तनीय समय अंतराल के अतिरिक्त, एक अपरिवर्तनीय स्पेसटाइम अंतराल होता है। | ||
विशेष सापेक्षता | भौतिकी के अन्य नियमों के साथ, विशेष सापेक्षता के दो अभिगृहीत [[ द्रव्यमान | द्रव्यमान]] और [[ ऊर्जा | ऊर्जा]] की तुल्यता की भविष्यवाणी करते हैं, जैसा कि द्रव्यमान-ऊर्जा तुल्यता सूत्र में व्यक्त किया गया है। <math>E = mc^2</math>, जहाँ <math>c</math> निर्वात में प्रकाश की गति है।<ref name="relativity">{{cite book |author=Albert Einstein |title=Relativity: The Special and the General Theory |page= 48 |url=https://books.google.com/books?id=idb7wJiB6SsC&pg=PA50 |isbn=978-0-415-25384-0 |publisher=Routledge |date=2001 |edition=Reprint of 1920 translation by Robert W. Lawson}}</ref><ref name="Feynman">[https://feynmanlectures.caltech.edu/I_15.html#Ch15-S9 The Feynman Lectures on Physics Vol. I Ch. 15-9: Equivalence of mass and energy]</ref> यह इस बात की पुष्टि करता है कि बिजली और चुंबकत्व की घटनाएं कैसे संबंधित हैं।<ref name=":0" /><ref name=":1" /> | ||
विशेष सापेक्षता की एक परिभाषित विशेषता [[ लोरेंत्ज़ परिवर्तन | लोरेंत्ज़ परिवर्तन]] के साथ न्यूटनियन यांत्रिकी के [[ गैलीलियन परिवर्तन | गैलीलियन परिवर्तन]] का प्रतिस्थापन है। समय और स्थान को एक दूसरे से अलग-अलग परिभाषित नहीं किया जा सकता (जैसा कि पहले माना जाता था)। बल्कि, अंतरिक्ष और समय को स्पेसटाइम में जोड़ा जाता है | किसी एकल सातत्य जिसे स्पेसटाइम के रूप में जाना जाता है, किसी पर्यवेक्षक के लिए एक ही समय में होने वाली घटनाएँ दूसरे के लिए अलग-अलग समय पर घटित हो सकती हैं। | |||
यह सिद्धांत इस | कई वर्षों बाद तक जब आइंस्टीन ने [[ सामान्य सापेक्षता | सामान्य सापेक्षता]] विकसित की, जिसने गुरुत्वाकर्षण को सम्मिलित करने के लिए एक गतिशील स्पेसटाइम पेश किया, जिसमे विशेष सापेक्षता वाक्यांश का उपयोग नहीं किया गया था। कभी-कभी उपयोग किया जाने वाला स्थानांतरण प्रतिबंधित सापेक्षता है, विशेष सापेक्षता वास्तव में एक विशिष्ट परिस्थिति है।<ref group="p">"Science and Common Sense", P. W. Bridgman, ''The Scientific Monthly'', Vol. 79, No. 1 (Jul. 1954), pp. 32–39.</ref><ref group="p">The Electromagnetic Mass and Momentum of a Spinning Electron, G. Breit, Proceedings of the National Academy of Sciences, Vol. 12, p.451, 1926</ref><ref group="p">Kinematics of an electron with an axis. Phil. Mag. 3:1-22. L. H. Thomas.]</ref><ref group="note">Einstein himself, in The Foundations of the General Theory of Relativity, Ann. Phys. 49 (1916), writes "The word 'special' is meant to intimate that the principle is restricted to the case ...". See p. 111 of The Principle of Relativity, A. Einstein, H. A. Lorentz, H. Weyl, H. Minkowski, Dover reprint of 1923 translation by Methuen and Company.]</ref> विशेष सापेक्षता में अल्बर्ट आइंस्टीन के कुछ काम [[ हेंड्रिक लोरेंत्ज़ो | हेंड्रिक लोरेंत्ज़ो]] और हेनरी पोंकारे द्वारा पहले के काम पर बनाए गए हैं। सिद्धांत अनिवार्य रूप से 1907 में पूर्ण हो गया।<ref name=":2" /> | ||
जिस तरह [[ गैलीलियन इनवेरिएंस ]] को अब विशेष सापेक्षता का अनुमान माना जाता है जो कम गति के लिए मान्य है, विशेष सापेक्षता को सामान्य सापेक्षता का अनुमान माना जाता है जो कमजोर [[ गुरुत्वाकर्षण क्षेत्र ]] | |||
यह सिद्धांत इस सन्दर्भ में विशेष है कि यह केवल उस विशेष परिस्थिति में लागू होता है जहां स्पेसटाइम एकसमान होता है, अर्थात जहां [[ स्पेसटाइम की वक्रता | स्पेसटाइम की वक्रता]] (ऊर्जा-गति टेंसर का परिणाम और [[ गुरुत्वाकर्षण | गुरुत्वाकर्षण]] का प्रतिनिधित्व) नगण्य है।<ref>Sean Carroll, Lecture Notes on General Relativity, ch. 1, "Special relativity and flat spacetime," http://ned.ipac.caltech.edu/level5/March01/Carroll3/Carroll1.html</ref><ref group="note">Wald, General Relativity, p. 60: "... the special theory of relativity asserts that spacetime is the manifold <math>\mathbb{R}^4</math> with a flat metric of Lorentz signature defined on it. Conversely, the entire content of special relativity ... is contained in this statement ..."</ref> गुरुत्वाकर्षण को सही ढंग से समायोजित करने के लिए, आइंस्टीन ने 1915 में सामान्य सापेक्षता तैयार की। विशेष सापेक्षता, कुछ ऐतिहासिक विवरणों के विपरीत, [[ त्वरण (विशेष सापेक्षता) | त्वरण (विशेष सापेक्षता)]] के साथ-साथ रिंडलर निर्देशांक को समायोजित करती है।<ref>{{cite book |title=Explorations in Mathematical Physics: The Concepts Behind an Elegant Language |edition=illustrated |first1=Don |last1=Koks |publisher=Springer Science & Business Media |year=2006 |isbn=978-0-387-32793-8 |page=234 |url=https://books.google.com/books?id=ObMb7l9-9loC}} [https://books.google.com/books?id=ObMb7l9-9loC&pg=PA234 Extract of page 234]</ref><ref>{{cite book |title=Relativity Made Relatively Easy |edition=illustrated |first1=Andrew M. |last1=Steane |publisher=OUP Oxford |year=2012 |isbn=978-0-19-966286-9 |page=226 |url=https://books.google.com/books?id=75rCErZkh7EC}} [https://books.google.com/books?id=75rCErZkh7EC&pg=PA226 Extract of page 226]</ref> | |||
जिस तरह [[ गैलीलियन इनवेरिएंस | गैलीलियन इनवेरिएंस]] को अब विशेष सापेक्षता का अनुमान माना जाता है जो कम गति के लिए मान्य है, विशेष सापेक्षता को सामान्य सापेक्षता का अनुमान माना जाता है जो कमजोर [[ गुरुत्वाकर्षण क्षेत्र | गुरुत्वाकर्षण क्षेत्र]] के लिए मान्य है, अर्थात पर्याप्त रूप से छोटे पैमाने पर(उदाहरण के लिए, जब ज्वारीय बल नगण्य हो) और मुक्त पतन की स्थितियों में। यद्यपि, सामान्य सापेक्षता में [[ गैर-यूक्लिडियन ज्यामिति | गैर-यूक्लिडियन ज्यामिति]] को सम्मिलित किया जाता है ताकि गुरुत्वाकर्षण प्रभाव को स्पेसटाइम के ज्यामितीय वक्रता के रूप में दर्शाया जा सके। विशेष सापेक्षता फ्लैट स्पेसटाइम तक cमित है जिसे [[ मिंकोव्स्की स्पेस | मिंकोव्स्की स्पेस]] के रूप में जाना जाता है। जब तक ब्रह्मांड को [[ छद्म रीमैनियन मैनिफोल्ड | छद्म रीमैनियन मैनिफोल्ड]] के रूप में तैयार किया जा सकता है। एक लोरेंत्ज़-अपरिवर्तनीय सीमा रेखा जो विशेष सापेक्षता का पालन करता है, जिसे इस [[ घुमावदार स्पेसटाइम | वक्राकार स्पेसटाइम]] में प्रत्येक बिंदु के पर्याप्त छोटे पड़ोस के लिए परिभाषित किया जा सकता है। | |||
[[ गैलिलियो गैलिली | गैलिलियो गैलिली]] ने पहले ही माना था कि विराम की कोई पूर्ण और यथार्थ रूप से परिभाषित स्थिति नहीं है(कोई [[ पसंदीदा फ्रेम |परिशुद्ध सीमा रेखा]] नहीं), एक सिद्धांत जिसे अब गैलीलियन इनवेरिएंस गैलीलियो का सापेक्षता का सिद्धांत कहा जाता है। आइंस्टीन ने इस सिद्धांत का विस्तार इस प्रकार किया कि यह प्रकाश की निरंतर गति के लिए उत्तरदायी हो गया,<ref>{{cite book|title=Spacetime Physics: Introduction to Special Relativity|date=1992|publisher=W. H. Freeman|isbn=978-0-7167-2327-1|author1=Edwin F. Taylor|author2=John Archibald Wheeler|name-list-style=amp|url=https://archive.org/details/spacetimephysics00edwi_0}}</ref> जिसे माइकलसन-मॉर्ले प्रयोग में देखा गया था। उन्होंने यह भी माना कि यह भौतिकी के सभी नियमों के लिए है, जिसमें यांत्रिकी और [[ बिजली का गतिविज्ञान | बिजली का गतिविज्ञान]] दोनों के नियम सम्मिलित हैं।<ref name="Rindler0">{{cite book |title=Essential Relativity: Special, General, and Cosmological |first1= Wolfgang |edition=illustrated |last1=Rindler |page= §1,11 p. 7 |url=https://books.google.com/books?id=0J_dwCmQThgC&pg=PT148 |isbn=978-3-540-07970-5 |publisher=Springer Science & Business Media|date=1977 }}</ref> | |||
== {{anchor|Postulates}} विशेष सापेक्षता के लिए पारंपरिक दो अभिधारणाएं == | == {{anchor|Postulates}} विशेष सापेक्षता के लिए पारंपरिक दो अभिधारणाएं == | ||
{{Quote box | {{Quote box | ||
| quote = " | | quote = "इस प्रकार के प्रतिबिंबों ने 1900 के कुछ समय बाद ही, अर्थात प्लैंक के ट्रेलब्लेज़िंग कार्य के तुरंत बाद, मुझे यह स्पष्ट कर दिया कि न तो यांत्रिकी और न ही विद्युत् गतिकी(सीमित परिस्थितियों को छोड़कर) सटीक वैधता का दावा कर सकते हैं। धीरे-धीरे मैं खोज की संभावना से निराश हो गया, ज्ञात तथ्यों पर आधारित रचनात्मक प्रयासों के माध्यम से सार्वभौमिक नियमो का जितना अधिक मैंने प्रयास किया, उतना ही मुझे यह विश्वास हुआ कि केवल एक सार्वभौमिक औपचारिक सिद्धांत की खोज ही हमें सुनिश्चित परिणामों तक ले जा सकती है। अतः किस प्रकार ऐसा सार्वभौमिक सिद्धांत पाया जा सकता है?" | ||
| source = | | source = अल्बर्ट आइंस्टीन: ''आत्मकथात्मक लेख''<ref name="autogenerated1" group=p>Einstein, Autobiographical Notes, 1949.</ref> | ||
| align = right | | align = right | ||
| width = 40% | | width = 40% | ||
}} | }} | ||
प्रकाश की गति की स्थिरता मैक्सवेल के विद्युत चुम्बकत्व के सिद्धांत [उद्धरण वांछित] और[[ चमकदार ईथर ]] के लिए | आइंस्टीन ने दो मूलभूत प्रस्तावों की पहचान की, जो यांत्रिकी या विद्युत गतिकी के(तत्कालीन) ज्ञात नियमो की सटीक वैधता की परवाह किए बिना, सबसे अधिक आश्वस्त प्रतीत होते थे। ये प्रस्ताव निर्वात में प्रकाश की गति की स्थिरता और जड़त्वीय प्रणाली की पसंद से भौतिक नियमो(विशेषकर प्रकाश की गति की स्थिरता) की स्वतंत्रता थे। 1905 में विशेष सापेक्षता की अपनी प्रारंभिक प्रस्तुति में उन्होंने इन अभिधारणाओं को इस रूप में व्यक्त किया:<ref name=electro group=p/>* [[ सापेक्षता का सिद्धांत ]] - वे नियम जिनके द्वारा भौतिक प्रणालियों की अवस्थाओं में परिवर्तन होता है, प्रभावित नहीं होते हैं, राज्य के इन परिवर्तनों को एक दूसरे के सापेक्ष एकसमान स्थानांतरणकीय गति में दो प्रणालियों में से एक या दूसरे को संदर्भित किया जा सकता था।<ref name=electro group=p/>* अपरिवर्तनीय प्रकाश गति का सिद्धांत - "... प्रकाश सदैव खाली स्थान में एक निश्चित वेग[गति] c के साथ प्रसारित होता है जो उत्सर्जक पिंड की गति की स्थिति से स्वतंत्र होता है"<ref name=electro group=p/>यह, निर्वात में प्रकाश स्रोत की गति की स्थिति की परवाह किए बिना, जड़त्वीय निर्देशांक की कम से कम एक प्रणाली ("स्थिर प्रणाली") में गति c (एक निश्चित स्थिर, दिशा से स्वतंत्र) के साथ फैलता है। | ||
प्रकाश की गति की स्थिरता मैक्सवेल के विद्युत चुम्बकत्व के सिद्धांत [उद्धरण वांछित] और[[ चमकदार ईथर | प्रकाशवाही ईथर]] के लिए प्रमाण की कमी से प्रेरित थी। मिशेलसन-मॉर्ले प्रयोग के शून्य परिणाम से आइंस्टीन किस सीमा तक प्रभावित थे, इस पर परस्पर विरोधी प्रमाण हैं।<ref>[[Michael Polanyi]] (1974) ''Personal Knowledge: Towards a Post-Critical Philosophy'', {{isbn|0-226-67288-3}}, footnote page 10–11: Einstein reports, via Dr N Balzas in response to Polanyi's query, that "The Michelson–Morley experiment had no role in the foundation of the theory." and "..the theory of relativity was not founded to explain its outcome at all." [https://books.google.com/books?id=0Rtu8kCpvz4C&lpg=PP1&pg=PT19]</ref><ref name="mM1905"/>किसी भी परिस्थिति में, माइकलसन-मॉर्ले प्रयोग के शून्य परिणाम ने प्रकाश की गति की गति की व्यापकता और तेजी से स्वीकृति की धारणा में मदद की। | |||
विशेष सापेक्षता की व्युत्पत्ति न केवल इन दो स्पष्ट अभिधारणाओं पर निर्भर करती है, बल्कि कई मौन धारणाओं (भौतिकी के लगभग सभी सिद्धांतों में बनाई गई) पर भी निर्भर करती है, जिसमें अंतरिक्ष की | विशेष सापेक्षता की व्युत्पत्ति न केवल इन दो स्पष्ट अभिधारणाओं पर निर्भर करती है, बल्कि कई मौन धारणाओं(भौतिकी के लगभग सभी सिद्धांतों में बनाई गई) पर भी निर्भर करती है, जिसमें अंतरिक्ष की समरूपता और उनके पिछले इतिहास से रेखा और समय को मापने की स्वतंत्रता सम्मिलित है।<ref group=p>Einstein, "Fundamental Ideas and Methods of the Theory of Relativity", 1920</ref> | ||
1905 में आइंस्टीन की विशेष सापेक्षता की मूल प्रस्तुति के बाद, विभिन्न वैकल्पिक व्युत्पत्तियों में अभिधारणाओं के कई अलग-अलग सेट प्रस्तावित किए गए हैं।<ref>For a survey of such derivations, see Lucas and Hodgson, Spacetime and Electromagnetism, 1990</ref> | 1905 में आइंस्टीन की विशेष सापेक्षता की मूल प्रस्तुति के बाद, विभिन्न वैकल्पिक व्युत्पत्तियों में अभिधारणाओं के कई अलग-अलग सेट प्रस्तावित किए गए हैं।<ref>For a survey of such derivations, see Lucas and Hodgson, Spacetime and Electromagnetism, 1990</ref>यद्यपि, आइंस्टीन द्वारा अपने मूल पेपर में नियोजित पदों का सबसे साधारण संग्रह बना हुआ है। बाद में आइंस्टीन द्वारा दिए गए सापेक्षता के सिद्धांत का एक और गणितीय कथन, जो ऊपर वर्णित सहजता की अवधारणा का परिचय नहीं देता है: | ||
{{quote|'' | {{quote|''सापेक्षता का विशेष सिद्धांत'': यदि निर्देशांक K की एक प्रणाली को चुना जाता है, ताकि इसके संबंध में, भौतिक नियम अपने सरलतम रूप में उपयुक्त हों, तो 'समान' नियम किसी भी अन्य समन्वय प्रणाली के संबंध में उपयुक्त होते हैं, जो समान रूप से स्थानांतरित होते हैं।<ref name=Einstein>{{cite book |title=The Principle of Relativity: a collection of original memoirs on the special and general theory of relativity |author=Einstein, A., Lorentz, H. A., Minkowski, H., & Weyl, H. |page=111 |url=https://books.google.com/books?id=yECokhzsJYIC&pg=PA111 | ||
|isbn=978-0-486-60081-9 |publisher=Courier Dover Publications |date=1952 }}</ref><!--Albert Einstein: ''The foundation of the general theory of relativity'', Section A, §1 -->}} | |isbn=978-0-486-60081-9 |publisher=Courier Dover Publications |date=1952 }}</ref><!--Albert Einstein: ''The foundation of the general theory of relativity'', Section A, §1 -->}} | ||
हेनरी पोंकारे ने यह साबित करके सापेक्षता सिद्धांत के लिए गणितीय ढांचा प्रदान किया कि [[ लोरेंत्ज़ परिवर्तन ]] समरूपता | हेनरी पोंकारे ने यह साबित करके सापेक्षता सिद्धांत के लिए गणितीय ढांचा प्रदान किया कि [[ लोरेंत्ज़ परिवर्तन ]] समरूपता परिवर्तन उनके पोंकारे समूह का एक उपसमूह है। आइंस्टीन ने बाद में इन परिवर्तनों को अपने स्वयंसिद्ध सिद्धांतों से प्राप्त किया। | ||
आइंस्टीन के कई पत्र इन दो सिद्धांतों के आधार पर लोरेंत्ज़ परिवर्तन की व्युत्पत्तियों को प्रस्तुत करते हैं।<ref group=p>Einstein, On the Relativity Principle and the Conclusions Drawn from It, 1907; "The Principle of Relativity and Its Consequences in Modern Physics", 1910; "The Theory of Relativity", 1911; Manuscript on the Special Theory of Relativity, 1912; Theory of Relativity, 1913; Einstein, Relativity, the Special and General Theory, 1916; The Principal Ideas of the Theory of Relativity, 1916; What Is The Theory of Relativity?, 1919; The Principle of Relativity (Princeton Lectures), 1921; Physics and Reality, 1936; The Theory of Relativity, 1949.</ref> | आइंस्टीन के कई पत्र इन दो सिद्धांतों के आधार पर लोरेंत्ज़ परिवर्तन की व्युत्पत्तियों को प्रस्तुत करते हैं।<ref group=p>Einstein, On the Relativity Principle and the Conclusions Drawn from It, 1907; "The Principle of Relativity and Its Consequences in Modern Physics", 1910; "The Theory of Relativity", 1911; Manuscript on the Special Theory of Relativity, 1912; Theory of Relativity, 1913; Einstein, Relativity, the Special and General Theory, 1916; The Principal Ideas of the Theory of Relativity, 1916; What Is The Theory of Relativity?, 1919; The Principle of Relativity (Princeton Lectures), 1921; Physics and Reality, 1936; The Theory of Relativity, 1949.</ref> | ||
| Line 43: | Line 47: | ||
== सापेक्षता का सिद्धांत == | == सापेक्षता का सिद्धांत == | ||
{{main| | {{main|सापेक्षता का सिद्धांत}} | ||
=== | === निर्देश तंत्र और सापेक्ष गति === | ||
[[File:Frames of reference in relative motion.svg|thumb|right|300px|चित्र 2-1। प्राइमेड सिस्टम अनप्रिम्ड सिस्टम के सापेक्ष गति में है, केवल एक्स- | [[File:Frames of reference in relative motion.svg|thumb|right|300px|चित्र 2-1। प्राइमेड सिस्टम अनप्रिम्ड सिस्टम के सापेक्ष गति में है, केवल एक्स-अक्ष के साथ निरंतर वेग वी के साथ, अनप्रिम्ड सिस्टम में एक पर्यवेक्षक स्थिर के दृष्टिकोण से। सापेक्षता के सिद्धांत के अनुसार, प्राइमेड सिस्टम में स्थिर पर्यवेक्षक एक समान निर्माण को देखेगा, सिवाय इसके कि वे जिस वेग को रिकॉर्ड करते हैं वह -v होगा। गैर-सापेक्ष यांत्रिकी में अनंत से अंतःक्रिया के प्रसार की गति को एक परिमित मूल्य में बदलने के लिए रूपांतरण समीकरणों की मैपिंग घटनाओं को एक सीमा रेखा में दूसरे सीमा रेखा में बदलने की आवश्यकता होगी।]] | ||
निर्देश तंत्र सापेक्षता सिद्धांत में एक महत्वपूर्ण भूमिका निभाते हैं। यहां उपयोग किया गया निर्देश तंत्र शब्द अंतरिक्ष में एक अवलोकन परिप्रेक्ष्य है जो गति(त्वरण) में किसी भी बदलाव से नहीं गुजरता है, जिससे एक स्थिति को 3 स्थानिक अक्षों के साथ मापा जा सकता है (इसलिए, विराम या स्थिर वेग पर)। इसके अलावा, एक निर्देश तंत्र में 'चालमापी' (समान आवधिकता के साथ कोई भी संदर्भ उपकरण) का उपयोग करके घटनाओं के समय के माप को निर्धारित करने की क्षमता होती है। | |||
एक [[ घटना (सापेक्षता) ]] | एक [[ घटना (सापेक्षता) ]]जिसे एक निर्देश तंत्र के सापेक्ष अंतरिक्ष में एक अद्वितीय क्षण और स्थान दिया जा सकता है: यह स्पेसटाइम में एक "बिंदु" है। चूंकि निर्देश तंत्र के बावजूद प्रकाश की गति सापेक्षता में स्थिर है, प्रकाश की स्पंदनों का उपयोग स्पष्ट रूप से दूरियों को मापने के लिए किया जा सकता है और उस समय को वापस संदर्भित किया जा सकता है जब घटना चालमापी में हुई थी, भले ही प्रकाश को घटना के बाद चालमापी तक पहुंचने में समय लगता है। | ||
उदाहरण के लिए, पटाखों के विस्फोट को एक "घटना" माना जा सकता है। हम किसी घटना को उसके चार स्पेसटाइम निर्देशांकों द्वारा पूरी तरह से निर्दिष्ट कर सकते हैं: घटना का समय और इसकी त्रि-आयामी स्थानिक स्थिति एक संदर्भ बिंदु को परिभाषित करती है। | उदाहरण के लिए, पटाखों के विस्फोट को एक "घटना" माना जा सकता है। हम किसी घटना को उसके चार स्पेसटाइम निर्देशांकों द्वारा पूरी तरह से निर्दिष्ट कर सकते हैं: घटना का समय और इसकी त्रि-आयामी स्थानिक स्थिति एक संदर्भ बिंदु को परिभाषित करती है। इस निर्देश तंत्र को S कहते हैं। | ||
सापेक्षता सिद्धांत में, हम | सापेक्षता सिद्धांत में, हम अधिकांशतः भिन्न संदर्भ फ़्रेमों से किसी घटना के निर्देशांकों की गणना करना चाहते हैं। विभिन्न सीमा रेखाों में किए गए मापों को जोड़ने वाले समीकरण रूपांतरण समीकरण कहलाते हैं। | ||
=== मानक विन्यास === | === मानक विन्यास === | ||
विभिन्न संदर्भ फ़्रेमों में पर्यवेक्षकों द्वारा मापा गया स्पेसटाइम निर्देशांक एक दूसरे के साथ तुलना करने के तरीके में अंतर्दृष्टि प्राप्त करने के लिए, मानक | विभिन्न संदर्भ फ़्रेमों में पर्यवेक्षकों द्वारा मापा गया स्पेसटाइम निर्देशांक एक दूसरे के साथ तुलना करने के तरीके में अंतर्दृष्टि प्राप्त करने के लिए, मानक विन्यास में फ़्रेम के साथ सरलीकृत सेटअप के साथ काम करना उपयोगी होता है।<ref name="Collier">{{cite book|title=A Most Incomprehensible Thing: Notes Towards a Very Gentle Introduction to the Mathematics of Relativity|last1=Collier|first1=Peter|publisher=Incomprehensible Books|year=2017|isbn=9780957389465|edition=3rd}}</ref>{{rp|107}} यह गणित के सरलीकरण की अनुमति देता है। निष्कर्षों में व्यापकता का कोई नुकसान नहीं होता है। चित्र 2-1 में, दो गैलीलियन संदर्भ फ़्रेम (अर्थात, पारंपरिक 3-स्पेस फ़्रेम) सापेक्ष गति में प्रदर्शित होते हैं। फ़्रेम S पहले पर्यवेक्षक O से संबंधित है, और फ़्रेम S′ दूसरे पर्यवेक्षक O′ से संबंधित है। | ||
* | * सीमा रेखा S के x, y, z अक्ष सीमा रेखा S′ के संबंधित प्राइमेड अक्षों के समानांतर उन्मुख होते हैं। | ||
* फ़्रेम S′ सरलता के लिए, एक ही दिशा में चलता है: फ़्रेम S की x-दिशा स्थिर वेग v के साथ, जैसा कि फ़्रेम S में मापा जाता है। | * फ़्रेम S′ सरलता के लिए, एक ही दिशा में चलता है: फ़्रेम S की x-दिशा स्थिर वेग v के साथ, जैसा कि फ़्रेम S में मापा जाता है। | ||
* | * सीमा रेखा S और S′ के उद्गम संपाती होते हैं जब सीमा रेखा S के लिए समय t = 0 और सीमा रेखा S′ के लिए t′ = 0 होता है। | ||
चूंकि सापेक्षता सिद्धांत में कोई पूर्ण | चूंकि सापेक्षता सिद्धांत में कोई पूर्ण निर्देश तंत्र नहीं है, इसलिए 'चलती' की अवधारणा सख्ती से उपलब्ध नहीं है, क्योंकि सब कुछ किसी अन्य निर्देश तंत्र के संबंध में आगे बढ़ रहा है। इसके अतिरिक्त, कोई भी दो सीमा रेखा जो एक ही गति से एक ही दिशा में चलते हैं, उन्हें मूविंग कहा जाता है। इसलिए, S और S′ गतिमान नहीं हैं। | ||
=== एक पूर्ण | === एक पूर्ण निर्देश तंत्र का अभाव === | ||
सापेक्षता का सिद्धांत, जिसमें कहा गया है कि प्रत्येक [[ जड़त्वीय संदर्भ फ्रेम ]] में भौतिक | सापेक्षता का सिद्धांत, जिसमें कहा गया है कि प्रत्येक [[ जड़त्वीय संदर्भ फ्रेम | जड़त्वीय निर्देश तंत्र]] में भौतिक नियमो का एक ही रूप है, गैलीलियो से पहले का है, और न्यूटनियन भौतिकी में सम्मिलित किया गया था। यद्यपि, 19वीं शताब्दी के अंत में, [[ विद्युत चुम्बकीय विकिरण ]] के अस्तित्व ने कुछ भौतिकविदों को यह सुझाव देने के लिए प्रेरित किया कि ब्रह्मांड एक पदार्थ से भरा हुआ है जिसे वे प्रकाशवाही ईथर कहते हैं, उन्होंने माना कि यह, माध्यम के रूप में कार्य करेगा जिसके माध्यम से ये तरंगें या कंपन प्रचारित होती हैं (जिस तरह से ध्वनि हवा के माध्यम से फैलती है, उc तरह कई मायनों में)। ईथर को एक परिशुद्ध सीमा रेखा माना जाता था जिसके विपरीत सभी गति को मापा जा सकता था, और इसे पृथ्वी या किसी अन्य निश्चित संदर्भ बिंदु के सापेक्ष स्थिर और गतिहीन माना जा सकता था। ईथर को विद्युत चुम्बकीय तरंगों का समर्थन करने के लिए पर्याप्त रूप से लोचदार माना जाता था, जबकि वे तरंगें पदार्थ के साथ परस्पर प्रभाव डाल सकती थीं, फिर भी इससे गुजरने वाले निकायों के लिए कोई प्रतिरोध नहीं था (इसकी एक संपत्ति यह थी कि यह विद्युत चुम्बकीय तरंगों को फैलाने की अनुमति देती थी)। 1887 में माइकलसन-मॉर्ले प्रयोग (बाद में अधिक सटीक और नवीन प्रयोगों के साथ सत्यापित) सहित विभिन्न प्रयोगों के परिणामों ने विशेष सापेक्षता के सिद्धांत को जन्म दिया, यह दिखाते हुए कि ईथर उपलब्ध नहीं था।<ref>Staley, Richard (2009), "Albert Michelson, the Velocity of Light, and the Ether Drift", ''Einstein's generation. The origins of the relativity revolution,'' Chicago: University of Chicago Press, {{isbn|0-226-77057-5}}</ref> आइंस्टीन का समाधान एक ईथर की धारणा और विराम की पूर्ण स्थिति को त्यागना था। सापेक्षता में, एकसमान गति से गतिमान कोई भी निर्देश तंत्र भौतिकी के समान नियमों का पालन करेगा। विशेष रूप से, निर्वात में प्रकाश की गति को सदैव c के रूप में मापा जाता है, भले ही इसे कई प्रणालियों द्वारा मापा जाता है जो अलग-अलग (लेकिन स्थिर) वेग से आगे बढ़ रहे हैं। | ||
=== दूसरी अभिधारणा के बिना सापेक्षता === | === दूसरी अभिधारणा के बिना सापेक्षता === | ||
केवल सापेक्षता के सिद्धांत से प्रकाश की गति की स्थिरता को ग्रहण किए बिना (अर्थात, अंतरिक्ष की समरूपता और विशेष सापेक्षता के सिद्धांत द्वारा निहित समरूपता का उपयोग करके) यह दिखाया जा सकता है कि जड़त्वीय | केवल सापेक्षता के सिद्धांत से प्रकाश की गति की स्थिरता को ग्रहण किए बिना (अर्थात, अंतरिक्ष की समरूपता और विशेष सापेक्षता के सिद्धांत द्वारा निहित समरूपता का उपयोग करके) यह दिखाया जा सकता है कि जड़त्वीय सीमा रेखा के बीच स्पेसटाइम परिवर्तन या तो यूक्लिडियन, गैलीलियन हैं , या लोरेंत्ज़ियन। लोरेंत्ज़ियन परिस्थिति में, तब कोई सापेक्षतावादी अंतराल संरक्षण और एक निश्चित cमित cमित गति प्राप्त कर सकता है। प्रयोगों से पता चलता है कि यह गति निर्वात में प्रकाश की चाल है।<ref name=Friedman group=p>{{cite book|author=Yaakov Friedman|title=Physical Applications of Homogeneous Balls|series=Progress in Mathematical Physics|volume=40|date=2004|pages=1–21|isbn=978-0-8176-3339-4}}</ref><ref name=Morin2007>David Morin (2007) ''Introduction to Classical Mechanics'', Cambridge University Press, Cambridge, chapter 11, Appendix I, {{isbn|1-139-46837-5}}.</ref> | ||
== {{anchor|Lorentz transformation}} विशेष सापेक्षता के आवश्यक मूल के रूप में लोरेंत्ज़ इनवेरिएंस == | == {{anchor|Lorentz transformation}} विशेष सापेक्षता के आवश्यक मूल के रूप में लोरेंत्ज़ इनवेरिएंस == | ||
{{Main| | {{Main|लोरेंत्ज़ परिवर्तन}} | ||
=== विशेष सापेक्षता के लिए वैकल्पिक दृष्टिकोण === | === विशेष सापेक्षता के लिए वैकल्पिक दृष्टिकोण === | ||
{{main| | {{main|लोरेंत्ज़ परिवर्तनों की व्युत्पत्ति}} | ||
आइंस्टीन लगातार लोरेंत्ज़ इनवेरिएंस (विशेष सापेक्षता का आवश्यक मूल) की व्युत्पत्ति सापेक्षता और प्रकाश-गति के अपरिवर्तन के केवल दो मूल सिद्धांतों पर आधारित थे। उन्होंने लिखा है: | आइंस्टीन लगातार लोरेंत्ज़ इनवेरिएंस (विशेष सापेक्षता का आवश्यक मूल) की व्युत्पत्ति सापेक्षता और प्रकाश-गति के अपरिवर्तन के केवल दो मूल सिद्धांतों पर आधारित थे। उन्होंने लिखा है: | ||
{{quote| | {{quote|सापेक्षता के विशेष सिद्धांत के लिए मूलभूत अंतर्दृष्टि यह है: धारणाएं सापेक्षता और प्रकाश की गति अपरिवर्तनीयता संगत होती हैं यदि एक नए प्रकार के संबंध ("लोरेंत्ज़ परिवर्तन") को निर्देशांक और घटनाओं के समय के रूपांतरण के लिए संक्षिप्त किया जाता है ... सार्वभौमिक सिद्धांत सापेक्षता के विशेष सिद्धांत की परिकल्पना में निहित है: भौतिकी के नियम लोरेंत्ज़ परिवर्तनों के संबंध में अपरिवर्तनीय हैं (एक जड़त्वीय प्रणाली से किसी अन्य मनमाने ढंग से चुने गए जड़त्वीय प्रणाली में संक्रमण के लिए)। यह प्राकृतिक नियमों के लिए एक प्रतिबंधित सिद्धांत है...<ref name="autogenerated1" group=p/>}} | ||
इस प्रकार विशेष सापेक्षता के कई आधुनिक उपचार इसे सार्वभौमिक लोरेंत्ज़ सहप्रसरण के एकल अभिधारणा पर, या, समान रूप से [[ मिंकोव्स्की स्पेसटाइम ]] के एकल अभिधारणा पर आधारित करते हैं।<ref group=p>Das, A. (1993) ''The Special Theory of Relativity, A Mathematical Exposition'', Springer, {{isbn|0-387-94042-1}}.</ref><ref group=p>Schutz, J. (1997) Independent Axioms for Minkowski Spacetime, Addison Wesley Longman Limited, {{isbn|0-582-31760-6}}.</ref> | इस प्रकार विशेष सापेक्षता के कई आधुनिक उपचार इसे सार्वभौमिक लोरेंत्ज़ सहप्रसरण के एकल अभिधारणा पर, या, समान रूप से [[ मिंकोव्स्की स्पेसटाइम ]] के एकल अभिधारणा पर आधारित करते हैं।<ref group=p>Das, A. (1993) ''The Special Theory of Relativity, A Mathematical Exposition'', Springer, {{isbn|0-387-94042-1}}.</ref><ref group=p>Schutz, J. (1997) Independent Axioms for Minkowski Spacetime, Addison Wesley Longman Limited, {{isbn|0-582-31760-6}}.</ref> | ||
सार्वभौमिक लोरेंत्ज़ सहप्रसरण को एक व्युत्पन्न सिद्धांत मानने के | सार्वभौमिक लोरेंत्ज़ सहप्रसरण को एक व्युत्पन्न सिद्धांत मानने के अतिरिक्त, यह लेख इसे विशेष सापेक्षता का मौलिक अभिधारणा मानता है। विशेष सापेक्षता के लिए पारंपरिक दो अभिधारणा दृष्टिकोण को असंख्य कॉलेज पाठ्यपुस्तकों और लोकप्रिय प्रस्तुतियों में प्रस्तुत किया गया है।<ref name="Miller2009">{{cite journal |last1=Miller |first1=D. J. |title=A constructive approach to the special theory of relativity |journal=American Journal of Physics |volume=78 |issue=6 |pages=633–638 |arxiv=0907.0902 |doi=10.1119/1.3298908 |year=2010 |bibcode=2010AmJPh..78..633M |s2cid=20444859 }}</ref> मिंकोवस्की स्पेसटाइम के एकल अभिधारणा से शुरू होने वाली पाठ्यपुस्तकों में टेलर, व्हीलर और कैलाहन द्वारा लिखित पुस्तकें सम्मिलित हैं।<ref name="Taylor_Wheeler">{{cite book |last1=Taylor |first1=Edwin |last2=Wheeler |first2=John Archibald |title=Spacetime Physics |date=1992 |publisher=W.H. Freeman & Co. |isbn=978-0-7167-2327-1 |edition=2nd |url=https://archive.org/details/spacetimephysics00edwi_0 }}</ref> विकिपीडिया लेख स्पेसटाइम और [[ मिंकोव्स्की आरेख ]] के बाद भी यही दृष्टिकोण है। | ||
=== लोरेंत्ज़ परिवर्तन और उसका प्रतिलोम === | === लोरेंत्ज़ परिवर्तन और उसका प्रतिलोम === | ||
स्पेसटाइम को परिभाषित करें | स्पेसटाइम को परिभाषित करें, स्पेसटाइम निर्देशांक रखने के लिए बुनियादी अवधारणाएं {{nowrap|(''t'', ''x'', ''y'', ''z'')}} सिस्टम S और . में {{nowrap|(''t''′, ''x''′, ''y''′, ''z''′)}} एक निर्देश तंत्र में उस सीमा रेखा के संबंध में वेग v से आगे बढ़ते हुए, S′ फिर लोरेंत्ज़ परिवर्तन निर्दिष्ट करता है कि ये निर्देशांक निम्नलिखित तरीके से संबंधित हैं: | ||
<math display="block">\begin{align} | <math display="block">\begin{align} | ||
t' &= \gamma \ (t - vx/c^2) \\ | t' &= \gamma \ (t - vx/c^2) \\ | ||
| Line 92: | Line 96: | ||
z' &= z , | z' &= z , | ||
\end{align}</math> | \end{align}</math> | ||
जहाँ <math display="block">\gamma = \frac{1}{\sqrt{1 - \frac{v^2}{c^2}}}</math> [[ लोरेंत्ज़ कारक ]] है और c निर्वात में प्रकाश की गति है, और S′ का वेग v, S के सापेक्ष, x-अक्ष के समानांतर है। सरलता के लिए, y और z निर्देशांक अप्रभावित हैं, केवल x और t निर्देशांक रूपांतरित होते हैं। ये लोरेंत्ज़ रूपांतरण रैखिक मैपिंग का [[ एक-पैरामीटर समूह ]]बनाते हैं, उस पैरामीटर को [[ तेज़ी ]] कहा जाता है। | |||
अप्रकाशित निर्देशांक के लिए उपरोक्त चार परिवर्तन समीकरणों को हल करने से व्युत्क्रम लोरेंत्ज़ परिवर्तन प्राप्त होता है: | अप्रकाशित निर्देशांक के लिए उपरोक्त चार परिवर्तन समीकरणों को हल करने से व्युत्क्रम लोरेंत्ज़ परिवर्तन प्राप्त होता है: | ||
| Line 101: | Line 105: | ||
z &= z'. | z &= z'. | ||
\end{align}</math> | \end{align}</math> | ||
इस व्युत्क्रम लोरेंत्ज़ परिवर्तन को प्राइमेड से अनप्रिम्ड सिस्टम में लोरेंत्ज़ परिवर्तन के साथ | इस व्युत्क्रम लोरेंत्ज़ परिवर्तन को प्राइमेड से अनप्रिम्ड सिस्टम में लोरेंत्ज़ परिवर्तन के साथ समानता के लिए लागू करना, अप्रकाशित सीमा रेखा को वेग के साथ आगे बढ़ने के रूप में दिखाता है {{math|1=''v′'' = −''v''}}, जैसा कि प्राइमेड सीमा रेखा में मापा जाता है। | ||
एक्स-अक्ष के बारे में कुछ खास नहीं है। परिवर्तन y- या z- अक्ष पर लागू हो सकता है, या वास्तव में गति के समानांतर किसी भी दिशा में (जो कारक द्वारा विकृत होते हैं) और लंबवत; विवरण के लिए लेख लोरेंत्ज़ परिवर्तन देखें। | एक्स-अक्ष के बारे में कुछ खास नहीं है। परिवर्तन y- या z- अक्ष पर लागू हो सकता है, या वास्तव में गति के समानांतर किसी भी दिशा में (जो कारक द्वारा विकृत होते हैं) और लंबवत; विवरण के लिए लेख लोरेंत्ज़ परिवर्तन देखें। | ||
| Line 113: | Line 117: | ||
*{{EquationRef|3|Eq. 3:}} <math>\Delta x' = \gamma \ (\Delta x - v \,\Delta t) \ ,\ \ </math> <math>\Delta t' = \gamma \ \left(\Delta t - v \ \Delta x / c^{2} \right) \ . </math> | *{{EquationRef|3|Eq. 3:}} <math>\Delta x' = \gamma \ (\Delta x - v \,\Delta t) \ ,\ \ </math> <math>\Delta t' = \gamma \ \left(\Delta t - v \ \Delta x / c^{2} \right) \ . </math> | ||
*{{EquationRef|4|Eq. 4:}} <math>\Delta x = \gamma \ (\Delta x' + v \,\Delta t') \ , \ </math> <math>\Delta t = \gamma \ \left(\Delta t' + v \ \Delta x' / c^{2} \right) \ . </math> | *{{EquationRef|4|Eq. 4:}} <math>\Delta x = \gamma \ (\Delta x' + v \,\Delta t') \ , \ </math> <math>\Delta t = \gamma \ \left(\Delta t' + v \ \Delta x' / c^{2} \right) \ . </math> | ||
यदि हम अंतर लेने के | यदि हम अंतर लेने के अतिरिक्त हमे दिखता है | ||
*{{EquationRef|5|Eq. 5:}} <math>dx' = \gamma \ (dx - v \, dt) \ ,\ \ </math> <math>dt' = \gamma \ \left( dt - v \ dx / c^{2} \right) \ . </math> | *{{EquationRef|5|Eq. 5:}} <math>dx' = \gamma \ (dx - v \, dt) \ ,\ \ </math> <math>dt' = \gamma \ \left( dt - v \ dx / c^{2} \right) \ . </math> | ||
| Line 125: | Line 129: | ||
| image3 = Spacetime diagram development C.svg |width3=535|height3=535 | | image3 = Spacetime diagram development C.svg |width3=535|height3=535 | ||
| image4 = Spacetime diagram development D.svg|width4=535|height4=535 | | image4 = Spacetime diagram development D.svg|width4=535|height4=535 | ||
| footer = | | footer = चित्र 3-1। लोरेंत्ज़ रूपांतरण को दर्शाने के लिए मिन्कोव्स्की स्पेसटाइम आरेख बनाना।}} | ||
स्पेसटाइम आरेख (मिन्कोव्स्की आरेख) यह देखने के लिए एक अत्यंत उपयोगी सहायता है कि विभिन्न संदर्भ फ़्रेमों के बीच निर्देशांक कैसे परिवर्तित होते हैं। यद्यपि उनका उपयोग करके सही गणना करना उतना आसान नहीं है जितना कि लोरेंत्ज़ परिवर्तनों को सीधे लागू करना, उनकी मुख्य शक्ति सापेक्षतावादी परिदृश्य के परिणामों की सहज समझ प्रदान करने की उनकी क्षमता है।<ref name=Morin2007/> | स्पेसटाइम आरेख (मिन्कोव्स्की आरेख) यह देखने के लिए एक अत्यंत उपयोगी सहायता है कि विभिन्न संदर्भ फ़्रेमों के बीच निर्देशांक कैसे परिवर्तित होते हैं। यद्यपि उनका उपयोग करके सही गणना करना उतना आसान नहीं है जितना कि लोरेंत्ज़ परिवर्तनों को सीधे लागू करना, उनकी मुख्य शक्ति सापेक्षतावादी परिदृश्य के परिणामों की सहज समझ प्रदान करने की उनकी क्षमता है।<ref name=Morin2007/> | ||
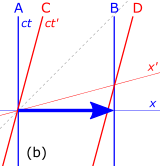
स्पेसटाइम आरेख बनाने के लिए, मानक | स्पेसटाइम आरेख बनाने के लिए, मानक विन्यास में दो गैलीलियन संदर्भ फ़्रेम, S और S' पर विचार करके प्रारंभ करें, जैसा कि चित्र 2-1 में दिखाया गया है।<ref name=Morin2007/><ref name="Mermin1968">{{cite book |last1=Mermin |first1=N. David |title=Space and Time in Special Relativity |url=https://archive.org/details/spacetimeinspeci0000merm |url-access=registration |date=1968 |publisher=McGraw-Hill |isbn=978-0881334203}}</ref>{{rp|155–199}}। 3-1a।, <math>x</math> तथा <math>t</math> सीमा रेखा s की अक्षों <math>x</math>, h अक्ष क्षैतिज है और <math>t</math> (वास्तव में <math>ct</math>) अक्ष लंबवत है, जो कि कीनेमेटिक्स में सामान्य परंपरा के विपरीत है। <math>ct</math> h> अक्ष को के एक कारक द्वारा बढ़ाया जाता है <math>c</math> ताकि दोनों अक्षों की लंबाई की सामान्य इकाइयाँ हों। दिखाए गए आरेख में, ग्रिडलाइनों को एक इकाई की दूरी पर रखा गया है। 45° विकर्ण रेखाएं समय पर मूल से गुजरने वाले दो फोटॉनों की विश्व रेखाओं का प्रतिनिधित्व करती हैं <math>t = 0.</math> इन विश्वरेखाओं की प्रवणता 1 है क्योंकि फोटॉन प्रति इकाई समय में एक इकाई अंतरिक्ष में आगे बढ़ते हैं। दो घटनाएँ, <math>\text{A}</math> तथा <math>\text{B},</math> इस ग्राफ पर प्लॉट किए गए हैं ताकि उनके निर्देशांकों की तुलना S और S के सीमा रेखा में की जा सके। | ||
चित्र 3-1 बी। खींचना <math>x'</math> तथा <math>ct'</math> सीमा रेखा S के अक्षों '। <math>ct'</math> h> अक्ष सीमा रेखा S में मापा गया S 'समन्वय प्रणाली की उत्पत्ति की विश्व रेखा का प्रतिनिधित्व करता है। इस आंकड़े में, <math>v = c/2.</math> दोनों <math>ct'</math> तथा <math>x'</math> अक्षों को एक कोण द्वारा अप्रकाशित अक्षों से झुकाया जाता है <math>\alpha = \tan^{-1}(\beta),</math> जहाँ <math>\beta = v/c.</math> प्राइमेड और अनप्रिम्ड अक्ष एक सामान्य मूल साझा करते हैं क्योंकि सीमा रेखा S और S 'मानक विन्यास में स्थापित किए गए थे, ताकि <math>t=0</math> जब <math>t'=0.</math> | |||
चित्र 3-1 c। प्राइमेड अक्ष में यूनिट्स का स्केल अनप्रिम्ड अक्ष में यूनिट्स से अलग होता है। लोरेंत्ज़ परिवर्तनों से, हम देखते हैं कि <math>(x', ct')</math> के निर्देशांक <math>(0, 1)</math> प्राइमेड निर्देशांक सिस्टम में रूपांतरित करें <math> (\beta \gamma, \gamma)</math> अप्रकाशित समन्वय प्रणाली में वैसे ही, <math>(x', ct')</math> के निर्देशांक <math>(1, 0)</math> प्राइमेड निर्देशांक सिस्टम में रूपांतरित करें <math>(\gamma, \beta \gamma)</math> अप्रशिक्षित प्रणाली में के समानांतर ग्रिडलाइन बनाएं <math>ct'</math> बिंदुओं के माध्यम से अक्ष <math>(k \gamma, k \beta \gamma)</math> जैसा कि अप्रकाशित सीमा रेखा में मापा जाता है, जहां <math> k </math> एक पूर्णांक है। इसी तरह, ग्रिडलाइन को समानांतर बनाएं <math>x'</math> अक्ष के माध्यम से <math>(k \beta \gamma, k \gamma)</math> जैसा कि अनप्रिमेड सीमा रेखा में मापा जाता है। पाइथागोरस प्रमेय का उपयोग करते हुए, हम देखते हैं कि के बीच की दूरी <math>ct'</math> इकाइयाँ बराबर होती हैं <math display="inline">\sqrt{(1 + \beta ^2)/(1 - \beta ^2)}</math> के बीच की दूरी का गुना <math>ct</math> इकाइयाँ, जैसा कि सीमा रेखा S में मापा जाता है। यह अनुपात सदैव 1 से अधिक होता है, और अंततः यह अनंत तक पहुँचता है <math>\beta \to 1.</math> | |||
चित्र 3-1d। चूंकि प्रकाश की गति एक अपरिवर्तनीय है, इसलिए समय पर मूल से गुजरने वाले दो फोटोन की ''सांसारिक रेखाएं'' <math>t' = 0</math> अभी भी 45° विकर्ण रेखाओं के रूप में प्लॉट करें। के प्राइमेड निर्देशांक <math>\text{A}</math> तथा <math>\text{B}</math> लोरेंत्ज़ परिवर्तनों के माध्यम से अप्रकाशित निर्देशांक से संबंधित हैं और लगभग ग्राफ से मापा जा सकता है (यह मानते हुए कि इसे सटीक रूप से पर्याप्त रूप से प्लॉट किया गया है), लेकिन मिंकोव्स्की आरेख की वास्तविक योग्यता हमें परिदृश्य का एक ज्यामितीय दृश्य प्रदान करना है। उदाहरण के लिए, इस आकृति में, हम देखते हैं कि दो समय-समान-पृथक घटनाएँ जिनके अप्रकाशित सीमा रेखा में अलग-अलग x-निर्देशांक थे, अब अंतरिक्ष में एक ही स्थिति में हैं। | |||
जबकि अप्रकाशित | जबकि अप्रकाशित सीमा रेखा को अंतरिक्ष और समय अक्षों के साथ खींचा जाता है जो समकोण पर मिलते हैं, प्राइमेड सीमा रेखा अक्षों के साथ खींचा जाता है जो तीव्र या अधिक कोणों पर मिलते हैं। यह विषमता अपरिहार्य विकृतियों के कारण है कि कैसे स्पेसटाइम एक कार्टेशियन विमान पर मानचित्र का समन्वय करता है, लेकिन सीमा रेखा वास्तव में समकक्ष हैं। | ||
== लोरेंत्ज़ परिवर्तन से प्राप्त परिणाम == | == लोरेंत्ज़ परिवर्तन से प्राप्त परिणाम == | ||
{{See also| | {{See also|युग्मीय विरोधाभास|सापेक्षवादी यांत्रिकी}} | ||
विशेष सापेक्षता के परिणाम लोरेंत्ज़ रूपांतरण समीकरणों से प्राप्त किए जा सकते हैं।<ref>{{cite book |title=Introduction to special relativity |author=Robert Resnick |publisher=Wiley |date=1968|pages=62–63 |isbn=9780471717249 |url=https://books.google.com/books?id=fsIRAQAAIAAJ}}</ref> ये परिवर्तन, और इसलिए विशेष सापेक्षता, सभी सापेक्ष वेगों पर न्यूटनियन यांत्रिकी की तुलना में अलग-अलग भौतिक भविष्यवाणियों की ओर ले जाते हैं, और सबसे स्पष्ट जब सापेक्ष वेग प्रकाश की गति के बराबर हो जाते हैं।अधिकांश मनुष्यों का सामना करने वाली किसी भी चीज़ की तुलना में प्रकाश की गति इतनी अधिक होती है कि सापेक्षता द्वारा भविष्यवाणी किए गए कुछ प्रभाव शुरू में विपरीत होते हैं। | विशेष सापेक्षता के परिणाम लोरेंत्ज़ रूपांतरण समीकरणों से प्राप्त किए जा सकते हैं।<ref>{{cite book |title=Introduction to special relativity |author=Robert Resnick |publisher=Wiley |date=1968|pages=62–63 |isbn=9780471717249 |url=https://books.google.com/books?id=fsIRAQAAIAAJ}}</ref> ये परिवर्तन, और इसलिए विशेष सापेक्षता, सभी सापेक्ष वेगों पर न्यूटनियन यांत्रिकी की तुलना में अलग-अलग भौतिक भविष्यवाणियों की ओर ले जाते हैं, और सबसे स्पष्ट जब सापेक्ष वेग प्रकाश की गति के बराबर हो जाते हैं।अधिकांश मनुष्यों का सामना करने वाली किसी भी चीज़ की तुलना में प्रकाश की गति इतनी अधिक होती है कि सापेक्षता द्वारा भविष्यवाणी किए गए कुछ प्रभाव शुरू में विपरीत होते हैं। | ||
| Line 147: | Line 151: | ||
<br/>{{pad|4}} | <br/>{{pad|4}} | ||
Impressed by Lorentz's "most ingenious idea", Poincaré saw more in local time than a mere mathematical trick. It represented the actual time that would be shown on a moving observer's clocks. On the other hand, Poincaré did not consider this measured time to be the "true time" that would be exhibited by clocks at rest in the aether. Poincaré made no attempt to redefine the concepts of space and time. To Poincaré, Lorentz transformation described the ''apparent'' states of the field for a moving observer. ''True states'' remained those defined with respect to the ether.<ref name="Darrigol2005">{{cite journal |last1=Darrigol |first1=Olivier |title=The Genesis of the Theory of Relativity |journal=Séminaire Poincaré |date=2005 |volume=1 |pages=1–22 |url=http://www.bourbaphy.fr/darrigol2.pdf |access-date=15 November 2018 |bibcode=2006eins.book....1D }}</ref>}} | Impressed by Lorentz's "most ingenious idea", Poincaré saw more in local time than a mere mathematical trick. It represented the actual time that would be shown on a moving observer's clocks. On the other hand, Poincaré did not consider this measured time to be the "true time" that would be exhibited by clocks at rest in the aether. Poincaré made no attempt to redefine the concepts of space and time. To Poincaré, Lorentz transformation described the ''apparent'' states of the field for a moving observer. ''True states'' remained those defined with respect to the ether.<ref name="Darrigol2005">{{cite journal |last1=Darrigol |first1=Olivier |title=The Genesis of the Theory of Relativity |journal=Séminaire Poincaré |date=2005 |volume=1 |pages=1–22 |url=http://www.bourbaphy.fr/darrigol2.pdf |access-date=15 November 2018 |bibcode=2006eins.book....1D }}</ref>}} | ||
विशेष सापेक्षता में, | विशेष सापेक्षता में, यद्यपि, स्थानिक और लौकिक निर्देशांकों की परस्पर बुनाई एक अपरिवर्तनीय अंतराल की अवधारणा को उत्पन्न करती है, जिसे निरूपित किया जाता है {{nowrap|<math>\Delta s^2</math>:}}<ref group="note">This concept is counterintuitive at least for the fact that, in contrast to usual concepts of [[distance]], it may assume ''negative'' values (is not [[Positive-definite bilinear form|positive definite]] for non-coinciding events), and that the ''square''-denotation is misleading. This ''negative square'' lead to, now not broadly used, concepts of [[Minkowski space#History|''imaginary time'']]. It is immediate that the negative of <math>\Delta s^2</math> is also an invariant, generated by a variant of the [[metric signature]] of spacetime.</ref> | ||
<math display="block"> \Delta s^2 \; \overset\text{def}{=} \; c^2 \Delta t^2 - (\Delta x^2 + \Delta y^2 + \Delta z^2) </math> | <math display="block"> \Delta s^2 \; \overset\text{def}{=} \; c^2 \Delta t^2 - (\Delta x^2 + \Delta y^2 + \Delta z^2) </math> | ||
अंतरिक्ष और समय की इंटरविविंग गैर-कोविंग | अंतरिक्ष और समय की इंटरविविंग गैर-कोविंग सीमा रेखा में पूर्ण एक साथ और सिंक्रनाइज़ेशन की अंतर्निहित रूप से ग्रहण की गई अवधारणाओं को रद्द कर देती है। | ||
<math>\Delta s^2 ,</math> | <math>\Delta s^2 ,</math> रुंडित समय व्यतीत होने और रुंडित स्थानिक दूरी का अंतर होने के कारण, यूक्लिडियन और स्पेसटाइम दूरियों के बीच एक मूलभूत विसंगति को प्रदर्शित करता है।{{refn| group=note|The invariance of Δs<sup>2</sup> under standard Lorentz transformation in analogous to the invariance of squared distances Δr<sup>2</sup> under rotations in Euclidean space. Although space and time have an equal ''footing'' in relativity, the minus sign in front of the spatial terms marks space and time as being of essentially different character. They are not the same. Because it treats time differently than it treats the 3 spatial dimensions, [[Minkowski space]] differs from [[four-dimensional Euclidean space]].}} इस अंतराल का अपरिवर्तन सामान्य लोरेंत्ज़ रूपांतरित (जिसे पोंकारे रूपांतरण भी कहा जाता है) की एक संपत्ति है, जिससे यह स्पेसटाइम का एक [[ आइसोमेट्री ]] बन जाता है। सामान्य लोरेंत्ज़ रूपांतरित मानक लोरेंत्ज़ रूपांतरित का विस्तार करता है (जो घूर्णन के बिना स्थानांतरणों से संबंधित है, अर्थात, लोरेंत्ज़ एक्स-दिशा में बूस्ट करता है) अन्य सभी स्थानांतरण (ज्यामिति), परावर्तन (गणित), और घूर्णन (गणित) के बीच किसी भी कार्टेशियन के बीच जड़त्वीय सीमा रेखा।<ref name="Rindler1977">{{cite book |last1=Rindler |first1=Wolfgang |title=Essential Relativity |date=1977 | publisher=Springer-Verlag |location=New York |isbn=978-0-387-10090-6 |edition=2nd}}</ref>{{rp|33–34}} | ||
सरलीकृत परिदृश्यों के विश्लेषण में, जैसे कि स्पेसटाइम आरेख, अपरिवर्तनीय अंतराल का एक कम-आयामी रूप | सरलीकृत परिदृश्यों के विश्लेषण में, जैसे कि स्पेसटाइम आरेख, अपरिवर्तनीय अंतराल का एक कम-आयामी रूप अधिकांशतः नियोजित होता है: | ||
<math display="block">\Delta s^2 \, = \, c^2 \Delta t^2 - \Delta x^2</math> | <math display="block">\Delta s^2 \, = \, c^2 \Delta t^2 - \Delta x^2</math> | ||
यह दर्शाता है कि अंतराल अपरिवर्तनीय है, कम-आयामी | यह दर्शाता है कि अंतराल अपरिवर्तनीय है, कम-आयामी परिस्थिति के लिए और मानक विन्यास में फ़्रेम के साथ सीधा है:<ref name=Morin2007/> | ||
<math display="block">\begin{align} | <math display="block">\begin{align} | ||
c^2 \Delta t^2 - \Delta x^2 &= c^2 \gamma ^2 \left(\Delta t' + \dfrac{v \Delta x'}{c^2} \right)^2 - \gamma ^2 \ (\Delta x' + v \Delta t')^2 \\ | c^2 \Delta t^2 - \Delta x^2 &= c^2 \gamma ^2 \left(\Delta t' + \dfrac{v \Delta x'}{c^2} \right)^2 - \gamma ^2 \ (\Delta x' + v \Delta t')^2 \\ | ||
| Line 162: | Line 166: | ||
&= c^2 \Delta t' ^{\, 2} - \Delta x' ^{\, 2} | &= c^2 \Delta t' ^{\, 2} - \Delta x' ^{\, 2} | ||
\end{align}</math> | \end{align}</math> | ||
का मूल्य <math>\Delta s^2</math> इसलिए उस | का मूल्य <math>\Delta s^2</math> इसलिए उस सीमा रेखा से स्वतंत्र है जिसमें इसे मापा जाता है। | ||
के भौतिक महत्व को देखते हुए <math>\Delta s^2</math>, ध्यान देने योग्य तीन | के भौतिक महत्व को देखते हुए <math>\Delta s^2</math>, ध्यान देने योग्य तीन परिस्थिति हैं:<ref name=Morin2007/><ref name="Taylor1966"/>{{rp|25–39}} | ||
*Δs<sup>2</sup> > 0: इस | *Δs<sup>2</sup> > 0: इस परिस्थिति में, दो घटनाओं को अंतरिक्ष की तुलना में अधिक समय से अलग किया जाता है, और इसलिए उन्हें 'समय की तरह' अलग कहा जाता है। यह बताता है कि <math>| \Delta x / \Delta t | < c ,</math> और लोरेंत्ज़ परिवर्तन दिया <math>\Delta x' = \gamma \ (\Delta x - v \,\Delta t) ,</math> यह स्पष्ट है कि वहाँ उपलब्ध है a <math>v</math> से कम <math>c</math> जिसके लिए <math>\Delta x' = 0</math> (विशेष रूप से, <math>v = \Delta x / \Delta t</math>) दूसरे शब्दों में, दो घटनाओं को देखते हुए जो समयबद्ध रूप से अलग हैं, एक सीमा रेखा खोजना संभव है जिसमें दो घटनाएं एक ही स्थान पर होती हैं। इस सीमा रेखा में, समय में अलगाव, <math> \Delta s / c,</math> उचित समय कहा जाता है। | ||
*'Δs<sup>2</sup> < 0: इस | *'Δs<sup>2</sup> < 0: इस परिस्थिति में, दो घटनाओं को समय की तुलना में अधिक स्थान से अलग किया जाता है, और इसलिए उन्हें अलग किया गया ''स्पेसलाइक'' कहा जाता है। यह बताता है कि <math>| \Delta x / \Delta t | > c ,</math> और लोरेंत्ज़ परिवर्तन दिया <math>\Delta t' = \gamma \ (\Delta t - v \Delta x / c^2) ,</math> वहाँ एक उपलब्ध है <math>v</math> से कम <math>c</math> जिसके लिए <math>\Delta t' = 0</math> (विशेष रूप से, <math> v = c^2 \Delta t / \Delta x</math>) दूसरे शब्दों में, दो घटनाओं को देखते हुए जो अंतरिक्ष की तरह अलग हैं, एक सीमा रेखा खोजना संभव है जिसमें दो घटनाएं एक ही समय में होती हैं। इस सीमा रेखा में, अंतरिक्ष में अलगाव, <math> \sqrt { - \Delta s^2 }, </math> उचित दूरी, या उचित लंबाई कहा जाता है। के मूल्यों के लिए <math>v</math> से बड़ा और कम <math> c^2 \Delta t / \Delta x , </math> का चिन्ह <math>\Delta t'</math> परिवर्तन, जिसका अर्थ है कि अंतरिक्ष-समान-पृथक घटनाओं का अस्थायी क्रम उस सीमा रेखा के आधार पर बदलता है जिसमें घटनाओं को देखा जाता है। हालाँकि, समयबद्ध-पृथक घटनाओं का अस्थायी क्रम निरपेक्ष है, क्योंकि एकमात्र तरीका है कि <math>v</math> से बड़ा हो सकता है <math> c^2 \Delta t / \Delta x</math> होगा अगर <math> v > c .</math> | ||
*Δs<sup>2</sup> = 0: इस | *Δs<sup>2</sup> = 0: इस परिस्थिति में, दो घटनाओं को अलग-अलग ''हल्का सा''' कहा जाता है। यह बताता है कि <math>| \Delta x / \Delta t | = c ,</math> और यह संबंध के अपरिवर्तन के कारण सीमा रेखा स्वतंत्र है <math>s^2 .</math> इससे हम देखते हैं कि प्रकाश की गति है <math>c</math> हर जड़त्वीय सीमा रेखा में। दूसरे शब्दों में, सार्वभौमिक लोरेंत्ज़ सहप्रसरण की धारणा से शुरू होकर, प्रकाश की निरंतर गति एक व्युत्पन्न परिणाम है, न कि एक विशेष सिद्धांत के दो-अभिधारणाओं के निर्माण के रूप में। | ||
=== एक साथ सापेक्षता === | === एक साथ सापेक्षता === | ||
{{See also| | {{See also|समकालिकता की सापेक्षता|लैडर विरोधाभास}} | ||
[[File:Relativity of Simultaneity Animation.gif|thumb|चित्र 4-1। तीन घटनाएँ (ए, बी, | [[File:Relativity of Simultaneity Animation.gif|thumb|चित्र 4-1। तीन घटनाएँ (ए, बी, c) कुछ पर्यवेक्षक ओ के निर्देश तंत्र में एक साथ हैं। एक निर्देश तंत्र में ''v'' = 0.3''c'' पर चलते हुए, जैसा कि O द्वारा मापा जाता है, घटनाएँ होती हैं क्रम c, बी, ए। एक निर्देश तंत्र में चल रहा है {{nowrap|1=''v'' = −0.5''c''}} O के संबंध में, घटनाएँ A, B, C के क्रम में घटित होती हैं। सफेद रेखाएँ, ''एक साथ रेखाएँ'', अतीत से भविष्य की ओर संबंधित फ़्रेमों (हरे रंग की समन्वय अक्षों) में चलती हैं, जो रहने वाली घटनाओं को उजागर करती हैं उन पर। वे संबंधित सीमा रेखा में एक ही समय में होने वाली सभी घटनाओं का स्थान हैं। सभी माने गए फ़्रेमों की उत्पत्ति के संबंध में ग्रे क्षेत्र [[ प्रकाश शंकु ]] है।]] | ||
दो अलग-अलग स्थानों में होने वाली दो घटनाओं पर विचार करें जो एक ही जड़त्वीय प्रेक्षक के | दो अलग-अलग स्थानों में होने वाली दो घटनाओं पर विचार करें जो एक ही जड़त्वीय प्रेक्षक के निर्देश तंत्र में एक साथ घटित होती हैं। वे गैर-एक साथ एक अन्य जड़त्वीय पर्यवेक्षक (पूर्ण एक साथ की कमी) के निर्देश तंत्र में हो सकते हैं। | ||
से {{EquationNote|3| | से {{EquationNote|3|समीकरण 3}} (समन्वय अंतर के संदर्भ में आगे लोरेंत्ज़ परिवर्तन) | ||
<math display="block">\Delta t' = \gamma \left(\Delta t - \frac{v \,\Delta x}{c^{2}} \right)</math> | <math display="block">\Delta t' = \gamma \left(\Delta t - \frac{v \,\Delta x}{c^{2}} \right)</math> | ||
यह स्पष्ट है कि दो घटनाएँ जो एक साथ | यह स्पष्ट है कि दो घटनाएँ जो एक साथ सीमा रेखा S (संतोषजनक .) में हैं {{nowrap|1=Δ''t'' = 0}}), जरूरी नहीं कि एक और जड़त्वीय सीमा रेखा S′ (संतोषजनक .) में एक साथ हों {{nowrap|1=Δ''t''′ = 0}}) केवल तभी जब ये घटनाएँ सीमा रेखा S में अतिरिक्त रूप से सह-स्थानीय हों (संतोषजनक .) {{nowrap|1=Δ''x'' = 0}}), क्या वे एक साथ दूसरे सीमा रेखा S′ में होंगे। | ||
सैगनैक प्रभाव को एक साथ सापेक्षता की अभिव्यक्ति माना जा सकता है।<ref name="Ashby2003">{{cite journal |last1=Ashby |first1=Neil |title=Relativity in the Global Positioning System |journal=Living Reviews in Relativity |volume=6 |issue=1 |pages=1 |doi=10.12942/lrr-2003-1 |pmid=28163638 |pmc=5253894 |year=2003 |bibcode=2003LRR.....6....1A }}</ref> चूँकि समकालिकता की सापेक्षता प्रथम कोटि का प्रभाव है <math>v</math>,<ref name=Morin2007/>उनके संचालन के लिए सैगनैक प्रभाव पर आधारित उपकरण, जैसे कि रिंग लेजर गायरोस्कोप और [[ फाइबर ऑप्टिक जाइरोस्कोप ]], संवेदनशीलता के चरम स्तर में सक्षम हैं।<ref name="Lin1979" group="p">{{cite journal |last1=Lin |first1=Shih-Chun |last2=Giallorenzi |first2=Thomas G. |title=Sensitivity analysis of the Sagnac-effect optical-fiber ring interferometer |journal=Applied Optics |date=1979 |volume=18 |issue=6 |pages=915–931 |doi=10.1364/AO.18.000915|pmid=20208844 |bibcode=1979ApOpt..18..915L |s2cid=5343180 |url=https://semanticscholar.org/paper/753964d7afc914de57f7d5186e70b01c1dcefeb6 }}</ref> | |||
=== समय | === समय विस्तार === | ||
{{See also| | {{See also|समय विस्तार}} | ||
दो घटनाओं के बीच का समय एक पर्यवेक्षक से दूसरे पर्यवेक्षक के लिए अपरिवर्तनीय नहीं है, लेकिन पर्यवेक्षकों के | दो घटनाओं के बीच का समय एक पर्यवेक्षक से दूसरे पर्यवेक्षक के लिए अपरिवर्तनीय नहीं है, लेकिन पर्यवेक्षकों के निर्देश तंत्र की सापेक्ष गति पर निर्भर है (उदाहरण के लिए, युगल विरोधाभास जो एक युगल से संबंधित है जो प्रकाश की गति के निकट यात्रा करने वाले अंतरिक्ष यान में उड़ जाता है और यह पता लगाने के लिए लौटता है कि गैर-यात्रा करने वाले युगल भाई की उम्र बहुत अधिक है, विरोधाभास यह है कि निरंतर वेग से हम यह समझने में असमर्थ हैं कि कौन सा युगल यात्रा नहीं कर रहा है और कौन सा युगल यात्रा करता है)। | ||
मान लीजिए कि एक [[ घड़ी ]] बिना प्राइमेड सिस्टम | मान लीजिए कि एक [[ घड़ी | चालमापी]] बिना प्राइमेड सिस्टम S में विराम पर है। दो अलग-अलग टिकों पर चालमापी की स्थिति को Δx = 0 से चिह्नित किया जाता है। दोनों प्रणालियों में मापा गया इन टिकों के बीच के समय के बीच संबंध खोजने के लिए, {{EquationNote|3|समीकरण 3}} का उपयोग किया जा सकता है : | ||
:<math>\Delta t' = \gamma\, \Delta t </math>{{pad|4}}संतोषजनक घटनाओं के लिए{{pad|4}}<math>\Delta x = 0 \ .</math> | :<math>\Delta t' = \gamma\, \Delta t </math>{{pad|4}}संतोषजनक घटनाओं के लिए{{pad|4}}<math>\Delta x = 0 \ .</math> | ||
इससे पता चलता है कि दो टिकों के बीच का समय (Δt′) जैसा कि उस | इससे पता चलता है कि दो टिकों के बीच का समय (Δt′) जैसा कि उस सीमा रेखा में देखा गया है जिसमें चालमापी चल रही है (S′), इन टिकों के बीच के समय (Δt) से अधिक लंबा है जैसा कि चालमापी के बाकी सीमा रेखा में मापा जाता है ( S)। समय का विस्तार कई भौतिक घटनाओं की व्याख्या करता है; उदाहरण के लिए, पृथ्वी के बाहरी वायुमंडल में कणों के साथ कॉस्मिक किरणों के टकराने और सतह की ओर बढ़ने से निर्मित उच्च गति वाले म्यूऑन का जीवनकाल, प्रयोगशाला में निर्मित और क्षय होने वाले धीरे-धीरे चलने वाले म्यूऑन के जीवनकाल से अधिक होता है।<ref>{{cite book|author1=Daniel Kleppner|author2=David Kolenkow|name-list-style=amp|title=An Introduction to Mechanics|date=1973|pages=[https://archive.org/details/introductiontome00dani/page/468 468–70]|isbn=978-0-07-035048-9|url=https://archive.org/details/introductiontome00dani/page/468}}</ref> | ||
=== लंबाई संकुचन === | === लंबाई संकुचन === | ||
{{See also| | {{See also|लोरेंत्ज़ संकुचन}} | ||
एक पर्यवेक्षक द्वारा मापी गई वस्तु के आयाम (जैसे, लंबाई) दूसरे पर्यवेक्षक द्वारा किए गए | एक पर्यवेक्षक द्वारा मापी गई किसी वस्तु के आयाम (जैसे, लंबाई) दूसरे पर्यवेक्षक द्वारा किए गए उc वस्तु के माप के परिणामों से छोटे हो सकते हैं (उदाहरण के लिए, [[ सीढ़ी विरोधाभास | cढ़ी विरोधाभास]] में प्रकाश की गति के निकट यात्रा करने वाली और समाहित होने वाली एक लंबी cढ़ी सम्मिलित है) एक छोटे गैरेज के भीतर)। | ||
इसी तरह, मान लीजिए कि एक मापने वाली छड़ | इसी तरह, मान लीजिए कि एक मापने वाली छड़ विराम पर है और अनप्रिम्ड सिस्टम S में x-अक्ष के साथ संरेखित है। इस प्रणाली में, इस छड़ की लंबाई Δx के रूप में लिखी जाती है। सिस्टम S′ में इस रॉड की लंबाई को मापने के लिए, जिसमें रॉड चलती है, रॉड के अंतिम बिंदुओं के लिए x′ की दूरी को उc सिस्टम S′ में एक साथ मापा जाना चाहिए। दूसरे शब्दों में, माप की विशेषता है {{nowrap|1=Δ''t''′ = 0}} है, जिसे x और Δx′ की {{EquationNote|4|समीकरण 4}} लंबाई के बीच संबंध खोजने के लिए समीकरण 4 के साथ जोड़ा जा सकता है: | ||
:<math>\Delta x' = \frac{\Delta x}{\gamma} </math>{{pad|4}}{{pad|4}}संतोषजनक घटनाओं के लिए{{pad|4}}<math>\Delta t' = 0 \ .</math> | :<math>\Delta x' = \frac{\Delta x}{\gamma} </math>{{pad|4}}{{pad|4}}संतोषजनक घटनाओं के लिए{{pad|4}}<math>\Delta t' = 0 \ .</math> | ||
इससे पता चलता है कि छड़ की लंबाई (Δx′) जिस | इससे पता चलता है कि छड़ की लंबाई (Δx′) जिस सीमा रेखा में चलती है (S′) में मापी जाती है, वह अपने स्वयं के विराम सीमा रेखा (S) में इसकी लंबाई (Δx) से कम होती है। | ||
समय का | समय का विस्तार और लंबाई का संकुचन केवल दिखावे नहीं हैं। समय विस्तार स्पष्ट रूप से किसी दिए गए समन्वय प्रणाली में एक ही स्थान पर होने वाली घटनाओं के बीच समय अंतराल को मापने के हमारे तरीके से संबंधित है (जिसे "सह-स्थानीय" घटनाएं कहा जाता है)। ये समय अंतराल (जो प्रासंगिक पर्यवेक्षकों द्वारा वास्तव में प्रयोगात्मक रूप से मापा जा सकता है, और हैं) पहले के संबंध में आगे बढ़ने वाली एक अन्य समन्वय प्रणाली में भिन्न हैं, जब तक कि सह-स्थानीय होने के अलावा घटनाएं भी एक साथ नहीं होती हैं। इसी तरह, लंबाई संकुचन पसंद के दिए गए समन्वय प्रणाली में अलग लेकिन एक साथ घटनाओं के बीच हमारी मापी गई दूरियों से संबंधित है। यदि ये घटनाएँ सह-स्थानीय नहीं हैं, लेकिन दूरी (अंतरिक्ष) द्वारा अलग की जाती हैं, तो वे एक दूसरे से समान स्थानिक दूरी पर नहीं घटित होंगी जब किसी अन्य चलती समन्वय प्रणाली से देखा जाए। | ||
=== वेगों का लोरेंत्ज़ परिवर्तन === | === वेगों का लोरेंत्ज़ परिवर्तन === | ||
{{See also| | {{See also|वेग-जोड़ सूत्र}} | ||
मानक विन्यास में दो | मानक विन्यास में दो सीमा रेखा S और S′ पर विचार करें। S में एक कण x दिशा में वेग सदिश के साथ गति करता है <math>\mathbf{u}.</math> इसका वेग क्या है <math>\mathbf{u'}</math> सीमा रेखा में S′ ? | ||
हम लिख सकते हैं | हम लिख सकते हैं | ||
| Line 208: | Line 212: | ||
{{NumBlk||<math display="block"> \mathbf{|u'|} = u' = dx' / dt' \, . </math>|{{EquationRef|8}}}} | {{NumBlk||<math display="block"> \mathbf{|u'|} = u' = dx' / dt' \, . </math>|{{EquationRef|8}}}} | ||
व्यंजकों को के लिए प्रतिस्थापित करना <math>dx'</math> तथा <math>dt'</math> से {{EquationNote|5| | व्यंजकों को के लिए प्रतिस्थापित करना <math>dx'</math> तथा <math>dt'</math> से {{EquationNote|5|समीकरण 5}} में {{EquationNote|8|समीकरण 8}}, इसके बाद सीधे गणितीय जोड़तोड़ और बैक-प्रतिस्थापन से {{EquationNote|7|समीकरण 7}} गति के लोरेंत्ज़ परिवर्तन उत्पन्न करता है <math>u</math> प्रति <math>u'</math>: | ||
{{NumBlk||<math display="block">u' = \frac{dx'}{dt'}=\frac{\gamma(dx-v dt)}{\gamma \left (dt-\frac{v dx}{c^2} \right )} = \frac{\frac{dx}{dt}-v}{1-\left ( \frac{v}{c^2} \right )\left ( \frac{dx}{dt} \right ) } =\frac{u-v}{1- uv / c^2}. </math>|{{EquationRef|9}}}} | {{NumBlk||<math display="block">u' = \frac{dx'}{dt'}=\frac{\gamma(dx-v dt)}{\gamma \left (dt-\frac{v dx}{c^2} \right )} = \frac{\frac{dx}{dt}-v}{1-\left ( \frac{v}{c^2} \right )\left ( \frac{dx}{dt} \right ) } =\frac{u-v}{1- uv / c^2}. </math>|{{EquationRef|9}}}} | ||
| Line 218: | Line 222: | ||
{{NumBlk||<math display="block"> \mathbf{u'} = (u_1', \ u_2', \ u_3') = ( dx' / dt', \ dy'/dt', \ dz'/dt') \ . </math>|{{EquationRef|12}}}} | {{NumBlk||<math display="block"> \mathbf{u'} = (u_1', \ u_2', \ u_3') = ( dx' / dt', \ dy'/dt', \ dz'/dt') \ . </math>|{{EquationRef|12}}}} | ||
इस | इस परिस्थिति के लिए आगे और उलटा परिवर्तन हैं: | ||
{{NumBlk||<math display="block">u_1'=\frac{u_1 -v}{1-u_1 v / c^2 } \ , \qquad u_2'=\frac{u_2}{\gamma \left( 1-u_1 v / c^2 \right) } \ , \qquad u_3'=\frac{u_3}{\gamma \left( 1- u_1 v / c^2 \right) } \ . </math>|{{EquationRef|13}}}} | {{NumBlk||<math display="block">u_1'=\frac{u_1 -v}{1-u_1 v / c^2 } \ , \qquad u_2'=\frac{u_2}{\gamma \left( 1-u_1 v / c^2 \right) } \ , \qquad u_3'=\frac{u_3}{\gamma \left( 1- u_1 v / c^2 \right) } \ . </math>|{{EquationRef|13}}}} | ||
{{NumBlk||<math display="block">u_1=\frac{u_1' +v}{1+ u_1' v / c^2 } \ , \qquad u_2=\frac{u_2'}{ \gamma \left( 1+ u_1' v / c^2 \right) } \ , \qquad u_3=\frac{u_3'}{\gamma \left( 1+ u_1' v / c^2 \right)} \ . </math>|{{EquationRef|14}}}} | {{NumBlk||<math display="block">u_1=\frac{u_1' +v}{1+ u_1' v / c^2 } \ , \qquad u_2=\frac{u_2'}{ \gamma \left( 1+ u_1' v / c^2 \right) } \ , \qquad u_3=\frac{u_3'}{\gamma \left( 1+ u_1' v / c^2 \right)} \ . </math>|{{EquationRef|14}}}} | ||
{{EquationNote|10| | {{EquationNote|10|समीकरण 10}} तथा {{EquationNote|14|समीकरण 14}} परिणामी देने के रूप में व्याख्या की जा सकती है <math> \mathbf{u} </math> दो वेगों के <math> \mathbf{v} </math> तथा <math> \mathbf{u'}, </math> और वे सूत्र की जगह लेते हैं <math> \mathbf{u = u' + v} </math> जो गैलीलियन सापेक्षता में मान्य है। इस तरह से व्याख्या की गई, उन्हें सामान्यतः पर सापेक्षिक वेग जोड़ (या संरचना) सूत्रों के रूप में संदर्भित किया जाता है, जो S और S के तीन अक्षों के लिए एक दूसरे के साथ गठबंधन होने के लिए मान्य है (यद्यपि मानक विन्यास में जरूरी नहीं है)।<ref name="Rindler0"/>{{rp|47–49}} | ||
हम निम्नलिखित बिंदुओं को लिखते हैं: | हम निम्नलिखित बिंदुओं को लिखते हैं: | ||
* यदि कोई वस्तु (जैसे, एक फोटान) एक | * यदि कोई वस्तु (जैसे, एक फोटान) एक सीमा रेखा में प्रकाश की गति से घूम रही हो {{nowrap|1=(i.e., ''u'' = ±''c''}} {{nowrap|1=or ''u′'' = ±''c''),}} तो यह किसी अन्य सीमा रेखा में प्रकाश की गति से भी गतिमान हो रहा होगा {{nowrap|{{abs|''v''}} < ''c''}}. | ||
* c से कम परिमाण वाले दो वेगों की परिणामी गति | * c से कम परिमाण वाले दो वेगों की परिणामी गति सदैव c से कम परिमाण वाला वेग होता है। | ||
*यदि दोनों |u| और |v| (और फिर भी |u′| और |v′|) प्रकाश की गति के संबंध में छोटे हैं (अर्थात, {{nowrap|e.g., {{abs|{{sfrac|''u''|''c''}}}} ≪ {{math|1}}),}} तब विशेष सापेक्षता के लिए परिवर्तन समीकरणों से सहज गैलीलियन परिवर्तन पुनर्प्राप्त किए जाते हैं | *यदि दोनों |u| और |v| (और फिर भी |u′| और |v′|) प्रकाश की गति के संबंध में छोटे हैं (अर्थात, {{nowrap|e.g., {{abs|{{sfrac|''u''|''c''}}}} ≪ {{math|1}}),}} तब विशेष सापेक्षता के लिए परिवर्तन समीकरणों से सहज गैलीलियन परिवर्तन पुनर्प्राप्त किए जाते हैं | ||
* एक फोटॉन को एक | * एक फोटॉन को एक सीमा रेखा संलग्न करना (आइंस्टीन की तरह एक प्रकाश किरण की सवारी करना) को परिवर्तनों के विशेष उपचार की आवश्यकता होती है। | ||
मानक विन्यास में x दिशा के बारे में कुछ खास नहीं है। उपरोक्त [[ औपचारिकता (गणित) ]] किसी भी दिशा में लागू होती है; और तीन ओर्थोगोनल दिशाएं इन दिशाओं में उनके घटकों के वेग वैक्टर को विघटित करके अंतरिक्ष में सभी दिशाओं से निपटने की अनुमति देती हैं। विवरण के लिए वेग-जोड़ सूत्र देखें। | मानक विन्यास में x दिशा के बारे में कुछ खास नहीं है। उपरोक्त [[ औपचारिकता (गणित) ]] किसी भी दिशा में लागू होती है; और तीन ओर्थोगोनल दिशाएं इन दिशाओं में उनके घटकों के वेग वैक्टर को विघटित करके अंतरिक्ष में सभी दिशाओं से निपटने की अनुमति देती हैं। विवरण के लिए वेग-जोड़ सूत्र देखें। | ||
=== थॉमस | === थॉमस घूर्णन === | ||
{{See also| | {{See also|थॉमस रोटेशन}} | ||
{{multiple image | {{multiple image | ||
| direction = vertical | | direction = vertical | ||
| Line 240: | Line 244: | ||
| image2 = Thomas-Wigner Rotation 2.svg | | image2 = Thomas-Wigner Rotation 2.svg | ||
}} | }} | ||
दो गैर-कोलिनियर लोरेंत्ज़ | दो गैर-कोलिनियर लोरेंत्ज़ बूस्ट की संरचना (अर्थात, दो गैर-कोलिनियर लोरेंत्ज़ रूपांतरण, जिनमें से कोई भी घूर्णन सम्मिलित नहीं है) के परिणामस्वरूप लोरेंत्ज़ परिवर्तन होता है जो शुद्ध वृद्धि नहीं है बल्कि एक वृद्धि और घूर्णन की संरचना है। | ||
थॉमस | थॉमस घूर्णन एक साथ सापेक्षता का परिणाम है। चित्र में। 4-2a, लंबाई की एक छड़ <math>L</math> इसके बाकी सीमा रेखा में (अर्थात, जिसकी [[ उचित लंबाई ]] है) <math>L</math>) जमीन के सीमा रेखा में y-अक्ष के अनुदिश लंबवत रूप से ऊपर उठती है। | ||
चित्र में। 4-2b, गति से चलते हुए रॉकेट के सीमा रेखा से एक ही छड़ देखी जाती है <math>v</math> दांई ओर। यदि हम रॉड के बाएं और दाएं छोर पर स्थित दो समयों की कल्पना करते हैं जो रॉड के सीमा रेखा में सिंक्रोनाइज्ड हैं, तो एक साथ सापेक्षता की वजह से रॉकेट सीमा रेखा में ऑब्जर्वर प्रेक्षक (#Measurement_versus_visual_appearance नहीं) चालमापी के दाहिने छोर पर स्थित है। रॉड द्वारा समय में उन्नत किया जा रहा है <math>Lv/c^2 ,</math> और छड़ को तदनुरूप झुके हुए के रूप में देखा जाता है।<ref name="Taylor1966">{{cite book |last1=Taylor |first1=Edwin F. |last2=Wheeler |first2=John Archibald |title=Spacetime Physics |url=https://archive.org/details/spacetimephysics0000tayl |url-access=registration |date=1966 |publisher=W. H. Freeman and Company |location=San Francisco |edition=1st}}</ref>{{rp|98–99}} | |||
दूसरे क्रम के सापेक्षतावादी प्रभावों जैसे कि लंबाई संकुचन या समय | दूसरे क्रम के सापेक्षतावादी प्रभावों जैसे कि लंबाई संकुचन या समय विस्तार के विपरीत, यह प्रभाव काफी कम वेग पर भी काफी महत्वपूर्ण हो जाता है। उदाहरण के लिए, इसे स्पिन-ऑर्बिट इंटरैक्शन में देखा जा सकता है, जहां थॉमस प्रीसेशन एक सापेक्ष सुधार है जो एक प्राथमिक कण के स्पिन (भौतिकी) या मैक्रोस्कोपिक [[ जाइरोस्कोप ]] के घूर्णन पर लागू होता है, जो स्पिन के कोणीय वेग से संबंधित होता है। कक्षीय गति के कोणीय वेग के लिए एक [[ वक्रीय ]] कक्षा का अनुसरण करने वाला कण।<ref name="Taylor1966"/>{{rp|169–174}} | ||
थॉमस | थॉमस घूर्णन प्रसिद्ध मीटर स्टिक और होल विरोधाभास को संकल्प प्रदान करता है।<ref name="Shaw" group=p>{{cite journal |last1=Shaw |first1=R. |title=Length Contraction Paradox |journal=American Journal of Physics |date=1962 |volume=30 |issue=1 |page=72 |doi=10.1119/1.1941907 |bibcode=1962AmJPh..30...72S |s2cid=119855914 |url=https://semanticscholar.org/paper/2bf0293bf38ed3c56949f6f889dde16fe5b26c31 }}</ref><ref name="Taylor1966"/>{{rp|98–99}} | ||
===कारण और प्रकाश की गति से तेज गति का निषेध === | ===कारण और प्रकाश की गति से तेज गति का निषेध === | ||
{{See also| | {{See also|कारण-कार्य-सिद्धान्त(भौतिकी)|टैच्योनिक एंटीटेलीफोन}} | ||
[[File:Simple light cone diagram.svg|thumb|चित्र 4–3। प्रकाश शंकु]] | [[File:Simple light cone diagram.svg|thumb|चित्र 4–3। प्रकाश शंकु]] | ||
चित्र 4-3 में, घटनाओं | चित्र 4-3 में, घटनाओं ए ("कारण") और बी ("प्रभाव") के बीच का समय अंतराल 'समय की तरह' है; अर्थात्, संदर्भ का एक ढांचा है जिसमें घटनाएँ A और B अंतरिक्ष में एक ही स्थान पर घटित होती हैं, केवल अलग-अलग समय पर घटित होने से अलग होती हैं। यदि ए उस सीमा रेखा में बी से पहले है, तो ए लोरेंत्ज़ रूपांतरितेशन द्वारा सुलभ सभी सीमा रेखाों में बी से पहले है। पदार्थ (या सूचना) के लिए A के स्थान से (प्रकाश की गति से कम) यात्रा करना संभव है, A के समय से शुरू होकर, B के स्थान तक, B के समय पर पहुँचता है, इसलिए एक कारण संबंध हो सकता है ( ए के साथ कारण और बी प्रभाव)। | ||
आरेख में अंतराल AC ' | आरेख में अंतराल AC 'अंतरिक्ष के समान' है; अर्थात्, संदर्भ का एक ढांचा है जिसमें घटनाएँ A और C एक साथ घटित होती हैं, केवल अंतरिक्ष में अलग होती हैं। ऐसे फ़्रेम भी हैं जिनमें A, C से पहले आता है (जैसा कि दिखाया गया है) और फ़्रेम जिसमें C, A से पहले है। यद्यपि, लोरेंत्ज़ रूपांतरण द्वारा कोई फ़्रेम एक्सेस नहीं किया जा सकता है, जिसमें ईवेंट A और C एक ही स्थान पर होते हैं। यदि घटना ए और c के बीच एक कारण और प्रभाव संबंध उपलब्ध होना संभव होता, तो कार्य-कारण के विरोधाभास का परिणाम होता हैं। | ||
उदाहरण के लिए, यदि संकेतों को प्रकाश की तुलना में तेजी से भेजा जा सकता है, तो संकेतों को प्रेषक के अतीत (आरेखों में पर्यवेक्षक बी) में भेजा जा सकता है।<ref>{{cite book | first = Richard C.|last = Tolman|title =The Theory of the Relativity of Motion |location=Berkeley|publisher = University of California Press|date = 1917|page = 54|url = https://books.google.com/books?id=8yodAAAAMAAJ&q=54}}</ref><ref group=p>{{cite journal|author1=G. A. Benford |author2=D. L. Book |author3=W. A. Newcomb |name-list-style=amp |doi=10.1103/PhysRevD.2.263|title=The Tachyonic Antitelephone|date=1970|journal=Physical Review D|volume=2|issue=2|pages=263–265|bibcode = 1970PhRvD...2..263B |s2cid=121124132 |url=https://semanticscholar.org/paper/0fbd29db01362f5bf2859ba8d30f528a29ee6cb9 }}</ref> तब विभिन्न प्रकार के कारण विरोधाभासों का निर्माण किया जा सकता था। | उदाहरण के लिए, यदि संकेतों को प्रकाश की तुलना में तेजी से भेजा जा सकता है, तो संकेतों को प्रेषक के अतीत (आरेखों में पर्यवेक्षक बी) में भेजा जा सकता है।<ref>{{cite book | first = Richard C.|last = Tolman|title =The Theory of the Relativity of Motion |location=Berkeley|publisher = University of California Press|date = 1917|page = 54|url = https://books.google.com/books?id=8yodAAAAMAAJ&q=54}}</ref><ref group=p>{{cite journal|author1=G. A. Benford |author2=D. L. Book |author3=W. A. Newcomb |name-list-style=amp |doi=10.1103/PhysRevD.2.263|title=The Tachyonic Antitelephone|date=1970|journal=Physical Review D|volume=2|issue=2|pages=263–265|bibcode = 1970PhRvD...2..263B |s2cid=121124132 |url=https://semanticscholar.org/paper/0fbd29db01362f5bf2859ba8d30f528a29ee6cb9 }}</ref> तब विभिन्न प्रकार के कारण विरोधाभासों का निर्माण किया जा सकता था। | ||
| Line 265: | Line 269: | ||
| alt2 = Three small white and yellow flowers before green-leaf background | | alt2 = Three small white and yellow flowers before green-leaf background | ||
| footer_align = center | | footer_align = center | ||
| footer = | | footer = चित्र 4-4. काल्पनिक के उपयोग से कारणता का उल्लंघन<br/>"तात्कालिक संचारक" | ||
}} | }} | ||
चित्र 4-4 में स्पेसटाइम आरेखों पर विचार करें। A और B एक रेल ट्रैक के साथ खड़े होते हैं, जब एक हाई-स्पीड ट्रेन गुजरती है, जिसमें C ट्रेन की आखिरी कार में सवार होता है और D अग्रणी कार में सवार होता है। ए और बी की विश्व रेखाएं लंबवत ( | चित्र 4-4 में स्पेसटाइम आरेखों पर विचार करें। A और B एक रेल ट्रैक के साथ खड़े होते हैं, जब एक हाई-स्पीड ट्रेन गुजरती है, जिसमें C ट्रेन की आखिरी कार में सवार होता है और D अग्रणी कार में सवार होता है। ए और बी की विश्व रेखाएं लंबवत (cटी) हैं, जो जमीन पर इन पर्यवेक्षकों की स्थिर स्थिति को अलग करती हैं, जबकि c और डी की विश्व रेखाएं आगे (cटी′) झुकी हुई हैं, जो पर्यवेक्षकों c और डी की तीव्र गति को दर्शाती हैं। उनकी ट्रेन में स्थिर, जैसा कि जमीन से देखा गया है। | ||
# | # चित्र 4-4a। B द्वारा D को संदेश भेजने की घटना, जैसे ही प्रमुख कार गुजरती है, D के सीमा रेखा के मूल में होती है। D एक काल्पनिक तात्कालिक संचारक का उपयोग करके पिछली कार में C को ट्रेन के साथ संदेश भेजता है। इस संदेश की दुनिया के साथ मोटा लाल तीर है <math>-x'</math> अक्ष, जो c और डी के प्राइमेड सीमा रेखा में एक साथ एक पंक्ति है। (अनप्रिम्ड) ग्राउंड सीमा रेखा में सिग्नल भेजे जाने से पहले आता है। | ||
# | # चित्र 4-4 बी। c द्वारा ए को संदेश भेजने की घटना, जो रेल की पटरियों के पास खड़ा है, उनके सीमा रेखा के मूल में है। अब A तात्कालिक संचारक के माध्यम से ट्रैक के साथ B को संदेश भेजता है। इस संदेश की विश्वरेखा नीला मोटा तीर है, साथ में <math>+x</math> अक्ष, जो ए और बी के सीमा रेखा के लिए एक साथ की एक पंक्ति है। जैसा कि स्पेसटाइम आरेख से देखा गया है, बी इसे भेजने से पहले संदेश प्राप्त करें, जो कार्य-कारण का उल्लंघन है।<ref name="Takeuchi">{{cite web |last1=Takeuchi |first1=Tatsu |title=Special Relativity Lecture Notes – Section 10 |url=https://www1.phys.vt.edu/~takeuchi/relativity/notes/section10.html |publisher=Virginia Tech |access-date=31 October 2018}}</ref> | ||
कार्य-कारण का उल्लंघन करने के लिए | संकेतों के लिए कार्य-कारण का उल्लंघन करने के लिए तात्कालिक होना आवश्यक नहीं है।भले ही D से C तक का सिग्नल की तुलना में थोड़ा उथला हो <math>x'</math> अक्ष (और ए से बी तक का संकेत . की तुलना में थोड़ा तेज है) <math>x</math> अक्ष), बी के लिए संदेश भेजने से पहले उसे प्राप्त करना अभी भी संभव होगा। ट्रेन की गति को हल्की गति के निकट बढ़ाकर, <math>ct'</math> तथा <math>x'</math> अक्षों को प्रकाश की गति का प्रतिनिधित्व करने वाली धराशायी रेखा के बहुत करीब निचोड़ा जा सकता है। इस संशोधित सेटअप के साथ, यह प्रदर्शित किया जा सकता है कि प्रकाश की गति की तुलना में केवल थोड़ा तेज संकेत भी कार्य-कारण उल्लंघन का परिणाम देगा।<ref name="Morin2017">{{cite book|last1=Morin|first1=David|title=Special Relativity for the Enthusiastic Beginner|date=2017|publisher=CreateSpace Independent Publishing Platform|pages=90–92|isbn=9781542323512}}</ref> | ||
इसलिए, यदि कार्य-कारण को संरक्षित किया जाना है, तो विशेष सापेक्षता के परिणामों में से एक यह है कि कोई भी सूचना संकेत या भौतिक वस्तु निर्वात में प्रकाश की तुलना में तेजी से यात्रा नहीं कर सकती है। | इसलिए, यदि कार्य-कारण को संरक्षित किया जाना है, तो विशेष सापेक्षता के परिणामों में से एक यह है कि कोई भी सूचना संकेत या भौतिक वस्तु निर्वात में प्रकाश की तुलना में तेजी से यात्रा नहीं कर सकती है। | ||
इसका मतलब यह नहीं है कि प्रकाश की गति से तेज ''सब'' असंभव है। विभिन्न तुच्छ स्थितियों का वर्णन किया जा सकता है जहां कुछ चीजें (वास्तविक पदार्थ या ऊर्जा नहीं) प्रकाश से तेज चलती हैं।<ref>{{cite web |last1=Gibbs |first1=Philip |title=Is Faster-Than-Light Travel or Communication Possible? |url=http://math.ucr.edu/home/baez/physics/Relativity/SpeedOfLight/FTL.html |website=Physics FAQ |publisher=Department of Mathematics, University of California, Riverside |access-date=31 October 2018}}</ref> उदाहरण के लिए, जिस स्थान पर खोज प्रकाश की किरण बादल के तल से टकराती है, वह प्रकाश की तुलना में तेजी से आगे बढ़ सकती है जब खोज प्रकाश तेजी से चालू होता है ( | इसका मतलब यह नहीं है कि प्रकाश की गति से तेज ''सब'' असंभव है। विभिन्न तुच्छ स्थितियों का वर्णन किया जा सकता है जहां कुछ चीजें (वास्तविक पदार्थ या ऊर्जा नहीं) प्रकाश से तेज चलती हैं।<ref>{{cite web |last1=Gibbs |first1=Philip |title=Is Faster-Than-Light Travel or Communication Possible? |url=http://math.ucr.edu/home/baez/physics/Relativity/SpeedOfLight/FTL.html |website=Physics FAQ |publisher=Department of Mathematics, University of California, Riverside |access-date=31 October 2018}}</ref> उदाहरण के लिए, जिस स्थान पर खोज प्रकाश की किरण बादल के तल से टकराती है, वह प्रकाश की तुलना में तेजी से आगे बढ़ सकती है जब खोज प्रकाश तेजी से चालू होता है (यद्यपि यह कार्य-कारण या किसी अन्य सापेक्षतावादी घटना का उल्लंघन नहीं करता है)।<ref>{{cite book |title=Applications of Electrodynamics in Theoretical Physics and Astrophysics |edition=illustrated |first1=David |last1=Ginsburg |publisher=CRC Press |year=1989 |isbn=978-2-88124-719-4 |page=206 |url=https://books.google.com/books?id=Lh0tjaBNzg0C|bibcode=1989aetp.book.....G }} [https://books.google.com/books?id=Lh0tjaBNzg0C&pg=PA206 Extract of page 206]</ref><ref>{{cite book |title=Four Decades of Scientific Explanation |author=Wesley C. Salmon |publisher=University of Pittsburgh |date=2006 |isbn=978-0-8229-5926-7 |page=107 |url=https://books.google.com/books?id=FHqOXCd06e8C}}, [https://books.google.com/books?id=FHqOXCd06e8C&pg=PA107 Section 3.7 page 107]</ref><!-- a pair of diagrams, with x–t and x'–t' coordinates would help here --> | ||
| Line 279: | Line 283: | ||
=== खींच प्रभाव === | === खींच प्रभाव === | ||
{{main| | {{main|फ़िज़ियो प्रयोग}} | ||
[[File:Fizeau experiment schematic.svg|thumb|300px|चित्रा 5-1। Fizeau के 1851 के प्रयोग का अत्यधिक सरलीकृत आरेख।]] | [[File:Fizeau experiment schematic.svg|thumb|300px|चित्रा 5-1। Fizeau के 1851 के प्रयोग का अत्यधिक सरलीकृत आरेख।]] | ||
1850 में, हिप्पोलीटे फ़िज़ौ और लियोन फौकॉल्ट ने स्वतंत्र रूप से स्थापित किया कि प्रकाश हवा की तुलना में पानी में अधिक धीरे-धीरे यात्रा करता है, इस प्रकार ऑगस्टिन-जीन फ्रेस्नेल की भविष्यवाणी को मान्य करता है।<ref name=Lauginie2004>{{cite journal |last1=Lauginie |first1=P. |title=Measuring Speed of Light: Why? Speed of what? |journal=Proceedings of the Fifth International Conference for History of Science in Science Education |date=2004 |url=http://sci-ed.org/documents/Lauginie-M.pdf|access-date=3 July 2015 |archive-url=https://web.archive.org/web/20150704043700/http://sci-ed.org/documents/Lauginie-M.pdf |archive-date=4 July 2015}}</ref> प्रकाश की गति को शांत जल में मापा जाता था। बहते जल में प्रकाश की चाल कितनी होगी? | 1850 में, हिप्पोलीटे फ़िज़ौ और लियोन फौकॉल्ट ने स्वतंत्र रूप से स्थापित किया कि प्रकाश हवा की तुलना में पानी में अधिक धीरे-धीरे यात्रा करता है, इस प्रकार ऑगस्टिन-जीन फ्रेस्नेल की भविष्यवाणी को मान्य करता है।<ref name=Lauginie2004>{{cite journal |last1=Lauginie |first1=P. |title=Measuring Speed of Light: Why? Speed of what? |journal=Proceedings of the Fifth International Conference for History of Science in Science Education |date=2004 |url=http://sci-ed.org/documents/Lauginie-M.pdf|access-date=3 July 2015 |archive-url=https://web.archive.org/web/20150704043700/http://sci-ed.org/documents/Lauginie-M.pdf |archive-date=4 July 2015}}</ref> प्रकाश की गति को शांत जल में मापा जाता था। बहते जल में प्रकाश की चाल कितनी होगी? | ||
| Line 285: | Line 289: | ||
1851 में, फ़िज़ौ ने इस प्रश्न का उत्तर देने के लिए एक प्रयोग किया, जिसका एक सरलीकृत निरूपण चित्र 5-1 में दिखाया गया है। प्रकाश की एक किरण को एक बीम फाड़नेवाला द्वारा विभाजित किया जाता है, और विभाजित बीम को विपरीत दिशाओं में बहते पानी की एक ट्यूब के माध्यम से पारित किया जाता है। उन्हें इंटरफेरेंस फ्रिंज बनाने के लिए पुनर्संयोजित किया जाता है, जो ऑप्टिकल पथ की लंबाई में अंतर को दर्शाता है, जिसे एक पर्यवेक्षक देख सकता है। प्रयोग ने प्रदर्शित किया कि बहते पानी द्वारा प्रकाश को खींचने से फ्रिंजों का विस्थापन हुआ, यह दर्शाता है कि पानी की गति ने प्रकाश की गति को प्रभावित किया था। | 1851 में, फ़िज़ौ ने इस प्रश्न का उत्तर देने के लिए एक प्रयोग किया, जिसका एक सरलीकृत निरूपण चित्र 5-1 में दिखाया गया है। प्रकाश की एक किरण को एक बीम फाड़नेवाला द्वारा विभाजित किया जाता है, और विभाजित बीम को विपरीत दिशाओं में बहते पानी की एक ट्यूब के माध्यम से पारित किया जाता है। उन्हें इंटरफेरेंस फ्रिंज बनाने के लिए पुनर्संयोजित किया जाता है, जो ऑप्टिकल पथ की लंबाई में अंतर को दर्शाता है, जिसे एक पर्यवेक्षक देख सकता है। प्रयोग ने प्रदर्शित किया कि बहते पानी द्वारा प्रकाश को खींचने से फ्रिंजों का विस्थापन हुआ, यह दर्शाता है कि पानी की गति ने प्रकाश की गति को प्रभावित किया था। | ||
उस समय प्रचलित सिद्धांतों के अनुसार, एक गतिमान माध्यम से यात्रा करने वाला प्रकाश माध्यम के माध्यम से अपनी गति और माध्यम की गति का एक साधारण योग होगा। अपेक्षा के विपरीत, फ़िज़ौ ने पाया कि यद्यपि प्रकाश को पानी द्वारा खींचा गया प्रतीत होता है, लेकिन खींचने का परिमाण अपेक्षा से बहुत कम था। यदि <math>u' = c/n</math> शांत जल में प्रकाश की गति है, और <math>v</math> पानी की गति है, और <math> u_{\pm} </math> प्रयोगशाला के | उस समय प्रचलित सिद्धांतों के अनुसार, एक गतिमान माध्यम से यात्रा करने वाला प्रकाश माध्यम के माध्यम से अपनी गति और माध्यम की गति का एक साधारण योग होगा। अपेक्षा के विपरीत, फ़िज़ौ ने पाया कि यद्यपि प्रकाश को पानी द्वारा खींचा गया प्रतीत होता है, लेकिन खींचने का परिमाण अपेक्षा से बहुत कम था। यदि <math>u' = c/n</math> शांत जल में प्रकाश की गति है, और <math>v</math> पानी की गति है, और <math> u_{\pm} </math> प्रयोगशाला के सीमा रेखा में प्रकाश की जल-जनित गति है जिसमें पानी का प्रवाह प्रकाश की गति से जुड़ता या घटाता है, तो | ||
<math display="block">u_{\pm} =\frac{c}{n} \pm v\left(1-\frac{1}{n^2}\right) \ . </math> | <math display="block">u_{\pm} =\frac{c}{n} \pm v\left(1-\frac{1}{n^2}\right) \ . </math> | ||
फ़िज़ौ के परिणाम, | फ़िज़ौ के परिणाम, यद्यपि फ्रेस्नेल की [[ एथर ड्रैग परिकल्पना ]] के पहले की परिकल्पना के अनुरूप थे, उस समय के भौतिकविदों के लिए बेसीमा निराशाजनक थे। अन्य बातों के अलावा, अपवर्तन पद के एक सूचकांक की उपस्थिति का मतलब है कि, चूंकि <math>n</math> तरंग दैर्ध्य पर निर्भर करता है, ईथर को एक ही समय में विभिन्न गतियों को बनाए रखने में सक्षम होना चाहिए।{{refn|group=note|The refractive index dependence of the presumed partial aether-drag was eventually confirmed by [[Pieter Zeeman]] in 1914–1915, long after special relativity had been accepted by the mainstream. Using a scaled-up version of Michelson's apparatus connected directly to [[Amsterdam]]'s main water conduit, Zeeman was able to perform extended measurements using monochromatic light ranging from violet (4358 Å) through red (6870 Å).<ref name=zee1 group=p>{{Cite journal|author=Zeeman, Pieter |title=Fresnel's coefficient for light of different colours. (First part) |journal=Proc. Kon. Acad. Van Weten.|volume=17|year=1914|pages=445–451|url=https://archive.org/details/p1proceedingsofs17akad|bibcode=1914KNAB...17..445Z}}</ref><ref name=zee2 group=p>{{Cite journal|author=Zeeman, Pieter |title=Fresnel's coefficient for light of different colours. (Second part)|journal=Proc. Kon. Acad. Van Weten.|volume=18|year=1915 |pages=398–408 |url=https://archive.org/details/proceedingsofsec181koni|bibcode=1915KNAB...18..398Z}}</ref>}} फ्रेस्नेल के ड्रैगिंग गुणांक की व्याख्या करने के लिए कई तरह के सैद्धांतिक स्पष्टीकरण प्रस्तावित किए गए थे जो पूरी तरह से एक-दूसरे के साथ थे। माइकलसन-मॉर्ले प्रयोग से पहले भी, फ़िज़ौ के प्रयोगात्मक परिणाम कई अवलोकनों में से थे, जिन्होंने चलती निकायों के प्रकाशिकी को समझाने में एक महत्वपूर्ण स्थिति पैदा की।<ref name=Stachel2005>{{cite book |last=Stachel |first=J. |title=The universe of general relativity |year=2005 |publisher=Birkhäuser |location=Boston |isbn=978-0-8176-4380-5 |pages=1–13 |chapter-url=https://books.google.com/books?id=-KlBhDwUKF8C&pg=PA1 |editor=Kox, A.J. |editor2=Eisenstaedt, J |access-date=17 April 2012 |chapter=Fresnel's (dragging) coefficient as a challenge to 19th century optics of moving bodies}}</ref> | ||
विशेष सापेक्षता के दृष्टिकोण से, फ़िज़्यू का परिणाम और कुछ नहीं, बल्कि एक सन्निकटन है {{EquationNote|10| | विशेष सापेक्षता के दृष्टिकोण से, फ़िज़्यू का परिणाम और कुछ नहीं, बल्कि एक सन्निकटन है {{EquationNote|10|समीकरण 10}}, वेगों की संरचना के लिए सापेक्षतावादी सूत्र।<ref name=Rindler1977/> | ||
: <math>u_{\pm} = \frac{u' \pm v}{ 1 \pm u'v/c^2 } =</math> <math> \frac {c/n \pm v}{ 1 \pm v/cn } \approx</math> <math> c \left( \frac{1}{n} \pm \frac{v}{c} \right) \left( 1 \mp \frac{v}{cn} \right) \approx </math> <math> \frac{c}{n} \pm v \left( 1 - \frac{1}{n^2} \right) </math> | : <math>u_{\pm} = \frac{u' \pm v}{ 1 \pm u'v/c^2 } =</math> <math> \frac {c/n \pm v}{ 1 \pm v/cn } \approx</math> <math> c \left( \frac{1}{n} \pm \frac{v}{c} \right) \left( 1 \mp \frac{v}{cn} \right) \approx </math> <math> \frac{c}{n} \pm v \left( 1 - \frac{1}{n^2} \right) </math> | ||
| Line 295: | Line 299: | ||
=== प्रकाश का सापेक्षिक विपथन === | === प्रकाश का सापेक्षिक विपथन === | ||
{{main| | {{main|प्रकाश का विचलन|प्रकाशिक समय सुधार}} | ||
[[File:Stellar aberration illustration.svg|thumb|चित्र 5-2। तारकीय विपथन का चित्रण]] | [[File:Stellar aberration illustration.svg|thumb|चित्र 5-2। तारकीय विपथन का चित्रण]] | ||
प्रकाश की परिमित गति के कारण, यदि किसी स्रोत और रिसीवर की सापेक्ष गति में एक अनुप्रस्थ घटक | प्रकाश की परिमित गति के कारण, यदि किसी स्रोत और रिसीवर की सापेक्ष गति में एक अनुप्रस्थ घटक सम्मिलित है, तो जिस दिशा से प्रकाश रिसीवर तक पहुंचता है, वह रिसीवर के सापेक्ष स्रोत के स्थान में ज्यामितीय स्थिति से विस्थापित हो जाएगा। विस्थापन की शास्त्रीय गणना दो रूप लेती है और माध्यम के संबंध में रिसीवर, स्रोत, या दोनों गति में हैं या नहीं, इसके आधार पर अलग-अलग भविष्यवाणियां करती हैं। (1) यदि रिसीवर गति में है, तो विस्थापन प्रकाश के विपथन का परिणाम होगा। रिसीवर के सापेक्ष बीम का घटना कोण रिसीवर की गति के वेक्टर योग और आपतित प्रकाश के वेग से परिकलित होगा।<ref name=Mould>{{cite book |title=Basic Relativity |page=8 |url=https://books.google.com/books?id=lfGE-wyJYIUC&pg=PA8 |isbn=978-0-387-95210-9 |date=2001 |publisher=Springer |author=Richard A. Mould |edition=2nd}}</ref> (2) यदि स्रोत गति में है, तो विस्थापन [[ प्रकाश-समय सुधार ]] का परिणाम होगा। अपनी ज्यामितीय स्थिति से स्रोत की स्पष्ट स्थिति का विस्थापन उस समय के दौरान स्रोत की गति का परिणाम होगा जब इसका प्रकाश रिसीवर तक पहुंचता है।<ref name="Seidelmann">{{cite book |editor1-last=Seidelmann |editor1-first=P. Kenneth |title=Explanatory Supplement to the Astronomical Almanac |date=1992 |publisher=University Science Books |location=ill Valley, Calif. |isbn=978-0-935702-68-2 |page=393 |url=https://archive.org/details/131123ExplanatorySupplementAstronomicalAlmanac/page/n209}}</ref> | ||
शास्त्रीय व्याख्या प्रयोगात्मक परीक्षण में विफल रही। चूंकि विपथन कोण रिसीवर के वेग और आपतित प्रकाश की गति के बीच संबंध पर निर्भर करता है, अपवर्तक माध्यम से आपतित प्रकाश के गुजरने से विपथन कोण बदल जाना चाहिए। 1810 में, फ्रांकोइस अरागो ने प्रकाश की गति को मापने के असफल प्रयास में इस अपेक्षित घटना का | शास्त्रीय व्याख्या प्रयोगात्मक परीक्षण में विफल रही। चूंकि विपथन कोण रिसीवर के वेग और आपतित प्रकाश की गति के बीच संबंध पर निर्भर करता है, अपवर्तक माध्यम से आपतित प्रकाश के गुजरने से विपथन कोण बदल जाना चाहिए। 1810 में, फ्रांकोइस अरागो ने प्रकाश की गति को मापने के असफल प्रयास में इस अपेक्षित घटना का उपयोग किया,<ref name="Ferraro">{{cite journal |last1=Ferraro |first1=Rafael |last2=Sforza |first2=Daniel M. |title=European Physical Society logo Arago (1810): the first experimental result against the ether |journal=European Journal of Physics |volume=26 |pages=195–204 |doi=10.1088/0143-0807/26/1/020 |arxiv=physics/0412055 |year=2005 |issue=1 |bibcode=2005EJPh...26..195F |s2cid=119528074 }}</ref> और 1870 में, [[ जॉर्ज एयरी ]] ने पानी से भरे दूरबीन का उपयोग करके परिकल्पना का परीक्षण किया, यह पाया कि, अपेक्षा के विपरीत, मापा विचलन एक हवा से भरे दूरबीन से मापा विचलन के समान था।<ref name="Dolan">{{cite web |last1=Dolan |first1=Graham |title=Airy's Water Telescope (1870) |url=http://www.royalobservatorygreenwich.org/articles.php?article=1069 |publisher=The Royal Observatory Greenwich |access-date=20 November 2018}}</ref> इन परिणामों को समझाने के लिए एक भारी प्रयास में आंशिक ईथर-ड्रैग की परिकल्पना का उपयोग किया गया,<ref name="Hollis">{{cite journal |last1=Hollis |first1=H. P. |title=Airy's water telescope |journal=The Observatory |date=1937 |volume=60 |pages=103–107 |url=http://adsbit.harvard.edu//full/1937Obs....60..103H/0000105.000.html |access-date=20 November 2018|bibcode=1937Obs....60..103H }}</ref> लेकिन माइकलसन-मॉर्ले प्रयोग के परिणामों के साथ असंगत था, जो स्पष्ट रूप से पूर्ण एथर-ड्रैग की मांग करता था।<ref>{{cite book |author1=Janssen, Michel |author2=Stachel, John |editor1-last=Stachel |editor1-first=John |title=Going Critical |date=2004 |publisher=Springer |isbn=978-1-4020-1308-9 |chapter=The Optics and Electrodynamics of Moving Bodies |chapter-url=https://www.mpiwg-berlin.mpg.de/Preprints/P265.PDF}}</ref> | ||
जड़त्वीय फ़्रेमों को मानते हुए, प्रकाश के विपथन के लिए सापेक्षतावादी अभिव्यक्ति रिसीवर के गतिमान और स्रोत गतिमान मामलों दोनों पर लागू होती है। विभिन्न प्रकार के त्रिकोणमितीय समकक्ष सूत्र प्रकाशित किए गए हैं। चित्र 5-2 में चरों के रूप में व्यक्त किए गए, इनमें | जड़त्वीय फ़्रेमों को मानते हुए, प्रकाश के विपथन के लिए सापेक्षतावादी अभिव्यक्ति रिसीवर के गतिमान और स्रोत गतिमान मामलों दोनों पर लागू होती है। विभिन्न प्रकार के त्रिकोणमितीय समकक्ष सूत्र प्रकाशित किए गए हैं। चित्र 5-2 में चरों के रूप में व्यक्त किए गए, इनमें सम्मिलित हैं<ref name="Rindler1977"/>{{rp|57–60}} | ||
: <math>\cos \theta ' = \frac{ \cos \theta + v/c}{ 1 + (v/c)\cos \theta}</math> या <math> \sin \theta ' = \frac{\sin \theta}{\gamma [ 1 + (v/c) \cos \theta ]}</math> या <math> \tan \frac{\theta '}{2} = \left( \frac{c - v}{c + v} \right)^{1/2} \tan \frac {\theta}{2}</math> | : <math>\cos \theta ' = \frac{ \cos \theta + v/c}{ 1 + (v/c)\cos \theta}</math> या <math> \sin \theta ' = \frac{\sin \theta}{\gamma [ 1 + (v/c) \cos \theta ]}</math> या <math> \tan \frac{\theta '}{2} = \left( \frac{c - v}{c + v} \right)^{1/2} \tan \frac {\theta}{2}</math> | ||
=== सापेक्ष डॉपलर प्रभाव === | === सापेक्ष डॉपलर प्रभाव === | ||
{{main| | {{main|सापेक्षवादी डॉपलर प्रभाव}} | ||
==== सापेक्ष अनुदैर्ध्य डॉपलर प्रभाव ==== | ==== सापेक्ष अनुदैर्ध्य डॉपलर प्रभाव ==== | ||
शास्त्रीय डॉपलर प्रभाव इस बात पर निर्भर करता है कि माध्यम के संबंध में स्रोत, रिसीवर या दोनों गति में हैं या नहीं। सापेक्षतावादी डॉपलर प्रभाव किसी भी माध्यम से स्वतंत्र होता है। फिर भी, अनुदैर्ध्य | शास्त्रीय डॉपलर प्रभाव इस बात पर निर्भर करता है कि माध्यम के संबंध में स्रोत, रिसीवर या दोनों गति में हैं या नहीं। सापेक्षतावादी डॉपलर प्रभाव किसी भी माध्यम से स्वतंत्र होता है। फिर भी, अनुदैर्ध्य परिस्थिति के लिए सापेक्षवादी डॉप्लर शिफ्ट, स्रोत और रिसीवर एक दूसरे से सीधे या दूर जाने के साथ, इसे शास्त्रीय घटना के रूप में प्राप्त किया जा सकता है, लेकिन एक समय विस्तार शब्द के अतिरिक्त संशोधित किया जाता है, और यही उपचार है यहाँ वर्णित है।<ref>{{cite journal |last1=Sher |first1=D. |title=The Relativistic Doppler Effect |journal=Journal of the Royal Astronomical Society of Canada |date=1968 |volume=62 |pages=105–111 |bibcode=1968JRASC..62..105S |url=http://adsbit.harvard.edu//full/1968JRASC..62..105S/0000105.000.html |access-date=11 October 2018}}</ref><ref name="Gill">{{cite book |last1=Gill |first1=T. P. |title=The Doppler Effect |date=1965 |publisher=Logos Press Limited |location=London |pages=6–9 |ol=5947329M }}</ref> | ||
मान लें कि रिसीवर और स्रोत एक दूसरे से सापेक्ष गति से दूर जा रहे हैं <math>v\,</math> जैसा कि रिसीवर या स्रोत पर एक पर्यवेक्षक द्वारा मापा जाता है (यहां अपनाया गया संकेत सम्मेलन यह है कि <math>v</math> नकारात्मक है यदि रिसीवर और स्रोत एक दूसरे की ओर बढ़ रहे हैं)। मान लें कि स्रोत माध्यम में स्थिर है। | मान लें कि रिसीवर और स्रोत एक दूसरे से सापेक्ष गति से दूर जा रहे हैं <math>v\,</math> जैसा कि रिसीवर या स्रोत पर एक पर्यवेक्षक द्वारा मापा जाता है (यहां अपनाया गया संकेत सम्मेलन यह है कि <math>v</math> नकारात्मक है यदि रिसीवर और स्रोत एक दूसरे की ओर बढ़ रहे हैं)। मान लें कि स्रोत माध्यम में स्थिर है। | ||
<math display="block">f_{r} = \left(1 - \frac v {c_s} \right) f_s</math> | <math display="block">f_{r} = \left(1 - \frac v {c_s} \right) f_s</math> | ||
जहाँ <math>c_s</math> ध्वनि की गति है। | |||
प्रकाश के लिए, और रिसीवर सापेक्ष गति से आगे बढ़ रहा है, रिसीवर पर | प्रकाश के लिए, और रिसीवर सापेक्ष गति से आगे बढ़ रहा है, रिसीवर पर समय स्रोत पर समयों के सापेक्ष समय विस्तार हैं। रिसीवर प्राप्त आवृत्ति को होने के लिए मापेगा | ||
<math display="block">f_r = \gamma\left(1 - \beta\right) f_s = \sqrt{\frac{1 - \beta}{1 + \beta}}\,f_s.</math> | <math display="block">f_r = \gamma\left(1 - \beta\right) f_s = \sqrt{\frac{1 - \beta}{1 + \beta}}\,f_s.</math> | ||
जहाँ | |||
*<math>\beta = v/c </math>तथा | *<math>\beta = v/c </math>तथा | ||
*<math>\gamma = \frac{1}{\sqrt{1 - \beta^2}}</math> लोरेंत्ज़ कारक है। | *<math>\gamma = \frac{1}{\sqrt{1 - \beta^2}}</math> लोरेंत्ज़ कारक है। | ||
एक गतिमान स्रोत के साथ रिसीवर के | एक गतिमान स्रोत के साथ रिसीवर के निर्देश तंत्र में विश्लेषण करते समय सापेक्षतावादी डॉपलर शिफ्ट के लिए एक समान अभिव्यक्ति प्राप्त की जाती है।<ref name=Feynman1977>{{cite book| title=The Feynman Lectures on Physics: Volume 1 | publisher=[[Addison-Wesley]] | location=Reading, Massachusetts |date=February 1977 | last1=Feynman | first1=Richard P. | author-link1=Richard Feynman | last2=Leighton | first2=Robert B. | author-link2=Robert B. Leighton | last3=Sands | first3=Matthew | author-link3=Matthew Sands | lccn=2010938208 | isbn=9780201021165 | pages=34–7 f |chapter-url=https://feynmanlectures.caltech.edu/I_34.html |chapter=Relativistic Effects in Radiation}}</ref><ref name=Morin2007/> | ||
| Line 329: | Line 333: | ||
शास्त्रीय रूप से, कोई यह उम्मीद कर सकता है कि यदि स्रोत और रिसीवर एक दूसरे के संबंध में अनुप्रस्थ रूप से आगे बढ़ रहे हैं, उनके सापेक्ष गति के लिए कोई अनुदैर्ध्य घटक नहीं है, तो रिसीवर तक पहुंचने वाले प्रकाश में कोई डॉपलर बदलाव नहीं होना चाहिए। | शास्त्रीय रूप से, कोई यह उम्मीद कर सकता है कि यदि स्रोत और रिसीवर एक दूसरे के संबंध में अनुप्रस्थ रूप से आगे बढ़ रहे हैं, उनके सापेक्ष गति के लिए कोई अनुदैर्ध्य घटक नहीं है, तो रिसीवर तक पहुंचने वाले प्रकाश में कोई डॉपलर बदलाव नहीं होना चाहिए। | ||
विशेष सापेक्षता अन्यथा भविष्यवाणी करती है। चित्र 5-3 इस परिदृश्य के दो सामान्य रूपों को दिखाता है। सरल समय | विशेष सापेक्षता अन्यथा भविष्यवाणी करती है। चित्र 5-3 इस परिदृश्य के दो सामान्य रूपों को दिखाता है। सरल समय विस्तार तर्कों का उपयोग करके दोनों प्रकारों का विश्लेषण किया जा सकता है।<ref name=Morin2007/>चित्र 5-3a में, रिसीवर स्रोत से प्रकाश को के कारक द्वारा ब्लूशिफ्ट के रूप में देखता है <math>\gamma</math>. चित्र में। 5-3b, प्रकाश को उc कारक द्वारा फिर से स्थानांतरित किया जाता है। | ||
=== माप बनाम दृश्य उपस्थिति === | === माप बनाम दृश्य उपस्थिति === | ||
समय का | समय का विस्तार और लंबाई का संकुचन ऑप्टिकल भ्रम नहीं हैं, बल्कि वास्तविक प्रभाव हैं। इन प्रभावों का मापन [[ डॉपलर शिफ्ट ]] का एक आर्टिफैक्ट नहीं है, न ही वे किसी घटना से पर्यवेक्षक तक यात्रा करने में लगने वाले समय को ध्यान में रखते हुए उपेक्षा का परिणाम हैं। | ||
वैज्ञानिक एक ओर माप या अवलोकन, बनाम दृश्य उपस्थिति, या जो देखता है, के बीच एक मूलभूत अंतर बनाते हैं। किसी वस्तु की मापी गई आकृति वस्तु के सभी बिंदुओं का एक काल्पनिक स्नैपशॉट है क्योंकि वे समय में एक ही क्षण में | वैज्ञानिक एक ओर माप या अवलोकन, बनाम दृश्य उपस्थिति, या जो देखता है, के बीच एक मूलभूत अंतर बनाते हैं। किसी वस्तु की मापी गई आकृति वस्तु के सभी बिंदुओं का एक काल्पनिक स्नैपशॉट है क्योंकि वे समय में एक ही क्षण में उपलब्ध होते हैं। हालाँकि, किसी वस्तु का दृश्य स्वरूप उस समय की अलग-अलग लंबाई से प्रभावित होता है, जो प्रकाश को वस्तु के विभिन्न बिंदुओं से किसी की आंख तक जाने में लगता है। | ||
[[File:Animated Terrell Rotation - Cube.gif|thumb|330px|चित्र 5-4. घन की मापी गई लंबाई के संकुचन की तुलना उसकी दृश्य उपस्थिति के विरुद्ध।]] | [[File:Animated Terrell Rotation - Cube.gif|thumb|330px|चित्र 5-4. घन की मापी गई लंबाई के संकुचन की तुलना उसकी दृश्य उपस्थिति के विरुद्ध।]] | ||
कई वर्षों तक, दोनों के बीच के अंतर को | कई वर्षों तक, दोनों के बीच के अंतर को सामान्यतः पर सराहा नहीं गया था, और सामान्यतः पर यह सोचा गया था कि एक पर्यवेक्षक द्वारा गुजरने वाली एक लंबी अनुबंधित वस्तु वास्तव में लंबाई के अनुबंध के रूप में देखी जाएगी। 1959 में, जेम्स टेरेल और रोजर पेनरोज़ ने स्वतंत्र रूप से बताया कि गतिमान वस्तु के विभिन्न भागों से प्रेक्षक तक पहुँचने वाले संकेतों में अंतर समय अंतराल प्रभाव के परिणामस्वरूप एक तेज़ गति वाली वस्तु का दृश्य रूप उसके मापा आकार से काफी भिन्न होता है। उदाहरण के लिए, एक घटती हुई वस्तु सिकुड़ी हुई दिखाई देगी, एक निकट आने वाली वस्तु लम्बी दिखाई देगी, और एक गुजरने वाली वस्तु में एक तिरछी उपस्थिति होगी जिसकी तुलना एक घुमाव से की गई है।<ref name="Terrell" group=p>{{cite journal|last1=Terrell|first1=James|title=Invisibility of the Lorentz Contraction|journal=[[Physical Review]]|date=15 November 1959|volume=116|issue=4|pages=1041–1045|doi=10.1103/PhysRev.116.1041|bibcode=1959PhRv..116.1041T}}</ref><ref name="Penrose" group=p>{{cite journal|last1=Penrose|first1=Roger|title=The Apparent Shape of a Relativistically Moving Sphere|journal=[[Proceedings of the Cambridge Philosophical Society|Mathematical Proceedings of the Cambridge Philosophical Society]]|date=24 October 2008|volume=55|issue=1|pages=137–139|doi=10.1017/S0305004100033776|bibcode=1959PCPS...55..137P|s2cid=123023118 }}</ref><ref>{{cite web|last1=Cook|first1=Helen|title=Relativistic Distortion|url=http://www.math.ubc.ca/~cass/courses/m309-01a/cook/|publisher=Mathematics Department, University of British Columbia|access-date=12 April 2017}}</ref><ref>{{cite web|last1=Signell|first1=Peter|title=Appearances at Relativistic Speeds|url=https://stuff.mit.edu/afs/athena/course/8/8.20/www/m44.pdf|website=Project PHYSNET|publisher=Michigan State University, East Lansing, MI|access-date=12 April 2017|archive-url=https://web.archive.org/web/20170413153459/https://stuff.mit.edu/afs/athena/course/8/8.20/www/m44.pdf|archive-date=13 April 2017|url-status=dead}}</ref> गति में एक गोला गोलाकार रूपरेखा को बरकरार रखता है, यद्यपि | ||
गोले की सतह और उस पर बने चित्र विकृत दिखाई देंगे।<ref>{{cite web|last1=Kraus|first1=Ute|title=The Ball is Round|url=http://www.spacetimetravel.org/fussball/fussball.html|website=Space Time Travel: Relativity visualized|publisher=Institut für Physik Universität Hildesheim|access-date=16 April 2017|archive-url=https://web.archive.org/web/20170512165032/http://www.spacetimetravel.org/fussball/fussball.html|archive-date=12 May 2017|url-status=dead}}</ref> | गोले की सतह और उस पर बने चित्र विकृत दिखाई देंगे।<ref>{{cite web|last1=Kraus|first1=Ute|title=The Ball is Round|url=http://www.spacetimetravel.org/fussball/fussball.html|website=Space Time Travel: Relativity visualized|publisher=Institut für Physik Universität Hildesheim|access-date=16 April 2017|archive-url=https://web.archive.org/web/20170512165032/http://www.spacetimetravel.org/fussball/fussball.html|archive-date=12 May 2017|url-status=dead}}</ref> | ||
[[File:M87 jet (1).jpg|thumb|चित्र 5-5। | [[File:M87 jet (1).jpg|thumb|चित्र 5-5। गैलेक्c [[ मेसियर 87 ]] इलेक्ट्रॉनों और अन्य उप-परमाणु कणों के एक ब्लैक-होल-संचालित जेट को लगभग प्रकाश की गति से यात्रा करता है।]] | ||
चित्र 5-4 एक घन को उसकी भुजाओं की लंबाई के चार गुना की दूरी से देखता है। उच्च गति पर, घन की जो भुजाएँ गति की दिशा के लंबवत होती हैं, आकार में अतिपरवलयिक दिखाई देती हैं। घन वास्तव में घुमाया नहीं गया है। बल्कि, क्यूब के पीछे से प्रकाश सामने से प्रकाश की तुलना में किसी की आंखों तक पहुंचने में अधिक समय लेता है, इस दौरान क्यूब दाईं ओर चला गया है। इस भ्रम को टेरेल घूर्णन या टेरेल-पेनरोज प्रभाव के रूप में जाना जाने लगा है।<ref group=note>Even though it has been many decades since Terrell and Penrose published their observations, popular writings continue to conflate measurement versus appearance. For example, Michio Kaku wrote in ''Einstein's Cosmos'' (W. W. Norton & Company, 2004. p. 65): "... imagine that the speed of light is only 20 miles per hour. If a car were to go down the street, it might look compressed in the direction of motion, being squeezed like an accordion down to perhaps 1 inch in length."</ref> | |||
एक और उदाहरण जहां दृश्य उपस्थिति माप के साथ बाधाओं पर है, विभिन्न [[ रेडियो आकाशगंगा ]]ओं, बीएल लाख वस्तुओं, [[ कैसर ]], और अन्य खगोलीय वस्तुओं में स्पष्ट सुपरल्यूमिनल गति के अवलोकन से आता है जो कि खगोलीय जेट को बाहर निकालते | एक और उदाहरण जहां दृश्य उपस्थिति माप के साथ बाधाओं पर है, विभिन्न [[ रेडियो आकाशगंगा ]]ओं, बीएल लाख वस्तुओं, [[ कैसर ]], और अन्य खगोलीय वस्तुओं में स्पष्ट सुपरल्यूमिनल गति के अवलोकन से आता है जो कि खगोलीय जेट को बाहर निकालते है। एक स्पष्ट ऑप्टिकल भ्रम के परिणाम प्रकाश यात्रा की तुलना में तेज होने का आभास देते हैं।<ref>{{cite book|last1=Zensus|first1=J. Anton|last2=Pearson|first2=Timothy J.|title=Superluminal Radio Sources|date=1987|publisher=Cambridge University Press|location=Cambridge, New York|isbn=9780521345606|page=3|edition=1st}}</ref><ref>{{cite web|last1=Chase|first1=Scott I.|title=Apparent Superluminal Velocity of Galaxies|url=http://math.ucr.edu/home/baez/physics/Relativity/SpeedOfLight/Superluminal/superluminal.html|website=The Original Usenet Physics FAQ|publisher=Department of Mathematics, University of California, Riverside|access-date=12 April 2017}}</ref><ref>{{cite web|last1=Richmond|first1=Michael|title="Superluminal" motions in astronomical sources|url=http://spiff.rit.edu/classes/phys200/lectures/superlum/superlum.html|website=Physics 200 Lecture Notes|publisher=School of Physics and Astronomy, Rochester Institute of Technology|access-date=20 April 2017|archive-url=https://web.archive.org/web/20170216155045/http://spiff.rit.edu/classes/phys200/lectures/superlum/superlum.html|archive-date=16 February 2017|url-status=dead}}</ref> चित्र 5-5 में, आकाशगंगा मेसियर 87 उप-परमाणु कणों के एक उच्च गति वाले जेट को लगभग सीधे हमारी ओर प्रवाहित करता है, लेकिन पेनरोज़-टेरेल घूर्णन के कारण जेट उc तरह से आगे बढ़ता हुआ दिखाई देता है जैसे कि क्यूब की उपस्थिति में चित्र 5-4 को बढ़ाया गया है।<ref>{{cite web|last1=Keel|first1=Bill|title=Jets, Superluminal Motion, and Gamma-Ray Bursts|url=http://pages.astronomy.ua.edu/keel/galaxies/jets.html|website=Galaxies and the Universe - WWW Course Notes|publisher=Department of Physics and Astronomy, University of Alabama|access-date=29 April 2017|archive-url=https://web.archive.org/web/20170301030027/http://pages.astronomy.ua.edu/keel/galaxies/jets.html|archive-date=1 March 2017|url-status=dead}}</ref> | ||
== गतिशीलता == | == गतिशीलता == | ||
लोरेंत्ज़ परिवर्तन से प्राप्त धारा #परिणाम गति का कारण बनने वाली ताकतों पर विचार किए बिना [[ गतिकी ]], बिंदुओं, निकायों और निकायों की प्रणालियों की गति के अध्ययन के साथ सख्ती से निपटा। यह खंड जनता, बलों, ऊर्जा और आगे की चर्चा करता है, और इस तरह लोरेंत्ज़ परिवर्तन द्वारा | लोरेंत्ज़ परिवर्तन से प्राप्त धारा #परिणाम गति का कारण बनने वाली ताकतों पर विचार किए बिना [[ गतिकी ]], बिंदुओं, निकायों और निकायों की प्रणालियों की गति के अध्ययन के साथ सख्ती से निपटा। यह खंड जनता, बलों, ऊर्जा और आगे की चर्चा करता है, और इस तरह लोरेंत्ज़ परिवर्तन द्वारा सम्मिलित लोगों से परे भौतिक प्रभावों पर विचार करने की आवश्यकता है। | ||
=== द्रव्यमान और ऊर्जा की तुल्यता === | === द्रव्यमान और ऊर्जा की तुल्यता === | ||
{{Main| | {{Main|द्रव्यमान-ऊर्जा तुल्यता}} | ||
जैसे ही किसी वस्तु की गति पर्यवेक्षक के दृष्टिकोण से प्रकाश की गति के करीब पहुंचती है, उसका [[ सापेक्षतावादी द्रव्यमान ]] बढ़ता है जिससे पर्यवेक्षक के संदर्भ के सीमा रेखा के भीतर से इसे तेज करना अधिक कठिन हो जाता है। | |||
ऊपर संदर्भित पत्रों के अलावा - जो लोरेंत्ज़ परिवर्तन की व्युत्पत्ति देते हैं और विशेष सापेक्षता की नींव का वर्णन करते हैं - आइंस्टीन ने द्रव्यमान और ऊर्जा की तुल्यता (और संप्रेषणीयता) के लिए [[ अनुमानी ]] तर्क देते हुए कम से कम चार पत्र भी लिखे। {{nowrap|1=''E'' = ''mc''<sup>2</sup>}}. | द्रव्यमान m के साथ किसी वस्तु की ऊर्जा सामग्री mc के बराबर होती है, ऊपर संदर्भित पत्रों के अलावा - जो लोरेंत्ज़ परिवर्तन की व्युत्पत्ति देते हैं और विशेष सापेक्षता की नींव का वर्णन करते हैं - आइंस्टीन ने द्रव्यमान और ऊर्जा की तुल्यता (और संप्रेषणीयता) के लिए [[ अनुमानी | अनुमानी]] तर्क देते हुए कम से कम चार पत्र भी लिखे। {{nowrap|1=''E'' = ''mc''<sup>2</sup>}}. | ||
द्रव्यमान-ऊर्जा तुल्यता विशेष सापेक्षता का परिणाम है। न्यूटोनियन यांत्रिकी में अलग-अलग ऊर्जा और गति, सापेक्षता में चार-सदिश बनाते हैं, और यह समय घटक (ऊर्जा) को अंतरिक्ष घटकों (गति) से गैर-तुच्छ तरीके से संबंधित करता है। किसी स्थिर वस्तु के लिए, ऊर्जा-गति चार-सदिश है {{nowrap|(''E''/''c'', 0, 0, 0)}}: इसमें एक समय घटक है जो ऊर्जा है, और तीन अंतरिक्ष घटक जो शून्य हैं। वेग v के एक छोटे मान के साथ x दिशा में लोरेंत्ज़ परिवर्तन के साथ | द्रव्यमान-ऊर्जा तुल्यता विशेष सापेक्षता का परिणाम है। न्यूटोनियन यांत्रिकी में अलग-अलग ऊर्जा और गति, सापेक्षता में चार-सदिश बनाते हैं, और यह समय घटक (ऊर्जा) को अंतरिक्ष घटकों (गति) से गैर-तुच्छ तरीके से संबंधित करता है। किसी स्थिर वस्तु के लिए, ऊर्जा-गति चार-सदिश है {{nowrap|(''E''/''c'', 0, 0, 0)}}: इसमें एक समय घटक है जो ऊर्जा है, और तीन अंतरिक्ष घटक जो शून्य हैं। वेग v के एक छोटे मान के साथ x दिशा में लोरेंत्ज़ परिवर्तन के साथ सीमा रेखा बदलने से, ऊर्जा गति चार-वेक्टर बन जाती है {{nowrap|(''E''/''c'', ''Ev''/''c''<sup>2</sup>, 0, 0)}}. संवेग c . द्वारा विभाजित वेग से गुणा की गई ऊर्जा के बराबर है। | ||
ऊर्जा और संवेग पदार्थ और विकिरण के गुण हैं, और यह निष्कर्ष निकालना असंभव है कि वे अपने आप में विशेष सापेक्षता के दो बुनियादी अभिधारणाओं से चार-सदिश बनाते हैं, क्योंकि ये पदार्थ या विकिरण के बारे में बात नहीं करते हैं, वे केवल बात करते हैं अंतरिक्ष और समय के बारे में। इसलिए व्युत्पत्ति के लिए कुछ अतिरिक्त भौतिक तर्क की आवश्यकता होती है। अपने 1905 के पेपर में, आइंस्टीन ने उन अतिरिक्त सिद्धांतों का उपयोग किया जो न्यूटोनियन यांत्रिकी को धीमी गति के लिए धारण करना चाहिए, ताकि धीमी गति पर एक ऊर्जा स्केलर और एक तीन-वेक्टर गति हो, और ऊर्जा और गति के लिए संरक्षण नियम सापेक्षता में बिल्कुल सही हो। . इसके अलावा, उन्होंने माना कि प्रकाश की ऊर्जा उc डॉपलर-शिफ्ट कारक द्वारा इसकी आवृत्ति के रूप में बदल जाती है, जिसे उन्होंने मैक्सवेल के समीकरणों के आधार पर पहले दिखाया था।<ref name="electro" group="p" />इस विषय पर आइंस्टीन का पहला पेपर था क्या किसी पिंड की जड़ता उसकी ऊर्जा सामग्री पर निर्भर करती है? 1905 में।<ref name="inertia" group="p">[http://www.fourmilab.ch/etexts/einstein/E_mc2/www/ Does the inertia of a body depend upon its energy content?] A. Einstein, ''Annalen der Physik.'' '''18''':639, 1905 (English translation by W. Perrett and G.B. Jeffery)</ref> यद्यपि इस पत्र में आइंस्टीन के तर्क को लगभग सार्वभौमिक रूप से भौतिकविदों द्वारा सही, यहां तक कि स्वयं-स्पष्ट के रूप में स्वीकार किया गया है, वर्षों से कई लेखकों ने सुझाव दिया है कि यह गलत है।<ref name="Jammer">{{cite book |title=Concepts of Mass in Classical and Modern Physics |author=[[Max Jammer]] |pages=177–178 |url=https://books.google.com/books?id=lYvz0_8aGsMC&pg=PA177 |isbn=978-0-486-29998-3 |publisher=Courier Dover Publications |date=1997 }}</ref> अन्य लेखकों का सुझाव है कि तर्क केवल अनिर्णायक था क्योंकि यह कुछ निहित मान्यताओं पर निर्भर था।<ref name="Stachel">{{cite book |title=Einstein from ''B'' to ''Z'' |page= 221 |author=John J. Stachel |url=https://books.google.com/books?id=OAsQ_hFjhrAC&pg=PA215 |isbn=978-0-8176-4143-6 |publisher=Springer |date=2002}}</ref> | |||
आइंस्टीन ने विशेष सापेक्षता पर अपने 1907 के सर्वेक्षण पत्र में अपनी व्युत्पत्ति पर विवाद को स्वीकार किया। वहां उन्होंने नोट किया कि अनुमानी द्रव्यमान-ऊर्जा तर्क के लिए मैक्सवेल के समीकरणों पर भरोसा करना समस्याग्रस्त है। उनके 1905 के पत्र में तर्क किसी भी द्रव्यमान रहित कणों के उत्सर्जन के साथ किया जा सकता है, लेकिन मैक्सवेल समीकरणों का उपयोग स्पष्ट रूप से यह स्पष्ट करने के लिए किया जाता है कि विशेष रूप से प्रकाश का उत्सर्जन केवल कार्य करके ही प्राप्त किया जा सकता है। विद्युत चुम्बकीय तरंगों का उत्सर्जन करने के लिए, आपको केवल एक आवेशित कण को हिलाना है, और यह स्पष्ट रूप से काम कर रहा है, ताकि उत्सर्जन ऊर्जा का हो।<ref name="survey" group="p">[https://www.webcitation.org/query?url=http://www.geocities.com/physics_world/abstracts/Einstein_1907A_abstract.htm&date=2009-10-26+00:34:19 ''On the Inertia of Energy Required by the Relativity Principle''], A. Einstein, Annalen der Physik 23 (1907): 371–384</ref><ref group="note">In a letter to Carl Seelig in 1955, Einstein wrote "I had already previously found that Maxwell's theory did not account for the micro-structure of radiation and could therefore have no general validity.", Einstein letter to Carl Seelig, 1955.</ref> | |||
=== आप पृथ्वी से कितनी दूर यात्रा कर सकते हैं?=== | === आप पृथ्वी से कितनी दूर यात्रा कर सकते हैं?=== | ||
{{See also| | {{See also|अंतरिक्ष यात्रा निरंतर त्वरण का उपयोग कर}} | ||
चूँकि कोई भी चीज प्रकाश से तेज गति से यात्रा नहीं कर सकती है, इसलिए यह निष्कर्ष निकाला जा सकता है कि मानव पृथ्वी से ~ 100 प्रकाश वर्ष से अधिक दूर कभी नहीं जा सकता है। आप आसानी से सोच सकते हैं कि एक यात्री पृथ्वी से 100 प्रकाश वर्ष की सीमा के भीतर | |||
चूँकि कोई भी चीज प्रकाश से तेज गति से यात्रा नहीं कर सकती है, इसलिए यह निष्कर्ष निकाला जा सकता है कि मानव पृथ्वी से ~ 100 प्रकाश वर्ष से अधिक दूर कभी नहीं जा सकता है। आप आसानी से सोच सकते हैं कि एक यात्री पृथ्वी से 100 प्रकाश वर्ष की सीमा के भीतर उपलब्ध कुछ सौर मंडलों से अधिक कभी नहीं पहुंच पाएगा। यद्यपि, समय के विस्तार के कारण, एक काल्पनिक अंतरिक्ष यान एक यात्री के जीवनकाल में हजारों प्रकाश वर्ष की यात्रा कर सकता है। यदि एक अंतरिक्ष यान का निर्माण किया जा सकता है जो पृथ्वी के निरंतर गुरुत्वाकर्षण पर गति करता है, तो यह एक वर्ष के बाद लगभग प्रकाश की गति से यात्रा करेगा जैसा कि पृथ्वी से देखा जाता है। यह इसके द्वारा वर्णित है: | |||
<math display="block">v(t) = \frac{at}{\sqrt{1+\frac{a^2t^2}{c^2}}}</math> | <math display="block">v(t) = \frac{at}{\sqrt{1+\frac{a^2t^2}{c^2}}}</math> | ||
जहाँ v(t) समय t पर वेग है, a अंतरिक्ष यान का त्वरण है और t पृथ्वी पर लोगों द्वारा मापा गया समन्वय समय है।<ref group=p>{{cite web|url = http://www.normalesup.org/~baglio/physique/acceleration.pdf|title = Acceleration in special relativity: What is the meaning of "uniformly accelerated movement" ?|date = 26 May 2007|access-date = 22 January 2016|publisher = Physics Department, ENS Cachan|last = Baglio|first = Julien}}</ref> इसलिए, 9.81 m/s . पर त्वरण के एक वर्ष बाद<sup>2</sup>, अंतरिक्ष यान पृथ्वी के सापेक्ष तीन वर्षों के बाद v = 0.712c और 0.946c पर यात्रा करेगा। इस त्वरण के तीन वर्षों के बाद, अंतरिक्ष यान पृथ्वी के सापेक्ष प्रकाश की गति के 94.6% के वेग को प्राप्त करने के साथ, समय के | जहाँ v(t) समय t पर वेग है, a अंतरिक्ष यान का त्वरण है और t पृथ्वी पर लोगों द्वारा मापा गया समन्वय समय है।<ref group=p>{{cite web|url = http://www.normalesup.org/~baglio/physique/acceleration.pdf|title = Acceleration in special relativity: What is the meaning of "uniformly accelerated movement" ?|date = 26 May 2007|access-date = 22 January 2016|publisher = Physics Department, ENS Cachan|last = Baglio|first = Julien}}</ref> इसलिए, 9.81 m/s . पर त्वरण के एक वर्ष बाद<sup>2</sup>, अंतरिक्ष यान पृथ्वी के सापेक्ष तीन वर्षों के बाद v = 0.712c और 0.946c पर यात्रा करेगा। इस त्वरण के तीन वर्षों के बाद, अंतरिक्ष यान पृथ्वी के सापेक्ष प्रकाश की गति के 94.6% के वेग को प्राप्त करने के साथ, समय के विस्तार के परिणामस्वरूप अंतरिक्ष यान पर पृथ्वी पर 3.1 सेकंड पहले के अनुभव के अनुसार प्रत्येक सेकंड का अनुभव होगा। अपनी यात्रा के दौरान, पृथ्वी पर लोगों को उनके मुकाबले अधिक समय का अनुभव होगा - क्योंकि उनकी समय (सभी भौतिक घटनाएं) वास्तव में अंतरिक्ष यान की तुलना में 3.1 गुना तेजी से टिक रही होंगी। यात्री के लिए 5 साल की गोल यात्रा 6.5 पृथ्वी वर्ष लेगी और 6 प्रकाश-वर्ष से अधिक की दूरी तय करेगी। उनके लिए 20 साल की राउंड ट्रिप (5 साल तेज, 5 डिक्लेरेटिंग, दो बार प्रत्येक) उन्हें 335 पृथ्वी वर्ष और 331 प्रकाश वर्ष की दूरी तय करके पृथ्वी पर वापस लाएगी।<ref name=gibbskoks>{{cite web|author1=Philip Gibbs |author2=Don Koks |name-list-style=amp |title=The Relativistic Rocket |url=http://math.ucr.edu/home/baez/physics/Relativity/SR/Rocket/rocket.html |access-date=30 August 2012}}</ref> 1g पर पूरे 40 साल की यात्रा पृथ्वी पर 58,000 वर्षों तक दिखाई देगी और 55,000 प्रकाश वर्ष की दूरी तय करेगी। 1.1g पर 40 साल की यात्रा में 148,000 पृथ्वी वर्ष लगेंगे और लगभग 140,000 प्रकाश वर्ष होंगे। एकतरफा 28 साल (14 साल का त्वरण, 14 अंतरिक्ष यात्री की चालमापी के साथ मापा गया) 1g त्वरण पर यात्रा एंड्रोमेडा गैलेक्c तक 2,000,000 प्रकाश-वर्ष तक पहुंच सकती है।<ref name=gibbskoks />इसी समय के विस्तार के कारण c के करीब यात्रा करने वाले म्यूऑन को अपने आधे जीवन (जब विराम से) की तुलना में बहुत अधिक यात्रा करने के लिए मनाया जाता है।<ref>[http://library.thinkquest.org/C0116043/specialtheorytext.htm The special theory of relativity shows that time and space are affected by motion] {{Webarchive|url=https://web.archive.org/web/20121021183616/http://library.thinkquest.org/C0116043/specialtheorytext.htm |date=2012-10-21 }}. Library.thinkquest.org. Retrieved on 2013-04-24.</ref> | ||
== सापेक्षता और एकीकृत विद्युत चुंबकत्व == | == सापेक्षता और एकीकृत विद्युत चुंबकत्व == | ||
{{Main| | {{Main|शास्त्रीय विद्युत चुंबकत्व और विशेष सापेक्षता|शास्त्रीय विद्युत चुंबकत्व का सहपरिवर्ती सूत्रीकरण}} | ||
[[ शास्त्रीय विद्युत चुंबकत्व ]] में सैद्धांतिक जांच ने तरंग प्रसार की खोज की। विद्युत चुम्बकीय प्रभावों को सामान्य करने वाले समीकरणों में पाया गया कि ई और बी क्षेत्रों की परिमित प्रसार गति को आवेशित कणों पर कुछ व्यवहार की आवश्यकता होती है। गतिमान आवेशों का सामान्य अध्ययन लीनार्ड-वाइचर्ट विभव का निर्माण करता है, जो विशेष सापेक्षता की ओर एक कदम है। | [[ शास्त्रीय विद्युत चुंबकत्व ]] में सैद्धांतिक जांच ने तरंग प्रसार की खोज की। विद्युत चुम्बकीय प्रभावों को सामान्य करने वाले समीकरणों में पाया गया कि ई और बी क्षेत्रों की परिमित प्रसार गति को आवेशित कणों पर कुछ व्यवहार की आवश्यकता होती है। गतिमान आवेशों का सामान्य अध्ययन लीनार्ड-वाइचर्ट विभव का निर्माण करता है, जो विशेष सापेक्षता की ओर एक कदम है। | ||
एक गतिमान आवेश के [[ विद्युत क्षेत्र ]] के एक गैर-गतिशील पर्यवेक्षक के | एक गतिमान आवेश के [[ विद्युत क्षेत्र ]] के एक गैर-गतिशील पर्यवेक्षक के निर्देश तंत्र में परिवर्तन के परिणामस्वरूप एक गणितीय शब्द की उपस्थिति होती है जिसे सामान्यतः पर [[ चुंबकीय क्षेत्र ]] कहा जाता है। इसके विपरीत, एक गतिमान आवेश द्वारा उत्पन्न 'चुंबकीय' क्षेत्र गायब हो जाता है और संदर्भ के एक गतिशील सीमा रेखा में विशुद्ध रूप से 'इलेक्ट्रोस्टैटिक' क्षेत्र बन जाता है। मैक्सवेल के समीकरण इस प्रकार ब्रह्मांड के शास्त्रीय मॉडल में विशेष सापेक्षतावादी प्रभावों के लिए केवल एक अनुभवजन्य फिट हैं। चूंकि विद्युत और चुंबकीय क्षेत्र निर्देश तंत्र पर निर्भर हैं और इस प्रकार आपस में जुड़े हुए हैं, इसलिए कोई भी ''विद्युत चुम्बकीय'' क्षेत्रों की बात करता है। विशेष सापेक्षता परिवर्तन नियम प्रदान करती है कि कैसे एक जड़त्वीय सीमा रेखा में एक विद्युत चुम्बकीय क्षेत्र दूसरे जड़त्वीय सीमा रेखा में प्रकट होता है। | ||
3डी रूप में मैक्सवेल के समीकरण पहले से ही विशेष सापेक्षता की भौतिक सामग्री के अनुरूप हैं, | 3डी रूप में मैक्सवेल के समीकरण पहले से ही विशेष सापेक्षता की भौतिक सामग्री के अनुरूप हैं, यद्यपि उन्हें [[ स्पष्ट रूप से सहसंयोजक ]] रूप में हेरफेर करना आसान है, अर्थात टेंसर कैलकुलस की भाषा में।<ref>{{cite book|title=Formal Structure of Electromagnetics: General Covariance and Electromagnetics|date=1962|publisher=Dover Publications Inc.|isbn=978-0-486-65427-0|author=E. J. Post}}</ref> | ||
| Line 383: | Line 388: | ||
[[ सापेक्षतावादी क्वांटम यांत्रिकी ]] और [[ क्वांटम इलेक्ट्रोडायनामिक्स ]] बनाने के लिए विशेष सापेक्षता को क्वांटम यांत्रिकी के साथ जोड़ा जा सकता है। सामान्य सापेक्षता और क्वांटम यांत्रिकी को कैसे एकीकृत किया जा सकता है यह [[ भौतिकी में अनसुलझी समस्याओं की सूची ]] है; [[ क्वांटम गुरुत्व ]] और हर चीज का एक सिद्धांत, जिसमें सामान्य सापेक्षता सहित एकीकरण की आवश्यकता होती है, सैद्धांतिक अनुसंधान में सक्रिय और चल रहे क्षेत्र हैं। | [[ सापेक्षतावादी क्वांटम यांत्रिकी ]] और [[ क्वांटम इलेक्ट्रोडायनामिक्स ]] बनाने के लिए विशेष सापेक्षता को क्वांटम यांत्रिकी के साथ जोड़ा जा सकता है। सामान्य सापेक्षता और क्वांटम यांत्रिकी को कैसे एकीकृत किया जा सकता है यह [[ भौतिकी में अनसुलझी समस्याओं की सूची ]] है; [[ क्वांटम गुरुत्व ]] और हर चीज का एक सिद्धांत, जिसमें सामान्य सापेक्षता सहित एकीकरण की आवश्यकता होती है, सैद्धांतिक अनुसंधान में सक्रिय और चल रहे क्षेत्र हैं। | ||
प्रारंभिक बोहर मॉडल | प्रारंभिक बोहर मॉडल शोधन बोहर-सोमरफेल्ड परमाणु मॉडल ने विशेष सापेक्षता और उस समय के क्वांटम यांत्रिकी पर प्रारंभिक ज्ञान दोनों का उपयोग करते हुए क्षार धातु परमाणुओं की बारीक संरचना की व्याख्या की।<ref>{{cite book|title=Quantum Physics of Atoms, Molecules, Solids, Nuclei and Particles|edition=2nd|pages=[https://archive.org/details/quantumphysicsof00eisb/page/114 114–116]|author1=R. Resnick|author2=R. Eisberg|publisher=John Wiley & Sons|date=1985|isbn=978-0-471-87373-0|url=https://archive.org/details/quantumphysicsof00eisb/page/114}}</ref> | ||
1928 में, [[ पॉल डिराका ]] ने एक प्रभावशाली सापेक्षतावादी तरंग समीकरण का निर्माण किया, जिसे अब उनके सम्मान में [[ डिराक समीकरण ]] के रूप में जाना जाता है,<ref name="Dirac" group=p>{{cite journal | author = P.A.M. Dirac | author-link = P.A.M. Dirac | date =1930 | title = A Theory of Electrons and Protons | journal =Proceedings of the Royal Society | volume = A126 |bibcode=1930RSPSA.126..360D | jstor=95359 | doi=10.1098/rspa.1930.0013 | issue = 801| pages = 360–365 | doi-access = free }}</ref> यह विशेष सापेक्षता और 1926 के बाद | 1928 में, [[ पॉल डिराका ]] ने एक प्रभावशाली सापेक्षतावादी तरंग समीकरण का निर्माण किया, जिसे अब उनके सम्मान में [[ डिराक समीकरण ]] के रूप में जाना जाता है,<ref name="Dirac" group=p>{{cite journal | author = P.A.M. Dirac | author-link = P.A.M. Dirac | date =1930 | title = A Theory of Electrons and Protons | journal =Proceedings of the Royal Society | volume = A126 |bibcode=1930RSPSA.126..360D | jstor=95359 | doi=10.1098/rspa.1930.0013 | issue = 801| pages = 360–365 | doi-access = free }}</ref> यह विशेष सापेक्षता और 1926 के बाद उपलब्ध क्वांटम सिद्धांत के अंतिम संस्करण के साथ पूरी तरह से संगत है। इस समीकरण ने न केवल स्पिन (भौतिकी) नामक इलेक्ट्रॉनों के आंतरिक कोणीय गति का वर्णन किया, बल्कि इससे इलेक्ट्रॉन के [[ कण ]] की भविष्यवाणी भी हुई। (पॉज़िट्रॉन),<ref name="Dirac" group=p /><ref group=p>{{cite journal|author=C.D. Anderson|author-link=Carl David Anderson |title=The Positive Electron|journal=Phys. Rev. |volume=43|pages=491–494 |date=1933|doi=10.1103/PhysRev.43.491|issue=6|bibcode = 1933PhRv...43..491A |doi-access=free}}</ref> और महीन संरचना को केवल विशेष सापेक्षता के साथ ही पूरी तरह से समझाया जा सकता है। यह सापेक्षतावादी क्वांटम यांत्रिकी की पहली नींव थी। | ||
दूसरी ओर, एंटीपार्टिकल्स का अस्तित्व इस निष्कर्ष की ओर ले जाता है कि सापेक्षतावादी क्वांटम यांत्रिकी कण अंतःक्रियाओं के अधिक सटीक और पूर्ण सिद्धांत के लिए पर्याप्त नहीं है। इसके | दूसरी ओर, एंटीपार्टिकल्स का अस्तित्व इस निष्कर्ष की ओर ले जाता है कि सापेक्षतावादी क्वांटम यांत्रिकी कण अंतःक्रियाओं के अधिक सटीक और पूर्ण सिद्धांत के लिए पर्याप्त नहीं है। इसके अतिरिक्त, [[ क्वांटम क्षेत्र सिद्धांत ]] कहे जाने वाले मात्रात्मक क्षेत्रों के रूप में व्याख्या किए गए कणों का एक सिद्धांत आवश्यक हो जाता है; जिसमें पूरे अंतरिक्ष और समय में कणों का सर्वनाश हो सकता है। | ||
== स्थिति == | == स्थिति == | ||
{{Main| | {{Main|विशेष सापेक्षता के परीक्षण|सापेक्षता सिद्धांत की आलोचना}} | ||
इसके मिंकोव्स्की स्पेसटाइम में विशेष सापेक्षता तभी सटीक होती है जब [[ गुरुत्वाकर्षण क्षमता ]] का निरपेक्ष मान c से बहुत कम हो | इसके मिंकोव्स्की स्पेसटाइम में विशेष सापेक्षता तभी सटीक होती है जब [[ गुरुत्वाकर्षण क्षमता ]] का निरपेक्ष मान c से बहुत कम हो रुचि के क्षेत्र में<ref>{{cite book | ||
|title=Einstein's general theory of relativity: with modern applications in cosmology | |title=Einstein's general theory of relativity: with modern applications in cosmology | ||
|author1=Øyvind Grøn |author2=Sigbjørn Hervik | |author1=Øyvind Grøn |author2=Sigbjørn Hervik | ||
| Line 398: | Line 403: | ||
|page=195 | |page=195 | ||
|url=https://books.google.com/books?id=IyJhCHAryuUC}} [https://books.google.com/books?id=IyJhCHAryuUC&pg=PA195 Extract of page 195 (with units where c=1)] | |url=https://books.google.com/books?id=IyJhCHAryuUC}} [https://books.google.com/books?id=IyJhCHAryuUC&pg=PA195 Extract of page 195 (with units where c=1)] | ||
</ref> एक मजबूत गुरुत्वाकर्षण क्षेत्र में, सामान्य सापेक्षता का उपयोग करना चाहिए। सामान्य सापेक्षता कमजोर क्षेत्र की सीमा पर विशेष सापेक्षता बन जाती है। बहुत छोटे पैमाने पर, जैसे कि प्लैंक की लंबाई और नीचे, क्वांटम प्रभावों को ध्यान में रखा जाना चाहिए, जिसके परिणामस्वरूप क्वांटम गुरुत्व होता है। | </ref> एक मजबूत गुरुत्वाकर्षण क्षेत्र में, सामान्य सापेक्षता का उपयोग करना चाहिए। सामान्य सापेक्षता कमजोर क्षेत्र की सीमा पर विशेष सापेक्षता बन जाती है। बहुत छोटे पैमाने पर, जैसे कि प्लैंक की लंबाई और नीचे, क्वांटम प्रभावों को ध्यान में रखा जाना चाहिए, जिसके परिणामस्वरूप क्वांटम गुरुत्व होता है। यद्यपि, मैक्रोस्कोपिक पैमानों पर और मजबूत गुरुत्वाकर्षण क्षेत्रों की अनुपस्थिति में, विशेष सापेक्षता का परीक्षण अत्यंत उच्च स्तर की सटीकता के लिए प्रयोगात्मक रूप से किया जाता है (10)<sup>-20</sup>)<ref>The number of works is vast, see as example:<br /> | ||
{{cite journal|author1=Sidney Coleman |author2=Sheldon L. Glashow |title=Cosmic Ray and Neutrino Tests of Special Relativity|journal= Physics Letters B |volume=405 |date=1997|pages= 249–252|arxiv=hep-ph/9703240|doi=10.1016/S0370-2693(97)00638-2|issue=3–4|bibcode = 1997PhLB..405..249C |s2cid=17286330 }}<br /> | {{cite journal|author1=Sidney Coleman |author2=Sheldon L. Glashow |title=Cosmic Ray and Neutrino Tests of Special Relativity|journal= Physics Letters B |volume=405 |date=1997|pages= 249–252|arxiv=hep-ph/9703240|doi=10.1016/S0370-2693(97)00638-2|issue=3–4|bibcode = 1997PhLB..405..249C |s2cid=17286330 }}<br /> | ||
An overview can be found on [http://www.edu-observatory.org/physics-faq/Relativity/SR/experiments.html this page]</ref> | An overview can be found on [http://www.edu-observatory.org/physics-faq/Relativity/SR/experiments.html this page]</ref> | ||
और इस प्रकार भौतिकी समुदाय द्वारा स्वीकार किया गया। प्रायोगिक परिणाम जो इसके विपरीत प्रतीत होते हैं, वे प्रतिलिपि प्रस्तुत करने योग्य नहीं हैं और इस प्रकार व्यापक रूप से प्रयोगात्मक त्रुटियों के कारण माना जाता है। | और इस प्रकार भौतिकी समुदाय द्वारा स्वीकार किया गया। प्रायोगिक परिणाम जो इसके विपरीत प्रतीत होते हैं, वे प्रतिलिपि प्रस्तुत करने योग्य नहीं हैं और इस प्रकार व्यापक रूप से प्रयोगात्मक त्रुटियों के कारण माना जाता है। | ||
विशेष सापेक्षता गणितीय रूप से आत्म-संगत है, और यह सभी आधुनिक भौतिक सिद्धांतों का एक कार्बनिक हिस्सा है, विशेष रूप से क्वांटम क्षेत्र सिद्धांत, स्ट्रिंग सिद्धांत, और सामान्य सापेक्षता (नगण्य गुरुत्वाकर्षण क्षेत्रों के | विशेष सापेक्षता गणितीय रूप से आत्म-संगत है, और यह सभी आधुनिक भौतिक सिद्धांतों का एक कार्बनिक हिस्सा है, विशेष रूप से क्वांटम क्षेत्र सिद्धांत, स्ट्रिंग सिद्धांत, और सामान्य सापेक्षता (नगण्य गुरुत्वाकर्षण क्षेत्रों के cमित परिस्थिति में)। | ||
न्यूटोनियन यांत्रिकी गणितीय रूप से छोटे वेगों (प्रकाश की गति की तुलना में) पर विशेष सापेक्षता से अनुसरण करती है - इस प्रकार न्यूटनियन यांत्रिकी को धीमी गति से चलने वाले पिंडों की एक विशेष सापेक्षता के रूप में माना जा सकता है। अधिक विस्तृत चर्चा के लिए [[ शास्त्रीय यांत्रिकी ]] देखें। | न्यूटोनियन यांत्रिकी गणितीय रूप से छोटे वेगों (प्रकाश की गति की तुलना में) पर विशेष सापेक्षता से अनुसरण करती है - इस प्रकार न्यूटनियन यांत्रिकी को धीमी गति से चलने वाले पिंडों की एक विशेष सापेक्षता के रूप में माना जा सकता है। अधिक विस्तृत चर्चा के लिए [[ शास्त्रीय यांत्रिकी ]] देखें। | ||
| Line 410: | Line 415: | ||
* [[ फ़िज़ौ प्रयोग ]] (1851, माइकलसन और मॉर्ले द्वारा 1886 में दोहराया गया) ने चलती मीडिया में प्रकाश की गति को मापा, जिसके परिणाम कॉलिनियर वेगों के सापेक्षतावादी जोड़ के अनुरूप हैं। | * [[ फ़िज़ौ प्रयोग ]] (1851, माइकलसन और मॉर्ले द्वारा 1886 में दोहराया गया) ने चलती मीडिया में प्रकाश की गति को मापा, जिसके परिणाम कॉलिनियर वेगों के सापेक्षतावादी जोड़ के अनुरूप हैं। | ||
* प्रसिद्ध माइकलसन-मॉर्ले प्रयोग (1881, 1887) ने इस अभिधारणा को और समर्थन दिया कि एक निरपेक्ष संदर्भ वेग का पता लगाना संभव नहीं था। यहां यह कहा जाना चाहिए कि, कई वैकल्पिक दावों के विपरीत, इसने स्रोत और पर्यवेक्षक के वेग के संबंध में प्रकाश की गति के अपरिवर्तन के बारे में बहुत कम कहा, क्योंकि स्रोत और पर्यवेक्षक दोनों एक ही वेग से हर समय एक साथ यात्रा कर रहे थे। | * प्रसिद्ध माइकलसन-मॉर्ले प्रयोग (1881, 1887) ने इस अभिधारणा को और समर्थन दिया कि एक निरपेक्ष संदर्भ वेग का पता लगाना संभव नहीं था। यहां यह कहा जाना चाहिए कि, कई वैकल्पिक दावों के विपरीत, इसने स्रोत और पर्यवेक्षक के वेग के संबंध में प्रकाश की गति के अपरिवर्तन के बारे में बहुत कम कहा, क्योंकि स्रोत और पर्यवेक्षक दोनों एक ही वेग से हर समय एक साथ यात्रा कर रहे थे। | ||
* ट्राउटन-नोबल प्रयोग (1903) ने दिखाया कि संधारित्र पर टोक़ स्थिति और जड़त्वीय | * ट्राउटन-नोबल प्रयोग (1903) ने दिखाया कि संधारित्र पर टोक़ स्थिति और जड़त्वीय निर्देश तंत्र से स्वतंत्र है। | ||
* [[ रेले और ब्रेस के प्रयोग ]] (1902, 1904) ने दिखाया कि लंबाई के संकुचन से सापेक्षता सिद्धांत के अनुसार, एक सह-चलती पर्यवेक्षक के लिए द्विअर्थीता नहीं होती है। | * [[ रेले और ब्रेस के प्रयोग ]] (1902, 1904) ने दिखाया कि लंबाई के संकुचन से सापेक्षता सिद्धांत के अनुसार, एक सह-चलती पर्यवेक्षक के लिए द्विअर्थीता नहीं होती है। | ||
कण त्वरक नियमित रूप से प्रकाश की गति के निकट गति करने वाले कणों के गुणों को मापते हैं और मापते हैं, जहां उनका व्यवहार पूरी तरह से सापेक्षता सिद्धांत के अनुरूप होता है और पहले न्यूटनियन यांत्रिकी के साथ असंगत होता है। ये मशीनें केवल काम नहीं करेंगी यदि वे सापेक्षतावादी सिद्धांतों के अनुसार इंजीनियर नहीं होतीं। इसके अलावा, विशेष सापेक्षता का परीक्षण करने के लिए काफी संख्या में आधुनिक प्रयोग किए गए हैं। कुछ उदाहरण: | कण त्वरक नियमित रूप से प्रकाश की गति के निकट गति करने वाले कणों के गुणों को मापते हैं और मापते हैं, जहां उनका व्यवहार पूरी तरह से सापेक्षता सिद्धांत के अनुरूप होता है और पहले न्यूटनियन यांत्रिकी के साथ असंगत होता है। ये मशीनें केवल काम नहीं करेंगी यदि वे सापेक्षतावादी सिद्धांतों के अनुसार इंजीनियर नहीं होतीं। इसके अलावा, विशेष सापेक्षता का परीक्षण करने के लिए काफी संख्या में आधुनिक प्रयोग किए गए हैं। कुछ उदाहरण: | ||
* आपेक्षिक ऊर्जा और संवेग का परीक्षण - कणों की | * आपेक्षिक ऊर्जा और संवेग का परीक्षण - कणों की cमित गति का परीक्षण | ||
* इव्स-स्टिलवेल प्रयोग - सापेक्षतावादी डॉपलर प्रभाव और समय | * इव्स-स्टिलवेल प्रयोग - सापेक्षतावादी डॉपलर प्रभाव और समय विस्तार का परीक्षण | ||
* [[ समय फैलाव का प्रायोगिक परीक्षण ]] - एक तेज गति वाले कण के आधे जीवन पर सापेक्ष प्रभाव | * [[ समय फैलाव का प्रायोगिक परीक्षण | समय विस्तार का प्रायोगिक परीक्षण]] - एक तेज गति वाले कण के आधे जीवन पर सापेक्ष प्रभाव | ||
* कैनेडी-थॉर्नडाइक प्रयोग - लोरेंत्ज़ परिवर्तनों के अनुसार समय का | * कैनेडी-थॉर्नडाइक प्रयोग - लोरेंत्ज़ परिवर्तनों के अनुसार समय का विस्तार | ||
* ह्यूजेस-ड्रेवर प्रयोग - अंतरिक्ष और द्रव्यमान की आइसोट्रॉपी का परीक्षण | * ह्यूजेस-ड्रेवर प्रयोग - अंतरिक्ष और द्रव्यमान की आइसोट्रॉपी का परीक्षण | ||
* लोरेंत्ज़ उल्लंघन के लिए आधुनिक खोज - विभिन्न आधुनिक परीक्षण | * लोरेंत्ज़ उल्लंघन के लिए आधुनिक खोज - विभिन्न आधुनिक परीक्षण | ||
| Line 424: | Line 429: | ||
== स्पेसटाइम की तकनीकी चर्चा == | == स्पेसटाइम की तकनीकी चर्चा == | ||
{{Main| | {{Main|मिन्कोवस्की अंतरिक्ष}} | ||
| Line 430: | Line 435: | ||
==== फ्लैट यूक्लिडियन अंतरिक्ष और मिंकोव्स्की अंतरिक्ष के बीच तुलना ==== | ==== फ्लैट यूक्लिडियन अंतरिक्ष और मिंकोव्स्की अंतरिक्ष के बीच तुलना ==== | ||
{{see also| | {{see also|रेखा तत्व}} | ||
[[File:Orthogonality and rotation.svg|thumb|350px|चित्र 10–1। बाएं के बीच की तुलना में समन्वय प्रणालियों की ऑर्थोगोनैलिटी और | [[File:Orthogonality and rotation.svg|thumb|350px|चित्र 10–1। बाएं के बीच की तुलना में समन्वय प्रणालियों की ऑर्थोगोनैलिटी और घूर्णन: सर्कुलर [[ कोण ]] ''φ'' के माध्यम से [[ यूक्लिडियन स्पेस ]], दाएं: मिंकोव्स्की स्पेसटाइम में हाइपरबॉलिक कोण ''φ'' के माध्यम से ('c' लेबल वाली लाल रेखाएं प्रकाश सिग्नल की दुनिया की रेखाओं को दर्शाती हैं , एक सदिश अपने आप में लंबकोणीय होता है यदि वह इस रेखा पर स्थित हो)।<ref>{{cite book|title=Gravitation|author1=J.A. Wheeler |author2=C. Misner |author3=K.S. Thorne |publisher=W.H. Freeman & Co|page=58|date=1973|isbn=978-0-7167-0344-0}}</ref>]] | ||
विशेष सापेक्षता एक 'फ्लैट' 4-आयामी मिंकोव्स्की स्पेस का उपयोग करती है - स्पेसटाइम का एक उदाहरण। मिंकोव्स्की स्पेसटाइम मानक 3-आयामी यूक्लिडियन स्पेस के समान प्रतीत होता है, लेकिन समय के संबंध में एक महत्वपूर्ण अंतर है। | विशेष सापेक्षता एक 'फ्लैट' 4-आयामी मिंकोव्स्की स्पेस का उपयोग करती है - स्पेसटाइम का एक उदाहरण। मिंकोव्स्की स्पेसटाइम मानक 3-आयामी यूक्लिडियन स्पेस के समान प्रतीत होता है, लेकिन समय के संबंध में एक महत्वपूर्ण अंतर है। | ||
| Line 437: | Line 442: | ||
<math display="block"> ds^2 = d\mathbf{x} \cdot d\mathbf{x} = dx_1^2 + dx_2^2 + dx_3^2, </math> | <math display="block"> ds^2 = d\mathbf{x} \cdot d\mathbf{x} = dx_1^2 + dx_2^2 + dx_3^2, </math> | ||
जहाँ {{nowrap|1=''d'''''x''' = (''dx''<sub>1</sub>, ''dx''<sub>2</sub>, ''dx''<sub>3</sub>)}} तीन स्थानिक आयामों के अंतर हैं। मिंकोव्स्की ज्यामिति में, निर्देशांक X . के साथ एक अतिरिक्त आयाम है<sup>0</sup> समय से व्युत्पन्न, जैसे दूरी अंतर पूरा करता है | |||
<math display="block"> ds^2 = -dX_0^2 + dX_1^2 + dX_2^2 + dX_3^2, </math> | <math display="block"> ds^2 = -dX_0^2 + dX_1^2 + dX_2^2 + dX_3^2, </math> | ||
जहाँ {{nowrap|1=''d'''''X''' = (''dX''<sub>0</sub>, ''dX''<sub>1</sub>, ''dX''<sub>2</sub>, ''dX''<sub>3</sub>)}} चार स्पेसटाइम आयामों के अंतर हैं। यह एक गहरी सैद्धांतिक अंतर्दृष्टि का सुझाव देता है: विशेष सापेक्षता हमारे स्पेसटाइम की एक घूर्णी समरूपता है, जो यूक्लिडियन अंतरिक्ष की घूर्णी समरूपता के अनुरूप है (चित्र 10-1 देखें)।<ref>{{cite book|title=Dynamics and Relativity|author1=J.R. Forshaw |author2=A.G. Smith |publisher=Wiley|page=247|date=2009|isbn=978-0-470-01460-8}}</ref> जैसे यूक्लिडियन स्पेस [[ यूक्लिडियन मीट्रिक ]] का उपयोग करता है, वैसे ही स्पेसटाइम [[ मिंकोव्स्की मीट्रिक ]] का उपयोग करता है। {{Anchor|interval}}मूल रूप से, किसी भी जड़त्वीय निर्देश तंत्र से देखे जाने पर, विशेष सापेक्षता को किसी भी स्पेसटाइम अंतराल (जो कि किसी भी दो घटनाओं के बीच 4D दूरी है) के आक्रमण के रूप में कहा जा सकता है। विशेष सापेक्षता के सभी समीकरण और प्रभाव मिंकोवस्की स्पेसटाइम के इस घूर्णी समरूपता (पोंकारे समूह) से प्राप्त किए जा सकते हैं। | |||
उपरोक्त ds का वास्तविक रूप मीट्रिक और X . के विकल्पों पर निर्भर करता है<sup>0</sup> समन्वय करें। | उपरोक्त ds का वास्तविक रूप मीट्रिक और X . के विकल्पों पर निर्भर करता है<sup>0</sup> समन्वय करें। | ||
समय निर्देशांक को अंतरिक्ष निर्देशांक की तरह बनाने के लिए, इसे [[ काल्पनिक संख्या ]] के रूप में माना जा सकता है: {{nowrap|1=''X''<sub>0</sub> = ''ict''}} (इसे विक | समय निर्देशांक को अंतरिक्ष निर्देशांक की तरह बनाने के लिए, इसे [[ काल्पनिक संख्या ]] के रूप में माना जा सकता है: {{nowrap|1=''X''<sub>0</sub> = ''ict''}} (इसे विक घूर्णन कहा जाता है)। | ||
ग्रेविटेशन (पुस्तक) | मिसनर, थॉर्न और व्हीलर (1971, 2.3) के अनुसार, अंततः विशेष और सामान्य सापेक्षता दोनों की गहरी समझ मिंकोव्स्की मीट्रिक (नीचे वर्णित) के अध्ययन से आएगी और लेने के लिए {{nowrap|1=''X''<sup>0</sup> = ''ct''}}, समय के समन्वय के रूप में ict का उपयोग करते हुए एक प्रच्छन्न यूक्लिडियन मीट्रिक के | ग्रेविटेशन (पुस्तक) | मिसनर, थॉर्न और व्हीलर (1971, 2.3) के अनुसार, अंततः विशेष और सामान्य सापेक्षता दोनों की गहरी समझ मिंकोव्स्की मीट्रिक (नीचे वर्णित) के अध्ययन से आएगी और लेने के लिए {{nowrap|1=''X''<sup>0</sup> = ''ct''}}, समय के समन्वय के रूप में ict का उपयोग करते हुए एक प्रच्छन्न यूक्लिडियन मीट्रिक के अतिरिक्त। | ||
कुछ लेखक उपयोग करते हैं {{nowrap|1=''X''<sup>0</sup> = ''t''}}, | कुछ लेखक उपयोग करते हैं {{nowrap|1=''X''<sup>0</sup> = ''t''}}, c के कारकों के साथ कहीं और क्षतिपूर्ति करने के लिए; उदाहरण के लिए, स्थानिक निर्देशांक c या c . के कारकों से विभाजित होते हैं<sup>±2</sup> मीट्रिक टेंसर में सम्मिलित हैं।<ref>{{cite book |author=R. Penrose| title=The Road to Reality| publisher= Vintage books| date=2007 | isbn=978-0-679-77631-4| title-link=The Road to Reality}}</ref> | ||
प्राकृतिक इकाइयों का उपयोग करके इन कई सम्मेलनों को हटा दिया जा सकता है जहां {{nowrap|1=''c'' = 1}}. तब स्थान और समय की समान इकाइयाँ होती हैं, और c का कोई भी गुणनखंड कहीं भी प्रकट नहीं होता है। | प्राकृतिक इकाइयों का उपयोग करके इन कई सम्मेलनों को हटा दिया जा सकता है जहां {{nowrap|1=''c'' = 1}}. तब स्थान और समय की समान इकाइयाँ होती हैं, और c का कोई भी गुणनखंड कहीं भी प्रकट नहीं होता है। | ||
| Line 474: | Line 479: | ||
जैसा कि चित्र 10-3 में दिखाया गया है, अशक्त भूगणित को त्रिज्या = c dt के साथ निरंतर संकेंद्रित क्षेत्रों के एक सेट के रूप में देखा जा सकता है। | जैसा कि चित्र 10-3 में दिखाया गया है, अशक्त भूगणित को त्रिज्या = c dt के साथ निरंतर संकेंद्रित क्षेत्रों के एक सेट के रूप में देखा जा सकता है। | ||
यह अशक्त दोहरा-शंकु अंतरिक्ष में एक बिंदु की दृष्टि की रेखा का प्रतिनिधित्व करता है। | यह अशक्त दोहरा-शंकु अंतरिक्ष में एक बिंदु की दृष्टि की रेखा का प्रतिनिधित्व करता है। अर्थात, जब हम तारों को देखते हैं और कहते हैं कि उस तारे का प्रकाश जो मुझे प्राप्त हो रहा है, वह X वर्ष पुराना है, तो हम इस दृष्टि रेखा को नीचे देख रहे हैं: एक अशक्त भूगणित। हम एक घटना को दूर से देख रहे हैं <math display="inline">d = \sqrt{x_1^2 + x_2^2 + x_3^2} </math> दूर और अतीत में एक समय डी / c। इस कारण से शून्य दोहरे शंकु को 'प्रकाश शंकु' के रूप में भी जाना जाता है। (चित्र 10-2 के निचले बाएँ बिंदु तारे का प्रतिनिधित्व करता है, मूल प्रेक्षक का प्रतिनिधित्व करता है, और रेखा दृष्टि की शून्य भूगणितीय रेखा का प्रतिनिधित्व करती है।) | ||
−t क्षेत्र में शंकु वह सूचना है जो बिंदु 'प्राप्त' कर रहा है, जबकि +t खंड में शंकु वह जानकारी है जो बिंदु 'भेज रहा है'। | −t क्षेत्र में शंकु वह सूचना है जो बिंदु 'प्राप्त' कर रहा है, जबकि +t खंड में शंकु वह जानकारी है जो बिंदु 'भेज रहा है'। | ||
| Line 484: | Line 489: | ||
=== स्पेसटाइम में भौतिकी === | === स्पेसटाइम में भौतिकी === | ||
==== | ==== निर्देश तंत्र के बीच भौतिक मात्राओं का परिवर्तन ==== | ||
ऊपर, समय के लिए लोरेंत्ज़ परिवर्तन | ऊपर, समय के समन्वय के लिए लोरेंत्ज़ परिवर्तन और तीन अंतरिक्ष निर्देशांक दर्शाते हैं कि वे आपस में जुड़े हुए हैं। यह अधिक व्यापक रूप से सच है: "टाइमलाइक" और "स्पेसेलिक" मात्राओं के कुछ जोड़े स्वाभाविक रूप से समान लोरेंत्ज़ परिवर्तन के तहत समान स्तर पर संयोजित होते हैं। | ||
उपरोक्त मानक विन्यास में लोरेंत्ज़ परिवर्तन, जो कि एक्स-दिशा में वृद्धि के लिए है, को निम्नानुसार मैट्रिक्स रूप में पुन: व्यवस्थित किया जा सकता है: | उपरोक्त मानक विन्यास में लोरेंत्ज़ परिवर्तन, जो कि एक्स-दिशा में वृद्धि के लिए है, को निम्नानुसार मैट्रिक्स रूप में पुन: व्यवस्थित किया जा सकता है: | ||
| Line 506: | Line 511: | ||
\end{pmatrix}. | \end{pmatrix}. | ||
</math> | </math> | ||
न्यूटोनियन यांत्रिकी में, परिमाण और दिशा वाली मात्राओं को गणितीय रूप से यूक्लिडियन अंतरिक्ष में 3 डी वैक्टर के रूप में वर्णित किया जाता है, और सामान्य तौर पर वे समय के | न्यूटोनियन यांत्रिकी में, परिमाण और दिशा वाली मात्राओं को गणितीय रूप से यूक्लिडियन अंतरिक्ष में 3 डी वैक्टर के रूप में वर्णित किया जाता है, और सामान्य तौर पर वे समय के साथ पैरामीट्रिज्ड होते हैं। विशेष आपेक्षिकता में, इस धारणा का विस्तार स्पेसलाइक वेक्टर मात्रा में उपयुक्त समय-सामान मात्रा को जोड़कर किया जाता है, और हमारे पास मिंकोवस्की स्पेसटाइम में 4d वैक्टर, या "चार वैक्टर" हैं। वैक्टर के घटक टेंसर इंडेक्स नोटेशन का उपयोग करके लिखे गए हैं, क्योंकि इसके कई फायदे हैं। संकेतन यह स्पष्ट करता है कि पोंकारे समूह के तहत समीकरण स्पष्ट रूप से सहसंयोजक हैं, इस प्रकार इस तथ्य की जांच करने के लिए कठिन गणनाओं को दरकिनार करते हैं। ऐसे समीकरणों के निर्माण में, हम अधिकांशतः पाते हैं कि जिन समीकरणों को पहले असंबंधित माना जाता था, वे वास्तव में एक ही टेंसर समीकरण का हिस्सा होने के कारण निकटता से जुड़े हुए हैं।अन्य [[ भौतिक मात्रा ]]ओं को टेंसर के रूप में पहचानना उनके परिवर्तन नियमो को सरल बनाता है। जब वे एक वर्ग (यह संदर्भ से स्पष्ट होना चाहिए) को इंगित करते हैं, और निचले सूचकांक (सबस्क्रिप्ट) सहसंयोजक सूचकांकों को छोड़कर, ऊपरी सूचकांक (सुपरस्क्रिप्ट) घातांक के अतिरिक्त विरोधाभाc सूचकांक होते हैं। पहले के समीकरणों के साथ सरलता और स्थिरता के लिए, कार्टेशियन निर्देशांक का उपयोग किया जाएगा। | ||
चार-सदिश का सबसे सरल उदाहरण स्पेसटाइम में एक घटना की स्थिति है, जो एक | चार-सदिश का सबसे सरल उदाहरण स्पेसटाइम में एक घटना की स्थिति है, जो एक समयबद्ध घटक ct और स्पेसलाइक घटक x = (x, y, z) का गठन करता है, एक विपरीत स्थिति में घटकों के साथ चार वेक्टर: | ||
<math display="block">X^\nu = (X^0, X^1, X^2, X^3)= (ct, x, y, z) = (ct, \mathbf{x} ).</math> | <math display="block">X^\nu = (X^0, X^1, X^2, X^3)= (ct, x, y, z) = (ct, \mathbf{x} ).</math> | ||
जहां हम परिभाषित करते हैं {{nowrap|1=''X''<sup>0</sup> = ''ct''}} ताकि समय समन्वय में अन्य स्थानिक आयामों के समान दूरी का आयाम हो; ताकि स्थान और समय के साथ समान व्यवहार किया जा सके।<ref>Jean-Bernard Zuber & Claude Itzykson, ''Quantum Field Theory'', pg 5, {{isbn|0-07-032071-3}}</ref><ref>[[Charles W. Misner]], [[Kip S. Thorne]] & [[John A. Wheeler]], ''Gravitation'', pg 51, {{isbn|0-7167-0344-0}}</ref><ref>[[George Sterman]], ''An Introduction to Quantum Field Theory'', pg 4, {{isbn|0-521-31132-2}}</ref> अब 4-वेक्टर की स्थिति के विपरीत घटकों के परिवर्तन को संक्षेप में इस प्रकार लिखा जा सकता है: | जहां हम परिभाषित करते हैं {{nowrap|1=''X''<sup>0</sup> = ''ct''}} ताकि समय समन्वय में अन्य स्थानिक आयामों के समान दूरी का आयाम हो; ताकि स्थान और समय के साथ समान व्यवहार किया जा सके।<ref>Jean-Bernard Zuber & Claude Itzykson, ''Quantum Field Theory'', pg 5, {{isbn|0-07-032071-3}}</ref><ref>[[Charles W. Misner]], [[Kip S. Thorne]] & [[John A. Wheeler]], ''Gravitation'', pg 51, {{isbn|0-7167-0344-0}}</ref><ref>[[George Sterman]], ''An Introduction to Quantum Field Theory'', pg 4, {{isbn|0-521-31132-2}}</ref> अब 4-वेक्टर की स्थिति के विपरीत घटकों के परिवर्तन को संक्षेप में इस प्रकार लिखा जा सकता है: | ||
| Line 515: | Line 520: | ||
जहां पर आइंस्टीन का अंकन है <math>\nu</math> 0 से 3 तक, और <math>\Lambda^{\mu'}{}_{\nu}</math> एक [[ मैट्रिक्स (गणित) ]] है। | जहां पर आइंस्टीन का अंकन है <math>\nu</math> 0 से 3 तक, और <math>\Lambda^{\mu'}{}_{\nu}</math> एक [[ मैट्रिक्स (गणित) ]] है। | ||
अधिक | अधिक सामान्यतः पर, चार-वेक्टर के सभी प्रतिपरिवर्तघटक <math>T^\nu</math> लोरेंत्ज़ परिवर्तन द्वारा एक सीमा रेखा से दूसरे सीमा रेखा में बदलना: | ||
<math display="block">T^{\mu'} = \Lambda^{\mu'}{}_{\nu} T^\nu</math> | <math display="block">T^{\mu'} = \Lambda^{\mu'}{}_{\nu} T^\nu</math> | ||
अन्य 4-वैक्टर के उदाहरणों में चार-वेग | अन्य 4-वैक्टर के उदाहरणों में चार-वेग सम्मिलित हैं <math>U^\mu,</math> [[ उचित समय ]] के संबंध में स्थिति 4-वेक्टर के व्युत्पन्न के रूप में परिभाषित: | ||
<math display="block">U^\mu = \frac{dX^\mu}{d\tau} = \gamma(v)( c , v_x , v_y, v_z ) = \gamma(v) (c, \mathbf{v} ). </math> | <math display="block">U^\mu = \frac{dX^\mu}{d\tau} = \gamma(v)( c , v_x , v_y, v_z ) = \gamma(v) (c, \mathbf{v} ). </math> | ||
जहां लोरेंत्ज़ कारक है: | जहां लोरेंत्ज़ कारक है: | ||
| Line 530: | Line 535: | ||
त्रि-आयामी वेग और त्वरण के लिए परिवर्तन नियम बहुत अजीब हैं; मानक विन्यास में भी ऊपर वेग समीकरण उनकी गैर-रैखिकता के कारण काफी जटिल हैं। दूसरी ओर, लोरेंत्ज़ परिवर्तन मैट्रिक्स के माध्यम से चार-वेग और चार-त्वरण का परिवर्तन सरल होता है। | त्रि-आयामी वेग और त्वरण के लिए परिवर्तन नियम बहुत अजीब हैं; मानक विन्यास में भी ऊपर वेग समीकरण उनकी गैर-रैखिकता के कारण काफी जटिल हैं। दूसरी ओर, लोरेंत्ज़ परिवर्तन मैट्रिक्स के माध्यम से चार-वेग और चार-त्वरण का परिवर्तन सरल होता है। | ||
एक अदिश क्षेत्र का [[ चार-ढाल ]] φ कॉन्ट्रावेरिएंट के | एक अदिश क्षेत्र का [[ चार-ढाल ]] φ कॉन्ट्रावेरिएंट के अतिरिक्त सहसंयोजक रूप से रूपांतरित होता है: | ||
<math display="block">\begin{pmatrix} | <math display="block">\begin{pmatrix} | ||
\dfrac{1}{c} \dfrac{\partial \phi}{\partial t'} & | \dfrac{1}{c} \dfrac{\partial \phi}{\partial t'} & | ||
| Line 556: | Line 561: | ||
अधिक सामान्यतः, 4-वेक्टर के सहसंयोजक घटक व्युत्क्रम लोरेंत्ज़ परिवर्तन के अनुसार बदलते हैं: | अधिक सामान्यतः, 4-वेक्टर के सहसंयोजक घटक व्युत्क्रम लोरेंत्ज़ परिवर्तन के अनुसार बदलते हैं: | ||
<math display="block"> T_{\mu'} = \Lambda_{\mu'}{}^{\nu} T_\nu,</math> | <math display="block"> T_{\mu'} = \Lambda_{\mu'}{}^{\nu} T_\nu,</math> | ||
जहाँ <math>\Lambda_{\mu'}{}^{\nu}</math> का पारस्परिक मैट्रिक्स है <math>\Lambda^{\mu'}{}_{\nu}</math>. | |||
विशेष सापेक्षता के अभिगृहीत लोरेंत्ज़ रूपांतरण मैट्रिक्स के सटीक रूप को बाधित करते हैं। | विशेष सापेक्षता के अभिगृहीत लोरेंत्ज़ रूपांतरण मैट्रिक्स के सटीक रूप को बाधित करते हैं। | ||
सामान्यतः पर, अधिकांश भौतिक मात्राओं को सबसे अच्छा (घटकों के) टेंसर के रूप में वर्णित किया जाता है। तो एक सीमा रेखा से दूसरे सीमा रेखा में बदलने के लिए, हम प्रसिद्ध टेंसर का उपयोग करते हैं<ref>{{cite book |title = Spacetime and Geometry: An Introduction to General Relativity |author=Sean M. Carroll |publisher=Addison Wesley |date=2004 |isbn=978-0-8053-8732-2 |page=22 |url=https://books.google.com/books?id=1SKFQgAACAAJ}}</ref> | |||
<math display="block">T^{\alpha' \beta' \cdots \zeta'}_{\theta' \iota' \cdots \kappa'} = \Lambda^{\alpha'}{}_{\mu} \Lambda^{\beta'}{}_{\nu} \cdots \Lambda^{\zeta'}{}_{\rho} \Lambda_{\theta'}{}^{\sigma} \Lambda_{\iota'}{}^{\upsilon} \cdots \Lambda_{\kappa'}{}^{\phi} T^{\mu \nu \cdots \rho}_{\sigma \upsilon \cdots \phi}</math> | <math display="block">T^{\alpha' \beta' \cdots \zeta'}_{\theta' \iota' \cdots \kappa'} = \Lambda^{\alpha'}{}_{\mu} \Lambda^{\beta'}{}_{\nu} \cdots \Lambda^{\zeta'}{}_{\rho} \Lambda_{\theta'}{}^{\sigma} \Lambda_{\iota'}{}^{\upsilon} \cdots \Lambda_{\kappa'}{}^{\phi} T^{\mu \nu \cdots \rho}_{\sigma \upsilon \cdots \phi}</math> | ||
जहाँ <math>\Lambda_{\chi'}{}^{\psi}</math> का पारस्परिक मैट्रिक्स है <math>\Lambda^{\chi'}{}_{\psi}</math>. इस नियम से सभी टेंसर बदल जाते हैं। | |||
चार-आयामी दूसरे क्रम के [[ एंटीसिमेट्रिक टेंसर ]] का एक उदाहरण सापेक्षतावादी [[ कोणीय गति ]] है, जिसमें छह घटक हैं: तीन शास्त्रीय कोणीय गति हैं, और अन्य तीन सिस्टम के द्रव्यमान के केंद्र के | चार-आयामी दूसरे क्रम के [[ एंटीसिमेट्रिक टेंसर ]] का एक उदाहरण सापेक्षतावादी [[ कोणीय गति ]] है, जिसमें छह घटक हैं: तीन शास्त्रीय कोणीय गति हैं, और अन्य तीन सिस्टम के द्रव्यमान के केंद्र के वृद्धि से संबंधित हैं। उचित समय के संबंध में सापेक्षतावादी कोणीय गति का व्युत्पन्न सापेक्षतावादी टोक़ है, दूसरा क्रम एंटीसिमेट्रिक टेंसर भी है। | ||
[[ विद्युत चुम्बकीय क्षेत्र टेंसर ]] एक और दूसरा क्रम एंटीसिमेट्रिक टेंसर क्षेत्र है | [[ विद्युत चुम्बकीय क्षेत्र टेंसर ]] छह घटकों के साथ एक और दूसरा क्रम एंटीसिमेट्रिक टेंसर क्षेत्र है: तीन विद्युत क्षेत्र के लिए और अन्य तीन चुंबकीय क्षेत्र के लिए। विद्युत चुम्बकीय क्षेत्र के लिए तनाव-ऊर्जा टेंसर भी है, अर्थात् विद्युत चुम्बकीय तनाव-ऊर्जा टेंसर। | ||
==== मीट्रिक ==== | ==== मीट्रिक ==== | ||
[[ मीट्रिक टेंसर ]] एक को दो वैक्टर के आंतरिक उत्पाद को परिभाषित करने की अनुमति देता है, जो बदले में वेक्टर को परिमाण | [[ मीट्रिक टेंसर ]] एक को दो वैक्टर के आंतरिक उत्पाद को परिभाषित करने की अनुमति देता है, जो बदले में एक को वेक्टर को एक परिमाण प्रदान करने की अनुमति देता है। स्पेसटाइम की चार-आयामी प्रकृति को देखते हुए मिंकोव्स्की मीट्रिक में घटक होते हैं (उपयुक्त रूप से चुने गए निर्देशांक के साथ मान्य) जिन्हें 4 × 4 मैट्रिक्स में व्यवस्थित किया जा सकता है: | ||
<math display="block">\eta_{\alpha\beta} = \begin{pmatrix} | <math display="block">\eta_{\alpha\beta} = \begin{pmatrix} | ||
-1 & 0 & 0 & 0\\ | -1 & 0 & 0 & 0\\ | ||
| Line 577: | Line 582: | ||
0 & 0 & 0 & 1 | 0 & 0 & 0 & 1 | ||
\end{pmatrix}</math> | \end{pmatrix}</math> | ||
जो इसके पारस्परिक के बराबर है, <math>\eta^{\alpha\beta}</math>, उन | जो इसके पारस्परिक के बराबर है, <math>\eta^{\alpha\beta}</math>, उन सीमा रेखाों में। ऊपर के रूप में हम संकेतों का उपयोग करते हैं, विभिन्न लेखक विभिन्न सम्मेलनों का उपयोग करते हैं - मिंकोव्स्की मीट्रिक वैकल्पिक संकेत देखें। | ||
पोंकारे समूह परिवर्तनों का सबसे सामान्य समूह है जो मिंकोव्स्की मीट्रिक को संरक्षित करता है: | पोंकारे समूह परिवर्तनों का सबसे सामान्य समूह है जो मिंकोव्स्की मीट्रिक को संरक्षित करता है: | ||
| Line 584: | Line 589: | ||
और यह भौतिक समरूपता है जो विशेष सापेक्षता में अंतर्निहित है। | और यह भौतिक समरूपता है जो विशेष सापेक्षता में अंतर्निहित है। | ||
मीट्रिक का उपयोग वैक्टर और टेंसर पर सूचकांक बढ़ाने और घटाने के लिए किया जा सकता है। मीट्रिक का उपयोग करके इनवेरिएंट का निर्माण किया जा सकता है, 4-वेक्टर टी का आंतरिक उत्पाद 4-वेक्टर | मीट्रिक का उपयोग वैक्टर और टेंसर पर सूचकांक बढ़ाने और घटाने के लिए किया जा सकता है। मीट्रिक का उपयोग करके इनवेरिएंट का निर्माण किया जा सकता है, 4-वेक्टर टी का आंतरिक उत्पाद 4-वेक्टर S के साथ है: | ||
<math display="block">T^{\alpha}S_{\alpha}=T^{\alpha}\eta_{\alpha\beta}S^{\beta} = T_{\alpha}\eta^{\alpha\beta}S_{\beta} = \text{invariant scalar}</math> | <math display="block">T^{\alpha}S_{\alpha}=T^{\alpha}\eta_{\alpha\beta}S^{\beta} = T_{\alpha}\eta^{\alpha\beta}S_{\beta} = \text{invariant scalar}</math> | ||
| Line 597: | Line 602: | ||
समन्वय अंतर भी विपरीत रूप से बदलते हैं: | समन्वय अंतर भी विपरीत रूप से बदलते हैं: | ||
<math display="block">dX^{\mu'}=\Lambda^{\mu'}{}_\nu dX^\nu</math> | <math display="block">dX^{\mu'}=\Lambda^{\mu'}{}_\nu dX^\nu</math> | ||
तो स्थिति के अंतर की | तो स्थिति के अंतर की रुंडित लंबाई चार-सदिश dX<sup>μ</sup> का उपयोग करके बनाया गया | ||
<math display="block">d\mathbf{X}^2 = dX^\mu \,dX_\mu = \eta_{\mu\nu}\,dX^\mu \,dX^\nu = -(c dt)^2+(dx)^2+(dy)^2+(dz)^2</math> | <math display="block">d\mathbf{X}^2 = dX^\mu \,dX_\mu = \eta_{\mu\nu}\,dX^\mu \,dX^\nu = -(c dt)^2+(dx)^2+(dy)^2+(dz)^2</math> | ||
एक अपरिवर्तनीय है। ध्यान दें कि जब [[ रेखा तत्व ]] d'X'<sup>2</sup> नकारात्मक है कि {{math|{{sqrt|−''d'''''X'''<sup>2</sup>}}}} उचित समय का अंतर है, जबकि जब d'X'<sup>2</sup> सकारात्मक है, {{math|{{sqrt|''d'''''X'''<sup>2</sup>}}}} [[ उचित दूरी ]] का अंतर है। | एक अपरिवर्तनीय है। ध्यान दें कि जब [[ रेखा तत्व ]] d'X'<sup>2</sup> नकारात्मक है कि {{math|{{sqrt|−''d'''''X'''<sup>2</sup>}}}} उचित समय का अंतर है, जबकि जब d'X'<sup>2</sup> सकारात्मक है, {{math|{{sqrt|''d'''''X'''<sup>2</sup>}}}} [[ उचित दूरी ]] का अंतर है। | ||
| Line 603: | Line 608: | ||
4-वेग U<sup>μ</sup> का एक अपरिवर्तनीय रूप है: | 4-वेग U<sup>μ</sup> का एक अपरिवर्तनीय रूप है: | ||
<math display="block">\mathbf U^2 = \eta_{\nu\mu} U^\nu U^\mu = -c^2 \,,</math> | <math display="block">\mathbf U^2 = \eta_{\nu\mu} U^\nu U^\mu = -c^2 \,,</math> | ||
जिसका अर्थ है कि सभी वेग चार-सदिशों का परिमाण c है। यह इस तथ्य की अभिव्यक्ति है कि सापेक्षता में समन्वय विश्राम | जिसका अर्थ है कि सभी वेग चार-सदिशों का परिमाण c है। यह इस तथ्य की अभिव्यक्ति है कि सापेक्षता में समन्वय विश्राम जैc कोई चीज नहीं है: कम से कम, आप सदैव समय के साथ आगे बढ़ रहे हैं। उपरोक्त समीकरण को द्वारा विभेदित करने पर उत्पन्न होता है: | ||
<math display="block">2\eta_{\mu\nu}A^\mu U^\nu = 0.</math> | <math display="block">2\eta_{\mu\nu}A^\mu U^\nu = 0.</math> | ||
तो विशेष सापेक्षता में, त्वरण चार-वेक्टर और वेग चार-वेक्टर ऑर्थोगोनल हैं। | तो विशेष सापेक्षता में, त्वरण चार-वेक्टर और वेग चार-वेक्टर ऑर्थोगोनल हैं। | ||
| Line 611: | Line 616: | ||
चार-गति का अपरिवर्तनीय परिमाण | गति 4-वेक्टर ऊर्जा-गति संबंध उत्पन्न करता है: | चार-गति का अपरिवर्तनीय परिमाण | गति 4-वेक्टर ऊर्जा-गति संबंध उत्पन्न करता है: | ||
<math display="block">\mathbf{P}^2 = \eta^{\mu\nu}P_\mu P_\nu = -\left (\frac{E}{c} \right )^2 + p^2 .</math> | <math display="block">\mathbf{P}^2 = \eta^{\mu\nu}P_\mu P_\nu = -\left (\frac{E}{c} \right )^2 + p^2 .</math> | ||
हम पहले यह तर्क देकर यह पता लगा सकते हैं कि यह अपरिवर्तनीय क्या है, क्योंकि यह एक अदिश राशि है, इससे कोई फर्क नहीं पड़ता कि हम किस | हम पहले यह तर्क देकर यह पता लगा सकते हैं कि यह अपरिवर्तनीय क्या है, क्योंकि यह एक अदिश राशि है, इससे कोई फर्क नहीं पड़ता कि हम किस निर्देश तंत्र में इसकी गणना करते हैं, और फिर एक सीमा रेखा में बदलकर जहां कुल गति शून्य है। | ||
<math display="block">\mathbf{P}^2 = - \left (\frac{E_\text{rest}}{c} \right )^2 = - (m c)^2 .</math> | <math display="block">\mathbf{P}^2 = - \left (\frac{E_\text{rest}}{c} \right )^2 = - (m c)^2 .</math> | ||
हम देखते हैं कि शेष ऊर्जा एक स्वतंत्र अपरिवर्तनीय है। गति में कणों और प्रणालियों के लिए भी एक | हम देखते हैं कि शेष ऊर्जा एक स्वतंत्र अपरिवर्तनीय है। गति में कणों और प्रणालियों के लिए भी एक विराम ऊर्जा की गणना की जा सकती है, एक सीमा रेखा में स्थानांतरण करके जिसमें गति शून्य है। | ||
शेष ऊर्जा ऊपर चर्चा किए गए प्रसिद्ध समीकरण के अनुसार द्रव्यमान से संबंधित है: | शेष ऊर्जा ऊपर चर्चा किए गए प्रसिद्ध समीकरण के अनुसार द्रव्यमान से संबंधित है: | ||
<math display="block">E_\text{rest} = m c^2.</math> | <math display="block">E_\text{rest} = m c^2.</math> | ||
उनके संवेग | उनके संवेग सीमा रेखा के केंद्र में मापा गया सिस्टम का द्रव्यमान (जहां कुल गति शून्य है) इस सीमा रेखा में सिस्टम की कुल ऊर्जा द्वारा दिया जाता है। यह अन्य फ़्रेमों में मापे गए व्यक्तिगत सिस्टम द्रव्यमान के योग के बराबर नहीं हो सकता है। | ||
न्यूटन के गति के तीसरे नियम का उपयोग करने के लिए, दोनों बलों को एक ही समय के समन्वय के संबंध में गति के परिवर्तन की दर के रूप में परिभाषित किया जाना चाहिए। अर्थात्, इसके लिए ऊपर परिभाषित 3D बल की आवश्यकता होती है। दुर्भाग्य से, 4D में कोई | न्यूटन के गति के तीसरे नियम का उपयोग करने के लिए, दोनों बलों को एक ही समय के समन्वय के संबंध में गति के परिवर्तन की दर के रूप में परिभाषित किया जाना चाहिए। अर्थात्, इसके लिए ऊपर परिभाषित 3D बल की आवश्यकता होती है। दुर्भाग्य से, 4D में कोई टेन्सर नहीं है जिसमें इसके घटकों के बीच 3D बल वेक्टर के घटक सम्मिलित हैं। | ||
यदि कोई कण c पर यात्रा नहीं कर रहा है, तो कोई कण के सह-चलती | यदि कोई कण c पर यात्रा नहीं कर रहा है, तो कोई कण के सह-चलती निर्देश तंत्र से 3D बल को पर्यवेक्षक के निर्देश तंत्र में बदल सकता है। यह एक 4-वेक्टर उत्पन्न करता है जिसे चार-बल कहा जाता है। यह उचित समय के संबंध में उपरोक्त ऊर्जा गति चार-सदिश के परिवर्तन की दर है। चार-बलों का सहसंयोजक संस्करण है: | ||
<math display="block">F_\nu = \frac{d P_{\nu}}{d \tau} = m A_\nu </math> | <math display="block">F_\nu = \frac{d P_{\nu}}{d \tau} = m A_\nu </math> | ||
वस्तु के बाकी | वस्तु के बाकी सीमा रेखा में, चार बल का समय घटक शून्य होता है जब तक कि वस्तु का "अपरिवर्तनीय द्रव्यमान" नहीं बदल रहा हो (इसके लिए एक गैर-बंद प्रणाली की आवश्यकता होती है जिसमें ऊर्जा/द्रव्यमान सीधे वस्तु से जोड़ा या हटाया जा रहा हो) ) जिस स्थिति में यह द्रव्यमान परिवर्तन की उस दर का ऋणात्मक होता है, समय c. सामान्य तौर पर, यद्यपि, चार बल के घटक तीन-बल के घटकों के बराबर नहीं होते हैं, क्योंकि तीन बल को समन्वय समय के संबंध में गति के परिवर्तन की दर से परिभाषित किया जाता है, अर्थात dp/dt जबकि चार बल को उचित समय के संबंध में संवेग के परिवर्तन की दर से परिभाषित किया गया है, अर्थात dp/dτ। | ||
एक सतत माध्यम में, बल का 3D घनत्व शक्ति के घनत्व के साथ मिलकर एक सहसंयोजक 4-वेक्टर बनाता है। स्थानिक भाग उस कोशिका के आयतन | एक सतत माध्यम में, बल का 3D घनत्व शक्ति के घनत्व के साथ मिलकर एक सहसंयोजक 4-वेक्टर बनाता है। स्थानिक भाग उस कोशिका के आयतन से एक छोटी कोशिका (3-स्थान में) पर बल को विभाजित करने का परिणाम है। समय घटक सेल के आयतन से विभाजित उस सेल को हस्तांतरित शक्ति का −1/c गुना है। इसका उपयोग नीचे विद्युत चुंबकत्व पर अनुभाग में किया जाएगा। | ||
==यह भी देखें== | ==यह भी देखें== | ||
| Line 720: | Line 725: | ||
=== मूल कार्य === | === मूल कार्य === | ||
* [http://www.physik.uni-augsburg.de/annalen/history/einstein-papers/1905_17_891-921.pdf मूविंग बॉडीज के इलेक्ट्रोडायनामिक्स पर] आइंस्टीन का मूल काम जर्मन में, [[ भौतिकी के इतिहास ]], [[ बर्नो ]] 1905 | * [http://www.physik.uni-augsburg.de/annalen/history/einstein-papers/1905_17_891-921.pdf मूविंग बॉडीज के इलेक्ट्रोडायनामिक्स पर] आइंस्टीन का मूल काम जर्मन में, [[ भौतिकी के इतिहास ]], [[ बर्नो ]] 1905 | ||
* [http://www.fourmilab.ch/etexts/einstein/specrel/specrel.pdf मूविंग बॉडीज के इलेक्ट्रोडायनामिक्स पर] 1923 की किताब द प्रिंसिपल ऑफ रिलेटिविटी में प्रकाशित अंग्रेजी | * [http://www.fourmilab.ch/etexts/einstein/specrel/specrel.pdf मूविंग बॉडीज के इलेक्ट्रोडायनामिक्स पर] 1923 की किताब द प्रिंसिपल ऑफ रिलेटिविटी में प्रकाशित अंग्रेजी स्थानांतरण। | ||
=== सामान्य दर्शकों के लिए विशेष सापेक्षता (गणितीय ज्ञान की आवश्यकता नहीं) === | === सामान्य दर्शकों के लिए विशेष सापेक्षता (गणितीय ज्ञान की आवश्यकता नहीं) === | ||
| Line 749: | Line 754: | ||
* [http://www.adamauton.com/warp/ ताना विशेष सापेक्षता सिम्युलेटर] प्रकाश की गति के करीब यात्रा करने के प्रभावों को दिखाने के लिए एक कंप्यूटर प्रोग्राम। | * [http://www.adamauton.com/warp/ ताना विशेष सापेक्षता सिम्युलेटर] प्रकाश की गति के करीब यात्रा करने के प्रभावों को दिखाने के लिए एक कंप्यूटर प्रोग्राम। | ||
* {{YouTube|C2VMO7pcWhg|Animation clip}} लोरेंत्ज़ परिवर्तन की कल्पना करना। | * {{YouTube|C2VMO7pcWhg|Animation clip}} लोरेंत्ज़ परिवर्तन की कल्पना करना। | ||
* [http://math.ucr.edu/~jdp/Relativity/SpecialRelativity.html ओरिजिनल इंटरएक्टिव फ्लैश एनिमेशन] लोरेंत्ज़ और गैलीलियन | * [http://math.ucr.edu/~jdp/Relativity/SpecialRelativity.html ओरिजिनल इंटरएक्टिव फ्लैश एनिमेशन] लोरेंत्ज़ और गैलीलियन सीमा रेखा, ट्रेन और टनल पैराडॉक्स, ट्विन पैराडॉक्स, वेव प्रोपेगेशन, क्लॉक सिंक्रोनाइज़ेशन का चित्रण करते हुए जॉन डी पिलिस से, आदि। | ||
* [http://lightspeed.sourceforge.net/ lightspeed] एक ओपनजीएल-आधारित प्रोग्राम जिसे चलती वस्तुओं की उपस्थिति पर विशेष सापेक्षता के प्रभावों को स्पष्ट करने के लिए विकसित किया गया है। | * [http://lightspeed.sourceforge.net/ lightspeed] एक ओपनजीएल-आधारित प्रोग्राम जिसे चलती वस्तुओं की उपस्थिति पर विशेष सापेक्षता के प्रभावों को स्पष्ट करने के लिए विकसित किया गया है। | ||
* [http://specialrelativity.net/animations/starfield/starfield.html?beta=0.8&color=on&circles=on&avgstellardensity=0.11&starpopulation=yalebsc&limitingMag=5&projection=stereographic&anim=on&runningTime=8 एनिमेशन] पृथ्वी के पास के तारे दिखा रहा है, जैसा कि यहां से देखा जा सकता है एक अंतरिक्ष यान तेजी से प्रकाश की गति में तेजी ला रहा है। | * [http://specialrelativity.net/animations/starfield/starfield.html?beta=0.8&color=on&circles=on&avgstellardensity=0.11&starpopulation=yalebsc&limitingMag=5&projection=stereographic&anim=on&runningTime=8 एनिमेशन] पृथ्वी के पास के तारे दिखा रहा है, जैसा कि यहां से देखा जा सकता है एक अंतरिक्ष यान तेजी से प्रकाश की गति में तेजी ला रहा है। | ||
| Line 765: | Line 770: | ||
श्रेणी:अल्बर्ट आइंस्टीन | श्रेणी:अल्बर्ट आइंस्टीन | ||
[[Category:AC with 0 elements|Special Relativity]] | |||
[[Category: | [[Category:Articles with hatnote templates targeting a nonexistent page|Special Relativity]] | ||
[[Category:Created On 09/09/2022]] | [[Category:Articles with short description|Special Relativity]] | ||
[[Category:CS1 maint]] | |||
[[Category:Collapse templates|Special Relativity]] | |||
[[Category:Created On 09/09/2022|Special Relativity]] | |||
[[Category:Machine Translated Page|Special Relativity]] | |||
[[Category:Navigational boxes| ]] | |||
[[Category:Navigational boxes without horizontal lists|Special Relativity]] | |||
[[Category:Pages using multiple image with manual scaled images|Special Relativity]] | |||
[[Category:Pages with empty portal template|Special Relativity]] | |||
[[Category:Pages with script errors|Special Relativity]] | |||
[[Category:Portal templates with redlinked portals|Special Relativity]] | |||
[[Category:Short description with empty Wikidata description|Special Relativity]] | |||
[[Category:Sidebars with styles needing conversion|Special Relativity]] | |||
[[Category:Template documentation pages|Documentation/doc]] | |||
[[Category:Templates generating microformats|Special Relativity]] | |||
[[Category:Templates that are not mobile friendly|Special Relativity]] | |||
[[Category:Templates using TemplateData|Special Relativity]] | |||
[[Category:Webarchive template wayback links]] | |||
[[Category:Wikipedia metatemplates|Special Relativity]] | |||
Latest revision as of 10:32, 22 November 2022

| Special relativity |
|---|
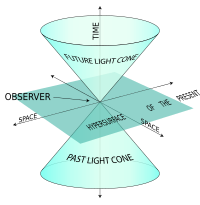 |
भौतिक विज्ञान में, सापेक्षता का विशेष सिद्धांत, या संक्षेप में विशेष सापेक्षता, अंतरिक्ष और समय के बीच संबंध में एक वैज्ञानिक सिद्धांत है। अल्बर्ट आइंस्टीन के मूल उपचार में दिया गया सिद्धांत दो अभिधारणाओं पर आधारित है:[p 1][1][2]
- संदर्भ के सभी जड़त्वीय सीमा रेखा(अर्थात, बिना किसी त्वरण के संदर्भ के सीमा रेखा) में भौतिकी के नियम अपरिवर्तनीय (भौतिकी) (अर्थात समान) हैं।
- निर्वात में प्रकाश की गति सभी प्रेक्षकों के लिए समान होती है, चाहे प्रकाश स्रोत या प्रेक्षक की गति कुछ भी हो।
मूल और महत्व
विशेष सापेक्षता मूल रूप से अल्बर्ट आइंस्टीन द्वारा 26 सितंबर 1905 को "विद्युतगतिकी पर गतिमान पिंड" शीर्षक से प्रकाशित एक पेपर में प्रस्तावित की गई थी।[p 1] मैक्सवेल के विद्युत चुंबकत्व के समीकरणों के साथ न्यूटनियन यांत्रिकी असंगति और, प्रयोगात्मक रूप से, माइकलसन-मॉर्ले नल परिणाम(और बाद में इसी तरह के प्रयोगों) ने प्रदर्शित किया कि ऐतिहासिक रूप से परिकल्पित प्रकाशवाही ईथर उपलब्ध नहीं था। इसने आइंस्टीन के विशेष सापेक्षता के विकास को जन्म दिया, जो सभी गतियों को सम्मिलित करने वाली स्थितियों को संभालने के लिए यांत्रिकी को विनिर्मित करता है और विशेष रूप से प्रकाश की गति के निकटतम गति पर(जिसे आपेक्षित वेग के नाम से जाना जाता है) आज, विशेष सापेक्षता किसी भी गति से गति का सबसे सटीक मॉडल साबित होती है जब गुरुत्वाकर्षण और क्वांटम प्रभाव नगण्य होते हैं।[3][4] फिर भी, न्यूटोनियन मॉडल अभी भी कम वेग(प्रकाश की गति के सापेक्ष) पर एक सरल और सटीक सन्निकटन के रूप में मान्य है, उदाहरण के लिए, पृथ्वी पर प्रतिदिन परिक्रमण की गति।
विशेष सापेक्षता के व्यापक परिणाम हैं जिन्हें प्रयोगात्मक रूप से सत्यापित किया गया है। वे एक साथ सापेक्षता, लंबाई संकुचन, समय विस्तार, सापेक्षतावादी वेग जोड़ सूत्र, सापेक्षतावादी डॉपलर प्रभाव, विशेष सापेक्षता में द्रव्यमान, प्रकाश की गति पर ऊपरी सीमा, द्रव्यमान-ऊर्जा तुल्यता, कार्य-कारण और थॉमस पूर्वसर्ग इत्यादि की गति सम्मिलित हैं ।[1][2]उदाहरण के लिए, इसने एक पूर्ण सार्वभौमिक समय की पारंपरिक धारणा को उस समय की धारणा से बदल दिया है जो निर्देश तंत्र और अंतरिक्ष स्थिति पर निर्भर है। दो घटनाओं के बीच एक अपरिवर्तनीय समय अंतराल के अतिरिक्त, एक अपरिवर्तनीय स्पेसटाइम अंतराल होता है।
भौतिकी के अन्य नियमों के साथ, विशेष सापेक्षता के दो अभिगृहीत द्रव्यमान और ऊर्जा की तुल्यता की भविष्यवाणी करते हैं, जैसा कि द्रव्यमान-ऊर्जा तुल्यता सूत्र में व्यक्त किया गया है। , जहाँ निर्वात में प्रकाश की गति है।[5][6] यह इस बात की पुष्टि करता है कि बिजली और चुंबकत्व की घटनाएं कैसे संबंधित हैं।[1][2]
विशेष सापेक्षता की एक परिभाषित विशेषता लोरेंत्ज़ परिवर्तन के साथ न्यूटनियन यांत्रिकी के गैलीलियन परिवर्तन का प्रतिस्थापन है। समय और स्थान को एक दूसरे से अलग-अलग परिभाषित नहीं किया जा सकता (जैसा कि पहले माना जाता था)। बल्कि, अंतरिक्ष और समय को स्पेसटाइम में जोड़ा जाता है | किसी एकल सातत्य जिसे स्पेसटाइम के रूप में जाना जाता है, किसी पर्यवेक्षक के लिए एक ही समय में होने वाली घटनाएँ दूसरे के लिए अलग-अलग समय पर घटित हो सकती हैं।
कई वर्षों बाद तक जब आइंस्टीन ने सामान्य सापेक्षता विकसित की, जिसने गुरुत्वाकर्षण को सम्मिलित करने के लिए एक गतिशील स्पेसटाइम पेश किया, जिसमे विशेष सापेक्षता वाक्यांश का उपयोग नहीं किया गया था। कभी-कभी उपयोग किया जाने वाला स्थानांतरण प्रतिबंधित सापेक्षता है, विशेष सापेक्षता वास्तव में एक विशिष्ट परिस्थिति है।[p 2][p 3][p 4][note 1] विशेष सापेक्षता में अल्बर्ट आइंस्टीन के कुछ काम हेंड्रिक लोरेंत्ज़ो और हेनरी पोंकारे द्वारा पहले के काम पर बनाए गए हैं। सिद्धांत अनिवार्य रूप से 1907 में पूर्ण हो गया।[4]
यह सिद्धांत इस सन्दर्भ में विशेष है कि यह केवल उस विशेष परिस्थिति में लागू होता है जहां स्पेसटाइम एकसमान होता है, अर्थात जहां स्पेसटाइम की वक्रता (ऊर्जा-गति टेंसर का परिणाम और गुरुत्वाकर्षण का प्रतिनिधित्व) नगण्य है।[7][note 2] गुरुत्वाकर्षण को सही ढंग से समायोजित करने के लिए, आइंस्टीन ने 1915 में सामान्य सापेक्षता तैयार की। विशेष सापेक्षता, कुछ ऐतिहासिक विवरणों के विपरीत, त्वरण (विशेष सापेक्षता) के साथ-साथ रिंडलर निर्देशांक को समायोजित करती है।[8][9] जिस तरह गैलीलियन इनवेरिएंस को अब विशेष सापेक्षता का अनुमान माना जाता है जो कम गति के लिए मान्य है, विशेष सापेक्षता को सामान्य सापेक्षता का अनुमान माना जाता है जो कमजोर गुरुत्वाकर्षण क्षेत्र के लिए मान्य है, अर्थात पर्याप्त रूप से छोटे पैमाने पर(उदाहरण के लिए, जब ज्वारीय बल नगण्य हो) और मुक्त पतन की स्थितियों में। यद्यपि, सामान्य सापेक्षता में गैर-यूक्लिडियन ज्यामिति को सम्मिलित किया जाता है ताकि गुरुत्वाकर्षण प्रभाव को स्पेसटाइम के ज्यामितीय वक्रता के रूप में दर्शाया जा सके। विशेष सापेक्षता फ्लैट स्पेसटाइम तक cमित है जिसे मिंकोव्स्की स्पेस के रूप में जाना जाता है। जब तक ब्रह्मांड को छद्म रीमैनियन मैनिफोल्ड के रूप में तैयार किया जा सकता है। एक लोरेंत्ज़-अपरिवर्तनीय सीमा रेखा जो विशेष सापेक्षता का पालन करता है, जिसे इस वक्राकार स्पेसटाइम में प्रत्येक बिंदु के पर्याप्त छोटे पड़ोस के लिए परिभाषित किया जा सकता है।
गैलिलियो गैलिली ने पहले ही माना था कि विराम की कोई पूर्ण और यथार्थ रूप से परिभाषित स्थिति नहीं है(कोई परिशुद्ध सीमा रेखा नहीं), एक सिद्धांत जिसे अब गैलीलियन इनवेरिएंस गैलीलियो का सापेक्षता का सिद्धांत कहा जाता है। आइंस्टीन ने इस सिद्धांत का विस्तार इस प्रकार किया कि यह प्रकाश की निरंतर गति के लिए उत्तरदायी हो गया,[10] जिसे माइकलसन-मॉर्ले प्रयोग में देखा गया था। उन्होंने यह भी माना कि यह भौतिकी के सभी नियमों के लिए है, जिसमें यांत्रिकी और बिजली का गतिविज्ञान दोनों के नियम सम्मिलित हैं।[11]
विशेष सापेक्षता के लिए पारंपरिक दो अभिधारणाएं
"इस प्रकार के प्रतिबिंबों ने 1900 के कुछ समय बाद ही, अर्थात प्लैंक के ट्रेलब्लेज़िंग कार्य के तुरंत बाद, मुझे यह स्पष्ट कर दिया कि न तो यांत्रिकी और न ही विद्युत् गतिकी(सीमित परिस्थितियों को छोड़कर) सटीक वैधता का दावा कर सकते हैं। धीरे-धीरे मैं खोज की संभावना से निराश हो गया, ज्ञात तथ्यों पर आधारित रचनात्मक प्रयासों के माध्यम से सार्वभौमिक नियमो का जितना अधिक मैंने प्रयास किया, उतना ही मुझे यह विश्वास हुआ कि केवल एक सार्वभौमिक औपचारिक सिद्धांत की खोज ही हमें सुनिश्चित परिणामों तक ले जा सकती है। अतः किस प्रकार ऐसा सार्वभौमिक सिद्धांत पाया जा सकता है?"
अल्बर्ट आइंस्टीन: आत्मकथात्मक लेख[p 5]
आइंस्टीन ने दो मूलभूत प्रस्तावों की पहचान की, जो यांत्रिकी या विद्युत गतिकी के(तत्कालीन) ज्ञात नियमो की सटीक वैधता की परवाह किए बिना, सबसे अधिक आश्वस्त प्रतीत होते थे। ये प्रस्ताव निर्वात में प्रकाश की गति की स्थिरता और जड़त्वीय प्रणाली की पसंद से भौतिक नियमो(विशेषकर प्रकाश की गति की स्थिरता) की स्वतंत्रता थे। 1905 में विशेष सापेक्षता की अपनी प्रारंभिक प्रस्तुति में उन्होंने इन अभिधारणाओं को इस रूप में व्यक्त किया:[p 1]* सापेक्षता का सिद्धांत - वे नियम जिनके द्वारा भौतिक प्रणालियों की अवस्थाओं में परिवर्तन होता है, प्रभावित नहीं होते हैं, राज्य के इन परिवर्तनों को एक दूसरे के सापेक्ष एकसमान स्थानांतरणकीय गति में दो प्रणालियों में से एक या दूसरे को संदर्भित किया जा सकता था।[p 1]* अपरिवर्तनीय प्रकाश गति का सिद्धांत - "... प्रकाश सदैव खाली स्थान में एक निश्चित वेग[गति] c के साथ प्रसारित होता है जो उत्सर्जक पिंड की गति की स्थिति से स्वतंत्र होता है"[p 1]यह, निर्वात में प्रकाश स्रोत की गति की स्थिति की परवाह किए बिना, जड़त्वीय निर्देशांक की कम से कम एक प्रणाली ("स्थिर प्रणाली") में गति c (एक निश्चित स्थिर, दिशा से स्वतंत्र) के साथ फैलता है।
प्रकाश की गति की स्थिरता मैक्सवेल के विद्युत चुम्बकत्व के सिद्धांत [उद्धरण वांछित] और प्रकाशवाही ईथर के लिए प्रमाण की कमी से प्रेरित थी। मिशेलसन-मॉर्ले प्रयोग के शून्य परिणाम से आइंस्टीन किस सीमा तक प्रभावित थे, इस पर परस्पर विरोधी प्रमाण हैं।[12][13]किसी भी परिस्थिति में, माइकलसन-मॉर्ले प्रयोग के शून्य परिणाम ने प्रकाश की गति की गति की व्यापकता और तेजी से स्वीकृति की धारणा में मदद की।
विशेष सापेक्षता की व्युत्पत्ति न केवल इन दो स्पष्ट अभिधारणाओं पर निर्भर करती है, बल्कि कई मौन धारणाओं(भौतिकी के लगभग सभी सिद्धांतों में बनाई गई) पर भी निर्भर करती है, जिसमें अंतरिक्ष की समरूपता और उनके पिछले इतिहास से रेखा और समय को मापने की स्वतंत्रता सम्मिलित है।[p 6] 1905 में आइंस्टीन की विशेष सापेक्षता की मूल प्रस्तुति के बाद, विभिन्न वैकल्पिक व्युत्पत्तियों में अभिधारणाओं के कई अलग-अलग सेट प्रस्तावित किए गए हैं।[14]यद्यपि, आइंस्टीन द्वारा अपने मूल पेपर में नियोजित पदों का सबसे साधारण संग्रह बना हुआ है। बाद में आइंस्टीन द्वारा दिए गए सापेक्षता के सिद्धांत का एक और गणितीय कथन, जो ऊपर वर्णित सहजता की अवधारणा का परिचय नहीं देता है:
सापेक्षता का विशेष सिद्धांत: यदि निर्देशांक K की एक प्रणाली को चुना जाता है, ताकि इसके संबंध में, भौतिक नियम अपने सरलतम रूप में उपयुक्त हों, तो 'समान' नियम किसी भी अन्य समन्वय प्रणाली के संबंध में उपयुक्त होते हैं, जो समान रूप से स्थानांतरित होते हैं।[15]
हेनरी पोंकारे ने यह साबित करके सापेक्षता सिद्धांत के लिए गणितीय ढांचा प्रदान किया कि लोरेंत्ज़ परिवर्तन समरूपता परिवर्तन उनके पोंकारे समूह का एक उपसमूह है। आइंस्टीन ने बाद में इन परिवर्तनों को अपने स्वयंसिद्ध सिद्धांतों से प्राप्त किया।
आइंस्टीन के कई पत्र इन दो सिद्धांतों के आधार पर लोरेंत्ज़ परिवर्तन की व्युत्पत्तियों को प्रस्तुत करते हैं।[p 7]
सापेक्षता का सिद्धांत
निर्देश तंत्र और सापेक्ष गति

निर्देश तंत्र सापेक्षता सिद्धांत में एक महत्वपूर्ण भूमिका निभाते हैं। यहां उपयोग किया गया निर्देश तंत्र शब्द अंतरिक्ष में एक अवलोकन परिप्रेक्ष्य है जो गति(त्वरण) में किसी भी बदलाव से नहीं गुजरता है, जिससे एक स्थिति को 3 स्थानिक अक्षों के साथ मापा जा सकता है (इसलिए, विराम या स्थिर वेग पर)। इसके अलावा, एक निर्देश तंत्र में 'चालमापी' (समान आवधिकता के साथ कोई भी संदर्भ उपकरण) का उपयोग करके घटनाओं के समय के माप को निर्धारित करने की क्षमता होती है।
एक घटना (सापेक्षता) जिसे एक निर्देश तंत्र के सापेक्ष अंतरिक्ष में एक अद्वितीय क्षण और स्थान दिया जा सकता है: यह स्पेसटाइम में एक "बिंदु" है। चूंकि निर्देश तंत्र के बावजूद प्रकाश की गति सापेक्षता में स्थिर है, प्रकाश की स्पंदनों का उपयोग स्पष्ट रूप से दूरियों को मापने के लिए किया जा सकता है और उस समय को वापस संदर्भित किया जा सकता है जब घटना चालमापी में हुई थी, भले ही प्रकाश को घटना के बाद चालमापी तक पहुंचने में समय लगता है।
उदाहरण के लिए, पटाखों के विस्फोट को एक "घटना" माना जा सकता है। हम किसी घटना को उसके चार स्पेसटाइम निर्देशांकों द्वारा पूरी तरह से निर्दिष्ट कर सकते हैं: घटना का समय और इसकी त्रि-आयामी स्थानिक स्थिति एक संदर्भ बिंदु को परिभाषित करती है। इस निर्देश तंत्र को S कहते हैं।
सापेक्षता सिद्धांत में, हम अधिकांशतः भिन्न संदर्भ फ़्रेमों से किसी घटना के निर्देशांकों की गणना करना चाहते हैं। विभिन्न सीमा रेखाों में किए गए मापों को जोड़ने वाले समीकरण रूपांतरण समीकरण कहलाते हैं।
मानक विन्यास
विभिन्न संदर्भ फ़्रेमों में पर्यवेक्षकों द्वारा मापा गया स्पेसटाइम निर्देशांक एक दूसरे के साथ तुलना करने के तरीके में अंतर्दृष्टि प्राप्त करने के लिए, मानक विन्यास में फ़्रेम के साथ सरलीकृत सेटअप के साथ काम करना उपयोगी होता है।[16]: 107 यह गणित के सरलीकरण की अनुमति देता है। निष्कर्षों में व्यापकता का कोई नुकसान नहीं होता है। चित्र 2-1 में, दो गैलीलियन संदर्भ फ़्रेम (अर्थात, पारंपरिक 3-स्पेस फ़्रेम) सापेक्ष गति में प्रदर्शित होते हैं। फ़्रेम S पहले पर्यवेक्षक O से संबंधित है, और फ़्रेम S′ दूसरे पर्यवेक्षक O′ से संबंधित है।
- सीमा रेखा S के x, y, z अक्ष सीमा रेखा S′ के संबंधित प्राइमेड अक्षों के समानांतर उन्मुख होते हैं।
- फ़्रेम S′ सरलता के लिए, एक ही दिशा में चलता है: फ़्रेम S की x-दिशा स्थिर वेग v के साथ, जैसा कि फ़्रेम S में मापा जाता है।
- सीमा रेखा S और S′ के उद्गम संपाती होते हैं जब सीमा रेखा S के लिए समय t = 0 और सीमा रेखा S′ के लिए t′ = 0 होता है।
चूंकि सापेक्षता सिद्धांत में कोई पूर्ण निर्देश तंत्र नहीं है, इसलिए 'चलती' की अवधारणा सख्ती से उपलब्ध नहीं है, क्योंकि सब कुछ किसी अन्य निर्देश तंत्र के संबंध में आगे बढ़ रहा है। इसके अतिरिक्त, कोई भी दो सीमा रेखा जो एक ही गति से एक ही दिशा में चलते हैं, उन्हें मूविंग कहा जाता है। इसलिए, S और S′ गतिमान नहीं हैं।
एक पूर्ण निर्देश तंत्र का अभाव
सापेक्षता का सिद्धांत, जिसमें कहा गया है कि प्रत्येक जड़त्वीय निर्देश तंत्र में भौतिक नियमो का एक ही रूप है, गैलीलियो से पहले का है, और न्यूटनियन भौतिकी में सम्मिलित किया गया था। यद्यपि, 19वीं शताब्दी के अंत में, विद्युत चुम्बकीय विकिरण के अस्तित्व ने कुछ भौतिकविदों को यह सुझाव देने के लिए प्रेरित किया कि ब्रह्मांड एक पदार्थ से भरा हुआ है जिसे वे प्रकाशवाही ईथर कहते हैं, उन्होंने माना कि यह, माध्यम के रूप में कार्य करेगा जिसके माध्यम से ये तरंगें या कंपन प्रचारित होती हैं (जिस तरह से ध्वनि हवा के माध्यम से फैलती है, उc तरह कई मायनों में)। ईथर को एक परिशुद्ध सीमा रेखा माना जाता था जिसके विपरीत सभी गति को मापा जा सकता था, और इसे पृथ्वी या किसी अन्य निश्चित संदर्भ बिंदु के सापेक्ष स्थिर और गतिहीन माना जा सकता था। ईथर को विद्युत चुम्बकीय तरंगों का समर्थन करने के लिए पर्याप्त रूप से लोचदार माना जाता था, जबकि वे तरंगें पदार्थ के साथ परस्पर प्रभाव डाल सकती थीं, फिर भी इससे गुजरने वाले निकायों के लिए कोई प्रतिरोध नहीं था (इसकी एक संपत्ति यह थी कि यह विद्युत चुम्बकीय तरंगों को फैलाने की अनुमति देती थी)। 1887 में माइकलसन-मॉर्ले प्रयोग (बाद में अधिक सटीक और नवीन प्रयोगों के साथ सत्यापित) सहित विभिन्न प्रयोगों के परिणामों ने विशेष सापेक्षता के सिद्धांत को जन्म दिया, यह दिखाते हुए कि ईथर उपलब्ध नहीं था।[17] आइंस्टीन का समाधान एक ईथर की धारणा और विराम की पूर्ण स्थिति को त्यागना था। सापेक्षता में, एकसमान गति से गतिमान कोई भी निर्देश तंत्र भौतिकी के समान नियमों का पालन करेगा। विशेष रूप से, निर्वात में प्रकाश की गति को सदैव c के रूप में मापा जाता है, भले ही इसे कई प्रणालियों द्वारा मापा जाता है जो अलग-अलग (लेकिन स्थिर) वेग से आगे बढ़ रहे हैं।
दूसरी अभिधारणा के बिना सापेक्षता
केवल सापेक्षता के सिद्धांत से प्रकाश की गति की स्थिरता को ग्रहण किए बिना (अर्थात, अंतरिक्ष की समरूपता और विशेष सापेक्षता के सिद्धांत द्वारा निहित समरूपता का उपयोग करके) यह दिखाया जा सकता है कि जड़त्वीय सीमा रेखा के बीच स्पेसटाइम परिवर्तन या तो यूक्लिडियन, गैलीलियन हैं , या लोरेंत्ज़ियन। लोरेंत्ज़ियन परिस्थिति में, तब कोई सापेक्षतावादी अंतराल संरक्षण और एक निश्चित cमित cमित गति प्राप्त कर सकता है। प्रयोगों से पता चलता है कि यह गति निर्वात में प्रकाश की चाल है।[p 8][18]
विशेष सापेक्षता के आवश्यक मूल के रूप में लोरेंत्ज़ इनवेरिएंस
विशेष सापेक्षता के लिए वैकल्पिक दृष्टिकोण
आइंस्टीन लगातार लोरेंत्ज़ इनवेरिएंस (विशेष सापेक्षता का आवश्यक मूल) की व्युत्पत्ति सापेक्षता और प्रकाश-गति के अपरिवर्तन के केवल दो मूल सिद्धांतों पर आधारित थे। उन्होंने लिखा है:
सापेक्षता के विशेष सिद्धांत के लिए मूलभूत अंतर्दृष्टि यह है: धारणाएं सापेक्षता और प्रकाश की गति अपरिवर्तनीयता संगत होती हैं यदि एक नए प्रकार के संबंध ("लोरेंत्ज़ परिवर्तन") को निर्देशांक और घटनाओं के समय के रूपांतरण के लिए संक्षिप्त किया जाता है ... सार्वभौमिक सिद्धांत सापेक्षता के विशेष सिद्धांत की परिकल्पना में निहित है: भौतिकी के नियम लोरेंत्ज़ परिवर्तनों के संबंध में अपरिवर्तनीय हैं (एक जड़त्वीय प्रणाली से किसी अन्य मनमाने ढंग से चुने गए जड़त्वीय प्रणाली में संक्रमण के लिए)। यह प्राकृतिक नियमों के लिए एक प्रतिबंधित सिद्धांत है...[p 5]
इस प्रकार विशेष सापेक्षता के कई आधुनिक उपचार इसे सार्वभौमिक लोरेंत्ज़ सहप्रसरण के एकल अभिधारणा पर, या, समान रूप से मिंकोव्स्की स्पेसटाइम के एकल अभिधारणा पर आधारित करते हैं।[p 9][p 10] सार्वभौमिक लोरेंत्ज़ सहप्रसरण को एक व्युत्पन्न सिद्धांत मानने के अतिरिक्त, यह लेख इसे विशेष सापेक्षता का मौलिक अभिधारणा मानता है। विशेष सापेक्षता के लिए पारंपरिक दो अभिधारणा दृष्टिकोण को असंख्य कॉलेज पाठ्यपुस्तकों और लोकप्रिय प्रस्तुतियों में प्रस्तुत किया गया है।[19] मिंकोवस्की स्पेसटाइम के एकल अभिधारणा से शुरू होने वाली पाठ्यपुस्तकों में टेलर, व्हीलर और कैलाहन द्वारा लिखित पुस्तकें सम्मिलित हैं।[20] विकिपीडिया लेख स्पेसटाइम और मिंकोव्स्की आरेख के बाद भी यही दृष्टिकोण है।
लोरेंत्ज़ परिवर्तन और उसका प्रतिलोम
स्पेसटाइम को परिभाषित करें, स्पेसटाइम निर्देशांक रखने के लिए बुनियादी अवधारणाएं (t, x, y, z) सिस्टम S और . में (t′, x′, y′, z′) एक निर्देश तंत्र में उस सीमा रेखा के संबंध में वेग v से आगे बढ़ते हुए, S′ फिर लोरेंत्ज़ परिवर्तन निर्दिष्ट करता है कि ये निर्देशांक निम्नलिखित तरीके से संबंधित हैं:
अप्रकाशित निर्देशांक के लिए उपरोक्त चार परिवर्तन समीकरणों को हल करने से व्युत्क्रम लोरेंत्ज़ परिवर्तन प्राप्त होता है:
एक्स-अक्ष के बारे में कुछ खास नहीं है। परिवर्तन y- या z- अक्ष पर लागू हो सकता है, या वास्तव में गति के समानांतर किसी भी दिशा में (जो कारक द्वारा विकृत होते हैं) और लंबवत; विवरण के लिए लेख लोरेंत्ज़ परिवर्तन देखें।
लोरेंत्ज़ परिवर्तनों के तहत एक मात्रा अपरिवर्तनीय को लोरेंत्ज़ स्केलार के रूप में जाना जाता है।
लोरेंत्ज़ परिवर्तन और इसके व्युत्क्रम को समन्वय अंतर के संदर्भ में लिखना, जहां एक घटना में निर्देशांक होते हैं (x1, t1) तथा (x′1, t′1), एक अन्य घटना के निर्देशांक हैं (x2, t2) तथा (x′2, t′2), और अंतर के रूप में परिभाषित कर रहे हैं
- Eq. 1:
- Eq. 2:
हम पाते हैं
- Eq. 3:
- Eq. 4:
यदि हम अंतर लेने के अतिरिक्त हमे दिखता है
- Eq. 5:
- Eq. 6:
लोरेंत्ज़ परिवर्तन का चित्रमय प्रतिनिधित्व
स्पेसटाइम आरेख (मिन्कोव्स्की आरेख) यह देखने के लिए एक अत्यंत उपयोगी सहायता है कि विभिन्न संदर्भ फ़्रेमों के बीच निर्देशांक कैसे परिवर्तित होते हैं। यद्यपि उनका उपयोग करके सही गणना करना उतना आसान नहीं है जितना कि लोरेंत्ज़ परिवर्तनों को सीधे लागू करना, उनकी मुख्य शक्ति सापेक्षतावादी परिदृश्य के परिणामों की सहज समझ प्रदान करने की उनकी क्षमता है।[18]
स्पेसटाइम आरेख बनाने के लिए, मानक विन्यास में दो गैलीलियन संदर्भ फ़्रेम, S और S' पर विचार करके प्रारंभ करें, जैसा कि चित्र 2-1 में दिखाया गया है।[18][21]: 155–199 । 3-1a।, तथा सीमा रेखा s की अक्षों , h अक्ष क्षैतिज है और (वास्तव में ) अक्ष लंबवत है, जो कि कीनेमेटिक्स में सामान्य परंपरा के विपरीत है। h> अक्ष को के एक कारक द्वारा बढ़ाया जाता है ताकि दोनों अक्षों की लंबाई की सामान्य इकाइयाँ हों। दिखाए गए आरेख में, ग्रिडलाइनों को एक इकाई की दूरी पर रखा गया है। 45° विकर्ण रेखाएं समय पर मूल से गुजरने वाले दो फोटॉनों की विश्व रेखाओं का प्रतिनिधित्व करती हैं इन विश्वरेखाओं की प्रवणता 1 है क्योंकि फोटॉन प्रति इकाई समय में एक इकाई अंतरिक्ष में आगे बढ़ते हैं। दो घटनाएँ, तथा इस ग्राफ पर प्लॉट किए गए हैं ताकि उनके निर्देशांकों की तुलना S और S के सीमा रेखा में की जा सके।
चित्र 3-1 बी। खींचना तथा सीमा रेखा S के अक्षों '। h> अक्ष सीमा रेखा S में मापा गया S 'समन्वय प्रणाली की उत्पत्ति की विश्व रेखा का प्रतिनिधित्व करता है। इस आंकड़े में, दोनों तथा अक्षों को एक कोण द्वारा अप्रकाशित अक्षों से झुकाया जाता है जहाँ प्राइमेड और अनप्रिम्ड अक्ष एक सामान्य मूल साझा करते हैं क्योंकि सीमा रेखा S और S 'मानक विन्यास में स्थापित किए गए थे, ताकि जब चित्र 3-1 c। प्राइमेड अक्ष में यूनिट्स का स्केल अनप्रिम्ड अक्ष में यूनिट्स से अलग होता है। लोरेंत्ज़ परिवर्तनों से, हम देखते हैं कि के निर्देशांक प्राइमेड निर्देशांक सिस्टम में रूपांतरित करें अप्रकाशित समन्वय प्रणाली में वैसे ही, के निर्देशांक प्राइमेड निर्देशांक सिस्टम में रूपांतरित करें अप्रशिक्षित प्रणाली में के समानांतर ग्रिडलाइन बनाएं बिंदुओं के माध्यम से अक्ष जैसा कि अप्रकाशित सीमा रेखा में मापा जाता है, जहां एक पूर्णांक है। इसी तरह, ग्रिडलाइन को समानांतर बनाएं अक्ष के माध्यम से जैसा कि अनप्रिमेड सीमा रेखा में मापा जाता है। पाइथागोरस प्रमेय का उपयोग करते हुए, हम देखते हैं कि के बीच की दूरी इकाइयाँ बराबर होती हैं के बीच की दूरी का गुना इकाइयाँ, जैसा कि सीमा रेखा S में मापा जाता है। यह अनुपात सदैव 1 से अधिक होता है, और अंततः यह अनंत तक पहुँचता है चित्र 3-1d। चूंकि प्रकाश की गति एक अपरिवर्तनीय है, इसलिए समय पर मूल से गुजरने वाले दो फोटोन की सांसारिक रेखाएं अभी भी 45° विकर्ण रेखाओं के रूप में प्लॉट करें। के प्राइमेड निर्देशांक तथा लोरेंत्ज़ परिवर्तनों के माध्यम से अप्रकाशित निर्देशांक से संबंधित हैं और लगभग ग्राफ से मापा जा सकता है (यह मानते हुए कि इसे सटीक रूप से पर्याप्त रूप से प्लॉट किया गया है), लेकिन मिंकोव्स्की आरेख की वास्तविक योग्यता हमें परिदृश्य का एक ज्यामितीय दृश्य प्रदान करना है। उदाहरण के लिए, इस आकृति में, हम देखते हैं कि दो समय-समान-पृथक घटनाएँ जिनके अप्रकाशित सीमा रेखा में अलग-अलग x-निर्देशांक थे, अब अंतरिक्ष में एक ही स्थिति में हैं।
जबकि अप्रकाशित सीमा रेखा को अंतरिक्ष और समय अक्षों के साथ खींचा जाता है जो समकोण पर मिलते हैं, प्राइमेड सीमा रेखा अक्षों के साथ खींचा जाता है जो तीव्र या अधिक कोणों पर मिलते हैं। यह विषमता अपरिहार्य विकृतियों के कारण है कि कैसे स्पेसटाइम एक कार्टेशियन विमान पर मानचित्र का समन्वय करता है, लेकिन सीमा रेखा वास्तव में समकक्ष हैं।
लोरेंत्ज़ परिवर्तन से प्राप्त परिणाम
विशेष सापेक्षता के परिणाम लोरेंत्ज़ रूपांतरण समीकरणों से प्राप्त किए जा सकते हैं।[22] ये परिवर्तन, और इसलिए विशेष सापेक्षता, सभी सापेक्ष वेगों पर न्यूटनियन यांत्रिकी की तुलना में अलग-अलग भौतिक भविष्यवाणियों की ओर ले जाते हैं, और सबसे स्पष्ट जब सापेक्ष वेग प्रकाश की गति के बराबर हो जाते हैं।अधिकांश मनुष्यों का सामना करने वाली किसी भी चीज़ की तुलना में प्रकाश की गति इतनी अधिक होती है कि सापेक्षता द्वारा भविष्यवाणी किए गए कुछ प्रभाव शुरू में विपरीत होते हैं।
अपरिवर्तनीय अंतराल
गैलीलियन सापेक्षता में, लंबाई ()[note 3] और दो घटनाओं के बीच अस्थायी अलगाव () स्वतंत्र अपरिवर्तनीय हैं, जिनके मान संदर्भ के विभिन्न फ़्रेमों से देखे जाने पर नहीं बदलते हैं।[note 4][note 5] विशेष सापेक्षता में, यद्यपि, स्थानिक और लौकिक निर्देशांकों की परस्पर बुनाई एक अपरिवर्तनीय अंतराल की अवधारणा को उत्पन्न करती है, जिसे निरूपित किया जाता है :[note 6]
रुंडित समय व्यतीत होने और रुंडित स्थानिक दूरी का अंतर होने के कारण, यूक्लिडियन और स्पेसटाइम दूरियों के बीच एक मूलभूत विसंगति को प्रदर्शित करता है।[note 7] इस अंतराल का अपरिवर्तन सामान्य लोरेंत्ज़ रूपांतरित (जिसे पोंकारे रूपांतरण भी कहा जाता है) की एक संपत्ति है, जिससे यह स्पेसटाइम का एक आइसोमेट्री बन जाता है। सामान्य लोरेंत्ज़ रूपांतरित मानक लोरेंत्ज़ रूपांतरित का विस्तार करता है (जो घूर्णन के बिना स्थानांतरणों से संबंधित है, अर्थात, लोरेंत्ज़ एक्स-दिशा में बूस्ट करता है) अन्य सभी स्थानांतरण (ज्यामिति), परावर्तन (गणित), और घूर्णन (गणित) के बीच किसी भी कार्टेशियन के बीच जड़त्वीय सीमा रेखा।[26]: 33–34 सरलीकृत परिदृश्यों के विश्लेषण में, जैसे कि स्पेसटाइम आरेख, अपरिवर्तनीय अंतराल का एक कम-आयामी रूप अधिकांशतः नियोजित होता है:
के भौतिक महत्व को देखते हुए , ध्यान देने योग्य तीन परिस्थिति हैं:[18][27]: 25–39
- Δs2 > 0: इस परिस्थिति में, दो घटनाओं को अंतरिक्ष की तुलना में अधिक समय से अलग किया जाता है, और इसलिए उन्हें 'समय की तरह' अलग कहा जाता है। यह बताता है कि और लोरेंत्ज़ परिवर्तन दिया यह स्पष्ट है कि वहाँ उपलब्ध है a से कम जिसके लिए (विशेष रूप से, ) दूसरे शब्दों में, दो घटनाओं को देखते हुए जो समयबद्ध रूप से अलग हैं, एक सीमा रेखा खोजना संभव है जिसमें दो घटनाएं एक ही स्थान पर होती हैं। इस सीमा रेखा में, समय में अलगाव, उचित समय कहा जाता है।
- 'Δs2 < 0: इस परिस्थिति में, दो घटनाओं को समय की तुलना में अधिक स्थान से अलग किया जाता है, और इसलिए उन्हें अलग किया गया स्पेसलाइक कहा जाता है। यह बताता है कि और लोरेंत्ज़ परिवर्तन दिया वहाँ एक उपलब्ध है से कम जिसके लिए (विशेष रूप से, ) दूसरे शब्दों में, दो घटनाओं को देखते हुए जो अंतरिक्ष की तरह अलग हैं, एक सीमा रेखा खोजना संभव है जिसमें दो घटनाएं एक ही समय में होती हैं। इस सीमा रेखा में, अंतरिक्ष में अलगाव, उचित दूरी, या उचित लंबाई कहा जाता है। के मूल्यों के लिए से बड़ा और कम का चिन्ह परिवर्तन, जिसका अर्थ है कि अंतरिक्ष-समान-पृथक घटनाओं का अस्थायी क्रम उस सीमा रेखा के आधार पर बदलता है जिसमें घटनाओं को देखा जाता है। हालाँकि, समयबद्ध-पृथक घटनाओं का अस्थायी क्रम निरपेक्ष है, क्योंकि एकमात्र तरीका है कि से बड़ा हो सकता है होगा अगर
- Δs2 = 0: इस परिस्थिति में, दो घटनाओं को अलग-अलग हल्का सा' कहा जाता है। यह बताता है कि और यह संबंध के अपरिवर्तन के कारण सीमा रेखा स्वतंत्र है इससे हम देखते हैं कि प्रकाश की गति है हर जड़त्वीय सीमा रेखा में। दूसरे शब्दों में, सार्वभौमिक लोरेंत्ज़ सहप्रसरण की धारणा से शुरू होकर, प्रकाश की निरंतर गति एक व्युत्पन्न परिणाम है, न कि एक विशेष सिद्धांत के दो-अभिधारणाओं के निर्माण के रूप में।
एक साथ सापेक्षता

दो अलग-अलग स्थानों में होने वाली दो घटनाओं पर विचार करें जो एक ही जड़त्वीय प्रेक्षक के निर्देश तंत्र में एक साथ घटित होती हैं। वे गैर-एक साथ एक अन्य जड़त्वीय पर्यवेक्षक (पूर्ण एक साथ की कमी) के निर्देश तंत्र में हो सकते हैं।
से समीकरण 3 (समन्वय अंतर के संदर्भ में आगे लोरेंत्ज़ परिवर्तन)
सैगनैक प्रभाव को एक साथ सापेक्षता की अभिव्यक्ति माना जा सकता है।[28] चूँकि समकालिकता की सापेक्षता प्रथम कोटि का प्रभाव है ,[18]उनके संचालन के लिए सैगनैक प्रभाव पर आधारित उपकरण, जैसे कि रिंग लेजर गायरोस्कोप और फाइबर ऑप्टिक जाइरोस्कोप , संवेदनशीलता के चरम स्तर में सक्षम हैं।[p 14]
समय विस्तार
दो घटनाओं के बीच का समय एक पर्यवेक्षक से दूसरे पर्यवेक्षक के लिए अपरिवर्तनीय नहीं है, लेकिन पर्यवेक्षकों के निर्देश तंत्र की सापेक्ष गति पर निर्भर है (उदाहरण के लिए, युगल विरोधाभास जो एक युगल से संबंधित है जो प्रकाश की गति के निकट यात्रा करने वाले अंतरिक्ष यान में उड़ जाता है और यह पता लगाने के लिए लौटता है कि गैर-यात्रा करने वाले युगल भाई की उम्र बहुत अधिक है, विरोधाभास यह है कि निरंतर वेग से हम यह समझने में असमर्थ हैं कि कौन सा युगल यात्रा नहीं कर रहा है और कौन सा युगल यात्रा करता है)।
मान लीजिए कि एक चालमापी बिना प्राइमेड सिस्टम S में विराम पर है। दो अलग-अलग टिकों पर चालमापी की स्थिति को Δx = 0 से चिह्नित किया जाता है। दोनों प्रणालियों में मापा गया इन टिकों के बीच के समय के बीच संबंध खोजने के लिए, समीकरण 3 का उपयोग किया जा सकता है :
- संतोषजनक घटनाओं के लिए
इससे पता चलता है कि दो टिकों के बीच का समय (Δt′) जैसा कि उस सीमा रेखा में देखा गया है जिसमें चालमापी चल रही है (S′), इन टिकों के बीच के समय (Δt) से अधिक लंबा है जैसा कि चालमापी के बाकी सीमा रेखा में मापा जाता है ( S)। समय का विस्तार कई भौतिक घटनाओं की व्याख्या करता है; उदाहरण के लिए, पृथ्वी के बाहरी वायुमंडल में कणों के साथ कॉस्मिक किरणों के टकराने और सतह की ओर बढ़ने से निर्मित उच्च गति वाले म्यूऑन का जीवनकाल, प्रयोगशाला में निर्मित और क्षय होने वाले धीरे-धीरे चलने वाले म्यूऑन के जीवनकाल से अधिक होता है।[29]
लंबाई संकुचन
एक पर्यवेक्षक द्वारा मापी गई किसी वस्तु के आयाम (जैसे, लंबाई) दूसरे पर्यवेक्षक द्वारा किए गए उc वस्तु के माप के परिणामों से छोटे हो सकते हैं (उदाहरण के लिए, cढ़ी विरोधाभास में प्रकाश की गति के निकट यात्रा करने वाली और समाहित होने वाली एक लंबी cढ़ी सम्मिलित है) एक छोटे गैरेज के भीतर)।
इसी तरह, मान लीजिए कि एक मापने वाली छड़ विराम पर है और अनप्रिम्ड सिस्टम S में x-अक्ष के साथ संरेखित है। इस प्रणाली में, इस छड़ की लंबाई Δx के रूप में लिखी जाती है। सिस्टम S′ में इस रॉड की लंबाई को मापने के लिए, जिसमें रॉड चलती है, रॉड के अंतिम बिंदुओं के लिए x′ की दूरी को उc सिस्टम S′ में एक साथ मापा जाना चाहिए। दूसरे शब्दों में, माप की विशेषता है Δt′ = 0 है, जिसे x और Δx′ की समीकरण 4 लंबाई के बीच संबंध खोजने के लिए समीकरण 4 के साथ जोड़ा जा सकता है:
- संतोषजनक घटनाओं के लिए
इससे पता चलता है कि छड़ की लंबाई (Δx′) जिस सीमा रेखा में चलती है (S′) में मापी जाती है, वह अपने स्वयं के विराम सीमा रेखा (S) में इसकी लंबाई (Δx) से कम होती है।
समय का विस्तार और लंबाई का संकुचन केवल दिखावे नहीं हैं। समय विस्तार स्पष्ट रूप से किसी दिए गए समन्वय प्रणाली में एक ही स्थान पर होने वाली घटनाओं के बीच समय अंतराल को मापने के हमारे तरीके से संबंधित है (जिसे "सह-स्थानीय" घटनाएं कहा जाता है)। ये समय अंतराल (जो प्रासंगिक पर्यवेक्षकों द्वारा वास्तव में प्रयोगात्मक रूप से मापा जा सकता है, और हैं) पहले के संबंध में आगे बढ़ने वाली एक अन्य समन्वय प्रणाली में भिन्न हैं, जब तक कि सह-स्थानीय होने के अलावा घटनाएं भी एक साथ नहीं होती हैं। इसी तरह, लंबाई संकुचन पसंद के दिए गए समन्वय प्रणाली में अलग लेकिन एक साथ घटनाओं के बीच हमारी मापी गई दूरियों से संबंधित है। यदि ये घटनाएँ सह-स्थानीय नहीं हैं, लेकिन दूरी (अंतरिक्ष) द्वारा अलग की जाती हैं, तो वे एक दूसरे से समान स्थानिक दूरी पर नहीं घटित होंगी जब किसी अन्य चलती समन्वय प्रणाली से देखा जाए।
वेगों का लोरेंत्ज़ परिवर्तन
मानक विन्यास में दो सीमा रेखा S और S′ पर विचार करें। S में एक कण x दिशा में वेग सदिश के साथ गति करता है इसका वेग क्या है सीमा रेखा में S′ ?
हम लिख सकते हैं
|
(7) |
|
(8) |
व्यंजकों को के लिए प्रतिस्थापित करना तथा से समीकरण 5 में समीकरण 8, इसके बाद सीधे गणितीय जोड़तोड़ और बैक-प्रतिस्थापन से समीकरण 7 गति के लोरेंत्ज़ परिवर्तन उत्पन्न करता है प्रति :
|
(9) |
व्युत्क्रम संबंध प्राइमेड और अनप्रिम्ड प्रतीकों को आपस में बदलकर और प्रतिस्थापित करके प्राप्त किया जाता है साथ
|
(10) |
के लिये x-अक्ष के अनुदिश संरेखित नहीं है, हम लिखते हैं:[11]: 47–49
|
(11) |
|
(12) |
इस परिस्थिति के लिए आगे और उलटा परिवर्तन हैं:
|
(13) |
|
(14) |
समीकरण 10 तथा समीकरण 14 परिणामी देने के रूप में व्याख्या की जा सकती है दो वेगों के तथा और वे सूत्र की जगह लेते हैं जो गैलीलियन सापेक्षता में मान्य है। इस तरह से व्याख्या की गई, उन्हें सामान्यतः पर सापेक्षिक वेग जोड़ (या संरचना) सूत्रों के रूप में संदर्भित किया जाता है, जो S और S के तीन अक्षों के लिए एक दूसरे के साथ गठबंधन होने के लिए मान्य है (यद्यपि मानक विन्यास में जरूरी नहीं है)।[11]: 47–49 हम निम्नलिखित बिंदुओं को लिखते हैं:
- यदि कोई वस्तु (जैसे, एक फोटान) एक सीमा रेखा में प्रकाश की गति से घूम रही हो (i.e., u = ±c or u′ = ±c), तो यह किसी अन्य सीमा रेखा में प्रकाश की गति से भी गतिमान हो रहा होगा |v| < c.
- c से कम परिमाण वाले दो वेगों की परिणामी गति सदैव c से कम परिमाण वाला वेग होता है।
- यदि दोनों |u| और |v| (और फिर भी |u′| और |v′|) प्रकाश की गति के संबंध में छोटे हैं (अर्थात, e.g., |u/c| ≪ 1), तब विशेष सापेक्षता के लिए परिवर्तन समीकरणों से सहज गैलीलियन परिवर्तन पुनर्प्राप्त किए जाते हैं
- एक फोटॉन को एक सीमा रेखा संलग्न करना (आइंस्टीन की तरह एक प्रकाश किरण की सवारी करना) को परिवर्तनों के विशेष उपचार की आवश्यकता होती है।
मानक विन्यास में x दिशा के बारे में कुछ खास नहीं है। उपरोक्त औपचारिकता (गणित) किसी भी दिशा में लागू होती है; और तीन ओर्थोगोनल दिशाएं इन दिशाओं में उनके घटकों के वेग वैक्टर को विघटित करके अंतरिक्ष में सभी दिशाओं से निपटने की अनुमति देती हैं। विवरण के लिए वेग-जोड़ सूत्र देखें।
थॉमस घूर्णन
दो गैर-कोलिनियर लोरेंत्ज़ बूस्ट की संरचना (अर्थात, दो गैर-कोलिनियर लोरेंत्ज़ रूपांतरण, जिनमें से कोई भी घूर्णन सम्मिलित नहीं है) के परिणामस्वरूप लोरेंत्ज़ परिवर्तन होता है जो शुद्ध वृद्धि नहीं है बल्कि एक वृद्धि और घूर्णन की संरचना है।
थॉमस घूर्णन एक साथ सापेक्षता का परिणाम है। चित्र में। 4-2a, लंबाई की एक छड़ इसके बाकी सीमा रेखा में (अर्थात, जिसकी उचित लंबाई है) ) जमीन के सीमा रेखा में y-अक्ष के अनुदिश लंबवत रूप से ऊपर उठती है।
चित्र में। 4-2b, गति से चलते हुए रॉकेट के सीमा रेखा से एक ही छड़ देखी जाती है दांई ओर। यदि हम रॉड के बाएं और दाएं छोर पर स्थित दो समयों की कल्पना करते हैं जो रॉड के सीमा रेखा में सिंक्रोनाइज्ड हैं, तो एक साथ सापेक्षता की वजह से रॉकेट सीमा रेखा में ऑब्जर्वर प्रेक्षक (#Measurement_versus_visual_appearance नहीं) चालमापी के दाहिने छोर पर स्थित है। रॉड द्वारा समय में उन्नत किया जा रहा है और छड़ को तदनुरूप झुके हुए के रूप में देखा जाता है।[27]: 98–99 दूसरे क्रम के सापेक्षतावादी प्रभावों जैसे कि लंबाई संकुचन या समय विस्तार के विपरीत, यह प्रभाव काफी कम वेग पर भी काफी महत्वपूर्ण हो जाता है। उदाहरण के लिए, इसे स्पिन-ऑर्बिट इंटरैक्शन में देखा जा सकता है, जहां थॉमस प्रीसेशन एक सापेक्ष सुधार है जो एक प्राथमिक कण के स्पिन (भौतिकी) या मैक्रोस्कोपिक जाइरोस्कोप के घूर्णन पर लागू होता है, जो स्पिन के कोणीय वेग से संबंधित होता है। कक्षीय गति के कोणीय वेग के लिए एक वक्रीय कक्षा का अनुसरण करने वाला कण।[27]: 169–174 थॉमस घूर्णन प्रसिद्ध मीटर स्टिक और होल विरोधाभास को संकल्प प्रदान करता है।[p 15][27]: 98–99
कारण और प्रकाश की गति से तेज गति का निषेध
चित्र 4-3 में, घटनाओं ए ("कारण") और बी ("प्रभाव") के बीच का समय अंतराल 'समय की तरह' है; अर्थात्, संदर्भ का एक ढांचा है जिसमें घटनाएँ A और B अंतरिक्ष में एक ही स्थान पर घटित होती हैं, केवल अलग-अलग समय पर घटित होने से अलग होती हैं। यदि ए उस सीमा रेखा में बी से पहले है, तो ए लोरेंत्ज़ रूपांतरितेशन द्वारा सुलभ सभी सीमा रेखाों में बी से पहले है। पदार्थ (या सूचना) के लिए A के स्थान से (प्रकाश की गति से कम) यात्रा करना संभव है, A के समय से शुरू होकर, B के स्थान तक, B के समय पर पहुँचता है, इसलिए एक कारण संबंध हो सकता है ( ए के साथ कारण और बी प्रभाव)।
आरेख में अंतराल AC 'अंतरिक्ष के समान' है; अर्थात्, संदर्भ का एक ढांचा है जिसमें घटनाएँ A और C एक साथ घटित होती हैं, केवल अंतरिक्ष में अलग होती हैं। ऐसे फ़्रेम भी हैं जिनमें A, C से पहले आता है (जैसा कि दिखाया गया है) और फ़्रेम जिसमें C, A से पहले है। यद्यपि, लोरेंत्ज़ रूपांतरण द्वारा कोई फ़्रेम एक्सेस नहीं किया जा सकता है, जिसमें ईवेंट A और C एक ही स्थान पर होते हैं। यदि घटना ए और c के बीच एक कारण और प्रभाव संबंध उपलब्ध होना संभव होता, तो कार्य-कारण के विरोधाभास का परिणाम होता हैं।
उदाहरण के लिए, यदि संकेतों को प्रकाश की तुलना में तेजी से भेजा जा सकता है, तो संकेतों को प्रेषक के अतीत (आरेखों में पर्यवेक्षक बी) में भेजा जा सकता है।[30][p 16] तब विभिन्न प्रकार के कारण विरोधाभासों का निर्माण किया जा सकता था।
चित्र 4-4 में स्पेसटाइम आरेखों पर विचार करें। A और B एक रेल ट्रैक के साथ खड़े होते हैं, जब एक हाई-स्पीड ट्रेन गुजरती है, जिसमें C ट्रेन की आखिरी कार में सवार होता है और D अग्रणी कार में सवार होता है। ए और बी की विश्व रेखाएं लंबवत (cटी) हैं, जो जमीन पर इन पर्यवेक्षकों की स्थिर स्थिति को अलग करती हैं, जबकि c और डी की विश्व रेखाएं आगे (cटी′) झुकी हुई हैं, जो पर्यवेक्षकों c और डी की तीव्र गति को दर्शाती हैं। उनकी ट्रेन में स्थिर, जैसा कि जमीन से देखा गया है।
- चित्र 4-4a। B द्वारा D को संदेश भेजने की घटना, जैसे ही प्रमुख कार गुजरती है, D के सीमा रेखा के मूल में होती है। D एक काल्पनिक तात्कालिक संचारक का उपयोग करके पिछली कार में C को ट्रेन के साथ संदेश भेजता है। इस संदेश की दुनिया के साथ मोटा लाल तीर है अक्ष, जो c और डी के प्राइमेड सीमा रेखा में एक साथ एक पंक्ति है। (अनप्रिम्ड) ग्राउंड सीमा रेखा में सिग्नल भेजे जाने से पहले आता है।
- चित्र 4-4 बी। c द्वारा ए को संदेश भेजने की घटना, जो रेल की पटरियों के पास खड़ा है, उनके सीमा रेखा के मूल में है। अब A तात्कालिक संचारक के माध्यम से ट्रैक के साथ B को संदेश भेजता है। इस संदेश की विश्वरेखा नीला मोटा तीर है, साथ में अक्ष, जो ए और बी के सीमा रेखा के लिए एक साथ की एक पंक्ति है। जैसा कि स्पेसटाइम आरेख से देखा गया है, बी इसे भेजने से पहले संदेश प्राप्त करें, जो कार्य-कारण का उल्लंघन है।[31]
संकेतों के लिए कार्य-कारण का उल्लंघन करने के लिए तात्कालिक होना आवश्यक नहीं है।भले ही D से C तक का सिग्नल की तुलना में थोड़ा उथला हो अक्ष (और ए से बी तक का संकेत . की तुलना में थोड़ा तेज है) अक्ष), बी के लिए संदेश भेजने से पहले उसे प्राप्त करना अभी भी संभव होगा। ट्रेन की गति को हल्की गति के निकट बढ़ाकर, तथा अक्षों को प्रकाश की गति का प्रतिनिधित्व करने वाली धराशायी रेखा के बहुत करीब निचोड़ा जा सकता है। इस संशोधित सेटअप के साथ, यह प्रदर्शित किया जा सकता है कि प्रकाश की गति की तुलना में केवल थोड़ा तेज संकेत भी कार्य-कारण उल्लंघन का परिणाम देगा।[32] इसलिए, यदि कार्य-कारण को संरक्षित किया जाना है, तो विशेष सापेक्षता के परिणामों में से एक यह है कि कोई भी सूचना संकेत या भौतिक वस्तु निर्वात में प्रकाश की तुलना में तेजी से यात्रा नहीं कर सकती है।
इसका मतलब यह नहीं है कि प्रकाश की गति से तेज सब असंभव है। विभिन्न तुच्छ स्थितियों का वर्णन किया जा सकता है जहां कुछ चीजें (वास्तविक पदार्थ या ऊर्जा नहीं) प्रकाश से तेज चलती हैं।[33] उदाहरण के लिए, जिस स्थान पर खोज प्रकाश की किरण बादल के तल से टकराती है, वह प्रकाश की तुलना में तेजी से आगे बढ़ सकती है जब खोज प्रकाश तेजी से चालू होता है (यद्यपि यह कार्य-कारण या किसी अन्य सापेक्षतावादी घटना का उल्लंघन नहीं करता है)।[34][35]
ऑप्टिकल प्रभाव
खींच प्रभाव
1850 में, हिप्पोलीटे फ़िज़ौ और लियोन फौकॉल्ट ने स्वतंत्र रूप से स्थापित किया कि प्रकाश हवा की तुलना में पानी में अधिक धीरे-धीरे यात्रा करता है, इस प्रकार ऑगस्टिन-जीन फ्रेस्नेल की भविष्यवाणी को मान्य करता है।[36] प्रकाश की गति को शांत जल में मापा जाता था। बहते जल में प्रकाश की चाल कितनी होगी?
1851 में, फ़िज़ौ ने इस प्रश्न का उत्तर देने के लिए एक प्रयोग किया, जिसका एक सरलीकृत निरूपण चित्र 5-1 में दिखाया गया है। प्रकाश की एक किरण को एक बीम फाड़नेवाला द्वारा विभाजित किया जाता है, और विभाजित बीम को विपरीत दिशाओं में बहते पानी की एक ट्यूब के माध्यम से पारित किया जाता है। उन्हें इंटरफेरेंस फ्रिंज बनाने के लिए पुनर्संयोजित किया जाता है, जो ऑप्टिकल पथ की लंबाई में अंतर को दर्शाता है, जिसे एक पर्यवेक्षक देख सकता है। प्रयोग ने प्रदर्शित किया कि बहते पानी द्वारा प्रकाश को खींचने से फ्रिंजों का विस्थापन हुआ, यह दर्शाता है कि पानी की गति ने प्रकाश की गति को प्रभावित किया था।
उस समय प्रचलित सिद्धांतों के अनुसार, एक गतिमान माध्यम से यात्रा करने वाला प्रकाश माध्यम के माध्यम से अपनी गति और माध्यम की गति का एक साधारण योग होगा। अपेक्षा के विपरीत, फ़िज़ौ ने पाया कि यद्यपि प्रकाश को पानी द्वारा खींचा गया प्रतीत होता है, लेकिन खींचने का परिमाण अपेक्षा से बहुत कम था। यदि शांत जल में प्रकाश की गति है, और पानी की गति है, और प्रयोगशाला के सीमा रेखा में प्रकाश की जल-जनित गति है जिसमें पानी का प्रवाह प्रकाश की गति से जुड़ता या घटाता है, तो
प्रकाश का सापेक्षिक विपथन
प्रकाश की परिमित गति के कारण, यदि किसी स्रोत और रिसीवर की सापेक्ष गति में एक अनुप्रस्थ घटक सम्मिलित है, तो जिस दिशा से प्रकाश रिसीवर तक पहुंचता है, वह रिसीवर के सापेक्ष स्रोत के स्थान में ज्यामितीय स्थिति से विस्थापित हो जाएगा। विस्थापन की शास्त्रीय गणना दो रूप लेती है और माध्यम के संबंध में रिसीवर, स्रोत, या दोनों गति में हैं या नहीं, इसके आधार पर अलग-अलग भविष्यवाणियां करती हैं। (1) यदि रिसीवर गति में है, तो विस्थापन प्रकाश के विपथन का परिणाम होगा। रिसीवर के सापेक्ष बीम का घटना कोण रिसीवर की गति के वेक्टर योग और आपतित प्रकाश के वेग से परिकलित होगा।[38] (2) यदि स्रोत गति में है, तो विस्थापन प्रकाश-समय सुधार का परिणाम होगा। अपनी ज्यामितीय स्थिति से स्रोत की स्पष्ट स्थिति का विस्थापन उस समय के दौरान स्रोत की गति का परिणाम होगा जब इसका प्रकाश रिसीवर तक पहुंचता है।[39] शास्त्रीय व्याख्या प्रयोगात्मक परीक्षण में विफल रही। चूंकि विपथन कोण रिसीवर के वेग और आपतित प्रकाश की गति के बीच संबंध पर निर्भर करता है, अपवर्तक माध्यम से आपतित प्रकाश के गुजरने से विपथन कोण बदल जाना चाहिए। 1810 में, फ्रांकोइस अरागो ने प्रकाश की गति को मापने के असफल प्रयास में इस अपेक्षित घटना का उपयोग किया,[40] और 1870 में, जॉर्ज एयरी ने पानी से भरे दूरबीन का उपयोग करके परिकल्पना का परीक्षण किया, यह पाया कि, अपेक्षा के विपरीत, मापा विचलन एक हवा से भरे दूरबीन से मापा विचलन के समान था।[41] इन परिणामों को समझाने के लिए एक भारी प्रयास में आंशिक ईथर-ड्रैग की परिकल्पना का उपयोग किया गया,[42] लेकिन माइकलसन-मॉर्ले प्रयोग के परिणामों के साथ असंगत था, जो स्पष्ट रूप से पूर्ण एथर-ड्रैग की मांग करता था।[43] जड़त्वीय फ़्रेमों को मानते हुए, प्रकाश के विपथन के लिए सापेक्षतावादी अभिव्यक्ति रिसीवर के गतिमान और स्रोत गतिमान मामलों दोनों पर लागू होती है। विभिन्न प्रकार के त्रिकोणमितीय समकक्ष सूत्र प्रकाशित किए गए हैं। चित्र 5-2 में चरों के रूप में व्यक्त किए गए, इनमें सम्मिलित हैं[26]: 57–60
- या या
सापेक्ष डॉपलर प्रभाव
सापेक्ष अनुदैर्ध्य डॉपलर प्रभाव
शास्त्रीय डॉपलर प्रभाव इस बात पर निर्भर करता है कि माध्यम के संबंध में स्रोत, रिसीवर या दोनों गति में हैं या नहीं। सापेक्षतावादी डॉपलर प्रभाव किसी भी माध्यम से स्वतंत्र होता है। फिर भी, अनुदैर्ध्य परिस्थिति के लिए सापेक्षवादी डॉप्लर शिफ्ट, स्रोत और रिसीवर एक दूसरे से सीधे या दूर जाने के साथ, इसे शास्त्रीय घटना के रूप में प्राप्त किया जा सकता है, लेकिन एक समय विस्तार शब्द के अतिरिक्त संशोधित किया जाता है, और यही उपचार है यहाँ वर्णित है।[44][45] मान लें कि रिसीवर और स्रोत एक दूसरे से सापेक्ष गति से दूर जा रहे हैं जैसा कि रिसीवर या स्रोत पर एक पर्यवेक्षक द्वारा मापा जाता है (यहां अपनाया गया संकेत सम्मेलन यह है कि नकारात्मक है यदि रिसीवर और स्रोत एक दूसरे की ओर बढ़ रहे हैं)। मान लें कि स्रोत माध्यम में स्थिर है।
प्रकाश के लिए, और रिसीवर सापेक्ष गति से आगे बढ़ रहा है, रिसीवर पर समय स्रोत पर समयों के सापेक्ष समय विस्तार हैं। रिसीवर प्राप्त आवृत्ति को होने के लिए मापेगा
- तथा
- लोरेंत्ज़ कारक है।
एक गतिमान स्रोत के साथ रिसीवर के निर्देश तंत्र में विश्लेषण करते समय सापेक्षतावादी डॉपलर शिफ्ट के लिए एक समान अभिव्यक्ति प्राप्त की जाती है।[46][18]
अनुप्रस्थ डॉपलर प्रभाव
अनुप्रस्थ डॉपलर प्रभाव सापेक्षता के विशेष सिद्धांत की मुख्य उपन्यास भविष्यवाणियों में से एक है।
शास्त्रीय रूप से, कोई यह उम्मीद कर सकता है कि यदि स्रोत और रिसीवर एक दूसरे के संबंध में अनुप्रस्थ रूप से आगे बढ़ रहे हैं, उनके सापेक्ष गति के लिए कोई अनुदैर्ध्य घटक नहीं है, तो रिसीवर तक पहुंचने वाले प्रकाश में कोई डॉपलर बदलाव नहीं होना चाहिए।
विशेष सापेक्षता अन्यथा भविष्यवाणी करती है। चित्र 5-3 इस परिदृश्य के दो सामान्य रूपों को दिखाता है। सरल समय विस्तार तर्कों का उपयोग करके दोनों प्रकारों का विश्लेषण किया जा सकता है।[18]चित्र 5-3a में, रिसीवर स्रोत से प्रकाश को के कारक द्वारा ब्लूशिफ्ट के रूप में देखता है . चित्र में। 5-3b, प्रकाश को उc कारक द्वारा फिर से स्थानांतरित किया जाता है।
माप बनाम दृश्य उपस्थिति
समय का विस्तार और लंबाई का संकुचन ऑप्टिकल भ्रम नहीं हैं, बल्कि वास्तविक प्रभाव हैं। इन प्रभावों का मापन डॉपलर शिफ्ट का एक आर्टिफैक्ट नहीं है, न ही वे किसी घटना से पर्यवेक्षक तक यात्रा करने में लगने वाले समय को ध्यान में रखते हुए उपेक्षा का परिणाम हैं।
वैज्ञानिक एक ओर माप या अवलोकन, बनाम दृश्य उपस्थिति, या जो देखता है, के बीच एक मूलभूत अंतर बनाते हैं। किसी वस्तु की मापी गई आकृति वस्तु के सभी बिंदुओं का एक काल्पनिक स्नैपशॉट है क्योंकि वे समय में एक ही क्षण में उपलब्ध होते हैं। हालाँकि, किसी वस्तु का दृश्य स्वरूप उस समय की अलग-अलग लंबाई से प्रभावित होता है, जो प्रकाश को वस्तु के विभिन्न बिंदुओं से किसी की आंख तक जाने में लगता है।
कई वर्षों तक, दोनों के बीच के अंतर को सामान्यतः पर सराहा नहीं गया था, और सामान्यतः पर यह सोचा गया था कि एक पर्यवेक्षक द्वारा गुजरने वाली एक लंबी अनुबंधित वस्तु वास्तव में लंबाई के अनुबंध के रूप में देखी जाएगी। 1959 में, जेम्स टेरेल और रोजर पेनरोज़ ने स्वतंत्र रूप से बताया कि गतिमान वस्तु के विभिन्न भागों से प्रेक्षक तक पहुँचने वाले संकेतों में अंतर समय अंतराल प्रभाव के परिणामस्वरूप एक तेज़ गति वाली वस्तु का दृश्य रूप उसके मापा आकार से काफी भिन्न होता है। उदाहरण के लिए, एक घटती हुई वस्तु सिकुड़ी हुई दिखाई देगी, एक निकट आने वाली वस्तु लम्बी दिखाई देगी, और एक गुजरने वाली वस्तु में एक तिरछी उपस्थिति होगी जिसकी तुलना एक घुमाव से की गई है।[p 19][p 20][47][48] गति में एक गोला गोलाकार रूपरेखा को बरकरार रखता है, यद्यपि गोले की सतह और उस पर बने चित्र विकृत दिखाई देंगे।[49]

चित्र 5-4 एक घन को उसकी भुजाओं की लंबाई के चार गुना की दूरी से देखता है। उच्च गति पर, घन की जो भुजाएँ गति की दिशा के लंबवत होती हैं, आकार में अतिपरवलयिक दिखाई देती हैं। घन वास्तव में घुमाया नहीं गया है। बल्कि, क्यूब के पीछे से प्रकाश सामने से प्रकाश की तुलना में किसी की आंखों तक पहुंचने में अधिक समय लेता है, इस दौरान क्यूब दाईं ओर चला गया है। इस भ्रम को टेरेल घूर्णन या टेरेल-पेनरोज प्रभाव के रूप में जाना जाने लगा है।[note 9] एक और उदाहरण जहां दृश्य उपस्थिति माप के साथ बाधाओं पर है, विभिन्न रेडियो आकाशगंगा ओं, बीएल लाख वस्तुओं, कैसर , और अन्य खगोलीय वस्तुओं में स्पष्ट सुपरल्यूमिनल गति के अवलोकन से आता है जो कि खगोलीय जेट को बाहर निकालते है। एक स्पष्ट ऑप्टिकल भ्रम के परिणाम प्रकाश यात्रा की तुलना में तेज होने का आभास देते हैं।[50][51][52] चित्र 5-5 में, आकाशगंगा मेसियर 87 उप-परमाणु कणों के एक उच्च गति वाले जेट को लगभग सीधे हमारी ओर प्रवाहित करता है, लेकिन पेनरोज़-टेरेल घूर्णन के कारण जेट उc तरह से आगे बढ़ता हुआ दिखाई देता है जैसे कि क्यूब की उपस्थिति में चित्र 5-4 को बढ़ाया गया है।[53]
गतिशीलता
लोरेंत्ज़ परिवर्तन से प्राप्त धारा #परिणाम गति का कारण बनने वाली ताकतों पर विचार किए बिना गतिकी , बिंदुओं, निकायों और निकायों की प्रणालियों की गति के अध्ययन के साथ सख्ती से निपटा। यह खंड जनता, बलों, ऊर्जा और आगे की चर्चा करता है, और इस तरह लोरेंत्ज़ परिवर्तन द्वारा सम्मिलित लोगों से परे भौतिक प्रभावों पर विचार करने की आवश्यकता है।
द्रव्यमान और ऊर्जा की तुल्यता
जैसे ही किसी वस्तु की गति पर्यवेक्षक के दृष्टिकोण से प्रकाश की गति के करीब पहुंचती है, उसका सापेक्षतावादी द्रव्यमान बढ़ता है जिससे पर्यवेक्षक के संदर्भ के सीमा रेखा के भीतर से इसे तेज करना अधिक कठिन हो जाता है।
द्रव्यमान m के साथ किसी वस्तु की ऊर्जा सामग्री mc के बराबर होती है, ऊपर संदर्भित पत्रों के अलावा - जो लोरेंत्ज़ परिवर्तन की व्युत्पत्ति देते हैं और विशेष सापेक्षता की नींव का वर्णन करते हैं - आइंस्टीन ने द्रव्यमान और ऊर्जा की तुल्यता (और संप्रेषणीयता) के लिए अनुमानी तर्क देते हुए कम से कम चार पत्र भी लिखे। E = mc2.
द्रव्यमान-ऊर्जा तुल्यता विशेष सापेक्षता का परिणाम है। न्यूटोनियन यांत्रिकी में अलग-अलग ऊर्जा और गति, सापेक्षता में चार-सदिश बनाते हैं, और यह समय घटक (ऊर्जा) को अंतरिक्ष घटकों (गति) से गैर-तुच्छ तरीके से संबंधित करता है। किसी स्थिर वस्तु के लिए, ऊर्जा-गति चार-सदिश है (E/c, 0, 0, 0): इसमें एक समय घटक है जो ऊर्जा है, और तीन अंतरिक्ष घटक जो शून्य हैं। वेग v के एक छोटे मान के साथ x दिशा में लोरेंत्ज़ परिवर्तन के साथ सीमा रेखा बदलने से, ऊर्जा गति चार-वेक्टर बन जाती है (E/c, Ev/c2, 0, 0). संवेग c . द्वारा विभाजित वेग से गुणा की गई ऊर्जा के बराबर है।
ऊर्जा और संवेग पदार्थ और विकिरण के गुण हैं, और यह निष्कर्ष निकालना असंभव है कि वे अपने आप में विशेष सापेक्षता के दो बुनियादी अभिधारणाओं से चार-सदिश बनाते हैं, क्योंकि ये पदार्थ या विकिरण के बारे में बात नहीं करते हैं, वे केवल बात करते हैं अंतरिक्ष और समय के बारे में। इसलिए व्युत्पत्ति के लिए कुछ अतिरिक्त भौतिक तर्क की आवश्यकता होती है। अपने 1905 के पेपर में, आइंस्टीन ने उन अतिरिक्त सिद्धांतों का उपयोग किया जो न्यूटोनियन यांत्रिकी को धीमी गति के लिए धारण करना चाहिए, ताकि धीमी गति पर एक ऊर्जा स्केलर और एक तीन-वेक्टर गति हो, और ऊर्जा और गति के लिए संरक्षण नियम सापेक्षता में बिल्कुल सही हो। . इसके अलावा, उन्होंने माना कि प्रकाश की ऊर्जा उc डॉपलर-शिफ्ट कारक द्वारा इसकी आवृत्ति के रूप में बदल जाती है, जिसे उन्होंने मैक्सवेल के समीकरणों के आधार पर पहले दिखाया था।[p 1]इस विषय पर आइंस्टीन का पहला पेपर था क्या किसी पिंड की जड़ता उसकी ऊर्जा सामग्री पर निर्भर करती है? 1905 में।[p 21] यद्यपि इस पत्र में आइंस्टीन के तर्क को लगभग सार्वभौमिक रूप से भौतिकविदों द्वारा सही, यहां तक कि स्वयं-स्पष्ट के रूप में स्वीकार किया गया है, वर्षों से कई लेखकों ने सुझाव दिया है कि यह गलत है।[54] अन्य लेखकों का सुझाव है कि तर्क केवल अनिर्णायक था क्योंकि यह कुछ निहित मान्यताओं पर निर्भर था।[55] आइंस्टीन ने विशेष सापेक्षता पर अपने 1907 के सर्वेक्षण पत्र में अपनी व्युत्पत्ति पर विवाद को स्वीकार किया। वहां उन्होंने नोट किया कि अनुमानी द्रव्यमान-ऊर्जा तर्क के लिए मैक्सवेल के समीकरणों पर भरोसा करना समस्याग्रस्त है। उनके 1905 के पत्र में तर्क किसी भी द्रव्यमान रहित कणों के उत्सर्जन के साथ किया जा सकता है, लेकिन मैक्सवेल समीकरणों का उपयोग स्पष्ट रूप से यह स्पष्ट करने के लिए किया जाता है कि विशेष रूप से प्रकाश का उत्सर्जन केवल कार्य करके ही प्राप्त किया जा सकता है। विद्युत चुम्बकीय तरंगों का उत्सर्जन करने के लिए, आपको केवल एक आवेशित कण को हिलाना है, और यह स्पष्ट रूप से काम कर रहा है, ताकि उत्सर्जन ऊर्जा का हो।[p 22][note 10]
आप पृथ्वी से कितनी दूर यात्रा कर सकते हैं?
चूँकि कोई भी चीज प्रकाश से तेज गति से यात्रा नहीं कर सकती है, इसलिए यह निष्कर्ष निकाला जा सकता है कि मानव पृथ्वी से ~ 100 प्रकाश वर्ष से अधिक दूर कभी नहीं जा सकता है। आप आसानी से सोच सकते हैं कि एक यात्री पृथ्वी से 100 प्रकाश वर्ष की सीमा के भीतर उपलब्ध कुछ सौर मंडलों से अधिक कभी नहीं पहुंच पाएगा। यद्यपि, समय के विस्तार के कारण, एक काल्पनिक अंतरिक्ष यान एक यात्री के जीवनकाल में हजारों प्रकाश वर्ष की यात्रा कर सकता है। यदि एक अंतरिक्ष यान का निर्माण किया जा सकता है जो पृथ्वी के निरंतर गुरुत्वाकर्षण पर गति करता है, तो यह एक वर्ष के बाद लगभग प्रकाश की गति से यात्रा करेगा जैसा कि पृथ्वी से देखा जाता है। यह इसके द्वारा वर्णित है:
सापेक्षता और एकीकृत विद्युत चुंबकत्व
शास्त्रीय विद्युत चुंबकत्व में सैद्धांतिक जांच ने तरंग प्रसार की खोज की। विद्युत चुम्बकीय प्रभावों को सामान्य करने वाले समीकरणों में पाया गया कि ई और बी क्षेत्रों की परिमित प्रसार गति को आवेशित कणों पर कुछ व्यवहार की आवश्यकता होती है। गतिमान आवेशों का सामान्य अध्ययन लीनार्ड-वाइचर्ट विभव का निर्माण करता है, जो विशेष सापेक्षता की ओर एक कदम है।
एक गतिमान आवेश के विद्युत क्षेत्र के एक गैर-गतिशील पर्यवेक्षक के निर्देश तंत्र में परिवर्तन के परिणामस्वरूप एक गणितीय शब्द की उपस्थिति होती है जिसे सामान्यतः पर चुंबकीय क्षेत्र कहा जाता है। इसके विपरीत, एक गतिमान आवेश द्वारा उत्पन्न 'चुंबकीय' क्षेत्र गायब हो जाता है और संदर्भ के एक गतिशील सीमा रेखा में विशुद्ध रूप से 'इलेक्ट्रोस्टैटिक' क्षेत्र बन जाता है। मैक्सवेल के समीकरण इस प्रकार ब्रह्मांड के शास्त्रीय मॉडल में विशेष सापेक्षतावादी प्रभावों के लिए केवल एक अनुभवजन्य फिट हैं। चूंकि विद्युत और चुंबकीय क्षेत्र निर्देश तंत्र पर निर्भर हैं और इस प्रकार आपस में जुड़े हुए हैं, इसलिए कोई भी विद्युत चुम्बकीय क्षेत्रों की बात करता है। विशेष सापेक्षता परिवर्तन नियम प्रदान करती है कि कैसे एक जड़त्वीय सीमा रेखा में एक विद्युत चुम्बकीय क्षेत्र दूसरे जड़त्वीय सीमा रेखा में प्रकट होता है।
3डी रूप में मैक्सवेल के समीकरण पहले से ही विशेष सापेक्षता की भौतिक सामग्री के अनुरूप हैं, यद्यपि उन्हें स्पष्ट रूप से सहसंयोजक रूप में हेरफेर करना आसान है, अर्थात टेंसर कैलकुलस की भाषा में।[58]
सापेक्षता और क्वांटम यांत्रिकी के सिद्धांत
सापेक्षतावादी क्वांटम यांत्रिकी और क्वांटम इलेक्ट्रोडायनामिक्स बनाने के लिए विशेष सापेक्षता को क्वांटम यांत्रिकी के साथ जोड़ा जा सकता है। सामान्य सापेक्षता और क्वांटम यांत्रिकी को कैसे एकीकृत किया जा सकता है यह भौतिकी में अनसुलझी समस्याओं की सूची है; क्वांटम गुरुत्व और हर चीज का एक सिद्धांत, जिसमें सामान्य सापेक्षता सहित एकीकरण की आवश्यकता होती है, सैद्धांतिक अनुसंधान में सक्रिय और चल रहे क्षेत्र हैं।
प्रारंभिक बोहर मॉडल शोधन बोहर-सोमरफेल्ड परमाणु मॉडल ने विशेष सापेक्षता और उस समय के क्वांटम यांत्रिकी पर प्रारंभिक ज्ञान दोनों का उपयोग करते हुए क्षार धातु परमाणुओं की बारीक संरचना की व्याख्या की।[59] 1928 में, पॉल डिराका ने एक प्रभावशाली सापेक्षतावादी तरंग समीकरण का निर्माण किया, जिसे अब उनके सम्मान में डिराक समीकरण के रूप में जाना जाता है,[p 24] यह विशेष सापेक्षता और 1926 के बाद उपलब्ध क्वांटम सिद्धांत के अंतिम संस्करण के साथ पूरी तरह से संगत है। इस समीकरण ने न केवल स्पिन (भौतिकी) नामक इलेक्ट्रॉनों के आंतरिक कोणीय गति का वर्णन किया, बल्कि इससे इलेक्ट्रॉन के कण की भविष्यवाणी भी हुई। (पॉज़िट्रॉन),[p 24][p 25] और महीन संरचना को केवल विशेष सापेक्षता के साथ ही पूरी तरह से समझाया जा सकता है। यह सापेक्षतावादी क्वांटम यांत्रिकी की पहली नींव थी।
दूसरी ओर, एंटीपार्टिकल्स का अस्तित्व इस निष्कर्ष की ओर ले जाता है कि सापेक्षतावादी क्वांटम यांत्रिकी कण अंतःक्रियाओं के अधिक सटीक और पूर्ण सिद्धांत के लिए पर्याप्त नहीं है। इसके अतिरिक्त, क्वांटम क्षेत्र सिद्धांत कहे जाने वाले मात्रात्मक क्षेत्रों के रूप में व्याख्या किए गए कणों का एक सिद्धांत आवश्यक हो जाता है; जिसमें पूरे अंतरिक्ष और समय में कणों का सर्वनाश हो सकता है।
स्थिति
इसके मिंकोव्स्की स्पेसटाइम में विशेष सापेक्षता तभी सटीक होती है जब गुरुत्वाकर्षण क्षमता का निरपेक्ष मान c से बहुत कम हो रुचि के क्षेत्र में[60] एक मजबूत गुरुत्वाकर्षण क्षेत्र में, सामान्य सापेक्षता का उपयोग करना चाहिए। सामान्य सापेक्षता कमजोर क्षेत्र की सीमा पर विशेष सापेक्षता बन जाती है। बहुत छोटे पैमाने पर, जैसे कि प्लैंक की लंबाई और नीचे, क्वांटम प्रभावों को ध्यान में रखा जाना चाहिए, जिसके परिणामस्वरूप क्वांटम गुरुत्व होता है। यद्यपि, मैक्रोस्कोपिक पैमानों पर और मजबूत गुरुत्वाकर्षण क्षेत्रों की अनुपस्थिति में, विशेष सापेक्षता का परीक्षण अत्यंत उच्च स्तर की सटीकता के लिए प्रयोगात्मक रूप से किया जाता है (10)-20)[61] और इस प्रकार भौतिकी समुदाय द्वारा स्वीकार किया गया। प्रायोगिक परिणाम जो इसके विपरीत प्रतीत होते हैं, वे प्रतिलिपि प्रस्तुत करने योग्य नहीं हैं और इस प्रकार व्यापक रूप से प्रयोगात्मक त्रुटियों के कारण माना जाता है।
विशेष सापेक्षता गणितीय रूप से आत्म-संगत है, और यह सभी आधुनिक भौतिक सिद्धांतों का एक कार्बनिक हिस्सा है, विशेष रूप से क्वांटम क्षेत्र सिद्धांत, स्ट्रिंग सिद्धांत, और सामान्य सापेक्षता (नगण्य गुरुत्वाकर्षण क्षेत्रों के cमित परिस्थिति में)।
न्यूटोनियन यांत्रिकी गणितीय रूप से छोटे वेगों (प्रकाश की गति की तुलना में) पर विशेष सापेक्षता से अनुसरण करती है - इस प्रकार न्यूटनियन यांत्रिकी को धीमी गति से चलने वाले पिंडों की एक विशेष सापेक्षता के रूप में माना जा सकता है। अधिक विस्तृत चर्चा के लिए शास्त्रीय यांत्रिकी देखें।
आइंस्टीन के 1905 के पेपर से पहले के कई प्रयोगों को अब सापेक्षता के प्रमाण के रूप में व्याख्यायित किया जाता है। इनमें से यह ज्ञात है कि आइंस्टीन को 1905 से पहले Fizeau प्रयोग के बारे में पता था,[62] और इतिहासकारों ने निष्कर्ष निकाला है कि आइंस्टीन को कम से कम 1899 की शुरुआत में माइकलसन-मॉर्ले प्रयोग के बारे में पता था, इसके बावजूद उन्होंने अपने बाद के वर्षों में दावा किया कि इसने सिद्धांत के विकास में कोई भूमिका नहीं निभाई।[13]
- फ़िज़ौ प्रयोग (1851, माइकलसन और मॉर्ले द्वारा 1886 में दोहराया गया) ने चलती मीडिया में प्रकाश की गति को मापा, जिसके परिणाम कॉलिनियर वेगों के सापेक्षतावादी जोड़ के अनुरूप हैं।
- प्रसिद्ध माइकलसन-मॉर्ले प्रयोग (1881, 1887) ने इस अभिधारणा को और समर्थन दिया कि एक निरपेक्ष संदर्भ वेग का पता लगाना संभव नहीं था। यहां यह कहा जाना चाहिए कि, कई वैकल्पिक दावों के विपरीत, इसने स्रोत और पर्यवेक्षक के वेग के संबंध में प्रकाश की गति के अपरिवर्तन के बारे में बहुत कम कहा, क्योंकि स्रोत और पर्यवेक्षक दोनों एक ही वेग से हर समय एक साथ यात्रा कर रहे थे।
- ट्राउटन-नोबल प्रयोग (1903) ने दिखाया कि संधारित्र पर टोक़ स्थिति और जड़त्वीय निर्देश तंत्र से स्वतंत्र है।
- रेले और ब्रेस के प्रयोग (1902, 1904) ने दिखाया कि लंबाई के संकुचन से सापेक्षता सिद्धांत के अनुसार, एक सह-चलती पर्यवेक्षक के लिए द्विअर्थीता नहीं होती है।
कण त्वरक नियमित रूप से प्रकाश की गति के निकट गति करने वाले कणों के गुणों को मापते हैं और मापते हैं, जहां उनका व्यवहार पूरी तरह से सापेक्षता सिद्धांत के अनुरूप होता है और पहले न्यूटनियन यांत्रिकी के साथ असंगत होता है। ये मशीनें केवल काम नहीं करेंगी यदि वे सापेक्षतावादी सिद्धांतों के अनुसार इंजीनियर नहीं होतीं। इसके अलावा, विशेष सापेक्षता का परीक्षण करने के लिए काफी संख्या में आधुनिक प्रयोग किए गए हैं। कुछ उदाहरण:
- आपेक्षिक ऊर्जा और संवेग का परीक्षण - कणों की cमित गति का परीक्षण
- इव्स-स्टिलवेल प्रयोग - सापेक्षतावादी डॉपलर प्रभाव और समय विस्तार का परीक्षण
- समय विस्तार का प्रायोगिक परीक्षण - एक तेज गति वाले कण के आधे जीवन पर सापेक्ष प्रभाव
- कैनेडी-थॉर्नडाइक प्रयोग - लोरेंत्ज़ परिवर्तनों के अनुसार समय का विस्तार
- ह्यूजेस-ड्रेवर प्रयोग - अंतरिक्ष और द्रव्यमान की आइसोट्रॉपी का परीक्षण
- लोरेंत्ज़ उल्लंघन के लिए आधुनिक खोज - विभिन्न आधुनिक परीक्षण
- उत्सर्जन सिद्धांत के परीक्षण के प्रयोगों ने प्रदर्शित किया कि प्रकाश की गति उत्सर्जक की गति से स्वतंत्र होती है।
- एथर ड्रैग परिकल्पना का परीक्षण करने के लिए प्रयोग - कोई ईथर प्रवाह बाधा नहीं।
स्पेसटाइम की तकनीकी चर्चा
स्पेसटाइम की ज्यामिति
फ्लैट यूक्लिडियन अंतरिक्ष और मिंकोव्स्की अंतरिक्ष के बीच तुलना

विशेष सापेक्षता एक 'फ्लैट' 4-आयामी मिंकोव्स्की स्पेस का उपयोग करती है - स्पेसटाइम का एक उदाहरण। मिंकोव्स्की स्पेसटाइम मानक 3-आयामी यूक्लिडियन स्पेस के समान प्रतीत होता है, लेकिन समय के संबंध में एक महत्वपूर्ण अंतर है।
3डी स्पेस में, दूरी (लाइन एलिमेंट) ds का डिफरेंशियल (अनंतिमल) द्वारा परिभाषित किया जाता है
उपरोक्त ds का वास्तविक रूप मीट्रिक और X . के विकल्पों पर निर्भर करता है0 समन्वय करें। समय निर्देशांक को अंतरिक्ष निर्देशांक की तरह बनाने के लिए, इसे काल्पनिक संख्या के रूप में माना जा सकता है: X0 = ict (इसे विक घूर्णन कहा जाता है)। ग्रेविटेशन (पुस्तक) | मिसनर, थॉर्न और व्हीलर (1971, 2.3) के अनुसार, अंततः विशेष और सामान्य सापेक्षता दोनों की गहरी समझ मिंकोव्स्की मीट्रिक (नीचे वर्णित) के अध्ययन से आएगी और लेने के लिए X0 = ct, समय के समन्वय के रूप में ict का उपयोग करते हुए एक प्रच्छन्न यूक्लिडियन मीट्रिक के अतिरिक्त।
कुछ लेखक उपयोग करते हैं X0 = t, c के कारकों के साथ कहीं और क्षतिपूर्ति करने के लिए; उदाहरण के लिए, स्थानिक निर्देशांक c या c . के कारकों से विभाजित होते हैं±2 मीट्रिक टेंसर में सम्मिलित हैं।[65] प्राकृतिक इकाइयों का उपयोग करके इन कई सम्मेलनों को हटा दिया जा सकता है जहां c = 1. तब स्थान और समय की समान इकाइयाँ होती हैं, और c का कोई भी गुणनखंड कहीं भी प्रकट नहीं होता है।
3डी स्पेसटाइम
यदि हम स्थानिक आयामों को घटाकर 2 कर दें, ताकि हम 3D अंतरिक्ष में भौतिकी का प्रतिनिधित्व कर सकें
4डी स्पेसटाइम
यदि हम इसे तीन स्थानिक आयामों तक बढ़ाते हैं, तो शून्य भूगणित 4-आयामी शंकु हैं:
जैसा कि चित्र 10-3 में दिखाया गया है, अशक्त भूगणित को त्रिज्या = c dt के साथ निरंतर संकेंद्रित क्षेत्रों के एक सेट के रूप में देखा जा सकता है।
यह अशक्त दोहरा-शंकु अंतरिक्ष में एक बिंदु की दृष्टि की रेखा का प्रतिनिधित्व करता है। अर्थात, जब हम तारों को देखते हैं और कहते हैं कि उस तारे का प्रकाश जो मुझे प्राप्त हो रहा है, वह X वर्ष पुराना है, तो हम इस दृष्टि रेखा को नीचे देख रहे हैं: एक अशक्त भूगणित। हम एक घटना को दूर से देख रहे हैं दूर और अतीत में एक समय डी / c। इस कारण से शून्य दोहरे शंकु को 'प्रकाश शंकु' के रूप में भी जाना जाता है। (चित्र 10-2 के निचले बाएँ बिंदु तारे का प्रतिनिधित्व करता है, मूल प्रेक्षक का प्रतिनिधित्व करता है, और रेखा दृष्टि की शून्य भूगणितीय रेखा का प्रतिनिधित्व करती है।)
−t क्षेत्र में शंकु वह सूचना है जो बिंदु 'प्राप्त' कर रहा है, जबकि +t खंड में शंकु वह जानकारी है जो बिंदु 'भेज रहा है'।
मिंकोव्स्की अंतरिक्ष की ज्यामिति को मिंकोव्स्की आरेखों का उपयोग करके चित्रित किया जा सकता है, जो विशेष सापेक्षता में कई विचार प्रयोगों को समझने में भी उपयोगी होते हैं।
ध्यान दें कि, 4d स्पेसटाइम में, द्रव्यमान के केंद्र की अवधारणा अधिक जटिल हो जाती है, द्रव्यमान का केंद्र (सापेक्षतावादी) देखें।
स्पेसटाइम में भौतिकी
निर्देश तंत्र के बीच भौतिक मात्राओं का परिवर्तन
ऊपर, समय के समन्वय के लिए लोरेंत्ज़ परिवर्तन और तीन अंतरिक्ष निर्देशांक दर्शाते हैं कि वे आपस में जुड़े हुए हैं। यह अधिक व्यापक रूप से सच है: "टाइमलाइक" और "स्पेसेलिक" मात्राओं के कुछ जोड़े स्वाभाविक रूप से समान लोरेंत्ज़ परिवर्तन के तहत समान स्तर पर संयोजित होते हैं।
उपरोक्त मानक विन्यास में लोरेंत्ज़ परिवर्तन, जो कि एक्स-दिशा में वृद्धि के लिए है, को निम्नानुसार मैट्रिक्स रूप में पुन: व्यवस्थित किया जा सकता है:
चार-सदिश का सबसे सरल उदाहरण स्पेसटाइम में एक घटना की स्थिति है, जो एक समयबद्ध घटक ct और स्पेसलाइक घटक x = (x, y, z) का गठन करता है, एक विपरीत स्थिति में घटकों के साथ चार वेक्टर:
अधिक सामान्यतः पर, चार-वेक्टर के सभी प्रतिपरिवर्तघटक लोरेंत्ज़ परिवर्तन द्वारा एक सीमा रेखा से दूसरे सीमा रेखा में बदलना:
चार-त्वरण 4-वेग का उचित समय व्युत्पन्न है:
एक अदिश क्षेत्र का चार-ढाल φ कॉन्ट्रावेरिएंट के अतिरिक्त सहसंयोजक रूप से रूपांतरित होता है:
अधिक सामान्यतः, 4-वेक्टर के सहसंयोजक घटक व्युत्क्रम लोरेंत्ज़ परिवर्तन के अनुसार बदलते हैं:
विशेष सापेक्षता के अभिगृहीत लोरेंत्ज़ रूपांतरण मैट्रिक्स के सटीक रूप को बाधित करते हैं।
सामान्यतः पर, अधिकांश भौतिक मात्राओं को सबसे अच्छा (घटकों के) टेंसर के रूप में वर्णित किया जाता है। तो एक सीमा रेखा से दूसरे सीमा रेखा में बदलने के लिए, हम प्रसिद्ध टेंसर का उपयोग करते हैं[69]
चार-आयामी दूसरे क्रम के एंटीसिमेट्रिक टेंसर का एक उदाहरण सापेक्षतावादी कोणीय गति है, जिसमें छह घटक हैं: तीन शास्त्रीय कोणीय गति हैं, और अन्य तीन सिस्टम के द्रव्यमान के केंद्र के वृद्धि से संबंधित हैं। उचित समय के संबंध में सापेक्षतावादी कोणीय गति का व्युत्पन्न सापेक्षतावादी टोक़ है, दूसरा क्रम एंटीसिमेट्रिक टेंसर भी है।
विद्युत चुम्बकीय क्षेत्र टेंसर छह घटकों के साथ एक और दूसरा क्रम एंटीसिमेट्रिक टेंसर क्षेत्र है: तीन विद्युत क्षेत्र के लिए और अन्य तीन चुंबकीय क्षेत्र के लिए। विद्युत चुम्बकीय क्षेत्र के लिए तनाव-ऊर्जा टेंसर भी है, अर्थात् विद्युत चुम्बकीय तनाव-ऊर्जा टेंसर।
मीट्रिक
मीट्रिक टेंसर एक को दो वैक्टर के आंतरिक उत्पाद को परिभाषित करने की अनुमति देता है, जो बदले में एक को वेक्टर को एक परिमाण प्रदान करने की अनुमति देता है। स्पेसटाइम की चार-आयामी प्रकृति को देखते हुए मिंकोव्स्की मीट्रिक में घटक होते हैं (उपयुक्त रूप से चुने गए निर्देशांक के साथ मान्य) जिन्हें 4 × 4 मैट्रिक्स में व्यवस्थित किया जा सकता है:
पोंकारे समूह परिवर्तनों का सबसे सामान्य समूह है जो मिंकोव्स्की मीट्रिक को संरक्षित करता है:
मीट्रिक का उपयोग वैक्टर और टेंसर पर सूचकांक बढ़ाने और घटाने के लिए किया जा सकता है। मीट्रिक का उपयोग करके इनवेरिएंट का निर्माण किया जा सकता है, 4-वेक्टर टी का आंतरिक उत्पाद 4-वेक्टर S के साथ है:
सापेक्षिक किनेमेटिक्स और इनवेरिएंस
समन्वय अंतर भी विपरीत रूप से बदलते हैं:
4-वेग Uμ का एक अपरिवर्तनीय रूप है:
सापेक्ष गतिकी और अपरिवर्तन
चार-गति का अपरिवर्तनीय परिमाण | गति 4-वेक्टर ऊर्जा-गति संबंध उत्पन्न करता है:
शेष ऊर्जा ऊपर चर्चा किए गए प्रसिद्ध समीकरण के अनुसार द्रव्यमान से संबंधित है:
न्यूटन के गति के तीसरे नियम का उपयोग करने के लिए, दोनों बलों को एक ही समय के समन्वय के संबंध में गति के परिवर्तन की दर के रूप में परिभाषित किया जाना चाहिए। अर्थात्, इसके लिए ऊपर परिभाषित 3D बल की आवश्यकता होती है। दुर्भाग्य से, 4D में कोई टेन्सर नहीं है जिसमें इसके घटकों के बीच 3D बल वेक्टर के घटक सम्मिलित हैं।
यदि कोई कण c पर यात्रा नहीं कर रहा है, तो कोई कण के सह-चलती निर्देश तंत्र से 3D बल को पर्यवेक्षक के निर्देश तंत्र में बदल सकता है। यह एक 4-वेक्टर उत्पन्न करता है जिसे चार-बल कहा जाता है। यह उचित समय के संबंध में उपरोक्त ऊर्जा गति चार-सदिश के परिवर्तन की दर है। चार-बलों का सहसंयोजक संस्करण है:
एक सतत माध्यम में, बल का 3D घनत्व शक्ति के घनत्व के साथ मिलकर एक सहसंयोजक 4-वेक्टर बनाता है। स्थानिक भाग उस कोशिका के आयतन से एक छोटी कोशिका (3-स्थान में) पर बल को विभाजित करने का परिणाम है। समय घटक सेल के आयतन से विभाजित उस सेल को हस्तांतरित शक्ति का −1/c गुना है। इसका उपयोग नीचे विद्युत चुंबकत्व पर अनुभाग में किया जाएगा।
यह भी देखें
- लोग:
- सापेक्षता:
- विशेष सापेक्षता का इतिहास
- दोगुनी विशेष सापेक्षता
- बौंडी के-कैलकुलस
- आइंस्टीन तुल्यकालन
- Rietdijk–Putnam तर्क
- विशेष सापेक्षता (वैकल्पिक सूत्रीकरण)
- सापेक्षता प्राथमिकता विवाद
- भौतिक विज्ञान:
- आइंस्टीन के विचार प्रयोग
- भौतिक ब्रह्मांड विज्ञान
- सापेक्ष यूलर समीकरण
- लोरेंत्ज़ ईथर सिद्धांत
- चलती चुंबक और कंडक्टर समस्या
- आकार तरंगें
- आपेक्षिक ऊष्मा चालन
- सापेक्ष डिस्क
- जन्म कठोरता
- जन्म निर्देशांक
- गणित:
- दर्शन:
- वास्तविकता
- परंपरावाद
- विरोधाभास:
- एरेनफेस्ट विरोधाभास
- बेल का अंतरिक्ष यान विरोधाभास
- मोकानू की वेग रचना विरोधाभास
- प्रकाशस्तंभ विरोधाभास
टिप्पणियाँ
- ↑ Einstein himself, in The Foundations of the General Theory of Relativity, Ann. Phys. 49 (1916), writes "The word 'special' is meant to intimate that the principle is restricted to the case ...". See p. 111 of The Principle of Relativity, A. Einstein, H. A. Lorentz, H. Weyl, H. Minkowski, Dover reprint of 1923 translation by Methuen and Company.]
- ↑ Wald, General Relativity, p. 60: "... the special theory of relativity asserts that spacetime is the manifold with a flat metric of Lorentz signature defined on it. Conversely, the entire content of special relativity ... is contained in this statement ..."
- ↑ In a spacetime setting, the length of a rigid object is the spatial distance between the ends of the object measured at the same time.
- ↑ The results of the Michelson–Morley experiment led George Francis FitzGerald and Hendrik Lorentz independently to propose the phenomenon of length contraction. Lorentz believed that length contraction represented a physical contraction of the atoms making up an object. He envisioned no fundamental change in the nature of space and time.[23]: 62–68
Lorentz expected that length contraction would result in compressive strains in an object that should result in measurable effects. Such effects would include optical effects in transparent media, such as optical rotation[p 11] and induction of double refraction,[p 12] and the induction of torques on charged condensers moving at an angle with respect to the aether.[p 12] Lorentz was perplexed by experiments such as the Trouton–Noble experiment and the experiments of Rayleigh and Brace which failed to validate his theoretical expectations.[23] - ↑ For mathematical consistency, Lorentz proposed a new time variable, the "local time", called that because it depended on the position of a moving body, following the relation .[p 13] Lorentz considered local time not to be "real"; rather, it represented an ad hoc change of variable.[24]: 51, 80
Impressed by Lorentz's "most ingenious idea", Poincaré saw more in local time than a mere mathematical trick. It represented the actual time that would be shown on a moving observer's clocks. On the other hand, Poincaré did not consider this measured time to be the "true time" that would be exhibited by clocks at rest in the aether. Poincaré made no attempt to redefine the concepts of space and time. To Poincaré, Lorentz transformation described the apparent states of the field for a moving observer. True states remained those defined with respect to the ether.[25] - ↑ This concept is counterintuitive at least for the fact that, in contrast to usual concepts of distance, it may assume negative values (is not positive definite for non-coinciding events), and that the square-denotation is misleading. This negative square lead to, now not broadly used, concepts of imaginary time. It is immediate that the negative of is also an invariant, generated by a variant of the metric signature of spacetime.
- ↑ The invariance of Δs2 under standard Lorentz transformation in analogous to the invariance of squared distances Δr2 under rotations in Euclidean space. Although space and time have an equal footing in relativity, the minus sign in front of the spatial terms marks space and time as being of essentially different character. They are not the same. Because it treats time differently than it treats the 3 spatial dimensions, Minkowski space differs from four-dimensional Euclidean space.
- ↑ The refractive index dependence of the presumed partial aether-drag was eventually confirmed by Pieter Zeeman in 1914–1915, long after special relativity had been accepted by the mainstream. Using a scaled-up version of Michelson's apparatus connected directly to Amsterdam's main water conduit, Zeeman was able to perform extended measurements using monochromatic light ranging from violet (4358 Å) through red (6870 Å).[p 17][p 18]
- ↑ Even though it has been many decades since Terrell and Penrose published their observations, popular writings continue to conflate measurement versus appearance. For example, Michio Kaku wrote in Einstein's Cosmos (W. W. Norton & Company, 2004. p. 65): "... imagine that the speed of light is only 20 miles per hour. If a car were to go down the street, it might look compressed in the direction of motion, being squeezed like an accordion down to perhaps 1 inch in length."
- ↑ In a letter to Carl Seelig in 1955, Einstein wrote "I had already previously found that Maxwell's theory did not account for the micro-structure of radiation and could therefore have no general validity.", Einstein letter to Carl Seelig, 1955.
प्राथमिक स्रोत
- ↑ 1.0 1.1 1.2 1.3 1.4 1.5 Albert Einstein (1905) "Zur Elektrodynamik bewegter Körper", Annalen der Physik 17: 891; English translation On the Electrodynamics of Moving Bodies by George Barker Jeffery and Wilfrid Perrett (1923); Another English translation On the Electrodynamics of Moving Bodies by Megh Nad Saha (1920).
- ↑ "Science and Common Sense", P. W. Bridgman, The Scientific Monthly, Vol. 79, No. 1 (Jul. 1954), pp. 32–39.
- ↑ The Electromagnetic Mass and Momentum of a Spinning Electron, G. Breit, Proceedings of the National Academy of Sciences, Vol. 12, p.451, 1926
- ↑ Kinematics of an electron with an axis. Phil. Mag. 3:1-22. L. H. Thomas.]
- ↑ 5.0 5.1 Einstein, Autobiographical Notes, 1949.
- ↑ Einstein, "Fundamental Ideas and Methods of the Theory of Relativity", 1920
- ↑ Einstein, On the Relativity Principle and the Conclusions Drawn from It, 1907; "The Principle of Relativity and Its Consequences in Modern Physics", 1910; "The Theory of Relativity", 1911; Manuscript on the Special Theory of Relativity, 1912; Theory of Relativity, 1913; Einstein, Relativity, the Special and General Theory, 1916; The Principal Ideas of the Theory of Relativity, 1916; What Is The Theory of Relativity?, 1919; The Principle of Relativity (Princeton Lectures), 1921; Physics and Reality, 1936; The Theory of Relativity, 1949.
- ↑ Yaakov Friedman (2004). Physical Applications of Homogeneous Balls. Progress in Mathematical Physics. Vol. 40. pp. 1–21. ISBN 978-0-8176-3339-4.
- ↑ Das, A. (1993) The Special Theory of Relativity, A Mathematical Exposition, Springer, ISBN 0-387-94042-1.
- ↑ Schutz, J. (1997) Independent Axioms for Minkowski Spacetime, Addison Wesley Longman Limited, ISBN 0-582-31760-6.
- ↑ Lorentz, H.A. (1902). "The rotation of the plane of polarization in moving media" (PDF). Huygens Institute - Royal Netherlands Academy of Arts and Sciences (KNAW). 4: 669–678. Bibcode:1901KNAB....4..669L. Retrieved 15 November 2018.
- ↑ 12.0 12.1 Lorentz, H. A. (1904). "Electromagnetic phenomena in a system moving with any velocity smaller than that of light" (PDF). Huygens Institute - Royal Netherlands Academy of Arts and Sciences (KNAW). 6: 809–831. Bibcode:1903KNAB....6..809L. Retrieved 15 November 2018.
- ↑ Lorentz, Hendrik (1895). "Investigation of oscillations excited by oscillating ions". Attempt at a Theory of Electrical and Optical Phenomena in Moving Bodies (Versuch einer Theorie der electrischen und optischen Erscheinungen in bewegten Körpern). Leiden: E. J. Brill. (subsection § 31).
- ↑ Lin, Shih-Chun; Giallorenzi, Thomas G. (1979). "Sensitivity analysis of the Sagnac-effect optical-fiber ring interferometer". Applied Optics. 18 (6): 915–931. Bibcode:1979ApOpt..18..915L. doi:10.1364/AO.18.000915. PMID 20208844. S2CID 5343180.
- ↑ Shaw, R. (1962). "Length Contraction Paradox". American Journal of Physics. 30 (1): 72. Bibcode:1962AmJPh..30...72S. doi:10.1119/1.1941907. S2CID 119855914.
- ↑ G. A. Benford; D. L. Book & W. A. Newcomb (1970). "The Tachyonic Antitelephone". Physical Review D. 2 (2): 263–265. Bibcode:1970PhRvD...2..263B. doi:10.1103/PhysRevD.2.263. S2CID 121124132.
- ↑ Zeeman, Pieter (1914). "Fresnel's coefficient for light of different colours. (First part)". Proc. Kon. Acad. Van Weten. 17: 445–451. Bibcode:1914KNAB...17..445Z.
- ↑ Zeeman, Pieter (1915). "Fresnel's coefficient for light of different colours. (Second part)". Proc. Kon. Acad. Van Weten. 18: 398–408. Bibcode:1915KNAB...18..398Z.
- ↑ Terrell, James (15 November 1959). "Invisibility of the Lorentz Contraction". Physical Review. 116 (4): 1041–1045. Bibcode:1959PhRv..116.1041T. doi:10.1103/PhysRev.116.1041.
- ↑ Penrose, Roger (24 October 2008). "The Apparent Shape of a Relativistically Moving Sphere". Mathematical Proceedings of the Cambridge Philosophical Society. 55 (1): 137–139. Bibcode:1959PCPS...55..137P. doi:10.1017/S0305004100033776. S2CID 123023118.
- ↑ Does the inertia of a body depend upon its energy content? A. Einstein, Annalen der Physik. 18:639, 1905 (English translation by W. Perrett and G.B. Jeffery)
- ↑ On the Inertia of Energy Required by the Relativity Principle, A. Einstein, Annalen der Physik 23 (1907): 371–384
- ↑ Baglio, Julien (26 May 2007). "Acceleration in special relativity: What is the meaning of "uniformly accelerated movement" ?" (PDF). Physics Department, ENS Cachan. Retrieved 22 January 2016.
- ↑ 24.0 24.1 P.A.M. Dirac (1930). "A Theory of Electrons and Protons". Proceedings of the Royal Society. A126 (801): 360–365. Bibcode:1930RSPSA.126..360D. doi:10.1098/rspa.1930.0013. JSTOR 95359.
- ↑ C.D. Anderson (1933). "The Positive Electron". Phys. Rev. 43 (6): 491–494. Bibcode:1933PhRv...43..491A. doi:10.1103/PhysRev.43.491.
संदर्भ
- ↑ 1.0 1.1 1.2 Griffiths, David J. (2013). "Electrodynamics and Relativity". Introduction to Electrodynamics (4th ed.). Pearson. Chapter 12. ISBN 978-0-321-85656-2.
- ↑ 2.0 2.1 2.2 Jackson, John D. (1999). "Special Theory of Relativity". Classical Electrodynamics (3rd ed.). John Wiley & Sons, Inc. Chapter 11. ISBN 0-471-30932-X.
- ↑ Goldstein, Herbert (1980). "Chapter 7: Special Relativity in Classical Mechanics". Classical Mechanics (2nd ed.). Addison-Wesley Publishing Company. ISBN 0-201-02918-9.
- ↑ 4.0 4.1 Lanczos, Cornelius (1970). "Chapter IX: Relativistic Mechanics". The Variational Principles of Mechanics (4th ed.). Dover Publications. ISBN 978-0-486-65067-8.
- ↑ Albert Einstein (2001). Relativity: The Special and the General Theory (Reprint of 1920 translation by Robert W. Lawson ed.). Routledge. p. 48. ISBN 978-0-415-25384-0.
- ↑ The Feynman Lectures on Physics Vol. I Ch. 15-9: Equivalence of mass and energy
- ↑ Sean Carroll, Lecture Notes on General Relativity, ch. 1, "Special relativity and flat spacetime," http://ned.ipac.caltech.edu/level5/March01/Carroll3/Carroll1.html
- ↑ Koks, Don (2006). Explorations in Mathematical Physics: The Concepts Behind an Elegant Language (illustrated ed.). Springer Science & Business Media. p. 234. ISBN 978-0-387-32793-8. Extract of page 234
- ↑ Steane, Andrew M. (2012). Relativity Made Relatively Easy (illustrated ed.). OUP Oxford. p. 226. ISBN 978-0-19-966286-9. Extract of page 226
- ↑ Edwin F. Taylor & John Archibald Wheeler (1992). Spacetime Physics: Introduction to Special Relativity. W. H. Freeman. ISBN 978-0-7167-2327-1.
- ↑ 11.0 11.1 11.2 Rindler, Wolfgang (1977). Essential Relativity: Special, General, and Cosmological (illustrated ed.). Springer Science & Business Media. p. §1,11 p. 7. ISBN 978-3-540-07970-5.
- ↑ Michael Polanyi (1974) Personal Knowledge: Towards a Post-Critical Philosophy, ISBN 0-226-67288-3, footnote page 10–11: Einstein reports, via Dr N Balzas in response to Polanyi's query, that "The Michelson–Morley experiment had no role in the foundation of the theory." and "..the theory of relativity was not founded to explain its outcome at all." [1]
- ↑ 13.0 13.1 Jeroen van Dongen (2009). "On the role of the Michelson–Morley experiment: Einstein in Chicago". Archive for History of Exact Sciences. 63 (6): 655–663. arXiv:0908.1545. Bibcode:2009arXiv0908.1545V. doi:10.1007/s00407-009-0050-5. S2CID 119220040.
- ↑ For a survey of such derivations, see Lucas and Hodgson, Spacetime and Electromagnetism, 1990
- ↑ Einstein, A., Lorentz, H. A., Minkowski, H., & Weyl, H. (1952). The Principle of Relativity: a collection of original memoirs on the special and general theory of relativity. Courier Dover Publications. p. 111. ISBN 978-0-486-60081-9.
{{cite book}}: CS1 maint: multiple names: authors list (link) - ↑ Collier, Peter (2017). A Most Incomprehensible Thing: Notes Towards a Very Gentle Introduction to the Mathematics of Relativity (3rd ed.). Incomprehensible Books. ISBN 9780957389465.
- ↑ Staley, Richard (2009), "Albert Michelson, the Velocity of Light, and the Ether Drift", Einstein's generation. The origins of the relativity revolution, Chicago: University of Chicago Press, ISBN 0-226-77057-5
- ↑ 18.0 18.1 18.2 18.3 18.4 18.5 18.6 18.7 David Morin (2007) Introduction to Classical Mechanics, Cambridge University Press, Cambridge, chapter 11, Appendix I, ISBN 1-139-46837-5.
- ↑ Miller, D. J. (2010). "A constructive approach to the special theory of relativity". American Journal of Physics. 78 (6): 633–638. arXiv:0907.0902. Bibcode:2010AmJPh..78..633M. doi:10.1119/1.3298908. S2CID 20444859.
- ↑ Taylor, Edwin; Wheeler, John Archibald (1992). Spacetime Physics (2nd ed.). W.H. Freeman & Co. ISBN 978-0-7167-2327-1.
- ↑ Mermin, N. David (1968). Space and Time in Special Relativity. McGraw-Hill. ISBN 978-0881334203.
- ↑ Robert Resnick (1968). Introduction to special relativity. Wiley. pp. 62–63. ISBN 9780471717249.
- ↑ 23.0 23.1 Miller, Arthur I. (1998). Albert Einstein's Special Theory of Relativity: Emergence (1905) and Early Interpretation (1905–1911). Mew York: Springer-Verlag. ISBN 978-0-387-94870-6.
- ↑ Bernstein, Jeremy (2006). Secrets of the Old One: Einstein, 1905. Copernicus Books (imprint of Springer Science + Business Media). ISBN 978-0387-26005-1.
- ↑ Darrigol, Olivier (2005). "The Genesis of the Theory of Relativity" (PDF). Séminaire Poincaré. 1: 1–22. Bibcode:2006eins.book....1D. Retrieved 15 November 2018.
- ↑ 26.0 26.1 26.2 Rindler, Wolfgang (1977). Essential Relativity (2nd ed.). New York: Springer-Verlag. ISBN 978-0-387-10090-6.
- ↑ 27.0 27.1 27.2 27.3 Taylor, Edwin F.; Wheeler, John Archibald (1966). Spacetime Physics (1st ed.). San Francisco: W. H. Freeman and Company.
- ↑ Ashby, Neil (2003). "Relativity in the Global Positioning System". Living Reviews in Relativity. 6 (1): 1. Bibcode:2003LRR.....6....1A. doi:10.12942/lrr-2003-1. PMC 5253894. PMID 28163638.
- ↑ Daniel Kleppner & David Kolenkow (1973). An Introduction to Mechanics. pp. 468–70. ISBN 978-0-07-035048-9.
- ↑ Tolman, Richard C. (1917). The Theory of the Relativity of Motion. Berkeley: University of California Press. p. 54.
- ↑ Takeuchi, Tatsu. "Special Relativity Lecture Notes – Section 10". Virginia Tech. Retrieved 31 October 2018.
- ↑ Morin, David (2017). Special Relativity for the Enthusiastic Beginner. CreateSpace Independent Publishing Platform. pp. 90–92. ISBN 9781542323512.
- ↑ Gibbs, Philip. "Is Faster-Than-Light Travel or Communication Possible?". Physics FAQ. Department of Mathematics, University of California, Riverside. Retrieved 31 October 2018.
- ↑ Ginsburg, David (1989). Applications of Electrodynamics in Theoretical Physics and Astrophysics (illustrated ed.). CRC Press. p. 206. Bibcode:1989aetp.book.....G. ISBN 978-2-88124-719-4. Extract of page 206
- ↑ Wesley C. Salmon (2006). Four Decades of Scientific Explanation. University of Pittsburgh. p. 107. ISBN 978-0-8229-5926-7., Section 3.7 page 107
- ↑ Lauginie, P. (2004). "Measuring Speed of Light: Why? Speed of what?" (PDF). Proceedings of the Fifth International Conference for History of Science in Science Education. Archived from the original (PDF) on 4 July 2015. Retrieved 3 July 2015.
- ↑ Stachel, J. (2005). "Fresnel's (dragging) coefficient as a challenge to 19th century optics of moving bodies". In Kox, A.J.; Eisenstaedt, J (eds.). The universe of general relativity. Boston: Birkhäuser. pp. 1–13. ISBN 978-0-8176-4380-5. Retrieved 17 April 2012.
- ↑ Richard A. Mould (2001). Basic Relativity (2nd ed.). Springer. p. 8. ISBN 978-0-387-95210-9.
- ↑ Seidelmann, P. Kenneth, ed. (1992). Explanatory Supplement to the Astronomical Almanac. ill Valley, Calif.: University Science Books. p. 393. ISBN 978-0-935702-68-2.
- ↑ Ferraro, Rafael; Sforza, Daniel M. (2005). "European Physical Society logo Arago (1810): the first experimental result against the ether". European Journal of Physics. 26 (1): 195–204. arXiv:physics/0412055. Bibcode:2005EJPh...26..195F. doi:10.1088/0143-0807/26/1/020. S2CID 119528074.
- ↑ Dolan, Graham. "Airy's Water Telescope (1870)". The Royal Observatory Greenwich. Retrieved 20 November 2018.
- ↑ Hollis, H. P. (1937). "Airy's water telescope". The Observatory. 60: 103–107. Bibcode:1937Obs....60..103H. Retrieved 20 November 2018.
- ↑ Janssen, Michel; Stachel, John (2004). "The Optics and Electrodynamics of Moving Bodies" (PDF). In Stachel, John (ed.). Going Critical. Springer. ISBN 978-1-4020-1308-9.
- ↑ Sher, D. (1968). "The Relativistic Doppler Effect". Journal of the Royal Astronomical Society of Canada. 62: 105–111. Bibcode:1968JRASC..62..105S. Retrieved 11 October 2018.
- ↑ Gill, T. P. (1965). The Doppler Effect. London: Logos Press Limited. pp. 6–9. OL 5947329M.
- ↑ Feynman, Richard P.; Leighton, Robert B.; Sands, Matthew (February 1977). "Relativistic Effects in Radiation". The Feynman Lectures on Physics: Volume 1. Reading, Massachusetts: Addison-Wesley. pp. 34–7 f. ISBN 9780201021165. LCCN 2010938208.
- ↑ Cook, Helen. "Relativistic Distortion". Mathematics Department, University of British Columbia. Retrieved 12 April 2017.
- ↑ Signell, Peter. "Appearances at Relativistic Speeds" (PDF). Project PHYSNET. Michigan State University, East Lansing, MI. Archived from the original (PDF) on 13 April 2017. Retrieved 12 April 2017.
- ↑ Kraus, Ute. "The Ball is Round". Space Time Travel: Relativity visualized. Institut für Physik Universität Hildesheim. Archived from the original on 12 May 2017. Retrieved 16 April 2017.
- ↑ Zensus, J. Anton; Pearson, Timothy J. (1987). Superluminal Radio Sources (1st ed.). Cambridge, New York: Cambridge University Press. p. 3. ISBN 9780521345606.
- ↑ Chase, Scott I. "Apparent Superluminal Velocity of Galaxies". The Original Usenet Physics FAQ. Department of Mathematics, University of California, Riverside. Retrieved 12 April 2017.
- ↑ Richmond, Michael. ""Superluminal" motions in astronomical sources". Physics 200 Lecture Notes. School of Physics and Astronomy, Rochester Institute of Technology. Archived from the original on 16 February 2017. Retrieved 20 April 2017.
- ↑ Keel, Bill. "Jets, Superluminal Motion, and Gamma-Ray Bursts". Galaxies and the Universe - WWW Course Notes. Department of Physics and Astronomy, University of Alabama. Archived from the original on 1 March 2017. Retrieved 29 April 2017.
- ↑ Max Jammer (1997). Concepts of Mass in Classical and Modern Physics. Courier Dover Publications. pp. 177–178. ISBN 978-0-486-29998-3.
- ↑ John J. Stachel (2002). Einstein from B to Z. Springer. p. 221. ISBN 978-0-8176-4143-6.
- ↑ 56.0 56.1 Philip Gibbs & Don Koks. "The Relativistic Rocket". Retrieved 30 August 2012.
- ↑ The special theory of relativity shows that time and space are affected by motion Archived 2012-10-21 at the Wayback Machine. Library.thinkquest.org. Retrieved on 2013-04-24.
- ↑ E. J. Post (1962). Formal Structure of Electromagnetics: General Covariance and Electromagnetics. Dover Publications Inc. ISBN 978-0-486-65427-0.
- ↑ R. Resnick; R. Eisberg (1985). Quantum Physics of Atoms, Molecules, Solids, Nuclei and Particles (2nd ed.). John Wiley & Sons. pp. 114–116. ISBN 978-0-471-87373-0.
- ↑ Øyvind Grøn & Sigbjørn Hervik (2007). Einstein's general theory of relativity: with modern applications in cosmology. Springer. p. 195. ISBN 978-0-387-69199-2. Extract of page 195 (with units where c=1)
- ↑ The number of works is vast, see as example:
Sidney Coleman; Sheldon L. Glashow (1997). "Cosmic Ray and Neutrino Tests of Special Relativity". Physics Letters B. 405 (3–4): 249–252. arXiv:hep-ph/9703240. Bibcode:1997PhLB..405..249C. doi:10.1016/S0370-2693(97)00638-2. S2CID 17286330.
An overview can be found on this page - ↑ John D. Norton, John D. (2004). "Einstein's Investigations of Galilean Covariant Electrodynamics prior to 1905". Archive for History of Exact Sciences. 59 (1): 45–105. Bibcode:2004AHES...59...45N. doi:10.1007/s00407-004-0085-6. S2CID 17459755.
- ↑ J.A. Wheeler; C. Misner; K.S. Thorne (1973). Gravitation. W.H. Freeman & Co. p. 58. ISBN 978-0-7167-0344-0.
- ↑ J.R. Forshaw; A.G. Smith (2009). Dynamics and Relativity. Wiley. p. 247. ISBN 978-0-470-01460-8.
- ↑ R. Penrose (2007). The Road to Reality. Vintage books. ISBN 978-0-679-77631-4.
- ↑ Jean-Bernard Zuber & Claude Itzykson, Quantum Field Theory, pg 5, ISBN 0-07-032071-3
- ↑ Charles W. Misner, Kip S. Thorne & John A. Wheeler, Gravitation, pg 51, ISBN 0-7167-0344-0
- ↑ George Sterman, An Introduction to Quantum Field Theory, pg 4, ISBN 0-521-31132-2
- ↑ Sean M. Carroll (2004). Spacetime and Geometry: An Introduction to General Relativity. Addison Wesley. p. 22. ISBN 978-0-8053-8732-2.
अग्रिम पठन
पाठ्यपुस्तकें
- Einstein, Albert (1920). Relativity: The Special and General Theory.
- Einstein, Albert (1996). The Meaning of Relativity. Fine Communications. ISBN 1-56731-136-9
- Logunov, Anatoly A. (2005). Henri Poincaré and the Relativity Theory (transl. from Russian by G. Pontocorvo and V. O. Soloviev, edited by V. A. Petrov). Nauka, Moscow.
- Charles Misner, Kip Thorne, and John Archibald Wheeler (1971) Gravitation. W. H. Freeman & Co. ISBN 0-7167-0334-3
- Post, E.J., 1997 (1962) Formal Structure of Electromagnetics: General Covariance and Electromagnetics. Dover Publications.
- Wolfgang Rindler (1991). Introduction to Special Relativity (2nd ed.), Oxford University Press. ISBN 978-0-19-853952-0; ISBN 0-19-853952-5
- Harvey R. Brown (2005). Physical relativity: space–time structure from a dynamical perspective, Oxford University Press, ISBN 0-19-927583-1; ISBN 978-0-19-927583-0
- Qadir, Asghar (1989). Relativity: An Introduction to the Special Theory. Singapore: World Scientific Publications. p. 128. Bibcode:1989rist.book.....Q. ISBN 978-9971-5-0612-4.
- French, A. P. (1968). Special Relativity (M.I.T. Introductory Physics) (1st ed.). W. W. Norton & Company. ISBN 978-0393097931.
- Silberstein, Ludwik (1914). The Theory of Relativity.
- Lawrence Sklar (1977). Space, Time and Spacetime. University of California Press. ISBN 978-0-520-03174-6.
- Lawrence Sklar (1992). Philosophy of Physics. Westview Press. ISBN 978-0-8133-0625-4.
- Sergey Stepanov (2018). Relativistic World. De Gruyter. ISBN 9783110515879.
- Taylor, Edwin, and John Archibald Wheeler (1992). Spacetime Physics (2nd ed.). W. H. Freeman & Co. ISBN 0-7167-2327-1.
- Tipler, Paul, and Llewellyn, Ralph (2002). Modern Physics (4th ed.). W. H. Freeman & Co. ISBN 0-7167-4345-0.
जर्नल लेख
- Alvager, T.; Farley, F. J. M.; Kjellman, J.; Wallin, L.; et al. (1964). "Test of the Second Postulate of Special Relativity in the GeV region". Physics Letters. 12 (3): 260–262. Bibcode:1964PhL....12..260A. doi:10.1016/0031-9163(64)91095-9.
- Darrigol, Olivier (2004). "The Mystery of the Poincaré–Einstein Connection". Isis. 95 (4): 614–26. doi:10.1086/430652. PMID 16011297. S2CID 26997100.
- Wolf, Peter; Petit, Gerard (1997). "Satellite test of Special Relativity using the Global Positioning System". Physical Review A. 56 (6): 4405–09. Bibcode:1997PhRvA..56.4405W. doi:10.1103/PhysRevA.56.4405.
- विशेष सापेक्षता स्कॉलरपीडिया
- Rindler, Wolfgang (2011). "Special relativity: Kinematics". Scholarpedia. 6 (2): 8520. Bibcode:2011SchpJ...6.8520R. doi:10.4249/scholarpedia.8520.
बाहरी संबंध
मूल कार्य
- मूविंग बॉडीज के इलेक्ट्रोडायनामिक्स पर आइंस्टीन का मूल काम जर्मन में, भौतिकी के इतिहास , बर्नो 1905
- मूविंग बॉडीज के इलेक्ट्रोडायनामिक्स पर 1923 की किताब द प्रिंसिपल ऑफ रिलेटिविटी में प्रकाशित अंग्रेजी स्थानांतरण।
सामान्य दर्शकों के लिए विशेष सापेक्षता (गणितीय ज्ञान की आवश्यकता नहीं)
- आइंस्टीन लाइट एक पुरस्कार- जीत, गैर-तकनीकी परिचय (फिल्म क्लिप और प्रदर्शन) गणित के साथ या बिना स्तरों पर आगे के स्पष्टीकरण और एनिमेशन के दर्जनों पृष्ठों द्वारा समर्थित।
- आइंस्टीन ऑनलाइन मैक्स प्लैंक इंस्टीट्यूट फॉर ग्रेविटेशनल फिजिक्स से सापेक्षता सिद्धांत का परिचय।
- ऑडियो: केन/गे (2006) - Astronomy Cast। आइंस्टीन की विशेष सापेक्षता का सिद्धांत
विशेष सापेक्षता की व्याख्या (सरल या अधिक उन्नत गणित का उपयोग करके)
- बौंडी के-कैलकुलस - सापेक्षता के विशेष सिद्धांत का एक सरल परिचय।
- ग्रेग ईगन की नींव।
- विशेष सापेक्षता पर हॉग नोट्स कलन का उपयोग करते हुए स्नातक स्तर पर विशेष सापेक्षता का एक अच्छा परिचय।
- सापेक्षता कैलकुलेटर: विशेष सापेक्षता - के लिए एक बीजीय और अभिन्न कलन व्युत्पत्ति E = mc2.
- MathPages - Rellections on Relativity एक व्यापक ग्रंथ सूची के साथ सापेक्षता पर एक पूर्ण ऑनलाइन पुस्तक।
- विशेष सापेक्षता स्नातक स्तर पर विशेष सापेक्षता का परिचय।
- Relativity: the Special and General Theory at Project Gutenbergअल्बर्ट आइंस्टीन द्वारा
- स्पेशल रिलेटिविटी लेक्चर नोट्स वर्जीनिया पॉलिटेक्निक इंस्टीट्यूट और स्टेट यूनिवर्सिटी से ड्रॉइंग और स्पेसटाइम डायग्राम के आधार पर विशेष सापेक्षता के लिए एक मानक परिचय है।
- विशेष सापेक्षता को समझना आसानी से समझने योग्य तरीके से विशेष सापेक्षता का सिद्धांत।
- सापेक्षता के विशेष सिद्धांत का एक परिचय (1964) रॉबर्ट काट्ज़ द्वारा, एक परिचय ... जो किसी भी छात्र के लिए सुलभ है, जिसका सामान्य परिचय है भौतिकी और कलन के साथ कुछ मामूली परिचित (130 पीपी; पीडीएफ प्रारूप)।
- विशेष सापेक्षता पर व्याख्यान नोट्स भौतिकी मैक्वेरी विश्वविद्यालय के जे डी क्रेसर विभाग द्वारा।
- SpecialRelativity.net - विज़ुअलाइज़ेशन और न्यूनतम गणित के साथ एक सिंहावलोकन।
- सापेक्षता 4-एवर? सुपरल्यूमिनल मोशन की समस्या पर मनोरंजक तरीके से चर्चा की गई है।
विज़ुअलाइज़ेशन
- रेट्रेसिंग स्पेशल रिलेटिविटी सॉफ्टवेयर विशेष सापेक्षता के प्रभाव में कई परिदृश्यों की कल्पना करता है।
- रियल टाइम रिलेटिविटी ऑस्ट्रेलियन नेशनल यूनिवर्सिटी। एक संवादात्मक कार्यक्रम के माध्यम से अनुभव किए गए सापेक्ष दृश्य प्रभाव।
- Spacetime travel सापेक्षतावादी गति से लेकर ब्लैक होल तक, सापेक्षतावादी प्रभावों के विभिन्न प्रकार के दृश्यावलोकन।
- आइंस्टीन की आंखों के माध्यम से ऑस्ट्रेलियाई राष्ट्रीय विश्वविद्यालय। फिल्मों और छवियों के साथ सापेक्षतावादी दृश्य प्रभावों की व्याख्या की गई।
- ताना विशेष सापेक्षता सिम्युलेटर प्रकाश की गति के करीब यात्रा करने के प्रभावों को दिखाने के लिए एक कंप्यूटर प्रोग्राम।
- Animation clip on YouTube लोरेंत्ज़ परिवर्तन की कल्पना करना।
- ओरिजिनल इंटरएक्टिव फ्लैश एनिमेशन लोरेंत्ज़ और गैलीलियन सीमा रेखा, ट्रेन और टनल पैराडॉक्स, ट्विन पैराडॉक्स, वेव प्रोपेगेशन, क्लॉक सिंक्रोनाइज़ेशन का चित्रण करते हुए जॉन डी पिलिस से, आदि।
- lightspeed एक ओपनजीएल-आधारित प्रोग्राम जिसे चलती वस्तुओं की उपस्थिति पर विशेष सापेक्षता के प्रभावों को स्पष्ट करने के लिए विकसित किया गया है।
- एनिमेशन पृथ्वी के पास के तारे दिखा रहा है, जैसा कि यहां से देखा जा सकता है एक अंतरिक्ष यान तेजी से प्रकाश की गति में तेजी ला रहा है।
श्रेणी:विशेष सापेक्षता
श्रेणी:अल्बर्ट आइंस्टीन