माइक्रोकैनोनिकल एन्सेम्बल: Difference between revisions
No edit summary |
No edit summary |
||
| (8 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
{{Short description|Ensemble of states with an exactly specified total energy}} | {{Short description|Ensemble of states with an exactly specified total energy}} | ||
{{Statistical mechanics|cTopic=Ensembles}} | {{Statistical mechanics|cTopic=Ensembles}} | ||
[[सांख्यिकीय यांत्रिकी]] में, माइक्रोकैनोनिकल | [[सांख्यिकीय यांत्रिकी]] में, '''माइक्रोकैनोनिकल एन्सेम्बल''' [[सांख्यिकीय पहनावा (गणितीय भौतिकी)|सांख्यिकीय एन्सेम्बल (गणितीय भौतिकी)]] है जो यांत्रिक प्रणाली की संभावित अवस्थाओं का प्रतिनिधित्व करता है जिसकी कुल ऊर्जा बिल्कुल निर्दिष्ट होती है।<ref name="gibbs">{{cite book |last=Gibbs |first=Josiah Willard |author-link=Josiah Willard Gibbs |title=सांख्यिकीय यांत्रिकी में प्राथमिक सिद्धांत|year=1902 |publisher=[[Charles Scribner's Sons]] |location=New York|title-link=सांख्यिकीय यांत्रिकी में प्राथमिक सिद्धांत}}</ref> प्रणाली को इस अर्थ में अलग-थलग माना जाता है कि यह अपने पर्यावरण के साथ ऊर्जा या कणों का आदान-प्रदान नहीं कर सकता है, ताकि (ऊर्जा के संरक्षण से) प्रणाली की ऊर्जा समय के साथ न बदले। | ||
माइक्रोकैनोनिकल | माइक्रोकैनोनिकल एन्सेम्बल के प्राथमिक मैक्रोस्कोपिक चर प्रणाली में कणों की कुल संख्या हैं (प्रतीक: {{math|''N''}}), प्रणाली का वॉल्यूम (प्रतीक: {{math|''V''}}), साथ ही प्रणाली में कुल ऊर्जा (प्रतीक: {{math|''E''}}). इनमें से प्रत्येक को एन्सेम्बल में स्थिर माना जाता है। इस कारण से, माइक्रोकैनोनिकल एन्सेम्बल को कभी-कभी {{math|''NVE''}} एन्सेम्बल कहा जाता है। | ||
सरल शब्दों में, प्रत्येक [[माइक्रोस्टेट (सांख्यिकीय यांत्रिकी)]] के लिए समान संभावना निर्दिष्ट करके माइक्रोकैनोनिकल | सरल शब्दों में, प्रत्येक [[माइक्रोस्टेट (सांख्यिकीय यांत्रिकी)]] के लिए समान संभावना निर्दिष्ट करके माइक्रोकैनोनिकल एन्सेम्बल परिभाषित किया जाता है, जिसकी ऊर्जा {{math|''E''}} एक सीमा के अन्दर आती है अन्य सभी माइक्रोस्टेट्स को शून्य की संभावना दी जाती है। चूंकि प्रायिकताओं को 1 तक जोड़ना चाहिए, प्रायिकता {{math|''P''}} ऊर्जा की सीमा के अन्दर माइक्रोस्टेट्स {{math|''W''}} की संख्या का व्युत्क्रम है। | ||
:<math>P = 1/W,</math> | :<math>P = 1/W,</math> | ||
ऊर्जा की सीमा तब तक चौड़ाई में कम हो जाती है जब तक कि यह असीम रूप से संकीर्ण न हो जाए, फिर भी केंद्रित हो {{math|''E''}}. इस प्रक्रिया की [[सीमा (गणित)]] में, माइक्रोकैनोनिकल | ऊर्जा की सीमा तब तक चौड़ाई में कम हो जाती है जब तक कि यह असीम रूप से संकीर्ण न हो जाए, फिर भी केंद्रित हो {{math|''E''}}. इस प्रक्रिया की [[सीमा (गणित)]] में, माइक्रोकैनोनिकल एन्सेम्बल प्राप्त होता है।<ref name="gibbs"/> | ||
== प्रयोज्यता == | == प्रयोज्यता == | ||
संतुलन सांख्यिकीय यांत्रिकी (विशेष रूप से उदासीनता के सिद्धांत) की प्राथमिक मान्यताओं के साथ इसके संबंध के कारण, माइक्रोकैनोनिकल | संतुलन सांख्यिकीय यांत्रिकी (विशेष रूप से उदासीनता के सिद्धांत) की प्राथमिक मान्यताओं के साथ इसके संबंध के कारण, माइक्रोकैनोनिकल एन्सेम्बल सिद्धांत में महत्वपूर्ण वैचारिक निर्माण खंड है।<ref name="Balescu1975">{{Citation|last1=Balescu|first1=Radu|author-link=Radu Bălescu|title=Equilibrium and Nonequilibrium Statistical Mechanics|publisher=John Wiley & Sons|year=1975|isbn=978-0-471-04600-4}}</ref> इसे कभी-कभी संतुलन सांख्यिकीय यांत्रिकी का मूलभूत वितरण माना जाता है। यह कुछ संख्यात्मक अनुप्रयोगों में भी उपयोगी है, जैसे [[आणविक गतिकी]]।<ref name="PearsonHalicioglu1985">{{cite journal|last1=Pearson|first1=Eric M.|last2=Halicioglu|first2=Timur|last3=Tiller|first3=William A.|title=शास्त्रीय माइक्रोकैनोनिकल पहनावा से थर्मोडायनामिक समीकरणों को प्राप्त करने के लिए लाप्लास-रूपांतरण तकनीक|journal=Physical Review A|volume=32|issue=5|year=1985|pages=3030–3039|issn=0556-2791|doi=10.1103/PhysRevA.32.3030|pmid=9896445 |bibcode=1985PhRvA..32.3030P }}</ref><ref name="Lustig1994">{{cite journal|last1=Lustig|first1=Rolf|title=शास्त्रीय आणविक गतिकी पहनावा में सांख्यिकीय ऊष्मप्रवैगिकी। मैं बुनियादी बातों|journal=The Journal of Chemical Physics|volume=100|issue=4|year=1994|pages=3048–3059|issn=0021-9606|doi=10.1063/1.466446|bibcode=1994JChPh.100.3048L }}</ref> दूसरी ओर, अधिकांश गैर-तुच्छ प्रणालियाँ माइक्रोकैनोनिकल एन्सेम्बल में वर्णन करने के लिए गणितीय रूप से बोझिल हैं, और एंट्रॉपी और तापमान की परिभाषाओं के बारे में भी अस्पष्टताएँ हैं। इन कारणों से, सैद्धांतिक गणना के लिए अधिकांशत अन्य एन्सेम्बल पसंद किया जाता है।<ref name="Balescu1975" /><ref name="Hill1986">{{cite book|title=सांख्यिकीय ऊष्मप्रवैगिकी का एक परिचय|first=Terrell L.|last=Hill|publisher=Dover Publications|year=1986|isbn=978-0-486-65242-9}}</ref><ref>{{cite book|title=सांख्यिकीय यांत्रिकी|first=Kerson|last=Huang|publisher=John Wiley & Sons|year=1967}}</ref> | ||
वास्तविक दुनिया प्रणालियों के लिए माइक्रोकैनोनिकल | वास्तविक दुनिया प्रणालियों के लिए माइक्रोकैनोनिकल एन्सेम्बल की प्रयोज्यता ऊर्जा के उतार-चढ़ाव के महत्व पर निर्भर करती है, जो प्रणाली और उसके पर्यावरण के साथ-साथ प्रणाली को तैयार करने में अनियंत्रित कारकों के बीच बातचीत का परिणाम हो सकता है। सामान्यतः, उतार-चढ़ाव नगण्य होते हैं यदि कोई प्रणाली मैक्रोस्कोपिक रूप से बड़ी होती है, या यदि यह ठीक-ठीक ज्ञात ऊर्जा के साथ निर्मित होती है और उसके बाद अपने पर्यावरण से निकट अलगाव में बनी रहती है।<ref name="HilbertHänggi2014"><nowiki>{{cite journal|last1=Hilbert|first1=Stefan|last2=Hänggi|first2=Peter|last3=Dunkel|first3=Jörn|title=पृथक प्रणालियों में थर्मोडायनामिक कानून|journal=Physical Review E|volume=90|issue=6|year=2014|page=062116 |issn=1539-3755|doi=10.1103/PhysRevE.90.062116|pmid=25615053 |arxiv=1408.5382 |bibcode=2014PhRvE..90f2116H |hdl=1721.1/92269|s2cid=5365820 |hdl-access=free}</nowiki></ref> ऐसे स्थितियों में माइक्रोकैनोनिकल एन्सेम्बल प्रयुक्त होता है। अन्यथा, अलग-अलग पहनावे अधिक उपयुक्त हैं - जैसे कि [[विहित पहनावा|विहित एन्सेम्बल]] (उतार-चढ़ाव वाली ऊर्जा) या [[भव्य विहित पहनावा|भव्य विहित एन्सेम्बल]] (उतार-चढ़ाव वाली ऊर्जा और कण संख्या)। | ||
== गुण == | == गुण == | ||
=== थर्मोडायनामिक मात्रा === | === थर्मोडायनामिक मात्रा === | ||
माइक्रोकैनोनिकल | माइक्रोकैनोनिकल एन्सेम्बल की मौलिक [[थर्मोडायनामिक क्षमता]] [[एन्ट्रापी]] है। कम से कम तीन संभावित परिभाषाएँ हैं, जिनमें से प्रत्येक को चरण आयतन फलन {{math|''v''(''E'')}} के संदर्भ में दिया गया है ''',''' जो इससे कम ऊर्जा वाले स्थिति की कुल संख्या की गणना करता है। {{math|''E''}} ({{math|''v''}} की गणितीय परिभाषा के लिए समेकन अनुभाग के लिए सही व्यंजक देखें | ||
{{unordered list | {{unordered list | ||
| 1 = the [[Boltzmann entropy]]<ref group=note>{{math|''S''<sub>B</sub>}} is the [[information entropy]], or [[Gibbs entropy]], for the specific case of the microcanonical ensemble. Note that it depends on the energy width {{math|''ω''}}.</ref> | | 1 = the [[Boltzmann entropy]]<ref group=note>{{math|''S''<sub>B</sub>}} is the [[information entropy]], or [[Gibbs entropy]], for the specific case of the microcanonical ensemble. Note that it depends on the energy width {{math|''ω''}}.</ref> | ||
| Line 32: | Line 30: | ||
}} | }} | ||
माइक्रोकैनोनिकल | माइक्रोकैनोनिकल एन्सेम्बल में, तापमान बाहरी नियंत्रण पैरामीटर के अतिरिक्त व्युत्पन्न मात्रा है। इसे ऊर्जा के संबंध में चुनी गई एन्ट्रापी के व्युत्पन्न के रूप में परिभाषित किया गया है।<ref>{{cite web |title=माइक्रोकैनोनिकल एनसेंबल|url=https://chem.libretexts.org/Bookshelves/Physical_and_Theoretical_Chemistry_Textbook_Maps/Supplemental_Modules_(Physical_and_Theoretical_Chemistry)/Statistical_Mechanics/Advanced_Statistical_Mechanics/Liouville's_Theorem%2C_non-Hamiltonian_systems%2C_the_microcanonical_ensemble/Equilibrium_ensembles/The_Microcanonical_Ensemble |website=chem.libretexts|access-date=3 May 2020}}</ref> उदाहरण के लिए, कोई तापमान {{math|''T<sub>v</sub>''}} और {{math|''T<sub>s</sub>''}} को निम्नलिखित नुसार परिभाषित कर सकता है। | ||
:<math>1/T_v = dS_v/dE,</math> | :<math>1/T_v = dS_v/dE,</math> | ||
:<math>1/T_s = dS_s/dE = dS_\text{B}/dE.</math> | :<math>1/T_s = dS_s/dE = dS_\text{B}/dE.</math> | ||
एंट्रॉपी की तरह, माइक्रोकैनोनिकल समेकन में तापमान को समझने के कई विधियाँ हैं। अधिक सामान्यतः, इन समेकन-आधारित परिभाषाओं और उनके थर्मोडायनामिक समकक्षों के बीच पत्राचार विशेष रूप से परिमित प्रणालियों के लिए सही नहीं है। | एंट्रॉपी की तरह, माइक्रोकैनोनिकल समेकन में तापमान को समझने के कई विधियाँ हैं। अधिक सामान्यतः, इन समेकन-आधारित परिभाषाओं और उनके थर्मोडायनामिक समकक्षों के बीच पत्राचार विशेष रूप से परिमित प्रणालियों के लिए सही नहीं है। | ||
माइक्रोकैनोनिकल दबाव और रासायनिक क्षमता द्वारा दिया जाता | माइक्रोकैनोनिकल दबाव और रासायनिक क्षमता द्वारा दिया जाता है।<ref>{{cite book|title=सांख्यिकीय ऊष्मप्रवैगिकी का एक परिचय|first=Terrell L.|last=Hill|publisher=Dover Publications|year=1986|isbn=978-0-486-65242-9}}</ref> | ||
:<math> \frac{p}{T}=\frac{\partial S}{\partial V}; \qquad \frac{\mu}{T}=-\frac{\partial S}{\partial N}</math> | :<math> \frac{p}{T}=\frac{\partial S}{\partial V}; \qquad \frac{\mu}{T}=-\frac{\partial S}{\partial N}</math> | ||
=== [[चरण संक्रमण]] === | === [[चरण संक्रमण]] === | ||
उनकी सख्त परिभाषा के अंतर्गत, चरण संक्रमण थर्मोडायनामिक क्षमता या इसके डेरिवेटिव में [[विश्लेषणात्मक कार्य]] व्यवहार के अनुरूप होते हैं।<ref name="Goldenfeld">[[Nigel Goldenfeld]]; ''Lectures on Phase Transitions and the Renormalization Group'', Frontiers in Physics 85, Westview Press (June, 1992) {{ISBN|0-201-55409-7}}</ref> इस परिभाषा का उपयोग करते हुए, माइक्रोकैनोनिकल | उनकी सख्त परिभाषा के अंतर्गत, चरण संक्रमण थर्मोडायनामिक क्षमता या इसके डेरिवेटिव में [[विश्लेषणात्मक कार्य]] व्यवहार के अनुरूप होते हैं।<ref name="Goldenfeld">[[Nigel Goldenfeld]]; ''Lectures on Phase Transitions and the Renormalization Group'', Frontiers in Physics 85, Westview Press (June, 1992) {{ISBN|0-201-55409-7}}</ref> इस परिभाषा का उपयोग करते हुए, माइक्रोकैनोनिकल एन्सेम्बल में चरण संक्रमण किसी भी आकार की प्रणालियों में हो सकता है। यह कैनोनिकल और ग्रैंड कैनोनिकल एनसेंबल के साथ विरोधाभासी है, जिसके लिए चरण संक्रमण केवल [[थर्मोडायनामिक सीमा]] में ही हो सकता है- यानी, असीम रूप से स्वतंत्रता के कई डिग्री वाले प्रणाली में।<ref name="Goldenfeld"/><ref name="DunkelHilbert2006">{{cite journal|last1=Dunkel|first1=Jörn|last2=Hilbert|first2=Stefan|title=Phase transitions in small systems: Microcanonical vs. canonical ensembles|journal=Physica A: Statistical Mechanics and Its Applications|volume=370|issue=2|year=2006|pages=390–406|issn=0378-4371|doi=10.1016/j.physa.2006.05.018|arxiv=cond-mat/0511501|bibcode=2006PhyA..370..390D |s2cid=13900006 }}</ref> सामान्यतः, कैनोनिकल या ग्रैंड कैनोनिकल समेकन को परिभाषित करने वाले जलाशय उतार-चढ़ाव पेश करते हैं जो परिमित प्रणालियों की मुक्त ऊर्जा में किसी भी गैर-विश्लेषणात्मक व्यवहार को सुगम बनाते हैं। यह चौरसाई प्रभाव सामान्यतः मैक्रोस्कोपिक प्रणालियों में नगण्य होता है, जो पर्याप्त रूप से बड़े होते हैं कि मुक्त ऊर्जा गैर-विश्लेषणात्मक व्यवहार को बहुत अच्छी तरह से अनुमानित कर सकती है। चूंकि, छोटी प्रणालियों के सैद्धांतिक विश्लेषण में एन्सेम्बल में तकनीकी अंतर महत्वपूर्ण हो सकता है।<ref name="DunkelHilbert2006"/> | ||
=== सूचना एन्ट्रॉपी === | === सूचना एन्ट्रॉपी === | ||
किसी दिए गए मैकेनिकल प्रणाली के लिए (फिक्स्ड {{math|''N''}}, {{math|''V''}}) और दी गई ऊर्जा की सीमा, संभाव्यता का समान वितरण {{math|''P''}} माइक्रोस्टेट्स पर (माइक्रोकैनोनिकल | किसी दिए गए मैकेनिकल प्रणाली के लिए (फिक्स्ड {{math|''N''}}, {{math|''V''}}) और दी गई ऊर्जा की सीमा, संभाव्यता का समान वितरण {{math|''P''}} माइक्रोस्टेट्स पर (माइक्रोकैनोनिकल एन्सेम्बल के रूप में) एन्सेम्बल औसत को अधिकतम {{math|−⟨log ''P''⟩}}.<ref name="gibbs"/> करता है। | ||
== थर्मोडायनामिक उपमाएँ == | == थर्मोडायनामिक उपमाएँ == | ||
[[लुडविग बोल्ट्जमैन]] द्वारा सांख्यिकीय यांत्रिकी में प्रारंभिक कार्य ने दी गई कुल ऊर्जा की प्रणाली के लिए अपने [[बोल्ट्जमैन एंट्रॉपी फॉर्मूला]] का नेतृत्व किया, {{math|''S'' {{=}} ''k'' log ''W''}}, जहाँ {{math|''W''}} उस ऊर्जा पर प्रणाली द्वारा सुलभ विभिन्न स्थितियों की संख्या है। आदर्श गैस के विशेष स्थितियों के अतिरिक्त, बोल्ट्जमैन ने इस बात पर बहुत गहराई से विस्तार नहीं किया कि वास्तव में प्रणाली के अलग-अलग स्थितियों के सेट का गठन क्या होता है। इस विषय की जांच [[योशिय्याह विलार्ड गिब्स]] द्वारा पूरी करने के लिए की गई थी जिन्होंने मनमाना यांत्रिक प्रणालियों के लिए सामान्यीकृत सांख्यिकीय यांत्रिकी विकसित की थी, और इस लेख में वर्णित माइक्रोकैनोनिकल | [[लुडविग बोल्ट्जमैन]] द्वारा सांख्यिकीय यांत्रिकी में प्रारंभिक कार्य ने दी गई कुल ऊर्जा की प्रणाली के लिए अपने [[बोल्ट्जमैन एंट्रॉपी फॉर्मूला]] का नेतृत्व किया, {{math|''S'' {{=}} ''k'' log ''W''}}, जहाँ {{math|''W''}} उस ऊर्जा पर प्रणाली द्वारा सुलभ विभिन्न स्थितियों की संख्या है। आदर्श गैस के विशेष स्थितियों के अतिरिक्त, बोल्ट्जमैन ने इस बात पर बहुत गहराई से विस्तार नहीं किया कि वास्तव में प्रणाली के अलग-अलग स्थितियों के सेट का गठन क्या होता है। इस विषय की जांच [[योशिय्याह विलार्ड गिब्स]] द्वारा पूरी करने के लिए की गई थी जिन्होंने मनमाना यांत्रिक प्रणालियों के लिए सामान्यीकृत सांख्यिकीय यांत्रिकी विकसित की थी, और इस लेख में वर्णित माइक्रोकैनोनिकल एन्सेम्बल को परिभाषित किया था।<ref name="gibbs"/> गिब्स ने माइक्रोकैनोनिकल एन्सेम्बल और ऊष्मप्रवैगिकी के बीच समानता की सावधानीपूर्वक जांच की, विशेष रूप से वे स्वतंत्रता की कुछ डिग्री की प्रणालियों के स्थितियों में कैसे टूटते हैं। उन्होंने माइक्रोकैनोनिकल एन्ट्रापी की दो और परिभाषाएँ प्रस्तुत कीं जो निर्भर नहीं करती हैं {{math|''ω''}} - ऊपर वर्णित मात्रा और सतह एन्ट्रॉपी। (ध्यान दें कि सतह एन्ट्रापी केवल बोल्ट्जमैन एंट्रॉपी से भिन्न होती है {{math|''ω''}}-निर्भर ऑफसेट है।) | ||
वॉल्यूम एन्ट्रापी {{math|''S''<sub>v</sub>}} और संबद्ध {{math|''T''<sub>v</sub>}} थर्मोडायनामिक एंट्रॉपी और तापमान के समीप सादृश्य बनाते हैं। ठीक वैसा ही दिखाना संभव | वॉल्यूम एन्ट्रापी {{math|''S''<sub>v</sub>}} और संबद्ध {{math|''T''<sub>v</sub>}} थर्मोडायनामिक एंट्रॉपी और तापमान के समीप सादृश्य बनाते हैं। ठीक वैसा ही दिखाना संभव है। | ||
:<math>dE = T_{\rm v} dS_{\rm v} - \langle P\rangle dV,</math> | :<math>dE = T_{\rm v} dS_{\rm v} - \langle P\rangle dV,</math> | ||
({{math|⟨''P''⟩}} | ({{math|⟨''P''⟩}} एन्सेम्बल औसत दबाव है) जैसा कि ऊष्मप्रवैगिकी के पहले नियम के लिए अपेक्षित है। सतह (बोल्ट्ज़मैन) एन्ट्रापी और उससे जुड़े {{math|''T''<sub>s</sub>}}, के लिए समान समीकरण पाया जा सकता है इस समीकरण में दबाव जटिल मात्रा है जिसका औसत दबाव से कोई संबंध नहीं है।<ref name="gibbs"/> | ||
माइक्रोकैनोनिकल {{math|''T''<sub>v</sub>}} और {{math|''T''<sub>s</sub>}} तापमान के अनुरूप पूरी तरह से संतोषजनक नहीं हैं। ऊष्मप्रवैगिकी सीमा के बाहर, कई कलाकृतियाँ होती हैं। | माइक्रोकैनोनिकल {{math|''T''<sub>v</sub>}} और {{math|''T''<sub>s</sub>}} तापमान के अनुरूप पूरी तरह से संतोषजनक नहीं हैं। ऊष्मप्रवैगिकी सीमा के बाहर, कई कलाकृतियाँ होती हैं। | ||
* दो प्रणालियों के संयोजन का गैर-तुच्छ परिणाम: दो प्रणालियां, जिनमें से प्रत्येक स्वतंत्र माइक्रोकैनोनिकल | * दो प्रणालियों के संयोजन का गैर-तुच्छ परिणाम: दो प्रणालियां, जिनमें से प्रत्येक स्वतंत्र माइक्रोकैनोनिकल एन्सेम्बल द्वारा वर्णित है, को थर्मल संपर्क में लाया जा सकता है और संयुक्त प्रणाली में संतुलित करने की अनुमति दी जा सकती है जिसे माइक्रोकैनोनिकल एन्सेम्बल द्वारा वर्णित किया गया है। दुर्भाग्य से, प्रारंभिक ''T'''s <nowiki/>के आधार पर दो प्रणालियों के बीच ऊर्जा प्रवाह की भविष्यवाणी नहीं की जा सकती है यहां तक कि जब प्रारंभिक मूल्यों से'''''<nowiki/>''''' अलग है। यह अंतर्ज्ञान का खंडन करता है कि तापमान गहन मात्रा होना चाहिए, और दो समान <nowiki/>तापमान प्रणालियों को थर्मल संपर्क में लाकर अप्रभावित होना चाहिए।<ref name="gibbs"/> | ||
** कुछ-कण प्रणालियों के लिए अजीब व्यवहार: कई परिणाम जैसे कि माइक्रोकैनोनिकल [[समविभाजन प्रमेय]] | ** कुछ-कण प्रणालियों के लिए अजीब व्यवहार: कई परिणाम जैसे कि माइक्रोकैनोनिकल [[समविभाजन प्रमेय]] {{math|''T''<sub>s</sub>}} एक- या दो-डिग्री की स्वतंत्रता ऑफसेट प्राप्त करते हैं, जब इसके संदर्भ में लिखा जाता है '''{{math|''T''<sub>s</sub>}}.''' छोटे प्रणाली के लिए यह ऑफ़सेट महत्वपूर्ण है, और इसलिए यदि हम {{math|''S''<sub>s</sub>}} को एन्ट्रापी के अनुरूप बनाते है तो, स्वतंत्रता की केवल एक या दो डिग्री वाले प्रणाली के लिए कई अपवादों की आवश्यकता होती है।<ref name="gibbs" /> | ||
*नकली नकारात्मक तापमान: नकारात्मक {{math|''T''<sub>s</sub>}} होता है कुछ प्रणालियों में स्थितियों का घनत्व ऊर्जा में [[मोनोटोनिक फ़ंक्शन|मोनोटोनिक फलन]] नहीं है, और इसी तरह ऊर्जा बढ़ने पर {{math|''T''<sub>s</sub>}} कई बार संकेत बदल सकता है।<ref>{{cite journal|arxiv=1304.2066|author1=Jörn Dunkel|author2=Stefan Hilbert|title=असंगत थर्मोस्टैटिस्टिक्स और नकारात्मक पूर्ण तापमान|year=2013|doi=10.1038/nphys2815|volume=10|issue=1|journal=Nature Physics|pages=67–72|bibcode=2014NatPh..10...67D|s2cid=16757018 }}</ref><ref>See further references at https://sites.google.com/site/entropysurfaceorvolume/</ref> | *नकली नकारात्मक तापमान: नकारात्मक {{math|''T''<sub>s</sub>}} होता है कुछ प्रणालियों में स्थितियों का घनत्व ऊर्जा में [[मोनोटोनिक फ़ंक्शन|मोनोटोनिक फलन]] नहीं है, और इसी तरह ऊर्जा बढ़ने पर {{math|''T''<sub>s</sub>}} कई बार संकेत बदल सकता है।<ref>{{cite journal|arxiv=1304.2066|author1=Jörn Dunkel|author2=Stefan Hilbert|title=असंगत थर्मोस्टैटिस्टिक्स और नकारात्मक पूर्ण तापमान|year=2013|doi=10.1038/nphys2815|volume=10|issue=1|journal=Nature Physics|pages=67–72|bibcode=2014NatPh..10...67D|s2cid=16757018 }}</ref><ref>See further references at https://sites.google.com/site/entropysurfaceorvolume/</ref> | ||
इन समस्याओं का पसंदीदा समाधान माइक्रोकैनोनिकल | इन समस्याओं का पसंदीदा समाधान माइक्रोकैनोनिकल एन्सेम्बल के उपयोग से बचना है। कई यथार्थवादी स्थितियों में प्रणाली को ताप स्नान के लिए थर्मोस्टेट किया जाता है ताकि ऊर्जा ठीक से ज्ञात न हो। फिर, अधिक सही विवरण विहित एन्सेम्बल या भव्य विहित एन्सेम्बल है, दोनों का ऊष्मप्रवैगिकी के साथ पूर्ण पत्राचार है।<ref name="tolman">{{cite book | last=Tolman |first=R. C. | year=1938 | title=सांख्यिकीय यांत्रिकी के सिद्धांत| publisher=[[Oxford University Press]]}}</ref> | ||
== कलाकारों की टुकड़ी के लिए सही | == कलाकारों की टुकड़ी के लिए सही अभिव्यक्तियाँ == | ||
सांख्यिकीय समुच्चय के लिए सही गणितीय अभिव्यक्ति विचाराधीन यांत्रिकी के प्रकार पर निर्भर करती है - क्वांटम या शास्त्रीय - क्योंकि इन दो स्थितियों में माइक्रोस्टेट की धारणा काफी भिन्न होती है। क्वांटम यांत्रिकी में, मैट्रिक्स विकर्णीकरण विशिष्ट ऊर्जाओं के साथ माइक्रोस्टेट (सांख्यिकीय यांत्रिकी) का असतत सेट प्रदान करता है। शास्त्रीय यांत्रिक स्थितियों में इसके अतिरिक्त विहित [[चरण स्थान]] पर अभिन्न अंग सम्मिलित है, और चरण स्थान में माइक्रोस्टेट्स के आकार को कुछ हद तक मनमाने ढंग से चुना जा सकता है। | सांख्यिकीय समुच्चय के लिए सही गणितीय अभिव्यक्ति विचाराधीन यांत्रिकी के प्रकार पर निर्भर करती है - क्वांटम या शास्त्रीय - क्योंकि इन दो स्थितियों में माइक्रोस्टेट की धारणा काफी भिन्न होती है। क्वांटम यांत्रिकी में, मैट्रिक्स विकर्णीकरण विशिष्ट ऊर्जाओं के साथ माइक्रोस्टेट (सांख्यिकीय यांत्रिकी) का असतत सेट प्रदान करता है। शास्त्रीय यांत्रिक स्थितियों में इसके अतिरिक्त विहित [[चरण स्थान]] पर अभिन्न अंग सम्मिलित है, और चरण स्थान में माइक्रोस्टेट्स के आकार को कुछ हद तक मनमाने ढंग से चुना जा सकता है। | ||
| Line 98: | Line 96: | ||
{{details|topic=क्वांटम यांत्रिकी में पहनावा का प्रतिनिधित्व|सांख्यिकीय पहनावा (गणितीय भौतिकी)}} | {{details|topic=क्वांटम यांत्रिकी में पहनावा का प्रतिनिधित्व|सांख्यिकीय पहनावा (गणितीय भौतिकी)}} | ||
क्वांटम यांत्रिकी में सांख्यिकीय | क्वांटम यांत्रिकी में सांख्यिकीय एन्सेम्बल [[घनत्व मैट्रिक्स]] द्वारा दर्शाया जाता है, जिसे निरूपित किया जाता है <math>\hat\rho</math>. प्रणाली की [[स्थिर अवस्था]] और ऊर्जा आइजन मूल्य के संदर्भ में, माइक्रोकैनोनिकल एनसेंबल को ब्रा-केट नोटेशन का उपयोग करके लिखा जा सकता है। ऊर्जा आइजन स्टेट्स का पूरा आधार दिया {{math|{{!}}''ψ''<sub>''i''</sub>⟩}}, द्वारा अनुक्रमित {{math|''i''}}, माइक्रोकैनोनिकल एन्सेम्बल है। | ||
:<math>\hat\rho = \frac{1}{W} \sum_i f\left(\tfrac{H_i - E}{\omega}\right) |\psi_i\rangle \langle \psi_i |,</math> | :<math>\hat\rho = \frac{1}{W} \sum_i f\left(\tfrac{H_i - E}{\omega}\right) |\psi_i\rangle \langle \psi_i |,</math> | ||
जहां {{math|''H''<sub>''i''</sub>}} द्वारा निर्धारित ऊर्जा आइजन मूल्य हैं <math>\hat H |\psi_i\rangle = H_i |\psi_i\rangle</math> (यहाँ {{math|''Ĥ''}} प्रणाली का कुल ऊर्जा संचालन है, i. '''ई।,''' [[हैमिल्टनियन (क्वांटम यांत्रिकी)]])। का मान है {{math|''W''}} की मांग करके निर्धारित किया जाता है <math>\hat\rho</math> सामान्यीकृत घनत्व मैट्रिक्स है, और इसलिए | जहां {{math|''H''<sub>''i''</sub>}} द्वारा निर्धारित ऊर्जा आइजन मूल्य हैं <math>\hat H |\psi_i\rangle = H_i |\psi_i\rangle</math> (यहाँ {{math|''Ĥ''}} प्रणाली का कुल ऊर्जा संचालन है, i. '''ई।,''' [[हैमिल्टनियन (क्वांटम यांत्रिकी)]])। का मान है {{math|''W''}} की मांग करके निर्धारित किया जाता है <math>\hat\rho</math> सामान्यीकृत घनत्व मैट्रिक्स है, और इसलिए | ||
:<math>W = \sum_i f\left(\tfrac{H_i - E}{\omega}\right).</math> | :<math>W = \sum_i f\left(\tfrac{H_i - E}{\omega}\right).</math> | ||
अवस्था आयतन फलन (एन्ट्रापी की गणना करने के लिए प्रयुक्त) किसके द्वारा दिया जाता | अवस्था आयतन फलन (एन्ट्रापी की गणना करने के लिए प्रयुक्त) किसके द्वारा दिया जाता है। | ||
:<math>v(E) = \sum_{H_i < E} 1.</math> | :<math>v(E) = \sum_{H_i < E} 1.</math> | ||
माइक्रोकैनोनिकल | माइक्रोकैनोनिकल एन्सेम्बल घनत्व मैट्रिक्स की सीमा को ले कर परिभाषित किया जाता है क्योंकि ऊर्जा की चौड़ाई शून्य हो जाती है, चूंकि ऊर्जा की चौड़ाई ऊर्जा स्तरों के बीच की दूरी से कम हो जाने पर समस्याग्रस्त स्थिति उत्पन्न होती है। बहुत कम ऊर्जा चौड़ाई के लिए, अधिकांश मूल्यों के लिए एन्सेम्बल बिल्कुल भी उपस्थित नहीं है {{math|''E''}}, क्योंकि कोई भी स्थिति सीमा के अन्दर नहीं आता है। जब एन्सेम्बल उपस्थित होता है, तो इसमें सामान्यतः केवल (क्रेमर्स प्रमेय) अवस्थाएँ होती हैं, क्योंकि जटिल प्रणाली में ऊर्जा का स्तर केवल दुर्घटना के बराबर होता है (इस बिंदु पर अधिक चर्चा के लिए [[यादृच्छिक मैट्रिक्स सिद्धांत]] देखें)। इसके अतिरिक्त, स्थिति-मात्रा फलन भी असतत वृद्धि में ही बढ़ता है, और इसलिए इसका व्युत्पन्न केवल कभी अनंत या शून्य होता है, जिससे स्थितियों की घनत्व को परिभाषित करना मुश्किल हो जाता है। इस समस्या को ऊर्जा सीमा को पूरी तरह से शून्य तक नहीं ले जाने और स्थिति-मात्रा फलन को सुचारू बनाने से हल किया जा सकता है, चूंकि यह एन्सेम्बल की परिभाषा को और अधिक जटिल बना देता है, क्योंकि यह तब आवश्यक हो जाता है जब अन्य चर (एक साथ) के अतिरिक्त ऊर्जा सीमा निर्दिष्ट करने के लिए , {{math|''NVEω''}} एन्सेम्बल) है। | ||
=== शास्त्रीय यांत्रिक === | === शास्त्रीय यांत्रिक === | ||
| Line 129: | Line 127: | ||
{{details|topic=शास्त्रीय यांत्रिकी में पहनावा का प्रतिनिधित्व|सांख्यिकीय पहनावा (गणितीय भौतिकी)}} | {{details|topic=शास्त्रीय यांत्रिकी में पहनावा का प्रतिनिधित्व|सांख्यिकीय पहनावा (गणितीय भौतिकी)}} | ||
शास्त्रीय यांत्रिकी में, | शास्त्रीय यांत्रिकी में, एन्सेम्बल संयुक्त संभाव्यता घनत्व फलन द्वारा दर्शाया जाता है {{math|''ρ''(''p''<sub>1</sub>, … ''p''<sub>''n''</sub>, ''q''<sub>1</sub>, … ''q''<sub>''n''</sub>)}} प्रणाली के चरण स्थान पर परिभाषित।<ref name="gibbs"/> चरण स्थान है {{math|''n''}} [[सामान्यीकृत निर्देशांक]] कहा जाता है {{math|''q''<sub>1</sub>, … ''q''<sub>''n''</sub>}}, और {{math|''n''}} संबंधित [[विहित गति]] कहा जाता है। {{math|''p''<sub>1</sub>, … ''p''<sub>''n''</sub>}}. | ||
माइक्रोकैनोनिकल | माइक्रोकैनोनिकल एन्सेम्बल के लिए प्रायिकता घनत्व फलन है: | ||
:<math>\rho = \frac{1}{h^n C} \frac{1}{W} f(\tfrac{H-E}{\omega}),</math> | :<math>\rho = \frac{1}{h^n C} \frac{1}{W} f(\tfrac{H-E}{\omega}),</math> | ||
जहाँ | जहाँ | ||
* {{math|''H''}} प्रणाली की कुल ऊर्जा ([[हैमिल्टनियन यांत्रिकी]]) है, चरण का कार्य {{math|(''p''<sub>1</sub>, … ''q''<sub>''n''</sub>)}}, | * {{math|''H''}} प्रणाली की कुल ऊर्जा ([[हैमिल्टनियन यांत्रिकी]]) है, चरण का कार्य {{math|(''p''<sub>1</sub>, … ''q''<sub>''n''</sub>)}}, | ||
* {{math|''h''}} ऊर्जा × समय की इकाइयों के साथ मनमाना लेकिन पूर्व निर्धारित स्थिरांक है जो माइक्रोस्टेट की सीमा निर्धारित करता है और | * {{math|''h''}} ऊर्जा × समय की इकाइयों के साथ मनमाना लेकिन पूर्व निर्धारित स्थिरांक है जो माइक्रोस्टेट की सीमा निर्धारित करता है और {{math|''ρ''}} सही आयाम प्रदान करता है.<ref group=note>(Historical note) Gibbs' original ensemble effectively set {{math|''h'' {{=}} 1 [energy unit]×[time unit]}}, leading to unit-dependence in the values of some thermodynamic quantities like entropy and chemical potential. Since the advent of quantum mechanics, {{math|''h''}} is often taken to be equal to [[Planck's constant]] in order to obtain a semiclassical correspondence with quantum mechanics.</ref> | ||
* {{math|''C''}} अतिगणना सुधार कारक है, जो अधिकांशत कण प्रणालियों के लिए उपयोग किया जाता है जहां समान कण एक दूसरे के साथ जगह बदलने में सक्षम होते हैं।<ref group=note>In a system of {{math|''N''}} identical particles, {{math|''C'' {{=}} ''N''!}} ([[factorial]] of {{math|''N''}}). This factor corrects the overcounting in phase space due to identical physical states being found in multiple locations. See the [[Statistical ensemble (mathematical physics)#Correcting overcounting in phase space|statistical ensemble]] article for more information on this overcounting.</ref> | * {{math|''C''}} अतिगणना सुधार कारक है, जो अधिकांशत कण प्रणालियों के लिए उपयोग किया जाता है जहां समान कण एक दूसरे के साथ जगह बदलने में सक्षम होते हैं।<ref group=note>In a system of {{math|''N''}} identical particles, {{math|''C'' {{=}} ''N''!}} ([[factorial]] of {{math|''N''}}). This factor corrects the overcounting in phase space due to identical physical states being found in multiple locations. See the [[Statistical ensemble (mathematical physics)#Correcting overcounting in phase space|statistical ensemble]] article for more information on this overcounting.</ref> | ||
फिर से, का मूल्य {{math|''W''}} की मांग करके निर्धारित किया जाता है {{math|''ρ''}} सामान्यीकृत प्रायिकता घनत्व फलन है: | फिर से, का मूल्य {{math|''W''}} की मांग करके निर्धारित किया जाता है {{math|''ρ''}} सामान्यीकृत प्रायिकता घनत्व फलन है: | ||
:<math>W = \int \ldots \int \frac{1}{h^n C} f(\tfrac{H-E}{\omega}) \, dp_1 \ldots dq_n </math> | :<math>W = \int \ldots \int \frac{1}{h^n C} f(\tfrac{H-E}{\omega}) \, dp_1 \ldots dq_n </math> | ||
यह इंटीग्रल पूरे फेज स्पेस पर ले लिया जाता है। अवस्था आयतन फलन (एन्ट्रॉपी की गणना के लिए प्रयुक्त) किसके द्वारा परिभाषित किया जाता | यह इंटीग्रल पूरे फेज स्पेस पर ले लिया जाता है। अवस्था आयतन फलन (एन्ट्रॉपी की गणना के लिए प्रयुक्त) किसके द्वारा परिभाषित किया जाता है। | ||
:<math>v(E) = \int \ldots \int_{H < E} \frac{1}{h^n C} \, dp_1 \ldots dq_n .</math> | :<math>v(E) = \int \ldots \int_{H < E} \frac{1}{h^n C} \, dp_1 \ldots dq_n .</math> | ||
ऊर्जा चौड़ाई के रूप में {{math|''ω''}} को शून्य पर ले जाया जाता है, का मान {{math|''W''}} के अनुपात में घटता है {{math|''ω''}} जैसा {{math|''W'' {{=}} ''ω'' (''dv''/''dE'')}}. | ऊर्जा चौड़ाई के रूप में {{math|''ω''}} को शून्य पर ले जाया जाता है, का मान {{math|''W''}} के अनुपात में घटता है {{math|''ω''}} जैसा {{math|''W'' {{=}} ''ω'' (''dv''/''dE'')}}. | ||
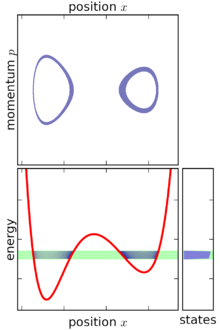
उपरोक्त परिभाषा के आधार पर, माइक्रोकैनोनिकल | उपरोक्त परिभाषा के आधार पर, माइक्रोकैनोनिकल एन्सेम्बल को स्थिर-ऊर्जा सतह पर केंद्रित चरण अंतरिक्ष में असीम रूप से पतले खोल के रूप में देखा जा सकता है। चूंकि माइक्रोकैनोनिकल एन्सेम्बल इस सतह तक ही सीमित है, यह आवश्यक रूप से उस सतह पर समान रूप से वितरित नहीं है: यदि चरण स्थान में ऊर्जा का ढाल भिन्न होता है, तो माइक्रोकैनोनिकल एन्सेम्बल दूसरों की तुलना में सतह के कुछ भागों में अधिक मोटा (अधिक केंद्रित) होता है। यह सुविधा आवश्यक होने का अपरिहार्य परिणाम है कि माइक्रोकैनोनिकल एन्सेम्बल स्थिर-अवस्था का एन्सेम्बल है। | ||
== उदाहरण == | == उदाहरण == | ||
===आदर्श गैस=== | ===आदर्श गैस=== | ||
माइक्रोकैनोनिकल | माइक्रोकैनोनिकल एन्सेम्बल में मौलिक मात्रा है <math>W(E, V, N)</math>, जो दिए गए के साथ संगत चरण स्थान की मात्रा के बराबर है <math>(E, V, N)</math>. से <math>W</math>, सभी थर्मोडायनामिक मात्राओं की गणना की जा सकती है। [[आदर्श गैस]] के लिए, ऊर्जा कणों की स्थिति से स्वतंत्र होती है, जो इसलिए कारक का योगदान करती है <math>V^N</math> को <math>W</math>. संवेग, इसके विपरीत, एक के लिए विवश हैं <math>3N</math>-आयामी [[एन-क्षेत्र|n-क्षेत्र]] (हाइपर-) त्रिज्या का गोलाकार खोल <math>\sqrt{2mE}</math>; उनका योगदान इस खोल की सतह के आयतन के बराबर है। के लिए परिणामी अभिव्यक्ति <math>W</math> है:<ref name="Kardar2007">{{cite book|title=कणों का सांख्यिकीय भौतिकी|first=Mehran|last=Kardar|author-link=Mehran Kardar|publisher=Cambridge University Press|year=2007|isbn=978-0-521-87342-0|pages=105–109}}</ref> | ||
:<math> | :<math> | ||
W = \frac{V^N}{N!} \frac{2\pi^{3N/2}}{\Gamma(3N/2)}\left(2mE\right)^{(3N-1)/2} | W = \frac{V^N}{N!} \frac{2\pi^{3N/2}}{\Gamma(3N/2)}\left(2mE\right)^{(3N-1)/2} | ||
</math> | </math> | ||
जहाँ <math> \Gamma(.) </math> [[गामा समारोह|गामा फलन]] और कारक है <math>N!</math> [[समान कण]] के लिए खाते में सम्मिलित किया गया है ([[गिब्स विरोधाभास]] देखें)। बड़े में <math>N</math> सीमा, बोल्ट्जमान एंट्रॉपी <math>S = k_{\mathrm{B}} \log W</math> | जहाँ <math> \Gamma(.) </math> [[गामा समारोह|गामा फलन]] और कारक है <math>N!</math> [[समान कण]] के लिए खाते में सम्मिलित किया गया है ([[गिब्स विरोधाभास]] देखें)। बड़े में <math>N</math> सीमा, बोल्ट्जमान एंट्रॉपी <math>S = k_{\mathrm{B}} \log W</math> है। | ||
:<math> | :<math> | ||
S = k_{\rm B} N \log \left[ \frac VN \left(\frac{4\pi m}{3}\frac EN\right)^{3/2}\right]+{\frac 52} k_{\rm B} N + O\left( \log N \right) | S = k_{\rm B} N \log \left[ \frac VN \left(\frac{4\pi m}{3}\frac EN\right)^{3/2}\right]+{\frac 52} k_{\rm B} N + O\left( \log N \right) | ||
| Line 166: | Line 164: | ||
\frac{p}{T} \equiv \frac{\partial S}{\partial V} = \frac{N k_{\mathrm{B}}}{V} \quad \rightarrow \quad pV = N k_{\mathrm{B}} T | \frac{p}{T} \equiv \frac{\partial S}{\partial V} = \frac{N k_{\mathrm{B}}}{V} \quad \rightarrow \quad pV = N k_{\mathrm{B}} T | ||
</math> | </math> | ||
अंत में, [[रासायनिक क्षमता]] <math>\mu</math> | अंत में, [[रासायनिक क्षमता]] <math>\mu</math> है। | ||
:<math> | :<math> | ||
\mu \equiv -T \frac{\partial S}{\partial N} = k_{\rm B} T \log \left[\frac{V}{N} \, \left(\frac{4 \pi m E}{3N} \right)^{3/2} \right] | \mu \equiv -T \frac{\partial S}{\partial N} = k_{\rm B} T \log \left[\frac{V}{N} \, \left(\frac{4 \pi m E}{3N} \right)^{3/2} \right] | ||
| Line 175: | Line 173: | ||
एक समान गुरुत्वाकर्षण क्षेत्र में आदर्श गैस के लिए माइक्रोकैनोनिकल चरण की मात्रा की भी स्पष्ट रूप से गणना की जा सकती है।<ref name="RomanWhite1995">{{cite journal|last1=Roman|first1=F L|last2=White|first2=J A|last3=Velasco|first3=S|title=गुरुत्वाकर्षण क्षेत्र में एक आदर्श गैस के लिए माइक्रोकैनोनिकल एकल-कण वितरण|journal=European Journal of Physics|volume=16|issue=2|year=1995|pages=83–90|issn=0143-0807|doi=10.1088/0143-0807/16/2/008|bibcode=1995EJPh...16...83R |s2cid=250840083 }}</ref> | एक समान गुरुत्वाकर्षण क्षेत्र में आदर्श गैस के लिए माइक्रोकैनोनिकल चरण की मात्रा की भी स्पष्ट रूप से गणना की जा सकती है।<ref name="RomanWhite1995">{{cite journal|last1=Roman|first1=F L|last2=White|first2=J A|last3=Velasco|first3=S|title=गुरुत्वाकर्षण क्षेत्र में एक आदर्श गैस के लिए माइक्रोकैनोनिकल एकल-कण वितरण|journal=European Journal of Physics|volume=16|issue=2|year=1995|pages=83–90|issn=0143-0807|doi=10.1088/0143-0807/16/2/008|bibcode=1995EJPh...16...83R |s2cid=250840083 }}</ref> | ||
'''के''' 3-आयामी आदर्श गैस के लिए परिणाम नीचे दिए गए हैं <math>N</math> कण, प्रत्येक द्रव्यमान के साथ <math>m</math>, ऊष्मीय रूप से पृथक कंटेनर में सीमित है जो कि z-दिशा में असीम रूप से लंबा है और निरंतर पार-अनुभागीय क्षेत्र है <math>A</math>. माना जाता है कि गुरुत्वाकर्षण क्षेत्र ताकत के साथ माइनस z दिशा में कार्य करता है <math>g</math>. चरण मात्रा <math>W(E, N)</math> | '''के''' 3-आयामी आदर्श गैस के लिए परिणाम नीचे दिए गए हैं <math>N</math> कण, प्रत्येक द्रव्यमान के साथ <math>m</math>, ऊष्मीय रूप से पृथक कंटेनर में सीमित है जो कि z-दिशा में असीम रूप से लंबा है और निरंतर पार-अनुभागीय क्षेत्र है <math>A</math>. माना जाता है कि गुरुत्वाकर्षण क्षेत्र ताकत के साथ माइनस z दिशा में कार्य करता है <math>g</math>. चरण मात्रा <math>W(E, N)</math> है। | ||
:<math> | :<math> | ||
W(E, N) = \frac{(2 \pi)^{3N/2}A^{N}m^{N/2}}{g^N \Gamma(5N/2)} E^{\frac{5N}{2}-1} | W(E, N) = \frac{(2 \pi)^{3N/2}A^{N}m^{N/2}}{g^N \Gamma(5N/2)} E^{\frac{5N}{2}-1} | ||
| Line 185: | Line 183: | ||
\rho(z) = \left(\frac{5N}{2} - 1 \right) \frac{mg}{E}\left(1 - \frac{mgz}{E} \right)^{\frac{5N}{2}-2} | \rho(z) = \left(\frac{5N}{2} - 1 \right) \frac{mg}{E}\left(1 - \frac{mgz}{E} \right)^{\frac{5N}{2}-2} | ||
</math> | </math> | ||
इसी प्रकार, वेग परिमाण का वितरण <math>|\vec{v}|</math> (सभी ऊंचाइयों पर औसत) | इसी प्रकार, वेग परिमाण का वितरण <math>|\vec{v}|</math> (सभी ऊंचाइयों पर औसत) है। | ||
:<math> | :<math> | ||
f(|\vec{v}|) = \frac{\Gamma(5N/2)}{\Gamma(3/2)\Gamma(5N/2-3/2)} \times \frac{m^{3/2}|\vec{v}|^{2}}{2^{1/2}E^{3/2}} \times \left(1 - \frac{m |\vec{v}|^{2}}{2 E} \right)^{\frac{5(N-1)}{2}} | f(|\vec{v}|) = \frac{\Gamma(5N/2)}{\Gamma(3/2)\Gamma(5N/2-3/2)} \times \frac{m^{3/2}|\vec{v}|^{2}}{2^{1/2}E^{3/2}} \times \left(1 - \frac{m |\vec{v}|^{2}}{2 E} \right)^{\frac{5(N-1)}{2}} | ||
</math> | </math> | ||
कैनोनिकल समेकन में इन समीकरणों के अनुरूप क्रमशः [[बैरोमीटर का सूत्र]] और मैक्सवेल-बोल्टज़मान वितरण हैं। सीमा में <math>N \rightarrow \infty</math>, माइक्रोकैनोनिकल और कैनन का भाव मेल खाते हैं; चूंकि, वे परिमित के लिए भिन्न हैं <math>N</math>. विशेष रूप से, माइक्रोकैनोनिकल | कैनोनिकल समेकन में इन समीकरणों के अनुरूप क्रमशः [[बैरोमीटर का सूत्र]] और मैक्सवेल-बोल्टज़मान वितरण हैं। सीमा में <math>N \rightarrow \infty</math>, माइक्रोकैनोनिकल और कैनन का भाव मेल खाते हैं; चूंकि, वे परिमित के लिए भिन्न हैं <math>N</math>. विशेष रूप से, माइक्रोकैनोनिकल एन्सेम्बल में, स्थिति और वेग सांख्यिकीय रूप से स्वतंत्र नहीं होते हैं। परिणामस्वरूप, गतिज तापमान, निश्चित मात्रा में औसत गतिज ऊर्जा के रूप में परिभाषित किया गया <math>A \, dz</math>, पूरे कंटेनर में असमान है: | ||
:<math> | :<math> | ||
T_{\mathrm{kinetic}} = \frac{3 E}{5 N - 2}\left(1 - \frac{mgz}{E} \right) | T_{\mathrm{kinetic}} = \frac{3 E}{5 N - 2}\left(1 - \frac{mgz}{E} \right) | ||
</math> | </math> | ||
इसके विपरीत, किसी भी के लिए कैनोनिकल | इसके विपरीत, किसी भी के लिए कैनोनिकल एन्सेम्बल में तापमान समान <math>N</math> है।<ref name="VelascoRomán1996">{{cite journal|last1=Velasco|first1=S|last2=Román|first2=F L|last3=White|first3=J A|title=एक गुरुत्वाकर्षण क्षेत्र में एक आदर्श गैस के तापमान वितरण से संबंधित एक विरोधाभास पर|journal=European Journal of Physics|volume=17|issue=1|year=1996|pages=43–44|issn=0143-0807|doi=10.1088/0143-0807/17/1/008|s2cid=250885860}}</ref> | ||
== यह भी देखें == | == यह भी देखें == | ||
| Line 208: | Line 206: | ||
{{Statistical mechanics topics}} | {{Statistical mechanics topics}} | ||
[[Category: | [[Category:Articles with hatnote templates targeting a nonexistent page]] | ||
[[Category:Collapse templates]] | |||
[[Category:Created On 31/03/2023]] | [[Category:Created On 31/03/2023]] | ||
[[Category:Lua-based templates]] | |||
[[Category:Machine Translated Page]] | |||
[[Category:Navigational boxes| ]] | |||
[[Category:Navigational boxes without horizontal lists]] | |||
[[Category:Pages with script errors]] | |||
[[Category:Short description with empty Wikidata description]] | |||
[[Category:Sidebars with styles needing conversion]] | |||
[[Category:Template documentation pages|Documentation/doc]] | |||
[[Category:Templates Translated in Hindi]] | |||
[[Category:Templates Vigyan Ready]] | |||
[[Category:Templates generating microformats]] | |||
[[Category:Templates that add a tracking category]] | |||
[[Category:Templates that are not mobile friendly]] | |||
[[Category:Templates that generate short descriptions]] | |||
[[Category:Templates using TemplateData]] | |||
[[Category:Wikipedia metatemplates]] | |||
[[Category:सांख्यिकीय पहनावा]] | |||
Latest revision as of 11:57, 25 September 2023
| Statistical mechanics |
|---|
 |
सांख्यिकीय यांत्रिकी में, माइक्रोकैनोनिकल एन्सेम्बल सांख्यिकीय एन्सेम्बल (गणितीय भौतिकी) है जो यांत्रिक प्रणाली की संभावित अवस्थाओं का प्रतिनिधित्व करता है जिसकी कुल ऊर्जा बिल्कुल निर्दिष्ट होती है।[1] प्रणाली को इस अर्थ में अलग-थलग माना जाता है कि यह अपने पर्यावरण के साथ ऊर्जा या कणों का आदान-प्रदान नहीं कर सकता है, ताकि (ऊर्जा के संरक्षण से) प्रणाली की ऊर्जा समय के साथ न बदले।
माइक्रोकैनोनिकल एन्सेम्बल के प्राथमिक मैक्रोस्कोपिक चर प्रणाली में कणों की कुल संख्या हैं (प्रतीक: N), प्रणाली का वॉल्यूम (प्रतीक: V), साथ ही प्रणाली में कुल ऊर्जा (प्रतीक: E). इनमें से प्रत्येक को एन्सेम्बल में स्थिर माना जाता है। इस कारण से, माइक्रोकैनोनिकल एन्सेम्बल को कभी-कभी NVE एन्सेम्बल कहा जाता है।
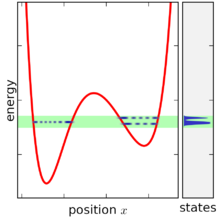
सरल शब्दों में, प्रत्येक माइक्रोस्टेट (सांख्यिकीय यांत्रिकी) के लिए समान संभावना निर्दिष्ट करके माइक्रोकैनोनिकल एन्सेम्बल परिभाषित किया जाता है, जिसकी ऊर्जा E एक सीमा के अन्दर आती है अन्य सभी माइक्रोस्टेट्स को शून्य की संभावना दी जाती है। चूंकि प्रायिकताओं को 1 तक जोड़ना चाहिए, प्रायिकता P ऊर्जा की सीमा के अन्दर माइक्रोस्टेट्स W की संख्या का व्युत्क्रम है।
ऊर्जा की सीमा तब तक चौड़ाई में कम हो जाती है जब तक कि यह असीम रूप से संकीर्ण न हो जाए, फिर भी केंद्रित हो E. इस प्रक्रिया की सीमा (गणित) में, माइक्रोकैनोनिकल एन्सेम्बल प्राप्त होता है।[1]
प्रयोज्यता
संतुलन सांख्यिकीय यांत्रिकी (विशेष रूप से उदासीनता के सिद्धांत) की प्राथमिक मान्यताओं के साथ इसके संबंध के कारण, माइक्रोकैनोनिकल एन्सेम्बल सिद्धांत में महत्वपूर्ण वैचारिक निर्माण खंड है।[2] इसे कभी-कभी संतुलन सांख्यिकीय यांत्रिकी का मूलभूत वितरण माना जाता है। यह कुछ संख्यात्मक अनुप्रयोगों में भी उपयोगी है, जैसे आणविक गतिकी।[3][4] दूसरी ओर, अधिकांश गैर-तुच्छ प्रणालियाँ माइक्रोकैनोनिकल एन्सेम्बल में वर्णन करने के लिए गणितीय रूप से बोझिल हैं, और एंट्रॉपी और तापमान की परिभाषाओं के बारे में भी अस्पष्टताएँ हैं। इन कारणों से, सैद्धांतिक गणना के लिए अधिकांशत अन्य एन्सेम्बल पसंद किया जाता है।[2][5][6]
वास्तविक दुनिया प्रणालियों के लिए माइक्रोकैनोनिकल एन्सेम्बल की प्रयोज्यता ऊर्जा के उतार-चढ़ाव के महत्व पर निर्भर करती है, जो प्रणाली और उसके पर्यावरण के साथ-साथ प्रणाली को तैयार करने में अनियंत्रित कारकों के बीच बातचीत का परिणाम हो सकता है। सामान्यतः, उतार-चढ़ाव नगण्य होते हैं यदि कोई प्रणाली मैक्रोस्कोपिक रूप से बड़ी होती है, या यदि यह ठीक-ठीक ज्ञात ऊर्जा के साथ निर्मित होती है और उसके बाद अपने पर्यावरण से निकट अलगाव में बनी रहती है।[7] ऐसे स्थितियों में माइक्रोकैनोनिकल एन्सेम्बल प्रयुक्त होता है। अन्यथा, अलग-अलग पहनावे अधिक उपयुक्त हैं - जैसे कि विहित एन्सेम्बल (उतार-चढ़ाव वाली ऊर्जा) या भव्य विहित एन्सेम्बल (उतार-चढ़ाव वाली ऊर्जा और कण संख्या)।
गुण
थर्मोडायनामिक मात्रा
माइक्रोकैनोनिकल एन्सेम्बल की मौलिक थर्मोडायनामिक क्षमता एन्ट्रापी है। कम से कम तीन संभावित परिभाषाएँ हैं, जिनमें से प्रत्येक को चरण आयतन फलन v(E) के संदर्भ में दिया गया है , जो इससे कम ऊर्जा वाले स्थिति की कुल संख्या की गणना करता है। E (v की गणितीय परिभाषा के लिए समेकन अनुभाग के लिए सही व्यंजक देखें
- the Boltzmann entropy[note 1]
- the 'volume entropy'
- the 'surface entropy'
माइक्रोकैनोनिकल एन्सेम्बल में, तापमान बाहरी नियंत्रण पैरामीटर के अतिरिक्त व्युत्पन्न मात्रा है। इसे ऊर्जा के संबंध में चुनी गई एन्ट्रापी के व्युत्पन्न के रूप में परिभाषित किया गया है।[8] उदाहरण के लिए, कोई तापमान Tv और Ts को निम्नलिखित नुसार परिभाषित कर सकता है।
एंट्रॉपी की तरह, माइक्रोकैनोनिकल समेकन में तापमान को समझने के कई विधियाँ हैं। अधिक सामान्यतः, इन समेकन-आधारित परिभाषाओं और उनके थर्मोडायनामिक समकक्षों के बीच पत्राचार विशेष रूप से परिमित प्रणालियों के लिए सही नहीं है।
माइक्रोकैनोनिकल दबाव और रासायनिक क्षमता द्वारा दिया जाता है।[9]
चरण संक्रमण
उनकी सख्त परिभाषा के अंतर्गत, चरण संक्रमण थर्मोडायनामिक क्षमता या इसके डेरिवेटिव में विश्लेषणात्मक कार्य व्यवहार के अनुरूप होते हैं।[10] इस परिभाषा का उपयोग करते हुए, माइक्रोकैनोनिकल एन्सेम्बल में चरण संक्रमण किसी भी आकार की प्रणालियों में हो सकता है। यह कैनोनिकल और ग्रैंड कैनोनिकल एनसेंबल के साथ विरोधाभासी है, जिसके लिए चरण संक्रमण केवल थर्मोडायनामिक सीमा में ही हो सकता है- यानी, असीम रूप से स्वतंत्रता के कई डिग्री वाले प्रणाली में।[10][11] सामान्यतः, कैनोनिकल या ग्रैंड कैनोनिकल समेकन को परिभाषित करने वाले जलाशय उतार-चढ़ाव पेश करते हैं जो परिमित प्रणालियों की मुक्त ऊर्जा में किसी भी गैर-विश्लेषणात्मक व्यवहार को सुगम बनाते हैं। यह चौरसाई प्रभाव सामान्यतः मैक्रोस्कोपिक प्रणालियों में नगण्य होता है, जो पर्याप्त रूप से बड़े होते हैं कि मुक्त ऊर्जा गैर-विश्लेषणात्मक व्यवहार को बहुत अच्छी तरह से अनुमानित कर सकती है। चूंकि, छोटी प्रणालियों के सैद्धांतिक विश्लेषण में एन्सेम्बल में तकनीकी अंतर महत्वपूर्ण हो सकता है।[11]
सूचना एन्ट्रॉपी
किसी दिए गए मैकेनिकल प्रणाली के लिए (फिक्स्ड N, V) और दी गई ऊर्जा की सीमा, संभाव्यता का समान वितरण P माइक्रोस्टेट्स पर (माइक्रोकैनोनिकल एन्सेम्बल के रूप में) एन्सेम्बल औसत को अधिकतम −⟨log P⟩.[1] करता है।
थर्मोडायनामिक उपमाएँ
लुडविग बोल्ट्जमैन द्वारा सांख्यिकीय यांत्रिकी में प्रारंभिक कार्य ने दी गई कुल ऊर्जा की प्रणाली के लिए अपने बोल्ट्जमैन एंट्रॉपी फॉर्मूला का नेतृत्व किया, S = k log W, जहाँ W उस ऊर्जा पर प्रणाली द्वारा सुलभ विभिन्न स्थितियों की संख्या है। आदर्श गैस के विशेष स्थितियों के अतिरिक्त, बोल्ट्जमैन ने इस बात पर बहुत गहराई से विस्तार नहीं किया कि वास्तव में प्रणाली के अलग-अलग स्थितियों के सेट का गठन क्या होता है। इस विषय की जांच योशिय्याह विलार्ड गिब्स द्वारा पूरी करने के लिए की गई थी जिन्होंने मनमाना यांत्रिक प्रणालियों के लिए सामान्यीकृत सांख्यिकीय यांत्रिकी विकसित की थी, और इस लेख में वर्णित माइक्रोकैनोनिकल एन्सेम्बल को परिभाषित किया था।[1] गिब्स ने माइक्रोकैनोनिकल एन्सेम्बल और ऊष्मप्रवैगिकी के बीच समानता की सावधानीपूर्वक जांच की, विशेष रूप से वे स्वतंत्रता की कुछ डिग्री की प्रणालियों के स्थितियों में कैसे टूटते हैं। उन्होंने माइक्रोकैनोनिकल एन्ट्रापी की दो और परिभाषाएँ प्रस्तुत कीं जो निर्भर नहीं करती हैं ω - ऊपर वर्णित मात्रा और सतह एन्ट्रॉपी। (ध्यान दें कि सतह एन्ट्रापी केवल बोल्ट्जमैन एंट्रॉपी से भिन्न होती है ω-निर्भर ऑफसेट है।)
वॉल्यूम एन्ट्रापी Sv और संबद्ध Tv थर्मोडायनामिक एंट्रॉपी और तापमान के समीप सादृश्य बनाते हैं। ठीक वैसा ही दिखाना संभव है।
(⟨P⟩ एन्सेम्बल औसत दबाव है) जैसा कि ऊष्मप्रवैगिकी के पहले नियम के लिए अपेक्षित है। सतह (बोल्ट्ज़मैन) एन्ट्रापी और उससे जुड़े Ts, के लिए समान समीकरण पाया जा सकता है इस समीकरण में दबाव जटिल मात्रा है जिसका औसत दबाव से कोई संबंध नहीं है।[1]
माइक्रोकैनोनिकल Tv और Ts तापमान के अनुरूप पूरी तरह से संतोषजनक नहीं हैं। ऊष्मप्रवैगिकी सीमा के बाहर, कई कलाकृतियाँ होती हैं।
- दो प्रणालियों के संयोजन का गैर-तुच्छ परिणाम: दो प्रणालियां, जिनमें से प्रत्येक स्वतंत्र माइक्रोकैनोनिकल एन्सेम्बल द्वारा वर्णित है, को थर्मल संपर्क में लाया जा सकता है और संयुक्त प्रणाली में संतुलित करने की अनुमति दी जा सकती है जिसे माइक्रोकैनोनिकल एन्सेम्बल द्वारा वर्णित किया गया है। दुर्भाग्य से, प्रारंभिक T's के आधार पर दो प्रणालियों के बीच ऊर्जा प्रवाह की भविष्यवाणी नहीं की जा सकती है यहां तक कि जब प्रारंभिक मूल्यों से अलग है। यह अंतर्ज्ञान का खंडन करता है कि तापमान गहन मात्रा होना चाहिए, और दो समान तापमान प्रणालियों को थर्मल संपर्क में लाकर अप्रभावित होना चाहिए।[1]
- कुछ-कण प्रणालियों के लिए अजीब व्यवहार: कई परिणाम जैसे कि माइक्रोकैनोनिकल समविभाजन प्रमेय Ts एक- या दो-डिग्री की स्वतंत्रता ऑफसेट प्राप्त करते हैं, जब इसके संदर्भ में लिखा जाता है Ts. छोटे प्रणाली के लिए यह ऑफ़सेट महत्वपूर्ण है, और इसलिए यदि हम Ss को एन्ट्रापी के अनुरूप बनाते है तो, स्वतंत्रता की केवल एक या दो डिग्री वाले प्रणाली के लिए कई अपवादों की आवश्यकता होती है।[1]
- नकली नकारात्मक तापमान: नकारात्मक Ts होता है कुछ प्रणालियों में स्थितियों का घनत्व ऊर्जा में मोनोटोनिक फलन नहीं है, और इसी तरह ऊर्जा बढ़ने पर Ts कई बार संकेत बदल सकता है।[12][13]
इन समस्याओं का पसंदीदा समाधान माइक्रोकैनोनिकल एन्सेम्बल के उपयोग से बचना है। कई यथार्थवादी स्थितियों में प्रणाली को ताप स्नान के लिए थर्मोस्टेट किया जाता है ताकि ऊर्जा ठीक से ज्ञात न हो। फिर, अधिक सही विवरण विहित एन्सेम्बल या भव्य विहित एन्सेम्बल है, दोनों का ऊष्मप्रवैगिकी के साथ पूर्ण पत्राचार है।[14]
कलाकारों की टुकड़ी के लिए सही अभिव्यक्तियाँ
सांख्यिकीय समुच्चय के लिए सही गणितीय अभिव्यक्ति विचाराधीन यांत्रिकी के प्रकार पर निर्भर करती है - क्वांटम या शास्त्रीय - क्योंकि इन दो स्थितियों में माइक्रोस्टेट की धारणा काफी भिन्न होती है। क्वांटम यांत्रिकी में, मैट्रिक्स विकर्णीकरण विशिष्ट ऊर्जाओं के साथ माइक्रोस्टेट (सांख्यिकीय यांत्रिकी) का असतत सेट प्रदान करता है। शास्त्रीय यांत्रिक स्थितियों में इसके अतिरिक्त विहित चरण स्थान पर अभिन्न अंग सम्मिलित है, और चरण स्थान में माइक्रोस्टेट्स के आकार को कुछ हद तक मनमाने ढंग से चुना जा सकता है।
माइक्रोकैनोनिकल समेकन का निर्माण करने के लिए, दोनों प्रकार के यांत्रिकी में पहले ऊर्जा की सीमा निर्दिष्ट करना आवश्यक है। फलन के नीचे के भावों में (का फलन H, शिखर पर E चौड़ाई के साथ ω) स्थितियों को सम्मिलित करने के लिए ऊर्जा की सीमा का प्रतिनिधित्व करने के लिए उपयोग किया जाएगा। इस फलन का उदाहरण होगा[1]:
या, अधिक सुचारू रूप से,
क्वांटम मैकेनिकल
क्वांटम यांत्रिकी में सांख्यिकीय एन्सेम्बल घनत्व मैट्रिक्स द्वारा दर्शाया जाता है, जिसे निरूपित किया जाता है . प्रणाली की स्थिर अवस्था और ऊर्जा आइजन मूल्य के संदर्भ में, माइक्रोकैनोनिकल एनसेंबल को ब्रा-केट नोटेशन का उपयोग करके लिखा जा सकता है। ऊर्जा आइजन स्टेट्स का पूरा आधार दिया |ψi⟩, द्वारा अनुक्रमित i, माइक्रोकैनोनिकल एन्सेम्बल है।
जहां Hi द्वारा निर्धारित ऊर्जा आइजन मूल्य हैं (यहाँ Ĥ प्रणाली का कुल ऊर्जा संचालन है, i. ई।, हैमिल्टनियन (क्वांटम यांत्रिकी))। का मान है W की मांग करके निर्धारित किया जाता है सामान्यीकृत घनत्व मैट्रिक्स है, और इसलिए
अवस्था आयतन फलन (एन्ट्रापी की गणना करने के लिए प्रयुक्त) किसके द्वारा दिया जाता है।
माइक्रोकैनोनिकल एन्सेम्बल घनत्व मैट्रिक्स की सीमा को ले कर परिभाषित किया जाता है क्योंकि ऊर्जा की चौड़ाई शून्य हो जाती है, चूंकि ऊर्जा की चौड़ाई ऊर्जा स्तरों के बीच की दूरी से कम हो जाने पर समस्याग्रस्त स्थिति उत्पन्न होती है। बहुत कम ऊर्जा चौड़ाई के लिए, अधिकांश मूल्यों के लिए एन्सेम्बल बिल्कुल भी उपस्थित नहीं है E, क्योंकि कोई भी स्थिति सीमा के अन्दर नहीं आता है। जब एन्सेम्बल उपस्थित होता है, तो इसमें सामान्यतः केवल (क्रेमर्स प्रमेय) अवस्थाएँ होती हैं, क्योंकि जटिल प्रणाली में ऊर्जा का स्तर केवल दुर्घटना के बराबर होता है (इस बिंदु पर अधिक चर्चा के लिए यादृच्छिक मैट्रिक्स सिद्धांत देखें)। इसके अतिरिक्त, स्थिति-मात्रा फलन भी असतत वृद्धि में ही बढ़ता है, और इसलिए इसका व्युत्पन्न केवल कभी अनंत या शून्य होता है, जिससे स्थितियों की घनत्व को परिभाषित करना मुश्किल हो जाता है। इस समस्या को ऊर्जा सीमा को पूरी तरह से शून्य तक नहीं ले जाने और स्थिति-मात्रा फलन को सुचारू बनाने से हल किया जा सकता है, चूंकि यह एन्सेम्बल की परिभाषा को और अधिक जटिल बना देता है, क्योंकि यह तब आवश्यक हो जाता है जब अन्य चर (एक साथ) के अतिरिक्त ऊर्जा सीमा निर्दिष्ट करने के लिए , NVEω एन्सेम्बल) है।
शास्त्रीय यांत्रिक
शास्त्रीय यांत्रिकी में, एन्सेम्बल संयुक्त संभाव्यता घनत्व फलन द्वारा दर्शाया जाता है ρ(p1, … pn, q1, … qn) प्रणाली के चरण स्थान पर परिभाषित।[1] चरण स्थान है n सामान्यीकृत निर्देशांक कहा जाता है q1, … qn, और n संबंधित विहित गति कहा जाता है। p1, … pn.
माइक्रोकैनोनिकल एन्सेम्बल के लिए प्रायिकता घनत्व फलन है:
जहाँ
- H प्रणाली की कुल ऊर्जा (हैमिल्टनियन यांत्रिकी) है, चरण का कार्य (p1, … qn),
- h ऊर्जा × समय की इकाइयों के साथ मनमाना लेकिन पूर्व निर्धारित स्थिरांक है जो माइक्रोस्टेट की सीमा निर्धारित करता है और ρ सही आयाम प्रदान करता है.[note 2]
- C अतिगणना सुधार कारक है, जो अधिकांशत कण प्रणालियों के लिए उपयोग किया जाता है जहां समान कण एक दूसरे के साथ जगह बदलने में सक्षम होते हैं।[note 3]
फिर से, का मूल्य W की मांग करके निर्धारित किया जाता है ρ सामान्यीकृत प्रायिकता घनत्व फलन है:
यह इंटीग्रल पूरे फेज स्पेस पर ले लिया जाता है। अवस्था आयतन फलन (एन्ट्रॉपी की गणना के लिए प्रयुक्त) किसके द्वारा परिभाषित किया जाता है।
ऊर्जा चौड़ाई के रूप में ω को शून्य पर ले जाया जाता है, का मान W के अनुपात में घटता है ω जैसा W = ω (dv/dE).
उपरोक्त परिभाषा के आधार पर, माइक्रोकैनोनिकल एन्सेम्बल को स्थिर-ऊर्जा सतह पर केंद्रित चरण अंतरिक्ष में असीम रूप से पतले खोल के रूप में देखा जा सकता है। चूंकि माइक्रोकैनोनिकल एन्सेम्बल इस सतह तक ही सीमित है, यह आवश्यक रूप से उस सतह पर समान रूप से वितरित नहीं है: यदि चरण स्थान में ऊर्जा का ढाल भिन्न होता है, तो माइक्रोकैनोनिकल एन्सेम्बल दूसरों की तुलना में सतह के कुछ भागों में अधिक मोटा (अधिक केंद्रित) होता है। यह सुविधा आवश्यक होने का अपरिहार्य परिणाम है कि माइक्रोकैनोनिकल एन्सेम्बल स्थिर-अवस्था का एन्सेम्बल है।
उदाहरण
आदर्श गैस
माइक्रोकैनोनिकल एन्सेम्बल में मौलिक मात्रा है , जो दिए गए के साथ संगत चरण स्थान की मात्रा के बराबर है . से , सभी थर्मोडायनामिक मात्राओं की गणना की जा सकती है। आदर्श गैस के लिए, ऊर्जा कणों की स्थिति से स्वतंत्र होती है, जो इसलिए कारक का योगदान करती है को . संवेग, इसके विपरीत, एक के लिए विवश हैं -आयामी n-क्षेत्र (हाइपर-) त्रिज्या का गोलाकार खोल ; उनका योगदान इस खोल की सतह के आयतन के बराबर है। के लिए परिणामी अभिव्यक्ति है:[15]
जहाँ गामा फलन और कारक है समान कण के लिए खाते में सम्मिलित किया गया है (गिब्स विरोधाभास देखें)। बड़े में सीमा, बोल्ट्जमान एंट्रॉपी है।
इसे सैकुर-टेट्रोड समीकरण के रूप में भी जाना जाता है।
द्वारा तापमान दिया जाता है
जो गैसों के गतिज सिद्धांत के अनुरूप परिणाम से सहमत है। दबाव की गणना आदर्श गैस नियम देती है:
अंत में, रासायनिक क्षमता है।
एक समान गुरुत्वाकर्षण क्षेत्र में आदर्श गैस
एक समान गुरुत्वाकर्षण क्षेत्र में आदर्श गैस के लिए माइक्रोकैनोनिकल चरण की मात्रा की भी स्पष्ट रूप से गणना की जा सकती है।[16]
के 3-आयामी आदर्श गैस के लिए परिणाम नीचे दिए गए हैं कण, प्रत्येक द्रव्यमान के साथ , ऊष्मीय रूप से पृथक कंटेनर में सीमित है जो कि z-दिशा में असीम रूप से लंबा है और निरंतर पार-अनुभागीय क्षेत्र है . माना जाता है कि गुरुत्वाकर्षण क्षेत्र ताकत के साथ माइनस z दिशा में कार्य करता है . चरण मात्रा है।
जहाँ कुल ऊर्जा, गतिज प्लस गुरुत्वाकर्षण है।
गैस घनत्व ऊंचाई के कार्य के रूप में चरण मात्रा निर्देशांक पर एकीकृत करके प्राप्त किया जा सकता है। परिणाम है:
इसी प्रकार, वेग परिमाण का वितरण (सभी ऊंचाइयों पर औसत) है।
कैनोनिकल समेकन में इन समीकरणों के अनुरूप क्रमशः बैरोमीटर का सूत्र और मैक्सवेल-बोल्टज़मान वितरण हैं। सीमा में , माइक्रोकैनोनिकल और कैनन का भाव मेल खाते हैं; चूंकि, वे परिमित के लिए भिन्न हैं . विशेष रूप से, माइक्रोकैनोनिकल एन्सेम्बल में, स्थिति और वेग सांख्यिकीय रूप से स्वतंत्र नहीं होते हैं। परिणामस्वरूप, गतिज तापमान, निश्चित मात्रा में औसत गतिज ऊर्जा के रूप में परिभाषित किया गया , पूरे कंटेनर में असमान है:
इसके विपरीत, किसी भी के लिए कैनोनिकल एन्सेम्बल में तापमान समान है।[17]
यह भी देखें
- पृथक प्रणाली
- एर्गोडिक परिकल्पना
- लॉस्च्मिड्ट का विरोधाभास
टिप्पणियाँ
- ↑ SB is the information entropy, or Gibbs entropy, for the specific case of the microcanonical ensemble. Note that it depends on the energy width ω.
- ↑ (Historical note) Gibbs' original ensemble effectively set h = 1 [energy unit]×[time unit], leading to unit-dependence in the values of some thermodynamic quantities like entropy and chemical potential. Since the advent of quantum mechanics, h is often taken to be equal to Planck's constant in order to obtain a semiclassical correspondence with quantum mechanics.
- ↑ In a system of N identical particles, C = N! (factorial of N). This factor corrects the overcounting in phase space due to identical physical states being found in multiple locations. See the statistical ensemble article for more information on this overcounting.
संदर्भ
- ↑ 1.0 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 Gibbs, Josiah Willard (1902). सांख्यिकीय यांत्रिकी में प्राथमिक सिद्धांत. New York: Charles Scribner's Sons.
- ↑ 2.0 2.1 Balescu, Radu (1975), Equilibrium and Nonequilibrium Statistical Mechanics, John Wiley & Sons, ISBN 978-0-471-04600-4
- ↑ Pearson, Eric M.; Halicioglu, Timur; Tiller, William A. (1985). "शास्त्रीय माइक्रोकैनोनिकल पहनावा से थर्मोडायनामिक समीकरणों को प्राप्त करने के लिए लाप्लास-रूपांतरण तकनीक". Physical Review A. 32 (5): 3030–3039. Bibcode:1985PhRvA..32.3030P. doi:10.1103/PhysRevA.32.3030. ISSN 0556-2791. PMID 9896445.
- ↑ Lustig, Rolf (1994). "शास्त्रीय आणविक गतिकी पहनावा में सांख्यिकीय ऊष्मप्रवैगिकी। मैं बुनियादी बातों". The Journal of Chemical Physics. 100 (4): 3048–3059. Bibcode:1994JChPh.100.3048L. doi:10.1063/1.466446. ISSN 0021-9606.
- ↑ Hill, Terrell L. (1986). सांख्यिकीय ऊष्मप्रवैगिकी का एक परिचय. Dover Publications. ISBN 978-0-486-65242-9.
- ↑ Huang, Kerson (1967). सांख्यिकीय यांत्रिकी. John Wiley & Sons.
- ↑ {{cite journal|last1=Hilbert|first1=Stefan|last2=Hänggi|first2=Peter|last3=Dunkel|first3=Jörn|title=पृथक प्रणालियों में थर्मोडायनामिक कानून|journal=Physical Review E|volume=90|issue=6|year=2014|page=062116 |issn=1539-3755|doi=10.1103/PhysRevE.90.062116|pmid=25615053 |arxiv=1408.5382 |bibcode=2014PhRvE..90f2116H |hdl=1721.1/92269|s2cid=5365820 |hdl-access=free}
- ↑ "माइक्रोकैनोनिकल एनसेंबल". chem.libretexts. Retrieved 3 May 2020.
- ↑ Hill, Terrell L. (1986). सांख्यिकीय ऊष्मप्रवैगिकी का एक परिचय. Dover Publications. ISBN 978-0-486-65242-9.
- ↑ 10.0 10.1 Nigel Goldenfeld; Lectures on Phase Transitions and the Renormalization Group, Frontiers in Physics 85, Westview Press (June, 1992) ISBN 0-201-55409-7
- ↑ 11.0 11.1 Dunkel, Jörn; Hilbert, Stefan (2006). "Phase transitions in small systems: Microcanonical vs. canonical ensembles". Physica A: Statistical Mechanics and Its Applications. 370 (2): 390–406. arXiv:cond-mat/0511501. Bibcode:2006PhyA..370..390D. doi:10.1016/j.physa.2006.05.018. ISSN 0378-4371. S2CID 13900006.
- ↑ Jörn Dunkel; Stefan Hilbert (2013). "असंगत थर्मोस्टैटिस्टिक्स और नकारात्मक पूर्ण तापमान". Nature Physics. 10 (1): 67–72. arXiv:1304.2066. Bibcode:2014NatPh..10...67D. doi:10.1038/nphys2815. S2CID 16757018.
- ↑ See further references at https://sites.google.com/site/entropysurfaceorvolume/
- ↑ Tolman, R. C. (1938). सांख्यिकीय यांत्रिकी के सिद्धांत. Oxford University Press.
- ↑ Kardar, Mehran (2007). कणों का सांख्यिकीय भौतिकी. Cambridge University Press. pp. 105–109. ISBN 978-0-521-87342-0.
- ↑ Roman, F L; White, J A; Velasco, S (1995). "गुरुत्वाकर्षण क्षेत्र में एक आदर्श गैस के लिए माइक्रोकैनोनिकल एकल-कण वितरण". European Journal of Physics. 16 (2): 83–90. Bibcode:1995EJPh...16...83R. doi:10.1088/0143-0807/16/2/008. ISSN 0143-0807. S2CID 250840083.
- ↑ Velasco, S; Román, F L; White, J A (1996). "एक गुरुत्वाकर्षण क्षेत्र में एक आदर्श गैस के तापमान वितरण से संबंधित एक विरोधाभास पर". European Journal of Physics. 17 (1): 43–44. doi:10.1088/0143-0807/17/1/008. ISSN 0143-0807. S2CID 250885860.