फूरियर रूपांतरण: Difference between revisions
m (12 revisions imported from alpha:फूरियर_रूपांतरण) |
|||
| (One intermediate revision by one other user not shown) | |||
| Line 2,156: | Line 2,156: | ||
[[Category:Pages with math errors|Fourier Transform]] | [[Category:Pages with math errors|Fourier Transform]] | ||
[[Category:Pages with math render errors|Fourier Transform]] | [[Category:Pages with math render errors|Fourier Transform]] | ||
[[Category:Vigyan Ready]] | |||
Latest revision as of 07:42, 17 October 2023

फूरियर रूपांतरण (एफटी) एक गणित का समाकलन रूपांतरण है | जो फलन (गणित) को आवृत्ति घटकों में विघटित करता है | जो आवृत्ति के फलन के रूप में ट्रांसफ़ॉर्म के आउटपुट द्वारा दर्शाए जाते हैं। सामान्यतः समय या स्थान के कार्यों को रूपांतरित किया जाता है | जो क्रमशः आवृत्ति या स्थानिक आवृत्ति के आधार पर एक फलन का उत्पादन करेगा। उस प्रक्रिया को 'विश्लेषण ' भी कहते हैं। एक उदाहरण अनुप्रयोग एक संगीत तार (संगीत) के तरंग को उसके घटक पिच (संगीत) की ध्वनि तीव्रता के संदर्भ में विघटित कर देगा। 'फूरियर रूपांतरण' शब्द आवृत्ति डोमेन प्रतिनिधित्व और संचालन (गणित) दोनों को संदर्भित करता है | जो आवृत्ति डोमेन प्रतिनिधित्व को अंतरिक्ष या समय के कार्य से जोड़ता है।
किसी फलन का फूरियर ट्रांसफ़ॉर्म एक सम्मिश्र-मूल्यवान फलन है | जो यूलर के सूत्र का प्रतिनिधित्व करता है | जिसमें मूल फलन सम्मिलित होता है। प्रत्येक आवृत्ति के लिए, सम्मिश्र संख्या मापांक और तर्क का परिमाण (पूर्ण मान सम्मिश्र संख्या) उस आवृत्ति के साथ एक घटक सम्मिश्र साइन लहर के आयाम का प्रतिनिधित्व करता है, और तर्क (सम्मिश्र विश्लेषण) उस सम्मिश्र साइनसॉइड के चरण ऑफसेट का प्रतिनिधित्व करता है। यदि कोई आवृत्ति उपस्थित नहीं है, तो उस आवृत्ति के लिए रूपांतरण का मान 0 होता है। फूरियर रूपांतरण समय के कार्यों तक ही सीमित नहीं है | किन्तु मूल कार्य के एक कार्य के डोमेन को सामान्यतः समय डोमेन के रूप में संदर्भित किया जाता है। फूरियर व्युत्क्रम प्रमेय एक संश्लेषण प्रक्रिया प्रदान करता है | जो मूल कार्य को उसके आवृत्ति डोमेन प्रतिनिधित्व से पुन: बनाता है।
टाइम डोमेन में स्थानीयकृत कार्यों में फूरियर रूपांतरण होते हैं | जो आवृत्ति डोमेन में फैले होते हैं और इसके विपरीत, एक घटना जिसे अनिश्चितता सिद्धांत के रूप में जाना जाता है। इस सिद्धांत के लिए महत्वपूर्ण बिंदु (गणित) गाऊसी फलन है | संभाव्यता सिद्धांत और सांख्यिकी के साथ-साथ सामान्य वितरण (जैसे, प्रसार ) को प्रदर्शित करने वाली भौतिक घटनाओं के अध्ययन में पर्याप्त महत्व है। गाऊसी फलन का फूरियर रूपांतरण एक अन्य गाऊसी फलन है। जोसेफ फूरियर ने गर्मी हस्तांतरण के अपने अध्ययन में परिवर्तन की प्रारंभ की, जहां गॉसियन कार्य गर्मी समीकरण के समाधान के रूप में दिखाई देते हैं।
फूरियर रूपांतरण को औपचारिक रूप से एक अनुचित इंटीग्रल रीमैन इंटीग्रल के रूप में परिभाषित किया जा सकता है | जिससे यह एक इंटीग्रल ट्रांसफॉर्मेशन बन जाता है, चूँकि यह परिभाषा अधिक परिष्कृत एकीकरण सिद्धांत की आवश्यकता वाले कई अनुप्रयोगों के लिए उपयुक्त नहीं है। उदाहरण के लिए, कई अपेक्षाकृत सरल अनुप्रयोग डिराक डेल्टा फलन का उपयोग करते हैं | जिसे औपचारिक रूप से माना जा सकता है | जैसे कि यह एक फलन था | किन्तु औचित्य के लिए गणितीय रूप से अधिक परिष्कृत दृष्टिकोण की आवश्यकता होती है।
यूक्लिडियन अंतरिक्ष पर कई चर के कार्यों के लिए फूरियर रूपांतरण को भी सामान्यीकृत किया जा सकता है, जिसका एक कार्य भेज रहा है | 3-आकार के एक फलन के लिए 'स्थिति स्थान' 3-आकार संवेग (या 4-संवेग के कार्य के लिए स्थान और समय का एक कार्य)। यह विचार स्थानिक फूरियर को तरंगों के अध्ययन के साथ-साथ क्वांटम यांत्रिकी में बहुत स्वाभाविक बनाता है, जहां स्थिति या गति और कभी-कभी दोनों के कार्यों के रूप में तरंग समाधानों का प्रतिनिधित्व करने में सक्षम होना महत्वपूर्ण है। सामान्यतः, फ़्यूरियर विधियाँ जिन कार्यों पर प्रयुक्त होती हैं | वे सम्मिश्र-मूल्यवान होते हैं, और संभवतः वेक्टर-मूल्यवान फलन होते हैं।[note 1] अभी भी समूह (गणित) पर कार्य करने के लिए और सामान्यीकरण संभव है | जो मूल फूरियर के अतिरिक्त रूपांतरित होता है R या Rn (जोड़ के अनुसार समूहों के रूप में देखा गया), विशेष रूप से असतत-समय फूरियर रूपांतरण (डीटीएफटी, समूह = Z), असतत फूरियर रूपांतरण (डीएफटी, समूह = चक्रीय समूह |Z mod N) और फूरियर श्रृंखला या परिपत्र फूरियर रूपांतरण (समूह = S1, यूनिट सर्कल ≈ समापन बिंदु के साथ बंद परिमित अंतराल की पहचान)। उत्तरार्द्ध नियमित रूप से आवधिक कार्यों को संभालने के लिए नियोजित होता है। फास्ट फूरियर ट्रांसफॉर्म (एफएफटी) डीएफटी की गणना के लिए एक एल्गोरिथम है।
परिभाषाएँ
विश्लेषण सूत्र
फूरियर रूपांतरण फूरियर श्रृंखला का एक विस्तार है | जो अपने सबसे सामान्य रूप में यूलर के फार्मूले के उपयोग का परिचय देता है। उदाहरण के लिए, एक फलन के लिए , आवृत्ति पर एक आवृत्ति घटक का आयाम और चरण , इस सम्मिश्र संख्या द्वारा दिया जाता है |
विस्तार घटकों की आवृत्ति निरंतरता प्रदान करता है | एकीकरण के अनंत अभिन्न का उपयोग करता है |
|
(Eq.1) |
यहाँ, कार्य का परिवर्तन आवृत्ति पर सम्मिश्र संख्या द्वारा निरूपित किया जाता है | जो कई सामान्य सम्मेलनों में से एक है। जिसका मूल्यांकन Eq.1 के सभी मूल्यों के लिए आवृत्ति-डोमेन फलन उत्पन्न करता है। जब स्वतंत्र चर () समय का प्रतिनिधित्व करता है (अधिकांशतः द्वारा निरूपित किया जाता है ), परिवर्तन चर () आवृत्ति का प्रतिनिधित्व करता है |(अधिकांशतः द्वारा निरूपित किया जाता है ). उदाहरण के लिए, यदि समय दूसरा में मापा जाता है, तो आवृत्ति हेटर्स में होती है।
व्याख्या करने की कुंजी Eq.1 यह गुणन का प्रभाव है | द्वारा घटाना है फलन के हर आवृत्ति घटक से [note 2] (नकारात्मक आवृत्ति भी देखें फूरियर रूपांतरण को सरल बनाना) तो वह घटक जो पर था | शून्य हर्ट्ज़ पर समाप्त होता है, और अभिन्न अपना आयाम उत्पन्न करता है | क्योंकि अन्य सभी घटक दोलनशील होते हैं और एक अनंत अंतराल पर शून्य में एकीकृत होते हैं।
कार्य और अधिकांशतः फूरियर रूपांतरण जोड़ी के रूप में जाना जाता है ।[1] रूपांतरण जोड़े को नामित करने के लिए एक सामान्य संकेतन है |[2]
फूरियर श्रृंखला गैर-आवधिक तरंगों का प्रतिनिधित्व नहीं कर सकती है। चूँकि, फूरियर रूपांतरण गैर-आवधिक तरंगों का भी प्रतिनिधित्व करने में सक्षम है। यह किसी भी तरंग की अवधि को अनंत (गणित) तक बढ़ाने के लिए एक सीमा (गणित) प्रयुक्त करके इसे प्राप्त करता है और फिर उसे आवधिक तरंग के रूप में मानता है।[3]
संश्लेषण सूत्र
वास्तविक फूरियर श्रृंखला एक संश्लेषण सूत्र है |
और फूरियर ट्रांसफॉर्म एक्सटेंशन है |
|
(Eq.2) |
सम्मिश्र संख्या, , आवृत्ति के आयाम और चरण दोनों को व्यक्त करता है | . इसलिए Eq.2 का प्रतिनिधित्व है | सम्मिश्र घातीय कार्यों के भारित योग के रूप में इसे फूरियर व्युत्क्रम प्रमेय के रूप में जाना जाता है, और इसे पहली बार जोसेफ फूरियर के गर्मी के विश्लेषणात्मक सिद्धांत में प्रस्तुत किया गया था |[4][5] चूँकि आधुनिक मानकों द्वारा प्रमाण बहुत बाद तक नहीं दिया गया था।[6][7]
अन्य नोटेशनल कन्वेंशन
कोणीय आवृत्ति का उपयोग करने सहित अन्य सामान्य सम्मेलनों और अंकन के लिए ω आवृत्ति के अतिरिक्त ξ, नीचे अन्य कन्वेंशन और अन्य नोटेशन देखें। फूरियर ट्रांसफॉर्म ऑन यूक्लिडियन स्पेस को अलग से ट्रीट किया जाता है | जिसमें वेरिएबल x अधिकांशतः स्थिति का प्रतिनिधित्व करता है और ξ गति इस आलेख में चुने गए सम्मेलन हार्मोनिक विश्लेषण के हैं, और उन्हें अद्वितीय सम्मेलनों के रूप में वर्णित किया गया है | जैसे कि फूरियर रूपांतरण दोनों एकात्मक संचालक है | L2 और एक बीजगणित समरूपता से L1 को L∞, लेबेस्ग माप को फिर से सामान्य किए बिना होता है |[8]
फूरियर रूपांतरण के कई अन्य लक्षण उपस्थित हैं। उदाहरण के लिए, कोई स्टोन-वॉन न्यूमैन प्रमेय का उपयोग करता है | फूरियर रूपांतरण हाइजेनबर्ग समूह के सहानुभूतिपूर्ण और यूक्लिडियन श्रोडिंगर अभ्यावेदन के लिए अद्वितीय एकात्मक इंटरट्विनर है।
पृष्ठभूमि
इतिहास
1822 में, फूरियर ने प्रमाणित किया (देखें जोसेफ फूरियर § द एनालिटिक थ्योरी ऑफ हीट) कि कोई भी फलन, चाहे सतत हो या असंतत, ज्याओं की एक श्रृंखला में विस्तारित किया जा सकता है।[9] उस महत्वपूर्ण कार्य को सुधारा गया और अन्य लोगों द्वारा उस पर विस्तार किया गया | जिससे उसके बाद से उपयोग किए जाने वाले फूरियर रूपांतरण के विभिन्न रूपों के लिए आधार प्रदान किया जा सके।
वास्तविक साइनसोइड्स का प्रतिनिधित्व करने के लिए सम्मिश्र साइनसोइड्स का उपयोग
गणित को सरल बनाने के लिए, फूरियर श्रृंखला को यूलर के सूत्र के योग के रूप में लिखना वांछनीय है (देखें फोरियर श्रेणी § घातीय रूप). आवृत्ति के प्रत्येक सम्मिश्र घातीय या सम्मिश्र साइनसॉइड ξ आवृत्ति की कोसाइन तरंग के योग के रूप में यूलर के सूत्र का उपयोग करके व्यक्त किया जा सकता है | वास्तविक घटक ξ के साथ-साथ आवृत्ति की साइन लहर भी ξ काल्पनिक घटक के लिए:
वास्तविक साइनसोइड्स को सम्मिश्र साइनसॉइड्स के रूप में व्यक्त करना फूरियर गुणांक के लिए आवश्यक बनाता है | सम्मिश्र मूल्य होने के लिए, किन्तु प्रत्येक आवृत्ति के बारे में सभी आवश्यक जानकारी को संक्षिप्त रूप से प्रस्तुत करने का लाभ है। इस सम्मिश्र संख्या की सामान्य व्याख्या यह है | (इसका एक सम्मिश्र संख्या का परिमाण) आयाम देता है और (इसका तर्क (सम्मिश्र विश्लेषण)) उस गुणांक के लिए सम्मिश्र साइनसॉइड का चरण (तरंगें) देता है।
इन सम्मिश्र घातांकों की ऋणात्मक आवृत्ति हो सकती है। उदाहरण के लिए, दोनों सम्मिश्र साइनसोइड्स e2πiξx और e−2πiξx प्रति यूनिट एक चक्र पूरा करें x, किन्तु पहला सकारात्मक आवृत्ति का प्रतिनिधित्व करता है | जबकि दूसरा नकारात्मक आवृत्ति का प्रतिनिधित्व करता है। सकारात्मक आवृत्ति को सम्मिश्र तल के बारे में वामावर्त घुमाने के रूप में समझा जा सकता है | जबकि ऋणात्मक आवृत्ति को सम्मिश्र तल के बारे में दक्षिणावर्त घुमाने के रूप में समझा जा सकता है। जब सम्मिश्र साइनसोइड्स को तीन-आयामों में एक कुंडलित वक्रता के रूप में व्याख्या किया जाता है (तीसरा आयाम काल्पनिक घटक होता है), तो आवृत्ति को नकारने से हेलिक्स हैंडेडनेस बदल जाती है।[10]
साइनसोइड्स के सम्मिश्र घातीय प्रतिनिधित्व से वास्तविक साइन और कोसाइन तरंगों को पुनर्प्राप्त किया जा सकता है। उदाहरण के लिए, एक यूलर का_फॉर्मूला रिलेशनशिप_टू_ट्रिगोनोमेट्री|यूलर के फॉर्मूले का कोरोलरी कोसाइन और साइन तरंगों को एक सम्मिश्र साइनसॉइड के वास्तविक या काल्पनिक भाग के रूप में या विपरीत आवृत्ति के दो सम्मिश्र साइनसॉइड के भारित योग के रूप में व्यक्त करने की अनुमति देता है |
परिणाम स्वरुप, किसी भी वास्तविक साइनसॉइड का एक सामान्य रूप (आवृत्ति के साथ ξ, चरण में बदलाव θ, और आयाम A) विपरीत आवृत्ति के दो सम्मिश्र साइनसोइड्स के योग के रूप में व्यक्त किया जा सकता है | (ξ और -ξ) किन्तु समान परिमाण (A/2) और फेज शिफ्ट के साथ θ उनके दोनों सम्मिश्र गुणांकों में सन्निहित:
इसलिए, प्रत्येक वास्तविक साइनसॉइड (और वास्तविक संकेत) को एक सकारात्मक और नकारात्मक आवृत्ति से युक्त माना जा सकता है | जिनके काल्पनिक घटक रद्द हो जाते हैं किन्तु जिनके वास्तविक घटक वास्तविक संकेत बनाने में समान रूप से योगदान करते हैं।
सम्मिश्र संख्याओं और नकारात्मक आवृत्तियों के उपयोग से बचने के लिए, साइन और कोसाइन रूपांतरित होते हैं | जिसको एक साथ फूरियर ट्रांसफॉर्म के समकक्ष वैकल्पिक रूप के रूप में उपयोग किया जा सकता है।
आवधिक कार्यों के लिए फूरियर रूपांतरण
निम्नलिखित एक फूरियर ट्रांसफॉर्म जोड़ी है | (डायराक डेल्टा फलन फूरियर ट्रांसफॉर्म देखें):
यह इस प्रकार है कि ए फूरियर_सीरीज़ कॉम्प्लेक्स-वैल्यूड_फंक्शन के साथ आवधिक कार्य है |
फूरियर रूपांतरण है |
जो एक डिराक कंघी फलन है | जिसके दांत फूरियर श्रृंखला गुणांक द्वारा संशोधित होते हैं।
फूरियर रूपांतरण का नमूना
ए का फूरियर रूपांतरण -आवधिक फलन गैर-शून्य होता है | केवल के अंतराल पर आवृत्तियों के असतत समुच्चय पर इसके अतिरिक्त, अनंत अभिन्न, केवल एक चक्र में एकीकरण द्वारा प्रतिस्थापित किया जाता है | इसी तरह, जब एपेरियोडिक फलन के फूरियर रूपांतरण को इच्छानुसार अंतराल पर नमूना लिया जाता है | अभिन्न को भी घटाया जा सकता है निम्नलिखित अनुसार:
एक आवधिक-सारांश को दर्शाता है | केवल एकीकरण के अंतराल पर गणना की जाती है, और हम पहचान सकते हैं | जिसके उत्पाद के रूप में और यह के फूरियर श्रृंखला विस्तार में गुणांक कब कॉम्पैक्ट समर्थन है | शब्दों की एक सीमित संख्या है। विशेष रूप से, के साथ और का गैर-शून्य भाग समाहित करने के लिए अधिक बड़ा है | अंदर यह सरलता से कम हो जाता है |
कब कॉम्पैक्ट समर्थन, की संख्यात्मक मूल्यांकन नहीं है | एक सन्निकटन की आवश्यकता होती है | जैसे टेपरिंग या संख्या शब्दों को छोटा करना है ।
उदाहरण
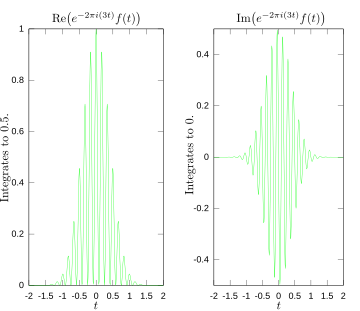
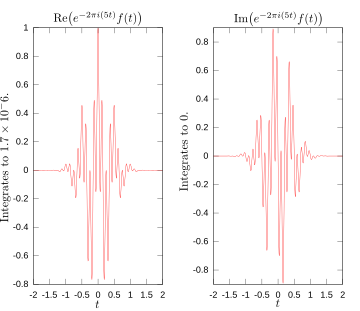
निम्नलिखित आंकड़े एक दृश्य चित्रण प्रदान करते हैं कि कैसे फूरियर किसी विशेष फलन में आवृत्ति उपस्थित है या नहीं, यह मापता है। चित्रित कार्य f(t) = cos(6πt) e−πt2 3 हर्ट्ज पर दोलन करता है (यदि t सेकंड्स को मापता है) और जल्दी से 0. तक जाता है। (इस समीकरण में दूसरा कारक एक लिफाफा (तरंगें) है जो निरंतर साइनसॉइड को एक छोटी नाड़ी में आकार देता है। इसका सामान्य रूप एक गॉसियन फलन है)। यह फलन विशेष रूप से वास्तविक फूरियर रूपांतरण के लिए चुना गया था जिसे आसानी से प्लॉट किया जा सकता है। पहली छवि में इसका ग्राफ है। गणना करने के लिए हमें एकीकृत करना चाहिए e−2πi(3t)f(t). दूसरी छवि इस फलन के वास्तविक और काल्पनिक भागों की साजिश दिखाती है। इंटीग्रैंड का वास्तविक भाग लगभग सदैव सकारात्मक होता है, क्योंकि कब f(t) नकारात्मक है, का वास्तविक भाग है e−2πi(3t) नकारात्मक भी है। क्योंकि वे उसी दर से दोलन करते हैं, जब f(t) सकारात्मक है, तो इसका असली भाग है e−2πi(3t). नतीजा यह है कि जब आप एकीकृत के वास्तविक हिस्से को एकीकृत करते हैं तो आपको अपेक्षाकृत बड़ी संख्या मिलती है (इस स्थिति में 1/2). दूसरी ओर, जब आप एक ऐसी आवृत्ति को मापने का प्रयास करते हैं जो उपस्थित नहीं है, जैसा कि हम देखते हैं , आप देखते हैं कि इस फलन के वास्तविक और काल्पनिक दोनों घटक धनात्मक और ऋणात्मक मानों के बीच तेज़ी से बदलते हैं, जैसा कि तीसरी छवि में दिखाया गया है। इसलिए, इस स्थिति में, इंटीग्रैंड अधिक तेजी से दोलन करता है जिससे इंटीग्रल बहुत छोटा हो और उस आवृत्ति के लिए फूरियर रूपांतरण का मान लगभग शून्य हो।
सामान्य स्थिति इससे थोड़ी अधिक सम्मिश्र हो सकती है | किन्तु आत्मा में यह है कि फूरियर कैसे मापता है कि एक फलन f(t) में कितनी व्यक्तिगत आवृत्ति उपस्थित है |
फूरियर रूपांतरण के गुण
यहाँ हम मानते हैं f(x), g(x) और h(x) पूर्णांक कार्य हैं | लेबेस्ग-मापने योग्य वास्तविक रेखा पर संतोषजनक:
मूल गुण
फूरियर रूपांतरण में निम्नलिखित मूल गुण होते हैं |[11]
रैखिकता
- किसी भी सम्मिश्र संख्या a और b, के लिए यदि h(x) = a f (x) + b g(x), तब ĥ(ξ) = a f̂(ξ) + b ĝ(ξ).
अनुवाद / समय परिवर्तन
किसी भी वास्तविक संख्या के लिए x0, यदि h(x) = f(x − x0), तब ĥ(ξ) = e−2πix0ξ f̂(ξ).
मॉड्यूलेशन / आवृत्ति शिफ्टिंग
- किसी भी वास्तविक संख्या के लिए ξ0, यदि h(x) = e2πixξ0 f(x), तब ĥ(ξ) = f̂(ξ − ξ0).
समय स्केलिंग
- शून्येतर वास्तविक संख्या के लिए a, यदि h(x) = f(ax), तब
- मुकदमा a = −1 टाइम-रिवर्सल प्रॉपर्टी की ओर जाता है | जो बताता है | यदि h(x) = f(−x), तब ĥ(ξ) = f̂(−ξ).
समरूपता
जब एक सम्मिश्र कार्य के वास्तविक और काल्पनिक भागों को उनके सम और विषम कार्यों सम-विषम अपघटन में विघटित किया जाता है, तो चार घटक होते हैं | जिन्हें सबस्क्रिप्ट आरई, आरओ, आईई और आईओ द्वारा निरूपित किया जाता है। और एक सम्मिश्र समय फलन के चार घटकों और इसके सम्मिश्र आवृत्ति परिवर्तन के चार घटकों के बीच एक-से-एक मानचित्रण होता है |[12]
इससे विभिन्न संबंध स्पष्ट होते हैं, उदाहरण के लिए:
- वास्तविक-मूल्यवान फलन का रूपांतरण (fRE+ f̂RO) सम और विषम फलन सम्मिश्र-मूल्यवान फलन f̂RE+ i f̂IO है | इसके विपरीत, एक सम-सममित परिवर्तन का तात्पर्य वास्तविक-मूल्यवान समय-डोमेन से है।
- एक काल्पनिक-मूल्यवान फलन का रूपांतरण (i fIE+ i fIO) सम और विषम फलन जटिल-मूल्यवान फलन फलन है | f̂RO+ i fIE, और इसका विलोम सत्य है।
- सम-सममित फलन का परिवर्तन (fRE+ i fIO) वास्तविक-मूल्यवान कार्य है | f̂RE+ 'fRO, और इसका विलोम सत्य है।
- एक विषम-सममित फलन का रूपांतरण (fRO+ i f̂IE) काल्पनिक-मूल्यवान कार्य है | i f̂IE+ i f̂IO, और इसका विलोम सत्य है।
सम्मिश्र संयुग्म
- यदि h(x) = f(x), तब
- विशेष रूप से, यदि f वास्तविक है, तो उसके पास वास्तविकता की स्थिति होती है |
- वह है, f̂ एक हर्मिटियन फलन है और यदि f विशुद्ध रूप से काल्पनिक है | फिर
समय में वास्तविक और काल्पनिक भाग
- यदि , तब .
- यदि , तब .
शून्य आवृत्ति घटक
- प्रतिस्थापन ξ = 0 परिभाषा में, हम प्राप्त करते हैं |
- यह का समाकलन के समान है | f अपने सभी डोमेन पर और फलन के औसत मूल्य या डीसी पूर्वाग्रह के रूप में भी जाना जाता है।
उलटापन और आवधिकता
फलन पर उपयुक्त परिस्थितियों में , इसे इसके फूरियर रूपांतरण से पुनर्प्राप्त किया जा सकता है | . दरअसल, फूरियर ट्रांसफॉर्म संचालक को निरूपित करते हुए , इसलिए , फिर उपयुक्त कार्यों के लिए, फूरियर ट्रांसफॉर्म को दो बार प्रयुक्त करने से फलन फ़्लिप हो जाता है | , जिसे उलटने के समय के रूप में व्याख्या किया जा सकता है। चूंकि उलटने का समय दो-आवधिक है | इसे दो बार प्रयुक्त करने से उपज मिलती है | , इसलिए फूरियर ट्रांसफॉर्म संचालक चार-आवधिक है, और इसी प्रकार फूरियर ट्रांसफॉर्म को तीन बार प्रयुक्त करके उलटा फूरियर ट्रांसफॉर्म प्राप्त किया जा सकता है | . विशेष रूप से फूरियर रूपांतरण उलटा (उपयुक्त परिस्थितियों में) है।
अधिक स्पष्ट, समता संचालक को परिभाषित करना ऐसा है कि , अपने पास:
संचालको की इन समानताओं के लिए प्रश्न में कार्यों के स्थान की सावधानीपूर्वक परिभाषा की आवश्यकता होती है | कार्यों की समानता को परिभाषित करना (प्रत्येक बिंदु पर समानता; लगभग हर स्थान समानता?) और संचालको की समानता को परिभाषित करना अर्थात, कार्य स्थान और संचालक स्थान पर टोपोलॉजी को परिभाषित करना प्रश्न ये सभी कार्यों के लिए सत्य नहीं हैं | किन्तु विभिन्न परिस्थितियों में सत्य हैं | जो फूरियर व्युत्क्रम प्रमेय के विभिन्न रूपों की पदार्थ हैं।
फूरियर रूपांतरण की यह चौगुना आवधिकता 90 डिग्री तक विमान के घूर्णन के समान है | विशेष रूप से दो गुना पुनरावृति एक उत्क्रमण उत्पन्न करती है, और वास्तव में इस सादृश्य को स्पष्ट बनाया जा सकता है। जबकि फूरियर रूपांतरण को केवल समय डोमेन और आवृत्ति डोमेन को बदलने के रूप में व्याख्या किया जा सकता है | व्युत्क्रम फूरियर रूपांतरण के साथ उन्हें वापस स्विच करना, अधिक ज्यामितीय रूप से इसे समय-आवृत्ति डोमेन में 90 ° द्वारा रोटेशन के रूप में व्याख्या किया जा सकता है | (समय को ध्यान में रखते हुए) x-अक्ष और आवृत्ति के रूप में y-एक्सिस), और फूरियर ट्रांसफॉर्म को आंशिक फूरियर रूपांतरण के लिए सामान्यीकृत किया जा सकता है | जिसमें अन्य कोणों से रोटेशन सम्मिलित है। इसे रैखिक विहित परिवर्तन के लिए और सामान्यीकृत किया जा सकता है | जिसे विशेष रैखिक समूह की क्रिया के रूप में देखा जा सकता है | SL2(R) समय-आवृत्ति तल पर, नीचे अनिश्चितता सिद्धांत के अनुरूप संरक्षित सहानुभूतिपूर्ण रूप के साथ यह दृष्टिकोण विशेष रूप से समय-आवृत्ति विश्लेषण के अनुसार संकेत प्रसंस्करण में अध्ययन किया जाता है।
इकाइयां और द्वैत
आवृत्ति वेरिएबल में मूल फलन के डोमेन की इकाइयों की व्युत्क्रम इकाइयाँ होनी चाहिए (सामान्यतः नामित t या x). उदाहरण के लिए, यदि t सेकंड में मापा जाता है | ξ प्रति सेकंड चक्र में होना चाहिए। यदि समय का मापदंड 2 की इकाई में है | π सेकंड, फिर एक और ग्रीक अक्षर ω सामान्यतः इसके अतिरिक्त कोणीय आवृत्ति का प्रतिनिधित्व करने के लिए प्रयोग किया जाता है (जहां ω = 2πξ) कांति प्रति सेकंड की इकाइयों में। यदि उपयोग कर रहे हैं | x लंबाई की इकाइयों के लिए, फिर ξ व्युत्क्रम लंबाई में होना चाहिए, उदाहरण के लिए, तरंग संख्या कहने का तात्पर्य यह है कि वास्तविक रेखा के दो संस्करण हैं | एक जो एक फलन की श्रेणी है | t और टी की इकाइयों में मापा जाता है, और दूसरा जो की सीमा है | ξ और की इकाइयों के व्युत्क्रम इकाइयों में मापा जाता है | t. वास्तविक रेखा के इन दो अलग-अलग संस्करणों की एक दूसरे के साथ बराबरी नहीं की जा सकती। इसलिए, फूरियर रूपांतरण कार्यों के एक स्थान से कार्यों के एक अलग स्थान पर जाता है | ऐसे कार्य जिनकी परिभाषा का एक अलग डोमेन है।
सामान्य रूप में, ξ इसे सदैव अपने डोमेन के स्थान पर एक रैखिक रूप में लिया जाना चाहिए, जिसका अर्थ है कि दूसरी वास्तविक रेखा पहली वास्तविक रेखा का दोहरा स्थान है। अधिक औपचारिक स्पष्टीकरण और अधिक विवरण के लिए रेखीय बीजगणित पर लेख देखें। फूरियर श्रृंखला के स्थिति सहित सामान्य समरूपता समूह में फूरियर रूपांतरण के सामान्यीकरण में यह दृष्टिकोण आवश्यक हो जाता है।
वास्तविक रेखा के दो संस्करणों की तुलना करने के लिए कोई एक पसंदीदा विधि नहीं है (अधिकांशतः, कोई कहता है कि कोई विहित विधि नहीं है) जो फूरियर रूपांतरण में सम्मिलित हैं | एक पंक्ति पर इकाइयों को ठीक करने से दूसरी पर इकाइयों के मापदंड को बाध्य नहीं किया जाता है। लाइन-फूरियर रूपांतरण की परिभाषा पर प्रतिद्वंद्वी सम्मेलनों की अधिकता का कारण है। इकाइयों के विभिन्न विकल्पों से उत्पन्न विभिन्न परिभाषाएँ विभिन्न स्थिरांकों से भिन्न होती हैं।
माना सामान्य आवृत्ति ξ के संदर्भ में फूरियर रूपांतरण का रूप हो .
चूंकि , वैकल्पिक रूप (कौन कौन से फूरियर रूपांतरण § अन्य परम्पराएँ कोणीय आवृत्ति में गैर-एकात्मक रूप कहता है) इसकी परिभाषा में कोई कारक नहीं है |
किन्तु का एक कारक है | इसके संगत उलटा सूत्र में
एक वैकल्पिक रूप (कौन कौन से फूरियर रूपांतरण § अन्य परम्पराएँ कोणीय आवृत्ति में एकात्मक रूप कहते हैं) का एक कारक है | इसकी परिभाषा में
और का भी वही कारक है | इसके संगत व्युत्क्रम सूत्र में, एक सममित संबंध का निर्माण
अन्य सम्मेलनों में, फूरियर रूपांतरण है | i के अतिरिक्त एक्सपोनेंट में −i, और उलटा सूत्र के लिए इसके विपरीत यह सम्मेलन आधुनिक भौतिकी में सामान्य है |[13] और वोल्फ्राम अल्फा के लिए डिफ़ॉल्ट है, और इसका कारण यह नहीं है कि आवृत्ति नकारात्मक हो गई है | क्योंकि एक सम्मिश्र तरंग की आवृत्ति के लिए सकारात्मकता की कोई प्रामाणिक परिभाषा नहीं है। इसका सीधा सा कारण है तरंग का आयाम है | लहर के अतिरिक्त (पूर्व, इसके ऋण चिह्न के साथ, अधिकांशतः विद्युत चुम्बकीय तरंग समीकरण के साइनसॉइडल प्लेन-वेव समाधान के लिए समय निर्भरता में या वेव फलन समय निर्भरता में देखा जाता है)। फूरियर रूपांतरण से जुड़ी कई पहचान उन सम्मेलनों में मान्य रहती हैं | परंतु वे सभी शब्द हों जिनमें स्पष्ट रूप से सम्मिलित हो i इसके द्वारा प्रतिस्थापित किया गया है | −i. विद्युत अभियन्त्रण में पत्र j के अतिरिक्त सामान्यतः काल्पनिक इकाई के लिए उपयोग किया जाता है | i चूंकि i करंट के लिए प्रयोग किया जाता है।
आयाम रहित इकाइयों का उपयोग करते समय, परिवर्तन की परिभाषा में स्थिर कारकों को भी नहीं लिखा जा सकता है। उदाहरण के लिए, संभाव्यता सिद्धांत में, विशेषता कार्य Φ संभाव्यता घनत्व फलन की f एक यादृच्छिक चर का X निरंतर प्रकार के घातीय में एक नकारात्मक चिह्न के बिना परिभाषित किया गया है, और की इकाइयों के बाद से x कोई 2 नहीं है π याउपेक्षित हैं |
(संभाव्यता सिद्धांत में, और गणितीय आँकड़ों में, फूरियर-स्टील्टजेस रूपांतरण के उपयोग को प्राथमिकता दी जाती है | क्योंकि इतने सारे यादृच्छिक चर निरंतर प्रकार के नहीं होते हैं, और उनके पास घनत्व कार्य नहीं होता है, और किसी को कार्य नहीं किन्तु वितरण (गणित) का इलाज करना चाहिए ), अर्थात वे उपाय जिनमें परमाणु होते हैं।)
चरित्र सिद्धांत के उच्च दृष्टिकोण से, जो बहुत अधिक सारगर्भित है | ये सभी इच्छानुसार विकल्प गायब हो जाते हैं | जैसा कि इस लेख के बाद के खंड में बताया जाएगा, जो स्थानीय रूप से कॉम्पैक्ट एबेलियन पर एक फलन के फूरियर रूपांतरण की धारणा का इलाज करता है।
एक समान निरंतरता और रीमैन-लेबेस्गु लेम्मा
फूरियर रूपांतरण को कुछ स्थितियों में गैर-पूर्ण कार्यों के लिए परिभाषित किया जा सकता है | किन्तु पूर्णांक कार्यों के फूरियर रूपांतरण में कई शक्तिशाली गुण होते हैं।
फूरियर रूपांतरण f̂ किसी भी पूर्णांक फलन की f समान रूप से निरंतर है और [14]
रीमैन-लेबेस्गु लेम्मा द्वारा,[15]
चूँकि, अभिन्न होने की आवश्यकता नहीं है। उदाहरण के लिए, आयताकार फलन का फूरियर रूपांतरण, जो पूर्णांक है, सिंक फलन है | जो लेबेसेग पूर्णांक नहीं है | क्योंकि इसके अनुचित इंटीग्रल वैकल्पिक हार्मोनिक श्रृंखला के समान रूप से व्यवहार करते हैं | जो पूरी तरह से अभिसरण के बिना योग में अभिसरण करते हैं।
लेबेस्ग इंटीग्रल के रूप में व्युत्क्रम परिवर्तन को लिखना सामान्यतः संभव नहीं है। चूँकि, जब दोनों f और पूर्णांक हैं, व्युत्क्रम समानता
लगभग हर स्थान रखता है। यही है, फूरियर ट्रांसफॉर्म इंजेक्शन पर है | L1(R). (किन्तु यदि f निरंतर है, तो समानता सभी के लिए है x.)
प्लैंकेरल प्रमेय और पारसेवल प्रमेय
माना f(x) और g(x) पूर्णांक बनें, और दें f̂(ξ) और ĝ(ξ) उनके फूरियर रूपांतरण बनें। यदि f(x) और g(x) भी वर्ग-पूर्णांक हैं, तो पारसेवल सूत्र इस प्रकार है:[16]
जहाँ बार सम्मिश्र संयुग्मन को दर्शाता है।
प्लैंकेरल प्रमेय, जो ऊपर से अनुसरण करता है, कहता है कि [17]
प्लैंचरेल की प्रमेय एक निरंतरता तर्क L2(R). पर L1(R) ∩ L2(R) द्वारा फूरियर रूपांतरण को एकात्मक संचालिका तक विस्तारित करना संभव बनाती है | यह एक्सटेंशन परिभाषित मूल फूरियर रूपांतरण से सहमत है | L1(R), इस प्रकार फूरियर रूपांतरण के डोमेन का विस्तार करना L1(R) + L2(R) (और इसके परिणामस्वरूप Lp(आर) के लिए 1 ≤ p ≤ 2). प्लैंकरेल के प्रमेय की विज्ञान में व्याख्या है कि फूरियर रूपांतरण मूल मात्रा की ऊर्जा को संरक्षित करता है। इन सूत्रों की शब्दावली अधिक मानकीकृत नहीं है। पारसेवल का प्रमेय केवल फूरियर श्रृंखला के लिए सिद्ध किया गया था, और सबसे पहले लायपुनोव द्वारा सिद्ध किया गया था। किन्तु पारसेवल का सूत्र फूरियर रूपांतरण के लिए भी समझ में आता है, और इसलिए तथापि फूरियर रूपांतरण के संदर्भ में यह प्लांचरेल द्वारा सिद्ध किया गया था | फिर भी इसे अधिकांशतः पारसेवल के सूत्र, या पारसेवल के संबंध, या यहां तक कि पारसेवल के प्रमेय के रूप में भी जाना जाता है।
स्थानीय रूप से कॉम्पैक्ट एबेलियन समूहों के संदर्भ में इस अवधारणा के सामान्य सूत्रीकरण के लिए पोंट्रीगिन द्वैत देखें।
विष योग सूत्र
प्वासों योग सूत्र (पीएसएफ) एक समीकरण है जो किसी फलन के आवधिक योग के फूरियर श्रृंखला गुणांकों को फलन के निरंतर फूरियर रूपांतरण के मानों से संबंधित करता है। प्वासों योग सूत्र कहता है कि पर्याप्त नियमित कार्यों के लिए f,
इसके कई प्रकार के उपयोगी रूप हैं | जो फूरियर ट्रांसफॉर्म के स्केलिंग और टाइम-शिफ्टिंग गुणों के अनुप्रयोग द्वारा मूल रूप से प्राप्त किए गए हैं। सूत्र में इंजीनियरिंग, भौतिकी और संख्या सिद्धांत में अनुप्रयोग हैं। मानक प्वासों संकलन सूत्र के आवृत्ति-डोमेन दोहरे को असतत-समय फूरियर रूपांतरण भी कहा जाता है।
पोइसन योग सामान्यतः आवधिक मीडिया के भौतिकी से जुड़ा होता है | जैसे कि एक वृत्त पर ऊष्मा चालन। एक वृत्त पर ऊष्मा समीकरण के मूलभूत समाधान को थीटा फलन कहा जाता है। यह थीटा कार्यों के परिवर्तन गुणों को सिद्ध करने के लिए संख्या सिद्धांत में प्रयोग किया जाता है | जो एक प्रकार का मॉड्यूलर रूप बन जाता है, और यह सामान्यतः ऑटोमोर्फिक रूपों के सिद्धांत से जुड़ा होता है | जहां यह सेलबर्ग ट्रेस सूत्र के एक तरफ दिखाई देता है।
भेद
मान लीजिए f(x) एक बिल्कुल निरंतर अलग-अलग कार्य है, और दोनों f और इसका व्युत्पन्न f′ पूर्णांक हैं। फिर व्युत्पन्न के फूरियर रूपांतरण द्वारा दिया जाता है |
अधिक सामान्यतः, nवें व्युत्पन्न f(n) द्वारा दिया गया है |
सादृश्य, फूरियर रूपांतरण प्रयुक्त करके और इन सूत्रों का उपयोग करके, कुछ सामान्य अंतर समीकरणों को बीजगणितीय समीकरणों में रूपांतरित किया जा सकता है, जिन्हें हल करना बहुत सरल है। ये सूत्र अंगूठे के नियम को भी जन्म देते हैं | f(x) चिकना है यदि और केवल यदि f̂(ξ) के लिए जल्दी से 0 पर गिर जाता है | |ξ| → ∞. व्युत्क्रम फूरियर रूपांतरण के लिए समान नियमों का उपयोग करके, कोई भी कह सकता है | f(x) के लिए जल्दी से 0 पर गिर जाता है |x| → ∞ यदि और केवल यदि f̂(ξ) चिकना है।
कनवल्शन प्रमेय
फूरियर रूपांतरण रूपांतरण और कार्यों के गुणन के बीच अनुवाद करता है। यदि f(x) और g(x) फूरियर रूपांतरण के साथ पूर्णांकीय कार्य हैं | f̂(ξ) और ĝ(ξ) क्रमशः, फिर कनवल्शन का फूरियर रूपांतरण फूरियर रूपांतरण के उत्पाद द्वारा दिया जाता है | f̂(ξ) और ĝ(ξ) (फूरियर रूपांतरण की परिभाषा के लिए अन्य सम्मेलनों के अनुसार एक स्थिर कारक प्रकट हो सकता है)।
इसका कारण है कि यदि:
जहाँ ∗ कनवल्शन संचालन को दर्शाता है, फिर:
एलटीआई प्रणाली थ्योरी में लीनियर टाइम इनवेरिएंट (एलटीआईएलटीआई प्रणाली सिद्धांत , इसकी व्याख्या करना सामान्य है g(x) इनपुट के साथ एलटीआई प्रणाली की आवेग प्रतिक्रिया के रूप में f(x) और आउटपुट h(x), के लिए डिराक डेल्टा फलन को प्रतिस्थापित करने के बाद से f(x) उतपन्न h(x) = g(x). इस स्थिति में, ĝ(ξ) प्रणाली की आवृत्ति प्रतिक्रिया का प्रतिनिधित्व करता है।
इसके विपरीत यदि f(x) दो वर्ग पूर्णांक कार्यों के उत्पाद के रूप में विघटित किया जा सकता है | p(x) और q(x), फिर फूरियर का रूपांतरण f(x) संबंधित फूरियर रूपांतरणों p̂(ξ) और q̂(ξ). के कनवल्शन द्वारा दिया जाता है |
क्रॉस-सहसंबंध प्रमेय
एक समान विधि से, यह दिखाया जा सकता है कि यदि h(x) का परस्पर-संबंध f(x) और g(x): है |
फिर फूरियर का रूपांतरण h(x) है |
एक विशेष स्थिति के रूप में, कार्य का स्वत: संबंध f(x) है |
जिसके लिए
ईजेनफंक्शन
फूरियर रूपांतरण एक रेखीय रूपांतरण है जिसका ईजेनफंक्शन पालन करता है | साथ सजातीय अंतर समीकरण को ध्यान में रखते हुए आइगेनफंक्शन का एक समुच्चय पाया जाता है
- ईजेनफंक्शन की ओर ले जाता है | फूरियर रूपांतरण का जब तक फूरियर रूपांतरण के अनुसार समीकरण का रूप अपरिवर्तित रहता है।[note 3] दूसरे शब्दों में, हर समाधान और इसका फूरियर रूपांतरण उसी समीकरण का पालन करें। साधारण अवकल समीकरण को मानते हुए अस्तित्व और समाधान के समाधान की विशिष्टता, हर समाधान इसलिए फूरियर रूपांतरण का एक आइगेनफंक्शन होना चाहिए। फूरियर रूपांतरण के अनुसार समीकरण का रूप अपरिवर्तित रहता है | यदि एक शक्ति श्रृंखला में विस्तारित किया जा सकता है | जिसमें सभी नियमो में से किसी एक का समान कारक कारकों से उत्पन्न होता है | सजातीय अंतर समीकरण को बदलने पर फूरियर पर विभेदीकरण नियमों द्वारा प्रस्तुत किया गया क्योंकि यह कारक तब रद्द किया जा सकता है। सबसे सरल स्वीकार्य सामान्य वितरण फूरियर रूपांतरण और विशेषता कार्य की ओर जाता है।[18]
अधिक सामान्यतः, आइगेनफंक्शन का एक समुच्चय यह भी ध्यान में रखते हुए पाया जाता है कि विभेदीकरण नियम का अर्थ है कि सामान्य अंतर समीकरण
साथ स्थिर और फूरियर रूपांतरण प्रयुक्त करते समय एक गैर-निरंतर सम कार्य होने के कारण रूप में अपरिवर्तनीय रहता है | समीकरण के दोनों पक्षों के लिए द्वारा सरलतम उदाहरण दिया गया है | जो क्वांटम हार्मोनिक ऑसिलेटर प्राकृतिक लंबाई और ऊर्जा पैमानों के लिए श्रोडिंगर समीकरण पर विचार करने के समान है।[19] संबंधित समाधान एक ऑर्थोनॉर्मल आधार का एक महत्वपूर्ण विकल्प प्रदान करते हैं | L2(R) और भौतिक विज्ञानी के हरमाइट बहुपदों द्वारा दिए गए हैं | हर्मिट फलन फूरियर रूपांतरण के आइगेनफंक्शन के रूप में समान रूप से प्रयोग कर सकते हैं |
जहाँ Hen(x) संभाव्यतावादी हर्मिट बहुपद हैं | जिन्हें परिभाषित किया गया है |
फूरियर रूपांतरण के लिए इस सम्मेलन के अनुसार, हमारे पास वह है |
दूसरे शब्दों में, हर्मिट कार्य फूरियर रूपांतरण के लिए ईजेनफंक्शन की एक पूर्ण ऑर्थोनॉर्मल प्रणाली बनाते हैं | L2(R).[11][20] चूँकि, आइगेनफंक्शन का यह विकल्प अद्वितीय नहीं है। वजह से फूरियर रूपांतरण के केवल चार अलग-अलग आइगेनवैल्यू एस हैं (एकता की चौथी जड़ें ±1 और ±i) और समान आइगेनवैल्यू के साथ आइगेनफंक्शन का कोई भी रैखिक संयोजन एक और आइगेनफंक्शन देता है।[21] इसके परिणामस्वरूप, इसका विघटन संभव है | L2(R) चार रिक्त स्थान के प्रत्यक्ष योग के रूप में H0, H1, H2, और H3 जहां फूरियर रूपांतरण कार्य करता है | Hek केवल ik गुणा करके किया जाता है |
चूंकि हर्मिट कार्यों का पूरा समुच्चय ψn पहचान का एक संकल्प प्रदान करता है | जो वे फूरियर संचालक को विकर्ण करते हैं, अर्थात फूरियर रूपांतरण को उपरोक्त आइगेनवैल्यू द्वारा भारित नियमो के ऐसे योग द्वारा दर्शाया जा सकता है, और इन योगों को स्पष्ट रूप से अभिव्यक्त किया जा सकता है |
फूरियर रूपांतरण को परिभाषित करने का यह दृष्टिकोण सबसे पहले नॉर्बर्ट वीनर द्वारा प्रस्तावित किया गया था।[22] अन्य गुणों के बीच, हर्मिट फ़ंक्शंस आवृत्ति और टाइम डोमेन दोनों में तेजी से घटते हैं, और इस प्रकार वे फूरियर रूपांतरण के सामान्यीकरण को परिभाषित करने के लिए उपयोग किए जाते हैं, अर्थात् समय-आवृत्ति विश्लेषण में प्रयुक्त आंशिक फूरियर रूपांतरण।[23] भौतिकी में, यह परिवर्तन एडवर्ड कोंडोन द्वारा प्रस्तुत किया गया था।[24] आधार कार्यों का यह परिवर्तन संभव हो जाता है क्योंकि सही अन्य सम्मेलनों का उपयोग करते समय फूरियर रूपांतरण एक एकात्मक परिवर्तन है। परिणाम स्वरुप, उचित परिस्थितियों में यह उम्मीद की जा सकती है कि यह स्व-संलग्न जनरेटर से परिणामित हो के जरिए |[25]
परिचालक क्वांटम हार्मोनिक ऑसिलेटर लैडर संचालक विधि है | जिसे क्वांटम हार्मोनिक ऑसिलेटर के रूप में लिखा गया है |[26][27]
- इसे मेहलर कर्नेल के क्वांटम यांत्रिकी में समरूपता के रूप में व्याख्या किया जा सकता है | इच्छानुसार मूल्यों के लिए आंशिक फूरियर परिवर्तन t, और पारंपरिक निरंतर फूरियर रूपांतरण विशेष मूल्य के लिए मेहलर कर्नेल के साथ #भौतिकी संस्करण संबंधित सक्रिय और निष्क्रिय परिवर्तन को प्रयुक्त करता है अमूर्त वेक्टर_स्पेस में। के ईजेनफंक्शन हर्मिट बहुपद हैं | हर्माइट फलन जो इसलिए भी आइगेनफंक्शन हैं | वितरण (गणित) में फूरियर रूपांतरण का विस्तार करने पर डायराक कंघी फूरियर रूपांतरण भी फूरियर रूपांतरण का एक ईजेनफंक्शन है।
हाइजेनबर्ग समूह के साथ संबंध
हाइजेनबर्ग समूह हिल्बर्ट अंतरिक्ष पर एकात्मक संचालको का एक निश्चित समूह (गणित) है L2(R) स्क्वायर इंटीग्रेबल सम्मिश्र मूल्यवान कार्यों का f वास्तविक रेखा पर, अनुवादों द्वारा उत्पन्न (Ty f)(x) = f (x + y) और गुणा करके e2πixξ, (Mξ f)(x) = e2πixξ f (x). ये संचालक यात्रा नहीं करते हैं | जैसा कि उनका (समूह) कम्यूटेटर है |
जो स्थिरांक से गुणा है (से स्वतंत्र x) e2πiyξ ∈ U(1) (इकाई मापांक सम्मिश्र संख्याओं का वृत्त समूह)। एक सार समूह के रूप में, हाइजेनबर्ग समूह ट्रिपल का त्रि-आयामी झूठ समूह है (x, ξ, z) ∈ R2 × U(1), समूह नियम के साथ
द्वारा हाइजेनबर्ग समूह को निरूपित करें H1. उपरोक्त प्रक्रिया न केवल समूह संरचना का वर्णन करती है | किन्तु एक मानक एकात्मक प्रतिनिधित्व भी करती है | H1 एक हिल्बर्ट स्थान पर, जिसे हम निरूपित करते हैं ρ : H1 → B(L2(R)) के रैखिक ऑटोमोर्फिज्म को परिभाषित करें R2 द्वारा
जिससे J2 = −I. यह J के एक अद्वितीय ऑटोमोर्फिज्म H1 तक बढ़ाया जा सकता है |
स्टोन-वॉन न्यूमैन प्रमेय के अनुसार, एकात्मक निरूपण ρ और ρ ∘ j एकात्मक रूप से समतुल्य हैं | इसलिए एक अद्वितीय इंटरविनर है | W ∈ U(L2(R)) ऐसा है कि
यह संचालिका W फूरियर रूपांतरण है।
फूरियर रूपांतरण के कई मानक गुण इस अधिक सामान्य ढांचे के तत्काल परिणाम हैं।[28] उदाहरण के लिए, फूरियर रूपांतरण का वर्ग, W2, से जुड़ा एक इंटरटाइनर है | J2 = −I, और इसलिए हमारे पास है |(W2f)(x) = f (−x) मूल कार्य f का प्रतिबिंब है |
सम्मिश्र डोमेन
फूरियर रूपांतरण के लिए अभिन्न
इसके तर्क के सम्मिश्र संख्या मूल्यों के लिए अध्ययन किया जा सकता है | ξ. के गुणों पर निर्भर करता है | f, यह वास्तविक अक्ष से बिल्कुल भी अभिसरण नहीं हो सकता है, या यह सभी मूल्यों के लिए एक सम्मिश्र विश्लेषण विश्लेषणात्मक कार्य में अभिसरण हो सकता है | ξ = σ + iτ, या बीच में कुछ।[29] पाले-वीनर प्रमेय कहता है कि f चिकना है (अर्थात, n सभी धनात्मक पूर्णांकों के लिए गुणन अवकलनीय n) और संक्षिप्त रूप से समर्थित यदि और केवल यदि f̂ (σ + iτ) एक होलोमॉर्फिक फलन है जिसके लिए एक [[स्थिर (गणित) |स्थिर (गणित) a > 0 ऐसा कि किसी भी]] पूर्णांक के लिए n ≥ 0, उपस्थित है
कुछ स्थिर के लिए C. (इस स्थिति में, f पर समर्थित है | [−a, a]।) यह कहकर व्यक्त किया जा सकता है | f̂ एक संपूर्ण कार्य है जो तेजी से घट रहा है σ (निश्चित के लिए τ) और में घातीय वृद्धि की τ (समान रूप से σ).[30] (यदि f चिकना नहीं है, किन्तु केवल L2, कथन अभी भी प्रदान किया गया है n = 0.[31]) एक सम्मिश्र विश्लेषण के ऐसे कार्यों के स्थान को पाले-वीनर स्थान कहा जाता है। इस प्रमेय को अर्धसरल झूठ समूहों के लिए सामान्यीकृत किया गया है।[32] यदि f आधा लाइन पर समर्थित है t ≥ 0, तब f कारणात्मक कहा जाता है क्योंकि शारीरिक रूप से वसूली योग्य फ़िल्टर (गणित) के आवेग प्रतिक्रिया फलन में यह संपत्ति होनी चाहिए, क्योंकि कोई प्रभाव इसके कारण से पहले नहीं हो सकता है। रेमंड पाले और वीनर ने तब दिखाया f̂ सम्मिश्र निचले आधे विमान पर एक होलोमोर्फिक फलन तक फैला हुआ है | τ < 0 जो शून्य हो जाता है τ अनंत तक जाता है।[33] इसका विलोम झूठा है और यह ज्ञात नहीं है कि एक कारण कार्य के फूरियर रूपांतरण को कैसे चित्रित किया जाए।[34]
लाप्लास रूपांतरण
फूरियर रूपांतरण f̂(ξ) लाप्लास परिवर्तन से संबंधित है | F(s), जिसका उपयोग अंतर समीकरण के समाधान और फ़िल्टर (सिग्नल प्रोसेसिंग) के विश्लेषण के लिए भी किया जाता है।
ऐसा हो सकता है कि एक फलन f जिसके लिए फूरियर इंटीग्रल वास्तविक अक्ष पर बिल्कुल भी अभिसरण नहीं करता है | फिर भी सम्मिश्र विमान के कुछ क्षेत्र में परिभाषित एक सम्मिश्र फूरियर रूपांतरण है।
उदाहरण के लिए, यदि f(t) घातीय वृद्धि का है, अर्थात,
कुछ स्थिरांक के लिए C, a ≥ 0, तब[35]
सभी के लिए अभिसरण 2πτ < −a, का दो तरफा f लाप्लास रूपांतर है |.
लाप्लास रूपांतरण का अधिक सामान्य संस्करण (एक तरफा) है |
यदि f कारणात्मक और विश्लेषणात्मक भी है, तब: इस प्रकार, फूरियर ट्रांसफॉर्म को सम्मिश्र डोमेन में विस्तारित करने का कारण है कि इसमें लाप्लास ट्रांसफॉर्म को कारण कार्यों के स्थिति में एक विशेष स्थिति के रूप में सम्मिलित किया गया है | किन्तु चर के परिवर्तन के साथ s = 2πiξ. है |
दूसरे, संभवतः अधिक मौलिक दृष्टिकोण से, लाप्लास अपने रूप से रूपांतरित होता है | जिसमें एक अतिरिक्त घातीय विनियमन शब्द सम्मिलित होता है | जो इसे काल्पनिक रेखा के बाहर अभिसरण करने देता है | जहां फूरियर रूपांतरण परिभाषित होता है। जैसे कि यह सबसे अधिक घातीय रूप से भिन्न श्रृंखला और इंटीग्रल के लिए अभिसरण कर सकता है | जबकि मूल फूरियर अपघटन नहीं कर सकता है | जो भिन्न या महत्वपूर्ण तत्वों के साथ प्रणाली के विश्लेषण को सक्षम करता है। रैखिक सिग्नल प्रोसेसिंग से दो विशेष उदाहरण यूनिट सर्कल पर स्पष्ट ध्रुव-शून्य रद्दीकरण के माध्यम से महत्वपूर्ण कंघी और मिटिगेटिंग फिल्टर से ऑलपास फिल्टर नेटवर्क का निर्माण है। इस तरह के डिजाइन ऑडियो प्रसंस्करण में सामान्य हैं, जहां पुनः क्रिया के रूप में अत्यधिक गैर-रैखिक चरण प्रतिक्रिया की मांग की जाती है।
इसके अतिरिक्त, जब सिग्नल प्रोसेसिंग कार्य के लिए विस्तारित पल्सलाइक आवेग प्रतिक्रियाओं की मांग की जाती है, तो उन्हें उत्पन्न करने का सबसे सरल विधि एक परिपथ होता है | जो एक अलग समय प्रतिक्रिया उत्पन्न करता है, और फिर विलंबित विपरीत और प्रतिपूरक प्रतिक्रिया के माध्यम से इसके विचलन को रद्द कर देता है। वहां, बीच में केवल देरी परिपथ मौलिक फूरियर विवरण स्वीकार करता है, जो महत्वपूर्ण है। पक्ष के दोनों परिपथ अस्थिर हैं, और अभिसारी फूरियर अपघटन को स्वीकार नहीं करते हैं। चूँकि, वे सम्मिश्र विमान (या असतत स्थिति में, जेड-प्लेन) में अभिसरण के समान अर्ध-विमानों के साथ एक लाप्लास डोमेन विवरण स्वीकार करते हैं, जिसमें उनके प्रभाव रद्द हो जाते हैं।
आधुनिक गणित में लाप्लास परिवर्तन को पारंपरिक रूप से एजिस फूरियर विधियों के अनुसार सम्मिलित किया गया है। उन दोनों को कहीं अधिक सामान्य, और अधिक सारगर्भित, हार्मोनिक विश्लेषण के विचार से सम्मिलित किया गया है।
उलटा
यदि f̂ के लिए a ≤ τ ≤ b सम्मिश्र विश्लेषणात्मक है |, तब
कॉची के अभिन्न प्रमेय द्वारा इसलिए, फूरियर व्युत्क्रम सूत्र वास्तविक अक्ष के समानांतर विभिन्न रेखाओं के साथ एकीकरण का उपयोग कर सकता है।[36]
प्रमेय: यदि f(t) = 0 के लिए t < 0, और |f(t)| < Cea|t| कुछ स्थिरांक के लिए C, a > 0, तब
किसी के लिए τ < −a/2π.
इस प्रमेय का अर्थ है लाप्लास परिवर्तन के लिए व्युत्क्रम लाप्लास परिवर्तन,[35]:
किसी के लिए b > a, जहाँ F(s) का f(t) लाप्लास रूपांतरण है |
परिकल्पनाओं को अशक्त किया जा सकता है, जैसा कि कार्लमैन और हंट के परिणामों में है | f(t) e−at प्राणी L1, उसे उपलब्ध कराया f के बंद पड़ोस में सीमित भिन्नता है | t (cf. डिरिचलेट-दिनी प्रमेय ), का मान f पर t बाएँ और दाएँ सीमा के अंकगणितीय माध्य के रूप में लिया जाता है, और परंतु कि इंटीग्रल को कौशी प्रमुख मूल्यों के अर्थ में लिया जाए।[37]
L2 इन उलटा सूत्रों के संस्करण भी उपलब्ध हैं।[38]
यूक्लिडियन अंतरिक्ष पर फूरियर रूपांतरण को किसी भी इच्छानुसार संख्या में n आयामों में परिभाषित किया जा सकता है | जैसा कि एक आयामी स्थिति में होता है | कई परंपराएँ होती हैं। एक अभिन्न फलन के लिए f(x), यह लेख परिभाषा लेता है |
जहाँ x और ξ n-आयामी वेक्टर (गणित) , और x · ξ वैक्टर का डॉट उत्पाद है। वैकल्पिक रूप से, ξ दोहरे स्थान से संबंधित के रूप में देखा जा सकता है | , जिस स्थिति में डॉट उत्पाद का टेन्सर संकुचन बन जाता है | x और ξ, सामान्यतः लिखा जाता है .
ऊपर सूचीबद्ध सभी मूल गुण इसके लिए धारण करते हैं | n-डायमेंशनल फूरियर रूपांतरण, जैसा कि प्लांचरेल और पारसेवल के प्रमेय करते हैं। जब फलन पूर्णांक होता है, तो फूरियर रूपांतरण अभी भी समान रूप से निरंतर होता है और रीमैन-लेबेस्गु लेम्मा धारण करता है।[15]
अनिश्चितता सिद्धांत
सामान्यतया, अधिक केंद्रित f(x) है, इसका फूरियर रूपांतरण जितना अधिक फैला हुआ है | f̂(ξ) होना चाहिए विशेष रूप से, फूरियर रूपांतरण की स्केलिंग संपत्ति को यह कहते हुए देखा जा सकता है | यदि हम किसी फलन को निचोड़ते हैं | x, इसका फूरियर रूपांतरण अंदर की ओर फैला हुआ है | ξ. किसी फलन और उसके फूरियर रूपांतरण दोनों पर इच्छानुसार से ध्यान केंद्रित करना संभव नहीं है।
किसी फलन के संघनन और उसके फूरियर रूपांतरण के बीच व्यापार-बंद को एक अनिश्चितता सिद्धांत के रूप में एक फलन को देखकर औपचारिक रूप दिया जा सकता है और इसके फूरियर समय-आवृत्ति प्रतिनिधित्व पर सहानुभूतिपूर्ण रूप के संबंध में संयुग्मित चर के रूप में बदलते हैं। आवृत्ति डोमेन: लीनियर कैनोनिकल ट्रांसफ़ॉर्मेशन के दृष्टिकोण से, फूरियर ट्रांसफ़ॉर्म टाइम आवृत्ति डोमेन में 90 ° से घूमता है, और सहानुभूतिपूर्ण वेक्टर स्थान को संरक्षित करता है।
मान लीजिए f(x) एक पूर्णांक और वर्ग-पूर्णांक कार्य है। सामान्यता के हानि के बिना, मान लीजिए f(x) सामान्यीकृत है |
यह प्लैंकेरल प्रमेय से अनुसरण करता है f̂(ξ) सामान्यीकृत भी है।
चारों ओर फैल गया x = 0 शून्य के बारे में फैलाव द्वारा मापा जा सकता है |[39]
संभाव्यता के संदर्भ में, यह का क्षण (गणित) है |f(x)|2 शून्य के बारे में।
अनिश्चितता सिद्धांत बताता है कि, यदि f(x) बिल्कुल निरंतर है और कार्य करता है | x·f(x) और f′(x) वर्ग पूर्णांक हैं, तब[11]
- .
समानता केवल स्थिति में प्राप्त की जाती है |
जहाँ σ > 0 इच्छानुसार है और C1 = 4√2/√σ जिससे f है L2-सामान्यीकृत [11] दूसरे शब्दों में, कहाँ f विचरण के साथ एक (सामान्यीकृत) गॉसियन फलन है | σ2/2π, शून्य पर केंद्रित है, और इसका फूरियर रूपांतरण विचरण वाला गॉसियन σ−2/2π फलन है |
वास्तव में, इस असमानता का तात्पर्य है कि:
किसी के लिए x0, ξ0 ∈ R.[40] क्वांटम यांत्रिकी में, संवेग और स्थिति तरंग कार्य प्लैंक के स्थिरांक के एक कारक के अंदर फूरियर रूपांतरण जोड़े हैं। इस स्थिरांक को उचित रूप से ध्यान में रखते हुए, उपरोक्त असमानता हाइजेनबर्ग अनिश्चितता सिद्धांत का कथन बन जाती है।[41] एक शक्तिशाली अनिश्चितता सिद्धांत हिर्शमैन अनिश्चितता है | जिसे इस प्रकार व्यक्त किया गया है |
जहाँ H(p) प्रायिकता घनत्व फलन की अवकल p(x) एन्ट्रॉपी है |
जहाँ लघुगणक किसी भी ऐसे आधार में हो सकते हैं जो सुसंगत हो गॉसियन के लिए समानता प्राप्त की जाती है, जैसा कि पिछले स्थिति में है।
ज्या और कोसाइन रूपांतरित
रूपांतरण के फूरियर के मूल सूत्रीकरण में सम्मिश्र संख्याओं का उपयोग नहीं किया गया, किन्तु ज्या और कोज्या का उपयोग किया गया। सांख्यिकीविद् और अन्य अभी भी इस फॉर्म का उपयोग करते हैं। एक बिल्कुल अभिन्न कार्य f जिसके लिए फूरियर इनवर्जन होल्ड को वास्तविक आवृत्तियों के संदर्भ में विस्तारित किया जा सकता है (नकारात्मक आवृत्तियों से बचना, जिन्हें कभी-कभी शारीरिक रूप से व्याख्या करना कठिन माना जाता है)[42]) λ द्वारा
इसे त्रिकोणमितीय इंटीग्रल या फूरियर इंटीग्रल एक्सपेंशन के रूप में विस्तार कहा जाता है। गुणांक कार्य करता है a और b फूरियर कोसाइन ट्रांसफॉर्म और फूरियर साइन ट्रांसफॉर्म के वेरिएंट का उपयोग करके पाया जा सकता है (सामान्यीकरण, फिर से, मानकीकृत नहीं हैं):
और
पुराना साहित्य दो रूपांतरण कार्यों को संदर्भित करता है, फूरियर कोसाइन रूपांतरण, a, और फूरियर साइन रूपांतरण, b. प्रोग्राम f साइन और कोसाइन ट्रांसफॉर्म का उपयोग करके पुनर्प्राप्त किया जा सकता है |
त्रिकोणमितीय पहचान के साथ। इसे फूरियर का अभिन्न सूत्र कहा जाता है।[35][43][44][45]
गोलाकार हार्मोनिक्स
डिग्री के सजातीय बहुपद हार्मोनिक फलन बहुपदों का समुच्चय दें k पर Rn द्वारा निरूपित किया जाए Ak. समुच्चय Ak डिग्री के ठोस गोलाकार हार्मोनिक्स होते हैं | k. ठोस गोलाकार हार्मोनिक्स आयाम एक में हर्मिट बहुपदों के लिए उच्च आयामों में समान भूमिका निभाते हैं। विशेष रूप से, यदि f(x) = e−π|x|2P(x) कुछ के लिए P(x) में Ak, तब f̂(ξ) = i−k f(ξ). समुच्चय करने दो Hk में बंद हो L2(Rn) प्रपत्र के कार्यों के रैखिक संयोजनों का f(|x|)P(x) जहाँ P(x) में है Ak. अंतरिक्ष L2(Rn) तब रिक्त स्थान का प्रत्यक्ष योग है | Hk और फूरियर प्रत्येक स्थान के नक्शे को रूपांतरित करता है | Hk स्वयं के लिए और प्रत्येक स्थान पर फूरियर रूपांतरण की क्रिया को चिह्नित Hk करना संभव है |[15]
माना f(x) = f0(|x|)P(x) (साथ P(x) में Ak), तब
जहाँ
यहां J(n + 2k − 2)/2 प्रथम प्रकार के बेसेल फलन को क्रम सहित निरूपित करता है | n + 2k − 2/2. कब k = 0 यह रेडियल फलन के फूरियर रूपांतरण के लिए एक उपयोगी सूत्र देता है।[46] यह अनिवार्य रूप से हैंकेल रूपांतरण है। इसके अतिरिक्त, स्थितियों से संबंधित एक साधारण पुनरावृत्ति है | n + 2 और n [47] गणना करने की इजाजत देता है, उदाहरण के लिए, एक आयामी एक से रेडियल फलन के त्रि-आयामी फूरियर रूपांतरण है ।
प्रतिबंध की समस्या
उच्च आयामों में फूरियर रूपांतरण के लिए प्रतिबंध की समस्याओं का अध्ययन करना रोचक हो जाता है। एक समाकलनीय फलन का फूरियर परिवर्तन सतत है और इस फलन का किसी भी समुच्चय पर प्रतिबंध परिभाषित है। किन्तु एक स्क्वायर-इंटीग्रेबल कार्य के लिए फूरियर ट्रांसफॉर्म स्क्वायर इंटीग्रेबल फंक्शन्स का एक सामान्य वर्ग हो सकता है। जैसे, एक के फूरियर रूपांतरण का प्रतिबंध L2(Rn) फलन को माप 0 के समुच्चय पर परिभाषित नहीं किया जा सकता है। यह अभी भी अध्ययन का एक सक्रिय क्षेत्र है जिसमें प्रतिबंध की समस्याओं को समझा जा सकता है Lp के लिए 1 < p < 2. आश्चर्यजनक रूप से, कुछ स्थितियों में एक फूरियर रूपांतरण के प्रतिबंध को एक समुच्चय में परिभाषित करना संभव है S, परंतु S गैर-शून्य वक्रता है। स्थिति जब S इकाई क्षेत्र है Rn विशेष रूचि है। इस स्थिति में इलियास स्टीन प्रतिबंध प्रमेय कहता है कि फूरियर का प्रतिबंध इकाई क्षेत्र में बदल जाता है Rn पर परिबद्ध संचालिका है | Lp परंतु 1 ≤ p ≤ 2n + 2/n + 3.
1 आयाम बनाम उच्च आयामों में फूरियर रूपांतरण के बीच एक उल्लेखनीय अंतर आंशिक योग संचालक से संबंधित है। मापने योग्य सेटों के बढ़ते संग्रह पर विचार करें ER द्वारा अनुक्रमित R ∈ (0,∞): जैसे त्रिज्या की गेंदें R मूल पर केंद्रित, या पक्ष के घन 2R. किसी दिए गए अभिन्न कार्य के लिए f, फलन पर विचार करें fR द्वारा परिभाषित:
इसके अतिरिक्त मान लीजिए f ∈ Lp(Rn). के लिए n = 1 और 1 < p < ∞, यदि कोई लेता है ER = (−R, R), तब fR में विलीन हो जाता है f में Lp जैसा R हिल्बर्ट परिवर्तन की सीमा से अनंत तक जाता है। भोलेपन से उम्मीद की जा सकती है कि वही सच है n > 1. उस स्थिति में ER भुजा की लंबाई वाला घन माना जाता है R, तो अभिसरण अभी भी कायम है। एक अन्य प्राकृतिक उम्मीदवार यूक्लिडियन बॉल है ER = {ξ : |ξ| < R}. इस आंशिक योग संचालक को अभिसरण करने के लिए, यह आवश्यक है कि यूनिट बॉल के लिए गुणक को बाध्य किया जाए Lp(Rn). के लिए n ≥ 2 यह चार्ल्स फ़ेफ़रमैन का एक प्रसिद्ध प्रमेय है कि यूनिट बॉल के लिए गुणक कभी भी परिबद्ध नहीं होता है p = 2.[22]वास्तव में, कब p ≠ 2, इससे पता चलता है कि न केवल हो सकता है fR अभिसरण करने में विफल f में Lp, किन्तु कुछ कार्यों के लिए f ∈ Lp(Rn), fR का Lp अंग भी नहीं है |
कार्य स्पेस पर फूरियर ट्रांसफॉर्म
चालू Lp रिक्त स्थान
चालू L1
फूरियर की परिभाषा अभिन्न सूत्र द्वारा रूपांतरित होती है |
लेबेस्ग पूर्णांक कार्यों के लिए मान्य है f; वह f ∈ L1(Rn) है |
फूरियर रूपांतरण F : L1(Rn) → L∞(Rn) एक परिबद्ध संकारक है। यह उस अवलोकन से अनुसरण करता है |
जो दिखाता है कि इसका संचालक मानदंड 1 से घिरा है। वास्तव में, यह 1 के समान है, जिसे उदाहरण के लिए रेक्ट से देखा जा सकता है। जिसकी छवि L1 अंतरिक्ष का उपसमुच्चय है | C0(Rn) निरंतर कार्यों की संख्या जो अनंत पर शून्य हो जाती है | (रीमैन-लेबेस्गु लेम्मा), चूँकि यह संपूर्ण स्थान नहीं है। दरअसल, छवि का कोई सरल लक्षण वर्णन नहीं है।
चालू L2
चूँकि कॉम्पैक्ट रूप से समर्थित सुचारू कार्य पूर्ण और घने होते हैं | L2(Rn)प्लैंकरेल प्रमेय हमें फूरियर रूपांतरण की परिभाषा को सामान्य कार्यों में विस्तारित करने की अनुमति देता है | L2(Rn) निरंतरता तर्कों द्वारा।फूरियर रूपांतरित होता है | L2(Rn) अब एक साधारण लेबेसेग इंटीग्रल द्वारा नहीं दिया जाता है | चूँकि इसकी गणना एक अनुचित इंटीग्रल द्वारा की जा सकती है | यहाँ इसका अर्थ है कि एक L2 फलन f,
जहां सीमा में लिया जाता है L2 समझ (अधिक सामान्यतः, आप उन कार्यों का अनुक्रम ले सकते हैं जो चौराहे में हैं | L1 और L2 और वह अभिसरण करता है | f में L2-नॉर्म, और फूरियर रूपांतरण को परिभाषित करें f के रूप में L2 इन कार्यों के फूरियर रूपांतरण की सीमा।[48])
फूरियर की कई संपत्तियां रूपांतरित हो जाती हैं L1 तक ले जाना L2, एक उपयुक्त सीमित तर्क द्वारा होता है ।
आगे, F : L2(Rn) → L2(Rn) एकात्मक संचालिका है।[49] एक संचालक के एकात्मक होने के लिए यह दिखाने के लिए पर्याप्त है कि यह विशेषण है और आंतरिक उत्पाद को संरक्षित करता है, इसलिए इस स्थिति में ये फूरियर व्युत्क्रम प्रमेय से इस तथ्य के साथ संयुक्त होते हैं कि किसी भी f, g ∈ L2(Rn) अपने पास
विशेष रूप से, की छवि L2(Rn) स्वयं फूरियर रूपांतरण के अधीन है।
दूसरे पर Lp
फूरियर रूपांतरण की परिभाषा को कार्यों में विस्तारित किया जा सकता है | Lp(Rn) के लिए 1 ≤ p ≤ 2 इस तरह के कार्यों को एक मोटी पूंछ वाले हिस्से में विघटित करके L2 प्लस एक मोटा शरीर का भाग L1. इनमें से प्रत्येक स्थान में, फूरियर एक फलन का रूपांतरण करता है | Lp(Rn) में है Lq(Rn), जहाँ q = p/p − 1 का होल्डर संयुग्म है p (हॉसडॉर्फ-यंग असमानता द्वारा)। चूँकि, को छोड़कर p = 2, छवि आसानी से विशेषता नहीं है। आगे के विस्तार अधिक विधि हो जाते हैं। फूरियर में कार्यों का रूपांतरण Lp रेंज के लिए 2 < p < ∞ वितरण के अध्ययन की आवश्यकता है।[14]वास्तव में, यह दिखाया जा सकता है कि इसमें कार्य हैं Lp साथ p > 2 जिससे फूरियर रूपांतरण को एक कार्य के रूप में परिभाषित न किया जा सके।[15]
टेम्पर्ड वितरण
कोई फूरियर ट्रांसफॉर्म के डोमेन को विस्तारित करने पर विचार कर सकता है | L1 + L2 सामान्यीकृत कार्यों, या वितरण पर विचार करके। वितरण चालू है | Rn अंतरिक्ष पर एक सतत रैखिक कार्यात्मक है | Cc(Rn) एक उपयुक्त टोपोलॉजी से सुसज्जित, कॉम्पैक्ट रूप से समर्थित सुचारू कार्यों का फिर फूरियर रूपांतरण की कार्रवाई पर विचार करने की रणनीति है | Cc(Rn) और द्वैत द्वारा वितरण को पास करें ऐसा करने में बाधा यह है कि फूरियर ट्रांसफॉर्म मैप नहीं करता है | Cc(Rn) को Cc(Rn). वास्तव में एक तत्व का फूरियर रूपांतरित होता है | Cc(Rn) एक खुले समुच्चय पर गायब नहीं हो सकता अनिश्चितता सिद्धांत पर उपरोक्त चर्चा देखें। यहाँ सही स्थान श्वार्ट्ज स्थान का थोड़ा बड़ा स्थान है। फूरियर ट्रांस्फ़ॉर्म श्वार्ट्ज अंतरिक्ष पर एक टोपोलॉजिकल वेक्टर स्पेस के रूप में एक ऑटोमोर्फिज़्म है, और इस तरह इसके दोहरे, टेम्पर्ड डिस्ट्रीब्यूशन के स्पेस पर एक ऑटोमोर्फिज़्म को प्रेरित करता है।[15] टेम्पर्ड डिस्ट्रीब्यूशन में ऊपर बताए गए सभी इंटिग्रेबल कार्य के साथ-साथ पॉलीनॉमियल ग्रोथ के अच्छे व्यवहार वाले कार्य और कॉम्पैक्ट सपोर्ट के डिस्ट्रीब्यूशन सम्मिलित हैं।
टेम्पर्ड डिस्ट्रीब्यूशन के फूरियर रूपांतरण की परिभाषा के लिए, आइए f और g अभिन्न कार्य हो, और चलो f̂ और ĝ उनके फूरियर रूपांतरण क्रमशः हो फिर फूरियर रूपांतरण निम्न गुणन सूत्र का पालन करता है |[15]
हर पूर्णांक फलन f एक वितरण को परिभाषित Tf संबंध द्वारा (प्रेरित) करता है |
श्वार्ट्ज के सभी कार्यों के लिए φ. तो फूरियर रूपांतरण को T̂f का Tf द्वारा परिभाषित करना समझ में आता है |
श्वार्ट्ज के सभी कार्यों के लिए φ. इसे सभी टेम्पर्ड वितरणों तक विस्तारित करना T फूरियर रूपांतरण की सामान्य परिभाषा देता है।
वितरण को विभेदित किया जा सकता है और फूरियर की उपर्युक्त अनुकूलता भिन्नता और कनवल्शन के साथ परिवर्तित होती है, जो टेम्पर्ड वितरण के लिए सही रहती है।
सामान्यीकरण
फूरियर-स्टील्टजेस ट्रांसफॉर्म
एक परिमित माप बोरेल माप का फूरियर रूपांतरण μ पर Rn द्वारा दिया गया है:[50]
यह रूपांतरण पूर्णांकीय कार्यों के फूरियर रूपांतरण के कई गुणों का आनंद लेना जारी रखता है। एक उल्लेखनीय अंतर यह है कि रीमैन-लेबेस्गु लेम्मा उपायों के लिए विफल रहता है।[14] उस स्थिति में dμ = f(x) dx, तो उपरोक्त सूत्र फूरियर रूपांतरण के लिए सामान्य परिभाषा को कम कर देता है | f. उस स्थिति में μ एक यादृच्छिक चर से जुड़ा प्रायिकता वितरण है | X, फूरियर-स्टिल्टजेस ट्रांसफ़ॉर्म विशेषता फलन (संभाव्यता सिद्धांत) से निकटता से संबंधित है, किन्तु संभाव्यता सिद्धांत में विशिष्ट सम्मेलनों को लेते हैं | eixξ के अतिरिक्त e−2πixξ.[11]इस स्थिति में जब वितरण में संभाव्यता घनत्व फलन होता है, तो यह परिभाषा संभाव्यता घनत्व फलन पर प्रयुक्त फूरियर ट्रांसफॉर्म को कम कर देती है, फिर से स्थिरांक की एक अलग पसंद के साथ होते है ।
उपायों के लक्षण वर्णन के लिए फूरियर रूपांतरण का उपयोग किया जा सकता है। बोचनर की प्रमेय बताती है कि फूरियर-स्टिल्टजेस सर्कल पर एक सकारात्मक माप के परिवर्तन के रूप में कौन से कार्य उत्पन्न हो सकते हैं ।[14]
इसके अतिरिक्त, डिराक डेल्टा फलन, चूँकि एक फलन नहीं है, एक परिमित बोरेल माप है। इसका फूरियर रूपांतरण एक स्थिर कार्य है (जिसका विशिष्ट मूल्य उपयोग किए गए फूरियर रूपांतरण के रूप पर निर्भर करता है)।
कनियादकिस κ-फूरियर रूपांतरण
कनिदाकिस सांख्यिकी κ-फूरियर रूपांतरण कनिदाकिस κ-फूरियर रूपांतरण, कनिदाकिस सांख्यिकी से संबद्ध फूरियर रूपांतरण का κ-विरूपण है | जिसे इस प्रकार परिभाषित किया गया है |[51]
जहाँ एक κ-नंबर है और कनियाडाकिस सांख्यिकी#कनियाडाकिस एंट्रॉपी से जुड़ा एंट्रोपिक इंडेक्स है।
कनिदाकिस सांख्यिकी#κ-फूरियर रूपांतरण κ-फूरियर रूपांतरण κ-फूरियर श्रृंखला पर आधारित है |[52] जिसमें मौलिक फूरियर श्रृंखला और फूरियर रूपांतरण विशेष स्थिति हैं | सीमित स्थिति यह परिवर्तन विषम रूप से लॉग-आवधिक व्यवहार (या विकृत द्वारा κ-विकृत चरण) को प्रयुक्त करता है ) और तरंगिका जैसे व्यवहार के बाद एक अवमंदन कारक (). है |
स्थानीय रूप से कॉम्पैक्ट एबेलियन समूह
फूरियर रूपांतरण को किसी भी स्थानीय कॉम्पैक्ट एबेलियन समूह के लिए सामान्यीकृत किया जा सकता है। एक स्थानीय रूप से कॉम्पैक्ट एबेलियन समूह एक एबेलियन समूह है | जो एक ही समय में स्थानीय रूप से कॉम्पैक्ट हॉसडॉर्फ स्पेस है | जिससे समूह संचालन निरंतर हो यदि G स्थानीय रूप से कॉम्पैक्ट एबेलियन समूह है | इसका एक अनुवाद अपरिवर्तनीय उपाय है μ, हार उपाय कहा जाता है। स्थानीय रूप से कॉम्पैक्ट एबेलियन समूह के लिए G, अलघुकरणीय का समुच्चय, अर्थात एक-आयामी, एकात्मक अभ्यावेदन इसके वर्ण समूह कहलाते हैं। इसकी प्राकृतिक समूह संरचना और बिंदुवार अभिसरण की टोपोलॉजी के साथ, वर्णों का समूह Ĝ खुद एक स्थानीय रूप से कॉम्पैक्ट एबेलियन समूह है, जिसे पोंट्रीगिन डुअल ऑफ कहा जाता है G. एक फलन के लिए f में L1(G), इसके फूरियर रूपांतरण द्वारा परिभाषित किया गया है |[14]
रीमैन-लेबेस्गु लेम्मा इस स्थिति में है | f̂(ξ) अनंत पर Ĝ लुप्त होने वाला कार्य है |
फूरियर चालू हो गया T= आर/जेड एक उदाहरण है | यहाँ T स्थानीय रूप से कॉम्पैक्ट एबेलियन समूह और हार माप है | μ पर T [0,1) पर लेबेस्ग माप के रूप में सोचा जा सकता है। प्रतिनिधित्व पर विचार करें T सम्मिश्र तल पर C यह एक 1-आयामी सम्मिश्र वेक्टर स्पेस है। अभ्यावेदन का एक समूह है (जो तब से अप्रासंगिक हैं C 1-मंद है) जहाँ के लिए .
ऐसे प्रतिनिधित्व का चरित्र, वह निशान है प्रत्येक के लिए और , है | अपने आप परिमित समूह के प्रतिनिधित्व के स्थिति में, समूह की वर्ण तालिका G सदिशों की पंक्तियाँ हैं जैसे कि प्रत्येक पंक्ति एक अलघुकरणीय प्रतिनिधित्व का चरित्र है | G, और ये वैक्टर मैप करने वाले क्लास फ़ंक्शंस के स्थान का एक ऑर्थोनॉर्मल आधार बनाते हैं | G को C शूर की लेम्मा द्वारा अब समूह T अब परिमित नहीं है | किन्तु फिर भी कॉम्पैक्ट है, और यह वर्ण तालिका की ऑर्थोनॉर्मलिटी को निरंतर रखता है। तालिका की प्रत्येक पंक्ति कार्य है | का और दो वर्ग कार्यों के बीच आंतरिक उत्पाद (सभी कार्य तब से वर्ग कार्य हैं T एबेलियन है) की तरह परिभाषित किया गया है | सामान्यीकरण कारक के साथ . क्रम वर्ग कार्यों के स्थान का एक अलौकिक आधार है |
किसी भी प्रतिनिधित्व के लिए V एक परिमित समूह का G, स्पैन के रूप में व्यक्त किया जा सकता है | ( के इर्रेप्स हैं | G), ऐसा है कि . इसी प्रकार के लिए और , . पोंट्रियागिन दोहरी है | और के लिए , इसका फूरियर रूपांतरण है |
गेलफैंड ट्रांसफॉर्म
फूरियर रूपांतरण भी गेलफैंड रूपांतरण का एक विशेष स्थिति है। इस विशेष संदर्भ में, यह ऊपर परिभाषित पोंट्रीगिन द्वैत मानचित्र से निकटता से संबंधित है।
एक एबेलियन स्थानीय रूप स्थानीय रूप से कॉम्पैक्ट स्थान हॉसडॉर्फ स्पेस टोपोलॉजिकल समूह दिया गया G, जैसा कि पहले हम अंतरिक्ष पर विचार करते हैं | L1(G), एक हार उपाय का उपयोग करके परिभाषित किया गया गुणन के रूप में कनवल्शन के साथ, L1(G) एक एबेलियन बनच बीजगणित है। इसमें एक इनवोल्यूशन (गणित) भी दिया गया है |
संभवतः सबसे बड़े के संबंध में पूर्णता लेना C*-नॉर्म अपना आवरण देता है | C*- बीजगणित, समूह कहलाता है | C*-बीजगणित C*(G) का G. (कोई भी C*-आदर्श चालू L1(G) से घिरा हुआ है | L1 मानदंड, इसलिए उनका सर्वोच्च अस्तित्व है।)
किसी एबेलियन को दिया C*-बीजगणित A, गेलफैंड रूपांतरण के बीच एक समरूपता देता है | A और C0(A^), जहाँ A^ गुणक रेखीय फलन है, अर्थात एक आयामी निरूपण, पर A अशक्त के साथ- * टोपोलॉजी मानचित्र केवल द्वारा दिया गया है |
यह पता चला है कि के गुणक रैखिक कार्य C*(G), उपयुक्त पहचान के बाद, बिल्कुल के पात्र हैं | G, और गेलफैंड रूपांतरण, जब सघन उपसमुच्चय तक सीमित होता है | L1(G) फूरियर-पोंट्रीगिन रूपांतरण है।
कॉम्पैक्ट गैर-अबेलियन समूह
फूरियर रूपांतरण को गैर-अबेलियन समूह पर कार्यों के लिए भी परिभाषित किया जा सकता है, परंतु कि समूह कॉम्पैक्ट स्थान हो। इस धारणा को हटाते हुए कि अंतर्निहित समूह एबेलियन है | अलघुकरणीय एकात्मक अभ्यावेदन को सदैव एक आयामी नहीं होना चाहिए। इसका कारण यह है कि एक गैर-अबेलियन समूह पर फूरियर रूपांतरण हिल्बर्ट अंतरिक्ष संचालको के रूप में मान लेता है ।[53] कॉम्पैक्ट समूहों पर फूरियर परिवर्तन प्रतिनिधित्व सिद्धांत में एक प्रमुख उपकरण है |[54] और गैर-कम्यूटेटिव हार्मोनिक विश्लेषण है ।
माना G एक कॉम्पैक्ट हॉसडॉर्फ स्पेस टोपोलॉजिकल ग्रुप बनें माना Σ निरूपण के एक निश्चित विकल्प के साथ, परिमित-आयामी इरेड्यूसेबल एकात्मक निरूपण के सभी समरूपता वर्गों के संग्रह को निरूपित करें U(σ) हिल्बर्ट अंतरिक्ष पर Hσ परिमित आयाम का dσ प्रत्येक के लिए σ ∈ Σ. यदि μ एक परिमित बोरेल माप है | G, फिर फूरियर-स्टील्टजेस का रूपांतरण μ संचालक चालू है Hσ द्वारा परिभाषित है |
जहाँ U(σ) का सम्मिश्र-संयुग्मित प्रतिनिधित्व है U(σ) अभिनय कर रहे Hσ. है | यदि μ हार माप के संबंध में बिल्कुल निरंतर है | बाएं-अपरिवर्तनीय संभाव्यता माप λ पर G, रैडॉन-निकोडिम प्रमेय के रूप में
कुछ के लिए f ∈ L1(λ), एक के फूरियर रूपांतरण की पहचान करता है f के फूरियर-स्टील्टजेस रूपांतरण के साथ μ. है |
मानचित्रण
बनच अंतरिक्ष के बीच एक समरूपता को परिभाषित करता है | M(G) परिमित बोरेल उपायों ( आरसीए अंतरिक्ष देखें) और बनच अंतरिक्ष के एक बंद उप-स्थान C∞(Σ) सभी अनुक्रमों से मिलकर E = (Eσ) द्वारा अनुक्रमित Σ (बाध्य) रैखिक संचालको की Eσ : Hσ → Hσ जिसके लिए मानदंड है |
कनवल्शन प्रमेय का प्रमाणित है कि, इसके अतिरिक्त, बनच रिक्त स्थान का यह समरूपता वास्तव में C* सी * - बीजगणित का एक उप-स्थान में एक सममितीय समरूपता है। C∞(Σ). गुणा चालू M(G) उपायों के कनवल्शन और इन्वॉल्वमेंट * द्वारा परिभाषित किया गया है |
और C∞(Σ) एक प्राकृतिक है C*हिल्बर्ट अंतरिक्ष संचालको के रूप में बीजगणित संरचना है \।
पीटर-वेइल प्रमेय धारण करता है, और फूरियर व्युत्क्रम सूत्र (प्लान्चेरेल प्रमेय) का एक संस्करण इस प्रकार है | यदि f ∈ L2(G), तब
जहां L2 योग को अभिसरण के रूप में समझा जाता है |
फूरियर के गैर-अनुवर्ती स्थिति में परिवर्तन के सामान्यीकरण ने भी आंशिक रूप से गैर-अनुसूचित ज्यामिति के विकास में योगदान दिया है। इस संदर्भ में, गैर-अनुवर्ती समूहों में फूरियर रूपांतरण का एक स्पष्ट सामान्यीकरण तन्नाका-क्रेइन द्वैत है | जो प्रतिनिधित्व की श्रेणी के साथ वर्णों के समूह को प्रतिस्थापित करता है। चूँकि, यह हार्मोनिक कार्यों के साथ संबंध खो देता है।
विकल्प
सिग्नल प्रोसेसिंग नियमो में, एक फलन (समय का) सही समय संकल्प के साथ सिग्नल का प्रतिनिधित्व होता है | किन्तु कोई आवृत्ति जानकारी नहीं होती है | जबकि फूरियर ट्रांसफॉर्म में पूर्ण आवृत्ति संकल्प होता है | किन्तु कोई समय की जानकारी नहीं होती है | फूरियर की परिमाण एक बिंदु पर बदलती है कितनी आवृत्ति पदार्थ है | किन्तु स्थान केवल चरण (एक बिंदु पर फूरियर रूपांतरण का तर्क) द्वारा दिया जाता है, और स्थायी तरंगें समय में स्थानीयकृत नहीं होती हैं - एक साइन लहर बिना क्षय के अनंत तक जारी रहती है। यह उन संकेतों का विश्लेषण करने के लिए फूरियर रूपांतरण की उपयोगिता को सीमित करता है जो समय में स्थानीयकृत होते हैं, विशेष रूप से क्षणिक (ध्वनिकी) , या परिमित सीमा के किसी भी संकेत का उपयोग होता है ।
फूरियर रूपांतरण के विकल्प के रूप में, समय-आवृत्ति विश्लेषण में, समय-आवृत्ति रूपांतरण या समय-आवृत्ति वितरण का उपयोग एक ऐसे रूप में संकेतों का प्रतिनिधित्व करने के लिए किया जाता है | जिसमें कुछ समय की जानकारी और कुछ आवृत्ति की जानकारी होती है | अनिश्चितता सिद्धांत द्वारा, एक व्यापार होता है | इन के बीच बंद ये फूरियर रूपांतरण के सामान्यीकरण हो सकते हैं | जैसे कम समय के फूरियर रूपांतरण या भिन्नात्मक फूरियर रूपांतरण, या संकेतों का प्रतिनिधित्व करने के लिए अन्य कार्य, जैसा कि वेवलेट रूपांतरण और चिरलेट रूपांतरण में होता है | (निरंतर) फूरियर रूपांतरण के तरंगिका एनालॉग के साथ निरंतर तरंगिका परिवर्तन है।[23]
अनुप्रयोग
एक डोमेन (समय या आवृत्ति) में किए गए रैखिक संचालन के दूसरे डोमेन में संबंधित संचालन होते हैं | जो कभी-कभी प्रदर्शन करना सरल होता है। समय डोमेन में व्युत्पन्न का संचालन आवृत्ति से गुणा के अनुरूप होता है | इसलिए आवृत्ति डोमेन में विश्लेषण करने के लिए कुछ अंतर समीकरण सरल होते हैं। साथ ही, समय डोमेन में दृढ़ संकल्प आवृत्ति डोमेन में सामान्य गुणा के अनुरूप होता है | (कनवॉल्यूशन प्रमेय देखें)। वांछित संचालन करने के बाद, परिणाम के परिवर्तन को समय डोमेन में वापस लाया जा सकता है। हार्मोनिक विश्लेषण आवृत्ति और समय डोमेन के बीच संबंधों का व्यवस्थित अध्ययन है | जिसमें एक या दूसरे में सरल प्रकार के कार्य या संचालन सम्मिलित हैं, और आधुनिक गणित के कई क्षेत्रों से गहरे संबंध हैं।
अंतर समीकरणों का विश्लेषण
फूरियर रूपांतरण का संभवतः सबसे महत्वपूर्ण उपयोग आंशिक अंतर समीकरणों को हल करना है। उन्नीसवीं सदी के गणितीय भौतिकी के कई समीकरणों को इस तरह से समझा जा सकता है। फूरियर ने ऊष्मा समीकरण का अध्ययन किया, जो एक आयाम में और आयामहीन इकाइयों में है |
हम जो उदाहरण देंगे, वह थोड़ा अधिक कठिन है, एक आयाम में तरंग समीकरण है, |
सदैव की तरह, समस्या समाधान खोजने की नहीं है: अपरिमित रूप से अनेक हैं। समस्या तथाकथित सीमा समस्या की है: एक समाधान खोजें जो सीमा की नियमो को पूरा करता है \
यहां, f और g कार्य दिए गए हैं। ऊष्मा समीकरण के लिए, केवल एक सीमा स्थिति की आवश्यकता हो सकती है |(सामान्यतः पहली वाली)। किन्तु तरंग समीकरण के लिए अभी भी अपरिमित रूप से अनेक हल हैं | y जो पहली सीमा नियम को पूरा करते हैं। किन्तु जब कोई दोनों शर्तें लगाता है, तो केवल एक ही संभव समाधान होता है।
फूरियर रूपांतरण को खोजना सरल है | ŷ समाधान की तुलना में सीधे समाधान खोजने के लिए ऐसा इसलिए है क्योंकि फूरियर रूपांतरण फूरियर-द्वैत चर द्वारा गुणन में भिन्नता लेता है, और इसलिए मूल फलन पर प्रयुक्त आंशिक अंतर समीकरण रूपांतरित फलन पर प्रयुक्त दोहरे चर के बहुपद कार्यों द्वारा गुणन में परिवर्तित हो जाता है। बाद में ŷ निर्धारित है, हम खोजने के लिए उलटा फूरियर रूपांतरण प्रयुक्त कर सकते हैं | y.
फूरियर की विधि इस प्रकार है। सबसे पहले, ध्यान दें कि रूपों का कोई भी कार्य
तरंग समीकरण को संतुष्ट करता है। इन्हें प्राथमिक समाधान कहा जाता है।
दूसरा, ध्यान दें कि इसलिए कोई भी अभिन्न
अब यह फलन के फूरियर संश्लेषण के सूत्र जैसा दिखता है। वास्तव में, यह का वास्तविक व्युत्क्रम फूरियर रूपांतरण है
a± और b± चर में x. तीसरा कदम यह जांचना है कि विशिष्ट अज्ञात गुणांक कार्यों को कैसे खोजा जाए a± और b± कि करने के लिए नेतृत्व करेंगे y सीमा नियमो को पूरा करना हम इन समाधानों के मूल्यों में रुचि रखते हैं | t = 0. तो हम समुच्चय करेंगे t = 0. यह मानते हुए कि फूरियर व्युत्क्रम के लिए आवश्यक शर्तें संतुष्ट हैं | फिर हम फूरियर साइन और कोज्या रूपांतरण (चर में) पा सकते हैं | x) दोनों पक्षों की और प्राप्त करें |
और
इसी प्रकार, का व्युत्पन्न लेना y इसके संबंध में t और फिर फूरियर साइन और कोसाइन ट्रांसफॉर्मेशन को प्रयुक्त करने से उतपन्न होती है |
और
ये चार अज्ञात के लिए चार रेखीय समीकरण हैं | a± और b±, सीमा स्थितियों के फूरियर साइन और कोसाइन रूपांतरण के संदर्भ में, जो प्राथमिक बीजगणित द्वारा आसानी से हल किए जाते हैं | परंतु कि ये परिवर्तन पाए जा सकें ।
सारांश में, हमने प्राथमिक समाधानों का एक समुच्चय चुना, जिसके द्वारा पैरामीट्रिज्ड किया गया ξ, जिनमें से सामान्य समाधान मापदंड पर एक अभिन्न के रूप में एक (निरंतर) रैखिक संयोजन होगा | ξ. किन्तु यह इंटीग्रल फूरियर इंटीग्रल के रूप में था। अगला कदम इन इंटीग्रल के संदर्भ में सीमा नियमो को व्यक्त करना था, और उन्हें दिए गए कार्यों के समान समुच्चय करना था | f और g. किन्तु व्युत्पन्न के फूरियर रूपांतरण के गुणों के कारण इन भावों ने फूरियर इंटीग्रल का रूप भी ले लिया। अंतिम चरण दोनों पक्षों में फूरियर परिवर्तन को प्रयुक्त करके फूरियर व्युत्क्रम का लाभ उठाना था, इस प्रकार गुणांक कार्यों के लिए भाव प्राप्त करना a± और b± दी गई सीमा नियमो के संदर्भ में f और g. है |
उच्च दृष्टिकोण से, फूरियर की प्रक्रिया को अवधारणात्मक रूप से अधिक सुधारा जा सकता है। चूंकि दो चर हैं, हम दोनों में फूरियर रूपांतरण का उपयोग करेंगे x और t फूरियर के रूप में काम करने के अतिरिक्त, जो केवल स्थानिक चर में परिवर्तित हो गया। ध्यान दें कि ŷ वितरण के अर्थ में विचार किया जाना चाहिए y(x, t) नहीं होने जा रहा है | L1: एक लहर के रूप में, यह समय के माध्यम से बनी रहेगी और इस प्रकार यह एक क्षणिक घटना नहीं है। किन्तु यह बाउंड होगा और इसलिए इसके फूरियर रूपांतरण को वितरण के रूप में परिभाषित किया जा सकता है। इस समीकरण के लिए प्रासंगिक फूरियर रूपांतरण के परिचालन गुण हैं कि इसमें भिन्नता होती है x से गुणा करना 2πiξ और के संबंध में भेदभाव t से गुणा करना 2πif जहाँ f आवृत्ति है। तब तरंग समीकरण एक बीजगणितीय समीकरण ŷ बन जाता है |
यह आवश्यकता के समान है | ŷ(ξ, f) = 0 जब तक ξ = ±f. तुरंत, यह बताता है कि हमने पहले किए गए प्राथमिक समाधानों का चुनाव इतना अच्छा काम क्यों किया: प्रकट है | f̂ = δ(ξ ± f) समाधान होंगे इन डेल्टा कार्यों के लिए फूरियर व्युत्क्रम को प्रयुक्त करते हुए, हम उन प्रारंभिक समाधानों को प्राप्त करते हैं | जिन्हें हमने पहले चुना था। किन्तु उच्च दृष्टिकोण से, कोई प्राथमिक समाधान नहीं चुनता है | किन्तु उन सभी वितरणों के स्थान पर विचार करता है | जो (पतित) शांकव पर समर्थित हैं ξ2 − f2 = 0. है |
हम शांकव पर समर्थित वितरणों पर भी विचार कर सकते हैं | जो रेखा पर एक चर के वितरण द्वारा दिए गए हैं ξ = f लाइन पर प्लस वितरण ξ = −f इस प्रकार है | यदि Φ कोई परीक्षण कार्य है |
जहाँ s+, और s−, एक चर के वितरण हैं।
फिर फूरियर उलटा देता है | सीमा की स्थिति के लिए, कुछ ऐसा ही जो हमारे पास अधिक ठोस रूप से ऊपर था (पुट Φ(ξ, f) = e2πi(xξ+tf), जो स्पष्ट रूप से बहुपद वृद्धि का है):
और
अब, पहले की तरह, चर में एक-चर फूरियर रूपांतरण प्रयुक्त करना x इन कार्यों के लिए x दो अज्ञात बंटनों में दो समीकरण देता है | s± (यदि सीमा की स्थितियाँ हैं तो इसे सामान्य कार्यों के रूप में लिया जा सकता है | L1 या L2).
एक गणनात्मक दृष्टिकोण से, निश्चित रूप से दोष यह है कि किसी को पहले सीमा स्थितियों के फूरियर रूपांतरणों की गणना करनी चाहिए | फिर इनसे समाधान इकट्ठा करना चाहिए, और फिर एक व्युत्क्रम फूरियर रूपांतरण की गणना करनी चाहिए। बंद फार्म सूत्र दुर्लभ हैं सिवाय इसके कि जब कुछ ज्यामितीय समरूपता का शोषण किया जा सकता है, और संख्यात्मक गणनाएं इंटीग्रल की दोलनशील प्रकृति के कारण कठिन होती हैं | जो अभिसरण को धीमा और अनुमान लगाने में कठिन बनाती हैं। व्यावहारिक गणनाओं के लिए, अन्य विधियों का अधिकांशतः उपयोग किया जाता है।
बीसवीं शताब्दी ने बहुपद गुणांकों के साथ सभी रेखीय आंशिक अंतर समीकरणों के लिए इन विधियों का विस्तार देखा है, और फूरियर अभिन्न संचालकों को सम्मिलित करने के लिए फूरियर रूपांतरण की धारणा का विस्तार करते हुए, कुछ गैर-रैखिक समीकरणों को भी सम्मिलित किया है।
फूरियर रूपांतरण स्पेक्ट्रोस्कोपी
फूरियर रूपांतरण का उपयोग परमाणु चुंबकीय अनुनाद (एनएमआर) और अन्य प्रकार की स्पेक्ट्रोस्कोपी में भी किया जाता है, उदाहरण इन्फ्रारेड (फूरियर रूपांतरण अवरक्त स्पेक्ट्रोस्कोपी )। एनएमआर में एक घातीय आकार का मुक्त प्रेरण क्षय (एफआईडी) संकेत समय डोमेन में प्राप्त किया जाता है और फूरियर-रूपांतरित आवृत्ति डोमेन में लोरेंट्ज़ियन लाइन-आकार में बदल जाता है। फूरियर रूपांतरण का उपयोग चुंबकीय अनुनाद इमेजिंग (एमआरआई) और मास स्पेक्ट्रोमेट्री में भी किया जाता है।
क्वांटम यांत्रिकी
फूरियर रूपांतरण क्वांटम यांत्रिकी में कम से कम दो अलग-अलग विधिया से उपयोगी है। आरंभ करने के लिए, क्वांटम यांत्रिकी की मूलभूत वैचारिक संरचना हाइजेनबर्ग अनिश्चितता सिद्धांत द्वारा जुड़े पूरक चर के जोड़े के अस्तित्व को दर्शाती है। उदाहरण के लिए, एक आयाम में, स्थानिक चर q का कहना है, एक कण, केवल क्वांटम यांत्रिक स्थिति संचालक द्वारा संवेग के बारे में जानकारी खोने की कीमत पर मापा जा सकता है p कण का। इसलिए, कण की भौतिक स्थिति या तो एक फलन द्वारा वर्णित की जा सकती है, जिसे वेव फलन कहा जाता है q या के एक फलन द्वारा p किन्तु दोनों चरों के कार्य द्वारा नहीं। चर p को संयुग्मी चर कहा जाता है q. मौलिक यांत्रिकी में, एक कण की भौतिक स्थिति (प्रदर्शन की सादगी के लिए एक आयाम में विद्यमान) दोनों को निश्चित मान निर्दिष्ट करके दी जाएगी। p और q साथ-साथ। इस प्रकार, सभी संभावित भौतिक अवस्थाओं का समुच्चय एक द्वि-आयामी वास्तविक सदिश समष्टि है p-अक्ष और ए q-अक्ष को चरण स्थान कहा जाता है।
इसके विपरीत, क्वांटम यांत्रिकी इस स्थान के ध्रुवीकरण को इस अर्थ में चुनती है कि यह एक-आधे आयाम का एक उप-स्थान चुनता है, उदाहरण के लिए, q-अक्ष अकेले, किन्तु केवल बिंदुओं पर विचार करने के अतिरिक्त, इस अक्ष पर सभी सम्मिश्र-मूल्यवान तरंग कार्यों का समुच्चय लेता है। फिर भी, का चयन p-एक्सिस एक समान रूप से वैध ध्रुवीकरण है, जो कण के संभावित भौतिक अवस्थाओं के समुच्चय का एक अलग प्रतिनिधित्व प्रदान करता है जो फूरियर परिवर्तन द्वारा पहले प्रतिनिधित्व से संबंधित है |
शारीरिक रूप से वसूली योग्य राज्य हैं L2, और इसलिए प्लांचरेल प्रमेय द्वारा, उनके फूरियर रूपांतर भी हैं | L2. (ध्यान दें कि चूंकि q दूरी की इकाइयों में है और p संवेग की इकाइयों में है, घातांक में प्लैंक के स्थिरांक की उपस्थिति प्रतिपादक को गैरविमीयकरण बनाती है, जैसा कि होना चाहिए।)
इसलिए, फूरियर रूपांतरण का उपयोग कण की स्थिति का प्रतिनिधित्व करने के एक विधि से, स्थिति के एक तरंग फलन द्वारा, कण की स्थिति का प्रतिनिधित्व करने के दूसरे विधि से: गति के तरंग फलन द्वारा किया जा सकता है। असीम रूप से कई अलग-अलग ध्रुवीकरण संभव हैं और सभी समान रूप से मान्य हैं। फूरियर रूपांतरण द्वारा राज्यों को एक प्रतिनिधित्व से दूसरे में बदलने में सक्षम होना न केवल सुविधाजनक है किन्तु हाइजेनबर्ग अनिश्चितता सिद्धांत का अंतर्निहित कारण भी है।
क्वांटम यांत्रिकी और क्वांटम क्षेत्र सिद्धांत दोनों में फूरियर रूपांतरण का अन्य उपयोग प्रयुक्त तरंग समीकरण को हल करना है। गैर-सापेक्षवादी क्वांटम यांत्रिकी में, एक-आयाम में एक समय-भिन्न तरंग फलन के लिए श्रोडिंगर का समीकरण, बाहरी शक्तियों के अधीन नहीं है, है |
यह काल्पनिक इकाई की उपस्थिति को छोड़कर ऊष्मा समीकरण के समान है | i. इस समीकरण को हल करने के लिए फूरियर विधियों का उपयोग किया जा सकता है।
संभावित ऊर्जा फलन द्वारा दी गई क्षमता की उपस्थिति में V(x), समीकरण बन जाता है |
प्रारंभिक समाधान, जैसा कि हमने उन्हें ऊपर बताया, कण के तथाकथित स्थिर राज्य हैं, और फूरियर के एल्गोरिदम, जैसा कि ऊपर वर्णित है, अभी भी भविष्य के विकास की सीमा मूल्य समस्या को हल करने के लिए उपयोग किया जा सकता है। ψ के लिए इसके मान दिए गए हैं t = 0. क्वांटम यांत्रिकी में इनमें से कोई भी दृष्टिकोण बहुत व्यावहारिक उपयोग नहीं है। सीमा मूल्य की समस्याएं और तरंग फलन का समय-विकास अधिक व्यावहारिक हित नहीं है: यह स्थिर राज्य हैं जो सबसे महत्वपूर्ण हैं।
सापेक्षवादी क्वांटम यांत्रिकी में, श्रोडिंगर का समीकरण मौलिक भौतिकी में सामान्य रूप से एक लहर समीकरण बन जाता है, सिवाय इसके कि सम्मिश्र-मूल्यवान तरंगों पर विचार किया जाता है। एक सरल उदाहरण, अन्य कणों या क्षेत्रों के साथ बातचीत के अभाव में, मुक्त एक आयामी क्लेन-गॉर्डन-श्रोडिंगर-फॉक समीकरण है |
यह, गणितीय दृष्टिकोण से, ऊपर हल किए गए मौलिक भौतिकी के तरंग समीकरण के समान है (किन्तु एक सम्मिश्र-मूल्यवान तरंग के साथ, जो विधियों में कोई अंतर नहीं करता है)। क्वांटम क्षेत्र सिद्धांत में यह बहुत उपयोगी है: तरंग के प्रत्येक अलग फूरियर घटक को एक अलग हार्मोनिक ऑसिलेटर के रूप में माना जा सकता है और फिर परिमाणित किया जा सकता है, एक प्रक्रिया जिसे दूसरी परिमाणीकरण के रूप में जाना जाता है। गैर-तुच्छ अंतःक्रियाओं से निपटने के लिए फूरियर विधियों को भी अनुकूलित किया गया है।
अंत में, क्वांटम हार्मोनिक ऑसिलेटर लैडर संचालक विधि की क्वांटम हार्मोनिक ऑसिलेटर की व्याख्या की जा सकती है, उदाहरण के लिए मेहलर कर्नेल भौतिकी संस्करण के माध्यम से, आइगेनफंक्शन के क्वांटम यांत्रिकी में समरूपता के रूप में होता है |[55]
सिग्नल प्रोसेसिंग
फूरियर रूपांतरण का उपयोग समय-श्रृंखला के वर्णक्रमीय विश्लेषण के लिए किया जाता है। सांख्यिकीय सिग्नल प्रोसेसिंग का विषय, चूँकि, सामान्यतः फूरियर रूपांतरण को सिग्नल में ही प्रयुक्त नहीं करता है। यहां तक कि यदि एक वास्तविक संकेत वास्तव में क्षणिक है, तो व्यवहार में यह पाया गया है कि एक फलन (या, वैकल्पिक रूप से, एक स्टोचैस्टिक प्रक्रिया) द्वारा सिग्नल को मॉडल करने की सलाह दी जाती है | जो कि इस अर्थ में स्थिर है कि इसकी विशेषता गुण सभी समय पर स्थिर हैं। इस तरह के एक फलन का फूरियर रूपांतरण सामान्य अर्थों में उपस्थित नहीं है, और संकेतों के विश्लेषण के लिए इसे अधिक उपयोगी पाया गया है | इसके अतिरिक्त अपने स्वत: सहसंबंध फलन के फूरियर रूपांतरण को लेना है ।
स्वतः सहसंबंध फलन R एक फलन का f द्वारा परिभाषित किया गया है |
यह कार्य समय-अंतराल का एक कार्य है | τ के f सहसंबद्ध होना मूल्यों के बीच समाप्त हो रहा है।
अधिकांश कार्यों के लिए f जो व्यवहार में होता है, R समय-अंतराल का एक परिबद्ध सम फलन है τ और ठेठ ध्वनि संकेतों के लिए यह अधिकतम के साथ τ = 0 समान रूप से निरंतर हो जाता है |
ऑटोकोरिलेशन फलन, अधिक उचित रूप से ऑटोकोवेरियन फलन कहा जाता है, जब तक कि यह कुछ उचित फैशन में सामान्य नहीं होता है, मूल्यों के बीच सहसंबंध की ताकत को मापता है f एक समय अंतराल से अलग। यह सहसंबंध खोजने का एक विधि है | f अपने अतीत के साथ। यह संकेतों के विश्लेषण के अतिरिक्त अन्य सांख्यिकीय कार्यों के लिए भी उपयोगी है। उदाहरण के लिए, यदि f(t) समय पर तापमान का प्रतिनिधित्व करता है | t24 घंटे के अंतराल पर तापमान के साथ एक शक्तिशाली सहसंबंध की अपेक्षा की जाती है ।
इसमें फूरियर रूपांतरण है |
इस फूरियर रूपांतरण को स्पेक्ट्रल घनत्व पावर स्पेक्ट्रल घनत्व फलन कहा जाता है | f. (जब तक सभी आवधिक घटकों को पहले फ़िल्टर नहीं किया जाता है | f, यह इंटीग्रल अलग हो जाएगा, किन्तु ऐसी आवधिकताओं को फ़िल्टर करना सरल है।)
पावर स्पेक्ट्रम, जैसा कि इस घनत्व फलन द्वारा इंगित किया गया है | P, आवृत्ति द्वारा डेटा में योगदान किए गए विचरण की मात्रा को मापता है | ξ. विद्युत संकेतों में, विचरण औसत शक्ति (ऊर्जा प्रति इकाई समय) के समानुपाती होता है, और इसलिए शक्ति स्पेक्ट्रम बताता है कि सिग्नल की औसत शक्ति में विभिन्न आवृत्तियों का कितना योगदान होता है। इस प्रक्रिया को समय-श्रृंखला का वर्णक्रमीय विश्लेषण कहा जाता है और डेटा के विचरण के सामान्य विश्लेषण के अनुरूप है जो समय-श्रृंखला (एनोवा ) नहीं है।
इस अर्थ में किस आवृत्ति का ज्ञान महत्वपूर्ण है | फिल्टर के उचित डिजाइन के लिए और उपकरणों को मापने के उचित मूल्यांकन के लिए महत्वपूर्ण है। यह डेटा के उत्पादन के लिए जिम्मेदार घटनाओं के वैज्ञानिक विश्लेषण के लिए भी उपयोगी हो सकता है।
एक सिग्नल के पावर स्पेक्ट्रम को एक संकीर्ण बैंड के बाहर सभी आवृत्तियों को फ़िल्टर करने के बाद सिग्नल में बनी औसत शक्ति को मापकर लगभग सीधे मापा जा सकता है।
वर्णक्रमीय विश्लेषण दृश्य संकेतों के लिए भी किया जाता है। पावर स्पेक्ट्रम सभी चरण संबंधों की उपेक्षा करता है, जो कई उद्देश्यों के लिए अधिक अच्छा है | किन्तु वीडियो संकेतों के लिए अन्य प्रकार के वर्णक्रमीय विश्लेषण को भी नियोजित किया जाना चाहिए, फिर भी एक उपकरण के रूप में फूरियर रूपांतरण का उपयोग करना है ।
अन्य नोटेशन
f̂(ξ) के लिए अन्य सामान्य संकेतन सम्मिलित करना है |
फ़्यूरियर ट्रांसफ़ॉर्म को कैपिटल लेटर द्वारा ट्रांसफ़ॉर्म किए जा रहे फलन के लेटर के अनुरूप नकारना (जैसे f(x) और F(ξ)) विशेष रूप से विज्ञान और इंजीनियरिंग में सामान्य है। इलेक्ट्रॉनिक्स में, ओमेगा (ω) के अतिरिक्त अधिकांशतः प्रयोग किया जाता है ξ कोणीय आवृत्ति के रूप में इसकी व्याख्या के कारण, कभी-कभी इसे लिखा जाता है F(jω), जहाँ j लाप्लास परिवर्तन के साथ अपने संबंध को इंगित करने के लिए काल्पनिक इकाई है, और कभी-कभी इसे अनौपचारिक रूप से लिखा जाता है F(2πf) सामान्य आवृत्ति का उपयोग करने के लिए। कण भौतिकी जैसे कुछ संदर्भों में, वही प्रतीक एक फलन के लिए दोनों के लिए उपयोग किया जा सकता है और साथ ही यह फूरियर रूपांतरण भी हो सकता है, दोनों केवल एक फलन के उनके तर्क से अलग हैं | संवेग तर्क के कारण फूरियर रूपांतरण को संदर्भित करेगा, जबकि स्थितीय तर्क के कारण मूल कार्य को संदर्भित करेगा। चूँकि टिल्ड्स का उपयोग इन के रूप में किया जा सकता है | फूरियर रूपांतरणों को इंगित करने के लिए, टिल्ड्स का उपयोग अधिक लोरेंत्ज़ अपरिवर्तनीय रूप के साथ मात्रा के संशोधन को इंगित करने के लिए भी किया जा सकता है, जैसे कि , इसलिए ध्यान रखना चाहिए। इसी प्रकार, अधिकांशतः हिल्बर्ट परिवर्तन को दर्शाता है | .
सम्मिश्र कार्य की व्याख्या f̂(ξ) इसे ध्रुवीय निर्देशांक रूप में व्यक्त करने में सहायता मिल सकती है |
दो वास्तविक कार्यों के संदर्भ में A(ξ) और φ(ξ) जहाँ:
आयाम है और
चरण (तरंगें) है (अर्ग (गणित) देखें)।
फिर उलटा परिवर्तन लिखा जा सकता है |
सभी आवृत्ति घटकों f(x) का पुनर्संयोजन है | प्रत्येक घटक फॉर्म का एक सम्मिश्र साइनसॉइड है | e2πixξ जिसका A(ξ) आयाम है और जिसका प्रारंभिक चरण (तरंगें) (पर x = 0) φ(ξ) है |
फूरियर ट्रांसफॉर्म को कार्य स्पेस पर मैपिंग के रूप में सोचा जा सकता है। यह मानचित्रण यहाँ निरूपित है | F और F(f) फलन के फूरियर रूपांतरण को निरूपित करने के लिए उपयोग किया जाता है | f. यह मानचित्रण रेखीय है | जिसका अर्थ है कि F कार्य स्थान पर एक रैखिक परिवर्तन के रूप में भी देखा जा सकता है और इसका तात्पर्य है कि रैखिक बीजगणित में एक वेक्टर के लिए एक रैखिक परिवर्तन प्रयुक्त करने के मानक अंकन (यहाँ फलन f) लिखने के लिए उपयोग किया जा सकता है | F f के अतिरिक्त F(f). चूंकि फूरियर ट्रांसफॉर्म को प्रयुक्त करने का परिणाम फिर से एक फलन है, हम मूल्य पर मूल्यांकित इस फलन के मूल्य में दिलचस्पी ले सकते हैं ξ इसके चर के लिए, और इसे या तो के रूप में दर्शाया गया है | F f(ξ) या के रूप में (F f)(ξ). ध्यान दें कि पूर्व स्थिति में, यह स्पष्ट रूप से समझा जाता है | F पहले प्रयुक्त होता है | f और फिर परिणामी फलन का मूल्यांकन ξ, उल्टा नहीं किया जाता है।
गणित और विभिन्न अनुप्रयुक्त विज्ञानों में, अधिकांशतः एक फलन के बीच अंतर करना आवश्यक होता है | f और का मूल्य f जब इसका चर समान होता है | x, निरूपित f(x). इसका कारण है कि एक संकेतन पसंद है | F(f(x)) औपचारिक रूप से के मूल्यों के फूरियर रूपांतरण के रूप में व्याख्या की जा सकती है | f पर x. इस दोष के अतिरिक्त, पिछला अंकन बार-बार प्रकट होता है, अधिकांशतः जब किसी विशेष कार्य या किसी विशेष चर के कार्य को बदलना होता है। उदाहरण के लिए,
कभी-कभी यह व्यक्त करने के लिए प्रयोग किया जाता है कि एक आयताकार फलन का फूरियर रूपांतरण एक सिंक कार्य है, या
फूरियर रूपांतरण की शिफ्ट संपत्ति को व्यक्त करने के लिए उपयोग किया जाता है।
ध्यान दें, कि अंतिम उदाहरण केवल इस धारणा के अनुसार सही है कि रूपांतरित कार्य एक कार्य है x का नहीं x0. है |
अन्य सम्मेलन
फूरियर रूपांतरण को कोणीय आवृत्ति के रूप में भी लिखा जा सकता है |
जिसकी इकाई रेडियन प्रति सेकेण्ड है।
प्रतिस्थापन ξ = ω/2π उपरोक्त सूत्रों में इस सम्मेलन का निर्माण करता है |
इस सम्मेलन के अनुसार, उलटा परिवर्तन बन जाता है |
इस लेख में अपनाई गई प्रथा के विपरीत, जब फूरियर रूपांतरण को इस तरह परिभाषित किया जाता है, तो यह अब एकात्मक रूपांतरण नहीं रह जाता है | L2(R). फूरियर रूपांतरण और इसके व्युत्क्रम के सूत्रों के बीच भी कम समरूपता है।
एक अन्य सम्मेलन के कारक को विभाजित करना है 2π समान रूप से फूरियर रूपांतरण और इसके व्युत्क्रम के बीच, जो परिभाषाओं की ओर जाता है:
इस सम्मेलन के अनुसार, फूरियर रूपांतरण फिर से एकात्मक परिवर्तन है | L2(R). यह फूरियर रूपांतरण और इसके व्युत्क्रम के बीच समरूपता को भी पुनर्स्थापित करता है।
सभी तीन सम्मेलनों के बदलाव आगे और रिवर्स ट्रांसफ़ॉर्म दोनों के सम्मिश्र-घातीय अभिन्न कर्नेल को मिलाकर बनाए जा सकते हैं। संकेत विपरीत होने चाहिए। इसके अतिरिक्त, चुनाव (फिर से) सम्मेलन का विषय है।
| सामान्य आवृत्ति ξ (Hz) | एकात्मक | |
|---|---|---|
| कोणीय आवृत्ति ω (rad/s) | एकात्मक | |
| गैर एकात्मक |
| सामान्य आवृत्ति ξ (Hz) | एकात्मक | |
|---|---|---|
| कोणीय आवृत्ति ω (rad/s) | एकात्मक | |
| गैर एकात्मक |
जैसा कि ऊपर चर्चा की गई है, एक यादृच्छिक चर का अभिलक्षणिक फलन (संभाव्यता सिद्धांत) इसके वितरण माप के रूपांतर के समान है, किन्तु इस संदर्भ में स्थिरांकों के लिए एक अलग परिपाटी लेना विशिष्ट है . सामान्यतः विशेषता कार्य परिभाषित किया गया है |
जैसा कि ऊपर गैर-एकात्मक कोणीय आवृत्ति सम्मेलन के स्थिति में, 2 का कारकπ न तो सामान्यीकरण स्थिरांक और न ही घातांक में प्रकट होता है। ऊपर दिखाई देने वाले किसी भी सम्मेलन के विपरीत, यह सम्मेलन एक्सपोनेंट में विपरीत चिन्ह लेता है।
गणना के विधि
उपयुक्त संगणना पद्धति अधिक सीमा तक निर्भर करती है कि मूल गणितीय फलन का प्रतिनिधित्व कैसे किया जाता है और आउटपुट फलन का वांछित रूप है ।
चूंकि एक फूरियर रूपांतरण की मौलिक परिभाषा एक अभिन्न है | ऐसे कार्य जिन्हें बंद-रूप अभिव्यक्ति के रूप में व्यक्त किया जा सकता है | सामान्यतः परिणाम के रूप में फूरियर रूपांतरण संयुग्म चर में एक बंद-रूप अभिव्यक्ति प्राप्त करने के लिए अभिन्न विश्लेषणात्मक रूप से काम करके गणना की जाती है। फूरियर रूपांतरणों की तालिकाएँ उत्पन्न करने के लिए इस विधि का उपयोग किया जाता है,[56] नीचे दी गई तालिका में पाए गए सहित (फूरियर रूपांतरण महत्वपूर्ण फूरियर रूपांतरण की तालिकाएँ)।
कई कंप्यूटर बीजगणित प्रणालियाँ जैसे मैटलैब और मेथेमेटिका जो प्रतीकात्मक एकीकरण में सक्षम हैं, फूरियर रूपांतरणों की गणना विश्लेषणात्मक रूप से करने में सक्षम हैं। उदाहरण के लिए, फूरियर रूपांतरण की गणना करने के लिए cos(6πt) e−πt2 कोई आदेश अंकित कर सकता है integrate cos(6*pi*t) exp(−pi*t^2) exp(-i*2*pi*f*t) from -inf to inf वोल्फरम अल्फा में।[note 4]
बंद-रूप कार्यों का संख्यात्मक एकीकरण
यदि इनपुट फलन बंद-रूप में है और वांछित आउटपुट फलन निर्दिष्ट डोमेन पर ऑर्डर किए गए जोड़े की एक श्रृंखला है (उदाहरण के लिए मूल्यों की एक तालिका जिसमें से एक ग्राफ उत्पन्न किया जा सकता है), तो फूरियर रूपांतरण संख्यात्मक एकीकरण द्वारा उत्पन्न किया जा सकता है फूरियर संयुग्म चर (उदाहरण के लिए आवृत्ति) के प्रत्येक मान पर जिसके लिए आउटपुट चर का मान वांछित है।[57] ध्यान दें कि इस विधि को आवृत्ति के प्रत्येक मूल्य के लिए एक अलग संख्यात्मक एकीकरण की गणना करने की आवश्यकता होती है जिसके लिए फूरियर रूपांतरण का मूल्य वांछित होता है।[58][59] संख्यात्मक एकीकरण दृष्टिकोण विश्लेषणात्मक दृष्टिकोण की तुलना में कार्यों के एक बहुत व्यापक वर्ग पर काम करता है, क्योंकि यह उन कार्यों के लिए परिणाम देता है जिनमें फूरियर ट्रांसफॉर्म इंटेग्रल्स बंद नहीं होते हैं।
आदेशित जोड़े की एक श्रृंखला का संख्यात्मक एकीकरण
यदि इनपुट फलन क्रमित जोड़े की एक श्रृंखला है (उदाहरण के लिए, एक समय अंतराल पर बार-बार आउटपुट चर को मापने से एक समय श्रृंखला) तो आउटपुट फलन भी क्रमबद्ध जोड़े की एक श्रृंखला होनी चाहिए (उदाहरण के लिए, एक सम्मिश्र संख्या बनाम आवृत्ति)। आवृत्ति के एक निर्दिष्ट डोमेन पर), जब तक कि कुछ धारणाएँ और सन्निकटन नहीं किए जाते हैं, जिससे आउटपुट फलन को एक बंद-फ़ॉर्म अभिव्यक्ति द्वारा अनुमानित किया जा सकता है। सामान्य स्थिति में जहां ऑर्डर किए गए जोड़े की उपलब्ध इनपुट श्रृंखला को एक अंतराल (आयाम बनाम समय, उदाहरण के लिए) पर एक सतत कार्य का प्रतिनिधित्व करने वाले नमूने माना जाता है, वांछित आउटपुट फलन का प्रतिनिधित्व करने वाले आदेशित जोड़े की श्रृंखला संख्यात्मक एकीकरण द्वारा प्राप्त की जा सकती है फूरियर संयुग्म चर (उदाहरण के लिए आवृत्ति) के प्रत्येक मूल्य पर उपलब्ध अंतराल पर इनपुट डेटा जिसके लिए फूरियर रूपांतरण का मूल्य वांछित है।[60] आदेशित जोड़े पर स्पष्ट संख्यात्मक एकीकरण संयुग्म फूरियर रूपांतरण चर (उदाहरण के लिए आवृत्ति) के किसी भी वांछित मूल्य के लिए फूरियर रूपांतरण उत्पादन मूल्य प्राप्त कर सकता है, जिससे किसी भी वांछित चरण आकार और किसी भी वांछित चर सीमा पर एक स्पेक्ट्रम का उत्पादन किया जा सके। अलग-अलग चोटियों के अनुरूप आयामों, आवृत्तियों और चरणों का स्पष्ट निर्धारण। डीएफटी और एफएफटी विधियों में सीमाओं के विपरीत, स्पष्ट संख्यात्मक एकीकरण में कोई वांछित चरण आकार हो सकता है और संयुग्म फूरियर रूपांतरण चर (उदाहरण के लिए, आवृत्ति) की किसी भी वांछित सीमा पर फूरियर रूपांतरण की गणना कर सकता है।
असतत फूरियर रूपांतरण और तेजी से फूरियर रूपांतरण
यदि मूल इनपुट फलन का प्रतिनिधित्व करने वाले आदेशित जोड़े समान रूप से उनके इनपुट चर (उदाहरण के लिए, समान समय चरण) में हैं, तो फूरियर रूपांतरण को असतत फूरियर रूपांतरण (डीएफटी) के रूप में जाना जाता है, जिसकी गणना या तो स्पष्ट संख्यात्मक एकीकरण द्वारा की जा सकती है। डीएफटी परिभाषा के स्पष्ट मूल्यांकन द्वारा, या फास्ट फूरियर ट्रांसफॉर्म (एफएफटी) विधियों द्वारा। इनपुट डेटा के स्पष्ट एकीकरण के विपरीत, डीएफटी और एफएफटी विधियों का उपयोग मूल नमूना अंतराल के व्युत्क्रम के समान चरण आकार के आदेशित जोड़े द्वारा वर्णित फूरियर रूपांतरण उत्पन्न करता है। उदाहरण के लिए, यदि इनपुट डेटा को हर 10 सेकंड में सैंपल किया जाता है, तो डीएफटी और एफएफटी विधियों के आउटपुट में 0.1 Hz आवृत्ति स्पेसिंग होगी।
महत्वपूर्ण फूरियर रूपांतरणों की सारणी
निम्नलिखित तालिकाएँ कुछ बंद-रूप फूरियर रूपांतरणों को रिकॉर्ड करती हैं। कार्यों के लिए f(x) और g(x) द्वारा उनके फूरियर रूपांतरण को निरूपित करें f̂ और ĝ. केवल तीन सबसे सामान्य सम्मेलनों को सम्मिलित किया गया है। यह नोटिस करना उपयोगी हो सकता है कि प्रविष्टि 105 एक फलन के फूरियर रूपांतरण और मूल फलन के बीच एक संबंध देता है, जिसे फूरियर रूपांतरण और इसके व्युत्क्रम से संबंधित के रूप में देखा जा सकता है।
कार्यात्मक संबंध, एक आयामी
इस तालिका में फूरियर रूपांतरण पाया जा सकता है | एर्डेली (1954) या कामलर (2000, अनुबंध).
| फलन | फूरियर रूपांतरण
एकात्मक, सामान्य आवृत्ति |
फूरियर रूपांतरण
एकात्मक, सामान्य आवृत्ति |
फूरियर रूपांतरण
गैर-एकात्मक, कोणीय आवृत्ति |
टिप्पणियां | |
|---|---|---|---|---|---|
| परिभाषाएं | |||||
| 101 | रैखिकता | ||||
| 102 | समय डोमेन में बदलाव | ||||
| 103 | फ़्रीक्वेंसी डोमेन में बदलाव, 102 का दोहरा | ||||
| 104 |
गणित> \frac{1}{|a|} \hat{f}\left( \frac{\omega}{a} \right)\,</math> |
गणित> \frac{1}{|a|} \hat{f}\left( \frac{\omega}{a} \right)\,</math> |
टाइम डोमेन में स्केलिंग। यदि |a| बड़ा है, तो f(ax) 0 और के आसपास केंद्रित है फैलता है और चपटा हो जाता है। | ||
| 105 | एक ही परिवर्तन दो बार प्रयुक्त किया जाता है, किन्तु x पहले परिवर्तन के बाद आवृत्ति चर (ξ या ω) को बदल देता है। | ||||
| 106 | जैसा f एक श्वार्ट्ज स्थान है | ||||
| 107 | यह 106 का द्वैत है | ||||
| 108 | संकेतन f ∗ g के कनवल्शन को दर्शाता है f और g - यह नियम कनवल्शन प्रमेय है | ||||
| 109 | यह 108 का द्वैत है | ||||
| 110 | के लिए f(x) विशुद्ध रूप से वास्तविक | हर्मिटियन समरूपता। z सम्मिश्र संयुग्म को इंगित करता है। | |||
| 113 | के लिए f(x) विशुद्ध रूप से काल्पनिक | z सम्मिश्र संयुग्म को इंगित करता है। | |||
| 114 | सम्मिश्र संयुग्म, 110 और 113 का सामान्यीकरण | ||||
| 115 | यह यूलर के सूत्र का उपयोग करते हुए नियम 101 और 103 से आता है: | ||||
| 116 | यह यूलर के सूत्र का उपयोग करते हुए 101 और 103 से आता है: |
वर्ग-पूर्ण कार्य, एक-आयामी
इस तालिका में फूरियर रूपांतरण पाया जा सकता है कैम्पबेल & पोषक (1948), एर्डेली (1954), या कामलर (2000, अनुबंध).
| फलन | फूरियर रूपांतरण
एकात्मक, सामान्य आवृत्ति |
फूरियर रूपांतरण
एकात्मक, सामान्य आवृत्ति |
फूरियर रूपांतरण
गैर-एकात्मक, कोणीय आवृत्ति |
टिप्पणियां | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| परिभाषाएं | |||||||||||
| 201 |
गणित> \frac{1}{\sqrt{2 \pi a^2}}\, \operatorname{सिंक}\left(\frac{\omega}{2\pi a}\right)</math> |
गणित> \frac{1}{|a|}\, \operatorname{सिंक}\left(\frac{\omega}{2\pi a}\right)</math> |
आयताकार फलन और सामान्यीकृत सिंक फलन, यहाँ इस रूप में परिभाषित किया गया है sinc(x) = sin(πx)/πx | ||||||||
| 202 | नियम 201 का दोहरा। आयताकार फलन एक आदर्श लो पास फिल्टर है, और सिंक फलन ऐसे फिल्टर का प्रतिकारणात्मक प्रणाली|गैर-कारण आवेग प्रतिक्रिया है। यहाँ सिंक फलन को इस प्रकार परिभाषित किया गया है sinc(x) = sin(πx)/πx | ||||||||||
| 203 | प्रोग्राम tri(x) त्रिकोणीय कार्य है | ||||||||||
| 204 | नियम 203 का दोहरा। | ||||||||||
| 205 | फलन u(x) हैवीसाइड स्टेप कार्य है और a > 0. | ||||||||||
| 206 | इससे पता चलता है कि, एकात्मक फूरियर रूपांतरण के लिए, गॉसियन फलन e−αx2 कुछ विकल्पों के लिए इसका अपना फूरियर रूपांतरण है α. इसके लिए अभिन्न होने के लिए हमारे पास होना चाहिए Re(α) > 0. | ||||||||||
| 207 | - | 208 | के लिए Re(a) > 0. यही है, लाप्लास वितरण का फूरियर रूपांतरण | दो तरफा क्षयकारी घातीय कार्य एक लोरेंत्ज़ियन कार्य है। | ||||||||
| 209 | अतिशयोक्तिपूर्ण फलन इसका अपना फूरियर रूपांतरण है | ||||||||||
| 210 | Hn है nवें क्रम हर्मिट बहुपद। यदि a = 1 तो गॉस-हर्माइट फ़ंक्शंस फूरियर ट्रांसफ़ॉर्म संचालक के ईजेनफ़ंक्शन हैं। एक व्युत्पत्ति के लिए, हर्मिट बहुपद #हर्मिट फ़ंक्शंस को फूरियर रूपांतरण के आइगेनफंक्शन s के रूप में देखें। सूत्र 206 के लिए कम हो जाता है n = 0. |
वितरण, एक आयामी
इस तालिका में फूरियर रूपांतरण पाया जा सकता है एर्डेली (1954) या कामलर (2000, अनुबंध).
| फलन | फूरियर रूपांतरण
एकात्मक, सामान्य आवृत्ति |
फूरियर रूपांतरण
एकात्मक, सामान्य आवृत्ति |
फूरियर रूपांतरण
गैर-एकात्मक, कोणीय आवृत्ति |
टिप्पणियां | |
|---|---|---|---|---|---|
| परिभाषाएं | |||||
| 301 | वितरण δ(ξ) डिराक डेल्टा फ़ंक्शन को दर्शाता है। | ||||
| 302 | नियम 301 का दोहरा। | ||||
| 303 | यह 103 और 301 से आता है। | ||||
| 304 | यह यूलर के सूत्र का उपयोग करते हुए नियम 101 और 303 से आता है: | ||||
| 305 | यह 101 और 303 के उपयोग से आता है | ||||
| 306 | यह 101 और 207 के उपयोग से आता है | ||||
| 307 | यह 101 और 207 के उपयोग से आता है | ||||
| 308 | यहाँ, n एक प्राकृतिक संख्या है और δ(n)(ξ) डिराक डेल्टा फ़ंक्शन का nवाँ वितरण व्युत्पन्न है। यह नियम नियम 107 और 301 से आता है। इस नियम को 101 के साथ जोड़कर, हम सभी बहुपदों को बदल सकते हैं। | ||||
| नियम 308 का दोहरा। δ(n)(ξ) डिराक डेल्टा फ़ंक्शन का nवां वितरण व्युत्पन्न है। यह नियम 106 और 302 से चलता है। | |||||
| 309 | यहाँ sgn(ξ) साइन फंक्शन है। ध्यान दें कि 1/x वितरण नहीं है। Schwartz प्रकार्यों के विरुद्ध परीक्षण करते समय कौशी प्रमुख मान का उपयोग करना आवश्यक है। हिल्बर्ट रूपांतरण के अध्ययन में यह नियम उपयोगी है। | ||||
| 310 | 1/xnवितरण व्युत्पन्न द्वारा परिभाषित सजातीय वितरण है | ||||
| 311 |
यह सूत्र के लिए मान्य है0 > α > −1. For α > 0मूल बिंदु पर कुछ विलक्षण शब्द उत्पन्न होते हैं जिन्हें 318 में अंतर करके पाया जा सकता है। यदिRe α > −1, then |x|αएक स्थानीय रूप से एकीकृत कार्य है, और इसलिए एक संयमित वितरण है। फलन α ↦ |x|α दाहिने आधे तल से अंतरिक्ष तक एक होलोमॉर्फिक फलन है टेम्पर्ड वितरण की। यह एक टेम्पर्ड डिस्ट्रीब्यूशन के लिए एक अद्वितीय मेरोमोर्फिक एक्सटेंशन को स्वीकार करता है, जिसे α के लिए |x|α भी कहा जाता है। ≠ −1, −3, ... (देखें सजातीय वितरण।) | ||||
| 314 |
फलन। यह परिणाम 302 और 102 से प्राप्त किया जा सकता है, इस तथ्य के साथ कि | ||||
| 315 | प्रोग्राम J0(x) प्रथम प्रकार का शून्य कोटि का बेसल फलन है। | ||||
| 316 | यह 315 का सामान्यीकरण है। कार्य Jn(x) है nप्रथम प्रकार का वां क्रम बेसेल फलन। प्रोग्राम Tn(x) चेबीशेव बहुपद है। | ||||
| 317 | γ यूलर-मास्चेरोनी स्थिरांक है। परीक्षण करते समय एक परिमित भाग अभिन्न का उपयोग करना आवश्यक है 1/|ξ| या 1/|ω|श्वार्ट्ज कार्य करता है के खिलाफ। इसका विवरण डेल्टा फ़ंक्शन के गुणांक को बदल सकता है। | ||||
| 318 | यह सूत्र के लिए मान्य है 1 > α > 0. उच्च घातांकों के लिए सूत्र व्युत्पन्न करने के लिए विभेदीकरण का उपयोग करें। u हीविसाइड फलन है। |
द्वि-आयामी कार्य
| फलन | फूरियर रूपांतरण
एकात्मक, सामान्य आवृत्ति |
फूरियर रूपांतरण
एकात्मक, सामान्य आवृत्ति |
फूरियर रूपांतरण
गैर-एकात्मक, कोणीय आवृत्ति |
टिप्पणियां | |
|---|---|---|---|---|---|
| 400 | चर ξx, ξy, ωx, ωy वास्तविक संख्याएँ हैं। इंटीग्रल को पूरे प्लेन में ले लिया जाता है। | ||||
| 403 |
का r−1, एक 2-डी फूरियर स्व-रूपांतरण।[61] | ||||
| 404 |
सामान्य के लिए सूत्र n-आयामी कार्य
| फलन | फूरियर रूपांतरण
एकात्मक, सामान्य आवृत्ति |
फूरियर रूपांतरण
एकात्मक, सामान्य आवृत्ति |
फूरियर रूपांतरण
गैर-एकात्मक, कोणीय आवृत्ति |
टिप्पणियां | |
|---|---|---|---|---|---|
| 500 | |||||
| 501 | फलन χ[0, 1] अंतराल [0, 1] का सूचक फलन है। फ़ंक्शन Γ(x) गामा फ़ंक्शन है। समारोह जेएन / 2 + δ ऑर्डर एन / 2 + δ के साथ पहली तरह का बेसेल फ़ंक्शन है। n = 2 और δ = 0 लेने पर 402 प्राप्त होता है.[62] | ||||
| 502 | See Riesz potential where the constant is given by The formula also holds for all α ≠ n, n + 2, ... by analytic continuation, but then the function and its Fourier transforms need to be understood as suitably regularized tempered distributions. See homogeneous distribution.[note 5] | ||||
| 503 | This is the formula for a multivariate normal distribution normalized to 1 with a mean of 0. Bold variables are vectors or matrices. Following the notation of the aforementioned page, Σ = σ σT and Σ−1 = σ−T σ−1 |
यह भी देखें
- एनालॉग सिग्नल प्रोसेसिंग
- बीवर-लिप्सन स्ट्रिप
- निरंतर-क्यू परिवर्तन
- असतत फूरियर रूपांतरण
- फास्ट फूरियर ट्रांसफॉर्म
- फूरियर इंटीग्रल ऑपरेटर
- फूरियर व्युत्क्रम प्रमेय
- फूरियर गुणक
- फोरियर श्रेणी
- फूरियर साइन ट्रांसफॉर्म
- फूरियर-डेलिग्ने रूपांतरण
- फूरियर-मुकाई रूपांतरण
- आंशिक फूरियर रूपांतरण
- अप्रत्यक्ष फूरियर रूपांतरण
- अभिन्न परिवर्तन
- हैंकेल ट्रांसफॉर्म
- हार्टले ट्रांसफॉर्म
- लाप्लास रूपांतरण
- कम से कम वर्ग वर्णक्रमीय विश्लेषण
- रैखिक विहित परिवर्तन
- मध्य परिवर्तन
- बहुआयामी परिवर्तन
- एनजीसी 4622 , विशेष रूप से छवि एनजीसी 4622 फूरियर रूपांतरण m = 2.
- गैर-स्थानीय ऑपरेटर
- क्वांटम फूरियर रूपांतरण
- शॉर्ट-टाइम फूरियर रूपांतरण
- वर्णक्रमीय घनत्व
- प्रतीकात्मक एकीकरण
- टाइम स्ट्रेच डिस्पर्सिव फूरियर ट्रांसफॉर्म
- रूपांतरण (गणित)
टिप्पणियाँ
- ↑ In relativistic quantum mechanics one encounters vector-valued Fourier transforms of multi-component wave functions. In quantum field theory, operator-valued Fourier transforms of operator-valued functions of spacetime are in frequent use, see for example Greiner & Reinhardt (1996).
- ↑ A possible source of confusion is the frequency-shifting property; i.e. the transform of function is The value of this function at is meaning that a frequency has been shifted to zero.
- ↑ The operator is defined by replacing by in the Taylor expansion of
- ↑ The direct command
fourier transform of cos(6*pi*t) exp(−pi*t^2)would also work for Wolfram Alpha. - ↑ In Gelfand & Shilov 1964, p. 363, with the non-unitary conventions of this table, the transform of is given to be
from which this follows, with .
उद्धरण
- ↑ Rahman 2011, p. 10.
- ↑ Oppenheim 1999, p. 58
- ↑ Taneja 2008, p. 192.
- ↑ Fourier 1822, p. 525.
- ↑ Fourier 1878, p. 408.
- ↑ (Jordan 1883) proves on pp. 216–226 the Fourier integral theorem before studying Fourier series.
- ↑ Titchmarsh 1986, p. 1.
- ↑ Folland 1989.
- ↑ Fourier 1822.
- ↑ Lyons, Richard (November 2001). "डिजिटल सिग्नल प्रोसेसिंग फ्रीक्वेंसी डोमेन को समझना". RF Design magazine. Retrieved March 14, 2022.
{{cite web}}: CS1 maint: url-status (link) - ↑ Jump up to: 11.0 11.1 11.2 11.3 11.4 Pinsky 2002.
- ↑ Proakis 1996, p. 291
- ↑ Arfken, George (1985). भौतिकविदों के लिए गणितीय तरीके (3rd ed.). Academic Press. ISBN 9780120598205.
- ↑ Jump up to: 14.0 14.1 14.2 14.3 14.4 Katznelson 1976.
- ↑ Jump up to: 15.0 15.1 15.2 15.3 15.4 15.5 Stein & Weiss 1971.
- ↑ Rudin 1987, p. 187.
- ↑ Rudin 1987, p. 186.
- ↑ Folland 1992, p. 216.
- ↑ Wolf 1979, p. 307ff
- ↑ Folland 1989, p. 53.
- ↑ Celeghini, Enrico; Gadella, Manuel; del Olmo, Mariano A. (2021). "Hermite Functions and Fourier Series". Symmetry. 13 (5). doi:10.3390/sym13050853.
- ↑ Jump up to: 22.0 22.1 Duoandikoetxea 2001.
- ↑ Jump up to: 23.0 23.1 Boashash 2003.
- ↑ Condon 1937.
- ↑ Wolf 1979, p. 320
- ↑ Wolf 1979, p. 312
- ↑ Folland 1989, p. 52.
- ↑ Howe 1980.
- ↑ Paley & Wiener 1934.
- ↑ Gelfand & Vilenkin 1964.
- ↑ Kirillov & Gvishiani 1982.
- ↑ Clozel & Delorme 1985, pp. 331–333.
- ↑ de Groot & Mazur 1984, p. 146.
- ↑ Champeney 1987, p. 80.
- ↑ Jump up to: 35.0 35.1 35.2 Kolmogorov & Fomin 1999.
- ↑ Wiener 1949.
- ↑ Champeney 1987, p. 63.
- ↑ Widder & Wiener 1938, p. 537.
- ↑ Pinsky 2002, p. 131.
- ↑ Stein & Shakarchi 2003.
- ↑ Stein & Shakarchi 2003, p. 158.
- ↑ Chatfield 2004, p. 113.
- ↑ Fourier 1822, p. 441.
- ↑ Poincaré 1895, p. 102.
- ↑ Whittaker & Watson 1927, p. 188.
- ↑ Grafakos 2004.
- ↑ Grafakos & Teschl 2013.
- ↑ "एप्लाइड फूरियर विश्लेषण और आधुनिक सिग्नल प्रोसेसिंग व्याख्यान के तत्व 3" (PDF). January 12, 2016. Retrieved 2019-10-11.
- ↑ Stein & Weiss 1971, Thm. 2.3.
- ↑ Pinsky 2002, p. 256.
- ↑ Scarfone, A.M. (2017). "κ -विकृत फूरियर रूपांतरण". Physica A: Statistical Mechanics and Its Applications (in English). 480: 63–78. arXiv:2206.06869. Bibcode:2017PhyA..480...63S. doi:10.1016/j.physa.2017.03.036. S2CID 126079408.
- ↑ Scarfone, Antonio (2015-05-04). "κ-विकृत चक्रीय कार्यों और κ-बीजगणित के ढांचे में सामान्यीकृत फूरियर श्रृंखला पर". Entropy (in English). 17 (5): 2812–2833. Bibcode:2015Entrp..17.2812S. doi:10.3390/e17052812. ISSN 1099-4300.
- ↑ Hewitt & Ross 1970, Chapter 8.
- ↑ Knapp 2001.
- ↑ Wolf 1979, p. 312
- ↑ Gradshteyn et al. 2015.
- ↑ Press et al. 1992.
- ↑ Bailey & Swarztrauber 1994.
- ↑ Lado 1971.
- ↑ Simonen & Olkkonen 1985.
- ↑ Jump up to: 61.0 61.1 Easton, Roger L. Jr. (2010). इमेजिंग में फूरियर तरीके (in English). John Wiley & Sons. ISBN 978-0-470-68983-7. Retrieved 26 May 2020.
- ↑ Stein & Weiss 1971, Thm. 4.15.
संदर्भ
- Bailey, David H.; Swarztrauber, Paul N. (1994), "A fast method for the numerical evaluation of continuous Fourier and Laplace transforms" (PDF), SIAM Journal on Scientific Computing, 15 (5): 1105–1110, Bibcode:1994SJSC...15.1105B, CiteSeerX 10.1.1.127.1534, doi:10.1137/0915067, archived from the original (PDF) on 2008-07-20, retrieved 2017-11-01.
- Boashash, B., ed. (2003), Time–Frequency Signal Analysis and Processing: A Comprehensive Reference, Oxford: Elsevier Science, ISBN 978-0-08-044335-5.
- Bochner, S.; Chandrasekharan, K. (1949), Fourier Transforms, Princeton University Press.
- Bracewell, R. N. (2000), The Fourier Transform and Its Applications (3rd ed.), Boston: McGraw-Hill, ISBN 978-0-07-116043-8.
- Campbell, George; Foster, Ronald (1948), Fourier Integrals for Practical Applications, New York: D. Van Nostrand Company, Inc..
- Champeney, D.C. (1987), A Handbook of Fourier Theorems, Cambridge University Press.
- Chatfield, Chris (2004), The Analysis of Time Series: An Introduction, Texts in Statistical Science (6th ed.), London: Chapman & Hall/CRC, ISBN 9780203491683.
- Clozel, Laurent; Delorme, Patrice (1985), "Sur le théorème de Paley-Wiener invariant pour les groupes de Lie réductifs réels", Comptes Rendus de l'Académie des Sciences, Série I, 300: 331–333.
- Condon, E. U. (1937), "Immersion of the Fourier transform in a continuous group of functional transformations", Proc. Natl. Acad. Sci., 23 (3): 158–164, Bibcode:1937PNAS...23..158C, doi:10.1073/pnas.23.3.158, PMC 1076889, PMID 16588141.
- de Groot, Sybren R.; Mazur, Peter (1984), Non-Equilibrium Thermodynamics (2nd ed.), New York: Dover.
- Duoandikoetxea, Javier (2001), Fourier Analysis, American Mathematical Society, ISBN 978-0-8218-2172-5.
- Dym, H.; McKean, H. (1985), Fourier Series and Integrals, Academic Press, ISBN 978-0-12-226451-1.
- Erdélyi, Arthur, ed. (1954), Tables of Integral Transforms, vol. 1, McGraw-Hill.
- Feller, William (1971), An Introduction to Probability Theory and Its Applications, vol. II (2nd ed.), New York: Wiley, MR 0270403.
- Folland, Gerald (1989), Harmonic analysis in phase space, Princeton University Press.
- Folland, Gerald (1992), Fourier analysis and its applications, Wadsworth & Brooks/Cole.
- Fourier, J.B. Joseph (1822), Théorie analytique de la chaleur (in français), Paris: Firmin Didot, père et fils, OCLC 2688081.
- Fourier, J.B. Joseph (1878) [1822], The Analytical Theory of Heat, translated by Alexander Freeman, The University Press (translated from French).
- Gradshteyn, Izrail Solomonovich; Ryzhik, Iosif Moiseevich; Geronimus, Yuri Veniaminovich; Tseytlin, Michail Yulyevich; Jeffrey, Alan (2015), Zwillinger, Daniel; Moll, Victor Hugo (eds.), Table of Integrals, Series, and Products (in English), translated by Scripta Technica, Inc. (8th ed.), Academic Press, ISBN 978-0-12-384933-5.
- Grafakos, Loukas (2004), Classical and Modern Fourier Analysis, Prentice-Hall, ISBN 978-0-13-035399-3.
- Grafakos, Loukas; Teschl, Gerald (2013), "On Fourier transforms of radial functions and distributions", J. Fourier Anal. Appl., 19: 167–179, arXiv:1112.5469, doi:10.1007/s00041-012-9242-5, S2CID 1280745.
- Greiner, W.; Reinhardt, J. (1996), Field Quantization, Springer, ISBN 978-3-540-59179-5.
- Gelfand, I.M.; Shilov, G.E. (1964), Generalized Functions, vol. 1, New York: Academic Press (translated from Russian).
- Gelfand, I.M.; Vilenkin, N.Y. (1964), Generalized Functions, vol. 4, New York: Academic Press (translated from Russian).
- Hewitt, Edwin; Ross, Kenneth A. (1970), Abstract harmonic analysis, Die Grundlehren der mathematischen Wissenschaften, Band 152, vol. II: Structure and analysis for compact groups. Analysis on locally compact Abelian groups, Springer, MR 0262773.
- Hörmander, L. (1976), Linear Partial Differential Operators, vol. 1, Springer, ISBN 978-3-540-00662-6.
- Howe, Roger (1980), "On the role of the Heisenberg group in harmonic analysis", Bulletin of the American Mathematical Society, 3 (2): 821–844, doi:10.1090/S0273-0979-1980-14825-9, MR 0578375.
- James, J.F. (2011), A Student's Guide to Fourier Transforms (3rd ed.), Cambridge University Press, ISBN 978-0-521-17683-5.
- Jordan, Camille (1883), Cours d'Analyse de l'École Polytechnique, vol. II, Calcul Intégral: Intégrales définies et indéfinies (2nd ed.), Paris
{{citation}}: CS1 maint: location missing publisher (link).
- Kaiser, Gerald (1994), "A Friendly Guide to Wavelets", Physics Today, 48 (7): 57–58, Bibcode:1995PhT....48g..57K, doi:10.1063/1.2808105, ISBN 978-0-8176-3711-8.
- Kammler, David (2000), A First Course in Fourier Analysis, Prentice Hall, ISBN 978-0-13-578782-3.
- Katznelson, Yitzhak (1976), An Introduction to Harmonic Analysis, Dover, ISBN 978-0-486-63331-2.
- Kirillov, Alexandre; Gvishiani, Alexei D. (1982) [1979], Theorems and Problems in Functional Analysis, Springer (translated from Russian).
- Knapp, Anthony W. (2001), Representation Theory of Semisimple Groups: An Overview Based on Examples, Princeton University Press, ISBN 978-0-691-09089-4.
- Kolmogorov, Andrey Nikolaevich; Fomin, Sergei Vasilyevich (1999) [1957], Elements of the Theory of Functions and Functional Analysis, Dover (translated from Russian).
- Lado, F. (1971), "Numerical Fourier transforms in one, two, and three dimensions for liquid state calculations", Journal of Computational Physics, 8 (3): 417–433, Bibcode:1971JCoPh...8..417L, doi:10.1016/0021-9991(71)90021-0.
- Müller, Meinard (2015), The Fourier Transform in a Nutshell. (PDF), Springer, doi:10.1007/978-3-319-21945-5, ISBN 978-3-319-21944-8, S2CID 8691186; also available at Fundamentals of Music Processing, Section 2.1, pages 40-56.
- Oppenheim, Alan V.; Schafer, Ronald W.; Buck, John R. (1999), Discrete-time signal processing (2nd ed.), Upper Saddle River, N.J.: Prentice Hall, ISBN 0-13-754920-2 Also available at https://d1.amobbs.com/bbs_upload782111/files_24/ourdev_523225.pdf.
- Paley, R.E.A.C.; Wiener, Norbert (1934), Fourier Transforms in the Complex Domain, American Mathematical Society Colloquium Publications, Providence, Rhode Island: American Mathematical Society.
- Pinsky, Mark (2002), Introduction to Fourier Analysis and Wavelets, Brooks/Cole, ISBN 978-0-534-37660-4.
- Poincaré, Henri (1895), Théorie analytique de la propagation de la chaleur, Paris: Carré.
- Polyanin, A. D.; Manzhirov, A. V. (1998), Handbook of Integral Equations, Boca Raton: CRC Press, ISBN 978-0-8493-2876-3.
- Press, William H.; Flannery, Brian P.; Teukolsky, Saul A.; Vetterling, William T. (1992), Numerical Recipes in C: The Art of Scientific Computing, Second Edition (2nd ed.), Cambridge University Press.
- Proakis, John G.; Manolakis, Dimitri G. (1996). Digital Signal Processing: Principles, Algorithms and Applications (in English) (3 ed.). New Jersey: Prentice-Hall International. Bibcode:1996dspp.book.....P. ISBN 9780133942897. sAcfAQAAIAAJ..
- Rahman, Matiur (2011), Applications of Fourier Transforms to Generalized Functions, WIT Press, ISBN 978-1-84564-564-9.
- Rudin, Walter (1987), Real and Complex Analysis (3rd ed.), Singapore: McGraw Hill, ISBN 978-0-07-100276-9.
- Simonen, P.; Olkkonen, H. (1985), "Fast method for computing the Fourier integral transform via Simpson's numerical integration", Journal of Biomedical Engineering, 7 (4): 337–340, doi:10.1016/0141-5425(85)90067-6, PMID 4057997.
- Stein, Elias; Shakarchi, Rami (2003), Fourier Analysis: An introduction, Princeton University Press, ISBN 978-0-691-11384-5.
- Stein, Elias; Weiss, Guido (1971), Introduction to Fourier Analysis on Euclidean Spaces, Princeton, N.J.: Princeton University Press, ISBN 978-0-691-08078-9.
- Taneja, H.C. (2008), "Chapter 18: Fourier integrals and Fourier transforms", Advanced Engineering Mathematics, vol. 2, New Delhi, India: I. K. International Pvt Ltd, ISBN 978-8189866563.
- Titchmarsh, E. (1986) [1948], Introduction to the theory of Fourier integrals (2nd ed.), Oxford University: Clarendon Press, ISBN 978-0-8284-0324-5.
- Vretblad, Anders (2000), Fourier Analysis and its Applications, Graduate Texts in Mathematics, vol. 223, New York: Springer, ISBN 978-0-387-00836-3.
- Whittaker, E. T.; Watson, G. N. (1927), A Course of Modern Analysis (4th ed.), Cambridge University Press.
- Widder, David Vernon; Wiener, Norbert (August 1938), "Remarks on the Classical Inversion Formula for the Laplace Integral", Bulletin of the American Mathematical Society, 44 (8): 573–575, doi:10.1090/s0002-9904-1938-06812-7.
- Wiener, Norbert (1949), Extrapolation, Interpolation, and Smoothing of Stationary Time Series With Engineering Applications, Cambridge, Mass.: Technology Press and John Wiley & Sons and Chapman & Hall.
- Wilson, R. G. (1995), Fourier Series and Optical Transform Techniques in Contemporary Optics, New York: Wiley, ISBN 978-0-471-30357-2.
- Wolf, Kurt B. (1979), Integral Transforms in Science and Engineering, Springer, doi:10.1007/978-1-4757-0872-1.
- Yosida, K. (1968), Functional Analysis, Springer, ISBN 978-3-540-58654-8.
बाहरी कड़ियाँ
 Media related to फूरियर रूपांतरण at Wikimedia Commons
Media related to फूरियर रूपांतरण at Wikimedia Commons- Encyclopedia of Mathematics
- Weisstein, Eric W. "Fourier Transform". MathWorld.