कालमान फिल्टर: Difference between revisions
No edit summary |
No edit summary |
||
| (16 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
[[File:Basic concept of Kalman filtering.svg|thumb|400px|कालमान फिल्टर प्रणाली की अनुमानित स्थिति और अनुमान की भिन्नता या अनिश्चितता का पंथ रखता है। एक अवस्था पारगमन प्रतिरूप और माप का उपयोग करके अनुमान को अद्यतन किया जाता है। <math>\hat{x}_{k\mid k-1}</math> ''k''-th माप ''y<sub>k</sub>'' को ध्यान में रखे जाने से पूर्व चरण ''k'' पर प्रणाली की स्थिति के अनुमान को दर्शाता है, <math>P_{k \mid k-1}</math> संगत अनिश्चितता है।]] | |||
सांख्यिकी और[[ नियंत्रण सिद्धांत | नियंत्रण सिद्धांत]] के लिए, '''कालमान फिल्टर''', जिसे रैखिक द्विघात अनुमान (LQE) के रूप में भी जाना जाता है, और यह एक [[ कलन विधि |कलन विधि]] है जो समय के साथ देखे गए मापों की एक श्रृंखला का उपयोग करता है, जिसमें [[ सांख्यिकीय शोर |सांख्यिकीय रव]] और अन्य अशुद्धियाँ सम्मिलित हैं, और अज्ञात चर के अनुमान उत्पन्न करता हैं, जो अधिक होते हैं। प्रत्येक समय-सीमा के लिए चरों पर एक असंग एक माप के आधार पर सटीक [[ संयुक्त संभाव्यता वितरण |संयुक्त संभाव्यता वितरण]] का अनुमान लगाकर किया जाता है। एक फिल्टर का नाम रुडोल्फ ई.कलमन के नाम पर रखा गया है, जो इसके सिद्धांत के प्राथमिक विकासकर्ताओं में से एक थे। | |||
इस अंकीय फिल्टर को कभी-कभी ''स्ट्रैटोनोविच-कालमान-बुकी फिल्टर'' कहा जाता है क्योंकि यह सोवियत [[ गणितज्ञ |गणितज्ञ]] [[ रुस्लान स्ट्रैटोनोविच |रुस्लान स्ट्रैटोनोविच]] द्वारा कुछ पूर्व में विकसित किए गए अधिक सामान्य, अरैखिक फिल्टर की एक विशेष स्थिति है।<ref>Stratonovich, R. L. (1959). ''Optimum nonlinear systems which bring about a separation of a signal with constant parameters from noise''. Radiofizika, 2:6, pp. 892–901.</ref><ref>Stratonovich, R. L. (1959). ''On the theory of optimal non-linear filtering of random functions''. Theory of Probability and Its Applications, 4, pp. 223–225.</ref><ref>Stratonovich, R. L. (1960) ''Application of the Markov processes theory to optimal filtering''. Radio Engineering and Electronic Physics, 5:11, pp. 1–19.</ref><ref>Stratonovich, R. L. (1960). ''Conditional Markov Processes''. Theory of Probability and Its Applications, 5, pp. 156–178.</ref> वास्तव में, कुछ विशेष स्थितिया रैखिक फिल्टर के समीकरण स्ट्रैटोनोविच के पत्रों में दिखाई दिए, जो 1960 की ग्रीष्म से पूर्व प्रकाशित हुए थे, जब कालमान मॉस्को में एक सम्मेलन के पर्यंत स्ट्रैटोनोविच से भेंट की थी।<ref name="stepanov_on_kalman">{{cite journal |last1=Stepanov |first1=O. A. |title=Kalman filtering: Past and present. An outlook from Russia. (On the occasion of the 80th birthday of Rudolf Emil Kalman) |journal=Gyroscopy and Navigation |date=15 May 2011 |volume=2 |issue=2 |page=105 |doi=10.1134/S2075108711020076 |s2cid=53120402 }}</ref> | |||
कालमान फिल्टर में कई प्रौद्योगिकीय अनुप्रयोग हैं। वाहनों, विशेष रूप से विमान, अंतरिक्ष यान और जहाजों के[[ गतिशील स्थिति | गतिशील स्थिति]] के मार्गदर्शन, नौ संचालन और नियंत्रण के लिए एक सामान्य अनुप्रयोग है। इसके अतिरिक्त, कालमान फिल्टर एक अवधारणा है जो [[ संकेत का प्रक्रमण | संकेत संसाधन]] और [[ अर्थमिति |अर्थमिति]] जैसे विषयों के लिए उपयोग की जाने वाली [[ समय श्रृंखला |समय श्रृंखला]] विश्लेषण में बहुत अधिक अनुप्रयुक्त होती है। कालमान फिल्टर भी यंत्रमानववत् [[ गति योजना |गति योजना]] और नियंत्रण के मुख्य विषयों में से एक है और इसका उपयोग [[ प्रक्षेपवक्र अनुकूलन |प्रक्षेपवक्र अनुकूलन]] के लिए किया जा सकता है। कालमान फिल्टर [[ केंद्रीय तंत्रिका तंत्र |केंद्रीय तंत्रिका तंत्र]] की गतिविधि के नियंत्रण के प्रतिरूप के लिए भी कार्य करता है। प्रेरक आदेश जारी करने और [[ संवेदी प्रतिक्रिया |संवेदी प्रतिक्रिया]] प्राप्त करने के मध्य समय की देरी के कारण, कालमान फिल्टर का उपयोग प्रेरक प्रणाली की वर्तमान स्थिति का अनुमान लगाने और अद्यतन आदेश जारी करने के लिए एक यथार्थवादी प्रतिरूप प्रदान करता है। | |||
कलन विधि दो-चरण प्रक्रिया द्वारा कार्य करते है। पूर्वाकलन चरण के लिए, कालमान फिल्टर वर्तमान स्थिति चरों के अनुमानों के साथ-साथ उनकी उनकी अनिश्चितताओं का अनुमान लगाता है। एक बार जब आगामी माप के परिणाम (अनिवार्य रूप से कुछ त्रुटि के साथ दूषित, यादृच्छिक रव सहित) देखे जाने के पश्चात, तो इन अनुमानों में [[ भारित माध्य |भारित औसतों]] का उपयोग करके अद्यतन किया जाता है, और अधिक निश्चितता के साथ अनुमानों को अधिक महत्व दिया जाता है। कलन विधि[[ रिकर्सन (कंप्यूटर विज्ञान) | पुनरावर्ती]] होती है। यह [[ वास्तविक समय नियंत्रण प्रणाली |वास्तविक समय नियंत्रण प्रणाली]] में कार्य कर सकती है, केवल वर्तमान इनपुट माप और पूर्व की गणना की स्थिति और इसकी अनिश्चितता आव्यूह का उपयोग करके; कोई अतिरिक्त पूर्व सूचना की आवश्यकता नहीं है। | |||
विधि के विस्तार और सामान्यीकरण भी विकसित किए गए हैं, जैसे कि [[ विस्तारित कलमन फ़िल्टर |विस्तारित | कालमान फिल्टर की इष्टतमता मानती है कि त्रुटियों का [[ सामान्य वितरण |सामान्य वितरण]] होता है। रुडोल्फ ई. कालमान के शब्दों में: संक्षेप में, यादृच्छिक प्रक्रियाओं के विषय में निम्नलिखित धारणाएँ बनाई गई हैं: भौतिक यादृच्छिक घटना को प्राथमिक यादृच्छिक स्रोतों के उत्तेजन गतिशील प्रणालियों के कारण माना जा सकता है। प्राथमिक स्रोतों को शून्य माध्य के साथ स्वतंत्र गॉसियन यादृच्छिक प्रक्रिया मानी जाती है; और गतिशील प्रणालियां रैखिक होंगी। हालांकि गॉसियनिटी की उपेक्षा किए बिना, यदि प्रक्रिया और माप सहप्रसरण ज्ञात हैं, तो कालमान फिल्टर [[ न्यूनतम माध्य वर्ग त्रुटि |न्यूनतम माध्य-वर्ग-त्रुटि]] के अर्थ में सर्वोत्तम संभव[[ रैखिकता | रैखिक]] अनुमानक है। | ||
विधि के विस्तार और सामान्यीकरण भी विकसित किए गए हैं, जैसे कि [[ विस्तारित कलमन फ़िल्टर |विस्तारित कालमान फिल्टर]] और असंतुलित कालमान फिल्टर जो [[ अरेखीय प्रणाली |अरैखिक प्रणालियों]] पर कार्य करते हैं। आधार एक [[ छिपा हुआ मार्कोव मॉडल |गुप्त मार्कोव प्रतिरूप]] है जैसे कि [[ अव्यक्त चर |अव्यक्त चर]] की अवस्था समष्टि सतत है और सभी अव्यक्त और देखे गए चर में गॉसियन वितरण हैं। इसके अतिरिक्त, कालमान फिल्टर का बहु-संवेदक संगलन में सफलतापूर्वक उपयोग किया गया है, और वितरित या सर्वसम्मति कालमान फिल्टर विकसित करने के लिए [[ सेंसर नेटवर्क |संवेदक जालक्रम]] वितरित किए। | |||
== इतिहास == | == इतिहास == | ||
निस्यंदन विधि का नाम हंगरी के प्रवासी रूडोल्फ ई. | निस्यंदन विधि का नाम हंगरी के प्रवासी रूडोल्फ ई. कालमान के नाम पर रखा गया है, हालांकि [[ थोरवाल्ड निकोलाई थिले |थोरवाल्ड निकोलाई थिले]] <ref>{{cite journal |last1=Lauritzen |first1=S. L. |date=December 1981 |title=Time series analysis in 1880. A discussion of contributions made by T.N. Thiele |journal=International Statistical Review |volume=49 |number=3 |pages=319–331 |doi=10.2307/1402616 |jstor=1402616 |quote=He derives a recursive procedure for estimating the regression component and predicting the Brownian motion. The procedure is now known as Kalman filtering.}}</ref><ref>{{cite book |last=Lauritzen |first=S. L. |date=2002 |title=Thiele: Pioneer in Statistics |url=https://books.google.com/books?id=irugmNUwuG4C&q=kalman |location=New York |publisher=[[Oxford University Press]] |page=41 |isbn=978-0-19-850972-1 |author-link=Steffen Lauritzen |quote=He solves the problem of estimating the regression coefficients and predicting the values of the Brownian motion by the method of least squares and gives an elegant recursive procedure for carrying out the calculations. The procedure is nowadays known as ''Kalman filtering''.}}</ref> और [[ पीटर स्वेर्लिंग |पीटर स्वेर्लिंग]] ने पूर्व में भी इसी प्रकार की कलन विधि विकसित की गयी थी। [[ जॉन्स हॉपकिन्स एप्लाइड फिजिक्स लेबोरेटरी |जॉन्स हॉपकिन्स अनुप्रयुक्त भौतिकी प्रयोगशाला]] के रिचर्ड एस बुकी ने सिद्धांत में योगदान दिया, जिससे इसे कभी-कभी कालमान-बुकी निस्यंदन के रूप में भी जाना जाता है। स्टेनली एफ. श्मिट को सामान्यतः कालमान फिल्टर के प्रथम कार्यान्वयन को विकसित करने का श्रेय दिया जाता है। उन्होंने अनुभव किया कि फिल्टर को दो अलग-अलग भागो में विभाजित किया जा सकता है, एक भाग संवेदक आउटपुट के मध्य की समयावधि के लिए और दूसरा भाग मापन को सम्मिलित करने के लिए किया जा सकता है।<ref>[http://ieeecss.org/CSM/library/2010/june10/11-HistoricalPerspectives.pdf Mohinder S. Grewal and Angus P. Andrews]</ref> यह कालमान द्वारा [[ नासा एम्स रिसर्च सेंटर |नासा एम्स अनुसंधान केंद्र]] के अभ्यागमन के पर्यंत, श्मिट ने [[ प्रोजेक्ट अपोलो |अपोलो प्रकल्प]] के लिए प्रक्षेपवक्र अनुमान की गैर-रैखिक समस्या के लिए कालमान के विचारों की प्रयोज्यता को देखा गया, जिसके परिणामस्वरूप [[ अपोलो गाइडेंस कंप्यूटर |अपोलो दिशाज्ञान परिकलक]] में इसका समावेश हुआ। | ||
इस | इस कालमान फिल्टर को सर्वप्रथम स्वेर्लिंग (1958), कालमान (1960) और कालमान और बुकी (1961) द्वारा प्रौद्योगिकी पत्रों में आंशिक रूप से वर्णित और विकसित किया गया था। | ||
{{blockquote|अपोलो परिकलक ने 2k चुम्बकीय कोर RAM और 36k तार रज्जु [...] का उपयोग किया। CPU को ICs [...] से बनाया गया था। घड़ी की गति 100 किलोहर्ट्ज़ [...] से कम थी। तथ्य यह है कि MIT के अभियन्ता इतने छोटे परिकलक में इतने अच्छे सॉफ्टवेयर (कलमैन निस्यंदक के सबसे पहले अनुप्रयोगों में से एक) को संविष्ट करने में सक्षम थे, वास्तव में उल्लेखनीय है।|मैथ्यू रीड द्वारा जैक क्रेंशॉ के साथ साक्षात्कार, TRS-80.org (2009) [http://www.trs-80.org/interview-jack-crenshaw/] }} | {{blockquote|अपोलो परिकलक ने 2k चुम्बकीय कोर RAM और 36k तार रज्जु [...] का उपयोग किया। CPU को ICs [...] से बनाया गया था। घड़ी की गति 100 किलोहर्ट्ज़ [...] से कम थी। तथ्य यह है कि MIT के अभियन्ता इतने छोटे परिकलक में इतने अच्छे सॉफ्टवेयर (कलमैन निस्यंदक के सबसे पहले अनुप्रयोगों में से एक) को संविष्ट करने में सक्षम थे, वास्तव में उल्लेखनीय है।|मैथ्यू रीड द्वारा जैक क्रेंशॉ के साथ साक्षात्कार, TRS-80.org (2009) [http://www.trs-80.org/interview-jack-crenshaw/] }} | ||
अमेरिकी नौसेना के परमाणु प्राक्षेपिकीय प्रक्षेपणास्त्र पनडुब्बियों के दिशाज्ञान प्रणाली के कार्यान्वयन में और अमेरिकी नौसेना की [[ टॉमहॉक मिसाइल |टॉमहॉक प्रक्षेपणास्त्र]] और अमेरिकी वायु सेना की [[ एजीएम-86 एएलसीएम |एजीएम-86 एएलसीएम]] प्रारंभ की गई जैसे क्रूज प्रक्षेपणास्त्र के मार्गदर्शन और दिशाज्ञान प्रणाली में | अमेरिकी नौसेना के परमाणु प्राक्षेपिकीय प्रक्षेपणास्त्र पनडुब्बियों के दिशाज्ञान प्रणाली के कार्यान्वयन में और अमेरिकी नौसेना की [[ टॉमहॉक मिसाइल |टॉमहॉक प्रक्षेपणास्त्र]] और अमेरिकी वायु सेना की [[ एजीएम-86 एएलसीएम |एजीएम-86 एएलसीएम]] प्रारंभ की गई जैसे क्रूज प्रक्षेपणास्त्र के मार्गदर्शन और दिशाज्ञान प्रणाली में कालमान फिल्टर महत्वपूर्ण हैं। उनका उपयोग पुन: प्रयोज्य प्रारंभ वाहनों के मार्गदर्शन, दिशाज्ञान प्रणाली और अंतरिक्ष यान के दृष्टिकोण नियंत्रण और दिशाज्ञान प्रणाली में भी किया जाता है, जो अंतर्राष्ट्रीय अंतरिक्ष केन्द्रो पर डॉक करते हैं।<ref>{{Cite book|doi=10.2514/6.2003-5445|chapter=GPS/INS Kalman Filter Design for Spacecraft Operating in the Proximity of International Space Station|title=AIAA Guidance, Navigation, and Control Conference and Exhibit|year=2003|last1=Gaylor|first1=David|last2=Lightsey|first2=E. Glenn|isbn=978-1-62410-090-1}}</ref> | ||
== गणना का अवलोकन == | |||
कालमान फिल्टर प्रणाली के गतिशील प्रतिरूप (जैसे, गति के भौतिक नियम), उस प्रणाली के लिए ज्ञात नियंत्रण इनपुट और प्रणाली की अलग-अलग मात्राओं (इसकी स्थिति) का अनुमान लगाने के लिए कई अनुक्रमिक माप (जैसे संवेदक से) का उपयोग करता है। जैसे, यह एक सामान्य संवेदक संयोजन और डेटा संयोजन कलन विधि है। | |||
रव संवेदक डेटा, समीकरणों में सन्निकटन जो प्रणाली के विकास का वर्णन करते हैं, और बाहरी कारक जिनका कोई दोषी नहीं हैं, और सभी पर्याप्त करते हैं कि प्रणाली की स्थिति को कितनी अच्छी तरह से निर्धारित करना संभव है। कालमान फिल्टर रव संवेदक डेटा के कारण अनिश्चितता और कुछ सीमा तक यादृच्छिक बाहरी कारकों से प्रभावकारी रूप से व्यवहार करता है। कालमान फिल्टर प्रणाली की अनुमानित स्थिति के औसत और भारित औसत का उपयोग करके एक नए मापन के रूप में प्रणाली की स्थिति का अनुमान लगाता है। भार का उद्देश्य यह है कि उत्तम (अर्थात्, छोटे) अनुमानित अनिश्चितता वाले मान अधिक विश्वसनीय है। भार की गणना [[ सहप्रसरण |सहप्रसरण]] द्वारा की जाती है, जो प्रणाली की स्थिति के पूर्वानुमान की अनुमानित अनिश्चितता का एक उपाय है। भारित औसत का परिणाम एक नयी अवस्था अनुमान है, जो अनुमानित और मापित स्थिति के मध्य स्थित है, और असंग की तुलना में उन्नत अनुमानित अनिश्चितता है। इस प्रक्रिया को प्रत्येक टाइमस्टेप पर दोहराया जाता है, और एक नए अनुमान और इसके सहप्रसरण के साथ निम्नलिखित पुनरावृत्ति में उपयोग की जाने वाली पूर्वानुमान को सूचित करते हैं। इसका अर्थ यह है कि कालमान फिल्टर[[ पुनरावर्ती फ़िल्टर | पुनरावर्ती फिल्टर]] के रूप में कार्य करता है और एक नयी अवस्था की गणना करने के लिए प्रणाली की स्थिति के सम्पूर्ण इतिहास के स्थान पर केवल अंतिम "सर्वोत्तम अनुमान" की आवश्यकता होती है। | |||
मापन की 'निश्चितता-स्तरीकरण और वर्तमान स्थिति पर अनुमान एक महत्वपूर्ण विचार हैं। कालमान फिल्टर के [[ लाभ (इलेक्ट्रॉनिक्स) |लब्धि]] के संदर्भ में फिल्टर की प्रतिक्रिया पर आलोचना करना एक सामान्य तथ्य है। कालमान-लब्धि मापन और वर्तमान-अवस्था अनुमान को दिया गया भार है, और इसे किसी विशेष प्रदर्शन को प्राप्त करने के लिए समायोजित किया जा सकता है। एक उच्च लब्धि के साथ, फिल्टर सबसे हाल के मापों पर अधिक भार डालता है, और इस प्रकार उनके लिए अधिक प्रतिक्रियात्मक रूप से अनुरूप होता है। | |||
फिल्टर के लिए वास्तविक गणना करते समय (जैसे नीचे चर्चा की गई है) गणना के एक समुच्चय में सम्मिलित कई आयामों के कारण अवस्था अनुमान और सहप्रसरणों को[[ मैट्रिक्स (गणित) | आव्यूह]] में कूटलेखित किया जाता है। यह किसी भी पारगमन प्रतिरूप या सहप्रसरण में विभिन्न अवस्था चर (जैसे स्थिति, वेग और त्वरण) के मध्य रैखिक संबंधों के प्रतिनिधित्व के लिए अनुमति देता है। | |||
== उदाहरण आवेदन == | |||
एक उदाहरण के रूप में, एक माल गाड़ी के सटीक स्थान को निर्धारित करने की समस्या पर विचार करें। माल गाड़ी एक [[ GPS |जीपीएस]] ईकाई से सुसज्जित किया जा सकता है, जो कुछ मीटर के भीतर स्थिति का अनुमान प्रदान करता है। जीपीएस अनुमान रव होने की संभावना है; पाठ्यांक तीव्रता से 'विषयांतर' करते हैं, हालांकि वास्तविक स्थिति के कुछ मीटर के भीतर रहते हैं। इसके अतिरिक्त, चूंकि माल गाड़ी से भौतिकी के नियमों का पालन करने की अपेक्षा की जाती है, इसलिए समय के साथ इसके वेग को एकीकृत करके इसकी स्थिति का अनुमान लगाया जा सकता है, जो चक्र क्रांतियों और चालन चक्र के कोण को पथानुसरण करके निर्धारित किया जाता है। यह एक ऐसी प्रविधि है जिसे [[ मृत गणना |मृत गणना]] के रूप में जाना जाता है। सामान्यतः, मृत गणना माल गाड़ी की स्थिति का एक बहुत ही सहज अनुमान प्रदान करती है, परन्तु जैसे-जैसे छोटी-छोटी त्रुटियां एकत्र होती जाएंगी, और यह समय के साथ प्रवाहित होती जाएंगी। | |||
इस उदाहरण के लिए, कालमान फिल्टर को दो अलग-अलग चरणों में कार्य करने के विषय में विचार किया जा सकता है: उदाहरण के लिए, पूर्वानुमान और नवीनीकरण। पूर्वानुमान के चरण में, माल गाड़ी की पूर्वतन स्थिति को भौतिक न्यूटन के गति के नियमों (गतिशील या अवस्था पारगमन प्रतिरूप) के अनुसार संशोधित किया जाएगा। न केवल एक नई स्थिति अनुमान की गणना की जाएगी, बल्कि एक नए सहप्रसरण की भी गणना की जाएगी। सम्भवतः सहप्रसरण माल गाड़ी की गति के समानुपाती होता है क्योंकि हम उच्च गति पर मृत गणना स्थिति अनुमान की सटीकता के विषय में अधिक अनिश्चित होते हैं, परन्तु कम गति पर स्थिति अनुमान के विषय में बहुत निश्चित होते हैं। आगामी, अद्यतन चरण में, जीपीएस ईकाई से माल गाड़ी की स्थिति का मापन लिया जा सकता है। इस मापन के साथ कुछ मात्रा में अनिश्चितता आती है, और पूर्व चरण के पूर्वानुमान के सापेक्ष इसका सहप्रसरण यह निर्धारित करता है कि एक नया मापन अद्यतन पूर्वानुमान को कितना प्रभावित करेगा। आदर्श रूप से, चूंकि मृत गणना अनुमान वास्तविक स्थिति से दूर हो जाते हैं, जीपीएस मापन के स्थिति अनुमान को वास्तविक स्थिति की ओर वापस खींचना चाहिए। | |||
== प्रौद्योगिकीय विवरण और संदर्भ == | |||
कालमान फिल्टर एक कुशल पुनरावर्ती फिल्टर अनुमानक है जो रव माप की एक श्रृंखला से एक [[ रैखिक गतिशील प्रणाली |रैखिक गतिशील प्रणाली]] की आंतरिक स्थिति का आकलन करता है। इसका उपयोग [[ राडार |रेडार]] और [[ कंप्यूटर दृष्टी |परिकलक दृष्टि]] से संरचनात्मक वृहत् अर्थशास्त्र प्रतिरूप के आकलन के लिए [[ अभियांत्रिकी |अभियांत्रिकी]] और [[ अर्थमितीय |अर्थमितीय]] अनुप्रयोगों की एक विस्तृत श्रृंखला में किया जाता है,<ref>{{cite journal| author1=Ingvar Strid |author2=Karl Walentin |date=April 2009|title=Block Kalman Filtering for Large-Scale DSGE Models |journal=Computational Economics |volume=33 |pages=277–304 |url=http://www.riksbank.se/en/Press-and-published/Published-from-the-Riksbank/Other-reports/Working-Paper-Series/2008/No-224-Block-Kalman-filtering-for-large-scale-DSGE-models/|issue=3| doi=10.1007/s10614-008-9160-4|hdl=10419/81929 |citeseerx=10.1.1.232.3790 |s2cid=3042206 }}</ref><ref>{{cite web|author=Martin Møller Andreasen |year=2008 |title=Non-linear DSGE Models, The Central Difference Kalman Filter, and The Mean Shifted Particle Filter |url=ftp://ftp.econ.au.dk/creates/rp/08/rp08_33.pdf}}</ref> और [[ नियंत्रण सिद्धांत |नियंत्रण सिद्धांत]] और[[ नियंत्रण प्रणाली ]]अभियान्त्रिकी में एक महत्वपूर्ण विषय है। [[ रैखिक-द्विघात नियामक |रैखिक-द्विघात नियामक]] (LQR) के साथ, कालमान फिल्टर रैखिक-द्विघात-गॉसियन नियंत्रण समस्या (LQG) को हल करता है। कालमान फिल्टर, रैखिक-द्विघात नियामक, और रैखिक-द्विघात-गॉसियन नियंत्रक नियंत्रण सिद्धांत की सबसे मौलिक समस्याओं के समाधान हैं। | |||
अधिकांश अनुप्रयोगों में, मापे जाने वाले कुछ "अवलोकनीय" मापदंडों की तुलना में आंतरिक स्थिति बहुत बड़ी होती है (इसमें स्वतंत्रता की डिग्री अधिक होती है)। हालांकि, माप की एक श्रृंखला के संयोजन से, कालमान फिल्टर संपूर्ण आंतरिक स्थिति का अनुमान लगाया जा सकता है। | |||
डेम्पस्टर-शेफ़र सिद्धांत के लिए, प्रत्येक अवस्था समीकरण या अवलोकन को एक रैखिक धारणाफलन की एक विशेष स्थिति मानी जाती है और कालमान फिल्टर एक जॉइन-ट्री या मार्कोव ट्री पर रैखिक धारणाफलनो के संयोजन की एक विशेष स्थिति है। अतिरिक्त विधियों में धारणा निस्यंदन सम्मिलित है जो अवस्था समीकरणों के लिए बेयस या साक्ष्य अद्यतन का उपयोग करती है। | |||
कालमान फिल्टर की एक विस्तृत विविधता अब तक उपस्थित है, जिसे कालमान के मूल सूत्रीकरण से - अब "साधारण" कालमान फिल्टर, कालमान-बुकी फिल्टर, श्मिट का "विस्तारित" फिल्टर, सूचना फिल्टर, और वर्ग-रूट फिल्टर की एक विविधता कहा जाता है। जिसे बर्मन, थॉर्नटन, और कई अन्य लोगों द्वारा विकसित किया गया था। सम्भवतः सबसे अधिक उपयोग किया जाने वाला सबसे सरल कालमान फिल्टर कला पाशित लूप है, जो अब रेडियो में सर्वव्यापी है, विशेष रूप से आवृत्ति प्रतिरुपण (FM) रेडियो, टेलीविजन समुच्चय,[[ उपग्रह संचार ]]प्राप्तकर्ता, बाह्य अंतरिक्ष संचार प्रणाली, और लगभग किसी भी अन्य [[ इलेक्ट्रानिक्स |विद्युत्]] संचार उपकरण आदि। | |||
== अंतर्निहित गतिशील प्रणाली प्रतिरूप == | |||
कालमान फिल्टर समय प्रभावक्षेत्र में अलग-अलग रैखिक गतिशील प्रणालियों पर आधारित है।वे त्रुटियों से क्षुब्ध रैखिक संचालको पर निर्मित मार्कोव श्रृंखला पर आधारित हैं, जिनमें गॉसियन रव सम्मिलित हो सकता है। लक्ष्य प्रणाली की स्थिति महत्व की आधार सत्यता (अभी तक अप्रत्यक्ष है) प्रणाली विन्यास को संदर्भित करती है, जिसे [[ वास्तविक संख्या |वास्तविक संख्याओं]] के [[ सदिश स्थल |सदिश]] के रूप में दर्शाया जाता है। प्रत्येक असतत समय वृद्धि पर, नए अवस्था को उत्पन्न करने के लिए एक रैखिक संचालको को अवस्था में अनुप्रयुक्त किया जाता है, जिसमें कुछ रव मिश्रित होते है, और वैकल्पिक रूप से प्रणाली पर नियंत्रण से कुछ सूचना ज्ञात होने पर पुनः अधिक रव के साथ मिश्रित एक और रैखिक संचालक वास्तविक (अप्रत्यक्ष) स्थिति से मापने योग्य आउटपुट (अर्थात्, अवलोकन) उत्पन्न करता है। कालमान फिल्टर को अप्रत्यक्ष मार्कोव प्रतिरूप के अनुरूप माना जा सकता है, इस अंतर के साथ कि अप्रत्यक्ष मार्कोव प्रतिरूप के लिए असतत अवस्था स्थान के विपरीत अप्रत्यक्ष अवस्था चर के मान निरंतर स्थान में होते हैं। कालमान फिल्टर के समीकरणों और अप्रत्यक्ष मार्कोव प्रतिरूप के समीकरणों के मध्य एक प्रबल सादृश्य है। इस और अन्य प्रतिरूपों की समीक्षा रोविस और[[ ज़ब्न जहरमान | ज़ब्न जहरमान]] (1999) और हैमिल्टन (1994), अध्याय 13 में दी गई है।<ref>{{cite journal|doi=10.1162/089976699300016674|pmid= 9950734|year= 1999|last1= Roweis|first1= S|title= A unifying review of linear gaussian models|journal= Neural Computation|volume= 11|issue= 2|pages= 305–45|last2= Ghahramani|first2= Z|s2cid= 2590898|url= https://authors.library.caltech.edu/13697/1/ROWnc99.pdf}}</ref> <ref name="hamilton">Hamilton, J. (1994), ''Time Series Analysis'', Princeton University Press. Chapter 13, 'The Kalman Filter'</ref> | |||
एक प्रक्रिया की आंतरिक स्थिति का अनुमान लगाने के लिए कालमान फिल्टर का उपयोग करने के लिए केवल रव अवलोकनों का अनुक्रम दिया जाता है, निम्नलिखित को रूपरेखा के अनुसार प्रक्रिया को प्रतिरूप करना चाहिए। इसका अर्थ है कि प्रत्येक समय-चरण k के लिए आव्यूह निर्दिष्ट करना, निम्नलिखित:'''F''', अवस्था-पारगमन प्रतिरूप; | |||
*'''H'''<sub>''k''</sub>, अवलोकन प्रतिरूप; | |||
*'''Q'''<sub>''k''</sub>, प्रक्रिया रव का सहप्रसरण; | |||
एक प्रक्रिया की आंतरिक स्थिति का अनुमान लगाने के लिए | *'''R'''<sub>''k''</sub>, प्रेक्षण रव का सहप्रसरण; | ||
*और कभी -कभी '''B'''<sub>''k''</sub>, नियंत्रण-इनपुट प्रतिरूप जैसा कि नीचे वर्णित है; यदि '''B'''<sub>''k''</sub> सम्मिलित है, तो भी है | |||
* | *'''u'''<sub>''k''</sub>, नियंत्रण सदिश, नियंत्रित इनपुट को नियंत्रण-इनपुट प्रतिरूप में दर्शाता है। | ||
* | |||
* | |||
*और कभी कभी | |||
* | |||
[[File:Kalman filter model 2.svg|right|thumb|631px| | [[File:Kalman filter model 2.svg|right|thumb|631px|कालमान फिल्टर के अंतर्निहित प्रतिरूप। वर्ग आव्यूह का प्रतिनिधित्व करते हैं। दीर्घवृत्त बहुभिन्नरूपी सामान्य वितरण का प्रतिनिधित्व करते हैं (माध्य और सहप्रसरण आव्यूह संलग्न के साथ) असंबद्ध मान सदिश होते हैं। साधारण स्थितियो के लिए, विभिन्न आव्यूह समय के साथ स्थिर होते हैं, और इस प्रकार पादांक का उपयोग नहीं किया जाता है, परन्तु कालमान फिल्टर उनमें से किसी को भी प्रत्येक बार चरण परिवर्तित करने की अनुमति देता है।]] | ||
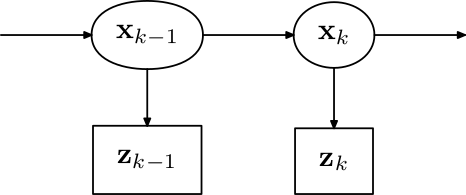
कालमान फिल्टर प्रतिरूप समय पर वास्तविक स्थिति को मानता है, जब k अवस्था से (k − 1) के अनुसार विकसित होता है; | |||
:<math> \mathbf{x}_k = \mathbf{F}_k \mathbf{x}_{k-1} +\mathbf{B}_k \mathbf{u}_{k} + \mathbf{w}_k </math> | :<math> \mathbf{x}_k = \mathbf{F}_k \mathbf{x}_{k-1} +\mathbf{B}_k \mathbf{u}_{k} + \mathbf{w}_k </math> | ||
जहां | |||
* | * '''F'''<sub>''k''</sub> अवस्था पारगमन प्रतिरूप है, जो पूर्व अवस्था '''x'''<sub>''k''−1</sub> पर अनुप्रयुक्त होता है; | ||
* | * '''B'''<sub>''k''</sub> नियंत्रण-इनपुट प्रतिरूप है, जो नियंत्रण सदिश '''u'''<sub>''k''</sub> पर अनुप्रयुक्त होता है; | ||
* | * '''w'''<sub>''k''</sub> प्रक्रिया रव है, जिसे शून्य माध्य बहुभिन्नरूपी सामान्य वितरण <math>\mathcal{N}</math> से आसंजित किया जाता है, सहप्रसरण आव्यूह के साथ, Q<sub>''k''</sub>: <math>\mathbf{w}_k \sim \mathcal{N}\left(0, \mathbf{Q}_k\right) </math>. | ||
समय k पर | समय k पर वास्तविक स्थिति x<sub>''k''</sub> का एक अवलोकन (या माप) z<sub>''k''</sub> के अनुसार किया जाता है | ||
:<math>\mathbf{z}_k = \mathbf{H}_k \mathbf{x}_k + \mathbf{v}_k</math> | :<math>\mathbf{z}_k = \mathbf{H}_k \mathbf{x}_k + \mathbf{v}_k</math> | ||
जहां | |||
* | * '''H'''<sub>''k''</sub> अवलोकन प्रतिरूप है, जो वास्तविक स्थिति स्थान को प्रेक्षित स्थान में मानचित्र करता है और | ||
* | * '''v'''<sub>''k''</sub> अवलोकन रव है, जिसे सहप्रसरण '''R'''<sub>''k''</sub> के साथ शून्य औसत गॉसियन श्वेत रव माना जाता है: <math>\mathbf{v}_k \sim \mathcal{N}\left(0, \mathbf{R}_k\right) </math>. | ||
प्रारंभिक अवस्था, और प्रत्येक चरण | प्रारंभिक अवस्था, और प्रत्येक चरण {'''x'''<sub>0</sub>, '''w'''<sub>1</sub>, ..., '''w'''<sub>''k''</sub>, '''v'''<sub>1</sub>, ... ,'''v'''<sub>''k''</sub>} पर रव सदिश सभी पारस्परिक रूप से स्वतंत्र माने जाते हैं। | ||
कई | कई वास्तविक समय सक्रिय प्रणाली इस प्रतिरूप के पूर्णतया अनुरूप नहीं हैं। वास्तव में, अप्रतिरूपित गतिशीलता फिल्टर के प्रदर्शन को गंभीरता से कम कर सकता है, तब भी जब इसे इनपुट के रूप में अज्ञात प्रसंभाव्य संकेतों के साथ कार्य करना चाहिए था। इसका कारण यह है कि अप्रतिरूपित गतिशीलता का प्रभाव इनपुट पर निर्भर करता है, और इसलिए, अनुमान कलन विधि को अस्थिरता में ला सकता है (यह विचलन करता है)। दूसरी ओर, स्वतंत्र श्वेत रव संकेत कलन विधि को विचलन नहीं करेंगे। मापन रव और अनप्रतिरूप गतिकी के मध्य अंतर करने की समस्या कठिन है और इसे [[ मजबूत नियंत्रण |सुदृढ़ नियंत्रण]] का उपयोग करके नियंत्रण सिद्धांत की समस्या के रूप में माना जाता है।<ref name="ishihara06">{{cite journal |doi=10.1109/TAC.2006.878741|title=Robust Kalman Filter for Descriptor Systems|journal=IEEE Transactions on Automatic Control|volume=51|issue=8|pages=1354|year=2006|last1=Ishihara|first1=J.Y.|last2=Terra|first2=M.H.|last3=Campos|first3=J.C.T.|s2cid=12741796}}</ref><ref name="terra14">{{cite journal |doi=10.1109/TAC.2014.2309282|title=Optimal Robust Linear Quadratic Regulator for Systems Subject to Uncertainties|journal=IEEE Transactions on Automatic Control|volume=59|issue=9|pages=2586–2591|year=2014|last1=Terra|first1=Marco H.|last2=Cerri|first2=Joao P.|last3=Ishihara|first3=Joao Y.|s2cid=8810105}}</ref> | ||
== '''विवरण''' == | == '''विवरण''' == | ||
कालमान फिल्टर एक [[ अनंत आवेग प्रतिक्रिया |पुनरावर्ती]] अनुमानक है। इसका अर्थ यह है कि वर्तमान स्थिति के अनुमान की गणना करने के लिए पूर्व समय के चरण और वर्तमान माप से केवल अनुमानित स्थिति की आवश्यकता है। प्रचय अनुमान प्रविधियों के विपरीत, अवलोकनों और/या अनुमानों के इतिहास की आवश्यकता नहीं है। निम्नलिखित में, अंकन <math>\hat{\mathbf{x}}_{n\mid m}</math> के अनुमान का प्रतिनिधित्व करता है, <math>\mathbf{x}</math> समय पर n दिए गए अवलोकनों को समय {{nowrap|''m'' ≤ ''n''}} तक सम्मिलित किया गया हैं | |||
फिल्टर की स्थिति को दो चर द्वारा दर्शाया जाता है: | |||
* <math>\hat{\mathbf{x}}_{k\mid k}</math>, एक पश्चवर्ती अवस्था का अनुमान समय k पर दिया गया है | * <math>\hat{\mathbf{x}}_{k\mid k}</math>, एक पश्चवर्ती अवस्था का अनुमान समय k पर दिया गया अवलोकन है, जिसमें समय k सम्मिलित है; | ||
* <math>\mathbf{P}_{k\mid k}</math>, एक | * <math>\mathbf{P}_{k\mid k}</math>, एक पश्चवर्ती सहप्रसरण आव्यूह (अवस्था अनुमान की अनुमानित सटीकता का एक माप)। | ||
कालमान फिल्टर की कलन विधि संरचना [[ अल्फा बीटा फ़िल्टर |अल्फा बीटा फिल्टर]] के समान होती है। कालमान फिल्टर को एकल समीकरण के रूप में लिखा जा सकता है; हालांकि, इसे प्रायः दो अलग-अलग चरणों के रूप में परिकल्पित किया जाता है: पूर्वानुमान और अद्यतन। पूर्वानुमान चरण वर्तमान टाइमस्टेप पर अवस्था का अनुमान लगाने के लिए पूर्व समय के अवस्था अनुमान का उपयोग करता है। इस पूर्वानुमानित अवस्था के अनुमान को प्राथमिक अवस्था के अनुमान के रूप में भी जाना जाता है क्योंकि, हालांकि यह वर्तमान समय पर अवस्था का अनुमान है, इसमें वर्तमान समय-चरण से अवलोकन की सूचना सम्मिलित नहीं है। अद्यतन चरण में, [[ नवाचार (सिग्नल प्रोसेसिंग) |नवाचार]] (पूर्व-सटीक अवशिष्ट), अर्थात् वर्तमान एक प्राथमिक पूर्वानुमान और वर्तमान अवलोकन सूचना के मध्य का अंतर, इष्टतम कालमान लब्धि से गुणा किया जाता है और अवस्था अनुमान को परिष्कृत करने के लिए पूर्व अवस्था अनुमान के साथ जोड़ा जाता है। वर्तमान अवलोकन के आधार पर इस उन्नत अनुमान को पश्चवर्ती अवस्था अनुमान कहा जाता है। | |||
सामान्यतः, दो चरण वैकल्पिक होते हैं, पूर्वानुमान अगले अनुसूचित अवलोकन तक अवस्था को आगे बढ़ाते है, और अद्यतन अवलोकन को सम्मिलित करते है। हालाँकि, यह आवश्यक नहीं है; यदि किसी कारण से कोई अवलोकन अनुपलब्ध है, तो अद्यतन को छोड़ दिया जा सकता है और कई पूर्वानुमान प्रक्रियाओं का प्रदर्शन किया जा सकता है। इसी प्रकार, यदि एक ही समय में कई स्वतंत्र अवलोकन उपलब्ध हैं, तो कई अद्यतन प्रक्रियाएं (सामान्यतः विभिन्न अवलोकन आव्यूह '''H'''<sub>''k''</sub> के साथ) की जा सकती हैं।<ref>{{cite journal|last1=Kelly|first1=Alonzo|title=A 3D state space formulation of a navigation Kalman filter for autonomous vehicles|journal=DTIC Document|date=1994|page=13|url=http://apps.dtic.mil/dtic/tr/fulltext/u2/a282853.pdf|archive-url=https://web.archive.org/web/20141230004557/http://www.dtic.mil/dtic/tr/fulltext/u2/a282853.pdf|url-status=live|archive-date=December 30, 2014}} [http://www.frc.ri.cmu.edu/~alonzo/pubs/reports/kalman_V2.pdf 2006 Corrected Version] {{Webarchive|url=https://web.archive.org/web/20170110204109/http://www.frc.ri.cmu.edu/~alonzo/pubs/reports/kalman_V2.pdf |date=2017-01-10 }}</ref><ref>{{cite web|last1=Reid|first1=Ian|last2=Term|first2=Hilary|title=Estimation II|url=http://www.robots.ox.ac.uk/~ian/Teaching/Estimation/LectureNotes2.pdf|website=www.robots.ox.ac.uk|publisher=Oxford University|access-date=6 August 2014}}</ref> | |||
=== | === पूर्वानुमान === | ||
{| | {| | ||
|- | |- | ||
| Line 111: | Line 109: | ||
| <math>\mathbf{S}_k = \mathbf{H}_k \mathbf{P}_{k\mid k-1} \mathbf{H}_k^\textsf{T} + \mathbf{R}_k</math> | | <math>\mathbf{S}_k = \mathbf{H}_k \mathbf{P}_{k\mid k-1} \mathbf{H}_k^\textsf{T} + \mathbf{R}_k</math> | ||
|- | |- | ||
| इष्टतम | | इष्टतम कालमान लब्धि | ||
| <math>\mathbf{K}_k = \mathbf{P}_{k\mid k-1}\mathbf{H}_k^\textsf{T} \mathbf{S}_k^{-1}</math> | | <math>\mathbf{K}_k = \mathbf{P}_{k\mid k-1}\mathbf{H}_k^\textsf{T} \mathbf{S}_k^{-1}</math> | ||
|- | |- | ||
| Line 129: | Line 127: | ||
:<math>\hat{\mathbf{x}}_{k\mid k} = (\mathbf{I} - \mathbf{K}_k \mathbf{H}_k) \hat{\mathbf{x}}_{k\mid k-1} + \mathbf{K}_k (\mathbf{H}_k \mathbf{x}_k + \mathbf{v}_k)</math> | :<math>\hat{\mathbf{x}}_{k\mid k} = (\mathbf{I} - \mathbf{K}_k \mathbf{H}_k) \hat{\mathbf{x}}_{k\mid k-1} + \mathbf{K}_k (\mathbf{H}_k \mathbf{x}_k + \mathbf{v}_k)</math> | ||
यह अभिव्यक्ति हमें एक रैखिक प्रक्षेप का स्मरण कराती है, <math>x = (1-t)(a) + t(b)</math> के लिये <math>t</math> [0,1] के मध्य हमारी स्थितियो में: | यह अभिव्यक्ति हमें एक रैखिक प्रक्षेप का स्मरण कराती है, <math>x = (1-t)(a) + t(b)</math> के लिये <math>t</math> [0,1] के मध्य हमारी स्थितियो में: | ||
* <math>t</math> | * <math>t</math> कालमान लब्धि (<math>\mathbf{K}_k</math>) है, एक आव्यूह जो <math>0</math> (संवेदक में उच्च त्रुटि) से <math>I</math> (कम त्रुटि) मान लेता है । | ||
* <math>a</math> प्रतिरूप से अनुमानित मान है। | * <math>a</math> प्रतिरूप से अनुमानित मान है। | ||
* <math>b</math> माप से मान है। | * <math>b</math> माप से मान है। | ||
यह व्यंजक अल्फ़ा बीटा | यह व्यंजक अल्फ़ा बीटा फिल्टर अद्यतन चरण के समान भी है। | ||
=== अपरिवर्तनीय === | === अपरिवर्तनीय === | ||
| Line 151: | Line 149: | ||
=== रव सहप्रसरण Q<sub>''k''</sub> और R<sub>''k''</sub> का अनुमान === | === रव सहप्रसरण Q<sub>''k''</sub> और R<sub>''k''</sub> का अनुमान === | ||
रव सहप्रसरण आव्यूह Q<sub>''k''</sub> और आर<sub>''k''</sub> का एक उत्तम अनुमान प्राप्त करने में कठिनाई के कारण | रव सहप्रसरण आव्यूह Q<sub>''k''</sub> और आर<sub>''k''</sub> का एक उत्तम अनुमान प्राप्त करने में कठिनाई के कारण कालमान फिल्टर का व्यावहारिक कार्यान्वयन प्रायः कठिन होता है। डेटा से इन सहप्रसरणों का अनुमान लगाने के लिए व्यापक अन्वेषण किया गया है। ऐसा करने की एक व्यावहारिक प्रणाली [[ स्वतः सहप्रसरण |स्वसहप्रसरण]] न्यूनतम वर्ग (''ALS'') प्रविधि है, जो सहप्रसरण का अनुमान लगाने के लिए नियमित संचालन डेटा के समय-अंतराल स्वसहप्रसरण का उपयोग करता है।<ref>{{cite thesis |url=http://jbrwww.che.wisc.edu/theses/rajamani.pdf |last=Rajamani |first=Murali |type=PhD Thesis |title=Data-based Techniques to Improve State Estimation in Model Predictive Control |location=University of Wisconsin–Madison |date=October 2007 |access-date=2011-04-04 |archive-url=https://web.archive.org/web/20160304194938/http://jbrwww.che.wisc.edu/theses/rajamani.pdf |archive-date=2016-03-04 |url-status=dead }}</ref><ref>{{cite journal |last1=Rajamani |first1=Murali R. |last2=Rawlings |first2=James B. |title=Estimation of the disturbance structure from data using semidefinite programming and optimal weighting |journal=Automatica |volume=45 |issue=1 |pages=142–148 |year=2009 |doi=10.1016/j.automatica.2008.05.032 }}</ref> [[ जीएनयू ऑक्टेव |जीएनयू अष्टक]] और मैटलैब कोड और एएलएस प्रविधि का उपयोग करके रव सहप्रसरण आव्यूह की गणना करने के लिए किया जाता है, जो[[ जीएनयू जनरल पब्लिक लाइसेंस | जीएनयू सामान्य जनता अनुज्ञप्ति]] का उपयोग करके लाइनेतर उपलब्ध है।<ref>{{cite web |url=https://sites.engineering.ucsb.edu/~jbraw/software/als/index.html |title=Autocovariance Least-Squares Toolbox |publisher=Jbrwww.che.wisc.edu |access-date=2021-08-18 }}</ref> क्षेत्र कालमान फिल्टर (FKF), एक बायेसियन कलन विधि, जो अवस्था, मापदंडों और रव सहप्रसरण के एक साथ आकलन की अनुमति देता है।<ref>{{cite conference |url= https://www.researchgate.net/publication/312029167|title= Field Kalman Filter and its approximation|last1= Bania|first1= P.|last2= Baranowski|first2=J.|publisher=IEEE |date=12 December 2016|pages= 2875–2880|location= Las Vegas, NV, USA|conference= IEEE 55th Conference on Decision and Control (CDC)}}</ref> एफकेएफ कलन विधियों में एक पुनरावर्ती सूत्रीकरण, उत्तम प्रेक्षित अभिसरण और अपेक्षाकृत कम जटिलता है। इस प्रकार यह संसूचन देता है कि एफकेएफ कलन विधि संभवतः स्वसहप्रसरण न्यूनतम वर्ग विधियों का एक सार्थक विकल्प हो सकता है। | ||
=== इष्टतमता और प्रदर्शन === | === इष्टतमता और प्रदर्शन === | ||
यह सिद्धांत से निम्नानुसार है कि | यह सिद्धांत से निम्नानुसार है कि कालमान फिल्टर उन स्थितियो में इष्टतम रैखिक फिल्टर है जहां ए) प्रतिरूप वास्तविक प्रणाली से पूरी तरह मेल खाता है, बी) प्रवेश रव सफेद (असंबद्ध) है और सी) रव के सहसंयोजक पूर्णतया ज्ञात हैं। कालमान फिल्टर का उपयोग करके सहसंबद्ध रव का भी इलाज किया जा सकता है।<ref>{{Cite book|last1=Bar-Shalom|first1=Yaakov|url=http://dx.doi.org/10.1002/0471221279|title=Estimation with Applications to Tracking and Navigation|last2=Li|first2=X.-Rong|last3=Kirubarajan|first3=Thiagalingam|date=2001|publisher=John Wiley & Sons, Inc.|isbn=0-471-41655-X|location=New York, USA|pages=319 ff|doi=10.1002/0471221279}}</ref> पूर्व दशकों के पर्यंत रव सहसंयोजक अनुमान के लिए कई प्रणाली प्रस्तावित की गयी हैं, जिनमें एएलएस भी सम्मिलित है, जिसका उल्लेख ऊपर के खंड में किया गया है। सहप्रसरणों का अनुमान लगाने के बाद, फिल्टर के प्रदर्शन का मूल्यांकन करना उपयोगी होता है; अर्थात् क्या अवस्था के आकलन की गुणवत्ता में सुधार संभव है। यदि कालमान फिल्टर उन्नत विधि से कार्य करता है, तो इनोवेशन सीक्वेंस (आउटपुट प्रेडिक्शन एरर) एक सफेद रव है, इसलिए इनोवेशन (सिग्नल प्रोसेसिंग) की व्हाइटनेस प्रॉपर्टी फिल्टर के प्रदर्शन को मापती है। इस उद्देश्य के लिए कई अलग-अलग प्रणालियो का उपयोग किया जा सकता है।<ref>Three optimality tests with numerical examples are described in {{cite book|doi=10.3182/20120711-3-BE-2027.00011|chapter=Optimality Tests and Adaptive Kalman Filter|title=16th IFAC Symposium on System Identification|journal=IFAC Proceedings Volumes|volume=45|issue=16|pages=1523–1528|series=16th IFAC Symposium on System Identification|year=2012|last1=Peter|first1=Matisko|isbn=978-3-902823-06-9}}</ref> यदि रव की शर्तों को गैर-गॉसियन विधि से वितरित किया जाता है, तो फिल्टर अनुमान के प्रदर्शन का आकलन करने के विधि, जो संभाव्यता असमानताओं या बड़े-प्रतिरूप सिद्धांत का उपयोग करते हैं, साहित्य में जाने जाते हैं।<ref>{{cite journal|doi=10.1016/0005-1098(95)00069-9|title=The Kantorovich inequality for error analysis of the Kalman filter with unknown noise distributions|journal=Automatica|volume=31|issue=10|pages=1513–1517|year=1995|last1=Spall|first1=James C.}}</ref><ref>{{cite journal|doi=10.1109/TAC.2003.821415|title=Use of the Kalman Filter for Inference in State-Space Models with Unknown Noise Distributions|journal=IEEE Transactions on Automatic Control|volume=49|pages=87–90|year=2004|last1=Maryak|first1=J.L.|last2=Spall|first2=J.C.|last3=Heydon|first3=B.D.|s2cid=21143516}}</ref> | ||
== उदाहरण आवेदन, प्रौद्योगिकीय == | == उदाहरण आवेदन, प्रौद्योगिकीय == | ||
[[File:kalman.png|thumb|{{color box|black}}{{nbsp}} | [[File:kalman.png|thumb|{{color box|black}}{{nbsp}}सत्यता; {{color box|green}}{{nbsp}}फिल्टर प्रक्रिया; {{color box|red}}{{nbsp}}अवलोकन।]] | ||
घर्षण रहित, पटरियों पर चलने वाले एक माल गाड़ी पर विचार करें। प्रारंभ में, माल गाड़ी की स्थिति 0 में स्थिर होती है, परन्तु यह यादृच्छिक अनियंत्रित बलों द्वारा इस प्रकार और उस प्रकार से टकराया जाता है। हम प्रत्येक Δt सेकंड में माल गाड़ी की स्थिति को मापते हैं, परन्तु ये माप सटीक नहीं होते हैं; हम माल गाड़ी की स्थिति और [[ वेग |वेग]] का एक प्रतिरूप बनाए रखना चाहते हैं। हम यहां दर्शाते हैं कि हम उस प्रतिरूप को कैसे प्राप्त करते हैं, जिससे हम अपना | घर्षण रहित, पटरियों पर चलने वाले एक माल गाड़ी पर विचार करें। प्रारंभ में, माल गाड़ी की स्थिति 0 में स्थिर होती है, परन्तु यह यादृच्छिक अनियंत्रित बलों द्वारा इस प्रकार और उस प्रकार से टकराया जाता है। हम प्रत्येक Δt सेकंड में माल गाड़ी की स्थिति को मापते हैं, परन्तु ये माप सटीक नहीं होते हैं; हम माल गाड़ी की स्थिति और [[ वेग |वेग]] का एक प्रतिरूप बनाए रखना चाहते हैं। हम यहां दर्शाते हैं कि हम उस प्रतिरूप को कैसे प्राप्त करते हैं, जिससे हम अपना कालमान फिल्टर निर्मित करते हैं। | ||
तब से <math>\mathbf{F}, \mathbf{H}, \mathbf{R}, \mathbf{Q}</math> स्थिर हैं, और उनका समय सूचकांक अवनत कर दिया जाता है। | तब से <math>\mathbf{F}, \mathbf{H}, \mathbf{R}, \mathbf{Q}</math> स्थिर हैं, और उनका समय सूचकांक अवनत कर दिया जाता है। | ||
| Line 171: | Line 169: | ||
जहां <math>\dot{x}</math> वेग है, जो समय के संबंध में स्थिति का व्युत्पन्न है। | जहां <math>\dot{x}</math> वेग है, जो समय के संबंध में स्थिति का व्युत्पन्न है। | ||
हम मानते हैं कि (k − 1) और k | हम मानते हैं कि (k − 1) और k टाइमस्टेप के मध्य अनियंत्रित बल a<sub>''k''</sub> के सतत त्वरण का कारण बनते हैं, सामान्य रूप से माध्य 0 और मानक विचलन ''σ<sub>a</sub>'' के साथ वितरित किया जाता है। न्यूटन के गति के नियमों से हम यह निष्कर्ष निकालते हैं कि | ||
:<math>\mathbf{x}_k = \mathbf{F} \mathbf{x}_{k-1} + \mathbf{G} a_k</math> | :<math>\mathbf{x}_k = \mathbf{F} \mathbf{x}_{k-1} + \mathbf{G} a_k</math> | ||
(<math>\mathbf{B}u</math> | (<math>\mathbf{B}u</math> पद का क्योंकि कोई ज्ञात नियंत्रण इनपुट नहीं हैं। इसके स्थान पर, ''a<sub>k</sub>'' एक अज्ञात इनपुट का प्रभाव है और जहां <math>\mathbf{G}</math> उस प्रभाव को अवस्था सदिश पर अनुप्रयुक्त करता है) | ||
:<math>\begin{align} | :<math>\begin{align} | ||
\mathbf{F} &= \begin{bmatrix} | \mathbf{F} &= \begin{bmatrix} | ||
| Line 196: | Line 194: | ||
\end{bmatrix}\sigma_a^2. | \end{bmatrix}\sigma_a^2. | ||
\end{align}</math> | \end{align}</math> | ||
एक आव्यूह <math>\mathbf{Q}</math> पूर्ण श्रेणी नहीं है (यह श्रेणी एक का <math>\Delta t \neq 0</math> है यदि) वितरण <math>N(0, \mathbf{Q})</math> पूर्णतया | एक आव्यूह <math>\mathbf{Q}</math> पूर्ण श्रेणी नहीं है (यह श्रेणी एक का <math>\Delta t \neq 0</math> है यदि) वितरण <math>N(0, \mathbf{Q})</math> पूर्णतया सतत नहीं है और इसमें कोई संभाव्यता घनत्व फलन नहीं है। इसे व्यक्त करने की एक अन्य प्रणाली, स्पष्ट पतित वितरणों से परिहरण करना है; | ||
:<math>\mathbf{w}_k \sim \mathbf{G} \cdot N\left(0, \sigma_a^2\right). </math> | :<math>\mathbf{w}_k \sim \mathbf{G} \cdot N\left(0, \sigma_a^2\right). </math> | ||
प्रत्येक | प्रत्येक टाइमस्टेप में, माल गाड़ी की वास्तविक स्थिति का रव माप किया जाता है, मान लें कि माप रव v<sub>''k''</sub> माध्य 0 और मानक विचलन ''σ<sub>z</sub>''के साथ सामान्य रूप से भी वितरित किया जाता है; | ||
:<math>\mathbf{z}_k = \mathbf{H x}_k + \mathbf{v}_k</math> | :<math>\mathbf{z}_k = \mathbf{H x}_k + \mathbf{v}_k</math> | ||
जहां | जहां | ||
| Line 209: | Line 207: | ||
हम माल गाड़ी की प्रारंभिक स्थिति को पूर्ण सटीकता के साथ स्पष्ट करते हैं, इसलिए हम प्रारंभ करते हैं | हम माल गाड़ी की प्रारंभिक स्थिति को पूर्ण सटीकता के साथ स्पष्ट करते हैं, इसलिए हम प्रारंभ करते हैं | ||
:<math>\hat{\mathbf{x}}_{0 \mid 0} = \begin{bmatrix} 0 \\ 0 \end{bmatrix} </math> | :<math>\hat{\mathbf{x}}_{0 \mid 0} = \begin{bmatrix} 0 \\ 0 \end{bmatrix} </math> | ||
और | और फिल्टर को यह सूचित के लिए कि हम सटीक स्थिति और वेग से परिचित हैं, हम इसे एक शून्य सहप्रसरण आव्यूह प्रदान करते हैं: | ||
:<math>\mathbf{P}_{0 \mid 0} = \begin{bmatrix} | :<math>\mathbf{P}_{0 \mid 0} = \begin{bmatrix} | ||
0 & 0 \\ | 0 & 0 \\ | ||
| Line 221: | Line 219: | ||
\end{bmatrix} | \end{bmatrix} | ||
</math> | </math> | ||
फिल्टर तब प्रतिरूप में पूर्व से ही उपस्थित सूचना पर प्रथम माप से सूचना को प्राथमिकता देता है। | |||
== स्पर्शोन्मुख रूप == | == स्पर्शोन्मुख रूप == | ||
सहजता के लिए, मान लें कि नियंत्रण इनपुट <math>\mathbf{u}_k=\mathbf{0}</math> है, तब | सहजता के लिए, मान लें कि नियंत्रण इनपुट <math>\mathbf{u}_k=\mathbf{0}</math> है, तब कालमान फिल्टर को लिखा जा सकता है: | ||
:<math>\hat{\mathbf{x}}_{k\mid k} = \mathbf{F}_k \hat{\mathbf{x}}_{k-1\mid k-1} + \mathbf{K}_k[\mathbf{z}_k - \mathbf{H}_k \mathbf{F}_k\hat{\mathbf{x}}_{k-1\mid k-1}].</math> | :<math>\hat{\mathbf{x}}_{k\mid k} = \mathbf{F}_k \hat{\mathbf{x}}_{k-1\mid k-1} + \mathbf{K}_k[\mathbf{z}_k - \mathbf{H}_k \mathbf{F}_k\hat{\mathbf{x}}_{k-1\mid k-1}].</math> | ||
यदि हम एक गैर-शून्य नियंत्रण इनपुट सम्मिलित करते हैं तो एक समान समीकरण प्राप्त होता है। लब्धि आव्यूह <math>\mathbf{K}_k</math> मापन <math>\mathbf{z}_k</math> से स्वतंत्र रूप से विकसित होते हैं। ऊपर से, | यदि हम एक गैर-शून्य नियंत्रण इनपुट सम्मिलित करते हैं तो एक समान समीकरण प्राप्त होता है। लब्धि आव्यूह <math>\mathbf{K}_k</math> मापन <math>\mathbf{z}_k</math> से स्वतंत्र रूप से विकसित होते हैं। ऊपर से, कालमान लब्धि को अद्यतन करने के लिए आवश्यक चार समीकरण इस प्रकार हैं: | ||
:<math>\begin{align} | :<math>\begin{align} | ||
| Line 238: | Line 236: | ||
चूंकि लब्धि आव्यूह केवल प्रतिरूप पर निर्भर करते हैं, न कि माप पर, उनकी गणना ऑफ़लाइन की जा सकती है। लब्धि आव्यूह का अभिसरण <math>\mathbf{K}_k</math> एक स्पर्शोन्मुख आव्यूह <math>\mathbf{K}_\infty</math> के लिए वालरैंड और डिमाकिस में स्थापित स्थितियों के लिए अनुप्रयुक्त होता है।<ref name=walrandnotes>{{cite book|last1=Walrand|first1=Jean|last2=Dimakis|first2=Antonis|date=August 2006 |title=Random processes in Systems -- Lecture Notes | url=https://people.eecs.berkeley.edu/~wlr/226F06/226a.pdf |pages=69–70}}</ref> अनुरूपण अभिसरण के चरणों की संख्या स्थापित करते हैं। ऊपर वर्णित चलती माल गाड़ी के उदाहरण के लिए <math>\Delta t = 1</math>. और <math>\sigma_a^2=\sigma_z^2 =\sigma_x^2= \sigma_\dot{x}^2=1</math>, अनुरूपण में अभिसरण <math>10</math> पुनरावृत्तियों को दर्शाता है; | चूंकि लब्धि आव्यूह केवल प्रतिरूप पर निर्भर करते हैं, न कि माप पर, उनकी गणना ऑफ़लाइन की जा सकती है। लब्धि आव्यूह का अभिसरण <math>\mathbf{K}_k</math> एक स्पर्शोन्मुख आव्यूह <math>\mathbf{K}_\infty</math> के लिए वालरैंड और डिमाकिस में स्थापित स्थितियों के लिए अनुप्रयुक्त होता है।<ref name=walrandnotes>{{cite book|last1=Walrand|first1=Jean|last2=Dimakis|first2=Antonis|date=August 2006 |title=Random processes in Systems -- Lecture Notes | url=https://people.eecs.berkeley.edu/~wlr/226F06/226a.pdf |pages=69–70}}</ref> अनुरूपण अभिसरण के चरणों की संख्या स्थापित करते हैं। ऊपर वर्णित चलती माल गाड़ी के उदाहरण के लिए <math>\Delta t = 1</math>. और <math>\sigma_a^2=\sigma_z^2 =\sigma_x^2= \sigma_\dot{x}^2=1</math>, अनुरूपण में अभिसरण <math>10</math> पुनरावृत्तियों को दर्शाता है; | ||
स्पर्शोन्मुख लब्धि का उपयोग करना, और मान लिया जाये <math>\mathbf{H}_k</math> तथा <math>\mathbf{F}_k</math> से <math>k</math> स्वतंत्र हैं, और | स्पर्शोन्मुख लब्धि का उपयोग करना, और मान लिया जाये <math>\mathbf{H}_k</math> तथा <math>\mathbf{F}_k</math> से <math>k</math> स्वतंत्र हैं, और कालमान फिल्टर एक रेखीय समय-अपरिवर्तनीय फिल्टर बन जाता है: | ||
:<math>\hat{\mathbf{x}}_{k} = \mathbf{F} \hat{\mathbf{x}}_{k-1} + \mathbf{K}_\infty[\mathbf{z}_k - \mathbf{H}\mathbf{F} \hat{\mathbf{x}}_{k-1}].</math> | :<math>\hat{\mathbf{x}}_{k} = \mathbf{F} \hat{\mathbf{x}}_{k-1} + \mathbf{K}_\infty[\mathbf{z}_k - \mathbf{H}\mathbf{F} \hat{\mathbf{x}}_{k-1}].</math> | ||
| Line 250: | Line 248: | ||
== व्युत्पत्ति == | == व्युत्पत्ति == | ||
कालमान फिल्टर को गत डेटा पर संचालित [[ सामान्यीकृत कम से कम वर्ग |सामान्यीकृत न्यूनतम वर्ग]] विधि के रूप में प्राप्त किया जा सकता है।<ref>Sant, Donald T. "Generalized least squares applied to time varying parameter models." Annals of Economic and Social Measurement, Volume 6, number 3. NBER, 1977. 301-314. [https://www.nber.org/system/files/chapters/c10557/c10557.pdf Online Pdf]</ref> | |||
=== पश्चवर्ती अनुमान सहप्रसरण आव्यूह प्राप्त करना === | === पश्चवर्ती अनुमान सहप्रसरण आव्यूह प्राप्त करना === | ||
त्रुटि सहप्रसरण '''P'''<sub>''k'' | ''k''</sub> पर हमारे अपरिवर्तनीय से प्रारंभ करना, उपरोक्तानुसार | त्रुटि सहप्रसरण '''P'''<sub>''k'' | ''k''</sub> पर हमारे अपरिवर्तनीय से प्रारंभ करना, उपरोक्तानुसार | ||
| Line 271: | Line 266: | ||
जो, '''P'''<sub>''k'' | ''k''−1</sub> पर हमारे अपरिवर्तनीय का उपयोग करते हुए और '''R'''<sub>''k''</sub> की परिभाषा का निर्माण हो जाता है | जो, '''P'''<sub>''k'' | ''k''−1</sub> पर हमारे अपरिवर्तनीय का उपयोग करते हुए और '''R'''<sub>''k''</sub> की परिभाषा का निर्माण हो जाता है | ||
:<math>\mathbf{P}_{k \mid k} = \left(\mathbf{I} - \mathbf{K}_k \mathbf{H}_k\right) \mathbf{P}_{k \mid k - 1} \left(\mathbf{I} - \mathbf{K}_k \mathbf{H}_k\right)^\textsf{T} + \mathbf{K}_k \mathbf{R}_k \mathbf{K}_k^\textsf{T}</math> | :<math>\mathbf{P}_{k \mid k} = \left(\mathbf{I} - \mathbf{K}_k \mathbf{H}_k\right) \mathbf{P}_{k \mid k - 1} \left(\mathbf{I} - \mathbf{K}_k \mathbf{H}_k\right)^\textsf{T} + \mathbf{K}_k \mathbf{R}_k \mathbf{K}_k^\textsf{T}</math> | ||
यह सूत्र (कभी-कभी सहप्रसरण अद्यतन समीकरण के जोसफ रूप के रूप में भी प्रचारित है), '''K'''<sub>''k''</sub> के किसी भी मान के लिए मान्य | यह सूत्र (कभी-कभी सहप्रसरण अद्यतन समीकरण के जोसफ रूप के रूप में भी प्रचारित है), '''K'''<sub>''k''</sub> के किसी भी मान के लिए मान्य है। इससे यह ज्ञात होता है कि यदि K<sub>''k''</sub> इष्टतम कालमान लब्धि है, इसे और सरल बनाया जा सकता है जैसा कि नीचे दर्शाया गया है। | ||
=== | === कालमान लब्धि व्युत्पत्ति === | ||
कालमान फिल्टर एक[[ न्यूनतम माध्य-वर्ग त्रुटि ]]अनुमानक है। पश्चवर्ती अवस्था के अनुमान में त्रुटि है; | |||
:<math>\mathbf{x}_k - \hat{\mathbf{x}}_{k \mid k}</math> | :<math>\mathbf{x}_k - \hat{\mathbf{x}}_{k \mid k}</math> | ||
हम इस सदिश | हम इस सदिश <math>\operatorname{E}\left[\left\|\mathbf{x}_{k} - \hat{\mathbf{x}}_{k|k}\right\|^2\right]</math>के परिमाण के वर्ग के अपेक्षित मान को कम करना चाहते हैं। यह पश्चगामी अनुमान सहप्रसरण आव्यूह <math> \mathbf{P}_{k|k} </math> के [[ ट्रेस (मैट्रिक्स) |अनुरेख]] को कम करने के समान है। उपरोक्त समीकरण में शर्तों का विस्तार करके और एकत्रित करके, हम प्राप्त करते हैं: | ||
:<math>\begin{align} | :<math>\begin{align} | ||
\mathbf{P}_{k\mid k} & = \mathbf{P}_{k\mid k-1} - \mathbf{K}_k \mathbf{H}_k \mathbf{P}_{k\mid k-1} - \mathbf{P}_{k\mid k-1} \mathbf{H}_k^\textsf{T} \mathbf{K}_k^\textsf{T} + \mathbf{K}_k \left(\mathbf{H}_k \mathbf{P}_{k\mid k-1} \mathbf{H}_k^\textsf{T} + \mathbf{R}_k\right) \mathbf{K}_k^\textsf{T} \\[6pt] | \mathbf{P}_{k\mid k} & = \mathbf{P}_{k\mid k-1} - \mathbf{K}_k \mathbf{H}_k \mathbf{P}_{k\mid k-1} - \mathbf{P}_{k\mid k-1} \mathbf{H}_k^\textsf{T} \mathbf{K}_k^\textsf{T} + \mathbf{K}_k \left(\mathbf{H}_k \mathbf{P}_{k\mid k-1} \mathbf{H}_k^\textsf{T} + \mathbf{R}_k\right) \mathbf{K}_k^\textsf{T} \\[6pt] | ||
&= \mathbf{P}_{k\mid k-1} - \mathbf{K}_k \mathbf{H}_k \mathbf{P}_{k\mid k-1} - \mathbf{P}_{k\mid k-1} \mathbf{H}_k^\textsf{T} \mathbf{K}_k^\textsf{T} + \mathbf{K}_k \mathbf{S}_k\mathbf{K}_k^\textsf{T} | &= \mathbf{P}_{k\mid k-1} - \mathbf{K}_k \mathbf{H}_k \mathbf{P}_{k\mid k-1} - \mathbf{P}_{k\mid k-1} \mathbf{H}_k^\textsf{T} \mathbf{K}_k^\textsf{T} + \mathbf{K}_k \mathbf{S}_k\mathbf{K}_k^\textsf{T} | ||
\end{align}</math> | \end{align}</math> | ||
अनुरेख को कम किया जाता है जब लब्धि आव्यूह के संबंध में इसका [[ मैट्रिक्स कैलकुलस |आव्यूह व्युत्पन्न]] शून्य होता है। अनुप्रवण आव्यूह नियमों और सम्मिलित आव्यूह की समरूपता का उपयोग करके हम प्राप्त करते हैं कि | |||
:<math>\frac{\partial \; \operatorname{tr}(\mathbf{P}_{k\mid k})}{\partial \;\mathbf{K}_k} = -2 \left(\mathbf{H}_k \mathbf{P}_{k\mid k-1}\right)^\textsf{T} + 2 \mathbf{K}_k \mathbf{S}_k = 0.</math> | :<math>\frac{\partial \; \operatorname{tr}(\mathbf{P}_{k\mid k})}{\partial \;\mathbf{K}_k} = -2 \left(\mathbf{H}_k \mathbf{P}_{k\mid k-1}\right)^\textsf{T} + 2 \mathbf{K}_k \mathbf{S}_k = 0.</math> | ||
K | K<sub>''k''</sub> के लिए इसे हल करने से कालमान लब्धि प्राप्त होती है: | ||
:<math>\begin{align} | :<math>\begin{align} | ||
\mathbf{K}_k \mathbf{S}_k &= \left(\mathbf{H}_k \mathbf{P}_{k\mid k-1}\right)^\textsf{T} = \mathbf{P}_{k\mid k-1} \mathbf{H}_k^\textsf{T} \\ | \mathbf{K}_k \mathbf{S}_k &= \left(\mathbf{H}_k \mathbf{P}_{k\mid k-1}\right)^\textsf{T} = \mathbf{P}_{k\mid k-1} \mathbf{H}_k^\textsf{T} \\ | ||
\Rightarrow \mathbf{K}_k &= \mathbf{P}_{k\mid k-1} \mathbf{H}_k^\textsf{T} \mathbf{S}_k^{-1} | \Rightarrow \mathbf{K}_k &= \mathbf{P}_{k\mid k-1} \mathbf{H}_k^\textsf{T} \mathbf{S}_k^{-1} | ||
\end{align}</math> | \end{align}</math> | ||
यह लब्धि, जिसे इष्टतम | यह लब्धि, जिसे इष्टतम कालमान लब्धि के रूप में जाना जाता है, वह है जो उपयोग किए जाने पर न्यूनतम माध्य वर्ग त्रुटि अनुमान प्रदान करता है। | ||
=== | === पश्चवर्ती त्रुटि सहप्रसरण सूत्र का सरलीकरण === | ||
पश्चवर्ती त्रुटि सहप्रसरण की गणना के लिए उपयोग किए जाने वाले सूत्र को सरल बनाया जा सकता है, जब कालमान लब्धि ऊपर प्राप्त इष्टतम मान के समान होती है। हमारे कालमान लब्धि सूत्र के दोनों पक्षों को '''S'''<sub>''k''</sub>'''K'''<sub>''k''</sub><sup>T</sup> दाईं ओर गुणा करने पर, यह इस प्रकार है; | |||
:<math>\mathbf{K}_k \mathbf{S}_k \mathbf{K}_k^\textsf{T} = \mathbf{P}_{k\mid k-1} \mathbf{H}_k^\textsf{T} \mathbf{K}_k^\textsf{T}</math> | :<math>\mathbf{K}_k \mathbf{S}_k \mathbf{K}_k^\textsf{T} = \mathbf{P}_{k\mid k-1} \mathbf{H}_k^\textsf{T} \mathbf{K}_k^\textsf{T}</math> | ||
पश्चवर्ती त्रुटि सहप्रसरण के लिए हमारे विस्तारित सूत्र का संदर्भ देते हुए, | |||
:<math> \mathbf{P}_{k\mid k} = \mathbf{P}_{k\mid k-1} - \mathbf{K}_k \mathbf{H}_k \mathbf{P}_{k\mid k-1} - \mathbf{P}_{k\mid k-1} \mathbf{H}_k^\textsf{T} \mathbf{K}_k^\textsf{T} + \mathbf{K}_k \mathbf{S}_k \mathbf{K}_k^\textsf{T}</math> | :<math> \mathbf{P}_{k\mid k} = \mathbf{P}_{k\mid k-1} - \mathbf{K}_k \mathbf{H}_k \mathbf{P}_{k\mid k-1} - \mathbf{P}_{k\mid k-1} \mathbf{H}_k^\textsf{T} \mathbf{K}_k^\textsf{T} + \mathbf{K}_k \mathbf{S}_k \mathbf{K}_k^\textsf{T}</math> | ||
हम पाते हैं कि अंतिम दो शर्तें | हम पाते हैं कि अंतिम दो शर्तें निरसित कर दी गई हैं | ||
:<math> \mathbf{P}_{k\mid k} = \mathbf{P}_{k\mid k-1} - \mathbf{K}_k \mathbf{H}_k \mathbf{P}_{k\mid k-1} = (\mathbf{I} - \mathbf{K}_k \mathbf{H}_k) \mathbf{P}_{k\mid k-1}.</math> | :<math> \mathbf{P}_{k\mid k} = \mathbf{P}_{k\mid k-1} - \mathbf{K}_k \mathbf{H}_k \mathbf{P}_{k\mid k-1} = (\mathbf{I} - \mathbf{K}_k \mathbf{H}_k) \mathbf{P}_{k\mid k-1}.</math> | ||
यह सूत्र | यह सूत्र अभिकलनीयतः रूप से अल्पमूल्य है और इस प्रकार लगभग सदैव व्यवहार में उपयोग किया जाता है, परन्तु यह केवल इष्टतम लब्धि के लिए सही है। यदि अंकगणितीय सटीकता असामान्य रूप से कम है, जिससे [[ संख्यात्मक स्थिरता ]]के साथ समस्याएं उत्पन्न होती हैं, या यदि एक गैर-इष्टतम कालमान लब्धि का विचारपूर्वक उपयोग किया जाता है, तो यह सरलीकरण अनुप्रयुक्त नहीं किया जा सकता है; उपरोक्त व्युत्पन्न (जोसेफ विधि) के रूप में एक पश्चवर्ती त्रुटि सहप्रसरण सूत्र का उपयोग किया जाना चाहिए। | ||
== | == सुग्राहिता विश्लेषण == | ||
कालमान फिल्टर समीकरण अवस्था <math>\hat{\mathbf{x}}_{k\mid k}</math> और इसकी त्रुटि सहप्रसरण <math>\mathbf{P}_{k\mid k}</math> पुनरावर्ती रूप से अनुमान प्रदान करते हैं। अनुमान और इसकी गुणवत्ता प्रणाली मापदंडों और अनुमानक को इनपुट के रूप में सिंचित किये गए रव आंकड़ों पर निर्भर करती है। यह खंड फिल्टर के सांख्यिकीय इनपुट में अनिश्चितताओं के प्रभाव का विश्लेषण करता है।<ref name=anderson>{{cite book|last1= Anderson|first1= Brian D. O.|last2=Moore|first2=John B.|year=1979 |title=Optimal Filtering |publisher=[[Prentice Hall]]|place=New York|pages=129–133|isbn= 978-0-13-638122-8}}</ref> विश्वसनीय आँकड़ों या रव सहप्रसरण आव्यूह <math>\mathbf{Q}_{k}</math> तथा <math>\mathbf{R}_k</math> के सटीक मानो के अभाव में, अभिव्यक्ति | |||
:<math>\mathbf{P}_{k\mid k} = \left(\mathbf{I} - \mathbf{K}_k\mathbf{H}_k\right)\mathbf{P}_{k\mid k-1}\left(\mathbf{I} - \mathbf{K}_k\mathbf{H}_k\right)^\textsf{T} + \mathbf{K}_k\mathbf{R}_k\mathbf{K}_k^\textsf{T}</math> | :<math>\mathbf{P}_{k\mid k} = \left(\mathbf{I} - \mathbf{K}_k\mathbf{H}_k\right)\mathbf{P}_{k\mid k-1}\left(\mathbf{I} - \mathbf{K}_k\mathbf{H}_k\right)^\textsf{T} + \mathbf{K}_k\mathbf{R}_k\mathbf{K}_k^\textsf{T}</math> | ||
अब वास्तविक त्रुटि सहप्रसरण प्रदान नहीं करता है। दूसरे शब्दों में, <math>\mathbf{P}_{k \mid k} \neq E\left[\left(\mathbf{x}_k - \hat{\mathbf{x}}_{k\mid k}\right)\left(\mathbf{x}_k - \hat{\mathbf{x}}_{k \mid k}\right)^\textsf{T}\right]</math>. अधिकांश वास्तविक समय के अनुप्रयोगों में, | अब वास्तविक त्रुटि सहप्रसरण प्रदान नहीं करता है। दूसरे शब्दों में, <math>\mathbf{P}_{k \mid k} \neq E\left[\left(\mathbf{x}_k - \hat{\mathbf{x}}_{k\mid k}\right)\left(\mathbf{x}_k - \hat{\mathbf{x}}_{k \mid k}\right)^\textsf{T}\right]</math>.अधिकांश वास्तविक समय के अनुप्रयोगों में, कालमान फिल्टर को प्रारुप करने में उपयोग किए जाने वाले सहप्रसरण आव्यूह वास्तविक रव सहप्रसरण आव्यूह से भिन्न होते हैं।{{citation needed|date=दिसंबर 2010}} यह सुग्राहिता विश्लेषण आकलन त्रुटि सहप्रसरण के व्यवहार का वर्णन करता है, जब रव सहप्रसरण के रूप में साथ ही प्रणाली आव्यूह <math>\mathbf{F}_k</math> तथा <math>\mathbf{H}_k</math> जो फिल्टर में इनपुट के रूप में सिंचित किए गए है, जोकि गलत हैं। इस प्रकार, सुग्राहिता विश्लेषण अनुमानक को गलत निर्दिष्ट सांख्यिकीय और प्राचलिक इनपुट के लिए अनुमानक की पृष्टता (या सुग्राहिता) का वर्णन करते है। | ||
यह | यह आलोचना सांख्यिकीय अनिश्चितताओं के स्थितियो में त्रुटि सुग्राहिता विश्लेषण तक पर्याप्त है। यहाँ वास्तविक रव सहप्रसरणों को <math>\mathbf{Q}^a_k</math> तथा <math>\mathbf{R}^a_k</math> क्रमशः द्वारा निरूपित किया जाता है, जबकि अनुमानक में प्रयुक्त प्रारुप मान <math>\mathbf{Q}_k</math> तथा <math>\mathbf{R}_k</math> क्रमशः हैं। वास्तविक त्रुटि सहप्रसरण <math>\mathbf{P}_{k \mid k}^a</math> तथा <math>\mathbf{P}_{k \mid k}</math> द्वारा निरूपित किया जाता है, जैसा कि कालमान फिल्टर द्वारा गणना की जाती है, उसे रिकाटी चर कहा जाता है। <math>\mathbf{Q}_k \equiv \mathbf{Q}^a_k</math> तथा <math>\mathbf{R}_k \equiv \mathbf{R}^a_k</math>, इसका है कि <math>\mathbf{P}_{k \mid k} = \mathbf{P}_{k \mid k}^a</math>. वास्तविक त्रुटि सहप्रसरण की गणना करते समय <math>\mathbf{P}_{k \mid k}^a = E\left[\left(\mathbf{x}_k - \hat{\mathbf{x}}_{k \mid k}\right)\left(\mathbf{x}_k - \hat{\mathbf{x}}_{k \mid k}\right)^\textsf{T}\right] </math>, के लिए प्रतिस्थापन <math>\widehat{\mathbf{x}}_{k \mid k}</math> और इस तथ्य का उपयोग करते हुए कि <math>E\left[\mathbf{w}_k\mathbf{w}_k^\textsf{T}\right] = \mathbf{Q}_k^a</math> तथा <math>E\left[\mathbf{v}_k \mathbf{v}_k^\textsf{T}\right] = \mathbf{R}_k^a</math>, निम्नलिखित पुनरावर्ती समीकरणों के लिए परिणाम <math>\mathbf{P}_{k \mid k}^a</math> हैंː | ||
:<math>\mathbf{P}_{k \mid k-1}^a = \mathbf{F}_k\mathbf{P}_{k-1 \mid k-1}^a \mathbf{F}_k^\textsf{T} + \mathbf{Q}_k^a </math> | :<math>\mathbf{P}_{k \mid k-1}^a = \mathbf{F}_k\mathbf{P}_{k-1 \mid k-1}^a \mathbf{F}_k^\textsf{T} + \mathbf{Q}_k^a </math> | ||
और | |||
:<math>\mathbf{P}_{k \mid k}^a = \left(\mathbf{I} - \mathbf{K}_k \mathbf{H}_k\right)\mathbf{P}_{k \mid k-1}^a \left(\mathbf{I} - \mathbf{K}_k \mathbf{H}_k\right)^\textsf{T} + \mathbf{K}_k \mathbf{R}_k^a \mathbf{K}_k^\textsf{T}</math> | :<math>\mathbf{P}_{k \mid k}^a = \left(\mathbf{I} - \mathbf{K}_k \mathbf{H}_k\right)\mathbf{P}_{k \mid k-1}^a \left(\mathbf{I} - \mathbf{K}_k \mathbf{H}_k\right)^\textsf{T} + \mathbf{K}_k \mathbf{R}_k^a \mathbf{K}_k^\textsf{T}</math> | ||
गणना करते समय <math>\mathbf{P}_{k \mid k}</math>, | गणना करते समय <math>\mathbf{P}_{k \mid k}</math>, प्रारुप द्वारा फिल्टर स्पष्ट रूप से मानता है कि <math>E\left[\mathbf{w}_k \mathbf{w}_k^\textsf{T}\right] = \mathbf{Q}_k</math> तथा <math>E\left[\mathbf{v}_k \mathbf{v}_k^\textsf{T}\right] = \mathbf{R}_k</math>, <math>\mathbf{P}_{k \mid k}^a</math> तथा <math>\mathbf{P}_{k \mid k}</math> के लिए पुनरावर्ती अभिव्यक्ति की उपस्थिति <math>\mathbf{Q}_k^a</math> तथा <math>\mathbf{R}_k^a</math> को छोड़कर समान हैं, प्रारुप मानो के स्थान पर <math>\mathbf{Q}_k</math> तथा <math>\mathbf{R}_k</math> क्रमशः हैं। कालमान फिल्टर प्रणाली की पृष्टता का विश्लेषण करने के लिए शोध किए गए हैं।<ref>Jingyang Lu. [https://ieeexplore.ieee.org/document/6916211, "False information injection attack on dynamic state estimation in multi-sensor systems"], Fusion 2014</ref> | ||
== वर्गमूल रूप == | == वर्गमूल रूप == | ||
कालमान फिल्टर के साथ एक समस्या इसकी संख्यात्मक स्थिरता है। यदि प्रक्रिया रव सहप्रसरण Q<sub>''k''</sub> छोटा होता है, तो पूर्णांक त्रुटि प्रायः अवस्था सहप्रसरण आव्यूह '''P''' एक छोटे धनात्मक आइगेन मान को ऋणात्मक संख्या के रूप में गणना करने का कारण बनती है। यह '''P''' [[ सकारात्मक-अर्ध-परिमित मैट्रिक्स |अनिश्चित]] के संख्यात्मक प्रतिनिधित्व को प्रस्तुत करता है, जबकि इसका वास्तविक रूप धनात्मक निश्चित आव्यूह है। | |||
धनात्मक निश्चित आव्यूहों में गुण होता है कि उनके पास एक | धनात्मक निश्चित आव्यूहों में गुण होता है कि उनके पास एक त्रिकोणीय आव्यूह वर्गमूल '''P''' = '''S'''·'''S'''<sup>T</sup> होता है। चोल्स्की गुणनखंड कलन विधि का उपयोग करके इसकी कुशलता से गणना की जा सकती है, परन्तु इससे भी महत्वपूर्ण तथ्य यह है कि यदि सहप्रसरण को इस रूप में रखा जाता है, तो इसमें कभी भी ऋणात्मक विकर्ण या असममित नहीं हो सकता है। एक समान रूप, जो आव्यूह वर्गमूल द्वारा आवश्यक कई वर्गमूल संचालन से से बचता है, फिर भी वांछनीय संख्यात्मक गुणों को संरक्षित करता है, U-D अपघटन रूप है, '''P''' = '''U'''·'''D'''·'''U'''<sup>T</sup> जहां U एक इकाई त्रिकोणीय आव्यूह (इकाई विकर्ण के साथ) है,और '''D''' एक विकर्ण आव्यूह है। | ||
दोनों के मध्य, U-D | दोनों के मध्य, U-D गुणनखंड समान मात्रा में भंडारण और कुछ स्थिति तक कम गणना का उपयोग करते है, और सबसे अधिक उपयोग किया जाने वाला वर्गमूल रूप है, (सापेक्ष दक्षता पर प्रारंभिक साहित्य कुछ स्थिति तक भ्रामक है, क्योंकि यह माना जाता है कि वर्गमूल विभाजनों की तुलना में अधिक समय लेने वाले थे,<ref name="thornton" />{{rp|69}} जबकि 21वीं सदी के परिकलको पर वे केवल थोड़े अधिक बहुमूल्य होते हैं)। | ||
जी जे बीरमैन और सी एल थॉर्नटन द्वारा कालमान पूर्वानुमान और वर्गमूल रूप में अद्यतन चरणों के लिए कुशल कलन विधि विकसित की गयी थी।<ref name="thornton">{{cite thesis|title=Triangular Covariance Factorizations for Kalman Filtering |url=https://ntrs.nasa.gov/citations/19770005172 |type=PhD |first=Catherine L. |last=Thornton |date=15 October 1976|id=NASA Technical Memorandum 33-798 |publisher=[[NASA]] }}</ref><ref name="bierman" /> | |||
नवप्रवर्तन सहप्रसरण आव्यूह '''S'''<sub>k</sub> का '''L'''·'''D'''·'''L'''<sup>T</sup> अपघटन एक अन्य प्रकार के संख्यात्मक रूप से कुशल और सुदृढ़ वर्गमूल फिल्टर का आधार है।<ref name="barshalom">{{cite book|last1=Bar-Shalom|first1= Yaakov|last2=Li|first2=X. Rong|last3=Kirubarajan|first3=Thiagalingam |date=July 2001 |title=Estimation with Applications to Tracking and Navigation |publisher=[[John Wiley & Sons]]|place=New York|isbn =978-0-471-41655-5 |pages=308–317}}</ref> कलन विधि LU अपघटन के साथ प्रारम्भ होता है जैसा कि रैखिक बीजगणित संवेष्टक ([[ LAPACK | LAPACK]] ) में अनुप्रयुक्त किया गया है। इन परिणामों को एक सममितीय व्युत्क्रमणीय आव्यूह के लिए गोलूब और वैन लोन (कलन विधि 4.1.2) द्वारा दी गयी प्रविधियों के साथ L·D·LT संरचना में आगे खंडित किया गया है। किसी भी एकल सहप्रसरण आव्यूह को कीलकित किया जाता है ताकि प्रथम विकर्ण विभाजन निरर्थक और अच्छी तरह से वातानुकूलित हो। कीलक एल्गोरिथम को नवप्रवर्तन सहप्रसरण आव्यूह के किसी भी भाग को सीधे देखे गए अवस्था-चर '''H'''<sub>k</sub>·'''x'''<sub>k|k-1</sub> से संबंधित होना चाहिए जो कि '''y'''<sub>k</sub> में सहायक अवलोकनों से जुड़े हुए हैं। '''l'''·'''d'''·'''l'''<sup>t</sup> वर्गमूल फिल्टर के लिए अवलोकन सदिश के लांबिकीकरण की आवश्यकता होती है। यह हिघम (2002, पृष्ठ 263) में विधि 2 का उपयोग करके सहायक चर के लिए सहप्रसरण आव्यूह के व्युत्क्रम वर्गमूल के साथ किया जा सकता है। | |||
== समानांतर रूप == | == समानांतर रूप == | ||
कालमान फिल्टर केंद्रीय प्रसंस्करण इकाइयों (CPUs) पर अनुक्रमिक डेटा प्रसंस्करण के लिए कुशल है, परन्तु अपने मूल रूप में यह समानांतर वास्तुकी जैसे [[ ग्राफिक्स प्रसंस्करण इकाइयाँ |आलेखिकी प्रसंस्करण इकाइयाँ]] (GPUs) पर अक्षम है। हालांकि, सरक्का (2021) में सूत्रीकरण का उपयोग करके एक सहयोगी संचालक के संदर्भ में फिल्टर-नवीनीकरण नित्यक्रम को व्यक्त करना संभव है।<ref name=parallel>{{cite journal | author = Särkkä, S.| author2 = Ángel F. García-Fernández | year = 2021 | title = Temporal Parallelization of Bayesian Smoothers | journal = IEEE Transactions on Automatic Control | volume = 66 | issue = 1 | pages = 299–306 | doi = 10.1109/TAC.2020.2976316 | arxiv = 1905.13002 | s2cid = 213695560 }}</ref> इसके पश्चात फिल्टर हल को [[ उपसर्ग योग |पूर्वयोजन योग]] कलन विधि के उपयोग द्वारा पुनः प्राप्त किया जा सकता है, जिसे जीपीयू पर कुशलता से अनुप्रयुक्त किया जा सकता है।<ref name=prefix-nvida>{{cite web |url=https://developer.nvidia.com/gpugems/gpugems3/part-vi-gpu-computing/chapter-39-parallel-prefix-sum-scan-cuda |title=Parallel Prefix Sum (Scan) with CUDA |author=<!--Not stated--> |website=developer.nvidia.com/ |access-date=2020-02-21 |quote=The scan operation is a simple and powerful parallel primitive with a broad range of applications. In this chapter we have explained an efficient implementation of scan using CUDA, which achieves a significant speedup compared to a sequential implementation on a fast CPU, and compared to a parallel implementation in OpenGL on the same GPU. Due to the increasing power of commodity parallel processors such as GPUs, we expect to see data-parallel algorithms such as scan to increase in importance over the coming years.}}</ref> यह अभिकलनात्मक जटिलता <math>O(N)</math> को टाइमस्टेपों की संख्या <math>O(\log(N))</math> में कम करता है। | |||
== | == पुनरावर्ती बायेसियन अनुमानसे संबंध == | ||
कालमान फिल्टर को सबसे सरल [[ गतिशील बायेसियन नेटवर्क |गतिशील बायेसियन जालक्रम]] में से एक के रूप में प्रस्तुत किया जा सकता है। कालमान फिल्टर आने वाले माप और गणितीय प्रक्रिया प्रतिरूप का उपयोग करके समय के साथ-साथ अवस्थाओं के वास्तविक मानो के अनुमानों की गणना करता है। इसी प्रकार, पुनरावर्ती बायेसियन अनुमान आने वाले माप और एक गणितीय प्रक्रिया प्रतिरूप का उपयोग करके समय के साथ एक अज्ञात संभाव्यता घनत्व प्रकार्य (PDF) के घनत्व अनुमान की गणना करते है।<ref>{{cite journal|first1=C. Johan |last1=Masreliez|first2= R D|last2= Martin |year=1977|title=Robust Bayesian estimation for the linear model and robustifying the Kalman filter|journal= IEEE Transactions on Automatic Control|volume= 22|issue= 3|pages= 361–371|doi=10.1109/TAC.1977.1101538|author-link1= C. Johan Masreliez}}</ref> | |||
पुनरावर्ती बायेसियन अनुमान में, वास्तविक स्थिति को एक | |||
पुनरावर्ती बायेसियन अनुमान में, वास्तविक स्थिति को एक अप्रतिबंधित [[ मार्कोव प्रक्रिया |मार्कोव प्रक्रिया]] माना जाता है, और माप एक अप्रत्यक्ष मार्कोव प्रतिरूप (HMM) की देखी गयी अवस्था हैं। | |||
[[File:HMM Kalman Filter Derivation.svg|center|हिडन मार्कोव प्रतिरूप]] | [[File:HMM Kalman Filter Derivation.svg|center|हिडन मार्कोव प्रतिरूप]] | ||
मार्कोव की धारणा के कारण, वास्तविक | मार्कोव की धारणा के कारण, वास्तविक स्थिति पूर्व के सभी अवस्थाओं से सशर्त रूप से स्वतंत्र है, जिसे पूर्व अवस्था दी गई है। | ||
:<math>p(\mathbf{x}_k\mid \mathbf{x}_0,\dots,\mathbf{x}_{k-1}) = p(\mathbf{x}_k\mid \mathbf{x}_{k-1})</math> | :<math>p(\mathbf{x}_k\mid \mathbf{x}_0,\dots,\mathbf{x}_{k-1}) = p(\mathbf{x}_k\mid \mathbf{x}_{k-1})</math> | ||
इसी | इसी प्रकार, k-वें टाइमस्टेप पर माप केवल वर्तमान स्थिति पर निर्भर है और वर्तमान स्थिति को देखते हुए अन्य सभी अवस्थाओं से सशर्त रूप से स्वतंत्र है। | ||
:<math>p(\mathbf{z}_k\mid\mathbf{x}_0,\dots,\mathbf{x}_k) = p(\mathbf{z}_k\mid \mathbf{x}_k )</math> | :<math>p(\mathbf{z}_k\mid\mathbf{x}_0,\dots,\mathbf{x}_k) = p(\mathbf{z}_k\mid \mathbf{x}_k )</math> | ||
इन मान्यताओं का उपयोग करते हुए, | इन मान्यताओं का उपयोग करते हुए, अप्रत्यक्ष मार्कोव प्रतिरूप के सभी अवस्थाओं में संभाव्यता वितरण को इस प्रकार लिखा जा सकता है: | ||
:<math>p\left(\mathbf{x}_0, \dots, \mathbf{x}_k, \mathbf{z}_1, \dots, \mathbf{z}_k\right) = p\left(\mathbf{x}_0\right)\prod_{i=1}^k p\left(\mathbf{z}_i \mid \mathbf{x}_i\right)p\left(\mathbf{x}_i \mid \mathbf{x}_{i-1}\right)</math> | :<math>p\left(\mathbf{x}_0, \dots, \mathbf{x}_k, \mathbf{z}_1, \dots, \mathbf{z}_k\right) = p\left(\mathbf{x}_0\right)\prod_{i=1}^k p\left(\mathbf{z}_i \mid \mathbf{x}_i\right)p\left(\mathbf{x}_i \mid \mathbf{x}_{i-1}\right)</math> | ||
हालांकि, जब अवस्था x का अनुमान लगाने के लिए एक | हालांकि, जब अवस्था x का अनुमान लगाने के लिए एक कालमान फिल्टर का उपयोग किया जाता है, तो हित की संभाव्यता वितरण वर्तमान वह होती है जो टाइमस्टेप तक माप पर वातानुकूलित वर्तमान अवस्थाओं से जुड़ी होती है। यह पूर्व अवस्थाओं को माप समुच्चय की संभाव्यता से विभाजित करके प्राप्त किया जाता है। | ||
यह संभावित रूप से लिखे गए कालमान फिल्टर के पूर्वानुमान और अद्यतन चरणों का परिणाम है। पूर्वानुमानित स्थिति से संबद्ध प्रायिकता वितरण, (''k'' − 1)-th टाइमस्टेप से ''k''-th और पूर्व स्थिति से जुड़े संभाव्यता वितरण के पारगमन से जुड़े संभाव्यता वितरण के उत्पादों का योग (अभिन्न) है, संपूर्ण संभव से अधिक <math>x_{k-1}</math>. | |||
:<math>p\left(\mathbf{x}_k \mid \mathbf{Z}_{k-1}\right) = \int p\left(\mathbf{x}_k \mid \mathbf{x}_{k-1}\right) p\left(\mathbf{x}_{k-1} \mid \mathbf{Z}_{k-1}\right)\, d\mathbf{x}_{k-1}</math> | :<math>p\left(\mathbf{x}_k \mid \mathbf{Z}_{k-1}\right) = \int p\left(\mathbf{x}_k \mid \mathbf{x}_{k-1}\right) p\left(\mathbf{x}_{k-1} \mid \mathbf{Z}_{k-1}\right)\, d\mathbf{x}_{k-1}</math> | ||
समय t | समय t तक निर्धारित माप है | ||
:<math>\mathbf{Z}_t = \left\{\mathbf{z}_1, \dots, \mathbf{z}_t\right\}</math> | :<math>\mathbf{Z}_t = \left\{\mathbf{z}_1, \dots, \mathbf{z}_t\right\}</math> | ||
अद्यतन का संभाव्यता वितरण माप की संभावना और अनुमानित स्थिति के उत्पाद के समानुपाती होता है। | अद्यतन का संभाव्यता वितरण माप की संभावना और अनुमानित स्थिति के उत्पाद के समानुपाती होता है। | ||
| Line 349: | Line 344: | ||
भाजक | भाजक | ||
:<math>p\left(\mathbf{z}_k \mid \mathbf{Z}_{k-1}\right) = \int p\left(\mathbf{z}_k \mid \mathbf{x}_k\right) p\left(\mathbf{x}_k \mid \mathbf{Z}_{k-1}\right)\, d\mathbf{x}_k</math> | :<math>p\left(\mathbf{z}_k \mid \mathbf{Z}_{k-1}\right) = \int p\left(\mathbf{z}_k \mid \mathbf{x}_k\right) p\left(\mathbf{x}_k \mid \mathbf{Z}_{k-1}\right)\, d\mathbf{x}_k</math> | ||
एक सामान्यीकरण | एक सामान्यीकरण पद है। | ||
शेष संभाव्यता घनत्व कार्य हैं | शेष संभाव्यता घनत्व कार्य हैं | ||
| Line 357: | Line 352: | ||
p\left(\mathbf{x}_{k-1} \mid \mathbf{Z}_{k-1}\right) &= \mathcal{N}\left(\hat{\mathbf{x}}_{k-1}, \mathbf{P}_{k-1}\right) | p\left(\mathbf{x}_{k-1} \mid \mathbf{Z}_{k-1}\right) &= \mathcal{N}\left(\hat{\mathbf{x}}_{k-1}, \mathbf{P}_{k-1}\right) | ||
\end{align}</math> | \end{align}</math> | ||
पूर्व टाइमस्टेप पर पीडीएफ को अभिगृहीत रूप से अनुमानित स्थिति और सहप्रसरण माना जाता है। यह उचित है क्योंकि, इष्टतम अनुमानक के रूप में, कालमान फिल्टर मापों का सर्वोत्तम उपयोग करता है, इसलिए पीडीएफ के लिए <math>\mathbf{x}_k</math> माप दिया गया,और <math>\mathbf{Z}_k</math> कालमान फिल्टर अनुमान है। | |||
== सीमांत | == सीमांत संभाव्यता == | ||
ऊपर वर्णित पुनरावर्ती बायेसियन व्याख्या से संबंधित, | ऊपर वर्णित पुनरावर्ती बायेसियन व्याख्या से संबंधित, कालमान फिल्टर को एक [[ जनरेटिव मॉडल |उत्पादक प्रतिरूप]] के रूप में देखा जा सकता है, अर्थात, यादृच्छिक अवलोकनों '''z''' = ('''z'''<sub>0</sub>, '''z'''<sub>1</sub>, '''z'''<sub>2</sub>, ...) का एक वर्ग उत्पन्न करने की प्रक्रिया है। विशेष रूप से, प्रक्रिया है | ||
# एक | # एक अप्रत्यक्ष स्थिति <math>\mathbf{x}_0</math>का प्रतिरूप, गॉसियन के पूर्व वितरण से <math>p\left(\mathbf{x}_0\right) = \mathcal{N}\left(\hat{\mathbf{x}}_{0 \mid 0}, \mathbf{P}_{0 \mid 0}\right)</math>. | ||
# एक अवलोकन | # एक अवलोकन <math>\mathbf{z}_0</math>का प्रतिरूप, अवलोकन प्रतिरूप से <math>p\left(\mathbf{z}_0 \mid \mathbf{x}_0\right) = \mathcal{N}\left(\mathbf{H}_0\mathbf{x}_0, \mathbf{R}_0\right)</math>. | ||
# | # <math>k = 1, 2, 3, \ldots</math>के लिये, करना | ||
## अगले | ## अगले अप्रत्यक्ष अवस्था <math>\mathbf{x}_k</math> का प्रतिरूप, पारगमन प्रतिरूप से <math>p\left(\mathbf{x}_k \mid \mathbf{x}_{k-1}\right) = \mathcal{N}\left(\mathbf{F}_k \mathbf{x}_{k-1} + \mathbf{B}_k\mathbf{u}_k, \mathbf{Q}_k\right).</math> | ||
## एक अवलोकन | ## एक अवलोकन <math>\mathbf{z}_k</math> का प्रतिरूप, अवलोकन प्रतिरूप से <math>p\left(\mathbf{z}_k \mid \mathbf{x}_k\right) = \mathcal{N}\left(\mathbf{H}_k\mathbf{x}_k, \mathbf{R}_k\right).</math> | ||
इस प्रक्रिया में | इस प्रक्रिया में अप्रत्यक्ष मार्कोव प्रतिरूप के समान संरचना है, अतिरिक्त इसके कि असतत स्थिति और अवलोकनों को गॉसियन वितरण से प्रतिरूप सतत चर के साथ परिवर्तित कर दिया जाता है। | ||
कुछ अनुप्रयोगों में, यह | कुछ अनुप्रयोगों में, यह संभाव्यता की गणना करने के लिए उपयोगी है कि दिए गए मापदंडों (पूर्व वितरण, पारगमन और अवलोकन प्रतिरूप, और नियंत्रण इनपुट) के साथ एक कालमान फिल्टर एक विशेष प्रेक्षित संकेत उत्पन्न करता है। इस संभाव्यता को [[ सीमांत संभावना |सीमांत संभाव्यता]] के रूप में जाना जाता है क्योंकि यह अप्रत्यक्ष अवस्था चर के मानो को एकीकृत करता है, इसलिए इसे केवल देखे गए संकेत का उपयोग करके गणना की जा सकती है। विभिन्न मापदण्ड विकल्पों का मूल्यांकन करने के लिए सीमांत संभाव्यता उपयोगी हो सकती है, या[[ बायेसियन मॉडल तुलना | बायेसियन प्रतिरूप तुलना]] का उपयोग करके अन्य प्रतिरूपों के विरुद्ध कालमान फिल्टर की तुलना करने के लिए उपयोगी हो सकती है। | ||
पुनरावर्ती निस्यंदन गणना के | पुनरावर्ती निस्यंदन गणना के पार्श्व प्रभाव के रूप में सीमांत संभावना की गणना करना सरल है। श्रृंखला नियम द्वारा, पूर्व अवलोकनों में दिए गए प्रत्येक अवलोकन की संभावना के उत्पाद के रूप में संभावना को ध्यान में रखा जा सकता है, | ||
:<math>p(\mathbf{z}) = \prod_{k=0}^T p\left(\mathbf{z}_k \mid \mathbf{z}_{k-1}, \ldots, \mathbf{z}_0\right)</math>, | :<math>p(\mathbf{z}) = \prod_{k=0}^T p\left(\mathbf{z}_k \mid \mathbf{z}_{k-1}, \ldots, \mathbf{z}_0\right)</math>, | ||
और क्योंकि | और क्योंकि कालमान फिल्टर एक मार्कोव प्रक्रिया का वर्णन करता है, पूर्व अवलोकनों से सभी प्रासंगिक सूचना वर्तमान स्थिति अनुमान <math>\hat{\mathbf{x}}_{k \mid k-1}, \mathbf{P}_{k \mid k-1}</math>में निहित है। इस प्रकार सीमांत संभावना द्वारा दी गई है | ||
:<math>\begin{align} | :<math>\begin{align} | ||
p(\mathbf{z}) &= \prod_{k=0}^T \int p\left(\mathbf{z}_k \mid \mathbf{x}_k\right) p\left(\mathbf{x}_k \mid \mathbf{z}_{k-1}, \ldots,\mathbf{z}_0\right) d\mathbf{x}_k\\ | p(\mathbf{z}) &= \prod_{k=0}^T \int p\left(\mathbf{z}_k \mid \mathbf{x}_k\right) p\left(\mathbf{x}_k \mid \mathbf{z}_{k-1}, \ldots,\mathbf{z}_0\right) d\mathbf{x}_k\\ | ||
| Line 381: | Line 376: | ||
&= \prod_{k=0}^T \mathcal{N}\left(\mathbf{z}_k; \mathbf{H}_k\hat{\mathbf{x}}_{k \mid k-1}, \mathbf{S}_k\right), | &= \prod_{k=0}^T \mathcal{N}\left(\mathbf{z}_k; \mathbf{H}_k\hat{\mathbf{x}}_{k \mid k-1}, \mathbf{S}_k\right), | ||
\end{align}</math> | \end{align}</math> | ||
अर्थात्, गॉसियन घनत्व का एक उत्पाद, प्रत्येक | अर्थात्, गॉसियन घनत्व का एक उत्पाद, प्रत्येक वर्तमान निस्यंदन वितरण <math>\mathbf{H}_k\hat{\mathbf{x}}_{k \mid k-1}, \mathbf{S}_k</math> के अंतर्गत एक अवलोकन z<sub>''k''</sub> के घनत्व के अनुरूप है। इसकी गणना सरल पुनरावर्ती अद्यतन के रूप में सरलता से की जा सकती है; हालांकि,[[ अंकगणितीय अंतर्प्रवाह |अंकगणितीय अंतर्प्रवाह]] से परिवर्जन के लिए, व्यावहारिक कार्यान्वयन में सामान्यतः लॉग सीमांत संभावना <math>\ell = \log p(\mathbf{z})</math> की गणना करना वांछनीय होता है। अधिवेशन <math>\ell^{(-1)} = 0</math> को अपनाना, यह पुनरावर्ती अद्यतन नियम के माध्यम से किया जा सकता है | ||
:<math>\ell^{(k)} = \ell^{(k-1)} - \frac{1}{2} \left(\tilde{\mathbf{y}}_k^\textsf{T} \mathbf{S}^{-1}_k \tilde{\mathbf{y}}_k + \log \left|\mathbf{S}_k\right| + d_y\log 2\pi \right),</math> | :<math>\ell^{(k)} = \ell^{(k-1)} - \frac{1}{2} \left(\tilde{\mathbf{y}}_k^\textsf{T} \mathbf{S}^{-1}_k \tilde{\mathbf{y}}_k + \log \left|\mathbf{S}_k\right| + d_y\log 2\pi \right),</math> | ||
जहां <math>d_y</math> माप सदिश का आयाम है।<ref>{{Cite book|last=Lütkepohl|first= Helmut|title=Introduction to Multiple Time Series Analysis|publisher= Springer-Verlag Berlin |location=Heidelberg|year= 1991|page=435}}</ref> | |||
एक महत्वपूर्ण अनुप्रयोग जहां अवलोकनों की ऐसी ( | |||
एक महत्वपूर्ण अनुप्रयोग जहां अवलोकनों की ऐसी (log) संभावना (फिल्टर मापदंडों को देखते हुए) बहु-लक्ष्य अनुपथन का उपयोग किया जाता है। उदाहरण के लिए, एक वस्तु अनुपथन परिदृश्य पर विचार करें जहां अवलोकन का एक वर्ग इनपुट है, हालांकि, यह अज्ञात है कि दृश्य में कितनी वस्तुएं हैं (या, वस्तुओं की संख्या ज्ञात है परन्तु एक से अधिक है)। ऐसे परिदृश्य के लिए, यह अज्ञात हो सकता है कि कौन से अवलोकन/माप किस वस्तु द्वारा उत्पन्न किए गए थे। एक बहु अवधारणा अनुपथक (MHT) सामान्यतः अलग-अलग पथ समिति परिकल्पनाओं का निर्माण करेगी, जहां प्रत्येक परिकल्पना को परिकल्पित वस्तु से जुड़े मापदंडों के एक विशिष्ट समुच्चयों के साथ कालमान फिल्टर (रैखिक गॉसियन स्थितियो के लिए) के रूप में माना जा सकता है। इस प्रकार, विचाराधीन विभिन्न परिकल्पनाओं के लिए टिप्पणियों की संभावना की गणना करना महत्वपूर्ण है। | |||
== सूचना | == सूचना फिल्टर == | ||
सूचना फिल्टर, या व्युत्क्रम सहप्रसरण फिल्टर में, अनुमानित सहप्रसरण और अनुमानित स्थिति को क्रमशः सूचना आव्यूह और सूचना सदिश द्वारा प्रतिस्थापित किया जाता है। इन्हें इस प्रकार परिभाषित किया गया है: | |||
सूचना | |||
:<math>\begin{align} | :<math>\begin{align} | ||
\mathbf{Y}_{k \mid k} &= \mathbf{P}_{k \mid k}^{-1} \\ | \mathbf{Y}_{k \mid k} &= \mathbf{P}_{k \mid k}^{-1} \\ | ||
\hat{\mathbf{y}}_{k \mid k} &= \mathbf{P}_{k \mid k}^{-1}\hat{\mathbf{x}}_{k \mid k} | \hat{\mathbf{y}}_{k \mid k} &= \mathbf{P}_{k \mid k}^{-1}\hat{\mathbf{x}}_{k \mid k} | ||
\end{align}</math> | \end{align}</math> | ||
इसी | इसी प्रकार अनुमानित सहप्रसरण और अवस्था के समान सूचना प्रपत्र हैं, जिन्हें इस प्रकार परिभाषित किया गया है: | ||
:<math>\begin{align} | :<math>\begin{align} | ||
\mathbf{Y}_{k \mid k-1} &= \mathbf{P}_{k \mid k-1}^{-1} \\ | \mathbf{Y}_{k \mid k-1} &= \mathbf{P}_{k \mid k-1}^{-1} \\ | ||
| Line 403: | Line 398: | ||
\mathbf{i}_k &= \mathbf{H}_k^\textsf{T} \mathbf{R}_k^{-1} \mathbf{z}_k | \mathbf{i}_k &= \mathbf{H}_k^\textsf{T} \mathbf{R}_k^{-1} \mathbf{z}_k | ||
\end{align}</math> | \end{align}</math> | ||
सूचना अद्यतन अब एक तुच्छ | सूचना अद्यतन अब एक तुच्छ योग बन जाता है।<ref name=terejanu>{{cite web|title=Discrete Kalman Filter Tutorial |author=Gabriel T. Terejanu |date=2012-08-04 |access-date=2016-04-13 |url=https://cse.sc.edu/~terejanu/files/tutorialKF.pdf}}</ref> | ||
:<math>\begin{align} | :<math>\begin{align} | ||
\mathbf{Y}_{k \mid k} &= \mathbf{Y}_{k \mid k-1} + \mathbf{I}_k \\ | \mathbf{Y}_{k \mid k} &= \mathbf{Y}_{k \mid k-1} + \mathbf{I}_k \\ | ||
\hat{\mathbf{y}}_{k \mid k} &= \hat{\mathbf{y}}_{k \mid k-1} + \mathbf{i}_k | \hat{\mathbf{y}}_{k \mid k} &= \hat{\mathbf{y}}_{k \mid k-1} + \mathbf{i}_k | ||
\end{align}</math> | \end{align}</math> | ||
सूचना | सूचना फिल्टर की मुख्य लब्धि यह है कि एन मापों को प्रत्येक चरणों में सूचना आव्यूहों और सदिशों को जोड़कर फिल्टर किया जा सकता है। | ||
:<math>\begin{align} | :<math>\begin{align} | ||
\mathbf{Y}_{k \mid k} &= \mathbf{Y}_{k \mid k-1} + \sum_{j=1}^N \mathbf{I}_{k,j} \\ | \mathbf{Y}_{k \mid k} &= \mathbf{Y}_{k \mid k-1} + \sum_{j=1}^N \mathbf{I}_{k,j} \\ | ||
\hat{\mathbf{y}}_{k \mid k} &= \hat{\mathbf{y}}_{k \mid k-1} + \sum_{j=1}^N \mathbf{i}_{k,j} | \hat{\mathbf{y}}_{k \mid k} &= \hat{\mathbf{y}}_{k \mid k-1} + \sum_{j=1}^N \mathbf{i}_{k,j} | ||
\end{align}</math> | \end{align}</math> | ||
सूचना | सूचना फिल्टर का पूर्वानुमान करने के लिए सूचना आव्यूहों और सदिशों को उनके अवस्था समष्टि समतुल्यता में वापस परिवर्तित किया जा सकता है, या वैकल्पिक रूप से सूचना स्थान पूर्वानुमान का उपयोग किया जा सकता है।<ref name=terejanu />: | ||
<math>\begin{align} | |||
\mathbf{M}_k &= | \mathbf{M}_k &= | ||
\left[\mathbf{F}_k^{-1}\right]^\textsf{T} \mathbf{Y}_{k-1 \mid k-1} \mathbf{F}_k^{-1} \\ | \left[\mathbf{F}_k^{-1}\right]^\textsf{T} \mathbf{Y}_{k-1 \mid k-1} \mathbf{F}_k^{-1} \\ | ||
| Line 428: | Line 425: | ||
== | |||
== निश्चित-अंतराल स्मूथर == | |||
इष्टतम | इष्टतम निश्चित अंतराल स्मूथर का इष्टतम अनुमान <math>\hat{\mathbf{x}}_{k-N \mid k}</math> प्रदान करता है, किसी निश्चित अंतराल <math>\mathbf{z}_1</math> प्रति <math>\mathbf{z}_k</math>के लिए <math>N</math> से मापन का उपयोग किया जाता है।<ref>{{cite book|last1=Anderson|first1=Brian D. O.|last2=Moore|first2=John B.|title=Optimal Filtering|date=1979|publisher=Prentice Hall, Inc.|location=Englewood Cliffs, NJ|isbn=978-0-13-638122-8|pages=176–190}}</ref> इसे एक संवर्धित अवस्था के माध्यम से पूर्व सिद्धांत का उपयोग करके प्राप्त किया जा सकता है, और फिल्टर का मुख्य समीकरण निम्नलिखित है: | ||
:<math> | :<math> | ||
\begin{bmatrix} | \begin{bmatrix} | ||
| Line 468: | Line 465: | ||
\mathbf{y}_{t \mid t-1} | \mathbf{y}_{t \mid t-1} | ||
</math> | </math> | ||
जहां: | |||
* <math> \hat{\mathbf{x}}_{t \mid t-1} </math> एक मानक | * <math> \hat{\mathbf{x}}_{t \mid t-1} </math> एक मानक कालमान फिल्टर के माध्यम से अनुमानित है; | ||
* <math> \mathbf{y}_{t \mid t-1} = \mathbf{z}_t - \mathbf{H}\hat{\mathbf{x}}_{t \mid t-1} </math> मानक | * <math> \mathbf{y}_{t \mid t-1} = \mathbf{z}_t - \mathbf{H}\hat{\mathbf{x}}_{t \mid t-1} </math> मानक कालमान फिल्टर के अनुमान को ध्यान में रखते हुए उत्पादित नवाचार है; | ||
* बहुत से <math> \hat{\mathbf{x}}_{t-i \mid t} </math> साथ <math> i = 1, \ldots, N-1 </math> नए चर हैं; अर्थात्, वे मानक | * बहुत से <math> \hat{\mathbf{x}}_{t-i \mid t} </math> साथ में <math> i = 1, \ldots, N-1 </math> नए चर हैं; अर्थात्, वे मानक कालमान फिल्टर में प्रकट नहीं होते हैं; | ||
* लब्धि की गणना निम्नलिखित योजना के माध्यम से की जाती है: | * लब्धि की गणना निम्नलिखित योजना के माध्यम से की जाती है: | ||
*:<math> | *:<math> | ||
| Line 490: | Line 487: | ||
\right]^i | \right]^i | ||
</math> | </math> | ||
: | :जहां <math> \mathbf{P} </math> तथा <math> \mathbf{K} </math> पूर्वानुमान त्रुटि सहप्रसरण और मानक कालमान फिल्टर की लब्धि हैं (अर्थात, <math> \mathbf{P}_{t \mid t-1} </math>) | ||
यदि अनुमान त्रुटि सहप्रसरण को परिभाषित किया जाता है ताकि | यदि अनुमान त्रुटि सहप्रसरण को परिभाषित किया जाता है ताकि | ||
| Line 506: | Line 503: | ||
\right], | \right], | ||
</math> | </math> | ||
तो हमारे पास अनुमान पर सुधार है <math> \mathbf{x}_{t-i} </math> द्वारा दिया गया है: | तो हमारे पास अनुमान पर सुधार है, <math> \mathbf{x}_{t-i} </math> द्वारा दिया गया है: | ||
:<math> | :<math> | ||
\mathbf{P} - \mathbf{P}_i = | \mathbf{P} - \mathbf{P}_i = | ||
| Line 520: | Line 517: | ||
== | == निश्चित-अंतराल स्मूथर्स == | ||
इष्टतम निश्चित-अंतराल | इष्टतम निश्चित-अंतराल स्मूथर का इष्टतम अनुमान <math>\hat{\mathbf{x}}_{k \mid n}</math> (<math>k < n</math>) प्रदान करता है, एक निश्चित अंतराल <math>\mathbf{z}_1</math>से <math>\mathbf{z}_n</math> के लिए मापन का उपयोग किया जाता है, इसे "कालमान समरेखण" भी कहा जाता है। सामान्य उपयोग में कई समरेखण कलन विधि हैं। | ||
=== राउच-तुंग-स्ट्रीबेल === | === राउच-तुंग-स्ट्रीबेल === | ||
रॉच-तुंग-स्ट्रीबेल ( | रॉच-तुंग-स्ट्रीबेल (RTS) स्मूथर निश्चित अंतराल समरेखण के लिए एक कुशल दो-पारण कलन विधि है।<ref>{{cite journal | last1 = Rauch | first1 = H.E. | last2 = Tung | first2 = F. | last3 = Striebel | first3 = C. T. | title = Maximum likelihood estimates of linear dynamic systems | journal = AIAA Journal| volume = 3 | issue = 8 | pages = 1445–1450 | date=August 1965 | doi = 10.2514/3.3166 | bibcode = 1965AIAAJ...3.1445.}}</ref> | ||
अग्रगामी पारण नियमित कालमान फिल्टर कलन विधि के समान है। ये ए-प्रीओरी और ए-पोस्टरियोरी अवस्था अनुमानों <math>\hat{\mathbf{x}}_{k \mid k-1}</math>, <math>\hat{\mathbf{x}}_{k \mid k}</math> और सहप्रसरण <math>\mathbf{P}_{k \mid k-1}</math>, <math>\mathbf{P}_{k \mid k}</math> को फिल्टर करते हैं। पश्चगामी पारण ([[ रेट्रोडिक्शन | रेट्रोडिक्शन]] के लिए) में उपयोग के लिए सेव किया जाता हैं। | |||
पश्चगामी पारण में, हम समकृत अवस्था अनुमानों <math>\hat{\mathbf{x}}_{k \mid n}</math> और सहप्रसरण <math>\mathbf{P}_{k \mid n}</math> की गणना करते हैं। हम अंतिम टाइमस्टेप से प्रारम्भ करते हैं और निम्नलिखित पुनरावर्ती समीकरणों का उपयोग करके समय में पश्चगामी की ओर बढ़ते हैं: | |||
:<math>\begin{align} | :<math>\begin{align} | ||
\hat{\mathbf{x}}_{k \mid n} &= \hat{\mathbf{x}}_{k \mid k} + \mathbf{C}_k \left(\hat{\mathbf{x}}_{k+1 \mid n} - \hat{\mathbf{x}}_{k+1 \mid k}\right) \\ | \hat{\mathbf{x}}_{k \mid n} &= \hat{\mathbf{x}}_{k \mid k} + \mathbf{C}_k \left(\hat{\mathbf{x}}_{k+1 \mid n} - \hat{\mathbf{x}}_{k+1 \mid k}\right) \\ | ||
\mathbf{P}_{k \mid n} &= \mathbf{P}_{k \mid k} + \mathbf{C}_k \left(\mathbf{P}_{k+1 \mid n} - \mathbf{P}_{k+1 \mid k}\right) \mathbf{C}_k^\textsf{T} | \mathbf{P}_{k \mid n} &= \mathbf{P}_{k \mid k} + \mathbf{C}_k \left(\mathbf{P}_{k+1 \mid n} - \mathbf{P}_{k+1 \mid k}\right) \mathbf{C}_k^\textsf{T} | ||
\end{align}</math> | \end{align}</math> | ||
जहां | |||
:<math>\mathbf{C}_k = \mathbf{P}_{k \mid k} \mathbf{F}_{k+1}^\textsf{T} \mathbf{P}_{k+1 \mid k}^{-1}.</math> | :<math>\mathbf{C}_k = \mathbf{P}_{k \mid k} \mathbf{F}_{k+1}^\textsf{T} \mathbf{P}_{k+1 \mid k}^{-1}.</math> | ||
<math> \mathbf{x}_{k \mid k}</math> टाइमस्टेप | <math> \mathbf{x}_{k \mid k}</math> टाइमस्टेप <math>k</math> तथा <math>\mathbf{x}_{k+1 \mid k}</math> की ए-पोस्टीरियरी अवस्था और टाइमस्टेप <math>k + 1</math> की ए-प्रीओरी अवस्था अनुमान है, सहप्रसरण पर भी यही संकेतन अनुप्रयुक्त होता है। | ||
=== संशोधित ब्रायसन-फ्रेज़ियर | === संशोधित ब्रायसन-फ्रेज़ियर स्मूथर === | ||
आरटीएस कलन विधि का एक विकल्प संशोधित ब्रायसन-फ्रेज़ियर ( | आरटीएस कलन विधि का एक विकल्प बीरमैन द्वारा विकसित संशोधित ब्रायसन-फ्रेज़ियर (MBF) निश्चित अंतराल स्मूथर है।<ref name="bierman">{{cite journal | last = Bierman | first = G.J. | title = Factorization Methods for Discrete Sequential Estimation | year = 1977 | bibcode = 1977fmds.book.....B | journal = Factorization Methods for Discrete Sequential Estimation }}</ref> यह एक पश्चगामी पारण का भी उपयोग करता है जो कालमान फिल्टर अग्रगामी पारण से सहेजे गए डेटा को संसाधित करता है। पश्चगामी पारण के समीकरणों में डेटा की पुनरावर्ती संगणना सम्मिलित होती है। जिसका उपयोग प्रत्येक अवलोकन समय पर समकृत अवस्था और सहप्रसरण की गणना के लिए किया जाता है । | ||
पुनरावर्ती समीकरण हैं | पुनरावर्ती समीकरण हैं | ||
| Line 550: | Line 547: | ||
\hat{\lambda}_n &= 0 | \hat{\lambda}_n &= 0 | ||
\end{align}</math> | \end{align}</math> | ||
जहां <math>\mathbf{S}_k</math> अवशिष्ट सहप्रसरण है और <math>\hat{\mathbf{C}}_k = \mathbf{I} - \mathbf{K}_k \mathbf{H}_k</math>.समकृत अवस्था और सहप्रसरण तब समीकरणों में प्रतिस्थापन द्वारा प्राप्त किया जा सकता है; | |||
:<math>\begin{align} | :<math>\begin{align} | ||
\mathbf{P}_{k \mid n} &= \mathbf{P}_{k \mid k} - \mathbf{P}_{k \mid k}\hat{\Lambda}_k\mathbf{P}_{k \mid k} \\ | \mathbf{P}_{k \mid n} &= \mathbf{P}_{k \mid k} - \mathbf{P}_{k \mid k}\hat{\Lambda}_k\mathbf{P}_{k \mid k} \\ | ||
| Line 560: | Line 557: | ||
\mathbf{x}_{k \mid n} &= \mathbf{x}_{k \mid k-1} - \mathbf{P}_{k \mid k-1}\tilde{\lambda}_k. | \mathbf{x}_{k \mid n} &= \mathbf{x}_{k \mid k-1} - \mathbf{P}_{k \mid k-1}\tilde{\lambda}_k. | ||
\end{align}</math> | \end{align}</math> | ||
एमबीएफ की एक महत्वपूर्ण लब्धि यह है कि इसमें सहप्रसरण आव्यूह के व्युत्क्रम को खोजने की आवश्यकता नहीं होती है। | |||
=== न्यूनतम-विचरण | === न्यूनतम-विचरण स्मूथर === | ||
न्यूनतम-विचरण | न्यूनतम-विचरण स्मूथर सर्वोत्तम संभव त्रुटि प्रदर्शन प्राप्त कर सकता है, बशर्ते कि प्रतिरूप रैखिक हों, उनके मापदण्ड और रव आंकड़े सटीक से ज्ञात हों।<ref>{{cite journal | last = Einicke | first = G.A. | title = Optimal and Robust Noncausal Filter Formulations | journal = IEEE Transactions on Signal Processing| volume = 54 | issue = 3 | pages = 1069–1077 | date=March 2006 | bibcode = 2006ITSP...54.1069E | doi = 10.1109/TSP.2005.863042 | s2cid = 15376718 }}</ref> यह स्मूथर इष्टतम गैर-कारण [[ विनीज़ फ़िल्टर |वीनर फिल्टर]] की एक समय-भिन्न अवस्था-स्थिति सामान्यीकरण है। | ||
स्मूथर गणना दो चरणों में की जाती है। इसमें एक चरण अग्रसर का पूर्वानुमान सम्मिलित होता है और इसके द्वारा दिया जाता है; | |||
:<math>\begin{align} | :<math>\begin{align} | ||
\hat{\mathbf{x}}_{k+1 \mid k} &= (\mathbf{F}_k - \mathbf{K}_k\mathbf{H}_k)\hat{\mathbf{x}}_{k \mid k-1} + \mathbf{K}_k\mathbf{z}_k \\ | \hat{\mathbf{x}}_{k+1 \mid k} &= (\mathbf{F}_k - \mathbf{K}_k\mathbf{H}_k)\hat{\mathbf{x}}_{k \mid k-1} + \mathbf{K}_k\mathbf{z}_k \\ | ||
\alpha_k &= -\mathbf{S}_k^{-\frac{1}{2}}\mathbf{H}_k\hat{\mathbf{x}}_{k \mid k-1} + \mathbf{S}_k^{-\frac{1}{2}}\mathbf{z}_k | \alpha_k &= -\mathbf{S}_k^{-\frac{1}{2}}\mathbf{H}_k\hat{\mathbf{x}}_{k \mid k-1} + \mathbf{S}_k^{-\frac{1}{2}}\mathbf{z}_k | ||
\end{align}</math> | \end{align}</math> | ||
उपरोक्त प्रणाली को व्युत्क्रम वीनर-हॉप कारक के रूप में जाना जाता है। | उपरोक्त प्रणाली को व्युत्क्रम वीनर-हॉप कारक के रूप में जाना जाता है। पश्चगामी पुनरावर्तन उपरोक्त पूर्वकालिक प्रणाली का जोड़ है। पश्चगामी पारण का परिणाम <math>\beta_k</math> कालोत्क्रमण <math>\alpha_k</math> पर आगे के समीकरणों को संचालित करके गणना की जा सकती है और समय परिणाम उत्क्रमणीय है। आउटपुट अनुमान की स्थितियो में, समकृत अनुमान द्वारा दिया जाता है | ||
:<math>\hat{\mathbf{y}}_{k \mid N} = \mathbf{z}_k - \mathbf{R}_k\beta_k</math> | :<math>\hat{\mathbf{y}}_{k \mid N} = \mathbf{z}_k - \mathbf{R}_k\beta_k</math> | ||
इस न्यूनतम-विचरण | इस न्यूनतम-विचरण के कारण स्मूथर प्रतिफल में भाग लेना | ||
:<math>\hat{\mathbf{y}}_{k \mid k} = \mathbf{z}_k - \mathbf{R}_k \mathbf{S}_k^{-\frac{1}{2}} \alpha_k</math> | :<math>\hat{\mathbf{y}}_{k \mid k} = \mathbf{z}_k - \mathbf{R}_k \mathbf{S}_k^{-\frac{1}{2}} \alpha_k</math> | ||
जो न्यूनतम-विचरण | जो न्यूनतम-विचरण कालमान फिल्टर के समान है। उपरोक्त उपाय आउटपुट अनुमान त्रुटि के विचरण को कम करते हैं। ध्यान दें कि रॉच-तुंग-स्ट्रीबेल स्मूथर व्युत्पत्ति का मानना है कि अंतर्निहित वितरण गॉसियन हैं, जबकि न्यूनतम-विचरण उपाय नहीं हैं। अवस्था के आकलन और इनपुट अनुमान के लिए इष्टतम स्मूथर्स का निर्माण इसी प्रकार किया जा सकता है। | ||
उपरोक्त स्मूथर का सतत-समय संस्करण में वर्णित है।<ref>{{cite journal | last = Einicke | first = G.A. | title = Asymptotic Optimality of the Minimum-Variance Fixed-Interval Smoother | journal = IEEE Transactions on Signal Processing| volume = 55 | issue = 4 | pages = 1543–1547 | date=April 2007 | bibcode = 2007ITSP...55.1543E | doi = 10.1109/TSP.2006.889402 | s2cid = 16218530 }}</ref><ref>{{cite journal | last1 = Einicke | first1 = G.A. | last2 = Ralston | first2 = J.C. | last3 = Hargrave | first3 = C.O. | last4 = Reid | first4 = D.C. | last5 = Hainsworth | first5 = D.W. | title = Longwall Mining Automation. An Application of Minimum-Variance Smoothing | journal = IEEE Control Systems Magazine | volume = 28 | issue = 6 |pages=28–37 |doi=10.1109/MCS.2008.929281 | date=December 2008 | s2cid = 36072082 }}</ref> | |||
अपेक्षा-अधिकतमकरण कलन विधि को न्यूनतम-विचरण फिल्टर और स्मूथर्स के भीतर अज्ञात अवस्था समष्टि मापदंडों के अनुमानित अधिकतम संभावना अनुमानों की गणना करने के लिए नियोजित किया जा सकता है। प्रायः अनिश्चितता समस्या धारणाओं के भीतर रहती है। रिकाटी समीकरण में एक सकारात्मक निश्चित पद जोड़कर अनिश्चितताओं को समायोजित करने वाला एक स्मूथर प्रारुप तैयार किया जा सकता है।<ref>{{cite journal | last = Einicke | first = G.A. | title = Asymptotic Optimality of the Minimum-Variance Fixed-Interval Smoother | journal = IEEE Transactions on Automatic Control | volume = 54 | issue = 12 | pages = 2904–2908 | date=December 2009 | bibcode = 2007ITSP...55.1543E | doi = 10.1109/TSP.2006.889402 | s2cid = 16218530 }}</ref> | |||
ऐसी स्थितियों में जहां प्रतिरूप गैर-रैखिक हैं, चरणगत रेखीयकरण न्यूनतम-विचरण फिल्टर और स्मूथ पुनरावर्तन (विस्तारित कालमान फिल्टर) के भीतर हो सकते है। | |||
== आवृत्ति-भारित | == आवृत्ति-भारित कालमान फिल्टर == | ||
1930 के दशक में फ्लेचर और मुनसन द्वारा विभिन्न आवृत्तियों पर | 1930 के दशक में फ्लेचर और मुनसन द्वारा विभिन्न आवृत्तियों पर ध्वनियों की धारणा पर अग्रणी शोध किया गया था। उनके कार्य ने औद्योगिक रव और श्रवण हानि की जांच के भीतर भार मापने के मानक विधियों का नेतृत्व किया। | ||
सामान्यतः, एक | सामान्यतः, एक आवृति आकार देने वाले प्रकार्य का उपयोग एक निर्दिष्ट आवृति बैंड में त्रुटि वर्णक्रमीय घनत्व की औसत शक्ति को भारित करने के लिए किया जाता है। माना <math>\mathbf{y} - \hat{\mathbf{y}}</math> एक सांकेतिक कालमान फिल्टर द्वारा प्रदर्शित आउटपुट अनुमान त्रुटि को निरूपित करता है। इसके अतिरिक्त, <math>\mathbf{W}</math> एक कारण आवृत्ति भार स्थानांतरण प्रकार्य को निरूपित करता है। इष्टतम समाधान जो <math>\mathbf{W}\left(\mathbf{y} - \hat{\mathbf{y}}\right)</math> के विचरण को कम करता है, <math>\mathbf{W}^{-1} \hat{\mathbf{y}}</math> केवल निर्माण करने से उत्पन्न होता है। | ||
<math>\mathbf{W}</math> का प्रारुप एक अनिर्णीत प्रश्न बना हुआ है। एक अग्रसर प्रणाली एक ऐसी प्रणाली की पहचान करती है जो अनुमान त्रुटि और समुच्चयन <math>\mathbf{W}</math> उत्पन्न करती है, उस प्रणाली के व्युत्क्रम के समान है।<ref>{{cite journal | last = Einicke | first = G.A. | title = Iterative Frequency-Weighted Filtering and Smoothing Procedures | journal = IEEE Signal Processing Letters | volume = 21 | issue = 12 | pages = 1467–1470 | date=December 2014 | doi = 10.1109/LSP.2014.2341641 |bibcode = 2014ISPL...21.1467E | s2cid = 13569109 }}</ref> बढ़े हुए फिल्टर क्रम की कीमत पर माध्य-वर्ग त्रुटि सुधार प्राप्त करने के लिए इस प्रक्रिया को पुनरावृत्त किया जा सकता है। स्मूथर्स पर भी यही प्रविधि अनुप्रयुक्त की जा सकती है। | |||
== | == अरेखीय फिल्टर == | ||
मूल | मूल कालमान फिल्टर एक रेखीय धारणा तक पर्याप्त है। हालाँकि, अधिक जटिल प्रणालियाँ अरैखिक हो सकती हैं। गैर-रैखिकता को या तो प्रक्रिया प्रतिरूप या अवलोकन प्रतिरूप के साथ या दोनों के साथ जोड़ा जा सकता है। | ||
गैर-रैखिक प्रणालियों के लिए | गैर-रैखिक प्रणालियों के लिए कालमान फिल्टर के सबसे सामान्य संस्करण विस्तारित कालमान फिल्टर और अनसेंटेड कालमान फिल्टर हैं। उपयोग करने के लिए किस फिल्टर की उपयुक्तता प्रक्रिया और अवलोकन प्रणाली के गैर-रैखिक सूचकांकों पर निर्भर करती है।<ref>{{Cite journal|last1=Biswas|first1=Sanat K.|last2=Qiao|first2=Li|last3=Dempster|first3=Andrew G.|date=2020-12-01|title=A quantified approach of predicting suitability of using the Unscented Kalman Filter in a non-linear application|url=http://www.sciencedirect.com/science/article/pii/S0005109820304398|journal=Automatica|language=en|volume=122|pages=109241|doi=10.1016/j.automatica.2020.109241|s2cid=225028760|issn=0005-1098}}</ref> | ||
=== विस्तारित | === विस्तारित कालमान फिल्टर === | ||
{{Main| | {{Main|विस्तारित कलमन निस्यंदक}} | ||
विस्तारित | विस्तारित कालमान फिल्टर (EKF) में, अवस्था पारगमन और अवलोकन प्रतिरूप को अवस्था के रैखिक कार्यों की आवश्यकता नहीं है, बल्कि इसके स्थान पर गैर-रेखीय कार्य हो सकते हैं। ये प्रकार्य अलग-अलग प्रकार के होते हैं। | ||
:<math>\begin{align} | :<math>\begin{align} | ||
\mathbf{x}_k &= f(\mathbf{x}_{k-1}, \mathbf{u}_k) + \mathbf{w}_k \\ | \mathbf{x}_k &= f(\mathbf{x}_{k-1}, \mathbf{u}_k) + \mathbf{w}_k \\ | ||
\mathbf{z}_k &= h(\mathbf{x}_k) + \mathbf{v}_k | \mathbf{z}_k &= h(\mathbf{x}_k) + \mathbf{v}_k | ||
\end{align}</math> | \end{align}</math> | ||
प्रकार्य f का उपयोग | प्रकार्य f का उपयोग पूर्व अनुमान से अनुमानित स्थिति की गणना करने के लिए किया जा सकता है और इसी तरह प्रकार्य h का उपयोग अनुमानित स्थिति से अनुमानित माप की गणना करने के लिए किया जा सकता है। हालाँकि, f और h को सीधे सहप्रसरण पर अनुप्रयुक्त नहीं किया जा सकता है। इसके स्थान पर आंशिक व्युत्पन्न ([[ जैकोबियन मैट्रिक्स |जैकोबियन]]) के एक आव्यूह की गणना की जाती है। | ||
प्रत्येक | प्रत्येक टाइमस्टेप पर जैकोबियन का वर्तमान पूर्वानुमानित अवस्थाओं के साथ मूल्यांकन किया जाता है। इन आव्यूह का उपयोग कालमान फिल्टर समीकरणों में किया जा सकता है। यह प्रक्रिया अनिवार्य रूप से वर्तमान अनुमान के आसपास गैर-रैखिक प्रकार्य को रैखिक बनाती है। | ||
=== अनसेंटेड | === अनसेंटेड कालमान फिल्टर === | ||
जब अवस्था | जब अवस्था पारगमन और अवलोकन प्रतिरूप, अर्थात, पूर्वानुमान और अद्यतन प्रकार्य <math>f</math> तथा <math>h</math>-अत्यधिक अरेखीय करते है , विस्तारित कालमान फिल्टर विशेष रूप से निःस्व प्रदर्शन दे सकता है।<ref name="JU97">{{cite book | ||
| author1 = Julier, Simon J. | | author1 = Julier, Simon J. | ||
| author2 = Uhlmann, Jeffrey K. | | author2 = Uhlmann, Jeffrey K. | ||
| Line 622: | Line 621: | ||
| editor1-last = Kadar | | editor1-last = Kadar | ||
| editor1-first = Ivan | | editor1-first = Ivan | ||
}}</ref> इसका कारण यह है कि सहप्रसरण अंतर्निहित अरेखीय प्रतिरूप के रेखीयकरण के माध्यम से प्रचारित किया जाता है। अनसेंटेड | }}</ref> इसका कारण यह है कि सहप्रसरण अंतर्निहित अरेखीय प्रतिरूप के रेखीयकरण के माध्यम से प्रचारित किया जाता है। अनसेंटेड कालमान फिल्टर ((UKF)<ref name="JU97" />माध्य के आसपास प्रतिरूप बिंदुओं (जिन्हें सिग्मा अंक कहा जाता है) के एक न्यूनतम समुच्चय का चयन करने के लिए एक नियतात्मक प्रतिरूपकरण प्रविधि का उपयोग करते है जिसे अनसेंटेड रूपांतरण (UT) के रूप में जाना जाता है। सिग्मा बिंदुओं को तब गैर-रेखीय कार्यों के माध्यम से प्रचारित किया जाता है, जिससे एक नया माध्य और सहप्रसरण अनुमान का निर्माण होता है। परिणामी फिल्टर इस तथ्य पर निर्भर करता है कि यूटी के रूपांतरित आँकड़ों की गणना कैसे की जाती है और सिग्मा बिंदुओं के किस समुच्चय का उपयोग किया जाता है। यह टिप्पणी की जानी चाहिए कि नए यूकेएफ का निर्माण एक सुसंगत विधि से करना सदैव संभव है।<ref>{{Cite journal|last1=Menegaz|first1=H. M. T.|last2=Ishihara|first2=J. Y.|last3=Borges|first3=G. A.|last4=Vargas|first4=A. N.|date=October 2015|title=A Systematization of the Unscented Kalman Filter Theory|journal=IEEE Transactions on Automatic Control|volume=60|issue=10|pages=2583–2598|doi=10.1109/tac.2015.2404511|issn=0018-9286|hdl=20.500.11824/251|s2cid=12606055|hdl-access=free}}</ref> कुछ प्रणालियों के लिए, परिणामी यूकेएफ सही माध्य और सहप्रसरण का अधिक सटीक अनुमान लगाता है।<ref name="GH2012">{{cite journal | ||
| author = Gustafsson, Fredrik | | author = Gustafsson, Fredrik | ||
| author2 = Hendeby, Gustaf | | author2 = Hendeby, Gustaf | ||
| Line 635: | Line 634: | ||
| s2cid = 17876531 | | s2cid = 17876531 | ||
| url = http://urn.kb.se/resolve?urn=urn:nbn:se:liu:diva-75272 | | url = http://urn.kb.se/resolve?urn=urn:nbn:se:liu:diva-75272 | ||
}}</ref> इसे [[ मोंटे कार्लो नमूनाकरण | मोंटे कार्लो | }}</ref> इसे [[ मोंटे कार्लो नमूनाकरण |मोंटे कार्लो प्रतिचयन]] या पश्च आँकड़ों के [[ टेलर श्रृंखला |टेलर श्रृंखला]] विस्तार के साथ सत्यापित किया जा सकता है। इसके अतिरिक्त, यह प्रविधि स्पष्ट रूप से जैकोबियन की गणना करने की आवश्यकता को निष्काषित कर देती है, जो जटिल कार्यों के लिए अपने आप में एक कठिन कार्य हो सकता है। | ||
==== सिग्मा अंक ==== | ==== सिग्मा अंक ==== | ||
एक यादृच्छिक सदिश | एक यादृच्छिक सदिश <math>\mathbf{x}=(x_1, \dots, x_L)</math> के लिए, सिग्मा बिंदु सदिशों का कोई भी समूह हैं, | ||
:<math> \{\mathbf{s}_0,\dots, \mathbf{s}_N \}=\bigl\{\begin{pmatrix} s_{0,1}& s_{0,2}&\ldots& s_{0,L} \end{pmatrix}, \dots, \begin{pmatrix} s_{N,1}& s_{N,2}&\ldots& s_{N,L} \end{pmatrix}\bigr\}</math> | :<math> \{\mathbf{s}_0,\dots, \mathbf{s}_N \}=\bigl\{\begin{pmatrix} s_{0,1}& s_{0,2}&\ldots& s_{0,L} \end{pmatrix}, \dots, \begin{pmatrix} s_{N,1}& s_{N,2}&\ldots& s_{N,L} \end{pmatrix}\bigr\}</math> | ||
के साथ | के साथ दोषी ठहराया | ||
* | * प्रथम क्रम भार <math>W_0^a, \dots, W_N^a</math> जो पूर्ण करते हैं | ||
# <math> \sum_{j=0}^N W_j^a=1 </math> | # <math> \sum_{j=0}^N W_j^a=1 </math> सभी के लिए <math>i=1, \dots, L</math>: <math> E[x_i]=\sum_{j=0}^N W_j^a s_{j,i} </math> | ||
* | * द्वितीय क्रम भार <math>W_0^c, \dots, W_N^c</math> जो पूर्ण करते हैं | ||
# <math> \sum_{j=0}^N W_j^c=1 </math> | # <math> \sum_{j=0}^N W_j^c=1 </math> सभी युग्मो के लिए <math> (i,l) \in \{1,\dots, L\}^2: E[x_ix_l]=\sum_{j=0}^N W_j^c s_{j,i}s_{j,l} </math>. | ||
के लिए सिग्मा अंक और भार | के लिए सिग्मा अंक और भार के लिए एक सरल विकल्प <math>\mathbf{x}_{k-1\mid k-1}</math> यूकेएफ कलन विधि में है; | ||
:<math>\begin{align} | :<math>\begin{align} | ||
\mathbf{s}_0&=\hat \mathbf{x}_{k-1\mid k-1}\\ | \mathbf{s}_0&=\hat \mathbf{x}_{k-1\mid k-1}\\ | ||
| Line 656: | Line 655: | ||
\end{align} | \end{align} | ||
</math> | </math> | ||
जहां <math>\hat \mathbf{x}_{k-1\mid k-1}</math> का औसत अनुमान <math>\mathbf{x}_{k-1\mid k-1}</math>है। सदिश <math>\mathbf{A}_j</math> का jth स्तम्भ <math>\mathbf{A}</math> है, जहां <math>\mathbf{P}_{k-1\mid k-1}=\mathbf{AA}^\textsf{T}</math>सामान्यतः, <math>\mathbf{A}</math> के [[ चोल्स्की अपघटन |चोल्स्की अपघटन <math>\mathbf{P}_{k-1\mid k-1}</math>]]के माध्यम से प्राप्त किया जाता है। कुछ सावधानी से फिल्टर समीकरण समीकरणों को इस प्रकार व्यक्त किया जा सकता है कि <math>\mathbf{A}</math> की मध्यवर्ती गणना के बिना <math>\mathbf{P}_{k-1\mid k-1}</math>का सीधे मूल्यांकन किया जाता है। इसे वर्गमूल अनसेंटेड कालमान फिल्टर के रूप में जाना जाता है।<ref>{{cite journal |last1=Van der Merwe |first1=R. |last2=Wan |first2=E.A. |title=The square-root unscented Kalman filter for state and parameter-estimation |journal=2001 IEEE International Conference on Acoustics, Speech, and Signal Processing. Proceedings (Cat. No.01CH37221) |date=2001 |volume=6 |pages=3461–3464 |doi=10.1109/ICASSP.2001.940586|isbn=0-7803-7041-4 |s2cid=7290857 }}</ref> | |||
औसत मान का भार, <math>W_0</math>, इच्छानुसार चयन किया जा सकता है। | |||
एक अन्य लोकप्रिय मानकीकरण (जो उपरोक्त को सामान्य करता है) है | एक अन्य लोकप्रिय मानकीकरण (जो उपरोक्त को सामान्य करता है) है; | ||
:<math>\begin{align} | :<math>\begin{align} | ||
\mathbf{s}_0&=\hat \mathbf{x}_{k-1\mid k-1}\\ | \mathbf{s}_0&=\hat \mathbf{x}_{k-1\mid k-1}\\ | ||
| Line 670: | Line 670: | ||
</math> | </math> | ||
<math>\alpha</math> तथा <math>\kappa</math> सिग्मा बिंदुओं के प्रसार को नियंत्रित | <math>\alpha</math> तथा <math>\kappa</math> सिग्मा बिंदुओं के प्रसार को नियंत्रित करता है और <math>\beta</math> के वितरण से संबंधित <math>x</math> है, | ||
उपयुक्त | उपयुक्त मान से सम्बंधित समस्याओं पर निर्भर करते हैं, परन्तु एक विशिष्ट सिफारिश <math>\alpha = 10^{-3}</math>, <math>\kappa = 1</math>, तथा <math>\beta = 2</math> है। हालांकि, <math>\alpha</math> का एक बड़ा मान (जैसे, <math>\alpha = 1</math>) वितरण के प्रसार और संभावित गैर-रैखिकताओं को उन्नत ढंग से अधिकृत करने के लिए लाभकारी हो सकता है।<ref>{{Cite journal|doi=10.5281/zenodo.44386|url=https://github.com/sbitzer/UKF-exposed |title=The UKF exposed: How it works, when it works and when it's better to sample |year=2016 |last1=Bitzer |first1=S. }}</ref> यदि <math>x</math> का सही वितरण गॉसियन है, और <math>\beta = 2</math> इष्टतम है।<ref>{{Cite book|doi=10.1109/ASSPCC.2000.882463|chapter-url=http://www.lara.unb.br/~gaborges/disciplinas/efe/papers/wan2000.pdf |chapter=The unscented Kalman filter for nonlinear estimation |title=Proceedings of the IEEE 2000 Adaptive Systems for Signal Processing, Communications, and Control Symposium (Cat. No.00EX373) |pages=153 |year=2000 |last1=Wan |first1=E.A. |last2=Van Der Merwe |first2=R. |isbn=978-0-7803-5800-3 |citeseerx=10.1.1.361.9373 |s2cid=13992571 }}</ref> | ||
माध्य और सहप्रसरण | ==== पूर्वानुमान ==== | ||
ईकेएफ के साथ, यूकेएफ पूर्वानुमान का उपयोग यूकेएफ नवीनीकरण से स्वतंत्र रूप से किया जा सकता है, एक रैखिक (या वास्तव में ईकेएफ) नवीनीकरण के संयोजन में, या इसके विपरीत। | |||
माध्य और सहप्रसरण, <math> \hat\mathbf{x}_{k-1\mid k-1}</math> तथा <math>\mathbf{P}_{k-1\mid k-1}</math> के अनुमानों को देखते हुए, एक प्राप्त <math> N = 2L+1 </math> सिग्मा अंक जैसा कि ऊपर अनुभाग में वर्णित है। सिग्मा बिंदुओं को पारगमन फलन f के माध्यम से प्रचारित किया जाता है। | |||
:<math>\mathbf{x}_{j} = f\left(\mathbf{s}_{j}\right) \quad j = 0, \dots, 2L </math>. | :<math>\mathbf{x}_{j} = f\left(\mathbf{s}_{j}\right) \quad j = 0, \dots, 2L </math>. | ||
अनुमानित माध्य और सहप्रसरण का उत्पादन करने के लिए प्रचारित सिग्मा बिंदुओं की तुलना की जाती है। | |||
:<math>\begin{align} | :<math>\begin{align} | ||
\hat{\mathbf{x}}_{k \mid k-1} &= \sum_{j=0}^{2L} W_j^a \mathbf{x}_j \\ | \hat{\mathbf{x}}_{k \mid k-1} &= \sum_{j=0}^{2L} W_j^a \mathbf{x}_j \\ | ||
\mathbf{P}_{k \mid k-1} &= \sum_{j=0}^{2L} W_j^c \left(\mathbf{x}_j - \hat{\mathbf{x}}_{k \mid k-1}\right)\left(\mathbf{x}_j - \hat{\mathbf{x}}_{k \mid k-1}\right)^\textsf{T}+\mathbf{Q}_k | \mathbf{P}_{k \mid k-1} &= \sum_{j=0}^{2L} W_j^c \left(\mathbf{x}_j - \hat{\mathbf{x}}_{k \mid k-1}\right)\left(\mathbf{x}_j - \hat{\mathbf{x}}_{k \mid k-1}\right)^\textsf{T}+\mathbf{Q}_k | ||
\end{align}</math> | \end{align}</math> | ||
जहां मूल सिग्मा बिंदुओं के प्रथम-क्रम का भार <math>W_j^a</math> हैं, और द्वितीय क्रम का भार <math>W_j^c</math> हैं। आव्यूह <math> \mathbf{Q}_k </math> पारगमन रव <math>\mathbf{w}_k</math> का सहप्रसरण है। | |||
==== | ==== नवीनीकरण ==== | ||
पूर्वानुमान अनुमानों <math>\hat{\mathbf{x}}_{k \mid k-1}</math> तथा <math>\mathbf{P}_{k \mid k-1}</math> को देखते हुए, <math>N = 2L+1</math> का एक नया समुच्चय सिग्मा अंक <math>\mathbf{s}_0, \dots, \mathbf{s}_{2L}</math> इसी प्रथम-क्रम भार के साथ <math> W_0^a,\dots W_{2L}^a</math> और दूसरे क्रम के भार <math>W_0^c,\dots, W_{2L}^c</math> की गणना की जाती है।<ref>{{cite journal |last1=Sarkka |first1=Simo |title=On Unscented Kalman Filtering for State Estimation of Continuous-Time Nonlinear Systems |journal=IEEE Transactions on Automatic Control |date=September 2007 |volume=52 |issue=9 |pages=1631–1641 |doi=10.1109/TAC.2007.904453}}</ref> ये सिग्मा अंक मापन प्रकार्य <math>h</math> के माध्यम से रूपांतरित होते हैं; | |||
:<math> \mathbf{z}_j=h(\mathbf{s}_j), \,\, j=0,1, \dots, 2L </math>. | :<math> \mathbf{z}_j=h(\mathbf{s}_j), \,\, j=0,1, \dots, 2L </math>. | ||
पुनः रूपांतरित बिंदुओं के अनुभवजन्य माध्य और सहप्रसरण की गणना की जाती है। | |||
:<math>\begin{align} | :<math>\begin{align} | ||
\hat{\mathbf{z}} &= \sum_{j=0}^{2L} W_j^a \mathbf{z}_j \\[6pt] | \hat{\mathbf{z}} &= \sum_{j=0}^{2L} W_j^a \mathbf{z}_j \\[6pt] | ||
\hat{\mathbf{S}}_k &= \sum_{j=0}^{2L} W_j^c (\mathbf{z}_j-\hat{\mathbf{z}})(\mathbf{z}_j-\hat{\mathbf{z}})^\textsf{T} + \mathbf{R}_k | \hat{\mathbf{S}}_k &= \sum_{j=0}^{2L} W_j^c (\mathbf{z}_j-\hat{\mathbf{z}})(\mathbf{z}_j-\hat{\mathbf{z}})^\textsf{T} + \mathbf{R}_k | ||
\end{align}</math> | \end{align}</math> | ||
जहां <math>\mathbf{R}_k</math> अवलोकन रव <math>\mathbf{v}_k</math> का सहप्रसरण आव्यूह है, इसके अतिरिक्त, तिर्यक् सहप्रसरण आव्यूह की भी आवश्यकता होती है | |||
:<math>\begin{align} | :<math>\begin{align} | ||
\mathbf{C_{xz}} &= \sum_{j=0}^{2L} W_j^c (\mathbf{x}_j-\hat\mathbf{x}_{k|k-1})(\mathbf{z}_j-\hat\mathbf{z})^\textsf{T}. | \mathbf{C_{xz}} &= \sum_{j=0}^{2L} W_j^c (\mathbf{x}_j-\hat\mathbf{x}_{k|k-1})(\mathbf{z}_j-\hat\mathbf{z})^\textsf{T}. | ||
\end{align}</math> | \end{align}</math> | ||
कालमान लब्धि है | |||
: <math>\begin{align} | : <math>\begin{align} | ||
\mathbf{K}_k=\mathbf{C_{xz}}\hat{\mathbf{S}}_k^{-1}. | \mathbf{K}_k=\mathbf{C_{xz}}\hat{\mathbf{S}}_k^{-1}. | ||
| Line 714: | Line 715: | ||
=== | === विभेदक कालमान फिल्टर === | ||
जब अवलोकन प्रतिरूप <math>p(\mathbf{z}_k\mid\mathbf{x}_k)</math> अत्यधिक गैर-रेखीय और/या गैर-गॉसियन है, यह बेयस के नियम और अनुमान को अनुप्रयुक्त करने के लिए | जब अवलोकन प्रतिरूप <math>p(\mathbf{z}_k\mid\mathbf{x}_k)</math> अत्यधिक गैर-रेखीय और/या गैर-गॉसियन है, तो यह बेयस के नियम और अनुमान को अनुप्रयुक्त करने के लिए लाभकारी सिद्ध हो सकता है; | ||
:<math> | :<math> | ||
p(\mathbf{z}_k\mid\mathbf{x}_k) \approx | p(\mathbf{z}_k\mid\mathbf{x}_k) \approx | ||
\frac{p(\mathbf{x}_k\mid\mathbf{z}_k)}{p(\mathbf{x}_k)} | \frac{p(\mathbf{x}_k\mid\mathbf{z}_k)}{p(\mathbf{x}_k)} | ||
</math> | </math> | ||
जहां <math>p(\mathbf{x}_k\mid\mathbf{z}_k) \approx \mathcal{N}(g(\mathbf{z}_k),Q(\mathbf{z}_k))</math> अरेखीय कार्यों <math>g,Q</math> के लिए, यह मानक कालमान फिल्टर के जनरेटिव विनिर्देश को अव्यक्त अवस्थाओं के लिए एक[[ भेदभावपूर्ण मॉडल | विभेदक प्रतिरूप]] के साथ को प्रतिस्थापित कर देता है। | |||
एक [[ स्थिर प्रक्रिया ]] | एक [[ स्थिर प्रक्रिया |स्थिर प्रक्रिया]] अवस्था प्रतिरूप के अंतर्गत | ||
:<math> | :<math> | ||
\begin{align} | \begin{align} | ||
| Line 730: | Line 731: | ||
\end{align} | \end{align} | ||
</math> | </math> | ||
जहां <math>\mathbf{T}= \mathbf{F}\mathbf{T}\mathbf{F}^\intercal + \mathbf{C}</math>, यदि | |||
:<math> | :<math> | ||
p(\mathbf{x}_k\mid\mathbf{z}_{1:k}) \approx \mathcal{N}(\hat{\mathbf{x}}_{k|k-1}, \mathbf{P}_{k|k-1}), | p(\mathbf{x}_k\mid\mathbf{z}_{1:k}) \approx \mathcal{N}(\hat{\mathbf{x}}_{k|k-1}, \mathbf{P}_{k|k-1}), | ||
</math> | </math> | ||
पुनः एक नया अवलोकन <math>\mathbf{z}_k</math> दिया गया, जो इस प्रकार है कि<ref name="Bur20">{{cite journal |last1=Burkhart |first1=Michael C. |last2=Brandman |first2=David M. |last3=Franco |first3=Brian |last4=Hochberg |first4=Leigh |last5=Harrison |first5=Matthew T. |title=The Discriminative Kalman Filter for Bayesian Filtering with Nonlinear and Nongaussian Observation Models |journal=Neural Computation |date=2020 |volume=32 |issue=5 |pages=969–1017 |doi=10.1162/neco_a_01275 |pmid=32187000 |pmc=8259355 |s2cid=212748230 |access-date=26 March 2021 | url=https://direct.mit.edu/neco/article/32/5/969/95592/The-Discriminative-Kalman-Filter-for-Bayesian}}</ref> | |||
:<math> | :<math> | ||
p(\mathbf{x}_{k+1}\mid\mathbf{z}_{1:k+1}) \approx \mathcal{N}(\hat{ \mathbf{x}}_{k+1|k}, \mathbf{P}_{k+1|k}) | p(\mathbf{x}_{k+1}\mid\mathbf{z}_{1:k+1}) \approx \mathcal{N}(\hat{ \mathbf{x}}_{k+1|k}, \mathbf{P}_{k+1|k}) | ||
</math> | </math> | ||
जहां | |||
:<math> | :<math> | ||
\begin{align} | \begin{align} | ||
| Line 746: | Line 747: | ||
\end{align} | \end{align} | ||
</math> | </math> | ||
ध्यान दें कि इस सन्निकटन | ध्यान दें कि इस सन्निकटन <math> Q(\mathbf{z}_k)^{-1} - \mathbf{T}^{-1} </math> की आवश्यकता है, जिनका धनात्मक निश्चित होना चाहिए; ऐसा न होने की दशा में, | ||
:<math> | :<math> | ||
\mathbf{P}_{k+1|k} = (\mathbf{M}_{k+1}^{-1} + Q(\mathbf{z}_k)^{-1})^{-1} | \mathbf{P}_{k+1|k} = (\mathbf{M}_{k+1}^{-1} + Q(\mathbf{z}_k)^{-1})^{-1} | ||
</math> | </math> | ||
के स्थान पर प्रयोग किया जाता है। | के स्थान पर प्रयोग किया जाता है। इस प्रकार का दृष्टिकोण विशेष रूप से तब उपयोगी सिद्ध होता है, जब अवलोकनों की आयामीता अव्यक्त अवस्थाओं की तुलना में बहुत अधिक होती है<ref name="Bur19">{{cite thesis |last1=Burkhart |first1=Michael C. |title=A Discriminative Approach to Bayesian Filtering with Applications to Human Neural Decoding |date=2019 |publisher=Brown University |location=Providence, RI, USA |doi=10.26300/nhfp-xv22 |url=https://doi.org/10.26300/nhfp-xv22 |access-date=26 March 2021}}</ref> और उन निस्यंदकों का निर्माण किया जा सकता है, जो अवलोकन प्रतिरूप में गैर-स्थिरता के लिए विशेष रूप से सुदृढ़ हैं।<ref name="Bra18">{{cite journal |last1=Brandman |first1=David M. |last2=Burkhart |first2=Michael C. |last3=Kelemen |first3=Jessica |last4=Franco |first4=Brian |last5=Harrison |first5=Matthew T. |last6=Hochberg |first6=Leigh R. |title=Robust Closed-Loop Control of a Cursor in a Person with Tetraplegia using Gaussian Process Regression |journal=Neural Computation |date=2018 |volume=30 |issue=11 |pages=2986–3008 |doi=10.1162/neco_a_01129 |pmid=30216140 |pmc=6685768 |url=https://direct.mit.edu/neco/article/30/11/2986/8418/Robust-Closed-Loop-Control-of-a-Cursor-in-a-Person |access-date=26 March 2021}}</ref> | ||
== अनुकूली कालमान फिल्टर == | |||
अनुकूली कालमान फिल्टर प्रक्रिया की गतिशीलता के अनुकूल होने की अनुमति देते हैं जो प्रक्रिया प्रतिरूप <math>\mathbf{F}(t)</math> में मॉडलिंग नहीं करते हैं, जो उदाहरण के लिए एक युक्तिपूर्ण लक्ष्य के संदर्भ में होते है, और जब अनुसरण के लिए एक स्थिर वेग (घटा हुआ क्रम) कालमान फिल्टर नियोजित किया जाता है।<ref>{{Cite book|last1=Bar-Shalom|first1=Yaakov|url=http://dx.doi.org/10.1002/0471221279|title=Estimation with Applications to Tracking and Navigation|last2=Li|first2=X.-Rong|last3=Kirubarajan|first3=Thiagalingam|date=2001|publisher=John Wiley & Sons, Inc.|isbn=0-471-41655-X|location=New York, USA|pages=421 ff|doi=10.1002/0471221279}}</ref> | |||
== कालमान-बुकी फिल्टर == | |||
कालमान-बुकी निस्यंदन (रिचर्ड स्नोडेन बुकी के नाम पर) कालमान फिल्टर का एक सतत समय संस्करण है।<ref>Bucy, R.S. and Joseph, P.D., ''Filtering for Stochastic Processes with Applications to Guidance,'' John Wiley & Sons, 1968; 2nd Edition, AMS Chelsea Publ., 2005. {{isbn|0-8218-3782-6}}</ref><ref>Jazwinski, Andrew H., ''Stochastic processes and filtering theory,'' Academic Press, New York, 1970. {{isbn|0-12-381550-9}}</ref> | |||
यह अवस्था समष्टि प्रतिरूप पर आधारित है | |||
यह अवस्था | |||
:<math>\begin{align} | :<math>\begin{align} | ||
\frac{d}{dt}\mathbf{x}(t) &= \mathbf{F}(t)\mathbf{x}(t) + \mathbf{B}(t)\mathbf{u}(t) + \mathbf{w}(t) \\ | \frac{d}{dt}\mathbf{x}(t) &= \mathbf{F}(t)\mathbf{x}(t) + \mathbf{B}(t)\mathbf{u}(t) + \mathbf{w}(t) \\ | ||
\mathbf{z}(t) &= \mathbf{H}(t) \mathbf{x}(t) + \mathbf{v}(t) | \mathbf{z}(t) &= \mathbf{H}(t) \mathbf{x}(t) + \mathbf{v}(t) | ||
\end{align}</math> | \end{align}</math> | ||
जहां <math>\mathbf{Q}(t)</math> तथा <math>\mathbf{R}(t)</math> दो श्वेत रव शब्दावली <math>\mathbf{w}(t)</math> तथा <math>\mathbf{v}(t)</math> की तीव्रता, (या, अधिक सटीक रूप से, ऊर्जा का वर्णक्रमीय घनत्व - PSD - आव्यूह) का प्रतिनिधित्व करते हैं; | |||
फिल्टर में दो अंतर समीकरण होते हैं, एक अवस्था अनुमान के लिए और एक सहप्रसरण के लिए: | |||
:<math>\begin{align} | :<math>\begin{align} | ||
\frac{d}{dt}\hat{\mathbf{x}}(t) &= \mathbf{F}(t)\hat{\mathbf{x}}(t) + \mathbf{B}(t)\mathbf{u}(t) + \mathbf{K}(t) \left(\mathbf{z}(t) - \mathbf{H}(t)\hat{\mathbf{x}}(t)\right) \\ | \frac{d}{dt}\hat{\mathbf{x}}(t) &= \mathbf{F}(t)\hat{\mathbf{x}}(t) + \mathbf{B}(t)\mathbf{u}(t) + \mathbf{K}(t) \left(\mathbf{z}(t) - \mathbf{H}(t)\hat{\mathbf{x}}(t)\right) \\ | ||
\frac{d}{dt}\mathbf{P}(t) &= \mathbf{F}(t)\mathbf{P}(t) + \mathbf{P}(t)\mathbf{F}^\textsf{T}(t) + \mathbf{Q}(t) - \mathbf{K}(t)\mathbf{R}(t)\mathbf{K}^\textsf{T}(t) | \frac{d}{dt}\mathbf{P}(t) &= \mathbf{F}(t)\mathbf{P}(t) + \mathbf{P}(t)\mathbf{F}^\textsf{T}(t) + \mathbf{Q}(t) - \mathbf{K}(t)\mathbf{R}(t)\mathbf{K}^\textsf{T}(t) | ||
\end{align}</math> | \end{align}</math> | ||
जहां | जहां कालमान लब्धि द्वारा प्रदान की जाती है | ||
:<math>\mathbf{K}(t) = \mathbf{P}(t)\mathbf{H}^\textsf{T}(t)\mathbf{R}^{-1}(t)</math> | :<math>\mathbf{K}(t) = \mathbf{P}(t)\mathbf{H}^\textsf{T}(t)\mathbf{R}^{-1}(t)</math> | ||
ध्यान दें कि इस अभिव्यक्ति में <math>\mathbf{K}(t)</math> अवलोकन रव का सहप्रसरण <math>\mathbf{R}(t)</math> एक ही समय में | ध्यान दें कि इस अभिव्यक्ति में <math>\mathbf{K}(t)</math>के लिए अवलोकन रव का सहप्रसरण <math>\mathbf{R}(t)</math> एक ही समय में पूर्वानुमान त्रुटि (या नवाचार) <math>\tilde{\mathbf{y}}(t) = \mathbf{z}(t) - \mathbf{H}(t)\hat{\mathbf{x}}(t)</math> के सहप्रसरण का प्रतिनिधित्व करता है। ये सहप्रसरण केवल सतत समय की स्थिति में समान होते हैं।<ref>{{cite journal|pages= 646–655|doi=10.1109/TAC.1968.1099025|title=An innovations approach to least-squares estimation--Part I: Linear filtering in additive white noise|journal=IEEE Transactions on Automatic Control|volume=13|issue=6|year=1968|last1=Kailath|first1=T.}}</ref> | ||
असतत-समय कालमान फिल्टर की पूर्वानुमान और अद्यतन चरणों के मध्य अंतर सतत समय में उपस्थित नहीं है। | |||
== | सहप्रसरण के लिए द्वितीय अवकल समीकरण, [[ रिकाटी समीकरण |रिकाटी समीकरण]] का एक उदाहरण है। कालमान-बुकी फिल्टर के गैर-रेखीय सामान्यीकरण में सतत समय विस्तारित कालमान फिल्टर सम्मिलित है। | ||
अधिकांश भौतिक प्रणालियों को | |||
== संकरित कालमान फिल्टर == | |||
अधिकांश भौतिक प्रणालियों को सतत-समय के प्रतिरूप के रूप में दर्शाया जाता है जबकि अंकीय संसाधक के माध्यम से अवस्था के आकलन के लिए प्रायः असतत-समय मापन किए जाते हैं। इसलिए, प्रणाली प्रतिरूप और माप प्रतिरूप द्वारा प्रदान की जाती है; | |||
:<math>\begin{align} | :<math>\begin{align} | ||
\dot{\mathbf{x}}(t) &= \mathbf{F}(t)\mathbf{x}(t) + \mathbf{B}(t)\mathbf{u}(t) + \mathbf{w}(t), | \dot{\mathbf{x}}(t) &= \mathbf{F}(t)\mathbf{x}(t) + \mathbf{B}(t)\mathbf{u}(t) + \mathbf{w}(t), | ||
| Line 786: | Line 789: | ||
&\mathbf{v}_k &\sim N(\mathbf{0},\mathbf{R}_k) | &\mathbf{v}_k &\sim N(\mathbf{0},\mathbf{R}_k) | ||
\end{align}</math> | \end{align}</math> | ||
जहां | |||
:<math>\mathbf{x}_k = \mathbf{x}(t_k)</math>. | :<math>\mathbf{x}_k = \mathbf{x}(t_k)</math>. | ||
| Line 793: | Line 796: | ||
=== | === पूर्वानुमान === | ||
:<math>\begin{align} | :<math>\begin{align} | ||
\dot{\hat{\mathbf{x}}}(t) &= \mathbf{F}(t) \hat{\mathbf{x}}(t) + \mathbf{B}(t) \mathbf{u}(t) | \dot{\hat{\mathbf{x}}}(t) &= \mathbf{F}(t) \hat{\mathbf{x}}(t) + \mathbf{B}(t) \mathbf{u}(t) | ||
| Line 802: | Line 805: | ||
\Rightarrow \mathbf{P}_{k \mid k-1} &= \mathbf{P}\left(t_k\right) | \Rightarrow \mathbf{P}_{k \mid k-1} &= \mathbf{P}\left(t_k\right) | ||
\end{align}</math> | \end{align}</math> | ||
पूर्वानुमान समीकरण माप से अद्यतन किए बिना सतत-समय कालमान फिल्टर से प्राप्त होते हैं, अर्थात्, <math> \mathbf{K}(t) = 0 </math>, पूर्व चरण में अनुमान के समान प्रारंभिक मानो के साथ अंतर समीकरणों के एक समुच्चय को हल करके अनुमानित अवस्था और सहप्रसरण की गणना की जाती है। | |||
[[ रैखिक समय अपरिवर्तनीय ]] प्रणालियों | [[ रैखिक समय अपरिवर्तनीय ]]प्रणालियों की स्थितियो में, सतत समय की गतिशीलता को [[ मैट्रिक्स घातांक |आव्यूह घातांक]] का उपयोग करके एक असतत समय प्रणाली में पूर्णतया विसर्जित किया जा सकता है। | ||
=== | === नवीनीकरण === | ||
:<math>\begin{align} | :<math>\begin{align} | ||
\mathbf{K}_k &= \mathbf{P}_{k \mid k-1}\mathbf{H}_k^\textsf{T} \left(\mathbf{H}_k\mathbf{P}_{k \mid k-1}\mathbf{H}_k^\textsf{T} + \mathbf{R}_k\right)^{-1} \\ | \mathbf{K}_k &= \mathbf{P}_{k \mid k-1}\mathbf{H}_k^\textsf{T} \left(\mathbf{H}_k\mathbf{P}_{k \mid k-1}\mathbf{H}_k^\textsf{T} + \mathbf{R}_k\right)^{-1} \\ | ||
| Line 812: | Line 815: | ||
\mathbf{P}_{k \mid k} &= \left(\mathbf{I} - \mathbf{K}_k\mathbf{H}_k\right)\mathbf{P}_{k \mid k-1} | \mathbf{P}_{k \mid k} &= \left(\mathbf{I} - \mathbf{K}_k\mathbf{H}_k\right)\mathbf{P}_{k \mid k-1} | ||
\end{align}</math> | \end{align}</math> | ||
अद्यतन समीकरण असतत-समय | अद्यतन समीकरण असतत-समय कालमान फिल्टर के समान हैं। | ||
== विरल संकेतों की पुनर्प्राप्ति के लिए परिवर्त्य == | == विरल संकेतों की पुनर्प्राप्ति के लिए परिवर्त्य == | ||
सांकेतिक कालमान फिल्टर को विरल, संभवतः गतिशील,रव अवलोकनों से संकेतों की पुनर्प्राप्ति के लिए भी नियोजित किया गया है। हाल ही में कार्य<ref>{{cite book|doi=10.1109/ICIP.2008.4711899|chapter=Kalman filtered Compressed Sensing|title=2008 15th IEEE International Conference on Image Processing|pages=893–896|year=2008|last1=Vaswani|first1=Namrata|author1-link= Namrata Vaswani |isbn=978-1-4244-1765-0|arxiv=0804.0819|s2cid=9282476}}</ref><ref>{{Cite journal|title=Methods for sparse signal recovery using Kalman filtering with embedded pseudo-measurement norms and quasi-norms|journal=IEEE Transactions on Signal Processing|volume=58|issue=4|pages=2405–2409|doi=10.1109/TSP.2009.2038959|year=2010|last1=Carmi|first1=Avishy|last2=Gurfil|first2=Pini|last3=Kanevsky|first3=Dimitri|bibcode=2010ITSP...58.2405C|s2cid=10569233}}</ref><ref>{{Cite journal|title=Dynamic Iterative Pursuit|journal=IEEE Transactions on Signal Processing|volume=60|issue=9|pages=4967–4972|doi=10.1109/TSP.2012.2203813|year=2012|last1=Zachariah|first1=Dave|last2=Chatterjee|first2=Saikat|last3=Jansson|first3=Magnus|arxiv=1206.2496|bibcode=2012ITSP...60.4967Z|s2cid=18467024}}</ref> संकुचित संवेदन/प्रतिरूपकरण के सिद्धांत से धारणाओं का उपयोग करते है, जैसे कि प्रतिबंधित समदूरीकता गुण और संबंधित संभाव्य पुनर्प्राप्ति विषय, आंतरिक रूप से निम्न-आयामी प्रणालियों में विरल अवस्था का क्रमिक रूप से अनुमान लगाने के लिए है। | |||
== गाउसीय प्रक्रम से संबंध == | == गाउसीय प्रक्रम से संबंध == | ||
चूंकि रैखिक गॉसियन अवस्था समष्टि प्रतिरूप गाउसीय प्रक्रियाओं की ओर ले जाते हैं, इसलिए | चूंकि रैखिक गॉसियन अवस्था समष्टि प्रतिरूप गाउसीय प्रक्रियाओं की ओर ले जाते हैं, इसलिए कालमान फिल्टर को गाउसीय प्रक्रम प्रतिगमन के लिए अनुक्रमिक समाधानकर्ता के रूप में देखा जा सकता है।<ref>{{cite arXiv|last1=Särkkä|first1=Simo|last2=Hartikainen|first2=Jouni|last3=Svensson|first3=Lennart|last4=Sandblom|first4=Fredrik|date=2015-04-22|title=On the relation between Gaussian process quadratures and sigma-point methods|class=stat.ME|eprint=1504.05994}}</ref> | ||
| Line 887: | Line 890: | ||
== अग्रिम पठन == | == अग्रिम पठन == | ||
{{refbegin|30em}} | {{refbegin|30em}} | ||
* {{cite book | author = Einicke, G.A. | year = 2019 | title = Smoothing, Filtering and Prediction: Estimating the Past, Present and Future (2nd ed.) | publisher = Amazon Prime Publishing | isbn = 978-0-6485115-0-2 }} | * {{cite book | author = Einicke, G.A. | year = 2019 | title = Smoothing, Filtering and Prediction: Estimating the Past, Present and Future (2nd ed.) | publisher = Amazon Prime Publishing | isbn = 978-0-6485115-0-2 }} | ||
| Line 916: | Line 918: | ||
== बाहरी संबंध == | == बाहरी संबंध == | ||
* [http://www.cs.unc.edu/~welch/kalman/kalmanPaper.html A New Approach to Linear Filtering and Prediction Problems], by R. E. Kalman, 1960 | * [http://www.cs.unc.edu/~welch/kalman/kalmanPaper.html A New Approach to Linear Filtering and Prediction Problems], by R. E. Kalman, 1960 | ||
* [https://github.com/rlabbe/Kalman-and-Bayesian-Filters-in-Python Kalman and Bayesian Filters in Python]. Open source Kalman filtering textbook. | * [https://github.com/rlabbe/Kalman-and-Bayesian-Filters-in-Python Kalman and Bayesian Filters in Python]. Open source Kalman filtering textbook. | ||
| Line 938: | Line 939: | ||
* [http://blog.sciencenet.cn/home.php?mod=space&uid=1565&do=blog&id=851754 Explaining Filtering (Estimation) in One Hour, Ten Minutes, One Minute, and One Sentence] by Yu-Chi Ho | * [http://blog.sciencenet.cn/home.php?mod=space&uid=1565&do=blog&id=851754 Explaining Filtering (Estimation) in One Hour, Ten Minutes, One Minute, and One Sentence] by Yu-Chi Ho | ||
*Simo Särkkä (2013). "Bayesian Filtering and Smoothing". ''Cambridge University Press.'' Full text available on author's webpage https://users.aalto.fi/~ssarkka/. | *Simo Särkkä (2013). "Bayesian Filtering and Smoothing". ''Cambridge University Press.'' Full text available on author's webpage https://users.aalto.fi/~ssarkka/. | ||
{{Authority control}} | |||
[[Category:All Wikipedia articles written in American English]] | |||
[[Category:All articles needing additional references]] | |||
[[Category:All articles to be expanded]] | |||
[[Category:All articles with unsourced statements]] | |||
[[Category:Articles needing additional references from अप्रैल 2016]] | |||
[[Category:Articles needing additional references from दिसंबर 2010]] | |||
[[Category:Articles to be expanded from अगस्त 2011]] | |||
[[Category:Articles using small message boxes]] | |||
[[Category:Articles with hatnote templates targeting a nonexistent page]] | |||
[[Category:Articles with invalid date parameter in template]] | |||
[[Category:Articles with unsourced statements from दिसंबर 2010]] | |||
[[Category:CS1]] | |||
[[Category:CS1 English-language sources (en)]] | |||
[[Category:CS1 errors]] | |||
[[Category:CS1 maint]] | |||
[[Category:Collapse templates]] | |||
[[Category:Lua-based templates]] | |||
[[Category:Multi-column templates]] | |||
[[Category:Navigational boxes| ]] | |||
[[Category:Navigational boxes without horizontal lists]] | |||
[[Category:Pages using div col with small parameter]] | |||
[[Category:Pages with script errors]] | |||
[[Category:Short description with empty Wikidata description]] | |||
[[Category:Sidebars with styles needing conversion]] | |||
[[Category:Template documentation pages|Documentation/doc]] | |||
[[Category:Templates Vigyan Ready]] | |||
[[Category:Templates generating microformats]] | |||
[[Category:Templates that add a tracking category]] | |||
[[Category:Templates that are not mobile friendly]] | |||
[[Category:Templates that generate short descriptions]] | |||
[[Category:Templates using TemplateData]] | |||
[[Category:Templates using under-protected Lua modules]] | |||
[[Category:Use American English from March 2018]] | |||
[[Category:Webarchive template wayback links]] | |||
[[Category:Wikipedia external links cleanup from June 2015]] | |||
[[Category:Wikipedia fully protected templates|Div col]] | |||
[[Category:Wikipedia further reading cleanup]] | |||
[[Category:Wikipedia metatemplates]] | |||
[[Category:Wikipedia spam cleanup from June 2015]] | |||
Latest revision as of 13:48, 6 November 2023
सांख्यिकी और नियंत्रण सिद्धांत के लिए, कालमान फिल्टर, जिसे रैखिक द्विघात अनुमान (LQE) के रूप में भी जाना जाता है, और यह एक कलन विधि है जो समय के साथ देखे गए मापों की एक श्रृंखला का उपयोग करता है, जिसमें सांख्यिकीय रव और अन्य अशुद्धियाँ सम्मिलित हैं, और अज्ञात चर के अनुमान उत्पन्न करता हैं, जो अधिक होते हैं। प्रत्येक समय-सीमा के लिए चरों पर एक असंग एक माप के आधार पर सटीक संयुक्त संभाव्यता वितरण का अनुमान लगाकर किया जाता है। एक फिल्टर का नाम रुडोल्फ ई.कलमन के नाम पर रखा गया है, जो इसके सिद्धांत के प्राथमिक विकासकर्ताओं में से एक थे।
इस अंकीय फिल्टर को कभी-कभी स्ट्रैटोनोविच-कालमान-बुकी फिल्टर कहा जाता है क्योंकि यह सोवियत गणितज्ञ रुस्लान स्ट्रैटोनोविच द्वारा कुछ पूर्व में विकसित किए गए अधिक सामान्य, अरैखिक फिल्टर की एक विशेष स्थिति है।[1][2][3][4] वास्तव में, कुछ विशेष स्थितिया रैखिक फिल्टर के समीकरण स्ट्रैटोनोविच के पत्रों में दिखाई दिए, जो 1960 की ग्रीष्म से पूर्व प्रकाशित हुए थे, जब कालमान मॉस्को में एक सम्मेलन के पर्यंत स्ट्रैटोनोविच से भेंट की थी।[5]
कालमान फिल्टर में कई प्रौद्योगिकीय अनुप्रयोग हैं। वाहनों, विशेष रूप से विमान, अंतरिक्ष यान और जहाजों के गतिशील स्थिति के मार्गदर्शन, नौ संचालन और नियंत्रण के लिए एक सामान्य अनुप्रयोग है। इसके अतिरिक्त, कालमान फिल्टर एक अवधारणा है जो संकेत संसाधन और अर्थमिति जैसे विषयों के लिए उपयोग की जाने वाली समय श्रृंखला विश्लेषण में बहुत अधिक अनुप्रयुक्त होती है। कालमान फिल्टर भी यंत्रमानववत् गति योजना और नियंत्रण के मुख्य विषयों में से एक है और इसका उपयोग प्रक्षेपवक्र अनुकूलन के लिए किया जा सकता है। कालमान फिल्टर केंद्रीय तंत्रिका तंत्र की गतिविधि के नियंत्रण के प्रतिरूप के लिए भी कार्य करता है। प्रेरक आदेश जारी करने और संवेदी प्रतिक्रिया प्राप्त करने के मध्य समय की देरी के कारण, कालमान फिल्टर का उपयोग प्रेरक प्रणाली की वर्तमान स्थिति का अनुमान लगाने और अद्यतन आदेश जारी करने के लिए एक यथार्थवादी प्रतिरूप प्रदान करता है।
कलन विधि दो-चरण प्रक्रिया द्वारा कार्य करते है। पूर्वाकलन चरण के लिए, कालमान फिल्टर वर्तमान स्थिति चरों के अनुमानों के साथ-साथ उनकी उनकी अनिश्चितताओं का अनुमान लगाता है। एक बार जब आगामी माप के परिणाम (अनिवार्य रूप से कुछ त्रुटि के साथ दूषित, यादृच्छिक रव सहित) देखे जाने के पश्चात, तो इन अनुमानों में भारित औसतों का उपयोग करके अद्यतन किया जाता है, और अधिक निश्चितता के साथ अनुमानों को अधिक महत्व दिया जाता है। कलन विधि पुनरावर्ती होती है। यह वास्तविक समय नियंत्रण प्रणाली में कार्य कर सकती है, केवल वर्तमान इनपुट माप और पूर्व की गणना की स्थिति और इसकी अनिश्चितता आव्यूह का उपयोग करके; कोई अतिरिक्त पूर्व सूचना की आवश्यकता नहीं है।
कालमान फिल्टर की इष्टतमता मानती है कि त्रुटियों का सामान्य वितरण होता है। रुडोल्फ ई. कालमान के शब्दों में: संक्षेप में, यादृच्छिक प्रक्रियाओं के विषय में निम्नलिखित धारणाएँ बनाई गई हैं: भौतिक यादृच्छिक घटना को प्राथमिक यादृच्छिक स्रोतों के उत्तेजन गतिशील प्रणालियों के कारण माना जा सकता है। प्राथमिक स्रोतों को शून्य माध्य के साथ स्वतंत्र गॉसियन यादृच्छिक प्रक्रिया मानी जाती है; और गतिशील प्रणालियां रैखिक होंगी। हालांकि गॉसियनिटी की उपेक्षा किए बिना, यदि प्रक्रिया और माप सहप्रसरण ज्ञात हैं, तो कालमान फिल्टर न्यूनतम माध्य-वर्ग-त्रुटि के अर्थ में सर्वोत्तम संभव रैखिक अनुमानक है।
विधि के विस्तार और सामान्यीकरण भी विकसित किए गए हैं, जैसे कि विस्तारित कालमान फिल्टर और असंतुलित कालमान फिल्टर जो अरैखिक प्रणालियों पर कार्य करते हैं। आधार एक गुप्त मार्कोव प्रतिरूप है जैसे कि अव्यक्त चर की अवस्था समष्टि सतत है और सभी अव्यक्त और देखे गए चर में गॉसियन वितरण हैं। इसके अतिरिक्त, कालमान फिल्टर का बहु-संवेदक संगलन में सफलतापूर्वक उपयोग किया गया है, और वितरित या सर्वसम्मति कालमान फिल्टर विकसित करने के लिए संवेदक जालक्रम वितरित किए।
इतिहास
निस्यंदन विधि का नाम हंगरी के प्रवासी रूडोल्फ ई. कालमान के नाम पर रखा गया है, हालांकि थोरवाल्ड निकोलाई थिले [6][7] और पीटर स्वेर्लिंग ने पूर्व में भी इसी प्रकार की कलन विधि विकसित की गयी थी। जॉन्स हॉपकिन्स अनुप्रयुक्त भौतिकी प्रयोगशाला के रिचर्ड एस बुकी ने सिद्धांत में योगदान दिया, जिससे इसे कभी-कभी कालमान-बुकी निस्यंदन के रूप में भी जाना जाता है। स्टेनली एफ. श्मिट को सामान्यतः कालमान फिल्टर के प्रथम कार्यान्वयन को विकसित करने का श्रेय दिया जाता है। उन्होंने अनुभव किया कि फिल्टर को दो अलग-अलग भागो में विभाजित किया जा सकता है, एक भाग संवेदक आउटपुट के मध्य की समयावधि के लिए और दूसरा भाग मापन को सम्मिलित करने के लिए किया जा सकता है।[8] यह कालमान द्वारा नासा एम्स अनुसंधान केंद्र के अभ्यागमन के पर्यंत, श्मिट ने अपोलो प्रकल्प के लिए प्रक्षेपवक्र अनुमान की गैर-रैखिक समस्या के लिए कालमान के विचारों की प्रयोज्यता को देखा गया, जिसके परिणामस्वरूप अपोलो दिशाज्ञान परिकलक में इसका समावेश हुआ।
इस कालमान फिल्टर को सर्वप्रथम स्वेर्लिंग (1958), कालमान (1960) और कालमान और बुकी (1961) द्वारा प्रौद्योगिकी पत्रों में आंशिक रूप से वर्णित और विकसित किया गया था।
अपोलो परिकलक ने 2k चुम्बकीय कोर RAM और 36k तार रज्जु [...] का उपयोग किया। CPU को ICs [...] से बनाया गया था। घड़ी की गति 100 किलोहर्ट्ज़ [...] से कम थी। तथ्य यह है कि MIT के अभियन्ता इतने छोटे परिकलक में इतने अच्छे सॉफ्टवेयर (कलमैन निस्यंदक के सबसे पहले अनुप्रयोगों में से एक) को संविष्ट करने में सक्षम थे, वास्तव में उल्लेखनीय है।
— मैथ्यू रीड द्वारा जैक क्रेंशॉ के साथ साक्षात्कार, TRS-80.org (2009) [1]
अमेरिकी नौसेना के परमाणु प्राक्षेपिकीय प्रक्षेपणास्त्र पनडुब्बियों के दिशाज्ञान प्रणाली के कार्यान्वयन में और अमेरिकी नौसेना की टॉमहॉक प्रक्षेपणास्त्र और अमेरिकी वायु सेना की एजीएम-86 एएलसीएम प्रारंभ की गई जैसे क्रूज प्रक्षेपणास्त्र के मार्गदर्शन और दिशाज्ञान प्रणाली में कालमान फिल्टर महत्वपूर्ण हैं। उनका उपयोग पुन: प्रयोज्य प्रारंभ वाहनों के मार्गदर्शन, दिशाज्ञान प्रणाली और अंतरिक्ष यान के दृष्टिकोण नियंत्रण और दिशाज्ञान प्रणाली में भी किया जाता है, जो अंतर्राष्ट्रीय अंतरिक्ष केन्द्रो पर डॉक करते हैं।[9]
गणना का अवलोकन
कालमान फिल्टर प्रणाली के गतिशील प्रतिरूप (जैसे, गति के भौतिक नियम), उस प्रणाली के लिए ज्ञात नियंत्रण इनपुट और प्रणाली की अलग-अलग मात्राओं (इसकी स्थिति) का अनुमान लगाने के लिए कई अनुक्रमिक माप (जैसे संवेदक से) का उपयोग करता है। जैसे, यह एक सामान्य संवेदक संयोजन और डेटा संयोजन कलन विधि है।
रव संवेदक डेटा, समीकरणों में सन्निकटन जो प्रणाली के विकास का वर्णन करते हैं, और बाहरी कारक जिनका कोई दोषी नहीं हैं, और सभी पर्याप्त करते हैं कि प्रणाली की स्थिति को कितनी अच्छी तरह से निर्धारित करना संभव है। कालमान फिल्टर रव संवेदक डेटा के कारण अनिश्चितता और कुछ सीमा तक यादृच्छिक बाहरी कारकों से प्रभावकारी रूप से व्यवहार करता है। कालमान फिल्टर प्रणाली की अनुमानित स्थिति के औसत और भारित औसत का उपयोग करके एक नए मापन के रूप में प्रणाली की स्थिति का अनुमान लगाता है। भार का उद्देश्य यह है कि उत्तम (अर्थात्, छोटे) अनुमानित अनिश्चितता वाले मान अधिक विश्वसनीय है। भार की गणना सहप्रसरण द्वारा की जाती है, जो प्रणाली की स्थिति के पूर्वानुमान की अनुमानित अनिश्चितता का एक उपाय है। भारित औसत का परिणाम एक नयी अवस्था अनुमान है, जो अनुमानित और मापित स्थिति के मध्य स्थित है, और असंग की तुलना में उन्नत अनुमानित अनिश्चितता है। इस प्रक्रिया को प्रत्येक टाइमस्टेप पर दोहराया जाता है, और एक नए अनुमान और इसके सहप्रसरण के साथ निम्नलिखित पुनरावृत्ति में उपयोग की जाने वाली पूर्वानुमान को सूचित करते हैं। इसका अर्थ यह है कि कालमान फिल्टर पुनरावर्ती फिल्टर के रूप में कार्य करता है और एक नयी अवस्था की गणना करने के लिए प्रणाली की स्थिति के सम्पूर्ण इतिहास के स्थान पर केवल अंतिम "सर्वोत्तम अनुमान" की आवश्यकता होती है।
मापन की 'निश्चितता-स्तरीकरण और वर्तमान स्थिति पर अनुमान एक महत्वपूर्ण विचार हैं। कालमान फिल्टर के लब्धि के संदर्भ में फिल्टर की प्रतिक्रिया पर आलोचना करना एक सामान्य तथ्य है। कालमान-लब्धि मापन और वर्तमान-अवस्था अनुमान को दिया गया भार है, और इसे किसी विशेष प्रदर्शन को प्राप्त करने के लिए समायोजित किया जा सकता है। एक उच्च लब्धि के साथ, फिल्टर सबसे हाल के मापों पर अधिक भार डालता है, और इस प्रकार उनके लिए अधिक प्रतिक्रियात्मक रूप से अनुरूप होता है।
फिल्टर के लिए वास्तविक गणना करते समय (जैसे नीचे चर्चा की गई है) गणना के एक समुच्चय में सम्मिलित कई आयामों के कारण अवस्था अनुमान और सहप्रसरणों को आव्यूह में कूटलेखित किया जाता है। यह किसी भी पारगमन प्रतिरूप या सहप्रसरण में विभिन्न अवस्था चर (जैसे स्थिति, वेग और त्वरण) के मध्य रैखिक संबंधों के प्रतिनिधित्व के लिए अनुमति देता है।
उदाहरण आवेदन
एक उदाहरण के रूप में, एक माल गाड़ी के सटीक स्थान को निर्धारित करने की समस्या पर विचार करें। माल गाड़ी एक जीपीएस ईकाई से सुसज्जित किया जा सकता है, जो कुछ मीटर के भीतर स्थिति का अनुमान प्रदान करता है। जीपीएस अनुमान रव होने की संभावना है; पाठ्यांक तीव्रता से 'विषयांतर' करते हैं, हालांकि वास्तविक स्थिति के कुछ मीटर के भीतर रहते हैं। इसके अतिरिक्त, चूंकि माल गाड़ी से भौतिकी के नियमों का पालन करने की अपेक्षा की जाती है, इसलिए समय के साथ इसके वेग को एकीकृत करके इसकी स्थिति का अनुमान लगाया जा सकता है, जो चक्र क्रांतियों और चालन चक्र के कोण को पथानुसरण करके निर्धारित किया जाता है। यह एक ऐसी प्रविधि है जिसे मृत गणना के रूप में जाना जाता है। सामान्यतः, मृत गणना माल गाड़ी की स्थिति का एक बहुत ही सहज अनुमान प्रदान करती है, परन्तु जैसे-जैसे छोटी-छोटी त्रुटियां एकत्र होती जाएंगी, और यह समय के साथ प्रवाहित होती जाएंगी।
इस उदाहरण के लिए, कालमान फिल्टर को दो अलग-अलग चरणों में कार्य करने के विषय में विचार किया जा सकता है: उदाहरण के लिए, पूर्वानुमान और नवीनीकरण। पूर्वानुमान के चरण में, माल गाड़ी की पूर्वतन स्थिति को भौतिक न्यूटन के गति के नियमों (गतिशील या अवस्था पारगमन प्रतिरूप) के अनुसार संशोधित किया जाएगा। न केवल एक नई स्थिति अनुमान की गणना की जाएगी, बल्कि एक नए सहप्रसरण की भी गणना की जाएगी। सम्भवतः सहप्रसरण माल गाड़ी की गति के समानुपाती होता है क्योंकि हम उच्च गति पर मृत गणना स्थिति अनुमान की सटीकता के विषय में अधिक अनिश्चित होते हैं, परन्तु कम गति पर स्थिति अनुमान के विषय में बहुत निश्चित होते हैं। आगामी, अद्यतन चरण में, जीपीएस ईकाई से माल गाड़ी की स्थिति का मापन लिया जा सकता है। इस मापन के साथ कुछ मात्रा में अनिश्चितता आती है, और पूर्व चरण के पूर्वानुमान के सापेक्ष इसका सहप्रसरण यह निर्धारित करता है कि एक नया मापन अद्यतन पूर्वानुमान को कितना प्रभावित करेगा। आदर्श रूप से, चूंकि मृत गणना अनुमान वास्तविक स्थिति से दूर हो जाते हैं, जीपीएस मापन के स्थिति अनुमान को वास्तविक स्थिति की ओर वापस खींचना चाहिए।
प्रौद्योगिकीय विवरण और संदर्भ
कालमान फिल्टर एक कुशल पुनरावर्ती फिल्टर अनुमानक है जो रव माप की एक श्रृंखला से एक रैखिक गतिशील प्रणाली की आंतरिक स्थिति का आकलन करता है। इसका उपयोग रेडार और परिकलक दृष्टि से संरचनात्मक वृहत् अर्थशास्त्र प्रतिरूप के आकलन के लिए अभियांत्रिकी और अर्थमितीय अनुप्रयोगों की एक विस्तृत श्रृंखला में किया जाता है,[10][11] और नियंत्रण सिद्धांत औरनियंत्रण प्रणाली अभियान्त्रिकी में एक महत्वपूर्ण विषय है। रैखिक-द्विघात नियामक (LQR) के साथ, कालमान फिल्टर रैखिक-द्विघात-गॉसियन नियंत्रण समस्या (LQG) को हल करता है। कालमान फिल्टर, रैखिक-द्विघात नियामक, और रैखिक-द्विघात-गॉसियन नियंत्रक नियंत्रण सिद्धांत की सबसे मौलिक समस्याओं के समाधान हैं।
अधिकांश अनुप्रयोगों में, मापे जाने वाले कुछ "अवलोकनीय" मापदंडों की तुलना में आंतरिक स्थिति बहुत बड़ी होती है (इसमें स्वतंत्रता की डिग्री अधिक होती है)। हालांकि, माप की एक श्रृंखला के संयोजन से, कालमान फिल्टर संपूर्ण आंतरिक स्थिति का अनुमान लगाया जा सकता है।
डेम्पस्टर-शेफ़र सिद्धांत के लिए, प्रत्येक अवस्था समीकरण या अवलोकन को एक रैखिक धारणाफलन की एक विशेष स्थिति मानी जाती है और कालमान फिल्टर एक जॉइन-ट्री या मार्कोव ट्री पर रैखिक धारणाफलनो के संयोजन की एक विशेष स्थिति है। अतिरिक्त विधियों में धारणा निस्यंदन सम्मिलित है जो अवस्था समीकरणों के लिए बेयस या साक्ष्य अद्यतन का उपयोग करती है।
कालमान फिल्टर की एक विस्तृत विविधता अब तक उपस्थित है, जिसे कालमान के मूल सूत्रीकरण से - अब "साधारण" कालमान फिल्टर, कालमान-बुकी फिल्टर, श्मिट का "विस्तारित" फिल्टर, सूचना फिल्टर, और वर्ग-रूट फिल्टर की एक विविधता कहा जाता है। जिसे बर्मन, थॉर्नटन, और कई अन्य लोगों द्वारा विकसित किया गया था। सम्भवतः सबसे अधिक उपयोग किया जाने वाला सबसे सरल कालमान फिल्टर कला पाशित लूप है, जो अब रेडियो में सर्वव्यापी है, विशेष रूप से आवृत्ति प्रतिरुपण (FM) रेडियो, टेलीविजन समुच्चय,उपग्रह संचार प्राप्तकर्ता, बाह्य अंतरिक्ष संचार प्रणाली, और लगभग किसी भी अन्य विद्युत् संचार उपकरण आदि।
अंतर्निहित गतिशील प्रणाली प्रतिरूप
कालमान फिल्टर समय प्रभावक्षेत्र में अलग-अलग रैखिक गतिशील प्रणालियों पर आधारित है।वे त्रुटियों से क्षुब्ध रैखिक संचालको पर निर्मित मार्कोव श्रृंखला पर आधारित हैं, जिनमें गॉसियन रव सम्मिलित हो सकता है। लक्ष्य प्रणाली की स्थिति महत्व की आधार सत्यता (अभी तक अप्रत्यक्ष है) प्रणाली विन्यास को संदर्भित करती है, जिसे वास्तविक संख्याओं के सदिश के रूप में दर्शाया जाता है। प्रत्येक असतत समय वृद्धि पर, नए अवस्था को उत्पन्न करने के लिए एक रैखिक संचालको को अवस्था में अनुप्रयुक्त किया जाता है, जिसमें कुछ रव मिश्रित होते है, और वैकल्पिक रूप से प्रणाली पर नियंत्रण से कुछ सूचना ज्ञात होने पर पुनः अधिक रव के साथ मिश्रित एक और रैखिक संचालक वास्तविक (अप्रत्यक्ष) स्थिति से मापने योग्य आउटपुट (अर्थात्, अवलोकन) उत्पन्न करता है। कालमान फिल्टर को अप्रत्यक्ष मार्कोव प्रतिरूप के अनुरूप माना जा सकता है, इस अंतर के साथ कि अप्रत्यक्ष मार्कोव प्रतिरूप के लिए असतत अवस्था स्थान के विपरीत अप्रत्यक्ष अवस्था चर के मान निरंतर स्थान में होते हैं। कालमान फिल्टर के समीकरणों और अप्रत्यक्ष मार्कोव प्रतिरूप के समीकरणों के मध्य एक प्रबल सादृश्य है। इस और अन्य प्रतिरूपों की समीक्षा रोविस और ज़ब्न जहरमान (1999) और हैमिल्टन (1994), अध्याय 13 में दी गई है।[12] [13]
एक प्रक्रिया की आंतरिक स्थिति का अनुमान लगाने के लिए कालमान फिल्टर का उपयोग करने के लिए केवल रव अवलोकनों का अनुक्रम दिया जाता है, निम्नलिखित को रूपरेखा के अनुसार प्रक्रिया को प्रतिरूप करना चाहिए। इसका अर्थ है कि प्रत्येक समय-चरण k के लिए आव्यूह निर्दिष्ट करना, निम्नलिखित:F, अवस्था-पारगमन प्रतिरूप;
- Hk, अवलोकन प्रतिरूप;
- Qk, प्रक्रिया रव का सहप्रसरण;
- Rk, प्रेक्षण रव का सहप्रसरण;
- और कभी -कभी Bk, नियंत्रण-इनपुट प्रतिरूप जैसा कि नीचे वर्णित है; यदि Bk सम्मिलित है, तो भी है
- uk, नियंत्रण सदिश, नियंत्रित इनपुट को नियंत्रण-इनपुट प्रतिरूप में दर्शाता है।

कालमान फिल्टर प्रतिरूप समय पर वास्तविक स्थिति को मानता है, जब k अवस्था से (k − 1) के अनुसार विकसित होता है;
जहां
- Fk अवस्था पारगमन प्रतिरूप है, जो पूर्व अवस्था xk−1 पर अनुप्रयुक्त होता है;
- Bk नियंत्रण-इनपुट प्रतिरूप है, जो नियंत्रण सदिश uk पर अनुप्रयुक्त होता है;
- wk प्रक्रिया रव है, जिसे शून्य माध्य बहुभिन्नरूपी सामान्य वितरण से आसंजित किया जाता है, सहप्रसरण आव्यूह के साथ, Qk: .
समय k पर वास्तविक स्थिति xk का एक अवलोकन (या माप) zk के अनुसार किया जाता है
जहां
- Hk अवलोकन प्रतिरूप है, जो वास्तविक स्थिति स्थान को प्रेक्षित स्थान में मानचित्र करता है और
- vk अवलोकन रव है, जिसे सहप्रसरण Rk के साथ शून्य औसत गॉसियन श्वेत रव माना जाता है: .
प्रारंभिक अवस्था, और प्रत्येक चरण {x0, w1, ..., wk, v1, ... ,vk} पर रव सदिश सभी पारस्परिक रूप से स्वतंत्र माने जाते हैं।
कई वास्तविक समय सक्रिय प्रणाली इस प्रतिरूप के पूर्णतया अनुरूप नहीं हैं। वास्तव में, अप्रतिरूपित गतिशीलता फिल्टर के प्रदर्शन को गंभीरता से कम कर सकता है, तब भी जब इसे इनपुट के रूप में अज्ञात प्रसंभाव्य संकेतों के साथ कार्य करना चाहिए था। इसका कारण यह है कि अप्रतिरूपित गतिशीलता का प्रभाव इनपुट पर निर्भर करता है, और इसलिए, अनुमान कलन विधि को अस्थिरता में ला सकता है (यह विचलन करता है)। दूसरी ओर, स्वतंत्र श्वेत रव संकेत कलन विधि को विचलन नहीं करेंगे। मापन रव और अनप्रतिरूप गतिकी के मध्य अंतर करने की समस्या कठिन है और इसे सुदृढ़ नियंत्रण का उपयोग करके नियंत्रण सिद्धांत की समस्या के रूप में माना जाता है।[14][15]
विवरण
कालमान फिल्टर एक पुनरावर्ती अनुमानक है। इसका अर्थ यह है कि वर्तमान स्थिति के अनुमान की गणना करने के लिए पूर्व समय के चरण और वर्तमान माप से केवल अनुमानित स्थिति की आवश्यकता है। प्रचय अनुमान प्रविधियों के विपरीत, अवलोकनों और/या अनुमानों के इतिहास की आवश्यकता नहीं है। निम्नलिखित में, अंकन के अनुमान का प्रतिनिधित्व करता है, समय पर n दिए गए अवलोकनों को समय m ≤ n तक सम्मिलित किया गया हैं
फिल्टर की स्थिति को दो चर द्वारा दर्शाया जाता है:
- , एक पश्चवर्ती अवस्था का अनुमान समय k पर दिया गया अवलोकन है, जिसमें समय k सम्मिलित है;
- , एक पश्चवर्ती सहप्रसरण आव्यूह (अवस्था अनुमान की अनुमानित सटीकता का एक माप)।
कालमान फिल्टर की कलन विधि संरचना अल्फा बीटा फिल्टर के समान होती है। कालमान फिल्टर को एकल समीकरण के रूप में लिखा जा सकता है; हालांकि, इसे प्रायः दो अलग-अलग चरणों के रूप में परिकल्पित किया जाता है: पूर्वानुमान और अद्यतन। पूर्वानुमान चरण वर्तमान टाइमस्टेप पर अवस्था का अनुमान लगाने के लिए पूर्व समय के अवस्था अनुमान का उपयोग करता है। इस पूर्वानुमानित अवस्था के अनुमान को प्राथमिक अवस्था के अनुमान के रूप में भी जाना जाता है क्योंकि, हालांकि यह वर्तमान समय पर अवस्था का अनुमान है, इसमें वर्तमान समय-चरण से अवलोकन की सूचना सम्मिलित नहीं है। अद्यतन चरण में, नवाचार (पूर्व-सटीक अवशिष्ट), अर्थात् वर्तमान एक प्राथमिक पूर्वानुमान और वर्तमान अवलोकन सूचना के मध्य का अंतर, इष्टतम कालमान लब्धि से गुणा किया जाता है और अवस्था अनुमान को परिष्कृत करने के लिए पूर्व अवस्था अनुमान के साथ जोड़ा जाता है। वर्तमान अवलोकन के आधार पर इस उन्नत अनुमान को पश्चवर्ती अवस्था अनुमान कहा जाता है।
सामान्यतः, दो चरण वैकल्पिक होते हैं, पूर्वानुमान अगले अनुसूचित अवलोकन तक अवस्था को आगे बढ़ाते है, और अद्यतन अवलोकन को सम्मिलित करते है। हालाँकि, यह आवश्यक नहीं है; यदि किसी कारण से कोई अवलोकन अनुपलब्ध है, तो अद्यतन को छोड़ दिया जा सकता है और कई पूर्वानुमान प्रक्रियाओं का प्रदर्शन किया जा सकता है। इसी प्रकार, यदि एक ही समय में कई स्वतंत्र अवलोकन उपलब्ध हैं, तो कई अद्यतन प्रक्रियाएं (सामान्यतः विभिन्न अवलोकन आव्यूह Hk के साथ) की जा सकती हैं।[16][17]
पूर्वानुमान
| अनुमानित (प्राथमिकता) अवस्था का अनुमान | |
| अनुमानित (प्राथमिकता) सहप्रसरण का अनुमान |
नवीनीकरण
| नवाचार या माप पूर्व-फिट अवशिष्ट | |
| नवोन्मेष (या पूर्व-फिट अवशिष्ट) सहप्रसरण | |
| इष्टतम कालमान लब्धि | |
| अद्यतित (एक उत्तरवर्ती) अवस्था का अनुमान | |
| अद्यतनीकृत (एक पश्चवर्ती) सहप्रसरण का अनुमान | |
| मापन पोस्ट-फिट अवशिष्ट |
उपरोक्त अद्यतन (एक पश्चवर्ती) अनुमान सहप्रसरण के लिए सूत्र इष्टतम Kk लब्धि के लिए मान्य है, जो अवशिष्ट त्रुटि को कम करता है, जिस रूप में यह अनुप्रयोगों में सबसे व्यापक रूप से उपयोग किया जाता है। सूत्रों का प्रमाण व्युत्पत्ति अनुभाग में मिलता है, जहाँ किसी Kk के लिए मान्य सूत्र भी दर्शाया गया है।
अद्यतन अवस्था अनुमान को व्यक्त करने का एक अधिक सहज प्रणाली () है:
यह अभिव्यक्ति हमें एक रैखिक प्रक्षेप का स्मरण कराती है, के लिये [0,1] के मध्य हमारी स्थितियो में:
- कालमान लब्धि () है, एक आव्यूह जो (संवेदक में उच्च त्रुटि) से (कम त्रुटि) मान लेता है ।
- प्रतिरूप से अनुमानित मान है।
- माप से मान है।
यह व्यंजक अल्फ़ा बीटा फिल्टर अद्यतन चरण के समान भी है।
अपरिवर्तनीय
यदि प्रतिरूप सटीक है, और तथा के लिए मान प्रारंभिक अवस्था मानो के वितरण को सटीक रूप से दर्शाता है, तोनिम्नलिखित अपरिवर्तनीय संरक्षित हैं:
जहां का अपेक्षित मान है, अर्थात् सभी अनुमानों में शून्य की औसत त्रुटि होती है।
और:
इसलिए सहप्रसरण आव्यूह अनुमानों के सहप्रसरण को सटीक रूप से दर्शाते हैं।
रव सहप्रसरण Qk और Rk का अनुमान
रव सहप्रसरण आव्यूह Qk और आरk का एक उत्तम अनुमान प्राप्त करने में कठिनाई के कारण कालमान फिल्टर का व्यावहारिक कार्यान्वयन प्रायः कठिन होता है। डेटा से इन सहप्रसरणों का अनुमान लगाने के लिए व्यापक अन्वेषण किया गया है। ऐसा करने की एक व्यावहारिक प्रणाली स्वसहप्रसरण न्यूनतम वर्ग (ALS) प्रविधि है, जो सहप्रसरण का अनुमान लगाने के लिए नियमित संचालन डेटा के समय-अंतराल स्वसहप्रसरण का उपयोग करता है।[18][19] जीएनयू अष्टक और मैटलैब कोड और एएलएस प्रविधि का उपयोग करके रव सहप्रसरण आव्यूह की गणना करने के लिए किया जाता है, जो जीएनयू सामान्य जनता अनुज्ञप्ति का उपयोग करके लाइनेतर उपलब्ध है।[20] क्षेत्र कालमान फिल्टर (FKF), एक बायेसियन कलन विधि, जो अवस्था, मापदंडों और रव सहप्रसरण के एक साथ आकलन की अनुमति देता है।[21] एफकेएफ कलन विधियों में एक पुनरावर्ती सूत्रीकरण, उत्तम प्रेक्षित अभिसरण और अपेक्षाकृत कम जटिलता है। इस प्रकार यह संसूचन देता है कि एफकेएफ कलन विधि संभवतः स्वसहप्रसरण न्यूनतम वर्ग विधियों का एक सार्थक विकल्प हो सकता है।
इष्टतमता और प्रदर्शन
यह सिद्धांत से निम्नानुसार है कि कालमान फिल्टर उन स्थितियो में इष्टतम रैखिक फिल्टर है जहां ए) प्रतिरूप वास्तविक प्रणाली से पूरी तरह मेल खाता है, बी) प्रवेश रव सफेद (असंबद्ध) है और सी) रव के सहसंयोजक पूर्णतया ज्ञात हैं। कालमान फिल्टर का उपयोग करके सहसंबद्ध रव का भी इलाज किया जा सकता है।[22] पूर्व दशकों के पर्यंत रव सहसंयोजक अनुमान के लिए कई प्रणाली प्रस्तावित की गयी हैं, जिनमें एएलएस भी सम्मिलित है, जिसका उल्लेख ऊपर के खंड में किया गया है। सहप्रसरणों का अनुमान लगाने के बाद, फिल्टर के प्रदर्शन का मूल्यांकन करना उपयोगी होता है; अर्थात् क्या अवस्था के आकलन की गुणवत्ता में सुधार संभव है। यदि कालमान फिल्टर उन्नत विधि से कार्य करता है, तो इनोवेशन सीक्वेंस (आउटपुट प्रेडिक्शन एरर) एक सफेद रव है, इसलिए इनोवेशन (सिग्नल प्रोसेसिंग) की व्हाइटनेस प्रॉपर्टी फिल्टर के प्रदर्शन को मापती है। इस उद्देश्य के लिए कई अलग-अलग प्रणालियो का उपयोग किया जा सकता है।[23] यदि रव की शर्तों को गैर-गॉसियन विधि से वितरित किया जाता है, तो फिल्टर अनुमान के प्रदर्शन का आकलन करने के विधि, जो संभाव्यता असमानताओं या बड़े-प्रतिरूप सिद्धांत का उपयोग करते हैं, साहित्य में जाने जाते हैं।[24][25]
उदाहरण आवेदन, प्रौद्योगिकीय
घर्षण रहित, पटरियों पर चलने वाले एक माल गाड़ी पर विचार करें। प्रारंभ में, माल गाड़ी की स्थिति 0 में स्थिर होती है, परन्तु यह यादृच्छिक अनियंत्रित बलों द्वारा इस प्रकार और उस प्रकार से टकराया जाता है। हम प्रत्येक Δt सेकंड में माल गाड़ी की स्थिति को मापते हैं, परन्तु ये माप सटीक नहीं होते हैं; हम माल गाड़ी की स्थिति और वेग का एक प्रतिरूप बनाए रखना चाहते हैं। हम यहां दर्शाते हैं कि हम उस प्रतिरूप को कैसे प्राप्त करते हैं, जिससे हम अपना कालमान फिल्टर निर्मित करते हैं।
तब से स्थिर हैं, और उनका समय सूचकांक अवनत कर दिया जाता है।
माल गाड़ी की स्थिति और वेग कोरै खिक अवस्था समष्टि द्वारा वर्णित किया जाता है;
जहां वेग है, जो समय के संबंध में स्थिति का व्युत्पन्न है।
हम मानते हैं कि (k − 1) और k टाइमस्टेप के मध्य अनियंत्रित बल ak के सतत त्वरण का कारण बनते हैं, सामान्य रूप से माध्य 0 और मानक विचलन σa के साथ वितरित किया जाता है। न्यूटन के गति के नियमों से हम यह निष्कर्ष निकालते हैं कि
( पद का क्योंकि कोई ज्ञात नियंत्रण इनपुट नहीं हैं। इसके स्थान पर, ak एक अज्ञात इनपुट का प्रभाव है और जहां उस प्रभाव को अवस्था सदिश पर अनुप्रयुक्त करता है)
ताकि
जहां
एक आव्यूह पूर्ण श्रेणी नहीं है (यह श्रेणी एक का है यदि) वितरण पूर्णतया सतत नहीं है और इसमें कोई संभाव्यता घनत्व फलन नहीं है। इसे व्यक्त करने की एक अन्य प्रणाली, स्पष्ट पतित वितरणों से परिहरण करना है;
प्रत्येक टाइमस्टेप में, माल गाड़ी की वास्तविक स्थिति का रव माप किया जाता है, मान लें कि माप रव vk माध्य 0 और मानक विचलन σzके साथ सामान्य रूप से भी वितरित किया जाता है;
जहां
और
हम माल गाड़ी की प्रारंभिक स्थिति को पूर्ण सटीकता के साथ स्पष्ट करते हैं, इसलिए हम प्रारंभ करते हैं
और फिल्टर को यह सूचित के लिए कि हम सटीक स्थिति और वेग से परिचित हैं, हम इसे एक शून्य सहप्रसरण आव्यूह प्रदान करते हैं:
यदि प्रारंभिक स्थिति और वेग पूर्णतया ज्ञात नहीं हैं, तो सहप्रसरण आव्यूह को इसके विकर्ण पर उपयुक्त भिन्नताओं के साथ प्रारंभ किया जाना चाहिए:
फिल्टर तब प्रतिरूप में पूर्व से ही उपस्थित सूचना पर प्रथम माप से सूचना को प्राथमिकता देता है।
स्पर्शोन्मुख रूप
सहजता के लिए, मान लें कि नियंत्रण इनपुट है, तब कालमान फिल्टर को लिखा जा सकता है:
यदि हम एक गैर-शून्य नियंत्रण इनपुट सम्मिलित करते हैं तो एक समान समीकरण प्राप्त होता है। लब्धि आव्यूह मापन से स्वतंत्र रूप से विकसित होते हैं। ऊपर से, कालमान लब्धि को अद्यतन करने के लिए आवश्यक चार समीकरण इस प्रकार हैं:
चूंकि लब्धि आव्यूह केवल प्रतिरूप पर निर्भर करते हैं, न कि माप पर, उनकी गणना ऑफ़लाइन की जा सकती है। लब्धि आव्यूह का अभिसरण एक स्पर्शोन्मुख आव्यूह के लिए वालरैंड और डिमाकिस में स्थापित स्थितियों के लिए अनुप्रयुक्त होता है।[26] अनुरूपण अभिसरण के चरणों की संख्या स्थापित करते हैं। ऊपर वर्णित चलती माल गाड़ी के उदाहरण के लिए . और , अनुरूपण में अभिसरण पुनरावृत्तियों को दर्शाता है;
स्पर्शोन्मुख लब्धि का उपयोग करना, और मान लिया जाये तथा से स्वतंत्र हैं, और कालमान फिल्टर एक रेखीय समय-अपरिवर्तनीय फिल्टर बन जाता है:
स्पर्शोन्मुख लब्धि , यदि यह उपस्थित है, तो उपगामी अवस्था सहप्रसरण के लिए निम्नलिखित असतत रिकाटी समीकरण को हल करके गणना की जा सकती है:[26]
स्पर्शोन्मुख लब्धि की गणना पूर्व की भाति की की जा सकती है।
व्युत्पत्ति
कालमान फिल्टर को गत डेटा पर संचालित सामान्यीकृत न्यूनतम वर्ग विधि के रूप में प्राप्त किया जा सकता है।[27]
पश्चवर्ती अनुमान सहप्रसरण आव्यूह प्राप्त करना
त्रुटि सहप्रसरण Pk | k पर हमारे अपरिवर्तनीय से प्रारंभ करना, उपरोक्तानुसार
की परिभाषा में स्थानापन्न
और स्थानापन्न
तथा
और त्रुटि सदिश को एकत्र करके हम प्राप्त करते हैं
चूंकि माप त्रुटि vk अन्य स्थितियों के साथ असंबंधित है, और यह निर्मित करता है
सहप्रसरण आव्यूह के गुणों से यह निर्मित करता है
जो, Pk | k−1 पर हमारे अपरिवर्तनीय का उपयोग करते हुए और Rk की परिभाषा का निर्माण हो जाता है
यह सूत्र (कभी-कभी सहप्रसरण अद्यतन समीकरण के जोसफ रूप के रूप में भी प्रचारित है), Kk के किसी भी मान के लिए मान्य है। इससे यह ज्ञात होता है कि यदि Kk इष्टतम कालमान लब्धि है, इसे और सरल बनाया जा सकता है जैसा कि नीचे दर्शाया गया है।
कालमान लब्धि व्युत्पत्ति
कालमान फिल्टर एकन्यूनतम माध्य-वर्ग त्रुटि अनुमानक है। पश्चवर्ती अवस्था के अनुमान में त्रुटि है;
हम इस सदिश के परिमाण के वर्ग के अपेक्षित मान को कम करना चाहते हैं। यह पश्चगामी अनुमान सहप्रसरण आव्यूह के अनुरेख को कम करने के समान है। उपरोक्त समीकरण में शर्तों का विस्तार करके और एकत्रित करके, हम प्राप्त करते हैं:
अनुरेख को कम किया जाता है जब लब्धि आव्यूह के संबंध में इसका आव्यूह व्युत्पन्न शून्य होता है। अनुप्रवण आव्यूह नियमों और सम्मिलित आव्यूह की समरूपता का उपयोग करके हम प्राप्त करते हैं कि
Kk के लिए इसे हल करने से कालमान लब्धि प्राप्त होती है:
यह लब्धि, जिसे इष्टतम कालमान लब्धि के रूप में जाना जाता है, वह है जो उपयोग किए जाने पर न्यूनतम माध्य वर्ग त्रुटि अनुमान प्रदान करता है।
पश्चवर्ती त्रुटि सहप्रसरण सूत्र का सरलीकरण
पश्चवर्ती त्रुटि सहप्रसरण की गणना के लिए उपयोग किए जाने वाले सूत्र को सरल बनाया जा सकता है, जब कालमान लब्धि ऊपर प्राप्त इष्टतम मान के समान होती है। हमारे कालमान लब्धि सूत्र के दोनों पक्षों को SkKkT दाईं ओर गुणा करने पर, यह इस प्रकार है;
पश्चवर्ती त्रुटि सहप्रसरण के लिए हमारे विस्तारित सूत्र का संदर्भ देते हुए,
हम पाते हैं कि अंतिम दो शर्तें निरसित कर दी गई हैं
यह सूत्र अभिकलनीयतः रूप से अल्पमूल्य है और इस प्रकार लगभग सदैव व्यवहार में उपयोग किया जाता है, परन्तु यह केवल इष्टतम लब्धि के लिए सही है। यदि अंकगणितीय सटीकता असामान्य रूप से कम है, जिससे संख्यात्मक स्थिरता के साथ समस्याएं उत्पन्न होती हैं, या यदि एक गैर-इष्टतम कालमान लब्धि का विचारपूर्वक उपयोग किया जाता है, तो यह सरलीकरण अनुप्रयुक्त नहीं किया जा सकता है; उपरोक्त व्युत्पन्न (जोसेफ विधि) के रूप में एक पश्चवर्ती त्रुटि सहप्रसरण सूत्र का उपयोग किया जाना चाहिए।
सुग्राहिता विश्लेषण
कालमान फिल्टर समीकरण अवस्था और इसकी त्रुटि सहप्रसरण पुनरावर्ती रूप से अनुमान प्रदान करते हैं। अनुमान और इसकी गुणवत्ता प्रणाली मापदंडों और अनुमानक को इनपुट के रूप में सिंचित किये गए रव आंकड़ों पर निर्भर करती है। यह खंड फिल्टर के सांख्यिकीय इनपुट में अनिश्चितताओं के प्रभाव का विश्लेषण करता है।[28] विश्वसनीय आँकड़ों या रव सहप्रसरण आव्यूह तथा के सटीक मानो के अभाव में, अभिव्यक्ति
अब वास्तविक त्रुटि सहप्रसरण प्रदान नहीं करता है। दूसरे शब्दों में, .अधिकांश वास्तविक समय के अनुप्रयोगों में, कालमान फिल्टर को प्रारुप करने में उपयोग किए जाने वाले सहप्रसरण आव्यूह वास्तविक रव सहप्रसरण आव्यूह से भिन्न होते हैं।[citation needed] यह सुग्राहिता विश्लेषण आकलन त्रुटि सहप्रसरण के व्यवहार का वर्णन करता है, जब रव सहप्रसरण के रूप में साथ ही प्रणाली आव्यूह तथा जो फिल्टर में इनपुट के रूप में सिंचित किए गए है, जोकि गलत हैं। इस प्रकार, सुग्राहिता विश्लेषण अनुमानक को गलत निर्दिष्ट सांख्यिकीय और प्राचलिक इनपुट के लिए अनुमानक की पृष्टता (या सुग्राहिता) का वर्णन करते है।
यह आलोचना सांख्यिकीय अनिश्चितताओं के स्थितियो में त्रुटि सुग्राहिता विश्लेषण तक पर्याप्त है। यहाँ वास्तविक रव सहप्रसरणों को तथा क्रमशः द्वारा निरूपित किया जाता है, जबकि अनुमानक में प्रयुक्त प्रारुप मान तथा क्रमशः हैं। वास्तविक त्रुटि सहप्रसरण तथा द्वारा निरूपित किया जाता है, जैसा कि कालमान फिल्टर द्वारा गणना की जाती है, उसे रिकाटी चर कहा जाता है। तथा , इसका है कि . वास्तविक त्रुटि सहप्रसरण की गणना करते समय , के लिए प्रतिस्थापन और इस तथ्य का उपयोग करते हुए कि तथा , निम्नलिखित पुनरावर्ती समीकरणों के लिए परिणाम हैंː
और
गणना करते समय , प्रारुप द्वारा फिल्टर स्पष्ट रूप से मानता है कि तथा , तथा के लिए पुनरावर्ती अभिव्यक्ति की उपस्थिति तथा को छोड़कर समान हैं, प्रारुप मानो के स्थान पर तथा क्रमशः हैं। कालमान फिल्टर प्रणाली की पृष्टता का विश्लेषण करने के लिए शोध किए गए हैं।[29]
वर्गमूल रूप
कालमान फिल्टर के साथ एक समस्या इसकी संख्यात्मक स्थिरता है। यदि प्रक्रिया रव सहप्रसरण Qk छोटा होता है, तो पूर्णांक त्रुटि प्रायः अवस्था सहप्रसरण आव्यूह P एक छोटे धनात्मक आइगेन मान को ऋणात्मक संख्या के रूप में गणना करने का कारण बनती है। यह P अनिश्चित के संख्यात्मक प्रतिनिधित्व को प्रस्तुत करता है, जबकि इसका वास्तविक रूप धनात्मक निश्चित आव्यूह है।
धनात्मक निश्चित आव्यूहों में गुण होता है कि उनके पास एक त्रिकोणीय आव्यूह वर्गमूल P = S·ST होता है। चोल्स्की गुणनखंड कलन विधि का उपयोग करके इसकी कुशलता से गणना की जा सकती है, परन्तु इससे भी महत्वपूर्ण तथ्य यह है कि यदि सहप्रसरण को इस रूप में रखा जाता है, तो इसमें कभी भी ऋणात्मक विकर्ण या असममित नहीं हो सकता है। एक समान रूप, जो आव्यूह वर्गमूल द्वारा आवश्यक कई वर्गमूल संचालन से से बचता है, फिर भी वांछनीय संख्यात्मक गुणों को संरक्षित करता है, U-D अपघटन रूप है, P = U·D·UT जहां U एक इकाई त्रिकोणीय आव्यूह (इकाई विकर्ण के साथ) है,और D एक विकर्ण आव्यूह है।
दोनों के मध्य, U-D गुणनखंड समान मात्रा में भंडारण और कुछ स्थिति तक कम गणना का उपयोग करते है, और सबसे अधिक उपयोग किया जाने वाला वर्गमूल रूप है, (सापेक्ष दक्षता पर प्रारंभिक साहित्य कुछ स्थिति तक भ्रामक है, क्योंकि यह माना जाता है कि वर्गमूल विभाजनों की तुलना में अधिक समय लेने वाले थे,[30]: 69 जबकि 21वीं सदी के परिकलको पर वे केवल थोड़े अधिक बहुमूल्य होते हैं)।
जी जे बीरमैन और सी एल थॉर्नटन द्वारा कालमान पूर्वानुमान और वर्गमूल रूप में अद्यतन चरणों के लिए कुशल कलन विधि विकसित की गयी थी।[30][31]
नवप्रवर्तन सहप्रसरण आव्यूह Sk का L·D·LT अपघटन एक अन्य प्रकार के संख्यात्मक रूप से कुशल और सुदृढ़ वर्गमूल फिल्टर का आधार है।[32] कलन विधि LU अपघटन के साथ प्रारम्भ होता है जैसा कि रैखिक बीजगणित संवेष्टक ( LAPACK ) में अनुप्रयुक्त किया गया है। इन परिणामों को एक सममितीय व्युत्क्रमणीय आव्यूह के लिए गोलूब और वैन लोन (कलन विधि 4.1.2) द्वारा दी गयी प्रविधियों के साथ L·D·LT संरचना में आगे खंडित किया गया है। किसी भी एकल सहप्रसरण आव्यूह को कीलकित किया जाता है ताकि प्रथम विकर्ण विभाजन निरर्थक और अच्छी तरह से वातानुकूलित हो। कीलक एल्गोरिथम को नवप्रवर्तन सहप्रसरण आव्यूह के किसी भी भाग को सीधे देखे गए अवस्था-चर Hk·xk|k-1 से संबंधित होना चाहिए जो कि yk में सहायक अवलोकनों से जुड़े हुए हैं। l·d·lt वर्गमूल फिल्टर के लिए अवलोकन सदिश के लांबिकीकरण की आवश्यकता होती है। यह हिघम (2002, पृष्ठ 263) में विधि 2 का उपयोग करके सहायक चर के लिए सहप्रसरण आव्यूह के व्युत्क्रम वर्गमूल के साथ किया जा सकता है।
समानांतर रूप
कालमान फिल्टर केंद्रीय प्रसंस्करण इकाइयों (CPUs) पर अनुक्रमिक डेटा प्रसंस्करण के लिए कुशल है, परन्तु अपने मूल रूप में यह समानांतर वास्तुकी जैसे आलेखिकी प्रसंस्करण इकाइयाँ (GPUs) पर अक्षम है। हालांकि, सरक्का (2021) में सूत्रीकरण का उपयोग करके एक सहयोगी संचालक के संदर्भ में फिल्टर-नवीनीकरण नित्यक्रम को व्यक्त करना संभव है।[33] इसके पश्चात फिल्टर हल को पूर्वयोजन योग कलन विधि के उपयोग द्वारा पुनः प्राप्त किया जा सकता है, जिसे जीपीयू पर कुशलता से अनुप्रयुक्त किया जा सकता है।[34] यह अभिकलनात्मक जटिलता को टाइमस्टेपों की संख्या में कम करता है।
पुनरावर्ती बायेसियन अनुमानसे संबंध
कालमान फिल्टर को सबसे सरल गतिशील बायेसियन जालक्रम में से एक के रूप में प्रस्तुत किया जा सकता है। कालमान फिल्टर आने वाले माप और गणितीय प्रक्रिया प्रतिरूप का उपयोग करके समय के साथ-साथ अवस्थाओं के वास्तविक मानो के अनुमानों की गणना करता है। इसी प्रकार, पुनरावर्ती बायेसियन अनुमान आने वाले माप और एक गणितीय प्रक्रिया प्रतिरूप का उपयोग करके समय के साथ एक अज्ञात संभाव्यता घनत्व प्रकार्य (PDF) के घनत्व अनुमान की गणना करते है।[35]
पुनरावर्ती बायेसियन अनुमान में, वास्तविक स्थिति को एक अप्रतिबंधित मार्कोव प्रक्रिया माना जाता है, और माप एक अप्रत्यक्ष मार्कोव प्रतिरूप (HMM) की देखी गयी अवस्था हैं।
मार्कोव की धारणा के कारण, वास्तविक स्थिति पूर्व के सभी अवस्थाओं से सशर्त रूप से स्वतंत्र है, जिसे पूर्व अवस्था दी गई है।
इसी प्रकार, k-वें टाइमस्टेप पर माप केवल वर्तमान स्थिति पर निर्भर है और वर्तमान स्थिति को देखते हुए अन्य सभी अवस्थाओं से सशर्त रूप से स्वतंत्र है।
इन मान्यताओं का उपयोग करते हुए, अप्रत्यक्ष मार्कोव प्रतिरूप के सभी अवस्थाओं में संभाव्यता वितरण को इस प्रकार लिखा जा सकता है:
हालांकि, जब अवस्था x का अनुमान लगाने के लिए एक कालमान फिल्टर का उपयोग किया जाता है, तो हित की संभाव्यता वितरण वर्तमान वह होती है जो टाइमस्टेप तक माप पर वातानुकूलित वर्तमान अवस्थाओं से जुड़ी होती है। यह पूर्व अवस्थाओं को माप समुच्चय की संभाव्यता से विभाजित करके प्राप्त किया जाता है।
यह संभावित रूप से लिखे गए कालमान फिल्टर के पूर्वानुमान और अद्यतन चरणों का परिणाम है। पूर्वानुमानित स्थिति से संबद्ध प्रायिकता वितरण, (k − 1)-th टाइमस्टेप से k-th और पूर्व स्थिति से जुड़े संभाव्यता वितरण के पारगमन से जुड़े संभाव्यता वितरण के उत्पादों का योग (अभिन्न) है, संपूर्ण संभव से अधिक .
समय t तक निर्धारित माप है
अद्यतन का संभाव्यता वितरण माप की संभावना और अनुमानित स्थिति के उत्पाद के समानुपाती होता है।
भाजक
एक सामान्यीकरण पद है।
शेष संभाव्यता घनत्व कार्य हैं
पूर्व टाइमस्टेप पर पीडीएफ को अभिगृहीत रूप से अनुमानित स्थिति और सहप्रसरण माना जाता है। यह उचित है क्योंकि, इष्टतम अनुमानक के रूप में, कालमान फिल्टर मापों का सर्वोत्तम उपयोग करता है, इसलिए पीडीएफ के लिए माप दिया गया,और कालमान फिल्टर अनुमान है।
सीमांत संभाव्यता
ऊपर वर्णित पुनरावर्ती बायेसियन व्याख्या से संबंधित, कालमान फिल्टर को एक उत्पादक प्रतिरूप के रूप में देखा जा सकता है, अर्थात, यादृच्छिक अवलोकनों z = (z0, z1, z2, ...) का एक वर्ग उत्पन्न करने की प्रक्रिया है। विशेष रूप से, प्रक्रिया है
- एक अप्रत्यक्ष स्थिति का प्रतिरूप, गॉसियन के पूर्व वितरण से .
- एक अवलोकन का प्रतिरूप, अवलोकन प्रतिरूप से .
- के लिये, करना
- अगले अप्रत्यक्ष अवस्था का प्रतिरूप, पारगमन प्रतिरूप से
- एक अवलोकन का प्रतिरूप, अवलोकन प्रतिरूप से
इस प्रक्रिया में अप्रत्यक्ष मार्कोव प्रतिरूप के समान संरचना है, अतिरिक्त इसके कि असतत स्थिति और अवलोकनों को गॉसियन वितरण से प्रतिरूप सतत चर के साथ परिवर्तित कर दिया जाता है।
कुछ अनुप्रयोगों में, यह संभाव्यता की गणना करने के लिए उपयोगी है कि दिए गए मापदंडों (पूर्व वितरण, पारगमन और अवलोकन प्रतिरूप, और नियंत्रण इनपुट) के साथ एक कालमान फिल्टर एक विशेष प्रेक्षित संकेत उत्पन्न करता है। इस संभाव्यता को सीमांत संभाव्यता के रूप में जाना जाता है क्योंकि यह अप्रत्यक्ष अवस्था चर के मानो को एकीकृत करता है, इसलिए इसे केवल देखे गए संकेत का उपयोग करके गणना की जा सकती है। विभिन्न मापदण्ड विकल्पों का मूल्यांकन करने के लिए सीमांत संभाव्यता उपयोगी हो सकती है, या बायेसियन प्रतिरूप तुलना का उपयोग करके अन्य प्रतिरूपों के विरुद्ध कालमान फिल्टर की तुलना करने के लिए उपयोगी हो सकती है।
पुनरावर्ती निस्यंदन गणना के पार्श्व प्रभाव के रूप में सीमांत संभावना की गणना करना सरल है। श्रृंखला नियम द्वारा, पूर्व अवलोकनों में दिए गए प्रत्येक अवलोकन की संभावना के उत्पाद के रूप में संभावना को ध्यान में रखा जा सकता है,
- ,
और क्योंकि कालमान फिल्टर एक मार्कोव प्रक्रिया का वर्णन करता है, पूर्व अवलोकनों से सभी प्रासंगिक सूचना वर्तमान स्थिति अनुमान में निहित है। इस प्रकार सीमांत संभावना द्वारा दी गई है
अर्थात्, गॉसियन घनत्व का एक उत्पाद, प्रत्येक वर्तमान निस्यंदन वितरण के अंतर्गत एक अवलोकन zk के घनत्व के अनुरूप है। इसकी गणना सरल पुनरावर्ती अद्यतन के रूप में सरलता से की जा सकती है; हालांकि,अंकगणितीय अंतर्प्रवाह से परिवर्जन के लिए, व्यावहारिक कार्यान्वयन में सामान्यतः लॉग सीमांत संभावना की गणना करना वांछनीय होता है। अधिवेशन को अपनाना, यह पुनरावर्ती अद्यतन नियम के माध्यम से किया जा सकता है
जहां माप सदिश का आयाम है।[36]
एक महत्वपूर्ण अनुप्रयोग जहां अवलोकनों की ऐसी (log) संभावना (फिल्टर मापदंडों को देखते हुए) बहु-लक्ष्य अनुपथन का उपयोग किया जाता है। उदाहरण के लिए, एक वस्तु अनुपथन परिदृश्य पर विचार करें जहां अवलोकन का एक वर्ग इनपुट है, हालांकि, यह अज्ञात है कि दृश्य में कितनी वस्तुएं हैं (या, वस्तुओं की संख्या ज्ञात है परन्तु एक से अधिक है)। ऐसे परिदृश्य के लिए, यह अज्ञात हो सकता है कि कौन से अवलोकन/माप किस वस्तु द्वारा उत्पन्न किए गए थे। एक बहु अवधारणा अनुपथक (MHT) सामान्यतः अलग-अलग पथ समिति परिकल्पनाओं का निर्माण करेगी, जहां प्रत्येक परिकल्पना को परिकल्पित वस्तु से जुड़े मापदंडों के एक विशिष्ट समुच्चयों के साथ कालमान फिल्टर (रैखिक गॉसियन स्थितियो के लिए) के रूप में माना जा सकता है। इस प्रकार, विचाराधीन विभिन्न परिकल्पनाओं के लिए टिप्पणियों की संभावना की गणना करना महत्वपूर्ण है।
सूचना फिल्टर
सूचना फिल्टर, या व्युत्क्रम सहप्रसरण फिल्टर में, अनुमानित सहप्रसरण और अनुमानित स्थिति को क्रमशः सूचना आव्यूह और सूचना सदिश द्वारा प्रतिस्थापित किया जाता है। इन्हें इस प्रकार परिभाषित किया गया है:
इसी प्रकार अनुमानित सहप्रसरण और अवस्था के समान सूचना प्रपत्र हैं, जिन्हें इस प्रकार परिभाषित किया गया है:
जैसा कि माप सहप्रसरण और माप सदिश है, जिसे इस प्रकार परिभाषित किया गया है:
सूचना अद्यतन अब एक तुच्छ योग बन जाता है।[37]
सूचना फिल्टर की मुख्य लब्धि यह है कि एन मापों को प्रत्येक चरणों में सूचना आव्यूहों और सदिशों को जोड़कर फिल्टर किया जा सकता है।
सूचना फिल्टर का पूर्वानुमान करने के लिए सूचना आव्यूहों और सदिशों को उनके अवस्था समष्टि समतुल्यता में वापस परिवर्तित किया जा सकता है, या वैकल्पिक रूप से सूचना स्थान पूर्वानुमान का उपयोग किया जा सकता है।[37]:
निश्चित-अंतराल स्मूथर
इष्टतम निश्चित अंतराल स्मूथर का इष्टतम अनुमान प्रदान करता है, किसी निश्चित अंतराल प्रति के लिए से मापन का उपयोग किया जाता है।[38] इसे एक संवर्धित अवस्था के माध्यम से पूर्व सिद्धांत का उपयोग करके प्राप्त किया जा सकता है, और फिल्टर का मुख्य समीकरण निम्नलिखित है:
जहां:
- एक मानक कालमान फिल्टर के माध्यम से अनुमानित है;
- मानक कालमान फिल्टर के अनुमान को ध्यान में रखते हुए उत्पादित नवाचार है;
- बहुत से साथ में नए चर हैं; अर्थात्, वे मानक कालमान फिल्टर में प्रकट नहीं होते हैं;
- लब्धि की गणना निम्नलिखित योजना के माध्यम से की जाती है:
- तथा
- जहां तथा पूर्वानुमान त्रुटि सहप्रसरण और मानक कालमान फिल्टर की लब्धि हैं (अर्थात, )
यदि अनुमान त्रुटि सहप्रसरण को परिभाषित किया जाता है ताकि
तो हमारे पास अनुमान पर सुधार है, द्वारा दिया गया है:
निश्चित-अंतराल स्मूथर्स
इष्टतम निश्चित-अंतराल स्मूथर का इष्टतम अनुमान () प्रदान करता है, एक निश्चित अंतराल से के लिए मापन का उपयोग किया जाता है, इसे "कालमान समरेखण" भी कहा जाता है। सामान्य उपयोग में कई समरेखण कलन विधि हैं।
राउच-तुंग-स्ट्रीबेल
रॉच-तुंग-स्ट्रीबेल (RTS) स्मूथर निश्चित अंतराल समरेखण के लिए एक कुशल दो-पारण कलन विधि है।[39]
अग्रगामी पारण नियमित कालमान फिल्टर कलन विधि के समान है। ये ए-प्रीओरी और ए-पोस्टरियोरी अवस्था अनुमानों , और सहप्रसरण , को फिल्टर करते हैं। पश्चगामी पारण ( रेट्रोडिक्शन के लिए) में उपयोग के लिए सेव किया जाता हैं।
पश्चगामी पारण में, हम समकृत अवस्था अनुमानों और सहप्रसरण की गणना करते हैं। हम अंतिम टाइमस्टेप से प्रारम्भ करते हैं और निम्नलिखित पुनरावर्ती समीकरणों का उपयोग करके समय में पश्चगामी की ओर बढ़ते हैं:
जहां
टाइमस्टेप तथा की ए-पोस्टीरियरी अवस्था और टाइमस्टेप की ए-प्रीओरी अवस्था अनुमान है, सहप्रसरण पर भी यही संकेतन अनुप्रयुक्त होता है।
संशोधित ब्रायसन-फ्रेज़ियर स्मूथर
आरटीएस कलन विधि का एक विकल्प बीरमैन द्वारा विकसित संशोधित ब्रायसन-फ्रेज़ियर (MBF) निश्चित अंतराल स्मूथर है।[31] यह एक पश्चगामी पारण का भी उपयोग करता है जो कालमान फिल्टर अग्रगामी पारण से सहेजे गए डेटा को संसाधित करता है। पश्चगामी पारण के समीकरणों में डेटा की पुनरावर्ती संगणना सम्मिलित होती है। जिसका उपयोग प्रत्येक अवलोकन समय पर समकृत अवस्था और सहप्रसरण की गणना के लिए किया जाता है ।
पुनरावर्ती समीकरण हैं
जहां अवशिष्ट सहप्रसरण है और .समकृत अवस्था और सहप्रसरण तब समीकरणों में प्रतिस्थापन द्वारा प्राप्त किया जा सकता है;
या
एमबीएफ की एक महत्वपूर्ण लब्धि यह है कि इसमें सहप्रसरण आव्यूह के व्युत्क्रम को खोजने की आवश्यकता नहीं होती है।
न्यूनतम-विचरण स्मूथर
न्यूनतम-विचरण स्मूथर सर्वोत्तम संभव त्रुटि प्रदर्शन प्राप्त कर सकता है, बशर्ते कि प्रतिरूप रैखिक हों, उनके मापदण्ड और रव आंकड़े सटीक से ज्ञात हों।[40] यह स्मूथर इष्टतम गैर-कारण वीनर फिल्टर की एक समय-भिन्न अवस्था-स्थिति सामान्यीकरण है।
स्मूथर गणना दो चरणों में की जाती है। इसमें एक चरण अग्रसर का पूर्वानुमान सम्मिलित होता है और इसके द्वारा दिया जाता है;
उपरोक्त प्रणाली को व्युत्क्रम वीनर-हॉप कारक के रूप में जाना जाता है। पश्चगामी पुनरावर्तन उपरोक्त पूर्वकालिक प्रणाली का जोड़ है। पश्चगामी पारण का परिणाम कालोत्क्रमण पर आगे के समीकरणों को संचालित करके गणना की जा सकती है और समय परिणाम उत्क्रमणीय है। आउटपुट अनुमान की स्थितियो में, समकृत अनुमान द्वारा दिया जाता है
इस न्यूनतम-विचरण के कारण स्मूथर प्रतिफल में भाग लेना
जो न्यूनतम-विचरण कालमान फिल्टर के समान है। उपरोक्त उपाय आउटपुट अनुमान त्रुटि के विचरण को कम करते हैं। ध्यान दें कि रॉच-तुंग-स्ट्रीबेल स्मूथर व्युत्पत्ति का मानना है कि अंतर्निहित वितरण गॉसियन हैं, जबकि न्यूनतम-विचरण उपाय नहीं हैं। अवस्था के आकलन और इनपुट अनुमान के लिए इष्टतम स्मूथर्स का निर्माण इसी प्रकार किया जा सकता है।
उपरोक्त स्मूथर का सतत-समय संस्करण में वर्णित है।[41][42]
अपेक्षा-अधिकतमकरण कलन विधि को न्यूनतम-विचरण फिल्टर और स्मूथर्स के भीतर अज्ञात अवस्था समष्टि मापदंडों के अनुमानित अधिकतम संभावना अनुमानों की गणना करने के लिए नियोजित किया जा सकता है। प्रायः अनिश्चितता समस्या धारणाओं के भीतर रहती है। रिकाटी समीकरण में एक सकारात्मक निश्चित पद जोड़कर अनिश्चितताओं को समायोजित करने वाला एक स्मूथर प्रारुप तैयार किया जा सकता है।[43]
ऐसी स्थितियों में जहां प्रतिरूप गैर-रैखिक हैं, चरणगत रेखीयकरण न्यूनतम-विचरण फिल्टर और स्मूथ पुनरावर्तन (विस्तारित कालमान फिल्टर) के भीतर हो सकते है।
आवृत्ति-भारित कालमान फिल्टर
1930 के दशक में फ्लेचर और मुनसन द्वारा विभिन्न आवृत्तियों पर ध्वनियों की धारणा पर अग्रणी शोध किया गया था। उनके कार्य ने औद्योगिक रव और श्रवण हानि की जांच के भीतर भार मापने के मानक विधियों का नेतृत्व किया।
सामान्यतः, एक आवृति आकार देने वाले प्रकार्य का उपयोग एक निर्दिष्ट आवृति बैंड में त्रुटि वर्णक्रमीय घनत्व की औसत शक्ति को भारित करने के लिए किया जाता है। माना एक सांकेतिक कालमान फिल्टर द्वारा प्रदर्शित आउटपुट अनुमान त्रुटि को निरूपित करता है। इसके अतिरिक्त, एक कारण आवृत्ति भार स्थानांतरण प्रकार्य को निरूपित करता है। इष्टतम समाधान जो के विचरण को कम करता है, केवल निर्माण करने से उत्पन्न होता है।
का प्रारुप एक अनिर्णीत प्रश्न बना हुआ है। एक अग्रसर प्रणाली एक ऐसी प्रणाली की पहचान करती है जो अनुमान त्रुटि और समुच्चयन उत्पन्न करती है, उस प्रणाली के व्युत्क्रम के समान है।[44] बढ़े हुए फिल्टर क्रम की कीमत पर माध्य-वर्ग त्रुटि सुधार प्राप्त करने के लिए इस प्रक्रिया को पुनरावृत्त किया जा सकता है। स्मूथर्स पर भी यही प्रविधि अनुप्रयुक्त की जा सकती है।
अरेखीय फिल्टर
मूल कालमान फिल्टर एक रेखीय धारणा तक पर्याप्त है। हालाँकि, अधिक जटिल प्रणालियाँ अरैखिक हो सकती हैं। गैर-रैखिकता को या तो प्रक्रिया प्रतिरूप या अवलोकन प्रतिरूप के साथ या दोनों के साथ जोड़ा जा सकता है।
गैर-रैखिक प्रणालियों के लिए कालमान फिल्टर के सबसे सामान्य संस्करण विस्तारित कालमान फिल्टर और अनसेंटेड कालमान फिल्टर हैं। उपयोग करने के लिए किस फिल्टर की उपयुक्तता प्रक्रिया और अवलोकन प्रणाली के गैर-रैखिक सूचकांकों पर निर्भर करती है।[45]
विस्तारित कालमान फिल्टर
विस्तारित कालमान फिल्टर (EKF) में, अवस्था पारगमन और अवलोकन प्रतिरूप को अवस्था के रैखिक कार्यों की आवश्यकता नहीं है, बल्कि इसके स्थान पर गैर-रेखीय कार्य हो सकते हैं। ये प्रकार्य अलग-अलग प्रकार के होते हैं।
प्रकार्य f का उपयोग पूर्व अनुमान से अनुमानित स्थिति की गणना करने के लिए किया जा सकता है और इसी तरह प्रकार्य h का उपयोग अनुमानित स्थिति से अनुमानित माप की गणना करने के लिए किया जा सकता है। हालाँकि, f और h को सीधे सहप्रसरण पर अनुप्रयुक्त नहीं किया जा सकता है। इसके स्थान पर आंशिक व्युत्पन्न (जैकोबियन) के एक आव्यूह की गणना की जाती है।
प्रत्येक टाइमस्टेप पर जैकोबियन का वर्तमान पूर्वानुमानित अवस्थाओं के साथ मूल्यांकन किया जाता है। इन आव्यूह का उपयोग कालमान फिल्टर समीकरणों में किया जा सकता है। यह प्रक्रिया अनिवार्य रूप से वर्तमान अनुमान के आसपास गैर-रैखिक प्रकार्य को रैखिक बनाती है।
अनसेंटेड कालमान फिल्टर
जब अवस्था पारगमन और अवलोकन प्रतिरूप, अर्थात, पूर्वानुमान और अद्यतन प्रकार्य तथा -अत्यधिक अरेखीय करते है , विस्तारित कालमान फिल्टर विशेष रूप से निःस्व प्रदर्शन दे सकता है।[46] इसका कारण यह है कि सहप्रसरण अंतर्निहित अरेखीय प्रतिरूप के रेखीयकरण के माध्यम से प्रचारित किया जाता है। अनसेंटेड कालमान फिल्टर ((UKF)[46]माध्य के आसपास प्रतिरूप बिंदुओं (जिन्हें सिग्मा अंक कहा जाता है) के एक न्यूनतम समुच्चय का चयन करने के लिए एक नियतात्मक प्रतिरूपकरण प्रविधि का उपयोग करते है जिसे अनसेंटेड रूपांतरण (UT) के रूप में जाना जाता है। सिग्मा बिंदुओं को तब गैर-रेखीय कार्यों के माध्यम से प्रचारित किया जाता है, जिससे एक नया माध्य और सहप्रसरण अनुमान का निर्माण होता है। परिणामी फिल्टर इस तथ्य पर निर्भर करता है कि यूटी के रूपांतरित आँकड़ों की गणना कैसे की जाती है और सिग्मा बिंदुओं के किस समुच्चय का उपयोग किया जाता है। यह टिप्पणी की जानी चाहिए कि नए यूकेएफ का निर्माण एक सुसंगत विधि से करना सदैव संभव है।[47] कुछ प्रणालियों के लिए, परिणामी यूकेएफ सही माध्य और सहप्रसरण का अधिक सटीक अनुमान लगाता है।[48] इसे मोंटे कार्लो प्रतिचयन या पश्च आँकड़ों के टेलर श्रृंखला विस्तार के साथ सत्यापित किया जा सकता है। इसके अतिरिक्त, यह प्रविधि स्पष्ट रूप से जैकोबियन की गणना करने की आवश्यकता को निष्काषित कर देती है, जो जटिल कार्यों के लिए अपने आप में एक कठिन कार्य हो सकता है।
सिग्मा अंक
एक यादृच्छिक सदिश के लिए, सिग्मा बिंदु सदिशों का कोई भी समूह हैं,
के साथ दोषी ठहराया
- प्रथम क्रम भार जो पूर्ण करते हैं
- सभी के लिए :
- द्वितीय क्रम भार जो पूर्ण करते हैं
- सभी युग्मो के लिए .
के लिए सिग्मा अंक और भार के लिए एक सरल विकल्प यूकेएफ कलन विधि में है;
जहां का औसत अनुमान है। सदिश का jth स्तम्भ है, जहां सामान्यतः, के चोल्स्की अपघटन के माध्यम से प्राप्त किया जाता है। कुछ सावधानी से फिल्टर समीकरण समीकरणों को इस प्रकार व्यक्त किया जा सकता है कि की मध्यवर्ती गणना के बिना का सीधे मूल्यांकन किया जाता है। इसे वर्गमूल अनसेंटेड कालमान फिल्टर के रूप में जाना जाता है।[49]
औसत मान का भार, , इच्छानुसार चयन किया जा सकता है।
एक अन्य लोकप्रिय मानकीकरण (जो उपरोक्त को सामान्य करता है) है;
तथा सिग्मा बिंदुओं के प्रसार को नियंत्रित करता है और के वितरण से संबंधित है,
उपयुक्त मान से सम्बंधित समस्याओं पर निर्भर करते हैं, परन्तु एक विशिष्ट सिफारिश , , तथा है। हालांकि, का एक बड़ा मान (जैसे, ) वितरण के प्रसार और संभावित गैर-रैखिकताओं को उन्नत ढंग से अधिकृत करने के लिए लाभकारी हो सकता है।[50] यदि का सही वितरण गॉसियन है, और इष्टतम है।[51]
पूर्वानुमान
ईकेएफ के साथ, यूकेएफ पूर्वानुमान का उपयोग यूकेएफ नवीनीकरण से स्वतंत्र रूप से किया जा सकता है, एक रैखिक (या वास्तव में ईकेएफ) नवीनीकरण के संयोजन में, या इसके विपरीत।
माध्य और सहप्रसरण, तथा के अनुमानों को देखते हुए, एक प्राप्त सिग्मा अंक जैसा कि ऊपर अनुभाग में वर्णित है। सिग्मा बिंदुओं को पारगमन फलन f के माध्यम से प्रचारित किया जाता है।
- .
अनुमानित माध्य और सहप्रसरण का उत्पादन करने के लिए प्रचारित सिग्मा बिंदुओं की तुलना की जाती है।
जहां मूल सिग्मा बिंदुओं के प्रथम-क्रम का भार हैं, और द्वितीय क्रम का भार हैं। आव्यूह पारगमन रव का सहप्रसरण है।
नवीनीकरण
पूर्वानुमान अनुमानों तथा को देखते हुए, का एक नया समुच्चय सिग्मा अंक इसी प्रथम-क्रम भार के साथ और दूसरे क्रम के भार की गणना की जाती है।[52] ये सिग्मा अंक मापन प्रकार्य के माध्यम से रूपांतरित होते हैं;
- .
पुनः रूपांतरित बिंदुओं के अनुभवजन्य माध्य और सहप्रसरण की गणना की जाती है।
जहां अवलोकन रव का सहप्रसरण आव्यूह है, इसके अतिरिक्त, तिर्यक् सहप्रसरण आव्यूह की भी आवश्यकता होती है
कालमान लब्धि है
अद्यतन माध्य और सहप्रसरण अनुमान हैं
विभेदक कालमान फिल्टर
जब अवलोकन प्रतिरूप अत्यधिक गैर-रेखीय और/या गैर-गॉसियन है, तो यह बेयस के नियम और अनुमान को अनुप्रयुक्त करने के लिए लाभकारी सिद्ध हो सकता है;
जहां अरेखीय कार्यों के लिए, यह मानक कालमान फिल्टर के जनरेटिव विनिर्देश को अव्यक्त अवस्थाओं के लिए एक विभेदक प्रतिरूप के साथ को प्रतिस्थापित कर देता है।
एक स्थिर प्रक्रिया अवस्था प्रतिरूप के अंतर्गत
जहां , यदि
पुनः एक नया अवलोकन दिया गया, जो इस प्रकार है कि[53]
जहां
ध्यान दें कि इस सन्निकटन की आवश्यकता है, जिनका धनात्मक निश्चित होना चाहिए; ऐसा न होने की दशा में,
के स्थान पर प्रयोग किया जाता है। इस प्रकार का दृष्टिकोण विशेष रूप से तब उपयोगी सिद्ध होता है, जब अवलोकनों की आयामीता अव्यक्त अवस्थाओं की तुलना में बहुत अधिक होती है[54] और उन निस्यंदकों का निर्माण किया जा सकता है, जो अवलोकन प्रतिरूप में गैर-स्थिरता के लिए विशेष रूप से सुदृढ़ हैं।[55]
अनुकूली कालमान फिल्टर
अनुकूली कालमान फिल्टर प्रक्रिया की गतिशीलता के अनुकूल होने की अनुमति देते हैं जो प्रक्रिया प्रतिरूप में मॉडलिंग नहीं करते हैं, जो उदाहरण के लिए एक युक्तिपूर्ण लक्ष्य के संदर्भ में होते है, और जब अनुसरण के लिए एक स्थिर वेग (घटा हुआ क्रम) कालमान फिल्टर नियोजित किया जाता है।[56]
कालमान-बुकी फिल्टर
कालमान-बुकी निस्यंदन (रिचर्ड स्नोडेन बुकी के नाम पर) कालमान फिल्टर का एक सतत समय संस्करण है।[57][58]
यह अवस्था समष्टि प्रतिरूप पर आधारित है
जहां तथा दो श्वेत रव शब्दावली तथा की तीव्रता, (या, अधिक सटीक रूप से, ऊर्जा का वर्णक्रमीय घनत्व - PSD - आव्यूह) का प्रतिनिधित्व करते हैं;
फिल्टर में दो अंतर समीकरण होते हैं, एक अवस्था अनुमान के लिए और एक सहप्रसरण के लिए:
जहां कालमान लब्धि द्वारा प्रदान की जाती है
ध्यान दें कि इस अभिव्यक्ति में के लिए अवलोकन रव का सहप्रसरण एक ही समय में पूर्वानुमान त्रुटि (या नवाचार) के सहप्रसरण का प्रतिनिधित्व करता है। ये सहप्रसरण केवल सतत समय की स्थिति में समान होते हैं।[59]
असतत-समय कालमान फिल्टर की पूर्वानुमान और अद्यतन चरणों के मध्य अंतर सतत समय में उपस्थित नहीं है।
सहप्रसरण के लिए द्वितीय अवकल समीकरण, रिकाटी समीकरण का एक उदाहरण है। कालमान-बुकी फिल्टर के गैर-रेखीय सामान्यीकरण में सतत समय विस्तारित कालमान फिल्टर सम्मिलित है।
संकरित कालमान फिल्टर
अधिकांश भौतिक प्रणालियों को सतत-समय के प्रतिरूप के रूप में दर्शाया जाता है जबकि अंकीय संसाधक के माध्यम से अवस्था के आकलन के लिए प्रायः असतत-समय मापन किए जाते हैं। इसलिए, प्रणाली प्रतिरूप और माप प्रतिरूप द्वारा प्रदान की जाती है;
जहां
- .
प्रारंभ
पूर्वानुमान
पूर्वानुमान समीकरण माप से अद्यतन किए बिना सतत-समय कालमान फिल्टर से प्राप्त होते हैं, अर्थात्, , पूर्व चरण में अनुमान के समान प्रारंभिक मानो के साथ अंतर समीकरणों के एक समुच्चय को हल करके अनुमानित अवस्था और सहप्रसरण की गणना की जाती है।
रैखिक समय अपरिवर्तनीय प्रणालियों की स्थितियो में, सतत समय की गतिशीलता को आव्यूह घातांक का उपयोग करके एक असतत समय प्रणाली में पूर्णतया विसर्जित किया जा सकता है।
नवीनीकरण
अद्यतन समीकरण असतत-समय कालमान फिल्टर के समान हैं।
विरल संकेतों की पुनर्प्राप्ति के लिए परिवर्त्य
सांकेतिक कालमान फिल्टर को विरल, संभवतः गतिशील,रव अवलोकनों से संकेतों की पुनर्प्राप्ति के लिए भी नियोजित किया गया है। हाल ही में कार्य[60][61][62] संकुचित संवेदन/प्रतिरूपकरण के सिद्धांत से धारणाओं का उपयोग करते है, जैसे कि प्रतिबंधित समदूरीकता गुण और संबंधित संभाव्य पुनर्प्राप्ति विषय, आंतरिक रूप से निम्न-आयामी प्रणालियों में विरल अवस्था का क्रमिक रूप से अनुमान लगाने के लिए है।
गाउसीय प्रक्रम से संबंध
चूंकि रैखिक गॉसियन अवस्था समष्टि प्रतिरूप गाउसीय प्रक्रियाओं की ओर ले जाते हैं, इसलिए कालमान फिल्टर को गाउसीय प्रक्रम प्रतिगमन के लिए अनुक्रमिक समाधानकर्ता के रूप में देखा जा सकता है।[63]
अनुप्रयोग
- प्रवृति और शीर्षक संदर्भ प्रणाली
- स्वचालित यंत्र
- विद्युत बैटरी प्रभार की अवस्था (SoC) अनुमान[64][65]
- मस्तिष्क-परिकलक अंतराफलक[53][55][54]
- अराजक संकेत
- कण संसूचक में आवेशित कणों का अनुसरण और शीर्ष अन्वायोजन[66]
- परिकलक दृष्टि में वस्तुओं का अनुसरण
- नौवहन में गतिशील स्थिति
- अर्थशास्त्र , विशेष रूप से वृहत् अर्थशास्त्र , समय श्रृंखला विश्लेषण , और अर्थमिति[67]
- जड़त्वीय मार्गदर्शन प्रणाली
- नाभिकीय औषधि - एकल फोटॉन उत्सर्जन गणना टोमोग्राफी छवि प्रत्यावर्तन[68]
- कक्षा निर्धारण
- ऊर्जा व्यवस्था की स्थिति का अनुमान
- रडार अनुपथक
- उपग्रह नौकानयन प्रणाली
- भूकंप विज्ञान [69]
- एसी चालक चर-आवृत्ति ड्राइव का संवेदक रहित नियंत्रण
- एक साथ स्थानीयकरण और मानचित्रण
- भाषण में वृद्धि
- दृश्य ओडोमेट्री
- मौसम की भविष्यवाणी
- दिशानिर्देशन प्रणाली
- 3 डी मॉडलिंग
- संरचनात्मक स्वास्थ्य अनुवीक्षण
- मानव संवेदीप्रेरक प्रसंस्करण [70]
यह भी देखें
- अल्फा बीटा निस्यंदक
- व्युत्क्रम-विचरण भार
- सहप्रसरण अंतरायोजी
- डेटा समीकरण
- कलमान निस्यंदक समूहन
- विस्तारित कलमन निस्यंदक
- स्थिर कलमन निस्यंदक
- निस्यंदन समस्या (प्रसंभाव्य प्रक्रियाएं)
- सामान्यीकृत निस्यंदन
- अपरिवर्तनीय विस्तारित कलमन निस्यंदक
- कर्नेल अनुकूली निस्यंदक
- मासरेलीज़ की प्रमेय
- गतिमान क्षितिज अनुमान
- कण निस्यंदक अनुमानक
- पीआईडी नियंत्रक
- भविष्यवक्ता-सुधारक विधि
- पुनरावर्ती न्यूनतम वर्ग निस्यंदक
- श्मिट-कलमैन निस्यंदक
- पृथक्करण सिद्धांत
- सर्पण प्रणाली नियंत्रण
- अवस्था-संक्रमण आव्यूह
- प्रसंभाव्य अंतर समीकरण
- कलमन निस्यंदक स्विच करना
- एक साथ अनुमान और मॉडलिंग
संदर्भ
- ↑ Stratonovich, R. L. (1959). Optimum nonlinear systems which bring about a separation of a signal with constant parameters from noise. Radiofizika, 2:6, pp. 892–901.
- ↑ Stratonovich, R. L. (1959). On the theory of optimal non-linear filtering of random functions. Theory of Probability and Its Applications, 4, pp. 223–225.
- ↑ Stratonovich, R. L. (1960) Application of the Markov processes theory to optimal filtering. Radio Engineering and Electronic Physics, 5:11, pp. 1–19.
- ↑ Stratonovich, R. L. (1960). Conditional Markov Processes. Theory of Probability and Its Applications, 5, pp. 156–178.
- ↑ Stepanov, O. A. (15 May 2011). "Kalman filtering: Past and present. An outlook from Russia. (On the occasion of the 80th birthday of Rudolf Emil Kalman)". Gyroscopy and Navigation. 2 (2): 105. doi:10.1134/S2075108711020076. S2CID 53120402.
- ↑ Lauritzen, S. L. (December 1981). "Time series analysis in 1880. A discussion of contributions made by T.N. Thiele". International Statistical Review. 49 (3): 319–331. doi:10.2307/1402616. JSTOR 1402616.
He derives a recursive procedure for estimating the regression component and predicting the Brownian motion. The procedure is now known as Kalman filtering.
- ↑ Lauritzen, S. L. (2002). Thiele: Pioneer in Statistics. New York: Oxford University Press. p. 41. ISBN 978-0-19-850972-1.
He solves the problem of estimating the regression coefficients and predicting the values of the Brownian motion by the method of least squares and gives an elegant recursive procedure for carrying out the calculations. The procedure is nowadays known as Kalman filtering.
- ↑ Mohinder S. Grewal and Angus P. Andrews
- ↑ Gaylor, David; Lightsey, E. Glenn (2003). "GPS/INS Kalman Filter Design for Spacecraft Operating in the Proximity of International Space Station". AIAA Guidance, Navigation, and Control Conference and Exhibit. doi:10.2514/6.2003-5445. ISBN 978-1-62410-090-1.
- ↑ Ingvar Strid; Karl Walentin (April 2009). "Block Kalman Filtering for Large-Scale DSGE Models". Computational Economics. 33 (3): 277–304. CiteSeerX 10.1.1.232.3790. doi:10.1007/s10614-008-9160-4. hdl:10419/81929. S2CID 3042206.
- ↑ Martin Møller Andreasen (2008). "Non-linear DSGE Models, The Central Difference Kalman Filter, and The Mean Shifted Particle Filter" (PDF).
- ↑ Roweis, S; Ghahramani, Z (1999). "A unifying review of linear gaussian models" (PDF). Neural Computation. 11 (2): 305–45. doi:10.1162/089976699300016674. PMID 9950734. S2CID 2590898.
- ↑ Hamilton, J. (1994), Time Series Analysis, Princeton University Press. Chapter 13, 'The Kalman Filter'
- ↑ Ishihara, J.Y.; Terra, M.H.; Campos, J.C.T. (2006). "Robust Kalman Filter for Descriptor Systems". IEEE Transactions on Automatic Control. 51 (8): 1354. doi:10.1109/TAC.2006.878741. S2CID 12741796.
- ↑ Terra, Marco H.; Cerri, Joao P.; Ishihara, Joao Y. (2014). "Optimal Robust Linear Quadratic Regulator for Systems Subject to Uncertainties". IEEE Transactions on Automatic Control. 59 (9): 2586–2591. doi:10.1109/TAC.2014.2309282. S2CID 8810105.
- ↑ Kelly, Alonzo (1994). "A 3D state space formulation of a navigation Kalman filter for autonomous vehicles" (PDF). DTIC Document: 13. Archived (PDF) from the original on December 30, 2014. 2006 Corrected Version Archived 2017-01-10 at the Wayback Machine
- ↑ Reid, Ian; Term, Hilary. "Estimation II" (PDF). www.robots.ox.ac.uk. Oxford University. Retrieved 6 August 2014.
- ↑ Rajamani, Murali (October 2007). Data-based Techniques to Improve State Estimation in Model Predictive Control (PDF) (PhD Thesis). University of Wisconsin–Madison. Archived from the original (PDF) on 2016-03-04. Retrieved 2011-04-04.
- ↑ Rajamani, Murali R.; Rawlings, James B. (2009). "Estimation of the disturbance structure from data using semidefinite programming and optimal weighting". Automatica. 45 (1): 142–148. doi:10.1016/j.automatica.2008.05.032.
- ↑ "Autocovariance Least-Squares Toolbox". Jbrwww.che.wisc.edu. Retrieved 2021-08-18.
- ↑ Bania, P.; Baranowski, J. (12 December 2016). Field Kalman Filter and its approximation. IEEE 55th Conference on Decision and Control (CDC). Las Vegas, NV, USA: IEEE. pp. 2875–2880.
- ↑ Bar-Shalom, Yaakov; Li, X.-Rong; Kirubarajan, Thiagalingam (2001). Estimation with Applications to Tracking and Navigation. New York, USA: John Wiley & Sons, Inc. pp. 319 ff. doi:10.1002/0471221279. ISBN 0-471-41655-X.
- ↑ Three optimality tests with numerical examples are described in Peter, Matisko (2012). "Optimality Tests and Adaptive Kalman Filter". 16th IFAC Symposium on System Identification. pp. 1523–1528. doi:10.3182/20120711-3-BE-2027.00011. ISBN 978-3-902823-06-9.
{{cite book}}:|journal=ignored (help) - ↑ Spall, James C. (1995). "The Kantorovich inequality for error analysis of the Kalman filter with unknown noise distributions". Automatica. 31 (10): 1513–1517. doi:10.1016/0005-1098(95)00069-9.
- ↑ Maryak, J.L.; Spall, J.C.; Heydon, B.D. (2004). "Use of the Kalman Filter for Inference in State-Space Models with Unknown Noise Distributions". IEEE Transactions on Automatic Control. 49: 87–90. doi:10.1109/TAC.2003.821415. S2CID 21143516.
- ↑ 26.0 26.1 Walrand, Jean; Dimakis, Antonis (August 2006). Random processes in Systems -- Lecture Notes (PDF). pp. 69–70.
- ↑ Sant, Donald T. "Generalized least squares applied to time varying parameter models." Annals of Economic and Social Measurement, Volume 6, number 3. NBER, 1977. 301-314. Online Pdf
- ↑ Anderson, Brian D. O.; Moore, John B. (1979). Optimal Filtering. New York: Prentice Hall. pp. 129–133. ISBN 978-0-13-638122-8.
- ↑ Jingyang Lu. "False information injection attack on dynamic state estimation in multi-sensor systems", Fusion 2014
- ↑ 30.0 30.1 Thornton, Catherine L. (15 October 1976). Triangular Covariance Factorizations for Kalman Filtering (PhD). NASA. NASA Technical Memorandum 33-798.
- ↑ 31.0 31.1 Bierman, G.J. (1977). "Factorization Methods for Discrete Sequential Estimation". Factorization Methods for Discrete Sequential Estimation. Bibcode:1977fmds.book.....B.
- ↑ Bar-Shalom, Yaakov; Li, X. Rong; Kirubarajan, Thiagalingam (July 2001). Estimation with Applications to Tracking and Navigation. New York: John Wiley & Sons. pp. 308–317. ISBN 978-0-471-41655-5.
- ↑ Särkkä, S.; Ángel F. García-Fernández (2021). "Temporal Parallelization of Bayesian Smoothers". IEEE Transactions on Automatic Control. 66 (1): 299–306. arXiv:1905.13002. doi:10.1109/TAC.2020.2976316. S2CID 213695560.
- ↑ "Parallel Prefix Sum (Scan) with CUDA". developer.nvidia.com/. Retrieved 2020-02-21.
The scan operation is a simple and powerful parallel primitive with a broad range of applications. In this chapter we have explained an efficient implementation of scan using CUDA, which achieves a significant speedup compared to a sequential implementation on a fast CPU, and compared to a parallel implementation in OpenGL on the same GPU. Due to the increasing power of commodity parallel processors such as GPUs, we expect to see data-parallel algorithms such as scan to increase in importance over the coming years.
- ↑ Masreliez, C. Johan; Martin, R D (1977). "Robust Bayesian estimation for the linear model and robustifying the Kalman filter". IEEE Transactions on Automatic Control. 22 (3): 361–371. doi:10.1109/TAC.1977.1101538.
- ↑ Lütkepohl, Helmut (1991). Introduction to Multiple Time Series Analysis. Heidelberg: Springer-Verlag Berlin. p. 435.
- ↑ 37.0 37.1 Gabriel T. Terejanu (2012-08-04). "Discrete Kalman Filter Tutorial" (PDF). Retrieved 2016-04-13.
- ↑ Anderson, Brian D. O.; Moore, John B. (1979). Optimal Filtering. Englewood Cliffs, NJ: Prentice Hall, Inc. pp. 176–190. ISBN 978-0-13-638122-8.
- ↑ Rauch, H.E.; Tung, F.; Striebel, C. T. (August 1965). "Maximum likelihood estimates of linear dynamic systems". AIAA Journal. 3 (8): 1445–1450. Bibcode:1965AIAAJ...3.1445.. doi:10.2514/3.3166.
- ↑ Einicke, G.A. (March 2006). "Optimal and Robust Noncausal Filter Formulations". IEEE Transactions on Signal Processing. 54 (3): 1069–1077. Bibcode:2006ITSP...54.1069E. doi:10.1109/TSP.2005.863042. S2CID 15376718.
- ↑ Einicke, G.A. (April 2007). "Asymptotic Optimality of the Minimum-Variance Fixed-Interval Smoother". IEEE Transactions on Signal Processing. 55 (4): 1543–1547. Bibcode:2007ITSP...55.1543E. doi:10.1109/TSP.2006.889402. S2CID 16218530.
- ↑ Einicke, G.A.; Ralston, J.C.; Hargrave, C.O.; Reid, D.C.; Hainsworth, D.W. (December 2008). "Longwall Mining Automation. An Application of Minimum-Variance Smoothing". IEEE Control Systems Magazine. 28 (6): 28–37. doi:10.1109/MCS.2008.929281. S2CID 36072082.
- ↑ Einicke, G.A. (December 2009). "Asymptotic Optimality of the Minimum-Variance Fixed-Interval Smoother". IEEE Transactions on Automatic Control. 54 (12): 2904–2908. Bibcode:2007ITSP...55.1543E. doi:10.1109/TSP.2006.889402. S2CID 16218530.
- ↑ Einicke, G.A. (December 2014). "Iterative Frequency-Weighted Filtering and Smoothing Procedures". IEEE Signal Processing Letters. 21 (12): 1467–1470. Bibcode:2014ISPL...21.1467E. doi:10.1109/LSP.2014.2341641. S2CID 13569109.
- ↑ Biswas, Sanat K.; Qiao, Li; Dempster, Andrew G. (2020-12-01). "A quantified approach of predicting suitability of using the Unscented Kalman Filter in a non-linear application". Automatica (in English). 122: 109241. doi:10.1016/j.automatica.2020.109241. ISSN 0005-1098. S2CID 225028760.
- ↑ 46.0 46.1 Julier, Simon J.; Uhlmann, Jeffrey K. (1997). "New extension of the Kalman filter to nonlinear systems" (PDF). In Kadar, Ivan (ed.). Signal Processing, Sensor Fusion, and Target Recognition VI. Proceedings of SPIE. Vol. 3. pp. 182–193. Bibcode:1997SPIE.3068..182J. CiteSeerX 10.1.1.5.2891. doi:10.1117/12.280797. S2CID 7937456. Retrieved 2008-05-03.
- ↑ Menegaz, H. M. T.; Ishihara, J. Y.; Borges, G. A.; Vargas, A. N. (October 2015). "A Systematization of the Unscented Kalman Filter Theory". IEEE Transactions on Automatic Control. 60 (10): 2583–2598. doi:10.1109/tac.2015.2404511. hdl:20.500.11824/251. ISSN 0018-9286. S2CID 12606055.
- ↑ Gustafsson, Fredrik; Hendeby, Gustaf (2012). "Some Relations Between Extended and Unscented Kalman Filters". IEEE Transactions on Signal Processing. 60 (2): 545–555. Bibcode:2012ITSP...60..545G. doi:10.1109/tsp.2011.2172431. S2CID 17876531.
- ↑ Van der Merwe, R.; Wan, E.A. (2001). "The square-root unscented Kalman filter for state and parameter-estimation". 2001 IEEE International Conference on Acoustics, Speech, and Signal Processing. Proceedings (Cat. No.01CH37221). 6: 3461–3464. doi:10.1109/ICASSP.2001.940586. ISBN 0-7803-7041-4. S2CID 7290857.
- ↑ Bitzer, S. (2016). "The UKF exposed: How it works, when it works and when it's better to sample". doi:10.5281/zenodo.44386.
{{cite journal}}: Cite journal requires|journal=(help) - ↑ Wan, E.A.; Van Der Merwe, R. (2000). "The unscented Kalman filter for nonlinear estimation" (PDF). Proceedings of the IEEE 2000 Adaptive Systems for Signal Processing, Communications, and Control Symposium (Cat. No.00EX373). p. 153. CiteSeerX 10.1.1.361.9373. doi:10.1109/ASSPCC.2000.882463. ISBN 978-0-7803-5800-3. S2CID 13992571.
- ↑ Sarkka, Simo (September 2007). "On Unscented Kalman Filtering for State Estimation of Continuous-Time Nonlinear Systems". IEEE Transactions on Automatic Control. 52 (9): 1631–1641. doi:10.1109/TAC.2007.904453.
- ↑ 53.0 53.1 Burkhart, Michael C.; Brandman, David M.; Franco, Brian; Hochberg, Leigh; Harrison, Matthew T. (2020). "The Discriminative Kalman Filter for Bayesian Filtering with Nonlinear and Nongaussian Observation Models". Neural Computation. 32 (5): 969–1017. doi:10.1162/neco_a_01275. PMC 8259355. PMID 32187000. S2CID 212748230. Retrieved 26 March 2021.
- ↑ 54.0 54.1 Burkhart, Michael C. (2019). A Discriminative Approach to Bayesian Filtering with Applications to Human Neural Decoding (Thesis). Providence, RI, USA: Brown University. doi:10.26300/nhfp-xv22. Retrieved 26 March 2021.
- ↑ 55.0 55.1 Brandman, David M.; Burkhart, Michael C.; Kelemen, Jessica; Franco, Brian; Harrison, Matthew T.; Hochberg, Leigh R. (2018). "Robust Closed-Loop Control of a Cursor in a Person with Tetraplegia using Gaussian Process Regression". Neural Computation. 30 (11): 2986–3008. doi:10.1162/neco_a_01129. PMC 6685768. PMID 30216140. Retrieved 26 March 2021.
- ↑ Bar-Shalom, Yaakov; Li, X.-Rong; Kirubarajan, Thiagalingam (2001). Estimation with Applications to Tracking and Navigation. New York, USA: John Wiley & Sons, Inc. pp. 421 ff. doi:10.1002/0471221279. ISBN 0-471-41655-X.
- ↑ Bucy, R.S. and Joseph, P.D., Filtering for Stochastic Processes with Applications to Guidance, John Wiley & Sons, 1968; 2nd Edition, AMS Chelsea Publ., 2005. ISBN 0-8218-3782-6
- ↑ Jazwinski, Andrew H., Stochastic processes and filtering theory, Academic Press, New York, 1970. ISBN 0-12-381550-9
- ↑ Kailath, T. (1968). "An innovations approach to least-squares estimation--Part I: Linear filtering in additive white noise". IEEE Transactions on Automatic Control. 13 (6): 646–655. doi:10.1109/TAC.1968.1099025.
- ↑ Vaswani, Namrata (2008). "Kalman filtered Compressed Sensing". 2008 15th IEEE International Conference on Image Processing. pp. 893–896. arXiv:0804.0819. doi:10.1109/ICIP.2008.4711899. ISBN 978-1-4244-1765-0. S2CID 9282476.
- ↑ Carmi, Avishy; Gurfil, Pini; Kanevsky, Dimitri (2010). "Methods for sparse signal recovery using Kalman filtering with embedded pseudo-measurement norms and quasi-norms". IEEE Transactions on Signal Processing. 58 (4): 2405–2409. Bibcode:2010ITSP...58.2405C. doi:10.1109/TSP.2009.2038959. S2CID 10569233.
- ↑ Zachariah, Dave; Chatterjee, Saikat; Jansson, Magnus (2012). "Dynamic Iterative Pursuit". IEEE Transactions on Signal Processing. 60 (9): 4967–4972. arXiv:1206.2496. Bibcode:2012ITSP...60.4967Z. doi:10.1109/TSP.2012.2203813. S2CID 18467024.
- ↑ Särkkä, Simo; Hartikainen, Jouni; Svensson, Lennart; Sandblom, Fredrik (2015-04-22). "On the relation between Gaussian process quadratures and sigma-point methods". arXiv:1504.05994 [stat.ME].
- ↑ Vasebi, Amir; Partovibakhsh, Maral; Bathaee, S. Mohammad Taghi (2007). "A novel combined battery model for state-of-charge estimation in lead-acid batteries based on extended Kalman filter for hybrid electric vehicle applications". Journal of Power Sources. 174 (1): 30–40. Bibcode:2007JPS...174...30V. doi:10.1016/j.jpowsour.2007.04.011.
- ↑ Vasebi, A.; Bathaee, S.M.T.; Partovibakhsh, M. (2008). "Predicting state of charge of lead-acid batteries for hybrid electric vehicles by extended Kalman filter". Energy Conversion and Management. 49: 75–82. doi:10.1016/j.enconman.2007.05.017.
- ↑ Fruhwirth, R. (1987). "Application of Kalman filtering to track and vertex fitting". Nuclear Instruments and Methods in Physics Research Section A. 262 (2–3): 444–450. Bibcode:1987NIMPA.262..444F. doi:10.1016/0168-9002(87)90887-4.
- ↑ Harvey, Andrew C. (1994). "Applications of the Kalman filter in econometrics". In Bewley, Truman (ed.). Advances in Econometrics. New York: Cambridge University Press. pp. 285f. ISBN 978-0-521-46726-1.
- ↑ Boulfelfel, D.; Rangayyan, R.M.; Hahn, L.J.; Kloiber, R.; Kuduvalli, G.R. (1994). "Two-dimensional restoration of single photon emission computed tomography images using the Kalman filter". IEEE Transactions on Medical Imaging. 13 (1): 102–109. doi:10.1109/42.276148. PMID 18218487.
- ↑ Bock, Y.; Crowell, B.; Webb, F.; Kedar, S.; Clayton, R.; Miyahara, B. (2008). "Fusion of High-Rate GPS and Seismic Data: Applications to Early Warning Systems for Mitigation of Geological Hazards". AGU Fall Meeting Abstracts. 43: G43B–01. Bibcode:2008AGUFM.G43B..01B.
- ↑ Wolpert, D. M.; Miall, R. C. (1996). "Forward Models for Physiological Motor Control". Neural Networks. 9 (8): 1265–1279. doi:10.1016/S0893-6080(96)00035-4. PMID 12662535.
अग्रिम पठन
- Einicke, G.A. (2019). Smoothing, Filtering and Prediction: Estimating the Past, Present and Future (2nd ed.). Amazon Prime Publishing. ISBN 978-0-6485115-0-2.
- Jinya Su; Baibing Li; Wen-Hua Chen (2015). "On existence, optimality and asymptotic stability of the Kalman filter with partially observed inputs". Automatica. 53: 149–154. doi:10.1016/j.automatica.2014.12.044.
- Gelb, A. (1974). Applied Optimal Estimation. MIT Press.
- Kalman, R.E. (1960). "A new approach to linear filtering and prediction problems" (PDF). Journal of Basic Engineering. 82 (1): 35–45. doi:10.1115/1.3662552. Archived from the original (PDF) on 2008-05-29. Retrieved 2008-05-03.
- Kalman, R.E.; Bucy, R.S. (1961). "New Results in Linear Filtering and Prediction Theory". Journal of Basic Engineering. 83: 95–108. CiteSeerX 10.1.1.361.6851. doi:10.1115/1.3658902.
- Harvey, A.C. (1990). Forecasting, Structural Time Series Models and the Kalman Filter. Cambridge University Press. ISBN 9780521405737.
- Roweis, S.; Ghahramani, Z. (1999). "A Unifying Review of Linear Gaussian Models" (PDF). Neural Computation. 11 (2): 305–345. doi:10.1162/089976699300016674. PMID 9950734. S2CID 2590898.
- Simon, D. (2006). Optimal State Estimation: Kalman, H Infinity, and Nonlinear Approaches. Wiley-Interscience.
- Warwick, K. (1987). "Optimal observers for ARMA models". International Journal of Control. 46 (5): 1493–1503. doi:10.1080/00207178708933989.
- Bierman, G.J. (1977). Factorization Methods for Discrete Sequential Estimation. ISBN 978-0-486-44981-4.
{{cite book}}:|journal=ignored (help) - Bozic, S.M. (1994). Digital and Kalman filtering. Butterworth–Heinemann.
- Haykin, S. (2002). Adaptive Filter Theory. Prentice Hall.
- Liu, W.; Principe, J.C. and Haykin, S. (2010). Kernel Adaptive Filtering: A Comprehensive Introduction. John Wiley.
{{cite book}}: CS1 maint: multiple names: authors list (link) - Manolakis, D.G. (1999). Statistical and Adaptive signal processing. Artech House.
- Welch, Greg; Bishop, Gary (1997). "SCAAT: incremental tracking with incomplete information" (PDF). SIGGRAPH '97 Proceedings of the 24th annual conference on Computer graphics and interactive techniques. ACM Press/Addison-Wesley Publishing Co. pp. 333–344. doi:10.1145/258734.258876. ISBN 978-0-89791-896-1. S2CID 1512754.
- Jazwinski, Andrew H. (1970). Stochastic Processes and Filtering. Mathematics in Science and Engineering. New York: Academic Press. p. 376. ISBN 978-0-12-381550-7.
- Maybeck, Peter S. (1979). "Chapter 1" (PDF). Stochastic Models, Estimation, and Control. Mathematics in Science and Engineering. Vol. 141–1. New York: Academic Press. ISBN 978-0-12-480701-3.
- Moriya, N. (2011). Primer to Kalman Filtering: A Physicist Perspective. New York: Nova Science Publishers, Inc. ISBN 978-1-61668-311-5.
- Dunik, J.; Simandl M.; Straka O. (2009). "Methods for Estimating State and Measurement Noise Covariance Matrices: Aspects and Comparison". 15th IFAC Symposium on System Identification, 2009. 15th IFAC Symposium on System Identification, 2009. France. pp. 372–377. doi:10.3182/20090706-3-FR-2004.00061. ISBN 978-3-902661-47-0.
{{cite book}}: CS1 maint: location missing publisher (link) - Chui, Charles K.; Chen, Guanrong (2009). Kalman Filtering with Real-Time Applications. Springer Series in Information Sciences. Vol. 17 (4th ed.). New York: Springer. p. 229. ISBN 978-3-540-87848-3.
- Spivey, Ben; Hedengren, J. D. and Edgar, T. F. (2010). "Constrained Nonlinear Estimation for Industrial Process Fouling". Industrial & Engineering Chemistry Research. 49 (17): 7824–7831. doi:10.1021/ie9018116.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - Thomas Kailath; Ali H. Sayed; Babak Hassibi (2000). Linear Estimation. NJ: Prentice–Hall. ISBN 978-0-13-022464-4.
- Ali H. Sayed (2008). Adaptive Filters. NJ: Wiley. ISBN 978-0-470-25388-5.
{{cite book}}: CS1 maint: uses authors parameter (link)
बाहरी संबंध
- A New Approach to Linear Filtering and Prediction Problems, by R. E. Kalman, 1960
- Kalman and Bayesian Filters in Python. Open source Kalman filtering textbook.
- How a Kalman filter works, in pictures. Illuminates the Kalman filter with pictures and colors
- Kalman–Bucy Filter, a derivation of the Kalman–Bucy Filter
- MIT Video Lecture on the Kalman filter on YouTube
- Kalman filter in Javascript. Open source Kalman filter library for node.js and the web browser.
- An Introduction to the Kalman Filter, SIGGRAPH 2001 Course, Greg Welch and Gary Bishop
- Kalman Filter webpage, with many links
- Kalman Filter Explained Simply, Step-by-Step Tutorial of the Kalman Filter with Equations
- "Kalman filters used in Weather models" (PDF). SIAM News. 36 (8). October 2003. Archived from the original (PDF) on 2011-05-17. Retrieved 2007-01-27.
- Haseltine, Eric L.; Rawlings, James B. (2005). "Critical Evaluation of Extended Kalman Filtering and Moving-Horizon Estimation". Industrial & Engineering Chemistry Research. 44 (8): 2451. doi:10.1021/ie034308l.
- Gerald J. Bierman's Estimation Subroutine Library: Corresponds to the code in the research monograph "Factorization Methods for Discrete Sequential Estimation" originally published by Academic Press in 1977. Republished by Dover.
- Matlab Toolbox implementing parts of Gerald J. Bierman's Estimation Subroutine Library: UD / UDU' and LD / LDL' factorization with associated time and measurement updates making up the Kalman filter.
- Matlab Toolbox of Kalman Filtering applied to Simultaneous Localization and Mapping: Vehicle moving in 1D, 2D and 3D
- The Kalman Filter in Reproducing Kernel Hilbert Spaces A comprehensive introduction.
- Matlab code to estimate Cox–Ingersoll–Ross interest rate model with Kalman Filter: Corresponds to the paper "estimating and testing exponential-affine term structure models by kalman filter" published by Review of Quantitative Finance and Accounting in 1999.
- Online demo of the Kalman Filter. Demonstration of Kalman Filter (and other data assimilation methods) using twin experiments.
- Botella, Guillermo; Martín h., José Antonio; Santos, Matilde; Meyer-Baese, Uwe (2011). "FPGA-Based Multimodal Embedded Sensor System Integrating Low- and Mid-Level Vision". Sensors. 11 (12): 1251–1259. Bibcode:2011Senso..11.8164B. doi:10.3390/s110808164. PMC 3231703. PMID 22164069.
- Examples and how-to on using Kalman Filters with MATLAB A Tutorial on Filtering and Estimation
- Explaining Filtering (Estimation) in One Hour, Ten Minutes, One Minute, and One Sentence by Yu-Chi Ho
- Simo Särkkä (2013). "Bayesian Filtering and Smoothing". Cambridge University Press. Full text available on author's webpage https://users.aalto.fi/~ssarkka/.