मुक्त ऊर्जा सिद्धांत: Difference between revisions
No edit summary |
No edit summary |
||
| Line 20: | Line 20: | ||
== सिंहावलोकन == | == सिंहावलोकन == | ||
जीव भौतिकी और संज्ञानात्मक विज्ञान में, मुक्त ऊर्जा सिद्धांत एक गणितीय सिद्धांत है जो भौतिक प्रणालियों की प्रतिनिधित्व क्षमताओं का औपचारिक विवरण बताता है: यही कारण है कि जो चीजें | जीव भौतिकी और संज्ञानात्मक विज्ञान में, मुक्त ऊर्जा सिद्धांत एक गणितीय सिद्धांत है जो भौतिक प्रणालियों की प्रतिनिधित्व क्षमताओं का औपचारिक विवरण बताता है: यही कारण है कि जो चीजें सम्मलित हैं वे ऐसी दिखती हैं मानो वे उन प्रणालियों के गुणों को ट्रैक करती हैं जिनसे वे जुड़े हुए हैं।<ref>{{cite journal | ||
| last1 = Friston | | last1 = Friston | ||
| first1 = Karl | | first1 = Karl | ||
| Line 38: | Line 38: | ||
यह स्थापित करता है कि भौतिक प्रणालियों की गतिशीलता आश्चर्य के रूप में ज्ञात मात्रा को कम करती है (जो कि कुछ परिणामों की नकारात्मक लॉग संभावना है); या समकक्ष, इसकी परिवर्तनशील ऊपरी सीमा, जिसे [[परिवर्तनशील मुक्त ऊर्जा]] कहा जाता है। इस सिद्धांत का उपयोग विशेष रूप से मस्तिष्क कार्य के लिए बायेसियन दृष्टिकोण में किया जाता है, लेकिन कृत्रिम बुद्धि के कुछ दृष्टिकोण में भी; यह औपचारिक रूप से वैरिएबल बायेसियन तरीकों से संबंधित है और मूल रूप से [[कार्ल फ्रिस्टन]] द्वारा [[तंत्रिका विज्ञान]] में सन्निहित धारणा-क्रिया लूप के स्पष्टीकरण के रूप में पेश किया गया था।<ref>{{cite journal | last1=Friston | first1=Karl | last2=Kilner | first2=James | last3=Harrison | first3=Lee | title=मस्तिष्क के लिए एक मुक्त ऊर्जा सिद्धांत| journal=Journal of Physiology-Paris | volume=100 | issue=1–3 | year=2006 | doi=10.1016/j.jphysparis.2006.10.001 | pmid=17097864 | pages=70–87| s2cid=637885 |url=http://www.fil.ion.ucl.ac.uk/~karl/A%20free%20energy%20principle%20for%20the%20brain.pdf}}</ref> | यह स्थापित करता है कि भौतिक प्रणालियों की गतिशीलता आश्चर्य के रूप में ज्ञात मात्रा को कम करती है (जो कि कुछ परिणामों की नकारात्मक लॉग संभावना है); या समकक्ष, इसकी परिवर्तनशील ऊपरी सीमा, जिसे [[परिवर्तनशील मुक्त ऊर्जा]] कहा जाता है। इस सिद्धांत का उपयोग विशेष रूप से मस्तिष्क कार्य के लिए बायेसियन दृष्टिकोण में किया जाता है, लेकिन कृत्रिम बुद्धि के कुछ दृष्टिकोण में भी; यह औपचारिक रूप से वैरिएबल बायेसियन तरीकों से संबंधित है और मूल रूप से [[कार्ल फ्रिस्टन]] द्वारा [[तंत्रिका विज्ञान]] में सन्निहित धारणा-क्रिया लूप के स्पष्टीकरण के रूप में पेश किया गया था।<ref>{{cite journal | last1=Friston | first1=Karl | last2=Kilner | first2=James | last3=Harrison | first3=Lee | title=मस्तिष्क के लिए एक मुक्त ऊर्जा सिद्धांत| journal=Journal of Physiology-Paris | volume=100 | issue=1–3 | year=2006 | doi=10.1016/j.jphysparis.2006.10.001 | pmid=17097864 | pages=70–87| s2cid=637885 |url=http://www.fil.ion.ucl.ac.uk/~karl/A%20free%20energy%20principle%20for%20the%20brain.pdf}}</ref> | ||
मुक्त ऊर्जा सिद्धांत उन प्रणालियों के व्यवहार को मॉडल करता है जो किसी अन्य प्रणाली (उदाहरण के लिए, एक अंत:स्थापन वातावरण) से अलग हैं, लेकिन युग्मित हैं, जहां दो प्रणालियों के बीच अंतरापृष्ठ को लागू करने वाली स्वतंत्रता की डिग्री को मार्कोव ब्लैंकेट के रूप में जाना जाता है। अधिक औपचारिक रूप से, मुक्त ऊर्जा सिद्धांत कहता है कि यदि किसी प्रणाली में "विशेष विभाजन" है ( | मुक्त ऊर्जा सिद्धांत उन प्रणालियों के व्यवहार को मॉडल करता है जो किसी अन्य प्रणाली (उदाहरण के लिए, एक अंत:स्थापन वातावरण) से अलग हैं, लेकिन युग्मित हैं, जहां दो प्रणालियों के बीच अंतरापृष्ठ को लागू करने वाली स्वतंत्रता की डिग्री को मार्कोव ब्लैंकेट के रूप में जाना जाता है। अधिक औपचारिक रूप से, मुक्त ऊर्जा सिद्धांत कहता है कि यदि किसी प्रणाली में "विशेष विभाजन" है (अर्थात, कणों में, उनके मार्कोव ब्लैंकेट के साथ), तो उस प्रणाली के उपसमुच्चय अन्य उपसमुच्चय की सांख्यिकीय संरचना को ट्रैक करेंगे (जिन्हें आंतरिक और के रूप में जाना जाता है) किसी प्रणाली की बाहरी अवस्थाएँ या पथ)। | ||
मुक्त ऊर्जा सिद्धांत मस्तिष्क के "[[Index.php?title=अनुमिति इंजन|अनुमिति इंजन]]" के बायेसियन विचार पर आधारित है। मुक्त ऊर्जा सिद्धांत के | मुक्त ऊर्जा सिद्धांत मस्तिष्क के "[[Index.php?title=अनुमिति इंजन|अनुमिति इंजन]]" के बायेसियन विचार पर आधारित है। मुक्त ऊर्जा सिद्धांत के अनुसरा, प्रणाली कम से कम आश्चर्य का रास्ता अपनाते हैं, या समकक्ष रूप से, दुनिया के अपने मॉडल और उनकी [[समझ]] और संबंधित धारणा के आधार पर पूर्वानुमान के बीच अंतर को कम करते हैं। इस अंतर को परिवर्तनशील मुक्त ऊर्जा द्वारा निर्धारित किया जाता है और प्रणाली के विश्व मॉडल के निरंतर सुधार या दुनिया को प्रणाली की पूर्वानुमान की तरह बनाकर कम किया जाता है। दुनिया को अपेक्षित स्थिति के करीब लाने के लिए इसे सक्रिय रूप से बदलकर, प्रणाली की मुक्त ऊर्जा को भी कम कर सकता है। फ्रिस्टन इसे सभी जैविक प्रतिक्रियाओं का सिद्धांत मानता है।<ref name="wired20181112">Shaun Raviv: [https://www.wired.com/story/karl-friston-free-energy-principle-artificial-intelligence/ The Genius Neuroscientist Who Might Hold the Key to True AI]. In: Wired, 13. November 2018</ref> फ्रिस्टन का यह भी मानना है कि उनका सिद्धांत [[Index.php?title=मानसिक विकारों|मानसिक विकारों]] के साथ-साथ कृत्रिम बुद्धिमत्ता पर भी लागू होता है। सक्रिय अनुमान सिद्धांत पर आधारित एआई कार्यान्वयन ने अन्य तरीकों की तुलना में लाभ दिखाया है।<ref name="wired20181112" /> | ||
मुक्त ऊर्जा [[सिद्धांत]] सूचना भौतिकी का एक गणितीय सिद्धांत है: अधिकतम एन्ट्रापी (परिक्षय) के सिद्धांत या कम से कम कार्रवाई के सिद्धांत की तरह, यह गणितीय आधार पर सत्य है। मुक्त ऊर्जा सिद्धांत को गलत | मुक्त ऊर्जा [[सिद्धांत]] सूचना भौतिकी का एक गणितीय सिद्धांत है: अधिकतम एन्ट्रापी (परिक्षय) के सिद्धांत या कम से कम कार्रवाई के सिद्धांत की तरह, यह गणितीय आधार पर सत्य है। मुक्त ऊर्जा सिद्धांत को गलत सिद्ध करने का प्रयास करना एक श्रेणी की गलती है, जो अनुभवजन्य अवलोकन करके [[ गणना | गणना]] को गलत सिद्ध करने की कोशिश करने के समान है। (कोई इस तरह से गणितीय सिद्धांत को अमान्य नहीं कर सकता है; इसके अतरिक्त, किसी को सिद्धांत से एक औपचारिक विरोधाभास प्राप्त करने की आवश्यकता होगी।) 2018 के एक साक्षात्कार में, फ्रिस्टन ने बताया कि मुक्त ऊर्जा सिद्धांत को [[मिथ्याकरणीयता]] के अधीन नहीं होने के लिए इसमें क्या सम्मलित है: मुझे लगता है इस बिंदु पर एक बुनियादी अंतर करना उपयोगी है - जिस पर हम बाद में अपील कर सकते हैं। अंतर एक अवस्था और प्रक्रिया सिद्धांत के बीच है; अर्थात, एक मानक सिद्धांत जिसके अनुरूप चीजें हो भी सकती हैं और नहीं भी, और उस सिद्धांत को कैसे साकार किया जाता है, इसके बारे में एक प्रक्रिया सिद्धांत या परिकल्पना के बीच अंतर है। इस भेद के अनुसरा, मुक्त ऊर्जा सिद्धांत [[Index.php?title=प्रागुक्तीय कोडन|प्रागुक्तीय कोडन]] और बायेसियन मस्तिष्क परिकल्पना जैसी चीजों से बिल्कुल अलग है। ऐसा इसलिए है क्योंकि मुक्त ऊर्जा सिद्धांत - एक सिद्धांत है। हैमिल्टन के सिद्धांत की तरह हैमिल्टन के स्थिर क्रिया के सिद्धांत को गलत सिद्ध नहीं किया जा सकता है। इसका खंडन नहीं किया जा सकता है, वास्तव में, आप इसमें बहुत कुछ नहीं कर सकते, जब तक कि आप यह न पूछें कि मापने योग्य प्रणालियाँ सिद्धांत के अनुरूप हैं या नहीं। दूसरी ओर, ऐसी परिकल्पनाएँ कि मस्तिष्क किसी प्रकार का बायेसियन अनुमान या पूर्वानुमानित कोडन करता है - वे परिकल्पनाएँ हैं। ये परिकल्पनाएँ अनुभवजन्य साक्ष्य द्वारा समर्थित हो भी सकती हैं और नहीं भी।<ref>{{Cite journal|last=Friston|first=Karl|date=2018|title=Of woodlice and men: A Bayesian account of cognition, life and consciousness. An interview with Karl Friston (by Martin Fortier & Daniel Friedman)|url=https://www.aliusresearch.org/bulletin02.html|journal=ALIUS Bulletin|volume=2|pages=17–43}}</ref> इन परिकल्पनाओं के अनुभवजन्य साक्ष्य द्वारा समर्थित होने के कई उदाहरण हैं।<ref>{{Cite book|last=Friston|first=Karl|date=2022|title=Active Inference: The Free Energy Principle in Mind, Brain, and Behavior|publisher=MIT Press |isbn=9780262045353 |url=https://books.google.com/books?id=KXZ_zgEACAAJ&q=Table+9.1}}</ref> | ||
== पृष्ठभूमि == | == पृष्ठभूमि == | ||
यह धारणा कि स्व-संगठित जैविक प्रणालियाँ - जैसे कोशिका या मस्तिष्क - को परिवर्तनशील मुक्त ऊर्जा को कम करने के रूप में समझा जा सकता है, [[हरमन वॉन हेल्महोल्ट्ज़]] के [[अचेतन अनुमान]] पर काम पर आधारित है<ref name="Helmholtz">Helmholtz, H. (1866/1962). Concerning the perceptions in general. In Treatise on physiological optics (J. Southall, Trans., 3rd ed., Vol. III). New York: Dover. Available at https://web.archive.org/web/20180320133752/http://poseidon.sunyopt.edu/BackusLab/Helmholtz/</ref> और मनोविज्ञान में बाद के उपचार<ref>{{cite journal | title=धारणाएँ परिकल्पना के रूप में| journal=Philosophical Transactions of the Royal Society of London. B, Biological Sciences | volume=290 | issue=1038 | date=1980-07-08 | doi=10.1098/rstb.1980.0090 | pmid=6106237 | bibcode=1980RSPTB.290..181G | pages=181–197|jstor=2395424| last1=Gregory | first1=R. L. | doi-access= }}</ref> और मशीन लर्निंग पर।<ref name="Dayan">{{cite journal | last1=Dayan | first1=Peter | last2=Hinton | first2=Geoffrey E. | last3=Neal | first3=Radford M. | last4=Zemel | first4=Richard S. | title=हेल्महोल्ट्ज़ मशीन| journal=Neural Computation | volume=7 | issue=5 | year=1995 | doi=10.1162/neco.1995.7.5.889 | pmid=7584891 | pages=889–904| s2cid=1890561 |url=http://www.gatsby.ucl.ac.uk/~dayan/papers/hm95.pdf| hdl=21.11116/0000-0002-D6D3-E | hdl-access=free }}</ref> परिवर्तनशील मुक्त ऊर्जा उनके छिपे कारणों पर अवलोकन और संभाव्यता घनत्व का एक कार्य है। इस परिवर्तनशील घनत्व को एक संभाव्य मॉडल के संबंध में परिभाषित किया गया है जो परिकल्पित कारणों से अनुमानित अवलोकन उत्पन्न करता है+। इस सेटिंग में, मुक्त ऊर्जा [[सीमांत संभावना]] का अनुमान प्रदान करती है।<ref>Beal, M. J. (2003). [http://www.cse.buffalo.edu/faculty/mbeal/papers/beal03.pdf Variational Algorithms for Approximate Bayesian Inference]. Ph.D. Thesis, University College London.</ref> इसलिए, इसके न्यूनतमकरण को बायेसियन अनुमान प्रक्रिया के रूप में देखा जा सकता है। जब कोई प्रणाली सक्रिय रूप से मुक्त ऊर्जा को कम करने के लिए अवलोकन करती है, तो यह अंतर्निहित रूप से सक्रिय अनुमान लगाती है और दुनिया के अपने मॉडल के लिए साक्ष्य को अधिकतम करती है। | यह धारणा कि स्व-संगठित जैविक प्रणालियाँ - जैसे कोशिका या मस्तिष्क - को परिवर्तनशील मुक्त ऊर्जा को कम करने के रूप में समझा जा सकता है, [[हरमन वॉन हेल्महोल्ट्ज़]] के [[अचेतन अनुमान]] पर काम पर आधारित है<ref name="Helmholtz">Helmholtz, H. (1866/1962). Concerning the perceptions in general. In Treatise on physiological optics (J. Southall, Trans., 3rd ed., Vol. III). New York: Dover. Available at https://web.archive.org/web/20180320133752/http://poseidon.sunyopt.edu/BackusLab/Helmholtz/</ref> और मनोविज्ञान में बाद के उपचार<ref>{{cite journal | title=धारणाएँ परिकल्पना के रूप में| journal=Philosophical Transactions of the Royal Society of London. B, Biological Sciences | volume=290 | issue=1038 | date=1980-07-08 | doi=10.1098/rstb.1980.0090 | pmid=6106237 | bibcode=1980RSPTB.290..181G | pages=181–197|jstor=2395424| last1=Gregory | first1=R. L. | doi-access= }}</ref> और मशीन लर्निंग पर।<ref name="Dayan">{{cite journal | last1=Dayan | first1=Peter | last2=Hinton | first2=Geoffrey E. | last3=Neal | first3=Radford M. | last4=Zemel | first4=Richard S. | title=हेल्महोल्ट्ज़ मशीन| journal=Neural Computation | volume=7 | issue=5 | year=1995 | doi=10.1162/neco.1995.7.5.889 | pmid=7584891 | pages=889–904| s2cid=1890561 |url=http://www.gatsby.ucl.ac.uk/~dayan/papers/hm95.pdf| hdl=21.11116/0000-0002-D6D3-E | hdl-access=free }}</ref> परिवर्तनशील मुक्त ऊर्जा उनके छिपे कारणों पर अवलोकन और संभाव्यता घनत्व का एक कार्य है। इस परिवर्तनशील घनत्व को एक संभाव्य मॉडल के संबंध में परिभाषित किया गया है जो परिकल्पित कारणों से अनुमानित अवलोकन उत्पन्न करता है+। इस सेटिंग में, मुक्त ऊर्जा [[सीमांत संभावना]] का अनुमान प्रदान करती है।<ref>Beal, M. J. (2003). [http://www.cse.buffalo.edu/faculty/mbeal/papers/beal03.pdf Variational Algorithms for Approximate Bayesian Inference]. Ph.D. Thesis, University College London.</ref> इसलिए, इसके न्यूनतमकरण को बायेसियन अनुमान प्रक्रिया के रूप में देखा जा सकता है। जब कोई प्रणाली सक्रिय रूप से मुक्त ऊर्जा को कम करने के लिए अवलोकन करती है, तो यह अंतर्निहित रूप से सक्रिय अनुमान लगाती है और दुनिया के अपने मॉडल के लिए साक्ष्य को अधिकतम करती है। | ||
चूंकि, मुक्त ऊर्जा भी परिणामों की आत्म-सूचना पर एक ऊपरी सीमा है, जहाँ आत्म-सूचना का दीर्घकालिक औसत एन्ट्रापी है। इसका मतलब यह है कि यदि कोई प्रणाली मुक्त ऊर्जा को कम करने के लिए कार्य करती है, तो यह परोक्ष रूप से परिणामों की एन्ट्रापी - या संवेदी अवस्थाओं - के नमूनों पर एक ऊपरी सीमा लगाएगी।<ref name="Towards a Geometry and Analysis for">{{cite arXiv | last1=Sakthivadivel | first1=Dalton | title=बायेसियन यांत्रिकी के लिए एक ज्यामिति और विश्लेषण की ओर| year=2022 | class=math-ph | eprint=2204.11900}}</ref><ref name="On Bayesian mechanics: A physics of">{{cite journal | last1=Ramstead | first1=Maxwell | last2=Sakthivadivel | first2=Dalton | last3=Heins | first3=Conor | last4 = Koudahl | first4 = Magnus | last5 = Millidge | first5 = Beren | last6 = Da Costa | first6 = Lancelot | last7 = Klein | first7 = Brennan | last8 = Friston | first8 = Karl | title=On Bayesian mechanics: A physics of and by beliefs | journal=Interface Focus | year=2023 | volume=13 | issue=3 | doi=10.1098/rsfs.2022.0029 | pmid=37213925 | pmc=10198254 | arxiv=2205.11543| s2cid=249017997 }}</ref> | |||
=== अन्य सिद्धांतों से संबंध === | === अन्य सिद्धांतों से संबंध === | ||
सक्रिय अनुमान अच्छे नियामक प्रमेय से निकटता से संबंधित है<ref>{{cite journal | doi=10.1080/00207727008920220 | title=किसी सिस्टम का प्रत्येक अच्छा नियामक उस सिस्टम का एक मॉडल होना चाहिए| year=1970 | last1=Conant | first1=Roger C. | last2=Ross Ashby | first2=W. | journal=International Journal of Systems Science | volume=1 | issue=2 | pages=89–97 }}</ref> और स्व-संगठन के संबंधित खाते,<ref>Kauffman, S. (1993). [https://books.google.com/books?id=lZcSpRJz0dgC&dq=%22The+Origins+of+Order%3A+Self-Organization+and+Selection+in+Evolution%22&pg=PR13 The Origins of Order: Self-Organization and Selection in Evolution]. Oxford: Oxford University Press.</ref><ref>Nicolis, G., & Prigogine, I. (1977). Self-organization in non-equilibrium systems. New York: John Wiley.</ref> जैसे स्व-संयोजन, पैटर्न निर्माण, [[आत्मनिर्णय का]]<ref>Maturana, H. R., & Varela, F. (1980). [http://topologicalmedialab.net/xinwei/classes/readings/Maturana/autopoesis_and_cognition.pdf Autopoiesis: the organization of the living]. In V. F. Maturana HR (Ed.), Autopoiesis and Cognition. Dordrecht, Netherlands: Reidel.</ref> और [[कार्यान्वयन]]<ref>{{cite journal | doi=10.1016/j.jtbi.2015.03.003 | title=Practopoiesis: Or how life fosters a mind | year=2015 | last1=Nikolić | first1=Danko | journal=Journal of Theoretical Biology | volume=373 | pages=40–61 | pmid=25791287 | arxiv=1402.5332 | bibcode=2015JThBi.373...40N | s2cid=12680941 }}</ref> यह [[साइबरनेटिक्स]], [[सिनर्जेटिक्स (हेकेन)]] में विचार किए गए विषयों को संबोधित करता है<ref>Haken, H. (1983). Synergetics: An introduction. Non-equilibrium phase transition and self-organisation in physics, chemistry and biology (3rd ed.). Berlin: Springer Verlag.</ref> और सन्निहित अनुभूति. क्योंकि मुक्त ऊर्जा को परिवर्तनशील घनत्व के अंतर्गत उसकी एन्ट्रापी को घटाकर प्रेक्षणों की अपेक्षित ऊर्जा के रूप में व्यक्त किया जा सकता है, यह [[अधिकतम एन्ट्रापी सिद्धांत]] से भी संबंधित है।<ref>{{cite journal |doi=10.1103/PhysRev.106.620 |url=http://bayes.wustl.edu/etj/articles/theory.1.pdf|title=सूचना सिद्धांत और सांख्यिकीय यांत्रिकी|year=1957 |last1=Jaynes |first1=E. T. |journal=Physical Review |volume=106 |issue=4 |pages=620–630 |bibcode=1957PhRv..106..620J |s2cid=17870175 }}</ref> अंततः, क्योंकि ऊर्जा का समय औसत क्रिया है, न्यूनतम परिवर्तनशील मुक्त ऊर्जा का सिद्धांत न्यूनतम क्रिया का सिद्धांत है। स्केल निश्चरता की अनुमति देने वाले सक्रिय अनुमान को अन्य सिद्धांतों और डोमेन पर भी लागू किया गया है। उदाहरण के लिए, इसे समाजशास्त्र पर लागू किया गया है,<ref>{{Cite journal |last1=Veissière |first1=Samuel P. L. |last2=Constant |first2=Axel |last3=Ramstead |first3=Maxwell J. D. |last4=Friston |first4=Karl J. |last5=Kirmayer |first5=Laurence J. |date=2020 |title=Thinking through other minds: A variational approach to cognition and culture |url=https://www.cambridge.org/core/journals/behavioral-and-brain-sciences/article/abs/thinking-through-other-minds-a-variational-approach-to-cognition-and-culture/9A10399BA85F428D5943DD847092C14A |journal=Behavioral and Brain Sciences |language=en |volume=43 |pages=e90 |doi=10.1017/S0140525X19001213 |pmid=31142395 |s2cid=169038428 |issn=0140-525X}}</ref><ref>{{Cite journal |last1=Ramstead |first1=Maxwell J. D. |last2=Constant |first2=Axel |last3=Badcock |first3=Paul B. |last4=Friston |first4=Karl J. |date=2019-12-01 |title=परिवर्तनशील पारिस्थितिकी और संवेदनशील प्रणालियों की भौतिकी|journal=Physics of Life Reviews |series=Physics of Mind |language=en |volume=31 |pages=188–205 |doi=10.1016/j.plrev.2018.12.002 |pmid=30655223 |pmc=6941227 |bibcode=2019PhLRv..31..188R |issn=1571-0645}}</ref><ref>{{Cite journal |last1=Albarracin |first1=Mahault |last2=Demekas |first2=Daphne |last3=Ramstead |first3=Maxwell J. D. |last4=Heins |first4=Conor |date=April 2022 |title=सक्रिय अनुमान के तहत ज्ञानमीमांसीय समुदाय|journal=Entropy |language=en |volume=24 |issue=4 |pages=476 |doi=10.3390/e24040476 |pmid=35455140 |pmc=9027706 |bibcode=2022Entrp..24..476A |issn=1099-4300 |doi-access=free }}</ref><ref>{{Cite journal |last1=Albarracin |first1=Mahault |last2=Constant |first2=Axel |last3=Friston |first3=Karl J. |last4=Ramstead |first4=Maxwell James D. |date=2021 |title=लिपियों के प्रति एक विविध दृष्टिकोण|journal=Frontiers in Psychology |volume=12 |page=585493 |doi=10.3389/fpsyg.2021.585493 |pmid=34354621 |pmc=8329037 |issn=1664-1078 |doi-access=free }}</ref> भाषाविज्ञान और संचार,<ref>{{Cite journal |last1=Friston |first1=Karl J. |last2=Parr |first2=Thomas |last3=Yufik |first3=Yan |last4=Sajid |first4=Noor |last5=Price |first5=Catherine J. |last6=Holmes |first6=Emma |date=2020-11-01 |title=जनरेटिव मॉडल, भाषाई संचार और सक्रिय अनुमान|journal=Neuroscience & Biobehavioral Reviews |language=en |volume=118 |pages=42–64 |doi=10.1016/j.neubiorev.2020.07.005 |pmid=32687883 |pmc=7758713 |issn=0149-7634}}</ref><ref>{{Cite journal |last1=Tison |first1=Remi |last2=Poirier |first2=Pierre |date=2021-10-02 |title=Communication as Socially Extended Active Inference: An Ecological Approach to Communicative Behavior |url=https://doi.org/10.1080/10407413.2021.1965480 |journal=Ecological Psychology |volume=33 |issue=3–4 |pages=197–235 |doi=10.1080/10407413.2021.1965480 |s2cid=238703201 |issn=1040-7413}}</ref><ref>{{Cite journal |last1=Friston |first1=Karl J. |last2=Frith |first2=Christopher D. |date=2015-07-01 |title=सक्रिय अनुमान, संचार और व्याख्याशास्त्र|journal=Cortex |series=Special issue: Prediction in speech and language processing |language=en |volume=68 |pages=129–143 |doi=10.1016/j.cortex.2015.03.025 |pmid=25957007 |pmc=4502445 |issn=0010-9452}}</ref> लाक्षणिकता,<ref>{{Cite journal |last=Kerusauskaite |first=Skaiste |date=2023-06-01 |title=Role of Culture in Meaning Making: Bridging Semiotic Cultural Psychology and Active Inference |url=https://doi.org/10.1007/s12124-022-09744-x |journal=Integrative Psychological and Behavioral Science |language=en |volume=57 |issue=2 |pages=432–443 |doi=10.1007/s12124-022-09744-x |pmid=36585542 |s2cid=255366405 |issn=1936-3567}}</ref><ref>{{Cite book |last1=García |first1=Adolfo M. |url=https://books.google.com/books?id=hPCKEAAAQBAJ&dq=active+inference+semiotics&pg=PT90 |title=सेमियोसिस और मस्तिष्क की रूटलेज हैंडबुक|last2=Ibáñez |first2=Agustín |date=2022-11-14 |publisher=Taylor & Francis |isbn=978-1-000-72877-4 |language=en}}</ref> और महामारी विज्ञान <ref>{{Cite journal |last1=Bottemanne |first1=Hugo |last2=Friston |first2=Karl J. |date=2021-12-01 |title=An active inference account of protective behaviours during the COVID-19 pandemic |url=https://doi.org/10.3758/s13415-021-00947-0 |journal=Cognitive, Affective, & Behavioral Neuroscience |language=en |volume=21 |issue=6 |pages=1117–1129 |doi=10.3758/s13415-021-00947-0 |issn=1531-135X |pmc=8518276 |pmid=34652601}}</ref> दूसरों के बीच में। | सक्रिय अनुमान अच्छे नियामक प्रमेय से निकटता से संबंधित है<ref>{{cite journal | doi=10.1080/00207727008920220 | title=किसी सिस्टम का प्रत्येक अच्छा नियामक उस सिस्टम का एक मॉडल होना चाहिए| year=1970 | last1=Conant | first1=Roger C. | last2=Ross Ashby | first2=W. | journal=International Journal of Systems Science | volume=1 | issue=2 | pages=89–97 }}</ref> और स्व-संगठन के संबंधित खाते,<ref>Kauffman, S. (1993). [https://books.google.com/books?id=lZcSpRJz0dgC&dq=%22The+Origins+of+Order%3A+Self-Organization+and+Selection+in+Evolution%22&pg=PR13 The Origins of Order: Self-Organization and Selection in Evolution]. Oxford: Oxford University Press.</ref><ref>Nicolis, G., & Prigogine, I. (1977). Self-organization in non-equilibrium systems. New York: John Wiley.</ref> जैसे स्व-संयोजन, पैटर्न निर्माण, [[आत्मनिर्णय का]]<ref>Maturana, H. R., & Varela, F. (1980). [http://topologicalmedialab.net/xinwei/classes/readings/Maturana/autopoesis_and_cognition.pdf Autopoiesis: the organization of the living]. In V. F. Maturana HR (Ed.), Autopoiesis and Cognition. Dordrecht, Netherlands: Reidel.</ref> और [[कार्यान्वयन]]<ref>{{cite journal | doi=10.1016/j.jtbi.2015.03.003 | title=Practopoiesis: Or how life fosters a mind | year=2015 | last1=Nikolić | first1=Danko | journal=Journal of Theoretical Biology | volume=373 | pages=40–61 | pmid=25791287 | arxiv=1402.5332 | bibcode=2015JThBi.373...40N | s2cid=12680941 }}</ref> यह [[साइबरनेटिक्स]], [[सिनर्जेटिक्स (हेकेन)]] में विचार किए गए विषयों को संबोधित करता है<ref>Haken, H. (1983). Synergetics: An introduction. Non-equilibrium phase transition and self-organisation in physics, chemistry and biology (3rd ed.). Berlin: Springer Verlag.</ref> और सन्निहित अनुभूति. क्योंकि मुक्त ऊर्जा को परिवर्तनशील घनत्व के अंतर्गत उसकी एन्ट्रापी को घटाकर प्रेक्षणों की अपेक्षित ऊर्जा के रूप में व्यक्त किया जा सकता है, यह [[अधिकतम एन्ट्रापी सिद्धांत]] से भी संबंधित है।<ref>{{cite journal |doi=10.1103/PhysRev.106.620 |url=http://bayes.wustl.edu/etj/articles/theory.1.pdf|title=सूचना सिद्धांत और सांख्यिकीय यांत्रिकी|year=1957 |last1=Jaynes |first1=E. T. |journal=Physical Review |volume=106 |issue=4 |pages=620–630 |bibcode=1957PhRv..106..620J |s2cid=17870175 }}</ref> अंततः, क्योंकि ऊर्जा का समय औसत क्रिया है, न्यूनतम परिवर्तनशील मुक्त ऊर्जा का सिद्धांत न्यूनतम क्रिया का सिद्धांत है। स्केल निश्चरता की अनुमति देने वाले सक्रिय अनुमान को अन्य सिद्धांतों और डोमेन पर भी लागू किया गया है। उदाहरण के लिए, इसे समाजशास्त्र पर लागू किया गया है,<ref>{{Cite journal |last1=Veissière |first1=Samuel P. L. |last2=Constant |first2=Axel |last3=Ramstead |first3=Maxwell J. D. |last4=Friston |first4=Karl J. |last5=Kirmayer |first5=Laurence J. |date=2020 |title=Thinking through other minds: A variational approach to cognition and culture |url=https://www.cambridge.org/core/journals/behavioral-and-brain-sciences/article/abs/thinking-through-other-minds-a-variational-approach-to-cognition-and-culture/9A10399BA85F428D5943DD847092C14A |journal=Behavioral and Brain Sciences |language=en |volume=43 |pages=e90 |doi=10.1017/S0140525X19001213 |pmid=31142395 |s2cid=169038428 |issn=0140-525X}}</ref><ref>{{Cite journal |last1=Ramstead |first1=Maxwell J. D. |last2=Constant |first2=Axel |last3=Badcock |first3=Paul B. |last4=Friston |first4=Karl J. |date=2019-12-01 |title=परिवर्तनशील पारिस्थितिकी और संवेदनशील प्रणालियों की भौतिकी|journal=Physics of Life Reviews |series=Physics of Mind |language=en |volume=31 |pages=188–205 |doi=10.1016/j.plrev.2018.12.002 |pmid=30655223 |pmc=6941227 |bibcode=2019PhLRv..31..188R |issn=1571-0645}}</ref><ref>{{Cite journal |last1=Albarracin |first1=Mahault |last2=Demekas |first2=Daphne |last3=Ramstead |first3=Maxwell J. D. |last4=Heins |first4=Conor |date=April 2022 |title=सक्रिय अनुमान के तहत ज्ञानमीमांसीय समुदाय|journal=Entropy |language=en |volume=24 |issue=4 |pages=476 |doi=10.3390/e24040476 |pmid=35455140 |pmc=9027706 |bibcode=2022Entrp..24..476A |issn=1099-4300 |doi-access=free }}</ref><ref>{{Cite journal |last1=Albarracin |first1=Mahault |last2=Constant |first2=Axel |last3=Friston |first3=Karl J. |last4=Ramstead |first4=Maxwell James D. |date=2021 |title=लिपियों के प्रति एक विविध दृष्टिकोण|journal=Frontiers in Psychology |volume=12 |page=585493 |doi=10.3389/fpsyg.2021.585493 |pmid=34354621 |pmc=8329037 |issn=1664-1078 |doi-access=free }}</ref> भाषाविज्ञान और संचार,<ref>{{Cite journal |last1=Friston |first1=Karl J. |last2=Parr |first2=Thomas |last3=Yufik |first3=Yan |last4=Sajid |first4=Noor |last5=Price |first5=Catherine J. |last6=Holmes |first6=Emma |date=2020-11-01 |title=जनरेटिव मॉडल, भाषाई संचार और सक्रिय अनुमान|journal=Neuroscience & Biobehavioral Reviews |language=en |volume=118 |pages=42–64 |doi=10.1016/j.neubiorev.2020.07.005 |pmid=32687883 |pmc=7758713 |issn=0149-7634}}</ref><ref>{{Cite journal |last1=Tison |first1=Remi |last2=Poirier |first2=Pierre |date=2021-10-02 |title=Communication as Socially Extended Active Inference: An Ecological Approach to Communicative Behavior |url=https://doi.org/10.1080/10407413.2021.1965480 |journal=Ecological Psychology |volume=33 |issue=3–4 |pages=197–235 |doi=10.1080/10407413.2021.1965480 |s2cid=238703201 |issn=1040-7413}}</ref><ref>{{Cite journal |last1=Friston |first1=Karl J. |last2=Frith |first2=Christopher D. |date=2015-07-01 |title=सक्रिय अनुमान, संचार और व्याख्याशास्त्र|journal=Cortex |series=Special issue: Prediction in speech and language processing |language=en |volume=68 |pages=129–143 |doi=10.1016/j.cortex.2015.03.025 |pmid=25957007 |pmc=4502445 |issn=0010-9452}}</ref> लाक्षणिकता,<ref>{{Cite journal |last=Kerusauskaite |first=Skaiste |date=2023-06-01 |title=Role of Culture in Meaning Making: Bridging Semiotic Cultural Psychology and Active Inference |url=https://doi.org/10.1007/s12124-022-09744-x |journal=Integrative Psychological and Behavioral Science |language=en |volume=57 |issue=2 |pages=432–443 |doi=10.1007/s12124-022-09744-x |pmid=36585542 |s2cid=255366405 |issn=1936-3567}}</ref><ref>{{Cite book |last1=García |first1=Adolfo M. |url=https://books.google.com/books?id=hPCKEAAAQBAJ&dq=active+inference+semiotics&pg=PT90 |title=सेमियोसिस और मस्तिष्क की रूटलेज हैंडबुक|last2=Ibáñez |first2=Agustín |date=2022-11-14 |publisher=Taylor & Francis |isbn=978-1-000-72877-4 |language=en}}</ref> और महामारी विज्ञान <ref>{{Cite journal |last1=Bottemanne |first1=Hugo |last2=Friston |first2=Karl J. |date=2021-12-01 |title=An active inference account of protective behaviours during the COVID-19 pandemic |url=https://doi.org/10.3758/s13415-021-00947-0 |journal=Cognitive, Affective, & Behavioral Neuroscience |language=en |volume=21 |issue=6 |pages=1117–1129 |doi=10.3758/s13415-021-00947-0 |issn=1531-135X |pmc=8518276 |pmid=34652601}}</ref> दूसरों के बीच में। | ||
नकारात्मक मुक्त ऊर्जा औपचारिक रूप से निचली सीमा के साक्ष्य के बराबर है, जिसका उपयोग | नकारात्मक मुक्त ऊर्जा औपचारिक रूप से निचली सीमा के साक्ष्य के बराबर है, जिसका उपयोग सामान्यत: [[ यंत्र अधिगम ]] में [[जनरेटिव मॉडल]], जैसे [[ वैरिएशनल ऑटोएनकोडर | विचरणी ऑटोकोडितर]] को प्रशिक्षित करने के लिए किया जाता है। | ||
== क्रिया और धारणा == | == क्रिया और धारणा == | ||
| Line 60: | Line 60: | ||
सक्रिय अनुमान एक जनरेटिव मॉडल से संवेदी आँकड़े के कारणों का अनुमान लगाने के लिए [[अनुमानित बायेसियन गणना]] की तकनीकों को लागू करता है। 'जनरेटिव' मॉडल के आँकड़े कैसे उत्पन्न होते है और फिर कार्रवाई का मार्गदर्शन करने के लिए इन अनुमानों का उपयोग करता है। | सक्रिय अनुमान एक जनरेटिव मॉडल से संवेदी आँकड़े के कारणों का अनुमान लगाने के लिए [[अनुमानित बायेसियन गणना]] की तकनीकों को लागू करता है। 'जनरेटिव' मॉडल के आँकड़े कैसे उत्पन्न होते है और फिर कार्रवाई का मार्गदर्शन करने के लिए इन अनुमानों का उपयोग करता है। | ||
बेयस नियम ऐसे कारण मॉडल के संभाव्य रूप से इष्टतम उलटा की विशेषता बताता है, लेकिन इसे लागू करना | बेयस नियम ऐसे कारण मॉडल के संभाव्य रूप से इष्टतम उलटा की विशेषता बताता है, लेकिन इसे लागू करना सामान्यत: अभिकलनीयतः रूप से कठिन होता है, जिससे अनुमानित तरीकों का उपयोग होता है। | ||
सक्रिय अनुमान में, ऐसे अनुमानित तरीकों का अग्रणी वर्ग व्यावहारिक और सैद्धांतिक दोनों कारणों से विचरणी बायेसियन विधियां हैं: व्यावहारिक, क्योंकि वे | सक्रिय अनुमान में, ऐसे अनुमानित तरीकों का अग्रणी वर्ग व्यावहारिक और सैद्धांतिक दोनों कारणों से विचरणी बायेसियन विधियां हैं: व्यावहारिक, क्योंकि वे अधिकांशत: सरल अनुमान प्रक्रियाओं की ओर ले जाते हैं; और सैद्धांतिक, क्योंकि वे मूलभूत भौतिक सिद्धांतों से संबंधित हैं, जैसा कि ऊपर चर्चा की गई है। | ||
ये परिवर्तनशील विधियाँ बेयस-इष्टतम अनुमान (या 'पश्च संभाव्यता') और विधि के अनुसार इसके सन्निकटन के बीच विचलन पर ऊपरी सीमा को कम करके आगे बढ़ती हैं। | ये परिवर्तनशील विधियाँ बेयस-इष्टतम अनुमान (या 'पश्च संभाव्यता') और विधि के अनुसार इसके सन्निकटन के बीच विचलन पर ऊपरी सीमा को कम करके आगे बढ़ती हैं। | ||
| Line 70: | Line 70: | ||
यह समग्र दोहरा अनुकूलन सक्रिय अनुमान की विशेषता है, और मुक्त ऊर्जा सिद्धांत यह परिकल्पना है कि सभी प्रणालियाँ जो अनुभव करती हैं और कार्य करती हैं, उन्हें इस तरह से चित्रित किया जा सकता है। | यह समग्र दोहरा अनुकूलन सक्रिय अनुमान की विशेषता है, और मुक्त ऊर्जा सिद्धांत यह परिकल्पना है कि सभी प्रणालियाँ जो अनुभव करती हैं और कार्य करती हैं, उन्हें इस तरह से चित्रित किया जा सकता है। | ||
मुक्त ऊर्जा सिद्धांत के माध्यम से सक्रिय अनुमान के यांत्रिकी का उदाहरण देने के लिए, एक जेनरेटिव मॉडल निर्दिष्ट किया जाना चाहिए, और इसमें | मुक्त ऊर्जा सिद्धांत के माध्यम से सक्रिय अनुमान के यांत्रिकी का उदाहरण देने के लिए, एक जेनरेटिव मॉडल निर्दिष्ट किया जाना चाहिए, और इसमें सामान्यत: संभाव्यता घनत्व कार्यों का संग्रह सम्मलित होता है जो एक साथ कारण मॉडल को चित्रित करता है। | ||
ऐसी ही एक विशिष्टता इस प्रकार है. | ऐसी ही एक विशिष्टता इस प्रकार है. | ||
| Line 79: | Line 79: | ||
चित्र 1 को ध्यान में रखते हुए, ध्यान दें कि निम्नलिखित में <math>\dot{\psi}, \psi, s, a</math> और <math>\mu</math> (निरंतर) समय के कार्य <math>t</math> हैं। जेनरेटिव मॉडल निम्नलिखित घनत्व कार्यों का विनिर्देश है: | चित्र 1 को ध्यान में रखते हुए, ध्यान दें कि निम्नलिखित में <math>\dot{\psi}, \psi, s, a</math> और <math>\mu</math> (निरंतर) समय के कार्य <math>t</math> हैं। जेनरेटिव मॉडल निम्नलिखित घनत्व कार्यों का विनिर्देश है: | ||
* एक संवेदी मॉडल, <math>p_S:S \times \Psi\times A \to \mathbb{R}</math>, | * एक संवेदी मॉडल, <math>p_S:S \times \Psi\times A \to \mathbb{R}</math>, अधिकांशत: के रूप में लिखा जाता है <math>p_S(s \mid \psi, a)</math>, बाहरी अवस्थाओं और क्रियाओं को देखते हुए संवेदी आँकड़े की संभावना को चिह्नित करना; | ||
*पर्यावरणीय गतिशीलता का एक स्टोकेस्टिक मॉडल, <math>p_\Psi: \Psi \times \Psi \times A \to \mathbb{R}</math>, | *पर्यावरणीय गतिशीलता का एक स्टोकेस्टिक मॉडल, <math>p_\Psi: \Psi \times \Psi \times A \to \mathbb{R}</math>, अधिकांशत: लिखा जाता है <math>p_\Psi(\dot{\psi} \mid \psi, a)</math>, यह वर्णन करते हुए कि कारक द्वारा समय के साथ बाहरी स्थितियों के विकसित होने की अपेक्षा कैसे की जाती है <math>t</math>, कारक के कार्यों को देखते हुए; | ||
* एक क्रिया मॉडल, <math>p_A: A \times R \times S \to \mathbb{R}</math>, लिखा हुआ <math>p_A(a \mid \mu, s)</math>, यह वर्णन करना कि कारक की गतिविधियां उसकी आंतरिक स्थिति और संवेदी आँकड़े पर कैसे निर्भर करती हैं; | * एक क्रिया मॉडल, <math>p_A: A \times R \times S \to \mathbb{R}</math>, लिखा हुआ <math>p_A(a \mid \mu, s)</math>, यह वर्णन करना कि कारक की गतिविधियां उसकी आंतरिक स्थिति और संवेदी आँकड़े पर कैसे निर्भर करती हैं; | ||
* एक आंतरिक मॉडल, <math>p_R: R \times S \to \mathbb{R}</math>, लिखा हुआ <math>p_R(\mu \mid s)</math>, यह वर्णन करते हुए कि कारक की आंतरिक स्थिति उसके संवेदी आँकड़े पर कैसे निर्भर करती है। | * एक आंतरिक मॉडल, <math>p_R: R \times S \to \mathbb{R}</math>, लिखा हुआ <math>p_R(\mu \mid s)</math>, यह वर्णन करते हुए कि कारक की आंतरिक स्थिति उसके संवेदी आँकड़े पर कैसे निर्भर करती है। | ||
| Line 101: | Line 101: | ||
a^* &= \underset{a}{\operatorname{arg\,min}} \{ F(\mu^*, a \,;\, s) \} | a^* &= \underset{a}{\operatorname{arg\,min}} \{ F(\mu^*, a \,;\, s) \} | ||
\end{align}</math> | \end{align}</math> | ||
जहाँ आंतरिक स्थिति है <math>\mu</math> | जहाँ आंतरिक स्थिति है <math>\mu</math> सामान्यत: 'परिवर्तनशील' घनत्व के मापदंडों को कोडित करने के लिए लिया जाता है, <math>q</math> के मापदंडों को एनकोड करने के लिए लिया जाता है और इसलिए एजेंट का पश्च विश्वास के बारे में "सर्वोत्तम अनुमान" होता है <math>\Psi</math>. | ||
ध्यान दें कि मुक्त ऊर्जा भी कारक ([[सीमांत वितरण]], या औसत) संवेदी सूचना सामग्री के माप पर एक ऊपरी सीमा है, और इसलिए मुक्त ऊर्जा न्यूनतमकरण | ध्यान दें कि मुक्त ऊर्जा भी कारक ([[सीमांत वितरण]], या औसत) संवेदी सूचना सामग्री के माप पर एक ऊपरी सीमा है, और इसलिए मुक्त ऊर्जा न्यूनतमकरण अधिकांशत: आश्चर्य को कम करने से प्रेरित होता है। | ||
== निःशुल्क ऊर्जा न्यूनतमकरण == | == निःशुल्क ऊर्जा न्यूनतमकरण == | ||
| Line 109: | Line 109: | ||
=== निःशुल्क ऊर्जा न्यूनतमकरण और स्व-संगठन === | === निःशुल्क ऊर्जा न्यूनतमकरण और स्व-संगठन === | ||
यादृच्छिक गतिशील प्रणालियों के रूप में डाले जाने पर मुक्त ऊर्जा न्यूनीकरण को स्व-संगठित प्रणालियों की एक पहचान के रूप में प्रस्तावित किया गया है।<ref>{{cite journal |doi=10.1007/BF01193705 |url=https://www.researchgate.net/publication/227072665|title=यादृच्छिक गतिशील प्रणालियों के लिए आकर्षण|year=1994 |last1=Crauel |first1=Hans |last2=Flandoli |first2=Franco |journal=Probability Theory and Related Fields |volume=100 |issue=3 |pages=365–393 |s2cid=122609512 |doi-access=free }}</ref> यह सूत्रीकरण एक मार्कोव ब्लैंकेट (जिसमें क्रिया और संवेदी अवस्थाएँ | यादृच्छिक गतिशील प्रणालियों के रूप में डाले जाने पर मुक्त ऊर्जा न्यूनीकरण को स्व-संगठित प्रणालियों की एक पहचान के रूप में प्रस्तावित किया गया है।<ref>{{cite journal |doi=10.1007/BF01193705 |url=https://www.researchgate.net/publication/227072665|title=यादृच्छिक गतिशील प्रणालियों के लिए आकर्षण|year=1994 |last1=Crauel |first1=Hans |last2=Flandoli |first2=Franco |journal=Probability Theory and Related Fields |volume=100 |issue=3 |pages=365–393 |s2cid=122609512 |doi-access=free }}</ref> यह सूत्रीकरण एक मार्कोव ब्लैंकेट (जिसमें क्रिया और संवेदी अवस्थाएँ सम्मलित हैं) पर टिकी हुई है जो आंतरिक और बाहरी अवस्थाओं को अलग करती है। यदि आंतरिक अवस्थाएँ और क्रियाएँ मुक्त ऊर्जा को कम करती हैं, तो वे संवेदी अवस्थाओं की एन्ट्रापी पर एक ऊपरी सीमा लगाते हैं: | ||
: <math> \lim_{T\to\infty} \frac{1}{T} \underset{\text{free-action}} {\underbrace{\int_0^T F(s(t),\mu (t))\,dt}} \ge | : <math> \lim_{T\to\infty} \frac{1}{T} \underset{\text{free-action}} {\underbrace{\int_0^T F(s(t),\mu (t))\,dt}} \ge | ||
\lim_{T\to\infty} \frac{1}{T} \int_0^T \underset{\text{surprise}}{\underbrace{-\log p(s(t)\mid m)}} \, dt = H[p(s\mid m)] </math> | \lim_{T\to\infty} \frac{1}{T} \int_0^T \underset{\text{surprise}}{\underbrace{-\log p(s(t)\mid m)}} \, dt = H[p(s\mid m)] </math> | ||
ऐसा इसलिए है क्योंकि - [[एर्गोडिक सिद्धांत]] मान्यताओं के | ऐसा इसलिए है क्योंकि - [[एर्गोडिक सिद्धांत]] मान्यताओं के अनुसरा - आश्चर्य का दीर्घकालिक औसत एन्ट्रापी है। यह बाध्यता अव्यवस्था की एक प्राकृतिक प्रवृत्ति का विरोध करती है - थर्मोडायनामिक्स (ऊष्मागतिकी) के दूसरे नियम और [[उतार-चढ़ाव प्रमेय]] से जुड़े प्रकार की, चूंकि, सांख्यिकीय भौतिकी से अवधारणाओं के संदर्भ में जीवन विज्ञान के लिए एक एकीकृत सिद्धांत तैयार करना, जैसे कि यादृच्छिक गतिशील प्रणाली, गैर-संतुलन स्थिर स्थिति और अभ्यतिप्रायता, सभी को अस्पष्ट करने के जोखिम के साथ जैविक प्रणालियों के सैद्धांतिक और अनुभवजन्य अध्ययन पर पर्याप्त बाधाएं डालता है। ऐसी विशेषताएँ जो जैविक प्रणालियों को रोचक प्रकार की स्व-संगठित प्रणालियाँ बनाती हैं।<ref>{{cite journal | doi=10.1007/s10539-021-09818-x | title=गैर-संतुलन थर्मोडायनामिक्स और जीव विज्ञान में मुक्त ऊर्जा सिद्धांत| year=2021 | last1=Colombo | first1=Matteo | last2=Palacios | first2=Patricia | journal=Biology & Philosophy | volume=36 | issue=5 | s2cid=235803361 | doi-access=free }}</ref> | ||
=== मुक्त ऊर्जा न्यूनीकरण और बायेसियन अनुमान === | === मुक्त ऊर्जा न्यूनीकरण और बायेसियन अनुमान === | ||
सभी बायेसियन अनुमान मुक्त ऊर्जा न्यूनीकरण के संदर्भ में लगाए जा सकते हैं<ref>{{cite journal |url=http://authors.library.caltech.edu/13697/1/ROWnc99.pdf |doi=10.1162/089976699300016674|title=रैखिक गाऊसी मॉडल की एक एकीकृत समीक्षा|year=1999 |last1=Roweis |first1=Sam |last2=Ghahramani |first2=Zoubin |journal=Neural Computation |volume=11 |issue=2 |pages=305–345 |pmid=9950734 |s2cid=2590898 }}</ref>{{Failed verification|date=April 2020}}. जब आंतरिक अवस्थाओं के संबंध में मुक्त ऊर्जा को कम किया जाता है, तो छिपी हुई अवस्थाओं पर परिवर्तनशील और पश्च घनत्व के बीच कुल्बैक-लीबलर विचलन कम हो जाता है। यह अनुमानित बायेसियन अनुमान से मेल खाता है - जब परिवर्तनशील घनत्व का रूप निश्चित होता है - और अन्यथा सटीक बायेसियन अनुमान होता है। इसलिए | सभी बायेसियन अनुमान मुक्त ऊर्जा न्यूनीकरण के संदर्भ में लगाए जा सकते हैं<ref>{{cite journal |url=http://authors.library.caltech.edu/13697/1/ROWnc99.pdf |doi=10.1162/089976699300016674|title=रैखिक गाऊसी मॉडल की एक एकीकृत समीक्षा|year=1999 |last1=Roweis |first1=Sam |last2=Ghahramani |first2=Zoubin |journal=Neural Computation |volume=11 |issue=2 |pages=305–345 |pmid=9950734 |s2cid=2590898 }}</ref>{{Failed verification|date=April 2020}}. जब आंतरिक अवस्थाओं के संबंध में मुक्त ऊर्जा को कम किया जाता है, तो छिपी हुई अवस्थाओं पर परिवर्तनशील और पश्च घनत्व के बीच कुल्बैक-लीबलर विचलन कम हो जाता है। यह अनुमानित बायेसियन अनुमान से मेल खाता है - जब परिवर्तनशील घनत्व का रूप निश्चित होता है - और अन्यथा सटीक बायेसियन अनुमान होता है। इसलिए मुक्त ऊर्जा न्यूनीकरण बायेसियन अनुमान और फ़िल्टरिंग (उदाहरण के लिए, [[कलमन फ़िल्टर]]) का एक सामान्य विवरण प्रदान करता है। इसका उपयोग बायेसियन [[मॉडल चयन]] में भी किया जाता है, जहां मुक्त ऊर्जा को जटिलता और सटीकता में उपयोगी रूप से विघटित किया जा सकता है: | ||
: <math> \underset{\text{free-energy}} {\underbrace{ F(s,\mu)}} = \underset{\text{complexity}} {\underbrace{ D_\mathrm{KL}[q(\psi\mid\mu)\parallel p(\psi\mid m)]}} - \underset{\mathrm{accuracy}} {\underbrace{E_q[\log p(s\mid\psi,m)]}}</math> | : <math> \underset{\text{free-energy}} {\underbrace{ F(s,\mu)}} = \underset{\text{complexity}} {\underbrace{ D_\mathrm{KL}[q(\psi\mid\mu)\parallel p(\psi\mid m)]}} - \underset{\mathrm{accuracy}} {\underbrace{E_q[\log p(s\mid\psi,m)]}}</math> | ||
न्यूनतम मुक्त ऊर्जा वाले मॉडल जटिलता लागत (सी.एफ., ओकैम के रेजर और अभिकलनीयतः लागत के अधिक औपचारिक उपचार) के | न्यूनतम मुक्त ऊर्जा वाले मॉडल जटिलता लागत (सी.एफ., ओकैम के रेजर और अभिकलनीयतः लागत के अधिक औपचारिक उपचार) के अनुसरा आँकड़े का सटीक स्पष्टीकरण प्रदान करते हैं।<ref>{{cite journal | url=http://rspa.royalsocietypublishing.org/content/469/2153/20120683 | doi=10.1098/rspa.2012.0683 | title=सूचना-प्रसंस्करण लागत के साथ निर्णय लेने के सिद्धांत के रूप में थर्मोडायनामिक्स| year=2013 | last1=Ortega | first1=Pedro A. | last2=Braun | first2=Daniel A. | journal=Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences | volume=469 | issue=2153 | arxiv=1204.6481 | bibcode=2013RSPSA.46920683O | s2cid=28080508 }}</ref> यहां, जटिलता परिवर्तनशील घनत्व और छुपे हुए स्थिति के बारे में पूर्व मान्यताओं (अर्थात, आँकड़े को समझाने के लिए उपयोग की जाने वाली स्वतंत्रता की प्रभावी डिग्री) के बीच विचलन है। | ||
=== मुक्त ऊर्जा न्यूनतमकरण और ऊष्मागतिकी === | === मुक्त ऊर्जा न्यूनतमकरण और ऊष्मागतिकी === | ||
परिवर्तनशील मुक्त ऊर्जा एक सूचना-सैद्धांतिक कार्यात्मक है और ऊष्मागतिक (हेल्महोल्ट्ज़) [[हेल्महोल्ट्ज़ मुक्त ऊर्जा]] से अलग है।<ref>{{cite journal |url=http://rscweb.anu.edu.au/~evans/papers/NEFET.pdf |doi=10.1080/0026897031000085173|title=नियतात्मक प्रणालियों के लिए एक गैर-संतुलन मुक्त ऊर्जा प्रमेय|year=2003 |last1=Evans |first1=Denis J. |journal=Molecular Physics |volume=101 |issue=10 |pages=1551–1554 |bibcode=2003MolPh.101.1551E |s2cid=15129000 }}</ref> | परिवर्तनशील मुक्त ऊर्जा एक सूचना-सैद्धांतिक कार्यात्मक है और ऊष्मागतिक (हेल्महोल्ट्ज़) [[हेल्महोल्ट्ज़ मुक्त ऊर्जा]] से अलग है।<ref>{{cite journal |url=http://rscweb.anu.edu.au/~evans/papers/NEFET.pdf |doi=10.1080/0026897031000085173|title=नियतात्मक प्रणालियों के लिए एक गैर-संतुलन मुक्त ऊर्जा प्रमेय|year=2003 |last1=Evans |first1=Denis J. |journal=Molecular Physics |volume=101 |issue=10 |pages=1551–1554 |bibcode=2003MolPh.101.1551E |s2cid=15129000 }}</ref> चूंकि, परिवर्तनशील मुक्त ऊर्जा की जटिलता अवधि हेल्महोल्त्ज़ मुक्त ऊर्जा के समान निश्चित बिंदु को साझा करती है (धारणा के अनुसरा प्रणाली ऊष्मागतिक रूप से बंद है लेकिन पृथक नहीं है)। ऐसा इसलिए है क्योंकि यदि संवेदी गड़बड़ी को (उपयुक्त लंबी अवधि के लिए) निलंबित कर दिया जाता है, तो जटिलता कम हो जाती है (क्योंकि सटीकता की उपेक्षा की जा सकती है)। इस बिंदु पर, प्रणाली संतुलन पर है और आंतरिक अवस्थाएं न्यूनतम ऊर्जा के सिद्धांत द्वारा हेल्महोल्ट्ज़ मुक्त ऊर्जा को कम करती हैं।<ref>{{cite journal | arxiv=cond-mat/9610209 | doi=10.1103/PhysRevLett.78.2690 | title=मुक्त ऊर्जा अंतर के लिए कोई भी संतुलन समानता नहीं| year=1997 | last1=Jarzynski | first1=C. | journal=Physical Review Letters | volume=78 | issue=14 | pages=2690–2693 | bibcode=1997PhRvL..78.2690J | s2cid=16112025 }}</ref> | ||
| Line 133: | Line 133: | ||
== तंत्रिका विज्ञान में मुक्त ऊर्जा न्यूनीकरण == | == तंत्रिका विज्ञान में मुक्त ऊर्जा न्यूनीकरण == | ||
मुक्त ऊर्जा न्यूनीकरण, अनिश्चितता के अनुसरा तंत्रिका अनुमान और सीखने के मानक (बेयस इष्टतम) मॉडल तैयार करने का एक उपयोगी तरीका प्रदान करता है।<ref>{{cite journal |url=http://www.fil.ion.ucl.ac.uk/~karl/The%20free-energy%20principle%20A%20unified%20brain%20theory.pdf |doi=10.1038/nrn2787|title=The free-energy principle: A unified brain theory? |year=2010 |last1=Friston |first1=Karl |journal=Nature Reviews Neuroscience |volume=11 |issue=2 |pages=127–138 |pmid=20068583 |s2cid=5053247 }}</ref> और इसलिए [[बायेसियन मस्तिष्क]] परिकल्पना की सदस्यता लेता है।<ref>{{cite journal |doi=10.1016/j.tins.2004.10.007 |url=http://mrl.isr.uc.pt/pub/bscw.cgi/d27540/ReviewKnillPouget2.pdf|title=The Bayesian brain: The role of uncertainty in neural coding and computation |year=2004 |last1=Knill |first1=David C. |last2=Pouget |first2=Alexandre |journal=Trends in Neurosciences |volume=27 |issue=12 |pages=712–719 |pmid=15541511 |s2cid=9870936 }}</ref> मुक्त ऊर्जा न्यूनतमकरण द्वारा वर्णित तंत्रिका प्रक्रियाएं छिपी हुई अवस्थाओं की प्रकृति पर निर्भर करती हैं: <math> \Psi = X \times \Theta \times \Pi </math> इसमें समय-निर्भर चर, समय-अपरिवर्तनीय पैरामीटर और यादृच्छिक उतार-चढ़ाव की सटीकता (उलटा विचरण या तापमान) सम्मलित हो सकते हैं। चर, पैरामीटर और परिशुद्धता को न्यूनतम करना क्रमशः अनुमान, सीखने और अनिश्चितता के कोडन के अनुरूप है। | |||
=== अवधारणात्मक अनुमान और वर्गीकरण === | === अवधारणात्मक अनुमान और वर्गीकरण === | ||
मुक्त ऊर्जा न्यूनीकरण धारणा में अचेतन अनुमान की धारणा को औपचारिक बनाता है<ref name="Helmholtz" /><ref name="Dayan" />और | मुक्त ऊर्जा न्यूनीकरण धारणा में अचेतन अनुमान की धारणा को औपचारिक बनाता है<ref name="Helmholtz" /><ref name="Dayan" />और तंत्रिका प्रसंस्करण का एक मानक (बायेसियन) सिद्धांत प्रदान करता है। तंत्रिका डायनेमिक्स का संबद्ध प्रक्रिया सिद्धांत प्रवणता अवरोह के माध्यम से मुक्त ऊर्जा को कम करने पर आधारित है। यह [[Index.php?title=सामान्यीकृत परिसरण|सामान्यीकृत परिसरण]] से मेल खाता है (जहां ~ गति के सामान्यीकृत निर्देशांक में एक चर को दर्शाता है और <math>D</math> एक व्युत्पन्न मैट्रिक्स ऑपरेटर है):<ref>{{cite journal | doi=10.1155/2010/621670 | doi-access=free | title=सामान्यीकृत फ़िल्टरिंग| year=2010 | last1=Friston | first1=Karl | last2=Stephan | first2=Klaas | last3=Li | first3=Baojuan | last4=Daunizeau | first4=Jean | journal=Mathematical Problems in Engineering | volume=2010 | pages=1–34 }}</ref> | ||
: <math>\dot{\tilde{\mu}} = D \tilde{\mu} - \partial_{\mu}F(s,\mu)\Big|_{\mu = \tilde{\mu}}</math> | : <math>\dot{\tilde{\mu}} = D \tilde{\mu} - \partial_{\mu}F(s,\mu)\Big|_{\mu = \tilde{\mu}}</math> | ||
सामान्यत:, मुक्त ऊर्जा को परिभाषित करने वाले उत्पादक मॉडल गैर-रैखिक और पदानुक्रमित होते हैं (मस्तिष्क में कॉर्टिकल पदानुक्रम की तरह)। सामान्यीकृत फ़िल्टरिंग के विशेष स्थितियों में कलमन फ़िल्टरिंग सम्मलित है, जो औपचारिक रूप से पूर्वानुमानित कोडन के बराबर है<ref>{{cite journal |doi=10.1016/j.tins.2004.10.007 |url=https://www.cs.utexas.edu/users/dana/nn.pdf|title=The Bayesian brain: The role of uncertainty in neural coding and computation |year=2004 |last1=Knill |first1=David C. |last2=Pouget |first2=Alexandre |journal=Trends in Neurosciences |volume=27 |issue=12 |pages=712–719 |pmid=15541511 |s2cid=9870936 }}</ref> - मस्तिष्क में संदेश भेजने का एक लोकप्रिय रूपक पदानुक्रमित मॉडल के अनुसरा, पूर्वकथन कहनेवाला कोडन में आरोही (नीचे से ऊपर) पूर्वानुमान त्रुटियों और अवरोही (ऊपर से नीचे) पूर्वानुमान का आवर्ती आदान-प्रदान सम्मलित होता है।<ref name="Mumford">{{cite journal |doi=10.1007/BF00198477 |url=http://cs.brown.edu/people/tld/projects/cortex/course/suggested_reading_list/supplements/documents/MumfordBC-92.pdf|title=नियोकोर्टेक्स की कम्प्यूटेशनल वास्तुकला पर|year=1992 |last1=Mumford |first1=D. |journal=Biological Cybernetics |volume=66 |issue=3 |pages=241–251 |pmid=1540675 |s2cid=14303625 }}</ref> यह संवेदी की शारीरिक रचना और शरीर विज्ञान के अनुरूप<ref>{{cite journal | doi=10.1016/j.neuron.2012.10.038 | title=पूर्वानुमानित कोडिंग के लिए कैनोनिकल माइक्रोसर्किट| year=2012 | last1=Bastos | first1=Andre M. | last2=Usrey | first2=W. Martin | last3=Adams | first3=Rick A. | last4=Mangun | first4=George R. | last5=Fries | first5=Pascal | last6=Friston | first6=Karl J. | journal=Neuron | volume=76 | issue=4 | pages=695–711 | pmid=23177956 | pmc=3777738 }}</ref> और मोटर प्रणाली है।<ref>{{cite journal | doi=10.1007/s00429-012-0475-5 | title=Predictions not commands: Active inference in the motor system | year=2013 | last1=Adams | first1=Rick A. | last2=Shipp | first2=Stewart | last3=Friston | first3=Karl J. | journal=Brain Structure and Function | volume=218 | issue=3 | pages=611–643 | pmid=23129312 | pmc=3637647 }}</ref> | |||
=== अवधारणात्मक शिक्षा और स्मृति === | === अवधारणात्मक शिक्षा और स्मृति === | ||
पूर्वकथन कहने वाला कोडन में, मुक्त ऊर्जा (मुक्त कार्रवाई) के अभिन्न अंग पर क्रमिक वंश के माध्यम से मॉडल मापदंडों का अनुकूलन साहचर्य या [[हेब्बियन सिद्धांत]] को कम करता है और मस्तिष्क में [[ सूत्रयुग्मक सुनम्यता ]]से जुड़ा होता है। | |||
=== अवधारणात्मक सटीकता, ध्यान और प्रमुखता === | === अवधारणात्मक सटीकता, ध्यान और प्रमुखता === | ||
परिशुद्धता मापदंडों का अनुकूलन | परिशुद्धता मापदंडों का अनुकूलन पूर्वानुमान त्रुटियों के लाभ को अनुकूलित करने से मेल खाता है (सी.एफ., कलमन लाभ)। पूर्वानुमानित कोडन के तंत्रिका रूप से प्रशंसनीय कार्यान्वयन में,<ref name="Mumford"/>यह सतही पिरामिड कोशिकाओं की उत्तेज्यता को अनुकूलित करने के अनुरूप है और इसकी व्याख्या ध्यानात्मक लाभ के संदर्भ में की गई है।<ref name="Feldman">{{cite journal | doi=10.3389/fnhum.2010.00215 | doi-access=free | title=ध्यान, अनिश्चितता, और मुक्त-ऊर्जा| year=2010 | last1=Friston | first1=Karl J. | last2=Feldman | first2=Harriet | journal=Frontiers in Human Neuroscience | volume=4 | page=215 | pmid=21160551 | pmc=3001758 }}</ref> | ||
[[File:PESAIM.jpg|thumb|कई वस्तुओं के वातावरण में पीई-एसएआईएम नामक एसएआईएम के बायेसियन सुधार द्वारा किए गए चयनात्मक ध्यान कार्य से प्राप्त परिणामों का अनुकरण। ग्राफ़ एफओए और नॉलेज नेटवर्क में दो टेम्पलेट इकाइयों के लिए सक्रियण का समय पाठ्यक्रम दिखाते हैं।]] | [[File:PESAIM.jpg|thumb|कई वस्तुओं के वातावरण में पीई-एसएआईएम नामक एसएआईएम के बायेसियन सुधार द्वारा किए गए चयनात्मक ध्यान कार्य से प्राप्त परिणामों का अनुकरण। ग्राफ़ एफओए और नॉलेज नेटवर्क में दो टेम्पलेट इकाइयों के लिए सक्रियण का समय पाठ्यक्रम दिखाते हैं।]]अधोशीर्ष बनाम ऊर्ध्वगामी विवाद के संबंध में, जिसे ध्यान की एक प्रमुख खुली समस्या के रूप में संबोधित किया गया है, एक अभिकलनीयतः मॉडल अधोशीर्ष और ऊर्ध्वगामी तंत्र के बीच परस्पर क्रिया की परिपत्र प्रकृति को चित्रित करने में सफल रहा है। ध्यान के एक स्थापित उभरते मॉडल, अर्थात् एसएआईएम का उपयोग करते हुए, लेखकों ने पीई-एसएआईएम नामक एक मॉडल का प्रस्ताव रखा, जो मानक संस्करण के विपरीत, ऊपर से नीचे की स्थिति से चयनात्मक ध्यान देता है। मॉडल पूर्वानुमानत्रुटियों के संचरण को समान स्तर या उससे ऊपर के स्तर पर ध्यान में रखता है, जिससे कि ऊर्जा फलन को कम किया जा सके जो आँकड़े और उसके कारण के बीच अंतर को इंगित करता है, या, दूसरे शब्दों में, जेनरेटिव मॉडल और पोस्टीरियर के बीच वैधता बढ़ाने के लिए, उन्होंने अपने मॉडल में उत्तेज्यताओं के बीच तंत्रिका प्रतिस्पर्धा को भी सम्मलित किया। इस मॉडल की एक उल्लेखनीय विशेषता केवल कार्य प्रदर्शन के दौरान पूर्वानुमानत्रुटियों के संदर्भ में मुक्त ऊर्जा फलन का पुनरुद्धार है: | ||
<math>\dfrac{\partial E^{total}(Y^{VP},X^{SN},x^{CN},y^{KN})}{\partial y^{SN}_{mn}}=x^{CN}_{mn}-b^{CN}\varepsilon^{CN}_{nm}+b^{CN}\sum_{k}(\varepsilon^{KN}_{knm})</math> | <math>\dfrac{\partial E^{total}(Y^{VP},X^{SN},x^{CN},y^{KN})}{\partial y^{SN}_{mn}}=x^{CN}_{mn}-b^{CN}\varepsilon^{CN}_{nm}+b^{CN}\sum_{k}(\varepsilon^{KN}_{knm})</math> | ||
दो मॉडलों की तुलना करने से उनके संबंधित परिणामों के बीच एक उल्लेखनीय समानता का पता चलता है, साथ ही एक उल्लेखनीय विसंगति भी उजागर होती है, जिससे - एसएआईएम के मानक संस्करण में - मॉडल का ध्यान मुख्य रूप से उत्तेजक कनेक्शन पर होता है, जबकि पीई-एसएआईएम में, निरोधात्मक कनेक्शन होते हैं। एक अनुमान लगाने के लिए उपयोग किया गया। यह मॉडल उच्च परिशुद्धता के साथ मानव प्रयोगों से प्राप्त ईईजी और एफएमआरआई आँकड़े की | जहाँ <math>E^{total}</math> तंत्रिका नेटवर्क का कुल ऊर्जा कार्य सम्मलित है, और <math>\varepsilon^{KN}_{knm}</math> समय के साथ जनरेटिव मॉडल (पूर्व) और पश्च परिवर्तन के बीच पूर्वानुमानत्रुटि है।<ref name="Abadi">{{cite journal | doi=10.1098/rsif.2018.0344 | title=दृश्य निर्माण के बायेसियन फॉर्मूलेशन में उत्तेजक बनाम निरोधात्मक प्रतिक्रिया| year=2019 | last1=Abadi | first1=Alireza Khatoon | last2=Yahya | first2=Keyvan | last3=Amini | first3=Massoud | last4=Friston | first4=Karl | last5=Heinke | first5=Dietmar | journal=Journal of the Royal Society Interface | volume=16 | issue=154 | pmid=31039693 | pmc=6544897 }}</ref> | ||
दो मॉडलों की तुलना करने से उनके संबंधित परिणामों के बीच एक उल्लेखनीय समानता का पता चलता है, साथ ही एक उल्लेखनीय विसंगति भी उजागर होती है, जिससे - एसएआईएम के मानक संस्करण में - मॉडल का ध्यान मुख्य रूप से उत्तेजक कनेक्शन पर होता है, जबकि पीई-एसएआईएम में, निरोधात्मक कनेक्शन होते हैं। एक अनुमान लगाने के लिए उपयोग किया गया। यह मॉडल उच्च परिशुद्धता के साथ मानव प्रयोगों से प्राप्त ईईजी और एफएमआरआई आँकड़े की पूर्वानुमानकरने के लिए भी उपयुक्त सिद्ध हुआ है। इसी तरह, याह्या एट अल। गुप्त चयनात्मक दृश्य ध्यान में टेम्पलेट मिलान के लिए एक अभिकलनीयतः मॉडल का प्रस्ताव करने के लिए मुक्त ऊर्जा सिद्धांत को भी लागू किया जो ज्यादातर एसएआईएम पर निर्भर करता है।<ref name="Yahya">{{cite journal | doi=10.1007/s10339-013-0597-6 | title=12th Biannual Conference of the German Cognitive Science Society (KogWis 2014) | journal=Cognitive Processing | year=2014 | volume=15 | page=107 | s2cid=10121398 | doi-access=free }}</ref> इस अध्ययन के अनुसार, पूरे स्थिति-समष्टि की कुल मुक्त ऊर्जा मूल तंत्रिका नेटवर्क में ऊपर से नीचे सिग्नल डालकर पहुंचाई जाती है, जिससे हम एक गतिशील प्रणाली प्राप्त करते हैं जिसमें अग्र प्रभरण और पश्चगामी पूर्वानुमानत्रुटि दोनों सम्मलित होती हैं। | |||
== सक्रिय अनुमान == | == सक्रिय अनुमान == | ||
जब | जब प्रवणता अवरोह को क्रिया पर लागू किया जाता है <math> \dot{a} = -\partial_aF(s,\tilde{\mu}) </math>, मोटर नियंत्रण को शास्त्रीय प्रतिवर्त चाप के संदर्भ में समझा जा सकता है जो अवरोही (कॉर्टिकोस्पाइनल) पूर्वानुमान से जुड़े होते हैं। यह एक औपचारिकता प्रदान करता है जो संतुलन बिंदु समाधान को सामान्यीकृत करता है - [[स्वतंत्रता समस्या की डिग्री]] तक<ref>{{cite journal |doi=10.1017/S0140525X0004070X |url=http://e.guigon.free.fr/rsc/article/FeldmanLevin95.pdf|title=मोटर नियंत्रण में स्थितीय संदर्भ फ्रेम की उत्पत्ति और उपयोग|year=1995 |last1=Feldman |first1=Anatol G. |last2=Levin |first2=Mindy F. |journal=Behavioral and Brain Sciences |volume=18 |issue=4 |pages=723–744 |s2cid=145164477 }}</ref> - आंदोलन प्रक्षेप पथ के लिए। | ||
=== सक्रिय अनुमान और [[इष्टतम नियंत्रण]] === | === सक्रिय अनुमान और [[इष्टतम नियंत्रण]] === | ||
सक्रिय अनुमान स्थिति परिवर्तन या प्रवाह के बारे में पूर्व मान्यताओं के साथ मूल्य या लागत-से-जाने वाले कार्यों को प्रतिस्थापित करके इष्टतम नियंत्रण से संबंधित है।<ref>{{cite journal |doi=10.1016/j.neuron.2011.10.018 |url=http://www.fil.ion.ucl.ac.uk/~karl/What%20Is%20Optimal%20about%20Motor%20Control.pdf|title=What is Optimal about Motor Control? |year=2011 |last1=Friston |first1=Karl |journal=Neuron |volume=72 |issue=3 |pages=488–498 |pmid=22078508 |s2cid=13912462 }}</ref> यह बायेसियन फ़िल्टरिंग और [[बेलमैन समीकरण]] के समाधान के बीच घनिष्ठ संबंध का फायदा उठाता है। | सक्रिय अनुमान स्थिति परिवर्तन या प्रवाह के बारे में पूर्व मान्यताओं के साथ मूल्य या लागत-से-जाने वाले कार्यों को प्रतिस्थापित करके इष्टतम नियंत्रण से संबंधित है।<ref>{{cite journal |doi=10.1016/j.neuron.2011.10.018 |url=http://www.fil.ion.ucl.ac.uk/~karl/What%20Is%20Optimal%20about%20Motor%20Control.pdf|title=What is Optimal about Motor Control? |year=2011 |last1=Friston |first1=Karl |journal=Neuron |volume=72 |issue=3 |pages=488–498 |pmid=22078508 |s2cid=13912462 }}</ref> यह बायेसियन फ़िल्टरिंग और [[बेलमैन समीकरण]] के समाधान के बीच घनिष्ठ संबंध का फायदा उठाता है। चूंकि, सक्रिय अनुमान प्रवाह से प्रारंभ होता है <math> f = \Gamma \cdot \nabla V + \nabla \times W </math> जो अदिश से निर्दिष्ट हैं <math> V(x) </math> और सदिश <math> W(x) </math> स्थिति स्थान के मूल्य कार्य (सी.एफ., [[हेल्महोल्ट्ज़ अपघटन]])। यहाँ, <math> \Gamma </math> यादृच्छिक उतार-चढ़ाव का आयाम है और लागत है <math> c(x) = f \cdot \nabla V + \nabla \cdot \Gamma \cdot V</math>. पूर्वज ओवर फ्लो <math> p(\tilde{x}\mid m) </math> स्थितिों पर पूर्व प्रेरित करें <math> p(x\mid m) = \exp (V(x)) </math> यह उपयुक्त अग्रगामी [[Index.php?title=कोलमोगोरोव समीकरणों|कोलमोगोरोव समीकरणों]] का समाधान है।<ref>{{cite journal | doi=10.1155/2012/937860 | doi-access=free | title=निःशुल्क ऊर्जा, मूल्य और आकर्षणकर्ता| year=2012 | last1=Friston | first1=Karl | last2=Ao | first2=Ping | journal=Computational and Mathematical Methods in Medicine | volume=2012 | pages=1–27 | pmid=22229042 | pmc=3249597 }}</ref> इसके विपरीत, इष्टतम नियंत्रण इस धारणा के अनुसरा, लागत फलन को देखते हुए, प्रवाह को अनुकूलित करता है <math> W = 0 </math> (अर्थात, प्रवाह कर्ल मुक्त है या विस्तृत संतुलन है)। सामान्यत:, इसमें पिछड़े कोलमोगोरोव समीकरणों को हल करना सम्मलित होता है।<ref>{{cite journal | arxiv=physics/0505066 | doi=10.1088/1742-5468/2005/11/P11011 | title=इष्टतम नियंत्रण सिद्धांत के लिए पथ अभिन्नता और समरूपता तोड़ना| year=2005 | last1=Kappen | first1=H. J. | journal=Journal of Statistical Mechanics: Theory and Experiment | volume=2005 | issue=11 | pages=P11011 | bibcode=2005JSMTE..11..011K | s2cid=87027 }}</ref> | ||
=== सक्रिय अनुमान और इष्टतम निर्णय (खेल) सिद्धांत === | === सक्रिय अनुमान और इष्टतम निर्णय (खेल) सिद्धांत === | ||
इष्टतम निर्णय समस्याओं (सामान्यत: आंशिक रूप से अवलोकन योग्य मार्कोव निर्णय प्रक्रियाओं के रूप में तैयार की जाती है) को पूर्व मान्यताओं में [[उपयोगिता]] को अवशोषित करके सक्रिय अनुमान के भीतर व्यवहार किया जाता है। इस सेटिंग में, जिन स्थितिों की उपयोगिता (कम लागत) अधिक है, वे ऐसे स्थिति हैं जिन पर कारक कब्ज़ा करने की उम्मीद करता है। जनरेटिव मॉडल को छिपे हुए स्थितिों से लैस करके मॉडल नियंत्रण, नीतियां (नियंत्रण अनुक्रम) जो परिवर्तनशील मुक्त ऊर्जा को कम करती हैं, उच्च उपयोगिता वाले स्थितिों की ओर ले जाती हैं।<ref>{{cite journal |doi=10.1007/s00422-012-0512-8 |doi-access=free|title=Active inference and agency: Optimal control without cost functions |year=2012 |last1=Friston |first1=Karl |last2=Samothrakis |first2=Spyridon |last3=Montague |first3=Read |journal=Biological Cybernetics |volume=106 |issue=8–9 |pages=523–541 |pmid=22864468 }}</ref> | |||
न्यूरोबायोलॉजिकल रूप से, [[डोपामाइन]] जैसे तंत्रिका मॉडुलेटर को पूर्वानुमानत्रुटि कोडन प्रमुख कोशिकाओं के लाभ को संशोधित करके पूर्वानुमानत्रुटियों की सटीकता की रिपोर्ट करने के लिए माना जाता है।<ref name="Friston_a">{{cite journal | doi=10.1371/journal.pcbi.1002327 | title=डोपामाइन, सामर्थ्य और सक्रिय अनुमान| year=2012 | last1=Friston | first1=Karl J. | last2=Shiner | first2=Tamara | last3=Fitzgerald | first3=Thomas | last4=Galea | first4=Joseph M. | last5=Adams | first5=Rick | last6=Brown | first6=Harriet | last7=Dolan | first7=Raymond J. | last8=Moran | first8=Rosalyn|author8-link=Rosalyn Moran | last9=Stephan | first9=Klaas Enno | last10=Bestmann | first10=Sven | journal=PLOS Computational Biology | volume=8 | issue=1 | pages=e1002327 | pmid=22241972 | pmc=3252266 | bibcode=2012PLSCB...8E2327F | doi-access=free }}</ref> यह पूर्वानुमानत्रुटियों की रिपोर्टिंग में डोपामाइन की भूमिका से निकटता से संबंधित है - लेकिन औपचारिक रूप से अलग है-प्रति भविष्यवाणी त्रुटियों की रिपोर्ट करने में डोपामाइन की भूमिका<ref>Fiorillo, Christopher D.; Tobler, Philippe N.; Schultz, Wolfram (2003). "Discrete Coding of Reward Probability and Uncertainty by Dopamine Neurons" (PDF). ''Science''. '''299''' (5614): 1898–1902. Bibcode:2003Sci...299.1898F. doi:10.1126/science.1077349. <nowiki>PMID 12649484</nowiki>. S2CID 2363255.</ref> और संबंधित कम्प्यूटेशनल खाते है।<ref>Frank, Michael J. (2005). "Dynamic Dopamine Modulation in the Basal Ganglia: A Neurocomputational Account of Cognitive Deficits in Medicated and Nonmedicated Parkinsonism" (PDF). ''Journal of Cognitive Neuroscience''. '''17''' (1): 51–72. doi:10.1162/0898929052880093. <nowiki>PMID 15701239</nowiki>. S2CID 7414727.</ref> | |||
न्यूरोबायोलॉजिकल रूप से, [[डोपामाइन]] जैसे | |||
=== सक्रिय अनुमान और [[संज्ञानात्मक तंत्रिका विज्ञान]] === | === सक्रिय अनुमान और [[संज्ञानात्मक तंत्रिका विज्ञान]] === | ||
सक्रिय अनुमान का उपयोग संज्ञानात्मक तंत्रिका विज्ञान, मस्तिष्क कार्य और न्यूरोसाइकिएट्री में कई मुद्दों को संबोधित करने के लिए किया गया है, जिसमें क्रिया अवलोकन भी | सक्रिय अनुमान का उपयोग संज्ञानात्मक तंत्रिका विज्ञान, मस्तिष्क कार्य और न्यूरोसाइकिएट्री (तंत्रिका मनश्चित्सा) में कई मुद्दों को संबोधित करने के लिए किया गया है, जिसमें क्रिया अवलोकन भी सम्मलित है।<ref>{{cite journal |doi=10.1007/s00422-011-0424-z |url=http://www.fil.ion.ucl.ac.uk/~karl/Action%20understanding%20and%20active%20inference.pdf|title=कार्रवाई की समझ और सक्रिय अनुमान|year=2011 |last1=Friston |first1=Karl |last2=Mattout |first2=Jérémie |last3=Kilner |first3=James |journal=Biological Cybernetics |volume=104 |issue=1–2 |pages=137–160 |pmid=21327826 |pmc=3491875 }}</ref> दर्पण स्नायु,<ref>{{cite journal |doi=10.1007/s10339-007-0170-2 |url=http://www.fil.ion.ucl.ac.uk/~karl/Predictive%20coding%20an%20account%20of%20the%20mirror%20neuron%20system.pdf|title=Predictive coding: An account of the mirror neuron system |year=2007 |last1=Kilner |first1=James M. |last2=Friston |first2=Karl J. |last3=Frith |first3=Chris D. |journal=Cognitive Processing |volume=8 |issue=3 |pages=159–166 |pmid=17429704 |pmc=2649419 }}</ref> सैकेडेस और दृश्य खोज,<ref>{{cite journal | doi=10.3389/fpsyg.2012.00151 | doi-access=free | title=Perceptions as Hypotheses: Saccades as Experiments | year=2012 | last1=Friston | first1=Karl | last2=Adams | first2=Rick A. | last3=Perrinet | first3=Laurent | last4=Breakspear | first4=Michael | journal=Frontiers in Psychology | volume=3 | page=151 | pmid=22654776 | pmc=3361132 }}</ref><ref>{{cite journal | doi=10.1371/journal.pone.0190429 | doi-access=free | title=मानव दृश्य अन्वेषण संवेदी दुनिया के बारे में अनिश्चितता को कम करता है| year=2018 | last1=Mirza | first1=M. Berk | last2=Adams | first2=Rick A. | last3=Mathys | first3=Christoph | last4=Friston | first4=Karl J. | journal=PLOS ONE | volume=13 | issue=1 | pages=e0190429 | pmid=29304087 | pmc=5755757 | bibcode=2018PLoSO..1390429M }}</ref> आँखों की हरकतें,<ref>{{cite journal | doi=10.1007/s00422-014-0620-8 | title=सक्रिय अनुमान, नेत्र गति और ओकुलोमोटर विलंब| year=2014 | last1=Perrinet | first1=Laurent U. | last2=Adams | first2=Rick A. | last3=Friston | first3=Karl J. | journal=Biological Cybernetics | volume=108 | issue=6 | pages=777–801 | pmid=25128318 | pmc=4250571 }}</ref> नींद,<ref>{{cite journal |doi=10.1016/j.pneurobio.2012.05.003 |doi-access=free|title=Waking and dreaming consciousness: Neurobiological and functional considerations |year=2012 |last1=Hobson |first1=J.A. |last2=Friston |first2=K.J. |journal=Progress in Neurobiology |volume=98 |issue=1 |pages=82–98 |pmid=22609044 |pmc=3389346 }}</ref> भ्रम,<ref>{{cite journal | doi=10.3389/fpsyg.2012.00043 | doi-access=free | title=Free-Energy and Illusions: The Cornsweet Effect | year=2012 | last1=Brown | first1=Harriet | last2=Friston | first2=Karl J. | journal=Frontiers in Psychology | volume=3 | page=43 | pmid=22393327 | pmc=3289982 }}</ref> ध्यान,<ref name="Feldman" />क्रिया चयन,<ref name="Friston_a" />चेतना,<ref>{{Cite journal|last1=Rudrauf|first1=David|last2=Bennequin|first2=Daniel|last3=Granic|first3=Isabela|last4=Landini|first4=Gregory|last5=Friston|first5=Karl|last6=Williford|first6=Kenneth|date=2017-09-07|title=सन्निहित चेतना का एक गणितीय मॉडल|journal=Journal of Theoretical Biology|volume=428|pages=106–131|doi=10.1016/j.jtbi.2017.05.032|pmid=28554611|bibcode=2017JThBi.428..106R |url=http://discovery.ucl.ac.uk/10057795/1/DR_et_al_A_math_model_of_embodied_consciousness_JTBiol_final_revision_for_submission.pdf}}</ref><ref>{{Cite journal|title=प्रक्षेप्य चेतना मॉडल और अभूतपूर्व स्वत्व|journal = Frontiers in Psychology|volume = 9|pages = 2571|last1=K|first1=Williford|last2=D|first2=Bennequin|date=2018-12-17|language=en|pmid=30618988|pmc = 6304424|last3=K|first3=Friston|last4=D|first4=Rudrauf|doi = 10.3389/fpsyg.2018.02571|doi-access = free}}</ref> हिस्टीरिया<ref>{{cite journal |doi=10.1093/brain/aws129 |url=http://www.fil.ion.ucl.ac.uk/~karl/A%20Bayesian%20account%20of%20hysteria.pdf|title='हिस्टीरिया' का बायेसियन विवरण|year=2012 |last1=Edwards |first1=M. J. |last2=Adams |first2=R. A. |last3=Brown |first3=H. |last4=Parees |first4=I. |last5=Friston |first5=K. J. |journal=Brain |volume=135 |issue=11 |pages=3495–3512 |pmid=22641838 |pmc=3501967 }}</ref> और मनोविकृति.<ref>{{cite journal | doi=10.1371/journal.pone.0047502 | doi-access=free | title=Smooth Pursuit and Visual Occlusion: Active Inference and Oculomotor Control in Schizophrenia | year=2012 | last1=Adams | first1=Rick A. | last2=Perrinet | first2=Laurent U. | last3=Friston | first3=Karl | journal=PLOS ONE | volume=7 | issue=10 | pages=e47502 | pmid=23110076 | pmc=3482214 | bibcode=2012PLoSO...747502A }}</ref> सक्रिय अनुमान में कार्रवाई की व्याख्या अधिकांशत: इस विचार पर निर्भर करती है कि मस्तिष्क में 'जिद्दी पूर्वकथनवाणियां' होती हैं जिन्हें वह अद्यतन नहीं कर सकता है, जिसके परिणामस्वरूप ऐसी गतिविधियां होती हैं जो इन पूर्वानुमान को सच कर देती हैं।<ref>{{Cite journal|last1=Yon|first1=Daniel|last2=Lange|first2=Floris P. de|last3=Press|first3=Clare|date=2019-01-01|title=एक जिद्दी वैज्ञानिक के रूप में पूर्वानुमानित मस्तिष्क|url=https://www.cell.com/trends/cognitive-sciences/abstract/S1364-6613(18)30239-0|journal=Trends in Cognitive Sciences|language=en|volume=23|issue=1|pages=6–8|doi=10.1016/j.tics.2018.10.003|pmid=30429054|s2cid=53280000}}</ref> | ||
== यह भी देखें == | == यह भी देखें == | ||
* {{annotated link| | * {{annotated link|क्रिया-विशेष धारणा}} | ||
* {{annotated link| | * {{annotated link|शक्यता}} | ||
* {{annotated link| | * {{annotated link|ऑटोपोइज़िस}} | ||
* {{annotated link| | * {{annotated link|मस्तिष्क के कार्य के लिए बायेसियन दृष्टिकोण}} | ||
* [[ एड्रिअन बेजान ]] - प्रकृति, चेतन और निर्जीव में डिजाइन विकास का नियम | * [[ एड्रिअन बेजान ]] - प्रकृति, चेतन और निर्जीव में डिजाइन विकास का नियम | ||
* {{annotated link| | * {{annotated link|निर्णय सिद्धांत}} | ||
* {{annotated link| | * {{annotated link|प्रतीकात्मक उपलब्धि}} | ||
* {{annotated link| | * {{annotated link|एंट्रोपिक बल}} | ||
* {{annotated link| | * {{annotated link|न्यूनतम ऊर्जा का सिद्धांत}} | ||
* {{annotated link| | * {{annotated link|सूचना-मेट्रिक्स}} | ||
* {{annotated link| | * {{annotated link|इष्टतम नियंत्रण}} | ||
* {{annotated link| | * {{annotated link|अनुकूली प्रणाली|aka=प्रैक्टोपोइज़िस}} | ||
* {{annotated link| | * {{annotated link|पूर्वानुमानित कोडिंग}} | ||
* {{annotated link| | * {{annotated link|आत्म संगठन}} | ||
* {{annotated link| | * {{annotated link|आश्चर्य}} | ||
* {{annotated link| | * {{annotated link|सिनर्जेटिक्स (हेकेन)}} | ||
* {{annotated link| | * {{annotated link|वैरिएशनल बायेसियन विधियाँ}} | ||
== संदर्भ == | == संदर्भ == | ||
Revision as of 23:04, 29 November 2023
मुक्त ऊर्जा सिद्धांत एक सैद्धांतिक रूपरेखा है जो सुझाव देता है कि मस्तिष्क आंतरिक मॉडल के आधार पर पूर्वानुमान और संवेदी इनपुट का उपयोग करके उन्हें अद्यतन करके आश्चर्य या अनिश्चितता को कम करता है। यह सटीकता और परिशुद्धता को बढ़ाने के लिए बाहरी दुनिया के साथ अपने आंतरिक मॉडल को संरेखित करने के मस्तिष्क के उद्देश्य पर प्रकाश डालता है। यह सिद्धांत बायेसियन अनुमान को सक्रिय अनुमान के साथ एकीकृत करता है, जहां क्रियाएं पूर्वानुमान द्वारा निर्देशित होती हैं और संवेदी प्रतिक्रिया उन्हें परिष्कृत करती है। मस्तिष्क के कार्य, धारणा और क्रिया (दर्शन) को समझने के लिए इसके व्यापक निहितार्थ हैं।[1]
सिंहावलोकन
जीव भौतिकी और संज्ञानात्मक विज्ञान में, मुक्त ऊर्जा सिद्धांत एक गणितीय सिद्धांत है जो भौतिक प्रणालियों की प्रतिनिधित्व क्षमताओं का औपचारिक विवरण बताता है: यही कारण है कि जो चीजें सम्मलित हैं वे ऐसी दिखती हैं मानो वे उन प्रणालियों के गुणों को ट्रैक करती हैं जिनसे वे जुड़े हुए हैं।[2]
यह स्थापित करता है कि भौतिक प्रणालियों की गतिशीलता आश्चर्य के रूप में ज्ञात मात्रा को कम करती है (जो कि कुछ परिणामों की नकारात्मक लॉग संभावना है); या समकक्ष, इसकी परिवर्तनशील ऊपरी सीमा, जिसे परिवर्तनशील मुक्त ऊर्जा कहा जाता है। इस सिद्धांत का उपयोग विशेष रूप से मस्तिष्क कार्य के लिए बायेसियन दृष्टिकोण में किया जाता है, लेकिन कृत्रिम बुद्धि के कुछ दृष्टिकोण में भी; यह औपचारिक रूप से वैरिएबल बायेसियन तरीकों से संबंधित है और मूल रूप से कार्ल फ्रिस्टन द्वारा तंत्रिका विज्ञान में सन्निहित धारणा-क्रिया लूप के स्पष्टीकरण के रूप में पेश किया गया था।[3]
मुक्त ऊर्जा सिद्धांत उन प्रणालियों के व्यवहार को मॉडल करता है जो किसी अन्य प्रणाली (उदाहरण के लिए, एक अंत:स्थापन वातावरण) से अलग हैं, लेकिन युग्मित हैं, जहां दो प्रणालियों के बीच अंतरापृष्ठ को लागू करने वाली स्वतंत्रता की डिग्री को मार्कोव ब्लैंकेट के रूप में जाना जाता है। अधिक औपचारिक रूप से, मुक्त ऊर्जा सिद्धांत कहता है कि यदि किसी प्रणाली में "विशेष विभाजन" है (अर्थात, कणों में, उनके मार्कोव ब्लैंकेट के साथ), तो उस प्रणाली के उपसमुच्चय अन्य उपसमुच्चय की सांख्यिकीय संरचना को ट्रैक करेंगे (जिन्हें आंतरिक और के रूप में जाना जाता है) किसी प्रणाली की बाहरी अवस्थाएँ या पथ)।
मुक्त ऊर्जा सिद्धांत मस्तिष्क के "अनुमिति इंजन" के बायेसियन विचार पर आधारित है। मुक्त ऊर्जा सिद्धांत के अनुसरा, प्रणाली कम से कम आश्चर्य का रास्ता अपनाते हैं, या समकक्ष रूप से, दुनिया के अपने मॉडल और उनकी समझ और संबंधित धारणा के आधार पर पूर्वानुमान के बीच अंतर को कम करते हैं। इस अंतर को परिवर्तनशील मुक्त ऊर्जा द्वारा निर्धारित किया जाता है और प्रणाली के विश्व मॉडल के निरंतर सुधार या दुनिया को प्रणाली की पूर्वानुमान की तरह बनाकर कम किया जाता है। दुनिया को अपेक्षित स्थिति के करीब लाने के लिए इसे सक्रिय रूप से बदलकर, प्रणाली की मुक्त ऊर्जा को भी कम कर सकता है। फ्रिस्टन इसे सभी जैविक प्रतिक्रियाओं का सिद्धांत मानता है।[4] फ्रिस्टन का यह भी मानना है कि उनका सिद्धांत मानसिक विकारों के साथ-साथ कृत्रिम बुद्धिमत्ता पर भी लागू होता है। सक्रिय अनुमान सिद्धांत पर आधारित एआई कार्यान्वयन ने अन्य तरीकों की तुलना में लाभ दिखाया है।[4]
मुक्त ऊर्जा सिद्धांत सूचना भौतिकी का एक गणितीय सिद्धांत है: अधिकतम एन्ट्रापी (परिक्षय) के सिद्धांत या कम से कम कार्रवाई के सिद्धांत की तरह, यह गणितीय आधार पर सत्य है। मुक्त ऊर्जा सिद्धांत को गलत सिद्ध करने का प्रयास करना एक श्रेणी की गलती है, जो अनुभवजन्य अवलोकन करके गणना को गलत सिद्ध करने की कोशिश करने के समान है। (कोई इस तरह से गणितीय सिद्धांत को अमान्य नहीं कर सकता है; इसके अतरिक्त, किसी को सिद्धांत से एक औपचारिक विरोधाभास प्राप्त करने की आवश्यकता होगी।) 2018 के एक साक्षात्कार में, फ्रिस्टन ने बताया कि मुक्त ऊर्जा सिद्धांत को मिथ्याकरणीयता के अधीन नहीं होने के लिए इसमें क्या सम्मलित है: मुझे लगता है इस बिंदु पर एक बुनियादी अंतर करना उपयोगी है - जिस पर हम बाद में अपील कर सकते हैं। अंतर एक अवस्था और प्रक्रिया सिद्धांत के बीच है; अर्थात, एक मानक सिद्धांत जिसके अनुरूप चीजें हो भी सकती हैं और नहीं भी, और उस सिद्धांत को कैसे साकार किया जाता है, इसके बारे में एक प्रक्रिया सिद्धांत या परिकल्पना के बीच अंतर है। इस भेद के अनुसरा, मुक्त ऊर्जा सिद्धांत प्रागुक्तीय कोडन और बायेसियन मस्तिष्क परिकल्पना जैसी चीजों से बिल्कुल अलग है। ऐसा इसलिए है क्योंकि मुक्त ऊर्जा सिद्धांत - एक सिद्धांत है। हैमिल्टन के सिद्धांत की तरह हैमिल्टन के स्थिर क्रिया के सिद्धांत को गलत सिद्ध नहीं किया जा सकता है। इसका खंडन नहीं किया जा सकता है, वास्तव में, आप इसमें बहुत कुछ नहीं कर सकते, जब तक कि आप यह न पूछें कि मापने योग्य प्रणालियाँ सिद्धांत के अनुरूप हैं या नहीं। दूसरी ओर, ऐसी परिकल्पनाएँ कि मस्तिष्क किसी प्रकार का बायेसियन अनुमान या पूर्वानुमानित कोडन करता है - वे परिकल्पनाएँ हैं। ये परिकल्पनाएँ अनुभवजन्य साक्ष्य द्वारा समर्थित हो भी सकती हैं और नहीं भी।[5] इन परिकल्पनाओं के अनुभवजन्य साक्ष्य द्वारा समर्थित होने के कई उदाहरण हैं।[6]
पृष्ठभूमि
यह धारणा कि स्व-संगठित जैविक प्रणालियाँ - जैसे कोशिका या मस्तिष्क - को परिवर्तनशील मुक्त ऊर्जा को कम करने के रूप में समझा जा सकता है, हरमन वॉन हेल्महोल्ट्ज़ के अचेतन अनुमान पर काम पर आधारित है[7] और मनोविज्ञान में बाद के उपचार[8] और मशीन लर्निंग पर।[9] परिवर्तनशील मुक्त ऊर्जा उनके छिपे कारणों पर अवलोकन और संभाव्यता घनत्व का एक कार्य है। इस परिवर्तनशील घनत्व को एक संभाव्य मॉडल के संबंध में परिभाषित किया गया है जो परिकल्पित कारणों से अनुमानित अवलोकन उत्पन्न करता है+। इस सेटिंग में, मुक्त ऊर्जा सीमांत संभावना का अनुमान प्रदान करती है।[10] इसलिए, इसके न्यूनतमकरण को बायेसियन अनुमान प्रक्रिया के रूप में देखा जा सकता है। जब कोई प्रणाली सक्रिय रूप से मुक्त ऊर्जा को कम करने के लिए अवलोकन करती है, तो यह अंतर्निहित रूप से सक्रिय अनुमान लगाती है और दुनिया के अपने मॉडल के लिए साक्ष्य को अधिकतम करती है।
चूंकि, मुक्त ऊर्जा भी परिणामों की आत्म-सूचना पर एक ऊपरी सीमा है, जहाँ आत्म-सूचना का दीर्घकालिक औसत एन्ट्रापी है। इसका मतलब यह है कि यदि कोई प्रणाली मुक्त ऊर्जा को कम करने के लिए कार्य करती है, तो यह परोक्ष रूप से परिणामों की एन्ट्रापी - या संवेदी अवस्थाओं - के नमूनों पर एक ऊपरी सीमा लगाएगी।[11][12]
अन्य सिद्धांतों से संबंध
सक्रिय अनुमान अच्छे नियामक प्रमेय से निकटता से संबंधित है[13] और स्व-संगठन के संबंधित खाते,[14][15] जैसे स्व-संयोजन, पैटर्न निर्माण, आत्मनिर्णय का[16] और कार्यान्वयन[17] यह साइबरनेटिक्स, सिनर्जेटिक्स (हेकेन) में विचार किए गए विषयों को संबोधित करता है[18] और सन्निहित अनुभूति. क्योंकि मुक्त ऊर्जा को परिवर्तनशील घनत्व के अंतर्गत उसकी एन्ट्रापी को घटाकर प्रेक्षणों की अपेक्षित ऊर्जा के रूप में व्यक्त किया जा सकता है, यह अधिकतम एन्ट्रापी सिद्धांत से भी संबंधित है।[19] अंततः, क्योंकि ऊर्जा का समय औसत क्रिया है, न्यूनतम परिवर्तनशील मुक्त ऊर्जा का सिद्धांत न्यूनतम क्रिया का सिद्धांत है। स्केल निश्चरता की अनुमति देने वाले सक्रिय अनुमान को अन्य सिद्धांतों और डोमेन पर भी लागू किया गया है। उदाहरण के लिए, इसे समाजशास्त्र पर लागू किया गया है,[20][21][22][23] भाषाविज्ञान और संचार,[24][25][26] लाक्षणिकता,[27][28] और महामारी विज्ञान [29] दूसरों के बीच में।
नकारात्मक मुक्त ऊर्जा औपचारिक रूप से निचली सीमा के साक्ष्य के बराबर है, जिसका उपयोग सामान्यत: यंत्र अधिगम में जनरेटिव मॉडल, जैसे विचरणी ऑटोकोडितर को प्रशिक्षित करने के लिए किया जाता है।
क्रिया और धारणा
सक्रिय अनुमान एक जनरेटिव मॉडल से संवेदी आँकड़े के कारणों का अनुमान लगाने के लिए अनुमानित बायेसियन गणना की तकनीकों को लागू करता है। 'जनरेटिव' मॉडल के आँकड़े कैसे उत्पन्न होते है और फिर कार्रवाई का मार्गदर्शन करने के लिए इन अनुमानों का उपयोग करता है।
बेयस नियम ऐसे कारण मॉडल के संभाव्य रूप से इष्टतम उलटा की विशेषता बताता है, लेकिन इसे लागू करना सामान्यत: अभिकलनीयतः रूप से कठिन होता है, जिससे अनुमानित तरीकों का उपयोग होता है।
सक्रिय अनुमान में, ऐसे अनुमानित तरीकों का अग्रणी वर्ग व्यावहारिक और सैद्धांतिक दोनों कारणों से विचरणी बायेसियन विधियां हैं: व्यावहारिक, क्योंकि वे अधिकांशत: सरल अनुमान प्रक्रियाओं की ओर ले जाते हैं; और सैद्धांतिक, क्योंकि वे मूलभूत भौतिक सिद्धांतों से संबंधित हैं, जैसा कि ऊपर चर्चा की गई है।
ये परिवर्तनशील विधियाँ बेयस-इष्टतम अनुमान (या 'पश्च संभाव्यता') और विधि के अनुसार इसके सन्निकटन के बीच विचलन पर ऊपरी सीमा को कम करके आगे बढ़ती हैं।
इस ऊपरी सीमा को मुक्त ऊर्जा के रूप में जाना जाता है, और हम तदनुसार आवक संवेदी जानकारी के संबंध में मुक्त ऊर्जा के न्यूनतमकरण के रूप में धारणा को चिह्नित कर सकते हैं, और जावक क्रिया जानकारी के संबंध में उसी मुक्त ऊर्जा के न्यूनतमकरण के रूप में कार्रवाई कर सकते हैं।
यह समग्र दोहरा अनुकूलन सक्रिय अनुमान की विशेषता है, और मुक्त ऊर्जा सिद्धांत यह परिकल्पना है कि सभी प्रणालियाँ जो अनुभव करती हैं और कार्य करती हैं, उन्हें इस तरह से चित्रित किया जा सकता है।
मुक्त ऊर्जा सिद्धांत के माध्यम से सक्रिय अनुमान के यांत्रिकी का उदाहरण देने के लिए, एक जेनरेटिव मॉडल निर्दिष्ट किया जाना चाहिए, और इसमें सामान्यत: संभाव्यता घनत्व कार्यों का संग्रह सम्मलित होता है जो एक साथ कारण मॉडल को चित्रित करता है।
ऐसी ही एक विशिष्टता इस प्रकार है.
प्रणाली को स्थिति स्थान में रहने के रूप में तैयार किया गया है , इस अर्थ में कि इसके स्थिति इस स्थान के बिंदु बनाते हैं।
फिर स्थिति स्थान को इसके अनुसार गुणनखंडित किया जाता है , जहाँ 'बाहरी' स्थितिों का स्थान है जो कारक से 'छिपा हुआ' है (प्रत्यक्ष रूप से माना या पहुंच योग्य नहीं होने के अर्थ में), संवेदी अवस्थाओं का स्थान है जिसे कारक द्वारा सीधे माना जाता है, कारक के संभावित कार्यों का स्थान है, और 'आंतरिक' स्थितिों का एक स्थान है जो कारक के लिए निजी है।
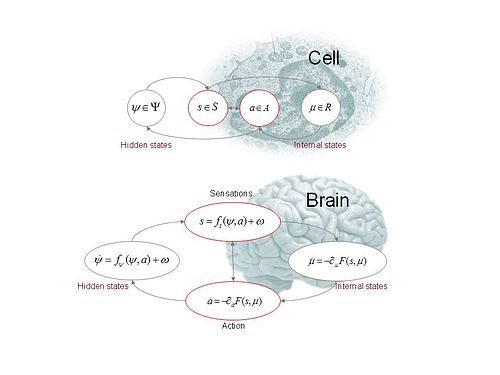
चित्र 1 को ध्यान में रखते हुए, ध्यान दें कि निम्नलिखित में और (निरंतर) समय के कार्य हैं। जेनरेटिव मॉडल निम्नलिखित घनत्व कार्यों का विनिर्देश है:
- एक संवेदी मॉडल, , अधिकांशत: के रूप में लिखा जाता है , बाहरी अवस्थाओं और क्रियाओं को देखते हुए संवेदी आँकड़े की संभावना को चिह्नित करना;
- पर्यावरणीय गतिशीलता का एक स्टोकेस्टिक मॉडल, , अधिकांशत: लिखा जाता है , यह वर्णन करते हुए कि कारक द्वारा समय के साथ बाहरी स्थितियों के विकसित होने की अपेक्षा कैसे की जाती है , कारक के कार्यों को देखते हुए;
- एक क्रिया मॉडल, , लिखा हुआ , यह वर्णन करना कि कारक की गतिविधियां उसकी आंतरिक स्थिति और संवेदी आँकड़े पर कैसे निर्भर करती हैं;
- एक आंतरिक मॉडल, , लिखा हुआ , यह वर्णन करते हुए कि कारक की आंतरिक स्थिति उसके संवेदी आँकड़े पर कैसे निर्भर करती है।
ये घनत्व फलन संयुक्त संभाव्यता वितरण के कारकों को निर्धारित करते हैं, जो जेनरेटिव मॉडल के पूर्ण विनिर्देश का प्रतिनिधित्व करता है, और जिसे इस प्रकार लिखा जा सकता है
- .
बेयस का नियम तब पश्च घनत्व निर्धारित करता है , जो बाहरी स्थिति के बारे में संभावित रूप से इष्टतम विश्वास व्यक्त करता है पूर्ववर्ती स्थिति और कारक के कार्यों, संवेदी संकेतों और आंतरिक स्थितियों को देखते हुए।
कंप्यूटिंग के बाद से अभिकलनीयतः रूप से कठिन है, मुक्त ऊर्जा सिद्धांत एक परिवर्तनशील घनत्व के अस्तित्व पर जोर देता है , जहाँ का एक अनुमान है .
फिर कोई मुक्त ऊर्जा को इस प्रकार परिभाषित करता है
और क्रिया और धारणा को संयुक्त अनुकूलन समस्या के रूप में परिभाषित करता है
जहाँ आंतरिक स्थिति है सामान्यत: 'परिवर्तनशील' घनत्व के मापदंडों को कोडित करने के लिए लिया जाता है, के मापदंडों को एनकोड करने के लिए लिया जाता है और इसलिए एजेंट का पश्च विश्वास के बारे में "सर्वोत्तम अनुमान" होता है .
ध्यान दें कि मुक्त ऊर्जा भी कारक (सीमांत वितरण, या औसत) संवेदी सूचना सामग्री के माप पर एक ऊपरी सीमा है, और इसलिए मुक्त ऊर्जा न्यूनतमकरण अधिकांशत: आश्चर्य को कम करने से प्रेरित होता है।
निःशुल्क ऊर्जा न्यूनतमकरण
निःशुल्क ऊर्जा न्यूनतमकरण और स्व-संगठन
यादृच्छिक गतिशील प्रणालियों के रूप में डाले जाने पर मुक्त ऊर्जा न्यूनीकरण को स्व-संगठित प्रणालियों की एक पहचान के रूप में प्रस्तावित किया गया है।[30] यह सूत्रीकरण एक मार्कोव ब्लैंकेट (जिसमें क्रिया और संवेदी अवस्थाएँ सम्मलित हैं) पर टिकी हुई है जो आंतरिक और बाहरी अवस्थाओं को अलग करती है। यदि आंतरिक अवस्थाएँ और क्रियाएँ मुक्त ऊर्जा को कम करती हैं, तो वे संवेदी अवस्थाओं की एन्ट्रापी पर एक ऊपरी सीमा लगाते हैं:
ऐसा इसलिए है क्योंकि - एर्गोडिक सिद्धांत मान्यताओं के अनुसरा - आश्चर्य का दीर्घकालिक औसत एन्ट्रापी है। यह बाध्यता अव्यवस्था की एक प्राकृतिक प्रवृत्ति का विरोध करती है - थर्मोडायनामिक्स (ऊष्मागतिकी) के दूसरे नियम और उतार-चढ़ाव प्रमेय से जुड़े प्रकार की, चूंकि, सांख्यिकीय भौतिकी से अवधारणाओं के संदर्भ में जीवन विज्ञान के लिए एक एकीकृत सिद्धांत तैयार करना, जैसे कि यादृच्छिक गतिशील प्रणाली, गैर-संतुलन स्थिर स्थिति और अभ्यतिप्रायता, सभी को अस्पष्ट करने के जोखिम के साथ जैविक प्रणालियों के सैद्धांतिक और अनुभवजन्य अध्ययन पर पर्याप्त बाधाएं डालता है। ऐसी विशेषताएँ जो जैविक प्रणालियों को रोचक प्रकार की स्व-संगठित प्रणालियाँ बनाती हैं।[31]
मुक्त ऊर्जा न्यूनीकरण और बायेसियन अनुमान
सभी बायेसियन अनुमान मुक्त ऊर्जा न्यूनीकरण के संदर्भ में लगाए जा सकते हैं[32][failed verification]. जब आंतरिक अवस्थाओं के संबंध में मुक्त ऊर्जा को कम किया जाता है, तो छिपी हुई अवस्थाओं पर परिवर्तनशील और पश्च घनत्व के बीच कुल्बैक-लीबलर विचलन कम हो जाता है। यह अनुमानित बायेसियन अनुमान से मेल खाता है - जब परिवर्तनशील घनत्व का रूप निश्चित होता है - और अन्यथा सटीक बायेसियन अनुमान होता है। इसलिए मुक्त ऊर्जा न्यूनीकरण बायेसियन अनुमान और फ़िल्टरिंग (उदाहरण के लिए, कलमन फ़िल्टर) का एक सामान्य विवरण प्रदान करता है। इसका उपयोग बायेसियन मॉडल चयन में भी किया जाता है, जहां मुक्त ऊर्जा को जटिलता और सटीकता में उपयोगी रूप से विघटित किया जा सकता है:
न्यूनतम मुक्त ऊर्जा वाले मॉडल जटिलता लागत (सी.एफ., ओकैम के रेजर और अभिकलनीयतः लागत के अधिक औपचारिक उपचार) के अनुसरा आँकड़े का सटीक स्पष्टीकरण प्रदान करते हैं।[33] यहां, जटिलता परिवर्तनशील घनत्व और छुपे हुए स्थिति के बारे में पूर्व मान्यताओं (अर्थात, आँकड़े को समझाने के लिए उपयोग की जाने वाली स्वतंत्रता की प्रभावी डिग्री) के बीच विचलन है।
मुक्त ऊर्जा न्यूनतमकरण और ऊष्मागतिकी
परिवर्तनशील मुक्त ऊर्जा एक सूचना-सैद्धांतिक कार्यात्मक है और ऊष्मागतिक (हेल्महोल्ट्ज़) हेल्महोल्ट्ज़ मुक्त ऊर्जा से अलग है।[34] चूंकि, परिवर्तनशील मुक्त ऊर्जा की जटिलता अवधि हेल्महोल्त्ज़ मुक्त ऊर्जा के समान निश्चित बिंदु को साझा करती है (धारणा के अनुसरा प्रणाली ऊष्मागतिक रूप से बंद है लेकिन पृथक नहीं है)। ऐसा इसलिए है क्योंकि यदि संवेदी गड़बड़ी को (उपयुक्त लंबी अवधि के लिए) निलंबित कर दिया जाता है, तो जटिलता कम हो जाती है (क्योंकि सटीकता की उपेक्षा की जा सकती है)। इस बिंदु पर, प्रणाली संतुलन पर है और आंतरिक अवस्थाएं न्यूनतम ऊर्जा के सिद्धांत द्वारा हेल्महोल्ट्ज़ मुक्त ऊर्जा को कम करती हैं।[35]
निःशुल्क ऊर्जा न्यूनीकरण और सूचना सिद्धांत
मुक्त ऊर्जा न्यूनीकरण संवेदी अवस्थाओं और आंतरिक अवस्थाओं के बीच पारस्परिक जानकारी को अधिकतम करने के बराबर है जो परिवर्तनशील घनत्व (एक निश्चित एन्ट्रापी परिवर्तनीय घनत्व के लिए) को मापता है। यह निःशुल्क ऊर्जा न्यूनीकरण को न्यूनतम अतिरेक के सिद्धांत से संबंधित करता है [36][12]
तंत्रिका विज्ञान में मुक्त ऊर्जा न्यूनीकरण
मुक्त ऊर्जा न्यूनीकरण, अनिश्चितता के अनुसरा तंत्रिका अनुमान और सीखने के मानक (बेयस इष्टतम) मॉडल तैयार करने का एक उपयोगी तरीका प्रदान करता है।[37] और इसलिए बायेसियन मस्तिष्क परिकल्पना की सदस्यता लेता है।[38] मुक्त ऊर्जा न्यूनतमकरण द्वारा वर्णित तंत्रिका प्रक्रियाएं छिपी हुई अवस्थाओं की प्रकृति पर निर्भर करती हैं: इसमें समय-निर्भर चर, समय-अपरिवर्तनीय पैरामीटर और यादृच्छिक उतार-चढ़ाव की सटीकता (उलटा विचरण या तापमान) सम्मलित हो सकते हैं। चर, पैरामीटर और परिशुद्धता को न्यूनतम करना क्रमशः अनुमान, सीखने और अनिश्चितता के कोडन के अनुरूप है।
अवधारणात्मक अनुमान और वर्गीकरण
मुक्त ऊर्जा न्यूनीकरण धारणा में अचेतन अनुमान की धारणा को औपचारिक बनाता है[7][9]और तंत्रिका प्रसंस्करण का एक मानक (बायेसियन) सिद्धांत प्रदान करता है। तंत्रिका डायनेमिक्स का संबद्ध प्रक्रिया सिद्धांत प्रवणता अवरोह के माध्यम से मुक्त ऊर्जा को कम करने पर आधारित है। यह सामान्यीकृत परिसरण से मेल खाता है (जहां ~ गति के सामान्यीकृत निर्देशांक में एक चर को दर्शाता है और एक व्युत्पन्न मैट्रिक्स ऑपरेटर है):[39]
सामान्यत:, मुक्त ऊर्जा को परिभाषित करने वाले उत्पादक मॉडल गैर-रैखिक और पदानुक्रमित होते हैं (मस्तिष्क में कॉर्टिकल पदानुक्रम की तरह)। सामान्यीकृत फ़िल्टरिंग के विशेष स्थितियों में कलमन फ़िल्टरिंग सम्मलित है, जो औपचारिक रूप से पूर्वानुमानित कोडन के बराबर है[40] - मस्तिष्क में संदेश भेजने का एक लोकप्रिय रूपक पदानुक्रमित मॉडल के अनुसरा, पूर्वकथन कहनेवाला कोडन में आरोही (नीचे से ऊपर) पूर्वानुमान त्रुटियों और अवरोही (ऊपर से नीचे) पूर्वानुमान का आवर्ती आदान-प्रदान सम्मलित होता है।[41] यह संवेदी की शारीरिक रचना और शरीर विज्ञान के अनुरूप[42] और मोटर प्रणाली है।[43]
अवधारणात्मक शिक्षा और स्मृति
पूर्वकथन कहने वाला कोडन में, मुक्त ऊर्जा (मुक्त कार्रवाई) के अभिन्न अंग पर क्रमिक वंश के माध्यम से मॉडल मापदंडों का अनुकूलन साहचर्य या हेब्बियन सिद्धांत को कम करता है और मस्तिष्क में सूत्रयुग्मक सुनम्यता से जुड़ा होता है।
अवधारणात्मक सटीकता, ध्यान और प्रमुखता
परिशुद्धता मापदंडों का अनुकूलन पूर्वानुमान त्रुटियों के लाभ को अनुकूलित करने से मेल खाता है (सी.एफ., कलमन लाभ)। पूर्वानुमानित कोडन के तंत्रिका रूप से प्रशंसनीय कार्यान्वयन में,[41]यह सतही पिरामिड कोशिकाओं की उत्तेज्यता को अनुकूलित करने के अनुरूप है और इसकी व्याख्या ध्यानात्मक लाभ के संदर्भ में की गई है।[44]
अधोशीर्ष बनाम ऊर्ध्वगामी विवाद के संबंध में, जिसे ध्यान की एक प्रमुख खुली समस्या के रूप में संबोधित किया गया है, एक अभिकलनीयतः मॉडल अधोशीर्ष और ऊर्ध्वगामी तंत्र के बीच परस्पर क्रिया की परिपत्र प्रकृति को चित्रित करने में सफल रहा है। ध्यान के एक स्थापित उभरते मॉडल, अर्थात् एसएआईएम का उपयोग करते हुए, लेखकों ने पीई-एसएआईएम नामक एक मॉडल का प्रस्ताव रखा, जो मानक संस्करण के विपरीत, ऊपर से नीचे की स्थिति से चयनात्मक ध्यान देता है। मॉडल पूर्वानुमानत्रुटियों के संचरण को समान स्तर या उससे ऊपर के स्तर पर ध्यान में रखता है, जिससे कि ऊर्जा फलन को कम किया जा सके जो आँकड़े और उसके कारण के बीच अंतर को इंगित करता है, या, दूसरे शब्दों में, जेनरेटिव मॉडल और पोस्टीरियर के बीच वैधता बढ़ाने के लिए, उन्होंने अपने मॉडल में उत्तेज्यताओं के बीच तंत्रिका प्रतिस्पर्धा को भी सम्मलित किया। इस मॉडल की एक उल्लेखनीय विशेषता केवल कार्य प्रदर्शन के दौरान पूर्वानुमानत्रुटियों के संदर्भ में मुक्त ऊर्जा फलन का पुनरुद्धार है:
जहाँ तंत्रिका नेटवर्क का कुल ऊर्जा कार्य सम्मलित है, और समय के साथ जनरेटिव मॉडल (पूर्व) और पश्च परिवर्तन के बीच पूर्वानुमानत्रुटि है।[45]
दो मॉडलों की तुलना करने से उनके संबंधित परिणामों के बीच एक उल्लेखनीय समानता का पता चलता है, साथ ही एक उल्लेखनीय विसंगति भी उजागर होती है, जिससे - एसएआईएम के मानक संस्करण में - मॉडल का ध्यान मुख्य रूप से उत्तेजक कनेक्शन पर होता है, जबकि पीई-एसएआईएम में, निरोधात्मक कनेक्शन होते हैं। एक अनुमान लगाने के लिए उपयोग किया गया। यह मॉडल उच्च परिशुद्धता के साथ मानव प्रयोगों से प्राप्त ईईजी और एफएमआरआई आँकड़े की पूर्वानुमानकरने के लिए भी उपयुक्त सिद्ध हुआ है। इसी तरह, याह्या एट अल। गुप्त चयनात्मक दृश्य ध्यान में टेम्पलेट मिलान के लिए एक अभिकलनीयतः मॉडल का प्रस्ताव करने के लिए मुक्त ऊर्जा सिद्धांत को भी लागू किया जो ज्यादातर एसएआईएम पर निर्भर करता है।[46] इस अध्ययन के अनुसार, पूरे स्थिति-समष्टि की कुल मुक्त ऊर्जा मूल तंत्रिका नेटवर्क में ऊपर से नीचे सिग्नल डालकर पहुंचाई जाती है, जिससे हम एक गतिशील प्रणाली प्राप्त करते हैं जिसमें अग्र प्रभरण और पश्चगामी पूर्वानुमानत्रुटि दोनों सम्मलित होती हैं।
सक्रिय अनुमान
जब प्रवणता अवरोह को क्रिया पर लागू किया जाता है , मोटर नियंत्रण को शास्त्रीय प्रतिवर्त चाप के संदर्भ में समझा जा सकता है जो अवरोही (कॉर्टिकोस्पाइनल) पूर्वानुमान से जुड़े होते हैं। यह एक औपचारिकता प्रदान करता है जो संतुलन बिंदु समाधान को सामान्यीकृत करता है - स्वतंत्रता समस्या की डिग्री तक[47] - आंदोलन प्रक्षेप पथ के लिए।
सक्रिय अनुमान और इष्टतम नियंत्रण
सक्रिय अनुमान स्थिति परिवर्तन या प्रवाह के बारे में पूर्व मान्यताओं के साथ मूल्य या लागत-से-जाने वाले कार्यों को प्रतिस्थापित करके इष्टतम नियंत्रण से संबंधित है।[48] यह बायेसियन फ़िल्टरिंग और बेलमैन समीकरण के समाधान के बीच घनिष्ठ संबंध का फायदा उठाता है। चूंकि, सक्रिय अनुमान प्रवाह से प्रारंभ होता है जो अदिश से निर्दिष्ट हैं और सदिश स्थिति स्थान के मूल्य कार्य (सी.एफ., हेल्महोल्ट्ज़ अपघटन)। यहाँ, यादृच्छिक उतार-चढ़ाव का आयाम है और लागत है . पूर्वज ओवर फ्लो स्थितिों पर पूर्व प्रेरित करें यह उपयुक्त अग्रगामी कोलमोगोरोव समीकरणों का समाधान है।[49] इसके विपरीत, इष्टतम नियंत्रण इस धारणा के अनुसरा, लागत फलन को देखते हुए, प्रवाह को अनुकूलित करता है (अर्थात, प्रवाह कर्ल मुक्त है या विस्तृत संतुलन है)। सामान्यत:, इसमें पिछड़े कोलमोगोरोव समीकरणों को हल करना सम्मलित होता है।[50]
सक्रिय अनुमान और इष्टतम निर्णय (खेल) सिद्धांत
इष्टतम निर्णय समस्याओं (सामान्यत: आंशिक रूप से अवलोकन योग्य मार्कोव निर्णय प्रक्रियाओं के रूप में तैयार की जाती है) को पूर्व मान्यताओं में उपयोगिता को अवशोषित करके सक्रिय अनुमान के भीतर व्यवहार किया जाता है। इस सेटिंग में, जिन स्थितिों की उपयोगिता (कम लागत) अधिक है, वे ऐसे स्थिति हैं जिन पर कारक कब्ज़ा करने की उम्मीद करता है। जनरेटिव मॉडल को छिपे हुए स्थितिों से लैस करके मॉडल नियंत्रण, नीतियां (नियंत्रण अनुक्रम) जो परिवर्तनशील मुक्त ऊर्जा को कम करती हैं, उच्च उपयोगिता वाले स्थितिों की ओर ले जाती हैं।[51]
न्यूरोबायोलॉजिकल रूप से, डोपामाइन जैसे तंत्रिका मॉडुलेटर को पूर्वानुमानत्रुटि कोडन प्रमुख कोशिकाओं के लाभ को संशोधित करके पूर्वानुमानत्रुटियों की सटीकता की रिपोर्ट करने के लिए माना जाता है।[52] यह पूर्वानुमानत्रुटियों की रिपोर्टिंग में डोपामाइन की भूमिका से निकटता से संबंधित है - लेकिन औपचारिक रूप से अलग है-प्रति भविष्यवाणी त्रुटियों की रिपोर्ट करने में डोपामाइन की भूमिका[53] और संबंधित कम्प्यूटेशनल खाते है।[54]
सक्रिय अनुमान और संज्ञानात्मक तंत्रिका विज्ञान
सक्रिय अनुमान का उपयोग संज्ञानात्मक तंत्रिका विज्ञान, मस्तिष्क कार्य और न्यूरोसाइकिएट्री (तंत्रिका मनश्चित्सा) में कई मुद्दों को संबोधित करने के लिए किया गया है, जिसमें क्रिया अवलोकन भी सम्मलित है।[55] दर्पण स्नायु,[56] सैकेडेस और दृश्य खोज,[57][58] आँखों की हरकतें,[59] नींद,[60] भ्रम,[61] ध्यान,[44]क्रिया चयन,[52]चेतना,[62][63] हिस्टीरिया[64] और मनोविकृति.[65] सक्रिय अनुमान में कार्रवाई की व्याख्या अधिकांशत: इस विचार पर निर्भर करती है कि मस्तिष्क में 'जिद्दी पूर्वकथनवाणियां' होती हैं जिन्हें वह अद्यतन नहीं कर सकता है, जिसके परिणामस्वरूप ऐसी गतिविधियां होती हैं जो इन पूर्वानुमान को सच कर देती हैं।[66]
यह भी देखें
- क्रिया-विशेष धारणा
- शक्यता
- ऑटोपोइज़िस
- मस्तिष्क के कार्य के लिए बायेसियन दृष्टिकोण – Explaining the brain's abilities through statistical principles
- एड्रिअन बेजान - प्रकृति, चेतन और निर्जीव में डिजाइन विकास का नियम
- निर्णय सिद्धांत – Branch of applied probability theory
- प्रतीकात्मक उपलब्धि
- एंट्रोपिक बल – Physical force that originates from thermodynamics instead of fundamental interactions
- न्यूनतम ऊर्जा का सिद्धांत
- सूचना-मेट्रिक्स – Interdisciplinary approach to scientific modelling and information processing
- इष्टतम नियंत्रण – Mathematical way of attaining a desired output from a dynamic system
- अनुकूली प्रणाली, also known as प्रैक्टोपोइज़िस
- पूर्वानुमानित कोडिंग
- आत्म संगठन – Process of creating order by local interactions
- आश्चर्य – Supercontinent from the late Paleozoic to early Mesozoic eras
- सिनर्जेटिक्स (हेकेन)
- वैरिएशनल बायेसियन विधियाँ – Mathematical methods used in Bayesian inference and machine learning
संदर्भ
- ↑ Bruineberg, Jelle; Kiverstein, Julian; Rietveld, Erik (2018). "The anticipating brain is not a scientist: the free-energy principle from an ecological-enactive perspective". Synthese. 195 (6): 2417–2444. doi:10.1007/s11229-016-1239-1. PMC 6438652. PMID 30996493.
- ↑ Friston, Karl (2010). "The free-energy principle: a unified brain theory?". Nature Reviews Neuroscience. 11 (2): 127–138. doi:10.1038/nrn2787. PMID 20068583. S2CID 5053247. Retrieved July 9, 2023.
- ↑ Friston, Karl; Kilner, James; Harrison, Lee (2006). "मस्तिष्क के लिए एक मुक्त ऊर्जा सिद्धांत" (PDF). Journal of Physiology-Paris. 100 (1–3): 70–87. doi:10.1016/j.jphysparis.2006.10.001. PMID 17097864. S2CID 637885.
- ↑ 4.0 4.1 Shaun Raviv: The Genius Neuroscientist Who Might Hold the Key to True AI. In: Wired, 13. November 2018
- ↑ Friston, Karl (2018). "Of woodlice and men: A Bayesian account of cognition, life and consciousness. An interview with Karl Friston (by Martin Fortier & Daniel Friedman)". ALIUS Bulletin. 2: 17–43.
- ↑ Friston, Karl (2022). Active Inference: The Free Energy Principle in Mind, Brain, and Behavior. MIT Press. ISBN 9780262045353.
- ↑ 7.0 7.1 Helmholtz, H. (1866/1962). Concerning the perceptions in general. In Treatise on physiological optics (J. Southall, Trans., 3rd ed., Vol. III). New York: Dover. Available at https://web.archive.org/web/20180320133752/http://poseidon.sunyopt.edu/BackusLab/Helmholtz/
- ↑ Gregory, R. L. (1980-07-08). "धारणाएँ परिकल्पना के रूप में". Philosophical Transactions of the Royal Society of London. B, Biological Sciences. 290 (1038): 181–197. Bibcode:1980RSPTB.290..181G. doi:10.1098/rstb.1980.0090. JSTOR 2395424. PMID 6106237.
- ↑ 9.0 9.1 Dayan, Peter; Hinton, Geoffrey E.; Neal, Radford M.; Zemel, Richard S. (1995). "हेल्महोल्ट्ज़ मशीन" (PDF). Neural Computation. 7 (5): 889–904. doi:10.1162/neco.1995.7.5.889. hdl:21.11116/0000-0002-D6D3-E. PMID 7584891. S2CID 1890561.
- ↑ Beal, M. J. (2003). Variational Algorithms for Approximate Bayesian Inference. Ph.D. Thesis, University College London.
- ↑ Sakthivadivel, Dalton (2022). "बायेसियन यांत्रिकी के लिए एक ज्यामिति और विश्लेषण की ओर". arXiv:2204.11900 [math-ph].
- ↑ 12.0 12.1 Ramstead, Maxwell; Sakthivadivel, Dalton; Heins, Conor; Koudahl, Magnus; Millidge, Beren; Da Costa, Lancelot; Klein, Brennan; Friston, Karl (2023). "On Bayesian mechanics: A physics of and by beliefs". Interface Focus. 13 (3). arXiv:2205.11543. doi:10.1098/rsfs.2022.0029. PMC 10198254. PMID 37213925. S2CID 249017997.
- ↑ Conant, Roger C.; Ross Ashby, W. (1970). "किसी सिस्टम का प्रत्येक अच्छा नियामक उस सिस्टम का एक मॉडल होना चाहिए". International Journal of Systems Science. 1 (2): 89–97. doi:10.1080/00207727008920220.
- ↑ Kauffman, S. (1993). The Origins of Order: Self-Organization and Selection in Evolution. Oxford: Oxford University Press.
- ↑ Nicolis, G., & Prigogine, I. (1977). Self-organization in non-equilibrium systems. New York: John Wiley.
- ↑ Maturana, H. R., & Varela, F. (1980). Autopoiesis: the organization of the living. In V. F. Maturana HR (Ed.), Autopoiesis and Cognition. Dordrecht, Netherlands: Reidel.
- ↑ Nikolić, Danko (2015). "Practopoiesis: Or how life fosters a mind". Journal of Theoretical Biology. 373: 40–61. arXiv:1402.5332. Bibcode:2015JThBi.373...40N. doi:10.1016/j.jtbi.2015.03.003. PMID 25791287. S2CID 12680941.
- ↑ Haken, H. (1983). Synergetics: An introduction. Non-equilibrium phase transition and self-organisation in physics, chemistry and biology (3rd ed.). Berlin: Springer Verlag.
- ↑ Jaynes, E. T. (1957). "सूचना सिद्धांत और सांख्यिकीय यांत्रिकी" (PDF). Physical Review. 106 (4): 620–630. Bibcode:1957PhRv..106..620J. doi:10.1103/PhysRev.106.620. S2CID 17870175.
- ↑ Veissière, Samuel P. L.; Constant, Axel; Ramstead, Maxwell J. D.; Friston, Karl J.; Kirmayer, Laurence J. (2020). "Thinking through other minds: A variational approach to cognition and culture". Behavioral and Brain Sciences (in English). 43: e90. doi:10.1017/S0140525X19001213. ISSN 0140-525X. PMID 31142395. S2CID 169038428.
- ↑ Ramstead, Maxwell J. D.; Constant, Axel; Badcock, Paul B.; Friston, Karl J. (2019-12-01). "परिवर्तनशील पारिस्थितिकी और संवेदनशील प्रणालियों की भौतिकी". Physics of Life Reviews. Physics of Mind (in English). 31: 188–205. Bibcode:2019PhLRv..31..188R. doi:10.1016/j.plrev.2018.12.002. ISSN 1571-0645. PMC 6941227. PMID 30655223.
- ↑ Albarracin, Mahault; Demekas, Daphne; Ramstead, Maxwell J. D.; Heins, Conor (April 2022). "सक्रिय अनुमान के तहत ज्ञानमीमांसीय समुदाय". Entropy (in English). 24 (4): 476. Bibcode:2022Entrp..24..476A. doi:10.3390/e24040476. ISSN 1099-4300. PMC 9027706. PMID 35455140.
- ↑ Albarracin, Mahault; Constant, Axel; Friston, Karl J.; Ramstead, Maxwell James D. (2021). "लिपियों के प्रति एक विविध दृष्टिकोण". Frontiers in Psychology. 12: 585493. doi:10.3389/fpsyg.2021.585493. ISSN 1664-1078. PMC 8329037. PMID 34354621.
- ↑ Friston, Karl J.; Parr, Thomas; Yufik, Yan; Sajid, Noor; Price, Catherine J.; Holmes, Emma (2020-11-01). "जनरेटिव मॉडल, भाषाई संचार और सक्रिय अनुमान". Neuroscience & Biobehavioral Reviews (in English). 118: 42–64. doi:10.1016/j.neubiorev.2020.07.005. ISSN 0149-7634. PMC 7758713. PMID 32687883.
- ↑ Tison, Remi; Poirier, Pierre (2021-10-02). "Communication as Socially Extended Active Inference: An Ecological Approach to Communicative Behavior". Ecological Psychology. 33 (3–4): 197–235. doi:10.1080/10407413.2021.1965480. ISSN 1040-7413. S2CID 238703201.
- ↑ Friston, Karl J.; Frith, Christopher D. (2015-07-01). "सक्रिय अनुमान, संचार और व्याख्याशास्त्र". Cortex. Special issue: Prediction in speech and language processing (in English). 68: 129–143. doi:10.1016/j.cortex.2015.03.025. ISSN 0010-9452. PMC 4502445. PMID 25957007.
- ↑ Kerusauskaite, Skaiste (2023-06-01). "Role of Culture in Meaning Making: Bridging Semiotic Cultural Psychology and Active Inference". Integrative Psychological and Behavioral Science (in English). 57 (2): 432–443. doi:10.1007/s12124-022-09744-x. ISSN 1936-3567. PMID 36585542. S2CID 255366405.
- ↑ García, Adolfo M.; Ibáñez, Agustín (2022-11-14). सेमियोसिस और मस्तिष्क की रूटलेज हैंडबुक (in English). Taylor & Francis. ISBN 978-1-000-72877-4.
- ↑ Bottemanne, Hugo; Friston, Karl J. (2021-12-01). "An active inference account of protective behaviours during the COVID-19 pandemic". Cognitive, Affective, & Behavioral Neuroscience (in English). 21 (6): 1117–1129. doi:10.3758/s13415-021-00947-0. ISSN 1531-135X. PMC 8518276. PMID 34652601.
- ↑ Crauel, Hans; Flandoli, Franco (1994). "यादृच्छिक गतिशील प्रणालियों के लिए आकर्षण". Probability Theory and Related Fields. 100 (3): 365–393. doi:10.1007/BF01193705. S2CID 122609512.
- ↑ Colombo, Matteo; Palacios, Patricia (2021). "गैर-संतुलन थर्मोडायनामिक्स और जीव विज्ञान में मुक्त ऊर्जा सिद्धांत". Biology & Philosophy. 36 (5). doi:10.1007/s10539-021-09818-x. S2CID 235803361.
- ↑ Roweis, Sam; Ghahramani, Zoubin (1999). "रैखिक गाऊसी मॉडल की एक एकीकृत समीक्षा" (PDF). Neural Computation. 11 (2): 305–345. doi:10.1162/089976699300016674. PMID 9950734. S2CID 2590898.
- ↑ Ortega, Pedro A.; Braun, Daniel A. (2013). "सूचना-प्रसंस्करण लागत के साथ निर्णय लेने के सिद्धांत के रूप में थर्मोडायनामिक्स". Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences. 469 (2153). arXiv:1204.6481. Bibcode:2013RSPSA.46920683O. doi:10.1098/rspa.2012.0683. S2CID 28080508.
- ↑ Evans, Denis J. (2003). "नियतात्मक प्रणालियों के लिए एक गैर-संतुलन मुक्त ऊर्जा प्रमेय" (PDF). Molecular Physics. 101 (10): 1551–1554. Bibcode:2003MolPh.101.1551E. doi:10.1080/0026897031000085173. S2CID 15129000.
- ↑ Jarzynski, C. (1997). "मुक्त ऊर्जा अंतर के लिए कोई भी संतुलन समानता नहीं". Physical Review Letters. 78 (14): 2690–2693. arXiv:cond-mat/9610209. Bibcode:1997PhRvL..78.2690J. doi:10.1103/PhysRevLett.78.2690. S2CID 16112025.
- ↑ Sakthivadivel, Dalton (2022). "बायेसियन यांत्रिकी के लिए एक ज्यामिति और विश्लेषण की ओर". arXiv:2204.11900 [math-ph].
- ↑ Friston, Karl (2010). "The free-energy principle: A unified brain theory?" (PDF). Nature Reviews Neuroscience. 11 (2): 127–138. doi:10.1038/nrn2787. PMID 20068583. S2CID 5053247.
- ↑ Knill, David C.; Pouget, Alexandre (2004). "The Bayesian brain: The role of uncertainty in neural coding and computation" (PDF). Trends in Neurosciences. 27 (12): 712–719. doi:10.1016/j.tins.2004.10.007. PMID 15541511. S2CID 9870936.
- ↑ Friston, Karl; Stephan, Klaas; Li, Baojuan; Daunizeau, Jean (2010). "सामान्यीकृत फ़िल्टरिंग". Mathematical Problems in Engineering. 2010: 1–34. doi:10.1155/2010/621670.
- ↑ Knill, David C.; Pouget, Alexandre (2004). "The Bayesian brain: The role of uncertainty in neural coding and computation" (PDF). Trends in Neurosciences. 27 (12): 712–719. doi:10.1016/j.tins.2004.10.007. PMID 15541511. S2CID 9870936.
- ↑ 41.0 41.1 Mumford, D. (1992). "नियोकोर्टेक्स की कम्प्यूटेशनल वास्तुकला पर" (PDF). Biological Cybernetics. 66 (3): 241–251. doi:10.1007/BF00198477. PMID 1540675. S2CID 14303625.
- ↑ Bastos, Andre M.; Usrey, W. Martin; Adams, Rick A.; Mangun, George R.; Fries, Pascal; Friston, Karl J. (2012). "पूर्वानुमानित कोडिंग के लिए कैनोनिकल माइक्रोसर्किट". Neuron. 76 (4): 695–711. doi:10.1016/j.neuron.2012.10.038. PMC 3777738. PMID 23177956.
- ↑ Adams, Rick A.; Shipp, Stewart; Friston, Karl J. (2013). "Predictions not commands: Active inference in the motor system". Brain Structure and Function. 218 (3): 611–643. doi:10.1007/s00429-012-0475-5. PMC 3637647. PMID 23129312.
- ↑ 44.0 44.1 Friston, Karl J.; Feldman, Harriet (2010). "ध्यान, अनिश्चितता, और मुक्त-ऊर्जा". Frontiers in Human Neuroscience. 4: 215. doi:10.3389/fnhum.2010.00215. PMC 3001758. PMID 21160551.
- ↑ Abadi, Alireza Khatoon; Yahya, Keyvan; Amini, Massoud; Friston, Karl; Heinke, Dietmar (2019). "दृश्य निर्माण के बायेसियन फॉर्मूलेशन में उत्तेजक बनाम निरोधात्मक प्रतिक्रिया". Journal of the Royal Society Interface. 16 (154). doi:10.1098/rsif.2018.0344. PMC 6544897. PMID 31039693.
- ↑ "12th Biannual Conference of the German Cognitive Science Society (KogWis 2014)". Cognitive Processing. 15: 107. 2014. doi:10.1007/s10339-013-0597-6. S2CID 10121398.
- ↑ Feldman, Anatol G.; Levin, Mindy F. (1995). "मोटर नियंत्रण में स्थितीय संदर्भ फ्रेम की उत्पत्ति और उपयोग" (PDF). Behavioral and Brain Sciences. 18 (4): 723–744. doi:10.1017/S0140525X0004070X. S2CID 145164477.
- ↑ Friston, Karl (2011). "What is Optimal about Motor Control?" (PDF). Neuron. 72 (3): 488–498. doi:10.1016/j.neuron.2011.10.018. PMID 22078508. S2CID 13912462.
- ↑ Friston, Karl; Ao, Ping (2012). "निःशुल्क ऊर्जा, मूल्य और आकर्षणकर्ता". Computational and Mathematical Methods in Medicine. 2012: 1–27. doi:10.1155/2012/937860. PMC 3249597. PMID 22229042.
- ↑ Kappen, H. J. (2005). "इष्टतम नियंत्रण सिद्धांत के लिए पथ अभिन्नता और समरूपता तोड़ना". Journal of Statistical Mechanics: Theory and Experiment. 2005 (11): P11011. arXiv:physics/0505066. Bibcode:2005JSMTE..11..011K. doi:10.1088/1742-5468/2005/11/P11011. S2CID 87027.
- ↑ Friston, Karl; Samothrakis, Spyridon; Montague, Read (2012). "Active inference and agency: Optimal control without cost functions". Biological Cybernetics. 106 (8–9): 523–541. doi:10.1007/s00422-012-0512-8. PMID 22864468.
- ↑ 52.0 52.1 Friston, Karl J.; Shiner, Tamara; Fitzgerald, Thomas; Galea, Joseph M.; Adams, Rick; Brown, Harriet; Dolan, Raymond J.; Moran, Rosalyn; Stephan, Klaas Enno; Bestmann, Sven (2012). "डोपामाइन, सामर्थ्य और सक्रिय अनुमान". PLOS Computational Biology. 8 (1): e1002327. Bibcode:2012PLSCB...8E2327F. doi:10.1371/journal.pcbi.1002327. PMC 3252266. PMID 22241972.
- ↑ Fiorillo, Christopher D.; Tobler, Philippe N.; Schultz, Wolfram (2003). "Discrete Coding of Reward Probability and Uncertainty by Dopamine Neurons" (PDF). Science. 299 (5614): 1898–1902. Bibcode:2003Sci...299.1898F. doi:10.1126/science.1077349. PMID 12649484. S2CID 2363255.
- ↑ Frank, Michael J. (2005). "Dynamic Dopamine Modulation in the Basal Ganglia: A Neurocomputational Account of Cognitive Deficits in Medicated and Nonmedicated Parkinsonism" (PDF). Journal of Cognitive Neuroscience. 17 (1): 51–72. doi:10.1162/0898929052880093. PMID 15701239. S2CID 7414727.
- ↑ Friston, Karl; Mattout, Jérémie; Kilner, James (2011). "कार्रवाई की समझ और सक्रिय अनुमान" (PDF). Biological Cybernetics. 104 (1–2): 137–160. doi:10.1007/s00422-011-0424-z. PMC 3491875. PMID 21327826.
- ↑ Kilner, James M.; Friston, Karl J.; Frith, Chris D. (2007). "Predictive coding: An account of the mirror neuron system" (PDF). Cognitive Processing. 8 (3): 159–166. doi:10.1007/s10339-007-0170-2. PMC 2649419. PMID 17429704.
- ↑ Friston, Karl; Adams, Rick A.; Perrinet, Laurent; Breakspear, Michael (2012). "Perceptions as Hypotheses: Saccades as Experiments". Frontiers in Psychology. 3: 151. doi:10.3389/fpsyg.2012.00151. PMC 3361132. PMID 22654776.
- ↑ Mirza, M. Berk; Adams, Rick A.; Mathys, Christoph; Friston, Karl J. (2018). "मानव दृश्य अन्वेषण संवेदी दुनिया के बारे में अनिश्चितता को कम करता है". PLOS ONE. 13 (1): e0190429. Bibcode:2018PLoSO..1390429M. doi:10.1371/journal.pone.0190429. PMC 5755757. PMID 29304087.
- ↑ Perrinet, Laurent U.; Adams, Rick A.; Friston, Karl J. (2014). "सक्रिय अनुमान, नेत्र गति और ओकुलोमोटर विलंब". Biological Cybernetics. 108 (6): 777–801. doi:10.1007/s00422-014-0620-8. PMC 4250571. PMID 25128318.
- ↑ Hobson, J.A.; Friston, K.J. (2012). "Waking and dreaming consciousness: Neurobiological and functional considerations". Progress in Neurobiology. 98 (1): 82–98. doi:10.1016/j.pneurobio.2012.05.003. PMC 3389346. PMID 22609044.
- ↑ Brown, Harriet; Friston, Karl J. (2012). "Free-Energy and Illusions: The Cornsweet Effect". Frontiers in Psychology. 3: 43. doi:10.3389/fpsyg.2012.00043. PMC 3289982. PMID 22393327.
- ↑ Rudrauf, David; Bennequin, Daniel; Granic, Isabela; Landini, Gregory; Friston, Karl; Williford, Kenneth (2017-09-07). "सन्निहित चेतना का एक गणितीय मॉडल" (PDF). Journal of Theoretical Biology. 428: 106–131. Bibcode:2017JThBi.428..106R. doi:10.1016/j.jtbi.2017.05.032. PMID 28554611.
- ↑ K, Williford; D, Bennequin; K, Friston; D, Rudrauf (2018-12-17). "प्रक्षेप्य चेतना मॉडल और अभूतपूर्व स्वत्व". Frontiers in Psychology (in English). 9: 2571. doi:10.3389/fpsyg.2018.02571. PMC 6304424. PMID 30618988.
- ↑ Edwards, M. J.; Adams, R. A.; Brown, H.; Parees, I.; Friston, K. J. (2012). "'हिस्टीरिया' का बायेसियन विवरण" (PDF). Brain. 135 (11): 3495–3512. doi:10.1093/brain/aws129. PMC 3501967. PMID 22641838.
- ↑ Adams, Rick A.; Perrinet, Laurent U.; Friston, Karl (2012). "Smooth Pursuit and Visual Occlusion: Active Inference and Oculomotor Control in Schizophrenia". PLOS ONE. 7 (10): e47502. Bibcode:2012PLoSO...747502A. doi:10.1371/journal.pone.0047502. PMC 3482214. PMID 23110076.
- ↑ Yon, Daniel; Lange, Floris P. de; Press, Clare (2019-01-01). "एक जिद्दी वैज्ञानिक के रूप में पूर्वानुमानित मस्तिष्क". Trends in Cognitive Sciences (in English). 23 (1): 6–8. doi:10.1016/j.tics.2018.10.003. PMID 30429054. S2CID 53280000.