सम्मिश्र विश्लेषण: Difference between revisions
No edit summary |
|||
| Line 33: | Line 33: | ||
सतही तौर पर, यह परिभाषा औपचारिक रूप से एक वास्तविक कार्य के व्युत्पन्न के अनुरूप है। हालांकि, सम्मिश्र डेरिवेटिव और अलग-अलग कार्य उनके वास्तविक समकक्षों की तुलना में काफी भिन्न तरीके से व्यवहार करते हैं। विशेष रूप से, इस सीमा के अस्तित्व के लिए, अंतर भागफल का मान समान सम्मिश्र संख्या तक पहुंचना चाहिए, चाहे हम जिस तरीके से दृष्टिकोण करें <math>z_0</math> सम्मिश्र विमान में। नतीजतन, सम्मिश्र भिन्नता का वास्तविक भिन्नता की तुलना में अधिक मजबूत प्रभाव पड़ता है। उदाहरण के लिए, होलोमोर्फिक फलन [[असीम रूप से भिन्न]] होते हैं, जबकि n वें व्युत्पन्न के अस्तित्व को वास्तविक कार्यों के लिए (n + 1) वें व्युत्पन्न के अस्तित्व की आवश्यकता नहीं होती है। इसके अलावा, सभी होलोमॉर्फिक फ़ंक्शन विश्लेषणात्मक फ़ंक्शन की मजबूत स्थिति को संतुष्ट करते हैं, जिसका अर्थ है कि फ़ंक्शन, अपने डोमेन में हर बिंदु पर, स्थानीय रूप से अभिसरण शक्ति श्रृंखला द्वारा दिया जाता है। संक्षेप में, इसका मतलब है कि होलोमोर्फिक कार्य करता है <math>\Omega</math> प्रत्येक बिंदु के कुछ पड़ोस में बहुपदों द्वारा मनमाने ढंग से अनुमानित किया जा सकता है <math>\Omega</math>. यह अलग-अलग वास्तविक कार्यों के ठीक विपरीत है; असीम रूप से अलग-अलग वास्तविक कार्य हैं जो कहीं भी विश्लेषणात्मक नहीं हैं; देखना {{slink|गैर-विश्लेषणात्मक सुचारू फलन|एक सहज फलन जो कहीं भी वास्तविक विश्लेषणात्मक नहीं है।}} | सतही तौर पर, यह परिभाषा औपचारिक रूप से एक वास्तविक कार्य के व्युत्पन्न के अनुरूप है। हालांकि, सम्मिश्र डेरिवेटिव और अलग-अलग कार्य उनके वास्तविक समकक्षों की तुलना में काफी भिन्न तरीके से व्यवहार करते हैं। विशेष रूप से, इस सीमा के अस्तित्व के लिए, अंतर भागफल का मान समान सम्मिश्र संख्या तक पहुंचना चाहिए, चाहे हम जिस तरीके से दृष्टिकोण करें <math>z_0</math> सम्मिश्र विमान में। नतीजतन, सम्मिश्र भिन्नता का वास्तविक भिन्नता की तुलना में अधिक मजबूत प्रभाव पड़ता है। उदाहरण के लिए, होलोमोर्फिक फलन [[असीम रूप से भिन्न]] होते हैं, जबकि n वें व्युत्पन्न के अस्तित्व को वास्तविक कार्यों के लिए (n + 1) वें व्युत्पन्न के अस्तित्व की आवश्यकता नहीं होती है। इसके अलावा, सभी होलोमॉर्फिक फ़ंक्शन विश्लेषणात्मक फ़ंक्शन की मजबूत स्थिति को संतुष्ट करते हैं, जिसका अर्थ है कि फ़ंक्शन, अपने डोमेन में हर बिंदु पर, स्थानीय रूप से अभिसरण शक्ति श्रृंखला द्वारा दिया जाता है। संक्षेप में, इसका मतलब है कि होलोमोर्फिक कार्य करता है <math>\Omega</math> प्रत्येक बिंदु के कुछ पड़ोस में बहुपदों द्वारा मनमाने ढंग से अनुमानित किया जा सकता है <math>\Omega</math>. यह अलग-अलग वास्तविक कार्यों के ठीक विपरीत है; असीम रूप से अलग-अलग वास्तविक कार्य हैं जो कहीं भी विश्लेषणात्मक नहीं हैं; देखना {{slink|गैर-विश्लेषणात्मक सुचारू फलन|एक सहज फलन जो कहीं भी वास्तविक विश्लेषणात्मक नहीं है।}} | ||
[[:hi:चरघातांकी फलन|चरघातांकी फलन]], [[:hi:त्रिकोणमितीय फलन|त्रिकोणमितीय फलन]], और सभी [[:hi:बहुपद|बहुपद फलन]] सहित अधिकांश प्रारंभिक फलन, फलन के रूप में जटिल तर्कों के लिए उचित रूप से विस्तृत किए गए हैं {{Nowrap|<math>\mathbb{C}\to\mathbb{C}</math>,}} समूचे जटिल तल पर होलोमॉर्फिक हैं, जिससे वे ''संपूर्ण'' ''कार्य'' करते हैं, जबकि तर्कसंगत कार्य <math>p/q</math> | [[:hi:चरघातांकी फलन|चरघातांकी फलन]], [[:hi:त्रिकोणमितीय फलन|त्रिकोणमितीय फलन]], और सभी [[:hi:बहुपद|बहुपद फलन]] सहित अधिकांश प्रारंभिक फलन, फलन के रूप में जटिल तर्कों के लिए उचित रूप से विस्तृत किए गए हैं {{Nowrap|<math>\mathbb{C}\to\mathbb{C}</math>,}} समूचे जटिल तल पर होलोमॉर्फिक हैं, जिससे वे ''संपूर्ण'' ''कार्य'' करते हैं, जबकि तर्कसंगत कार्य <math>p/q</math>, जहां ''p'' और ''q'' बहुपद हैं, उन डोमेन पर होलोमॉर्फिक हैं जो उन बिंदुओं को बाहर करते हैं जहां ''q'' शून्य है। ऐसे कार्य जो अलग-अलग बिंदुओं के एक सेट को छोड़कर हर जगह होलोमोर्फिक होते हैं, ''मेरोमोर्फिक फ़ंक्शन'' के रूप में जाने जाते हैं। दूसरी ओर, कार्य {{Nowrap|<math>z\mapsto \Re(z)</math>,}} {\displaystyle z\mapsto \Re (z)} | ||
{{nowrap|<math>z\mapsto \Re(z)</math>,}} {{nowrap|<math>z\mapsto |z|</math>,}} | |||
<math>z\mapsto |z|</math>, और <math>z\mapsto \bar{z}</math> | |||
<math>z\mapsto \bar{z}</math> जटिल तल पर कहीं भी होलोमोर्फिक नहीं हैं, जैसा कि कॉची-रीमैन शर्तों को पूरा करने में उनकी विफलता से दिखाया जा सकता है (नीचे देखें)।िक कार्यों की एक महत्वपूर्ण संपत्ति उनके वास्तविक और काल्पनिक घटकों के आंशिक डेरिवेटिव के बीच का संबंध है, जिसे कॉची-रीमैन शर्तों के रूप में जाना जाता है। यदि <math>f:\mathbb{C}\to\mathbb{C}</math>, द्वारा परिभाषित {{nowrap|<math>f(z) = f(x + iy) = u(x, y) + iv(x, y)</math>,}} कहाँ पे {{nowrap|<math>x, y, u(x, y),v(x, y) \in \R</math>,}} एक [[क्षेत्र (गणित)]] पर होलोमोर्फिक है {{nowrap|<math>\Omega</math>,}} फिर सभी के लिए <math>z_0\in \Omega</math>, | |||
:<math>\frac{\partial f}{\partial\bar{z}}(z_0) = 0,\ \text{where } \frac\partial{\partial\bar{z}} \mathrel{:=} \frac12\left(\frac\partial{\partial x} + i\frac\partial{\partial y}\right).</math> | :<math>\frac{\partial f}{\partial\bar{z}}(z_0) = 0,\ \text{where } \frac\partial{\partial\bar{z}} \mathrel{:=} \frac12\left(\frac\partial{\partial x} + i\frac\partial{\partial y}\right).</math> | ||
फलन, u और v के वास्तविक और काल्पनिक भागों के संदर्भ में, यह समीकरणों के युग्म के तुल्य है <math>u_x = v_y</math> तथा <math>u_y=-v_x</math>, जहां सबस्क्रिप्ट आंशिक विभेदन का संकेत देते हैं। हालांकि, कॉची-रीमैन स्थितियां अतिरिक्त निरंतरता स्थितियों के बिना, होलोमोर्फिक कार्यों को चिह्नित नहीं करती हैं (लूमन-मेन्चॉफ प्रमेय देखें)। | फलन, u और v के वास्तविक और काल्पनिक भागों के संदर्भ में, यह समीकरणों के युग्म के तुल्य है <math>u_x = v_y</math> तथा <math>u_y=-v_x</math>, जहां सबस्क्रिप्ट आंशिक विभेदन का संकेत देते हैं। हालांकि, कॉची-रीमैन स्थितियां अतिरिक्त निरंतरता स्थितियों के बिना, होलोमोर्फिक कार्यों को चिह्नित नहीं करती हैं (लूमन-मेन्चॉफ प्रमेय देखें)। | ||
| Line 45: | Line 47: | ||
==अनुरूप मानचित्र== | ==अनुरूप मानचित्र== | ||
{{main| | {{main|अनुरूप मानचित्रण}} | ||
अनुरूप मानचित्रण स्थानीय रूप से उलटा [[जटिल विश्लेषणात्मक|सम्मिश्र विश्लेषणात्मक]] है | अनुरूप मानचित्रण स्थानीय रूप से उलटा [[जटिल विश्लेषणात्मक|सम्मिश्र विश्लेषणात्मक]] है | ||
अभिविन्यास संरक्षण के लिए दो आयामों में कार्य करता है। | अभिविन्यास संरक्षण के लिए दो आयामों में कार्य करता है। | ||
==अनुरूप मानचित्रण का अनुप्रयोग == | ==अनुरूप मानचित्रण का अनुप्रयोग == | ||
*[[अंतरिक्ष इंजीनियरिंग]] में<ref>{{Cite journal |last1=Selig |first1=Michael S. |last2=Maughmer |first2=Mark D. |date=1992-05-01 |title=अनुरूप मानचित्रण के आधार पर मल्टीपॉइंट इनवर्स एयरफॉइल डिजाइन पद्धति|url=https://arc.aiaa.org/doi/10.2514/3.11046 |journal=AIAA Journal |volume=30 |issue=5 |pages=1162–1170 |doi=10.2514/3.11046 |bibcode=1992AIAAJ..30.1162S |issn=0001-1452}}</ref> | |||
* | *बायोमेडिकल विज्ञान में<ref>{{Cite journal |last1=Cortijo |first1=Vanessa |last2=Alonso |first2=Elena R. |last3=Mata |first3=Santiago |last4=Alonso |first4=José L. |date=2018-01-18 |title=फेनोलिक एसिड का गठनात्मक मानचित्र|url=https://pubmed.ncbi.nlm.nih.gov/29215883/ |journal=The Journal of Physical Chemistry A |volume=122 |issue=2 |pages=646–651 |doi=10.1021/acs.jpca.7b08882 |issn=1520-5215 |pmid=29215883|bibcode=2018JPCA..122..646C }}</ref> | ||
*ब्रेन मैपिंग में<ref>{{Cite web |title=अनुरूप मानचित्रण के गुण|url=https://www.researchgate.net/figure/Properties-of-Conformal-Mapping-Conformal-mappings-transform-infinitesimal-circles-to_fig1_228640184}}</ref> | |||
*जेनेटिक मैपिंग<ref>{{Cite web |title=7.1 आनुवंशिक मानचित्र विभिन्न रूपों में आते हैं|url=http://www.informatics.jax.org/silver/chapters/7-1.shtml |access-date=2022-08-22 |website=www.informatics.jax.org}}</ref><ref>{{Cite journal |url=https://hcvalidate.perfdrive.com/?ssa=71fed169-69c9-41b8-9877-416719f0d113&ssb=80077267131&ssc=https%3A%2F%2Fiopscience.iop.org%2Farticle%2F10.1088%2F1478-3975%2F13%2F5%2F05LT01%2Fpdf&ssi=e1a50ce6-8427-48c7-9e70-ece2b2f11df9&ssk=support@shieldsquare.com&ssm=73836051457188970102906276668717&ssn=bd1de37a5005eecad6da1d8bb5de43cdae96922a58cb-972c-4c61-bbf00b&sso=ce98748a-7da0b84595a0eb14c80eef4551a4a5763a991c17cd7fabdb&ssp=79762773411661113911166113142686120&ssq=67286667226024947028072260265646682776545&ssr=MjA4LjgwLjE1My4yNA==&sst=ZoteroTranslationServer/WMF%20(mailto:noc@wikimedia.org)&ssv=&ssw=&ssx=W10= |access-date=2022-08-22 |journal=Physical Biology |doi=10.1088/1478-3975/13/5/05lt01| title=पत्ती की वृद्धि अनुरूप है| year=2016 | last1=Alim | first1=Karen | last2=Armon | first2=Shahaf | last3=Shraiman | first3=Boris I. | last4=Boudaoud | first4=Arezki | volume=13 | issue=5 | pages=05LT01 | pmid=27597439 | arxiv=1611.07032 | bibcode=2016PhBio..13eLT01A | s2cid=9351765 }}</ref><ref>{{Cite journal |last1=González-Matesanz |first1=F. J. |last2=Malpica |first2=J. A. |date=2006-11-01 |title=परिवर्तनों के समन्वय के लिए लागू आनुवंशिक एल्गोरिदम के साथ अर्ध-अनुरूप मानचित्रण|url=https://www.sciencedirect.com/science/article/pii/S0098300406000161 |journal=Computers & Geosciences |language=en |volume=32 |issue=9 |pages=1432–1441 |doi=10.1016/j.cageo.2006.01.002 |bibcode=2006CG.....32.1432G |issn=0098-3004}}</ref> | *जेनेटिक मैपिंग<ref>{{Cite web |title=7.1 आनुवंशिक मानचित्र विभिन्न रूपों में आते हैं|url=http://www.informatics.jax.org/silver/chapters/7-1.shtml |access-date=2022-08-22 |website=www.informatics.jax.org}}</ref><ref>{{Cite journal |url=https://hcvalidate.perfdrive.com/?ssa=71fed169-69c9-41b8-9877-416719f0d113&ssb=80077267131&ssc=https%3A%2F%2Fiopscience.iop.org%2Farticle%2F10.1088%2F1478-3975%2F13%2F5%2F05LT01%2Fpdf&ssi=e1a50ce6-8427-48c7-9e70-ece2b2f11df9&ssk=support@shieldsquare.com&ssm=73836051457188970102906276668717&ssn=bd1de37a5005eecad6da1d8bb5de43cdae96922a58cb-972c-4c61-bbf00b&sso=ce98748a-7da0b84595a0eb14c80eef4551a4a5763a991c17cd7fabdb&ssp=79762773411661113911166113142686120&ssq=67286667226024947028072260265646682776545&ssr=MjA4LjgwLjE1My4yNA==&sst=ZoteroTranslationServer/WMF%20(mailto:noc@wikimedia.org)&ssv=&ssw=&ssx=W10= |access-date=2022-08-22 |journal=Physical Biology |doi=10.1088/1478-3975/13/5/05lt01| title=पत्ती की वृद्धि अनुरूप है| year=2016 | last1=Alim | first1=Karen | last2=Armon | first2=Shahaf | last3=Shraiman | first3=Boris I. | last4=Boudaoud | first4=Arezki | volume=13 | issue=5 | pages=05LT01 | pmid=27597439 | arxiv=1611.07032 | bibcode=2016PhBio..13eLT01A | s2cid=9351765 }}</ref><ref>{{Cite journal |last1=González-Matesanz |first1=F. J. |last2=Malpica |first2=J. A. |date=2006-11-01 |title=परिवर्तनों के समन्वय के लिए लागू आनुवंशिक एल्गोरिदम के साथ अर्ध-अनुरूप मानचित्रण|url=https://www.sciencedirect.com/science/article/pii/S0098300406000161 |journal=Computers & Geosciences |language=en |volume=32 |issue=9 |pages=1432–1441 |doi=10.1016/j.cageo.2006.01.002 |bibcode=2006CG.....32.1432G |issn=0098-3004}}</ref> | ||
*जियोडेसिक्स<ref>{{Cite journal |last1=Berezovski |first1=Volodymyr |last2=Cherevko |first2=Yevhen |last3=Rýparová |first3=Lenka |date=August 2019 |title=कुछ विशेष स्थानों पर अनुरूप और जियोडेसिक मानचित्रण|journal=Mathematics |language=en |volume=7 |issue=8 |pages=664 |doi=10.3390/math7080664 |issn=2227-7390|doi-access=free }}</ref> * ज्यामिति में<ref>{{Cite journal |last=Gronwall |first=T. H. |date=June 1920 |title=वास्तविक शंकुओं के परिवार का दूसरे पर अनुरूप मानचित्रण|journal=Proceedings of the National Academy of Sciences |language=en |volume=6 |issue=6 |pages=312–315 |doi=10.1073/pnas.6.6.312 |issn=0027-8424 |pmc=1084530 |pmid=16576504|bibcode=1920PNAS....6..312G |doi-access=free }}</ref> * भूभौतिकी में<ref>{{Cite web |title=एक वाक्य में मानचित्रण (खासकर अच्छा वाक्य जैसे बोली, कहावत...)|url=https://sentencedict.com/mapping_10.html |access-date=2022-08-22 |website=sentencedict.com}}</ref> * गूगल में<ref>{{Cite patent|number=US6820032B2|title=अनुरूप मानचित्रण का उपयोग करके किसी क्षेत्र को स्कैन करने की प्रणाली और विधि|gdate=2004-11-16|invent1=Wenzel|invent2=Rajagopal|invent3=Nair|invent4=Ting|inventor1-first=Lothar|inventor2-first=Ram|inventor3-first=Dinesh|inventor4-first=Joseph|url=https://patents.google.com/patent/US6820032B2/en}}</ref><ref>{{Cite journal |last=Lippus |first=J. |date=2004-09-01 |title=टुकड़ों के अनुरूप अनुरूप मानचित्रण का उपयोग करके निर्देशांक का परिवर्तन|url=https://doi.org/10.1007/s00190-003-0364-z |journal=Journal of Geodesy |language=en |volume=78 |issue=1 |pages=40–46 |doi=10.1007/s00190-003-0364-z |bibcode=2004JGeod..78...40L |s2cid=120123792 |issn=1432-1394}}</ref> | *जियोडेसिक्स<ref>{{Cite journal |last1=Berezovski |first1=Volodymyr |last2=Cherevko |first2=Yevhen |last3=Rýparová |first3=Lenka |date=August 2019 |title=कुछ विशेष स्थानों पर अनुरूप और जियोडेसिक मानचित्रण|journal=Mathematics |language=en |volume=7 |issue=8 |pages=664 |doi=10.3390/math7080664 |issn=2227-7390|doi-access=free }}</ref> | ||
*सहित्य में<ref>{{Cite patent|number=US6820032B2|title=अनुरूप मानचित्रण का उपयोग करके किसी क्षेत्र को स्कैन करने की प्रणाली और विधि|gdate=2004-11-16|invent1=Wenzel|invent2=Rajagopal|invent3=Nair|invent4=Ting|inventor1-first=Lothar|inventor2-first=Ram|inventor3-first=Dinesh|inventor4-first=Joseph|url=https://patents.google.com/patent/US6820032B2/en:/en.bab.la/dictionary/english-german/conformal-mapping}}</ref><ref>{{Cite journal |chapter= |doi=10.1101/048199 |url=https://www.biorxiv.org/content/10.1101/048199v1.full.pdf |archive-url=https://web.archive.org/web/20220822131019/https://www.biorxiv.org/content/10.1101/048199v1.full.pdf |archive-date=2022-08-22 |url-status=live|title=''अरबिडोप्सिसलीव्स'' की अनुरूप वृद्धि|year=2016 |last1=Mitchison |first1=Graeme |s2cid=197469442 }}</ref> * इंजीनियरिंग में<ref>{{Cite journal |last1=Calixto |first1=Wesley Pacheco |last2=Alvarenga |first2=Bernardo |last3=da Mota |first3=Jesus Carlos |last4=Brito |first4=Leonardo da Cunha |last5=Wu |first5=Marcel |last6=Alves |first6=Aylton José |last7=Neto |first7=Luciano Martins |last8=Antunes |first8=Carlos F. R. Lemos |date=2011-02-15 |title=कॉनफॉर्मल मैपिंग द्वारा इलेक्ट्रोमैग्नेटिक प्रॉब्लम्स सॉल्विंग: ए मैथमेटिकल ऑपरेटर फॉर ऑप्टिमाइज़ेशन|journal=Mathematical Problems in Engineering |language=en |volume=2010 |pages=e742039 |doi=10.1155/2010/742039 |issn=1024-123X|doi-access=free }}</ref><ref>{{Cite journal |last=Leonhardt |first=Ulf |date=2006-06-23 |title=ऑप्टिकल अनुरूप मानचित्रण|url=https://www.science.org/doi/10.1126/science.1126493 |journal=Science |language=en |volume=312 |issue=5781 |pages=1777–1780 |doi=10.1126/science.1126493 |pmid=16728596 |bibcode=2006Sci...312.1777L |s2cid=8334444 |issn=0036-8075}}</ref> * इलेक्ट्रॉनिक्स में<ref>{{Cite journal |last1=Singh |first1=Arun K. |last2=Auton |first2=Gregory |last3=Hill |first3=Ernie |last4=Song |first4=Aimin |date=2018-07-01 |title=अनुरूप मानचित्रण तकनीक का उपयोग करके ग्राफीन स्व-स्विचिंग डायोड की आंतरिक और बाह्य धारिता का अनुमान|url=https://ui.adsabs.harvard.edu/abs/2018TDM.....5c5023S |journal=2D Materials |volume=5 |issue=3 |pages=035023 |doi=10.1088/2053-1583/aac133 |bibcode=2018TDM.....5c5023S |s2cid=117531045 |issn=2053-1583}}</ref> | *ज्यामिति में<ref>{{Cite journal |last=Gronwall |first=T. H. |date=June 1920 |title=वास्तविक शंकुओं के परिवार का दूसरे पर अनुरूप मानचित्रण|journal=Proceedings of the National Academy of Sciences |language=en |volume=6 |issue=6 |pages=312–315 |doi=10.1073/pnas.6.6.312 |issn=0027-8424 |pmc=1084530 |pmid=16576504|bibcode=1920PNAS....6..312G |doi-access=free }}</ref> | ||
*प्रोटीन संश्लेषण में <ref>{{Cite journal |last1=Gangupomu |first1=Vamshi K. |last2=Wagner |first2=Jeffrey R. |last3=Park |first3=In-Hee |last4=Jain |first4=Abhinandan |last5=Vaidehi |first5=Nagarajan |date=2013-05-07 |title=टॉर्सनल डायनेमिक्स सिमुलेशन का उपयोग करके प्रोटीन के कन्फॉर्मल डायनेमिक्स का मानचित्रण करना|journal=Biophysical Journal |volume=104 |issue=9 |pages=1999–2008 |doi=10.1016/j.bpj.2013.01.050 |issn=1542-0086 |pmc=3647154 |pmid=23663843|bibcode=2013BpJ...104.1999G }}</ref><ref>{{Cite journal |last1=Jones |first1=Gareth Wyn |last2=Mahadevan |first2=L. |date=2013-05-08 |title=प्लानर मॉर्फोमेट्री, शीयर और इष्टतम अर्ध-अनुरूप मैपिंग|url=https://royalsocietypublishing.org/doi/10.1098/rspa.2012.0653 |journal=Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences |language=en |volume=469 |issue=2153 |pages=20120653 |doi=10.1098/rspa.2012.0653 |bibcode=2013RSPSA.46920653J |s2cid=123826235 |issn=1364-5021}}</ref> * भूगोल में,<ref>{{Cite web |title=ईएपी - एस्टोनियाई एकेडमी ऑफ साइंसेज की कार्यवाही - प्रकाशन।|url=https://kirj.ee/proceedings-of-the-estonian-academy-of-sciences-publications/ |access-date=2022-08-22 |language=en-GB}}</ref> | *भूभौतिकी में<ref>{{Cite web |title=एक वाक्य में मानचित्रण (खासकर अच्छा वाक्य जैसे बोली, कहावत...)|url=https://sentencedict.com/mapping_10.html |access-date=2022-08-22 |website=sentencedict.com}}</ref> | ||
*गूगल में<ref>{{Cite patent|number=US6820032B2|title=अनुरूप मानचित्रण का उपयोग करके किसी क्षेत्र को स्कैन करने की प्रणाली और विधि|gdate=2004-11-16|invent1=Wenzel|invent2=Rajagopal|invent3=Nair|invent4=Ting|inventor1-first=Lothar|inventor2-first=Ram|inventor3-first=Dinesh|inventor4-first=Joseph|url=https://patents.google.com/patent/US6820032B2/en}}</ref><ref>{{Cite journal |last=Lippus |first=J. |date=2004-09-01 |title=टुकड़ों के अनुरूप अनुरूप मानचित्रण का उपयोग करके निर्देशांक का परिवर्तन|url=https://doi.org/10.1007/s00190-003-0364-z |journal=Journal of Geodesy |language=en |volume=78 |issue=1 |pages=40–46 |doi=10.1007/s00190-003-0364-z |bibcode=2004JGeod..78...40L |s2cid=120123792 |issn=1432-1394}}</ref> | |||
*सहित्य में<ref>{{Cite patent|number=US6820032B2|title=अनुरूप मानचित्रण का उपयोग करके किसी क्षेत्र को स्कैन करने की प्रणाली और विधि|gdate=2004-11-16|invent1=Wenzel|invent2=Rajagopal|invent3=Nair|invent4=Ting|inventor1-first=Lothar|inventor2-first=Ram|inventor3-first=Dinesh|inventor4-first=Joseph|url=https://patents.google.com/patent/US6820032B2/en:/en.bab.la/dictionary/english-german/conformal-mapping}}</ref><ref>{{Cite journal |chapter= |doi=10.1101/048199 |url=https://www.biorxiv.org/content/10.1101/048199v1.full.pdf |archive-url=https://web.archive.org/web/20220822131019/https://www.biorxiv.org/content/10.1101/048199v1.full.pdf |archive-date=2022-08-22 |url-status=live|title=''अरबिडोप्सिसलीव्स'' की अनुरूप वृद्धि|year=2016 |last1=Mitchison |first1=Graeme |s2cid=197469442 }}</ref> | |||
*इंजीनियरिंग में<ref>{{Cite journal |last1=Calixto |first1=Wesley Pacheco |last2=Alvarenga |first2=Bernardo |last3=da Mota |first3=Jesus Carlos |last4=Brito |first4=Leonardo da Cunha |last5=Wu |first5=Marcel |last6=Alves |first6=Aylton José |last7=Neto |first7=Luciano Martins |last8=Antunes |first8=Carlos F. R. Lemos |date=2011-02-15 |title=कॉनफॉर्मल मैपिंग द्वारा इलेक्ट्रोमैग्नेटिक प्रॉब्लम्स सॉल्विंग: ए मैथमेटिकल ऑपरेटर फॉर ऑप्टिमाइज़ेशन|journal=Mathematical Problems in Engineering |language=en |volume=2010 |pages=e742039 |doi=10.1155/2010/742039 |issn=1024-123X|doi-access=free }}</ref><ref>{{Cite journal |last=Leonhardt |first=Ulf |date=2006-06-23 |title=ऑप्टिकल अनुरूप मानचित्रण|url=https://www.science.org/doi/10.1126/science.1126493 |journal=Science |language=en |volume=312 |issue=5781 |pages=1777–1780 |doi=10.1126/science.1126493 |pmid=16728596 |bibcode=2006Sci...312.1777L |s2cid=8334444 |issn=0036-8075}}</ref> | |||
*इलेक्ट्रॉनिक्स में<ref>{{Cite journal |last1=Singh |first1=Arun K. |last2=Auton |first2=Gregory |last3=Hill |first3=Ernie |last4=Song |first4=Aimin |date=2018-07-01 |title=अनुरूप मानचित्रण तकनीक का उपयोग करके ग्राफीन स्व-स्विचिंग डायोड की आंतरिक और बाह्य धारिता का अनुमान|url=https://ui.adsabs.harvard.edu/abs/2018TDM.....5c5023S |journal=2D Materials |volume=5 |issue=3 |pages=035023 |doi=10.1088/2053-1583/aac133 |bibcode=2018TDM.....5c5023S |s2cid=117531045 |issn=2053-1583}}</ref> | |||
*प्रोटीन संश्लेषण में <ref>{{Cite journal |last1=Gangupomu |first1=Vamshi K. |last2=Wagner |first2=Jeffrey R. |last3=Park |first3=In-Hee |last4=Jain |first4=Abhinandan |last5=Vaidehi |first5=Nagarajan |date=2013-05-07 |title=टॉर्सनल डायनेमिक्स सिमुलेशन का उपयोग करके प्रोटीन के कन्फॉर्मल डायनेमिक्स का मानचित्रण करना|journal=Biophysical Journal |volume=104 |issue=9 |pages=1999–2008 |doi=10.1016/j.bpj.2013.01.050 |issn=1542-0086 |pmc=3647154 |pmid=23663843|bibcode=2013BpJ...104.1999G }}</ref><ref>{{Cite journal |last1=Jones |first1=Gareth Wyn |last2=Mahadevan |first2=L. |date=2013-05-08 |title=प्लानर मॉर्फोमेट्री, शीयर और इष्टतम अर्ध-अनुरूप मैपिंग|url=https://royalsocietypublishing.org/doi/10.1098/rspa.2012.0653 |journal=Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences |language=en |volume=469 |issue=2153 |pages=20120653 |doi=10.1098/rspa.2012.0653 |bibcode=2013RSPSA.46920653J |s2cid=123826235 |issn=1364-5021}}</ref> | |||
*भूगोल में,<ref>{{Cite web |title=ईएपी - एस्टोनियाई एकेडमी ऑफ साइंसेज की कार्यवाही - प्रकाशन।|url=https://kirj.ee/proceedings-of-the-estonian-academy-of-sciences-publications/ |access-date=2022-08-22 |language=en-GB}}</ref> | |||
*मानचित्रकला में।<ref>{{Cite journal |last=López-Vázquez |first=Carlos |date=2012-01-01 |title=अनुभवजन्य विश्लेषणात्मक कार्यों का उपयोग करके स्थितीय सटीकता में सुधार|url=https://doi.org/10.1559/15230406393133 |journal=Cartography and Geographic Information Science |volume=39 |issue=3 |pages=133–139 |doi=10.1559/15230406393133 |s2cid=123894885 |issn=1523-0406}}</ref> | |||
==प्रमुख परिणाम== | ==प्रमुख परिणाम== | ||
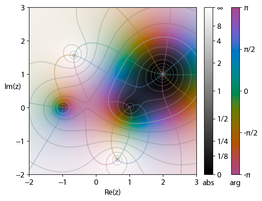
[[Image:Complex-plot.png|right|thumb|262px|फ़ंक्शन का [[डोमेन रंग]] | [[Image:Complex-plot.png|right|thumb|262px|फ़ंक्शन का [[डोमेन रंग]] | ||
{{math|''f''(''x'') {{=}} {{sfrac|(''x''<sup>2</sup> − 1)(''x'' − 2 − ''i'')<sup>2</sup>|''x''<sup>2</sup> + 2 + 2''i''}}}}.<br/> | {{math|''f''(''x'') {{=}} {{sfrac|(''x''<sup>2</sup> − 1)(''x'' − 2 − ''i'')<sup>2</sup>|''x''<sup>2</sup> + 2 + 2''i''}}}}.<br/> | ||
रंग [[तर्क (जटिल विश्लेषण)]] का प्रतिनिधित्व करता है, [[चमक]] निरपेक्ष मान#जटिल संख्या|परिमाण।]] | रंग [[तर्क (जटिल विश्लेषण)]] का प्रतिनिधित्व करता है, [[चमक]] निरपेक्ष मान#जटिल संख्या|परिमाण।]]जटिल विश्लेषण में केंद्रीय उपकरणों में से एक [[:hi:रेखा अभिन्न|लाइन समाकलन]] है। [[कॉची इंटीग्रल प्रमेय|कौशी समाकल प्रमेय]] द्वारा कहा गया है कि बंद पथ से घिरे क्षेत्र के अंदर हर जगह होलोमोर्फिक फ़ंक्शन के एक बंद पथ के चारों ओर अभिन्न रेखा हमेशा शून्य होती है। डिस्क के अंदर इस तरह के होलोमोर्फिक फ़ंक्शन के मूल्यों की गणना डिस्क की सीमा पर पथ अभिन्न द्वारा की जा सकती है (जैसा कि [[:hi:कौशी समाकल सूत्र|कॉची के अभिन्न सूत्र]] में दिखाया गया है)। जटिल विमान में पथ इंटीग्रल का उपयोग अक्सर जटिल वास्तविक इंटीग्रल को निर्धारित करने के लिए किया जाता है, और यहां दूसरों के बीच [[अवशेषों]] का सिद्धांत लागू होता है (समोच्च एकीकरण के तरीके देखें)। किसी फ़ंक्शन का "ध्रुव" (या [[पृथक विलक्षणता]] ) एक बिंदु है जहां फ़ंक्शन का मान असीमित हो जाता है, या "उड़ा" जाता है। यदि किसी फ़ंक्शन में ऐसा ध्रुव है, तो कोई फ़ंक्शन के अवशेष की गणना कर सकता है, जिसका उपयोग फ़ंक्शन से जुड़े पथ इंटीग्रल की गणना करने के लिए किया जा सकता है; यह शक्तिशाली [[:hi:अवशेष प्रमेय|अवशेष प्रमेय]] की सामग्री है। [[पिकार्ड के प्रमेय]] द्वारा आवश्यक विलक्षणताओं के पास होलोमोर्फिक कार्यों के उल्लेखनीय व्यवहार का वर्णन किया गया है। ऐसे कार्य जिनमें केवल ध्रुव होते हैं लेकिन कोई [[आवश्यक विलक्षणता]] नहीं होती है, [[:hi:मेरोमॉर्फिक|मेरोमोर्फिक]] कहलाते हैं। लॉरेंट श्रृंखला [[टेलर श्रृंखला]] के समतुल्य जटिल-मूल्यवान हैं, लेकिन बहुपद जैसे अधिक अच्छी तरह से समझे गए कार्यों के अनंत योगों के माध्यम से विलक्षणताओं के निकट कार्यों के व्यवहार का अध्ययन करने के लिए उपयोग किया जा सकता है।। | ||
एक परिबद्ध फलन जो पूरे सम्मिश्र तल में होलोमोर्फिक है, स्थिर होना चाहिए; यह लिउविल का प्रमेय है (सम्मिश्र विश्लेषण)|लिउविल का प्रमेय। इसका उपयोग बीजगणित के मौलिक प्रमेय के लिए एक [[प्राकृतिक]] और संक्षिप्त प्रमाण प्रदान करने के लिए किया जा सकता है जो बताता है कि सम्मिश्र संख्याओं का [[क्षेत्र (गणित)]] बीजगणितीय रूप से बंद क्षेत्र है। | एक परिबद्ध फलन जो पूरे सम्मिश्र तल में होलोमोर्फिक है, स्थिर होना चाहिए; यह लिउविल का प्रमेय है (सम्मिश्र विश्लेषण)|लिउविल का प्रमेय। इसका उपयोग बीजगणित के मौलिक प्रमेय के लिए एक [[प्राकृतिक]] और संक्षिप्त प्रमाण प्रदान करने के लिए किया जा सकता है जो बताता है कि सम्मिश्र संख्याओं का [[क्षेत्र (गणित)]] बीजगणितीय रूप से बंद क्षेत्र है। | ||
| Line 111: | Line 120: | ||
==इस पेज में लापता आंतरिक लिंक की सूची == | ==इस पेज में लापता आंतरिक लिंक की सूची == | ||
विश्लेषणात्मक संयोजन | |||
भौतिक विज्ञान | |||
व्यावहारिक गणित | |||
समारोह (गणित) | |||
नाभिकीय अभियांत्रिकी | |||
सम्मिश्र आंकड़े | |||
अलग करने योग्य समारोह | |||
सम्मिश्र गतिकी | |||
ज्यामितीय अनुक्रम | |||
किसी फ़ंक्शन का डोमेन | |||
खुला उपसमुच्चय | |||
वास्तविक मूल्यवान समारोह | |||
क्रमित युग्म | |||
अवकलनीयता | |||
जुड़ा हुआ स्थान | |||
विभेदक | |||
खुला सेट | |||
घातांक प्रकार्य | |||
त्रिकोणमितीय समारोह | |||
हुए | |||
कॉम्प्लेक्स हिल्बर्ट स्पेस | |||
कई सम्मिश्र चर का कार्य | |||
परिबद्ध समारोह | |||
बीजीय रूप से बंद क्षेत्र | |||
बीजगणित का मौलिक प्रमेय | |||
बिजली की श्रृंखला | |||
तरंग क्रिया | |||
वास्तविक विश्लेषण | |||
==बाहरी संबंध== | ==बाहरी संबंध== | ||
{{Sister project links| wikt=complex analysis | commons=Category:Complex analysis | b=no | n=no | q=Complex analysis | s=no | v=no | voy=no | species=no | d=no}} | {{Sister project links| wikt=complex analysis | commons=Category:Complex analysis | b=no | n=no | q=Complex analysis | s=no | v=no | voy=no | species=no | d=no}} | ||
Revision as of 01:17, 1 December 2022
| Mathematical analysis → Complex analysis |
| Complex analysis |
|---|
 |
| Complex numbers |
| Complex functions |
| Basic Theory |
| Geometric function theory |
| People |
|
|
सम्मिश्र विश्लेषण, परंपरागत रूप से एक सम्मिश्र चर के कार्यों के सिद्धांत के रूप में जाना जाता है, गणितीय विश्लेषण की शाखा है जो सम्मिश्र संख्याओं के कार्यों की जांच करती है। यह गणित की कई शाखाओं में सहायक है, जिसमें बीजगणितीय ज्यामिति, संख्या सिद्धांत, विश्लेषणात्मक संयोजक, व्यावहारिक गणित शामिल हैं; साथ ही भौतिकी में, हाइड्रोडायनामिक्स, ऊष्मप्रवैगिकी और विशेष रूप से प्रमात्रा यान्त्रिकी की शाखाएं शामिल हैं। विस्तार से, सम्मिश्र विश्लेषण के उपयोग में परमाणु, अंतरिक्ष इंजीनियरिंग, यान्त्रिक और विद्युत अभियान्त्रिकी जैसे इंजीनियरिंग क्षेत्रों में भी अनुप्रयोग हैं।
जटिल चर के एक भिन्न कार्य के रूप में इसकी टेलर श्रृंखला के बराबर है (अर्थात, यह विश्लेषणात्मक है), जटिल विश्लेषण विशेष रूप से एक जटिल चर (यानी, होलोमोर्फिक कार्यों ) के विश्लेषणात्मक कार्यों से संबंधित है।
इतिहास
जटिल विश्लेषण गणित की शास्त्रीय शाखाओं में से एक है, जिसकी जड़ें 18वीं शताब्दी में और उससे ठीक पहले हैं। जटिल संख्याओं से जुड़े महत्वपूर्ण गणितज्ञों में यूलर, गॉस, रीमैन, कॉची, वीयरस्ट्रास और 20वीं शताब्दी के कई अन्य शामिल हैं। जटिल विश्लेषण, विशेष रूप से अनुरूप मैपिंग के सिद्धांत में, कई भौतिक अनुप्रयोग हैं और पूरे विश्लेषणात्मक संख्या सिद्धांत में भी इसका उपयोग किया जाता है। आधुनिक समय में, यह जटिल गतिशीलता नए प्रोत्साहन के माध्यम से और होलोमार्फिक फलन को पुनरावृत्त करके उत्पादित फ्रैक्टल की चित्रों के माध्यम से बहुत लोकप्रिय हो गया है। जटिल विश्लेषण का एक अन्य महत्वपूर्ण अनुप्रयोग स्ट्रिंग सिद्धांत में है जो प्रमात्रा क्षेत्र सिद्धान्त में अनुरूप निश्चर का निरीक्षण करता है।
सम्मिश्र कार्य
जटिल कार्य जटिल संख्याओं से जटिल संख्याओं का एक कार्य है। दूसरे शब्दों में, यह एक ऐसा फलन है जिसमें डोमेन के रूप में सम्मिश्र संख्याओं का उपसमुच्चय होता है और सम्मिश्र संख्याएँ कोडोमेन के रूप में होती हैं। जटिल कार्यों को आम तौर पर एक डोमेन माना जाता है जिसमें समष्टि समतल का एक गैर-खाली खुला सेट होता है।
किसी भी सम्मिश्र कार्य के लिए, मान डोमेन और उनकी छवियों से श्रेणी में वास्तविक संख्या और काल्पनिक संख्या भागों में अलग किया जा सकता है:
कहाँ पे सभी वास्तविक मूल्यवान हैं।
दूसरे शब्दों में, एक सम्मिश्र कार्य में विघटित किया जा सकता है
- तथा
यानी, दो वास्तविक-मूल्यवान कार्यों में (, ) दो वास्तविक चरों का (, ).
इसी प्रकार, कोई सम्मिश्र-मूल्यवान फ़ंक्शन f एक मनमाना सेट (गणित) पर X दो वास्तविक-मूल्यवान कार्यों की एक आदेशित जोड़ी के रूप में माना जा सकता है: (Re f, Im f) या, वैकल्पिक रूप से, वेक्टर-मूल्यवान फ़ंक्शन के रूप में X में सम्मिश्र-मूल्यवान कार्यों के कुछ गुण (जैसे निरंतर कार्य) दो वास्तविक चर के वेक्टर मूल्यवान कार्यों के संबंधित गुणों से ज्यादा कुछ नहीं हैं। सम्मिश्र विश्लेषण की अन्य अवधारणाएँ, जैसे विभेदीकरण, वास्तविक कार्यों के लिए समान अवधारणाओं का प्रत्यक्ष सामान्यीकरण हैं, लेकिन बहुत भिन्न गुण हो सकते हैं। विशेष रूप से, प्रत्येक होलोमॉर्फिक फ़ंक्शन विश्लेषणात्मक फ़ंक्शन होता है (अगला अनुभाग देखें), और दो अलग-अलग फ़ंक्शन जो एक बिंदु के नेबरहुड (गणित) में बराबर होते हैं, उनके डोमेन के प्रतिच्छेदन पर बराबर होते हैं (यदि डोमेन जुड़े स्थान हैं)। परवर्ती गुण विश्लेषणात्मक निरंतरता के सिद्धांत का आधार है जो एक सम्मिश्र विश्लेषणात्मक फ़ंक्शन प्राप्त करने के लिए प्रत्येक वास्तविक विश्लेषणात्मक फ़ंक्शन को एक तरीके से विस्तारित करने की अनुमति देता है जिसका डोमेन संपूर्ण सम्मिश्र विमान है जिसमें चाप (ज्यामिति) की सीमित संख्या को हटा दिया गया है। कई बुनियादी और विशेष कार्य सम्मिश्र कार्यों को इस तरह से परिभाषित किया गया है, जिसमें घातीय कार्य सम्मिश्र विमान, सम्मिश्र लघुगणक, और त्रिकोणमितीय कार्य सम्मिश्र विमान शामिल हैं।
होलोमोर्फिक फ़ंक्शन
सम्मिश्र कार्य जो एक खुले सेट के हर बिंदु पर अलग-अलग होते हैं कहा जाता है कि सम्मिश्र तल पर होलोमोर्फिक होता है . सम्मिश्र विश्लेषण के संदर्भ में, के व्युत्पन्न पर होना परिभाषित किया गया है
सतही तौर पर, यह परिभाषा औपचारिक रूप से एक वास्तविक कार्य के व्युत्पन्न के अनुरूप है। हालांकि, सम्मिश्र डेरिवेटिव और अलग-अलग कार्य उनके वास्तविक समकक्षों की तुलना में काफी भिन्न तरीके से व्यवहार करते हैं। विशेष रूप से, इस सीमा के अस्तित्व के लिए, अंतर भागफल का मान समान सम्मिश्र संख्या तक पहुंचना चाहिए, चाहे हम जिस तरीके से दृष्टिकोण करें सम्मिश्र विमान में। नतीजतन, सम्मिश्र भिन्नता का वास्तविक भिन्नता की तुलना में अधिक मजबूत प्रभाव पड़ता है। उदाहरण के लिए, होलोमोर्फिक फलन असीम रूप से भिन्न होते हैं, जबकि n वें व्युत्पन्न के अस्तित्व को वास्तविक कार्यों के लिए (n + 1) वें व्युत्पन्न के अस्तित्व की आवश्यकता नहीं होती है। इसके अलावा, सभी होलोमॉर्फिक फ़ंक्शन विश्लेषणात्मक फ़ंक्शन की मजबूत स्थिति को संतुष्ट करते हैं, जिसका अर्थ है कि फ़ंक्शन, अपने डोमेन में हर बिंदु पर, स्थानीय रूप से अभिसरण शक्ति श्रृंखला द्वारा दिया जाता है। संक्षेप में, इसका मतलब है कि होलोमोर्फिक कार्य करता है प्रत्येक बिंदु के कुछ पड़ोस में बहुपदों द्वारा मनमाने ढंग से अनुमानित किया जा सकता है . यह अलग-अलग वास्तविक कार्यों के ठीक विपरीत है; असीम रूप से अलग-अलग वास्तविक कार्य हैं जो कहीं भी विश्लेषणात्मक नहीं हैं; देखना गैर-विश्लेषणात्मक सुचारू फलन § एक सहज फलन जो कहीं भी वास्तविक विश्लेषणात्मक नहीं है।
चरघातांकी फलन, त्रिकोणमितीय फलन, और सभी बहुपद फलन सहित अधिकांश प्रारंभिक फलन, फलन के रूप में जटिल तर्कों के लिए उचित रूप से विस्तृत किए गए हैं , समूचे जटिल तल पर होलोमॉर्फिक हैं, जिससे वे संपूर्ण कार्य करते हैं, जबकि तर्कसंगत कार्य , जहां p और q बहुपद हैं, उन डोमेन पर होलोमॉर्फिक हैं जो उन बिंदुओं को बाहर करते हैं जहां q शून्य है। ऐसे कार्य जो अलग-अलग बिंदुओं के एक सेट को छोड़कर हर जगह होलोमोर्फिक होते हैं, मेरोमोर्फिक फ़ंक्शन के रूप में जाने जाते हैं। दूसरी ओर, कार्य , {\displaystyle z\mapsto \Re (z)}
, ,
, और
जटिल तल पर कहीं भी होलोमोर्फिक नहीं हैं, जैसा कि कॉची-रीमैन शर्तों को पूरा करने में उनकी विफलता से दिखाया जा सकता है (नीचे देखें)।िक कार्यों की एक महत्वपूर्ण संपत्ति उनके वास्तविक और काल्पनिक घटकों के आंशिक डेरिवेटिव के बीच का संबंध है, जिसे कॉची-रीमैन शर्तों के रूप में जाना जाता है। यदि , द्वारा परिभाषित , कहाँ पे , एक क्षेत्र (गणित) पर होलोमोर्फिक है , फिर सभी के लिए ,
फलन, u और v के वास्तविक और काल्पनिक भागों के संदर्भ में, यह समीकरणों के युग्म के तुल्य है तथा , जहां सबस्क्रिप्ट आंशिक विभेदन का संकेत देते हैं। हालांकि, कॉची-रीमैन स्थितियां अतिरिक्त निरंतरता स्थितियों के बिना, होलोमोर्फिक कार्यों को चिह्नित नहीं करती हैं (लूमन-मेन्चॉफ प्रमेय देखें)।
होलोमॉर्फिक फ़ंक्शंस कुछ उल्लेखनीय विशेषताएं प्रदर्शित करते हैं। उदाहरण के लिए, पिकार्ड प्रमेय | पिकार्ड का प्रमेय दावा करता है कि एक संपूर्ण फ़ंक्शन की सीमा केवल तीन संभावित रूप ले सकती है: , , या कुछ के लिए . दूसरे शब्दों में, यदि दो भिन्न सम्मिश्र संख्याएँ तथा एक संपूर्ण फ़ंक्शन की सीमा में नहीं हैं , फिर एक निरंतर कार्य है। इसके अलावा, एक जुड़े हुए खुले सेट पर एक होलोमोर्फिक फ़ंक्शन किसी भी गैर-खाली खुले सबसेट के प्रतिबंध से निर्धारित होता है।
अनुरूप मानचित्र
अनुरूप मानचित्रण स्थानीय रूप से उलटा सम्मिश्र विश्लेषणात्मक है अभिविन्यास संरक्षण के लिए दो आयामों में कार्य करता है।
अनुरूप मानचित्रण का अनुप्रयोग
- अंतरिक्ष इंजीनियरिंग में[1]
- बायोमेडिकल विज्ञान में[2]
- ब्रेन मैपिंग में[3]
- जेनेटिक मैपिंग[4][5][6]
- जियोडेसिक्स[7]
- ज्यामिति में[8]
- भूभौतिकी में[9]
- गूगल में[10][11]
- सहित्य में[12][13]
- इंजीनियरिंग में[14][15]
- इलेक्ट्रॉनिक्स में[16]
- प्रोटीन संश्लेषण में [17][18]
- भूगोल में,[19]
- मानचित्रकला में।[20]
प्रमुख परिणाम
जटिल विश्लेषण में केंद्रीय उपकरणों में से एक लाइन समाकलन है। कौशी समाकल प्रमेय द्वारा कहा गया है कि बंद पथ से घिरे क्षेत्र के अंदर हर जगह होलोमोर्फिक फ़ंक्शन के एक बंद पथ के चारों ओर अभिन्न रेखा हमेशा शून्य होती है। डिस्क के अंदर इस तरह के होलोमोर्फिक फ़ंक्शन के मूल्यों की गणना डिस्क की सीमा पर पथ अभिन्न द्वारा की जा सकती है (जैसा कि कॉची के अभिन्न सूत्र में दिखाया गया है)। जटिल विमान में पथ इंटीग्रल का उपयोग अक्सर जटिल वास्तविक इंटीग्रल को निर्धारित करने के लिए किया जाता है, और यहां दूसरों के बीच अवशेषों का सिद्धांत लागू होता है (समोच्च एकीकरण के तरीके देखें)। किसी फ़ंक्शन का "ध्रुव" (या पृथक विलक्षणता ) एक बिंदु है जहां फ़ंक्शन का मान असीमित हो जाता है, या "उड़ा" जाता है। यदि किसी फ़ंक्शन में ऐसा ध्रुव है, तो कोई फ़ंक्शन के अवशेष की गणना कर सकता है, जिसका उपयोग फ़ंक्शन से जुड़े पथ इंटीग्रल की गणना करने के लिए किया जा सकता है; यह शक्तिशाली अवशेष प्रमेय की सामग्री है। पिकार्ड के प्रमेय द्वारा आवश्यक विलक्षणताओं के पास होलोमोर्फिक कार्यों के उल्लेखनीय व्यवहार का वर्णन किया गया है। ऐसे कार्य जिनमें केवल ध्रुव होते हैं लेकिन कोई आवश्यक विलक्षणता नहीं होती है, मेरोमोर्फिक कहलाते हैं। लॉरेंट श्रृंखला टेलर श्रृंखला के समतुल्य जटिल-मूल्यवान हैं, लेकिन बहुपद जैसे अधिक अच्छी तरह से समझे गए कार्यों के अनंत योगों के माध्यम से विलक्षणताओं के निकट कार्यों के व्यवहार का अध्ययन करने के लिए उपयोग किया जा सकता है।।
एक परिबद्ध फलन जो पूरे सम्मिश्र तल में होलोमोर्फिक है, स्थिर होना चाहिए; यह लिउविल का प्रमेय है (सम्मिश्र विश्लेषण)|लिउविल का प्रमेय। इसका उपयोग बीजगणित के मौलिक प्रमेय के लिए एक प्राकृतिक और संक्षिप्त प्रमाण प्रदान करने के लिए किया जा सकता है जो बताता है कि सम्मिश्र संख्याओं का क्षेत्र (गणित) बीजगणितीय रूप से बंद क्षेत्र है।
यदि एक कनेक्टेड स्पेस डोमेन में कोई फ़ंक्शन होलोमॉर्फिक है तो इसके मान किसी भी छोटे उपडोमेन पर इसके मानों द्वारा पूरी तरह से निर्धारित किए जाते हैं। बड़े डोमेन पर कार्य को छोटे डोमेन पर इसके मूल्यों से विश्लेषणात्मक निरंतरता कहा जाता है। यह कार्यों की परिभाषा के विस्तार की अनुमति देता है, जैसे कि रीमैन जीटा फ़ंक्शन, जो प्रारंभिक रूप से अनंत योगों के रूप में परिभाषित होते हैं जो केवल सीमित डोमेन पर लगभग पूरे सम्मिश्र विमान में अभिसरण करते हैं। कभी-कभी, जैसा कि प्राकृतिक लघुगणक के मामले में होता है, सम्मिश्र तल में एक गैर-सरल रूप से जुड़े डोमेन के लिए विश्लेषणात्मक रूप से एक होलोमोर्फिक फ़ंक्शन को जारी रखना असंभव है, लेकिन इसे निकट से संबंधित सतह पर एक होलोमोर्फिक फ़ंक्शन तक विस्तारित करना संभव है, जिसे एक के रूप में जाना जाता है। रीमैन सतह।
यह सब एक चर में सम्मिश्र विश्लेषण को संदर्भित करता है। कई सम्मिश्र चरों के कार्य का एक बहुत समृद्ध सिद्धांत भी है जिसमें विश्लेषणात्मक गुण जैसे कि शक्ति श्रृंखला विस्तार जारी रहता है जबकि एक सम्मिश्र आयाम (जैसे अनुरूपता) में होलोमोर्फिक कार्यों के अधिकांश ज्यामितीय गुण आगे नहीं बढ़ते हैं। सम्मिश्र विमान में कुछ डोमेन के अनुरूप संबंध के बारे में रीमैन मैपिंग प्रमेय, जो एक आयामी सिद्धांत में सबसे महत्वपूर्ण परिणाम हो सकता है, उच्च आयामों में नाटकीय रूप से विफल हो जाता है।
कुछ सम्मिश्र हिल्बर्ट रिक्त स्थान का एक प्रमुख अनुप्रयोग क्वांटम यांत्रिकी में तरंग कार्यों के रूप में है।
यह भी देखें
- हाइपरकॉम्प्लेक्स विश्लेषण
- वेक्टर पथरी
- सम्मिश्र गतिकी
- सम्मिश्र विश्लेषण विषयों की सूची
- प्रमेय मोनोड्रोम
- सच्चा विश्लेषण
- रीमैन-रोच प्रमेय
- रंज की प्रमेय
संदर्भ
- ↑ Selig, Michael S.; Maughmer, Mark D. (1992-05-01). "अनुरूप मानचित्रण के आधार पर मल्टीपॉइंट इनवर्स एयरफॉइल डिजाइन पद्धति". AIAA Journal. 30 (5): 1162–1170. Bibcode:1992AIAAJ..30.1162S. doi:10.2514/3.11046. ISSN 0001-1452.
- ↑ Cortijo, Vanessa; Alonso, Elena R.; Mata, Santiago; Alonso, José L. (2018-01-18). "फेनोलिक एसिड का गठनात्मक मानचित्र". The Journal of Physical Chemistry A. 122 (2): 646–651. Bibcode:2018JPCA..122..646C. doi:10.1021/acs.jpca.7b08882. ISSN 1520-5215. PMID 29215883.
- ↑ "अनुरूप मानचित्रण के गुण".
- ↑ "7.1 आनुवंशिक मानचित्र विभिन्न रूपों में आते हैं". www.informatics.jax.org. Retrieved 2022-08-22.
- ↑ Alim, Karen; Armon, Shahaf; Shraiman, Boris I.; Boudaoud, Arezki (2016). "पत्ती की वृद्धि अनुरूप है". Physical Biology. 13 (5): 05LT01. arXiv:1611.07032. Bibcode:2016PhBio..13eLT01A. doi:10.1088/1478-3975/13/5/05lt01. PMID 27597439. S2CID 9351765. Retrieved 2022-08-22.
- ↑ González-Matesanz, F. J.; Malpica, J. A. (2006-11-01). "परिवर्तनों के समन्वय के लिए लागू आनुवंशिक एल्गोरिदम के साथ अर्ध-अनुरूप मानचित्रण". Computers & Geosciences (in English). 32 (9): 1432–1441. Bibcode:2006CG.....32.1432G. doi:10.1016/j.cageo.2006.01.002. ISSN 0098-3004.
- ↑ Berezovski, Volodymyr; Cherevko, Yevhen; Rýparová, Lenka (August 2019). "कुछ विशेष स्थानों पर अनुरूप और जियोडेसिक मानचित्रण". Mathematics (in English). 7 (8): 664. doi:10.3390/math7080664. ISSN 2227-7390.
- ↑ Gronwall, T. H. (June 1920). "वास्तविक शंकुओं के परिवार का दूसरे पर अनुरूप मानचित्रण". Proceedings of the National Academy of Sciences (in English). 6 (6): 312–315. Bibcode:1920PNAS....6..312G. doi:10.1073/pnas.6.6.312. ISSN 0027-8424. PMC 1084530. PMID 16576504.
- ↑ "एक वाक्य में मानचित्रण (खासकर अच्छा वाक्य जैसे बोली, कहावत...)". sentencedict.com. Retrieved 2022-08-22.
- ↑ US6820032B2, Wenzel, Lothar; Rajagopal, Ram & Nair, Dinesh et al., "अनुरूप मानचित्रण का उपयोग करके किसी क्षेत्र को स्कैन करने की प्रणाली और विधि", issued 2004-11-16
- ↑ Lippus, J. (2004-09-01). "टुकड़ों के अनुरूप अनुरूप मानचित्रण का उपयोग करके निर्देशांक का परिवर्तन". Journal of Geodesy (in English). 78 (1): 40–46. Bibcode:2004JGeod..78...40L. doi:10.1007/s00190-003-0364-z. ISSN 1432-1394. S2CID 120123792.
- ↑ US6820032B2, Wenzel, Lothar; Rajagopal, Ram & Nair, Dinesh et al., "अनुरूप मानचित्रण का उपयोग करके किसी क्षेत्र को स्कैन करने की प्रणाली और विधि", issued 2004-11-16
- ↑ Mitchison, Graeme (2016). "अरबिडोप्सिसलीव्स की अनुरूप वृद्धि" (PDF). doi:10.1101/048199. S2CID 197469442. Archived (PDF) from the original on 2022-08-22.
{{cite journal}}: Cite journal requires|journal=(help) - ↑ Calixto, Wesley Pacheco; Alvarenga, Bernardo; da Mota, Jesus Carlos; Brito, Leonardo da Cunha; Wu, Marcel; Alves, Aylton José; Neto, Luciano Martins; Antunes, Carlos F. R. Lemos (2011-02-15). "कॉनफॉर्मल मैपिंग द्वारा इलेक्ट्रोमैग्नेटिक प्रॉब्लम्स सॉल्विंग: ए मैथमेटिकल ऑपरेटर फॉर ऑप्टिमाइज़ेशन". Mathematical Problems in Engineering (in English). 2010: e742039. doi:10.1155/2010/742039. ISSN 1024-123X.
- ↑ Leonhardt, Ulf (2006-06-23). "ऑप्टिकल अनुरूप मानचित्रण". Science (in English). 312 (5781): 1777–1780. Bibcode:2006Sci...312.1777L. doi:10.1126/science.1126493. ISSN 0036-8075. PMID 16728596. S2CID 8334444.
- ↑ Singh, Arun K.; Auton, Gregory; Hill, Ernie; Song, Aimin (2018-07-01). "अनुरूप मानचित्रण तकनीक का उपयोग करके ग्राफीन स्व-स्विचिंग डायोड की आंतरिक और बाह्य धारिता का अनुमान". 2D Materials. 5 (3): 035023. Bibcode:2018TDM.....5c5023S. doi:10.1088/2053-1583/aac133. ISSN 2053-1583. S2CID 117531045.
- ↑ Gangupomu, Vamshi K.; Wagner, Jeffrey R.; Park, In-Hee; Jain, Abhinandan; Vaidehi, Nagarajan (2013-05-07). "टॉर्सनल डायनेमिक्स सिमुलेशन का उपयोग करके प्रोटीन के कन्फॉर्मल डायनेमिक्स का मानचित्रण करना". Biophysical Journal. 104 (9): 1999–2008. Bibcode:2013BpJ...104.1999G. doi:10.1016/j.bpj.2013.01.050. ISSN 1542-0086. PMC 3647154. PMID 23663843.
- ↑ Jones, Gareth Wyn; Mahadevan, L. (2013-05-08). "प्लानर मॉर्फोमेट्री, शीयर और इष्टतम अर्ध-अनुरूप मैपिंग". Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences (in English). 469 (2153): 20120653. Bibcode:2013RSPSA.46920653J. doi:10.1098/rspa.2012.0653. ISSN 1364-5021. S2CID 123826235.
- ↑ "ईएपी - एस्टोनियाई एकेडमी ऑफ साइंसेज की कार्यवाही - प्रकाशन।" (in British English). Retrieved 2022-08-22.
- ↑ López-Vázquez, Carlos (2012-01-01). "अनुभवजन्य विश्लेषणात्मक कार्यों का उपयोग करके स्थितीय सटीकता में सुधार". Cartography and Geographic Information Science. 39 (3): 133–139. doi:10.1559/15230406393133. ISSN 1523-0406. S2CID 123894885.
- Ablowitz, M. J. & A. S. Fokas, Complex Variables: Introduction and Applications (Cambridge, 2003).
- Ahlfors, L., Complex Analysis (McGraw-Hill, 1953).
- Cartan, H., Théorie élémentaire des fonctions analytiques d'une ou plusieurs variables complexes. (Hermann, 1961). English translation, Elementary Theory of Analytic Functions of One or Several Complex Variables. (Addison-Wesley, 1963).
- Carathéodory, C., Funktionentheorie. (Birkhäuser, 1950). English translation, Theory of Functions of a Complex Variable (Chelsea, 1954). [2 volumes.]
- Carrier, G. F., M. Krook, & C. E. Pearson, Functions of a Complex Variable: Theory and Technique. (McGraw-Hill, 1966).
- Conway, J. B., Functions of One Complex Variable. (Springer, 1973).
- Fisher, S., Complex Variables. (Wadsworth & Brooks/Cole, 1990).
- Forsyth, A., Theory of Functions of a Complex Variable (Cambridge, 1893).
- Freitag, E. & R. Busam, Funktionentheorie. (Springer, 1995). English translation, Complex Analysis. (Springer, 2005).
- Goursat, E., Cours d'analyse mathématique, tome 2. (Gauthier-Villars, 1905). English translation, A course of mathematical analysis, vol. 2, part 1: Functions of a complex variable. (Ginn, 1916).
- Henrici, P., Applied and Computational Complex Analysis (Wiley). [Three volumes: 1974, 1977, 1986.]
- Kreyszig, E., Advanced Engineering Mathematics. (Wiley, 1962).
- Lavrentyev, M. & B. Shabat, Методы теории функций комплексного переменного. (Methods of the Theory of Functions of a Complex Variable). (1951, in Russian).
- Markushevich, A. I., Theory of Functions of a Complex Variable, (Prentice-Hall, 1965). [Three volumes.]
- Marsden & Hoffman, Basic Complex Analysis. (Freeman, 1973).
- Needham, T., Visual Complex Analysis. (Oxford, 1997). http://usf.usfca.edu/vca/
- Remmert, R., Theory of Complex Functions. (Springer, 1990).
- Rudin, W., Real and Complex Analysis. (McGraw-Hill, 1966).
- Shaw, W. T., Complex Analysis with Mathematica (Cambridge, 2006).
- Stein, E. & R. Shakarchi, Complex Analysis. (Princeton, 2003).
- Sveshnikov, A. G. & A. N. Tikhonov, Теория функций комплексной переменной. (Nauka, 1967). English translation, The Theory Of Functions Of A Complex Variable (MIR, 1978).
- Titchmarsh, E. C., The Theory of Functions. (Oxford, 1932).
- Wegert, E., Visual Complex Functions. (Birkhäuser, 2012).
- Whittaker, E. T. & G. N. Watson, A Course of Modern Analysis. (Cambridge, 1902). 3rd ed. (1920)
इस पेज में लापता आंतरिक लिंक की सूची
विश्लेषणात्मक संयोजन
भौतिक विज्ञान
व्यावहारिक गणित
समारोह (गणित)
नाभिकीय अभियांत्रिकी
सम्मिश्र आंकड़े
अलग करने योग्य समारोह
सम्मिश्र गतिकी
ज्यामितीय अनुक्रम
किसी फ़ंक्शन का डोमेन
खुला उपसमुच्चय
वास्तविक मूल्यवान समारोह
क्रमित युग्म
अवकलनीयता
जुड़ा हुआ स्थान
विभेदक
खुला सेट
घातांक प्रकार्य
त्रिकोणमितीय समारोह
हुए
कॉम्प्लेक्स हिल्बर्ट स्पेस
कई सम्मिश्र चर का कार्य
परिबद्ध समारोह
बीजीय रूप से बंद क्षेत्र
बीजगणित का मौलिक प्रमेय
बिजली की श्रृंखला
तरंग क्रिया
वास्तविक विश्लेषण