अंतःक्षेपक मॉड्यूल: Difference between revisions
(Created page with "{{Short description|Mathematical object in abstract algebra}} गणित में, विशेष रूप से अमूर्त बीजगणित के क्...") |
m (Sugatha moved page इंजेक्शन मॉड्यूल to अंतःक्षेपक मॉड्यूल) |
||
| (7 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
{{Short description|Mathematical object in abstract algebra}} | {{Short description|Mathematical object in abstract algebra}} | ||
गणित में, विशेष रूप से अमूर्त बीजगणित के क्षेत्र में | गणित में, विशेष रूप से अमूर्त बीजगणित के क्षेत्र में '''अंतःक्षेपक मॉड्यूल''' को सामान्यतः [[मॉड्यूल सिद्धांत]] के रूप में जाना जाता है। अंतःक्षेपक मॉड्यूल Q वह मॉड्यूल है जो सभी [[तर्कसंगत संख्या|तर्कसंगत संख्याओं]] के Z मॉड्यूल Q के साथ कुछ वांछनीय गुणों को साझा करता है। विशेष रूप से यदि Q किसी अन्य मॉड्यूल का उपमॉड्यूल है तो यह पहले से ही उस मॉड्यूल का प्रत्यक्ष योग होता है। इसके अतिरिक्त मॉड्यूल Y का एक उपमॉड्यूल दिया जाता है तो इस उपमॉड्यूल से Q तक किसी भी [[मॉड्यूल समरूपता]] को सभी Y से Q तक एक समान रूप से बढ़ाया जा सकता है। यह अवधारणा प्रक्षेपीय मॉड्यूल के लिए दोहरी है। अंतःक्षेपक मॉड्यूल को {{harv|बेयर|1940}} और {{harv|लेयम|1999|loc=§3}} ने प्रस्तुत किया था। जिनकी पाठ्यपुस्तक में विस्तार से चर्चा की गई है। | ||
अंतःक्षेपक मॉड्यूल का अत्यधिक अध्ययन किया गया है और विभिन्न प्रकार की अतिरिक्त धारणाओं को उनके संदर्भ में परिभाषित किया गया है। [[इंजेक्शन कोजेनरेटर|अंतःक्षेपक के उपनिर्माता]] अंतःक्षेपक मॉड्यूल हैं जो ईमानदारी से मॉड्यूल की पूरी श्रेणी का प्रतिनिधित्व करते हैं। यह मॉड्यूल अंतःक्षेपी विश्लेषण को मापता है कि अंतःक्षेपण आयाम के संदर्भ में एक मॉड्यूल अंतःक्षेपण से कितनी दूर है और व्युत्पन्न श्रेणी में मॉड्यूल का प्रतिनिधित्व करता है। अंतःक्षेपक हल्स अधिकतम आवश्यक विस्तार हैं और न्यूनतम अंतःक्षेपक भी विस्तार बन जाते हैं। [[नोथेरियन रिंग|नोथेरियन वलय]] पर प्रत्येक अंतःक्षेपक मॉड्यूल विशिष्ट रूप से अविघटनीय मॉड्यूल का प्रत्यक्ष योग है और उनकी संरचना अच्छी तरह से समझी जाती है। एक वलय पर अंतःक्षेपक मॉड्यूल, दूसरे पर अंतःक्षेपक नहीं हो सकता है। लेकिन वलयों को रूपांतरण की अच्छी तरह से समझी जाने वाली विधियां हैं जो विशेष स्थितियों को संभालती हैं। वलय जो स्वयं अंतःक्षेपक मॉड्यूल हैं उसमे कई विशेष गुण हैं और इसमें क्षेत्र पर [[परिमित समूह|परिमित समूहों]] के समूह वलय जैसे वलय सम्मिलित हैं। अंतःक्षेपक मॉड्यूल में [[विभाज्य समूह]] सम्मिलित होते हैं जो [[श्रेणी सिद्धांत]] में अंतःक्षेपक वाली वस्तुओं की धारणा से सामान्यीकृत होते हैं। | |||
== परिभाषा == | == परिभाषा == | ||
वलय R के ऊपर बायाँ मॉड्यूल Q अंतःक्षेपी होता है यदि यह निम्नलिखित समतुल्य शर्तों में से एक (और इसलिए सभी) को संतुष्ट करता है: | |||
* यदि Q किसी अन्य बाएँ R | * यदि Q किसी अन्य बाएँ R मॉड्यूल M का उपमॉड्यूल है, तो M का एक और उपमॉड्यूल K उपस्थित होता है। जैसे M, Q और K का आंतरिक प्रत्यक्ष Q + K = M और Q ∩ K = {0} योग है। | ||
* | * कोई भी छोटा शुद्ध क्रम 0 →Q → M → K → 0 बाएँ R-मॉड्यूल को विभाजित करता है। | ||
* यदि | * बाएँ R मॉड्यूल की श्रेणी से एबेलियन समूहों की श्रेणी के लिए प्रतिपरिवर्ती फलन Hom(-,''Q'') उपयुक्त है। | ||
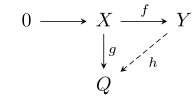
*यदि X और Y को R-मॉड्यूल के लिए छोड़ दिया जाए, तो f: X → Y अंतःक्षेपी मॉड्यूल समाकारिता है और g : X → Q अपेक्षाकृत मॉड्यूल समाकारिता है तो मॉड्यूल समाकारिता ''h'' : ''Y'' → ''Q'' सम्मिलित होती है जैसे कि hf = g को निम्न आरेख मे दर्शाया गया है: | |||
[[File:Injective module.svg|center|thumb|196x196px]] | |||
अंतःक्षेपक दाएँ R मॉड्यूल को पूर्ण सादृश्य में परिभाषित किया गया है। | |||
== उदाहरण == | == उदाहरण == | ||
=== | === प्रथम उदाहरण === | ||
तुच्छ रूप से | तुच्छ रूप से शून्य मॉड्यूल {0} अंतःक्षेपक मॉड्यूल है। | ||
एक | एक क्षेत्र k दिया गया है जहां प्रत्येक k-[[ सदिश स्थल |सदिश समष्टि]], Q अंतःक्षेपी और k मॉड्यूल है। यदि Q, V की उपसमष्टि है तो हम Q का एक आधार खोज सकते हैं और इसे V के आधार पर विस्तारित कर सकते हैं। नए विस्तारित आधार सदिशों में V की उपसमष्टि K है और V, Q और K का आंतरिक प्रत्यक्ष योग है। ध्यान दे कि Q का प्रत्यक्ष पूरक K विशिष्ट रूप से Q द्वारा निर्धारित नहीं किया गया है। इसी प्रकार उपरोक्त परिभाषा में विस्तारित मानचित्र h विशिष्ट रूप से अद्वितीय नहीं है। | ||
तर्कसंगत | तर्कसंगत Q (जोड़ के साथ) एक अंतःक्षेपक एबेलियन समूह (अर्थात अंतःक्षेपक Z-मॉड्यूल) बनाते हैं। कारक समूह Q/Z और वृत्तीय समूह अंतःक्षेपक Z-मॉड्यूल हैं। जो n> 1 के लिए कारक समूह <math>\mathfrak{Z/nZ}</math> एक Z/nZ-मॉड्यूल के रूप में अंतःक्षेपक है, लेकिन एक एबेलियन समूह के रूप में अंतःक्षेपक नहीं है। | ||
=== क्रमविनिमेय उदाहरण === | === क्रमविनिमेय उदाहरण === | ||
सामान्यतः किसी भी [[ अभिन्न डोमेन |समाकल डोमेन]] R के लिए अंश K के क्षेत्र के साथ R-मॉड्यूल K का अंतःक्षेपक R-मॉड्यूल है। वास्तव में R युक्त सबसे छोटा अंतःक्षेपक R-मॉड्यूल है। किसी भी डेडेकाइंड डोमेन के लिए [[भागफल मॉड्यूल]] K/R है। व्यंजक और इसका अविघटनीय योग स्थानीयकरण हैं। गैर-अभाज्य <math>R_{\mathfrak{p}}/R</math> अभाज्य अनुक्रम <math>\mathfrak{p}</math> के लिए शून्य आदर्श भी प्रमुख है और अंतःक्षेपक के के अनुरूप है। इस प्रकार से प्रमुख आदर्शों और अपरिवर्तनीय अंतःक्षेपक मॉड्यूल के बीच 1-1 सहसंबंध होता है। | |||
[[एबेन मैटलिस]] के कारण क्रमविनिमेय | [[एबेन मैटलिस]] (लैम 1999, §3I) के कारण क्रमविनिमेय नॉथेरियन वलयों के लिए विशेष रूप से समृद्ध सिद्धांत उपलब्ध है। प्रत्येक अंतःक्षेपक मॉड्यूल विशिष्ट रूप से अपरिवर्तनीय अंतःक्षेपक मॉड्यूल का प्रत्यक्ष योग है और अपरिवर्तनीय अंतःक्षेपक मॉड्यूल को विशिष्ट रूप से भागफल <math>R_{\mathfrak{p}}/R</math> के अंतःक्षेपक हल्स के रूप में पहचाना जाता है जहां <math>\mathfrak{p}</math> वलय के प्रमुख स्पेक्ट्रम पर भिन्न होता है। R मॉड्यूल के रूप में <math>R_{\mathfrak{p}}/R</math> का अंतःक्षेपक हल्स कैनोनिक रूप से ''R<sub>P</sub>'' मॉड्यूल है और ''R<sub>P</sub>'' का आरपी-अंतःक्षेपक हल्स है। दूसरे शब्दों में यह स्थानीय वलय पर विचार करने के लिए पर्याप्त है। R/P के अंतःक्षेपक हल्स का [[एंडोमोर्फिज्म रिंग|अंतःरूपांतरण वलय]], P पर R का पूरा <math>\hat R_P</math> है। | ||
दो उदाहरण Z-मॉड्यूल Z/ | |||
दो उदाहरण Z-मॉड्यूल Z/pZ (प्रूफ़र समूह) के अंतःक्षेपक हल्स हैं और k[x] मॉड्यूल k (व्युत्क्रम बहुपदों की वलय) के अंतःक्षेपक हल्स हैं। उत्तरार्द्ध को आसानी से ''k''[''x'',''x''<sup>−1</sup>]/''xk''[''x''] के रूप में वर्णित किया गया है। इस मॉड्यूल का आधार "व्युत्क्रम एकपदीय" है, जो कि n = 0, 1, 2, ... के लिए x<sup>−n</sup> है। अदिश द्वारा गुणन अपेक्षित है और x द्वारा गुणा सामान्य रूप से x·1 = 0 को छोड़कर व्यवहार करता है। [[एंडोमोर्फिज्म रिंग|अंतःरूपांतरण वलय]] केवल [[औपचारिक शक्ति श्रृंखला|औपचारिक घात श्रृंखला]] वलय है। | |||
=== आर्टिनियन उदाहरण === | === आर्टिनियन उदाहरण === | ||
यदि G | यदि G परिमित समूह है और k [[विशेषता (बीजगणित)]] 0 के साथ एक क्षेत्र है तो [[समूह प्रतिनिधित्व]] के सिद्धांत प्रदर्शित करता है कि किसी दिए गए उप-प्रतिनिधित्व पहले से ही दिए गए मॉड्यूल भाषा में अनुवादित एक का प्रत्यक्ष योग है। इसका अर्थ है कि समूह बीजगणित ''kG'' पर सभी मॉड्यूल अंतःक्षेपक हैं। यदि k का अभिलाक्षणिक मान शून्य नहीं है तो निम्न उदाहरण सहायता कर सकते है। | ||
यदि A, क्षेत्र k पर | यदि A, k पर परिमित आयाम के साथ क्षेत्र k पर इकाई [[साहचर्य बीजगणित]] है तो Hom<sub>k</sub>(-, k) अंतिम रूप से उत्पन्न बाएं A मॉड्यूल और अंतिम रूप से उत्पन्न दाएं A मॉड्यूल के बीच एक द्वैत है। इसलिए सूक्ष्म रूप से निर्मित किए गए अंतःक्षेपक बाएं A मॉड्यूल पूर्णतः Hom<sub>''k''</sub>(''P'', ''k'') के रूप में मॉड्यूल हैं जहां P अंतिम रूप से उत्पन्न प्रक्षेपीय सही A मॉड्यूल है। सममित बीजगणित के लिए अनुरूप विशेष रूप से अच्छी तरह से व्यवहार किया जाता है। प्रक्षेपीय मॉड्यूल और अंतःक्षेपक मॉड्यूल एक दूसरे के अनुरूप हैं। | ||
किसी भी [[आर्टिनियन रिंग]] के लिए | किसी भी [[आर्टिनियन रिंग|आर्टिनियन वलय]] के लिए जैसे कि कम्यूटेटिव वलय के लिए, अभाज्य क्रम और अंतःक्षेपक मॉड्यूल के बीच 1-1 सहसंबंध होता है। इस स्थिति में सहसंबंध लगभग और भी सरल है। एक प्रमुख आदर्श अद्वितीय सरल मॉड्यूल का विनाशक है और संबंधित अपरिवर्तनीय अंतःक्षेपक मॉड्यूल इसके अंतःक्षेपक हल्स है। क्षेत्र पर परिमित-आयामी बीजगणित के लिए ये अंतःक्षेपक हल्स सूक्ष्म रूप से उत्पन्न मॉड्यूल {{harv|लैम|1999|loc=§3G, §3J}} हैं। | ||
==== कम्प्यूटिंग | ==== कम्प्यूटिंग अंतःक्षेपक हल्स ==== | ||
यदि <math>R</math> एक नोथेरियन वलय है और <math>\mathfrak{p}</math> मुख्य आदर्श समुच्चय <math>E = E(R/\mathfrak{p})</math> अंतःक्षेपक हल्स के रूप में है। आर्टिनियन वलय के ऊपर <math>R/\mathfrak{p}</math> का अंतःक्षेपक हल्स {<math>R/\mathfrak{p}^k</math> की गणना मॉड्यूल <math>(0:_E\mathfrak{p}^k)</math> के रूप में की जा सकती है। यह <math>R/\mathfrak{p}^k</math> के समान लंबाई का एक मॉड्यूल है।<ref name=":0">{{Cite book|last=Eisenbud|title=क्रमविनिमेय बीजगणित का परिचय|pages=624, 625}}</ref> विशेष रूप से मानक ग्रेडेड वलय के लिए <math>R_\bullet = k[x_1,\ldots,x_n]_\bullet</math> और <math>\mathfrak{p}=(x_1,\ldots, x_n)</math>, <math>E = \oplus_i \text{Hom}(R_i, k)</math> अंतःक्षेपक मॉड्यूल है जो <math>k</math> से अधिक आर्टिनियन वलय के लिए अविघटनीय अंतःक्षेपक मॉड्यूल की गणना के लिए उपकरण है। | |||
==== स्व | ==== स्व अंतःक्षेपक ==== | ||
आर्टिन स्थानीय वलय <math>(R, \mathfrak{m}, K)</math> यदि और केवल यदि स्व अंतःक्षेपक <math>soc(R)</math> है। एक 1-आयामी सदिश समष्टि <math>K</math> है। इसका अर्थ यह है कि प्रत्येक स्थानीय गोरेंस्टीन वलय जो कि आर्टिन भी है। अपने आप में अंतःक्षेपक है क्योंकि इसमें 1-आयामी सोसल है।<ref>{{Cite web|url=https://www.math.purdue.edu/~walther/snowbird/inj.pdf|title=इंजेक्शन मॉड्यूल|page=10}}</ref> <math>R = \mathbb{C}[x,y]/(x^2,xy,y^2)</math> साधारण गैर-उदाहरण वलय है। जिसका अधिकतम आदर्श <math>(x,y)</math> और अवशेष क्षेत्र <math>\mathbb{C}</math> इसका सोसल <math>\mathbb{C}\cdot x \oplus\mathbb{C}\cdot y</math> है जो द्वि-आयामी है। अवशेष क्षेत्र <math>\text{Hom}_\mathbb{C}(\mathbb{C}\cdot x\oplus\mathbb{C}\cdot y, \mathbb{C})</math> में अंतःक्षेपक हल्स है। | |||
=== | ==== लाई बीजगणित मॉड्यूल ==== | ||
लाई बीजगणित के लिए <math>\mathfrak{g}</math> विशेषता 0 के क्षेत्र <math>k</math> पर मॉड्यूल की श्रेणी <math>\mathcal{M}(\mathfrak{g})</math> का अपेक्षाकृत प्रत्यक्ष वर्णन है अंतःक्षेपक मॉड्यूल सार्वभौमिक लाई बीजगणित का उपयोग करके किसी भी अंतःक्षेपक <math>\mathfrak{g}</math>-मॉड्यूल का निर्माण <math>\text{Hom}_k(U(\mathfrak{g}), V)</math> निम्न मॉड्यूल से किया जा सकता है:<ref>{{Cite web|last=Vogan|first=David|title=झूठ बीजगणित कोहोलॉजी|url=http://www-math.mit.edu/~dav/cohom.pdf}}</ref><blockquote><math>\mathfrak{g} \hookrightarrow U(\mathfrak{g})</math></blockquote>वास्तव में प्रत्येक <math>\mathfrak{g}</math>-मॉड्यूल में कुछ में अंतःक्षेपक <math>\text{Hom}_k(U(\mathfrak{g}), V)</math> है और प्रत्येक अंतःक्षेपक <math>\mathfrak{g}</math>-मॉड्यूल कुछ का प्रत्यक्ष योग <math>\text{Hom}_k(U(\mathfrak{g}), V)</math> है। | |||
== सिद्धांत == | == सिद्धांत == | ||
=== | === क्रमविनिमेय नोथेरियन वलय के लिए संरचना प्रमेय === | ||
एक कम्यूटेटिव नोथेरियन वलय <math>R</math> पर प्रत्येक अंतःक्षेपक मॉड्यूल अपरिवर्तनीय अंतःक्षेपक मॉड्यूल का प्रत्यक्ष योग होता है और प्रत्येक अपरिवर्तनीय अंतःक्षेपक मॉड्यूल अभाज्य <math>\mathfrak{p}</math> पर अवशेष क्षेत्र का अंतःक्षेपक हल्स होता है। अर्थात् एक अंतःक्षेपक <math>I \in \text{Mod}(R)</math> के लिए समरूपता है: | |||
<math>I \cong \bigoplus_{i} E(R/\mathfrak{p}_i)</math> | |||
=== | जहां <math>E(R/\mathfrak{p}_i)</math> मॉड्यूल के अंतःक्षेपक हल्स <math>R/\mathfrak{p}_i</math> हैं।<ref>{{Cite web|url=https://stacks.math.columbia.edu/tag/08YA|title=Structure of injective modules over Noetherian rings}}</ref> इसके अतिरिक्त यदि <math>I</math> मॉड्यूल <math>M</math> का अंतःक्षेपक हल्स है तो <math>\mathfrak{p}_i</math>, <math>M</math> के संबंधित अभाज्य संख्याएँ हैं।<ref name=":0" /> | ||
=== उपमॉड्यूल, भागफल, उत्पाद और योग === | |||
अंतःक्षेपक मॉड्यूल (यहां तक कि अपरिमित रूप से कई) अंतःक्षेपक मॉड्यूल का कोई भी उत्पाद अंतःक्षेपक है। इसके विपरीत यदि मॉड्यूल का प्रत्यक्ष उत्पाद अंतःक्षेपक है, तो प्रत्येक मॉड्यूल {{harv|लैम|1999|p=61}} अंतःक्षेपक है। सूक्ष्म रूप से अनेक अंतःक्षेपी मॉड्यूलों का प्रत्येक प्रत्यक्ष योग अंतःक्षेपी होता है। सामान्य रूप से उपमॉड्यूल्स, गणनांक मॉड्यूल या अंतःक्षेपक मॉड्यूल के अनंत प्रत्यक्ष योगों को अंतःक्षेपक नहीं होना चाहिए। प्रत्येक अंतःक्षेपक मॉड्यूल का प्रत्येक उपमॉड्यूल अंतःक्षेपक है यदि और केवल यदि वलय आर्टिनियन अर्ध साधारण है तब {{harv|गोलान|हेड|1991|p=152}} प्रत्येक अंतःक्षेपक मॉड्यूल का प्रत्येक कारक मॉड्यूल अंतःक्षेपक है यदि और केवल यदि वलय वंशानुगत है तब {{harv|लैम|1999|loc=Th. 3.22}} अंतःक्षेपी मॉड्यूल का प्रत्येक अनंत प्रत्यक्ष योग अंतःक्षेपी है यदि और केवल यदि वलय नोथेरियन {{harv|लैम|1999|loc=Th 3.46}} है।<ref>This is the [[Hyman Bass|Bass]]-Papp theorem, see {{harv|Papp|1959}} and {{harv|Chase|1960}}</ref> | |||
=== बेयर मानदंड === | |||
बेयर के मूल पेपर में उन्होंने एक उपयोगी परिणाम को सिद्ध किया है जिसे सामान्यतः बेयर के मानदंड के रूप में जाना जाता है। यह जांचने के लिए कि क्या मॉड्यूल अंतःक्षेपक है एक बायां R मॉड्यूल Q अंतःक्षेपक है यदि और केवल यदि कोई समरूपता g : I → Q बाएं आदर्श वलय से परिभाषित R का सभी R तक विस्तार किया जा सकता है। | |||
इस मानदंड का उपयोग करके कोई भी यह दिखा सकता है कि Q एक अंतःक्षेपी एबेलियन समूह है अर्थात Z पर एक अंतःक्षेपी मॉड्यूल अधिक सामान्यतः एक एबेलियन समूह अंतःक्षेपक है यदि और केवल यदि यह विभाज्य है। अधिक सामान्यतः अभी भी प्रमुख आदर्श डोमेन पर एक मॉड्यूल अंतःक्षेपक है यदि और केवल यदि यह विभाज्य है सदिश रिक्त समष्टि कि स्थिति इस प्रमेय का एक उदाहरण है, क्योंकि प्रत्येक क्षेत्र का प्रमुख आदर्श डोमेन है और प्रत्येक सदिश समष्टि विभाज्य है। सामान्य समाकल डोमेन पर हमारे पास अभी भी निहितार्थ है। समाकल डोमेन पर प्रत्येक अंतःक्षेपक मॉड्यूल विभाज्य होता है। | |||
बेयर के | बेयर के मानदंड को कई प्रकार {{harv|गोलान|हेड|1991|p=119}} से परिष्कृत किया गया है जिसमें {{harv|समित|1981}} और {{harv|वामोस|1983}} का परिणाम भी सम्मिलित है कि एक क्रमविनिमेय नोथेरियन वलय के लिए यह केवल प्रमुख आदर्शों पर विचार करने के लिए पर्याप्त है। दोहरी बेयर मानदंड जो प्रक्षेपीय मॉड्यूल के लिए परीक्षण सामान्य रूप से गलत है। उदाहरण के लिए Z-मॉड्यूल Q बेयर मानदंड के दोहरे नियम को संतुष्ट करता है लेकिन प्रक्षेपी नहीं है। | ||
=== अंतःक्षेपक सह निर्माता === | |||
{{Main|सह निर्माता}} | |||
लगभग सबसे महत्वपूर्ण अंतःक्षेपक मॉड्यूल एबेलियन समूह Q/Z है। यह [[एबेलियन समूहों की श्रेणी]] में एक अंतःक्षेपक उपनिर्माता है। जिसका अर्थ है कि यह अंतःक्षेपक है और कोई अन्य मॉड्यूल Q/Z की प्रतियों के उपयुक्त बड़े उत्पाद में निहित है। तो विशेष रूप से प्रत्येक एबेलियन समूह के अंतःक्षेपक का एक उपसमूह है। यह अपेक्षाकृत महत्वपूर्ण है कि यह किसी भी वलय पर भी सत्य है। प्रत्येक मॉड्यूल अंतःक्षेपक का एक उपसमूह है या बाएं R-मॉड्यूल की श्रेणी में पर्याप्त अंतःक्षेपक हैं। इसे सिद्ध करने के लिए बाएं R मॉड्यूल की श्रेणी में एक अंतःक्षेपक उपनिर्माता बनाने के लिए एबेलियन समूह Q/Z के अपेक्षाकृत गुणों का उपयोग किया जाता है। | |||
= | बाएं R-मॉड्यूल M के लिए तथाकथित चरित्र मॉड्यूल ''M''<sup>+</sup> = Hom<sub>'''Z'''</sub>(''M'','''Q'''/'''Z''') एक सही R मॉड्यूल है जो अंतःक्षेपक मॉड्यूल और प्रक्षेपीय मॉड्यूल के बीच नहीं बल्कि अंतःक्षेपक मॉड्यूल और [[फ्लैट मॉड्यूल|समतल मॉड्यूल]] के बीच रोचक द्विविधता {{harv|हनोक|जेंड़ा|2001|pp=78–80}} प्रदर्शित करता है। किसी भी वलय R के लिए एक बायां R मॉड्यूल समतल है यदि और केवल यदि इसका चरित्र मॉड्यूल अंतःक्षेपक है। यदि R नोथेरियन को छोड़ दिया गया है तो बाएं R मॉड्यूल अंतःक्षेपक है यदि और केवल यदि इसका चरित्र मॉड्यूल समतल है। | ||
{{ | |||
=== अंतःक्षेपक हल्स === | |||
{{Main|अंतःक्षेपक हल्स}} | |||
मॉड्यूल का अंतःक्षेपक हल्स सबसे छोटा अंतःक्षेपक मॉड्यूल है जिसमें दिए गए {{harv|एकमैनन|शॉपफ|1953}} को इसमें वर्णित किया गया था। एक न्यूनतम अंतःक्षेपक विश्लेषण (नीचे देखें) को परिभाषित करने के लिए अंतःक्षेपक हल्स का उपयोग कर सकते हैं। यदि अंतःक्षेपी समाकल का प्रत्येक पद पिछले मानचित्र के कोकर्नेल का अंतःक्षेपी हल्स है तो अंतःक्षेपी मॉड्यूल समाकल की न्यूनतम लंबाई होती है। | |||
मॉड्यूल का | |||
एक | === अंतःक्षेपक विश्लेषण === | ||
प्रत्येक मॉड्यूल M में एक अंतःक्षेपक विश्लेषण भी होता है जो निम्न रूप का उपयुक्त अनुक्रम है: | |||
: 0 → ''M'' → ''I''<sup>0</sup> → ''I''<sup>1</sup> → ''I''<sup>2</sup> → ... | |||
जहां ''I'' <sup>''j''</sup> अंतःक्षेपक मॉड्यूल हैं। व्युत्पन्न प्रस्तावों को परिभाषित करने के लिए अंतःक्षेपक विश्लेषण का उपयोग किया जा सकता है जैसे कि [[Ext functor|एक्सट गुणनाक]] एक परिमित अंतःक्षेपी समाकल की लंबाई सूचकांक n है जैसे कि I<sup>n</sup> शून्य नहीं है और I<sup>i</sup> = 0 के लिए n से अधिक है। यदि एक मॉड्यूल M एक परिमित अंतःक्षेपण संकल्प को स्वीकृत करता है, तो M के सभी परिमित अंतःक्षेपी संकल्पों के बीच न्यूनतम लंबाई को इसके अंतःक्षेपी आयाम और निरूपित id(''M'') कहा जाता है। यदि M परिमित अंतःक्षेपी संकल्प को स्वीकृत नहीं करता है तो मॉड्यूल द्वारा अंतःक्षेपी आयाम को अनंत कहा जाता है। उदाहरण के रूप में मॉड्यूल M पर विचार करें जैसे कि id(M) = 0 की इस स्थिति में अनुक्रम 0 → ''M'' → ''I''<sup>0</sup> → 0 की शुद्धता इंगित करती है कि केंद्र में (→) एक समरूपता है और इसलिए M स्वयं अंतःक्षेपी है।<ref>A module isomorphic to an injective module is of course injective.</ref> | |||
समान रूप से M का अंतःक्षेपी आयाम न्यूनतम पूर्णांक ∞ या n है जैसे कि Ext{{su|p=''N''|b=''A''}}(–,M) = 0 सभी N > n के लिए A(–, M) = 0 है। | |||
समान रूप से | |||
=== अविघटनीय === | === अविघटनीय === | ||
अंतःक्षेपक मॉड्यूल का प्रत्येक अंतःक्षेपक उपमॉड्यूल एक प्रत्यक्ष योग है। इसलिए अविघटनीय मॉड्यूल अंतःक्षेपक मॉड्यूल {{harv|लैम|1999|loc=§3F}} को समझना महत्वपूर्ण है। | |||
प्रत्येक अविघटनीय | प्रत्येक अविघटनीय अंतःक्षेपक मॉड्यूल में स्थानीय अंतःरूपांतरण वलय होती है। मॉड्यूल को एक समान मॉड्यूल कहा जाता है यदि प्रत्येक दो गैर-शून्य उपमॉड्यूल में गैर-शून्य प्रतिच्छेद होते है। एक अंतःक्षेपक मॉड्यूल M के लिए निम्नलिखित समतुल्य हैं: | ||
* | * M अविघटनीय है। | ||
* M | * M गैर-शून्य है और प्रत्येक गैर-शून्य उपमॉड्यूल का अंतःक्षेपक हल है। | ||
* | * M एकसमान है। | ||
* | * M एक समान मॉड्यूल का अंतःक्षेपक हल है। | ||
* | * M एक समान [[चक्रीय मॉड्यूल]] का अंतःक्षेपक हल है। | ||
* | * M में एक स्थानीय अंतःरूपांतरण वलय है | ||
नोथेरियन | नोथेरियन वलय के ऊपर प्रत्येक अंतःक्षेपक मॉड्यूल (विशिष्ट रूप से निर्धारित) अविघटनीय अंतःक्षेपक मॉड्यूल का प्रत्यक्ष योग है। क्रमविनिमेय नोथेरियन वलय के ऊपर यह (मैटलिस 1958) में वर्णित सभी अंतःक्षेपक मॉड्यूल की विशेष रूप से अच्छी समझ देता है। अविघटनीय अंतःक्षेपक मॉड्यूल वलय R के प्रमुख आदर्श के लिए मॉड्यूल R/P के अंतःक्षेपक हल्स हैं। इसके अतिरिक्त R/P के अंतःक्षेपक हल्स M में आदर्श ''p<sup>n</sup>'' के एनीहिलेटर द्वारा दिए गए मॉड्यूल ''M<sub>n</sub>'' द्वारा बढ़ते निस्पंदन हैं और ''M<sub>n</sub>''<sub>+1</sub>/''M<sub>n</sub>'' समरूपता है, जो R/p से Hom<sub>''R''/''p''</sub>(''p<sup>n</sup>''/''p<sup>n</sup>''<sup>+1</sup>, ''k''(''p'')) के भागफल क्षेत्र k(p) पर परिमित-आयामी सदिश समष्टि के रूप में है। | ||
=== | === वलय का परिवर्तन === | ||
विशेष रूप से बहुपद | विशेष रूप से बहुपद वलयों के लिए [[सबरिंग|उपवलय]] या भागफल के वलय या मॉड्यूल पर विचार करने में सक्षम होना महत्वपूर्ण है। सामान्यतः यह कठिन है, लेकिन कई परिणाम ज्ञात हैं। माना कि {{harv|लैम |1999|p=62}} S और R को वलय P के बाए R, दाए S [[bimodule|द्विमाड्यूल]] है जो बाए-R मॉड्यूल के रूप में समतल मॉड्यूल है। किसी भी अंतःक्षेपक दाए S मॉड्यूल M के लिए मॉड्यूल समरूपता Hom<sub>''S''</sub>( ''P'', ''M'' ) एक अंतःक्षेपक सही R मॉड्यूल है। बाएँ और दाएँ गुणों के आदान-प्रदान के बाद निश्चित रूप से यही कथन प्रयुक्त होता है। | ||
S | उदाहरण के लिए यदि R, S का उपवलय है जैसे कि S समतल R-मॉड्यूल है तो प्रत्येक अंतःक्षेपक S-मॉड्यूल अंतःक्षेपक R मॉड्यूल है। विशेष रूप से यदि R एक समाकल डोमेन है और S इसके [[अंशों का क्षेत्र]] है, तो S पर प्रत्येक सदिश समष्टि अंतःक्षेपी R-मॉड्यूल है। इसी प्रकार प्रत्येक अंतःक्षेपक ''R''[''x''] -मॉड्यूल अंतःक्षेपक R मॉड्यूल है। | ||
विपरीत दिशा में वलय समरूपता <math>f: S\to R</math> बाएँ और दाएँ गुणन द्वारा R को बाएँ-R, दाएँ-S द्विमॉड्यूल में बनाता है। अपने आप में मुक्त मॉड्यूल होने के कारण R भी [[मुफ्त मॉड्यूल]] और प्रक्षेपीय मॉड्यूल बाएं R मॉड्यूल के रूप में है। P = R के लिए उपरोक्त कथन की विशेषज्ञता यह कहती है कि जब M अंतःक्षेपक सही S मॉड्यूल का सह-प्रेरित मॉड्यूल है।<math> f_* M = \mathrm{Hom}_S(R, M)</math> एक अंतःक्षेपक सही R मॉड्यूल है। इस प्रकार f पर संयोग अंतःक्षेपक S मॉड्यूल से अंतःक्षेपक R मॉड्यूल उत्पन्न करता है। | |||
भागफल वलय R/I के लिए वलय का परिवर्तन भी बहुत स्पष्ट है। एक R मॉड्यूल ठीक उसी सम R/I-मॉड्यूल होता है जब इसे '''''I''''' द्वारा विलोपित किया जाता है। उपमॉड्यूल ann<sub>''I''</sub>(''M'') = { ''m'' in ''M'' : ''im'' = 0 बाएं R मॉड्यूल का एक बायां उपमॉड्यूल है। M और M का सबसे बड़ा उपमॉड्यूल है जो एक R/I-मॉड्यूल है। यदि M अंतःक्षेपी बायाँ R-मॉड्यूल है तो ann<sub>''I''</sub>(M) अंतःक्षेपी बायाँ R/I-मॉड्यूल है। इसे R=Z, I=nZ और M=Q/Z पर लागू करने पर, एक परिचित तथ्य प्राप्त होता है कि Z/nZ अपने आप में एक मॉड्यूल के रूप में अंतःक्षेपक है। हालांकि अंतःक्षेपक R मॉड्यूल को अंतःक्षेपक R/I-मॉड्यूल में परिवर्तित करना आसान होता है लेकिन यह प्रक्रिया अंतःक्षेपक वाले R विश्लेषण को अंतःक्षेपक वाले R/I-विश्लेषण में परिवर्तित नहीं करती है जो परिणामी समिश्र की होमोलॉजी अध्ययन के प्रारंभिक और मौलिक क्षेत्रों में से एक है। सहसंबंध समरूप बीजगणित की पाठ्यपुस्तक {{harv|रोटमैन|1979|p=103}} के पास एक गलत प्रमाण है कि वलय का स्थानीयकरण अंतःक्षेपक को संरक्षित करता है, लेकिन इसमें एक गणना {{harv| डेड|1981}} उदाहरण दिया गया है। | |||
=== स्व-अंतःक्षेपक वलय === | |||
समरूपता के साथ प्रत्येक वलय एक स्वतंत्र मॉड्यूल है और इसलिए अपने आप में मॉड्यूल के रूप में प्रक्षेपी है, लेकिन यह वलय के लिए अपने आप में एक मॉड्यूल के रूप में अंतःक्षेपक होना दुर्लभ है। यदि एक वलय सही मॉड्यूल के रूप में स्वयं पर अंतःक्षेपक है, तो इसे दायां स्व-अंतःक्षेपक वलय कहा जाता है। प्रत्येक फ्रोबेनियस बीजगणित स्व-अंतःक्षेपी है, लेकिन कोई भी समाकल डोमेन जो एक क्षेत्र नहीं है वह स्व-अंतःक्षेपी है। डेडेकाइंड डोमेन का प्रत्येक उपयुक्त भागफल स्व-अंतःक्षेपक है। | |||
एक दाएँ नोएथेरियन, दाएँ स्व-अंतःक्षेपक वाले वलय को [[अर्ध-फ्रोबेनियस रिंग|अर्ध-फ्रोबेनियस वलय]] कहा जाता है यदि यह दो तरफा आर्टिनियन और दो तरफा अंतःक्षेपक वाला होता है। अर्ध-फ्रोबेनियस वलयों का एक महत्वपूर्ण मॉड्यूल सैद्धांतिक गुण यह है कि प्रक्षेपी मॉड्यूल प्रायः अंतःक्षेपक मॉड्यूल होते हैं। | |||
== | == सामान्यीकरण और विशेषज्ञता == | ||
== | === अंतःक्षेपक वस्तुएं === | ||
{{Main|अंतःक्षेपक वस्तुएं}} | |||
मॉड्यूल श्रेणियों की तुलना में अधिक सामान्य श्रेणियों में अंतःक्षेपक वस्तुओ के विषय में भी चर्चा करता है, उदाहरण के लिए गुणनांक श्रेणियों में या कुछ वलय वाले समष्टि (''X'',O<sub>''X''</sub>) पर O<sub>''X''</sub> मॉड्यूल के शेव सिद्धांत की श्रेणियों में निम्नलिखित सामान्य परिभाषा का उपयोग श्रेणी C की एक वस्तु Q के लिए किया जाता है, यदि किसी समरूपता f: X → Y में C और किसी भी आकारिकी g: X → Q के लिए समरूपता h: Y → Q hf = g के साथ सम्मिलित है। | |||
=== विभाज्य समूह === | === विभाज्य समूह === | ||
{{Main| | {{Main|विभाज्य समूह}} | ||
= | एबेलियन समूहों की श्रेणी में अंतःक्षेपक वस्तु की धारणा को विभाज्य समूह शब्द के अंतर्गत अंतःक्षेपक मॉड्यूल से कुछ स्थिति तक स्वतंत्र रूप से अध्ययन किया गया था। यहां एक Z-मॉड्यूल M अंतःक्षेपक है यदि और केवल यदि ''n''⋅''M'' = ''M'' प्रत्येक गैर-शून्य पूर्णांक N के लिए यहां समतल मॉड्यूल, शुद्ध उपमॉड्यूल और अंतःक्षेपक मॉड्यूल के बीच संबंध अधिक स्पष्ट हैं क्योंकि यह केवल पूर्णांक द्वारा मॉड्यूल तत्वों के कुछ विभाज्य गुणों को संदर्भित करता है। | ||
=== शुद्ध अंतःक्षेपक मॉड्यूल === | |||
{{Main|शुद्ध अंतःक्षेपक मॉड्यूल}} | |||
सहसंबंध समरूपता बीजगणित में समरूपता के विस्तारण गुण के अतिरिक्त केवल उपमॉड्यूल के लिए आवश्यक हो सकती है। उदाहरण के लिए एक शुद्ध अंतःक्षेपी मॉड्यूल ऐसा मॉड्यूल होता है, जिसमें शुद्ध उपमॉड्यूल से समरूपता को समष्टि मॉड्यूल तक विस्तृत किया जा सकता है। | |||
== संदर्भ == | |||
=== टिप्पणियाँ === | === टिप्पणियाँ === | ||
{{Reflist}} | {{Reflist}} | ||
=== पाठ्यपुस्तकें === | === पाठ्यपुस्तकें === | ||
| Line 173: | Line 168: | ||
श्रेणी:मॉड्यूल सिद्धांत | श्रेणी:मॉड्यूल सिद्धांत | ||
[[Category:Articles with hatnote templates targeting a nonexistent page|Injective Module]] | |||
[[Category: | [[Category:Created On 25/05/2023|Injective Module]] | ||
[[Category:Created On 25/05/2023]] | [[Category:Lua-based templates|Injective Module]] | ||
[[Category:Machine Translated Page|Injective Module]] | |||
[[Category:Pages with script errors|Injective Module]] | |||
[[Category:Templates Vigyan Ready|Injective Module]] | |||
[[Category:Templates that add a tracking category|Injective Module]] | |||
[[Category:Templates that generate short descriptions|Injective Module]] | |||
[[Category:Templates using TemplateData|Injective Module]] | |||
Latest revision as of 16:16, 30 August 2023
गणित में, विशेष रूप से अमूर्त बीजगणित के क्षेत्र में अंतःक्षेपक मॉड्यूल को सामान्यतः मॉड्यूल सिद्धांत के रूप में जाना जाता है। अंतःक्षेपक मॉड्यूल Q वह मॉड्यूल है जो सभी तर्कसंगत संख्याओं के Z मॉड्यूल Q के साथ कुछ वांछनीय गुणों को साझा करता है। विशेष रूप से यदि Q किसी अन्य मॉड्यूल का उपमॉड्यूल है तो यह पहले से ही उस मॉड्यूल का प्रत्यक्ष योग होता है। इसके अतिरिक्त मॉड्यूल Y का एक उपमॉड्यूल दिया जाता है तो इस उपमॉड्यूल से Q तक किसी भी मॉड्यूल समरूपता को सभी Y से Q तक एक समान रूप से बढ़ाया जा सकता है। यह अवधारणा प्रक्षेपीय मॉड्यूल के लिए दोहरी है। अंतःक्षेपक मॉड्यूल को (बेयर 1940) और (लेयम 1999, §3) ने प्रस्तुत किया था। जिनकी पाठ्यपुस्तक में विस्तार से चर्चा की गई है।
अंतःक्षेपक मॉड्यूल का अत्यधिक अध्ययन किया गया है और विभिन्न प्रकार की अतिरिक्त धारणाओं को उनके संदर्भ में परिभाषित किया गया है। अंतःक्षेपक के उपनिर्माता अंतःक्षेपक मॉड्यूल हैं जो ईमानदारी से मॉड्यूल की पूरी श्रेणी का प्रतिनिधित्व करते हैं। यह मॉड्यूल अंतःक्षेपी विश्लेषण को मापता है कि अंतःक्षेपण आयाम के संदर्भ में एक मॉड्यूल अंतःक्षेपण से कितनी दूर है और व्युत्पन्न श्रेणी में मॉड्यूल का प्रतिनिधित्व करता है। अंतःक्षेपक हल्स अधिकतम आवश्यक विस्तार हैं और न्यूनतम अंतःक्षेपक भी विस्तार बन जाते हैं। नोथेरियन वलय पर प्रत्येक अंतःक्षेपक मॉड्यूल विशिष्ट रूप से अविघटनीय मॉड्यूल का प्रत्यक्ष योग है और उनकी संरचना अच्छी तरह से समझी जाती है। एक वलय पर अंतःक्षेपक मॉड्यूल, दूसरे पर अंतःक्षेपक नहीं हो सकता है। लेकिन वलयों को रूपांतरण की अच्छी तरह से समझी जाने वाली विधियां हैं जो विशेष स्थितियों को संभालती हैं। वलय जो स्वयं अंतःक्षेपक मॉड्यूल हैं उसमे कई विशेष गुण हैं और इसमें क्षेत्र पर परिमित समूहों के समूह वलय जैसे वलय सम्मिलित हैं। अंतःक्षेपक मॉड्यूल में विभाज्य समूह सम्मिलित होते हैं जो श्रेणी सिद्धांत में अंतःक्षेपक वाली वस्तुओं की धारणा से सामान्यीकृत होते हैं।
परिभाषा
वलय R के ऊपर बायाँ मॉड्यूल Q अंतःक्षेपी होता है यदि यह निम्नलिखित समतुल्य शर्तों में से एक (और इसलिए सभी) को संतुष्ट करता है:
- यदि Q किसी अन्य बाएँ R मॉड्यूल M का उपमॉड्यूल है, तो M का एक और उपमॉड्यूल K उपस्थित होता है। जैसे M, Q और K का आंतरिक प्रत्यक्ष Q + K = M और Q ∩ K = {0} योग है।
- कोई भी छोटा शुद्ध क्रम 0 →Q → M → K → 0 बाएँ R-मॉड्यूल को विभाजित करता है।
- बाएँ R मॉड्यूल की श्रेणी से एबेलियन समूहों की श्रेणी के लिए प्रतिपरिवर्ती फलन Hom(-,Q) उपयुक्त है।
- यदि X और Y को R-मॉड्यूल के लिए छोड़ दिया जाए, तो f: X → Y अंतःक्षेपी मॉड्यूल समाकारिता है और g : X → Q अपेक्षाकृत मॉड्यूल समाकारिता है तो मॉड्यूल समाकारिता h : Y → Q सम्मिलित होती है जैसे कि hf = g को निम्न आरेख मे दर्शाया गया है:
अंतःक्षेपक दाएँ R मॉड्यूल को पूर्ण सादृश्य में परिभाषित किया गया है।
उदाहरण
प्रथम उदाहरण
तुच्छ रूप से शून्य मॉड्यूल {0} अंतःक्षेपक मॉड्यूल है।
एक क्षेत्र k दिया गया है जहां प्रत्येक k-सदिश समष्टि, Q अंतःक्षेपी और k मॉड्यूल है। यदि Q, V की उपसमष्टि है तो हम Q का एक आधार खोज सकते हैं और इसे V के आधार पर विस्तारित कर सकते हैं। नए विस्तारित आधार सदिशों में V की उपसमष्टि K है और V, Q और K का आंतरिक प्रत्यक्ष योग है। ध्यान दे कि Q का प्रत्यक्ष पूरक K विशिष्ट रूप से Q द्वारा निर्धारित नहीं किया गया है। इसी प्रकार उपरोक्त परिभाषा में विस्तारित मानचित्र h विशिष्ट रूप से अद्वितीय नहीं है।
तर्कसंगत Q (जोड़ के साथ) एक अंतःक्षेपक एबेलियन समूह (अर्थात अंतःक्षेपक Z-मॉड्यूल) बनाते हैं। कारक समूह Q/Z और वृत्तीय समूह अंतःक्षेपक Z-मॉड्यूल हैं। जो n> 1 के लिए कारक समूह एक Z/nZ-मॉड्यूल के रूप में अंतःक्षेपक है, लेकिन एक एबेलियन समूह के रूप में अंतःक्षेपक नहीं है।
क्रमविनिमेय उदाहरण
सामान्यतः किसी भी समाकल डोमेन R के लिए अंश K के क्षेत्र के साथ R-मॉड्यूल K का अंतःक्षेपक R-मॉड्यूल है। वास्तव में R युक्त सबसे छोटा अंतःक्षेपक R-मॉड्यूल है। किसी भी डेडेकाइंड डोमेन के लिए भागफल मॉड्यूल K/R है। व्यंजक और इसका अविघटनीय योग स्थानीयकरण हैं। गैर-अभाज्य अभाज्य अनुक्रम के लिए शून्य आदर्श भी प्रमुख है और अंतःक्षेपक के के अनुरूप है। इस प्रकार से प्रमुख आदर्शों और अपरिवर्तनीय अंतःक्षेपक मॉड्यूल के बीच 1-1 सहसंबंध होता है।
एबेन मैटलिस (लैम 1999, §3I) के कारण क्रमविनिमेय नॉथेरियन वलयों के लिए विशेष रूप से समृद्ध सिद्धांत उपलब्ध है। प्रत्येक अंतःक्षेपक मॉड्यूल विशिष्ट रूप से अपरिवर्तनीय अंतःक्षेपक मॉड्यूल का प्रत्यक्ष योग है और अपरिवर्तनीय अंतःक्षेपक मॉड्यूल को विशिष्ट रूप से भागफल के अंतःक्षेपक हल्स के रूप में पहचाना जाता है जहां वलय के प्रमुख स्पेक्ट्रम पर भिन्न होता है। R मॉड्यूल के रूप में का अंतःक्षेपक हल्स कैनोनिक रूप से RP मॉड्यूल है और RP का आरपी-अंतःक्षेपक हल्स है। दूसरे शब्दों में यह स्थानीय वलय पर विचार करने के लिए पर्याप्त है। R/P के अंतःक्षेपक हल्स का अंतःरूपांतरण वलय, P पर R का पूरा है।
दो उदाहरण Z-मॉड्यूल Z/pZ (प्रूफ़र समूह) के अंतःक्षेपक हल्स हैं और k[x] मॉड्यूल k (व्युत्क्रम बहुपदों की वलय) के अंतःक्षेपक हल्स हैं। उत्तरार्द्ध को आसानी से k[x,x−1]/xk[x] के रूप में वर्णित किया गया है। इस मॉड्यूल का आधार "व्युत्क्रम एकपदीय" है, जो कि n = 0, 1, 2, ... के लिए x−n है। अदिश द्वारा गुणन अपेक्षित है और x द्वारा गुणा सामान्य रूप से x·1 = 0 को छोड़कर व्यवहार करता है। अंतःरूपांतरण वलय केवल औपचारिक घात श्रृंखला वलय है।
आर्टिनियन उदाहरण
यदि G परिमित समूह है और k विशेषता (बीजगणित) 0 के साथ एक क्षेत्र है तो समूह प्रतिनिधित्व के सिद्धांत प्रदर्शित करता है कि किसी दिए गए उप-प्रतिनिधित्व पहले से ही दिए गए मॉड्यूल भाषा में अनुवादित एक का प्रत्यक्ष योग है। इसका अर्थ है कि समूह बीजगणित kG पर सभी मॉड्यूल अंतःक्षेपक हैं। यदि k का अभिलाक्षणिक मान शून्य नहीं है तो निम्न उदाहरण सहायता कर सकते है।
यदि A, k पर परिमित आयाम के साथ क्षेत्र k पर इकाई साहचर्य बीजगणित है तो Homk(-, k) अंतिम रूप से उत्पन्न बाएं A मॉड्यूल और अंतिम रूप से उत्पन्न दाएं A मॉड्यूल के बीच एक द्वैत है। इसलिए सूक्ष्म रूप से निर्मित किए गए अंतःक्षेपक बाएं A मॉड्यूल पूर्णतः Homk(P, k) के रूप में मॉड्यूल हैं जहां P अंतिम रूप से उत्पन्न प्रक्षेपीय सही A मॉड्यूल है। सममित बीजगणित के लिए अनुरूप विशेष रूप से अच्छी तरह से व्यवहार किया जाता है। प्रक्षेपीय मॉड्यूल और अंतःक्षेपक मॉड्यूल एक दूसरे के अनुरूप हैं।
किसी भी आर्टिनियन वलय के लिए जैसे कि कम्यूटेटिव वलय के लिए, अभाज्य क्रम और अंतःक्षेपक मॉड्यूल के बीच 1-1 सहसंबंध होता है। इस स्थिति में सहसंबंध लगभग और भी सरल है। एक प्रमुख आदर्श अद्वितीय सरल मॉड्यूल का विनाशक है और संबंधित अपरिवर्तनीय अंतःक्षेपक मॉड्यूल इसके अंतःक्षेपक हल्स है। क्षेत्र पर परिमित-आयामी बीजगणित के लिए ये अंतःक्षेपक हल्स सूक्ष्म रूप से उत्पन्न मॉड्यूल (लैम 1999, §3G, §3J) हैं।
कम्प्यूटिंग अंतःक्षेपक हल्स
यदि एक नोथेरियन वलय है और मुख्य आदर्श समुच्चय अंतःक्षेपक हल्स के रूप में है। आर्टिनियन वलय के ऊपर का अंतःक्षेपक हल्स { की गणना मॉड्यूल के रूप में की जा सकती है। यह के समान लंबाई का एक मॉड्यूल है।[1] विशेष रूप से मानक ग्रेडेड वलय के लिए और , अंतःक्षेपक मॉड्यूल है जो से अधिक आर्टिनियन वलय के लिए अविघटनीय अंतःक्षेपक मॉड्यूल की गणना के लिए उपकरण है।
स्व अंतःक्षेपक
आर्टिन स्थानीय वलय यदि और केवल यदि स्व अंतःक्षेपक है। एक 1-आयामी सदिश समष्टि है। इसका अर्थ यह है कि प्रत्येक स्थानीय गोरेंस्टीन वलय जो कि आर्टिन भी है। अपने आप में अंतःक्षेपक है क्योंकि इसमें 1-आयामी सोसल है।[2] साधारण गैर-उदाहरण वलय है। जिसका अधिकतम आदर्श और अवशेष क्षेत्र इसका सोसल है जो द्वि-आयामी है। अवशेष क्षेत्र में अंतःक्षेपक हल्स है।
लाई बीजगणित मॉड्यूल
लाई बीजगणित के लिए विशेषता 0 के क्षेत्र पर मॉड्यूल की श्रेणी का अपेक्षाकृत प्रत्यक्ष वर्णन है अंतःक्षेपक मॉड्यूल सार्वभौमिक लाई बीजगणित का उपयोग करके किसी भी अंतःक्षेपक -मॉड्यूल का निर्माण निम्न मॉड्यूल से किया जा सकता है:[3]
वास्तव में प्रत्येक -मॉड्यूल में कुछ में अंतःक्षेपक है और प्रत्येक अंतःक्षेपक -मॉड्यूल कुछ का प्रत्यक्ष योग है।
सिद्धांत
क्रमविनिमेय नोथेरियन वलय के लिए संरचना प्रमेय
एक कम्यूटेटिव नोथेरियन वलय पर प्रत्येक अंतःक्षेपक मॉड्यूल अपरिवर्तनीय अंतःक्षेपक मॉड्यूल का प्रत्यक्ष योग होता है और प्रत्येक अपरिवर्तनीय अंतःक्षेपक मॉड्यूल अभाज्य पर अवशेष क्षेत्र का अंतःक्षेपक हल्स होता है। अर्थात् एक अंतःक्षेपक के लिए समरूपता है:
जहां मॉड्यूल के अंतःक्षेपक हल्स हैं।[4] इसके अतिरिक्त यदि मॉड्यूल का अंतःक्षेपक हल्स है तो , के संबंधित अभाज्य संख्याएँ हैं।[1]
उपमॉड्यूल, भागफल, उत्पाद और योग
अंतःक्षेपक मॉड्यूल (यहां तक कि अपरिमित रूप से कई) अंतःक्षेपक मॉड्यूल का कोई भी उत्पाद अंतःक्षेपक है। इसके विपरीत यदि मॉड्यूल का प्रत्यक्ष उत्पाद अंतःक्षेपक है, तो प्रत्येक मॉड्यूल (लैम 1999, p. 61) अंतःक्षेपक है। सूक्ष्म रूप से अनेक अंतःक्षेपी मॉड्यूलों का प्रत्येक प्रत्यक्ष योग अंतःक्षेपी होता है। सामान्य रूप से उपमॉड्यूल्स, गणनांक मॉड्यूल या अंतःक्षेपक मॉड्यूल के अनंत प्रत्यक्ष योगों को अंतःक्षेपक नहीं होना चाहिए। प्रत्येक अंतःक्षेपक मॉड्यूल का प्रत्येक उपमॉड्यूल अंतःक्षेपक है यदि और केवल यदि वलय आर्टिनियन अर्ध साधारण है तब (गोलान & हेड 1991, p. 152) प्रत्येक अंतःक्षेपक मॉड्यूल का प्रत्येक कारक मॉड्यूल अंतःक्षेपक है यदि और केवल यदि वलय वंशानुगत है तब (लैम 1999, Th. 3.22) अंतःक्षेपी मॉड्यूल का प्रत्येक अनंत प्रत्यक्ष योग अंतःक्षेपी है यदि और केवल यदि वलय नोथेरियन (लैम 1999, Th 3.46) है।[5]
बेयर मानदंड
बेयर के मूल पेपर में उन्होंने एक उपयोगी परिणाम को सिद्ध किया है जिसे सामान्यतः बेयर के मानदंड के रूप में जाना जाता है। यह जांचने के लिए कि क्या मॉड्यूल अंतःक्षेपक है एक बायां R मॉड्यूल Q अंतःक्षेपक है यदि और केवल यदि कोई समरूपता g : I → Q बाएं आदर्श वलय से परिभाषित R का सभी R तक विस्तार किया जा सकता है।
इस मानदंड का उपयोग करके कोई भी यह दिखा सकता है कि Q एक अंतःक्षेपी एबेलियन समूह है अर्थात Z पर एक अंतःक्षेपी मॉड्यूल अधिक सामान्यतः एक एबेलियन समूह अंतःक्षेपक है यदि और केवल यदि यह विभाज्य है। अधिक सामान्यतः अभी भी प्रमुख आदर्श डोमेन पर एक मॉड्यूल अंतःक्षेपक है यदि और केवल यदि यह विभाज्य है सदिश रिक्त समष्टि कि स्थिति इस प्रमेय का एक उदाहरण है, क्योंकि प्रत्येक क्षेत्र का प्रमुख आदर्श डोमेन है और प्रत्येक सदिश समष्टि विभाज्य है। सामान्य समाकल डोमेन पर हमारे पास अभी भी निहितार्थ है। समाकल डोमेन पर प्रत्येक अंतःक्षेपक मॉड्यूल विभाज्य होता है।
बेयर के मानदंड को कई प्रकार (गोलान & हेड 1991, p. 119) से परिष्कृत किया गया है जिसमें (समित 1981) और (वामोस 1983) का परिणाम भी सम्मिलित है कि एक क्रमविनिमेय नोथेरियन वलय के लिए यह केवल प्रमुख आदर्शों पर विचार करने के लिए पर्याप्त है। दोहरी बेयर मानदंड जो प्रक्षेपीय मॉड्यूल के लिए परीक्षण सामान्य रूप से गलत है। उदाहरण के लिए Z-मॉड्यूल Q बेयर मानदंड के दोहरे नियम को संतुष्ट करता है लेकिन प्रक्षेपी नहीं है।
अंतःक्षेपक सह निर्माता
लगभग सबसे महत्वपूर्ण अंतःक्षेपक मॉड्यूल एबेलियन समूह Q/Z है। यह एबेलियन समूहों की श्रेणी में एक अंतःक्षेपक उपनिर्माता है। जिसका अर्थ है कि यह अंतःक्षेपक है और कोई अन्य मॉड्यूल Q/Z की प्रतियों के उपयुक्त बड़े उत्पाद में निहित है। तो विशेष रूप से प्रत्येक एबेलियन समूह के अंतःक्षेपक का एक उपसमूह है। यह अपेक्षाकृत महत्वपूर्ण है कि यह किसी भी वलय पर भी सत्य है। प्रत्येक मॉड्यूल अंतःक्षेपक का एक उपसमूह है या बाएं R-मॉड्यूल की श्रेणी में पर्याप्त अंतःक्षेपक हैं। इसे सिद्ध करने के लिए बाएं R मॉड्यूल की श्रेणी में एक अंतःक्षेपक उपनिर्माता बनाने के लिए एबेलियन समूह Q/Z के अपेक्षाकृत गुणों का उपयोग किया जाता है।
बाएं R-मॉड्यूल M के लिए तथाकथित चरित्र मॉड्यूल M+ = HomZ(M,Q/Z) एक सही R मॉड्यूल है जो अंतःक्षेपक मॉड्यूल और प्रक्षेपीय मॉड्यूल के बीच नहीं बल्कि अंतःक्षेपक मॉड्यूल और समतल मॉड्यूल के बीच रोचक द्विविधता (हनोक & जेंड़ा 2001, pp. 78–80) प्रदर्शित करता है। किसी भी वलय R के लिए एक बायां R मॉड्यूल समतल है यदि और केवल यदि इसका चरित्र मॉड्यूल अंतःक्षेपक है। यदि R नोथेरियन को छोड़ दिया गया है तो बाएं R मॉड्यूल अंतःक्षेपक है यदि और केवल यदि इसका चरित्र मॉड्यूल समतल है।
अंतःक्षेपक हल्स
मॉड्यूल का अंतःक्षेपक हल्स सबसे छोटा अंतःक्षेपक मॉड्यूल है जिसमें दिए गए (एकमैनन & शॉपफ 1953) को इसमें वर्णित किया गया था। एक न्यूनतम अंतःक्षेपक विश्लेषण (नीचे देखें) को परिभाषित करने के लिए अंतःक्षेपक हल्स का उपयोग कर सकते हैं। यदि अंतःक्षेपी समाकल का प्रत्येक पद पिछले मानचित्र के कोकर्नेल का अंतःक्षेपी हल्स है तो अंतःक्षेपी मॉड्यूल समाकल की न्यूनतम लंबाई होती है।
अंतःक्षेपक विश्लेषण
प्रत्येक मॉड्यूल M में एक अंतःक्षेपक विश्लेषण भी होता है जो निम्न रूप का उपयुक्त अनुक्रम है:
- 0 → M → I0 → I1 → I2 → ...
जहां I j अंतःक्षेपक मॉड्यूल हैं। व्युत्पन्न प्रस्तावों को परिभाषित करने के लिए अंतःक्षेपक विश्लेषण का उपयोग किया जा सकता है जैसे कि एक्सट गुणनाक एक परिमित अंतःक्षेपी समाकल की लंबाई सूचकांक n है जैसे कि In शून्य नहीं है और Ii = 0 के लिए n से अधिक है। यदि एक मॉड्यूल M एक परिमित अंतःक्षेपण संकल्प को स्वीकृत करता है, तो M के सभी परिमित अंतःक्षेपी संकल्पों के बीच न्यूनतम लंबाई को इसके अंतःक्षेपी आयाम और निरूपित id(M) कहा जाता है। यदि M परिमित अंतःक्षेपी संकल्प को स्वीकृत नहीं करता है तो मॉड्यूल द्वारा अंतःक्षेपी आयाम को अनंत कहा जाता है। उदाहरण के रूप में मॉड्यूल M पर विचार करें जैसे कि id(M) = 0 की इस स्थिति में अनुक्रम 0 → M → I0 → 0 की शुद्धता इंगित करती है कि केंद्र में (→) एक समरूपता है और इसलिए M स्वयं अंतःक्षेपी है।[6]
समान रूप से M का अंतःक्षेपी आयाम न्यूनतम पूर्णांक ∞ या n है जैसे कि ExtN
A(–,M) = 0 सभी N > n के लिए A(–, M) = 0 है।
अविघटनीय
अंतःक्षेपक मॉड्यूल का प्रत्येक अंतःक्षेपक उपमॉड्यूल एक प्रत्यक्ष योग है। इसलिए अविघटनीय मॉड्यूल अंतःक्षेपक मॉड्यूल (लैम 1999, §3F) को समझना महत्वपूर्ण है।
प्रत्येक अविघटनीय अंतःक्षेपक मॉड्यूल में स्थानीय अंतःरूपांतरण वलय होती है। मॉड्यूल को एक समान मॉड्यूल कहा जाता है यदि प्रत्येक दो गैर-शून्य उपमॉड्यूल में गैर-शून्य प्रतिच्छेद होते है। एक अंतःक्षेपक मॉड्यूल M के लिए निम्नलिखित समतुल्य हैं:
- M अविघटनीय है।
- M गैर-शून्य है और प्रत्येक गैर-शून्य उपमॉड्यूल का अंतःक्षेपक हल है।
- M एकसमान है।
- M एक समान मॉड्यूल का अंतःक्षेपक हल है।
- M एक समान चक्रीय मॉड्यूल का अंतःक्षेपक हल है।
- M में एक स्थानीय अंतःरूपांतरण वलय है
नोथेरियन वलय के ऊपर प्रत्येक अंतःक्षेपक मॉड्यूल (विशिष्ट रूप से निर्धारित) अविघटनीय अंतःक्षेपक मॉड्यूल का प्रत्यक्ष योग है। क्रमविनिमेय नोथेरियन वलय के ऊपर यह (मैटलिस 1958) में वर्णित सभी अंतःक्षेपक मॉड्यूल की विशेष रूप से अच्छी समझ देता है। अविघटनीय अंतःक्षेपक मॉड्यूल वलय R के प्रमुख आदर्श के लिए मॉड्यूल R/P के अंतःक्षेपक हल्स हैं। इसके अतिरिक्त R/P के अंतःक्षेपक हल्स M में आदर्श pn के एनीहिलेटर द्वारा दिए गए मॉड्यूल Mn द्वारा बढ़ते निस्पंदन हैं और Mn+1/Mn समरूपता है, जो R/p से HomR/p(pn/pn+1, k(p)) के भागफल क्षेत्र k(p) पर परिमित-आयामी सदिश समष्टि के रूप में है।
वलय का परिवर्तन
विशेष रूप से बहुपद वलयों के लिए उपवलय या भागफल के वलय या मॉड्यूल पर विचार करने में सक्षम होना महत्वपूर्ण है। सामान्यतः यह कठिन है, लेकिन कई परिणाम ज्ञात हैं। माना कि (लैम 1999, p. 62) S और R को वलय P के बाए R, दाए S द्विमाड्यूल है जो बाए-R मॉड्यूल के रूप में समतल मॉड्यूल है। किसी भी अंतःक्षेपक दाए S मॉड्यूल M के लिए मॉड्यूल समरूपता HomS( P, M ) एक अंतःक्षेपक सही R मॉड्यूल है। बाएँ और दाएँ गुणों के आदान-प्रदान के बाद निश्चित रूप से यही कथन प्रयुक्त होता है।
उदाहरण के लिए यदि R, S का उपवलय है जैसे कि S समतल R-मॉड्यूल है तो प्रत्येक अंतःक्षेपक S-मॉड्यूल अंतःक्षेपक R मॉड्यूल है। विशेष रूप से यदि R एक समाकल डोमेन है और S इसके अंशों का क्षेत्र है, तो S पर प्रत्येक सदिश समष्टि अंतःक्षेपी R-मॉड्यूल है। इसी प्रकार प्रत्येक अंतःक्षेपक R[x] -मॉड्यूल अंतःक्षेपक R मॉड्यूल है।
विपरीत दिशा में वलय समरूपता बाएँ और दाएँ गुणन द्वारा R को बाएँ-R, दाएँ-S द्विमॉड्यूल में बनाता है। अपने आप में मुक्त मॉड्यूल होने के कारण R भी मुफ्त मॉड्यूल और प्रक्षेपीय मॉड्यूल बाएं R मॉड्यूल के रूप में है। P = R के लिए उपरोक्त कथन की विशेषज्ञता यह कहती है कि जब M अंतःक्षेपक सही S मॉड्यूल का सह-प्रेरित मॉड्यूल है। एक अंतःक्षेपक सही R मॉड्यूल है। इस प्रकार f पर संयोग अंतःक्षेपक S मॉड्यूल से अंतःक्षेपक R मॉड्यूल उत्पन्न करता है।
भागफल वलय R/I के लिए वलय का परिवर्तन भी बहुत स्पष्ट है। एक R मॉड्यूल ठीक उसी सम R/I-मॉड्यूल होता है जब इसे I द्वारा विलोपित किया जाता है। उपमॉड्यूल annI(M) = { m in M : im = 0 बाएं R मॉड्यूल का एक बायां उपमॉड्यूल है। M और M का सबसे बड़ा उपमॉड्यूल है जो एक R/I-मॉड्यूल है। यदि M अंतःक्षेपी बायाँ R-मॉड्यूल है तो annI(M) अंतःक्षेपी बायाँ R/I-मॉड्यूल है। इसे R=Z, I=nZ और M=Q/Z पर लागू करने पर, एक परिचित तथ्य प्राप्त होता है कि Z/nZ अपने आप में एक मॉड्यूल के रूप में अंतःक्षेपक है। हालांकि अंतःक्षेपक R मॉड्यूल को अंतःक्षेपक R/I-मॉड्यूल में परिवर्तित करना आसान होता है लेकिन यह प्रक्रिया अंतःक्षेपक वाले R विश्लेषण को अंतःक्षेपक वाले R/I-विश्लेषण में परिवर्तित नहीं करती है जो परिणामी समिश्र की होमोलॉजी अध्ययन के प्रारंभिक और मौलिक क्षेत्रों में से एक है। सहसंबंध समरूप बीजगणित की पाठ्यपुस्तक (रोटमैन 1979, p. 103) के पास एक गलत प्रमाण है कि वलय का स्थानीयकरण अंतःक्षेपक को संरक्षित करता है, लेकिन इसमें एक गणना (डेड 1981) उदाहरण दिया गया है।
स्व-अंतःक्षेपक वलय
समरूपता के साथ प्रत्येक वलय एक स्वतंत्र मॉड्यूल है और इसलिए अपने आप में मॉड्यूल के रूप में प्रक्षेपी है, लेकिन यह वलय के लिए अपने आप में एक मॉड्यूल के रूप में अंतःक्षेपक होना दुर्लभ है। यदि एक वलय सही मॉड्यूल के रूप में स्वयं पर अंतःक्षेपक है, तो इसे दायां स्व-अंतःक्षेपक वलय कहा जाता है। प्रत्येक फ्रोबेनियस बीजगणित स्व-अंतःक्षेपी है, लेकिन कोई भी समाकल डोमेन जो एक क्षेत्र नहीं है वह स्व-अंतःक्षेपी है। डेडेकाइंड डोमेन का प्रत्येक उपयुक्त भागफल स्व-अंतःक्षेपक है।
एक दाएँ नोएथेरियन, दाएँ स्व-अंतःक्षेपक वाले वलय को अर्ध-फ्रोबेनियस वलय कहा जाता है यदि यह दो तरफा आर्टिनियन और दो तरफा अंतःक्षेपक वाला होता है। अर्ध-फ्रोबेनियस वलयों का एक महत्वपूर्ण मॉड्यूल सैद्धांतिक गुण यह है कि प्रक्षेपी मॉड्यूल प्रायः अंतःक्षेपक मॉड्यूल होते हैं।
सामान्यीकरण और विशेषज्ञता
अंतःक्षेपक वस्तुएं
मॉड्यूल श्रेणियों की तुलना में अधिक सामान्य श्रेणियों में अंतःक्षेपक वस्तुओ के विषय में भी चर्चा करता है, उदाहरण के लिए गुणनांक श्रेणियों में या कुछ वलय वाले समष्टि (X,OX) पर OX मॉड्यूल के शेव सिद्धांत की श्रेणियों में निम्नलिखित सामान्य परिभाषा का उपयोग श्रेणी C की एक वस्तु Q के लिए किया जाता है, यदि किसी समरूपता f: X → Y में C और किसी भी आकारिकी g: X → Q के लिए समरूपता h: Y → Q hf = g के साथ सम्मिलित है।
विभाज्य समूह
एबेलियन समूहों की श्रेणी में अंतःक्षेपक वस्तु की धारणा को विभाज्य समूह शब्द के अंतर्गत अंतःक्षेपक मॉड्यूल से कुछ स्थिति तक स्वतंत्र रूप से अध्ययन किया गया था। यहां एक Z-मॉड्यूल M अंतःक्षेपक है यदि और केवल यदि n⋅M = M प्रत्येक गैर-शून्य पूर्णांक N के लिए यहां समतल मॉड्यूल, शुद्ध उपमॉड्यूल और अंतःक्षेपक मॉड्यूल के बीच संबंध अधिक स्पष्ट हैं क्योंकि यह केवल पूर्णांक द्वारा मॉड्यूल तत्वों के कुछ विभाज्य गुणों को संदर्भित करता है।
शुद्ध अंतःक्षेपक मॉड्यूल
सहसंबंध समरूपता बीजगणित में समरूपता के विस्तारण गुण के अतिरिक्त केवल उपमॉड्यूल के लिए आवश्यक हो सकती है। उदाहरण के लिए एक शुद्ध अंतःक्षेपी मॉड्यूल ऐसा मॉड्यूल होता है, जिसमें शुद्ध उपमॉड्यूल से समरूपता को समष्टि मॉड्यूल तक विस्तृत किया जा सकता है।
संदर्भ
टिप्पणियाँ
- ↑ 1.0 1.1 Eisenbud. क्रमविनिमेय बीजगणित का परिचय. pp. 624, 625.
- ↑ "इंजेक्शन मॉड्यूल" (PDF). p. 10.
- ↑ Vogan, David. "झूठ बीजगणित कोहोलॉजी" (PDF).
- ↑ "Structure of injective modules over Noetherian rings".
- ↑ This is the Bass-Papp theorem, see (Papp 1959) and (Chase 1960)
- ↑ A module isomorphic to an injective module is of course injective.
पाठ्यपुस्तकें
- Anderson, Frank Wylie; Fuller, Kent R (1992), Rings and Categories of Modules, Berlin, New York: Springer-Verlag, ISBN 978-0-387-97845-1, retrieved 30 July 2016
- Enochs, Edgar E.; Jenda, Overtoun M. G. (2000), Relative homological algebra, de Gruyter Expositions in Mathematics, vol. 30, Berlin: Walter de Gruyter & Co., doi:10.1515/9783110803662, ISBN 978-3-11-016633-0, MR 1753146
- Golan, Jonathan S.; Head, Tom (1991), Modules and the structure of rings, Monographs and पाठ्यपुस्तकें in Pure and Applied Mathematics, vol. 147, Marcel Dekker, ISBN 978-0-8247-8555-0, MR 1201818
- Lam, Tsit-Yuen (1999), Lectures on modules and rings, Graduate Texts in Mathematics No. 189, Berlin, New York: Springer-Verlag, doi:10.1007/978-1-4612-0525-8, ISBN 978-0-387-98428-5, MR 1653294
- Rotman, Joseph J. (1979), An introduction to homological algebra, Pure and Applied Mathematics, vol. 85, Boston, MA: Academic Press, ISBN 978-0-12-599250-3, MR 0538169
प्राथमिक स्रोत
- Baer, Reinhold (1940), "Abelian groups that are direct summands of every containing abelian group", Bulletin of the American Mathematical Society, 46 (10): 800–807, doi:10.1090/S0002-9904-1940-07306-9, MR 0002886, Zbl 0024.14902
- Chase, Stephen U. (1960), "Direct products of modules", Transactions of the American Mathematical Society, American Mathematical Society, Vol. 97, No. 3, 97 (3): 457–473, doi:10.2307/1993382, JSTOR 1993382, MR 0120260
- Dade, Everett C. (1981), "Localization of injective modules", Journal of Algebra, 69 (2): 416–425, doi:10.1016/0021-8693(81)90213-1, MR 0617087
- Eckmann, B.; Schopf, A. (1953), "Über injektive Moduln", Archiv der Mathematik, 4 (2): 75–78, doi:10.1007/BF01899665, MR 0055978
- Lambek, Joachim (1963), "On Utumi's ring of quotients", Canadian Journal of Mathematics, 15: 363–370, doi:10.4153/CJM-1963-041-4, ISSN 0008-414X, MR 0147509
- Matlis, Eben (1958), "Injective modules over Noetherian rings", Pacific Journal of Mathematics, 8: 511–528, doi:10.2140/pjm.1958.8.511, ISSN 0030-8730, MR 0099360
- Osofsky, B. L. (1964), "On ring properties of injective hulls", Canadian Mathematical Bulletin, 7: 405–413, doi:10.4153/CMB-1964-039-3, ISSN 0008-4395, MR 0166227
- Papp, Zoltán (1959), "On algebraically closed modules", Publicationes Mathematicae Debrecen, 6: 311–327, ISSN 0033-3883, MR 0121390
- Smith, P. F. (1981), "Injective modules and prime ideals", Communications in Algebra, 9 (9): 989–999, doi:10.1080/00927878108822627, MR 0614468
- Utumi, Yuzo (1956), "On quotient rings", Osaka Journal of Mathematics, 8: 1–18, ISSN 0030-6126, MR 0078966
- Vámos, P. (1983), "Ideals and modules testing injectivity", Communications in Algebra, 11 (22): 2495–2505, doi:10.1080/00927878308822975, MR 0733337
श्रेणी:समरूप बीजगणित
श्रेणी:मॉड्यूल सिद्धांत