SO(3) पर चार्ट: Difference between revisions
No edit summary |
m (11 revisions imported from alpha:SO(3)_पर_चार्ट) |
||
| (6 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
{{broader|रोटेशन समूह SO(3)}}गणित में, तीन आयामों में [[विशेष ऑर्थोगोनल समूह]], जिसे घूर्णन समूह | {{broader|रोटेशन समूह SO(3)}}गणित में, तीन आयामों में [[विशेष ऑर्थोगोनल समूह]], जिसे घूर्णन समूह SO(3) के रूप में जाना जाता है, [[ कई गुना |मैनिफोल्ड]] का स्वाभाविक रूप से घटित होने वाला उदाहरण है। '''SO(3) पर विभिन्न [[चार्ट (टोपोलॉजी)|चार्ट]]''' [[चार्ट (टोपोलॉजी)|(टोपोलॉजी)]] प्रतिद्वंद्वी समन्वय प्रणाली स्थापित करते हैं: इस विषय में घूर्णन का वर्णन करने वाले मान का मुख्य रूप से समुच्चय नहीं कहा जा सकता है। स्वतंत्रता की तीन डिग्री (भौतिकी और रसायन विज्ञान) हैं, जिससे SO(3) का आयाम तीन हो जाये। कई अनुप्रयोगों में एक या अन्य समन्वय प्रणाली का उपयोग किया जाता है, और प्रश्न उठता है कि किसी दिए गए प्रणाली से दूसरे प्रणाली में कैसे परिवर्तित किया जाए। | ||
==घूर्णन का स्थान== | ==घूर्णन का स्थान== | ||
[[ज्यामिति]] में घूर्णन समूह त्रि-आयामी यूक्लिडियन अंतराल R<sup>3</sup> की उत्पत्ति के बारे में सभी घुमावों का [[समूह (गणित)]] है I<ref>Jacobson (2009), p. 34, Ex. 14.</ref> परिभाषा के अनुसार, मूल के चारों ओर घूमना [[रैखिक परिवर्तन]] है, जो [[वेक्टर (ज्यामिति)|सदिश (ज्यामिति)]] की [[लंबाई]] को संरक्षित करता है (यह [[आइसोमेट्री]] है) और अंतराल के [[अभिविन्यास (गणित)]] ( | [[ज्यामिति]] में घूर्णन समूह त्रि-आयामी यूक्लिडियन अंतराल R<sup>3</sup> की उत्पत्ति के बारे में सभी घुमावों का [[समूह (गणित)]] है I<ref>Jacobson (2009), p. 34, Ex. 14.</ref> परिभाषा के अनुसार, मूल के चारों ओर घूमना [[रैखिक परिवर्तन]] है, जो [[वेक्टर (ज्यामिति)|सदिश (ज्यामिति)]] की [[लंबाई]] को संरक्षित करता है (यह [[आइसोमेट्री]] है) और अंतराल के [[अभिविन्यास (गणित)]] (अर्थात हैंडनेस) को संरक्षित करता है। लंबाई-संरक्षण परिवर्तन जो अभिविन्यास को विपरीत कर देता है, उसे अनुचित घूर्णन कहा जाता है। त्रि-आयामी यूक्लिडियन अंतराल का प्रत्येक अनुचित घूर्णन एक घूर्णन है, जिसके पश्चात् मूल के माध्यम से सतह में [[प्रतिबिंब (गणित)]] होता है। | ||
दो घूर्णनों को संयोजित करने से दूसरा घूर्णन उत्पन्न होता है; प्रत्येक घूर्णन में अद्वितीय व्युत्क्रम घूर्णन होता है; और [[पहचान मानचित्र]] घूर्णन की परिभाषा को संतुष्ट करता है। उपरोक्त गुणों के कारण, सभी घुमावों का समुच्चय संरचना के अंतर्गत समूह (गणित) है। इसके अतिरिक्त, घूर्णन समूह में प्राकृतिक मैनिफोल्ड संरचना होती है, जिसके लिए समूह संचालन [[सुचारू कार्य|सुचारू]] होता है, तो यह वास्तव में [[झूठ समूह|लाई समूह]] है। ऑर्थोगोनल और घूर्णन मैट्रिसेस बताए गए कारणों से घूर्णन समूह को प्रायः SO(3) के रूप में दर्शाया जाता है। | दो घूर्णनों को संयोजित करने से दूसरा घूर्णन उत्पन्न होता है; प्रत्येक घूर्णन में अद्वितीय व्युत्क्रम घूर्णन होता है; और [[पहचान मानचित्र]] घूर्णन की परिभाषा को संतुष्ट करता है। उपरोक्त गुणों के कारण, सभी घुमावों का समुच्चय संरचना के अंतर्गत समूह (गणित) है। इसके अतिरिक्त, घूर्णन समूह में प्राकृतिक मैनिफोल्ड संरचना होती है, जिसके लिए समूह संचालन [[सुचारू कार्य|सुचारू]] होता है, तो यह वास्तव में [[झूठ समूह|लाई समूह]] है। ऑर्थोगोनल और घूर्णन मैट्रिसेस बताए गए कारणों से घूर्णन समूह को प्रायः SO(3) के रूप में दर्शाया जाता है। | ||
| Line 12: | Line 12: | ||
यह 3डी ठोस गोला 4डी डिस्क की सतह के बराबर है, जो एक 3डी प्रकार भी है। इस तुल्यता को करने के लिए, हमें यह परिभाषित करना होगा कि हम इस 4D-एम्बेडेड सतह के साथ घूर्णन का प्रतिनिधित्व कैसे करेंगे। | यह 3डी ठोस गोला 4डी डिस्क की सतह के बराबर है, जो एक 3डी प्रकार भी है। इस तुल्यता को करने के लिए, हमें यह परिभाषित करना होगा कि हम इस 4D-एम्बेडेड सतह के साथ घूर्णन का प्रतिनिधित्व कैसे करेंगे। | ||
==घूर्णन का | ==घूर्णन का अतिपरवलय== | ||
[[Image:Space of rotations.png|200px|thumb|right|घूर्णन के स्थान में विभिन्न कोणों और विभिन्न अक्षों द्वारा दो घूर्णन। सदिश की लंबाई घूर्णन के परिमाण से संबंधित है।]] | [[Image:Space of rotations.png|200px|thumb|right|घूर्णन के स्थान में विभिन्न कोणों और विभिन्न अक्षों द्वारा दो घूर्णन। सदिश की लंबाई घूर्णन के परिमाण से संबंधित है।]] | ||
=== | ===अतिपरवलय की कल्पना करना=== | ||
समतल को त्रि-आयामी क्षेत्र S<sup>3</sup>,4-आयामी यूक्लिडियन समतल में डिस्क की सीमा रूप में मानना रूचिपूर्ण है। ऐसा करने के लिए, हमें यह परिभाषित करना होगा कि हम इस 4डी-एम्बेडेड सतह के साथ घूर्णन का प्रतिनिधित्व कैसे करते हैं। | |||
घूर्णन के कोण को निर्दिष्ट करने के लिए त्रिज्या का उपयोग करने का उपाय सीधा नहीं है। इसे परिभाषित उत्तरी ध्रुव वाले क्षेत्र में अक्षांश के वृत्तों से संबंधित किया जा सकता है और इसे इस प्रकार समझाया गया है: | घूर्णन के कोण को निर्दिष्ट करने के लिए त्रिज्या का उपयोग करने का उपाय सीधा नहीं है। इसे परिभाषित उत्तरी ध्रुव वाले क्षेत्र में अक्षांश के वृत्तों से संबंधित किया जा सकता है और इसे इस प्रकार समझाया गया है: | ||
त्रि-आयामी | त्रि-आयामी समतल में गोले के उत्तरी ध्रुव से प्रारम्भ करके, हम पहचान घूर्णन का प्रतिनिधित्व करने के लिए उत्तरी ध्रुव पर बिंदु निर्दिष्ट करते हैं। पहचान घूर्णन के विषय में, घूर्णन की कोई धुरी परिभाषित नहीं है, और घूर्णन का कोण (शून्य) अप्रासंगिक है। xy-तल में निहित अपनी धुरी और बहुत छोटे घूर्णन कोण के साथ घूर्णन को xy-तल के समानांतर और उत्तरी ध्रुव के बहुत निकट गोले के माध्यम से स्लाइस द्वारा निर्दिष्ट किया जा सकता है। इस स्लाइस द्वारा परिभाषित वृत्त घूर्णन के छोटे कोण के अनुरूप बहुत छोटा होगा। जैसे-जैसे घूर्णन कोण बड़े होते जाते हैं, टुकड़ा दक्षिण की ओर बढ़ता जाता है, और गोले के भूमध्य रेखा तक पहुंचने पर वृत्त बड़े होते जाते हैं, जो 180 डिग्री के घूर्णन कोण के अनुरूप होगा। दक्षिण की ओर बढ़ते हुए, वृत्तों की त्रिज्याएँ अब छोटी हो गई हैं (घूर्णन के कोण के निरपेक्ष मान के अनुरूप जिसे ऋणात्मक संख्या माना जाता है)। अंत में, जैसे ही दक्षिणी ध्रुव पर पहुँचते हैं, वृत्त एक बार फिर पहचान घुमाव में सिकुड़ जाते हैं, जिसे दक्षिणी ध्रुव पर बिंदु के रूप में भी निर्दिष्ट किया जाता है। ध्यान दें कि इस कल्पना द्वारा ऐसे घुमावों की कई विशेषताओं और उनके प्रतिनिधित्व को देखा जा सकता है। | ||
घूर्णन का स्थान निरंतर होता है, प्रत्येक घूर्णन में घूर्णन का प्रतिवेश होता है जो लगभग समान होता है, और प्रतिवेश के सिकुड़ने पर यह समतल हो जाता है। | घूर्णन का स्थान निरंतर होता है, प्रत्येक घूर्णन में घूर्णन का प्रतिवेश होता है जो लगभग समान होता है, और प्रतिवेश के सिकुड़ने पर यह समतल हो जाता है। | ||
===उपनाम=== | ===उपनाम=== | ||
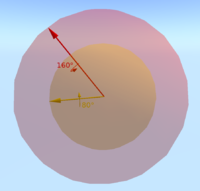
[[Image:Hypersphere of rotations.png|250px|thumb|right|घूर्णन के लिए घूर्णन का | [[Image:Hypersphere of rotations.png|250px|thumb|right|घूर्णन के लिए घूर्णन का अतिपरवलय जिसमें क्षैतिज अक्ष (xy-प्लेन में) होता है।]]इसके अतिरिक्त, प्रत्येक घुमाव को वास्तव में गोले पर दो एंटीपोडल बिंदुओं द्वारा दर्शाया जाता है, जो गोले के केंद्र के माध्यम से रेखा के विपरीत शीर्ष पर होते हैं। यह इस तथ्य को दर्शाता है कि प्रत्येक घूर्णन को किसी अक्ष के चारों ओर घूर्णन के रूप में दर्शाया जा सकता है, या, समकक्ष, विपरीत दिशा में इंगित करने वाले अक्ष के बारे में नकारात्मक घूर्णन के रूप में (तथाकथित डबल कवरिंग समूह) के रूप में दर्शाया जा सकता है। किसी विशेष घूर्णन कोण का प्रतिनिधित्व करने वाले वृत्त का अक्षांश उस घूर्णन द्वारा दर्शाए गए कोण का आधा होगा, क्योंकि जैसे ही बिंदु उत्तर से दक्षिण ध्रुव की ओर जाता है, अक्षांश शून्य से 180 डिग्री तक होता है, जबकि घूर्णन का कोण 0 से 360 डिग्री तक होता है। (तब बिंदु का "देशांतर" घूर्णन की विशेष धुरी का प्रतिनिधित्व करता है।) चूँकि ध्यान दें कि घुमावों का यह सेट संरचना के अंतर्गत संवृत नहीं है। | ||
xy-तल में अक्षों के साथ दो क्रमिक घूर्णन आवश्यक रूप से ऐसा घूर्णन नहीं देंगे जिसकी धुरी xy-तल में स्थित हो, और इस प्रकार इसे गोले पर | xy-तल में अक्षों के साथ दो क्रमिक घूर्णन आवश्यक रूप से ऐसा घूर्णन नहीं देंगे जिसकी धुरी xy-तल में स्थित हो, और इस प्रकार इसे गोले पर बिंदु के रूप में दर्शाया नहीं जा सकता है। 3-स्पेस में सामान्य घूर्णन के विषय में ऐसा नहीं होगा, जो संरचना के अंतर्गत संवृत समुच्चय बनाते हैं। | ||
इस | इस कल्पना को 3-आयामी समतल में सामान्य घुमाव तक बढ़ाया जा सकता है। पहचान घूर्णन बिंदु है, और कुछ अक्ष के सम्बन्ध में घूर्णन के छोटे कोण को छोटे त्रिज्या वाले गोले पर बिंदु के रूप में दर्शाया जा सकता है। जैसे-जैसे घूर्णन का कोण बढ़ता है, गोला तब तक बढ़ता है, जब तक कि घूर्णन का कोण 180 डिग्री तक नहीं पहुंच जाता, जिस बिंदु पर गोला सिकुड़ना प्रारम्भ हो जाता है, और कोण 360 डिग्री (या नकारात्मक दिशा से शून्य डिग्री) तक पहुंचने पर बिंदु बन जाता है। फैलते और सिकुड़ते गोले का यह समुच्चय चार-आयामी समतल (3-परवलय) में 3-परवलय अतिपरवलय का प्रतिनिधित्व करता है। | ||
जैसा कि ऊपर दिए गए सरल उदाहरण में है, | जैसा कि ऊपर दिए गए सरल उदाहरण में है, अतिपरवलय पर बिंदु के रूप में दर्शाया गया प्रत्येक घुमाव उस अतिपरवलय पर उसके एंटीपोडल बिंदु से मैच करता है। अतिपरवलय पर अक्षांश घूर्णन के संबंधित कोण का आधा होगा, और प्रतिवेश सिकुड़ने पर किसी भी बिंदु का प्रतिवेश चपटा हो जाएगा (अर्थात बिंदुओं के 3 डी यूक्लिडियन स्थान द्वारा दर्शाया जाएगा)। | ||
यह व्यवहार [[इकाई चतुर्भुज]] के समुच्चय से | यह व्यवहार [[इकाई चतुर्भुज]] के समुच्चय से मैच करता है: एक सामान्य चतुर्भुज चार-आयामी समतल में बिंदु का प्रतिनिधित्व करता है, किन्तु इसे इकाई परिमाण में सीमित करने से अतिपरवलय की सतह के बराबर त्रि-आयामी स्थान प्राप्त होता है। इकाई चतुर्भुज का परिमाण इकाई त्रिज्या के अतिपरवलय के अनुरूप इकाई होता है। | ||
इकाई चतुर्भुज का सदिश भाग घूर्णन अक्ष के अनुरूप 2-परवलय की त्रिज्या का प्रतिनिधित्व करता है, और इसका परिमाण घूर्णन के आधे कोण की ज्या है। प्रत्येक घूर्णन को विपरीत चिह्न के दो इकाई चतुर्भुजों द्वारा दर्शाया जाता है, और, जैसा कि तीन आयामों में घूर्णन के स्थान में होता है, दो इकाई चतुर्भुजों का चतुर्भुज उत्पाद इकाई चतुर्भुज का उत्पादन करता है। साथ ही, किसी दिए गए इकाई चतुर्भुज के किसी भी अतिसूक्ष्म प्रतिवेश में इकाई चतुर्भुज का स्थान समतल होता है। | |||
==पैरामीट्रिज़ेशन== | ==पैरामीट्रिज़ेशन== | ||
{{main|अभिविन्यास (ज्यामिति)}} | {{main|अभिविन्यास (ज्यामिति)}} | ||
हम घूर्णन के स्थान को कई | हम घूर्णन के स्थान को कई प्रकार से मानकीकृत कर सकते हैं, किन्तु अध:पतन सदैव दिखाई देता है। उदाहरण के लिए, यदि हम तीन कोणों ([[यूलर कोण]]) का उपयोग करते हैं, तो अतिपरवलय पर कुछ बिंदुओं पर इस प्रकार का पैरामीटर अव्यवस्थित हो जाता है, जिससे [[जिम्बल लॉक]] की समस्या उत्पन्न हो जाती है। हम w के साथ चार यूक्लिडियन निर्देशांक w,x,y,z का उपयोग करके ''w''<sup>2</sup> + ''x''<sup>2</sup> + ''y''<sup>2</sup> + ''z''<sup>2</sup> = 1 के साथ इससे बच सकते हैं I बिंदु (w,x,y,z) कोण द्वारा सदिश (x,y,z) द्वारा निर्देशित अक्ष के चारों ओर एक घूर्णन का प्रतिनिधित्व करता है:- | ||
:<math>\alpha = 2 \cos^{-1}(w) = 2 \sin^{-1} \left (\sqrt{1-(x^2+y^2+z^2)} \right ).</math> | :<math>\alpha = 2 \cos^{-1}(w) = 2 \sin^{-1} \left (\sqrt{1-(x^2+y^2+z^2)} \right ).</math> | ||
यह समस्या अक्षांश और देशांतर जैसे दो निर्देशांकों के साथ | यह समस्या अक्षांश और देशांतर जैसे दो निर्देशांकों के साथ गोले की द्विआयामी सतह को पैरामीटराइज़ करने के समान है। उत्तरी और दक्षिणी ध्रुवों पर अक्षांश और देशांतर अव्यवस्थित व्यवहार (अपक्षयी) हैं, चूँकि ध्रुव गोले पर किसी भी अन्य बिंदु से आंतरिक रूप से भिन्न नहीं हैं। ध्रुवों (अक्षांश +90° और −90°) पर, देशांतर अर्थहीन हो जाता है। यह दर्शाया जा सकता है कि कोई भी दो-पैरामीटर समन्वय प्रणाली ऐसी विकृति से बच नहीं सकती है। | ||
संभावित पैरामीट्रिज़ेशन | संभावित पैरामीट्रिज़ेशन कैंडिडेट में सम्मिलित हैं: | ||
*यूलर कोण (θ,φ,ψ), x, y और z अक्षों के | *यूलर कोण (θ,φ,ψ), x, y और z अक्षों के सम्बन्ध में घूर्णन के उत्पाद का प्रतिनिधित्व करते हैं; | ||
*टाइट-ब्रायन कोण (θ,φ,ψ), x, y और z अक्षों के | *टाइट-ब्रायन कोण (θ,φ,ψ), x, y और z अक्षों के सम्बन्ध में घूर्णन के उत्पाद का प्रतिनिधित्व करते हैं; | ||
* | *अक्ष का प्रतिनिधित्व करने वाले इकाई सदिश का [[अक्ष कोण]] युग्म ('n', θ), और इसके चारों ओर घूर्णन का कोण हैं; | ||
*लंबाई 1 का | *लंबाई 1 का चतुर्भुज 'q' (cf. [[ मैं मुड़ा |वर्सर]], [[चतुर्भुज और स्थानिक घूर्णन]], [[गोला|3-गोलाकार]]), जिसके घटकों को यूलर-रोड्रिग्स पैरामीटर भी कहा जाता है; | ||
* | *3 × 3 [[तिरछा-सममित मैट्रिक्स|तिरछा-सममित आव्यूह]], घातांक के माध्यम से; 3 × 3 तिरछा-सममित आव्यूह लाई बीजगणित SO(3) हैं, और यह लाई सिद्धांत में घातीय मानचित्र है; | ||
*केली तर्कसंगत पैरामीटर, [[केली परिवर्तन]] पर आधारित, सभी विशेषताओं में प्रयोग योग्य; | *केली तर्कसंगत पैरामीटर, [[केली परिवर्तन]] पर आधारित, सभी विशेषताओं में प्रयोग योग्य है; | ||
*मोबियस परिवर्तन, <math>w=\frac{az+b}{cz+d},</math> [[रीमैन क्षेत्र]] पर कार्य | *मोबियस परिवर्तन, <math>w=\frac{az+b}{cz+d},</math> [[रीमैन क्षेत्र]] पर कार्य करना है। | ||
===पैरामीट्रिज़ेशन की समस्याएँ=== | ===पैरामीट्रिज़ेशन की समस्याएँ === | ||
इनकी बहु-मूल्यवान प्रकृति और विलक्षणताओं के कारण इन्हें स्थानीय चार्ट से अधिक उपयोग करने में समस्याएँ हैं। अर्थात्, चार्ट (टोपोलॉजी) की परिभाषा में केवल [[भिन्नता]] के साथ काम करने के लिए सबसे ऊपर सावधान रहना चाहिए। इस प्रकार की समस्याएँ अपरिहार्य हैं, क्योंकि SO(3) [[वास्तविक प्रक्षेप्य स्थान]] P | इनकी बहु-मूल्यवान प्रकृति और विलक्षणताओं के कारण इन्हें स्थानीय चार्ट से अधिक उपयोग करने में समस्याएँ होती हैं। अर्थात्, चार्ट (टोपोलॉजी) की परिभाषा में केवल [[भिन्नता]] के साथ काम करने के लिए सबसे ऊपर सावधान रहना चाहिए। इस प्रकार की समस्याएँ अपरिहार्य हैं, क्योंकि SO(3) [[वास्तविक प्रक्षेप्य स्थान]] P<sup>3</sup>(R) से भिन्न है, जो एंटीपोडल बिंदुओं की पहचान करके S<sup>3</sup> का एक भागफल है, और चार्ट R<sup>3</sup> का उपयोग करके मैनिफोल्ड को मॉडल करने का प्रयास करते हैं। | ||
यह बताता है कि, उदाहरण के लिए, यूलर कोण 3-[[ टोरस्र्स ]] में | यह बताता है कि, उदाहरण के लिए, यूलर कोण 3-[[ टोरस्र्स ]]में चर और 3-गोले में इकाई चतुर्भुज क्यों देते प्रतीत होते हैं। यूलर कोणों द्वारा प्रतिनिधित्व की विशिष्टता कुछ बिंदुओं पर टूट जाती है (सीएफ. जिम्बल लॉक), किन्तु क्वाटरनियन प्रतिनिधित्व सदैव डबल कवरिंग समूह होता है, जिसमें ''q'' और −''q'' समान घूर्णन देते हैं। | ||
यदि हम | यदि हम तिरछा-सममित आव्यूह का उपयोग करते हैं, तो प्रत्येक 3 × 3 तिरछा-सममित आव्यूह 3 मानो द्वारा निर्धारित किया जाता है, और इसलिए प्रथम दृश्य में, पैरामीटर स्थान R<sup>3</sup> है I[[ मैट्रिक्स घातांक | आव्यूह घातांक]] ऐसे आव्यूह का परिणाम निर्धारक 1 के ऑर्थोगोनल 3 × 3 आव्यूह में होता है - दूसरे शब्दों में, घूर्णन आव्यूह, किन्तु यह कई-से-एक मानचित्र है। ध्यान दें कि यह [[ कवरिंग मानचित्र |कवरिंग मानचित्र]] नहीं है - किन्तु यह मूल के निकट स्थानीय होमोमोर्फिज्म है, यह 180 डिग्री तक घूमने वाला कवरिंग मैप नहीं है। इन आव्यूह को R<sup>3</sup> में मूल के चारों ओर गेंद तक सीमित करना संभव है, जिससे घूर्णन 180 डिग्री से अधिक न हो, और यह एक-से-एक होगा, 180 डिग्री के घूर्णन को त्यागकर, जो सीमा S<sup>2</sup> के अनुरूप है, और ये एंटीपोडल बिंदुओं की पहचान करते हैं - यह [[कट लोकस (रीमैनियन मैनिफोल्ड)]] है। सीमा की इस पहचान के साथ 3-गेंद P<sup>3</sup>(R) है I समान स्थिति में तिरछा-सममित आव्यूह में केली परिवर्तन को प्रारम्भ करने के लिए होती है। | ||
अक्ष कोण | अक्ष कोण S<sup>2</sup> × S<sup>1</sup> में पैरामीटर देता है, यदि हम इकाई सदिश को घूर्णन के वास्तविक अक्ष से प्रतिस्थापित करते हैं, जिससे ''n'' और −''n'' ही अक्ष रेखा दें, तो अक्ष का सेट [[वास्तविक प्रक्षेप्य तल]] P<sup>2</sup>(R) बन जाता है। । किन्तु चूँकि ''n'' और −''n'' के चारों ओर घूमने को θ के विपरीत मानों द्वारा मानकीकृत किया जाता है, परिणाम P<sup>2</sup>(R), पर S<sup>1</sup> बंडल है, जो P<sup>3</sup>(R) बन जाता है। | ||
आंशिक रैखिक परिवर्तन चार जटिल | आंशिक रैखिक परिवर्तन चार जटिल मानो, ''a'', ''b'', ''c'' और ''d'' का उपयोग करते हैं, इस नियम के साथ कि ad−bc गैर-शून्य है। चूँकि सभी चार मानो को एक ही जटिल संख्या से गुणा करने पर पैरामीटर नहीं परिवर्तित करता है, हम इस बात पर जोर दे सकते हैं कि ad−bc=1। यह (''a'',''b'',''c'',''d'') को निर्धारक 1 के 2 × 2 जटिल आव्यूह के रूप में लिखने का सुझाव देता है, अर्थात, विशेष रैखिक समूह SL(2,C) के तत्व के रूप में है। किन्तु ऐसे सभी मैट्रिक्स घूर्णन उत्पन्न नहीं करते: S2 पर अनुरूप मानचित्र भी सम्मिलित हैं। केवल घूर्णन प्राप्त करने के लिए हम इस बात पर जोर देते हैं कि d, a का सम्मिश्र संयुग्म है, और c, b के सम्मिश्र संयुग्म का ऋणात्मक है। फिर हमारे पास दो सम्मिश्र संख्याएँ, a और b हैं, जो |a|2+|b|2=1 के अधीन हैं। यदि हम a+bj लिखते हैं, तो यह इकाई लंबाई का चतुर्भुज है। | ||
अंततः, | अंततः, चूँकि R<sup>3</sup>,P<sup>3</sup>(R) नहीं है, इसलिए इनमें से प्रत्येक दृष्टिकोण के साथ समस्या होती है। कुछ विषय में, हमें यह याद रखने की आवश्यकता है कि कुछ पैरामीटर मानों का परिणाम समान घूर्णन होता है, और इस समस्या को दूर करने के लिए, सीमाएं स्थापित की जानी चाहिए, किन्तु फिर R<sup>3</sup> में इस क्षेत्र के माध्यम से पथ को पार करते समय अचानक अलग क्षेत्र में जाना चाहिए I सीमा. जिम्बल लॉक समस्या है, जब मानचित्र का व्युत्पन्न पूर्ण रैंक नहीं होता है, जो यूलर कोण और टैट-ब्रायन कोण के साथ होता है, किन्तु अन्य विकल्पों के लिए नहीं हैं। चतुर्भुज प्रतिनिधित्व में इनमें से कोई भी समस्या नहीं है (प्रत्येक स्थान दो-से-एक मैपिंग होने के साथ), किन्तु इसमें नियम (इकाई लंबाई) के साथ 4 पैरामीटर हैं, जो कभी-कभी उपलब्ध स्वतंत्रता की तीन डिग्री को देखना कठिन बना देता है। | ||
===अनुप्रयोग=== | ===अनुप्रयोग=== | ||
एक क्षेत्र जिसमें ये विचार, किसी न किसी रूप में, अपरिहार्य हो जाते हैं, | एक क्षेत्र जिसमें ये विचार, किसी न किसी रूप में, अपरिहार्य हो जाते हैं, कठोर बॉडी की [[गतिकी]] है। पहचान (प्रारंभिक स्थिति) से प्रारम्भ करके, त्रि-आयामी यूक्लिडियन समतल के [[यूक्लिडियन समूह]] ''E''(3) में [[वक्र]] के विचार को परिभाषा के रूप में लिया जा सकता है। E(3) का अनुवाद उपसमूह T [[सामान्य उपसमूह]] है, भागफल SO(3) के साथ यदि हम उपसमूह यूक्लिडियन समूह प्रत्यक्ष और अप्रत्यक्ष आइसोमेट्रीज़ ''E''(3) को देखें 3 यूक्लिडियन समूह केवल प्रत्यक्ष और अप्रत्यक्ष आइसोमेट्री (जो किनेमेटिक्स में उचित है) है। द्रव्यमान के केंद्र की गति और द्रव्यमान के केंद्र के सम्बन्ध में कठोर बॉडी के घूर्णन पर विचार करके मानक न्यूटोनियन किनेमेटिक्स में अनुवादात्मक भाग को घूर्णन भाग से पृथक किया जा सकता है। इसलिए, जब हम अनुवादात्मक भाग का कारक निकालते हैं, तो बॉडी की कोई भी कठोर गति सीधे SO(3) की ओर ले जाती है। | ||
ये पहचानें दर्शाती हैं कि SO(3) संयोजकता है | ये पहचानें दर्शाती हैं कि SO(3) संयोजकता है किन्तु केवल संबद्ध नहीं है। उत्तरार्द्ध के संबंध में, पहचाने गए एंटीपोडल सतह बिंदुओं वाली गेंद में, उत्तरी ध्रुव से सीधे केंद्र के माध्यम से दक्षिणी ध्रुव तक चलने वाले पथ पर विचार करें। यह संवृत लूप है, क्योंकि उत्तरी ध्रुव और दक्षिणी ध्रुव की पहचान की जाती है। इस लूप को बिंदु तक छोटा नहीं किया जा सकता है, क्योंकि इससे कोई फर्क नहीं पड़ता कि आप लूप को कैसे विकृत करते हैं, प्रारंभ और अंत बिंदु को एंटीपोडल रहना होगा, अन्यथा लूप टूट कर विवृत हो जाता है। घूर्णन के संदर्भ में, यह लूप पहचान घूर्णन पर प्रारम्भ और समाप्त होने वाले z-अक्ष के सम्बन्ध में घूर्णन के निरंतर अनुक्रम का प्रतिनिधित्व करता है (अर्थात कोण φ के माध्यम से घूर्णन की एक श्रृंखला जहां 0 से 2π तक चलता है)। | ||
आश्चर्य की बात है, यदि आप पथ पर दो बार दौड़ते हैं, | आश्चर्य की बात है, यदि आप पथ पर दो बार दौड़ते हैं, अर्थात, उत्तरी ध्रुव से नीचे दक्षिणी ध्रुव तक और वापस उत्तरी ध्रुव तक जिससे φ 0 से 4π तक चलता है, तो आपको संवृत लूप प्राप्त होता है, जिसे बिंदु तक छोटा किया जा सकता है: प्रथम पथ गेंद की सतह तक जाने वाले पथ अभी भी उत्तरी ध्रुव को दक्षिणी ध्रुव से दो बार जोड़ते हैं। पथ का दूसरा भाग पथ को परिवर्तित किये बिना एंटीपोडल पक्ष पर प्रतिबिंबित किया जा सकता है। अब हमारे पास गेंद की सतह पर साधारण संवृत लूप है, जो उत्तरी ध्रुव को बड़े वृत्त के साथ जोड़ता है। इस वृत्त को बिना किसी समस्या के उत्तरी ध्रुव तक छोटा किया जा सकता है।बालिनीज़ [[ प्लेट चाल |प्लेट ट्रिक]] और इसी प्रकार की ट्रिक्स इसे व्यावहारिक रूप से प्रदर्शित करती हैं। | ||
समान तर्क सामान्य रूप से किया जा सकता है, और यह दर्शाता है कि SO(3) का मूल समूह क्रम 2 का [[चक्रीय समूह]] है। भौतिकी अनुप्रयोगों में, मूल समूह की गैर-तुच्छता [[स्पिनर]] | समान तर्क सामान्य रूप से किया जा सकता है, और यह दर्शाता है कि SO(3) का मूल समूह क्रम 2 का [[चक्रीय समूह]] है। भौतिकी अनुप्रयोगों में, मूल समूह की गैर-तुच्छता [[स्पिनर|स्पिनर्स]] के रूप में ज्ञात वस्तुओं के अस्तित्व की अनुमति प्रदान करती है, और स्पिन-सांख्यिकी प्रमेय के विकास में महत्वपूर्ण उपकरण है। | ||
SO(3) का | SO(3) का सार्वभौमिक आवरण [[स्पिनर समूह|स्पिनर]] (3) नामक लाई समूह है। समूह स्पिन(3) [[विशेष एकात्मक समूह]] SU(2) का समरूपी है; यह इकाई 3-परवलय 'S<sup>3</sup>' से भी भिन्न है, और इसे चतुर्भुज के समूह के रूप में समझा जा सकता है (अर्थात जिनका पूर्ण मान 1 है)। चतुर्भुज और घूर्णन के मध्य संबंध, जो सामान्यतः [[ कंप्यूटर चित्रलेख |कंप्यूटर ग्राफिक्स]] में उपयोग किया जाता है, चतुर्भुज और स्थानिक घुमावों में समझाया गया है। S<sup>3</sup> से SO(3) तक का चित्र जो S<sup>3</sup> के एंटीपोडल बिंदुओं की पहचान करता है I [[कर्नेल (बीजगणित)]] {±1} के साथ, लाई समूहों का [[विशेषण]] [[समरूपता]] है। स्थलाकृतिक दृष्टि से, यह मानचित्र दो-से-एक कवर करने वाला मानचित्र है। | ||
==यह भी देखें== | ==यह भी देखें== | ||
| Line 91: | Line 91: | ||
[[Category: Machine Translated Page]] | [[Category: Machine Translated Page]] | ||
[[Category:Created On 17/11/2023]] | [[Category:Created On 17/11/2023]] | ||
[[Category:Vigyan Ready]] | |||
Latest revision as of 09:38, 1 December 2023
गणित में, तीन आयामों में विशेष ऑर्थोगोनल समूह, जिसे घूर्णन समूह SO(3) के रूप में जाना जाता है, मैनिफोल्ड का स्वाभाविक रूप से घटित होने वाला उदाहरण है। SO(3) पर विभिन्न चार्ट (टोपोलॉजी) प्रतिद्वंद्वी समन्वय प्रणाली स्थापित करते हैं: इस विषय में घूर्णन का वर्णन करने वाले मान का मुख्य रूप से समुच्चय नहीं कहा जा सकता है। स्वतंत्रता की तीन डिग्री (भौतिकी और रसायन विज्ञान) हैं, जिससे SO(3) का आयाम तीन हो जाये। कई अनुप्रयोगों में एक या अन्य समन्वय प्रणाली का उपयोग किया जाता है, और प्रश्न उठता है कि किसी दिए गए प्रणाली से दूसरे प्रणाली में कैसे परिवर्तित किया जाए।
घूर्णन का स्थान
ज्यामिति में घूर्णन समूह त्रि-आयामी यूक्लिडियन अंतराल R3 की उत्पत्ति के बारे में सभी घुमावों का समूह (गणित) है I[1] परिभाषा के अनुसार, मूल के चारों ओर घूमना रैखिक परिवर्तन है, जो सदिश (ज्यामिति) की लंबाई को संरक्षित करता है (यह आइसोमेट्री है) और अंतराल के अभिविन्यास (गणित) (अर्थात हैंडनेस) को संरक्षित करता है। लंबाई-संरक्षण परिवर्तन जो अभिविन्यास को विपरीत कर देता है, उसे अनुचित घूर्णन कहा जाता है। त्रि-आयामी यूक्लिडियन अंतराल का प्रत्येक अनुचित घूर्णन एक घूर्णन है, जिसके पश्चात् मूल के माध्यम से सतह में प्रतिबिंब (गणित) होता है।
दो घूर्णनों को संयोजित करने से दूसरा घूर्णन उत्पन्न होता है; प्रत्येक घूर्णन में अद्वितीय व्युत्क्रम घूर्णन होता है; और पहचान मानचित्र घूर्णन की परिभाषा को संतुष्ट करता है। उपरोक्त गुणों के कारण, सभी घुमावों का समुच्चय संरचना के अंतर्गत समूह (गणित) है। इसके अतिरिक्त, घूर्णन समूह में प्राकृतिक मैनिफोल्ड संरचना होती है, जिसके लिए समूह संचालन सुचारू होता है, तो यह वास्तव में लाई समूह है। ऑर्थोगोनल और घूर्णन मैट्रिसेस बताए गए कारणों से घूर्णन समूह को प्रायः SO(3) के रूप में दर्शाया जाता है।
घूर्णन का स्थान घूर्णन ऑपरेटर (सदिश स्थान) के समुच्चय और निर्धारक +1 के साथ ऑर्थोनॉर्मल आव्यूह के समुच्चय के साथ आइसोमोर्फिक है। यह उनके आंतरिक उत्पाद के साथ चतुर्भुज के समुच्चय के साथ-साथ घूर्णन सदिश के समुच्चय के साथ भी निकटता से संबंधित है, (चूँकि यहां संबंध का वर्णन करना कठिन है, विवरण के लिए नीचे देखें) अलग आंतरिक संरचना ऑपरेशन के साथ उनके समकक्ष आव्यूह के उत्पाद द्वारा दिया गया है।
घूर्णन सदिश संकेतन यूलर के घूर्णन प्रमेय से उत्पन्न होता है, जिसमें कहा गया है कि तीन आयामों में किसी भी घूर्णन को किसी अक्ष के चारों ओर किसी कोण और घूर्णन द्वारा वर्णित किया जा सकता है। इसे ध्यान में रखते हुए, हम इनमें से किसी घूर्णन की धुरी को दो कोणों द्वारा निर्दिष्ट कर सकते हैं, और हम घूर्णन के कोण को निर्दिष्ट करने के लिए सदिश की त्रिज्या का उपयोग कर सकते हैं। ये सदिश असामान्य टोपोलॉजी के साथ 3डी में गेंद (गणित) का प्रतिनिधित्व करते हैं।
यह 3डी ठोस गोला 4डी डिस्क की सतह के बराबर है, जो एक 3डी प्रकार भी है। इस तुल्यता को करने के लिए, हमें यह परिभाषित करना होगा कि हम इस 4D-एम्बेडेड सतह के साथ घूर्णन का प्रतिनिधित्व कैसे करेंगे।
घूर्णन का अतिपरवलय
अतिपरवलय की कल्पना करना
समतल को त्रि-आयामी क्षेत्र S3,4-आयामी यूक्लिडियन समतल में डिस्क की सीमा रूप में मानना रूचिपूर्ण है। ऐसा करने के लिए, हमें यह परिभाषित करना होगा कि हम इस 4डी-एम्बेडेड सतह के साथ घूर्णन का प्रतिनिधित्व कैसे करते हैं।
घूर्णन के कोण को निर्दिष्ट करने के लिए त्रिज्या का उपयोग करने का उपाय सीधा नहीं है। इसे परिभाषित उत्तरी ध्रुव वाले क्षेत्र में अक्षांश के वृत्तों से संबंधित किया जा सकता है और इसे इस प्रकार समझाया गया है:
त्रि-आयामी समतल में गोले के उत्तरी ध्रुव से प्रारम्भ करके, हम पहचान घूर्णन का प्रतिनिधित्व करने के लिए उत्तरी ध्रुव पर बिंदु निर्दिष्ट करते हैं। पहचान घूर्णन के विषय में, घूर्णन की कोई धुरी परिभाषित नहीं है, और घूर्णन का कोण (शून्य) अप्रासंगिक है। xy-तल में निहित अपनी धुरी और बहुत छोटे घूर्णन कोण के साथ घूर्णन को xy-तल के समानांतर और उत्तरी ध्रुव के बहुत निकट गोले के माध्यम से स्लाइस द्वारा निर्दिष्ट किया जा सकता है। इस स्लाइस द्वारा परिभाषित वृत्त घूर्णन के छोटे कोण के अनुरूप बहुत छोटा होगा। जैसे-जैसे घूर्णन कोण बड़े होते जाते हैं, टुकड़ा दक्षिण की ओर बढ़ता जाता है, और गोले के भूमध्य रेखा तक पहुंचने पर वृत्त बड़े होते जाते हैं, जो 180 डिग्री के घूर्णन कोण के अनुरूप होगा। दक्षिण की ओर बढ़ते हुए, वृत्तों की त्रिज्याएँ अब छोटी हो गई हैं (घूर्णन के कोण के निरपेक्ष मान के अनुरूप जिसे ऋणात्मक संख्या माना जाता है)। अंत में, जैसे ही दक्षिणी ध्रुव पर पहुँचते हैं, वृत्त एक बार फिर पहचान घुमाव में सिकुड़ जाते हैं, जिसे दक्षिणी ध्रुव पर बिंदु के रूप में भी निर्दिष्ट किया जाता है। ध्यान दें कि इस कल्पना द्वारा ऐसे घुमावों की कई विशेषताओं और उनके प्रतिनिधित्व को देखा जा सकता है।
घूर्णन का स्थान निरंतर होता है, प्रत्येक घूर्णन में घूर्णन का प्रतिवेश होता है जो लगभग समान होता है, और प्रतिवेश के सिकुड़ने पर यह समतल हो जाता है।
उपनाम
इसके अतिरिक्त, प्रत्येक घुमाव को वास्तव में गोले पर दो एंटीपोडल बिंदुओं द्वारा दर्शाया जाता है, जो गोले के केंद्र के माध्यम से रेखा के विपरीत शीर्ष पर होते हैं। यह इस तथ्य को दर्शाता है कि प्रत्येक घूर्णन को किसी अक्ष के चारों ओर घूर्णन के रूप में दर्शाया जा सकता है, या, समकक्ष, विपरीत दिशा में इंगित करने वाले अक्ष के बारे में नकारात्मक घूर्णन के रूप में (तथाकथित डबल कवरिंग समूह) के रूप में दर्शाया जा सकता है। किसी विशेष घूर्णन कोण का प्रतिनिधित्व करने वाले वृत्त का अक्षांश उस घूर्णन द्वारा दर्शाए गए कोण का आधा होगा, क्योंकि जैसे ही बिंदु उत्तर से दक्षिण ध्रुव की ओर जाता है, अक्षांश शून्य से 180 डिग्री तक होता है, जबकि घूर्णन का कोण 0 से 360 डिग्री तक होता है। (तब बिंदु का "देशांतर" घूर्णन की विशेष धुरी का प्रतिनिधित्व करता है।) चूँकि ध्यान दें कि घुमावों का यह सेट संरचना के अंतर्गत संवृत नहीं है।
xy-तल में अक्षों के साथ दो क्रमिक घूर्णन आवश्यक रूप से ऐसा घूर्णन नहीं देंगे जिसकी धुरी xy-तल में स्थित हो, और इस प्रकार इसे गोले पर बिंदु के रूप में दर्शाया नहीं जा सकता है। 3-स्पेस में सामान्य घूर्णन के विषय में ऐसा नहीं होगा, जो संरचना के अंतर्गत संवृत समुच्चय बनाते हैं।
इस कल्पना को 3-आयामी समतल में सामान्य घुमाव तक बढ़ाया जा सकता है। पहचान घूर्णन बिंदु है, और कुछ अक्ष के सम्बन्ध में घूर्णन के छोटे कोण को छोटे त्रिज्या वाले गोले पर बिंदु के रूप में दर्शाया जा सकता है। जैसे-जैसे घूर्णन का कोण बढ़ता है, गोला तब तक बढ़ता है, जब तक कि घूर्णन का कोण 180 डिग्री तक नहीं पहुंच जाता, जिस बिंदु पर गोला सिकुड़ना प्रारम्भ हो जाता है, और कोण 360 डिग्री (या नकारात्मक दिशा से शून्य डिग्री) तक पहुंचने पर बिंदु बन जाता है। फैलते और सिकुड़ते गोले का यह समुच्चय चार-आयामी समतल (3-परवलय) में 3-परवलय अतिपरवलय का प्रतिनिधित्व करता है।
जैसा कि ऊपर दिए गए सरल उदाहरण में है, अतिपरवलय पर बिंदु के रूप में दर्शाया गया प्रत्येक घुमाव उस अतिपरवलय पर उसके एंटीपोडल बिंदु से मैच करता है। अतिपरवलय पर अक्षांश घूर्णन के संबंधित कोण का आधा होगा, और प्रतिवेश सिकुड़ने पर किसी भी बिंदु का प्रतिवेश चपटा हो जाएगा (अर्थात बिंदुओं के 3 डी यूक्लिडियन स्थान द्वारा दर्शाया जाएगा)।
यह व्यवहार इकाई चतुर्भुज के समुच्चय से मैच करता है: एक सामान्य चतुर्भुज चार-आयामी समतल में बिंदु का प्रतिनिधित्व करता है, किन्तु इसे इकाई परिमाण में सीमित करने से अतिपरवलय की सतह के बराबर त्रि-आयामी स्थान प्राप्त होता है। इकाई चतुर्भुज का परिमाण इकाई त्रिज्या के अतिपरवलय के अनुरूप इकाई होता है।
इकाई चतुर्भुज का सदिश भाग घूर्णन अक्ष के अनुरूप 2-परवलय की त्रिज्या का प्रतिनिधित्व करता है, और इसका परिमाण घूर्णन के आधे कोण की ज्या है। प्रत्येक घूर्णन को विपरीत चिह्न के दो इकाई चतुर्भुजों द्वारा दर्शाया जाता है, और, जैसा कि तीन आयामों में घूर्णन के स्थान में होता है, दो इकाई चतुर्भुजों का चतुर्भुज उत्पाद इकाई चतुर्भुज का उत्पादन करता है। साथ ही, किसी दिए गए इकाई चतुर्भुज के किसी भी अतिसूक्ष्म प्रतिवेश में इकाई चतुर्भुज का स्थान समतल होता है।
पैरामीट्रिज़ेशन
हम घूर्णन के स्थान को कई प्रकार से मानकीकृत कर सकते हैं, किन्तु अध:पतन सदैव दिखाई देता है। उदाहरण के लिए, यदि हम तीन कोणों (यूलर कोण) का उपयोग करते हैं, तो अतिपरवलय पर कुछ बिंदुओं पर इस प्रकार का पैरामीटर अव्यवस्थित हो जाता है, जिससे जिम्बल लॉक की समस्या उत्पन्न हो जाती है। हम w के साथ चार यूक्लिडियन निर्देशांक w,x,y,z का उपयोग करके w2 + x2 + y2 + z2 = 1 के साथ इससे बच सकते हैं I बिंदु (w,x,y,z) कोण द्वारा सदिश (x,y,z) द्वारा निर्देशित अक्ष के चारों ओर एक घूर्णन का प्रतिनिधित्व करता है:-
यह समस्या अक्षांश और देशांतर जैसे दो निर्देशांकों के साथ गोले की द्विआयामी सतह को पैरामीटराइज़ करने के समान है। उत्तरी और दक्षिणी ध्रुवों पर अक्षांश और देशांतर अव्यवस्थित व्यवहार (अपक्षयी) हैं, चूँकि ध्रुव गोले पर किसी भी अन्य बिंदु से आंतरिक रूप से भिन्न नहीं हैं। ध्रुवों (अक्षांश +90° और −90°) पर, देशांतर अर्थहीन हो जाता है। यह दर्शाया जा सकता है कि कोई भी दो-पैरामीटर समन्वय प्रणाली ऐसी विकृति से बच नहीं सकती है।
संभावित पैरामीट्रिज़ेशन कैंडिडेट में सम्मिलित हैं:
- यूलर कोण (θ,φ,ψ), x, y और z अक्षों के सम्बन्ध में घूर्णन के उत्पाद का प्रतिनिधित्व करते हैं;
- टाइट-ब्रायन कोण (θ,φ,ψ), x, y और z अक्षों के सम्बन्ध में घूर्णन के उत्पाद का प्रतिनिधित्व करते हैं;
- अक्ष का प्रतिनिधित्व करने वाले इकाई सदिश का अक्ष कोण युग्म ('n', θ), और इसके चारों ओर घूर्णन का कोण हैं;
- लंबाई 1 का चतुर्भुज 'q' (cf. वर्सर, चतुर्भुज और स्थानिक घूर्णन, 3-गोलाकार), जिसके घटकों को यूलर-रोड्रिग्स पैरामीटर भी कहा जाता है;
- 3 × 3 तिरछा-सममित आव्यूह, घातांक के माध्यम से; 3 × 3 तिरछा-सममित आव्यूह लाई बीजगणित SO(3) हैं, और यह लाई सिद्धांत में घातीय मानचित्र है;
- केली तर्कसंगत पैरामीटर, केली परिवर्तन पर आधारित, सभी विशेषताओं में प्रयोग योग्य है;
- मोबियस परिवर्तन, रीमैन क्षेत्र पर कार्य करना है।
पैरामीट्रिज़ेशन की समस्याएँ
इनकी बहु-मूल्यवान प्रकृति और विलक्षणताओं के कारण इन्हें स्थानीय चार्ट से अधिक उपयोग करने में समस्याएँ होती हैं। अर्थात्, चार्ट (टोपोलॉजी) की परिभाषा में केवल भिन्नता के साथ काम करने के लिए सबसे ऊपर सावधान रहना चाहिए। इस प्रकार की समस्याएँ अपरिहार्य हैं, क्योंकि SO(3) वास्तविक प्रक्षेप्य स्थान P3(R) से भिन्न है, जो एंटीपोडल बिंदुओं की पहचान करके S3 का एक भागफल है, और चार्ट R3 का उपयोग करके मैनिफोल्ड को मॉडल करने का प्रयास करते हैं।
यह बताता है कि, उदाहरण के लिए, यूलर कोण 3-टोरस्र्स में चर और 3-गोले में इकाई चतुर्भुज क्यों देते प्रतीत होते हैं। यूलर कोणों द्वारा प्रतिनिधित्व की विशिष्टता कुछ बिंदुओं पर टूट जाती है (सीएफ. जिम्बल लॉक), किन्तु क्वाटरनियन प्रतिनिधित्व सदैव डबल कवरिंग समूह होता है, जिसमें q और −q समान घूर्णन देते हैं।
यदि हम तिरछा-सममित आव्यूह का उपयोग करते हैं, तो प्रत्येक 3 × 3 तिरछा-सममित आव्यूह 3 मानो द्वारा निर्धारित किया जाता है, और इसलिए प्रथम दृश्य में, पैरामीटर स्थान R3 है I आव्यूह घातांक ऐसे आव्यूह का परिणाम निर्धारक 1 के ऑर्थोगोनल 3 × 3 आव्यूह में होता है - दूसरे शब्दों में, घूर्णन आव्यूह, किन्तु यह कई-से-एक मानचित्र है। ध्यान दें कि यह कवरिंग मानचित्र नहीं है - किन्तु यह मूल के निकट स्थानीय होमोमोर्फिज्म है, यह 180 डिग्री तक घूमने वाला कवरिंग मैप नहीं है। इन आव्यूह को R3 में मूल के चारों ओर गेंद तक सीमित करना संभव है, जिससे घूर्णन 180 डिग्री से अधिक न हो, और यह एक-से-एक होगा, 180 डिग्री के घूर्णन को त्यागकर, जो सीमा S2 के अनुरूप है, और ये एंटीपोडल बिंदुओं की पहचान करते हैं - यह कट लोकस (रीमैनियन मैनिफोल्ड) है। सीमा की इस पहचान के साथ 3-गेंद P3(R) है I समान स्थिति में तिरछा-सममित आव्यूह में केली परिवर्तन को प्रारम्भ करने के लिए होती है।
अक्ष कोण S2 × S1 में पैरामीटर देता है, यदि हम इकाई सदिश को घूर्णन के वास्तविक अक्ष से प्रतिस्थापित करते हैं, जिससे n और −n ही अक्ष रेखा दें, तो अक्ष का सेट वास्तविक प्रक्षेप्य तल P2(R) बन जाता है। । किन्तु चूँकि n और −n के चारों ओर घूमने को θ के विपरीत मानों द्वारा मानकीकृत किया जाता है, परिणाम P2(R), पर S1 बंडल है, जो P3(R) बन जाता है।
आंशिक रैखिक परिवर्तन चार जटिल मानो, a, b, c और d का उपयोग करते हैं, इस नियम के साथ कि ad−bc गैर-शून्य है। चूँकि सभी चार मानो को एक ही जटिल संख्या से गुणा करने पर पैरामीटर नहीं परिवर्तित करता है, हम इस बात पर जोर दे सकते हैं कि ad−bc=1। यह (a,b,c,d) को निर्धारक 1 के 2 × 2 जटिल आव्यूह के रूप में लिखने का सुझाव देता है, अर्थात, विशेष रैखिक समूह SL(2,C) के तत्व के रूप में है। किन्तु ऐसे सभी मैट्रिक्स घूर्णन उत्पन्न नहीं करते: S2 पर अनुरूप मानचित्र भी सम्मिलित हैं। केवल घूर्णन प्राप्त करने के लिए हम इस बात पर जोर देते हैं कि d, a का सम्मिश्र संयुग्म है, और c, b के सम्मिश्र संयुग्म का ऋणात्मक है। फिर हमारे पास दो सम्मिश्र संख्याएँ, a और b हैं, जो |a|2+|b|2=1 के अधीन हैं। यदि हम a+bj लिखते हैं, तो यह इकाई लंबाई का चतुर्भुज है।
अंततः, चूँकि R3,P3(R) नहीं है, इसलिए इनमें से प्रत्येक दृष्टिकोण के साथ समस्या होती है। कुछ विषय में, हमें यह याद रखने की आवश्यकता है कि कुछ पैरामीटर मानों का परिणाम समान घूर्णन होता है, और इस समस्या को दूर करने के लिए, सीमाएं स्थापित की जानी चाहिए, किन्तु फिर R3 में इस क्षेत्र के माध्यम से पथ को पार करते समय अचानक अलग क्षेत्र में जाना चाहिए I सीमा. जिम्बल लॉक समस्या है, जब मानचित्र का व्युत्पन्न पूर्ण रैंक नहीं होता है, जो यूलर कोण और टैट-ब्रायन कोण के साथ होता है, किन्तु अन्य विकल्पों के लिए नहीं हैं। चतुर्भुज प्रतिनिधित्व में इनमें से कोई भी समस्या नहीं है (प्रत्येक स्थान दो-से-एक मैपिंग होने के साथ), किन्तु इसमें नियम (इकाई लंबाई) के साथ 4 पैरामीटर हैं, जो कभी-कभी उपलब्ध स्वतंत्रता की तीन डिग्री को देखना कठिन बना देता है।
अनुप्रयोग
एक क्षेत्र जिसमें ये विचार, किसी न किसी रूप में, अपरिहार्य हो जाते हैं, कठोर बॉडी की गतिकी है। पहचान (प्रारंभिक स्थिति) से प्रारम्भ करके, त्रि-आयामी यूक्लिडियन समतल के यूक्लिडियन समूह E(3) में वक्र के विचार को परिभाषा के रूप में लिया जा सकता है। E(3) का अनुवाद उपसमूह T सामान्य उपसमूह है, भागफल SO(3) के साथ यदि हम उपसमूह यूक्लिडियन समूह प्रत्यक्ष और अप्रत्यक्ष आइसोमेट्रीज़ E(3) को देखें 3 यूक्लिडियन समूह केवल प्रत्यक्ष और अप्रत्यक्ष आइसोमेट्री (जो किनेमेटिक्स में उचित है) है। द्रव्यमान के केंद्र की गति और द्रव्यमान के केंद्र के सम्बन्ध में कठोर बॉडी के घूर्णन पर विचार करके मानक न्यूटोनियन किनेमेटिक्स में अनुवादात्मक भाग को घूर्णन भाग से पृथक किया जा सकता है। इसलिए, जब हम अनुवादात्मक भाग का कारक निकालते हैं, तो बॉडी की कोई भी कठोर गति सीधे SO(3) की ओर ले जाती है।
ये पहचानें दर्शाती हैं कि SO(3) संयोजकता है किन्तु केवल संबद्ध नहीं है। उत्तरार्द्ध के संबंध में, पहचाने गए एंटीपोडल सतह बिंदुओं वाली गेंद में, उत्तरी ध्रुव से सीधे केंद्र के माध्यम से दक्षिणी ध्रुव तक चलने वाले पथ पर विचार करें। यह संवृत लूप है, क्योंकि उत्तरी ध्रुव और दक्षिणी ध्रुव की पहचान की जाती है। इस लूप को बिंदु तक छोटा नहीं किया जा सकता है, क्योंकि इससे कोई फर्क नहीं पड़ता कि आप लूप को कैसे विकृत करते हैं, प्रारंभ और अंत बिंदु को एंटीपोडल रहना होगा, अन्यथा लूप टूट कर विवृत हो जाता है। घूर्णन के संदर्भ में, यह लूप पहचान घूर्णन पर प्रारम्भ और समाप्त होने वाले z-अक्ष के सम्बन्ध में घूर्णन के निरंतर अनुक्रम का प्रतिनिधित्व करता है (अर्थात कोण φ के माध्यम से घूर्णन की एक श्रृंखला जहां 0 से 2π तक चलता है)।
आश्चर्य की बात है, यदि आप पथ पर दो बार दौड़ते हैं, अर्थात, उत्तरी ध्रुव से नीचे दक्षिणी ध्रुव तक और वापस उत्तरी ध्रुव तक जिससे φ 0 से 4π तक चलता है, तो आपको संवृत लूप प्राप्त होता है, जिसे बिंदु तक छोटा किया जा सकता है: प्रथम पथ गेंद की सतह तक जाने वाले पथ अभी भी उत्तरी ध्रुव को दक्षिणी ध्रुव से दो बार जोड़ते हैं। पथ का दूसरा भाग पथ को परिवर्तित किये बिना एंटीपोडल पक्ष पर प्रतिबिंबित किया जा सकता है। अब हमारे पास गेंद की सतह पर साधारण संवृत लूप है, जो उत्तरी ध्रुव को बड़े वृत्त के साथ जोड़ता है। इस वृत्त को बिना किसी समस्या के उत्तरी ध्रुव तक छोटा किया जा सकता है।बालिनीज़ प्लेट ट्रिक और इसी प्रकार की ट्रिक्स इसे व्यावहारिक रूप से प्रदर्शित करती हैं।
समान तर्क सामान्य रूप से किया जा सकता है, और यह दर्शाता है कि SO(3) का मूल समूह क्रम 2 का चक्रीय समूह है। भौतिकी अनुप्रयोगों में, मूल समूह की गैर-तुच्छता स्पिनर्स के रूप में ज्ञात वस्तुओं के अस्तित्व की अनुमति प्रदान करती है, और स्पिन-सांख्यिकी प्रमेय के विकास में महत्वपूर्ण उपकरण है।
SO(3) का सार्वभौमिक आवरण स्पिनर (3) नामक लाई समूह है। समूह स्पिन(3) विशेष एकात्मक समूह SU(2) का समरूपी है; यह इकाई 3-परवलय 'S3' से भी भिन्न है, और इसे चतुर्भुज के समूह के रूप में समझा जा सकता है (अर्थात जिनका पूर्ण मान 1 है)। चतुर्भुज और घूर्णन के मध्य संबंध, जो सामान्यतः कंप्यूटर ग्राफिक्स में उपयोग किया जाता है, चतुर्भुज और स्थानिक घुमावों में समझाया गया है। S3 से SO(3) तक का चित्र जो S3 के एंटीपोडल बिंदुओं की पहचान करता है I कर्नेल (बीजगणित) {±1} के साथ, लाई समूहों का विशेषण समरूपता है। स्थलाकृतिक दृष्टि से, यह मानचित्र दो-से-एक कवर करने वाला मानचित्र है।
यह भी देखें
- एटलस (टोपोलॉजी) – Set of charts that describes a manifold
- घूर्णन (गणित) – Motion of a certain space that preserves at least one point
- तीन आयामों में घूर्णन औपचारिकताएँ – Ways to represent 3D rotations
संदर्भ
- ↑ Jacobson (2009), p. 34, Ex. 14.