सिंपलेक्टिक मैनिफ़ोल्ड: Difference between revisions
(Created page with "{{Short description|Type of manifold in differential geometry}} {{Use American English|date = March 2019}} विभेदक ज्यामिति में, गण...") |
No edit summary |
||
| Line 1: | Line 1: | ||
[[ विभेदक ज्यामिति | विभेदक ज्यामिति]] में, गणित का विषय, सिम्प्लेक्टिक मैनिफोल्ड डिफरेंशियल मैनिफोल्ड#परिभाषा है, <math> M </math>, बंद और सटीक अंतर रूपों से सुसज्जित गैर-अपक्षयी रूप [[विभेदक रूप]] | अंतर 2-रूप <math> \omega </math>, सिंपलेक्टिक फॉर्म कहा जाता है। सिंपलेक्टिक मैनिफोल्ड्स के अध्ययन को [[सिंपलेक्टिक ज्यामिति]] या [[सिंपलेक्टिक टोपोलॉजी]] कहा जाता है। सिंपलेक्टिक मैनिफोल्ड्स [[शास्त्रीय यांत्रिकी]] और [[विश्लेषणात्मक यांत्रिकी]] के अमूर्त फॉर्मूलेशन में मैनिफोल्ड्स के [[कोटैंजेंट बंडल]]ों के रूप में स्वाभाविक रूप से उत्पन्न होते हैं। उदाहरण के लिए, शास्त्रीय यांत्रिकी के [[हैमिल्टनियन यांत्रिकी]] में, जो क्षेत्र के लिए प्रमुख प्रेरणाओं में से प्रदान करता है, प्रणाली के सभी संभावित विन्यासों के सेट को कई गुना के रूप में तैयार किया जाता है, और यह कई गुना कोटैंजेंट बंडल सिस्टम के [[चरण स्थान]] का वर्णन करता है। | |||
[[ विभेदक ज्यामिति ]] में, गणित का | |||
== प्रेरणा == | == प्रेरणा == | ||
शास्त्रीय यांत्रिकी से सिंपलेक्टिक मैनिफ़ोल्ड उत्पन्न होते हैं; विशेष रूप से, वे | शास्त्रीय यांत्रिकी से सिंपलेक्टिक मैनिफ़ोल्ड उत्पन्न होते हैं; विशेष रूप से, वे बंद प्रणाली के चरण स्थान का सामान्यीकरण हैं।<ref name="Webster">{{cite web |first=Ben |last=Webster |title=What is a symplectic manifold, really? |date=9 January 2012 |url=https://sbseminar.wordpress.com/2012/01/09/what-is-a-symplectic-manifold-really/ }}</ref> उसी तरह से [[हैमिल्टन समीकरण]] किसी को [[अंतर समीकरण]]ों के सेट से सिस्टम के समय के विकास को प्राप्त करने की अनुमति देते हैं, सहानुभूतिपूर्ण रूप से किसी को हैमिल्टनियन फ़ंक्शन एच के अंतर डीएच से सिस्टम के प्रवाह का वर्णन करने वाला वेक्टर क्षेत्र प्राप्त करने की अनुमति मिलनी चाहिए। .<ref name="Cohn">{{cite web |first=Henry |last=Cohn |title=शास्त्रीय यांत्रिकी के लिए सिंपलेक्टिक ज्यामिति प्राकृतिक सेटिंग क्यों है?|url=https://math.mit.edu/~cohn/Thoughts/symplectic.html }}</ref> इसलिए हमें रेखीय मानचित्र की आवश्यकता है {{nowrap|''TM'' → ''T''<sup>∗</sup>''M''}} स्पर्शरेखा मैनिफोल्ड टीएम से [[को[[ स्पर्शरेखा अनेक गुना ]]]] टी तक<sup>∗</sup>M, या समकक्ष, का तत्व {{nowrap|''T''<sup>∗</sup>''M'' ⊗ ''T''<sup>∗</sup>''M''}}. मान लीजिए कि ω खंड (फाइबर बंडल) को दर्शाता है {{nowrap|''T''<sup>∗</sup>''M'' ⊗ ''T''<sup>∗</sup>''M''}}, आवश्यकता यह है कि ω [[विकृत रूप]] हो | गैर-डीजेनरेट यह सुनिश्चित करता है कि प्रत्येक अंतर डीएच के लिए अद्वितीय संगत वेक्टर फ़ील्ड वी है<sub>H</sub>ऐसा है कि {{nowrap|1=''dH'' = ''ω''(''V<sub>H</sub>'', · )}}. चूँकि कोई चाहता है कि हैमिल्टनियन प्रवाह रेखाओं के साथ स्थिर रहे, तो उसे ऐसा करना चाहिए {{nowrap|1=''ω''(''V<sub>H</sub>'', ''V<sub>H</sub>'') = ''dH''(''V<sub>H</sub>'') = 0}}, जिसका अर्थ है कि ω [[वैकल्पिक रूप]] है और इसलिए 2-रूप है। अंत में, कोई यह आवश्यकता करता है कि ω को प्रवाह रेखाओं के तहत नहीं बदलना चाहिए, यानी कि वी के साथ ω का [[झूठ व्युत्पन्न]]<sub>H</sub>गायब हो जाता है. कार्टन होमोटॉपी फॉर्मूला|कार्टन के फॉर्मूला को लागू करने पर, इसका मतलब (यहाँ) है <math> \iota_X</math> [[आंतरिक उत्पाद]] है): | ||
:<math>\mathcal{L}_{V_H}(\omega) = 0\;\Leftrightarrow\;\mathrm d (\iota_{V_H} \omega) + \iota_{V_H} \mathrm d\omega= \mathrm d (\mathrm d\,H) + \mathrm d\omega(V_H) = \mathrm d\omega(V_H)=0</math> | :<math>\mathcal{L}_{V_H}(\omega) = 0\;\Leftrightarrow\;\mathrm d (\iota_{V_H} \omega) + \iota_{V_H} \mathrm d\omega= \mathrm d (\mathrm d\,H) + \mathrm d\omega(V_H) = \mathrm d\omega(V_H)=0</math> | ||
| Line 11: | Line 8: | ||
== परिभाषा == | == परिभाषा == | ||
चिकने [[ कई गुना ]] पर | चिकने [[ कई गुना |कई गुना]] पर सिम्प्लेक्टिक रूप <math> M </math> बंद गैर-पतित अंतर 2-रूप है <math> \omega </math>.<ref name="Gosson">{{cite book |first=Maurice |last=de Gosson |title=सिंपलेक्टिक ज्यामिति और क्वांटम यांत्रिकी|year=2006 |publisher=Birkhäuser Verlag |location=Basel |isbn=3-7643-7574-4 |page=10 }} | ||
</ref><ref name="Arnold">{{Cite book|first1=V. I.|last1=Arnold|first2=A. N.|last2=Varchenko|first3=S. M.|last3=Gusein-Zade|author-link1=Vladimir Arnold|author-link3=Sabir Gusein-Zade|author-link2=Alexander Varchenko|title=The Classification of Critical Points, Caustics and Wave Fronts: Singularities of Differentiable Maps, Vol 1|publisher=Birkhäuser|year=1985|isbn=0-8176-3187-9}}</ref> यहां अ-विक्षिप्त का मतलब है कि हर बिंदु के लिए <math> p \in M </math>, [[स्पर्शरेखा स्थान]] पर तिरछा-सममित युग्मन <math> T_p M </math> द्वारा परिभाषित <math> \omega </math> गैर पतित है. कहने का तात्पर्य यह है कि यदि कोई अस्तित्व में है <math> X \in T_p M </math> ऐसा है कि <math> \omega( X, Y ) = 0 </math> सभी के लिए <math> Y \in T_p M </math>, तब <math> X = 0 </math>. चूँकि विषम आयामों में, [[तिरछा-सममित मैट्रिक्स]] हमेशा एकवचन होता है, इसलिए यह आवश्यक है <math> \omega </math> अविक्षिप्त होना इसका तात्पर्य है <math> M </math> | </ref><ref name="Arnold">{{Cite book|first1=V. I.|last1=Arnold|first2=A. N.|last2=Varchenko|first3=S. M.|last3=Gusein-Zade|author-link1=Vladimir Arnold|author-link3=Sabir Gusein-Zade|author-link2=Alexander Varchenko|title=The Classification of Critical Points, Caustics and Wave Fronts: Singularities of Differentiable Maps, Vol 1|publisher=Birkhäuser|year=1985|isbn=0-8176-3187-9}}</ref> यहां अ-विक्षिप्त का मतलब है कि हर बिंदु के लिए <math> p \in M </math>, [[स्पर्शरेखा स्थान]] पर तिरछा-सममित युग्मन <math> T_p M </math> द्वारा परिभाषित <math> \omega </math> गैर पतित है. कहने का तात्पर्य यह है कि यदि कोई अस्तित्व में है <math> X \in T_p M </math> ऐसा है कि <math> \omega( X, Y ) = 0 </math> सभी के लिए <math> Y \in T_p M </math>, तब <math> X = 0 </math>. चूँकि विषम आयामों में, [[तिरछा-सममित मैट्रिक्स]] हमेशा एकवचन होता है, इसलिए यह आवश्यक है <math> \omega </math> अविक्षिप्त होना इसका तात्पर्य है <math> M </math> सम आयाम है.<ref name="Gosson"/><ref name="Arnold"/>बंद स्थिति का मतलब है कि [[बाहरी व्युत्पन्न]] <math> \omega </math> गायब हो जाता है. सिम्प्लेक्टिक मैनिफोल्ड जोड़ी है <math> (M, \omega) </math> कहाँ <math> M </math> चिकनी विविधता है और <math> \omega </math> सांकेतिक रूप है. को सिम्पलेक्सिक फॉर्म निर्दिष्ट करना <math> M </math> देना कहा जाता है <math> M </math> सिम्पलेक्सिक संरचना. | ||
== उदाहरण == | == उदाहरण == | ||
| Line 19: | Line 16: | ||
{{main|Symplectic vector space}} | {{main|Symplectic vector space}} | ||
होने देना <math>\{v_1, \ldots, v_{2n}\}</math> के लिए | होने देना <math>\{v_1, \ldots, v_{2n}\}</math> के लिए आधार बनें <math>\R^{2n}.</math> हम इस आधार पर अपने सहानुभूतिपूर्ण रूप ω को इस प्रकार परिभाषित करते हैं: | ||
:<math>\omega(v_i, v_j) = \begin{cases} 1 & j-i =n \text{ with } 1 \leqslant i \leqslant n \\ -1 & i-j =n \text{ with } 1 \leqslant j \leqslant n \\ 0 & \text{otherwise} \end{cases}</math> | :<math>\omega(v_i, v_j) = \begin{cases} 1 & j-i =n \text{ with } 1 \leqslant i \leqslant n \\ -1 & i-j =n \text{ with } 1 \leqslant j \leqslant n \\ 0 & \text{otherwise} \end{cases}</math> | ||
इस मामले में सिंपलेक्टिक रूप | इस मामले में सिंपलेक्टिक रूप सरल [[द्विघात रूप]] में कम हो जाता है। अगर मुझे<sub>n</sub>n × n पहचान मैट्रिक्स को दर्शाता है तो इस द्विघात रूप का मैट्रिक्स, Ω, द्वारा दिया जाता है {{nowrap|1=2''n'' × 2''n''}} [[ब्लॉक मैट्रिक्स]]: | ||
:<math>\Omega = \begin{pmatrix} 0 & I_n \\ -I_n & 0 \end{pmatrix}. </math> | :<math>\Omega = \begin{pmatrix} 0 & I_n \\ -I_n & 0 \end{pmatrix}. </math> | ||
=== कोटैंजेंट बंडल === | === कोटैंजेंट बंडल === | ||
होने देना <math>Q</math> आयाम की | होने देना <math>Q</math> आयाम की सहज विविधता बनें <math>n</math>. फिर कोटैंजेंट बंडल का कुल स्थान <math>T^* Q</math> इसका प्राकृतिक सहानुभूतिपूर्ण रूप है, जिसे पोंकारे दो-रूप या [[विहित सहानुभूतिपूर्ण रूप]] कहा जाता है | ||
:<math>\omega = \sum_{i=1}^n dp_i \wedge dq^i </math> | :<math>\omega = \sum_{i=1}^n dp_i \wedge dq^i </math> | ||
यहाँ <math>(q^1, \ldots, q^n)</math> क्या कोई स्थानीय निर्देशांक चालू हैं? <math>Q</math> और <math>(p_1, \ldots, p_n)</math> कोटैंजेंट वैक्टर के संबंध में फाइबरवाइज निर्देशांक हैं <math>dq^1, \ldots, dq^n</math>. कोटैंजेंट बंडल शास्त्रीय यांत्रिकी के प्राकृतिक चरण स्थान हैं। ऊपरी और निचले सूचकांकों को अलग करने का बिंदु [[मीट्रिक टेंसर]] वाले मैनिफोल्ड के मामले से प्रेरित होता है, जैसा कि [[रीमैनियन मैनिफोल्ड]]्स के मामले में होता है। ऊपरी और निचले सूचकांक समन्वय फ्रेम के परिवर्तन के तहत विपरीत और सहसंयोजक रूप से बदलते हैं। कोटैंजेंट वैक्टर के संबंध में फ़ाइबरवाइज कोऑर्डिनेट वाक्यांश का अर्थ यह बताना है कि संवेग <math>p_i</math> वेगों के सोल्डर रूप हैं <math>dq^i</math>. सोल्डरिंग इस विचार की अभिव्यक्ति है कि वेग और संवेग एकरेखीय हैं, इसमें दोनों | यहाँ <math>(q^1, \ldots, q^n)</math> क्या कोई स्थानीय निर्देशांक चालू हैं? <math>Q</math> और <math>(p_1, \ldots, p_n)</math> कोटैंजेंट वैक्टर के संबंध में फाइबरवाइज निर्देशांक हैं <math>dq^1, \ldots, dq^n</math>. कोटैंजेंट बंडल शास्त्रीय यांत्रिकी के प्राकृतिक चरण स्थान हैं। ऊपरी और निचले सूचकांकों को अलग करने का बिंदु [[मीट्रिक टेंसर]] वाले मैनिफोल्ड के मामले से प्रेरित होता है, जैसा कि [[रीमैनियन मैनिफोल्ड]]्स के मामले में होता है। ऊपरी और निचले सूचकांक समन्वय फ्रेम के परिवर्तन के तहत विपरीत और सहसंयोजक रूप से बदलते हैं। कोटैंजेंट वैक्टर के संबंध में फ़ाइबरवाइज कोऑर्डिनेट वाक्यांश का अर्थ यह बताना है कि संवेग <math>p_i</math> वेगों के सोल्डर रूप हैं <math>dq^i</math>. सोल्डरिंग इस विचार की अभिव्यक्ति है कि वेग और संवेग एकरेखीय हैं, इसमें दोनों ही दिशा में चलते हैं, और पैमाने के कारक से भिन्न होते हैं। | ||
=== काहलर मैनिफोल्ड्स === | === काहलर मैनिफोल्ड्स === | ||
काहलर मैनिफोल्ड | काहलर मैनिफोल्ड संगत एकीकृत जटिल संरचना से सुसज्जित सहानुभूतिपूर्ण मैनिफोल्ड है। वे जटिल विविधताओं का विशेष वर्ग बनाते हैं। उदाहरणों का बड़ा वर्ग जटिल [[बीजगणितीय ज्यामिति]] से आता है। कोई भी चिकनी जटिल [[प्रक्षेप्य किस्म]] <math>V \subset \mathbb{CP}^n</math> इसका सहानुभूतिपूर्ण रूप है जो फ़ुबिनी-अध्ययन मीट्रिक का प्रतिबंध है|फ़ुबिनी-[[प्रक्षेप्य स्थान]] पर अध्ययन प्रपत्र <math>\mathbb{CP}^n</math>. | ||
=== लगभग-जटिल कई गुना === | === लगभग-जटिल कई गुना === | ||
रीमैनियन | रीमैनियन के साथ कई गुना होता है <math>\omega</math>-संगत [[लगभग जटिल संरचना]] को लगभग-जटिल मैनिफोल्ड्स कहा जाता है। वे काहलर मैनिफोल्ड्स का सामान्यीकरण करते हैं, जिसमें उन्हें एकीकृत होने की आवश्यकता नहीं है। अर्थात्, वे आवश्यक रूप से अनेक गुना जटिल संरचना से उत्पन्न नहीं होते हैं। | ||
== लैग्रेंजियन और अन्य सबमेनिफोल्ड्स == | == लैग्रेंजियन और अन्य सबमेनिफोल्ड्स == | ||
सिम्प्लेक्टिक मैनिफोल्ड के [[सबमैनिफोल्ड]] की कई प्राकृतिक ज्यामितीय धारणाएँ हैं <math> (M, \omega) </math>: | सिम्प्लेक्टिक मैनिफोल्ड के [[सबमैनिफोल्ड]] की कई प्राकृतिक ज्यामितीय धारणाएँ हैं <math> (M, \omega) </math>: | ||
* के सिम्प्लेक्टिक सबमैनिफोल्ड्स <math> M </math> (संभावित रूप से किसी भी सम आयाम के) उपमानव हैं <math> S \subset M </math> ऐसा है कि <math> \omega|_S </math> पर | * के सिम्प्लेक्टिक सबमैनिफोल्ड्स <math> M </math> (संभावित रूप से किसी भी सम आयाम के) उपमानव हैं <math> S \subset M </math> ऐसा है कि <math> \omega|_S </math> पर प्रतीकात्मक रूप है <math> S </math>. | ||
* आइसोट्रोपिक सबमैनिफोल्ड्स सबमैनिफोल्ड्स हैं जहां सहानुभूति रूप शून्य तक सीमित है, यानी प्रत्येक स्पर्शरेखा स्थान परिवेश मैनिफोल्ड के स्पर्शरेखा स्थान का | * आइसोट्रोपिक सबमैनिफोल्ड्स सबमैनिफोल्ड्स हैं जहां सहानुभूति रूप शून्य तक सीमित है, यानी प्रत्येक स्पर्शरेखा स्थान परिवेश मैनिफोल्ड के स्पर्शरेखा स्थान का [[आइसोट्रोपिक उपस्थान]] है। इसी प्रकार, यदि किसी सबमैनिफोल्ड का प्रत्येक स्पर्शरेखा उप-स्थान सह-आइसोट्रोपिक (एक आइसोट्रोपिक उप-स्थान का द्वैत) है, तो सबमैनिफोल्ड को सह-आइसोट्रोपिक कहा जाता है। | ||
* सिंपलेक्टिक मैनिफोल्ड के लैग्रेंजियन सबमैनिफोल्ड्स <math>(M,\omega)</math> उपमानव हैं जहां सहानुभूति रूप का प्रतिबंध है <math>\omega</math> को <math>L\subset M</math> लुप्त हो रहा है, अर्थात <math>\omega|_L=0</math> और <math>\text{dim }L=\tfrac{1}{2}\dim M</math>. लैग्रेंजियन सबमैनिफोल्ड्स अधिकतम आइसोट्रोपिक सबमैनिफोल्ड्स हैं। | * सिंपलेक्टिक मैनिफोल्ड के लैग्रेंजियन सबमैनिफोल्ड्स <math>(M,\omega)</math> उपमानव हैं जहां सहानुभूति रूप का प्रतिबंध है <math>\omega</math> को <math>L\subset M</math> लुप्त हो रहा है, अर्थात <math>\omega|_L=0</math> और <math>\text{dim }L=\tfrac{1}{2}\dim M</math>. लैग्रेंजियन सबमैनिफोल्ड्स अधिकतम आइसोट्रोपिक सबमैनिफोल्ड्स हैं। | ||
एक प्रमुख उदाहरण यह है कि उत्पाद सिंपलेक्टिक मैनिफोल्ड में | एक प्रमुख उदाहरण यह है कि उत्पाद सिंपलेक्टिक मैनिफोल्ड में [[लक्षणरूपता]] का ग्राफ {{nowrap|1=(''M'' × ''M'', ''ω'' × −''ω'')}} लैग्रेन्जियन है। उनके चौराहे कठोरता गुणों को प्रदर्शित करते हैं जो चिकनी मैनिफोल्ड्स के पास नहीं होते हैं; [[अर्नोल्ड अनुमान]] स्मूथ केस में [[यूलर विशेषता]] के बजाय, स्मूथ लैग्रेंजियन सबमैनिफोल्ड के स्वयं प्रतिच्छेदन की संख्या के लिए निचली सीमा के रूप में सबमैनिफोल्ड की बेट्टी संख्याओं का योग देता है। | ||
=== उदाहरण === | === उदाहरण === | ||
होने देना <math>\R^{2n}_{\textbf{x},\textbf{y}}</math> वैश्विक निर्देशांक लेबल किए गए हैं <math>(x_1, \dotsc, x_n, y_1, \dotsc, y_n)</math>. फिर, हम सुसज्जित कर सकते हैं <math>\R_{\textbf{x},\textbf{y}}^{2n}</math> विहित सहानुभूतिपूर्ण रूप के साथ | होने देना <math>\R^{2n}_{\textbf{x},\textbf{y}}</math> वैश्विक निर्देशांक लेबल किए गए हैं <math>(x_1, \dotsc, x_n, y_1, \dotsc, y_n)</math>. फिर, हम सुसज्जित कर सकते हैं <math>\R_{\textbf{x},\textbf{y}}^{2n}</math> विहित सहानुभूतिपूर्ण रूप के साथ | ||
:<math>\omega =\mathrm{d}x_1\wedge \mathrm{d}y_1 + \dotsb + \mathrm{d}x_n\wedge \mathrm{d}y_n.</math> द्वारा दिया गया | :<math>\omega =\mathrm{d}x_1\wedge \mathrm{d}y_1 + \dotsb + \mathrm{d}x_n\wedge \mathrm{d}y_n.</math> द्वारा दिया गया मानक लैग्रेंजियन सबमैनिफोल्ड है <math>\R^n_{\mathbf{x}} \to \R^{2n}_{\mathbf{x},\mathbf{y}}</math>. फार्म <math>\omega</math> पर गायब हो जाता है <math>\R^n_{\mathbf{x}}</math> क्योंकि स्पर्शरेखा सदिशों का कोई जोड़ा दिया गया है <math>X= f_i(\textbf{x}) \partial_{x_i}, Y=g_i(\textbf{x})\partial_{x_i},</math> हमारे पास वह है <math>\omega(X,Y) = 0.</math> स्पष्ट करने के लिए, मामले पर विचार करें <math>n=1</math>. तब, <math>X = f(x)\partial_x, Y=g(x)\partial_x,</math> और <math>\omega = \mathrm{d}x\wedge \mathrm{d}y</math>. ध्यान दें कि जब हम इसका विस्तार करते हैं | ||
:<math>\omega(X,Y) = \omega(f(x)\partial_x,g(x)\partial_x) = \frac{1}{2}f(x)g(x)(\mathrm{d}x(\partial_x)\mathrm{d}y(\partial_x) - \mathrm{d}y(\partial_x)\mathrm{d}x(\partial_x))</math> | :<math>\omega(X,Y) = \omega(f(x)\partial_x,g(x)\partial_x) = \frac{1}{2}f(x)g(x)(\mathrm{d}x(\partial_x)\mathrm{d}y(\partial_x) - \mathrm{d}y(\partial_x)\mathrm{d}x(\partial_x))</math> | ||
| Line 57: | Line 52: | ||
====उदाहरण: कोटैंजेंट बंडल==== | ====उदाहरण: कोटैंजेंट बंडल==== | ||
मैनिफोल्ड के कोटैंजेंट बंडल को पहले उदाहरण के समान स्थान पर स्थानीय रूप से तैयार किया गया है। यह दिखाया जा सकता है कि हम इन एफ़िन सिम्प्लेक्टिक रूपों को गोंद कर सकते हैं इसलिए यह बंडल | मैनिफोल्ड के कोटैंजेंट बंडल को पहले उदाहरण के समान स्थान पर स्थानीय रूप से तैयार किया गया है। यह दिखाया जा सकता है कि हम इन एफ़िन सिम्प्लेक्टिक रूपों को गोंद कर सकते हैं इसलिए यह बंडल सिम्प्लेक्टिक मैनिफोल्ड बनाता है। लैग्रेंजियन सबमैनिफोल्ड का कम तुच्छ उदाहरण मैनिफोल्ड के कोटैंजेंट बंडल का शून्य खंड है। उदाहरण के लिए, चलो | ||
:<math>X = \{(x,y) \in \R^2 : y^2 - x = 0\}.</math> | :<math>X = \{(x,y) \in \R^2 : y^2 - x = 0\}.</math> | ||
| Line 66: | Line 61: | ||
====उदाहरण: पैरामीट्रिक सबमैनिफोल्ड ==== | ====उदाहरण: पैरामीट्रिक सबमैनिफोल्ड ==== | ||
विहित स्थान पर विचार करें <math>\R^{2n}</math> निर्देशांक के साथ <math>(q_1,\dotsc ,q_n,p_1,\dotsc ,p_n)</math>. | विहित स्थान पर विचार करें <math>\R^{2n}</math> निर्देशांक के साथ <math>(q_1,\dotsc ,q_n,p_1,\dotsc ,p_n)</math>. पैरामीट्रिक सबमैनिफोल्ड <math>L</math> का <math>\R^{2n}</math> वह है जो निर्देशांक द्वारा मानकीकृत है <math>(u_1,\dotsc,u_n)</math> ऐसा है कि | ||
:<math>q_i=q_i(u_1,\dotsc,u_n) \quad p_i=p_i(u_1,\dotsc,u_n)</math> | :<math>q_i=q_i(u_1,\dotsc,u_n) \quad p_i=p_i(u_1,\dotsc,u_n)</math> | ||
यदि [[लैग्रेंज ब्रैकेट]] है तो यह मैनिफोल्ड | यदि [[लैग्रेंज ब्रैकेट]] है तो यह मैनिफोल्ड लैग्रेंजियन सबमैनिफोल्ड है <math>[u_i,u_j]</math> सभी के लिए गायब हो जाता है <math>i,j</math>. अर्थात यह लैग्रेन्जियन है यदि | ||
:<math>[u_i,u_j]=\sum_k \frac {\partial q_k}{\partial u_i}\frac {\partial p_k}{\partial u_j} | :<math>[u_i,u_j]=\sum_k \frac {\partial q_k}{\partial u_i}\frac {\partial p_k}{\partial u_j} | ||
| Line 88: | Line 83: | ||
और अन्य सभी गायब हो रहे हैं। | और अन्य सभी गायब हो रहे हैं। | ||
जैसा कि सिंपलेक्टिक मैनिफोल्ड पर [[चार्ट (टोपोलॉजी)]] विहित रूप लेता है, यह उदाहरण बताता है कि लैग्रेंजियन सबमैनिफोल्ड अपेक्षाकृत अप्रतिबंधित हैं। सिंपलेक्टिक मैनिफ़ोल्ड्स का वर्गीकरण [[फ़्लोर होमोलॉजी]] के माध्यम से किया जाता है - यह लैग्रेंजियन सबमैनिफ़ोल्ड्स के बीच मानचित्रों के लिए एक्शन (भौतिकी) के लिए [[मोर्स सिद्धांत]] का | जैसा कि सिंपलेक्टिक मैनिफोल्ड पर [[चार्ट (टोपोलॉजी)]] विहित रूप लेता है, यह उदाहरण बताता है कि लैग्रेंजियन सबमैनिफोल्ड अपेक्षाकृत अप्रतिबंधित हैं। सिंपलेक्टिक मैनिफ़ोल्ड्स का वर्गीकरण [[फ़्लोर होमोलॉजी]] के माध्यम से किया जाता है - यह लैग्रेंजियन सबमैनिफ़ोल्ड्स के बीच मानचित्रों के लिए एक्शन (भौतिकी) के लिए [[मोर्स सिद्धांत]] का अनुप्रयोग है। भौतिकी में, क्रिया भौतिक प्रणाली के समय विकास का वर्णन करती है; यहां, इसे ब्रैन्स की गतिशीलता के विवरण के रूप में लिया जा सकता है। | ||
====उदाहरण: मोर्स सिद्धांत==== | ====उदाहरण: मोर्स सिद्धांत==== | ||
लैग्रेंजियन सबमैनिफोल्ड्स का | लैग्रेंजियन सबमैनिफोल्ड्स का अन्य उपयोगी वर्ग मोर्स सिद्धांत में पाया जाता है। [[मोर्स फ़ंक्शन]] दिया गया <math>f:M\to\R</math> और काफी छोटे के लिए <math>\varepsilon</math> कोई लुप्त हो रहे स्थान द्वारा दिए गए लैग्रेंजियन सबमैनिफोल्ड का निर्माण कर सकता है <math>\mathbb{V}(\varepsilon\cdot \mathrm{d}f) \subset T^*M</math>. सामान्य मोर्स फ़ंक्शन के लिए हमारे पास लैग्रेन्जियन प्रतिच्छेदन है जो इसके द्वारा दिया गया है <math>M \cap \mathbb{V}(\varepsilon\cdot \mathrm{d}f) = \text{Crit}(f)</math>. | ||
{{See also|symplectic category}} | {{See also|symplectic category}} | ||
=== विशेष लैग्रेंजियन सबमैनिफोल्ड्स === | === विशेष लैग्रेंजियन सबमैनिफोल्ड्स === | ||
काहलर मैनिफोल्ड्स (या कैलाबी-यॉ मैनिफोल्ड्स) के मामले में हम | काहलर मैनिफोल्ड्स (या कैलाबी-यॉ मैनिफोल्ड्स) के मामले में हम विकल्प चुन सकते हैं <math>\Omega=\Omega_1+\mathrm{i}\Omega_2</math> पर <math>M</math> होलोमोर्फिक एन-फॉर्म के रूप में, जहां <math>\Omega_1</math> असली हिस्सा है और <math>\Omega_2</math> काल्पनिक. लैग्रेंजियन सबमैनिफोल्ड <math>L</math> विशेष कहा जाता है यदि उपरोक्त लैग्रेंजियन स्थिति के अतिरिक्त प्रतिबंध हो <math>\Omega_2</math> को <math>L</math> लुप्त हो रहा है. दूसरे शब्दों में, वास्तविक भाग <math>\Omega_1</math> पर प्रतिबंधित <math>L</math> वॉल्यूम फॉर्म को आगे ले जाता है <math>L</math>. निम्नलिखित उदाहरणों को विशेष लैग्रेंजियन सबमैनिफोल्ड्स के रूप में जाना जाता है, | ||
# हाइपरकेहलर मैनिफोल्ड्स के जटिल लैग्रेंजियन सबमैनिफोल्ड्स, | # हाइपरकेहलर मैनिफोल्ड्स के जटिल लैग्रेंजियन सबमैनिफोल्ड्स, | ||
कैलाबी-याउ मैनिफोल्ड्स की वास्तविक संरचना के # निश्चित बिंदु। | कैलाबी-याउ मैनिफोल्ड्स की वास्तविक संरचना के # निश्चित बिंदु। | ||
[[एसवाईजेड अनुमान]] [[दर्पण समरूपता (स्ट्रिंग सिद्धांत)]] में विशेष लैग्रेंजियन सबमैनिफोल्ड्स के अध्ययन से संबंधित है; देखना {{harv|Hitchin|1999}}. | [[एसवाईजेड अनुमान]] [[दर्पण समरूपता (स्ट्रिंग सिद्धांत)]] में विशेष लैग्रेंजियन सबमैनिफोल्ड्स के अध्ययन से संबंधित है; देखना {{harv|Hitchin|1999}}. | ||
थॉमस-याउ अनुमान भविष्यवाणी करता है कि लैग्रैंगियंस के हैमिल्टनियन आइसोटोप वर्गों में कैलाबी-याउ मैनिफोल्ड्स पर | थॉमस-याउ अनुमान भविष्यवाणी करता है कि लैग्रैंगियंस के हैमिल्टनियन आइसोटोप वर्गों में कैलाबी-याउ मैनिफोल्ड्स पर विशेष लैग्रैन्जियन सबमैनिफोल्ड्स का अस्तित्व मैनिफोल्ड की फुकाया श्रेणी पर [[ब्रिजलैंड स्थिरता की स्थिति]] के संबंध में स्थिरता के बराबर है। | ||
== लैग्रेंजियन [[कंपन]] == | == लैग्रेंजियन [[कंपन]] == | ||
सिम्प्लेक्टिक मैनिफोल्ड ''एम'' का लैग्रेंजियन फ़िब्रेशन | सिम्प्लेक्टिक मैनिफोल्ड ''एम'' का लैग्रेंजियन फ़िब्रेशन फ़िब्रेशन है जहां सभी फ़ाइबर बंडल#औपचारिक परिभाषा लैग्रैन्जियन सबमैनिफ़ोल्ड्स हैं। चूंकि ''एम'' सम-आयामी है इसलिए हम स्थानीय निर्देशांक ले सकते हैं {{nowrap|1=(''p''<sub>1</sub>,…,''p''<sub>''n''</sub>, ''q''<sup>1</sup>,…,''q''<sup>''n''</sup>),}} और डार्बौक्स के प्रमेय द्वारा सहानुभूतिपूर्ण रूप ω को, कम से कम स्थानीय रूप से, इस प्रकार लिखा जा सकता है {{nowrap|1=''ω'' = ∑ d''p''<sub>''k''</sub> ∧ d''q''<sup>''k''</sup>}}, जहां d बाहरी व्युत्पन्न को दर्शाता है और ∧ [[बाहरी उत्पाद]] को दर्शाता है। इस फॉर्म को पोंकारे टू-फॉर्म या कैनोनिकल टू-फॉर्म कहा जाता है। इस सेट-अप का उपयोग करके हम स्थानीय रूप से एम को कोटैंजेंट बंडल के रूप में सोच सकते हैं <math>T^*\R^n,</math> और लैग्रेंजियन फ़िब्रेशन को तुच्छ फ़िब्रेशन के रूप में <math>\pi: T^*\R^n \to \R^n.</math> यह विहित चित्र है. | ||
== लैग्रेंजियन मैपिंग == | == लैग्रेंजियन मैपिंग == | ||
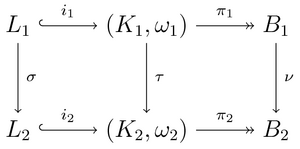
[[File:TIKZ PICT FBN.png|thumb|]]मान लीजिए कि L | [[File:TIKZ PICT FBN.png|thumb|]]मान लीजिए कि L इमर्शन (गणित) द्वारा दिए गए सिंपलेक्टिक मैनिफोल्ड (K,ω) का लैग्रेंजियन सबमैनिफोल्ड है। {{nowrap|1=''i'' : ''L'' ↪ ''K''}} (i को 'लैग्रेंजियन इमर्शन' कहा जाता है)। होने देना {{nowrap|1=''π'' : ''K'' ↠ ''B''}} K का लैग्रेंजियन फ़िब्रेशन दें। समग्र {{nowrap|1=(''π'' ∘ ''i'') : ''L'' ↪ ''K'' ↠ ''B''}} लैग्रेंजियन मैपिंग है। ''π'' ∘ ''i'' के क्रांतिक मान को [[कास्टिक (गणित)]] कहा जाता है। | ||
दो लैग्रेंजियन मानचित्र {{nowrap|1=(''π''<sub>1</sub> ∘ ''i''<sub>1</sub>) : ''L''<sub>1</sub> ↪ ''K''<sub>1</sub> ↠ ''B''<sub>1</sub>}} और {{nowrap|1=(''π''<sub>2</sub> ∘ ''i''<sub>2</sub>) : ''L''<sub>2</sub> ↪ ''K''<sub>2</sub> ↠ ''B''<sub>2</sub>}} को लैग्रेंजियन समतुल्य कहा जाता है यदि ''σ'', ''τ'' और ''ν'' [[भिन्नता]]एं मौजूद हैं जैसे कि सही [[क्रमविनिमेय आरेख]] पर दिए गए आरेख के दोनों पक्ष, और ''τ'' सहानुभूति रूप को संरक्षित करते हैं .<ref name="Arnold"/>प्रतीकात्मक रूप से: | दो लैग्रेंजियन मानचित्र {{nowrap|1=(''π''<sub>1</sub> ∘ ''i''<sub>1</sub>) : ''L''<sub>1</sub> ↪ ''K''<sub>1</sub> ↠ ''B''<sub>1</sub>}} और {{nowrap|1=(''π''<sub>2</sub> ∘ ''i''<sub>2</sub>) : ''L''<sub>2</sub> ↪ ''K''<sub>2</sub> ↠ ''B''<sub>2</sub>}} को लैग्रेंजियन समतुल्य कहा जाता है यदि ''σ'', ''τ'' और ''ν'' [[भिन्नता]]एं मौजूद हैं जैसे कि सही [[क्रमविनिमेय आरेख]] पर दिए गए आरेख के दोनों पक्ष, और ''τ'' सहानुभूति रूप को संरक्षित करते हैं .<ref name="Arnold"/>प्रतीकात्मक रूप से: | ||
| Line 114: | Line 109: | ||
== विशेष मामले और सामान्यीकरण == | == विशेष मामले और सामान्यीकरण == | ||
* एक सिंपलेक्टिक मैनिफोल्ड <math>(M, \omega)</math> यदि सिंपलेक्टिक रूप सटीक है <math>\omega</math> बंद और सटीक विभेदक रूप है। उदाहरण के लिए, | * एक सिंपलेक्टिक मैनिफोल्ड <math>(M, \omega)</math> यदि सिंपलेक्टिक रूप सटीक है <math>\omega</math> बंद और सटीक विभेदक रूप है। उदाहरण के लिए, चिकने मैनिफोल्ड का कोटैंजेंट बंडल सटीक सिंपलेक्टिक मैनिफोल्ड है। विहित सहानुभूतिपूर्ण रूप सटीक है। | ||
* एक मीट्रिक टेंसर से संपन्न | * एक मीट्रिक टेंसर से संपन्न सिंपलेक्टिक मैनिफोल्ड, जो लगभग जटिल मैनिफोल्ड है # सिंपलेक्टिक रूप के साथ संगत त्रिगुण इस अर्थ में लगभग काहलर मैनिफोल्ड है कि स्पर्शरेखा बंडल में लगभग जटिल संरचना होती है, लेकिन इसके लिए इंटीग्रेबिलिटी स्थिति की आवश्यकता नहीं होती है। | ||
* सिंपलेक्टिक मैनिफोल्ड्स [[पॉइसन मैनिफ़ोल्ड]] के विशेष मामले हैं। | * सिंपलेक्टिक मैनिफोल्ड्स [[पॉइसन मैनिफ़ोल्ड]] के विशेष मामले हैं। | ||
* डिग्री ''के'' का | * डिग्री ''के'' का मल्टीसिम्पलेक्टिक मैनिफोल्ड बंद गैर-अपक्षयी ''के''-फॉर्म से सुसज्जित मैनिफोल्ड है।<ref>{{cite journal |first1=F. |last1=Cantrijn |first2=L. A. |last2=Ibort |first3=M. |last3=de León |title=मल्टीसिम्प्लेक्टिक मैनिफोल्ड्स की ज्यामिति पर|journal=J. Austral. Math. Soc. |series=Ser. A |volume=66 |year=1999 |issue=3 |pages=303–330 |doi=10.1017/S1446788700036636 |doi-access=free }}</ref> | ||
* एक पॉलीसिम्पलेक्टिक मैनिफोल्ड | * एक पॉलीसिम्पलेक्टिक मैनिफोल्ड [[लीजेंड्रे बंडल]] है जो पॉलीसिम्पलेक्टिक स्पर्शरेखा-मूल्य के साथ प्रदान किया जाता है <math>(n+2)</math>-प्रपत्र; इसका उपयोग [[हैमिल्टनियन क्षेत्र सिद्धांत]] में किया जाता है।<ref>{{cite journal |first1=G. |last1=Giachetta |first2=L. |last2=Mangiarotti |first3=G. |last3=Sardanashvily |author-link3=Gennadi Sardanashvily |title=क्षेत्र सिद्धांत के लिए सहसंयोजक हैमिल्टनियन समीकरण|journal=Journal of Physics |volume=A32 |year=1999 |issue=38 |pages=6629–6642 |doi=10.1088/0305-4470/32/38/302 |arxiv=hep-th/9904062 |bibcode=1999JPhA...32.6629G |s2cid=204899025 }}</ref> | ||
== यह भी देखें == | == यह भी देखें == | ||
{{Portal|Mathematics}} | {{Portal|Mathematics}} | ||
| Line 158: | Line 151: | ||
* {{cite web |author-link=Dusa McDuff |last=McDuff |first=D. |url=https://www.ams.org/notices/199808/mcduff.pdf |title=Symplectic Structures—A New Approach to Geometry |work=Notices of the AMS |date=November 1998 }} | * {{cite web |author-link=Dusa McDuff |last=McDuff |first=D. |url=https://www.ams.org/notices/199808/mcduff.pdf |title=Symplectic Structures—A New Approach to Geometry |work=Notices of the AMS |date=November 1998 }} | ||
* {{cite arXiv |first1=Nigel |last1=Hitchin |year=1999 |title=Lectures on Special Lagrangian Submanifolds |eprint=math/9907034 }} | * {{cite arXiv |first1=Nigel |last1=Hitchin |year=1999 |title=Lectures on Special Lagrangian Submanifolds |eprint=math/9907034 }} | ||
{{DEFAULTSORT:Symplectic Manifold}}[[Category: विभेदक टोपोलॉजी]] [[Category: हैमिल्टनियन यांत्रिकी]] [[Category: चिकनी कई गुना]] [[Category: सिंपलेक्टिक ज्यामिति]] | {{DEFAULTSORT:Symplectic Manifold}}[[Category: विभेदक टोपोलॉजी]] [[Category: हैमिल्टनियन यांत्रिकी]] [[Category: चिकनी कई गुना]] [[Category: सिंपलेक्टिक ज्यामिति]] | ||
Revision as of 22:55, 8 July 2023
विभेदक ज्यामिति में, गणित का विषय, सिम्प्लेक्टिक मैनिफोल्ड डिफरेंशियल मैनिफोल्ड#परिभाषा है, , बंद और सटीक अंतर रूपों से सुसज्जित गैर-अपक्षयी रूप विभेदक रूप | अंतर 2-रूप , सिंपलेक्टिक फॉर्म कहा जाता है। सिंपलेक्टिक मैनिफोल्ड्स के अध्ययन को सिंपलेक्टिक ज्यामिति या सिंपलेक्टिक टोपोलॉजी कहा जाता है। सिंपलेक्टिक मैनिफोल्ड्स शास्त्रीय यांत्रिकी और विश्लेषणात्मक यांत्रिकी के अमूर्त फॉर्मूलेशन में मैनिफोल्ड्स के कोटैंजेंट बंडलों के रूप में स्वाभाविक रूप से उत्पन्न होते हैं। उदाहरण के लिए, शास्त्रीय यांत्रिकी के हैमिल्टनियन यांत्रिकी में, जो क्षेत्र के लिए प्रमुख प्रेरणाओं में से प्रदान करता है, प्रणाली के सभी संभावित विन्यासों के सेट को कई गुना के रूप में तैयार किया जाता है, और यह कई गुना कोटैंजेंट बंडल सिस्टम के चरण स्थान का वर्णन करता है।
प्रेरणा
शास्त्रीय यांत्रिकी से सिंपलेक्टिक मैनिफ़ोल्ड उत्पन्न होते हैं; विशेष रूप से, वे बंद प्रणाली के चरण स्थान का सामान्यीकरण हैं।[1] उसी तरह से हैमिल्टन समीकरण किसी को अंतर समीकरणों के सेट से सिस्टम के समय के विकास को प्राप्त करने की अनुमति देते हैं, सहानुभूतिपूर्ण रूप से किसी को हैमिल्टनियन फ़ंक्शन एच के अंतर डीएच से सिस्टम के प्रवाह का वर्णन करने वाला वेक्टर क्षेत्र प्राप्त करने की अनुमति मिलनी चाहिए। .[2] इसलिए हमें रेखीय मानचित्र की आवश्यकता है TM → T∗M स्पर्शरेखा मैनिफोल्ड टीएम से [[कोस्पर्शरेखा अनेक गुना ]] टी तक∗M, या समकक्ष, का तत्व T∗M ⊗ T∗M. मान लीजिए कि ω खंड (फाइबर बंडल) को दर्शाता है T∗M ⊗ T∗M, आवश्यकता यह है कि ω विकृत रूप हो | गैर-डीजेनरेट यह सुनिश्चित करता है कि प्रत्येक अंतर डीएच के लिए अद्वितीय संगत वेक्टर फ़ील्ड वी हैHऐसा है कि dH = ω(VH, · ). चूँकि कोई चाहता है कि हैमिल्टनियन प्रवाह रेखाओं के साथ स्थिर रहे, तो उसे ऐसा करना चाहिए ω(VH, VH) = dH(VH) = 0, जिसका अर्थ है कि ω वैकल्पिक रूप है और इसलिए 2-रूप है। अंत में, कोई यह आवश्यकता करता है कि ω को प्रवाह रेखाओं के तहत नहीं बदलना चाहिए, यानी कि वी के साथ ω का झूठ व्युत्पन्नHगायब हो जाता है. कार्टन होमोटॉपी फॉर्मूला|कार्टन के फॉर्मूला को लागू करने पर, इसका मतलब (यहाँ) है आंतरिक उत्पाद है):
ताकि, विभिन्न सुचारू कार्यों के लिए इस तर्क को दोहराया जा सके इस प्रकार कि संगत प्रत्येक बिंदु पर स्पर्शरेखा स्थान का विस्तार करें जिस पर तर्क लागू किया गया है, हम देखते हैं कि प्रवाह के साथ लुप्त होने वाले लाई व्युत्पन्न की आवश्यकता है मनमाने ढंग से चिकनी के अनुरूप इस आवश्यकता के समतुल्य है कि ω को बंद किया जाना चाहिए और सटीक अंतर रूप होना चाहिए।
परिभाषा
चिकने कई गुना पर सिम्प्लेक्टिक रूप बंद गैर-पतित अंतर 2-रूप है .[3][4] यहां अ-विक्षिप्त का मतलब है कि हर बिंदु के लिए , स्पर्शरेखा स्थान पर तिरछा-सममित युग्मन द्वारा परिभाषित गैर पतित है. कहने का तात्पर्य यह है कि यदि कोई अस्तित्व में है ऐसा है कि सभी के लिए , तब . चूँकि विषम आयामों में, तिरछा-सममित मैट्रिक्स हमेशा एकवचन होता है, इसलिए यह आवश्यक है अविक्षिप्त होना इसका तात्पर्य है सम आयाम है.[3][4]बंद स्थिति का मतलब है कि बाहरी व्युत्पन्न गायब हो जाता है. सिम्प्लेक्टिक मैनिफोल्ड जोड़ी है कहाँ चिकनी विविधता है और सांकेतिक रूप है. को सिम्पलेक्सिक फॉर्म निर्दिष्ट करना देना कहा जाता है सिम्पलेक्सिक संरचना.
उदाहरण
सिंपलेक्टिक वेक्टर रिक्त स्थान
होने देना के लिए आधार बनें हम इस आधार पर अपने सहानुभूतिपूर्ण रूप ω को इस प्रकार परिभाषित करते हैं:
इस मामले में सिंपलेक्टिक रूप सरल द्विघात रूप में कम हो जाता है। अगर मुझेnn × n पहचान मैट्रिक्स को दर्शाता है तो इस द्विघात रूप का मैट्रिक्स, Ω, द्वारा दिया जाता है 2n × 2n ब्लॉक मैट्रिक्स:
कोटैंजेंट बंडल
होने देना आयाम की सहज विविधता बनें . फिर कोटैंजेंट बंडल का कुल स्थान इसका प्राकृतिक सहानुभूतिपूर्ण रूप है, जिसे पोंकारे दो-रूप या विहित सहानुभूतिपूर्ण रूप कहा जाता है
यहाँ क्या कोई स्थानीय निर्देशांक चालू हैं? और कोटैंजेंट वैक्टर के संबंध में फाइबरवाइज निर्देशांक हैं . कोटैंजेंट बंडल शास्त्रीय यांत्रिकी के प्राकृतिक चरण स्थान हैं। ऊपरी और निचले सूचकांकों को अलग करने का बिंदु मीट्रिक टेंसर वाले मैनिफोल्ड के मामले से प्रेरित होता है, जैसा कि रीमैनियन मैनिफोल्ड्स के मामले में होता है। ऊपरी और निचले सूचकांक समन्वय फ्रेम के परिवर्तन के तहत विपरीत और सहसंयोजक रूप से बदलते हैं। कोटैंजेंट वैक्टर के संबंध में फ़ाइबरवाइज कोऑर्डिनेट वाक्यांश का अर्थ यह बताना है कि संवेग वेगों के सोल्डर रूप हैं . सोल्डरिंग इस विचार की अभिव्यक्ति है कि वेग और संवेग एकरेखीय हैं, इसमें दोनों ही दिशा में चलते हैं, और पैमाने के कारक से भिन्न होते हैं।
काहलर मैनिफोल्ड्स
काहलर मैनिफोल्ड संगत एकीकृत जटिल संरचना से सुसज्जित सहानुभूतिपूर्ण मैनिफोल्ड है। वे जटिल विविधताओं का विशेष वर्ग बनाते हैं। उदाहरणों का बड़ा वर्ग जटिल बीजगणितीय ज्यामिति से आता है। कोई भी चिकनी जटिल प्रक्षेप्य किस्म इसका सहानुभूतिपूर्ण रूप है जो फ़ुबिनी-अध्ययन मीट्रिक का प्रतिबंध है|फ़ुबिनी-प्रक्षेप्य स्थान पर अध्ययन प्रपत्र .
लगभग-जटिल कई गुना
रीमैनियन के साथ कई गुना होता है -संगत लगभग जटिल संरचना को लगभग-जटिल मैनिफोल्ड्स कहा जाता है। वे काहलर मैनिफोल्ड्स का सामान्यीकरण करते हैं, जिसमें उन्हें एकीकृत होने की आवश्यकता नहीं है। अर्थात्, वे आवश्यक रूप से अनेक गुना जटिल संरचना से उत्पन्न नहीं होते हैं।
लैग्रेंजियन और अन्य सबमेनिफोल्ड्स
सिम्प्लेक्टिक मैनिफोल्ड के सबमैनिफोल्ड की कई प्राकृतिक ज्यामितीय धारणाएँ हैं :
- के सिम्प्लेक्टिक सबमैनिफोल्ड्स (संभावित रूप से किसी भी सम आयाम के) उपमानव हैं ऐसा है कि पर प्रतीकात्मक रूप है .
- आइसोट्रोपिक सबमैनिफोल्ड्स सबमैनिफोल्ड्स हैं जहां सहानुभूति रूप शून्य तक सीमित है, यानी प्रत्येक स्पर्शरेखा स्थान परिवेश मैनिफोल्ड के स्पर्शरेखा स्थान का आइसोट्रोपिक उपस्थान है। इसी प्रकार, यदि किसी सबमैनिफोल्ड का प्रत्येक स्पर्शरेखा उप-स्थान सह-आइसोट्रोपिक (एक आइसोट्रोपिक उप-स्थान का द्वैत) है, तो सबमैनिफोल्ड को सह-आइसोट्रोपिक कहा जाता है।
- सिंपलेक्टिक मैनिफोल्ड के लैग्रेंजियन सबमैनिफोल्ड्स उपमानव हैं जहां सहानुभूति रूप का प्रतिबंध है को लुप्त हो रहा है, अर्थात और . लैग्रेंजियन सबमैनिफोल्ड्स अधिकतम आइसोट्रोपिक सबमैनिफोल्ड्स हैं।
एक प्रमुख उदाहरण यह है कि उत्पाद सिंपलेक्टिक मैनिफोल्ड में लक्षणरूपता का ग्राफ (M × M, ω × −ω) लैग्रेन्जियन है। उनके चौराहे कठोरता गुणों को प्रदर्शित करते हैं जो चिकनी मैनिफोल्ड्स के पास नहीं होते हैं; अर्नोल्ड अनुमान स्मूथ केस में यूलर विशेषता के बजाय, स्मूथ लैग्रेंजियन सबमैनिफोल्ड के स्वयं प्रतिच्छेदन की संख्या के लिए निचली सीमा के रूप में सबमैनिफोल्ड की बेट्टी संख्याओं का योग देता है।
उदाहरण
होने देना वैश्विक निर्देशांक लेबल किए गए हैं . फिर, हम सुसज्जित कर सकते हैं विहित सहानुभूतिपूर्ण रूप के साथ
- द्वारा दिया गया मानक लैग्रेंजियन सबमैनिफोल्ड है . फार्म पर गायब हो जाता है क्योंकि स्पर्शरेखा सदिशों का कोई जोड़ा दिया गया है हमारे पास वह है स्पष्ट करने के लिए, मामले पर विचार करें . तब, और . ध्यान दें कि जब हम इसका विस्तार करते हैं
दोनों शर्तें हमारे पास हैं कारक, जो परिभाषा के अनुसार 0 है।
उदाहरण: कोटैंजेंट बंडल
मैनिफोल्ड के कोटैंजेंट बंडल को पहले उदाहरण के समान स्थान पर स्थानीय रूप से तैयार किया गया है। यह दिखाया जा सकता है कि हम इन एफ़िन सिम्प्लेक्टिक रूपों को गोंद कर सकते हैं इसलिए यह बंडल सिम्प्लेक्टिक मैनिफोल्ड बनाता है। लैग्रेंजियन सबमैनिफोल्ड का कम तुच्छ उदाहरण मैनिफोल्ड के कोटैंजेंट बंडल का शून्य खंड है। उदाहरण के लिए, चलो
फिर, हम प्रस्तुत कर सकते हैं जैसा
जहां हम प्रतीकों का इलाज कर रहे हैं के निर्देशांक के रूप में . हम उस उपसमुच्चय पर विचार कर सकते हैं जहां निर्देशांक हैं और , हमें शून्य अनुभाग दे रहा है। इस उदाहरण को सुचारु कार्यों के लुप्त हो रहे स्थान द्वारा परिभाषित किसी भी मैनिफोल्ड के लिए दोहराया जा सकता है और उनके अंतर .
उदाहरण: पैरामीट्रिक सबमैनिफोल्ड
विहित स्थान पर विचार करें निर्देशांक के साथ . पैरामीट्रिक सबमैनिफोल्ड का वह है जो निर्देशांक द्वारा मानकीकृत है ऐसा है कि
यदि लैग्रेंज ब्रैकेट है तो यह मैनिफोल्ड लैग्रेंजियन सबमैनिफोल्ड है सभी के लिए गायब हो जाता है . अर्थात यह लैग्रेन्जियन है यदि
- सभी के लिए . इसे विस्तार करके देखा जा सकता है
लैग्रेंजियन सबमैनिफोल्ड की स्थिति में . इसका मतलब यह है कि स्पर्शरेखा मैनिफोल्ड पर सहानुभूतिपूर्ण रूप गायब हो जाना चाहिए ; अर्थात्, यह सभी स्पर्शरेखा सदिशों के लिए लुप्त हो जाना चाहिए:
सभी के लिए . विहित सहानुभूति प्रपत्र का उपयोग करके परिणाम को सरल बनाएं :
और अन्य सभी गायब हो रहे हैं।
जैसा कि सिंपलेक्टिक मैनिफोल्ड पर चार्ट (टोपोलॉजी) विहित रूप लेता है, यह उदाहरण बताता है कि लैग्रेंजियन सबमैनिफोल्ड अपेक्षाकृत अप्रतिबंधित हैं। सिंपलेक्टिक मैनिफ़ोल्ड्स का वर्गीकरण फ़्लोर होमोलॉजी के माध्यम से किया जाता है - यह लैग्रेंजियन सबमैनिफ़ोल्ड्स के बीच मानचित्रों के लिए एक्शन (भौतिकी) के लिए मोर्स सिद्धांत का अनुप्रयोग है। भौतिकी में, क्रिया भौतिक प्रणाली के समय विकास का वर्णन करती है; यहां, इसे ब्रैन्स की गतिशीलता के विवरण के रूप में लिया जा सकता है।
उदाहरण: मोर्स सिद्धांत
लैग्रेंजियन सबमैनिफोल्ड्स का अन्य उपयोगी वर्ग मोर्स सिद्धांत में पाया जाता है। मोर्स फ़ंक्शन दिया गया और काफी छोटे के लिए कोई लुप्त हो रहे स्थान द्वारा दिए गए लैग्रेंजियन सबमैनिफोल्ड का निर्माण कर सकता है . सामान्य मोर्स फ़ंक्शन के लिए हमारे पास लैग्रेन्जियन प्रतिच्छेदन है जो इसके द्वारा दिया गया है .
विशेष लैग्रेंजियन सबमैनिफोल्ड्स
काहलर मैनिफोल्ड्स (या कैलाबी-यॉ मैनिफोल्ड्स) के मामले में हम विकल्प चुन सकते हैं पर होलोमोर्फिक एन-फॉर्म के रूप में, जहां असली हिस्सा है और काल्पनिक. लैग्रेंजियन सबमैनिफोल्ड विशेष कहा जाता है यदि उपरोक्त लैग्रेंजियन स्थिति के अतिरिक्त प्रतिबंध हो को लुप्त हो रहा है. दूसरे शब्दों में, वास्तविक भाग पर प्रतिबंधित वॉल्यूम फॉर्म को आगे ले जाता है . निम्नलिखित उदाहरणों को विशेष लैग्रेंजियन सबमैनिफोल्ड्स के रूप में जाना जाता है,
- हाइपरकेहलर मैनिफोल्ड्स के जटिल लैग्रेंजियन सबमैनिफोल्ड्स,
कैलाबी-याउ मैनिफोल्ड्स की वास्तविक संरचना के # निश्चित बिंदु। एसवाईजेड अनुमान दर्पण समरूपता (स्ट्रिंग सिद्धांत) में विशेष लैग्रेंजियन सबमैनिफोल्ड्स के अध्ययन से संबंधित है; देखना (Hitchin 1999).
थॉमस-याउ अनुमान भविष्यवाणी करता है कि लैग्रैंगियंस के हैमिल्टनियन आइसोटोप वर्गों में कैलाबी-याउ मैनिफोल्ड्स पर विशेष लैग्रैन्जियन सबमैनिफोल्ड्स का अस्तित्व मैनिफोल्ड की फुकाया श्रेणी पर ब्रिजलैंड स्थिरता की स्थिति के संबंध में स्थिरता के बराबर है।
लैग्रेंजियन कंपन
सिम्प्लेक्टिक मैनिफोल्ड एम का लैग्रेंजियन फ़िब्रेशन फ़िब्रेशन है जहां सभी फ़ाइबर बंडल#औपचारिक परिभाषा लैग्रैन्जियन सबमैनिफ़ोल्ड्स हैं। चूंकि एम सम-आयामी है इसलिए हम स्थानीय निर्देशांक ले सकते हैं (p1,…,pn, q1,…,qn), और डार्बौक्स के प्रमेय द्वारा सहानुभूतिपूर्ण रूप ω को, कम से कम स्थानीय रूप से, इस प्रकार लिखा जा सकता है ω = ∑ dpk ∧ dqk, जहां d बाहरी व्युत्पन्न को दर्शाता है और ∧ बाहरी उत्पाद को दर्शाता है। इस फॉर्म को पोंकारे टू-फॉर्म या कैनोनिकल टू-फॉर्म कहा जाता है। इस सेट-अप का उपयोग करके हम स्थानीय रूप से एम को कोटैंजेंट बंडल के रूप में सोच सकते हैं और लैग्रेंजियन फ़िब्रेशन को तुच्छ फ़िब्रेशन के रूप में यह विहित चित्र है.
लैग्रेंजियन मैपिंग
मान लीजिए कि L इमर्शन (गणित) द्वारा दिए गए सिंपलेक्टिक मैनिफोल्ड (K,ω) का लैग्रेंजियन सबमैनिफोल्ड है। i : L ↪ K (i को 'लैग्रेंजियन इमर्शन' कहा जाता है)। होने देना π : K ↠ B K का लैग्रेंजियन फ़िब्रेशन दें। समग्र (π ∘ i) : L ↪ K ↠ B लैग्रेंजियन मैपिंग है। π ∘ i के क्रांतिक मान को कास्टिक (गणित) कहा जाता है।
दो लैग्रेंजियन मानचित्र (π1 ∘ i1) : L1 ↪ K1 ↠ B1 और (π2 ∘ i2) : L2 ↪ K2 ↠ B2 को लैग्रेंजियन समतुल्य कहा जाता है यदि σ, τ और ν भिन्नताएं मौजूद हैं जैसे कि सही क्रमविनिमेय आरेख पर दिए गए आरेख के दोनों पक्ष, और τ सहानुभूति रूप को संरक्षित करते हैं .[4]प्रतीकात्मक रूप से:
कहां τ∗o2 ω के विभेदक रूपों के पुलबैक (विभेदक ज्यामिति)#पुलबैक को दर्शाता है2 τ द्वारा.
विशेष मामले और सामान्यीकरण
- एक सिंपलेक्टिक मैनिफोल्ड यदि सिंपलेक्टिक रूप सटीक है बंद और सटीक विभेदक रूप है। उदाहरण के लिए, चिकने मैनिफोल्ड का कोटैंजेंट बंडल सटीक सिंपलेक्टिक मैनिफोल्ड है। विहित सहानुभूतिपूर्ण रूप सटीक है।
- एक मीट्रिक टेंसर से संपन्न सिंपलेक्टिक मैनिफोल्ड, जो लगभग जटिल मैनिफोल्ड है # सिंपलेक्टिक रूप के साथ संगत त्रिगुण इस अर्थ में लगभग काहलर मैनिफोल्ड है कि स्पर्शरेखा बंडल में लगभग जटिल संरचना होती है, लेकिन इसके लिए इंटीग्रेबिलिटी स्थिति की आवश्यकता नहीं होती है।
- सिंपलेक्टिक मैनिफोल्ड्स पॉइसन मैनिफ़ोल्ड के विशेष मामले हैं।
- डिग्री के का मल्टीसिम्पलेक्टिक मैनिफोल्ड बंद गैर-अपक्षयी के-फॉर्म से सुसज्जित मैनिफोल्ड है।[5]
- एक पॉलीसिम्पलेक्टिक मैनिफोल्ड लीजेंड्रे बंडल है जो पॉलीसिम्पलेक्टिक स्पर्शरेखा-मूल्य के साथ प्रदान किया जाता है -प्रपत्र; इसका उपयोग हैमिल्टनियन क्षेत्र सिद्धांत में किया जाता है।[6]
यह भी देखें
- Almost symplectic manifold
- Contact manifold-सिम्प्लेक्टिक मैनिफोल्ड का एक विषम-आयामी समकक्ष।
- Covariant Hamiltonian field theory
- Fedosov manifold
- Poisson bracket
- Symplectic group
- Symplectic matrix
- Symplectic topology
- Symplectic vector space
- Symplectomorphism
- Tautological one-form
- Wirtinger inequality (2-forms)
उद्धरण
- ↑ Webster, Ben (9 January 2012). "What is a symplectic manifold, really?".
- ↑ Cohn, Henry. "शास्त्रीय यांत्रिकी के लिए सिंपलेक्टिक ज्यामिति प्राकृतिक सेटिंग क्यों है?".
- ↑ 3.0 3.1 de Gosson, Maurice (2006). सिंपलेक्टिक ज्यामिति और क्वांटम यांत्रिकी. Basel: Birkhäuser Verlag. p. 10. ISBN 3-7643-7574-4.
- ↑ 4.0 4.1 4.2 Arnold, V. I.; Varchenko, A. N.; Gusein-Zade, S. M. (1985). The Classification of Critical Points, Caustics and Wave Fronts: Singularities of Differentiable Maps, Vol 1. Birkhäuser. ISBN 0-8176-3187-9.
- ↑ Cantrijn, F.; Ibort, L. A.; de León, M. (1999). "मल्टीसिम्प्लेक्टिक मैनिफोल्ड्स की ज्यामिति पर". J. Austral. Math. Soc. Ser. A. 66 (3): 303–330. doi:10.1017/S1446788700036636.
- ↑ Giachetta, G.; Mangiarotti, L.; Sardanashvily, G. (1999). "क्षेत्र सिद्धांत के लिए सहसंयोजक हैमिल्टनियन समीकरण". Journal of Physics. A32 (38): 6629–6642. arXiv:hep-th/9904062. Bibcode:1999JPhA...32.6629G. doi:10.1088/0305-4470/32/38/302. S2CID 204899025.
सामान्य और उद्धृत संदर्भ
- McDuff, Dusa; Salamon, D. (1998). सिंपलेक्टिक टोपोलॉजी का परिचय. Oxford Mathematical Monographs. ISBN 0-19-850451-9.
- Auroux, Denis. "दर्पण समरूपता पर संगोष्ठी".
- Meinrenken, Eckhard. "सिंपलेक्टिक ज्यामिति" (PDF).
- Abraham, Ralph; Marsden, Jerrold E. (1978). यांत्रिकी की नींव. London: Benjamin-Cummings. See Section 3.2. ISBN 0-8053-0102-X.
- de Gosson, Maurice A. (2006). सिंपलेक्टिक ज्यामिति और क्वांटम यांत्रिकी. Basel: Birkhäuser Verlag. ISBN 3-7643-7574-4.
- Alan Weinstein (1971). "सिंपलेक्टिक मैनिफोल्ड्स और उनके लैग्रेंजियन सबमैनिफोल्ड्स". Advances in Mathematics. 6 (3): 329–46. doi:10.1016/0001-8708(71)90020-X.
- Arnold, V. I. (1990). "Ch.1, Symplectic geometry". कास्टिक्स और तरंग मोर्चों की विलक्षणताएँ. Mathematics and Its Applications. Vol. 62. Dordrecht: Springer Netherlands. doi:10.1007/978-94-011-3330-2. ISBN 978-1-4020-0333-2. OCLC 22509804.
अग्रिम पठन
- Dunin-Barkowski, Petr (2022). "Symplectic duality for topological recursion". arXiv:2206.14792 [math-ph].
- "How to find Lagrangian Submanifolds". Stack Exchange. December 17, 2014.
- Lumist, Ü. (2001) [1994], "Symplectic Structure", Encyclopedia of Mathematics, EMS Press
- Sardanashvily, G. (2009). "Fibre bundles, jet manifolds and Lagrangian theory". Lectures for Theoreticians. arXiv:0908.1886.
- McDuff, D. (November 1998). "Symplectic Structures—A New Approach to Geometry" (PDF). Notices of the AMS.
- Hitchin, Nigel (1999). "Lectures on Special Lagrangian Submanifolds". arXiv:math/9907034.