अनुनादी अल्ट्रासाउंड स्पेक्ट्रोस्कोपी

अनुनाद अल्ट्रासाउंड स्पेक्ट्रोस्कोपी (आरयूएस) एक प्रयोगशाला तकनीक है जिसका उपयोग लोच (भौतिकी) से जुड़े मौलिक भौतिक गुणों को मापने के लिए भूविज्ञान और भौतिक विज्ञान में किया जाता है। यह तकनीक इस तथ्य पर निर्भर करती है कि ठोस वस्तुओं में प्राकृतिक आवृत्तियाँ होती हैं जिस पर वे यांत्रिक रूप से उत्तेजित होने पर कंपन करती हैं। प्राकृतिक आवृत्ति वस्तु की लोच, आकार और बनावट पर निर्भर करती है - आरयूएस सामग्री की रैखिक लोच को निर्धारित करने के लिए ठोस पदार्थों की इस संपत्ति को शोषित करता है। इस तकनीक का सबसे बड़ा लाभ यह है कि संपूर्ण लोचदार टेन्सर (तानिका) एकल त्वरित माप में एकल क्रिस्टल नमूने से प्राप्त किया जाता है। कम या अधिक सामान्य आवृत्तियों पर इस विधि को ध्वनिक अनुनाद स्पेक्ट्रोस्कोपी के रूप में जाना जाता है।

इतिहास

17 वीं शताब्दी के दार्शनिकों ने लोचदार गुणों में रुचि के साथ प्रवेश किया लेकिन लोच का वास्तविक सिद्धांत यह दर्शाता है कि सामग्री के लोचदार स्थिरांक को उस सामग्री में ध्वनि वेगों को मापकर प्राप्त किया जा सकता है यह दो सौ साल बाद केवल सारांशित किया गया था। सन 1964 में डी.बी. फ्रेज़ियर और आरसी लेक्रॉ ने आगे की समस्या को हल करने के लिए सन 1880 में जी. लामे और एच. लैम्ब द्वारा गणना किए गए समाधान का उपयोग किया, और फिर इसे ग्राफिकल रूप से उल्टा कर दिया, जो कि पहला आरयूएस माप हो सकता है। फिर भी, हमें भूभौतिकी समुदाय की भागीदारी के लिए इंतजार करना पड़ा, जो पृथ्वी की संरचना का निर्धारण करने में रुचि रखते थे। पृथ्वी की आंतरिक संरचना, उलटी समस्या को हल करने के लिए: 1970 में तीन भूभौतिकीविदों ने पिछली पद्धति में सुधार किया और अनुनाद क्षेत्र तकनीक (RST) शब्द पेश किया। . चाँद की चट्टान के साथ प्राप्त उत्साहजनक परिणामों से उत्साहित, उनमें से एक ने अपने छात्रों में से एक को क्यूब के आकार के नमूनों के उपयोग के लिए विधि का विस्तार करने का कार्य दिया। यह विधि, जिसे अब आयताकार समांतर चतुर्भुज प्रतिध्वनि (RPR) विधि के रूप में जाना जाता है, को 1976 में I. ओहनो द्वारा आगे बढ़ाया गया था। अंत में, 1980 के दशक के अंत में, ए. मिग्लियोरी और जे. लोडिंग और निम्न-स्तरीय इलेक्ट्रॉनिक मापन, और W. Visscher के साथ कंप्यूटर एल्गोरिदम को उनकी वर्तमान स्थिति में लाया, अंतिम शब्द गुंजयमान अल्ट्रासाउंड स्पेक्ट्रोस्कोपी (RUS) का परिचय दिया।

सिद्धांत

सबसे पहले, नमूना आयामों, द्रव्यमान और काल्पनिक लोचदार स्थिरांक (आगे की समस्या) के एक सेट के संदर्भ में प्राकृतिक आवृत्तियों की गणना करने की समस्या को हल करना चाहिए। फिर मापा प्राकृतिक आवृत्तियों (उलटा समस्या) से लोचदार स्थिरांक खोजने के लिए एक गैर-रैखिक उलटा एल्गोरिदम लागू करना चाहिए।

Lagrangian न्यूनीकरण

सभी आरयूएस माप नमूनों पर किए जाते हैं जो फ्री वाइब्रेटर हैं। क्योंकि ठोस पदार्थों के मुक्त कंपन के लिए एक पूर्ण विश्लेषणात्मक समाधान मौजूद नहीं है, किसी को सन्निकटन पर भरोसा करना चाहिए। परिमित तत्व विधियाँ एक विभेदक आयतन तत्व पर लागू बलों को संतुलित करने पर आधारित होती हैं, फिर उसकी प्रतिक्रिया की गणना करती हैं। दूसरी ओर ऊर्जा न्यूनीकरण के तरीके न्यूनतम ऊर्जा निर्धारित करते हैं, और इस प्रकार वस्तु के लिए संतुलन विन्यास। ऊर्जा न्यूनीकरण तकनीकों के बीच, गति में इसके लाभ (परिमित-तत्व विधियों की तुलना में छोटे परिमाण का एक क्रम) के कारण आरयूएस विश्लेषण में लैग्रैन्जियन न्यूनीकरण का सबसे अधिक उपयोग किया जाता है।

यह प्रक्रिया आयतन V की एक वस्तु से शुरू होती है, जो इसकी मुक्त सतह S से बंधी होती है। Lagrangian (क्षेत्र सिद्धांत) द्वारा दिया जाता है

$L=\int _{V}(KE-PE)dV(1)$ जहाँ KE गतिज ऊर्जा घनत्व है

$KE={\frac {1}{2}}\sum _{i}\rho \omega ^{2}u_{i}^{2}(2)$ और पीई संभावित ऊर्जा घनत्व है

$PE={\frac {1}{2}}\sum _{i,j,k,l}c_{i,j,k,l}{\frac {du_{i}}{dx_{j}}}{\frac {du_{k}}{dx_{l}}}(3)$

अंजीर। 1: एक आयताकार समांतर चतुर्भुज नमूने के लिए कंपन के कुछ सामान्य तरीकों के कंप्यूटर जनित चित्रण।

यहाँ, $u_{i}$ विस्थापन वेक्टर का iवां घटक है, ω हार्मोनिक समय निर्भरता से कोणीय आवृत्ति है, $c_{i,j,k,l}$ लोचदार कठोरता टेंसर का एक घटक है, और ρ घनत्व है। सबस्क्रिप्ट i, j, आदि, कार्टेशियन निर्देशांक दिशाओं को संदर्भित करते हैं।

Lagrangian का न्यूनतम ज्ञात करने के लिए, L के एक फ़ंक्शन के अंतर को u के एक फ़ंक्शन के रूप में परिकलित करें, V में और S पर u की मनमाना भिन्नता। यह देता है:

$\delta L=\int _{V}{\Bigl \{}\sum _{i}{\Bigl [}\rho \omega ^{2}u_{i}-\sum _{j,k,l}c_{i,j,k,l}{\frac {\delta ^{2}u_{k}}{\delta x_{j}\delta x_{l}}}{\Bigr ]}\delta u_{i}{\Bigr \}}dV-\int _{S}{\Bigl \{}\sum _{i}{\Bigl [}\sum _{j,k,l}{\vec {n}}c_{i,j,k,l}{\frac {\delta u_{k}}{\delta x_{l}}}{\Bigr ]}du_{i}{\Bigr \}}dS(4)$ क्योंकि $u_{i}$ वी और एस में मनमाना है, वर्ग कोष्ठक में दोनों शब्द शून्य होने चाहिए। पहले पद को शून्य के बराबर सेट करने से प्रत्यास्थ तरंग समीकरण प्राप्त होता है। दूसरा वर्ग कोष्ठक पद मुक्त सतह सीमा स्थितियों की अभिव्यक्ति है; ${\vec {n}}$ एस के लिए इकाई वेक्टर सामान्य है। एक मुक्त शरीर के लिए (जैसा कि हम इसे मानते हैं), बाद की अवधि शून्य के बराबर होती है और इसे अनदेखा किया जा सकता है।

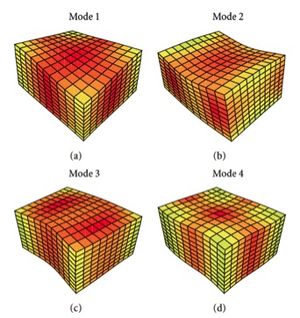
इस प्रकार का सेट $u_{i}$ जो पहले बताई गई शर्तों को संतुष्ट करता है, वे विस्थापन हैं जो ω सिस्टम की सामान्य मोड आवृत्ति के अनुरूप हैं। इससे पता चलता है कि किसी वस्तु के सामान्य कंपन (चित्र 1) की गणना एक भिन्नता विधि (हमारे मामले में रेले-रिट्ज विधि | रेले-रिट्ज भिन्नता विधि, अगले पैराग्राफ में समझाया गया है) को लागू करके दोनों सामान्य मोड को निर्धारित करने के लिए की जा सकती है। आवृत्तियों और भौतिक दोलनों का विवरण। विशर को उद्धृत करने के लिए, दोनों समीकरणों को मूल लैग्रेंजियन से प्राप्त करना एक गणितीय भाग्य है जो मर्फी के नियम में एक चूक के दौरान हुआ हो सकता है|मर्फी की सतर्कता।

रेले-रिट्ज परिवर्तनशील विधि

इस दृष्टिकोण की सक्रियता के विस्तार की आवश्यकता है $u_{i}$ शरीर की ज्यामिति के लिए उपयुक्त आधार कार्यों के एक सेट में, उस अभिव्यक्ति को Eq में प्रतिस्थापित करना। (1) और N×N मैट्रिक्स (आइगेनवैल्यू प्रॉब्लम) को डायगोनलाइज़ करने की समस्या को कम करना। Eq से उत्पन्न eigenvalue समस्या को हल करके Lagrangian के स्थिर बिंदुओं को पाया जाता है। (4), अर्थात्,

$\omega ^{2}Ea=\Gamma a(5)$ जहाँ a पूर्ण आधार सेट में विस्तारित गति के सन्निकटन हैं, E गतिज ऊर्जा शब्द से आता है, और Γ लोचदार ऊर्जा शब्द से आता है। अच्छे सन्निकटन के लिए मेट्रिसेस का क्रम ~10^3 है।

समीकरण (5) लोचदार मापांक से अनुनाद आवृत्तियों को निर्धारित करता है।

व्युत्क्रम समस्या

यांत्रिक अनुनादों के एक मापा स्पेक्ट्रम से लोचदार स्थिरांक निकालने की व्युत्क्रम समस्या का कोई विश्लेषणात्मक समाधान नहीं है, इसलिए इसे कम्प्यूटेशनल विधियों द्वारा हल करने की आवश्यकता है। अप्रत्यक्ष विधि के लिए, एक प्रारंभिक गुंजयमान आवृत्ति स्पेक्ट्रम, $f_{n}^{cal}$ (n=1,2,...) लोचदार स्थिरांक और ज्ञात नमूना आयाम और घनत्व के लिए अनुमानित मानों का उपयोग करके गणना की जाती है। गणना की गई और मापी गई अनुनाद आवृत्ति स्पेक्ट्रम के बीच का अंतर, $f_{n}^{mea}$ (n=1,2,...) मेरिट फ़ंक्शन के एक आंकड़े द्वारा परिमाणित है,

$F=\sum _{n}w_{n}(f_{n}^{cal}-f_{n}^{mea})^{2}(6)$ कहाँ $w_{n}$ (n=1,2,...) वजन गुणांक हैं जो अलग-अलग अनुनाद मापों पर विश्वास को दर्शाते हैं। फिर, इस प्रक्रिया के लिए विकसित कंप्यूटर सॉफ्टवेयर का उपयोग करके सभी लोचदार स्थिरांक के मूल्यों को वापस करके फ़ंक्शन एफ का न्यूनतमकरण मांगा जाता है।

माप

अंजीर। चित्र 2: दो ट्रांसड्यूसर गुंजयमान अल्ट्रासाउंड स्पेक्ट्रोस्कोपी की योजना की स्थापना।

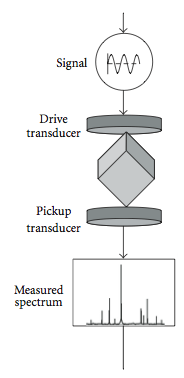
यांत्रिक गुंजयमान स्पेक्ट्रम का पता लगाने के लिए सबसे आम तरीका चित्र 2 में दिखाया गया है, जहां दो पीजोइलेक्ट्रिक ट्रांसड्यूसर के बीच एक छोटे समानांतर आकार के नमूने को हल्के से रखा जाता है। एक ट्रांसड्यूसर का उपयोग निरंतर आयाम और अलग-अलग आवृत्ति की लोचदार तरंग उत्पन्न करने के लिए किया जाता है, जबकि दूसरे का उपयोग नमूना के अनुनाद का पता लगाने के लिए किया जाता है। जैसे ही फ़्रीक्वेंसी रेंज बह जाती है, अनुनाद चोटियों का एक क्रम दर्ज किया जाता है। इन चोटियों की स्थिति प्राकृतिक आवृत्तियों पर होती है $f_{n}$ (जिससे लोचदार स्थिरांक निर्धारित किए जाते हैं) और गुणवत्ता कारक क्यू (अनुनाद कितना संकीर्ण है इसका एक उपाय) लोचदार ऊर्जा के अपव्यय के बारे में जानकारी प्रदान करता है।

एक पारंपरिक अल्ट्रासोनिक माप के विपरीत, एक विधि में जो नमूने को प्रतिध्वनित करती है, ट्रांसड्यूसर और नमूने के बीच एक मजबूत युग्मन की आवश्यकता नहीं होती है, क्योंकि नमूना एक प्राकृतिक एम्पलीफायर के रूप में व्यवहार करता है।इसके बजाय, उनके बीच कम से कम जोड़े को रखते हुए, आप मुक्त सतह सीमा स्थितियों के लिए एक अच्छा अनुमान प्राप्त करते हैं और क्यू को भी संरक्षित करते हैं। चर-तापमान मापन के लिए नमूने को दो बफर छड़ों के सिरों के बीच रखा जाता है जो नमूने को ट्रांसड्यूसर (चित्र 3) से जोड़ते हैं क्योंकि ट्रांसड्यूसर को कमरे के तापमान पर रखा जाना चाहिए। दबाव के मामले में, इसके विपरीत, केवल कुछ सलाखों की सीमा होती है, क्योंकि उच्च दबावों के आवेदन से नमूने के अनुनादों में कमी आती है।

नमूने

RUS को नमूनों के आकार की एक बड़ी श्रृंखला पर लागू किया जा सकता है, न्यूनतम क्रम में या कुछ सौ माइक्रोमीटर के साथ, लेकिन खनिज लोच की माप के लिए इसका उपयोग आमतौर पर 1 मिमी और 1 सेमी आकार के बीच के नमूनों पर किया जाता है।

नमूना, या तो पूरी तरह से सघन polycrystalline समुच्चय या एकल क्रिस्टल, एक नियमित आकार में मशीनीकृत होता है।सैद्धांतिक रूप से किसी भी नमूना आकार का उपयोग किया जा सकता है, लेकिन आप आयताकार समांतर चतुर्भुज अनुनादक (RPR), गोलाकार या बेलनाकार वाले (सिलेंडर के साथ कम समय की बचत) का उपयोग करके कम्प्यूटेशनल समय में पर्याप्त बचत प्राप्त करते हैं।

अंजीर। 3: RUS चर-तापमान माप के लिए नमूना असेंबली।

चूंकि माप की सटीकता नमूना तैयार करने में सटीकता पर सख्ती से निर्भर करती है, इसलिए कई सावधानियां बरती जाती हैं: आरपीआर क्रिस्टलोग्राफिक दिशाओं के समानांतर किनारों के साथ तैयार किए जाते हैं; सिलेंडरों के लिए केवल अक्ष को नमूना समरूपता से मिलान किया जा सकता है। कम समरूपता के नमूनों के लिए RUS का उपयोग शायद ही कभी किया जाता है, और समदैशिक नमूनों के लिए, संरेखण अप्रासंगिक है। उच्च समरूपता के लिए, निरर्थक प्रतिध्वनि को रोकने के लिए अलग-अलग लंबाई के किनारों का होना सुविधाजनक है।

एकल क्रिस्टल पर मापन के लिए आरपीआर के किनारों के साथ नमूना क्रिस्टलोग्राफिक कुल्हाड़ियों के उन्मुखीकरण की आवश्यकता होती है, ताकि अभिविन्यास गणना की उपेक्षा की जा सके और केवल लोचदार मापांक से निपटा जा सके।

पॉलीक्रिस्टलाइन के नमूने आदर्श रूप से पूरी तरह से घने, दरारों से मुक्त और अनाज के अधिमान्य अभिविन्यास के बिना होने चाहिए। एकल क्रिस्टल नमूने क्रिस्टल ट्विनिंग जैसे आंतरिक क्रिस्टलोग्राफिक दोषों से मुक्त होने चाहिए। सभी नमूनों की सतहों को पॉलिश किया जाना चाहिए और विपरीत चेहरे समानांतर होने चाहिए। एक बार तैयार होने के बाद, घनत्व को सटीक रूप से मापा जाना चाहिए क्योंकि यह लोचदार मोडुली के पूरे सेट को मापता है।

ट्रांसड्यूसर

अन्य सभी अल्ट्रासोनिक तकनीकों के विपरीत, RUS अल्ट्रासोनिक ट्रांसड्यूसर को नमूने के साथ शुष्क बिंदु संपर्क बनाने के लिए डिज़ाइन किया गया है। यह आवृत्तियों से लोचदार मापांक की गणना के लिए मुक्त सतह सीमा की स्थिति की आवश्यकता के कारण है। आरपीआर के लिए इसके लिए नमूने के कोनों और ट्रांसड्यूसर के बीच बहुत हल्के स्पर्श की आवश्यकता होती है। कोनों का उपयोग किया जाता है क्योंकि वे लोचदार रूप से कमजोर युग्मन प्रदान करते हैं, लोडिंग को कम करते हैं, और क्योंकि वे कभी भी कंपन नोड बिंदु नहीं होते हैं। पर्याप्त रूप से कमजोर संपर्क सुनिश्चित करता है कि ट्रांसड्यूस्ड सुधार की आवश्यकता नहीं है।

अनुप्रयोग

ठोस सामग्री के लोचदार गुणों को चिह्नित करने के लिए एक बहुमुखी उपकरण के रूप में, आरयूएस ने विभिन्न क्षेत्रों में आवेदन पाया है। भूविज्ञान में सबसे महत्वपूर्ण अनुप्रयोगों में से एक पृथ्वी की संरचना में भूकंपीय तरंग के निर्धारण से संबंधित है। पृथ्वी के आंतरिक भाग। हाल के एक काम में, उदाहरण के लिए, जलीय forsterite के लोचदार स्थिरांक को परिवेश के तापमान पर 14.1 GPa तक मापा गया। इस अध्ययन से पता चला है कि हाइड्रस फोर्सटेराइट का कुल बल्क मापांक और कतरनी मापांक इसी निर्जल चरण की तुलना में अधिक दर से दबाव के साथ बढ़ता है। इसका तात्पर्य यह है कि परिवेशी परिस्थितियों में वीपी और वीएस हाइड्रस फोर्सटेराइट निर्जल की तुलना में धीमे होते हैं; इसके विपरीत, बढ़ते दबाव और फलस्वरूप गहराई के साथ, वी_P और वी_S हाइड्रस फोर्सटेराइट निर्जल से अधिक है। इसके अलावा हाइड्रेशन V को घटाता है_P/में_S फ़ॉर्स्टराइट का अनुपात, अधिकतम संपीड़न तरंग अज़ीमुथल असमदिग्वर्ती होने की दशा और अधिकतम कतरनी तरंग विभाजन। ये डेटा हमें पृथ्वी की मेंटल संरचना को बाधित करने और उच्च तापमान या आंशिक पिघल के क्षेत्रों से हाइड्रोजन संवर्धन के क्षेत्रों में अंतर करने में मदद करते हैं।