अपवाह वेग: Difference between revisions
(Created page with "{{Short description|Average velocity of particles mainly moving randomly}} भौतिकी में, बहाव वेग एक विद्युत क्षेत...") |
m (Abhishek moved page बहाव का वेग to अपवाह वेग without leaving a redirect) |
(No difference)
| |
Revision as of 13:12, 10 March 2023
भौतिकी में, बहाव वेग एक विद्युत क्षेत्र के कारण पदार्थ में आवेशित कणों, जैसे इलेक्ट्रॉनों द्वारा प्राप्त औसत वेग है। सामान्य तौर पर, एक विद्युत कंडक्टर में एक इलेक्ट्रॉन बेतरतीब ढंग से फर्मी वेग से फैलेगा, जिसके परिणामस्वरूप शून्य का औसत वेग होगा। एक विद्युत क्षेत्र को लागू करने से इस यादृच्छिक गति में एक दिशा में एक छोटा शुद्ध प्रवाह जुड़ जाता है; यह बहाव है।
बहाव वेग वर्तमान (बिजली) के समानुपाती होता है। एक प्रतिरोध (बिजली) सामग्री में, यह बाहरी विद्युत क्षेत्र के परिमाण के समानुपाती भी होता है। इस प्रकार ओम के नियम को बहाव वेग के संदर्भ में समझाया जा सकता है। कानून की सबसे प्रारंभिक अभिव्यक्ति है:
कहाँ u बहाव वेग है, μ सामग्री की इलेक्ट्रॉन गतिशीलता है, और E विद्युत क्षेत्र है। इकाइयों की एमकेएस प्रणाली में, इन मात्राओं की इकाइयां एम/एस, एम हैं2/(वाल्ट ·s), और V/m, क्रमशः।
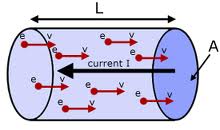
जब एक कंडक्टर में एक संभावित अंतर लागू किया जाता है, मुक्त इलेक्ट्रॉन दिशा में वेग प्राप्त करते हैं, लगातार टकरावों के बीच विद्युत क्षेत्र के विपरीत (और क्षेत्र की दिशा में यात्रा करते समय वेग खो देते हैं), इस प्रकार उस दिशा में वेग घटक प्राप्त करने के अलावा इसके यादृच्छिक तापीय वेग के लिए। नतीजतन, इलेक्ट्रॉनों का एक निश्चित छोटा बहाव वेग होता है, जो मुक्त इलेक्ट्रॉनों की यादृच्छिक गति पर आरोपित होता है। इस अपवाह वेग के कारण क्षेत्र की दिशा के विपरीत इलेक्ट्रॉनों का शुद्ध प्रवाह होता है।
प्रायोगिक माप
निरंतर क्रॉस-सेक्शन (ज्यामिति) | क्रॉस-सेक्शनल क्षेत्र की सामग्री में आवेश वाहकों के बहाव वेग के मूल्यांकन के लिए सूत्र द्वारा दिया गया है:[1]
कहाँ u इलेक्ट्रॉनों का बहाव वेग है, j सामग्री के माध्यम से प्रवाहित होने वाला वर्तमान घनत्व है, n आवेश-वाहक संख्या घनत्व है, और q आवेश-वाहक पर विद्युत आवेश है।
इसे इस प्रकार भी लिखा जा सकता है:
लेकिन वर्तमान घनत्व और बहाव वेग, जे और यू वास्तव में वैक्टर हैं, इसलिए इस संबंध को अक्सर इस प्रकार लिखा जाता है:
कहाँ
आवेश घनत्व है (SI इकाई: कूलम्ब प्रति घन मीटर)।
सही-बेलनाकार विद्युत प्रवाह-वाहक धातु विद्युत कंडक्टर के मूल गुणों के संदर्भ में, जहां चार्ज-वाहक इलेक्ट्रॉनों होते हैं, इस अभिव्यक्ति को फिर से लिखा जा सकता है:[citation needed]
कहाँ
- u फिर से इलेक्ट्रॉनों का बहाव वेग है, मीटर⋅दूसरा में-1
- m धातु का आणविक द्रव्यमान है, किग्रा में
- σ सीमेंस (इकाई)/मीटर में माने गए तापमान पर माध्यम की विद्युत चालकता है।
- ΔV वोल्ट में कंडक्टर पर लागू वोल्टेज है
- ρ कंडक्टर का घनत्व (द्रव्यमान प्रति इकाई आयतन) किग्रा⋅मीटर में है−3
- e प्राथमिक आवेश है, कूलम्ब (इकाई) में
- f प्रति परमाणु इलेक्ट्रॉन की संख्या है
- ℓ मीटर में कंडक्टर की लंबाई है
संख्यात्मक उदाहरण
बिजली आमतौर पर तांबे के तारों के माध्यम से आयोजित की जाती है। ताँबा का घनत्व होता है 8.94 g/cm3 और का परमाणु भार 63.546 g/mol, तो हैं 140685.5 mol/m3. किसी भी तत्व के एक मोल (इकाई) में होते हैं 6.022×1023 परमाणु (अवोगाद्रो संख्या)। इसलिए, में 1 m3 ताँबे के लगभग होते हैं 8.5×1028 परमाणु (6.022×1023 × 140685.5 mol/m3). कॉपर में प्रति परमाणु एक मुक्त इलेक्ट्रॉन होता है, इसलिए n के बराबर है 8.5×1028 इलेक्ट्रॉन प्रति घन मीटर।
करंट मान लीजिए I = 1 ampere, और का एक तार 2 mm व्यास (त्रिज्या = 0.001 m). इस तार का अनुप्रस्थ काट क्षेत्रफल होता है {{math|A}π × (0.001 m)2 = 3.14×10−6 m2 = 3.14 mm2. एक इलेक्ट्रॉन का आवेश होता है q = −1.6×10−19 C. इसलिए बहाव वेग की गणना की जा सकती है:
तुलनात्मक रूप से, इन इलेक्ट्रॉनों का फर्मी प्रवाह वेग (जो, कमरे के तापमान पर, विद्युत प्रवाह की अनुपस्थिति में उनके अनुमानित वेग के रूप में सोचा जा सकता है) लगभग है 1570 km/s.[2]
यह भी देखें
- प्रवाह वेग
- इलेक्ट्रॉन गतिशीलता
- बिजली की गति
- बहाव कक्ष
- मार्गदर्शक केंद्र
संदर्भ
- ↑ Griffiths, David (1999). इलेक्ट्रोडायनामिक्स का परिचय (3 ed.). Upper Saddle River, NJ: Prentice-Hall. p. 289. ISBN 9780138053260.
- ↑ http://hyperphysics.phy-astr.gsu.edu/hbase/electric/ohmmic.html Ohm's Law, Microscopic View, retrieved 2015-11-16
बाहरी संबंध
- Ohm's Law: Microscopic View at Hyperphysics