बार्न्स जी-फ़ंक्शन

गणित में, बार्न्स G-फलन G(z) फलन (गणित) है जोकी जटिल संख्याओं के लिए सुपरफैक्टोरियल का विस्तार है। यह गामा फलन , K-फलन और ग्लैशर-किंकलिन स्थिरांक से संबंधित है, और इसका नाम गणितज्ञ अर्नेस्ट विलियम बार्न्स के नाम पर रखा गया था। इसे दोहरे गामा फलन के संदर्भ में लिखा जा सकता है।

इस प्रकार से औपचारिक रूप से, बार्न्स G-फलन को निम्नलिखित वीयरस्ट्रैस उत्पाद रूप में परिभाषित किया गया है:

$G(1+z)=(2\pi )^{z/2}\exp \left(-{\frac {z+z^{2}(1+\gamma )}{2}}\right)\,\prod _{k=1}^{\infty }\left\{\left(1+{\frac {z}{k}}\right)^{k}\exp \left({\frac {z^{2}}{2k}}-z\right)\right\}$

जहाँ $\,\gamma$ यूलर-माशेरोनी स्थिरांक है, घातीय फलन(x) = e^xघातांकीय फलन है, और Π गुणन (कैपिटल पाई नोटेशन) को दर्शाता है।

जहां $\,\gamma$ यूलर-माशेरोनी स्थिरांक है, exp(x) = e^x घातीय फलन है, और Π गुणन (कैपिटल पाई नोटेशन) को दर्शाता जाता है।

संपूर्ण फलन के रूप में, G क्रम दो का और अनंत प्रकार का है। इसका अनुमान दिए गए स्पर्शोन्मुख विस्तार से लगाया जा सकता हैgiven below.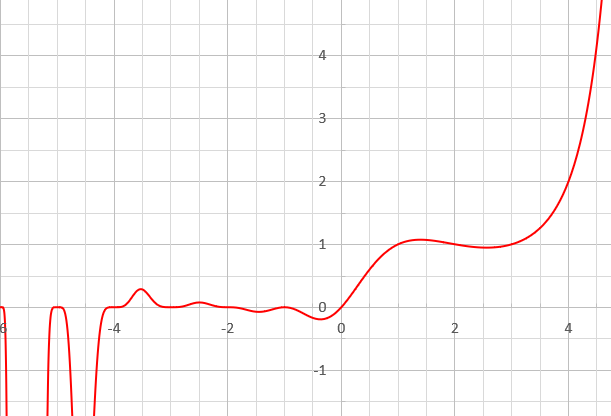

कार्यात्मक समीकरण और पूर्णांक तर्क

बार्न्स G -फलन कार्यात्मक समीकरण को संतुष्ट करता है

$G(z+1)=\Gamma (z)\,G(z)$

सामान्यीकरण G(1) = 1 के साथ। बार्न्स G -फलन के कार्यात्मक समीकरण और यूलर गामा फलन के कार्यात्मक समीकरण के बीच समानता पर ध्यान दें:

$\Gamma (z+1)=z\,\Gamma (z).$

कार्यात्मक समीकरण का तात्पर्य है कि G पूर्णांक तर्कों पर निम्नलिखित मान लेता है:

$G(n)={\begin{cases}0&{\text{if }}n=0,-1,-2,\dots \\\prod _{i=0}^{n-2}i!&{\text{if }}n=1,2,\dots \end{cases}}$

(विशेष रूप से, $\,G(0)=0,G(1)=1$)

और इस प्रकार से

$G(n)={\frac {(\Gamma (n))^{n-1}}{K(n)}}$

जहाँ $\,\Gamma (x)$ गामा फलन को दर्शाता है और K, K-फलन को दर्शाता है। कार्यात्मक समीकरण विशिष्ट रूप से G फलन को परिभाषित करता है यदि उत्तलता की स्थिति,

$\,{\frac {d^{3}}{dx^{3}}}G(x)\geq 0$ जोड़ दिया गया है। इसके अतिरिक्त, बार्न्स G फलन दोहराव सूत्र को संतुष्ट करता है,

$G(x)G\left(x+{\frac {1}{2}}\right)^{2}G(x+1)=e^{\frac {1}{4}}A^{-3}2^{-2x^{2}+3x-{\frac {11}{12}}}\pi ^{x-{\frac {1}{2}}}G\left(2x\right)$

लक्षण वर्णन

गामा फलन के लिए बोहर-मोलेरुप प्रमेय|बोहर-मोलेरुप प्रमेय के समान, स्थिरांक $c>0$,के लिए हमारे समीप $f(x)=cG(x)$

$f(x+1)=\Gamma (x)f(x)$ के लिए है

और के लिए $x>0$

$f(x+n)\sim \Gamma (x)^{n}n^{x \choose 2}f(n)$

जैसा $n\to \infty$.

मान 1/2 पर

$G\left({\tfrac {1}{2}}\right)=2^{\frac {1}{24}}e^{{\frac {3}{2}}\zeta '(-1)}\pi ^{-{\frac {1}{4}}}.$

परावर्तन सूत्र 1.0

इस प्रकार से G-फलन के लिए अंतर समीकरण, गामा फलन के कार्यात्मक समीकरण के साथ, बार्न्स G-फलन के लिए निम्नलिखित प्रतिबिंब सूत्र प्राप्त करने के लिए उपयोग किया जा सकता है (मूल रूप से हरमन किंकेलिन द्वारा सिद्ध) किया गया है:

$\log G(1-z)=\log G(1+z)-z\log 2\pi +\int _{0}^{z}\pi x\cot \pi x\,dx.$

दाहिनी ओर लॉगटैन्जेंट इंटीग्रल का मूल्यांकन क्लॉज़ेन फलन (क्रम 2 के) के संदर्भ में किया जा सकता है, जैसा कि नीचे दिखाया गया है:

$2\pi \log \left({\frac {G(1-z)}{G(1+z)}}\right)=2\pi z\log \left({\frac {\sin \pi z}{\pi }}\right)+\operatorname {Cl} _{2}(2\pi z)$

इस परिणाम का प्रमाण कोटैंजेंट इंटीग्रल के निम्नलिखित मूल्यांकन पर निर्भर करता है: अंकन का परिचय $\operatorname {Lc} (z)$ लॉगकोटैंजेंट इंटीग्रल के लिए, और इस तथ्य का उपयोग करते हुए $\,(d/dx)\log(\sin \pi x)=\pi \cot \pi x$, भागों द्वारा एकीकरण देता है

इस परिणाम का प्रमाण कोटैंजेंट इंटीग्रल के निम्नलिखित मूल्यांकन पर निर्भर करता है: लॉगकोटैंजेंट इंटीग्रल के लिए नोटेशन $\operatorname {Lc} (z)$ का परिचय देना, और इस तथ्य का उपयोग करना कि $\,(d/dx)\log(\sin \pi x)=\pi \cot \pi x$ भागों द्वारा एक एकीकरण देता है

${\begin{aligned}\operatorname {Lc} (z)&=\int _{0}^{z}\pi x\cot \pi x\,dx\\&=z\log(\sin \pi z)-\int _{0}^{z}\log(\sin \pi x)\,dx\\&=z\log(\sin \pi z)-\int _{0}^{z}{\Bigg [}\log(2\sin \pi x)-\log 2{\Bigg ]}\,dx\\&=z\log(2\sin \pi z)-\int _{0}^{z}\log(2\sin \pi x)\,dx.\end{aligned}}$

अभिन्न प्रतिस्थापन करना $\,y=2\pi x\Rightarrow dx=dy/(2\pi )$ देता है

$z\log(2\sin \pi z)-{\frac {1}{2\pi }}\int _{0}^{2\pi z}\log \left(2\sin {\frac {y}{2}}\right)\,dy.$

क्लॉज़ेन फलन - दूसरे क्रम का - अभिन्न प्रतिनिधित्व है

$\operatorname {Cl} _{2}(\theta )=-\int _{0}^{\theta }\log {\Bigg |}2\sin {\frac {x}{2}}{\Bigg |}\,dx.$

चूंकि , अंतराल के अंदर $\,0<\theta <2\pi$, एकीकृत के अंदर पूर्ण मूल्य चिह्न को छोड़ा जा सकता है, क्योंकि सीमा के अंदर इंटीग्रल में 'अर्ध-साइन' फलन जटिलता से सकारात्मक माने जाते है, और यह जटिलता से गैर-शून्य होते है। लॉगटैन्जेंट इंटीग्रल के लिए उपरोक्त परिणाम के साथ इस परिभाषा की तुलना करने पर, निम्नलिखित संबंध स्पष्ट रूप से सामने आते है:

$\operatorname {Lc} (z)=z\log(2\sin \pi z)+{\frac {1}{2\pi }}\operatorname {Cl} _{2}(2\pi z).$

इस प्रकार, शब्दों की थोड़ी सी पुनर्व्यवस्था के पश्चात , प्रमाण पूर्ण हो जाता है:

$2\pi \log \left({\frac {G(1-z)}{G(1+z)}}\right)=2\pi z\log \left({\frac {\sin \pi z}{\pi }}\right)+\operatorname {Cl} _{2}(2\pi z)\,.\,\Box$

संबंध $\,G(1+z)=\Gamma (z)\,G(z)$का उपयोग करना और प्रतिबिंब सूत्र को $\,2\pi$ कारक से विभाजित करना समतुल्य रूप दिया जाता है:

$\log \left({\frac {G(1-z)}{G(z)}}\right)=z\log \left({\frac {\sin \pi z}{\pi }}\right)+\log \Gamma (z)+{\frac {1}{2\pi }}\operatorname {Cl} _{2}(2\pi z)$

संदर्भ: प्रतिबिंब सूत्र के समतुल्य रूप के लिए नीचे एडमचिक देखें, किन्तु इसे अलग प्रमाण के साथ उपयोग किया जाता है ।

परावर्तन सूत्र 2.0

पिछले प्रतिबिंब सूत्र में z को (1/2) − z'' से परिवर्तित करने पर, कुछ सरलीकरण के पश्चात , नीचे दिखाया गया समतुल्य सूत्र मिलता है (बर्नौली बहुपद को सम्मिलित करते हुए): किया जाता है।

$\log \left({\frac {G\left({\frac {1}{2}}+z\right)}{G\left({\frac {1}{2}}-z\right)}}\right)=\log \Gamma \left({\frac {1}{2}}-z\right)+B_{1}(z)\log 2\pi +{\frac {1}{2}}\log 2+\pi \int _{0}^{z}B_{1}(x)\tan \pi x\,dx$

टेलर श्रृंखला विस्तार

टेलर के प्रमेय द्वारा, और बार्न्स फलन के लघुगणकीय व्युत्पन्न पर विचार करते हुए, निम्नलिखित श्रृंखला विस्तार प्राप्त किया जा सकता है:

$\log G(1+z)={\frac {z}{2}}\log 2\pi -\left({\frac {z+(1+\gamma )z^{2}}{2}}\right)+\sum _{k=2}^{\infty }(-1)^{k}{\frac {\zeta (k)}{k+1}}z^{k+1}.$

यह $\,0<z<1$, के लिए मान्य है . यहाँ $\,\zeta (x)$ रीमैन ज़ेटा फलन है:

$\zeta (s)=\sum _{n=1}^{\infty }{\frac {1}{n^{s}}}.$

टेलर विस्तार के दोनों पक्षों का प्रतिपादन करने पर यह प्राप्त होता है:

${\begin{aligned}G(1+z)&=\exp \left[{\frac {z}{2}}\log 2\pi -\left({\frac {z+(1+\gamma )z^{2}}{2}}\right)+\sum _{k=2}^{\infty }(-1)^{k}{\frac {\zeta (k)}{k+1}}z^{k+1}\right]\\&=(2\pi )^{z/2}\exp \left[-{\frac {z+(1+\gamma )z^{2}}{2}}\right]\exp \left[\sum _{k=2}^{\infty }(-1)^{k}{\frac {\zeta (k)}{k+1}}z^{k+1}\right].\end{aligned}}$

इसकी तुलना बार्न्स फलन के वीयरस्ट्रैस उत्पाद रूप से करने पर निम्नलिखित संबंध देखने को मिलते है:

$\exp \left[\sum _{k=2}^{\infty }(-1)^{k}{\frac {\zeta (k)}{k+1}}z^{k+1}\right]=\prod _{k=1}^{\infty }\left\{\left(1+{\frac {z}{k}}\right)^{k}\exp \left({\frac {z^{2}}{2k}}-z\right)\right\}$

गुणन सूत्र

गामा फलन की तरह, G-फलन में भी गुणन सूत्र होता है:

$G(nz)=K(n)n^{n^{2}z^{2}/2-nz}(2\pi )^{-{\frac {n^{2}-n}{2}}z}\prod _{i=0}^{n-1}\prod _{j=0}^{n-1}G\left(z+{\frac {i+j}{n}}\right)$

जहाँ $K(n)$ द्वारा दिया गया स्थिरांक है:

$K(n)=e^{-(n^{2}-1)\zeta ^{\prime }(-1)}\cdot n^{\frac {5}{12}}\cdot (2\pi )^{(n-1)/2}\,=\,(Ae^{-{\frac {1}{12}}})^{n^{2}-1}\cdot n^{\frac {5}{12}}\cdot (2\pi )^{(n-1)/2}.$

यहाँ $\zeta ^{\prime }$ रीमैन ज़ेटा फलन का व्युत्पन्न है और $A$ ग्लैशर-किंकलिन स्थिरांक माना जाता है।

पूर्ण मान

यह सच है $G({\overline {z}})={\overline {G(z)}}$, इस प्रकार $|G(z)|^{2}=G(z)G({\overline {z}})$. इस संबंध से और ऊपर प्रस्तुत वीयरस्ट्रैस उत्पाद प्रपत्र से कोई यह दिखा सकता है

$|G(x+iy)|=|G(x)|\exp \left(y^{2}{\frac {1+\gamma }{2}}\right){\sqrt {1+{\frac {y^{2}}{x^{2}}}}}{\sqrt {\prod _{k=1}^{\infty }\left(1+{\frac {y^{2}}{(x+k)^{2}}}\right)^{k+1}\exp \left(-{\frac {y^{2}}{k}}\right)}}.$

यह संबंध मनमाने ढंग $x\in \mathbb {R} \setminus \{0,-1,-2,\dots \}$ से मान्य है और $y\in \mathbb {R}$. अगर $x=0$ तो इसके अतिरिक्त नीचे दिया गया सूत्र मान्य है:

यह संबंध इच्छा अनुसार $x\in \mathbb {R} \setminus \{0,-1,-2,\dots \}$ , और $y\in \mathbb {R}$ के लिए मान्य है यदि $x=0$, तो इसके अतिरिक्त नीचे दिया गया सूत्र मान्य है

$|G(iy)|=y\exp \left(y^{2}{\frac {1+\gamma }{2}}\right){\sqrt {\prod _{k=1}^{\infty }\left(1+{\frac {y^{2}}{k^{2}}}\right)^{k+1}\exp \left(-{\frac {y^{2}}{k}}\right)}}$

इच्छा अनुसार वास्तविक y के लिए।

स्पर्शोन्मुख विस्तार

G(z + 1) के लघुगणक में निम्नलिखित स्पर्शोन्मुख विस्तार है, जैसा कि बार्न्स द्वारा स्थापित किया गया है:

${\begin{aligned}\log G(z+1)={}&{\frac {z^{2}}{2}}\log z-{\frac {3z^{2}}{4}}+{\frac {z}{2}}\log 2\pi -{\frac {1}{12}}\log z\\&{}+\left({\frac {1}{12}}-\log A\right)+\sum _{k=1}^{N}{\frac {B_{2k+2}}{4k\left(k+1\right)z^{2k}}}~+~O\left({\frac {1}{z^{2N+2}}}\right).\end{aligned}}$

यहां ही $B_{k}$ बर्नौली संख्याएँ हैं और $A$ ग्लैशर-किंकलिन स्थिरांक है। (ध्यान दें कि बार्न्स के समय यह कुछ सीमा तक भ्रमित करने वाला था बर्नौली संख्या $B_{2k}$ के रूप में लिखा गया होगा $(-1)^{k+1}B_{k}$, किन्तु यह परिपाटी अब प्रचलित नहीं है।) यह विस्तार इसके लिए मान्य $z$ है किसी भी ऐसे सेक्टर में जिसमें नकारात्मक वास्तविक अक्ष $|z|$ उच्चय न हो।

लॉगगामा इंटीग्रल से संबंध

पैरामीट्रिक लॉगगामा का मूल्यांकन बार्न्स G-फलन के संदर्भ में किया जा सकता है (संदर्भ: यह परिणाम नीचे एडमचिक में पाया गया है, किन्तु बिना प्रमाण में दर्शाया गया है):

$\int _{0}^{z}\log \Gamma (x)\,dx={\frac {z(1-z)}{2}}+{\frac {z}{2}}\log 2\pi +z\log \Gamma (z)-\log G(1+z)$

प्रमाण कुछ सीमा तक अप्रत्यक्ष होते है, और इसमें पहले गामा फलन और बार्न्स G-फलन के लघुगणकीय अंतर पर विचार करना सम्मिलित होता है:

$z\log \Gamma (z)-\log G(1+z)$

जहाँ

${\frac {1}{\Gamma (z)}}=ze^{\gamma z}\prod _{k=1}^{\infty }\left\{\left(1+{\frac {z}{k}}\right)e^{-z/k}\right\}$

और $\,\gamma$ यूलर-माशेरोनी स्थिरांक है।

बार्न्स फलन और गामा फलन के वीयरस्ट्रैस उत्पाद रूपों का लघुगणक लेने पर यह मिलता है:

${\begin{aligned}&z\log \Gamma (z)-\log G(1+z)=-z\log \left({\frac {1}{\Gamma (z)}}\right)-\log G(1+z)\\[5pt]={}&{-z}\left[\log z+\gamma z+\sum _{k=1}^{\infty }{\Bigg \{}\log \left(1+{\frac {z}{k}}\right)-{\frac {z}{k}}{\Bigg \}}\right]\\[5pt]&{}-\left[{\frac {z}{2}}\log 2\pi -{\frac {z}{2}}-{\frac {z^{2}}{2}}-{\frac {z^{2}\gamma }{2}}+\sum _{k=1}^{\infty }{\Bigg \{}k\log \left(1+{\frac {z}{k}}\right)+{\frac {z^{2}}{2k}}-z{\Bigg \}}\right]\end{aligned}}$

शब्दों का थोड़ा सरलीकरण और पुनः क्रम लगाने से श्रृंखला का विस्तार होता है:

${\begin{aligned}&\sum _{k=1}^{\infty }{\Bigg \{}(k+z)\log \left(1+{\frac {z}{k}}\right)-{\frac {z^{2}}{2k}}-z{\Bigg \}}\\[5pt]={}&{-z}\log z-{\frac {z}{2}}\log 2\pi +{\frac {z}{2}}+{\frac {z^{2}}{2}}-{\frac {z^{2}\gamma }{2}}-z\log \Gamma (z)+\log G(1+z)\end{aligned}}$

अंत में, गामा फलन के वीयरस्ट्रैस उत्पाद रूप का लघुगणक लें, और अंतराल $\,[0,\,z]$ पर एकीकृत करें प्राप्त करने के लिए:

${\begin{aligned}&\int _{0}^{z}\log \Gamma (x)\,dx=-\int _{0}^{z}\log \left({\frac {1}{\Gamma (x)}}\right)\,dx\\[5pt]={}&{-(z\log z-z)}-{\frac {z^{2}\gamma }{2}}-\sum _{k=1}^{\infty }{\Bigg \{}(k+z)\log \left(1+{\frac {z}{k}}\right)-{\frac {z^{2}}{2k}}-z{\Bigg \}}\end{aligned}}$

दोनों मूल्यांकनों को समान करने से प्रमाण पूर्ण हो जाता है:

$\int _{0}^{z}\log \Gamma (x)\,dx={\frac {z(1-z)}{2}}+{\frac {z}{2}}\log 2\pi +z\log \Gamma (z)-\log G(1+z)$

और जब से $\,G(1+z)=\Gamma (z)\,G(z)$ जब ,

$\int _{0}^{z}\log \Gamma (x)\,dx={\frac {z(1-z)}{2}}+{\frac {z}{2}}\log 2\pi -(1-z)\log \Gamma (z)-\log G(z)\,.$

संदर्भ

• Askey, R.A.; Roy, R. (2010), "बार्न्स जी-फ़ंक्शन", in Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W. (eds.), NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0-521-19225-5, MR 2723248

• Adamchik, Viktor S. (2003). "Contributions to the Theory of the Barnes function". arXiv:math/0308086.