प्रतिनिधित्व सिद्धांत

This article is about रेखीय परिवर्तनों और आव्यूहों द्वारा बीजगणितीय संरचनाओं के निरूपण का सिद्धांत. For प्रतिनिधित्व सिद्धांत अन्य विषयों में, see प्रतिनिधित्व (बहुविकल्पी).

Not to be confused with समूह प्रस्तुति.

प्रतिनिधित्व सिद्धांत गणित की एक शाखा है जो वेक्टर रिक्त स्थान के रैखिक परिवर्तनों के रूप में अपने तत्वों का प्रतिनिधित्व करके सार बीजगणितीय संरचनाओं का अध्ययन करता है, और इन अमूर्त बीजगणितीय संरचनाओं पर मॉड्यूल का अध्ययन करता है। संक्षेप में, एक प्रतिनिधित्व मैट्रिक्स और उनके बीजगणितीय संचालन (उदाहरण के लिए, मैट्रिक्स जोड़, मैट्रिक्स गुणा) द्वारा अपने तत्वों का वर्णन करके एक अमूर्त बीजगणितीय वस्तु को और अधिक ठोस बनाता है। मैट्रिसेस और रैखिक संचालकों का सिद्धांत अच्छी तरह से समझा जाता है, इसलिए परिचित रैखिक बीजगणित वस्तुओं के संदर्भ में अधिक अमूर्त वस्तुओं का प्रतिनिधित्व गुणों को चमकाने में मदद करता है और कभी-कभी अधिक सार सिद्धांतों पर गणना को सरल करता है।

प्रतिनिधित्व सिद्धांत अध्ययन करता है कि कैसे बीजगणितीय संरचनाएं वस्तुओं पर कार्य करती हैं। एक सरल उदाहरण यह है कि डायहेड्रल समूह, जिसमें प्रतिबिंब और घुमाव शामिल हैं, बहुभुज को रूपांतरित करते हैं।

इस तरह के विवरण के लिए उपयुक्त बीजगणितीय वस्तुओं में समूह, सहयोगी बीजगणित और लाई बीजगणित शामिल हैं। इनमें से सबसे प्रमुख (और ऐतिहासिक रूप से पहला) समूहों का प्रतिनिधित्व सिद्धांत है, जिसमें एक समूह के तत्वों को इनवर्टिबल मैट्रिसेस द्वारा इस तरह से दर्शाया जाता है कि समूह संचालन मैट्रिक्स गुणन है।

प्रतिनिधित्व सिद्धांत एक उपयोगी तरीका है क्योंकि यह अमूर्त बीजगणित की समस्याओं को रेखीय बीजगणित की समस्याओं में कम कर देता है, एक ऐसा विषय जिसे अच्छी तरह से समझा जाता है। इसके अलावा, सदिश स्थान जिस पर एक समूह (उदाहरण के लिए) का प्रतिनिधित्व किया जाता है, अनंत-आयामी हो सकता है, और उदाहरण के लिए, एक हिल्बर्ट स्थान होने की अनुमति देकर, विश्लेषण के तरीकों को समूहों के सिद्धांत पर लागू किया जा सकता है। भौतिकी में प्रतिनिधित्व सिद्धांत भी महत्वपूर्ण है क्योंकि, उदाहरण के लिए, यह वर्णन करता है कि भौतिक प्रणाली का समरूपता समूह उस प्रणाली का वर्णन करने वाले समीकरणों के समाधान को कैसे प्रभावित करता है।

प्रतिनिधित्व सिद्धांत गणित के सभी क्षेत्रों में दो कारणों से व्यापक है। सबसे पहले, प्रतिनिधित्व सिद्धांत के अनुप्रयोग विविध हैं: बीजगणित पर इसके प्रभाव के अतिरिक्त, प्रतिनिधित्व सिद्धांत:

• हार्मोनिक विश्लेषण के माध्यम से फूरियर विश्लेषण को प्रकाशित और सामान्य करता है,
• अपरिवर्तनीय सिद्धांत और एर्लांगेन कार्यक्रम के माध्यम से ज्यामिति से जुड़ा है,
• संख्या सिद्धांत में ऑटोमोर्फिक रूपों और लैंगलैंड्स कार्यक्रम के माध्यम से प्रभाव पड़ता है।

दूसरा, प्रतिनिधित्व सिद्धांत के विविध दृष्टिकोण हैं। बीजगणितीय ज्यामिति, मॉड्यूल सिद्धांत, विश्लेषणात्मक संख्या सिद्धांत, अंतर ज्यामिति, संचालिका सिद्धांत, बीजगणितीय संयोजक और टोपोलॉजी से विधियों का उपयोग करके समान वस्तुओं का अध्ययन किया जा सकता है।

प्रतिनिधित्व सिद्धांत की सफलता ने कई सामान्यीकरणों को जन्म दिया है। श्रेणी सिद्धांत में सबसे सामान्य में से एक है। जिन बीजगणितीय वस्तुओं पर प्रतिनिधित्व सिद्धांत लागू होता है, उन्हें विशेष प्रकार की श्रेणियों के रूप में देखा जा सकता है, और ऑब्जेक्ट श्रेणी से सदिश रिक्त स्थान की श्रेणी के ऑपरेटर के रूप में प्रस्तुतियों को देखा जा सकता है।यह विवरण दो स्पष्ट सामान्यीकरणों की ओर इशारा करता है: पहला, बीजगणितीय वस्तुओं को अधिक सामान्य श्रेणियों द्वारा प्रतिस्थापित किया जा सकता है; दूसरा, सदिश स्थानों की लक्ष्य श्रेणी को अन्य सुविचारित श्रेणियों से बदला जा सकता है।

परिभाषाएं और अवधारणाएं

मान लीजिए V क्षेत्र F पर एक सदिश समष्टि है। उदाहरण के लिए, मान लें कि V, Rⁿ या Cⁿ है, जो क्रमशः वास्तविक या जटिल संख्याओं पर स्तंभ सदिशों का मानक n-आयामी स्थान है। इस मामले में, प्रतिनिधित्व सिद्धांत का विचार वास्तविक या जटिल संख्याओं के n × n आव्यूहों का उपयोग करके ठोस रूप से सार बीजगणित करना है।

बीजगणितीय वस्तुओं के तीन मुख्य प्रकार हैं जिनके लिए यह किया जा सकता है: समूह (गणित), साहचर्य बीजगणित और लाई बीजगणित।

• सभी व्युत्क्रमणीय n × n आव्यूहों का समुच्चय आव्यूह गुणन के अंतर्गत एक समूह है, और समूहों का प्रतिनिधित्व सिद्धांत व्युत्क्रमणीय आव्यूहों के संदर्भ में इसके तत्वों का वर्णन ("प्रतिनिधित्व") करके एक समूह का विश्लेषण करता है।
• मैट्रिक्स जोड़ और गुणन सभी n × n मैट्रिक्स के सेट को एक साहचर्य बीजगणित में बनाते हैं, और इसलिए साहचर्य बीजगणित का एक संगत प्रतिनिधित्व सिद्धांत है।
• यदि हम मैट्रिक्स गुणन MN को मैट्रिक्स कम्यूटेटर MN - NM से प्रतिस्थापित करते हैं, तो n × n मैट्रिक्स इसके बजाय एक लाई बीजगणित बन जाते हैं, जो लाई बीजगणित के एक प्रतिनिधित्व सिद्धांत की ओर ले जाता है।

यह किसी भी क्षेत्र F और F पर किसी भी सदिश स्थान V के लिए सामान्यीकरण करता है, मैट्रिक्स गुणन की जगह मैट्रिक्स और रचना की जगह रैखिक मानचित्रों के साथ: V के ऑटोमोर्फिज्म का एक समूह GL (V, F) है, जो सभी एंडोमोर्फिज्म का एक सहयोगी बीजगणित End_F(V) है। V का, और एक संगत लाई बीजगणित gl(V,F).

परिभाषा

See also: समूह प्रतिनिधित्व, बीजगणित प्रतिनिधित्व, and लाई बीजगणित प्रतिनिधित्व

गतिविधि

प्रतिनिधित्व क्या है, यह कहने के दो तरीके हैं। पहले एक क्रिया के विचार का उपयोग करता है, मैट्रिक्स गुणन द्वारा कॉलम वैक्टर पर मेट्रिसेस के कार्य करने के तरीके को सामान्य करता है। सदिश समष्टि V पर समूह G या (साहचर्य या लाई) बीजगणित A का निरूपण एक मानचित्र है

$\Phi \colon G\times V\to V\quad {\text{or}}\quad \Phi \colon A\times V\to V$

दो गुणों के साथ। सबसे पहले, g में किसी भी G के लिए (या A में), मानचित्र

${\begin{aligned}\Phi (g)\colon V&\to V\\v&\mapsto \Phi (g,v)\end{aligned}}$

रैखिक है (F से अधिक)। दूसरा, अगर हम 'g · v के लिए संकेतन का परिचय देते हैं $\Phi$ (g, v), फिर किसी भी g₁, g₂ के लिए और v में V:

$(1)\quad e\cdot v=v$

$(2)\quad g_{1}\cdot (g_{2}\cdot v)=(g_{1}g_{2})\cdot v$

जहां e, G का पहचान तत्व है और g₁g₂ G में उत्पाद है। सहयोगी बीजगणित की आवश्यकता समान है, सिवाय इसके कि सहयोगी बीजगणित में हमेशा एक पहचान तत्व नहीं होता है, जिसमें समीकरण (1) को अनदेखा किया जाता है। समीकरण (2) आव्यूह गुणन की साहचर्यता की एक अमूर्त अभिव्यक्ति है। यह मैट्रिक्स कम्यूटेटर के लिए नहीं है और कम्यूटेटर के लिए कोई पहचान तत्व नहीं है। इसलिए लाई बीजगणित के लिए, केवल आवश्यकता यह है कि किसी भी x₁, x₂ में A और v में V के लिए:

$(2')\quad x_{1}\cdot (x_{2}\cdot v)-x_{2}\cdot (x_{1}\cdot v)=[x_{1},x_{2}]\cdot v$

जहां [x₁, x₂] झूठ बीजगणित परिभाषा और पहला गुण है, जो मैट्रिक्स कम्यूटेटर mn - nm को सामान्यीकृत करता है।

मैपिंग

एक प्रतिनिधित्व को परिभाषित करने का दूसरा तरीका मानचित्र पर केंद्रित है φ जी को एक रैखिक मानचित्र φ(g): V → V में भेज रहा है, जो संतुष्ट करता है

$\varphi (g_{1}g_{2})=\varphi (g_{1})\circ \varphi (g_{2})\quad {\text{for all }}g_{1},g_{2}\in G$

और इसी तरह अन्य मामलों में। यह दृष्टिकोण अधिक संक्षिप्त और अधिक सारगर्भित दोनों है।

इस दृष्टि से:

• सदिश समष्टि V पर समूह G का निरूपण एक समूह समरूपता φ: G → GL(V,'F');* एक सदिश स्थान V पर एक साहचर्य बीजगणित A का प्रतिनिधित्व एक बीजगणित समरूपता है φ: A → अंत_F(में);* सदिश स्थान V पर लाई बीजगणित 𝖆 का प्रतिनिधित्व एक लाई बीजगणित समरूपता φ: 𝖆 → 'gl'(V,'F') है।

शब्दावली

सदिश समष्टि V को φ का 'प्रतिनिधित्व स्थान' कहा जाता है और इसके सदिश समष्टि के आयाम (यदि परिमित) को निरूपण का 'आयाम' कहा जाता है (कभी-कभी डिग्री, जैसे कि ). जब समरूपता φ संदर्भ से स्पष्ट हो तो स्वयं V को निरूपण के रूप में संदर्भित करना भी एक सामान्य प्रथा है; अन्यथा अंकन (V, φ) का उपयोग प्रतिनिधित्व को निरूपित करने के लिए किया जा सकता है।

जब V परिमित आयाम n का हो, तो V के लिए 'F' के साथ V की पहचान करने के लिए कोई आधार (रैखिक बीजगणित) चुन सकता हैⁿ, और इसलिए फ़ील्ड 'F' में प्रविष्टियों के साथ एक मैट्रिक्स प्रतिनिधित्व पुनर्प्राप्त करें।

एक प्रभावी या विश्वसनीय निरूपण एक निरूपण (V, φ) है, जिसके लिए समाकारिता φ अंतःक्षेपी है।

समतुल्य मानचित्र और समरूपता

See also: समांतर मानचित्र

यदि V और W 'F' पर सदिश समष्टियाँ हैं, जो समूह G के प्रतिनिधित्व φ और ψ से सुसज्जित हैं, तो V से W तक 'समतुल्य मानचित्र' रैखिक मानचित्र α: V → W ऐसा है कि

$\alpha (g\cdot v)=g\cdot \alpha (v)$

G में सभी g और V में v के लिए। φ: G → GL(V) और ψ: G → GL(W) के संदर्भ में, इसका मतलब है

$\alpha \circ \varphi (g)=\psi (g)\circ \alpha$

G में सभी g के लिए, अर्थात् निम्न क्रमविनिमेय आरेख:

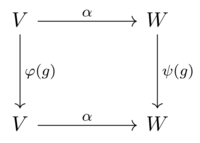एक साहचर्य या लाई बीजगणित के निरूपण के लिए समतुल्य मानचित्र इसी तरह परिभाषित किए गए हैं। यदि α व्युत्क्रमणीय है, तो इसे एक समरूपता कहा जाता है, जिस स्थिति में V और W (या, अधिक सटीक रूप से, φ और ψ) समरूपी निरूपण हैं, जिन्हें समतुल्य निरूपण भी कहा जाता है। एक समपरिवर्ती मानचित्र को अक्सर निरूपणों का एक आपस में ग्रन्थिल हुआ मानचित्र कहा जाता है। साथ ही, समूह की स्थिति में G, कभी-कभी इसे ए कहा जाता है G-मानचित्र।

व्यावहारिक उद्देश्यों के लिए आइसोमोर्फिक प्रतिनिधित्व समान हैं; वे प्रतिनिधित्व किए जा रहे समूह या बीजगणित के बारे में समान जानकारी प्रदान करते हैं। प्रतिनिधित्व सिद्धांत इसलिए समरूपता तक के प्रतिनिधित्व को वर्गीकृत करना चाहता है।

उप-प्रतिनिधित्व, उद्धरण, और अलघुकरणीय निरूपण

See also: अपरिवर्तनीय प्रतिनिधित्व and साधारण मॉड्यूल

अगर $(V,\psi )$ एक समूह (कहते हैं) का प्रतिनिधित्व है $G$, और $W$ की एक रेखीय उपसमष्टि है $V$ की क्रिया द्वारा संरक्षित है $G$ इस अर्थ में कि सभी के लिए $w\in W$ और $g\in G$, $g\cdot w\in W$ (जीन पियरे सेरे इन्हें कहते हैं $W$ के नीचे स्थिर $G$), तब $W$ उपनिरूपण कहा जाता है: परिभाषित करके

$$\phi :G\to {\text{Aut}}(W)$$

जहाँ $\phi (g)$ का प्रतिबंध है $\psi (g)$ को $W$, $(W,\phi )$ का प्रतिनिधित्व है $G$ और का समावेश $W\hookrightarrow V$ समतुल्य नक्शा है। भागफल स्थान (रैखिक बीजगणित) $V/W$ का प्रतिनिधित्व भी किया जा सकता है $G$. अगर $V$ ठीक दो उप-निरूपण हैं, अर्थात् शून्य सदिश स्थान {0} और $V$ स्वयं, तब प्रतिनिधित्व को 'इरेड्यूसिबल' कहा जाता है; अगर $V$ एक उचित गैर-तुच्छ उप-प्रतिनिधित्व है, प्रतिनिधित्व को 'कम करने योग्य' कहा जाता है।

इरेड्यूसिबल प्रतिनिधित्व की परिभाषा का तात्पर्य शूर की लेम्मा से है: एक समतुल्य मानचित्र

$$\alpha :(V,\psi )\to (V',\psi ')$$

=अप्रासंगिक अभ्यावेदन के बीच या तो शून्य नक्शा या एक समरूपता है, क्योंकि इसकी कर्नेल (रैखिक बीजगणित) और छवि (गणित) उप-प्रतिनिधित्व हैं। विशेष रूप से, कब $V=V'$, इससे पता चलता है कि के समतुल्य एंडोमोर्फिज्म $V$ अंतर्निहित क्षेत्र F पर एक साहचर्य विभाजन बीजगणित बनाते हैं। यदि F बीजगणितीय रूप से बंद है, तो एक अलघुकरणीय प्रतिनिधित्व के एकमात्र समतुल्य एंडोमोर्फिज्म पहचान के अदिश गुणक हैं।

कई समूहों के लिए इर्रिड्यूसिबल प्रतिनिधित्व प्रतिनिधित्व सिद्धांत के निर्माण खंड हैं: यदि एक प्रतिनिधित्व $V$ अप्रासंगिक नहीं है तो यह एक उप-प्रस्तुतिकरण और एक भागफल से बनाया गया है जो दोनों कुछ अर्थों में सरल हैं; उदाहरण के लिए, यदि $V$ परिमित-आयामी है, तो उप-निरूपण और भागफल दोनों का आयाम छोटा है। ऐसे प्रति उदाहरण हैं जहां एक प्रतिनिधित्व में एक उप-प्रतिनिधित्व होता है, लेकिन केवल एक गैर-तुच्छ इर्रेड्यूबल घटक होता है। उदाहरण के लिए, योगात्मक समूह $(\mathbb {R} ,+)$ दो आयामी प्रतिनिधित्व है

$$\phi (a)={\begin{bmatrix}1&a\\0&1\end{bmatrix}}$$

इस समूह में वेक्टर है ${\begin{bmatrix}1&0\end{bmatrix}}^{\mathsf {T}}$ इस समरूपता द्वारा तय किया गया है, लेकिन पूरक उप-स्थान मैप करता है

$${\begin{bmatrix}0\\1\end{bmatrix}}\mapsto {\begin{bmatrix}a\\1\end{bmatrix}}$$

केवल एक अलघुकरणीय उपनिरूपण दे रही है। यह सभी एकांगी समूहों के लिए सही है।

प्रत्यक्ष योग और अविघटनीय निरूपण

See also: Direct sum, indecomposable module, and semisimple module

यदि (V, φ) और (W, ψ) एक समूह G का प्रतिनिधित्व करते हैं (कहते हैं), तो V और W के सदिश स्थानों का प्रत्यक्ष योग एक प्रतिनिधित्व है, एक विहित तरीके से, समीकरण के माध्यम से

$g\cdot (v,w)=(g\cdot v,g\cdot w).$

अभ्यावेदन के प्रत्यक्ष योग में समूह G के बारे में दो निरूपणों की तुलना में व्यक्तिगत रूप से अधिक जानकारी नहीं होती है। यदि एक प्रतिनिधित्व दो उचित गैर-तुच्छ उप-प्रतिनिधियों का प्रत्यक्ष योग है, तो इसे अपघटन योग्य कहा जाता है। अन्यथा इसे अपघटनीय कहा जाता है।

पूर्ण न्यूनीकरण

अनुकूल परिस्थितियों में, प्रत्येक परिमित-आयामी प्रतिनिधित्व अलघुकरणीय अभ्यावेदन का प्रत्यक्ष योग होता है: ऐसे अभ्यावेदन को अर्धसरल कहा जाता है। इस मामले में, यह केवल अलघुकरणीय अभ्यावेदन को समझने के लिए पर्याप्त है। ऐसे उदाहरण जहां पूर्ण न्यूनीकरण की घटना पर वेइल का प्रमेय होता है, उनमें परिमित समूह शामिल हैं (मास्कके प्रमेय देखें), कॉम्पैक्ट समूह, और अर्ध-सरल लाई बीजगणित।

ऐसे मामलों में जहां पूर्ण रिड्यूसबिलिटी धारण नहीं करती है, किसी को यह समझना चाहिए कि एक उप-प्रतिनिधित्व द्वारा भागफल के विस्तार के रूप में इर्रिडिएबल अभ्यावेदन से कैसे अपघटनीय अभ्यावेदन बनाया जा सकता है।

अभ्यावेदन के टेंसर उत्पाद

Main article: Tensor product of representations

कल्पना करना $\phi _{1}:G\rightarrow \mathrm {GL} (V_{1})$ और $\phi _{2}:G\rightarrow \mathrm {GL} (V_{2})$ समूह के प्रतिनिधि हैं $G$. तब हम एक प्रतिनिधित्व बना सकते हैं $\phi _{1}\otimes \phi _{2}$ टेंसर उत्पाद सदिश स्थान पर अभिनय करने वाले G का $V_{1}\otimes V_{2}$ निम्नलिखित नुसार:

$(\phi _{1}\otimes \phi _{2})(g)=\phi _{1}(g)\otimes \phi _{2}(g)$.

अगर $\phi _{1}$ और $\phi _{2}$ लाई बीजगणित के निरूपण हैं, तो उपयोग करने के लिए सही सूत्र है

$(\phi _{1}\otimes \phi _{2})(X)=\phi _{1}(X)\otimes I+I\otimes \phi _{2}(X)$.

इस उत्पाद को कोलजेब्रा पर Tensor algebra#Coproduct के रूप में पहचाना जा सकता है। सामान्य तौर पर, अलघुकरणीय अभ्यावेदन का टेंसर उत्पाद अलघुकरणीय नहीं होता है; इरेड्यूसिबल प्रस्तुतियों के प्रत्यक्ष योग के रूप में एक टेन्सर उत्पाद को अपघटित करने की प्रक्रिया को क्लेब्स-गॉर्डन_कोएफिशिएंट्स | क्लेब्स-गॉर्डन सिद्धांत के रूप में जाना जाता है।

SU(2) के प्रतिनिधित्व सिद्धांत के मामले में | समूह SU(2) का प्रतिनिधित्व सिद्धांत (या समतुल्य रूप से, इसके जटिल झूठ बीजगणित का $\mathrm {sl} (2;\mathbb {C} )$), अपघटन को काम करना आसान है। अलघुकरणीय अभ्यावेदन को एक पैरामीटर द्वारा लेबल किया जाता है $l$ वह एक गैर-ऋणात्मक पूर्णांक या आधा पूर्णांक है; प्रतिनिधित्व तो आयाम है $2l+1$. मान लीजिए कि हम लेबल के साथ दो अभ्यावेदन के प्रतिनिधित्व के टेंसर उत्पाद को लेते हैं $l_{1}$ और $l_{2},$ जहां हम मानते हैं $l_{1}\geq l_{2}$. तब टेंसर उत्पाद लेबल के साथ प्रत्येक प्रतिनिधित्व की एक प्रति के प्रत्यक्ष योग के रूप में विघटित हो जाता है $l$, कहाँ $l$ से लेकर $l_{1}-l_{2}$ को $l_{1}+l_{2}$ 1 की वृद्धि में। यदि, उदाहरण के लिए, $l_{1}=l_{2}=1$, फिर के मान $l$ जो 0, 1 और 2 होते हैं। इस प्रकार, टेन्सर उत्पाद आयाम का प्रतिनिधित्व करता है $(2l_{1}+1)\times (2l_{2}+1)=3\times 3=9$ 1-आयामी प्रतिनिधित्व के प्रत्यक्ष योग के रूप में विघटित होता है $(l=0),$ एक 3-आयामी प्रतिनिधित्व $(l=1),$ और एक 5-आयामी प्रतिनिधित्व $(l=2)$.

शाखाएँ और विषय

See also: Group representation

प्रतिनिधित्व सिद्धांत इसकी शाखाओं की संख्या और समूहों और बीजगणितों के प्रतिनिधित्व के अध्ययन के लिए दृष्टिकोण की विविधता के लिए उल्लेखनीय है। हालांकि, सभी सिद्धांतों में पहले से ही चर्चा की गई बुनियादी अवधारणाओं में समानता है, वे विस्तार से काफी भिन्न हैं। अंतर कम से कम 3 गुना हैं:

1. प्रतिनिधित्व सिद्धांत प्रतिनिधित्व किए जा रहे बीजगणितीय वस्तु के प्रकार पर निर्भर करता है। समूहों के कई अलग-अलग वर्ग हैं, साहचर्य बीजगणित और झूठ बीजगणित, और उनके प्रतिनिधित्व सिद्धांतों में सभी का एक अलग स्वाद है।
2. प्रतिनिधित्व सिद्धांत सदिश स्थान की प्रकृति पर निर्भर करता है जिस पर बीजगणितीय वस्तु का प्रतिनिधित्व किया जाता है। सबसे महत्वपूर्ण अंतर आयाम (वेक्टर स्पेस) | परिमित-आयामी प्रतिनिधित्व और अनंत-आयामी प्रतिनिधित्व के बीच है। अनंत-आयामी मामले में, अतिरिक्त संरचनाएं महत्वपूर्ण हैं (उदाहरण के लिए, स्थान एक हिल्बर्ट स्थान है या नहीं, बानाच स्थान, आदि)। परिमित-आयामी मामले में अतिरिक्त बीजगणितीय संरचनाएं भी लगाई जा सकती हैं।
3. प्रतिनिधित्व सिद्धांत उस क्षेत्र (गणित) के प्रकार पर निर्भर करता है जिस पर सदिश स्थान परिभाषित किया गया है। सबसे महत्वपूर्ण मामले जटिल संख्याओं के क्षेत्र, वास्तविक संख्याओं के क्षेत्र, परिमित क्षेत्रों और पी-एडिक संख्याओं के क्षेत्र हैं। अतिरिक्त कठिनाइयाँ सकारात्मक विशेषता वाले क्षेत्रों के लिए और उन क्षेत्रों के लिए उत्पन्न होती हैं जो बीजगणितीय रूप से बंद नहीं हैं।

परिमित समूह

Main article: Representation of a finite group

परिमित समूहों के अध्ययन में समूह प्रतिनिधित्व एक बहुत ही महत्वपूर्ण उपकरण है। वे परिमित समूह सिद्धांत के ज्यामिति और क्रिस्टलोग्राफिक समूह के अनुप्रयोगों में भी उत्पन्न होते हैं। परिमित समूहों के प्रतिनिधित्व सामान्य सिद्धांत की कई विशेषताओं को प्रदर्शित करते हैं और प्रतिनिधित्व सिद्धांत में अन्य शाखाओं और विषयों के लिए रास्ता बताते हैं।

विशेषता शून्य के एक क्षेत्र पर, एक परिमित समूह G के प्रतिनिधित्व में कई सुविधाजनक गुण हैं। सबसे पहले, G का निरूपण सेमीसिंपल (पूरी तरह से कम करने योग्य) है। यह माश्के के प्रमेय का एक परिणाम है, जिसमें कहा गया है कि जी-प्रतिनिधित्व डब्ल्यू के किसी भी उप-प्रतिनिधित्व वी में जी-अपरिवर्तनीय पूरक है। एक प्रमाण यह है कि किसी प्रक्षेपण (रैखिक बीजगणित) π को W से V तक चुनें और इसे इसके औसत π से बदलें_G द्वारा परिभाषित

$\pi _{G}(x)={\frac {1}{|G|}}\sum _{g\in G}g\cdot \pi (g^{-1}\cdot x).$

π_G समपरिवर्ती है, और इसकी गिरी आवश्यक पूरक है।

परिमित-आयामी जी-प्रतिनिधित्व को चरित्र सिद्धांत का उपयोग करके समझा जा सकता है: प्रतिनिधित्व का चरित्र φ: G → GL(V) वर्ग फ़ंक्शन χ है_φ: जी → 'एफ' द्वारा परिभाषित

$\chi _{\varphi }(g)=\mathrm {Tr} (\varphi (g))$

कहाँ $\mathrm {Tr}$ एक मैट्रिक्स का निशान है। G का एक अलघुकरणीय निरूपण पूरी तरह से इसके चरित्र द्वारा निर्धारित होता है।

Maschke की प्रमेय आम तौर पर सकारात्मक विशेषता p के क्षेत्रों के लिए अधिक होती है, जैसे कि परिमित क्षेत्र, जब तक कि प्रधान p, G के समूह क्रम का सहअभाज्य है। एक उपशाखा में अध्ययन किया जाता है जिसे मॉड्यूलर प्रतिनिधित्व सिद्धांत कहा जाता है।

औसत तकनीक यह भी दिखाती है कि यदि 'एफ' वास्तविक या जटिल संख्या है, तो कोई भी जी-प्रतिनिधित्व एक आंतरिक उत्पाद को संरक्षित करता है। $\langle \cdot ,\cdot \rangle$ वी पर इस अर्थ में कि

$\langle g\cdot v,g\cdot w\rangle =\langle v,w\rangle$

जी में सभी जी और डब्ल्यू में डब्ल्यू के लिए डब्ल्यू। इसलिए कोई भी जी-प्रतिनिधित्व एकात्मक प्रतिनिधित्व है।

एकात्मक अभ्यावेदन स्वचालित रूप से अर्ध-सरल होते हैं, क्योंकि मस्कके के परिणाम को उप-प्रतिनिधित्व के ऑर्थोगोनल पूरक द्वारा सिद्ध किया जा सकता है। ऐसे समूहों के निरूपण का अध्ययन करते समय जो परिमित नहीं हैं, एकात्मक अभ्यावेदन परिमित समूह के वास्तविक और जटिल अभ्यावेदन का एक अच्छा सामान्यीकरण प्रदान करते हैं।

माशके के प्रमेय और एकात्मक संपत्ति जैसे परिणाम जो औसत पर भरोसा करते हैं, औसत को एक अभिन्न के साथ बदलकर अधिक सामान्य समूहों के लिए सामान्यीकृत किया जा सकता है, बशर्ते कि अभिन्न की एक उपयुक्त धारणा को परिभाषित किया जा सके। यह कॉम्पैक्ट समूह (कॉम्पैक्ट झूठ समूहों सहित) के लिए किया जा सकता है, हार उपाय का उपयोग करके, और परिणामी सिद्धांत को सार हार्मोनिक विश्लेषण के रूप में जाना जाता है।

मनमाना क्षेत्रों पर, परिमित समूहों का एक अन्य वर्ग जिनके पास एक अच्छा प्रतिनिधित्व सिद्धांत है, वे ली प्रकार के परिमित समूह हैं। महत्वपूर्ण उदाहरण परिमित क्षेत्रों पर रैखिक बीजगणितीय समूह हैं। रेखीय बीजगणितीय समूहों और लाई समूहों का प्रतिनिधित्व सिद्धांत इन उदाहरणों को अनंत-आयामी समूहों तक फैलाता है, बाद वाला लाई बीजगणित निरूपण से घनिष्ठ रूप से संबंधित है। परिमित समूहों के लिए चरित्र सिद्धांत का महत्व झूठ समूहों और झूठ बीजगणित के प्रतिनिधित्व के लिए वजन के सिद्धांत (प्रतिनिधित्व सिद्धांत) में एक एनालॉग है।

परिमित समूह G के निरूपण भी समूह वलय 'F' [G] के माध्यम से बीजगणित निरूपण से सीधे जुड़े हुए हैं, जो G के तत्वों के आधार पर 'F' पर एक सदिश स्थान है, जो परिभाषित गुणन संक्रिया से सुसज्जित है। समूह संचालन, रैखिकता, और आवश्यकता है कि समूह संचालन और अदिश गुणन कम्यूट करें।

मॉड्यूलर प्रतिनिधित्व

Main article: Modular representation theory

एक परिमित समूह G का मॉड्यूलर प्रतिनिधित्व एक ऐसे क्षेत्र पर प्रतिनिधित्व करता है जिसकी विशेषता |G| के लिए सहअभाज्य नहीं है, इसलिए माश्के की प्रमेय अब मान्य नहीं है (क्योंकि |G| 'F' में व्युत्क्रमणीय नहीं है और इसलिए कोई इससे विभाजित नहीं हो सकता है)। फिर भी, रिचर्ड ब्राउर ने मॉड्यूलर अभ्यावेदन के लिए बहुत से चरित्र सिद्धांत का विस्तार किया, और इस सिद्धांत ने परिमित सरल समूहों के वर्गीकरण की दिशा में प्रारंभिक प्रगति में महत्वपूर्ण भूमिका निभाई, विशेष रूप से सरल समूहों के लिए जिनका लक्षण वर्णन विशुद्ध रूप से समूह-सैद्धांतिक तरीकों के लिए उत्तरदायी नहीं था क्योंकि उनका सिलो उपसमूह |साइलो 2-उपसमूह बहुत छोटे थे। साथ ही समूह सिद्धांत के अनुप्रयोगों के साथ, मॉड्यूलर प्रतिनिधित्व स्वाभाविक रूप से गणित की अन्य शाखाओं में उत्पन्न होता है, जैसे कि बीजगणितीय ज्यामिति, कोडिंग सिद्धांत, संयोजक और संख्या सिद्धांत।

एकात्मक प्रतिनिधित्व

Main article: Unitary representation

एक समूह G का एकात्मक प्रतिनिधित्व एक वास्तविक या (आमतौर पर) जटिल हिल्बर्ट स्पेस V पर G का एक रैखिक प्रतिनिधित्व φ है, जैसे कि φ(g) प्रत्येक g ∈ G के लिए एक एकात्मक ऑपरेटर है। इस तरह के प्रतिनिधित्व व्यापक रूप से क्वांटम यांत्रिकी में लागू किए गए हैं। 1920 के दशक से, विशेष रूप से हरमन वेइल के प्रभाव के लिए धन्यवाद, और इसने सिद्धांत के विकास को प्रेरित किया है, विशेष रूप से पोंकारे समूह के प्रतिनिधित्व सिद्धांत के विश्लेषण के माध्यम से | यूजीन विग्नर द्वारा पोंकारे समूह के प्रतिनिधित्व। एकात्मक अभ्यावेदन के एक सामान्य सिद्धांत के निर्माण में अग्रदूतों में से एक (किसी भी समूह जी के बजाय केवल अनुप्रयोगों में उपयोगी विशेष समूहों के लिए) जॉर्ज मैके थे, और 1950 और 1960 के दशक में हरीश-चंद्र और अन्य द्वारा एक व्यापक सिद्धांत विकसित किया गया था। एक प्रमुख लक्ष्य एकात्मक दोहरे का वर्णन करना है, जी के अलघुकरणीय एकात्मक अभ्यावेदन का स्थान। सिद्धांत इस मामले में सबसे अच्छी तरह से विकसित हुआ है कि जी स्थानीय रूप से कॉम्पैक्ट (हॉसडॉर्फ) टोपोलॉजिकल समूह है और प्रतिनिधित्व दृढ़ता से निरंतर हैं।जी एबेलियन के लिए, एकात्मक द्वैत सिर्फ चरित्र सिद्धांत का स्थान है, जबकि जी कॉम्पैक्ट के लिए, पीटर-वेइल प्रमेय दर्शाता है कि अलघुकरणीय एकात्मक निरूपण परिमित-आयामी हैं और एकात्मक द्वैत असतत है। <रेफरी नाम = पीटर-वेइल>Peter & Weyl 1927.</ref> उदाहरण के लिए, यदि G, वृत्त समूह S है¹, तो वर्ण पूर्णांकों द्वारा दिए गए हैं, और एकात्मक द्वैत Z है।

गैर-कॉम्पैक्ट जी के लिए, कौन से निरूपण एकात्मक हैं, यह प्रश्न एक सूक्ष्म है। हालांकि अलघुकरणीय एकात्मक अभ्यावेदन स्वीकार्य होना चाहिए (हरीश-चंद्र मॉड्यूल के रूप में) और यह पता लगाना आसान है कि कौन से स्वीकार्य अभ्यावेदन में एक गैर-अपरिवर्तनीय अपरिवर्तनीय सेस्क्विलिनियर रूप है, यह निर्धारित करना कठिन है कि यह रूप कब सकारात्मक निश्चित है। एकात्मक दोहरे का एक प्रभावी वर्णन, यहां तक ​​कि अपेक्षाकृत अच्छी तरह से व्यवहार किए गए समूहों जैसे कि वास्तविक सेमीसिम्पल लाइ समूह लाइ समूह (नीचे चर्चा की गई) के लिए, प्रतिनिधित्व सिद्धांत में एक महत्वपूर्ण खुली समस्या बनी हुई है। इसे कई विशेष समूहों के लिए हल किया गया है, जैसे कि SL2(R)|SL(2,R) का प्रतिनिधित्व सिद्धांत और लोरेंत्ज़ समूह का प्रतिनिधित्व सिद्धांत।

हार्मोनिक विश्लेषण

Main article: Abstract harmonic analysis

वृत्त समूह S के बीच द्वंद्व¹ और पूर्णांक Z, या अधिक सामान्यतः, एक टोरस T के बीचⁿ और 'Z'ⁿ विश्लेषण में फूरियर श्रृंखला के सिद्धांत के रूप में अच्छी तरह से जाना जाता है, और फूरियर रूपांतरण समान रूप से इस तथ्य को व्यक्त करता है कि वास्तविक सदिश स्थान पर वर्णों का स्थान दोहरी सदिश स्थान है। इस प्रकार एकात्मक प्रतिनिधित्व सिद्धांत और हार्मोनिक विश्लेषण अंतरंग रूप से संबंधित हैं, और अमूर्त हार्मोनिक विश्लेषण स्थानीय कॉम्पैक्टनेस और संबंधित स्थानों पर कार्यों के गणितीय विश्लेषण को विकसित करके इस संबंध का फायदा उठाता है।

एक प्रमुख लक्ष्य फूरियर रूपांतरण और प्लैंकेरल प्रमेय का एक सामान्य रूप प्रदान करना है। यह अंतरिक्ष एल पर जी के नियमित प्रतिनिधित्व के बीच एकात्मक दोहरे और एक समरूपता पर एक माप (गणित) का निर्माण करके किया जाता है।²(G) G पर वर्ग समाकलनीय फलन और L2-स्पेस|L के स्थान पर इसका प्रतिनिधित्व² एकात्मक दोहरे पर कार्य करता है। पोंट्रजगिन द्वैत और पीटर-वेइल प्रमेय इसे क्रमशः एबेलियन और कॉम्पैक्ट जी के लिए प्राप्त करते हैं। <रेफरी नाम = पीटर-वेइल /> एक अन्य दृष्टिकोण में सभी एकात्मक अभ्यावेदन पर विचार करना शामिल है, न कि केवल अप्रासंगिक वाले। ये एक श्रेणी (गणित) बनाते हैं, और तन्नाका-क्रेन द्वैत एक कॉम्पैक्ट समूह को एकात्मक प्रतिनिधित्व की श्रेणी से पुनर्प्राप्त करने का एक तरीका प्रदान करता है।

यदि समूह न तो एबेलियन है और न ही कॉम्पैक्ट है, तो प्लैंकेरल प्रमेय या फूरियर व्युत्क्रम के एनालॉग के साथ कोई सामान्य सिद्धांत ज्ञात नहीं है, हालांकि अलेक्जेंडर ग्रोथेंडिक ने रेखीय बीजगणितीय समूहों और तनाकियन श्रेणी के बीच संबंध के लिए तन्नाका-क्रेन द्वैत का विस्तार किया।

हार्मोनिक विश्लेषण को समूह जी पर कार्यों के विश्लेषण से जी के लिए सजातीय रिक्त स्थान पर कार्यों के विश्लेषण से भी विस्तारित किया गया है। सिद्धांत विशेष रूप से सममित रिक्त स्थान के लिए विकसित किया गया है और ऑटोमोर्फिक रूपों का सिद्धांत प्रदान करता है (नीचे चर्चा की गई)।

झूठ समूह

Main article: Representation of a Lie group

एक झूठ समूह एक ऐसा समूह है जो एक चिकनी मैनिफोल्ड भी है। वास्तविक या जटिल संख्याओं पर मैट्रिसेस के कई शास्त्रीय समूह लाई समूह हैं। भौतिकी और रसायन विज्ञान में महत्वपूर्ण कई समूह झूठ समूह हैं, और उनका प्रतिनिधित्व सिद्धांत उन क्षेत्रों में समूह सिद्धांत के अनुप्रयोग के लिए महत्वपूर्ण है।

कॉम्पैक्ट समूहों पर विचार करके पहले झूठ समूहों का प्रतिनिधित्व सिद्धांत विकसित किया जा सकता है, जिसके लिए कॉम्पैक्ट प्रतिनिधित्व सिद्धांत के परिणाम लागू होते हैं।इस सिद्धांत को वेइल की एकात्मक चाल का उपयोग करके सेमीसिम्पल लाइ समूहों के परिमित-आयामी प्रतिनिधित्व तक बढ़ाया जा सकता है: प्रत्येक सेमीसिंपल रियल लाई ग्रुप जी में एक जटिलता है, जो एक जटिल लाई ग्रुप जी है।^c, और इस जटिल लाई समूह में एक अधिकतम कॉम्पैक्ट उपसमूह K है। G का परिमित-आयामी प्रतिनिधित्व K के साथ निकटता से मेल खाता है।

एक सामान्य लाई समूह एक हल करने योग्य लाई समूह और एक अर्ध-सरल लाई समूह (लेवी अपघटन) का एक अर्ध-प्रत्यक्ष उत्पाद है। हल करने योग्य झूठ समूहों के प्रतिनिधित्व का वर्गीकरण सामान्य रूप से जटिल है, लेकिन व्यावहारिक मामलों में अक्सर आसान होता है। अर्ध-प्रत्यक्ष उत्पादों के अभ्यावेदन का तब मैके सिद्धांत नामक सामान्य परिणामों के माध्यम से विश्लेषण किया जा सकता है, जो विग्नेर के पॉइनकेयर समूह के अभ्यावेदन के वर्गीकरण में उपयोग की जाने वाली विधियों का एक सामान्यीकरण है।

झूठ बीजगणित

Main article: Lie algebra representation

फ़ील्ड F पर एक लाई बीजगणित एक तिरछा-सममित ग्राफ से सुसज्जित F पर एक सदिश स्थान है। तिरछा-सममित बिलिनियर ऑपरेशन जिसे लेट ब्रैकेट कहा जाता है, जो जैकोबी पहचान को संतुष्ट करता है। झूठ बीजगणित विशेष रूप से पहचान तत्व पर झूठ समूहों के लिए स्पर्शरेखा रिक्त स्थान के रूप में उत्पन्न होते हैं, जिससे उनकी व्याख्या अपरिमेय समरूपता के रूप में होती है।झूठ समूहों के प्रतिनिधित्व सिद्धांत के लिए एक महत्वपूर्ण दृष्टिकोण झूठ बीजगणित के संबंधित प्रतिनिधित्व सिद्धांत का अध्ययन करना है, लेकिन झूठ बीजगणित के प्रतिनिधित्व में भी एक आंतरिक रुचि है। झूठ बीजगणित, झूठ समूहों की तरह, अर्ध-सरल और हल करने योग्य भागों में एक लेवी अपघटन होता है, साथ ही हल करने योग्य झूठ बीजगणित के प्रतिनिधित्व सिद्धांत सामान्य रूप से अव्यवस्थित होते हैं। इसके विपरीत, एली कार्टन के काम के बाद, अर्ध-सरल लाई बीजगणित के परिमित-आयामी प्रतिनिधित्व को पूरी तरह से समझा जाता है। सेमीसिम्पल लाई बीजगणित 𝖌 का प्रतिनिधित्व यह सबलजेब्रा परीक्षण को चुनकर किया जाता है, जो अनिवार्य रूप से 𝖌 का एक सामान्य मैक्सिमल सबलजेब्रा 𝖍 है जिस पर लाइ ब्रैकेट शून्य (एबेलियन) है। 𝖌 के प्रतिनिधित्व को वजन (प्रतिनिधित्व सिद्धांत) में विघटित किया जा सकता है जो कि 𝖍 की कार्रवाई के लिए eigenspaces और वर्णों के अतिसूक्ष्म अनुरूप हैं। अर्ध-सरल झूठ बीजगणित की संरचना तब होने वाले संभावित वजन के आसानी से समझने वाले संयोजनों के प्रतिनिधित्व के विश्लेषण को कम कर देती है।

अनंत-आयामी झूठ बीजगणित

See also: Affine Lie algebra and Kac–Moody algebra

अनंत-आयामी झूठ बीजगणित के कई वर्ग हैं जिनके अभ्यावेदन का अध्ययन किया गया है। इनमें से एक महत्वपूर्ण वर्ग काक-मूडी बीजगणित हैं। उनका नाम विक्टर काक और रॉबर्ट मूडी के नाम पर रखा गया है, जिन्होंने उन्हें स्वतंत्र रूप से खोजा था। ये बीजगणित परिमित-आयामी अर्ध-सरल झूठ बीजगणित का एक सामान्यीकरण बनाते हैं, और उनके कई दहनशील गुणों को साझा करते हैं। इसका मतलब यह है कि उनके पास अभ्यावेदन का एक वर्ग है जिसे उसी तरह से समझा जा सकता है जैसे अर्ध-सरल झूठ बीजगणित का निरूपण।

Affine Lie algebras Kac-Moody algebras का एक विशेष मामला है, जिसका गणित और सैद्धांतिक भौतिकी में विशेष महत्व है, विशेष रूप से अनुरूप क्षेत्र सिद्धांत और बिल्कुल हल करने योग्य मॉडल का सिद्धांत। केएसी ने कुछ संयोजी पहचानों, मैकडोनाल्ड पहचानों का एक सुंदर प्रमाण खोजा, जो एफिन केएसी-मूडी बीजगणित के प्रतिनिधित्व सिद्धांत पर आधारित है।

लेट सुपरएलजेब्रस

Main article: Representation of a Lie superalgebra

लव सुपरएलजेब्रा लाई अलजेब्रा का सामान्यीकरण है जिसमें अंतर्निहित सदिश स्थान में एक Z होता है₂लाई ब्रैकेट के -ग्रेडिंग, और तिरछा-समरूपता और जैकोबी पहचान गुणों को संकेतों द्वारा संशोधित किया जाता है। उनका प्रतिनिधित्व सिद्धांत झूठ बीजगणित के प्रतिनिधित्व सिद्धांत के समान है।

रेखीय बीजगणितीय समूह

See also: Linear algebraic group

रेखीय बीजगणितीय समूह (या अधिक आम तौर पर, एफ़िन समूह योजनाएँ) लाई समूहों के बीजगणितीय ज्यामिति में अनुरूप हैं, लेकिन केवल आर या सी की तुलना में अधिक सामान्य क्षेत्रों में। विशेष रूप से, परिमित क्षेत्रों में, वे लाई प्रकार के परिमित समूहों को जन्म देते हैं। हालांकि रैखिक बीजगणितीय समूहों का एक वर्गीकरण है जो झूठ समूहों के समान है, उनका प्रतिनिधित्व सिद्धांत बल्कि अलग है (और बहुत कम अच्छी तरह से समझा जाता है) और विभिन्न तकनीकों की आवश्यकता होती है, क्योंकि जरिस्की टोपोलॉजी अपेक्षाकृत कमजोर है, और विश्लेषण से तकनीकें अब नहीं हैं उपलब्ध।

अपरिवर्तनीय सिद्धांत

Main article: Invariant theory

अपरिवर्तनीय सिद्धांत कार्यों पर उनके प्रभाव के दृष्टिकोण से बीजगणितीय विविधता पर समूह क्रिया (गणित) का अध्ययन करता है, जो समूह का प्रतिनिधित्व करता है। शास्त्रीय रूप से, सिद्धांत बहुपद कार्यों के स्पष्ट विवरण के प्रश्न से संबंधित है जो किसी दिए गए रैखिक समूह से परिवर्तनों के तहत बदलते नहीं हैं, या अपरिवर्तनीय हैं। आधुनिक दृष्टिकोण इन अभ्यावेदनों के अपघटन को इरेड्यूसिबल्स में विश्लेषित करता है। अनंत समूहों का अपरिवर्तनीय सिद्धांत रेखीय बीजगणित के विकास के साथ विशेष रूप से जुड़ा हुआ है, विशेष रूप से, द्विघात रूपों और निर्धारकों के सिद्धांत। मजबूत पारस्परिक प्रभाव वाला एक अन्य विषय प्रक्षेपी ज्यामिति है, जहां विषय को व्यवस्थित करने के लिए अपरिवर्तनीय सिद्धांत का उपयोग किया जा सकता है, और 1960 के दशक के दौरान डेविड ममफोर्ड द्वारा अपने ज्यामितीय अपरिवर्तनीय सिद्धांत के रूप में इस विषय में नई जान फूंक दी गई थी। सेमीसिंपल लाई समूहों के प्रतिनिधित्व सिद्धांत की जड़ें अपरिवर्तनीय सिद्धांत में हैंऔर प्रतिनिधित्व सिद्धांत और बीजगणितीय ज्यामिति के बीच मजबूत लिंक में अंतर ज्यामिति में कई समानताएं हैं, जिसकी शुरुआत फेलिक्स क्लेन के एर्लांगेन कार्यक्रम और एली कार्टन के कार्टन कनेक्शन से होती है, जो ज्यामिति के केंद्र में समूह और समरूपता रखते हैं। आधुनिक विकास प्रतिनिधित्व सिद्धांत और अपरिवर्तनीय सिद्धांत को समरूपता, अंतर संचालकों और कई जटिल चर के सिद्धांत के रूप में विविध क्षेत्रों से जोड़ता है।

स्वचालित रूप और संख्या सिद्धांत

Main article: Automorphic form

ऑटोमॉर्फिक रूप अधिक सामान्य विश्लेषणात्मक कार्यों के लिए मॉड्यूलर रूपों का एक सामान्यीकरण है, शायद समान परिवर्तन गुणों के साथ कई जटिल चर। सामान्यीकरण में मॉड्यूलर समूह PSL2(R)|PSL को बदलना शामिल है₂ (आर) और एक चुना हुआ सर्वांगसम उपसमूह एक अर्धसूत्रीय लाई समूह जी और एक असतत उपसमूह Γ द्वारा। जिस तरह मॉड्यूलर रूपों को ऊपरी आधे स्थान H = PSL के भागफल पर अंतर रूपों के रूप में देखा जा सकता है₂ (R)/SO(2), ऑटोमॉर्फिक रूपों को Γ\G/K पर अंतर रूपों (या समान वस्तुओं) के रूप में देखा जा सकता है, जहां K है (आमतौर पर ) जी का एक अधिकतम कॉम्पैक्ट उपसमूह। हालाँकि, कुछ देखभाल की आवश्यकता होती है, क्योंकि भागफल में आमतौर पर विलक्षणताएँ होती हैं। एक कॉम्पैक्ट उपसमूह द्वारा अर्ध-सरल लाई समूह का अंश एक सममित स्थान है और इसलिए ऑटोमोर्फिक रूपों का सिद्धांत सममित रिक्त स्थान पर हार्मोनिक विश्लेषण से घनिष्ठ रूप से संबंधित है।

सामान्य सिद्धांत के विकास से पहले, कई महत्वपूर्ण विशेष मामलों पर विस्तार से काम किया गया था, जिसमें हिल्बर्ट मॉड्यूलर फॉर्म और सील मॉड्यूलर रूप शामिल थे। सिद्धांत में महत्वपूर्ण परिणामों में सेलबर्ग ट्रेस फॉर्मूला और रॉबर्ट लैंगलैंड्स द्वारा प्राप्ति शामिल है कि ऑटोमोर्फिक रूपों के स्थान के आयाम की गणना करने के लिए रीमैन-रोच प्रमेय लागू किया जा सकता है। ऑटोमॉर्फिक प्रतिनिधित्व की बाद की धारणा इस मामले से निपटने के लिए महान तकनीकी मूल्य साबित हुई है कि 'जी' एक बीजगणितीय समूह है, जिसे एक एडिलिक बीजगणितीय समूह के रूप में माना जाता है। नतीजतन, एक संपूर्ण दर्शन, लैंगलैंड्स कार्यक्रम ऑटोमोर्फिक रूपों के प्रतिनिधित्व और संख्या सैद्धांतिक गुणों के बीच संबंध के आसपास विकसित हुआ है।

साहचर्य बीजगणित

Main article: Algebra representation

एक अर्थ में, साहचर्य बीजगणित निरूपण समूहों और लाई बीजगणित दोनों के अभ्यावेदन को सामान्य करता है। एक समूह का प्रतिनिधित्व एक संबंधित समूह की अंगूठी या समूह की अंगूठी के प्रतिनिधित्व को प्रेरित करता है, जबकि लाई बीजगणित का प्रतिनिधित्व विशेष रूप से इसके सार्वभौमिक लिफाफा बीजगणित के प्रतिनिधित्व के अनुरूप होता है। हालाँकि, सामान्य साहचर्य बीजगणित के प्रतिनिधित्व सिद्धांत में समूहों के प्रतिनिधित्व सिद्धांत और झूठ बीजगणित के सभी अच्छे गुण नहीं हैं।

मॉड्यूल सिद्धांत

Main article: Module theory

एक साहचर्य बीजगणित के प्रतिनिधित्व पर विचार करते समय, कोई अंतर्निहित क्षेत्र को भूल सकता है, और साहचर्य बीजगणित को एक अंगूठी के रूप में, और इसके प्रतिनिधित्व को मॉड्यूल के रूप में मान सकता है। यह दृष्टिकोण आश्चर्यजनक रूप से उपयोगी है: प्रतिनिधित्व सिद्धांत में कई परिणाम एक अंगूठी पर मॉड्यूल के परिणामों के विशेष मामलों के रूप में व्याख्या किए जा सकते हैं।

हॉफ बीजगणित और क्वांटम समूह

Main article: Representation theory of Hopf algebras

हॉफ बीजगणित समूहों के प्रतिनिधित्व सिद्धांत और विशेष मामलों के रूप में झूठ बीजगणित को बनाए रखते हुए सहयोगी बीजगणित के प्रतिनिधित्व सिद्धांत को बेहतर बनाने का एक तरीका प्रदान करते हैं। विशेष रूप से, दो अभ्यावेदन का टेन्सर उत्पाद एक प्रतिनिधित्व है, जैसा कि दोहरी सदिश स्थान है।

समूहों से जुड़े हॉफ बीजगणित में एक क्रमविनिमेय बीजगणित संरचना होती है, और इसलिए सामान्य हॉफ बीजगणित को क्वांटम समूह के रूप में जाना जाता है, हालांकि यह शब्द अक्सर समूहों के विरूपण या उनके सार्वभौमिक आवरण बीजगणित के रूप में उत्पन्न होने वाले कुछ हॉप बीजगणित तक ही सीमित होता है। क्वांटम समूहों के प्रतिनिधित्व सिद्धांत ने झूठ समूहों और झूठ बीजगणित के प्रतिनिधित्व सिद्धांत में आश्चर्यजनक अंतर्दृष्टि जोड़ दी है, उदाहरण के लिए काशीवाड़ा के क्रिस्टल आधार के माध्यम से।

सामान्यीकरण

सेट-सैद्धांतिक प्रतिनिधित्व

Main article: Group action (mathematics)

एक समुच्चय (गणित) X पर एक समूह (गणित) G का समुच्चय-सैद्धांतिक प्रतिनिधित्व (समूह क्रिया (गणित) या क्रमपरिवर्तन प्रतिनिधित्व के रूप में भी जाना जाता है) G से X तक एक फ़ंक्शन (गणित) ρ द्वारा दिया जाता है^X, X से X तक फ़ंक्शन (गणित) का सेट (गणित), ऐसा कि सभी g के लिए₁, जी₂ जी में और एक्स में सभी एक्स:

$\rho (1)[x]=x$

$\rho (g_{1}g_{2})[x]=\rho (g_{1})[\rho (g_{2})[x]].$

समूह के लिए यह स्थिति और अभिगृहीत का अर्थ है कि ρ(g) G में सभी g के लिए एक आक्षेप (या क्रमचय) है। इस प्रकार हम G से सममित समूह S के समूह समरूपता के रूप में एक क्रमचय निरूपण को समान रूप से परिभाषित कर सकते हैं।_X एक्स का।

अन्य श्रेणियों में प्रतिनिधित्व

See also: Category theory

प्रत्येक समूह G को एक वस्तु के साथ एक श्रेणी (गणित) के रूप में देखा जा सकता है; इस श्रेणी में morphisms सिर्फ G के तत्व हैं। एक मनमानी श्रेणी C को देखते हुए, C में G का प्रतिनिधित्व G से C तक एक फ़ंक्टर है। ऐसा फ़ंक्टर C में एक ऑब्जेक्ट X और G से Aut(X) के लिए एक समूह समरूपता का चयन करता है। ), एक्स का ऑटोमोर्फिज्म समूह।

मामले में जहां सी 'वेक्ट' है_F, क्षेत्र F पर वेक्टर रिक्त स्थान की श्रेणी, यह परिभाषा एक रैखिक प्रतिनिधित्व के बराबर है। इसी तरह, एक सेट-सैद्धांतिक प्रतिनिधित्व सेट की श्रेणी में जी का प्रतिनिधित्व मात्र है।

एक अन्य उदाहरण के लिए टोपोलॉजिकल स्पेस की श्रेणी पर विचार करें, टॉप। शीर्ष में प्रतिनिधित्व जी से एक सांस्थितिकीय स्थान एक्स के होमियोमोर्फिज्म समूह के लिए होमोमोर्फिज्म हैं।

रैखिक निरूपण से निकटता से संबंधित तीन प्रकार के निरूपण हैं:

• प्रक्षेपी अभ्यावेदन: प्रक्षेपी रिक्त स्थान की श्रेणी में। इन्हें स्केलर परिवर्तनों तक रैखिक प्रतिनिधित्व के रूप में वर्णित किया जा सकता है।
• affine प्रतिनिधित्व: affine रिक्त स्थान की श्रेणी में। उदाहरण के लिए, यूक्लिडियन समूह यूक्लिडियन अंतरिक्ष पर स्नेहपूर्ण रूप से कार्य करता है।
• एकात्मक और विरोधी एकात्मक समूहों की मुख्य प्रस्तुतियाँ: जटिल वेक्टर रिक्त स्थान की श्रेणी में morphisms के साथ रैखिक या एंटीलाइनर परिवर्तन होते हैं।

श्रेणियों का प्रतिनिधित्व

See also: Quiver (mathematics)

चूंकि समूह श्रेणियां हैं, कोई अन्य श्रेणियों के प्रतिनिधित्व पर भी विचार कर सकता है। सरलतम सामान्यीकरण मोनोइड्स के लिए है, जो एक वस्तु वाली श्रेणियां हैं। समूह मोनॉइड होते हैं जिनके लिए प्रत्येक रूपवाद उलटा होता है। सामान्य मोनोइड्स का किसी भी श्रेणी में प्रतिनिधित्व होता है। सेट की श्रेणी में, ये मोनोइड क्रियाएं हैं, लेकिन वेक्टर रिक्त स्थान और अन्य वस्तुओं पर मोनोइड प्रस्तुतियों का अध्ययन किया जा सकता है।

अधिक आम तौर पर, कोई इस धारणा को शिथिल कर सकता है कि जिस श्रेणी का प्रतिनिधित्व किया जा रहा है उसमें केवल एक वस्तु है। पूर्ण सामान्यता में, यह केवल श्रेणियों के बीच फ़ैक्टरों का सिद्धांत है, और बहुत कम कहा जा सकता है।

एक विशेष मामले का प्रतिनिधित्व सिद्धांत पर महत्वपूर्ण प्रभाव पड़ा है, अर्थात् तरकश का प्रतिनिधित्व सिद्धांत।एक तरकश केवल एक निर्देशित ग्राफ है (लूप और कई तीरों की अनुमति है), लेकिन इसे ग्राफ में पथों पर विचार करके एक श्रेणी (और बीजगणित भी) में बनाया जा सकता है। ऐसी श्रेणियों/बीजगणितों के निरूपण ने प्रतिनिधित्व सिद्धांत के कई पहलुओं पर प्रकाश डाला है, उदाहरण के लिए एक समूह के बारे में गैर-अर्ध-सरल प्रतिनिधित्व सिद्धांत प्रश्नों को अनुमति देकर कुछ मामलों में तरकश के बारे में अर्ध-सरल प्रतिनिधित्व सिद्धांत प्रश्नों को कम किया जा सकता है।

यह भी देखें

• गाल्वा प्रतिनिधित्व
• प्रतिनिधित्व सिद्धांत की शब्दावली
• समूह प्रतिनिधित्व
• इतो का प्रमेय
• प्रतिनिधित्व सिद्धांत विषयों की सूची
• हार्मोनिक विश्लेषण विषयों की सूची
• संख्यात्मक विश्लेषण
• पुच्छल रूपों का दर्शन
• प्रतिनिधित्व (गणित)
• प्रतिनिधित्व प्रमेय
• सार्वभौमिक बीजगणित

संदर्भ

• Alperin, J. L. (1986), Local Representation Theory: Modular Representations as an Introduction to the Local Representation Theory of Finite Groups, Cambridge University Press, ISBN 978-0-521-44926-7.
• Bargmann, V. (1947), "Irreducible unitary representations of the Lorenz group", Annals of Mathematics, 48 (3): 568–640, doi:10.2307/1969129, JSTOR 1969129.
• Borel, Armand (2001), Essays in the History of Lie Groups and Algebraic Groups, American Mathematical Society, ISBN 978-0-8218-0288-5.
• Borel, Armand; Casselman, W. (1979), Automorphic Forms, Representations, and L-functions, American Mathematical Society, ISBN 978-0-8218-1435-2.
• Curtis, Charles W.; Reiner, Irving (1962), Representation Theory of Finite Groups and Associative Algebras, John Wiley & Sons (Reedition 2006 by AMS Bookstore), ISBN 978-0-470-18975-7.
• Gelbart, Stephen (1984), "An Elementary Introduction to the Langlands Program", Bulletin of the American Mathematical Society, 10 (2): 177–219, doi:10.1090/S0273-0979-1984-15237-6.
• Folland, Gerald B. (1995), A Course in Abstract Harmonic Analysis, CRC Press, ISBN 978-0-8493-8490-5.
• Fulton, William; Harris, Joe (1991). Representation theory. A first course. Graduate Texts in Mathematics, Readings in Mathematics (in British English). Vol. 129. New York: Springer-Verlag. doi:10.1007/978-1-4612-0979-9. ISBN 978-0-387-97495-8. MR 1153249. OCLC 246650103..
• Goodman, Roe; Wallach, Nolan R. (1998), Representations and Invariants of the Classical Groups, Cambridge University Press, ISBN 978-0-521-66348-9.
• James, Gordon; Liebeck, Martin (1993), Representations and Characters of Groups, Cambridge: Cambridge University Press, ISBN 978-0-521-44590-0.
• Hall, Brian C. (2015), Lie Groups, Lie Algebras, and Representations: An Elementary Introduction, Graduate Texts in Mathematics, vol. 222 (2nd ed.), Springer, ISBN 978-3319134666
• Helgason, Sigurdur (1978), Differential Geometry, Lie groups and Symmetric Spaces, Academic Press, ISBN 978-0-12-338460-7
• Humphreys, James E. (1972a), Introduction to Lie Algebras and Representation Theory, Birkhäuser, ISBN 978-0-387-90053-7.
• Humphreys, James E. (1972b), Linear Algebraic Groups, Graduate Texts in Mathematics, vol. 21, Berlin, New York: Springer-Verlag, ISBN 978-0-387-90108-4, MR 0396773
• Jantzen, Jens Carsten (2003), Representations of Algebraic Groups, American Mathematical Society, ISBN 978-0-8218-3527-2.
• Kac, Victor G. (1977), "Lie superalgebras", Advances in Mathematics, 26 (1): 8–96, doi:10.1016/0001-8708(77)90017-2.
• Kac, Victor G. (1990), Infinite Dimensional Lie Algebras (3rd ed.), Cambridge University Press, ISBN 978-0-521-46693-6.
• Knapp, Anthony W. (2001), Representation Theory of Semisimple Groups: An Overview Based on Examples, Princeton University Press, ISBN 978-0-691-09089-4.
• Kim, Shoon Kyung (1999), Group Theoretical Methods and Applications to Molecules and Crystals: And Applications to Molecules and Crystals, Cambridge University Press, ISBN 978-0-521-64062-6.
• Kostrikin, A. I.; Manin, Yuri I. (1997), Linear Algebra and Geometry, Taylor & Francis, ISBN 978-90-5699-049-7.
• Lam, T. Y. (1998), "Representations of finite groups: a hundred years", Notices of the AMS, 45 (3, 4): 361–372 (Part I), 465–474 (Part II).
• Yurii I. Lyubich. Introduction to the Theory of Banach Representations of Groups. Translated from the 1985 Russian-language edition (Kharkov, Ukraine). Birkhäuser Verlag. 1988.
• Mumford, David; Fogarty, J.; Kirwan, F. (1994), Geometric invariant theory, Ergebnisse der Mathematik und ihrer Grenzgebiete (2) [Results in Mathematics and Related Areas (2)], vol. 34 (3rd ed.), Berlin, New York: Springer-Verlag, ISBN 978-3-540-56963-3, MR 0214602; MR0719371 (2nd ed.); MR1304906(3rd ed.)
• Olver, Peter J. (1999), Classical invariant theory, Cambridge: Cambridge University Press, ISBN 978-0-521-55821-1.
• Peter, F.; Weyl, Hermann (1927), "Die Vollständigkeit der primitiven Darstellungen einer geschlossenen kontinuierlichen Gruppe", Mathematische Annalen, 97 (1): 737–755, doi:10.1007/BF01447892, S2CID 120013521.
• Pontrjagin, Lev S. (1934), "The theory of topological commutative groups", Annals of Mathematics, 35 (2): 361–388, doi:10.2307/1968438, JSTOR 1968438.
• Sally, Paul; Vogan, David A. (1989), Representation Theory and Harmonic Analysis on Semisimple Lie Groups, American Mathematical Society, ISBN 978-0-8218-1526-7.
• Serre, Jean-Pierre (1977), Linear Representations of Finite Groups, Springer-Verlag, ISBN 978-0387901909.
• Sharpe, Richard W. (1997), Differential Geometry: Cartan's Generalization of Klein's Erlangen Program, Springer, ISBN 978-0-387-94732-7.
• Simson, Daniel; Skowronski, Andrzej; Assem, Ibrahim (2007), Elements of the Representation Theory of Associative Algebras, Cambridge University Press, ISBN 978-0-521-88218-7.
• Sternberg, Shlomo (1994), Group Theory and Physics, Cambridge University Press, ISBN 978-0-521-55885-3.
• Tung, Wu-Ki (1985). Group Theory in Physics (1st ed.). New Jersey·London·Singapore·Hong Kong: World Scientific. ISBN 978-9971966577.
• Weyl, Hermann (1928), Gruppentheorie und Quantenmechanik (The Theory of Groups and Quantum Mechanics, translated H.P. Robertson, 1931 ed.), S. Hirzel, Leipzig (reprinted 1950, Dover), ISBN 978-0-486-60269-1.
• Weyl, Hermann (1946), The Classical Groups: Their Invariants and Representations (2nd ed.), Princeton University Press (reprinted 1997), ISBN 978-0-691-05756-9.
• Wigner, Eugene P. (1939), "On unitary representations of the inhomogeneous Lorentz group", Annals of Mathematics, 40 (1): 149–204, Bibcode:1939AnMat..40..149W, doi:10.2307/1968551, JSTOR 1968551, S2CID 121773411.

बाहरी संबंध

• "Representation theory", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
• Alexander Kirillov Jr., An introduction to Lie groups and Lie algebras (2008). Textbook, preliminary version pdf downloadable from author's home page.
• Kevin Hartnett, (2020), article on representation theory in Quanta magazine