नुसेल्ट संख्या

ऊष्मीय द्रव गतिकी में, न्यूसेल्ट संख्या (Nu, विल्हेम न्यूसेल्ट के बाद) तरल पदार्थ में सीमा (ऊष्मागतिक) पर ऊष्मा चालन ताप हस्तांतरण के लिए संवहन का अनुपात है। संवहन में अभिवहन (द्रव गति) और प्रसार (चालन) दोनों सम्मिलित हैं। काल्पनिक रूप से गतिहीन द्रव के लिए प्रवाहकीय घटक को संवहन के समान शर्तों के तहत मापा जाता है। यह आयाम रहित संख्या है, जो द्रव के रेले संख्या से निकटता से संबंधित है। मूल्य एक (शून्य) की एक नुसेल्ट संख्या शुद्ध चालन द्वारा गर्मी हस्तांतरण का प्रतिनिधित्व करती है। एक (शून्य) और 10 के बीच का मान स्लग प्रवाह या लामिनार प्रवाह की विशेषता है।

मूल्य एक (शून्य) की न्यूसेल्ट संख्या शुद्ध चालन द्वारा ऊष्मा हस्तांतरण का प्रतिनिधित्व करती है। एक (शून्य) और 10 के बीच का मान स्लग (धातु का ठोस थक्का) प्रवाह या स्तरीय प्रवाह की विशेषता है। सामान्यतः 100-1000 सीमा में विक्षुब्ध प्रवाह के साथ बड़ा न्यूसेल्ट संख्या अधिक सक्रिय संवहन के अनुरूप है ।

एक समान गैर-आयामी गुण बायोट संख्या है, जो द्रव के स्थान पर ठोस पिंड के लिए तापीय चालकता से संबंधित है। न्यूसेल्ट संख्या का सामूहिक स्थानांतरण अनुरूप शेरवुड संख्या है।

परिभाषा

न्यूसेल्ट संख्या एक सीमा के पार प्रवाहकीय ऊष्मा हस्तांतरण के लिए संवहन का अनुपात है। संवहन और चालन ऊष्मा प्रवाह एक दूसरे के समानांतर (ज्यामिति) होते हैं और सीमा सतह के सामान्य सतह पर होते हैं, और साधारण स्थिति में औसत द्रव प्रवाह के लंबवत होते हैं।

$\mathrm {Nu} _{L}={\frac {\mbox{Convective heat transfer }}{\mbox{Conductive heat transfer }}}={\frac {h}{k/L}}={\frac {hL}{k}}$

जहाँ h प्रवाह का संवहन ऊष्मा अंतरण गुणांक है, L अभिलाक्षणिक लंबाई है, और k द्रव की तापीय चालकता है।

• विशेषता लंबाई का चयन सीमा परत के विकास (या मोटाई) की दिशा में होना चाहिए; विशेषता लंबाई के कुछ उदाहरण हैं: (बाहरी) अनुप्रस्थ प्रवाह (सिलेंडर अक्ष के लंबवत) में एक सिलेंडर का बाहरी व्यास, लंबाई प्राकृतिक संवहन, या एक गोले के व्यास से गुजरने वाली एक ऊर्ध्वाधर फलक की लंबाई है। जटिल आकृतियों के लिए, लंबाई को सतह क्षेत्र द्वारा विभाजित द्रव निकाय की मात्रा के रूप में परिभाषित किया जा सकता है।
• तरल पदार्थ की तापीय चालकता का सामान्यतः (लेकिन सदैव नहीं) आवरण तापमान पर मूल्यांकन किया जाता है, जिसे अभियान्त्रिकी उद्देश्यों के लिए समष्टि द्रव तापमान और दीवार की सतह के तापमान के मध्यमान-औसत के रूप में गणना की जा सकती है।

ऊपर दी गई परिभाषा के विपरीत, जिसे औसत न्यूसेल्ट संख्या के रूप में जाना जाता है, स्थानीय न्यूसेल्ट संख्या को रुचि के स्थानीय बिंदु के लिए सतह की सीमा से दूरी के रूप में लंबाई लेकर परिभाषित किया जाता है ।

$\mathrm {Nu} _{x}={\frac {h_{x}x}{k}}$

ब्याज की सीमा पर अभिव्यक्ति को एकीकृत करके माध्य या औसत संख्या प्राप्त की जाती है, जैसे:

${\overline {\mathrm {Nu} }}={\frac {{\frac {1}{L}}\int _{0}^{L}h_{x}\ dx\ L}{k}}={\frac {{\overline {h}}L}{k}}$

संदर्भ

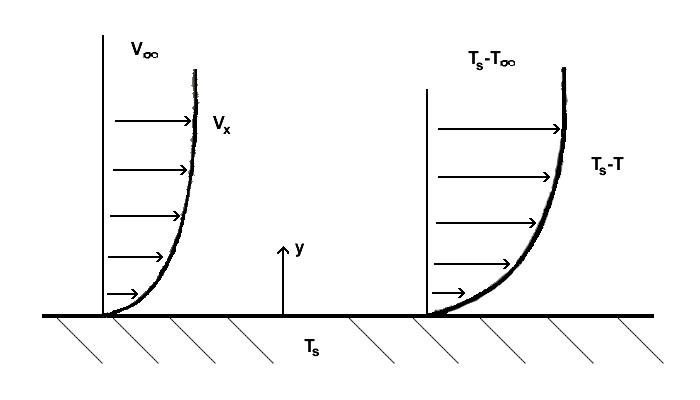
संवहन सीमा परतों की समझ एक सतह के बीच संवहन ताप हस्तांतरण और इसके पिछले प्रवाहित द्रव को समझने के लिए आवश्यक है। यदि द्रव मुक्त धारा तापमान और सतह का तापमान भिन्न होता है तो एक ऊष्मीय सीमा परत विकसित होती है । इस तापमान अंतर से उत्पन्न ऊर्जा विनिमय के कारण एक तापमान परिच्छेदिका सम्मिलित है।

ऊष्मीय सीमा परत

न्यूटन के शीतलन के नियम का उपयोग करके ऊष्मा अंतरण दर को लिखा जा सकता है

$Q_{y}=hA\left(T_{s}-T_{\infty }\right)$,

जहाँ h ऊष्मा अंतरण गुणांक है और A ऊष्मा अंतरण सतह क्षेत्र है। चूँकि सतह पर ऊष्मा का स्थानांतरण चालन द्वारा होता है, उसी मात्रा को तापीय चालकता k के रूप में व्यक्त किया जा सकता है:

$Q_{y}=-kA{\frac {\partial }{\partial y}}\left.\left(T-T_{s}\right)\right|_{y=0}$.

ये दो शब्द समान हैं; इस प्रकार

$-kA{\frac {\partial }{\partial y}}\left.\left(T-T_{s}\right)\right|_{y=0}=hA\left(T_{s}-T_{\infty }\right)$.

पुनर्व्यवस्थित,

${\frac {h}{k}}={\frac {\left.{\frac {\partial \left(T_{s}-T\right)}{\partial y}}\right|_{y=0}}{\left(T_{s}-T_{\infty }\right)}}$.

प्रतिनिधि लंबाई L से गुणा करने पर आयाम रहित व्यंजक मिलता है:

${\frac {hL}{k}}={\frac {\left.{\frac {\partial \left(T_{s}-T\right)}{\partial y}}\right|_{y=0}}{\frac {\left(T_{s}-T_{\infty }\right)}{L}}}$.

दाहिनी ओर अब संदर्भ तापमान प्रवणता के लिए सतह पर तापमान प्रवणता का अनुपात है, जबकि बाईं ओर बायोट मापांक के समान है। यह द्रव के संवहन तापीय प्रतिरोध के प्रवाहकीय तापीय प्रतिरोध का अनुपात बन जाता है, अन्यथा इसे न्यूसेल्ट संख्या, Nu के रूप में जाना जाता है।

$\mathrm {Nu} ={\frac {h}{k/L}}={\frac {hL}{k}}$.

व्युत्पत्ति

नूसेल्ट संख्या फूरियर के नियम के एक गैर-आयामी विश्लेषण द्वारा प्राप्त की जा सकती है क्योंकि यह सतह पर आयाम रहित तापमान प्रवणता के बराबर है:

$q=-kA\nabla T$, जहाँ q ऊष्मा अंतरण दर है, k स्थिर तापीय चालकता है और T द्रव तापमान है।

दरअसल, अगर: $\nabla '=L\nabla$ और $T'={\frac {T-T_{h}}{T_{h}-T_{c}}}$

हम निम्न पर पहुंचते हैं:

$-\nabla 'T'={\frac {L}{kA(T_{h}-T_{c})}}q={\frac {hL}{k}}$

फिर हम परिभाषित करते हैं

$\mathrm {Nu} _{L}={\frac {hL}{k}}$

तो समीकरण बन जाता है

$\mathrm {Nu} _{L}=-\nabla 'T'$

तत्व की सतह पर एकीकृत करके:

${\overline {\mathrm {Nu} }}=-{{1} \over {S'}}\int _{S'}^{}\mathrm {Nu} \,\mathrm {d} S'\!$,

जहाँ $S'={\frac {S}{L^{2}}}$.

अनुभवजन्य सहसंबंध

विशिष्ट रूप से, मुक्त संवहन के लिए, औसत न्यूसेल्ट संख्या को रेले संख्या और प्रांटल संख्या के फलन के रूप में व्यक्त किया जाता है, जिसे इस प्रकार लिखा जाता है:

$\mathrm {Nu} =f(\mathrm {Ra} ,\mathrm {Pr} )$

अन्यथा, बलपूर्वक संवहन के लिए, न्यूसेल्ट संख्या सामान्यतःरेनॉल्ड्स संख्या और प्रांडल संख्या का एक कार्य है, या

$\mathrm {Nu} =f(\mathrm {Re} ,\mathrm {Pr} )$

आनुभविक विभिन्न प्रकार की ज्यामिति के लिए अनुभवजन्य सहसंबंध उपलब्ध हैं जो उपरोक्त रूपों में न्यूसेल्ट संख्या को व्यक्त करते हैं।

मुक्त संवहन

एक ऊर्ध्वाधर दीवार पर मुक्त संवहन

उद्धृत जैसा कि चर्चिल और चू (CHU) से आया है:

${\overline {\mathrm {Nu} }}_{L}\ =0.68+{\frac {0.663\,\mathrm {Ra} _{L}^{1/4}}{\left[1+(0.492/\mathrm {Pr} )^{9/16}\,\right]^{4/9}\,}}\quad \mathrm {Ra} _{L}\leq 10^{8}$

क्षैतिज फलकों से मुक्त संवहन

यदि विशेषता लंबाई परिभाषित की गई है

$L\ ={\frac {A_{s}}{P}}$

जहाँ $\mathrm {A} _{s}$फलक का सतह क्षेत्र है और $P$ इसकी परिधि है।

फिर ठंडे वातावरण में गर्म वस्तु की ऊपरी सतह के लिए या गर्म वातावरण में ठंडी वस्तु की निचली सतह के लिए

${\overline {\mathrm {Nu} }}_{L}\ =0.54\,\mathrm {Ra} _{L}^{1/4}\,\quad 10^{4}\leq \mathrm {Ra} _{L}\leq 10^{7}$

${\overline {\mathrm {Nu} }}_{L}\ =0.15\,\mathrm {Ra} _{L}^{1/3}\,\quad 10^{7}\leq \mathrm {Ra} _{L}\leq 10^{11}$

और ठंडे वातावरण में गर्म वस्तु की निचली सतह या गर्म वातावरण में ठंडी वस्तु की ऊपरी सतह के लिए

${\overline {\mathrm {Nu} }}_{L}\ =0.52\,\mathrm {Ra} _{L}^{1/5}\,\quad 10^{5}\leq \mathrm {Ra} _{L}\leq 10^{10}$

पटलीय प्रवाह में समतल फलक

पटलीय प्रवाह के लिए स्थानीय न्यूसेल्ट संख्या एक समतल फलक पर, कुछ दूरी पर $x$ फलक के किनारे से नीचे की ओर, निम्न द्वारा दिया गया है

$\mathrm {Nu} _{x}\ =0.332\,\mathrm {Re} _{x}^{1/2}\,\mathrm {Pr} ^{1/3},(\mathrm {Pr} >0.6)$

फलक के किनारे से अधः प्रवाह दूरी तक एक समतल फलक पर लैमिनार प्रवाह के लिए औसत न्यूसेल्ट संख्या $x$, द्वारा दिया गया है

${\overline {\mathrm {Nu} }}_{x}\ ={2}\cdot 0.332\,\mathrm {Re} _{x}^{1/2}\,\mathrm {Pr} ^{1/3}\ =0.664\,\mathrm {Re} _{x}^{1/2}\,\mathrm {Pr} ^{1/3},(\mathrm {Pr} >0.6)$

संवहनी प्रवाह में गोला

कुछ अनुप्रयोगों में, जैसे हवा में गोलाकार तरल बूंदों का वाष्पीकरण, निम्नलिखित सहसंबंध का उपयोग किया जाता है:

$\mathrm {Nu} _{D}\ ={2}+0.4\,\mathrm {Re} _{D}^{1/2}\,\mathrm {Pr} ^{1/3}\,$

विक्षुब्ध नलिका प्रवाह में बलपूर्वक संवहन

ग्नीलिंस्की सहसंबंध

नलिकाओं में विक्षुब्ध प्रवाह के लिए ग्नीलिंस्की का सहसंबंध:

$\mathrm {Nu} _{D}={\frac {\left(f/8\right)\left(\mathrm {Re} _{D}-1000\right)\mathrm {Pr} }{1+12.7(f/8)^{1/2}\left(\mathrm {Pr} ^{2/3}-1\right)}}$

जहां f डार्सी घर्षण कारक है जिसे या तो मूडी लेखाचित्र से प्राप्त किया जा सकता है या पेटुखोव द्वारा विकसित सहसंबंध से सुचारू ट्यूबों के लिए प्राप्त किया जा सकता है:

$f=\left(0.79\ln \left(\mathrm {Re} _{D}\right)-1.64\right)^{-2}$

ग्नीलिंस्की सहसंबंध इसके लिए मान्य है:

$0.5\leq \mathrm {Pr} \leq 2000$

$3000\leq \mathrm {Re} _{D}\leq 5\times 10^{6}$

डिटस-बॉयलर समीकरण

डिट्टस-बोएल्टर समीकरण (विक्षुब्ध प्रवाह के लिए) जैसा कि W.H. मॅकएडम्स द्वारा प्रस्तुत किया गया है। न्यूसेल्ट संख्या की गणना के लिए एक स्पष्ट कार्य है। इसे हल करना आसान है, लेकिन जब तरल पदार्थ के तापमान में बड़ा अंतर होता है तो यह कम सटीक होता है। यह सुचारू ट्यूबों के अनुरूप है, इसलिए खुरदरी ट्यूबों (अधिकांश व्यावसायिक अनुप्रयोगों) के लिए उपयोग करने की चेतावनी दी जाती है। डिट्टस-बोएल्टर समीकरण निम्न है:

$\mathrm {Nu} _{D}=0.023\,\mathrm {Re} _{D}^{4/5}\,\mathrm {Pr} ^{n}$

जहाँ:

$D$ वृत्ताकार वाहिनी का भीतरी व्यास है

$\mathrm {Pr}$ प्रान्तल संख्या है

$n=0.4$ द्रव के गर्म होने के लिए, और $n=0.3$ द्रव को ठंडा करने के लिए है।

डिट्टस-बोएल्टर समीकरण निम्न लिए वैध है

$0.6\leq \mathrm {Pr} \leq 160$

$\mathrm {Re} _{D}\gtrsim 10\,000$

${\frac {L}{D}}\gtrsim 10$

डिट्टस-बॉयल्टर समीकरण एक अच्छा सन्निकटन है जहां थोक तरल पदार्थ और ऊष्मा हस्तांतरण सतह के बीच तापमान का अंतर न्यूनतम होता है, समीकरण जटिलता और पुनरावृत्त समाधान से बचा जाता है। औसत तापमान के थोक द्रव के साथ पानी लेना 20 °C (68 °F), श्यानता 10.07×10⁻⁴ Pa.s और एक ऊष्मा हस्तांतरण सतह का तापमान 40 °C (104 °F) (श्यानता 6.96×10⁻⁴ Pa.s, के लिए एक संलग्नशीलता सुधार कारक $({\mu }/{\mu _{s}})$ 1.45 के रूप में प्राप्त किया जा सकता है। यह ऊष्मा हस्तांतरण सतह के तापमान के साथ बढ़कर 3.57 हो जाता है 100 °C (212 °F) (श्यानता 2.82×10⁻⁴ Pa.s), न्यूसेल्ट संख्या और ताप अंतरण गुणांक में महत्वपूर्ण अंतर उत्पन्न करता है।

साइडर-टेट सहसंबंध

विक्षुब्ध प्रवाह के लिए साइडर-टेट सहसंबंध एक अंतर्निहित कार्य है, क्योंकि यह प्रणाली को एक गैर-रैखिक सीमा मूल्य समस्या के रूप में विश्लेषण करता है। साइडर-टेट परिणाम अधिक सटीक हो सकता है क्योंकि थोक द्रव औसत तापमान और ऊष्मा हस्तांतरण सतह के तापमान के बीच क्रमशः तापमान परिवर्तन के कारण यह संलग्नशीलता ($\mu$ और $\mu _{s}$) में परिवर्तन को ध्यान में रखता है। साइडर-टेट सहसंबंध सामान्य रूप से एक पुनरावृत्त प्रक्रिया द्वारा हल किया जाता है, क्योंकि संलग्नशीलता कारक बदल जाएगा क्योंकि न्यूसेल्ट संख्या में परिवर्तन होता है।

$\mathrm {Nu} _{D}=0.027\,\mathrm {Re} _{D}^{4/5}\,\mathrm {Pr} ^{1/3}\left({\frac {\mu }{\mu _{s}}}\right)^{0.14}$

जहाँ:

$\mu$ बल्क द्रव तापमान पर द्रव संलग्नशील है

$\mu _{s}$ ऊष्मा-हस्तांतरण सीमा सतह के तापमान पर द्रव संलग्नशील है

सीडर-टेट सहसंबंध के लिए निम्न मान्य है

$0.7\leq \mathrm {Pr} \leq 16\,700$

$\mathrm {Re} _{D}\geq 10\,000$

${\frac {L}{D}}\gtrsim 10$

पूर्ण विकसित पटलीय नलिका प्रवाह में जबरन संवहन

पूरी तरह से विकसित आंतरिक पटलीय प्रवाह के लिए, न्यूसेल्ट संख्याएं लम्बी नलिकाओं के लिए एक स्थिर मान की ओर होती हैं।

आंतरिक प्रवाह के लिए:

$\mathrm {Nu} ={\frac {hD_{h}}{k_{f}}}$

जहाँ:

D_h= द्रवचालित व्यास

k_f = द्रव की तापीय चालकता

h = संवहनी ऊष्मा हस्तांतरण गुणांक

परिपत्र नालिका के लिए समान तापमान के साथ संवहन

इनक्रोपेरा और डेविट से,

$\mathrm {Nu} _{D}=3.66$

OEIS अनुक्रम A282581 इस मान को निम्न प्रकार से देता है $\mathrm {Nu} _{D}=3.6567934577632923619...$.

परिपत्र नलिकाओं के लिए समान ताप प्रवाह के साथ संवहन

निरंतर सतह ताप प्रवाह की स्थिति में,

$\mathrm {Nu} _{D}=4.36$

यह भी देखें

• शेरवुड संख्या (समूह स्थान्तरण न्यूसेल्ट संख्या)
• चर्चिल-बर्नस्टीन समीकरण
• बिओट संख्या
• रेनॉल्ड्स संख्या
• संवहन (ऊष्मा हस्तांतरण)
• ऊष्मा हस्तांतरण गुणांक
• ऊष्मीय चालकता

बाहरी कड़ियाँ

• Simple derivation of the Nusselt number from Newton's law of cooling (Accessed 23 September 2009)